Modeling huanglongbing transmission within a citrus tree

Abstract

The citrus disease huanglongbing (HLB), associated with an uncultured bacterial pathogen, is threatening the citrus industry worldwide. A mathematical model of the transmission of HLB between its psyllid vector and citrus host has been developed to characterize the dynamics of the vector and disease development, focusing on the spread of the pathogen from flush to flush (a newly developing cluster of very young leaves on the expanding terminal end of a shoot) within a tree. This approach differs from that of prior models for vector-transmitted plant diseases where the entire plant is the unit of analysis. Dynamics of vector and host populations are simulated realistically as the flush population approaches complete infection. Model analysis indicates that vector activity is essential for initial infection but is not necessary for continued infection because infection can occur from flush to flush through internal movement in the tree. Flush production, within-tree spread, and latent period are the most important parameters influencing HLB development. The model shows that the effect of spraying of psyllids depends on time of initial spraying, frequency, and efficacy of the insecticides. Similarly, effects of removal of symptomatic flush depend on the frequency of removal and the time of initiation of this practice since the start of the epidemic. Within-tree resistance to spread, possibly affected by inherent or induced resistance, is a major factor affecting epidemic development, supporting the notion that alternate routes of transmission besides that by the vector can be important for epidemic development.

Huanglongbing (HLB) or citrus greening has been responsible for the near destruction of citrus industries in Asia and Africa (1). In 1998, the psyllid vector Diaphorina citri Kuwayama was first detected in Florida and by 2000 this pest had spread to 31 Florida counties (2). HLB was first detected in Florida in 2005 and has spread through most of Florida since then (3). In recent years, the disease has occasionally been found in other southeastern states of the United States, and recently in California. HLB is considered the most serious problem of citrus worldwide, and in the United States, a committee of the National Research Council investigated research priorities to control this disease (4). Since the introduction of the disease into the Americas, a lot of research has been conducted on the epidemiology of the disease and on the vector, but results of these two lines of inquiry have not been integrated.

HLB is associated with three noncultivable Gram-negative bacterial species belonging to Candidatus Liberibacter, recognized on the basis of 16S rDNA sequence analysis (1). The species observed in the United States is Candidatus Liberibacter asiaticus (CLas). The putative greening pathogens are fastidious phloem-inhabiting bacteria (2), but they could possibly occur in the xylem as well, because psyllids sometimes feed from the xylem (5). All HLB-associated species of Ca. Liberibacter are transmitted from infected to healthy plants through grafting or by citrus psyllids, particularly the Asian citrus psyllid (ACP) D. citri in Asia and the Americas (6). The transmission process through grafting depends on the plant part, amount of tissue used, and the pathogen strain (1). Ca. Liberibacter spp. can be transported both upward and downward throughout the tree, but their distribution is highly patchy (7). The highest concentrations can be found in stem and midribs of flush. Flush is a newly developing cluster of very young leaves on the expanding terminal end of a shoot.

The main symptoms on HLB-infected citrus trees are yellow shoots, leaves with blotchy mottle, and small lopsided fruits (1, 2). Ultimately, infected branches die back and the tree dies. The time from infection to symptom appearance is variable, depending on the time of year, environmental conditions, tree age, host species/cultivar, and horticultural health, ranging from less than 1 y to several years (3).

Population densities of D. citri on host plants correlate with quantity and nutritional quality of plant flush because eggs are laid on young flush and nymphs develop exclusively on tender flush (8). By the time flush expand and harden, turning dark green, nymphs have completed their development. Nymphs, which are always found on new growth, spend most of their time feeding on phloem juice close to where they were born, using piercing-sucking mouth parts. Adults may be found on leaves and along the stem, almost exclusively on new growth, except in the winter when there is no new growth. They leap when disturbed and may fly a short distance to other flush on the same or neighboring trees (9). Epidemic spread occurs more frequently within trees and rows in a grove than between rows, and long-distance spread occurs occasionally (3).

Disease management is complicated, because incubation periods are long and diagnosis is difficult. In Florida, there has been a three-pronged approach to HLB management: (i) production of disease-free nursery stock (mandatory for commercial citrus production in Florida); (ii) psyllid control by insecticides and removal of symptomatic trees that test positive for CLas in a qPCR test (adopted in large citrus groves with limited HLB incidence); and (iii) psyllid control and application of foliar nutritional sprays, often combined with salicylic acid and/or phosphite (widely adopted in areas with high HLB incidence). There is a fierce debate about the effectiveness of strategies ii and iii, but there is agreement that none of these control strategies completely eliminates HLB transmission.

Mathematical models have played an important role in understanding the epidemiology of vector-transmitted plant pathogens, in particular viral pathogens (10–12). Analytical models have also been developed for the spread of citrus canker (13), but models for vector-transmitted bacterial pathogens are still preliminary (14). Some existing vector-borne plant disease models have been used as experimental tools with which to investigate the relative effects of management practices on the spread of diseases (10) and of different modes of virus transmission on epidemic development (15).

Recently, a spatially explicit simulation model was constructed to predict the potential dynamics and spread of citrus psyllids in Australia, taking climate change into account (16). The model indicated that the flush period has a major influence on psyllid dynamics. However, infection of citrus by Ca. Liberibacter sp. was not considered. The report by the National Research Council stated “the construction of a mathematical model for the CLas/ ACP/ citrus-HLB system should be a long-term goal of HLB research” (ref. 4, p. 124). As the vector spends most of its life time on a particular flush, and adults move primarily from one flush to a nearby flush, a flush is the central epidemiological unit, and a tree is considered as a population of flush, similar to the model of Hassell et al. for whiteflies on a single plant (17). Thus, the main objective of this study was to develop a mathematical model of the dynamics of the developmental stages of D. citri, citrus flush development, and infection by CLas to obtain a clearer understanding of the interactions between the pathogen, the vector, and the tree. Additional objectives are to assess the epidemiological parameters that have a strong influence on HLB development, to evaluate effects of different management strategies on HLB development, and to identify the parameters that contribute to the effectiveness of these strategies.

Methods and Results

Differential Equations for Transmission Dynamics.

The psyllid life cycle has seven distinct nonoverlapping stages: (i) egg, (ii–vi) five nymphal instars, and (vii) adults (2). We group these stages into three developmental stages, namely the egg (E), nymph (N), and adult (A) stages. The populations of nymphs and adults are divided into five compartments, namely uninfected nymphs 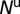, infected nymphs 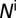, uninfected adult psyllids 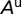, infected adults that acquired CLas during the nymphal stage 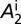, and infected adults that acquired CLas during the adult stage 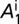. The flush population is categorized into four compartments: uninfected and healthy 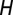, infected and asymptomatic but not yet infectious (latent) 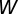, infectious and asymptomatic 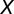, and infectious and symptomatic 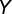. Fourth- to fifth-instar nymphs and adults can acquire the pathogen and adults emerging from those nymphs can transmit the pathogen in a shorter period than psyllids that feed on infected plants only as adults (18, 19). The difference in infectivity of these two groups of infected adults is modeled by the parameter 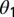. Initially, transovarial transmission was thought to be absent (19), but recently, there has been some evidence of transovarial transmission (20). Nevertheless, we assume there is no transovarial transmission because it is low, variable, and dependent on environmental conditions (20). Of most concern are the nymph and adult stages because acquisition feeding can occur during the last nymph stages and the adult stage. For the egg stage, the only concern is survival to the nymph stage. Therefore, we define as the rate of oviposition, 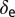as the rate at which an egg becomes nonviable, and 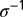as the duration from egg to first nymph stage. The parameter is the probability that a viable egg survives into a first instar nymph. It is assumed that CLas is not pathogenic to psyllids but makes infected psyllids more fertile and makes them lay more eggs than their noninfected counterparts (20). The rate at which susceptible plants are infected, 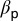can be described as 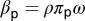, where 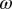is the average time spent per visit on a plant, 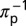is the mean time a psyllid must feed on a plant for inoculation to occur, and 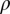is the number of flushes visited per day per vector. The product 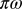is the probability of inoculation of a healthy plant during a visit by an infectious vector, and 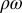is interpreted as a measure of vector activity. Similarly, the rate at which susceptible adult vectors are infected is 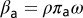, and the rate at which uninfected nymphs acquire the pathogen is 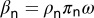, where 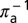and 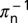are the mean times required for acquisition by the adult and nymph, respectively. The infected adults retain infectivity after acquisition throughout their lives and adult vectors emigrate from a flush at a rate .

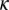For the flush population, the rate of growth of new healthy flush 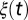is assumed periodic with

where 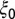is the baseline rate of growth, 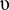is the strength of seasonal forcing, and and is the period. Growth of new foliage on mature citrus trees occurs approximately twice a year, a major flush in spring and a rebound in fall (21). Healthy flush are infected by infectious vectors that acquired the pathogen during the nymphal stages and those that acquire it during the adult stage. Healthy flush also acquire the pathogen directly from both the asymptomatic and the symptomatic infected flush at rates 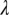and 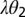, respectively. The flush mature at a rate 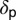. 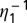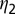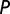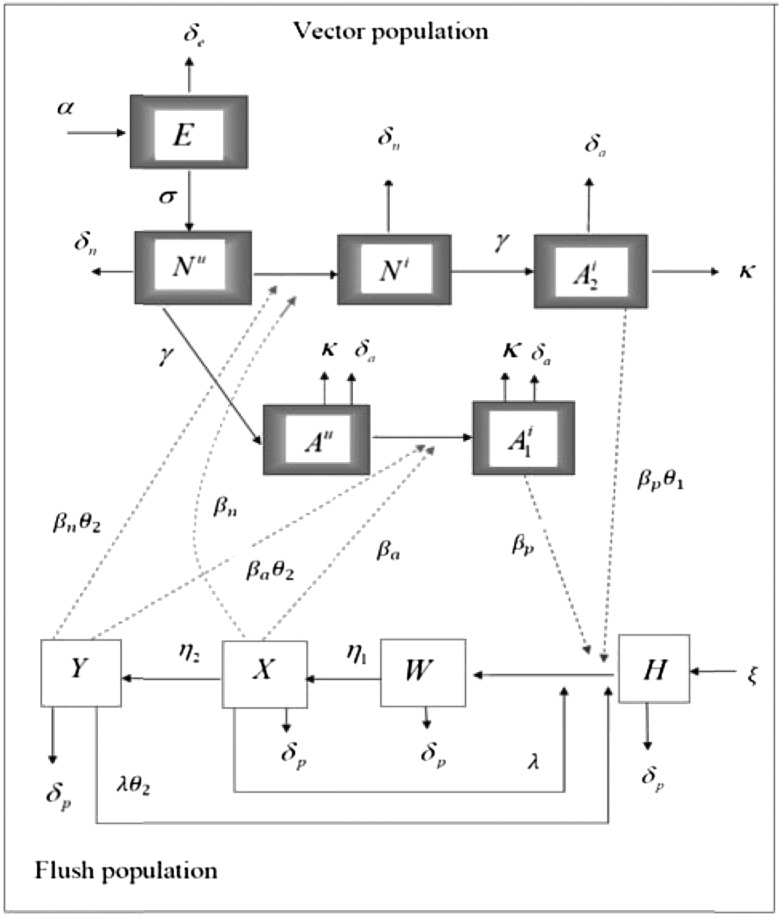is the flush latent period, is the rate at which an infectious flush becomes symptomatic, and is the flush population size (density). The asymptomatic flush become symptomatic due to an increase in concentration of the pathogen, making the symptomatic flush more infectious to vectors than the asymptomatic flush (22). In one study more active bacterial cells were observed in presymptomatic than in highly symptomatic leaf samples (23), suggesting that the bacteria are dormant or dead in highly symptomatic tissue. However, a positive correlation between concentration of CLas and HLB symptom expression has also been shown (22). In addition, symptomatic trees (yellow color) may be more attractive for the vector (24). Therefore, an increase in infectivity of early symptomatic flush is modeled by the parameter 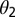. Incubation (time to symptom expression) and latency (time to infectivity) are two concurrent and related temporal processes, both beginning at infection (3). In most plant–pathogen systems, the incubation period is shorter than the latent period but in other systems like citrus HLB, latency ends when infectivity begins and is followed by the end of the incubation period. The flow diagram for the model is given in Fig. 1.

Fig. 1.

Model flow diagram showing the transmission of Ca. Liberibacter asiaticus between the psyllids and the host flush. The flush compartments are uninfected and healthy 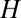, infected and asymptomatic but not yet infectious (latent) 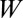, infectious and asymptomatic 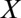, and infectious and symptomatic 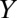. The vector compartments are uninfected nymphs 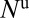, infected nymphs 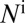, uninfected adult psyllids 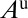, infected adults that acquired CLas during the adult stage 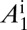, and infected adults that acquired CLas during the nymphal stage .

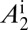The following system of differential equations specifies the model.

Analysis of the system (1) is simplified if we work with the nondimensionalized system (Eq. S3 in SI Text), where 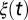is interpreted as a maturation rate.

Parameter Values.

We used parameter values from ref. 6, assuming a temperature of 28 °C. Table 2 in ref. 6 shows the survivorship of immature stages of D. citri at different temperatures (Table S1). The value for the mortality rate of nymphs per day 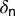is therefore estimated from table 2 in ref. 6. This table was also used to estimate the rate at which eggs become nonviable. On average D. citri takes about 2.5 h to prepare the stylet pathway and around 3.5 h to feed in the phloem, which represents a predominant activity (5). Effective time spent per visit on a flush is assumed to be 2.5–3.5 h, and it takes 15–30 min for adults to acquire the bacteria (25). Acquisition time for nymphs 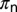is assumed to be 2 h. The maturation rate of flush was deduced from the fact that by the time flush expanded and hardened, nymphs would have completed their development (8). Thus, the time taken by the flush to harden is the same as the development time of the psyllid (6).

We assume that CLas bacteria are more numerous in symptomatic than in asymptomatic flush (22). We assume that the chance of picking up infective bacteria is three times more from symptomatic than from asymptomatic flush. Thus, infectiousness of symptomatic flush is given by 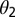= 3. Approximately 78% of the psyllids that fed as fifth-instar nymphs on CLas-infected trees and 13% of the psyllids that acquired the pathogen as adults were CLas positive at the end of an inoculation access period (18). The factor by which infectiousness of infected adults that acquired the pathogen in the nymphal stages 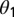is therefore assumed to be 6.

General Dynamics of the Model.

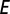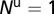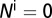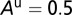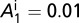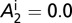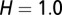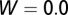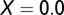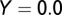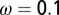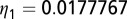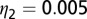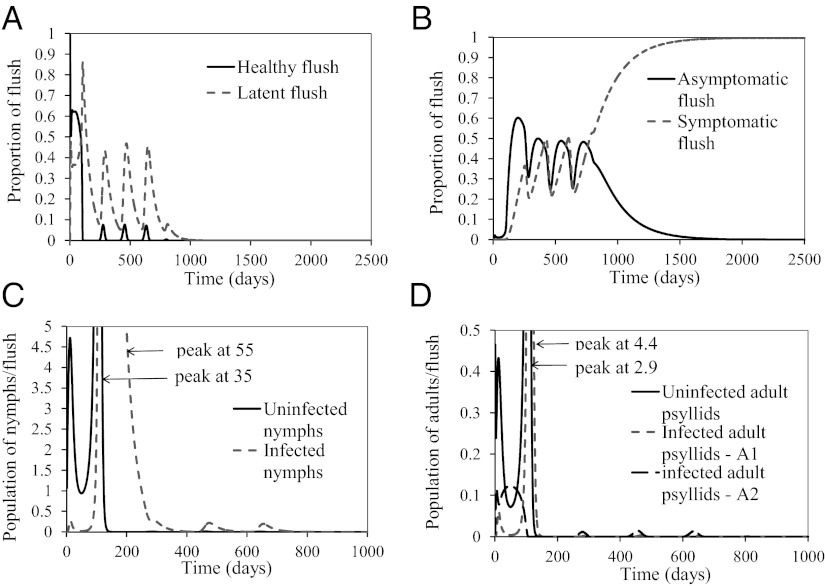
The graphs in Fig. 2 A–D are obtained by using the following initial conditions: = 5, , , , , , , , , and . The parameter values used are given in Table 1 with , , , and 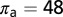. During the first 2–3 y, the different flush categories oscillate due to the forced oscillatory input of healthy flush twice a year. After about 3 y a saturation curve of symptomatic flush sets in and all of the flush become infected and symptomatic in about 5 y (Fig. 2 A and B). In accordance with the availability of young flush, the different stages of the vector population fluctuate with a large peak after the first peak in healthy flush. When healthy flush is diminished, the vector population decreases to a very low level, i.e., less than 0.5 psyllids (nymphs plus adults) per flush on average. Such low populations are realistic for a severely infected and symptomatic tree where little new healthy flush is produced.

Fig. 2.

(A–D) Proportions of healthy and latent flush (A), proportions of asymptomatic and symptomatic flush (B), populations of uninfected and infected nymphs per flush (C), and populations of uninfected and infected adult psyllids per flush (D). The latent flush is infected but not yet infectious. The asymptomatic and symptomatic flush are both infected and infectious. Infected adult psyllids are infectious and consist of categories A1 = 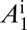and A2 = 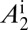. Input rate of healthy flush follows a periodic function with two peaks in 1 y. The parameter for internal movement of the pathogen in the tree, .

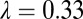Table 1.

Parameter definitions and values used for numerical simulations of the transmission of huanglongbing from infectious adult psyllids to citrus flush and from infectious flush to psyllid nymphs and adults

Parameter	Definition	Value	Units	Reference*
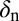	Mortality rate of nymphs	0.0035	d−1	(6)
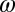	Effective time spent per visit on a flush	0.10–0.15	d	(5)
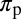	Feeding rate for inoculation to occur	4.8	d−1	(5, 18)
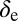	Rate at which eggs become non viable	0.011	d−1	(6)
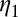	Rate at which infected flush becomes infectious	0.005–0.033	d−1	Estimate (3)
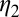	Rate at which asymptomatic infected flush becomes symptomatic	0.005–0.033	d−1	Estimate (3)
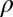	Number of flushes visited per day	1.0	d−1	Estimate
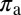	Feeding rate by adult vectors for acquisition to occur	48–96	d−1	(2)
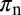	Feeding rate by nymphs for acquisition	12	d−1	Estimate†
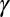	Rate at which nymphs become adults	0.078	d−1	(6)
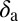	Mortality rate of adult	0.025	d−1	(6)
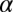	Rate of oviposition	15.77	d−1	(6)
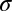	Rate at which eggs become nymphs	0.24	d−1	(6)
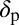	Maturation rate of flush‡	0.071	d−1	(6, 8)
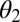	Infectiousness of symptomatic flush	3	—	(22)
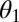	Increased infectiousness of	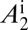6	—	(18)
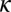	Emigration rate of adult psyllids	0.4	d−1	Estimate
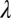	Internal transmission rate among flushes	0.2–0.35	d−1	Estimate
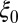	Baseline input rate of healthy flush	0.5	d−1	Estimate
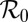	Strength of seasonality	0.9	1	Estimate
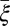	Period	π/90		Estimate

*Parameter values from ref. 6 were at an average temperature of 28 °C. See SI Text.

^†The assumption made is based on the fact that nymphs have a shorter piercing mouth; therefore, it would take longer to obtain Las for nymphs than for adults.

^‡The rate was deduced from the fact that Pluke et al. (8) noted that by the time flushes expanded and hardened, nymphs would have completed their development. (Value of development from egg to adult used is from ref. 6.)

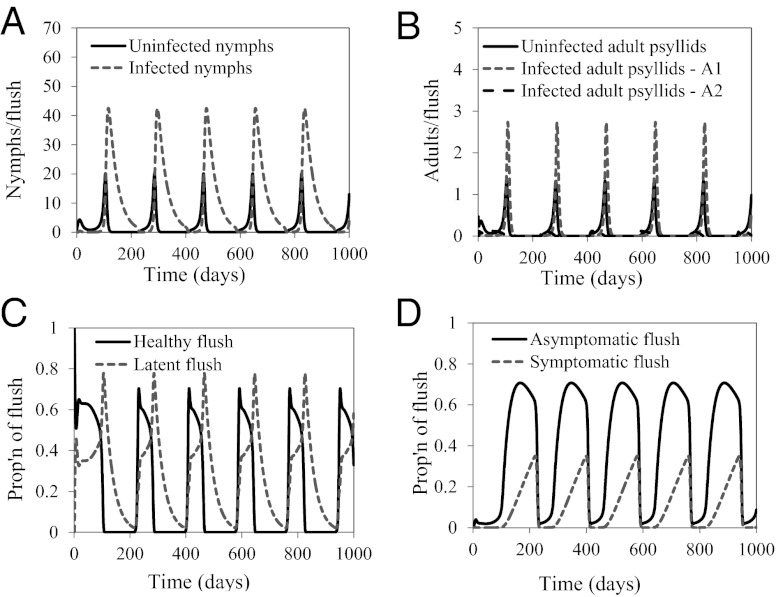
There are also field situations when psyllid populations remain relatively high even when a tree is infected and symptomatic. Parameter estimates were therefore adjusted to investigate whether such situations could be modeled in the present framework. When the value of the transmission rate of the bacteria from flush to flush, 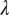, is decreased from 0.33 to 0.25, while keeping the other parameters and initial conditions the same as those used in Fig. 2, the psyllid populations increased to about 60 nymphs and 5 adults per flush (Fig. 3 A and B). In this situation, the different flush categories continue to oscillate and flush never become 100% symptomatic (Fig. 3 C and D). In this second scenario, both the uninfected and the infected components of psyllids and flush are at equilibrium. Other values of 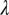always result in either scenario 1 or scenario 2. Thus, the model has two distinct equilibrium states with respect to disease, in addition to a disease-free equilibrium: (i) the state with ultimately 100% symptomatic flush represented by simulations with 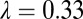= 0.33 and (ii) the state with all components continuously present represented by 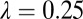= 0.25.

Fig. 3.

(A–D) Populations of uninfected and infected nymphs per flush (A), populations of uninfected and infected adult psyllids per flush (B), proportions of healthy and latent flush (C), and proportions of asymptomatic and symptomatic flush (D). The latent flush is infected but not yet infectious. The asymptomatic and symptomatic flush are both infected and infectious. Infected adult psyllids are infectious and consist of categories A1 = 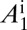and A2 = 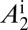. Input rate of healthy flush follows a periodic function with two peaks in 1 y. Internal movement parameter of the pathogen in the tree, .

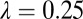Sensitivity Analysis.

The ratio of the relative change in a variable to that in a parameter is an index of the sensitivity of the variable to that parameter (26). Sensitivity analysis of the parameters of model Eq. S3 was carried out relative to the reproductive number 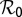because variation in 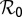is considered whenever optimal intervention strategies are sought. Equations for 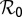and the calculation of sensitivity indexes are given in SI Text. The expression for the reproductive number is given by

where

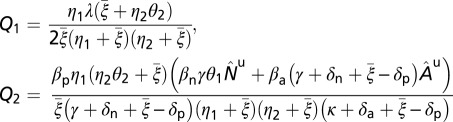with 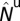, 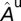as values at the disease-free equilibrium.

Parameters with negative sensitivity indexes decrease the value of 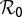as their values increase, whereas those with positive values increase the value of 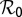as their values increase. The HLB model system is most sensitive to 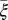followed by 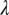and 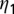(Table 2). The parameter that has the most effect on the dynamics of the HLB infection is the maturation rate 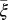. An increase in 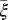of 10% decreases 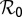by about 20% and decreasing 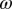or 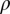by 10% decreases 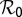by 0.6%.

Table 2.

Sensitivity indexes for the reproductive number 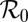(SI Text) of the development of huanglongbing in a citrus tree

Parameter	Index
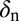	−0.0003529
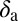	−0.001153
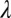	0.9373
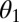	0.02229
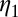	0.9354
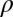	0.06265
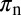	0.02229
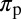	0.03132
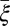	−1.9962
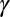	0.02346
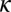	−0.01844
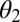	0.02820
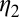	0.01861
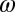	0.06265
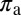	0.0090303

Other parameters that show a great influence on HLB are rate of pathogen transfer from infectious flush to healthy flush through plant material 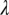and the latent period 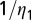. When 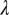is reduced, the dynamics of HLB development change drastically from continued expansion of HLB symptoms to a dynamic equilibrium between healthy, asymptomatic, and symptomatic flush (SI Text). When the latent period is varied between 30 d and 180 d, there are large differences in the maximal proportions of asymptomatic flush attained (35–70%), but there are only slight differences in the time needed to reach 100% symptomatic flush (Fig. S1).

Effects of Insecticide Applications.

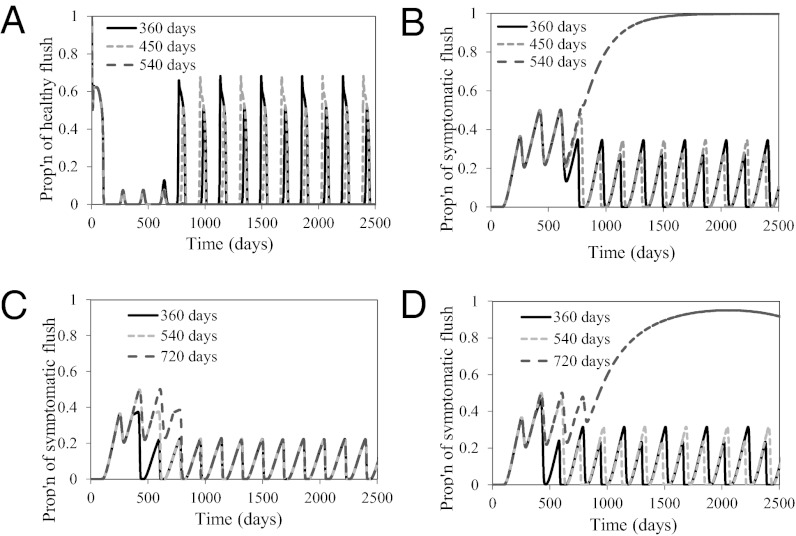
When the psyllid death rate is increased to 0.004 d⁻¹ to simulate the effect of insecticide spraying, while keeping the same initial conditions and other parameter values as used for Fig. 2, results vary, depending on the start of the spray program, namely 360 d, 450 d, and 540 d after initial inoculation, spraying twice a year with an insecticide that has an effectiveness of 75% (Fig. 4 A and B). If insecticide is applied starting from 360 d or 450 d after initial infection, increases in the proportion of healthy flush and decreases in the proportion of asymptomatic infected flush ensue (Fig. 4 A and B). The resulting oscillations in the different categories are ultimately very similar for the two spray starting dates and continue indefinitely. On the other hand, if spraying is started after 540 d, the dynamics of the different flush categories follow a similar pattern to that observed without spraying. Although early spraying reduces the temporal increase in infected flush, it does not eliminate the pathogen from a tree (Fig. 4B). As expected, spraying the vectors reduces the psyllid populations in all categories, but they continue to oscillate (Fig. S2).

Fig. 4.

(A–D) Proportion of healthy flush (A) and of asymptomatic flush (B) when psyllids are sprayed twice every year with an insecticide that is 0.75 effective, 360 d, 450 d, and 540 d after initial infection and proportions of symptomatic flush when symptomatic flush are removed every 3 mo (C) and every 6 mo (D) starting 360 d, 540 d, and 720 d after inoculation.

If insecticides are applied when λ = 0.25, all flush and vector categories continue to oscillate similar to the nonsprayed scenario (Fig. S3). However, the total population of adult psyllids is reduced from a maximum of 4.5 to 4.3 individuals per flush (Fig. S3A) and the maximum proportion of symptomatic flush is reduced from 0.35 to 0.29 (Fig. S3B).

Effects of Flush Removal.

When 90% of symptomatic flush is removed every 3 mo, although the latent period is 56 d, a stable equilibrium sets in after about 2 y for the proportion of symptomatic flush, oscillating between 0 and 21%, no matter if the flush removal is started 360 d, 540 d, or 720 d after inoculation (Fig. 4C). On the contrary, when symptomatic flush is removed by 90% every 6 mo, stable oscillations in symptomatic flush (0–30%) occur if flush removal is initiated after 360 d. A two-state equilibrium is reached with flush removal starting after 540 d. A long-term high plateau (about 92%) is reached when flush removal every 6 mo is started after 720 d (Fig. 4D).

Discussion

A mathematical model is presented to describe and analyze the transmission of a bacterial vector-borne disease within a tree. The model considers the transmission of the pathogen from flush to flush through the vector as well as by movement within a tree. An analogous comparison of multiple infection routes of human pathogens has been of growing interest, for example in the case of pneumonic plague (27). Selection of flush as the fundamental unit constitutes a vector-centered rather than a host-centered approach. This is similar to the approach taken by Hassell et al. (17), who modeled populations of whiteflies on individual leaves of a single plant to account for the patchy distribution within a plant.

There are several assumptions on which the model is based: (i) We assume that psyllid eggs are laid on healthy flush. This choice is based on the assumption that new flush emerges healthy and that one psyllid generation takes as much time as the maturation period of a flush (8). Therefore, eggs would need to be laid on very young flush to be able to complete development to adulthood. In reality, eggs also are laid on already infected flush and there is some indication that female psyllids might have some preference for infected flush (24), but an infected flush cannot become more infected than it already is. Also, a female psyllid does not lose infectivity after feeding on a flush. There are no epidemiological consequences if a female lays eggs on a recently infected rather than a healthy flush. (ii) Nymphs are not subdivided over five stages (2) in the model. Fourth- and fifth-instar nymphs acquire Liberibacter cells more readily than younger nymphs (18, 20), and the pathogen likely multiplies inside the nymphs (28), but multiplication of Liberibacter is not part of this model, because not enough is known about acquisition (3). Therefore, the only thing that matters for the outcome of the model is whether adult psyllids acquired the pathogen as nymphs or as adults, because they are more infectious in the first case (18, 20). (iii) The growth, death, and development rates are assumed to be similar for psyllids with and without CLas. In reality, the generation time is shorter for psyllids with the pathogen than for those without (20) and female psyllids with Liberibacter lay more eggs than those without (20). Moreover, the vectors may be more attracted to symptomatic than to asymptomatic flush (29), and this complex interrelationship is not addressed in this model. (iv) Symptomatic flush is assumed to be more infectious than asymptomatic flush on the basis of higher CLas DNA densities in symptomatic flush (22). Recently, large numbers of active CLas cells were found in tissue samples from presymptomatic young flushes whereas more inactive bacteria were observed in highly symptomatic samples (23). If we assume that the symptomatic flush is less infectious than the asymptomatic one, then the number of subsequent infections will be reduced. Similar conclusions can be drawn in cases where some of the infected psyllids fail to transmit the pathogen to a healthy flush after feeding. Finally, it is assumed that the psyllids are randomly distributed among the flush, which is not true (30), and that the development of the psyllid and flush populations is synchronous, which is partially true due to the environmental forcing of flush production (8, 9). However, this model gives realistic results and provides a first tool for comparison of management strategies.

The results of the model show that when internal movement of CLas in a tree is relatively fast (λ = 0.33) and insecticides are not applied, an infected tree will become 100% symptomatic and die after about 5 y. This time frame is in agreement with observations when trees become infected in an established grove. The time taken for an infected tree to become unproductive and die depends on the tree age, because multiplication of CLas is fastest in young citrus plants (22). In graft-inoculated young trees, production of additional new growth decreased until about 9 mo after inoculation, when severely affected branches stopped producing new growth (23). Most of the infected plants eventually died over the following year.

The model indicates that the psyllid populations drop to very low levels once the number of infected flush has increased. This might be attributed to the fact that as much of the tree becomes symptomatic, growth of new flush decreases (23), so that the vectors will search for other trees with flush to lay their eggs (31). Indeed, the parameter reflecting the flush maturation rate and thus the availability of flush (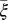) has the most effect on the dynamics of the HLB infection. Increasing the maturation rate or decreasing the growth rate of flush leads to a reduction in the spread of infection in a tree. This reduction is in agreement with decreased vector activity in a grove with diminished flush production (31).

Another parameter that shows a great influence on the expansion of HLB infection is the rate of pathogen transfer from infectious flush to healthy flush through the tree 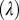. When 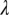is reduced to 0.25 d⁻¹, the dynamics of HLB development change drastically from a situation of continued expansion of HLB symptoms to a situation of a dynamic equilibrium between healthy, infected asymptomatic and symptomatic flush (Fig. S4). In practice, such a situation may be present when nutritional products and systemic acquired resistance inducers are used to ameliorate the effect of symptoms produced by HLB in citrus groves (3) or when a resistant rootstock or interstock is used (32). The actual movement of CLas through a tree is evident from systemic spread of the pathogen in plants that are inoculated through grafting in greenhouses where vectors are absent (23). However, the rates of movement and multiplication of the pathogen inside trees are not well understood (3). As a result, models that would take the concentration of the pathogen into account are as yet nonexistent. This finding of the importance of internal flush-to-flush spread has broader implications as well. For example, the spread of pneumonic plague through human-to-human aerosol contact (analogous to flush-to-flush spread) is more important than the spread by its vector, fleas (27).

Insecticidal control of the psyllids is another method adopted to reduce HLB spread (10). Effectiveness of this method depends on time of initial spraying, frequency of spraying, and efficacy of the insecticides. According to the model, spraying does not curb the infection after about half of the flush has become symptomatic. If spraying is initiated earlier, it will have beneficial effects but will not eliminate the bacteria from the tree. To achieve an effective reduction in disease spread, frequency and efficacy of insecticide sprays should be quite high, which can be expensive and may have potential side effects, including insecticide resistance. In addition, insecticide applications may have little or no effect when the resistance to internal movement is great (small 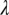) and a stable equilibrium exists between infected and noninfected flush (Fig. S3).

Effects of flush initiation and removal are quite complex. Periodic forcing of flush initiation affects the dynamics of the model (Fig. S5). Effects of flush removal depend on the type of flush removed (healthy or infected, asymptomatic or symptomatic), flush removal initiation relative to initial infection, and the removal frequency relative to the latent and incubation periods. According to our model simulations, removal of symptomatic flush could reduce the percentage of flush that becomes symptomatic, but the effect greatly depends on the frequency of flush removal and the time of initiation of this treatment. Flush removal every 6 mo initiated 2 y after initial infection does not reduce symptom development. Ineffectiveness of flush removal from highly infected trees is in agreement with experimental results (33). Rigorous psyllid control combined with removal of symptomatic trees from slightly infected, large groves has slowed down epidemic development (3). These practices may be comparable to frequent flush removal in the beginning of an epidemic simulated with our model, but spatial spread from tree to tree would need to be included in our model to determine effects of tree removal on epidemic development under various conditions, in particular different latent and incubation periods.

For mathematical tractability of the model several assumptions were made. Nevertheless, there is sufficient realism in our specifications that we were able to gain valuable insights into effects of spraying and flush removal and into crucial parameters to be considered when implementing intervention strategies. A better understanding of the transmission dynamics of the pathogen between the psyllid and a citrus tree and of the spread from tree to tree will provide further insight in planning and assessing the impact of current control strategies and development of effective control measures.