Coexistence of phage and bacteria on the boundary of self-organized refuges

Abstract

Bacteriophage are voracious predators of bacteria and a major determinant in shaping bacterial life strategies. Many phage species are virulent, meaning that infection leads to certain death of the host and immediate release of a large batch of phage progeny. Despite this apparent voraciousness, bacteria have stably coexisted with virulent phages for eons. Here, using individual-based stochastic spatial models, we study the conditions for achieving coexistence on the edge between two habitats, one of which is a bacterial refuge with conditions hostile to phage whereas the other is phage friendly. We show how bacterial density-dependent, or quorum-sensing, mechanisms such as the formation of biofilm can produce such refuges and edges in a self-organized manner. Coexistence on these edges exhibits the following properties, all of which are observed in real phage–bacteria ecosystems but difficult to achieve together in nonspatial ecosystem models: (i) highly efficient virulent phage with relatively long lifetimes, high infection rates and large burst sizes; (ii) large, stable, and high-density populations of phage and bacteria; (iii) a fast turnover of both phage and bacteria; and (iv) stability over evolutionary timescales despite imbalances in the rates of phage vs. bacterial evolution.

Virulent phage are remarkably efficient predators. For every bacterial infection, they produce on the order of 100 copies of themselves, in just a time span of around one bacterial generation (1). Such a high predator–prey conversion factor is unheard of for most macroscopic ecosystems. Questions related to phage bacteria coexistence, population dynamics, and evolution have been studied extensively both theoretically and experimentally, e.g., in refs. 2–8. However, it remains a puzzle exactly how virulent phage avoid driving their bacterial prey to extinction (9–11).

Perhaps the most prominent explanation for how virulent phage manage to coexist with their bacterial hosts is that they are continuously engaged in a balanced coevolutionary arms race where bacteria constantly avoid disaster by evolving resistance to existing phage and the phage then counterevolve to attack resistant bacteria. This “Red Queen” argument (12) has, however, been criticized by some on the grounds that the rates of evolution of phage and bacteria are not necessarily symmetric (13, 14). Recent measurements support this: In soil, phage appear to be “ahead of the bacteria in the coevolutionary arms race” (ref. 15, p. 833). For the Red Queen argument to work it is necessary that at every stage the phage and bacteria must coexist, without one or the other becoming extinct, for long enough to allow resistant bacteria to evolve. In our view, therefore, although coevolution is responsible for very long-term coexistence between virulent phage and bacteria (e.g., refs. 5 and 7), it is important to explore nonevolutionary mechanisms that can stabilize predator–prey populations. In this paper we focus on spatial heterogeneity as one such mechanism and show how enhanced coexistence in the short term ties in to stability of the longer-term coevolutionary arms race.

The degree of spatial heterogeneity is high in many typical phage bacteria environments, for example in soil and biofilm, and it has been suggested that spatial bacteria refuges aid coexistence to some degree in these milieus: Schrag and Mittler (16) showed that coexistence between virulent phage and bacteria is feasible in a chemostat but not in serial cultures, due to biofilm refuge formation. Experiments done by Brockhurst et al. (17) indicate that reduced phage dispersal can prolong coexistence for virulent phage and bacteria in spatial environments by creating ephemeral refuges for the bacteria. The impact of spatial heterogeneity on phage–bacteria coexistence has been explored computationally by Kerr et al. (6). Using a simple cellular automaton, modeling fragmented populations of phage and bacteria, they showed that coexistence was more easily achieved when the phage migration pattern induced spatial heterogeneity. In macroecology, it has been argued theoretically that prey refuges may help stabilize predator–prey interactions (18, 19). The formation of a spatial refuge invariably leads to the formation of a boundary zone or edge between two different environments and studies of natural macroecosystems have shown that there is an increased biodiversity on edges between different types of habitats (e.g., ref. 20).

Here we use an individual-based stochastic spatial model to explore the effect of bacterial refuges on coexistence of virulent phage and their bacterial hosts. We further explore density-dependent mechanisms, such as quorum-sensing–triggered biofilm formation, that allow bacteria to create refuges in a self-organized manner. Both for spatially fixed refuges and for self-organized ones, we find that the phage and bacteria can coexist along the edges of the refuges and that this coexistence is remarkably robust to changes of parameters that affect phage efficiency and to alterations in the details of the model rules. (Henceforth we use the term “phage efficiency” to mean the phage growth rate in an environment where the bacterial density is kept constant. Parameters that influence phage efficiency are, for example, the infection rate α, the burst size β, the phage degradation rate δ, and the phage diffusion constant.

Finally, we explore evolutionary models where phage efficiency can evolve and find that the possibility of creating spatial refuges pushes the system toward more stable coexistence.

Results

Coexistence in the Basic Model Occurs only for a Narrow Range of Parameters.

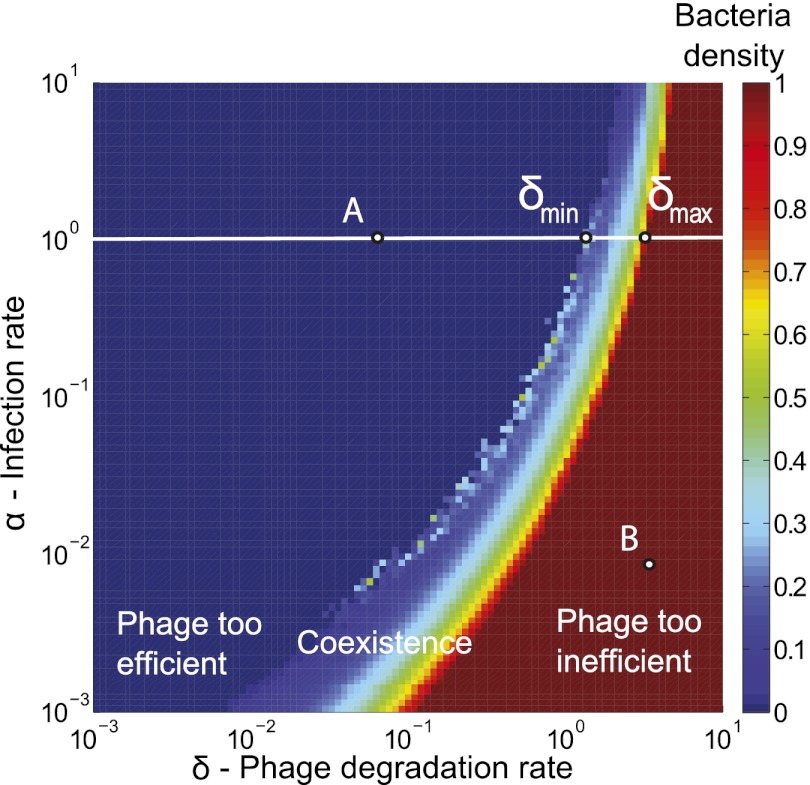
In a previous study (11), we established which parameter ranges allow stable coexistence in a 2D phage–bacteria ecosystem model (the basic model described in Materials and Methods). Fig. 1 shows that coexistence is possible only in a narrow range of the phage degradation rate (δ) and infection rate (α) values. (We define coexistence to mean that neither phage nor bacteria go extinct for up to 1,000 bacterial generations. The number 1,000 was chosen for practical reasons only—so simulations are completed in a reasonable time with the computational resources at our disposal—but is also long enough for our overall aim of testing mechanisms to determine whether they can stabilize the populations for long enough to allow bacteria to evolve resistance.)

Fig. 1.

Narrow coexistence region for basic model. Colors shows average bacterial density for simulations after 1,000 bacterial generations have passed as a function of phage infection rate (α) and degradation rate (δ). Dark red is the maximal bacterial density of one, and dark blue is zero; colors in between signify that bacteria and phage coexist. For each value of α there exists an interval 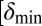, , 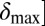outside of which there will be no coexistence. Here these points are marked for 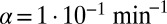. Points A and B show the parameters used for the simulation shown in Fig. 4. The grid size used in these simulations was 100 × 100, and initial conditions were randomly scattered uninfected bacteria (at density 0.05) and bacteria infected with phage (at density 0.005).

On either side of this region, phage and bacteria cannot coexist for two different reasons. On the right side (red region), phage are too inefficient and die out even at high bacterial density. On the left side (blue region), phage are too efficient; they drive the bacteria to extinction and subsequently die out themselves. In the narrow region in the middle, coexistence is possible because the degradation rate is high enough and/or the search times for new bacterial hosts are long enough to ensure that most phage offspring die before they can find and successfully infect a new host. Hence, for these parameters, the phage and bacteria can coexist despite the large phage burst size. However, the narrowness of the region indicates that coexistence in this basic model is fine-tuned and may not be robust to evolutionary or environmental changes that perturb the parameter values affecting phage efficiency.

Bacterial Refuges Enhance Coexistence.

To test whether bacterial refuges can stabilize phage–bacteria coexistence, we begin by introducing a spatial refuge in the basic model. We divide the plane in two halves and allow phage efficiency to take on different values in the two halves (see Materials and Methods for details). As expected, when parameter values in either one of the half-planes are chosen from within the coexistence region in Fig. 1 of the basic model, we get coexistence here too, whereas if parameters of both half-planes lie in the same noncoexistence region, then we do not observe coexistence.

Whenever parameters for one half are chosen from the right non-coexistence region of Fig. 1 (where phage are too inefficient to coexist in the basic model), whereas parameters in the other half are chosen from the left non-coexistence region (where phage are too efficient to coexist in the basic model), a more interesting phenomenon is seen. In this case, we observe coexistence of phage and bacteria, which is stable for at least 1,000 bacterial generations. The phage exist only in a zone around the edge between the two halves. The dynamics and width of this zone vary considerably, as seen in Fig. 2, which shows snapshots from three different simulations of the fixed bacterial refuge model where only δ, the phage degradation rate, differs between the two half-planes. The same is observed when the phage infection rate α is varied between the two half-planes, keeping all other parameters fixed, or when combinations of δ, α, β (burst size), and the phage diffusion constant are varied between the half-planes. It is interesting that it is thus possible to obtain long coexistence when the parameters in each half-plane in isolation would lead to fast extinction of phage or bacteria. The only condition required for long coexistence is that one half-plane must be a bacterial refuge (i.e., the parameter values there make phage too inefficient to survive), whereas the other is phage friendly. Thus, this stabilization of coexistence occurs for parameter values spanning many orders of magnitude: a vast set compared with the narrow band of parameters that allows coexistence in the basic model.

Fig. 2.

Snapshots of fixed bacterial refuge simulations. The plane is divided into two halves. The upper part is a bacterial refuge where phage cannot sustain themselves for long because of a high phage degradation rate. The three snapshots show simulations with three different 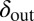values in the lower part of the system. The 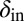value in the upper part of the system (the bacterial refuge) is kept constant at 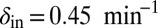. Grid size: 150 × 150. Initial conditions: upper plane was filled with uninfected bacteria and one line of infected bacteria was placed on the boundary between the two halves. (Top) 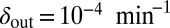. (Middle) 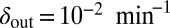. (Bottom) .

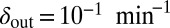Density-Dependent Mechanisms Can Create Self-Organized Bacterial Refuges.

In the above model, the bacterial refuge is determined before the simulation and occupies a fixed position in space. We wanted to test whether the same enhancement of coexistence is possible if bacterial refuges instead form dynamically. In particular, we examined whether mechanisms that create phage unfriendly conditions in areas of high bacterial density are sufficient to produce robust coexistence.

Substantial evidence exists in the literature that conditions for phage can be more difficult inside a dense bacterial colony. Nutrient depletion and limitation change the physiological condition for the cells and make them down-regulate receptors for phage adsorption (21, 22). Further, murein, which forms the cell wall, becomes hypercross-linked and richer in covalently bound lipoprotein (23), which may alter the kinetics of phage infection. Reduced infection rates, for cells in stationary phase, have for this reason also been used in other model studies (8). Reduced burst size and prolonged latent times have also been observed for cells with low growth rate/low metabolic activity, as well as for cells in stationary phase, in several studies (24–29). Another challenge for phage in high cell density is that bacterial quorum-sensing systems may trigger production of biofilm. Diffusibility inside a biofilm is locally significantly reduced due to high density of exopolymers produced by bacteria (30). Inside a biofilm, tight cell–cell binding may directly block phage receptors (31) and this action could also reduce phage infection. Also biofilms often contain proteolytic enzymes as well as endoglycanases that can lead to phage inactivation (26).

Self-Organized Bacterial Refuges also Enhance Coexistence.

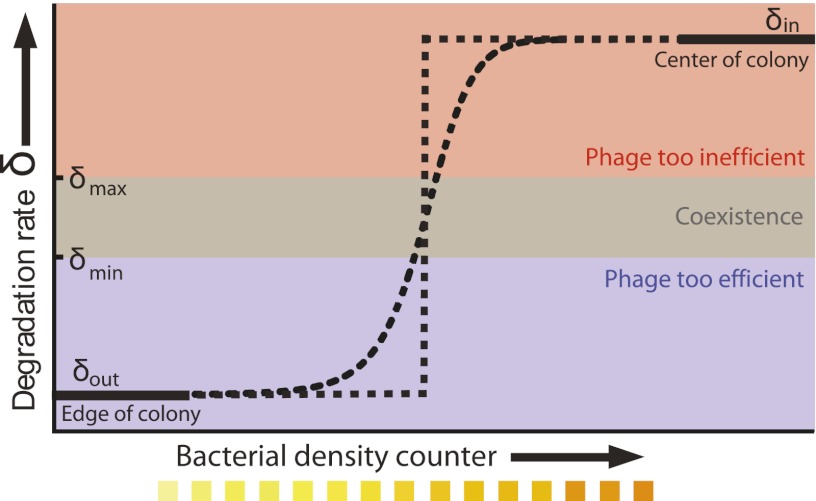
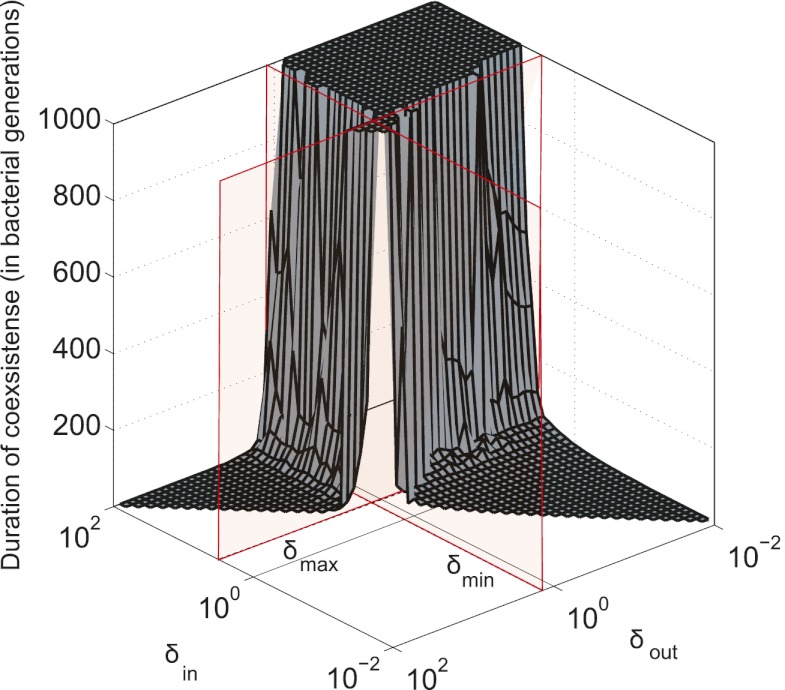
To test the effect of density-dependent formation of bacterial refuges, we constructed another version of the basic model where parameters such as the infection rate α and phage degradation rate δ can be different at different spatial locations. However, unlike the fixed bacterial refuge model, the values are not prespecified at each point in space. Instead they depend on local bacterial density as it develops dynamically during the course of the simulation (Materials and Methods). We implement the density-dependent effect by assigning to each bacterium a “density counter.” Each counter is an integer number that is incremented every time step that the bacterium spends with three or more neighbors and decremented otherwise. The value of these counters thus correlates with how long a bacterium has spent recently in high density. We then let the parameters of a specific site in the grid depend on the density counter of the bacterium that occupies that site, such that when the bacteria are young or alone, and thus have a low density-counter value, they are more susceptible to phage. Fig. 3 shows schematically how this rule can be implemented by making the phage degradation rate δ an increasing function of the density-counter value. Similarly phage infection rate or burst size or diffusion 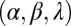, or combinations of all of these, can be made a decreasing function of the density counter. In this model we observe long-lived coexistence: Bacterial refuges self-organized and the system developed an almost static pattern of bacterial islands, with phage proliferating on new bacteria produced on the edges of the islands (Fig. 4). This phenomenon occurs for a huge range of parameter values and is stable against many changes in the model rules (see SI Appendix for details on this process). Fig. 5 shows the duration of coexistence as a function of 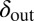and 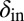, for simulations where only δ depends on the density counter ( 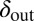and 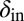are the values of δ for sites with minimal and maximal density-counter values, respectively) (Fig. 3). In the region where 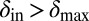and 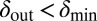, we find that coexistence times rise steeply compared with the values outside this region (Fig. 5 shows simulations that last at most 1,000 bacterial generations, but on the basis of a few longer simulations we suspect that coexistence times are much larger for parameter values deeper within this region). What is required for long-lived coexistence on the edge of bacterial refuges is merely that the bacteria in the center of the colony are so resilient that phage cannot sustain themselves in there, whereas recently divided bacteria on the edge of the colonies are (possibly very) susceptible to phage infection.

Fig. 3.

Phage degradation rate dependence on bacterial density counter. One way of implementing the self-organized bacterial refuge model is by making phage degradation rate an increasing function of the bacterial density counter. Thereby, bacteria that are young or alone occupy sites where the phage degradation rate is low, whereas bacteria that have spent some time at high density are at sites with high phage degradation rates. The plot shows schematically how this method may be done. 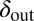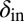The degradation rate at zero and maximal density counter values are denoted and , respectively. Also shown schematically is the region between 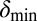and 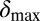, where phage and bacteria would coexist in the basic model. 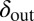and 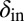can be chosen without restriction, but phage–bacteria coexistence is enhanced when they are chosen as shown, with 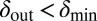and 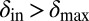. The dotted lines signify that we have also tried smoother, sigmoidal, functions and this method gives similar results.

Fig. 4.

Snapshots of simulations of the self-organized bacterial refuge model. After awhile bacteria in the center of colonies reach the maximal density-counter value and grid sites inside colonies become phage unfriendly (bacteria with low density counters are light yellow and bacteria with increasingly higher density counters are colored darker shades of yellow). New bacteria with density counter equal to zero are produced at the colony edges. Parameters were 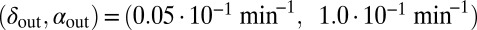and 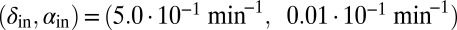marked by A and B in Fig. 1. The initial condition was randomly distributed bacteria with density counter equal to zero and a few infected with phage. Grid size: 200 × 200. 1, snapshot taken 4 bacterial generations (bac. gen.) after t = 0; 2, after 8 bac. gen.; 3, after 70 bac. gen.; 4, after 500 bac. gen.; 5, after 1,000 bac. gen.; and 6, after 2,000 bac. gen.

Fig. 5.

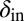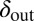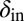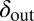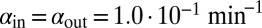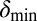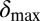Long-lived coexistence for a broad range of and . Shown is duration of coexistence as a function of and (). Red lines mark and for 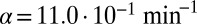in the basic model. If time reached 1,000 bacterial generations while there was still coexistence (i.e., both phage and bacteria were present), then the simulation was stopped. Only parameter sets where 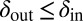were considered. Within the region where 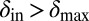and 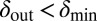the phage and bacteria coexisted for durations much longer than the bacterial generation time. In this region, the average infection front speeds were also relatively low (SI Appendix). 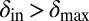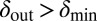When and , the phage live for a short time on the edge of the expanding bacterial colony before dying out. 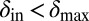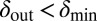When and , the phage infection fronts rapidly eat into the colonies and eventually wipe out the bacteria. In the small region where both 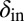and 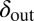are within the narrow range of 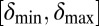, there is stable coexistence. Grid size: 100 × 100. Initial conditions: upper half-plane filled by uninfected bacteria and a single line of infected bacteria on the boundary between the upper part and the empty lower half-plane.

Evolution of Bacterial Refuges.

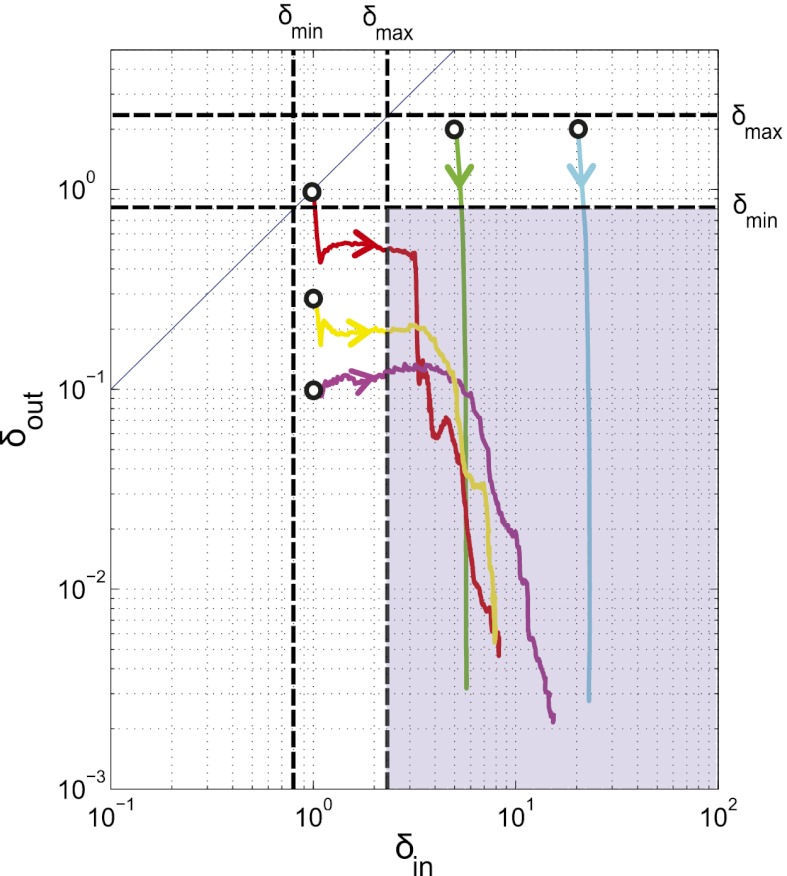
We next extended the self-organized refuge model to allow both bacteria and phage to evolve. Fig. 6 shows the results of one such implementation, where 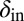was a property that bacteria pass on to their offspring and 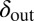a property inherited by phage offspring from their parents, and both were allowed to mutate (Materials and Methods and SI Appendix, Figs. S15–S18). The colored trajectories in Fig. 6 starting at different initial conditions each show, as time progresses, the changing values of 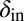and 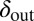, averaged over all phage and bacteria at that time. We see how the average parameters of the system are all pushed deeper into the blue-shaded region, toward more long-lived coexistence, by bacteria evolving to increase 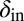and phage evolving to decrease 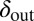. Note that we chose the initial values of 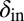and 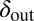in these simulations to be outside the coexistence region. Thus, in the absence of evolution, coexistence would not have lasted very long. A similar pattern is seen when we allow the infection rates, 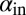and 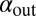, to mutate instead (SI Appendix, Fig. S18). Interestingly, this pattern was also maintained when the mean mutation step sizes of phage and bacteria were very different. For example, we observed that evolution of 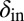and 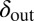from the initial condition of 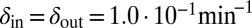was able to bring the system into the blue region of Fig. 6 both when 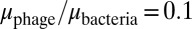and when .

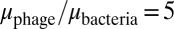Fig. 6.

Evolution pushes the self-organized bacterial refuge system deeper into the parameter region with long-lived coexistence. Trajectories show how the system averages of 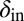and 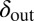change during five different simulations (each lasting 3,000 time steps) in the self-organized bacterial refuge model when bacteria and phage are permitted to evolve ( 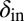was an inheritable characteristic of the bacteria whereas 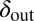was an inheritable characteristic of the phage, both passed on vertically to offspring with the chance of small changes; new offspring values were picked from a normal distribution with a mean equal to the parent value and a variance of 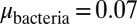and 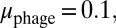respectively). We see that selection tends to push 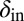to higher values and 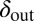toward lower values. This process drives the system deeper into the parameter region where 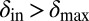and 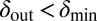(the light blue region), where the phage and bacteria coexist for much longer than the bacteria generation time. Grid size: 150 × 150. Initial conditions: randomly scattered uninfected bacteria and a few infected. Purple start point: 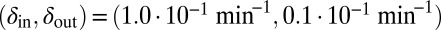. Yellow start point: 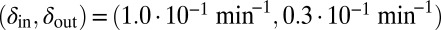. Red start point: 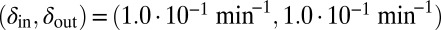. Green start point: 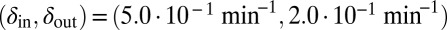. Blue start point: .

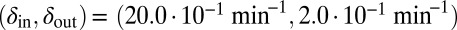Discussion

In this paper we explore bacterial refuges and their formation by density-dependent mechanisms as a mechanism for enhancing phage–bacteria coexistence. We find that coexistence between a virulent phage and its bacterial host is remarkably stable and robust on boundaries between habitats within each of which coexistence is not possible—provided one habitat is a bacterial refuge where conditions are hostile to phage, whereas the other is phage friendly. We further show that this enhancement of coexistence also stabilizes the long-term coevolution between phage and bacteria.

Spatial heterogeneity is a prominent feature of many real phage–bacteria ecosystems. This circumstance is reflected in the fact that soil or biofilms, and even ocean data, show high variability of phage and bacteria density over small length scales (32). In oceans, heterogeneity could be self-organized by cyanobacteria making colonies in the form of sheets and mats (33).

Many bacteria can at high density create a heterogenous and somewhat phage-hostile environment by themselves. One such density-dependent mechanism is the use of quorum-sensing systems to trigger biofilm formation. Biofilm is not invincible to phage attack (30) but many factors contribute to make phage existence in biofilm harsher as discussed earlier. Costerton et al. (34) report that Escherichia coli persist in the intestinal tract by adhering to tissue surfaces and food particles, where they live in encapsulated microcolonies akin to biofilms. Sternberg et al. (35) report that within biofilms, cells typically form clusters (microcolonies) with the most metabolically active cells located on the periphery of each microcolony. This formation resembles the self-organized bacterial clusters formed in our simulations. Corbin et al. (30) observe ongoing phage proliferation and sustained coexistence of bacteria and phage populations of T4 in E. coli glucose-limited biofilm. They suggest that virulent phage multiply only in the part of the E. coli biofilm population where bacteria are not in stationary phase. Other studies have also reported that phage may alter biofilm morphology but that bacteria and virulent phage are able to coexist stably inside biofilm (26, 36).

Characteristics of Phage–Bacteria Coexistence on Edges of Refuges.

In our simulations, we found that density-dependent, or quorum-sensing, mechanisms are a robust way of forming self-organized bacterial refuges. And having stable refuges is in turn a robust way to enhance phage–bacteria coexistence. We found that coexistence, in these simulations, has the following characteristics: (i) Phage and bacterial densities are quite high with phage being concentrated on the edges of dense bacterial colonies, (ii) phage can outnumber bacteria by easily an order of magnitude without destabilizing the system, and (iii) there is a high turnover of the phage population and also of the bacterial population at the edge of colonies (SI Appendix, Figs. S11–S13). Coexistence with these characteristics happens despite the phage being intrinsically very efficient predators, with a large burst size, long lifetimes, and high infection rates outside the bacterial refuge. In the absence of refuges, coexistence between phage and bacteria is difficult to obtain and has very different characteristics because a higher phage efficiency is incompatible with stable and high bacterial density and high turnover of both phage and bacteria populations. The only way to get coexistence with an efficient phage in the absence of refuges is to have a sufficiently low bacterial density so that it takes so long to find new host bacteria that on average only a single phage from a burst survives long enough to infect a new bacterium (11). Data from soil (37) and marine (38) phage–bacteria ecosystems seem to match the characteristics of the refuge model better; the population densities of both phage and bacteria are observed to be relatively high and the phage:bacteria ratio is around 10:1. Moreover, stable populations numbers and a high turnover rate of phage and bacteria are also observed: Virulent phage are estimated to kill 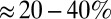of the bacteria in the oceans on a daily basis (38).

Our results suggest that it would be particularly interesting to measure parameters that affect phage efficiency, such as phage lifetime, infection rate, and diffusion constant, in natural ecosystems where such phage have been observed to coexist with bacteria. The lifetimes of nine different virulent phage were measured in laboratory conditions with bacteria growing on LB and found to be of the order of 10 d on average (39). However, the corresponding numbers are not known in natural ecosystems in soil or oceans. If measured parameters are found to lie outside the coexistence region of the basic model, that result would strongly suggest that there must be additional mechanisms that allow coexistence. The specific mechanism of coexistence along the edge of refuges also predicts that the variance of these parameters should be large, even over very short length scales. It would, for example, be interesting to know the variance of burst sizes in a biofilm instead of just the mean burst size. This is a qualitative prediction at the moment, but as more accurate measurements of parameters are made the more quantitative such predictions of our models will become.

The jump from our simple models to real phage–bacteria ecosystems is a substantial one, and any predictions should be treated with caution and first confirmed in simpler laboratory experiments with isogenic phage and bacteria. However, it is encouraging that the model behavior is robust to many alterations in the dynamical rules. In addition to the variants described above, we have also found qualitatively similar refuge formation and enhancement of coexistence when we added a third dimension, density-dependent bacterial growth, bacterial diffusion, and hydrodynamic flows that make bacteria and phage drift in a specific direction (SI Appendix, Figs. S14, S19, and S20).

Bacterial Refuges and the Coevolutionary Arms Race.

Bacterial refuges alone are not necessarily sufficient to ensure very long-term coexistence of phage and bacteria. In real ecosystems, very long-term coexistence certainly involves bacteria evolving to become resistant to phage and phage counter-evolving strategies to infect resistant bacteria. However, such a coevolutionary arms race cannot be stable if at any time conditions arise where either the phage or the bacteria rapidly die out. For example, if a particularly efficient phage arises, it could rapidly wipe out the whole system before bacteria have time to evolve resistance. Therefore, any nonevolutionary mechanisms that enhance coexistence could play a crucial role in allowing sufficient time for evolution to occur. Self-organized bacterial refuges are one of several such possible mechanisms. We have shown that, for a very broad region of parameter space, such refuges can slow down the rate of extinction immensely, while maintaining a high density of both phage and bacteria, for time spans of at least 1,000 times longer than the bacterial generation time. The evolutionary simulations we have done complete the second part of this argument. We found that even when the system starts with parameter values that do not allow coexistence for very long, evolution of the phage and bacteria pushes these parameter values into regions that do allow coexistence. Interestingly, this outcome was true both when the phage mutated faster than the bacteria and vice versa. As one of the referees pointed out, irrespective of the particular values chosen for the mutation rates, the self-organized refuges result in an asymmetry in the evolutionary rates of phage and bacteria. Bacterial mutations occur more often at the edges of colonies because that is where new bacteria are formed, but these mutations are often quickly eliminated by phage infections. On the other hand, phage mutations (which also occur mainly at the edges) can persist and spread through the population. This process likely explains the shape of the evolutionary trajectories shown in Fig. 6, Figs. S16–S18, and in SI Appendix: Changes in bacterial parameters typically occur early on when the refuges are still stabilizing, whereas later the trajectory moves mainly in the direction of changing phage parameters. In these evolutionary simulations, the properties of the ecosystem described above are maintained—highly efficient phage living on the edge of almost static refuges, with a high turnover of both phage and bacterial populations—and there is continuous evolution of phage that are more efficient and bacteria that create better refuges. A very interesting direction to take these models in the future would be to include multiple phage and bacteria species with a complex network of infection and immunity interactions between them.

To summarize, we have shown that self-organized bacterial refuge formation might be a mechanism that can help facilitate coexistence and perhaps resolve several apparently paradoxical features of the phage–bacteria coexistence observed in the real world. We have shown that self-organized bacterial refuges can produce coexistence with features similar to those observed in real-world ecosystems by concentrating phage–bacteria interaction to the edges of the refuges and have argued that selection pressures will push the system toward more robust coexistence.

Materials and Methods

Basic Model.

We use the simple virulent phage and bacteria ecosystem model introduced in ref. 11. Phage and bacteria interact on a 2D 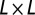grid of “sites”. Each site in the grid can be either occupied or unoccupied by a single bacterium. The bacterium may be uninfected or infected. In addition, there can be any number of free phage at that site. Time proceeds in discrete steps. Precise timers control bacterial cell division and the lysis of an infected bacterium, which releases a burst of free phage. Other processes are random, e.g., death and diffusion of phage, and are modeled as Poisson processes. In each time step the following can happen:

• i) Bacterial replication: A bacterium with at least one empty adjacent site will attempt to divide in every time step after the current time has become greater than the value of its replication timer. The probability of replication is set proportional to the number of empty neighbor sites. Once a bacterium divides, one daughter cell remains in the original site and the other is placed randomly in one of the adjacent empty sites. The replication timers of both cells are reset to the current time plus T, a parameter that thus sets the growth rate of the bacteria.

• ii) Bacterial infection: An uninfected bacterium at the same site as free phage may be infected with a probability that is set by the infection rate per phage per bacterium, α. When an infection occurs, then the number of free phage at that site is reduced by one, and the lysis timer of the newly infected bacterium is set to τ (the latent time of the infecting phage) time steps ahead. (Note that we disallow superinfection—phage can infect only uninfected bacteria in all of the models used in this paper.)

• iii) Bacterial lysis: An infected bacterium dies when its lysis time is reached. The number of phage at that site then increases by the burst size, β.

• iv) Phage degradation: Free phage die with a probability determined by the phage degradation rate δ.

• v) Phage diffusion: Each free phage may jump to a neighboring site with a probability set by the phage jump rate λ (which thus sets the phage diffusion constant).

The values of the parameters and the size of the time step depend on the choice of phage and bacteria species (see SI Appendix, Table S1 for explanation of symbols and parameters). For E. coli with a replication time of 300 min, a reasonable choice of time step would be 10 min, and each grid site would have an area of ∼1 μm². We choose λ to keep the phage diffusion constant fixed at 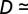1/4 (site area)/(time step), meaning that a phage on average will use 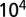time steps to move across a grid size of 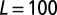. (For the choice of E. coli this number would correspond to at phage diffusion constant of 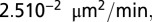which is relatively low.) See SI Appendix and ref. 11 for further details of model rules for bacterial replication, phage diffusion, infection, and lysis.

Fixed Bacterial Refuge Model.

We extend the basic model to include a bacterial refuge by dividing the 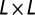grid into two halves. Grid points in one half are assigned one set of 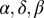, and λ values that make this half phage hostile—this is the bacterial refuge part of the grid. The other half is given another set of parameter values that make it phage friendly. This division is in contrast to the basic model where parameters are the same all over the grid. Phage-hostile and phage-friendly parts of the plane can be created in many ways. The simplest is where only a single phage parameter is changed. For example, δ could be high in the phage-hostile half and low in the phage-friendly half. Bacterial growth rate is the same throughout the system.

Self-Organized Bacterial Refuge Model.

In the self-organized bacterial refuge model we again allow 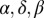, and λ to have different values for different grid points. However, unlike those in the fixed-refuge model, these values are not preassigned to each point. Instead they are determined dynamically during the course of simulation in a manner dependent on the density of bacteria. The rules that govern this determination mimic the formation of a biofilm within which phage efficiency is reduced. Each bacterium has a density counter, which is an integer number that goes up every time step that the bacterium spends with three neighbors or more and down each time step it spends with two neighbors or less (the counter stops increasing at a certain maximum value and never goes below zero). These counters thus keep track of how long a bacterium has spent recently in high cell density, which we assume is correlated to its being within the biofilm protection. We explore different ways, described in the main text, of making phage parameters depend on the biofilm protection, i.e., on the value of the density counter of the bacterium that occupies a site.

Evolutionary Version of Self-Organized Refuge Model.

In this variant, the parameter values at each grid point are again determined by the value of the density counter there, but additionally the function of the density counter from which the value is computed varies across grid points (unlike the self-organized refuge model where this function was the same for all grid points). The function used is determined by the bacteria and phage that occupy that grid point. The value chosen when the density counter is maximal is an inheritable property of the bacterium, whereas the value chosen when the density counter is zero is an inheritable property of each phage. When bacteria or phage replicate, the offspring properties are normally distributed around the parent properties with variance 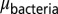and , respectively. We have implemented several variants of this method, and an algorithmic description of the different models can be found in SI Appendix. A Java applet implementing the self-organized refuge model is available from S.H. The applet is interactive and allows the user to modify phage degradation and infection rates.