Highly efficient and exact method for parallelization of grid-based algorithms and its implementation in DelPhi

Abstract

The Gauss-Seidel method is a standard iterative numerical method widely used to solve a system of equations and, in general, is more efficient comparing to other iterative methods, such as the Jacobi method. However, standard implementation of the Gauss-Seidel method restricts its utilization in parallel computing due to its requirement of using updated neighboring values (i.e., in current iteration) as soon as they are available. Here we report an efficient and exact (not requiring assumptions) method to parallelize iterations and to reduce the computational time as a linear/nearly linear function of the number of CPUs. In contrast to other existing solutions, our method does not require any assumptions and is equally applicable for solving linear and nonlinear equations. This approach is implemented in the DelPhi program, which is a finite difference Poisson-Boltzmann equation solver to model electrostatics in molecular biology. This development makes the iterative procedure on obtaining the electrostatic potential distribution in the parallelized DelPhi several folds faster than that in the serial code. Further we demonstrate the advantages of the new parallelized DelPhi by computing the electrostatic potential and the corresponding energies of large supramolecular structures.

Introduction

The ability to calculate electrostatic forces and energies is critical in modeling biological molecules and nano objects immersed in water and salt phase or another medium due to the fact that biological macromolecules are comprised of charged atoms. Their interactions and interactions with water and salt contribute to the structure, function and interactions of bio-molecules. At the same time, modeling the electrostatic potential of biological macro-molecules is not trivial, and in a continuum case, requires solving the Poisson-Boltzmann equation (PBE) ¹

$$\nabla ·[\epsilon (x)\nabla \phi (x)]-\kappa {(x)}^{2}sinh(\phi (x))=-4\pi \rho (x),$$ (1)

which is a second order nonlinear elliptic partial differential equation (PDE) discussed extensively in Ref. ². Here φ(x) is the electrostatic potential, ε(x) is the spatial dielectric function, κ(x) is a modified Debye-Huckel parameter, and ρ(x) is the charge distribution function.

The PBE does not have analytical solutions for irregularly shaped objects, and because of that, the solution must be obtained numerically. Numerous PBE solvers (PBES) have been designed and developed independently to utilize various mathematical methods to solve the PBE numerically. A short list includes AMBER ^3–6, CHARMM ⁷, ZAP ⁸, MEAD ⁹, UHBD ¹⁰, AFMPB ¹¹, MIBPB ^12,13, ACG-based PBE solver ¹⁴, Jaguar ¹⁵, APBS ^16,17 and DelPhi ^1,18. Among these PBES, three popular implementations deserve specific attention in the light of current work. The APBS is a popular multigrid finite-difference and adaptive finite element PBE solver developed by Dr. N. Baker and his colleagues and is aimed at providing force estimates and modeling large biomolecules and assemblages and pKa calculations. Another popular PB solver is MIBPB^{12,13,19–22}, developed by Dr. G-W. Wei and coworkers which utilizes interface technique to assure potential and flux continuity at the interface biomolecule and solvent. Due to this and Krylov subspace technique^12,19–22 implementation, the MIBPB was demonstrated to be very robust PBE solver achieving second-order convergence for solving linear PBE¹³. The third popular solver is DelPhi, developed in Dr. B. Honig’s lab ^1,18, which adopts the Gauss-Seidel (GS) method, combined with the successive over-relaxation (SOR) method which estimates the best relaxation parameter at run time ²³ to solve both linear and nonlinear PBEs. DelPhi has many unique features, such as abilities of modeling geometric objects (spheres, parallelepipeds, cones and cylinders) and assigning multiple dielectric regions and charge distributions, and capabilities of allowing users to specify different types of salts and boundary conditions, as well as various output maps.

However, existing methods implemented in serial PBES are only suitable for electrostatic calculations of relatively small bio-molecular systems due to time constraints. Nowadays, problems arising from computational biology are complex and usually of nano scale resulting in systems consisting of large amounts of charged atoms and tens of thousands of, even millions, of mesh points. The size and complexity of these problems make parallelization of current serial PBES highly desired to improve their performance to solve the problems in reasonable time. For example, APBS was parallelized by a “parallel focusing” method based on the (spatial) domain decomposition method, together with standard focusing techniques. The results of parallel solution of the PBE for supramolecular structures, such as microtubule and ribosome structures, are presented in Ref. ¹⁷. It should be mentioned that the solution obtained by this parallel method may not be identical to that obtained by the serial calculation, since, in order to perform calculations in parallel on subsets of global mesh, additional values at boundaries of subsets must be, for instance, interpolated from the solution on a much coarser mesh in the first place.

In contrast to the (spatial) domain decomposition approach implemented in APBS, this paper reports a novel approach to parallelize the GS method and its application to create a parallelized DelPhi. The implementation was facilitated due to the techniques already implemented in the serial DelPhi, such as the “checkerboard” ordering (also known as the “red-black” ordering ²⁴) and contiguous memory mapping ¹, to fulfill the GS method and latter, the SOR method. In addition, the parallelization was possible because of the message passing interface version 1.0 (MPI-1), which allows the high-performance message passing operations available for the advance distributed-memory communication environment supplied with parallel computers/clusters. Later on, MPI-2 was released to include new features such as parallel I/O, dynamic process management and remote memory operations ²⁵. With the aid of powerful MPI libraries, we developed an efficient and exact method to parallelize the serial DelPhi (from the algorithmic point of view) to achieve linear/nearly-linear speedup of its performance without compromising the accuracy and without introducing any assumptions. While the approach was implemented in DelPhi, the very same parallelization technique can be translated and employed by other software to implement/parallelize GS/SOR methods and other grid-based algorithms.

This paper is organized as follows: (a) the techniques of implementing GS/SOR methods reported in Ref. ¹ are described in the next section. Then, (b) parallel technique using MPI-2 remote memory operations is reported, and (c) implementation results and performance analysis on two examples of large supramolecular structures are demonstrated.

Efficient Implementation Techniques of the GS Method

In this section, we briefly describe the numerical methods and the techniques implemented in the serial DelPhi code. More details can be found in supporting information and original papers ^1,18,26.

Consider a three dimensional cubical domain Ω. We discretize Ω into L grids per side with uniform grid size h. The total number of grid points is N = L * L * L. Let K₀ (x₀, y₀, z₀) be an arbitrary grid point away from the boundary of Ω. Applying finite difference formulation yields an iteration equation for eqn. (1):

$${\phi }_0=\frac{{\displaystyle \sum _{i=1}^6}{\epsilon }_i{\phi }_i+4\pi q_0/h}{{\displaystyle \sum _{i=1}^6}{\epsilon }_i+{(\kappa h)}^2(sinh({\phi }_0))/{\phi }_0},$$ (2)

where φ and q₀ are the potential and charge assigned to K₀, φ_i, i =1,…,6 are potentials at six nearest neighboring grids of K₀, and ε_i, i =1,…,6 are the dielectric constants (taking value ε_i = ε_out outside the protein and ε_i =ε_in inside the protein), at midpoints of K₀ and its nearest neighbors (see supporting information for details). Eqn. (2) can be rewritten in matrix form as

$$\mathrm{\Phi }=T\mathrm{\Phi }+Q,$$ (3)

where T is the coefficient matrix, Φ and Q are column vectors.

Given appropriate boundary conditions at the edge of Ω and an initial guess for the potential at each grid point (usually zero for convenience), we may solve eqn. (3) iteratively using numerical methods such as Jacobi, GS or SOR methods. In the case of serial calculations, the GS method is, in general, superior to the Jacobi method in the sense that it converges faster than the Jacobi method. The gain of convergence rate comes from the fact that the GS method uses latest updated potentials at neighboring points in current iteration, instead of values obtained in the previous iteration as in the Jacobi method. However, without special treatment, the requirement of using latest updated neighboring values makes the GS method less favorable to parallel computing due to the fact that calculations at one point cannot start prior to the completion of calculations at its neighbors. In order to efficiently parallelize the GS method, an implementation technique, called the “checkerboard” ordering ¹, which has been implemented in serial DelPhi, will be discussed in the following section.

The “Checkerboard” Ordering

Solving eqn. (3) iteratively requires construct mapping to convert potentials and charges at three dimensional grid points to column vectors Φ and Q. One common mapping, alternating index in x-direction first, followed by indices in y- and z- direction, is given by

$$w=x+L\ast (y-1)+L^2\ast (z-1),$$ (4)

which maps the potential and charge at point P(x, y, z) to Φ(x) and Q(w), respectively.

The associated coefficient matrix T is determined by the order in which the grid points are mapped. However, it has been pointed out in Ref. ²⁷ that this mapping does not affect the spectral radius of matrix T. That is, the convergence rate of the iteration method is independent of the mapping order, which allows us to reorder the components of Φ and Q, and reconstruct associated matrix T in desired fashion without losing the overall convergence rate of the iteration method.

Another important observation on the grid-to-vector mapping is that each grid point P(x, y, z) can be assigned as odd or even by the sum of its grid coordinates, sum = x + y + z ¹. We call P an even point if sum is even, and P an odd point if sum is odd. The six nearest neighbors of P are of opposite nature, i.e., every even point is surrounded by odd points and vice versa since the sums of their coordinates only differ by one. As shown in eqn. (2), updating of the potential at any point only depends on the potentials at its six nearest neighbors, we see that even is updated by surrounding odds, and odd is updated by surrounding evens. Moreover, provided L an odd number, index w obtained by eqn. (4) is of the same even/odd nature as sum which leads to the following reorganization of Φ and Q simply by sum

$$\mathrm{\Phi }=\left[\begin{array}{c}{\mathrm{\Phi }}_{\text{even}}\\ {\mathrm{\Phi }}_{\text{odd}}\end{array}\right],Q=\left[\begin{array}{c}{Q}_{\text{even}}\\ Q_{\text{odd}}\end{array}\right],$$ (5)

where Φ_even and Q_even are potentials and charges at even points, and Φ_odd and Q_odd are those at odd points. The corresponding coefficient matrix T is then of the form

$$T=\left[\begin{array}{cc}0& T_{\text{odd}}\\ T_{\text{even}}& o\end{array}\right],$$ (6)

such that T_odd is the submatrix which updates Φ_even with Φ_odd, and in turn, T_even updates Φ_odd with newly obtained Φ_even. Eqn. (3) is thereby equivalent to

$$\{\begin{array}{c}{\mathrm{\Phi }}_{\text{even}}=T_{\text{odd}}{\mathrm{\Phi }}_{\text{odd}}+Q_{\mathit{even}}\\ {\mathrm{\Phi }}_{\text{odd}}=T_{\mathit{even}}{\mathrm{\Phi }}_{\mathit{even}}+Q_{\mathit{odd}}\end{array}.$$ (7)

Eqn. (7) allows the GS method to be implemented in Jacobi’s fashion and makes it suitable for parallelization.

Contiguous Memory Mapping

Before we move to the next section introducing techniques on how to parallelize the GS scheme effectively, one more implementation technique, namely contiguous memory mapping, needs to be described.

It is noticed ¹ that the performance of the “checkerboard” ordering implementing the GS method is slowed down by using a logical operation (“IF” statement) in the most inner loop of the algorithm in order to separate the process of updating Φ into odd and even cycles. Considering a case such that Φ is composed of millions of points and the numerical algorithm requires hundreds of iterations to converge, the cost of this logical operation is unaffordable. Therefore, it was suggested in Ref. ¹ that the best way to efficiently code the ordering is to map the odd and even points separately into two contiguous memory/arrays, i.e., Φ_odd and Φ_even. This leads to a more complex coding of the algorithm but avoids branching the inner loop ¹.

Discussions of Parallelization Techniques and Parallel Algorithm

After implementing the techniques described above, parallelizing eqn. (7) of the GS method is conceptually straightforward: Provided N_cpu processes or computing units (CPUs) at our disposal, we divide Φ_odd and Φ_even evenly into N_cpu segments. Each pair of segments of Φ_odd and Φ_even is given to one CPU for updating. In order to reproduce values obtained from serial calculations without imposing additional boundary conditions, additional memory is allocated to synchronize values near both ends of the segments. Synchronization takes place right after the segments of Φ_odd and Φ_even are updated locally.

Implementing the above idea effectively requires network communication to be reduced. An efficient algorithm must minimize the ratio between the amount of data to be synchronized and the amount of data to be computed locally per CPU, i.e. the CPU must spend more time computing than communicating.

Details of the Parallelization

Notice Φ is of the length L³ and therefore, segments of Φ_odd and Φ_even to be updated locally per CPU are of the same length L³ / (2N_CPU). Let p₀ (x₀, y₀, z₀) be an even point and the potential at p₀ is mapped to Φ_even(w₀) with $w_0=\frac{x_0+L(y_0-1)+L^2(z_0-1)+1}{2}$, the potentials at six nearest neighbors of p₀ are then mapped to six entries of Φ_odd shown in the second column of Table 1. Similarly, when p₀ is odd and the potential at p₀ is mapped to Φ_odd (w₀) with $w_0=\frac{x_0+L(y_0-1)+L^2(z_0-1)}{2}$, the potentials at its six neighbors are shown in the third column of Table 1.

Table 1.

Potentials at six nearest neighbor points of p₀ in Φ_odd and Φ_even

Neighboring points of p0(x0, y0, z0)	Entries of Φodd when p0 is even	Entries of Φeven when p0 is odd
p1(x0 − 1, y0, z0)	Φodd(w0 − 1)	Φeven(w0)
p2(x0 + 1, y0, z0)	Φodd(w0)	Φeven(w0+1)
p3(x0, y0 − 1, z0)	${\mathrm{\Phi }}_{\text{odd}}(w_0-\frac{L+1}{2})$	${\mathrm{\Phi }}_{\text{even}}(w_0-\frac{L-1}{2})$
p4(x0, y0 + 1, z0)	${\mathrm{\Phi }}_{\text{odd}}(w_0+\frac{L-1}{2})$	${\mathrm{\Phi }}_{\text{even}}(w_0+\frac{L+1}{2})$
p5(x0, y0, z0 − 1)	${\mathrm{\Phi }}_{\text{odd}}(w_0-\frac{L^2+1}{2})$	${\mathrm{\Phi }}_{\text{even}}(w_0-\frac{L^2-1}{2})$
p6(x0, y0, z0 + 1)	${\mathrm{\Phi }}_{\text{odd}}(w_0+\frac{L^2-1}{2})$	${\mathrm{\Phi }}_{\text{even}}(w_0+\frac{L^2+1}{2})$

We can see from Table 1 that, on each CPU, at most $\frac{L^2+1}{2}+\frac{L^2-1}{2}=L^2$ elements near the ends of segments of Φ_odd and Φ_even are required to be synchronized in iterations. Therefore, the ratio of the number of elements to be exchanged and the number of elements to be calculated locally is

$$r=\frac{L^2/2}{L^3/(2N_{\text{CPU}})}=\frac{N_{\text{CPU}}}{L}.$$ (8)

Eqn. (8) provides an insight to the speedup, efficiency and scalability of the parallel algorithm. For example, small r (r≪1, or equivalently, N_CPU ≪ L) indicates that communication cost in the parallel computation contributes only a minor portion of the overhead, assuming cost of network communication is comparable to that of CPU floating point calculations. In such cases, linear speedup of the parallel computing is very likely to be achieved.

Many other factors may affect the performance of the parallelized code. In particular, appropriate MPI communication operations must be chosen carefully to avoid unwanted delays due to queue in synchronization. Synchronization across all processors can be achieved by either blocking or non-blocking operations provided by MPI. Blocking operations require the sender to wait for receiving the confirmation from the receiver before the sender can process to the next operation. In our case, one processor needs to exchange boundary values with both neighboring processors on its left and right sides. If blocking operations are chosen to use, in the worst scenario, processor 2 needs to talk to processor 1 and wait for response from processor 1 before it can talk to processor 3, and so on. In this case, a communication queue is created and the last processor communicates the last. It is obviously not efficient. Therefore, non-blocking operations are more favorable for this application. Moreover, since the computer cluster is equipped with Myrinet, on which one-sided operations have potentials to perform better than two-sided operations, one-sided direct memory access operations were used in this method.

MPI-2 library provides two communication models: two-sided communication based on blocking/non-blocking send and receive operations and one-sided communication allowing direct remote memory access (DRMA) of a remote process ²⁸. Two-sided communication requires actions on both sides of sender and receiver. In contrast, one-sided communication specifies communication parameters only on the “requester” side (called the origin process) and leaves the “host” (called the target process) alone without interrupting its on-going work during communication. One-sided communication requires additional operations to create an area of memory (call a “window”) in the target process for the origin process to access prior to communication takes place.

One-sided communication fits in our requirements very well. It is more convenient to use, and has the potential to perform better on the networks like InfiniBand and Myrinet, where one-sided communication is supported natively ²⁹. One-side communication requires explicit synchronization to ensure the completion of communication. Three synchronization mechanisms are provided in MPI-2 ³⁰: the fence synchronization, the lock/unlock synchronization and the post-start-complete-wait synchronization. Among these three synchronization mechanisms, the scope of the post-start-complete-wait synchronization can be restricted to only a pair of communicating, which makes it the best candidate in our scenario: synchronizations between two successive processes take place at almost the same time, and moreover, provided the problem size is fixed (see eqn. (8)), the amount of data to be exchanged between two processes is of the same no matter how many processes are allocated.

Parallel Algorithm

In the light of above results and discussions, we followed the Master-Slaves paradigm and developed an efficient and exact algorithm to parallelize the iterations in the GS method using MPI-2 one-sided DRMA operations. It is shown in Table 2.

Table 2.

An algorithm for parallelizing iterations in the GS method using MPI-2 DRMA operations

Step 1: The master CPU assigns three dimensional points as even and odd according to the sum of its coordinates. An arbitrary grid point p(x, y, z) and its six nearest neighbors are shaded and shown in Figure 1(a). The master CPU maintains Qeven, Qodd, Φeven and Φodd. Relative positions of p in Φeven and its neighbors in Φodd are demonstrated in Figure 1(b). Qeven, Qodd, Φeven and Φodd are then divided evenly and distributed to every slave CPU. Step 2: Each slave CPU allocates contiguous memory for segments of Qeven and Qodd of length L3 / (2NCPU), and segments of Φeven and Φodd of length L3 / (2NCPU) + L2. In Φeven and Φodd, the first and last L2 / 2 elements (unshaded regions in Figure 1(c)) are for receiving updated potentials on the previous and next CPUs, and, in between (shaded regions in Figure 1(c)), L3 / (2NCPU) potentials are updated locally on this CPU. The colored regions in Figure 1(c) indicate where synchronization takes place. Step 3: The first (Ncpu − 1) slave CPUs create two windows, win1 and win2, of size L2 at the right end of Φeven and Φodd by MPI_WIN_CREATE (shown in Figure 1(d)). Step 4: Slave CPU(i) opens window win2 using MPI_WIN_POST. CPU(i+1) starts request of DRMA using MPI_WIN_START, copies L2 /2 elements in the shaded red region of Φodd to the unshaded red region of Φodd on CPU(i) by MPI_PUT, brings another L2 /2 elements in the shaded blue region of Φodd on CPU(i) back to the unshaded blue region of Φodd on CPU(i+1) by MPI_READ, and completes the request by MPI_WIN_COMPLETE. The whole access epoch is completed after CPU(i) calls MPI_WIN_WAIT, as shown in Figure 1(d). Step 5: Each slave CPU updates the elements of Φeven in the shaded region one by one using eqn. (2), or more efficiency method described in 1. Step 6: Follow the same procedures in Step 4–5 to update Φodd using updated Φeven. Step 7: Repeat Step 4–6 until pre-defined tolerance or the maximal number of iterations is achieved. The computed results are sent back to the master CPU for reassembling.

Implementation Results and Conclusions

Analyzing the performance of parallel programs requires background in parallel computing. For readers who are not familiar with parallel computing, it is suggested to refer to the supporting information for some commonly used quantities, such as speedup and efficiency, as well as some important theoretical results, for performance analysis of parallel algorithms.

The numerical experiments reported in this section were done with parallelized DelPhi (version 5.1, written in FORTRAN95) and performed on two types of computer nodes of the Palmetto cluster at Clemson University ³¹: (I) Computer node 1112-1541 of Sun X6250 with Intel Xeon L5420 @ 2.5 GHz x2 processors, 8 cores, 6 MB L2 cache, and 32 GB memory; (II) Computer node 1553-1622 of HP DL 165 G7 with AMD Opteron 6172 @ 2.1 GHz x2 processors, 24 cores, 12 MB L2 cache, and 48 GB memory. 10 GB Myrinet network is equipped on the Palmetto cluster. All experiments, except those of serial nonlinear implementations which require more than 30 GB memory, were performed on the first set of nodes for consistency. Each identical experiment was repeated 5 times and the average is reported here to reduce random fluctuations caused by system workload and network traffic in real time.

All calculations used the same Amber force field. Scale = 2.0 and 70% percentage filling of the box domain were set in the parameter file resulting in the dimensions of the box domain ≈ 407 Å× 407 Å × 407 Å and 815 × 815 × 815 mesh points in total.

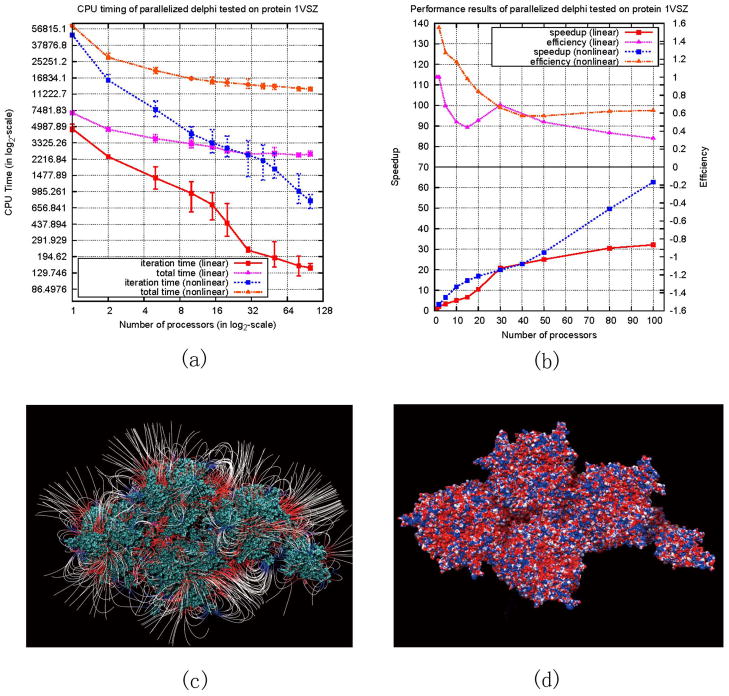
The first series of experiments, requiring solving linear and nonlinear PB equations, were performed on a fraction of the protein of human adenovirus 1VSZ downloaded from the Protein Data Bank (PDB) ³² and protonated by TINKER ³³. The CPU time achieved by solving the linear and nonlinear PBE as a function of increasing number of processors is shown in Figure 2(a) with vertical bars indicating variations of 5 runs. To compare their performance, log-scale plots of speedup and efficiency are shown in Figure 2(b). The resulting potential and electrostatic field are plotted by VMD ³⁴ and demonstrated in Figure 2(c)–(d).

Figure 2.

Performance results and electrostatic properties of 1VSZ. (a) Execution (purple) and iteration (red) time for solving the linear PBE, compared to execution (orange) and iteration (blue) time for solving the nonlinear PBE. (b) Speedup (red) and efficiency (purple) achieved by solving the linear PBE, compared to speedup (blue) and efficiency (orange) obtained by solving the nonlinear PBE. (c) Resulting electrostatic field. (d) Resulting electrostatic potential.

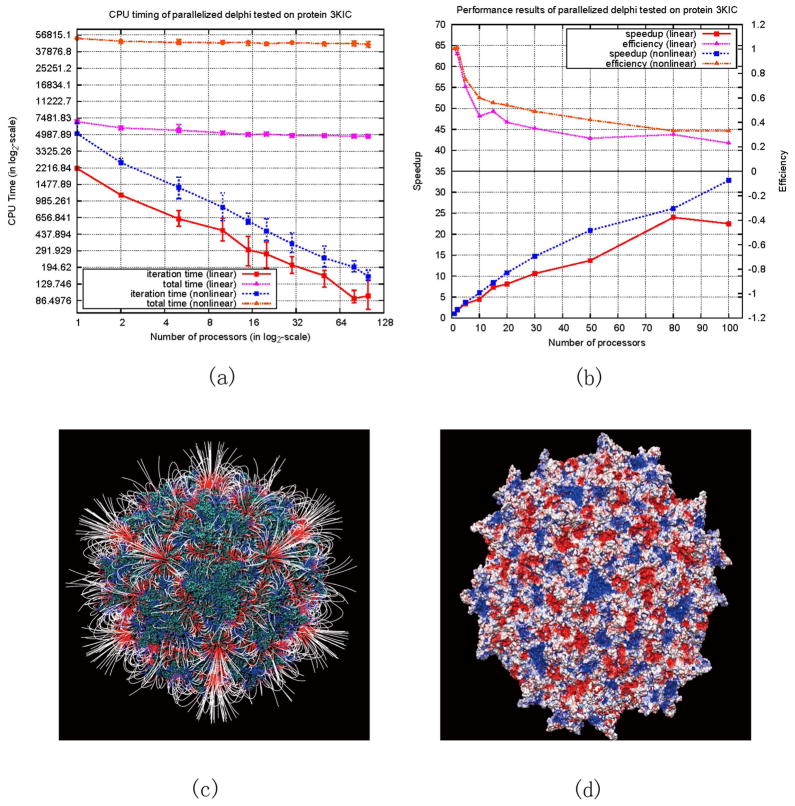
The next series of experiments were performed on the protein of adeno-associated virus 3KIC, which has significantly more atoms (≈ 484,500 atoms in a pdb file of size 25.4 MB) than those of 1VSZ (≈180,574 atoms in a pdb file of size 9.5 MB). The results are presented in Figure 3(a)–(d).

Figure 3.

Performance results and electrostatic properties of 3KIC. (a) Execution (purple) and iteration (red) time for solving the linear PBE, compared to execution (orange) and iteration (blue) time for solving the nonlinear PBE. (b) Speedup (red) and efficiency (purple) achieved by solving the linear PBE, compared to speedup (blue) and efficiency (orange) obtained by solving the nonlinear PBE. (c) Resulting electrostatic field. (d) Resulting electrostatic potential.

It should be emphasized that the reported parallelization and its implementation in DelPhi are exact. No approximations were made. This is demonstrated by the fact that the calculated potentials and energies are identical for serial and parallelized DelPhi (see supporting information). The importance of achieving exact solution stems from the fact that in many biologically relevant cases the potential and energy differences are of order of several kT/e or kT units or even less. Any assumption may induce an error larger than that, especially if computing large size systems, and thus to obscure the outcome.

It was shown that the parallelization drastically improves the speed of calculations, especially in case of solving non-linear PBE. The case of 1VSZ was purposely included in the testing, although the structure represents only part of the capsid, simply to illustrate a case of highly charged entity with very irregular (different from sphere) shape. This particular case, at the limits of our testing, utilizing 100 CPUs resulted in speed up of 63 for solving non-linear PBE. This illustrates that problems requiring heavy computations will benefit from parallelization substantially. Eqn. (8) provides an efficient formula to estimate the conditions at which the parallel algorithm will be outperforming the serial one. Obviously the cases involving large systems made of protein complexes will be the primary choice of investigation with the parallel DelPhi. In another words, the speedup of the parallel algorithm will depend on the ratio of the CPU time and communication time, as indicated by Eqn. (8). With decrease of the size of the system, as small biomolecules with small mesh, the CPU time will decrease, making the coefficient “r” in Eqn. (8) larger and reducing the efficiency of the algorithm. Because of that, calculations involving small biomolecules are not expected to take advantage of this approach.

Analysis of Figure 2(b) and 3(b) reveals another important aspect of parallelization in case of solving non-linear PB. The speedup is almost linear when running on a small number of processors. It keeps increasing with the increase of processors (up to 100 processors in our test) and even shows potential to increase further since its curve has not reached its peak and flattened out, as pointed out in the Amdahl’s law (introduced in supporting information). The best result we obtained is a speedup of 63 when running on 100 processors to solve the nonlinear PBE for 1VSZ. At the same time, the efficiency decreases slowly when the number of employed processors increases for solving both linear and nonlinear PBE (Figure 2(b) and 3(b)). This observation confirms our previous discussion and reflects the ratio outlined in Eqn. (8). However, one can see that the new parallel method maintains better efficiency when solving nonlinear PBE, because more computations are involved comparing with solving linear PBE. Moreover, Figure 2(b) shows that “super-linear” speedup is achieved when solving nonlinear PBE for 1VSZ on less than 15 processors (see the beginning of the graph when only a few processors are involved in the calculations). It is another indication of the high efficiency of the algorithm.

Figure 1.

Graphical demonstration of an algorithm for parallelizing the iterations in the GS/SOR method uisng MPI-2 DRMA operations. (a) The “checkerboard” ordering. (b) Contiguous memory mapping. (c) Distribution of Φ_even and Φ_odd to multiple CPUs. (d) DRMA to the previous CPU.