Spatial Structure and Lamarckian Adaptation Explain Extreme Genetic Diversity at CRISPR Locus

ABSTRACT

Even within similar bacterial strains, it has been found that the clustered, regularly interspaced short palindromic repeat (CRISPR) shows a large variability of spacers. Modeling bacterial strains with different levels of immunity to infection by a single virulent phage, we find that coexistence in a well-mixed environment is possible only when these levels are distinctly different. When bacterial strains are similar, one subpopulation collapses. In the case of bacteria with various levels of CRISPR immunity to a range of phages, small differences in spacer composition will accordingly be suppressed under well-mixed conditions. Using a numerical model of populations spreading in space, we predict that it is the Lamarckian nature of CRISPR evolution that combines with spatial correlations to sustain the experimentally observed distribution of spacer diversity.

Opinion/Hypothesis

Bacteria have evolved several effective defense mechanisms against their most abundant predators, the bacteriophages (1–4, 25). Among these mechanisms, the bacterial clustered, regularly interspaced short palindromic repeat (CRISPR) phage response system—first discovered in Escherichia coli by Ishino et al. in 1987 (5)—has recently drawn considerable attention (6–16). CRISPR is widespread and present in about half of bacterial genomes. The conditions under which CRISPR allows bacteria competitive advantages over other defense mechanisms are still under investigation (16). Part of the interest in CRISPR is due to its peculiar functioning, where the host first integrates short sections (26 to 72 bp) of the predator’s DNA—so-called protospacers—into the bacterial genome which are later used to inactivate invading phages carrying the same protospacer (17). This reaction to invading elements is unusual, as it may constitute a rare example of Lamarckian evolution (18, 19). Bacterial resistance to the phage is acquired as a product of phage infection and host range changes by mutation. This resistance is subsequently passed on to the offspring. The source of the inherited variation can be contrasted with Darwinian evolution, which is changes in the genome occurring by random mutations, i.e., independent of phage infection.

New spacers are inserted at the leader-proximal end of the CRISPR system (10, 20), implying a larger variety of spacers than at the leader-distal end (15). As spacer diversity diminishes for older and more selected spacers, one is left with the problem of understanding what actually sets the scale for the observed numbers of spacers in bacterial species. This number varies between 2 and 50 but typically is some intermediate value that will be much smaller than the expected diversity of phage species (9, 13). In fact, examination of spacers in geographically separated systems shows that spacer content differs widely. There is considerable variation of spacers in isolates of the same microbial species within habitats, such as Streptococcus strains in human saliva (21) or thermophilic Synechococcus sampled from hot springs (22). Many of the sampled spacers are found to be unique (only sampled once), and only a few have homologs with known viruses. Heidelberg et al. suggested that either the apparent diversity could be attributed to a very large diversity of the phage population—essentially overwhelming the CRISPR system—or that the CRISPR response to viral attacks could be very fast and very localized to the level of the microniche (22). While both explanations are reasonable, the former would be harder to reconcile with CRISPR as an effective system of defense against phages (20), as the addition of a new spacer would be unlikely to be used subsequently for defense against that particular phage. The latter explanation is in line with a spatially structured system constraining a bacterium’s surroundings and the local phage diversity. Further, these and other studies (23) find spacer content to vary with the geographic location, with a generally stronger overlap of spacers from similar geographic origins. Held and Whitaker (23) have studied the evolution of Sulfolobus islandicus and suggested that their coevolution should be seen in a biogeographic context and migration to play an important role in shaping the observed spatial pattern (24). They further concluded that viruses may benefit from migration, allowing them to escape local host defenses, such as CRISPR. Spacer abundance is accordingly expected to be far too low to give complete immunity and, on the other hand, shown to be exposed to dynamic reshuffling.

Childs et al. (6) introduced a model of phage and bacterial coevolution, with phages characterized by several protospacers and bacteria by a fixed number of spacers. Although only the nonspatial version of the model is studied, it predicts the sustainable coexistence of many strains of phages and bacteria. Strain diversity is maintained by a common evolutionary history where different phage strains typically share several protospacers, making particular spacers sufficient to target a majority of the phage strains. Abandoning the assumption of close evolutionary relationships between phages, we want to explore here how diversity can be sustained and, in particular, to understand why CRISPR systems often have an intermediate number of spacers. As we will see, a spatially distributed system is the key to obtaining both of these characteristics of real-world microbial ecosystems.

MODELING OF CRISPR

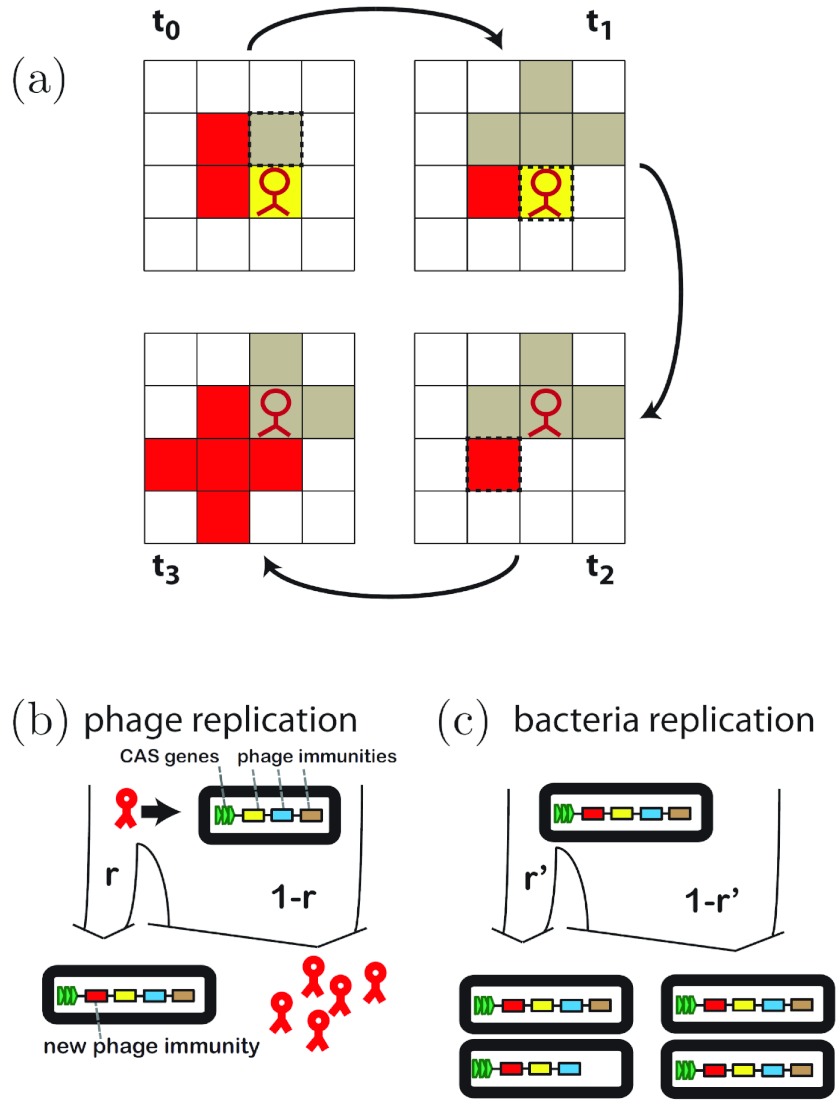
We model a system with a single bacterial species but n_p distinct phage species. To distinguish the latter, a unique index is assigned to each phage species. To describe the spatial CRISPR system, we allow each bacterium to carry a sequence of spacers (modeled by a list of indexes identifying the corresponding phage species) and cost is proportional to n_res, the number of spacers present in the bacterium. The bacterial growth rate is given by the equation 1/(1 + cn_res), with the cost parameter c, and the phage growth rate is unity. Growth of bacteria and phages proceeds as shown in Fig. 1a. Bacteria spread to all nearest-neighbor sites not occupied by phages. If a site is occupied by another uninfected bacterium, it is overwritten. In this way, faster bacteria will gradually displace slower ones. Phage spread only to nearest-neighbor sites occupied by infectible bacteria, i.e., those bacteria lacking the corresponding spacer. At each replication step, the phages at the previous site decay. A spacer is acquired at a fixed rate, r, when a bacterium is attacked by the corresponding phage but lost at a rate r′ upon reproduction (Fig. 1b and c). r′ evolves freely during simulation. In the steady state of a well-mixed system with n_p phage species, a bacterium with n_res spacers would have a probability of δ + (1 − δ)r, with δ = n_res/n_p, of resisting a random phage attack, hence the sum of the probability of having the correct spacer and the conditional probability of acquiring it upon attack. In general, the phage also undergo mutations. We model this by a rate of mutation, r_ph, per replication step. A phage is then assigned a new index and is able to evade the bacterial CRISPR defense. Our lattice model should be understood as a coarse-grained version of the microscopic bacterium-phage community, where a bacterial population at a given lattice site represents a microcolony of bacteria (i.e., 10⁵ individuals). The rate r correspondingly reflects the probability of an individual bacterium within such a microcolony acquiring a new spacer and subsequently replenishing the microcolony with immune bacteria. The insertion rate for a single bacterium was estimated to be 10⁻⁶ (1), resulting in an effective rate of r = 0.1 for a given microcolony. We explore the sensitivity of our results to parameters less constrained by experiments (burst size, phage mutations, diffusion, latency). The update of the lattice proceeds according to a Gillespie algorithm, linear lattice sizes range from 200 to 600 sites, and we treat the system as converged when the population densities stably fluctuate around a mean (the drift has vanished). In the following, we systematically focus our analysis on communities of bacteria and phages in their long-term sustainable state. Transient behavior is explored in the supplemental material (the model code is available at www.nbi.dk/~haerter/mbio/).

FIG 1 .

Schematic of CRISPR model. (a) Example of bacterial and phage spreading on a lattice in four consecutive time steps. Bacteria with distinct CRISPR arrays are shown as colored squares in different shades. Red bacteria are resistant to red phage. Phage are shown as red symbols. Spreading to all available nearest-neighbor sites occurs as follows: t₀ to t₁, brown-shaded bacteria spreading; t₁ to t₂, phage spreading; t₂ to t₃, red bacteria spreading. (b) Upon infection of bacteria, phage generally lyse and produce a number of progeny. At a small probability r, bacteria incorporate a new phage spacer into their CRISPR system (shown as a red insertion at a position closest to the CAS genes). Note that this process lengthens the CRISPR array by one spacer. (c) Replicating bacteria usually produce identical copies of their genomes. At a small probability r[prime], the offspring loses a spacer (note the lack of the brown spacer in the offspring genome).

A WELL-MIXED ENVIRONMENT MAKES CRISPR EVOLUTION DARWINIAN AND INEFFICIENT

The well-mixed model applies to an environment where the interaction between species is random and dependent only on the concentrations of the species. Because of the negative feedback from acquired CRISPR immunity, all species concentrations become roughly equal and we do not obtain large variations in population size (for details, see Fig. S5 in the supplemental material). Hence, the gain from any acquired immunity is ~1/n_p, as in the event of an attack, the probability of the attack originating from any given phage type is equally ~1/n_p.

The overall survival probability is thus δ = n_res/n_p, with n_res the number of spacers in the CRISPR system. Further, subsequent attacks are independent and therefore the bacteria do not “learn” anything when attacked by a phage. The inclusion in or removal from the CRISPR system of a new spacer becomes equivalent to a random mutation that increases or decreases, respectively, the probability of survival of the next attack by 1/n_p, with a rate of spacer acquisition proportional to the product of r and the density of phage species not present in the CRISPR array. In this sense, the evolution of the defense system is reminiscent of a Darwinian system with mutation rates set by the overall phage densities. Simulating this system numerically, we find that bacterial species similar in immunity in fact die out. Only the extremes of immunity (δ = 1 and δ = 0) are possible. As discussed previously (3) and detailed in the supplemental material, a mean-field system with completely resistant and completely susceptible bacteria can coexist with a phage population when resistance comes at a sufficiently small cost. In the case of n_p levels of immunity, intermediate levels of resistance, 0 < n_res/n_p < 1, are unstable and are drawn back to the two extremes, n_res = 0 and n_res = n_p. This is due to the convexity of the growth rate, g(n_res), which has a negative slope as n_res approaches zero but a positive slope as n_res approaches n_p (for details, see the supplemental material: Fig. S1 to S3 and Text S1). For large n_p values, the fully resistant state entirely breaks down.

DARWINIAN ACQUISITION OF IMMUNITY PUSHES FOR EXTREME SPACER NUMBERS IN THE BACTERIAL POPULATION

We have also explored a spatial system where bacteria and phages spread on a lattice but where spacer evolution is Darwinian. In practice, this is simulated by including a random spacer corresponding to one of the existing phages at a given rate—independent of phage attacks. At the same rate, spacers are removed from the host. Also here, the system settles for extreme values of immunity (data not shown), either complete susceptibility or complete defense, depending on the cost. This opting for extremes reflects an inefficiency in acquiring any needed spacer. That is, attempting random spacer insertions and removals is so inefficient that the bacterial immune system is essentially randomized before it acquires a spacer that is needed to survive in a given local environment.

LAMARCKIAN EVOLUTION OF SPATIALLY STRUCTURED POPULATIONS FAVORS INTERMEDIATE SPACER LEVELS

We now consider spreading of bacteria and phage in space (Fig. 1a) and new spacers to be included at the small probability r only when bacteria are challenged by a phage attack (Fig. 1b and c).

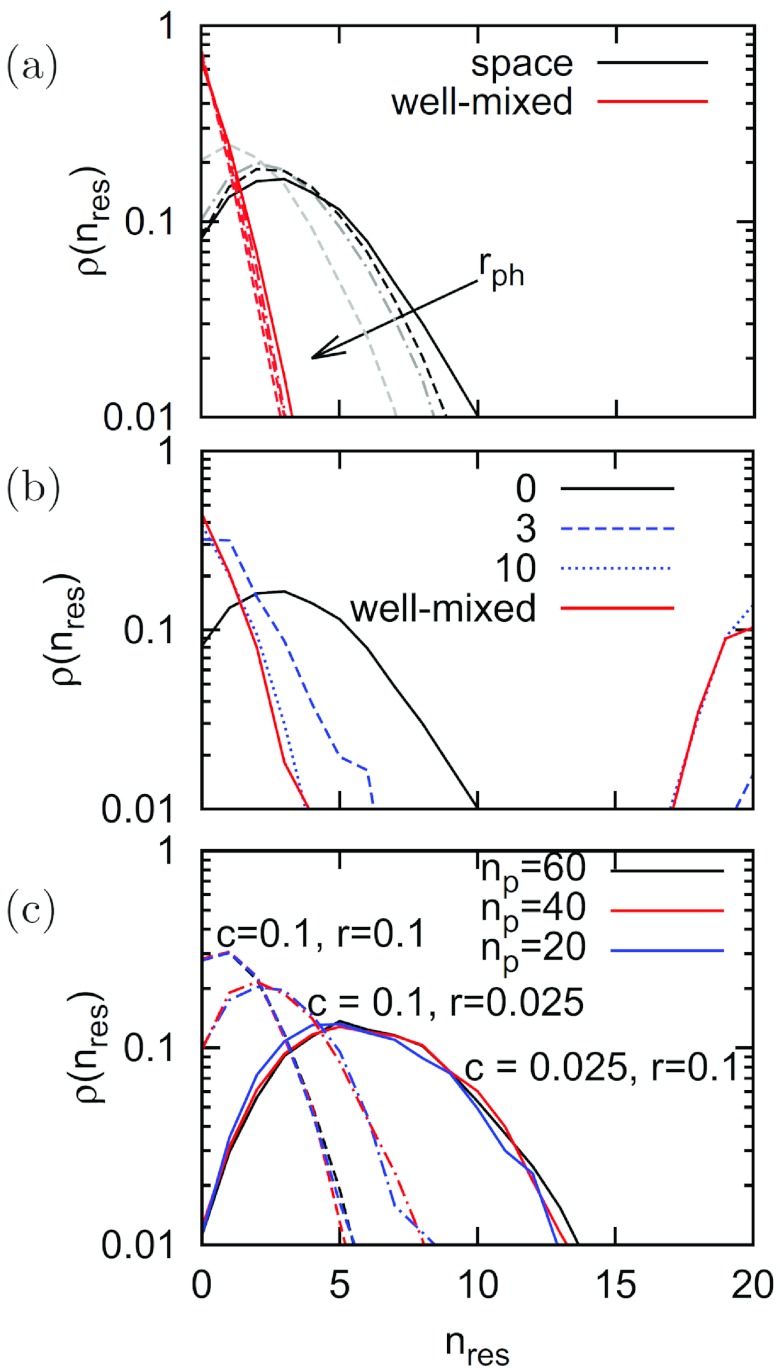
Figure 2a shows a comparison of the well-mixed and spatial systems for various rates of r_ph, including the limit of r_ph → 0. For the well-mixed model, the distribution of spacer numbers is a rapidly decaying exponential with zero as the dominant spacer number; in fact, all curves for different r_ph values collapse into one. In the spatial system, for all values of r_ph, peaked curves result which generally shift slightly to lower values of n_res as r_ph is increased. We use a spacer insertion rate of r = 0.05 but have determined that overall results remain similar for smaller r values as long as the system size is increased appropriately. Concerning the phage mutation rate, then, as long as r_ph is less than r, we also find that space supports a robust distribution of intermediate spacer numbers, whereas the well-mixed system fails to do this. We therefore continue our analysis in the limit r_ph → 0 using values of n_p where none of the phages collapse.

FIG 2 .

CRISPR spacer diversity. Panels show the distributions of spacer numbers. (a) Varying phage mutation rate r_ph in spatial (black and gray curves) and well-mixed (red) systems. r_ph values (0, 10⁻⁴, 10⁻³, 10⁻²) are indicated by the arrow. (b) Varying diffusion but r_ph fixed at 0 and n_p fixed at 20 in a spatial system (solid black line) with diffusion of up to 3 sites (dashed blue line) or 10 sites (dotted blue line) and a well-mixed system (solid red line). L = 200, r = 0.05, c = 0.05. (c) Varying number of phage types, n_p. Different colors correspond to different numbers of phage types, ranging from n_p = 20 to n_p = 60. Shown are three different sets of c and r values. Note the logarithmic vertical axes.

For n_p = 20 (Fig. 2b), we compare the well-mixed and spatial systems when diffusion is varied. The well-mixed system (shown in red) opts for the extremes of immunity, n_res = 0 or n_res = n_p. In contrast, the spatially correlated system (shown in black) favors intermediate values of n_res. Simulations with an intermediate diffusion range behave similarly, demonstrating the robustness of this result as long as phages are allowed to diffuse only a small distance compared to the system size. Our results were also robust upon variations in phage burst latency, as well as phage fitness quantified by the burst size (see the supplemental material).

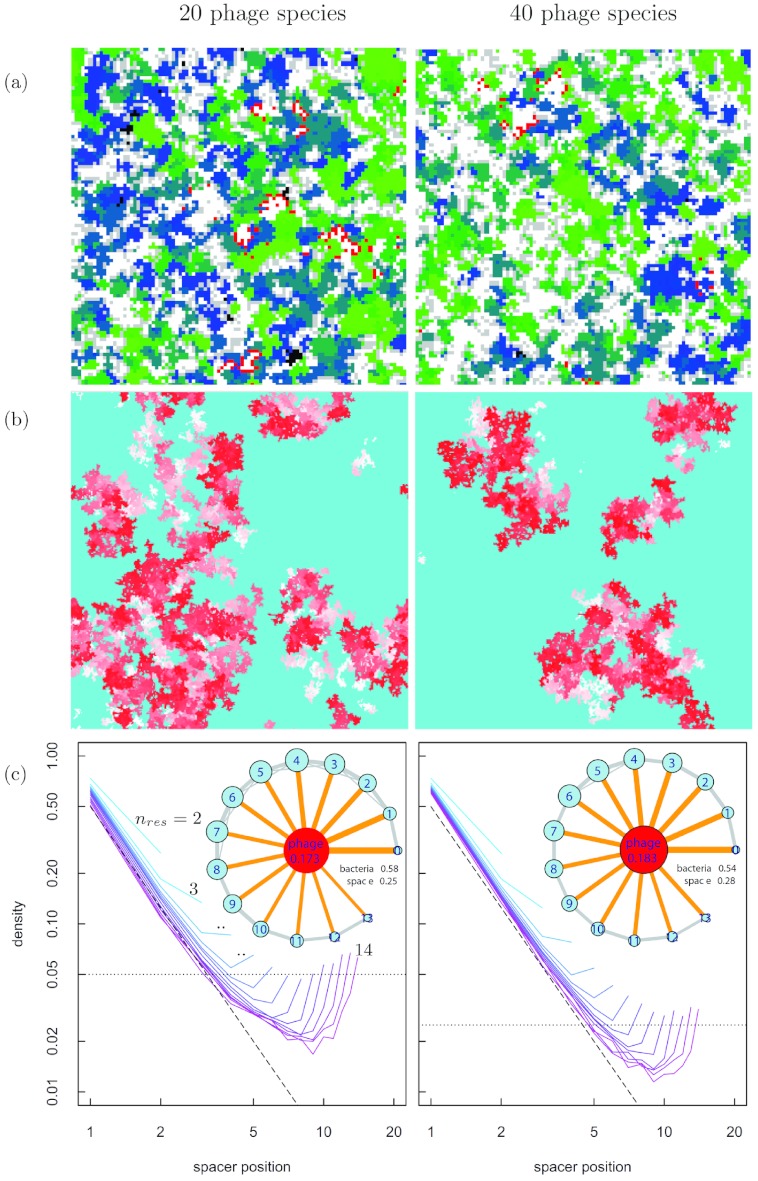
To characterize the spatial effects, Fig. 3a shows spatial plots of the bacterium-phage community in the steady state where 20 distinct phage types are present and the spacer inclusion rate is fixed at r = 0.1. Generally, the bacterial population shows a pattern characterized by patches of bacteria with similar CRISPR spacer numbers (similar colors in Fig. 3a). When comparing the left and right panels (n_p values of 20 and 40, respectively), we find little difference in the general pattern of the bacterial population. The only notable difference is that the phage density of any given type (the one shown in red) changes as the reciprocal of the increase in phage diversity, leaving the overall phage density roughly constant.

FIG 3 .

Phage-bacterium interaction pattern. The left and right columns show images for n_p = 20 and n_p = 40, respectively, c = 0.025, and r = 0.1. (a) Enlarged gridbox (100 by 100) image. One phage species (out of the n_p species present) is shown as red pixels; all others are shown in gray. Shades from green (long) to blue (short) show bacteria with various numbers of spacers. Bacteria shown in black have no spacers at all. (b) Gridbox image (300 by 300) for space explored in time by one phage shown by red shades. Time increases from white (past) to red (present). Light blue is space not occupied by the phage during this time. (c) Frequency of spacer use at a given position in the bacterial CRISPR system for c = 0.025 and r = 0.1 for different CRISPR array sizes. Short (long) arrays are shown in blue (purple). Note the log-log axis scaling. Insets in panel c show corresponding species interaction graphs of self-organization in space. The blue (red) circles represent bacterial subpopulations with spacer array lengths indicated by the values (phage population), and circle area corresponds to population size. Links correspond to the strength of the interaction between two populations.

PHAGES CLUSTER TOGETHER WITH WEAK BACTERIA, WHILE BACTERIA CLUSTER TOGETHER WITH BACTERIA WITH SIMILAR SPACER NUMBERS

The structured spatial pattern (Fig. 3a) can be characterized by determining the neighborhood of each bacterial subpopulation and the phage population (Fig. 3c, inset). Bacteria tend to organize in the neighborhood of other bacteria with a similar spacer number, and interactions between those very different in immunity are, in fact, rare. Thus, while bacteria similar in immunity repress each other in a well-mixed system, they cluster together in a spatially structured system. The phage cluster most strongly near bacteria with weak immunity, as strong immunity leads to a feedback upon phage presence, diminishing the phage population in their neighborhood.

SPACER DIVERSITY IS ROBUST UPON CHANGES IN COST, INSERTION FREQUENCY, AND PHAGE DIVERSITY

To systematically explore how spacer diversity depends on the model parameters, we now consider changes in r, c, and n_p (Fig. 2c). First, we find that smaller r values—hence, less frequent additions to the spacer sequence—favor more spacers with more immunity, as new immunities are not easily acquired. Second, lower cost of spacer additions also stretches the distribution function; while the benefit of many spacers may be low, acquiring them at a low cost can still be beneficial. Third, and perhaps most interestingly, varying n_p appears to have very little consequences for the shape of the distribution function, a result that also is reflected in a remarkable robustness upon variations in phage fitness (see Fig. S4 in the supplemental material). The last result may seem surprising, as higher n_p values could mean that phage diversity—both globally and locally—becomes larger. However, when we consider the space explored by a given phage type at a given time (Fig. 3b), it becomes obvious that phages in a large-n_p environment spread substantially more slowly to other parts of the system. Hence, the likelihood that a susceptible bacterium will encounter this phage is reduced by the same amount.

Another perspective on the origin of the self-organized spatial heterogeneity is obtained when we keep track of how frequently a spacer at a given position within the CRISPR array is used (Fig. 3c). Considering that a recently incorporated spacer has been triggered by phages in the neighborhood, it seems intuitive that spacers close to the CAS genes (at the beginning of the array) are more frequently used. This is shown in Fig. 3c, where the usage frequency falls off rapidly after a short distance along the CRISPR array. A somewhat peculiar feature of these curves is that they exhibit a slight increase toward the end of the array length. Imagine a bacterial population with a given spacer length with immunity to a given phage but with a location of the immunity close to the CRISPR array end. Eventually, by random loss of spacers, some of the individuals in this subpopulation will again become vulnerable to the phage. In this instance, the bacterium that has not yet lost its final spacer will undergo increased attacks by this phage.

CONCLUSION

The bacterial CRISPR defense system is fascinating as it appears to constitute Lamarckian adaptation, in the sense that a host picks up an appropriate response to a predator when challenged by it. We suggest that in models of well-mixed systems or systems with random (Darwinian) mutations, the observed spacer diversity breaks down and only extremes—i.e., complete or absent immunity—prevail. Both outcomes do not represent the observed spacer number variation seen in nature and in experiments.

Using a simple spatial model of spacer diversity in the bacterial CRISPR defense system allowing for spacer additions upon phage encounter and assuming that removals are caused by random evolutionary processes, we find that the ecology self-organizes to a state with a large diversity of spacer numbers. This diversity is a consequence of the Lamarckian aspect of the CRISPR mechanism as the process of spacer addition and removal naturally leads to clusters of defense- and replication-focused bacteria, respectively. A constant cycle of spreading, attack, defense, and again replacement by faster bacteria results. In a sense, a hierarchy of subpopulations self-organizes, with fast-growing yet less-protected bacteria being quickly depleted when phage are present but overrunning slower, more phage-protected bacteria when phage are absent. Our simulation suggests that self-organization of bacteria in space yields a diversity of spacer numbers, with intermediate spacer numbers most frequent, in accordance with previous observations (9, 13). Spacer numbers were found to cluster broadly around a mean of 20 or 30 spacers with a standard deviation of about half the mean. There were very few extreme spacer numbers, just as found in our simulations. In the real community, the cost of acquiring a spacer may be substantially smaller than in our simulations and the number n_p of distinct phages is likely much larger.

In experimental settings—such as biogeographic studies (21–23)—it may be interesting to use the CRISPR signature present in the bacterial immune system to draw conclusions about the details of the interaction between bacteria and phage. Interestingly, however, in a spatially structured environment, there should be no connection between phage diversity and spacer numbers, and thus, one cannot probe phage diversity by indirect measurements of spacer sequence lengths. Instead, our model shows that spacer numbers may be useful in probing the likelihood of spacer insertions and the cost associated with having a spacer insertion. Primarily, our predictions call for long-term evolutionary experiments comparing spacer sequence distributions in well-mixed versus spatially structured environments.

SUPPLEMENTAL MATERIAL

Figure S1

Bacteria with imperfect immunity. (a) Densities of susceptible (solid black lines) and resistant (dashed blue line) populations as a function of the cost difference Δc for various values of δ. Bold (thin) lines correspond to δ = 1 (δ = 0.6). Decreasing δ implies less immunity of the resistant (R) bacteria (lower survival chances) upon phage attack. (b) Well-mixed state coexistence diagram for δ and Δc. The areas marked R and S show parameter ranges with only resistant and susceptible bacteria, respectively; the shaded area marked R+S shows the coexistence regime. The inset in panel a shows a schematic of the interaction of susceptible (S), resistant (R), and infected (I) bacteria. Arrows indicate activation of species, blunt arrows indicate repression. Labels on arrows indicate rates. Download Figure S1, EPS file, 6.2 MB.

Figure S2

Growth rate g as a function of n_res for a single bacterium. The solid line shows g(n_res) for a given combination of c and n_p. The dashed (dotted-dashed) curve is similar but for half (1/10) of the cost; i.e., increasing cost enhances the separation of the absorbing states, while no cost would allow bacteria to migrate freely. $n_0=\sqrt{(1+{cn}_p)-1/c}$ indicates the resistance at the minimal growth rate. Download Figure S2, EPS file, 1.9 MB.

Figure S3

Transient behavior. Parameters: r = 0.05, r_ph = 0.0001, c = 0.05, L = 150. The time dependence of n_res (bold lines) and n_p (thin lines) is shown. For the well-mixed system, dashed crossed lines indicate the time point and corresponding value of n_p when n_res begins to decrease; i.e., the CRISPR system becomes too inefficient. Time is in units of system updates. Download Figure S3, EPS file, 3.2 MB.

Figure S4

Variations in the fitness of bacteria and phage. Parameters: r = 0.05, r_ph = 0.001, c = 0.05, L = 150. (a) Snapshot image of the state of the bacterium-phage community, similar to Fig. 3a but with phages shown in shades of red with larger p_bs (the phage burst size probability) shown as brighter red shades. Shades of black, blue, and green indicate increasing numbers of spacers. (b) Probability distribution functions of n_res for p_bs = 1 (dashed) and a variable p_bs (thin solid). (c) Transient behavior of n_p including variations in p_bs. Bold red (black) lines show n_p for the well-mixed (spatial) system with an evolving p_bs. Light red and gray lines show corresponding data for p_bs = 1. Time is in units of system updates. (d) Probability density functions of p_bs for phages. (e) Same as panel c but for mean spacer numbers n_res. (f) Same as panel d but for p_bs in host spacer count. Note the logarithmic vertical scales in panels b, d, and f. Download Figure S4, EPS file, 7.2 MB.

Figure S5

Fluctuations of phage species densities. Different columns show time dependence in units of system updates (histograms of population densities) for system size as labeled above the plot. Colors in time-dependent panels from red to blue distinguish different phage species. The mean of all phage species is shown as a gray curve. Parameters: r = 0.1, c = 0.1, n_p = 20. (a) Well-mixed system. (b) Spatial system. (c) Same as panel a but without CRISPR. (d) Same as panel b but without CRISPR. Note the logarithmic vertical scales in the histograms. Download Figure S5, EPS file, 13.8 MB.

Text S1

Supplemental methods. Download Text S1, PDF file, 0.1 MB.