Toward structure determination using membrane-protein nanocrystals and microcrystals

Abstract

Membrane proteins are very important for all living cells, being involved in respiration, photosynthesis, cellular uptake and signal transduction, amongst other vital functions. However, less than 300 unique membrane protein structures have been determined to date, often due to difficulties associated with the growth of sufficiently large and well-ordered crystals. This work has been focused on showing the first proof of concept for using membrane protein nanocrystals and microcrystals for high-resolution structure determination. Upon determining that crystals of the membrane protein Photosystem I, which is the largest and most complex membrane protein crystallized to date, exist with only a hundred unit cells with sizes of less than 200 nm on an edge, work was done to develop a technique that could exploit the growth of the Photosystem I nanocrystals and microcrystals. Femtosecond X-ray protein nanocrystallography was developed for use at the first high-energy X-ray free electron laser, the LCLS at SLAC National Accelerator Laboratory, in which a liquid jet brought fully-hydrated Photosystem I nanocrystals into the interaction region of the pulsed X-ray source. Diffraction patterns were recorded from millions of individual PSI nanocrystals and data from thousands of different, randomly oriented crystallites were integrated using Monte Carlo integration of the peak intensities. The short pulses (~ 70 fs) provided by the LCLS allowed the possibility to collect the diffraction data before the onset of radiation damage, exploiting the diffract-before-destroy principle. During the initial experiments at the AMO beamline using 6.9-Å wavelength, Bragg peaks were recorded to 8.5-Å resolution, and an electron-density map was determined that did not show any effects of X-ray-induced radiation damage [Chapman H.N., et al. Femtosecond X-ray protein nanocrystallography, Nature 470 (2011) ^73–81]. Many additional techniques still need to be developed to explore the femtosecond nanocrystallography technique for experimental phasing and time-resolved X-ray crystallography experiments. The first proof-of-principle results for the femtosecond nanocrystallography technique indicate the incredible potential of the technique to offer a new route to the structure determination of membrane proteins.

1. Introduction

1.1. Structural biology and the quest to solve life's mysteries

The structure and function of molecules are intimately related at the atomic and molecular levels. The desire to determine the structure of matter in order to infer the mechanisms and pathways has been a large motivational force in the disciplines of physics, chemistry, and biology. For instance, the structures of inorganic and organic molecules offer insights into catalysis and reaction pathways, and the information can be used to elucidate the action of drugs [1], or the potential environmental impact of an organometallic molecule [2], as two examples.

The biomacromolecules are the facilitators of life. Thereby the structure determination of biomacromolecules is one important clue to help understand the complexity observed in life. Whether the desire is to understand cellular respiration, nutrient uptake and transport by a cell, or various other cellular functions, one focus is to determine high-resolution structures of the molecules involved. The structure forms the basis to elucidate the reaction mechanisms and understand how the structure relates to the function and the dynamics of the molecules. Studying the structures of proteins by X-ray crystallography [3, 4], electron microscopy [5], electron crystallography [6], and nuclear magnetic resonance (NMR) [7, 8] is well established, with the majority of the 70,000+ structures determined by protein X-ray crystallography [9].

The impact of structural biology on the biological sciences becomes tangible when noting the examples of success for structure determination. One area of study that has seen considerable success through the use of structural biology is oxygenic Photosynthesis [10]—proteins involved in Photosynthesis are also a primary focus in the development of methods for femtosecond nanocrystallography. One breakthrough of X-ray protein crystallography was the structure determination of cyanobacterial Photosystem I [11].

1.1.1. Structure of cyanobacterial Photosystem I

Photosystem I (PSI) is a large membrane-intrinsic protein complex that is responsible for light-induced charge-separation, which transfers an electron from the luminal side to the stromal side of the thylakoid membrane. The electron transfer catalyzed by PSI provides the electrons utilized in reducing NADP⁺ to NADPH in oxygenic photosynthesis [12].

PSI exists in a number of oligomeric forms in nature. In plants, PSI exists as a monomer surrounded by four antenna proteins LHC-(I–IV), whereas in cyanobacteria, PSI exists predominantly as a trimer, but the monomer can be found when cells are grown under high-light conditions; the trimer-tomonomer ratio depends on the light conditions [13]. Cyanobacterial PSI is one of the largest and most complex membrane-protein complex to be crystallized [14] and its structure has been determined to 2.5-Å resolution [11].

The trimeric PSI, as shown in Fig. 1, has a mass of 1,056,000 Da, with each monomer consisting of 12 protein subunits and 127 non-covalently bound cofactors. Trimeric PSI has a diameter of approximately 220 Å and a height of approximately 90 Å, with a stromal hump that extends 40 Å into the stroma of the chlorplasts/ cytoplasm of the cyanobacteria. The cofactor composition in the monomer is 96 chlorophyll molecules, 22 carotenoid molecules, three 4Fe-4S clusters, three lipids, two phylloquinone molecules, and one Ca²⁺ ion [11].

Fig. 1. Structure of cyanobacterial Photosystem I.

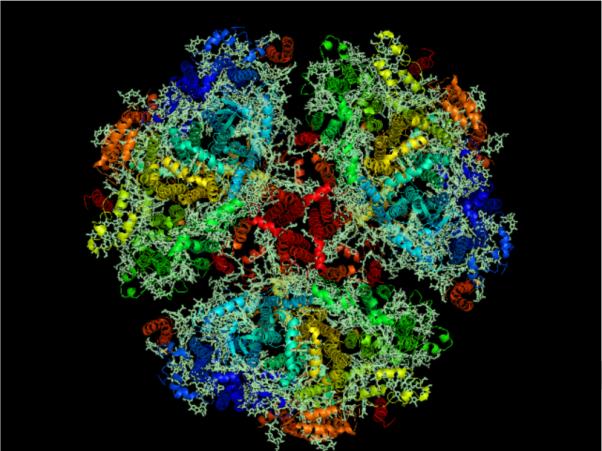
Membrane normal image of the trimeric Photosystem I from cyanobacteria using RSCB PDB (www.pdb.org, [9]) ID 1JB0 at 2.5-Å resolution [11] created using Py-Mol [116]. Cyanobacterial Photosystem I is the largest membrane protein complex solved to molecular resolution.

Overall, the structures of the major proteins involved in oxygenic photosynthesis have been solved using X-ray crystallography. X-ray crystallography does not have size restrictions on the protein of interest, unlike NMR and single-particle electron microscopy, which is one of the reasons for its ubiquitous role in structural biology [15]. Additionally, X-ray crystallography has proven to be an invaluable tool for the determination of the structure of many small molecules, and its extension to the large macromolecules of the cell was inevitable.

1.2. X-ray protein crystallography

1.2.1. Conventional X-ray protein crystallography

X-ray crystallography is the workhorse of structural biology, having accounted for the majority of the biomacromolecular structures determined to date. The power of X-ray crystallography resides in the ability of reproducibly ordered molecules in a lattice to scatter electromagnetic radiation coherently. Coherent scattering implies that the scattered waves have a defined phase relationship, which allows for the addition of the amplitudes of the scattered waves, creating a pronounced effect for the scattered signal [16].

The scattering of X-rays by molecules depends on the atomic number of the atoms incorporated, which corresponds to the number of electrons present. In the forward direction, the limit of the atomic scattering factor as the scattering approaches zero is Z [16]. However, biological macromolecules are composed mostly of H, C, N, O and minor amounts of S and P, with relatively low atomic numbers, causing the scattered intensity to be small. Additionally, unlike in the case of small inorganic or organic molecules, crystals of biomacromolecules contain a large percentage of water, commonly between 30 and 70% of the unit cell volume [17], creating large unit cells with few crystal contact sites. Consequently, in order to record X-ray diffraction to large angles and high resolution, large, well-ordered crystals of proteins are necessary for protein-crystallography experiments, due to the weak scattering of the constituent elements as well as the large unit cell solvent contents.

Photosystem I is used as a model protein for the work presented in this review, and as an example of the power and perils of X-ray crystallography, consider the time associated with the structure determination of PSI from the cyanobacterium Thermosynechococcus elongatus. The first micron-sized crystals of PSI extracted from T. elongatus were reported in 1988 [18]. The first structural model of PSI, based on crystal diffraction to 6-Å resolution, was determined in 1993 [19, 20], followed by a 4-Å structure in 1996 [21] and an improved structure at 4-Å in 1999 [22, 23]. In 2001, the structure of Photosystem I was unraveled at 2.5-Å resolution [11] from cryogenically cooled crystals that were incubated in sucrose before freezing. Therefore, it took 13 years from the growth of the first microcrystals to the determination of the first near-atomic-resolution structure of Photosystem I based on large, well-ordered single crystals under cryogenic conditions [12].

However, PSI is by no means the only membrane protein that has presented challenges during structural determination. The membrane-protein complexes involved in photosynthesis and respiration are studied using X-ray crystallography, and are examples of extremely complex, molecular machines; the proteins involved in these electron-transport chains include the b6f complex [24], the cytochrome c oxidase [25, 26, 27], the bc₁ complex [28, 29], Photosystem II [30, 31, 32], the LHCII [33], and the plant PSI-LHCI complex [34, 35, 36], amongst others. As is the case with PSI, the structures of these proteins have been solved (if solved) using X-ray crystallography by efforts that extend over more than a decade.

Photosystem I remains the largest membrane-protein complex solved to molecular resolution, and the use of X-ray crystallography to determine the structure of such a complicated molecule is a tour de force for the technique. However, the work on the project took the tireless effort, of many dedicated researchers, for over a decade.

A question that needs to be addressed pertains to the causes of the structure determination of a protein taking a decade, or longer. In order to address this question, the difficulties with X-ray protein crystallography will need to be discussed from the general point of view. Besides the problems associated with expression and purification of proteins, the major difficulties of X-ray crystallography are: the growth of large and simultaneously well-ordered crystals of proteins, X-ray-induced radiation damage, and the cryogenic cooling of protein crystals.

1.2.2. Protein crystallization and the necessity for large crystals

Obtaining a suitable crystal for X-ray protein crystallography is the least understood step of the structure determination of a protein [3]. The various properties of proteins allow for more complicated mechanisms of crystal growth with respect to small molecules. Protein molecules are much more complicated in regard to composition, structure, degrees of freedom, surface properties, as well as surface potential, than small organic molecules. Additionally, due to the much larger sizes, proteins have far different transport properties in solution, causing slower crystal growth relative to small organic crystals [37].

Protein crystal nucleation and growth are driven by supersaturation of the protein in solution. One of the difficulties associated with protein crystallization is the need for a much larger supersaturation—the supersaturation is defined as ln(c/s), where c is the concentration and s is the concentration at saturation—than what is typically needed in the case of small organic molecules [37]. The high supersaturation is necessary for the formation of the critical nuclei of the new phase, but high supersaturation is not desirable for the growth of large, well-ordered single crystals. Additionally, multiple protein-replete phases are possible in the case of proteins, such as amorphous precipitates, that are not ordered. High supersaturation will favor the formation of amorphous precipitates, as opposed to crystals due to kinetic factors [38]. An additional result of the high supersaturations used for protein crystallization is that the growth of protein microcrystals is much more common than the growth of macroscopic protein crystals [15]. The difficulties associated with the growth of protein crystals are major issues for protein crystallography because of the weak scattering of the constituents; therefore, much work and extensive optimization is often necessary to grow large protein crystals (if conditions are found at all).

In general, membrane proteins provide greater resistance to structure determination than their soluble counterparts due to difficulties associated with crystallization; although the crystallization of membrane proteins is, in principle, similar to that of soluble proteins, a major difference is that membrane proteins are amphiphilic, having both hydrophobic and hydrophilic domains [39]. Despite their extremely high impact, only four medically relevant human membrane-protein structures have been determined to date, that of a G protein-coupled receptor, the β₂-andronergic receptor [40, 41, 42], Aquaporin-5 [43], and leukotriene C₄ synthase [44], and the dopamine receptor [45]. Much work has been devoted to improving membrane-protein crystallization, including the use of in meso crystallization matrices [46, 47], such as the lipidic cubic phase [48] or the sponge phase [49, 50], and the use of amphipols [51], amongst others. The use of in meso crystallization matrices has shown much promise as an adaptable media for membrane-protein crystallization [52] and the growth of well-ordered membrane-protein crystals, although challenges remain in the optimization of the growth of membrane-proteins that are suitably large and well ordered for conventional X-ray crystallography.

Even when a large protein crystal grows, the crystal will often suffer from large internal disorder, as measured by the mosaicity. In the mosaic model of crystals, a crystal is considered to be composed of smaller mosaic domains, and mosaicity, or mosaic spread, is a term used to describe the degree of angular misalignment of mosaic domains within a crystal [16]. Working from the mosaic domain model, Bragg reflections can be broadened by the finite size of mosaic blocks, the angular misalignment of mosaic blocks, and additionally by variations in the unit cell parameters in different mosaic blocks [53]. However, the mosaic domain model is an incomplete picture in the case of membrane proteins, and if PSI crystals are considered, it is seen that only four salt bridges make up the crystal contacts, which would be a primary cause of misalignment. Misalignment of the unit cells could also occur due to excess surface area with respect to volume, because the molecules at the interface will have a reduced number of crystal contacts. Therefore, two effects can be seen as influencing the mosaicity of the crystal: for large crystals, it is the propagation of slight misalignments in different domains, whereas for small crystals, the increased surface area with respect to volume causes misalignment of a large number of molecules. Regardless of the cause of the internal disorder, the broadening of the reflections by mosaic spread causes the scattered intensity to be subtended over a larger solid angle as shown in Fig. 2. The broadening can result in severe consequences, such as being unable to resolve the high-resolution diffraction spots, making it impossible to evaluate the structure to the maximum resolution recorded in the diffraction pattern.

Fig. 2. Effects of mosaicity.

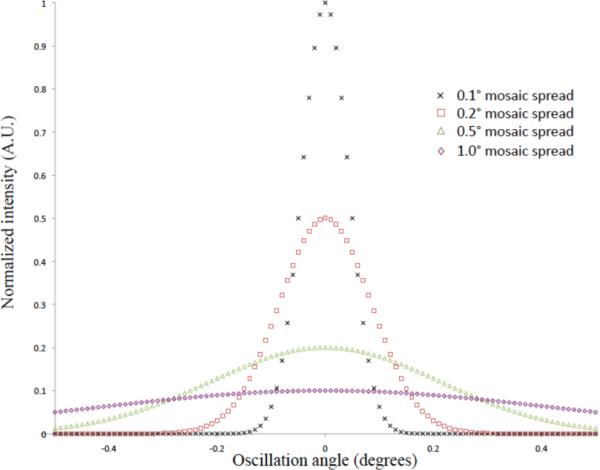
Plot of Gaussian peak profiles showing the effect of increase mosaicity. The mosaicity is defined as the full-width at half-maximum of the peak and is related to the variance by FWHM = 2.3548(σ²)^1/2. The peak height has a linear dependence on the standard deviation of the Gaussian peak. The higher the mosaicity, the lower the peak maximum and the broader the peak width, which can have major implications for high-resolution data.

The theoretical dependence of the scattered intensity on the size of a crystal can be readily understood though the kinematic theory of diffraction. The Darwin equation can be used to calculate the integrated scattered intensity in an X-ray crystallography experiment, when using the oscillation method, and shows the scattered intensity with the following form [54]:

$$I=I_0{r}_e^2\frac{(1-{\cos }^2\left(2\theta \right)){\lambda }^3{V}_x}{2\sin \left(2\theta \right)\omega V^2}{\mid F_{hkl}\mid }^2$$ (1)

in which I₀ is the incident intensity, r_e² is the classical electron radius, (1-cos²(2θ)) is the polarization factor and assumes unpolarized radiation, 2sin2θ is the Lorentz factor, λ is the wavelength, ω is the angular speed of rotation, V_x is the crystal volume, V is the unit cell volume, and F_hkl is the structure factor associated with the particular reflection. From Eq. 1, it becomes clear that the integrated intensity is proportional to the crystal volume relative to the unit cell volume. Consequently, the larger the crystal, without regarding the internal order, the stronger the scattered intensity.

As mentioned already, protein crystallization experiments may result in the production of a shower of microcrystals, without subsequent optimization experiments producing the large, well-ordered protein crystals necessary for data collection at conventional protein crystallography beamlines [55]. However, smaller protein crystals can be beneficial when issues such as high mosaicity or twinning plague the data [56], but the tradeo is weaker scattering. In addition to the weaker scattering provided by a smaller protein crystal, if the crystal is smaller than the X-ray beam focus, then an increased background relative to the signal will also be recorded. One technology development that has increased the usefulness of protein microcrystals for structure determination is the microfocussed beamline [57].

The microfocussed beamline compensates for the weaker scattering of a smaller crystal by increasing the flux density at the sample, I₀ on the RHS of Eq. 1. A (20-μm)³ crystal will scatter 1000× weaker than a (200-μm)³ crystal, which could be compensated for through a 1000× increase in the flux density on the sample by decreasing the focus spot radius by a factor of 1000^1/2 ≈ 31.6. The reduced beam focus will also result in a smaller background scattering from the mother liquor. However, radiation damage becomes a limiting factor in data collection at microfocused beamlines, as discussed in the following section.

1.2.3. Radiation damage and the unending quest to mitigate it

X-ray diffraction is inherently a destructive imaging technique because X-rays are a form of ionizing radiation. Unfortunately, the ionizing nature of the X-rays leads to radiation damage, which along with sample heterogeneity ultimately limits the resolution of a biomacromolecular structure determined using X-ray crystallography [58]. The problem that ultimately arises with the use of conventional X-ray sources to determine a structure is that the smaller the object one wishes to determine the structure of, the smaller the scattering cross-sectional area. Therefore, to obtain enough scattered intensity to high resolution, the total fluence incident on the sample must be increased [59], increasing the risk of X-ray-induced radiation damage and ultimately decreasing the effective resolution of the reconstructed object [60].

There are two types of X-ray-induced radiation damage during protein crystallography: global damage and local damage [61]. Global radiation damage appears quantitatively in the data set and is not associated with any one particular element of the electron density, and can become manifest as a reduced total scattered intensity, increased unit cell parameters, and increased mosaicity of the crystal (or some combination), amongst other effects, but has a dependence on the experimental conditions [58]. Local damage is damage affecting specific sites such as amino acids within the protein structure itself, and is often ascertained when looking at the electron density maps of the structure of interest [61]. An interesting use was found for site-specific radiation damage, in which the information is used to solve the crystallographic phase problem using a technique called Radiation-damage Induced Phasing (RIP) [62].

When protein crystals are irradiated by X-rays, an X-ray can either interact with the sample, or it can pass through without being affected by the presence of the sample. In the case of 12.4 keV X-rays (λ = 1 Å), the wavelength typically used for macromolecular crystallography, only approximately 2% of incident X-rays will interact with a 100-μm thick crystal. Of the interacting 2%, 84% will interact through the photoelectric effect, causing the ejection of photoelectrons. Only 8% of the interacting X-rays will produce elastic scattering events, whereas the remaining 8% will produce inelastic scattering [63]. The relatively low ratio of the scattering-cross-sectional area of the light elements for X-rays with respect to photo-ionization and inelastic scattering is one of the major weaknesses of X-ray crystallography with respect to related electron microscopy techniques [64].

The primary radiation damage occurs due to the inelastic events, i.e. the photoelectric effect and Compton scattering. The photoelectric effect will cause the ejection of energetic (tens of keV) electrons from the K-shells of many of the light elements (and of other shells in heavier metals). The energy deposited by the primary events will cause a cascade of additional photoelectrons, with energies of a few to tens of eV. Possible effects of the primary and secondary damage are the breakage of chemical bonds, oxidation-reduction reactions, the generation of free radicals, and the production of gaseous species. The accumulation of all of the damage at the microscopic level can lead to strain in the crystal and cause distortion of the long-range order of the molecules in a crystal, leading to tertiary damage, or global damage [58].

Cryogenic cooling of protein crystals was developed [65] to mitigate X-ray-induced radiation damage. The vitreous-solvent matrix that is formed does not reduce the number of radicals, but limits the diffusion of the destructive radicals throughout the unit cell and crystal [64]. However, once the use of 3^rd generation synchrotrons became more widespread for structural biology, the high X-ray doses lead to significant damage even under cryogenic conditions; therefore, data sets were still being recorded that were produced from damaged species. That the damage still occurred at cryogenic temperatures could be attributed to the high amount of radicals produced; ultimately there is an absolute limit to the dose a protein sample can tolerate, after which it requisitely deteriorates due to the detrimental effect of the large amount of radicals. The effects of the damage would ultimately be manifest in the degradation of the diffraction pattern, which is the global damage [66]. From cryogenic electron microscopy, the tolerable dose for a protein crystal—defined as the absorbed energy necessary to reduce the total scattered intensity to a value of 0.5 the initial value—was calculated to be 20 MGy [67]. More recently using synchrotron radiation, the number was empirically determined to be 42 MGy [68], but the authors recommended that data collection should cease once the scattered intensity decreased by a factor of ln(2) = 0.693 from the initial scattered intensity, which corresponded quite well with a 30 MGy limit.

Unfortunately, specific local damage, situated on individual amino acid residues, or at specific sites, can start well before the global damage thresholds are reached [58, 68]. In the case of Photosystem II, individual structure elements that are prone to oxidation-reduction chemistry—one prominent example is the Mn₄CaCl of Photosystem II that catalyzes the oxidation of water—could be damaged with much lower doses [69]; thereby, the allowed dose will depend very specifically on the biomacromolecule of interest; metal containing proteins; proteins with more radiation-damage susceptible amino acids in the catalytic site, solvent exposed, or at crystal contacts; as well as proteins with solvent exposed disulfide bridges, should have the data collection strategy carefully considered at reduced dose limits [58]. A (very general) rule of thumb for proteins that can be used is that for every 1 Å of resolution in the structure, 10 MGy can be absorbed, such that for a 3-Å structure, 30 MGy can be absorbed [59]. It should be noted, however, that photoreduction of metals can occur from a dose that is one to two orders of magnitude lower than the 30 MGy limit [69], and consequently, the rule of thumb from above should be applied cautiously and only for proteins that do not contain significant amounts of metals or cofactors that would increase the damage.

Ultimately, the use of cryoprotectants to avoid cubic ice formation can prove problematic. The addition of the cryoprotectant will change the properties of the solution and could lead to dissolution of the protein crystal, or in some cases, lead to the cracking or breaking of a protein crystal. A suitable cryo-solution must first be found for the crystal, typically the mother liquor plus an anti-freeze chemical such as glycerol, sucrose, and the lighter PEGS, amongst others; the anti-freeze agent should not dilute the concentration of the precipitant components, but replace the water of the solution instead [70]. The concentration of the anti-freeze agent must be tested to determine the necessary concentration to avoid cubic ice formation, which involves the collection of diffraction patterns of the cryogenically cooled solution in a loop [71]. If the protein crystal is not grown in conditions with suitable levels of cryoprotectants in the motherliquor, the time allowed for incubating the crystal in the cryo-solution must be determined empirically. Short incubations-such as through dragging a crystal through a cryo-solution-can minimize the degradation of the crystal by the cryoprotectant but may not allow for osmotic equilibration, whereas longer incubation times allow for osmotic equilibration but also have the potential for more damage to be done to the crystal by the cryoprotectant [70]. As seen from the above discussion, determining a proper cryogenic cooling protocol may be a daunting undertaking.

As can be seen, much effort is devoted to the minimization of radiation damage. Cryogenic cooling of protein crystals and the use of microfocused beams can allow for less of the crystal to be inundated with damaging X-rays, which allows for the frequent shifting of the crystal during data collection to unexposed regions. In sum, the main difficulty with X-ray protein crystallography emanates from the fact that X-ray diffraction is inherently a destructive structural determination technique.

1.3. Objective and Hypotheses for Nanocrystallography

The predominant hypothesis of the new concept of nanocrystallography was that the membrane protein microcrystals, which are more commonly found in protein crystallization screens than protein macrocrystals, could be used to determine high-resolution structures of membrane proteins. However, the membrane protein microcrystals could not be used with the currently available third-generation X-ray sources in a traditional single-crystal experiment, as X-ray-induced radiation damage becomes the major problem. Consequently, the main objective of the nanocrystallography project is to determine whether microcrystals of membrane proteins can be used to obtain molecular, or even atomic, resolution diffraction patterns. For the work, the intrinsic membrane protein Photosystem I was chosen as a model system.

1.3.1. Challenges Associated with Nanocrystallography

Questions and challenges that immediately arise from consideration of nanocrystallography involve protein crystallization, sample introduction, data collection, data analysis, as well as radiation physics and chemistry. Decades of work on protein crystallization were done to take the crystallization conditions that produced microcrystals and to generate macrocrystals from adjacent areas of the crystallization phase diagram. One major challenge was in determining the reproducibility and quality of protein microcrystals and to investigate the production of protein microcrystals. Since microcrystals of proteins were always (only) considered a stepping stone toward the generation of macrocrystals, the prevalence of formation was never thoroughly evaluated. An additional question to address was how small the membrane protein crystals can be, while still exhibiting enough order to be useful in a crystallographic experiment, and how could the nanocrystals be observed and measured. Additionally, the data quality of diffraction patterns and the merging of data from different crystals needed to be assessed. Most importantly, the way to arrive at high-resolution data that was not encumbered by data from damaged samples needed new, innovative ideas.

sectionPreparation of nanocrystals and microcrystals of PSI One of the first experiments initiated was to test the production of microcrystals of PSI, in order to gain insight into the prevalence, reproducibility, and quality of membrane-protein microcrystals.

1.4. Photosystem I purification and crystallization

Photosystem I (PSI) is isolated from the thermophilic cyanobacterium Thermosynechococcus elongatus and crystals are grown as described previously [14]. The cells are grown under low-light conditions allowing for a higher yield of trimeric PSI. The cells are harvested and lysed using a microfluidizer, and the PSI-containing thylakoids are cleaned by three centrifugation washing steps. The protein is solubilized by addition of 0.6% (m/v) N-dodecyl-beta-maltoside (βDDM) and purified using ultracentrifugation and anion-exchange chromatography. The eluent solutions for the chromatography consist of 20 mM MES pH 6.4, 0.02% (m/v) βDDM, and concentrations of MgSO₄ varying between 100 and 150 mM.

Photosystem I is crystallized by decreasing the ionic strength of the solution. This method is often referred to as the reverse of ”salting in” of the protein. The decrease of the ionic strength leads to a depletion of counter ions from charged groups at the surface of the protein, which lowers the solubility of the protein. Under low ionic-strength conditions, direct contacts of negatively and positively charged surface groups of adjacent protein molecules are facilitated, which could lead to the formation of crystal contacts.

Fractions containing the PSI-trimer peak from all FPLC runs are collected and concentrated using a 400-mL, stirred, ultrafiltration-unit concentrator (Stirred-cell model 8400, Millipore, Part No. 5124) using a 100-kDa-cuto membrane (Ultrafiltration Membrane Disc Filters, Pall Life Sciences, Part No. OM100076) at 4°C with gentle stirring, using less than 5 psi of pressure². Small amounts of the filtrate are taken and examined visually at different time points for green color. The sample is concentrated and subsequently diluted through the dropwise addition of a buffer containing 0 mM MgSO₄ to a MgSO₄ concentration between 4 and 12 mM, using a conductivity meter and a standard curve to determine the initial salt concentration.

The concentration of the PSI is determined through a chlorophyll assay, done in triplicate, by adding a small aliquot of the protein solution (0.5–5 μL, depending on the protein concentration) to an 80% (v/v) acetone in water solution. The chlorophyll is extracted into the acetone, and the absorbance of the chlorophyll-containing, acetone solution between 400 and 800 nm is measured. The following formula is used to calculate the chlorophyll concentration:

$$C_{\mathrm{Chl}}=\frac{A_{664}-A_{710}}{76780\left(M^{-1}{\mathit{cm}}^{-1}\right)\cdot l}\cdot \frac{1000\left(\mu L\right)}{V_{\mathrm{sample}}}$$ (2)

where C_Chl is the chlorophyll concentration of the sample in molar, A₆₆₄ and A₇₁₀ are the absorbance measurements at 664 nm and 710 nm, respectively, l is the path length in centimeters, 76780 M⁻¹cm⁻¹ is the molar absorption coe cient at 664 nm wavelength of chlorophyll in acetone [72], and V _sample is the volume of the sample, in microliters, used in the chlorophyll assay. The chlorophyll concentration is taken as the mean value of the three measurements produced by Eq. 2.

After diluting the salt, the protein is slowly concentrated to a chlorophyll concentration of 5–12 mM, with gentle stirring at 4°C, inducing crystallization at low ionic-strength conditions using a technique called ultrafiltration crystallization, shown schematically in Fig. 3. The PSI crystals are allowed to grow overnight.

Fig. 3. Schematic phase diagram of Photosystem I.

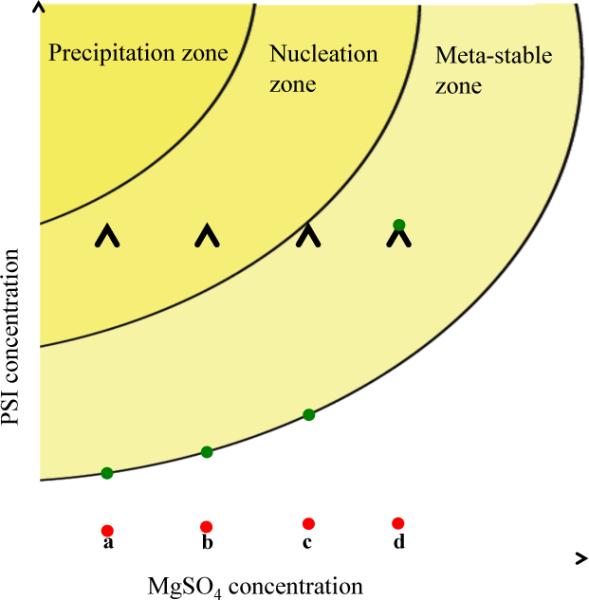
Schematic phase diagram of Photosystem I showing the ultrafiltration crystallization method. Lines a–d indicate different starting MgSO₄ concentrations for the crystallization experiments, in which the red circles indicate the starting position of a crystallization experiment and the green circles show the equilibrium positions of the sample in the phase diagram. The crystallization experiments (a,b,c) would lead to a shower of crystals and crystallites, whereas (d) would need further concentrating to produce crystalline sample. (a) would produce the conditions that led to the largest number and fastest growing crystals, whereas (c) would produce the smallest number of crystals that grew slowly comparative to (a).

The Photosystem I crystals are harvested from the membrane and 1-mL aliquots of the crystal suspensions are placed into 1.5-mL, reaction vessels forx fractional-sedimentation experiments. The crystals are washed using a bu er containing 3 mM MgSO₄, followed by two washes with a buffer containing 0 mM MgSO₄.

The PSI-crystal samples are re-suspended, and after 10 minutes the supernatant is carefully removed from the settled pellet and placed into a new 1.5-mL, reaction vessel, with gentle mixing. After 20 minutes, the supernatant is again removed from the settled pellet and placed into a new 1.5-mL, reaction vessel. This procedure is repeated for 30 min, 40 min, and 60 min settling steps. The settled crystals are combined into 1–3, 1.5-mL reaction vessels, and a 500-μL aliquot of a buffer containing 0 mM MgSO₄ is placed above each pellet; the pellets are stored at 4°C.

1.5. Results of the PSI purification and crystallization

The ultrafiltration crystallization method was used because it would intrinsically produce a large size distribution of PSI crystals. Images of the PSI crystals contained within the pellet of each fractional-sedimentation time point are shown in Fig. 4. The size distribution of the crystals in the pellet remaining after each settling experiment can be estimated. In the 10-min settled crystals of Fig. 4a, the size distribution is measured to be 2–100 μm in size, whereas in the 20-min PSI crystals of Fig. 4b, the size distribution is measured as 2–30 μm in size. The size distribution of the 30-min settled PSI crystals of Fig. 4c is measured to be 2–20 μm in size, and the size distribution of the 40-min settled PSI crystals of Fig. 4d is measured to be ≤ 2–5 μm in size.

4. Ultrafiltration crystallization results for PSI.

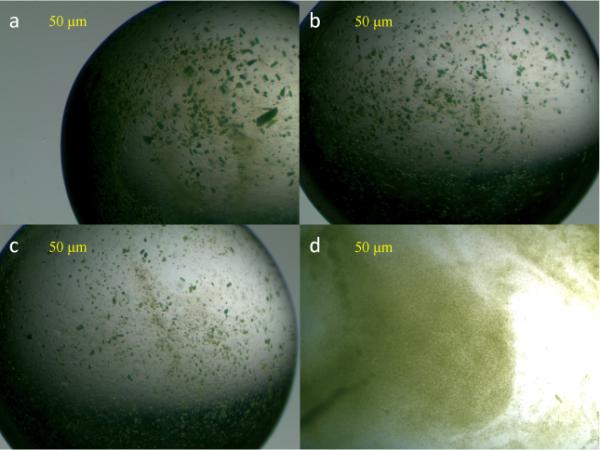
Images of the crystals contained within the Photosystem I crystal suspensions after the solution is allowed to settle for 10 min (a), 20 min (b), 30 min (c), and 40 min (d).

Unfortunately, it was not clear what the size distribution, smallest size, or quality of the PSI samples made were, and the only method available at the time to study these characteristics of the samples was X-ray diffraction. However, we were interested in the smallest crystals, and consequently, only the most intense X-ray sources could be used to measure signal to high resolution. The most intense conventional X-ray sources are the third-generation X-ray sources, but novel sample introduction techniques were necessary due to X-ray-induced radiation damage.

2. Serial crystallography and liquid jets

Third-generation X-ray sources, which refer to storage rings that utilize insertion devices such as undulators and wigglers, have revolutionized X-ray experiments in many fields of science. One prominent example of the influence of third-generation X-ray sources is X-ray protein crystallography. X-ray sources are usually described in terms of the brilliance (photons s⁻¹ mm⁻² mrad⁻² /0.1% bandwidth) of the source, which is a measure that takes into account many properties of the X-ray beam, such as photon flux, beam divergence, and bandwidth, and can succinctly be interpreted as a measure of the quality of the X-ray beam. Third-generation X-ray sources offer much higher brilliance than any previous X-ray source, with the APS, Spring-8, ESRF, and PETRA III being examples of third-generation X-ray sources [73]; the higher brilliance allows the use of smaller protein crystals. However, X-ray-induced radiation damage remains a major obstacle, and so the smallest PSI crystals grown using ultrafiltration crystallization method described in the preceding section could not be used in a traditional X-ray crystallography experiment, due to their small size.

One idea presented to avoid X-ray-induced radiation damage using conventional sources is serial crystallography [74]. Serial crystallography proposed the idea that by constantly replenishing a biological sample—in the case of the original paper, it was single biomacromolecules—the X-ray-induced radiation damage was avoided; the idea was that a stream of molecules could be introduced to the source and could diffract before significant radiation damage could occur. Specifically, a jet would be used to introduce the sample to an electron beam—the idea is easily generalized to an X-ray source—and an external alignment mechanism would be used to orient the molecules preferentially, allowing thousands of patterns of identically oriented molecules to be summed up to produce a diffraction pattern.

Sample introduction was key to the serial crystallography idea. The first method tested for sample introduction utilized a Rayleigh jet, in which a glass nozzle was used to produce the jet. A Rayleigh nozzle produces a liquid jet with a diameter equal to the inner diameter of the nozzle and droplets that are approximately twice the inner diameter [75]. However, as the jet diameter needs to be minimal, the inner diameter of the Rayleigh jet must be reduced, leading to issues of clogging. In order to avoid the clogging problems of the Rayleigh jets, a liquid jet system was developed that used a high-velocity accelerating gas to squeeze a liquid into a jet through an aperture [76]. The nozzle—termed a gas-dynamic virtual nozzle—could produce liquid jets from hundreds to thousands of nanometers in thickness [77]. By using a jet to constantly replenish the sample, signal averaging could be used to increase the signal-to-noise ratio of the data and possibly provide high-resolution data that was not plagued by diffraction from damaged species.

3. Serial powder diffraction of membrane-protein nanocrystals

An important initial experiment of the femtosecond nanocrystallography project was to test the reproducibility and quality of membrane protein microcrystals as well as attempting to gain insight into the frequency of occurrence of the submicron crystals. In order to study these aspects of the PSI samples produced using ultrafiltration crystallization, a gas-dynamic virtual nozzle was used to produce a liquid jet of fully-hydrated PSI-crystal sample that was introduced to the soft X-rays of beamline 9.0.1 of the Advanced Light Source (ALS) of Lawrence Berkeley National Laboratory (LBNL) utilizing the technique of serial crystallography (but replacing external alignment mechanisms with the crystallographic alignment within the crystalline samples) [78, 79].

A full description of the experimental setup can be found in [79]. Briefly, the serial powder diffraction experiments were done by using a liquid injector [75] to introduce a sample of fully-hydrated PSI crystals—grown in 6–8 mM MgSO₄—to the 520- or 1560-eV X-rays of beamline 9.0.1 of the ALS. Diffraction patterns were recorded with both an on-axis and off-axis detector, with maximum resolutions in the corners of the detector for the 1560-eV (520-eV) X-rays being 28 Å (84 Å) and 14 Å (42 Å), respectively. For the 1560 eV experiments with an off-axis detector, as many 30-s exposures as possible were taken and averaged together to produce the powder diffraction pattern.

In order to test whether sub-micron PSI crystals exist, 500-nm and 100-nm inline filters were used to restrict the maximum crystal size allowed to proceed into the interaction region. The PSI-crystal samples passed through the 500-nm filter produced measurable diffraction patterns to 28-Å resolution using 1560-eV X-rays on the off-axis detector, the resolution at which the powder lines of PSI crystals would start to overlap due to the large unit-cell volume of the PSI crystals. A PSI crystal passing through a 500-nm filter could maximally have 6000 unit cells, which is nine orders-of-magnitude smaller than PSI crystals used for conventional crystallography. The PSI-crystal samples passed through the 100-nm filter produced measurable diffraction patterns to 51-Å resolution, using 520-eV X-rays, on the off-axis detector; the resolution in the case of the ≤ 100-nm PSI crystals was limited by the small amount of sample used to collect the data. A PSI crystal passing through a 100-nm filter would have less than 100 unit cells. The diffraction patterns collected with an off-axis detector for the 500-nm and 100-nm PSI crystals, crystals referred to as nanocrystals, are shown in Fig. 5 and 6, respectively.

5. Powder diffraction from 500-nm PSI crystallites.

(a) Diffraction patterns from ≤ 500 nm PSI crystals using an off-axis detector to increase measurable scattering angle. The crystals were irradiated with 1560 eV X-rays (λ = 0.8 nm) and had a resolution of 1.3 nm in the upper-left corner. Less than 6000 unit cells are in each of the ≤ 500 nm PSI crystals, yet powder diffraction is seen to 28-Å resolution, at which point the semi-discrete powder rings come a continuous background due to the large unit cell dimensions of photosystem I. Image and caption modified from [79]

6. Powder diffraction from 100-nm PSI crystallites.

Diffraction pattern from 100-nm PSI crystals with an off-axis detector and an X-ray energy of 520 eV (λ = 2.4 nm). The resolution at the corner of the detector is 4.0 nm. Less than 100 PSI trimers are in each crystal. Image taken from and caption modified from [79].

The diffraction patterns shown in Figs. 5 and 6 were radially averaged and the one-dimensional plot is shown in Fig. 7. A very interesting feature of the overlaid plots is that the full-width at half maximum (FWHM) of the peaks is approximately the same for the 100-nm and 500-nm data sets. A Scherrer analysis done utilizing the FWHM of the peaks can estimate the size of the particle producing the powder diffraction patterns [80] and Scherrer analysis of the plots in Fig. 7 indicate that the crystals are the same size in each data set. Originally, it was argued that the (unexpectedly) large peak width in the 500-nm data could be explained by mosaicity effects [79], however, newer data show that the internal disorder of PSI nanocrystals is very small. Therefore the broad powder diffraction rings in the 500-nm patterns could be better explained by the dominance of 100-nm crystals in the 500-nm-filtered sample. This is an area of great interest moving forward.

Fig. 7. Radially integrated PSI powder diffraction patterns.

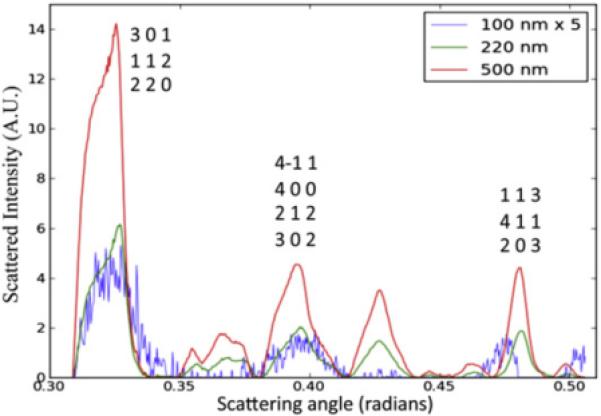
A comparison of the scattering power of the 100 nm, 220 nm, and 500 nm crystals at specific Bragg reflections using the scattered intensity as a function of scattering angle. Figure and caption taken from [79].

The serial powder diffraction experiments revealed the potential of membrane-protein nanocrystals and microcrystals for structure determination experiments, but cannot be used to solve the structures of large proteins directly. Although powder diffraction is a suitable method for structure determination for small molecules, peptides, and proteins, the technique becomes less effective as the unit-cell volume of the crystal of interest increases, due to a loss of information in powder diffraction [81]. This is due, in part, to the reduction of three-dimensional reciprocal space information into one-dimension, i.e., the diffraction data is treated as a function of d alone. In addition to the distinct possibility of peak overlap caused by the large unit-cell volume of typical protein crystals, peak broadening due to instrumental factors, such as beam divergence, energy spread, etc., will add to peak broadening caused by finite size effects and mosaicity effects. As the protein of interest transitions from small, soluble proteins, to membrane proteins and protein complexes, the overlap of the peaks can become an insurmountable factor in the analysis of powder diffraction data. Furthermore, the small spacing of the powder diffraction lines leads to a “continuum” at higher diffraction angles. Therefore, the serial powder diffraction experiments could not be a stand-alone experiment used as a general method for structure determination of membrane proteins using membrane protein nanocrystals and microcrystals, but it will be an effective way to characterize the nanocrystals and microcrystals of membrane proteins moving forward. A single-crystal method would be needed to allow the use of the PSI microcrystals for high-resolution structure determination, and, fortunately, a new type of X-ray source exhibits properties that may allow single-crystal experiments using protein nanocrystals.

4. The fourth-generation X-ray sources

4.1. VUV and X-ray free electron lasers

Recently, fourth-generation VUV and X-ray sources have been designed and built, with noticeable examples being FLASH at Deutsches Elektronen-Synchrotron (DESY) [82], the LCLS at SLAC National Accelerator Laboratory [83], the SPring-8 Compact SASE Source at SPring-8 [84], and the upcoming European XFEL at DESY [85]. The peak brilliance of these fourth-generation X-ray sources, known as the X-ray free electron lasers (XFELs), is up to 10 orders of magnitude higher than the peak brilliance currently available at the most brilliant third-generation X-ray sources [83]. Due to the incredible peak brilliance offered by the XFELs, many new areas of physics and chemistry could be examined with unprecedented spatial resolution.

XFELs involve relativistic electron bunches from a linear accelerator that are compressed in a bunch compressor and fed into a long undulator. In the undulator, X-rays with extremely high brilliance are created by self-amplified spontanteous emission (SASE). To achieve SASE, the XFEL is tuned such that when an electron bunch traverses one period of the undulator, the radiation emitted by the adjacent upstream electron bunch is in phase with that emitted by the downstream electron bunch. The ponderomotive force accelerates those electrons (in the downstream bunch) that are out of phase with the radiation, while decelerating those that are in phase, creating a fine structure of microbunches within the electron bunch. As a result, the spontaneously emitted radiation from the microbunches further amplifies the coherence of the X-ray wavefield, which in turn forces the microbunches downstream in a more well-defined bunch, thus emitting even more coherently. An exponential increase in the spontaneous emission through this resonant process leads to saturation of the XFEL and to the arrival of X-ray bunches of extremely high brilliance at the interaction region [86].

The peak intensity of an XFEL is much higher than that of any third-generation X-ray source and could be of use for X-ray protein crystallography. However, as discussed in Section 1.2, the increased intensity will not solve the problem of X-ray-induced radiation damage. Fortunately, the XFELs offer one important characteristic that may lend itself to mitigation or removal of X-ray-induced radiation damage altogether, the ability to produce ultra-short X-ray pulse durations.

4.2. Diffract before destroy

The X-ray beam produced at an XFEL arrives in pulses with pulse durations related to the electron bunch length in the undulator [87] between several and several-hundred femtoseconds. The time scale of the pulse duration offered by XFELs is on the same (or shorter) time scale as many of the physical and chemical processes involved in X-ray-induced radiation damage, such as the secondary damage pathways. As the secondary events are the main mechanism for the specific damage in X-ray protein crystallography [88], the short time scale of the X-ray pulses may allow diffraction data to be collected before significant damage degrades the crystal and the diffraction pattern.

In the year 2000, a paper was published showing simulations of the damage pathway of a lysozyme molecule in the gas phase that interacts with an intense X-ray pulse from an XFEL [89]. Ultimately, the large positive charge harbored by the lysozyme molecule led to a Coulomb explosion, but the simulations showed that the explosion occurred on the time scale of 5–10 femtoseconds. The simulation results can be interpreted such that if an X-ray pulse terminates before the onset of the Coulomb explosion, all of the diffraction data collected will be without the degraded signal from the damaged sample, which could add significant background to the diffraction patterns. The results led the authors to propose the diffract-before-destroy hypothesis, in which X-ray-induced radiation damage is avoided by the termination of the X-rays used before the onset of the secondary damage processes.

The lysozyme simulation results were published before any VUV or X-ray free electron laser became operational, and so it was not known whether the simulations would be commensurate with experimental data obtained using an XFEL. The first opportunity to experimentally test the diffract-before-destroy hypothesis was when the first VUV free-electron laser, the Free electron LASer in Hamburg Germany (FLASH), started operation in 2005. FLASH offered wavelengths between 47 and 470 Å [90] with the short, 10–50 fs, pulses expected from the upcoming XFELs, with high peak intensities of up to 10¹⁶ W/cm².

Using objects etched into silicon nitride windows, experiments were carried out showing that the diffraction patterns collected from FLASH could be used to produce an undamaged image of the object to 32-nm resolution [91]. Other results from FLASH showed that the presence of a layer of solvation around the sample of interest will cause the Coulomb explosion to be retarded, and the retarded explosion provided evidence that the pulse durations of the XFELs could be longer than the simulation of the gas-phase biomolecule, due to a sacrificial tampering by the solvent layer [92].

Although FLASH allowed for some interesting experiments, the wavelengths offered were too long to be of direct interest to the crystallography community. However, higher-energy free electron lasers, such as the Linac Coherent Light Source (LCLS) at SLAC National Accelerator Laboratory, offered the potential to operate at crystallography-relevant wavelengths. The first lasing of the LCLS occurred in April 2009, and the Atomic and Molecular Optics (AMO) beamline became available to users at the end of 2009 [93]. The initial operation of the LCLS generated X-rays with up to 1800 eV energy (6.9-Å wavelength) with a repetition rate of 30 Hz and a flux of 10¹²–10¹³ photons/pulse.

5. Initial femtosecond nanocrystallography experiments

At this point, the serial powder diffraction experiments had shown that nanocrystals and microcrystals of PSI, as small as a few hundred total unit cells, exist and exhibit enough order to diffract X-rays with measurable Bragg peaks. The preparation of PSI nanocrystals and microcrystals was shown to be reproducible and predictable. The growth of PSI nanocrystals likely indicates that nanocrystals of other membrane proteins can be grown and may even be produced more commonly than microcrystals of membrane proteins.

The motivation behind the initial femtosecond X-ray protein nanocrystallography experiments was to provide a proof of principle of the diffract-before-destroy concept for protein crystallography using membrane protein crystals. The experiments were set up so that one diffraction pattern would be collected from one nanocrystal, as described below. Success with the technique of femtosecond X-ray protein nanocrystallography would provide a new avenue for the structure determination of membrane proteins, offering the ability to use membrane protein crystals of any size for structure determination experiments. Crystals of Photosystem I were chosen as a model system because with a large hexagonal unit cell (a = b = 281 Å, c = 165 Å) and high solvent content (78%), it presents a most stringent test for the analysis of nanocrystals by femtosecond X-ray crystallography.

Three major experiments were done during these femtosecond nanocrystallography studies. The first experiment was to record diffraction data to the highest allowable resolution, of 8.5 Å, and use the data to produce merged intensities, calculate structure factors, and produce an electron-density map of PSI. Complementary experiments were conducted to assess the internal consistency of the LCLS data as well as to compare the LCLS data to conventional X-ray crystallography data for PSI. The second major experiment done was to compare the diffracted intensity for PSI nanocrystals at several different X-ray pulse durations, in order to gain insight into the X-ray-induced radiation damage to the PSI crystallites. The third major experiment was to record the interference patterns around the low-resolution Bragg reflections that are caused by the finite crystal size.

5.1. Preparation of the sample for femtosecond nanocrystallography

The PSI nanocrystal samples used for the first femtosecond X-ray protein nanocrystallography experiments were obtained from two different large-scale PSI preparations, which were completed directly before the LCLS experiments. The PSI nanocrystals from the 40-min settling steps that were used in the experiments were restricted in size by using a 2-μm inline filter; therefore, the PSI nanocrystals contained between 100 and (maximally) 500,000 unit cells for the 2-μm microcrystals. However, there were no visible crystals in the re-suspended sample, and most of the crystals were ≤ 1000 nm in size. It should be noted that even the 2-μm PSI crystallites were between 10⁷ and 10⁸ smaller than the PSI crystals used in conventional crystallography.

Based on crystal-density calculations, the PSI sample was diluted to 1 mg/mL PSI and loaded into the sample line of a dual-line system. The liquid injector was run with a flow rate between 10 and 12 μL/min, and the jet was centered in the X-ray beam by observing a streak on the back detector, due to scattering of the X-rays by the continuous column of the jet. Data for the PSI samples were collected over the course of 48 continuous hours of experiments. Millions of diffraction patterns were recorded, corresponding to 25 TB of data.

5.2. Diffraction experiments

Details of the first femtosecond X-ray protein nanocrystallography experiment, in addition to a full list of acknowledgements, can be found in [94]. Details of the data analysis can be found in [95, 96].

Concisely, the soft X-ray femtosecond nanocrystallography experiment was done by using a liquid jet to introduce a stream of fully-hydrated PSI crystallites to the LCLS—with X-ray pulse durations between 10 and 250 fs and a repetition rate of 30 Hz—at the AMO beamine [97] of the LCLS utilizing the CAMP chamber [98] as shown in Fig. 8. The X-ray energy used for the initial experiments was 1.8 keV (λ = 6.9 Å), and diffraction was recorded on two sets of detector modules: a “front” detector, able to record reflections to maximum resolution of 8.5 Å at the corner, and a “back” detector, able to record reflections between 4000 and 100 Å[94]. During the femtosecond nanocrystallography experiment, one pulse of the LCLS would ideally inundate one PSI crystallite, producing a diffraction pattern recorded on both the front and back detectors that is read out and digitized before the subsequent LCLS pulse arrives.

Fig. 8. Femtosecond nanocrystallography.

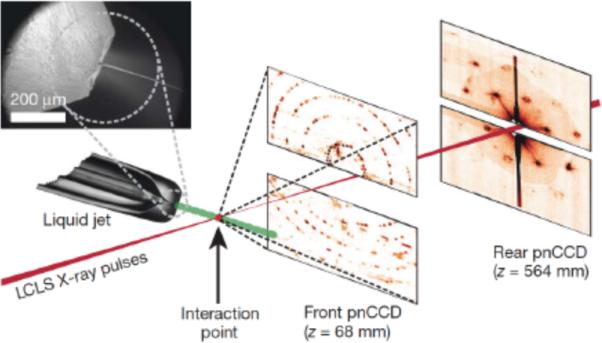
Photosystem I nanocrystals flow in their buffer G₀ in a gas-focused 4-μm diameter jet, perpendicular to the X-ray beam that is focused on the jet. The insert shows an environmental scanning electron micrograph of the nozzle, flowing jet, and focusing gas [76]. Two pairs of high-frame rate pnCCD detectors [98] record low and high-angle diffraction from single X-ray FEL pulses, at a rate of 30 Hz. Crystals arrive at random times and orientations in the beam, and the probability of hitting one is proportional to the crystal concentration. Figure and caption taken from [94] with slight modifications.

5.3. Data processing and analysis of snapshot diffraction patterns

A detailed description of the data analysis of the PSI data from the LCLS is provided in [96], but a brief description is given here. The diffraction patterns were processed by removal of any known bad detector pixels, followed by application of a flat-field correction, normalization of the pixel values with respect to the dark current and gain of the panel, and subtraction of the background. The background was defined as a moving-window selection of 50 frames, with the background for a given pixel defined as the median value over the range [96].

Once the diffraction data were fully processed, indexing and merging of the data were performed. However, for each X-ray pulse, the Ewald sphere would slice through the reciprocal lattice of the PSI crystal in a random position. Due to the sparse population of reciprocal points in the reciprocal space of the crystal system, most scattering would not occur due to the intersection of the Ewald sphere with a reciprocal lattice point. Instead, much of the scattering is due to intersection of the Ewald sphere with the shape transform laid down upon the reciprocal-lattice point. A peak finder was used to establish peaks, and the peak locations were given to MOSFLM [99], using the DPS algorithm [100], or DirAx [101] for indexing. Indexing the patterns would give the orientation of the crystal relative to the lab frame, and could be used for further processing. Each orientation matrix was further refined by a global optimization of the unit-cell constants and three Euler angles [96].

The structure factors extracted from the LCLS data were compared to structure factors extracted from a conventional crystallographic data set of PSI collected at beamline 8.2.2. of the ALS. The conventional data and LCLS data were collected on samples prepared quite differently, as the conventional data originated from a large single crystal of PSI that had been incubated in 2 M sucrose and cryogenically frozen using liquid propane. The conventional data were collected specifically with large working distance and a 100× attenuated beam, so that the low-resolution data were not from saturated detector pixels.

5.4. Femtosecond nanocrystallography results for PSI

A total of 1.85 million “snap-shot” diffraction patterns from PSI were collected at the 70-fs pulse duration. Bragg peaks from the PSI crystallites were recorded to resolution of 8.5 Å on the front detector, as shown in Fig. 9. The diffraction of the nanocrystals was so strong that even saturated peaks appeared occasionally in the diffraction patterns. Unlike in cryo-EM or traditional crystallography, the X-ray diffraction patterns were collected at room temperature, without any crystal mounting, freezing, or cryo-protectants. The diffraction patterns showed well-resolved peaks, and some orientations provided many Bragg peaks per pattern.

Fig. 9. Single-shot crystal diffraction patterns of PSI nanocrystals.

(a, Left) A pattern from a crystal oriented with its c axis almost horizontal, perpendicular to the X-ray beam. (b, Right) Reciprocal lattice planes are seen as arcs, due to the intersection of the Ewald sphere with the lattice. Cuts through the shape transform, due to the finite crystal size, are evident when the intersection of the Ewald sphere with the reciprocal lattice planes is close to tangential, such as the almost continuous lines of intensity in the bottom left of (a) and the spots in the complete circle of reflection in the top left of (b). Figure and caption taken from [94]

A 20% hit rate was achieved by crystal-density calculations. Most of the recorded crystallite diffraction patterns were from one X-ray pulse hitting one nanocrystal, with the patterns on the front and back detectors reading out before the arrival of the next pulse. Fine adjustment and optimization of the crystal density was done based upon the perceived hit rate as determined from the data stream at the LCLS control room.

Of the 1.85 million diffraction patterns of PSI crystallites that were collected at the 70-fs pulse duration, over 112,000 contained ten or more identifiable peaks, of which a total of 28,192 were indexed with unit cell parameters within 5% of the mean values, with a representative image shown in Fig. 10a. Indexing success was strongly correlated to the number of peaks contained within the pattern, as 60% of the patterns containing 75 or more peaks were indexed. However, approximately 42% of indexed patterns were rejected during the intensity-merging steps, due to disagreement between the predicted and observed peak positions. The reason for the disagreement is still unknown, but deviations between the predicted and observed peak positions likely resulted from slight indexing errors that produced large effects at the higher-resolution reflections. In total, 16,374 patterns were integrated and contributed to the structure-factor amplitudes used to produce the PSI structure shown in Fig. 10c [94].

Fig. 10. Indexed diffraction patterns and electron density of PSI from the LCLS data.

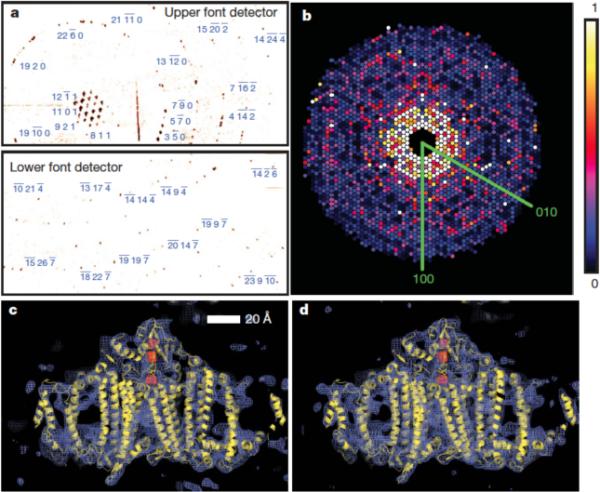
(a) Diffraction pattern recorded on the front pnCCDs with a single 70-fs pulse after background subtraction and correction of saturated pixels. Some peaks are labeled with their Miller indices. The resolution in the lower detector corner is 8.5 Å, (b) Precision-style pattern of the [001] zone for Photosystem I, obtained from merging femtosecond nanocrystal data from over 15,000 nanocrystal patterns, displayed on the linear color scale shown on the right. (c) Region of the the 2mF₀2DF_c electron density map at 1.0σ (purple mesh), calculated from the 70-fs data and (d) from conventional synchrotron data truncated at a resolution of 8.5 Å and collected at a temperature of 100 K. The refined model of PSI is depicted in yellow. Figure and caption modified from [94].

In order to further evaluate the nanocrystallography data to 8.5 Å, rigid body refinement of the published PSI structure (PDB code 1JB0) against the 70-fs pulse-duration nanocrystal structure factors was performed using the program REFMAC [102], yielding R/R_free = 0.284/0.327. In addition, rigid body refinement of the published PSI structure was performed against the structure factors extracted from a higher-resolution single-crystal PSI data set, in which good low-resolution data were measured and collected at beamline 8.2.2 of the ALS. The ALS data set was truncated to 8.5-Å resolution, yielding R/R_free of 0.285/0.298. Figure 10c shows a representative regions of the 2mF₀-2DF_c averaged-kick-map electron density at 8.5 Å from the LCLS data sets. The electron density map clearly show the transmembrane helices, as well as electron density from the membrane extrinsic subunits, and the loop regions are also visible at 8.5-Å resolution. The reference electron-density map shown in Fig 10d was generated using data from a large, single crystal of PSI using 12.4-keV X-rays, with a single crystal of Photosystem I that had been cryogenically cooled to 100 K and had 2.00 M sucrose as a cryo-protectant [94].

The refinement statistics for the PSI electron-density map calculated from the LCLS data are shown in Table 1. The data show good statistics for all categories until the highest resolution shell, in which case the data were measured in the corner of the detectors, causing a reduced number of total measurements, likely contributing to the poorer statistics.

Table 1.

Statistics for the merged dataset of PSI at 70-fs pulse duration R_iso(F) compares the LCLS structure factors to a conventional single-crystal dataset collected at the ALS beamline 8.2.2. The bottom center edge of the bottom detector occurs at a resolution length of 10.0 Å. Table and caption modified from [94]

Resolution shell (Å)	Number of unique reflections	Multiplicity	Completeness (%)	<Peak height/Noise>	Merged I/σ	Riso(F) (%)
30.0	416	1369	100	889	16.8	37.6
16.2	382	1278	100	29.3	15.9	15.1
13.6	362	1195	100	19.2	16.2	12.3
12.1	366	1009	100	20.3	14.7	12.9
11.1	357	678	100	19.5	12.7	14.6
10.4	355	492	100	15.4	10.6	28.7
9.85	349	283	100	14.0	9.20	22.2
9.39	352	111	100	11.8	7.12	28.1
9.01	352	28.6	99.4	9.50	4.99	24.8
8.68	88	3.92	25.1	6.70	3.29	30.8
Overall	3379	717	92.8	123	11.9	22.1

5.5. Comparison of the LCLS data to conventional data

One important comparison required for the new PSI femtosecond X-ray protein crystallography data is with conventional X-ray protein crystallography data of PSI collected at a conventional beamline. The comparison will allow the LCLS data to be compared against the standard for X-ray crystallography.

The LCLS structure factors were compared to structure factors determined from PSI data collected conventionally at beamline 8.2.2 of the ALS, on large crystals at cryogenic temperatures, as a measure of the relative accuracy of the LCLS structure factors. The ALS data were collected using a large, single crystal of PSI that was cryogenically frozen in liquid propane, in which the data were collected to a resolution of 2.3 Å, but the data were truncated at 8.5 Å Å. The overall R_iso between the LCLS and ALS structure factors was 23.5%, indicating the structure factors from the LCLS and ALS data are comparable. The linear correlation coeffcient, C_iso, comparing the LCLS and ALS structure factors for PSI, approached 0.9 around a resolution of 15 Å, and quickly fell o at higher resolutions, again indicating the similarity in the data sets for the resolutions in which a large number of reflections were recorded and processed (for the LCLS data) [96].

Deviations between the LCLS and ALS data sets for PSI were expected. The ALS data were collected on a crystal that was cryogenically frozen and contained 2.00 M sucrose within the unit cell, whereas the LCLS data were collected at room temperature and had no cryo-protectants. The unit cells had slightly different until cell parameters, and in addition, the different wavelengths would produce different scattering and absorption cross-sections. The LCLS data were not processed to take any absorption into account, although at 1.8 keV, the small absorbance correction for the protein crystal and liquid stream may allow for a better comparison between the data sets.

After showing the similarity of the LCLS data and reconstructed PSI electron-density map to the conventional data and resultant electron-density map, it is clear that the LCLS data, to 8.5-Å resolution, is the same—if not better than—the conventional case. That the LCLS data were collected using samples in which the majority of the crystallites could not be seen in a visible microscope is remarkable. This is in stark contrast to the large PSI crystal at a conventional beamline, where crystals larger than 1 mm are used. Yet, the LCLS data is similar to the conventional data to this resolution, indicating that the femtosecond X-ray protein crystallography could help to solve the structures of difficult-to-crystallize membrane proteins.

5.6. The diffract-before-destroy principle and radiation damage

The major reason that small crystals of proteins cannot be easily used in conventional X-ray crystallography experiments is that X-ray-induced radiation damage will ultimately limit the exposure time, thereby limiting the true resolution of the structure. A major premise of the femtosecond nanocrystallography project is that the femtosecond X-ray pulses are as fast as, or faster, than the time scale of the conventional X-ray damage processes, such as disulfide bond reduction, decarboxylation of amino acids, etc. Diffraction patterns were collected with X-ray pulse durations of 10 fs, 70 fs, and 250 fs, in order to compare the effects of the different pulse durations on the quality of the diffraction data.

Examining the electron density maps produced using the structure factors from the LCLS data sets, no specific damage was evident when using the 70 fs pulse durations. However, the onset of damage, when the secondary electrons were spawned, occurs on the 10–100-fs timescale [88]. To assess the damage induced by the XFEL beam, data from 10-fs and 250-fs-duration pulses were collected to directly compare the decay in scattering as a function of time. The 10-fs pulses were operated at a fluence about 10% of the fluence for the 70-fs pulses, corresponding to an absorbed dose of approximately 70 MGy. Fig. 12 shows the integrated structure factors obtained from the three different pulse durations, 10 fs, 70 fs, and 250 fs, using 97,883, 805,311, and 66,063 patterns respectively, normalized with respect to fluence. The plots of the scattering strength of the crystallites versus resolution were generated by selecting and summing Bragg spots from the patterns.

Fig. 12. Pulse-duration dependence of diffraction intensities.

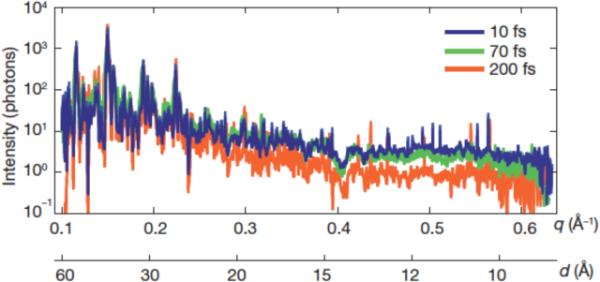
Plot of the integrated Bragg intensities of Photosystem-I-nanocrystal diffraction as a function of photon momentum transfer, q = (4π/λ)sin(θ) = 2π/d, (wavelength, λ; scattering angle, 2θ; resolution, d) for pulse durations of 10, 70 and 200 fs. Averages were obtained by isolating Bragg spots from 97,883, 805,311, and 66,063 patterns, respectively, normalized to pulse fluence. The error in each plot is indicated by the thickness of the line. The decrease in scattered intensity for 200-fs pulses and d < 25 Å indicates radiation damage for these long pulses, which is not apparent for 70-fs pulses and shorter.. Figure and caption modified from [94].

The thickness of the lines in Fig. 12 indicates the uncertainty of each plot. The 10- and 70-fs data sets are indistinguishable, indicating that the 70-fs pulse durations were short enough to avoid global damage to 8.5-Å resolution, relative to the 10-fs pulses. The decrease in integrated scattering intensity for the 250-fs pulses, beyond 25-Å resolution, indicates that the 250-fs pulse duration caused significant radiation damage. The data clearly show the onset of global radiation damage below 8.5-Å resolution occurs at time scales greater than 70 fs.

The dose received by the PSI crystallites was calculated to be as large as 700 MGy using RADDOSE [63] for a fluence of 900 J/cm². The dose of 700 MGy is more than a twenty-fold increase over the damage threshold of 30 MGy from conventional X-ray crystallography [68]. Owen et al. determined the D_1/2 limit of 43 MGy based upon empirical evidence of the totaled scaled-scattered-intensity ΣI_j over all reflections j, which is a measure of global damage. Although 43 MGy corresponded to D_1/2, the authors still concluded that the 30 MGy limit was the safer choice to ensure quality data. 30 MGy corresponded to a decrease in total scaled-scattered-intensity by a factor of ln(2) ≈ 69.3% of the initial total scaled-scattered-intensity in the study [68]. It should be noted that these damage numbers are for cryogenically-cooled protein crystals, and that cryogenic cooling increases the allowed dose by many orders of magnitude [65]. The LCLS experiments were carried out at room temperature; therefore, the stability of the crystals at room temperature, despite the increase in the absorbed dose by a factor of 23 when compared to conventional data collection, is even more remarkable.

The dose of 700 MGy in the LCLS experiment corresponds to K-shell ionization in 3% of all carbon atoms present in the protein molecules. The photoionization process can be considered an instantaneous process and can only be outrun with the shortest pulse durations. The loss of the K-shell electrons would requisitely cause a decrease in scattered intensity, as the X-rays are scattered from electrons in the sample. Consequently, the lack of radiation damage for the 70-fs-duration pulses is only relative to the shorter pulses, because a decrease in scattered intensity must occur due to the initial photoionization events. However, photoionization of K-shell electrons is also a problem in conventional crystallography, but relaxation of the system after the initial excitation by the electrons contributes a much larger effect to the damage than the initial photoionization by itself.

The energy absorbed during the X-ray exposure is released through photoionization and Auger decay, followed by a cascade of lower-energy electrons caused by the secondary electrons on the 10–100-fs time scale [88]. Additionally, simulations using plasma dynamics [103] indicate that each atom of the PSI crystallite was ionized once during a 100-fs interval after initial exposure and that nuclear motion had begun on the 100-fs timescale. A photoelectron produced in these experiments from the K-shell ionization of carbon would have a kinetic energy of approximately (1800 eV – 285 eV) 1500 eV, which could produce hundreds to thousands of low-energy electrons. The secondary electrons and low-energy electrons cause the radiation chemistry to initiate, which leads to specific damage at sensitive amino acid residues/sites. However, redox reactions occur in the ≤ 100-fs timescale and the loss of specific groups from amino acid residues occurs once nuclear motion initiates, which is greater than the 100-fs timescale. It is clearly noted that in conventional crystallography, the specific sample needs to be considered when determining the allowed dose, as the decrease in spot intensity does not give insight into the radiation chemistry occurring. Specific amino acids, such as cysteine, glutamate, and aspartate, are more susceptible to radiation damage than others, and if these radiation-sensitive residues appear in the active site of an enzyme or at the crystal contacts, this could lead to an inability to interpret the electron-density map [63, 104]. Additionally, metal-containing cofactors are acutely prone to local X-ray-induced radiation damage. Using the femtosecond nanocrystallography experiment, consideration of the specific biochemical makeup of the protein may not be necessary, as the experiments are done on a timescale at or faster than the onset of nuclear motion.

The results of the simulations presented in [89] created an expectation that the 70-fs pulse duration data would exhibit some damage effects relative to the 10-fs pulse duration data. The increased time could allow for more Auger relaxation, and secondary ionization events, as well as the Coulomb explosion, which is estimated to begin after just a few tens of femtoseconds [88]. There are multiple possible reasons for the lack of visible radiation damage in Fig. 12 for the 10-fs and 70-fs data. The most immediate reason is that the displacement of atoms in 70 fs is in the sub-Å range and is not visible at 8.5-Å resolution, and therefore the data do not attain a high enough resolution for the increased damage to manifest in the intensity plots of the 70-fs pulses. Another explanation is that the liquid jet surrounding the PSI crystallites acts as a sacrificial tamper for the nanocrystals, in which photoelectrons produced in the stream can neutralize some of the positive charge building up in the sample [92]. One additional explanation is that the nominal pulse durations given are from the length of the electron bunch and that the X-ray pulses are shorter in duration than the electron bunches; simulations of transparency effects in neon using data from the LCLS indicate that nominal 80-fs pulse duration data were more consistent with pulse durations between 20 and 40 fs [87]. Thereby, the lack of damage in the 70-fs data set relative to the 10-fs data set could be attributed to the resolution limit of the data, sacrificial tamper effect of the solvent, or shorter pulses than the nominally reported pulses.

The LCLS experiments collected crystallographic data on PSI nanocrystals at room temperature. The PSI nanocrystals prepared for the LCLS experiments did not require any freezing of crystals, making sample handling much easier. However, cryogenic cooling decreases the temperature factor of the molecules while also (potentially) increasing the internal disorder of the crystal, making the benefit of room temperature diffraction diffcult to quantify until higher-resolution data become available.

5.7. Shape transform results and discussion

Although the diffraction patterns collected on the front detector were used for the integration of the majority of the data used to reconstruct the PSI electron-density at 8.5-Å resolution, the back detector contained a wealth of information as well. In at least one regard, the information collected with the back detector was as equally exciting as the front-detector data.

The back detector measured high angular-resolution data and could be used to resolve interference fringes around Bragg reflections that are caused by the small number of unit cells of the PSI crystallites used in the experiment being irradiated by a transversely coherent X-ray beam. The result of the interference effects around the Bragg peaks would be to observe measurable intensities away from the Bragg peaks, which cannot be measured in conventional X-ray protein crystallography experiments using a protein macrocrystal. The “added” intensity contains a large amount of information that is normally lost in conventional crystallography, so the back detector results were greatly anticipated.

The large working distance of the back detector provided the necessary angular resolution to well-resolve subsidiary maxima, as shown in Fig. 11. Thereby, the crystal size could in principle be determined by counting the number of fringes between Bragg peaks (for instance the number of Bragg peaks between the (100) and (200) reflections would give the number of unit cells along a*). Patterns from crystals containing less than 10 unit cells per edge were recorded, which shows the PSI crystallites were in the size range of 200–1000 nm, consistent with the serial powder diffraction results. However, the smallest crystals may not have produced diffraction patterns that were identified by the hit-finding algorithm, as they may produce weaker Bragg reflections. Thereby, patterns from smaller crystals may also be present in the data sets. Re-examining the data to search for smaller crystals is still a possibility.

Fig. 11. Coherent crystal diffraction.

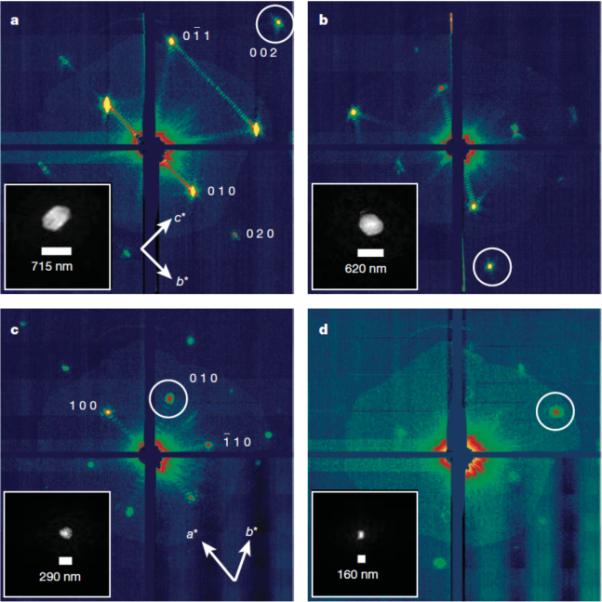
Low-angle diffraction patterns recorded on the rear pnCCDs, revealing coherent diffraction from the structure of the PSI nanocrystals, shown using a logarithmic, false-color scale. The intensities away from the Bragg condition are an interference effect caused by the small number of unit cells in the crystal. The Miller indices of the peaks in (a) were determined from the corresponding high-resolution pattern. In (c) seven fringes are counted in the b* direction, corresponding to nine unit cells, or 250-nm PSI crystal. Insets, real-space images of the nanocrystal, determined by phase retrieval (using the Shrinkwrap algorithm [105] of the circled coherent Bragg shape transform). Figure and caption modified from [94].

The interference fringes surrounding the Bragg peaks allow the use of image-reconstruction techniques from the coherent-diffractive-imaging field. Using phase retrieval methods [105, 106], a cross section of the crystal size and morphology can be determined from the interference pattern surrounding a Bragg peak, as shown in Figure 11a–d [94]. The information contained within the shape transform may facilitate a direct solution to the phase problem, according to Shannon's theorem [107], because the intensity between Bragg peaks allows for oversampling of the diffraction pattern [108].

Although the maximum size of the crystals was restricted by inline filtering, the shape transforms were observed because the minimum size could not be strictly chosen, so the minimum size was the soluble PSI_T. The size distribution of the PSI sample was not known in advance; however, the size of the crystal was observed to affect the produced diffraction pattern substantially, as shown in Figure 11a–d, with the observation of the shape transforms.

A diffraction grating with N slits will give rise to diffraction features that are finer than the Bragg peaks by a factor of 1/N. Therefore, a crystal with N unit cells in a given direction will produce diffraction patterns with N - 2 subsidiary maxima between the Bragg peaks, providing a method to determine the size of the crystal projection. The central maxima will have a width of approximately 2/N, whereas the width of all subsidiary maxima will be 1/N for a general parallelepiped crystal. An identical shape transform will be laid down upon each reciprocal lattice site, and the diffracted intensity will have the following form for a general parallelepiped [16]:

$$I\propto \frac{{\sin }^2(\pi N_a\mathbf{a}\cdot \mathbf{s}){\sin }^2(\pi N_b\mathbf{b}\cdot \mathbf{s}){\sin }^2(\pi N_c\mathbf{c}\cdot \mathbf{s})}{{\sin }^2(\pi \mathbf{a}\cdot \mathbf{s}){\sin }^2(\pi \mathbf{b}\cdot \mathbf{s}){\sin }^2(\mathbf{c}\cdot \mathbf{s})}$$ (3)

where a, b, and c are the unit cell vectors, i.e. a·s = h·x_j, N_a represents the number unit cells in the a direction, etc. The larger the number of unit cells, the smaller the shape transforms until the limit of the conventional crystallography case is reached, in which the inter-Bragg peak intensities are not observable. In the case of a crystal with 10 unit cells in the a direction, there will be 8 subsidiary maxima in that direction about the Bragg reflection, and the peak height will be proportional to 10², as calculated by Eq. 3.

5.7.1. Hit rates and sample settling

When examining the LCLS data for PSI, the low hit rate for the PSI data became a concern. The major issue for the low hit rate of the LCLS experiments is shown in Fig. 13 and is that the nanocrystals and microcrystals of PSI settled out of solution with time;. The plot shows the decrease in sample chlorophyll concentration as a function of time, as measured by absorbance at 280 nm (for peptide bonds) and 680 nm (for chlorophyll a). The plot was made by using a HPLC to run a suspension of PSI crystallites through a 15-m long sample line. Settling of the larger crystallites in the sample reservoir lines was likely the major cause of the decreased protein concentration shown in Fig. 13.

Fig. 13. Photosystem I crystallite settling with time.

Plot of the absorbance at 680 nm (red), 600 nm (fushia), and 280 nm (blue) of suspension of 2-μm-filtered Photosystem I crystallites as monitored using an HPLC flowing at 10 mL/min. Sudden increases in absorbance at around 75 min and 130 min correspond to the sample loop being inverted.

A few methods could be available to prevent the larger crystallites settling from solution at a faster rate than the smaller crystallites. One method would be to keep the crystallites in a neutral-buoyancy solution, which prevents any settling of the crystallites. In the case of PSI, a neutral buoyancy solution can be prepared using 1.4 M sucrose in G₀ buffer. A diffculty that arises with the sucrose-containing solution is that the viscosity increases with the amount of sucrose, and consequently, the liquid pressure in the jet needs to be increased. This can lead to an unstable jet or even a jet that will not run with a given inner-diameter fiber optic. As a result, the inner diameter of the fiber optic would need to be increased, making for a thicker, higher flow-rate jet. The thickness of the jet is a problem when higher-energy X-rays are used, as a strong solvent background will be recorded, which may reduce the dynamic range, or worse, fully saturate the detector pixels. One possibility to overcome the diffculties listed above is to use lower sucrose concentrations. The lower sucrose concentrations will allow for a decrease in viscosity while still increasing the settling time of the larger crystallites.

5.7.2. PSI sample consumption during femtosecond nanocrystallography

An issue that arose during the first femtosecond nanocrystallography experiments related to the low hit rate was that the PSI data were collected for 24 hours at a flow rate of 10 μL/min. Approximately 14 mg of PSI was used for the first femtosecond X-ray protein nanocrystallography experiments in Dec 2009. Operating at 30 Hz, the X-rays only interacted with 0.004% of the sample, hitting one out of every 25,000 nanocrystals at a concentration of one crystallite per four interaction volumes. The effciency increased as the LCLS moved to 120-Hz repetition rate, but this is only an improvement by a factor of four in the effciency of sample use. Once the European XFEL becomes operational, with tens of kilohertz repetition rate, the effciency will be increased by orders of magnitude, so that a larger percentage of nanocrystals within a sample interact with the XFEL beam [73]. Using 12 kHz with the same setup, one out of every 250 crystallites would be utilized.

In order to show the relative effciencies of protein use between the conventional experiments and the LCLS experiments, the amount of protein in each crystal, and the number of crystals used to collect a data set in each case, must be compared. Although may of the PSI crystallites used in the experiment were smaller than 2 μm in size, the assumption that all the PSI crystallites were 2 μm in size will allow for the most conservative comparison between the conventional and LCLS experiments.

There are approximately 10⁷ to 10⁸ crystallites with 2-μm edges within a 0.5 mmx 0.5 mm x 2 mm PSI crystal. Using the current hit rate from the LCLS experiments of one in 25,000, 5x10⁷ 2-μm PSI crystallites would produce 2000 diffraction patterns, whereas approximately 10,000 patterns were needed for the completeness of the LCLS data to approach 100%, without any type of post refinement—post-refinement may significantly decrease the number of patterns necessary for completion—and pure Monte Carlo integration of the intensities [96]. Now that the LCLS operates at 120 Hz, 5x10⁷ 2-μm PSI crystallites will produce 8000 diffraction patterns, generating the necessary amount of diffraction patterns for a full Monte-Carlo integration of the intensities.

When conventional X-ray crystallography experiments are done using large PSI crystals, up to 100 large crystals—each containing 10⁷–10⁸ of the 2-μm PSI microcrystals—are grown and shipped to the experiments. Therefore, the total amount of PSI used for the preliminary LCLS experiments, once scaled for the full repetition rate of the LCLS, is less than the amount of PSI used for data collection on single, large crystals, and the effciency of the femtosecond X-ray protein nanocrystallography technique will be increased by at least two orders of magnitude when the European XFEL becomes operational. Additionally, the conventional crystallization experiments will produce PSI crystals that are too small or too internally disordered (mosaicity ≥ 1.0°) to attain high-resolution, high-quality diffraction patterns. As a consequence, only 1–2% of all protein in a conventional PSI-crystallization experiment produces crystals allow high-quality data sets to be recorded. In fact, the femtosecond X-ray protein nanocrystallography experiments used less protein than one conventional X-ray crystallography experiment using PSI, especially since high protein concentrations of 80 mg/mL, in combination with micro and macroseeding experiments, are necessary to achieve the growth of large, single crystals of PSI with mosaicity below 1°.

Even though less PSI sample was used, relative to the conventional crystallographic case, than initially thought, decreasing sample consumption is still a major optimization factor for the femtosecond nanocrystallography project. One promising method to decrease the sample usage would be to decrease the flow rate of the jet. As the jet currently runs at approximately 10 μL/min, slowing the flow rate to a few hundreds of nanoliters per minute would offer a substantial improvement. However, the minimal flow rate is limited by the repetition rate of the X-rays. The linear velocity of the jet, which is related to the flow rate and jet diameter, must be large enough to deliver fresh sample to the X-ray interaction region that could not have received any ill effects of the previous pulse before the subsequent X-ray pulse. In the case of 120 Hz repetition rate, the lower limit of the flow rate will be ~10 nL/min, but the exact number will depend on the jet thickness. Jets running high-viscosity liquids could provide the necessary methods of reducing sample consumption while inhibiting crystallite sedimentation. However, much work remains to be done.

5.8. Resolution limits of the first femtosecond nanocrystallography data

The initial femtosecond nanocrystallography experiments were conducted at 1.8 keV X-rays (λ = 6.9 Å) as determined by the initial operating conditions of the LCLS. The resolution limit of approximately 8.5 Å in the PSI femtosecond nanocrystallography data set was due to the long wavelength used in the experiment, as well as the instrumental geometry.

The 8.5-Å resolution limit of the data also contributed to the small number of peaks in the patterns. The indexing success of MOSFLM or DirAx was correlated to the number of peaks contained within the diffraction pattern, which supports that moving to higher resolution will increase indexing success because the total number of measurable reflections in a given resolution sphere is calculated as follows:

$$N_{\mathrm{reflections}}=V_{\mathrm{unit}\mathrm{cell}}\cdot \frac{4}{3}\pi {\left(\frac{1}{d_{\min }}\right)}^3$$ (4)

Using equation 4, the total number of reflections to 8.5 Å for the PSI structure is calculated to be approximately 82000 non-unique reflections corresponding to 6800 unique reflections. However, the number of reflections in the 3.0-Å-resolution sphere is calculated to be 1.9 million non-unique reflections, corresponding to 158,000 unique reflections. Once the snapshot patterns contain a larger number of peaks, the indexing programs may be able to identify the unit cells with less ambiguity. Additionally, the size of the PSI crystallites may need to be increased to compensate for the reduced scattering cross-section at higher X-ray energies, which will decrease the measured intensities of the shape transforms, providing another benefit to auto-indexing.

6. The CXI instrument

The beamline that is of interest for X-ray protein crystallographers is the Coherent X-ray Imaging (CXI) beamline, which became available for users in February 2011 [109]. The CXI instrument will provide X-ray energies between 2 and 30 keV, with repetition rates up to 120 Hz and as much as 10¹² photons/pulse. The CXI instrument provides X-ray wavelengths as short as 1.3 Å using the first harmonic, which should allow atomic-resolution diffraction patterns to be recorded.

7. OUTLOOK AND CONCLUSIONS

Membrane proteins are involved in many vital cellular functions and pathways, such as photosynthesis, cellular respiration, and signal transduction, amongst many others. However, the number of solved (unique) membrane protein structures is less than 300. Although X-ray protein crystallography is the workhorse of structural biology, there are many diffculties associated with the technique. The two main di culties of conventional X-ray protein crystallography that the femtosecond nanocrystallography technique attempted to address were the necessity for large, well-ordered protein crystals—which could take years to grow and optimize, but the conditions may never be found in the first place—and the X-ray-induced radiation damage deteriorating the quality of the data and reconstructed electron-density map.

The femtosecond X-ray protein nanocrystallography project was initiated in order to determine whether membrane protein crystallites could be utilized to obtain high-resolution X-ray diffraction patterns, with the ultimate goal of producing molecular- and atomic-resolution electron-density maps to solve the structures of these complex proteins. Many experiments were necessary during the coarse of the project. Experiments were related to sample production, such as the development of methods to produce and characterize membrane protein nanocrystals, testing of the reproducibly of membrane protein crystallite production. Further, some experiments were related to sample quality, such as determining the diffraction potential and minimum size of membrane protein crystallites. Other experiments and theoretical developments were necessary for the development of sample handling and delivery systems, as well as the development of novel data acquisition and analysis schemes. Of course, none of the data to date could have been collected without the theoretical and experimental development of the LCLS itself, or the CAMP chamber and pnCCD detectors.

Although the first results of femtosecond X-ray protein nanocrystallography have been published in 2011 [94], the technique is rapidly improving and maturing. The excitement is rapidly building in the structural biology community to harness the potential of the femtosecond nanocrystallography technique to revolutionize the capabilities of the structural biology community.

Femtosecond X-ray protein nanocrystallography will offer a new path to the structure of diffcult-to-crystallize proteins, one in which a crystal of any size may be suffcient for structure determination. The most exciting aspect of the technique is that femtosecond X-ray protein nanocrystallography will allow the structures of membrane proteins to be determined without the ill-effects of X-ray-induced radiation damage on the sample.

Ultimately, the true power of femtosecond nanocrystallography will be in its ability to harness the full spatio-temporal resolution offered by X-ray free electron lasers. Time-resolved crystallography using Laue diffraction methods at third-generation synchrotrons have shown the abities of a technique that combines ultrafast spectroscopy with the spatial resolution of crystal-lography, and current time-resolved crystallography can track changes in the electron density on the time scales of hundreds of picoseconds to seconds [110, 111, 112, 113, 114, 115]. The short pulses of the XFELs may allow the time-resolved crystallography to be extended to even shorter time scales, such as hundreds of femtoseconds. Combined with the femtosecond nanocrystallography technique, time-resolved crystallography at XFELs may be more amenable to systems that produce non-cyclical or irreversible, light-induced changes. The immediate implications are in studying the photocatalytic cycles of the photosynthetic proteins, as well as watching light-induced undocking of the proteins involved in the electron transfer of photosynthesis. This could lead to a very fundamental understanding of the basic processes of life and could have implications in artificial protein design and engineering.

The potential applications for femtosecond nanocrystallography are far reaching and could have a major impact on many areas of science and engineering. Results obtained from the method could be used in every area from basic science to the rational design of drugs. However, as is true with most new technologies, some major uses of femtosecond nanocrystallograhy will not be realized or appreciated for many years or decades to come. Although much is left to be done in regard to bringing the femtosecond nanocrystallography method to its full potential, the impact of the technique may be felt in many disciplines. The future of structural biology will be bright, and femtosecond X-ray protein nanocrystallography may present the technique necessary for a paradigm shift from the (mostly) static X-ray protein crystal-lography of today to the (mostly) time-resolved X-ray protein crystallography of the future.