Abstract
Molecular motor proteins use the energy released from ATP hydrolysis to generate force and haul cargoes along cytoskeletal filaments. Thus, measuring the force motors generate amounts to directly probing their function. We report on optical trapping methodology capable of making precise in vivo stall-force measurements of individual cargoes hauled by molecular motors in their native environment. Despite routine measurement of motor forces in vitro, performing and calibrating such measurements in vivo has been challenging. We describe the methodology recently developed to overcome these difficulties, and used to measure stall forces of both kinesin-1 and cytoplasmic dynein-driven lipid droplets in Drosophila embryos. Critically, by measuring the cargo dynamics in the optical trap, we find that there is memory: it is more likely for a cargo to resume motion in the same direction—rather than reverse direction—after the motors transporting it detach from the microtubule under the force of the optical trap. This suggests that only motors of one polarity are active on the cargo at any instant in time and is not consistent with the tug-of-war models of bidirectional transport where both polarity motors can bind the microtubules at all times. We further use the optical trap to measure in vivo the detachment rates from microtubules of kinesin-1 and dynein-driven lipid droplets. Unlike what is commonly assumed, we find that dynein’s but not kinesin’s detachment time in vivo increases with opposing load. This suggests that dynein’s interaction with microtubules behaves like a catch bond.
Introduction
Although many small molecules can diffuse to reach where they are needed inside the cell, larger molecules and organelles need to be actively transported. This is accomplished by a set of specialized motor proteins that transport the cargoes to where they are needed by stepping along a network of intracellular filaments—microtubules and actin filaments (1). The importance of active transport is most evident in the case of neurons, where the axon extremity of the cell can be tens of centimeters long and of the order of a few micrometers thin. For a large cargo to diffuse from one end to the other would take more than a lifetime! Examples of transported cargoes include mRNA particles (2), mitochondria (3,4), endosomes and phagosomes (5,6), various vesicles (7), and lipid droplets (8). Cargoes are not always benign; pathogens like virus particles hijack the molecular motors of the cell that in turn deliver them to the nucleus where they can use the cellular machinery to replicate (9).
Much of our understanding of how individual motors function has benefitted from precise in vitro measurements at the single molecule level (10). However, the environment motors face inside the cell is very different from the buffer conditions: motor binding to the cargo, the existence of multiple similar and dissimilar motors on cargoes, motor cofactors, motor regulators, microtubule-associated proteins, and the crowded environment in the cell can all lead to motor function diverging from its behavior in vitro. It is hence important to understand how motors function in their native cellular environment. Given that motors generate force to haul cargoes, measuring that force amounts to directly probing their function. By applying the linear restoring force of an optical trap against the force of motors pulling a cargo, the maximum force the motors are able to exert is measured.
Force measurements have been instrumental in elucidating motor function in vitro (11–13). First attempts to measure motor forces in their native environment in living cells resulted in average escape force measurements rather than measuring the force needed to stall individual cargoes. Nevertheless, these early measurements demonstrated the power of optical trap measurements in suggesting that multiple motors haul cargoes (14) and probing motor function in different genetic backgrounds (8). Here, we report on the details of a methodology that enabled us to measure forces of molecular motors transporting individual cargoes in vivo (15). We use lipid droplets hauled by kinesin-1 and cytoplasmic dynein in Drosophila embryos as a model system to measure motor properties important for the transport of cargoes driven by similar and dissimilar teams of motors. Although kinesin-1 and cytoplasmic dynein move predominantly unidirectionally along microtubules and in opposite directions, cargoes they haul move bidirectionally (16). Two models have been proposed that would result in bidirectional transport: regulation and tug-of-war. The regulation model proposes that both polarity motors are bound to the cargo but only motors of one polarity are active at any instant of time, with the activity reversed by some motor cofactor. The tug-of-war model, on the other hand, proposes that both polarity motors are active and can bind simultaneously to the microtubule resulting in a fight followed by one polarity motors stochastically detaching under the opposing force of the other. Recent mathematical models of the tug-of-war scenario used some known properties of the single motors and hypothesized unknown properties to quantitatively reproduce the bidirectional transport observed in living cells (17). These models require the cooperative detachment of a team of motors under opposing load that results from an assumed exponential increase in the detachment rate of motors with opposing load as proposed by Bell (18). Here, using the optical trap in vivo, we show that motor detachment under load does not follow the model assumed in (17). Furthermore, we find that cargoes exhibit short-term memory in directionality, a feature inconsistent with a tug-of-war scenario, but consistent with a regulated switching mechanism.
Methods
Optical trapping setup and methodology
A schematic of the optical trap setup is shown in Fig. 1 A. The trap was built around an inverted optical microscope (Eclipse TE2000-U, Nikon, Tokyo, Japan) using a high numerical aperture oil immersion objective (100× Plan Fluor, Na = 1.3, Nikon, Japan). Imaging lipid droplets inside Drosophila embryos was achieved using differential interference contrast (DIC) with the green light of a mercury lamp (GIF filter). Sample preparation is described in the Supporting Material. A micrometer-driven translation stage (Mad City Labs, Madison, WI) was used for positioning the specimen in the field of view and the fine focusing knob of the microscope was used to determine the depth of field. The images obtained with a charge-coupled device camera (Dage-MTI-100, Michigan City, IN) were captured at 30 frames/s by a frame grabber for real-time computer analysis and recorded on video tape for offline analysis. A computer-controlled piezo-driven mirror steers the trap (Nano-MTA2, Mad City Labs). Fast positioning of the trap was essential as the cargo of interest could be anywhere in the field of view (see inset Fig. 1 A), is already moving, and needed to be rapidly trapped (see below). A 980 nm fiber-coupled laser diode (Thorlabs, Newton, NJ) was used for trapping; this wavelength minimizes optical damage (19). No optical damage was observed: droplets moved immediately upon release, even from repeated trapping periods of several seconds (see e.g., Fig. 2 C and Fig. 6 A), suggesting the motors on the droplets were still active.
Figure 1.
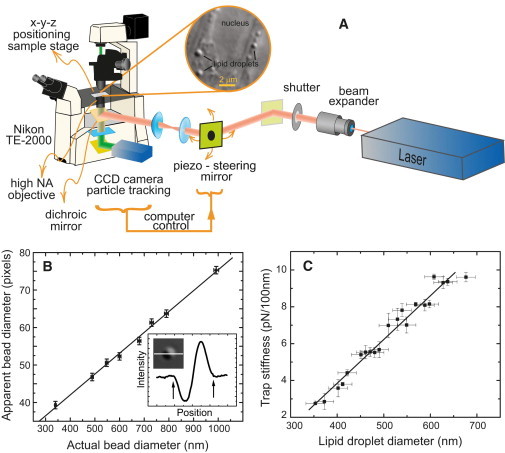
Experimental setup and its calibration. (A) Schematic of the optical trap used to measure molecular motor forces in vivo. Given that the moving lipid droplet cargoes can be anywhere in the field of view (inset), a piezo-driven mirror, controlled by the fast single-particle tracking software, rapidly and precisely positions the trap at the center of the moving cargo. (B) Polystyrene beads of varying size were imaged using DIC microscopy and their diameter measured in a cross section of the image as shown in the inset. The straight line is a fit to the apparent size as a function of the actual size data for beads immersed in an index liquid to match the refractive index mismatch between the lipid droplets and cytosol. This line was used to infer lipid droplet size from their (DIC) image. (C) The trap stiffness increases with lipid droplet diameter as measured using the power spectrum method for purified lipid droplets suspended in buffer. The stiffness is expected to peak around the wavelength in buffer (∼737 nm) of the trap laser light used. Error bars are mean ± SE.
Figure 2.
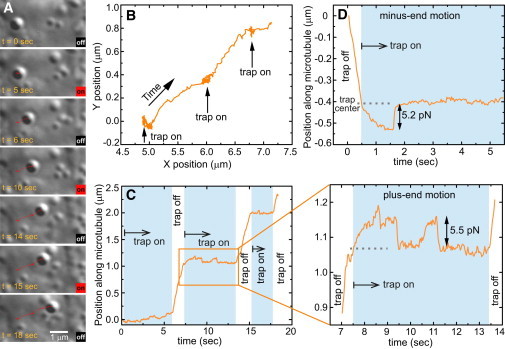
An example of in vivo stall force measurement for both kinesin-1 and cytoplasmic dynein. (A) Snapshots showing a lipid droplet in an OR-R embryo trapped at multiple positions along its trajectory shown in B. In C, the projection of the position of the lipid droplet along its direction of motion is plotted as a function of time. Highlighted periods indicate that the trap was on. The enlarged graph shows that the kinesin-1-driven droplet stalls when the trap is switched on and then drops to the trap center. The motors attempt to move the droplet away from the trap center to stall again. When the trap is switched off, the motors haul the cargo along. The trace in D is for a dynein-driven droplet that stalls, falls back to the center of the trap and stays there. Increasing position indicates plus-end-directed motion, whereas decreasing position indicates minus-end-directed motion.
Figure 6.
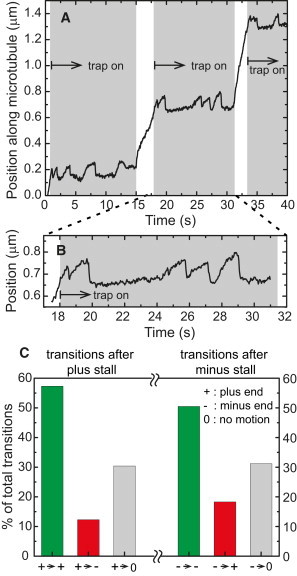
A lipid droplet is more likely to continue moving in its original direction after the trap detaches the motors from the microtubule. (A) A lipid droplet trapped at multiple positions along its trajectory shows successive excursions and detachments in the plus-end direction. (B) An enlarged section of the trajectory in A. (C) Excursions in the optical trap after a stall are counted and classified as either plus-end, minus-end, or no motion. Plus stalls are more likely to be followed by plus-end-directed motion and minus stalls are more likely to be followed by minus-end motion. (The total number of plus transitions is 358 and minus transitions is 186, the maximum waiting time after a stall was 0.5 s for an excursion to be counted).
We developed a single particle tracking algorithm that can follow the position of the cargo in real-time (described in the Supporting Material). This made possible multiple stall force measurements on the same cargo while it moved along its trajectory, as well as the ability to precisely localize the optical trap over the center of individual droplets so that the initial load on the cargo is minimized.
In a typical stall force measurement (Fig. 2), a moving droplet is spotted and selected in the video image using the mouse pointer. This triggers the real-time particle tracking program (see below) that tracks the droplet; the droplet’s location is used to control the piezo-driven mirror that moves the trap to that position and the program opens the shutter. The droplet is then trapped. The shutter can be closed, at which point the droplet can move again, although its position is still tracked. When the shutter is next opened, the trap will be at the new droplet position. This can be repeated, enabling multiple measurements on the same lipid droplet as it moves along the microtubule.
Calibration of the optical trap for in vivo stall force measurement
The trap stiffness is a function of both the properties of the laser beam (e.g., laser power, beam waist at focus) and the properties of the trapped object and surrounding medium (e.g., object size, its index of refraction and that of the medium) (20,21). For stall force measurements, the stiffness (k) of the trap needs to be calibrated and the cargo stall force is then calculated using Hooke’s law by measuring the stall distance (13,22).
Procedures typically used in vitro to calibrate trap stiffness cannot be directly applied in vivo because each cargo’s size is distinct, and the cytosol’s viscosity is unknown and can vary by location. Moreover, such methods either observe thermal motion of the trapped particle, or drag it in the medium until it escapes (23). In vivo, however, the cargo carries molecular motors that attach to cytoskeletal filaments, altering thermal jiggling or inducing premature escape from the trap. Hence, we developed an alternative method to account for these factors.
Determining the size of the trapped cargoes
The size of the cargo determines the stiffness it experiences in a trap (20,24,25), and lipid droplets range in size between ∼300 and 800 nm as inferred from electron micrographs (8). The lipid droplet size cannot be measured directly from its image because of diffraction. The contrast generated in DIC microscopy that we used to image the droplets is due to the change in the optical path length between light passing through the object and the medium, which have different refractive indices. We used this to determine the real size of the lipid droplets from their apparent size in the image. This was done by comparing the droplets to a sample of polystyrene beads of standard (known) size immersed in a matching liquid. Under these conditions the polystyrene beads looked like lipid droplets appear in the cell (see Fig. S1 in the Supporting Material). To determine the index of refraction needed for the immersion liquid, we measured the index of refraction of the cytosolic fraction (n = 1.355 ± 0.002) and the lipid droplets (cargo) (n = 1.465 ± 0.003) from Drosophila embryos. The index of refraction of the cytosolic fraction was measured using an Abbe-type refractometer (Bausch & Lomb, Rochester, NY). The index of refraction of lipid droplets (cargo) from Drosophila embryos was measured as follows: the droplets were purified as described (26) and deposited on a microscope coverslip. Liquids of progressively increasing indices of refraction (different aqueous dilutions of the Cargille index matching liquid, undiluted n =1.5560 (at 25 C)) were used to immerse the lipid droplets, which were visualized using an optical microscope in DIC mode. When the index of the immersion liquid matched that of the droplets they became invisible in the DIC image. With the indices of refractions measured, size calibration was achieved using polystyrene beads (polybead, Polysciences Inc., Warrington, PA; and PS beads, Bangs Laboratories, Fishers, IN) immersed in an index liquid (Cargille Laboratories, Cedar Grove, NJ) diluted in water to match the lipid-cytosol refractive index difference. A calibration curve of the apparent size as a function of the real size was constructed and used to determine the real size of individual lipid droplets (Fig. 1 B). The apparent size in pixels was determined using the cross section through the image of a droplet or bead (inset, Fig. 1 B). This procedure gave the size of the lipid droplets to within 5% (see the Supporting Material).
Calibrating the trap stiffness as a function of cargo size
Lipid droplets were purified as described previously (26) and dispersed in buffer matching the index of refraction of cytosol. The viscosity of the buffer was measured using a falling ball viscometer. The rolloff frequency of the position power spectrum of a trapped lipid droplet in buffer was used to calculate the trap stiffness (13,27). The laser power used for stiffness calibration was 100 mW at the source. The stiffness of the trap was measured as a function of the size of the lipid droplet, as determined from its calibrated DIC image (see above) (Fig. 1 C). The stiffness increases monotonically with droplet size for the laser wavelength used (980 nm) and the range of droplet sizes used. The stiffness is expected to peak at the wavelength of the trap light in the medium used (735 nm) (24), but lipid droplets average ∼500 nm and are rarely larger than 750 nm in diameter. We estimate the uncertainty in a force measurement to be ∼25% (see the Supporting Material).
Determination of the cargo’s center to allow trap positioning
In contrast to in vitro experiments, once the cargo to be probed is identified, it must be quickly trapped by rapidly and precisely determining its position, and then appropriately positioning the laser over it. The center of a cargo was determined from its image. Many cargoes are transparent, so we use DIC imaging, where objects appear shadowed and the cargo’s center cannot be found from a simple geometric determination of the peak intensity. We used a correlation-based method where the cargo image was compared to a template image of a cargo. This gave the center of the cargo a precision of a few nanometers (28).
Aligning the trap with the cargo can be done by moving the sample into a fixed laser beam, or by moving the trap beam to the cargo. We moved the beam with a piezo-driven mirror (Fig. 1 A). To calibrate the pixel position of the trap center in the field of view resulting from the beam movement, a polystyrene bead was trapped in buffer and its position was tracked as the piezo-mirror scanned the trap across the field of view. Once the trap was positioned at the cargo position, it stayed there until the shutter was toggled off and on again to trap the cargo at its new position as described below.
It is important that the trap be positioned at the cargo center so that the initial force acting on the cargo is zero. To confirm that our method did indeed position the trap at the precise center, we used beads, suspended in viscous solutions to slow down diffusion, and tracked the bead position before and after the shutter was opened. The distance the beads were pulled by the trap was indistinguishable from our particle tracking precision (few nanometers).
Results
Measuring motor forces in vivo
Optical trapping is well established for measuring molecular motor forces in vitro; here we adapted it to measurements in vivo. Several obstacles needed to be overcome to be able to measure the force motors exert in hauling individual cargoes. First, the optical trap needs to be quickly and precisely positioned at the center of the moving cargo so that the initial force acting on the motors is negligible and increases as the motors pull the cargo away from the trap center. Second, given the wide size distribution of endogenous cargoes and the dependence of the trap stiffness on the trapped particle size, a way to measure the cargo size needed to be developed. Finally, the optical density of both cargo and cytosol needed to be accounted for. To measure molecular motor forces in living Drosophila embryos, we developed an optical trap and calibration methodology to account for the index of refraction of the cargo (lipid droplets) and cytosol, as well as for the varied size of the lipid droplets. Details of the methodology are included in the Methods and Supporting Material. Trap stiffness calibration for different size lipid droplets suspended in buffer was achieved using the power spectrum method (27) by trapping purified droplets in an index-matching buffer of known viscosity (Fig. 1 C). This was necessary given the sticky and rheologically complex environment inside the embryos. Given that the stall force measurements are made on cargoes that stop moving, knowledge of the rheological properties of the cytosol is not necessary. Indeed, once the cargo size and corresponding trap stiffness are determined, the force at which a cargo stalls can be determined by measuring its stall distance from the center of the trap.
The alignment of the microtubules in the fly embryo with their minus ends in the perinuclear region at the periphery and their plus ends extending inward (Fig. S3 B) makes it possible to differentiate between kinesin and dynein-driven motion. Fig. 2 A shows snapshots of a lipid droplet being trapped at multiple locations along its trajectory. The trap laser is toggled on during the highlighted periods of time in the corresponding trace shown in Fig. 2 C and the droplet stalls twice after the motors pull it away from the trap center at around 7.5 s. As soon as the trap is switched off, the droplet is driven by the motor along the microtubule. By measuring the distance at which the droplet stalls relative to the trap center, the stall force can be calculated. An example of a dynein-driven lipid droplet stalled by the optical trap is shown in Fig. 2 D. For clarity, in all the traces shown, kinesin-driven motion is represented by moving up on the position versus time graph, whereas moving down corresponds to dynein-based transport.
Multiple motors cooperate to haul cargo
Stalled cargoes often start advancing further away from the trap center to reach another stall level before falling back to the trap center (Fig. 3 A). This double stall is a direct indication of the activity of multiple motors in hauling the cargo and that the number of motors available on the cargo can be larger than the number of motors participating in transport at any point in time. We find that molecular motor forces in vivo are additive as the second stall typically occurs at twice the distance of the first stall. The double stall and the additive forces are consistent with what has been observed in vitro when two or more motors are present on the cargo (29,30). A histogram of kinesin-1 stall forces measured in vivo is shown in Fig. 3 B. The histogram has three peaks, the first of which is at a force value of 2.6 pN and corresponds to the single motor level. Higher force peaks are at multiples of this single motor force, indicating that multiple motors cooperate in transporting the cargo. We have previously shown that minus-end forces show a similar force distribution, and that the distribution changes to coincide with the plus-end force distribution in mutants affecting kinesin-1 expression levels (15).
Figure 3.
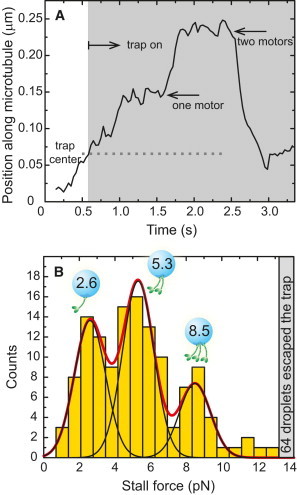
Multiple motors haul lipid droplets in Drosophila embryos. (A) The position of a lipid droplet pulled by kinesin motors in the optical trap shows a stall that is followed by another motor engaging to the microtubule and pulling the droplet further into the trap at ∼1.5 s. The two motors stall again at about twice the force of the single motor. (B) A histogram of kinesin stall forces of lipid droplets measured in vivo shows peaks at multiples of ∼2.6 pN indicating the action of multiple motors. No constraints on peak position were used in the Gaussian fits. Statistical analysis to confirm the position of the peaks can be found in the Supporting Material.
Opposite polarity motors are attached to a single cargo and exert similar forces
Like many other cargoes, lipid droplets move bidirectionally along microtubules. We have previously shown that cytoplasmic dynein (31) and kinesin-1 (15) drive the droplets toward the minus- and plus-ends of microtubules, respectively. Lipid droplets in the optical trap that stall in one direction often show rapid motion and stalling in the opposite direction after they fall back to the trap center. Fig. 4 A shows a trace of a lipid droplet moving in the minus-end direction and stalling when the trap is switched on. About a second after the trap is switched on, the stalled droplet drops to the center of the trap and immediately starts moving in the opposite direction and stalls. The plus-end motors then detach and the droplet falls back to the trap center and stays there for an extended time. The plus-end motors start pulling the cargo within one video frame (0.033 s) after it drops to the trap center at ∼1.6 s. Another trace with fast direction switching is shown in Fig. S2. This short time suggests that both polarity motors are attached to the cargo at the same time so that direction switching can happen without waiting for a motor to bind the cargo. This was previously suggested for lipid droplets based on the fast direction reversal of all lipid droplets observed (16,32). That both motors are simultaneously attached to the cargo is also consistent with findings in other systems where fluorescently labeled motors colocalized and moved with a cargo hauled by the opposite polarity motor (33–35).
Figure 4.
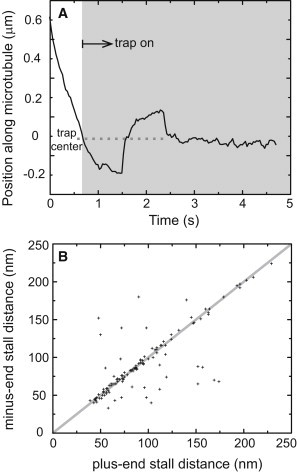
Opposite polarity motors are attached to a single cargo and exert equal forces. (A) A minus-end-directed lipid droplet stalls in the trap and drops to the trap center after the motors detach (at ∼1.6 s). It is then immediately pulled by the plus-end motors to stall again and detach. Another example is shown in Fig. S2. (B) Individual lipid droplets that stall in opposite directions during a measurement stall at the same distance away from the trap center in ∼80% of the times. This indicates that opposite polarity motor forces are balanced. The shaded line has a slope of 1 and is a guide to the eye. Stall distances rather than stall forces are plotted given that some excursions extend beyond the linear range of the trap. However, because the trap is symmetric, equal distances in opposite directions imply equal forces (115 individual lipid droplets from two wild-type fly strains, OR-R and YW).
Lipid droplets that switch direction during an optical trap measurement enable comparing the number of motors that engage in each direction. Fig. 4 B shows the measured stall distance in the minus-end direction versus its counterpart in the plus-end direction for individual lipid droplets. The overwhelming clustering of the measurements around a line of slope one indicates that the number of motors moving the cargo is the same in both directions.
Dynein’s detachment rate decreases with increasing opposing load
We have shown that multiple motors hauling a cargo attach and detach from the microtubule dynamically in the optical trap. Moreover, both polarity motors are simultaneously present on the bidirectionally moving lipid droplets. Recent mathematical models proposed that the opposite polarity motors could simultaneously pull in opposite directions until one polarity motors detach. This tug-of-war scenario had been proposed as a theoretical model for the observed bidirectional transport of cargoes and lipid droplets in particular (17), and recent works have suggested it as a mechanism in other biological systems (36,37) and studied it in vitro (38,39). We asked whether the detachment rates of both kinesin and dynein follow the exponential increase with opposing load that is generally used in, and crucial for, the tug-of-war models of bidirectional transport (17). Given that cargoes are transported by multiple motors, it is not possible to measure the detachment rate of the individual motor in vivo. However, using the optical trap we can compare the detachment rate under varying opposing loads of plus-end and minus-end moving cargoes. For that, we used the same methodology described previously for force measurements, but altered the positioning of the trap to be some fixed distance behind the moving cargo instead of being at its center. Thus, as soon as the shutter is opened, the moving cargo experiences a sudden opposing load and the time that elapses before it drops back to the center of the trap—the residence time—is measured. Because lipid droplets are of varying size, applying the trap of constant power at distances ranging between 50 and 160 nm generates forces of varying magnitude that also increase with the diameter of the cargo, as shown in Fig. 1 C. Given that we found that the number of motors on lipid droplets coincide for plus-end and minus-end motors (Fig. 4 B) (15), the measured residence time reflects the properties of the motors rather than differences in motor numbers. Fig. 5, A and B, show sample traces of a lipid droplet detaching immediately after applying the sudden load, and another holding on for 0.53 s before eventually falling back to the trap center.
Figure 5.
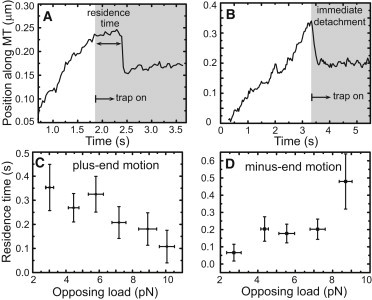
Kinesin, but not dynein, is more likely to detach from microtubules under larger opposing loads. By positioning the trap away from the center of the moving lipid droplet, a sudden opposing force is applied to the motors. The time the motors hold on before detaching—the residence time—is measured and can either be long (A) or short (B). (C and D) Show that kinesin-1 behaves differently from dynein under opposing load. Although kinesin is more likely to detach, dynein is less likely to detach under larger loads, which suggests a catch bond interaction between dynein and the microtubule. (The plots represent 90 binned measurements for kinesin and 61 binned measurements for dynein.)
We measured the residence times of both plus-end- and minus-end-driven lipid droplets (Fig. 5, C and D). Kinesin’s residence time drops with increasing opposing load, qualitatively consistent with Bell’s description of an increase in detachment rate under load. Surprisingly, however, the residence time of dynein under similar conditions increases with opposing load. This suggests that dynein might interact with the microtubules via a catch bond, unlike what is typically assumed in models. The implication on bidirectional transport of this difference between kinesin’s and dynein’s reaction to opposing load is addressed in the Discussion.
Opposite polarity motors are not simultaneously active
Given that both polarity motors are present on the cargo at the same time, we asked whether both could engage in pulling the cargo in opposite directions simultaneously as suggested by the tug-of-war models. To address this question we decided to compare the probability of a cargo switching direction after falling to the trap center, as in Fig. 4 A, to the probability of a cargo to restart moving in the same direction as in Fig. 6, A and B. This is summarized in Fig. 6 C, which shows that cargoes moving in some direction will more likely continue to move in the same direction after the optical trap detaches them from the microtubule. This is true for both plus-end and minus-end moving cargoes. These data suggest that, although both polarity motors are present on the cargo to move it bidirectionally, motors of one polarity only are active at any point in time, which argues against a tug-of-war model.
Discussion
We have developed a method to measure the stall forces of individual motor-driven cargoes in vivo. Although we used the method to measure forces hauling lipid droplets in Drosophila embryos as a model system, the applicability of the method transcends this system. Indeed, recent work reports similar measurements in a mammalian cell culture (40). Several requirements are needed to be able to use this methodology. First, the cargo needs to be refractile and spherical for quantitative force measurements. The spherical requirement is not needed if only manipulating the cargo is desired. Second, the indices of refraction of the cargo and the cytosol need to be measurable. Alternatively, a method to pull each cargo out of the cell and calibrate the trap stiffness for each cargo is needed. Third, the cargo needs to be rigid enough to maintain its shape in the optical trap, and the wavelength and power of the trap laser need to be chosen to avoid optical damage. Many vesicles are not refractile enough and thus require large laser powers to trap, which can potentially damage the motors and deform the vesicle shape rendering quantitative measurements difficult (41).
In vivo force measurements enabled us to establish that multiple motors move individual cargoes, as we observed motors attaching and detaching to the microtubule, resulting in the cargo stalling at multiple force levels. Stall force histograms show peaks at multiples of a fundamental value, confirming that stall forces are additive in vivo, similar to what has been observed in vitro (29,30). No such stall force addition was found for a two-kinesin construct linked via a short DNA and attached to beads (42,43). The two-kinesin mean detachment force coincided with that of the single kinesin which was, in turn, comparable to the single kinesin stall force. It would be interesting for future work to explore in what ways these in vitro works need to be modified to capture the in vivo observations. The value of the stall force for both kinesin-1 and cytoplasmic dynein hauling the lipid droplets in the fly embryos is around 2.5 pN. This is consistent with similar measurements in mammalian cells within the uncertainty (40). However, these values differ from the stall forces of the individual isolated motors hauling plastic beads in vitro (4–7 pN for kinesin and 1–7 pN for dynein) (11,13,30,44–46). Moreover, unlike the isolated motors in vitro, kinesin-1 and cytoplasmic dynein exert equal forces in vivo (15). This discrepancy could result because, inside the cell, both the motors and the microtubules can be altered by accessory proteins or by posttranslational modifications that can result in altered motor-microtubule interaction. Moreover, recent work reported that the motor-microtubule interaction in vitro depends significantly on whether they both originate from the same organism (47). This emphasizes the importance of the cellular context in determining motor properties and highlights the need for quantitative in vivo measurements.
The occasional fast reversal in direction after a stalled droplet falls to the trap center is indicative of the availability of both polarity motors on the cargo, as has previously been demonstrated using fluorescence colocalization measurements in other systems (33,35,34). We find that equal numbers of the opposite polarity motors move the cargo. However, the probability of direction reversal is lower than would be expected from a stochastic attachment of either polarity motors with the two being equally available for attachment. Moreover, although at the embryonic stage of development that we study the lipid droplets have a net plus-end transport, minus-end excursions in the trap are still more likely to be followed by minus-end motion. This finding is not consistent with the tug-of-war model (17), which would predict that both polarity excursions are equally likely after detachment. The short-term memory in cargo directionality that we observe is, however, consistent with a model where only motors of one polarity on a cargo are active at any instant in time and that a regulatory event is needed to switch that activity to the opposite polarity motors.
Using the in vivo optical trapping methodology, we investigated the effect of opposing load on the detachment rates of lipid droplets. We find that kinesin-1-driven droplets detach more rapidly at a larger opposing load, whereas dynein-driven droplets detach more slowly at higher loads, reminiscent of a catch bond (49). These results have implications on tug-of-war models of bidirectional transport. The essence of these models is that teams of opposite polarity motors fight by engaging simultaneously to the microtubule. Motors of one polarity detach under the effect of the load applied by the opposing motors as well as by the intrinsic detachment rate of the individual motors. With this process happening stochastically, the net effect is cargoes that move bidirectionally with the net directionality determined by the attachment and detachment rates of the individual motors of both directions. With the detachment rate increasing exponentially under opposing load as is typically assumed for both polarity motors, a team of motors will detach if one of the motors in the team happens to detach. This is because the remaining motors now experience a larger opposing load that increases their likelihood to detach. We find that kinesins’ detachment rate increases with opposing load; even if the dependence does not seem to be exponential, consistent with recent in vitro measurements on single kinesin molecules (50). However, our finding that dyneins’ detachment rate decreases rather than increasing with larger opposing load requires revisiting the tug-of-war models to account for this fact. Recent in vitro work showed that at superstall forces individual dynein motors remain attached to the microtubule for long periods of time and used these single molecule observations to revise the tug-of-war model (50). Our findings confirm that these single molecule properties hold for lipid droplet transport in the cellular context. Given that cytoplasmic dynein is conserved across many species, the implications of this catch-bond-like behavior of dynein on tug-of-war models are likely general, but that remains to be seen. It would be intriguing to see if the cell employs these motor properties by exploiting a tug-of-war between opposite polarity motors to perform biological function, such as the endosome fission reported in (37).
In summary, the in vivo quantitative force measurements that we report enabled us to probe the function of the molecular motors in their native environment in the cell. We establish that multiple motors cooperate in hauling a cargo and generate additive force, and that motors of opposite polarity are present on the cargo in equal numbers. Moreover, polarity switching of the motors in the optical trap suggests that only motors of one polarity are active at any point in time. This is inconsistent with theoretical models of bidirectional transport where opposite polarity motors engage in a tug-of-war. We further find that, unlike kinesin, dynein’s detachment rate from microtubules decreases with increasing opposing load. This suggests that dynein interacts with the microtubules via a catch bond, which would also alter the predictions of tug-of-war models. Given that measuring motor forces amounts to directly probing their function, the approach we present is well suited to study how that function is altered by mutation. For example, by altering kinesin expression levels we recently studied how transport characteristics correlate with motor numbers and showed that both polarity motor levels on the cargo are coupled (15). We have also used force measurements in vivo to study how glycogen synthase kinase 3 (GSK-3), which is a major player in Alzheimer’s pathology, regulates transport (C. Weaver, C. Leidel, L. Szpankowski, N. M. Farley, G. T. Shubeita, and L. S. B. Goldstein, unpublished).
Acknowledgments
The authors thank H. Swinney, E.-L. Florin, and S. P. Gross for critical reading of the manuscript, M. Marder for helpful discussions on data analysis, and B. Carter for help with developing the particle tracking algorithm.
This work was funded in part by The Welch Foundation grant No. F-1693 and the National Science Foundation grant PHY-0957811 to G.T.S.
Supporting Material
References
- 1.Vale R.D. The molecular motor toolbox for intracellular transport. Cell. 2003;112:467–480. doi: 10.1016/s0092-8674(03)00111-9. [DOI] [PubMed] [Google Scholar]
- 2.Bullock S.L., Stauber M., Schmidt-Ott U. Differential cytoplasmic mRNA localization adjusts pair-rule transcription factor activity to cytoarchitecture in dipteran evolution. Development. 2004;131:4251–4261. doi: 10.1242/dev.01289. [DOI] [PubMed] [Google Scholar]
- 3.Chada S.R., Hollenbeck P.J. Mitochondrial movement and positioning in axons: the role of growth factor signaling. J. Exp. Biol. 2003;206:1985–1992. doi: 10.1242/jeb.00263. [DOI] [PubMed] [Google Scholar]
- 4.Leopold P.L., McDowall A.W., Brady S.T. Association of kinesin with characterized membrane-bounded organelles. Cell Motil. Cytoskeleton. 1992;23:19–33. doi: 10.1002/cm.970230104. [DOI] [PubMed] [Google Scholar]
- 5.Blocker A., Severin F.F., Griffiths G. Molecular requirements for bi-directional movement of phagosomes along microtubules. J. Cell Biol. 1997;137:113–129. doi: 10.1083/jcb.137.1.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Murray J.W., Bananis E., Wolkoff A.W. Reconstitution of ATP-dependent movement of endocytic vesicles along microtubules in vitro: an oscillatory bidirectional process. Mol. Biol. Cell. 2000;11:419–433. doi: 10.1091/mbc.11.2.419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hayden J.H. Microtubule-associated organelle and vesicle transport in fibroblasts. Cell Motil. Cytoskeleton. 1988;10:255–262. doi: 10.1002/cm.970100130. [DOI] [PubMed] [Google Scholar]
- 8.Welte M.A., Gross S.P., Wieschaus E.F. Developmental regulation of vesicle transport in Drosophila embryos: forces and kinetics. Cell. 1998;92:547–557. doi: 10.1016/s0092-8674(00)80947-2. [DOI] [PubMed] [Google Scholar]
- 9.Smith G.A., Gross S.P., Enquist L.W. Herpes viruses use bidirectional fast-axonal transport to spread in sensory neurons. Proc. Natl. Acad. Sci. USA. 2001;98:3466–3470. doi: 10.1073/pnas.061029798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ishii Y., Yanagida T. How single molecule detection measures the dynamic actions of life. HFSP J. 2007;1:15–29. doi: 10.2976/1.2723643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mallik R., Carter B.C., Gross S.P. Cytoplasmic dynein functions as a gear in response to load. Nature. 2004;427:649–652. doi: 10.1038/nature02293. [DOI] [PubMed] [Google Scholar]
- 12.Mehta A.D., Rock R.S., Cheney R.E. Myosin-V is a processive actin-based motor. Nature. 1999;400:590–593. doi: 10.1038/23072. [DOI] [PubMed] [Google Scholar]
- 13.Svoboda K., Block S.M. Force and velocity measured for single kinesin molecules. Cell. 1994;77:773–784. doi: 10.1016/0092-8674(94)90060-4. [DOI] [PubMed] [Google Scholar]
- 14.Ashkin A., Schütze K., Schliwa M. Force generation of organelle transport measured in vivo by an infrared laser trap. Nature. 1990;348:346–348. doi: 10.1038/348346a0. [DOI] [PubMed] [Google Scholar]
- 15.Shubeita G.T., Tran S.L., Gross S.P. Consequences of motor copy number on the intracellular transport of kinesin-1-driven lipid droplets. Cell. 2008;135:1098–1107. doi: 10.1016/j.cell.2008.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gross S.P., Welte M.A., Wieschaus E.F. Coordination of opposite-polarity microtubule motors. J. Cell Biol. 2002;156:715–724. doi: 10.1083/jcb.200109047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Müller M.J.I., Klumpp S., Lipowsky R. Tug-of-war as a cooperative mechanism for bidirectional cargo transport by molecular motors. Proc. Natl. Acad. Sci. USA. 2008;105:4609–4614. doi: 10.1073/pnas.0706825105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 19.Gross S.P. Application of optical traps in vivo. Methods Enzymol. 2003;361:162–174. doi: 10.1016/s0076-6879(03)61010-4. [DOI] [PubMed] [Google Scholar]
- 20.Nahmias Y.K., Odde D.J. Analysis of radiation forces in laser trapping and laser-guided direct writing applications. IEEE J. Quantum Electron. 2002;38:131–141. [Google Scholar]
- 21.Neuman K.C., Block S.M. Optical trapping. Rev. Sci. Instrum. 2004;75:2787–2809. doi: 10.1063/1.1785844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Visscher K., Schnitzer M.J., Block S.M. Single kinesin molecules studied with a molecular force clamp. Nature. 1999;400:184–189. doi: 10.1038/22146. [DOI] [PubMed] [Google Scholar]
- 23.Visscher K., Block S.M. Versatile optical traps with feedback control. Methods Enzymol. 1998;298:460–489. doi: 10.1016/s0076-6879(98)98040-5. [DOI] [PubMed] [Google Scholar]
- 24.Rohrbach A. Stiffness of optical traps: quantitative agreement between experiment and electromagnetic theory. Phys. Rev. Lett. 2005;95:168102. doi: 10.1103/PhysRevLett.95.168102. [DOI] [PubMed] [Google Scholar]
- 25.Bartlett P., Henderson S. Three-dimensional force calibration of a single-beam optical gradient trap. J. Phys. Condens. Matter. 2002;14:7757–7768. [Google Scholar]
- 26.Cermelli S., Guo Y., Welte M.A. The lipid-droplet proteome reveals that droplets are a protein-storage depot. Curr. Biol. 2006;16:1783–1795. doi: 10.1016/j.cub.2006.07.062. [DOI] [PubMed] [Google Scholar]
- 27.Berg-Sorensen K., Flyvbjerg H. Power spectrum analysis for optical tweezers. Rev. Sci. Instrum. 2004;75:594–612. [Google Scholar]
- 28.Carter B.C., Shubeita G.T., Gross S.P. Tracking single particles: a user-friendly quantitative evaluation. Phys. Biol. 2005;2:60–72. doi: 10.1088/1478-3967/2/1/008. [DOI] [PubMed] [Google Scholar]
- 29.Mallik R., Petrov D., Gross S.P. Building complexity: an in vitro study of cytoplasmic dynein with in vivo implications. Curr. Biol. 2005;15:2075–2085. doi: 10.1016/j.cub.2005.10.039. [DOI] [PubMed] [Google Scholar]
- 30.Vershinin M., Carter B.C., Gross S.P. Multiple-motor based transport and its regulation by Tau. Proc. Natl. Acad. Sci. USA. 2007;104:87–92. doi: 10.1073/pnas.0607919104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gross S.P., Welte M.A., Wieschaus E.F. Dynein-mediated cargo transport in vivo. A switch controls travel distance. J. Cell Biol. 2000;148:945–956. doi: 10.1083/jcb.148.5.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Welte M.A., Cermelli S., Gross S.P. Regulation of lipid-droplet transport by the perilipin homolog LSD2. Curr. Biol. 2005;15:1266–1275. doi: 10.1016/j.cub.2005.06.062. [DOI] [PubMed] [Google Scholar]
- 33.Hirokawa N., Sato-Yoshitake R., Kawashima T. Brain dynein (MAP1C) localizes on both anterogradely and retrogradely transported membranous organelles in vivo. J. Cell Biol. 1990;111:1027–1037. doi: 10.1083/jcb.111.3.1027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ma S., Chisholm R.L. Cytoplasmic dynein-associated structures move bidirectionally in vivo. J. Cell Sci. 2002;115:1453–1460. doi: 10.1242/jcs.115.7.1453. [DOI] [PubMed] [Google Scholar]
- 35.Pedersen L.B., Geimer S., Rosenbaum J.L. Dissecting the molecular mechanisms of intraflagellar transport in chlamydomonas. Curr. Biol. 2006;16:450–459. doi: 10.1016/j.cub.2006.02.020. [DOI] [PubMed] [Google Scholar]
- 36.Hendricks A.G., Perlson E., Holzbaur E.L. Motor coordination via a tug-of-war mechanism drives bidirectional vesicle transport. Curr. Biol. 2010;20:697–702. doi: 10.1016/j.cub.2010.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Soppina V., Rai A.K., Mallik R. Tug-of-war between dissimilar teams of microtubule motors regulates transport and fission of endosomes. Proc. Natl. Acad. Sci. USA. 2009;106:19381–19386. doi: 10.1073/pnas.0906524106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ali M.Y., Kennedy G.G., Warshaw D.M. Myosin Va and myosin VI coordinate their steps while engaged in an in vitro tug of war during cargo transport. Proc. Natl. Acad. Sci. USA. 2011;108:E535–E541. doi: 10.1073/pnas.1104298108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Leduc C., Pavin N., Diez S. Collective behavior of antagonistically acting kinesin-1 motors. Phys. Rev. Lett. 2010;105:128103. doi: 10.1103/PhysRevLett.105.128103. [DOI] [PubMed] [Google Scholar]
- 40.Sims P.A., Xie X.S. Probing dynein and kinesin stepping with mechanical manipulation in a living cell. ChemPhysChem. 2009;10:1511–1516. doi: 10.1002/cphc.200900113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Guck J., Ananthakrishnan R., Käs J. Optical deformability of soft biological dielectrics. Phys. Rev. Lett. 2000;84:5451–5454. doi: 10.1103/PhysRevLett.84.5451. [DOI] [PubMed] [Google Scholar]
- 42.Jamison D.K., Driver J.W., Diehl M.R. Two kinesins transport cargo primarily via the action of one motor: implications for intracellular transport. Biophys. J. 2010;99:2967–2977. doi: 10.1016/j.bpj.2010.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Jamison D.K., Driver J.W., Diehl M.R. Cooperative responses of multiple kinesins to variable and constant loads. J. Biol. Chem. 2012;287:3357–3365. doi: 10.1074/jbc.M111.296582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Carter N.J., Cross R.A. Mechanics of the kinesin step. Nature. 2005;435:308–312. doi: 10.1038/nature03528. [DOI] [PubMed] [Google Scholar]
- 45.Cho C., Reck-Peterson S.L., Vale R.D. Regulatory ATPase sites of cytoplasmic dynein affect processivity and force generation. J. Biol. Chem. 2008;283:25839–25845. doi: 10.1074/jbc.M802951200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gennerich A., Carter A.P., Vale R.D. Force-induced bidirectional stepping of cytoplasmic dynein. Cell. 2007;131:952–965. doi: 10.1016/j.cell.2007.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Alper J., Tovar M., Howard J. In vitro gliding assays indicate that Chlamydomonas dynein moves microtubules polymerized from Chlamydomonas axonemal tubulin faster than those polymerized from porcine brain tubulin. Biophys. J. 2012;102:371a–372a. [Google Scholar]
- 48.Reference deleted in proof.
- 49.Dembo M., Torney D.C., Hammer D. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. B Biol. Sci. 1988;234:55–83. doi: 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
- 50.Kunwar A., Tripathy S.K., Gross S.P. Mechanical stochastic tug-of-war models cannot explain bidirectional lipid-droplet transport. Proc. Natl. Acad. Sci. USA. 2011;108:18960–18965. doi: 10.1073/pnas.1107841108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cheng D., Kannan R., Wang G. A divide-and-merge methodology for clustering. ACM Trans. Database Syst. 2006;31:1499–1525. [Google Scholar]
- 52.Kannan R., Vempala S., Vetta A. On clusterings: good, bad and spectral. J. ACM. 2004;51:497–515. [Google Scholar]
- 53.King B., Stone M., Swinney H.L. Buoyancy frequency profiles and internal semidiurnal tide turning depths in the oceans. J.Geophys. Res. 2012;117 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


