Rapid Calculation of Protein pK_a Values Using Rosetta

Abstract

We developed a Rosetta-based Monte Carlo method to calculate the pK_a values of protein residues that commonly exhibit variable protonation states (Asp, Glu, Lys, His, and Tyr). We tested the technique by calculating pK_a values for 264 residues from 34 proteins. The standard Rosetta score function, which is independent of any environmental conditions, failed to capture pK_a shifts. After incorporating a Coulomb electrostatic potential and optimizing the solvation reference energies for pK_a calculations, we employed a method that allowed side-chain flexibility and achieved a root mean-square deviation (RMSD) of 0.83 from experimental values (0.68 after discounting 11 predictions with an error over 2 pH units). Additional degrees of side-chain conformational freedom for the proximal residues facilitated the capture of charge-charge interactions in a few cases, resulting in an overall RMSD of 0.85 pH units. The addition of backbone flexibility increased the overall RMSD to 0.93 pH units but improved relative pK_a predictions for proximal catalytic residues. The method also captures large pK_a shifts of lysine and some glutamate point mutations in staphylococcal nuclease. Thus, a simple and fast method based on the Rosetta score function and limited conformational sampling produces pK_a values that will be useful when rapid estimation is essential, such as in docking, design, and folding.

Introduction

Biological processes are profoundly influenced by the pH of their local cellular environment. For example, protein folding, enzyme catalysis, and protein-protein interactions are all pH dependent (1–3). Variations in pH can affect protein-protein binding energies by as much as 50% (4), and variable amino acid protonation states due to pH can result in significantly different complex conformations during small-molecule docking calculations (5). Rosetta, a highly successful biomolecular modeling and design package, does not have any dependency on pH. In this work, we added a pH dependency to Rosetta and calibrated relevant parts of the energy function based on our ability to calculate residue pK_a values.

The ability to evaluate residue pK_a values rapidly and accurately will help investigators design better drugs and more robust industrial enzymes that are stable and active over a range of pH values. The calculation of pK_a values can identify the strengths and deficiencies of the energy function, particularly with regard to the electrostatic components (6). Also, the availability of a large number of experimentally determined pK_a values allows benchmarking of energy functions to capture the effects of pH (7). We are especially interested in improving Rosetta’s ability to dock protein or small-molecule ligands to proteins, which is currently limited in the case of binding sites that contain charged atoms, because Rosetta’s algorithms do not account for alternate residue charge states.

Existing computational pK_a prediction algorithms can be broadly classified into four major branches and hybrid approaches. The first branch solves or approximates the Poisson-Boltzmann equation using grid-based continuum electrostatic models (8–13) with diverse dielectric constants (typically in the range of four to 20) to represent the protein interior. These methods have sometimes been found to overestimate the effects of charge-charge interactions (14), and often require several minutes to hours to estimate the pK_a value for a single residue. The second branch employs all-atom molecular dynamics (MD) simulations (15–20) using either explicit (AMBER/CHARMM force fields) or implicit solvent models (generalized Born potential). The third branch comprises quantum mechanics/molecular mechanics (QM/MM)-based methods, which treat the part of protein containing the titratable residue using ab initio QM and the rest of the protein environment using MM (21,22). The fourth branch uses a variety of empirical approaches, some of which employ geometric-based dielectric constants and empirical approximations for solvation, electrostatic, and hydrogen-bonding models (23–28). Each of these branches offers a distinct set of advantages, with the empirical approaches generally being computationally less expensive and the more-rigorous approaches benefiting from fundamental explanations of the underlying physical interactions. Studies have typically reported a prediction root mean-square deviation (RMSD) of <1 pH unit from experimental pK_a values.

Although the diversity in the array of current pK_a prediction algorithms is encouraging, developing a method that can incorporate extensive conformational flexibility while retaining a relatively small computational resource footprint remains a significant challenge. Complex phenomena, such as local conformational changes and coupled ionization pairs, continue to make computational pK_a predictions difficult to achieve. Some approaches tackle conformational flexibility through the use of MD snapshots, explicit side-chain sampling, or NMR structures (9,11,29–32). However, capturing conformational flexibility is expensive. Fast computations are needed to enable the use of pK_a calculation methods in protocols such as protein-protein docking and design, which themselves require generation of a large set of target conformations.

The fast and efficient Rosetta framework can thus be used for rapid estimation of pK_a values that can be useful for further calculations in structure prediction and design. Rosetta’s physics-based all-atom energy function (with terms for van der Waals, solvation, hydrogen bonding, etc.) is pairwise-additive and has used successfully in a wide range of applications (33–41). Nevertheless, Rosetta’s energy function does not include any explicit dependence on environmental conditions such as temperature, salt, and pH. Instead, investigators have assembled the energy function by combining physical and statistical potentials, and calibrating by the ability to identify native-like structures and sequences (33,42–44) and to predict free-energy changes upon mutation (45,46). Therefore, in this work, we begin to incorporate environmental dependence into the Rosetta energy function by using pK_a shifts to calibrate the Rosetta score function’s dependence on environmental pH.

In the remainder of this article, we describe a fast and simple physics-based method, termed Rosetta-pH, to estimate the pK_a values of five types of residues with varied protonation states (Asp, Glu, His, Tyr, and Lys). After showing that the standard Rosetta energy function cannot alone predict pK_a shifts, we add electrostatic terms and modify the solvation potential to create an improved score function. We then explore varying levels of conformational flexibility and test the performance of the method on a set of large pK_a shifts used in recent blind predictions (47).

Methods

In Rosetta pK_a calculations, the pH is titrated from 1 to 14 with Monte Carlo (MC) sampling of protonated and deprotonated side chains with χ-angles sampled from a backbone-dependent rotamer library (48), irrespective of the protonation state. We used an expanded rotamer library that includes additional rotamers that are one and two standard deviations away from the base rotamers, because we noted slight improvements in pK_a prediction accuracy with extra side-chain sampling (data not shown). Each rotamer configuration is accepted or rejected using the Metropolis criterion and the Rosetta score function. The conformational degeneracy in the protonated variants of Asp and Glu (with H atoms on either of the terminal O_δ and O_ε atoms, respectively) is explicitly incorporated by accommodating both possible protonated versions for the residues during sampling. The χ-angles for protons in the protonated variants are sampled at their canonical angles (−60, 60, 180) and ±20°. For neutral His, both possible tautomers (with proton on either N_δ1 or N_ε2 atoms) are sampled.

The protonation states of the lowest-energy conformers sampled during the side-chain conformational search were recorded during every pH step of the calculation (Fig. S1 in the Supporting Material shows the flowchart for the algorithm). An initial titration was carried out in intervals of 1 pH unit, starting with pH = 1 until a change in protonation state was observed, and subsequently a finer sampling interval of 0.1 pH unit was employed in the appropriate coarse interval. The pK_a was identified as the pH value at which the lowest-energy conformer of the residue shifted from the protonated to the deprotonated state. In the case of NMR structures, the entire ensemble of available structural models was used, and the mean of the calculated pK_a values over the structural dataset was used as a representative pK_a for the residue.

The Supporting Material includes a complete description of the experimental pK_a dataset, the Rosetta score function, and the command-line syntax for performing pK_a predictions with Rosetta.

Results and Discussion

Preliminary pK_a predictions

The standard all-atom Rosetta score function comprises several terms, including a Lennard-Jones potential, an implicit solvation potential, and an orientation-dependent hydrogen-bonding term. However, none of Rosetta’s standard score terms depend on the pH of the environment. Consequently, Rosetta assumes constant, standard side-chain protonation states for the ionizable amino acids irrespective of pH: Asp and Glu are assumed to be deprotonated, His and Tyr are assumed to be neutral, and Lys and Arg are assumed to be protonated. To resolve this issue, we created a means to treat the variable protonation states of amino acids.

Protonation potential

First, we added a protonation potential based on the probability of protonation of individual amino acid residues at a given pH. We used a simplified version of the potential described by Onufriev et al. (49) that has been used in pK_a estimations (11,12) and prediction of binding affinities (50). The probability of protonation $\left(f_{\text{prot}}\right)$ of an amino acid is

$$f_{\text{prot}}=\frac{1}{{10}^{\text{pH}-\text{Ip}{K}_{\text{a}}}+1},$$

and the protonation potential $\left(E_{\text{pH}}\right)$ is

$$E_{\text{pH}}=\{\begin{array}{cc}-k_{\text{B}}T\ln f_{\text{prot}}& \text{if}\text{protonated}\\ -k_{\text{B}}T\ln \left(1-f_{\text{prot}}\right)& \text{if}\text{deprotonated}\end{array},$$

where pH is defined by the environment, and $\text{Ip}{K}_a$ is the unperturbed intrinsic pK_a value of the model compound in solution (4.0 for Asp, 4.4 for Glu, 6.3 for His, 10.0 for Tyr, and 10.4 for Lys). $k_{\text{B}}T$ was assigned a value of 0.59 kcal/mol, corresponding to a temperature of 298 K. The free-energy gap of protonation between protonated and deprotonated variants of a residue, $\Delta E_{\text{pH}}$, is $2.3k_{\text{B}}T\left(\text{pH}-\text{Ip}{K}_{\text{a}}\right)$. The Supporting Material includes a derivation of pK_a values from the scores of the protonated and deprotonated variants.

Updating residue atom types

Second, to accumulate nonstandard charge-state amino acid variants, we updated the residue atom types to reflect the changes in the protonation state (see Table S1). For example, in the case of protonated Asp, the definition of terminal O_δ atom was modified from a carboxyl oxygen (OOC) in the standard residue to a hydroxyl oxygen (OH) in the protonated variant. The atom types determine the solvation and van der Waals parameters, and the ability to donate or accept hydrogen bonds.

pK_a predictions fail using the standard Rosetta score function

We initially evaluated the pK_a values for the assembled dataset of 264 residues using the protonation potential and the standard Rosetta score function. We calculated the pK_a values by using a single backbone conformation for x-ray crystal structures and averaging over the ensemble of models for NMR structures. The predicted pK_a values plotted against experimental pK_a values in Fig. 1 a are flat, that is, the calculated pK_a values demonstrate negligible shifts from the reference values. Only a few residues, such as H43 from Streptomyces subtilisin inhibitor (3SSI), show shifts (with the pK_a shifting to 2.0 from the reference value of 6.3). Most shifts can be attributed to steric hindrance from the neighboring residues, which renders the protonated variants highly unfavorable. The RMSD of predicted pK_a values relative to experimental pK_a values is 1.0 pH units. In comparison, the null model, in which all pK_a values are assumed to be unshifted from the reference intrinsic pK_a values, produces an RMSD of 0.94 pH units.

Figure 1.

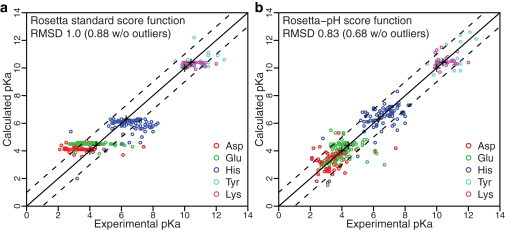
(a and b) Correlation between predicted and experimental pK_a values calculated using the standard Rosetta score function (a) without an explicit electrostatic potential and (b) with a distance-dependent Coulomb potential and calibrated solvation reference energies. In panel a, the prediction plots are flat (no shifts from the intrinsic pK_a values, denoted by + symbols) whereas in b, 78% of the pK_a predictions are within 1 pH unit from the experimental values (dashed lines) and only 4% of the predictions have errors > 2 pH units. Absolute pK_a values are plotted for clarity; see Fig. S2 for ΔpK_a correlation plots. Note that the RMSD values based on pK_a and ΔpK_a values are equivalent.

These results are not surprising, considering that Rosetta’s standard score function does not include a term for Coulomb electrostatics. Instead, Rosetta relies on a combination of an implicit solvation potential to capture the Born energy of ion burial (51), a statistical residue pair term to account for ion-ion pair interactions (52) and an orientation-dependent, hydrogen-bonding term (53) that rewards salt bridges. For the nonstandard residue protonation variants, the solvation and hydrogen-bonding scores are affected by the changed atom types. However, the residue pair-energy term (E_pair) is based on the probability of proximity of two amino acids in the PDB (normalized by the frequencies of residue-residue pairs in a given burial environment). Because the protonation states of residues in PDB crystal structures are not known, the pair statistics do not differentiate the protonated from the deprotonated forms.

Optimization of the Rosetta-pH score function for pK_a prediction

The shortcomings of the standard Rosetta energy function led us to modify it in two ways. First, to explicitly evaluate electrostatic effects, we added a simple form of a Coulomb electrostatic potential with a distance-dependent dielectric for gradual shielding at increasing interatomic distances (54). It includes a cap at short range and a shift to become zero at a long-range cutoff. The energy between atoms i and j is

$$E_{\text{elec}}^{ij}=\{\begin{array}{ll}322q_i{q}_j\left(\frac{1}{{\epsilon }_{\text{min}}{r}_{\text{min}}}-\frac{1}{{\epsilon }_{\text{max}}{r}_{\text{max}}}\right)& r_{ij}\le r_{\text{min}}\\ 322q_i{q}_j\left(\frac{1}{\epsilon r_{ij}}-\frac{1}{{\epsilon }_{\text{max}}{r}_{\text{max}}}\right)& r_{\text{min}}<r_{ij}<r_{\text{max}}\\ 0& r_{ij}\ge r_{\text{max}}\end{array},$$

where q₁ and q₂ are atomic charges, r_ij is the distance between atoms i and j, and ε is the dielectric constant, which is estimated as ε = 10r. The short- and long-range cutoff distances, r_min and r_max, are 1.5 Å and 5.5 Å, respectively, with ε_min = 10r_min and ε_max = 10r_max. The partial charges (q_i) for the side-chain atoms in standard amino acid variants and nonstandard protonation states were obtained from CHARMM27 (55). For deprotonated Tyr, the parameters were obtained from the quantum chemical calculations by Rabenstein et al. (56). The total Coulomb energy, E_elec, is evaluated by summing $E_{\text{elec}}^{ij}$ over all pairs of atoms in the protein.

Our second modification to the Rosetta score function arose from the solvation term. Rosetta uses the Lazaridis-Karplus implicit model for solvation (51), where the score for an atom i is evaluated as

$$E_{\text{solv}}^i=\Delta G_i^{\text{ref}}-\sum _{j\ne i}f\left(r_{ij}\right)V_j,$$

where r_ij is the distance between atoms i and j, V_j is the volume of neighbor atom j, $\Delta G_i^{\text{ref}}$ is reference solvation energy based on a fully solvated atom, and $f\left(r_{ij}\right)$ is the solvation free-energy density estimated by the Gaussian exclusion function (see Lazaridis and Karplus (51) for details). The total solvation energy for a residue, E_solv, is evaluated by summing $E_{\text{solv}}^i$ over all its atoms.

To test the effects of solvation on the side-chain protonation state, we plotted the difference in solvation energies between the protonated and deprotonated variants (ΔE_solv) against the degree of burial from solvent for all residues from the pK_a prediction dataset (Fig. S3). Negligible differences were observed in solvation scores between protonated and deprotonated variants in residues exposed to the solvent (<15 neighboring atoms), indicating equal preference for either variant. Solvation scores in Rosetta are zero for atoms exposed to solvent, because the Lazaridis-Karplus reference energy $(\Delta G_i^{\text{ref}})$ has been displaced by a separate reference score (aa_ref) derived using sequence recovery over a dataset of proteins (42). However, for solvent-exposed residues, considering alternate protonation states, the potential should favor the charged variant. Therefore, we derived reference scores for the five nonstandard protonation variants using a linear regression that minimizes the predicted pK_a RMSD over a subset of randomly selected 200 pK_a values (∼3/4 of the total dataset). For example, for Asp the pK_a predictions are optimal if the reference score for the protonated state shifts up by 0.59 score units relative to the deprotonated variant. Table S2 details the resulting reference scores.

Testing the effects of varying degrees of protein flexibility

Flexible target side chain

We employed the new energy function and evaluated pK_a values by sampling the χ-angles and protonation states of the target residue with the remaining protein held rigid. The method resulted in an RMSD of 0.83 pH units over the entire dataset (Fig. 1 b). Excluding 11 outliers that have prediction errors > 2 pH units, the remaining 253 residues have an RMSD of 0.68. We found that 92% of the predictions differed by <1.5 pH units from the experimental values, and more than half of them were accurate to within 0.5 pH units (Table S3).

The overall accuracy of the pK_a predictions usually decreased as the number of residue side-chain degrees of freedom increased (Table 1). The predictions were more accurate in the case of Asp, His, and Tyr (two χ-angles), with overall prediction RMSD values of 0.81, 0.82, and 0.77, respectively, compared with 0.92 in the case of Glu (three χ-angles). Although the RMSD for Lys residues (four χ-angles) is 0.67, it is still higher than the null-model RMSD of 0.59.

Table 1.

pK_a prediction RMSD by residue type and prediction method

	Number of χ angles	Null model	Standard Rosetta	Rosetta-pH score function
				Site repack	Neighbor repack	Ensemble average
Asp	2	0.96	1.1	0.81	0.87	0.83
Glu	3	0.83	0.88	0.92	0.88	0.92
His	2	1.0	1.2	0.82	0.86	1.0
Tyr	2	1.2	0.96	0.77	0.84	1.2
Lys	4	0.59	0.65	0.67	0.62	0.71
All	–	0.94	1.0	0.83	0.85	0.93

To improve the accuracy of predictions and understand the limitations of the method, we inspected residues with large pK_a errors. In the case of E17 and E26 from calbindin D9k (4ICB), calculating the pK_a values for each residue separately resulted in pK_a predictions of 5.3 and 5.2, compared with experimental values of 3.6 and 4.1, respectively (57). These two glutamate residues are structurally proximal (Fig. 2 a) and are involved in strong charge-charge interaction; hence, the large pK_a prediction errors can be attributed to the unrealistic assumption that the neighboring Glu residue is deprotonated across the entire range of pH values during titration. Therefore, the pK_a predictions are upshifted due to the high energetic penalty resulting from electrostatic repulsion.

Figure 2.

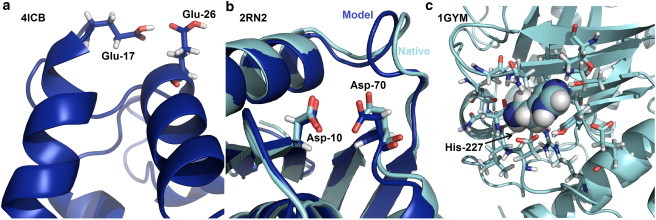
Conformational flexibility. (a) Interacting neighbor residues E17 and E26 from calbindin D9k (4ICB) are more accurately predicted when neighbor side-chain flexibility and protonation are allowed. (b) A structural model of RNase H (2RN2) generated using RosettaRelax (blue) compared with the native structure (cyan). D10 is closer to D70 in the model, resulting in a shift in the predicted pK_a value of the D10 from 4.0 using the native structure to 5.5 using the relaxed model. The experimental pK_a value for D10 is 6.1. (c) The structural model of H227 from phospholipase C (1GYM) has no space for a proton and thus highly favors the default (deprotonated) variant, resulting in a predicted pK_a of 2.7.

We also examined whether the pK_a predictions could identify the correct proton donor among the catalytic residues in hen egg white lysozyme (2LZT) and Bacillus circulans xylanase (1XNB). The catalytic sites of both lysozyme and xylanase have a Glu residue with a large upshifted pK_a value that acts as a proton donor, and a proximal carboxylic acid residue with a lower pK_a value that serves as a nucleophile (58,59). The Rosetta-pH method predicted pK_a values of 3.8 and 2.9 for the E35-D52 pair in lysozyme, and 3.0 and 4.1 for the E172-E78 pair in xylanase. The experimental pK_a values for the E35-D52 pair in lysozyme are 6.2 and 3.7, respectively, and those for the E172-E78 pair in xylanase are 6.7 and 4.6, respectively. Thus, a ranking of residues by their calculated pK_a values identified the correct proton donor in the case of lysozyme (pK_a^E35 > pK_a^D52) but failed in the case of xylanase. However, the method was unable to predict the large upward shifts in the pK_a values of Glu residues in either case. The upward shifts were likely absent because in this formulation, neighbor residues did not sample alternate protonation states. Thus, charge-charge interactions of proximal residues capable of adapting variable protonation states were not captured.

Flexible and protonatable neighbor side chains

In an effort to improve the treatment of local charge-charge interactions, we added conformational sampling of standard and alternate-charge-state side-chain rotamers of all the residues within 6 Å of the target residue. This approach allowed simultaneous sampling of variable protonation states for the E17-E26 pair from calbindin D9k (Fig. 2 a) and improved the predicted pK_a values to 3.7 and 4.1, respectively (experimental pK_a values are 3.6 and 4.1, respectively). The pK_a prediction accuracy for the E17-E26 pair is encouraging, because it is difficult to determine the optimal titration order in an ionizable pair when the difference between the respective residue pK_a values is small relative to the interaction energy involved (60).

However, the method still could not capture the large upward shift in the pK_a values of Glu residues in the catalytic sites of lysozyme and xylanase. The method predicted pK_a values of 3.7 and 2.7 for the E35-D52 pair in lysozyme, and 2.7 and 4.7 for the E172-E78 pair in xylanase. For xylanase, the method predicted a higher pK_a value for E78 relative to E172, thereby incorrectly identifying E78 as the proton donor and E172 as the nucleophile during catalysis. Thus, in this case, additional side-chain flexibility did not improve the accuracy of the pK_a predictions.

Over the complete dataset, adding neighbor side-chain sampling decreased the number of outliers from 11 to 7. However, in a few cases, sampling the extra side-chain conformations resulted in additional deviations (up to 0.3 pH units). Thus, the RMSD for predicted pK_a values (Fig. 3 a) over the complete dataset increased to 0.85 (0.73 excluding the outliers). The percentage of pK_a predictions within an error of 1 pH unit dropped slightly from 78% to 76%.

Figure 3.

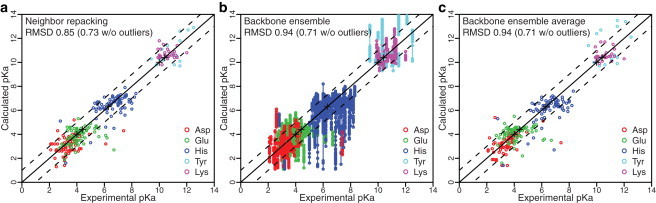
(a–c) Correlation between predicted and experimental pK_a values using (a) neighbor repacking and (b and c) a structural ensemble of 50 backbone conformations. (b) pK_a distribution for each generated structure in the ensemble. (c) Average pK_a value over the ensemble. The pK_a predictions are highly sensitive to local side-chain and backbone conformational changes.

Flexible backbone

For a second level of protein flexibility, we extended conformational sampling to the protein backbone. To explore the effects of a flexible backbone in x-ray crystal structures, it is first necessary to create an ensemble of backbone structures. To that end, we generated a conformational ensemble for each protein using RosettaRelax (33,61). RosettaRelax uses MC sampling employing small backbone dihedral angle (φ, ψ) perturbations followed by side-chain packing and minimization of the score function along the gradient in torsion space. We generated 50 structural models for each protein starting from its x-ray crystal structure. To enable comparisons with rigid backbone methods over the complete dataset, we also generated ensembles for NMR structures by choosing NMR Model 1 as the starting structure. The conformers generated using this protocol form a dense cluster with most models <1 Å C_α RMSD from the native structure (62).

For each residue, we evaluated the pK_a values separately using each of the 50 generated backbone models in the ensemble. As illustrated in Fig. 3 b, the predicted pK_a values for each residue were distributed over a wide range, demonstrating the sensitivity of pK_a predictions to even small changes in backbone conformation. Using the average pK_a value for each residue over the ensemble resulted in a distribution similar to that observed using a single representative structure (Fig. 3 c). The RMSD values for Asp, Glu, and Lys were comparable to those obtained without accounting for backbone flexibility (0.83, 0.92, and 0.71, respectively, compared with 0.81, 0.92, and 0.67), but the RMSD values for His and Tyr were far less accurate (1.0 and 1.2, respectively, compared with 0.82 and 0.77). The average pK_a values had an RMSD of 0.94 pH units over the complete dataset.

Fig. 2 b shows D10 from ribonuclease H (2RN2) as a representative example demonstrating the effect of backbone variation. A small backbone perturbation in one of the models generated with the use of backbone relaxation reduced the distance between D10 and D70, resulting in an increase in the predicted pK_a value from 5.0 with the crystal structure to 5.5, which is closer to the experimental pK_a value of 6.1. In contrast, in the case of H227 from phospholipase C (1GYM; Fig. 2 c), whose experimental pK_a value is 6.9, the predicted pK_a dropped dramatically from 6.6 with the crystal structure to 2.7 with the backbone ensemble. The pK_a shifted down because the backbone relaxation created a tightly packed core that fit only the deprotonated version of His, i.e., because the RosettaRelax protocol does not use alternate protonation states of residues in conformational sampling, it used the deprotonated His and compacted the structure too tightly to fit a hydrogen atom. Thus, the use of a backbone conformational ensemble improved the accuracy of some pK_a predictions but also resulted in significant downshifts in pK_a values for a few residues with stabilized deprotonated variants.

The increase in conformational degrees of freedom did not help in recovering the large upward shift in pK_a values of catalytic Glu residues in lysozyme and xylanase. Although the predicted pK_a value of 3.3 for D52 in lysozyme (experimental pK_a 3.7) was more accurate than predictions of 2.9 and 2.7 when sampling the target residue and neighboring side chains, respectively, the method predicted a pK_a value of 3.6 for E35, compared with the experimental pK_a value of 6.2. However, the additional backbone flexibility allowed the method to identify the correct proton donor among catalytic residues in xylanase, as the predicted pK_a value of 3.5 for E172 was higher than the predicted pK_a value of 2.2 for E78.

Extreme pK_a shifts—the staphylococcal nuclease set

In our main dataset, the majority of the residues had pK_a shifts of <1.5 pH units, and a few residues shifted up to 3.5 pH units. Members of the García-Moreno laboratory recently acquired experimental data for a large number of pK_a values for mutants at various positions in the highly stable Δ+PHS variant of staphylococcal nuclease (SNase). Some ionizable groups in hydrophobic regions shifted their pK_a values by as much as 5 pH units from their intrinsic pK_a values (63–70). The dataset of pK_a values was recently used in a large-scale, community-wide blind pK_a prediction challenge, called the pK_a Cooperative, for assessment of published pK_a prediction methods (47).

To test the efficacy of our method for predicting large pK_a shifts, we applied the optimized Rosetta-pH method to the SNase model system, with conformational flexibility limited to the target residue. Fig. 4 shows the correlation between predicted and experimental pK_a values represented relative to their shift from reference pK_a values. Encouragingly, the pK_a prediction RMSD for the set of Lys residues was 1.3 compared with a null-model RMSD of 3.4. The RMSDs for predictions in the case of Glu and Asp residue sets were 2.1 and 3 pH units respectively (the corresponding null-model RMSDs were 2.4 and 2.9). Although the large pK_a shift of the K66 mutant was predicted accurately (predicted pK_a = 5.3; experimental pK_a = 5.6), the method was unable to predict the large upshifts in the pK_a values of Asp and Glu mutants at the same position (predicted pK_a = 3.6 and 4.4; experimental pK_a = 8.7 and 8.5, respectively). Experimental studies revealed a network of internal water molecules in the case of E66 mutant (71) and a local conformational transition in the case of D66 mutant (72), and sensitivity of the pK_a values to the SNase global stability (66). These effects are difficult to capture. For other pK_a prediction methods using continuum electrostatics, investigators have resorted to the use of high dielectric constants (ε ≈ 10) to reproduce the magnitude of the pK_a shifts (68).

Figure 4.

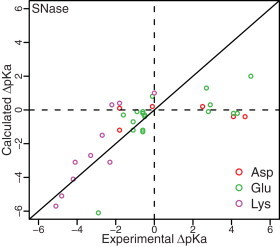
Correlation between predicted and experimental pK_a values for SNase mutants with large pK_a shifts.

Conclusion

We have developed a novel (to our knowledge) method, termed Rosetta-pH, that rapidly calculates the pK_a values of a diverse dataset. We find that 78% of the predictions are within 1 pH unit of the experimental pK_a values. The score function used for predictions includes a simple distance-based dielectric Coulomb potential that substantially increases the accuracy of pK_a predictions compared with the standard Rosetta score function. Coulomb interactions play a significant role in stabilizing the charged variants of buried residues to balance the effects of desolvation (47). However, it is perhaps surprising that employing a simple Coulomb potential generates pK_a predictions with an RMSD of 0.83 pH units using a single flexible target side chain. In comparison, the latest published versions of the widely used pK_a prediction algorithms MCCE2 (13) and PROPKA3 (25) report RMSDs of 0.90 and 0.79, respectively, over their corresponding datasets comprising 305 and 293 residues. (Note that using RMSD values to guide optimization of pK_a calculation algorithms does not guarantee physically realistic models, and RMSD values are highly dependent on the pK_a datasets used for calibration (7).) The successful prediction of large pK_a shifts in SNase point mutants also supports the efficacy of the fast and simple Coulomb electrostatic treatment.

In addition to the score function, pK_a prediction is influenced by the extent of conformational sampling. Other investigators have explored the effects of side-chain (11,29,32) and backbone (15,16,20) flexibility. For example, significant improvements in pK_a prediction accuracy were reported by Gunner et al. (73), Witham et al. (31), and Song (74), who employed Gromacs relaxation, MD snapshots, and Rosetta refinement, respectively, to incorporate backbone effects in MCCE pK_a calculations. Similarly, in Rosetta-pH, additional side-chain flexibility resulted in more accurate estimation of charge-charge interactions, and additional backbone flexibility improved relative pK_a predictions in catalytic residues. However, over the complete dataset, the prediction RMSD values increased from 0.83 to 0.85, and finally reached 0.94 pH units as we extended the sampling from a single side chain to multiple neighboring side chains and finally to the protein backbone (Table 1). One explanation for the reduced accuracy is simply the noise in the energy introduced by additional motions throughout the large protein. A second possible explanation for the dip is that the diversity of the generated backbone ensemble inaccurately represents the solution-state flexibility when alternate protonation states are possible. For example, during ensemble generation, the RosettaRelax protocol does not dynamically alter residue protonation states, thus biasing the structures toward standard protonation variants. Considering variable protonation states and calibrating RosettaRelax to generate an ensemble of thermodynamic states that can be used in Boltzmann weighting for pK_a estimations might improve the accuracy of the pK_a predictions.

Our treatment of the pK_a calculations is also very simple in that it defines the pK_a as the pH at which the lowest-energy state changes, instead of calculating the average over an ensemble of different protonated and deprotonated states at each pH. A more rigorous thermodynamic treatment would need to capture the titration dynamics by collecting side-chain rotamer frequencies during titration, and reproduce the titration curves to estimate the pK_a values. Such a treatment could better capture cases in which multiple structures make important contributions to the thermodynamic ensemble, or in which ionization effects are coupled.

The standard Rosetta standard score function has been applied very successfully to protein folding, design, and docking. However, before this work, the score function had not been developed to handle pK_a calculations. pK_a predictions are extremely sensitive to electrostatic treatments, so our hope is that these protocols will aid in improving and fine-tuning the Rosetta score function. Further studies employing the pK_a protocol can be used to test alternate electrostatic and solvation potentials in Rosetta, such as Poisson-Boltzmann treatments using matched interface- and boundary-method-based solvers (75) and semi-explicit solvation potentials (76). Ultimately, such calculations may also help introduce other environmental factors, such as temperature and salt concentration (77,78), into the Rosetta score function, but work is needed to reconcile the new score terms with the standard score function that is finely tuned for structure prediction and design applications.

The major goal of our study was to develop a fast method for identifying the most favorable protonation state at a given pH. Whereas a full titration requires ∼15–30 CPU seconds depending on the extent of conformational flexibility, Rosetta-pH can evaluate the most favorable protonation state at a given pH in less than a second. The meager computational requirements make Rosetta-pH sufficiently fast to dynamically sample, predict, and alter various probable protonation states on the fly during other calculations. Combined with the object-oriented design of the Rosetta modeling suite (79), our method makes it possible to integrate alternate protonation states and pH contexts into other protocols, such as protein folding, docking, and design.