Abstract
Longitudinal data analysis methods are powerful tools for exploring scientific questions regarding change and are well-suited to evaluate the impact of a new policy. However, there are challenging aspects of policy change data that require consideration, such as defining comparison groups, separating the effect of time from that of the policy, and accounting for heterogeneity in the policy effect. We compare currently available methods to evaluate a policy change and illustrate issues specific to a policy change analysis via a case study of laws that eliminate gun-use restrictions (shall-issue laws) and firearm-related homicide. We obtain homicide rate ratios estimating the effect of enacting a shall-issue law that vary between 0.903 and 1.101. We conclude that in a policy change analysis it is essential to select a mean model that most accurately characterizes the anticipated effect of the policy intervention, thoroughly model temporal trends, and select methods that accommodate unit-specific policy effects. We also conclude that several longitudinal data analysis methods are useful to evaluate a policy change, but not all may be appropriate in certain contexts. Analysts must carefully decide which methods are appropriate for their application and must be aware of the differences between methods to select a procedure that generates valid inference.
Keywords: Generalized estimating equations, generalized linear mixed models, meta-analysis, empirical Bayes
1 Introduction
1.1 Evaluating a Policy Change
Evaluations designed to generate inference regarding the impact of a policy change are common in the current literature of several disciplines, including biomedical research, injury prevention, and econometrics. Examples include contrasting repeated measures among patients receiving surgical treatment for lumbar spinal stenosis and those receiving non-surgical treatment [1], evaluating the effectiveness of centerline rumble strips in reducing opposing-direction automobile collisions [2], and determining the effect of welfare reform on health insurance coverage for women and children [3].
Even though studies of the impact of a new policy are common, there does not appear to be a unified approach to formally evaluate a policy change. In fact, the analysis methods employed vary considerably, from simple to sophisticated. For example, some policy researchers advocate the use of a simple “difference in differences” method, which involves calculating differences in the observed outcome, first for each study unit over time and then between a defined “treatment” and “control” group [3]. The “difference in differences” estimator allows different pre- and post-policy temporal trends and exploits the pre-policy temporal trends in the “control” group to represent the post-policy temporal trends in the “treatment” group. A simple method popular among medication use researchers is “segmented regression” analysis of interrupted time series data, which involves treating observations as a time series, fitting a least squares regression model for each study unit, and accounting for autocorrelation [4]. Econometricians frequently perform a “regression discontinuity” analysis, which involves fitting separate kernel-weighted linear regression models to the data before and after a policy change and forming contrasts based on the left and right limits of these models at the policy change [5].
More sophisticated methods, which we elaborate upon in this paper, include generalized estimating equations, generalized linear mixed models, and methods that use empirical Bayes estimators to form contrasts between observed and expected outcomes. Although there are important differences between these methods with respect to implementation and inference, they all utilize longitudinal methodology in some form to attempt to account for the correlation induced by repeatedly collecting observations over time and/or space. Surprisingly, there are studies in the current literature that ignore this correlation and provide inference that may be invalid [6].
Methods for analyzing longitudinal data are well studied, but there are unique aspects of policy change data with respect to implementation and inference that require careful thought and consideration. The primary challenge of a policy change analysis is defining groups between which to compare units with and without the policy change, while using all available data. Policy change data are typically comprised of outcomes collected over time on aggregate study units such as health care centers or governmental jurisdictions. Often some units experience the policy change during the study period, while others do not. This leads to partial crossover data. In this situation it is possible to exploit both within-unit and between-unit contrasts to generate inference regarding the policy effect. One approach is to control for time and contrast the mean outcome among all units with the policy to that among all units without the policy. Essentially, such an analysis captures the cross-sectional information regarding the difference in the average outcome with and without the policy. Another approach is to match on study unit and summarize the mean difference between outcomes within a unit after policy implementation and outcomes within the same unit prior to implementation. Such an analysis exploits the within-unit change in policy, but is not applicable for units that either never implemented the policy or implemented it prior to the study period.
Secondary challenges include properly separating the effect of time from that of the policy, accounting for heterogeneity in the policy effect, and accounting for serial correlation within study units. First, the outcome of interest may vary considerably over time due to a strong temporal trend. Therefore it is important to ascertain what amount of variability is due to the temporal trend and what amount is due to the new policy. Otherwise calendar time may confound the policy effect. Second, study units may be intrinsically different from one another. Therefore the impact of the policy may vary across units even after controlling for measured factors. To characterize the average policy effect it may be necessary to model unit-specific policy effects. Third, correlation may be induced within study units by repeatedly collecting observations on the same units over time. Failure to accurately account for longitudinal correlation may result in invalid inference.
In this paper we compare and contrast currently available statistical techniques for analyzing longitudinal data in the context of evaluating a policy change. Our goals are to explore the situations in which these methods are appropriate, educate researchers on the challenges of a policy change analysis, and provide a unified framework for proper analysis of policy change data. We describe the theoretical framework for these methods, discuss issues that are specific to evaluating a policy change, and provide an illustrative example. The goal of the example is to estimate the effect of state laws that eliminate gun-use restrictions, or shall-issue laws, on firearm-related homicide [7].
1.2 Evaluating Gun-use Laws
There is considerable debate as to whether eliminating gun-use restrictions increases or decreases violent crime [8]. Lott and Mustard [6] obtained crime, arrest, income, and demographic information for every county in the United States from 1977 to 1992 and determined when each state enacted a shall-issue law. They used ordinary least squares to estimate the effect of enacting a shall-issue law on the expected log crime rate, weighted by population size. They concluded that “allowing citizens to carry concealed weapons deters violent crimes.” However, Lott and Mustard’s conclusions were challenged. Webster and colleagues [9] discussed several flaws in Lott and Mustard’s statistical model, including measurement error in the shall-issue explanatory variable and inadequate adjustment for cyclical changes in crime. Webster and colleagues stated that these problems “are likely to bias results toward finding crime-reducing effects of shall-issue laws.”
Lott and Mustard’s inference was also undermined by their estimation method. Ordinary least squares assumes that observations repeatedly collected on a study unit are independent and assumes that units are independent of one another. Because Lott and Mustard collected county-level data from 1977 to 1992, observations collected within a county over time are temporally correlated. In addition, because a given county may be more similar to an adjacent county than to a non-adjacent county, county-level observations are spatially correlated. Ordinary least squares ignores both temporal and spatial correlation. If either one is non-zero, then standard errors are likely to be underestimated. Therefore confidence intervals and p-values are anti-conservative, which may provide invalid inference.
In Section 2 we describe statistical models to assess the impact of a new policy. We introduce two models for the outcome of interest in Section 2.1 and discuss issues related to specifying a mean model in Section 2.2. In Section 3 we review estimation methods that are currently available to evaluate a policy change: generalized estimating equations (Section 3.1), generalized linear mixed models (Section 3.2), random effects meta-analysis (Section 3.3), and methods based on empirical Bayes estimators (Section 3.4). We summarize a recently published evaluation of shall-issue laws and firearm-related homicide in Section 4. In Section 5 we analyze the data from this study using the methods we introduce. We provide concluding discussion in Section 6. In the Supplementary Material we detail variance estimation for empirical Bayes estimators.
2 Statistical Models
2.1 Notation
Let yij denote the observed outcome for unit i = 1, …, n during time period j = 1, …, mi. Similarly let xij denote the set of covariates collected for unit i during time period j and let Nij denote population size, or the total number of individuals in unit i during time period j. We are interested in a cross-sectional model for μij, the expectation of yij given covariates xij and parameters β to be estimated. We consider this model within two different frameworks: marginal and conditional.
The outcome of interest in our case study is the number of homicides due to firearms, which we assume to follow a Poisson distribution. As is standard when analyzing count data, we model the mean homicide rate instead of the mean number of homicides. We therefore include log Nij as an “offset” in both the marginal and conditional model. The marginal model relates the expectation of yij to xij via a log link function:
The marginal model assumes that the variance of yij is a known function ϕV (μij), where ϕ represents a dispersion parameter to be estimated. The model also assumes that the correlation between yij and yij′ (j ≠ j′) is a known function ρ(α), where α represents correlation parameters to be estimated.
In the marginal model β are fixed parameters. Conversely, the conditional model assumes that certain effects vary across units. The conditional model includes a set of covariates zij, which may be equal to xij or a subset of xij, and relates the expectation of yij to xij and zij via a log link function:
We write β⋆ for the parameters of interest in the conditional model because they may differ from those in the marginal model. Note that γi are vectors of mutually independent, unit-specific random effects with a common underlying distribution. These random effects induce a correlation structure between yij and yij′. The model assumes that given γi, {yi1, …, yimi} are mutually independent and have an exponential family density. Similar to the marginal model, the conditional model assumes that the variance of yij given γi is a known function .
2.2 Modeling the Mean
Perhaps the most important goal of any statistical analysis is to correctly model the mean, i.e. the systemic variation of yij across covariate values xij. This requires deciding which variables to include in the model and specifying their functional relationship with the outcome of interest. There are several features of policy change data that present challenges to analysts with respect to specifying a mean model.
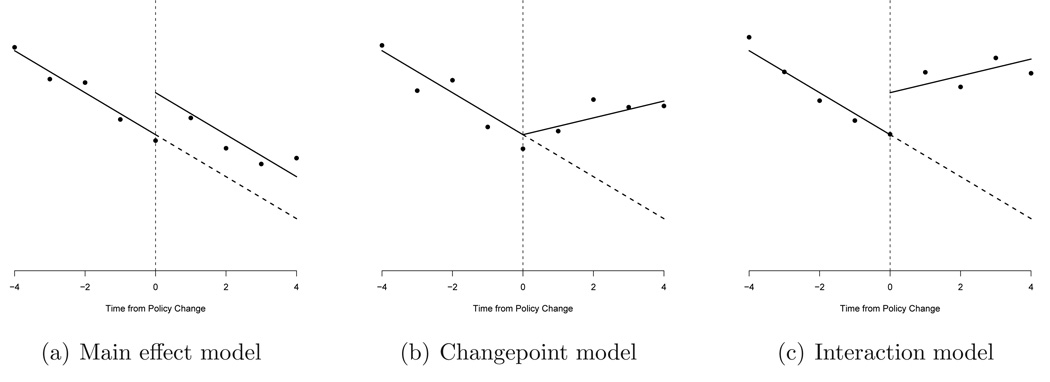
Figure 1 presents three hypothetical mean models to evaluate the impact of a new policy. The horizontal axis is time from policy change; a vertical line at zero represents the policy change. Circles represent the observed outcome during a given time period. Solid lines represent the estimated association between time and the outcome before and after implementing the policy. Dashed lines represent the expected association had the policy change not occurred. Of primary interest is the difference between the observed outcome after the policy change and the expected outcome had the policy change not occurred.
Figure 1.
Hypothetical mean models to evaluate a policy change
Figure 1(a) presents a main effect model, which is the simplest and least flexible model. The main effect model assumes that the policy change is associated with an immediate change in the expected outcome and that this effect is constant across time. In addition, it assumes that the temporal trend is the same before and after the policy change. Figure 1(b) presents a changepoint model, which is more flexible than a main effect model. The changepoint model assumes that the effect of time is different before after the policy change and that the policy change is not associated with an immediate change in the expected outcome. Figure 1(c) presents an interaction model, which relaxes the assumptions of the main effect and changepoint model. The interaction model allows the effect of time to be different before and after the policy change. It also allows an immediate change in the expected outcome associated with the policy change. Proponents of “segmented regression” recommend the interaction model [4]. Analysts must decide which of these models, if any, most accurately characterizes the anticipated effect of the policy intervention.
A variation of the main effect model is one in which the binary intervention is treated as continuous in the analysis. That is, instead of using an indicator variable, analysts could use a continuous variable, perhaps with a range between 0 and 1. For example, for years without the policy the continuous variable would be coded as 0. For the first year after the policy was implemented, the variable would be coded as 0.1, for the second year after as 0.2, and so on. Coding the intervention in this manner would emulate a more gradual effect of the policy change and may be more scientifically relevant in certain contexts.
The mean models presented in Figure 1 raise the central challenge of a policy change analysis: defining groups between which to compare units with and without the policy change. In Figure 1 the time scale is time from policy change. This is a convenient time scale for units that implemented the policy during the study period because each unit has a meaningful reference point in time. In addition, aligning units by time from policy change lends to a natural comparison between observed and expected outcomes across units. However, not all study units may have implemented the policy during the study period and hence time from policy change is not a meaningful scale for all units. To overcome this difficulty analysts may decide to only consider units with the policy change. This choice is often undesirable, however, because the information contained in units without the policy change is lost. Alternatively, analysts may choose a time scale such as calendar time to match units with and without the policy change.
A possibly attractive alternative to selecting one of the mean models presented in Figure 1 is to simply contrast the mean outcome before the policy change ȳB with the mean outcome after ȳA. However, this approach may be problematic. Suppose that in truth μij is linearly related to a continuous variable for calendar time tij and a policy indicator pij:
Interest lies in estimating β1, the policy effect. Consider a simple estimate Δ̂ = ȳA − ȳB and examine its expectation:
Therefore the estimate Δ̂ = ȳA − ȳB is a biased estimator for the policy effect if a linear temporal trend exists because the mean time after the policy change t̄A is not necessarily equal to the mean time before t̄B. For non-linear models the absolute difference between ȳA and ȳB may be an inappropriate summary measure. For example, the ratio of ȳA to ȳB would be a natural crude estimate associated with a log-linear model.
One approach to remove the bias associated with a temporal trend is to adjust for calendar time. Suppose that each unit has unique time and policy effects:
We assume that interest lies in estimating the average policy effect Eβ[β1i]. Consider unit-specific estimates and examine their expectation with respect to Y:
Next examine the expectation of EY [Δ̂i] with respect to βi:
Therefore the average of the unit-specific estimates is a biased estimator for the average policy effect if unit-specific temporal trends exist. However, Δ̄ is an unbiased estimator for the average policy effect if and only if Eβ[β2i] = 0. This will occur if the global temporal trend is negligible, i.e. if the average of the unit-specific temporal trends is approximately zero. This suggests that analysts should adjust for calendar time to remove temporal trends and correctly estimate the policy effect.
Another approach to remove the bias associated with a temporal trend is that of the “difference in differences” estimator. This approach exploits the pre-policy temporal trends in the “control” (C) group to represent the post-policy temporal trends in the “treatment” (T) group. Examine the expectation of the “difference in differences” estimator Δ̃:
Therefore the “difference in differences” estimator is an unbiased estimator for the policy effect assuming that the temporal trends in the “treatment” and “control” group are identical. The main difficulty of this approach is defining a pre- and post-policy time for the “control” group. This definition may be arbitrary for most observational data because no specific time is identified as the time of policy implementation for units without a policy change.
Defining groups between which to compare units with and without the policy change is of central importance. One simple approach is to contrast the mean outcome before the policy change with that after via an estimate such as Δ̂. Inference based on this approach assumes that temporal trends do not exist. Another simple approach is to calculate Δ̄, the average of the unit-specific estimates. Although this approach accommodates unit-specific temporal trends, inference based on this approach assumes that the global temporal trend is negligible. In addition, because a unit-specific estimate is only available for units that implemented the policy during the study period, this approach may not utilize all available data. Yet another approach is to calculate differences in the observed outcome, first for each study unit over time and then between a defined “treatment” and “control” group using the “difference in differences” estimate Δ̃. Inference based on this approach assumes that temporal trends in the “treatment” and “control” group are identical. In addition, this approach may not utilize all available data because the difference in the observed outcome for each unit over time is not available for units without a policy change. Therefore more sophisticated methods are required to allow analysts to specify a mean model of choice, include units without a policy change, and adjust for temporal trends (via calendar time) and other important factors.
2.3 Modeling Heterogeneity
Once the mean has been correctly modeled, analysts may explore models for the variance of the outcome of interest and the correlation between observations collected on the same study unit. This is especially important in longitudinal data analysis, for if the correlation between repeated measures is not correctly modeled, then the analysis method may be inefficient and inference may be invalid. There are several popular methods for modeling variance and correlation that are useful in the context of evaluating a policy change. We review them in the following section.
3 Estimation Methods
In this section we review existing longitudinal data analysis methods that are appropriate for assessing the impact of a new policy. We briefly review generalized estimating equations and generalized linear mixed models, which are standard longitudinal data analysis methods. We thoroughly review random effects meta-analysis and methods based on empirical Bayes estimators, which are not as commonly used in a longitudinal context. All of these methods allow analysts to specify a mean model of choice, include units without a policy change, and specify a flexible adjustment for temporal trends. However, we show that there are differences between these methods with respect to implementation and inference that are important in the context of evaluating a policy change. Table 2 previews these differences.
Table 2.
Relative merits of methods to evaluate a policy change
| Criterion | GEE | GLMM | Meta | EB |
|---|---|---|---|---|
| Allow flexible adjustment for time | + | + | + | + |
| Model heterogeneity in policy effect | − | + | + | + |
| Model longitudinal correlation | + | + | − | + |
| Provide direct inference to: | ||||
| “Level 1” (e.g., U.S. population) | + | +/− | − | +/− |
| “Level 2” (e.g., states) | − | +/− | + | +/− |
3.1 Generalized Estimating Equations (GEE)
GEE is a marginal method that estimates an population-level policy effect, which does not accommodate heterogeneity in the effect across units. GEE models longitudinal correlation by specifying a working covariance matrix [10]. A basic choice is working independence, in which observations collected on the same unit are assumed to be independent. Under this specification the variance estimate of β̂ is appropriately adjusted to account for longitudinal correlation using the so-called “robust” or “sandwich” variance estimate that is available in many statistical packages (e.g., Stata). Other popular choices for the working covariance matrix are exchangeable, in which the correlation between observations collected on the same unit is constant, and autoregressive, in which the correlation is a function of the time between observations. We implement GEE via the R package geepack [11]. Chapter 8 of Analysis of Longitudinal Data [12] provides a general overview of GEE. Carriere, Roos, and Dover [13] discuss an estimating equation approach to health care utilization data.
3.2 Generalized Linear Mixed Models (GLMM)
GLMM is a conditional method that accommodates heterogeneity in the policy effect and estimates an average policy effect via maximum likelihood. Recall that in the conditional model β⋆ represents the parameters of interest and γi represents unit-specific random effects, which induce a model for longitudinal correlation. The GLMM framework assumes that the repeated measures are independent given the random effects and that the random effects are independent and identically distributed given the covariates. Maximum likelihood estimation of β⋆ treats γi as unobserved nuisance random variables, which are typically assumed to follow a Normal distribution with mean zero with covariance matrix D [14]. We implement GLMM via the R package lme4 [15]. Chapter 9 of Analysis of Longitudinal Data [12] provides a general overview of GLMM for longitudinal data. Daniels and Gatsonis [16] present hierarchical generalized linear models and their application to health care utilization data. Tooze, Grunwald, and Jones [17] provide a mixed model approach to health policy data with “clumping” at zero.
3.3 Random Effects Meta-analysis
Meta-analysis is a conditional method that combines information across multiple studies, which typically involves averaging summary measures obtained via a literature review of independent studies of a similar comparison [18]. Our implementation is different from a classic epidemiological meta-analysis in that we treat study units as independent “studies” of the association between exposure and outcome. We estimate state-specific log homicide rate ratios β̂i by fitting a single Poisson regression model that includes an interaction between an indicator variable for a shall-issue law and an indicator variable for each state. We are able to include units without a policy change by fitting a single model in which all states contribute information regarding adjustment covariates such as calendar time. We average the state-specific estimates using the R package rmeta [19] to obtain an estimate of the average policy effect and a summary of the magnitude of state-to-state heterogeneity in the policy effect.
When implementing a meta-analysis analysts must decide between a fixed or random effects model. In the fixed effects model each study-specific estimate β̂i is assumed to arise from a population of estimates with common mean β and known variance . Each quantifies the amount of “within-study” variation. Although robust estimates of are not computable, estimation of each could accommodate correlation structures such as autoregressive. The model assumes that the fixed effects are independent and follow a Normal distribution:
In the random effects model each β̂i is assumed to arise from a subpopulation of estimates, each with mean βi and known variance . In addition, each βi is assumed to arise from a population of parameters with mean β and variance τ2. The parameter τ2 quantifies the amount of “between-study” variation. The model assumes that the random effects are independent and imposes a hierarchical structure:
We assume a random effects framework to accommodate state-specific effects and to allow for both “within-study” and “between-study” variation. We prefer the random effects framework because the fixed effects framework assumes that there is no “between-study” variation and it seems unlikely that there would be no variation in the policy effect between states. Note that rmeta uses the DerSimonian and Laird estimate of τ2 [20].
3.4 Empirical Bayes (EB) Estimators
In previous sections we presented methods based on simple summary statistics such as a difference in means and more sophisticated regression-based methods such as GEE and GLMM. An issue with these regression techniques is that time must be modeled appropriately and we have commented that analysts must carefully consider temporal trends both before and after a policy change. An alternative method exists that combines the sophistication of advanced regression-based methods, which model unit-specific policy effects and adjust for important covariates, with the attractive simplicity of contrasting post-policy means with their expectation under the absence of a policy change. This technique is known as empirical Bayes and is popular among road safety researchers [2].
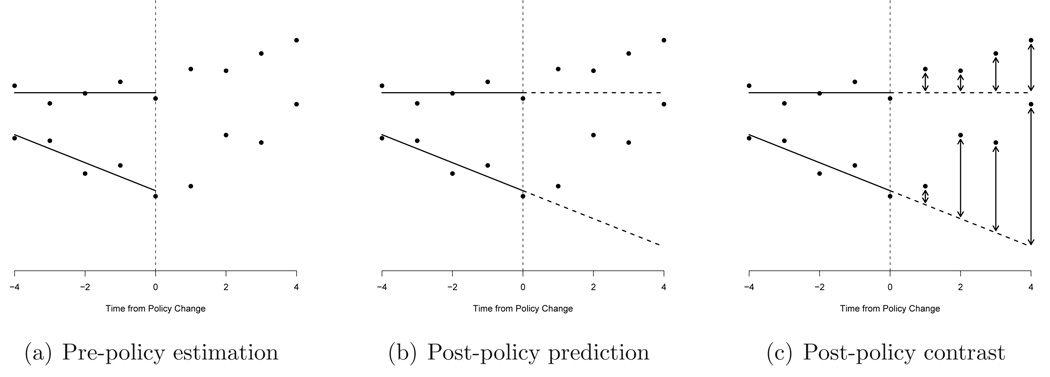
Although EB estimators represent a broad class of estimators [21], we focus on an EB procedure specifically designed to generate conditional inference from partial crossover data. The main idea is to use a hierarchical regression model to characterize the temporal trends prior to policy implementation and use this model to predict the outcome in time periods subsequent to the policy change. Thus the flexibility of regression-based methods is exploited to forecast expected outcomes, but a regression model for outcomes after the policy change is not required. We graphically summarize this procedure in Figure 2, in which circles represent hypothetical data observed for two units.
Figure 2.
Summary of empirical Bayes procedure
The EB procedure involves fitting a mixed effects model, represented by solid lines in Figure 2(a), to the data observed before the policy change. We recommend that in addition to random intercepts, this model include random time effects to account for unit-specific temporal trends. Units that never implemented the policy can be incorporated into the mixed effects model, but units that implemented the policy before the study period cannot. The fixed and random effects estimated from the pre-policy data are used to predict the expected outcomes after the policy change for each study unit, represented by dashed lines in Figure 2(b). These expected outcomes are contrasted with the data observed after the policy change for each unit. These contrasts, represented by vertical arrows in Figure 2(c), are averaged within each unit to estimate unit-specific policy effects. A simple statistic is used to estimate the average policy effect, such as a between-unit average of the unit-specific estimates. We are interested in estimating the homicide rate ratio associated with enacting a shall-issue law. In this case an EB estimate of the average log policy effect is:
An advantage of an EB analysis is that each unit-specific estimate Δ̂i is “shrunk” toward the average of the unit-specific estimates Δ̄. This tends to draw extreme estimates toward the rest of the individual estimates. The degree to which each unit-specific estimate is “shrunk” depends on the amount of data observed for each unit and the overall variability of the estimated unit-specific effects. If a large amount of data is observed for a study unit, then there will be little shrinkage in its estimated effect. Conversely, with little overall variability of the unit-specific estimates, there will be large shrinkage because the model suggests that there is little real variation in the effect between units.
The main difficulty of an EB analysis is calculating the standard error of Δ̄. This difficulty arises because unit-specific estimates Δ̂i share common fixed effects β̂⋆, implying that their correlation is non-zero. Standard error computation is simplified by assuming that the unit-specific estimates are uncorrelated, effectively ignoring variation due to estimation of pre-policy model parameters. In this case the variance of Δ̄ can be estimated by s2 = Var[Δ̂i], as in a one-sample t-test. Hence a (1 − α)% confidence interval for the average policy effect is . In the Supplementary Material we derive a simple estimator for the variance of Δ̄ that incorporates the variance in and correlation between unit-specific estimates.
3.5 Role of the Model
There are several interesting comparisons between a GLMM and an EB analysis. For example, both accommodate unit-level heterogeneity in the policy effect by conditioning on unit-specific policy effects, but estimate unit-specific effects differently by explicitly modeling different portions of the data. Recall our simple estimate, which is a summary statistic based on a contrast between observed outcomes before and after the policy change:
A GLMM employs a purely model-based approach to estimating unit-specific policy effects by including a random effect for policy in the model. As we showed in Figure 1, these estimates can be thought of as a contrast between expected outcomes given a post-policy model ℳA and expected outcomes given a pre-policy model ℳB that is extrapolated to post-policy times tA:
An EB analysis combines a model-based approach with a simple summary statistic and estimates unit-specific policy effects by contrasting observed and expected outcomes after the policy change for each unit. As we showed in Figure 2, these estimates can be thought of as a contrast between observed outcomes after the policy change and expected outcomes given an extrapolated pre-policy model:
Both a GLMM and an EB procedure rely on a pre-policy model ℳB to extrapolate to post-policy times. A GLMM additionally relies on a post-policy model ℳA, whereas an EB procedure simply exploits the observed data. Valid inference generated from a GLMM requires that both models are correct. If these models are correct, then a GLMM may be superior to an EB analysis. Conversely, if only the pre-policy model is correct, then an EB analysis may be superior.
3.6 Interpretation
Generally, the interpretation of a conditional parameter estimate is not the same as that of a marginal parameter estimate. The parameter estimates obtained from a marginal model estimate population-level contrasts and inference is made on the population level. Conversely, the parameter estimates obtained from a conditional model estimate unit-specific contrasts.
There are situations in which the estimates obtained from a marginal and conditional model both estimate a population-level contrast [22]. Consider an analysis with an outcome repeatedly collected on units in a sample. Suppose a single covariate is also measured and its cross-sectional relationship with the outcome is of interest. If the outcome is continuous and follows a Normal distribution and we fit a linear model with random intercepts and/or slopes, then β̂⋆ (the regression parameter estimated from the conditional model) estimates a population-level contrast. Moreover, if the outcome is a count and follows a Poisson distribution and we fit a log-linear model with random intercepts, then β̂⋆ estimates a population-level contrast. However, if we fit a log-linear model that includes random slopes, then β̂⋆ estimates a unit-specific contrast. In addition, if the outcome follows a Binomial distribution and we fit a logistic model with random intercepts and/or slopes, then β̂⋆ estimates a unit-specific contrast.
In our case study we assume that the number of homicides due to firearms follows a Poisson distribution. Therefore if we fit a log-linear model with random intercepts, then we interpret the estimated effect of enacting a shall-issue law as a population-level contrast. However, if the model includes random slopes, then we interpret the estimated effect as an average state-specific effect.
It is important to note that in our case study individual-level data were partially aggregated for strata defined by gender, race, and age; stratum-specific counts for population size and firearm-related homicide were available. The data were not fully aggregated into a single count with corresponding state demographic characteristics. Therefore the effects of these factors can be interpreted at the individual level and are not subject to the bias incurred from the ecological fallacy [23].
4 Case Study
4.1 Introduction
Rosengart and colleagues [7] described a study to determine whether state gun laws are associated with firearm-related homicide and suicide. Yearly deaths due to firearms were collected from all 50 states and the District of Columbia from 1979 to 1998. During this period 289,719 firearm-related homicides occurred in the United States. Data were grouped into gender, race, and age strata and stratum-specific counts for population size and firearm-related homicide were available. State-specific characteristics were also available, including measures of unemployment and poverty, and proportion of residents living in a metropolitan area. Although Rosengart and colleagues studied five state gun laws, we focused specifically on shall-issue laws, which permit an individual to carry a concealed handgun unless another statute provides a restriction. We also limited our focus to firearm-related homicide. Rosengart and colleagues provided additional details regarding this study, including data collection, covariate adjustment, and comprehensive results.
4.2 Graphical Displays
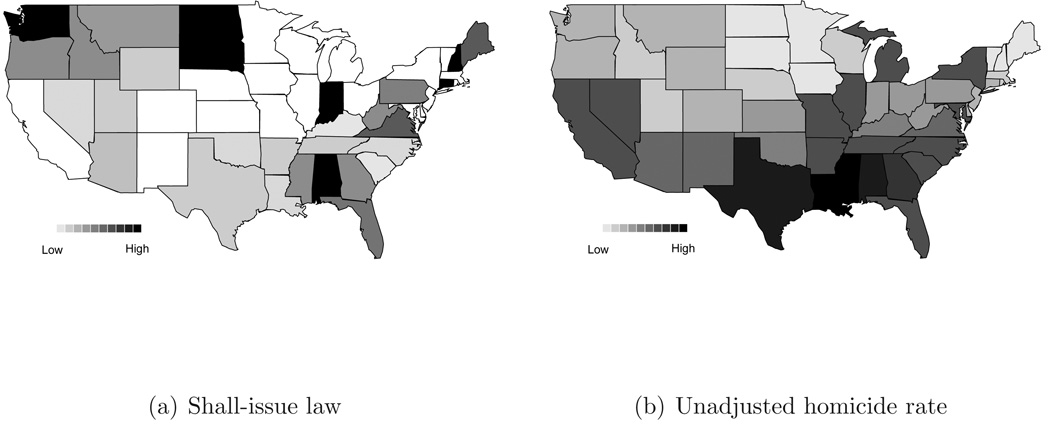
Figure 3(a) displays the total duration of a shall-issue law for each state in the contiguous United States. Darker states had a longer duration of a shall-issue law. Figure 3(b) displays the average unadjusted firearm-related homicide rate for each state. Darker states had a higher homicide rate. States with a greater duration of a shall-issue law appear to be clustered in the Northwest and the Upper Midwest, as well as in the Northeast and South. States with a higher firearm-related homicide rate appear to be clustered in the southern half of the United States. Comparing Figure 3(a) to Figure 3(b), at least two interesting patterns emerge. In the Northwest and Upper Midwest several states with greater exposure to a shall-issue law had a low firearm-related homicide rate (e.g., North Dakota, South Dakota, and Washington). Conversely, several states in the South with greater exposure to a shall-issue law had a high firearm-related homicide rate (e.g., Alabama, Georgia, and Mississippi).
Figure 3.
Total duration of a shall-issue law and average unadjusted homicide rate
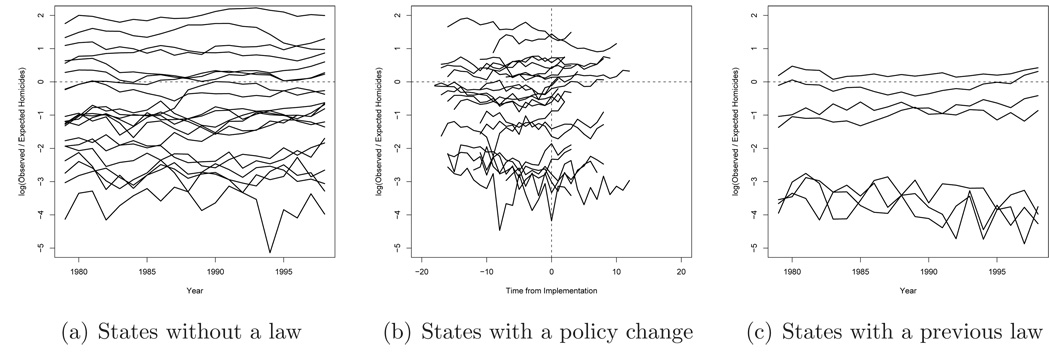
We estimated the expected number of homicides using a Poisson regression model with cubic splines for calendar year and calculated the log ratio of observed to expected homicides. A log ratio of zero implies that the number of observed and expected homicides was equal. A log ratio greater than (less than) zero implies a greater (smaller) number of homicides were observed than would be expected. Figure 4(a) displays the log ratio of observed to expected homicides for states that never enacted a shall-issue law. Note that 20 states and the District of Columbia never enacted a shall-issue law during the study period. There do not appear to be noticeable temporal trends after adjusting for the expected number of homicides. There is large variation in the response between states, but there appears to be little variation in the temporal trends.
Figure 4.
Log ratio of observed to expected homicides
Figure 4(b) displays the log ratio of observed to expected homicides for the 23 states that enacted a shall-issue law during the study period. The time scale is time from implementation, i.e. the number of years before or after a law was enacted. Large variation in the response between states is evident in Figure 4(b). There are noticeable temporal trends for several states, but there does not appear to be substantial variation in the temporal trends. Interestingly, firearm-related homicides appear to increase for most states after a shall-issue law was enacted. In addition, there are several states for which firearm-related homicides appear to decrease before a law was enacted and increase afterward. Figure 4(c) displays the log ratio of observed to expected homicides for the 7 states that enacted a shall-issue law before 1979. As in Figure 4(a), there do not appear to be a noticeable temporal trends after adjusting for the expected number of homicides.
5 Results
5.1 Simple Summaries
We calculated the unadjusted homicide rate ratio Δ̂ as the mean homicide rate after shall-issue laws were enacted divided by that before. The unadjusted homicide rate ratio associated with enacting a shall-issue law was 0.748, 95% CI: (0.668, 0.836). Hence shall-issue laws were associated with a significant 25.2% decrease in firearm-related homicide rates. However, this estimate is biased if temporal trends exist. This estimate is also likely biased because it does not adjust for other factors that are associated with firearm-related homicide.
For the 23 states that enacted a shall-issue law during the study period, we first calculated Δ̂i as the mean homicide rate after a shall-issue law was enacted divided by that before. We adjusted these estimates for temporal trends by dividing the observed number of homicides by the expected number of homicides (estimated from a Poisson regression model with cubic splines for calendar year). We then calculated , the average state-specific homicide rate ratio. The homicide rate ratio associated with enacting a shall-issue law was 0.948, 95% CI: (0.911, 0.988). Hence shall-issue laws were associated with a significant 5.2% decrease in firearm-related homicide rates. Although this estimate adjusts for temporal trends, it is likely biased because it does not adjust for other important factors. It also does not utilize all available data because states without a policy change do not contribute any information.
5.2 Generalized Estimating Equations
We implemented GEE to estimate the population-level effect of enacting a shall-issue law. We adjusted for calendar year using a cubic spline to allow for a thorough, flexible adjustment for time. We also adjusted for demographic characteristics (gender, race, and age category) using indicator variables, for state-specific characteristics (proportion unemployed, proportion living in poverty, proportion living in a metropolitan area) using linear splines, and for other state gun laws using indicator variables. We included an offset for log population size and allowed for over-dispersion. The regression formula was:
This model generated inference for exp β1, the population-level effect of enacting a shall-issue law.
We defined states as clusters and assumed an independence correlation structure. Because states defined the clusters in the covariance calculation, state-specific estimates of homicide, of enacting a shall-issue law, and of temporal trends were not estimable. The adjusted homicide rate ratio associated with enacting a shall-issue law was 0.915, 95% CI: (0.814, 1.029). Hence shall-issue laws were associated with an 8.5% decrease in firearm-related homicide rates, although this decrease was not statistically significant (p = 0.140). We obtained similar results via marginal quasi-likelihood, which induces a correlation model using unit-specific random effects, but provides a point estimate with a population-level interpretation.
Assuming an exchangeable correlation structure the adjusted homicide rate ratio was 0.903, 95% CI: (0.785, 1.039). Hence shall-issue laws were associated with an 9.7% decrease in firearm-related homicide rates, although this decrease was not statistically significant (p = 0.154). These results are similar to those obtained assuming an independence correlation structure. If we ignored within-state correlation and used the naïve standard error estimate, then the confidence interval for the homicide rate ratio was (0.899, 0.932), indicating that the reduction in homicide rates was highly significant (p < 0.001). However, this confidence interval is invalid because it ignores within-state correlation.
5.3 Generalized Linear Mixed Models
We implemented GLMM with increasing levels of complexity. In each model we allowed for over-dispersion and correlated random effects. In each model we adjusted for calendar year, demographic characteristics, state-specific characteristics, other state gun laws, and log population size. First, we considered a model that included random intercepts, which allowed the homicide rate to vary across states. This model estimated the population-level effect of enacting a shall-issue law. Second, we considered a model that included random intercepts and random effects of time, which allowed the homicide rate and the effect of time to vary across states. Third, we considered a model that included random intercepts and random effects of enacting a shall-issue law, which allowed the homicide rate and the effect of enacting a shall-issue law to vary across states. Fourth, we considered a model that included random intercepts, random effects of time, and random effects of enacting a shall-issue law. Each of these three models estimated an average state-specific effect. The regression formulae were:
| (1) |
| (2) |
| (3) |
| (4) |
A key distinction is that (1) and (2) assumed a fixed shall-issue law effect, whereas (3) and (4) explicitly allowed random shall-issue law effects.
Table 1 provides adjusted homicide rate ratios associated with enacting a shall-issue law. These results provide conflicting inference. According to (1) shall-issue laws were associated with a significant 3.1% decrease in firearm-related homicide rates (p = 0.036). According to (2) and (3) shall-issue laws were not significantly associated with firearm-related homicide rates (p = 0.355 and 0.926, respectively). According to (4) shall-issue laws were associated with a 5.8% increase in firearm-related homicide rates, although this increase was not statistically signficant (p = 0.059). Results obtained via a conditional Poisson model were similar to those from (1).
Table 1.
Adjusted homicide rate ratios estimated via GLMM
| Model | Homicide Rate Ratio | 95% Confidence Interval |
|---|---|---|
| Random intercepts | 0.969 | (0.941, 0.998) |
| + Random time effects | 1.017 | (0.982, 1.053) |
| + Random law effects | 0.996 | (0.911, 1.089) |
| + Random time and law effects | 1.058 | (0.998, 1.121) |
The confidence intervals obtained from (1) and (2) are substantially tighter than other GLMM confidence intervals. We are skeptical of these two confidence intervals because both these models ignore state-level heterogeneity in the law effect, which our other analyses show to be important. Therefore we believe that these two confidence intervals are likely to be anti-conservative.
5.4 Random Effects Meta-analysis
We used a Poisson regression model, allowing for over-dispersion, to estimate state-specific homicide rate ratios and incorporated them into a meta-analysis. We adjusted for calendar year, demographic characteristics, state-specific characteristics, other state gun laws, and log population size. To allow the effect of time to vary across states, we included an interaction between a linear term for calendar year and indicator variables for each state. This two-stage model mirrored (4).
Recall that 23 states enacted a shall-issue law between 1979 and 1998. In a traditional meta-analysis only states with variation in the exposure, i.e. states that enacted a law during the study period, would be available to estimate the effect of enacting a shall-issue law. In our meta-analysis we included the 7 states that previously enacted and the 21 states that never enacted a law, which substantially increased the sample size. In addition, we were able to pool information across states to estimate the effect of adjustment variables. This and the increased sample size increased the power of our meta-analysis.
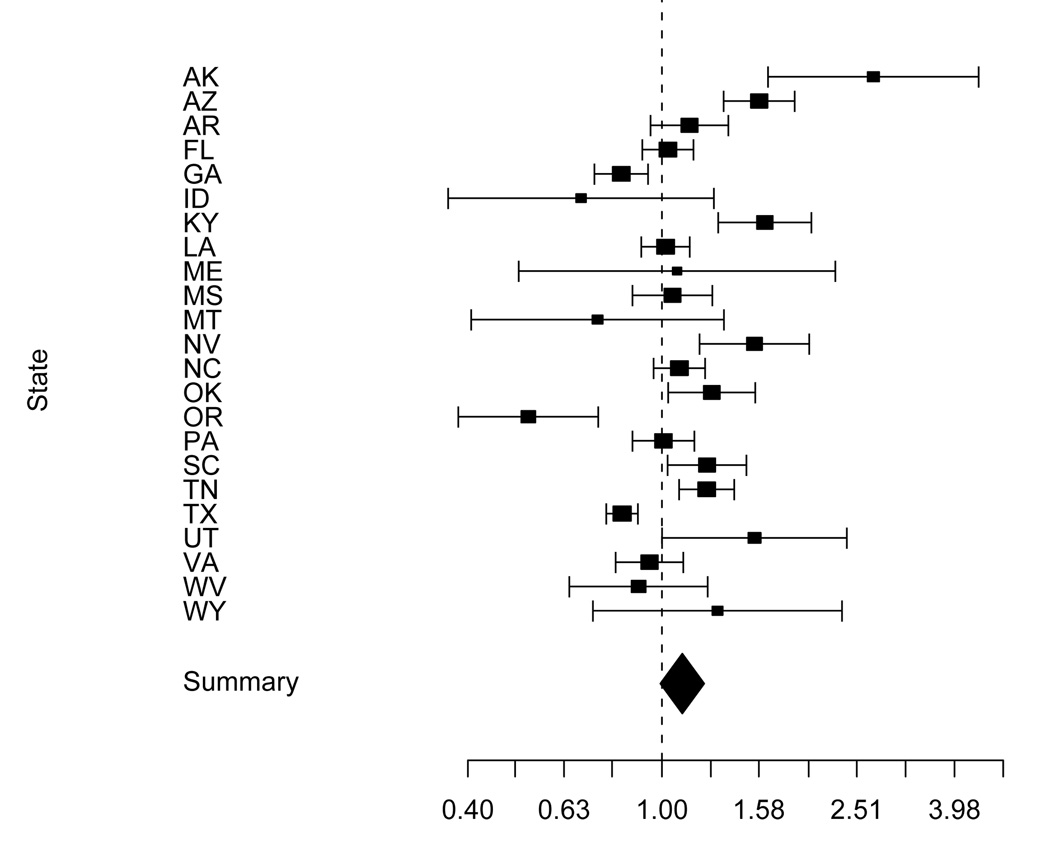
Figure 5 displays the estimated homicide rate ratio associated with enacting a shall-issue law for each state that enacted a law between 1979 and 1998. Estimated homicide rate ratios are represented by squares with size proportional to their inverse variance and confidence interval end-points are represented by vertical dashes. A diamond represents the summary homicide rate ratio. It appears that for most states enacting a shall-issue law was associated with an increase in firearm-related homicides. For several states the increase was statistically significant. The adjusted homicide rate ratio associated with enacting a shall-issue law was 1.101, 95% CI: (0.993, 1.220). Hence shall-issue laws were associated with a 10.1% increase in firearm-related homicide rates, although this increase was not statistically significant (p = 0.068). The estimated between-state heterogeneity in the policy effect was 0.045. There was strong evidence to suggest that the true between-state heterogeneity in the policy effect was not equal to zero (p < 0.001).
Figure 5.
Homicide rate ratios for states that enacted a shall-issue law
5.5 Empirical Bayes Estimators
We fit a GLMM to the data observed before shall-issue laws were enacted, which included the 23 states that enacted a shall-issue law between 1979 and 1998 and the 21 states that never enacted a law. We allowed for over-dispersion and correlated random effects. We adjusted for calendar year, demographic characteristics, state-specific characteristics, other state gun laws, and log population size. In addition, we included random intercepts and random time effects in the model. This model was similar to (2) with pij = 0. We used the estimated fixed and random effects from this model to calculate expected log homicide rates for each state after a shall-issue law was enacted. We subtracted these expected log rates from the observed log homicide rates for each state and averaged the differences to estimate state-specific log homicide rate ratios. We averaged the state-specific estimates and exponentiated the result to obtain an estimate of the average effect of enacting a shall-issue law.
The adjusted homicide rate ratio associated with enacting a shall-issue law was 1.097, 95% CI: (0.987, 1.220). Hence shall-issue laws were associated with a 9.7% increase in firearm-related homicide rates, although this increase was not statistically significant (p = 0.083). We obtained this confidence interval and p-value by assuming that state-specific log homicide rate ratios were uncorrelated. The variance and covariance calculations derived in the Supplementary Material yielded slightly more conservative inference. The confidence interval was (0.956, 1.258) and the p-value was 0.199.
6 Discussion
6.1 Evaluating Gun-use Laws
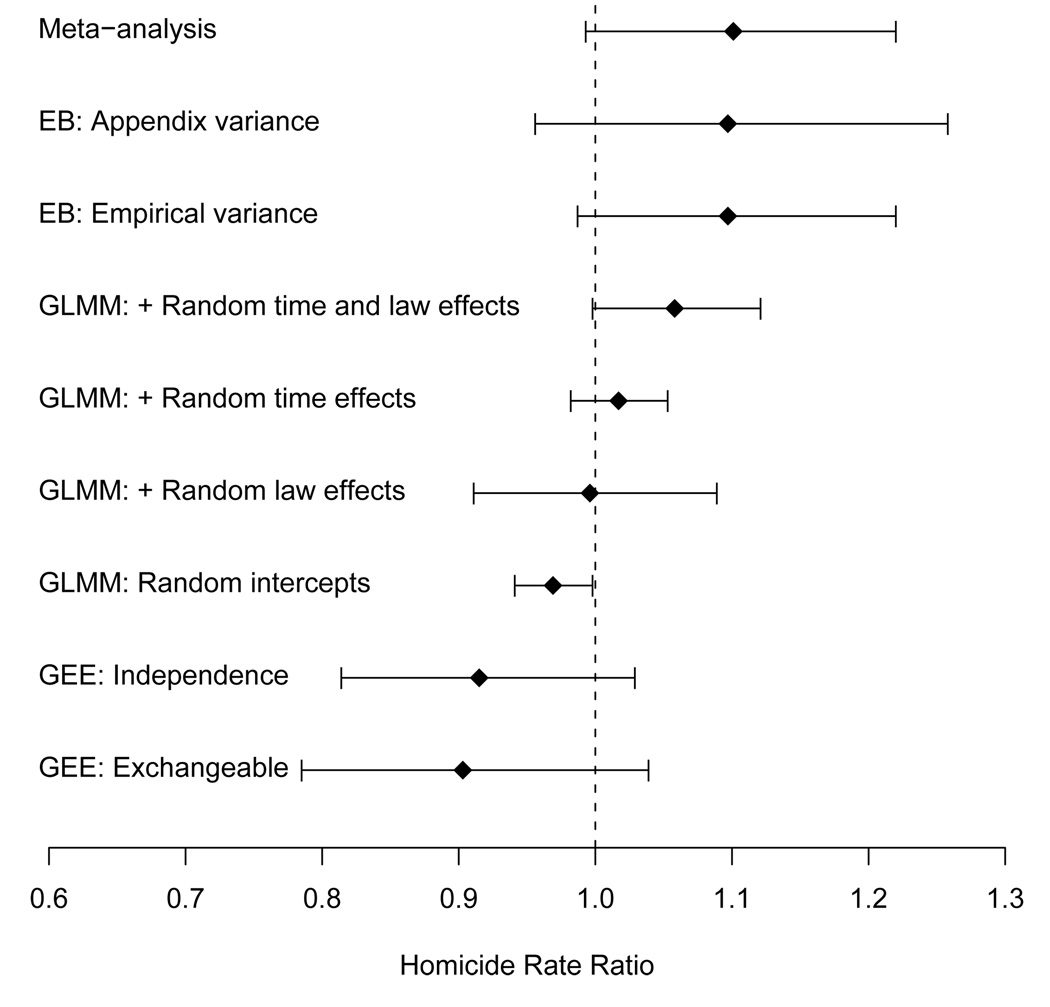
As discussed in Section 1.2, researchers continue to debate whether eliminating gun-use restrictions increases or decreases firearm-related homicide. Indeed, our results provide evidence for both conclusions. We summarize our main results in Figure 6, which displays the estimated homicide rate ratio and 95% confidence interval obtained from each analysis. Diamonds represent estimated homicide rate ratios and vertical dashes represent confidence interval end-points.
Figure 6.
Summary of case study analyses
The differences between our results beg the question, which analyses are appropriate in our context? Given the observed heterogeneity in state-specific estimates of homicide over time (see Figure 4) and of enacting a shall-issue law (see Figure 5), we believe that an appropriate analysis includes state-specific time and law effects. Other gun-use researchers share this view [8]. The GEE analysis is limited in this respect because state-specific estimates are not available due to the clustering defined in the standard error computation. GLMM (4), meta-analysis, and EB accommodate state-level heterogeneity in time and law effects. Based on these analyses we conclude that enacting a shall-issue law is associated with a weak but non-significant increase in firearm-related homicide rates.
A more subtle and perhaps more important question is, how does the target of inference differ between our analyses? Table 2 contains a summary of the direct target of inference for each estimation method. A GEE generates inference to a population of individuals (“Level 1”); in our case study, residents of the United States. A random effects meta-analysis generates inference to a population of units (“Level 2”); in our case study, the 50 states and the District of Columbia. GLMM and EB are given a +/− for both “Level 1” and “Level 2” inference because, as we discussed in Section 3.6, a conditional model may generate inference to either a population of individuals or a population of units (depending on the distribution of the outcome and the choice of random effects). For example, of the GLMMs we presented in Section 5.3, model (1) generates inference to a population of individuals, whereas models (2), (3), and (4) generate inference to a population of states. Although these latter models rely on different assumptions regarding the homogeneity or hetereogeniety in the policy effect across states, their target of inference is the same. Because the intervention in our case study is at the state level, we are perhaps more interested in generalizing to a population of states rather than to a population of individuals.
A characteristic of the data that we did not consider in our analyses is spatial structure (see Figure 3). Because a given state may be more similar to an adjacent state than to a non-adjacent state, correlation may be induced between neighboring states. Ignoring spatial correlation is likely to produce standard error estimates that are too small. Therefore our inference may be anti-conservative. In our application it may be difficult to properly address the issue of spatial correlation because of the small number of geographic units. However, in applications with a richer spatial structure there are options for incorporating it into an estimating equation [24] or mixed model approach [16].
A critical aspect of any statistical analysis is evaluating the assumptions of the model used to generate inference, such as verifying the correct functional form of adjustment variables. In the context of longitudinal data additional assumptions must be evaluated. In an estimating equation approach analysts must verify that the sample size is large enough to ensure consistent sandwich variance estimation; n ≥ 40 is usually sufficient [25]. In a mixed model approach analysts should consider the distribution of the random effects and verify that the variance-covariance model is correct. Distributional assumptions may be evaluated using quantile-quantile plots of the estimated random effects, although it may be difficult to detect violations in certain situations [26]. The variance model may be evaluated by plotting the squared normalized residuals versus the fitted values and including a lowess smoother. The covariance model may be evaluated by calculating the empirical semi-variogram or sample autocorrelation function [12]. Several chapters in Linear Mixed Models for Longitudinal Data [26] provide details on methods to assess model fit.
Another important model assumption concerns missing data. Biased estimation may result from various missingness mechanisms. A likelihood-based mixed model approach accommodates data that are missing at random, i.e. missingness depends only on the observed data. An estimating equation approach more rigidly requires that data are missing completely at random, i.e. missingness does not depend on either the observed or unobserved data. There are well-researched options for extending these complete-case approaches to accommodate missing data. These options include modeling the missingness mechanism and weighting by the estimated probability of missingness, or imputing the missing data using methods such as multiple imputation [27]. Chapter 13 of Analysis of Longitudinal Data [12] provides details on several approaches for addressing missing values in longitudinal data. In our application there was no missing data.
6.2 Evaluating a Policy Change
We conclude that existing longitudinal data analysis methods are well-suited to assess the impact of a new policy: commonly used methods such as generalized estimating equations and generalized linear mixed models, as well as less commonly used methods such as random effects meta-analysis and methods based on empirical Bayes estimators. We have shown that these methods should be used only after considering the primary challenge of a policy change analysis: defining groups between which to compare units with and without the policy change, while using all available data. Central to this definition is selecting a mean model that most accurately characterizes the anticipated effect of the policy intervention.
We also conclude that secondary challenges of a policy change analysis warrant careful consideration. First, analysts must properly separate the effect of time from that of the policy by thoroughly adjusting for temporal trends. Second, analysts must account for heterogeneity in the policy effect by selecting methods that accommodate unit-specific policy effects. Third, analysts must account for serial correlation within study units by selecting a model for the correlation between observations collected on the same unit. We have shown that failure to address these challenges may result in misleading and invalid inference.
We recommend the following steps as a outline from which to approach a policy change analysis:
Exploratory Longitudinal Analysis: Form a contrast (such as a difference or ratio, as appropriate) between observed and expected outcomes adjusted for calendar time. Plot these estimates versus time from policy change for units with a change and versus calendar time for units without, as in Figure 4.
Unit-specific Summaries: Calculate unit-specific estimates of the policy effect Δ̂i adjusted for calendar time and average these estimates to obtain Δ̄, a crude estimate of the average policy effect. A confidence interval may be obtained via bootstrap [28].
Effect Heterogeneity: Create a meta-analysis plot of unit-specific policy effects adjusted for calendar time and other covariates, as in Figure 5.
Average Effect: Generate inference for the average policy effect using either GEE, GLMM, meta-analysis, or EB, remaining mindful of the important differences between these estimation methods with respect to implementation and inference. Table 2 summarizes these differences.
Analysts may be drawn to simple methods such as “difference in differences,” “segmented regression,” and “regression discontinuity.” These methods are useful in certain contexts, but have several limitations. “Difference in differences” assumes that unit-level heterogeneity is constant across time and that temporal trends are identical in the “treatment” and “control” groups [3]. “Segmented regression” relies on the rigid assumption of linearity and does not allow adjustment for covariates [4]. “Regression discontinuity” may be sensitive to choice of kernel and bandwidth [5].
After deciding on an appropriate mean model, correlation model, and target of inference, another challenge for analysts is obtaining software to fit the model. The methods we described are available in most statistical programs. We used R [29] and several packages therein. Standard software such as Stata [30] is also available to implement these methods. Sophisticated methods for analyzing policy change data such as those accommodating both temporal and spatial correlation are difficult to implement, even in specialized software. However, software continues to evolve and will simplify detailed policy change evaluations in the future.
Supplementary Material
Acknowledgments
We gratefully acknowledge the National Heart, Lung, and Blood Institute (HL 072966) and the University of Washington for supporting this research; Matthew Rosengart for providing the data; Cecilia Cotton, Katherine Davis, Yuying Jin, Tessa Rue, and Paramita Saha for helpful discussion; and three reviewers and an Associate Editor for useful comments.
Grant Support: National Heart, Lung, and Blood Institute; HL 072966
References
- 1.Atlas SJ, Keller RB, Robson D, Deyo RA, Singer DE. Surgical and nonsurgical management of lumbar spinal stenosis. Spine. 2000;25:556–562. doi: 10.1097/00007632-200003010-00005. [DOI] [PubMed] [Google Scholar]
- 2.Persaud BN, Retting RA, Lyon CA. Crash reduction following installation of centerline rumble strips on rural two-lane roads. Accident Analysis and Prevention. 2004;36:1073–1079. doi: 10.1016/j.aap.2004.03.002. [DOI] [PubMed] [Google Scholar]
- 3.Cawley J, Schroeder M, Simon KI. How did welfare reform affect the health insurance coverage of women and children? Health Services Research. 2006;41:486–506. doi: 10.1111/j.1475-6773.2005.00501.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wagner AK, Soumerai SB, Zhang F, Ross-Degnan D. Segmented regression analysis of interrupted time series studies in medication use research. Journal of Clinical Pharmacy and Therapeutics. 2002;27:299–309. doi: 10.1046/j.1365-2710.2002.00430.x. [DOI] [PubMed] [Google Scholar]
- 5.Ludwig J, Miller DL. Does Head Start improve children’s life chances? Evidence from a regression discontinuity design. Quarterly Journal of Economics. 2007;122:159–208. [Google Scholar]
- 6.Lott JR, Mustard DB. Crime, deterrence, and right-to-carry concealed handguns. Journal of Legal Studies. 1997;26:1–68. [Google Scholar]
- 7.Rosengart M, Cummings P, Nathens A, Heagerty P, Maier R, Rivara F. An evaluation of state firearm regulations and homicide and suicide death rates. Injury Prevention. 2005;11:77–83. doi: 10.1136/ip.2004.007062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kovandzic TV, Marvell TB, Vieraitis LM. The impact of “shall-issue” concealed handgun laws on violent crime rates: Evidence from panel data for large urban cities. Homicide Studies. 2005;9:292–323. [Google Scholar]
- 9.Webster DW, Vernick JS, Ludwig J, Lester KJ. Flawed gun policy research could endanger public safety. American Journal of Public Health. 1997;87:918–921. doi: 10.2105/ajph.87.6.918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liang K-Y, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- 11.Yan J. geepack: Generalized estimating equation package. R package version 1.0-13 [Google Scholar]
- 12.Diggle PJ, Heagerty P, Liang K-Y, Zeger SL. Analysis of Longitudinal Data. New York: Oxford University Press; 2002. [Google Scholar]
- 13.Carriere KC, Roos LL, Dover DC. Across time and space: Variations in hospital use during Canadian health reform. Health Services Research. 2000;35:467–487. [PMC free article] [PubMed] [Google Scholar]
- 14.Breslow NE, Clayton DG. Approximate inference in generalized linear mixed models. Journal of the American Statistical Association. 1993;88:9–25. [Google Scholar]
- 15.Bates D. lme4: Linear mixed-effects models using S4 classes. R package version 0.99875-9 [Google Scholar]
- 16.Daniels MJ, Gatsonis C. Hierarchical generalized linear models in the analysis of variations in health care utilization. Journal of the American Statistical Association. 1999;94:29–42. [Google Scholar]
- 17.Tooze JA, Grunwald GK, Jones RH. Analysis of repeated measures data with clumping at zero. Statistical Methods in Medical Research. 2002;11:341–355. doi: 10.1191/0962280202sm291ra. [DOI] [PubMed] [Google Scholar]
- 18.Normand SLT. Meta-analysis: Formulating, evaluating, combining, and reporting. Statistics in Medicine. 1999;18:321–359. doi: 10.1002/(sici)1097-0258(19990215)18:3<321::aid-sim28>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]
- 19.Lumley T. rmeta: Meta-analysis. R package version 2.14 [Google Scholar]
- 20.DerSimonian R, Laird N. Meta-analysis in clinical trials. Controlled Clinical Trials. 1986;7:177–188. doi: 10.1016/0197-2456(86)90046-2. [DOI] [PubMed] [Google Scholar]
- 21.Casella G. An introduction to empirical Bayes data analysis. The American Statistician. 1985;39:83–87. [Google Scholar]
- 22.Zeger SL, Liang K-Y, Albert PS. Models for longitudinal data: A generalized estimating equation approach. Biometrics. 1988;44:1049–1060. [PubMed] [Google Scholar]
- 23.Piantadosi S, Byar DP, Green SB. The ecological fallacy. American Journal of Epidemiology. 1988;127:893–904. doi: 10.1093/oxfordjournals.aje.a114892. [DOI] [PubMed] [Google Scholar]
- 24.Heagerty PJ, Lumley T. Window subsampling of estimating functions with application to regression models. Journal of the American Statistical Association. 2000;95:197–211. [Google Scholar]
- 25.Mancl LA, DeRouen TA. A covariance estimator for GEE with improved small-sample properties. Biometrics. 2001;57:126–134. doi: 10.1111/j.0006-341x.2001.00126.x. [DOI] [PubMed] [Google Scholar]
- 26.Verbeke G, Molenberghs G. Linear Mixed Models for Longitudinal Data. New York: Springer; 2000. [Google Scholar]
- 27.Little RJA, Rubin DB. Statistical Analysis with Missing Data. New York: John Wiley; 2002. [Google Scholar]
- 28.Efron B, Tibshirani RJ. An Introduction to the Bootstrap. New York: Chapman & Hall; 1993. [Google Scholar]
- 29.R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2007. [Google Scholar]
- 30.StataCorp. Stata Statistical Software: Release 10. StataCorp LP: College Station, Texas; 2007. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.