Abstract
Cooperative binding of a ligand to multiple subsites on a protein is a common theme among enzymes and receptors. The analysis of cooperative binding data (either positive or negative) often relies on the assumption that free ligand concentration, L, can be approximated by the total ligand concentration, LT. When this approximation does not hold, such analyses result in inaccurate estimates of dissociation constants. Presented here are exact analytical expressions for equilibrium concentrations of all enzyme and ligand species (in terms of Kd values and total concentrations of protein and ligand) for homotropic dimeric and trimeric protein–ligand systems. These equations circumvent the need to approximate L and are provided in Excel worksheets suitable for simulation and least-squares fitting. The equations and worksheets are expanded to treat cases where binding signals vary with distinct site occupancy.
Keywords: Ligand binding, Cooperativity, Homotropic, Quartic polynomial, Cubic polynomial, Excel, Receptor, Enzyme, Substrate, Dissociation constant, Dimer, Trimer, Protein
Protein–ligand interactions are fundamental to numerous biological processes, including hormone signaling, allosteric regulation, metabolism, and cell-to-cell communication. A key metric for such interactions is the dissociation constant (Kd), which is often determined in equilibrium binding titrations where the concentration of saturated receptor or bound ligand is measured as a function of the total ligand (LT) concentration. Methods used to obtain ligand binding information include various forms of spectroscopy [1], surface plasmon resonance [2], calorimetry [3], radioactivity [4], and assays that couple protein saturation to biological or chemical– enzymatic signals. Such measurements report on the concentration of bound and/or free ligand and are often interpreted as the fractional saturation (Y) of protein.
The simplest equations for fitting ligand binding data (cf. Eq. (1)) require knowledge of free ligand (L), which may be either measured directly or estimated by virtue of experimental designs in which L can be approximated by LT such as when protein concentration (ET) is very low relative to Kd or LT. Signal detection limits often preclude the use of such designs. When L is not known, the data are best modeled using an expression for Y in terms of LT, ET, and Kd (Eq. (2)). Eq. (2) (obtained from mass conservation laws and the quadratic formula) provides such an analytical expression for the elementary case of ligand binding to a single site (or multiple noninteracting sites). Using such an expression, a best-fit Kd value can be extracted from titration data by least-squares fitting.
For higher order processes, such as cooperative binding to a multimeric protein (where ligand occupancy at one protomer alters ligand affinity at the others), fitting methods must take into account each of the multiply liganded forms. Such behavior manifests experimentally as multiphasic saturation curves or nonlinear Hill and Scatchard plots, whose shapes indicate enhanced (positive cooperativity) or diminished (negative cooperativity) binding of successive ligands [5,6]. Among the many proteins and protein classes that exhibit homotropic cooperativity are the dimeric G-protein-coupled receptors [7], sulfotransferases [8], trimeric metabolic enzymes [9–12], monomeric cytochrome P450s [13], AcrB bacterial drug efflux pump [14], bacteriorhodopsin trimers [15], and DegS protease that regulates the Escherichia coli stress response [16].
The Hill [17,18] and Adair [19] equations (Eqs. (3) and (4)) address the cases where L is known and report cooperativity either indirectly as the Hill coefficient (n) or explicitly as Kd values (given by Ki for the ith ligand to bind) that reflect changes in affinity between successive binding steps. Derivation of parallel analytical equations in terms of LT is nontrivial given that the equilibrium concentration of any species of a dimeric or trimeric protein is the root of a cubic or quartic polynomial, respectively. Analytical solutions for higher order oligomers are not possible, and fitting the titrations of such systems requires the use of numerical methods [20]:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Although analytical expressions for the roots of cubic and quartic functions have been known for 400 years [21–23], they require knowledge of advanced algebra. Recent articles have treated the cubic polynomial in ligand binding systems; Wang and Sigurskjold described competitive binding of two ligands to identical independent binding sites [24,25], and Whitesides and co-workers used exact analysis to describe binding of homodivalent ligands to monomeric proteins, producing expressions that apply equally to homodimeric proteins binding to monovalent ligands [26]. However, to our knowledge, application of the quartic polynomial to trimer–ligand binding has not yet been addressed, and no exact analysis has been applied to heteroligomers that exhibit homotropic cooperativity.
Current approaches to modeling trimeric systems rely on numerical methods that employ differential equations or stochastic models to estimate the equilibrium distributions of enzyme forms. Typically, these algorithms require the user to provide total reactant concentrations and equilibrium or rate constants [27–29]. Equilibrium distributions are then calculated at each “point” or condition in a titration, and the concentrations of the relevant species from the distributions are then compared with experimental measurements to assess how well a given set of input constants predicts binding behavior. These procedures can be iterated to produce a best-fit set of constants. Notably, such efforts typically require high-level mathematical software or original programming [30]. The analytical equations described here provide a relatively simple means of obtaining exact distributions. The equations take into account both positive and negative cooperativity and can be applied to any chemical equilibrium involving homotropic binding to a diva-lent or trivalent species. For convenience, the equations are provided in Excel worksheet implementations suitable for prediction and multiparameter estimation by least-squares fitting. An expansion of the equations and worksheets to treat spectroscopic titration is also described.
Results and discussion
The models
Early models of allostery proposed that linked subunits undergo concerted transitions between two conformational states, each with a different ligand affinity [31]. Later models allowed subunits to undergo independent, substrate-induced conformational changes and held that affinities at the unoccupied sites would change progressively as ligands added to the complex [19,32]. Even more general models allowed subunits to undergo conformational transitions with or without bound ligand and allowed the affinity of all sites to vary with each unique configuration of the system [33,34].
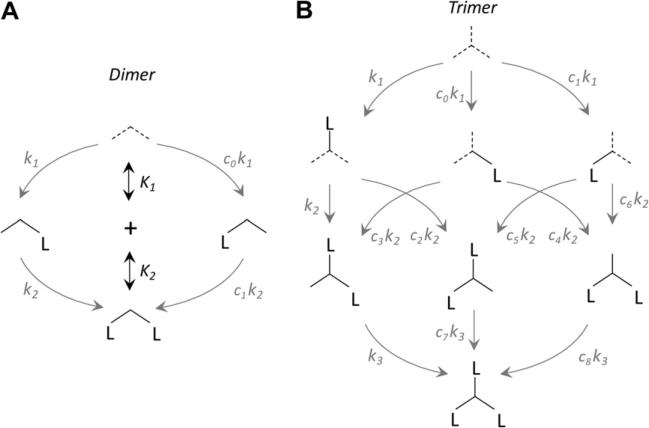
The dimer and trimer ligand binding models used as the basis for the algebra described below are presented in Fig. 1A and B. Oligomers are represented by intersecting lines; each line represents a subunit. Dotted lines indicate the subunits that may inter-convert via isomerization; however, subunits need not be identical. Site and dissociation constants are given by ki and Ki, respectively, where i represents the ith subunit to bind. Site constants are given for each subunit in all possible configurations and are related by cj values, which define the magnitude and nature of the cooperative interactions. The cj values are related by the fact that the product of the site constants connecting any two enzyme forms is path independent, a consequence of the first law of thermodynamics. The model assumes that ligand binding, which is stochastic, stabilizes a subunit in the state that it was in when binding occurred; hence, dotted lines become solid on the addition of ligand.
Fig.1.
Binding of ligand to protein dimers (A) and trimers (B). Proteins are represented by intersecting lines, each of which represents a subunit. Site constants and dissociation constants are given as ki and Ki, respectively, where i represents the ith ligand to bind (e.g., i = 2 indicates the addition of the second ligand). All arrows correspond to reversible equilibria. Site constants are related by coefficients, cj, that are themselves related by the fact that the product of the site constants connecting any two complexes must be equal and independent of the path that connects them (a consequence of the first law of thermodynamics). The k1, k2, and k3 coefficients are not shown and have arbitrarily been set to 1. Dotted arrows indicate subunits that may interconvert via isomerization.
Theory
The equilibria describing binding of the first and second ligands L to a dimeric protein E are shown in Fig. 1A. When considering ligand binding to a multisubunit system, it is important to note that binding measurements yield aggregate constants (e.g., Kd values) that report on all enzyme forms capable of transitioning between two stoichiometric states (e.g., singly to doubly liganded) [35]. The dissociation constants for binding of the first (K1) and second (K2) ligands to a dimer are given by Eqs. (6) and (7). The denominator of Eq. (6) is the sum of all the singly liganded enzyme forms:
| (6) |
| (7) |
Complexes EL and LE represent ligand bound to different subunits of a heterodimer or to either symmetric subunit of a homodimer. By treating the subunits separately, we isolate the interaction of ligand with a single protomer. This interaction is defined by a “site” dissociation constant [35] that reports directly on the strength of the interaction at a particular binding site. These constants are given by lowercase ki for the ith ligand to bind and are modified by coefficients cj for heterodimeric proteins (Eq. (8)):
| (8) |
The aggregate constants Ki (Eqs. (6) and (7)) are a function of the individual site ki values at each ligand binding step. For multimeric proteins with n equivalent binding sites, cj = 1 and dissociation constants are related by a statistical coefficient (Eq. (9)):
| (9) |
where i corresponds to the ith ligand to bind [36]. Equivalencies among aggregate and site constants in cases where cj ≠ 1 are described below (trimers) and in the Supplementary material.
For a trimeric protein, binding of both the second and third ligands may show ligand occupancy dependence. In this case, one additional equilibrium relationship is needed (Eq. (10)):
| (10) |
Binding of ligand to a trimeric protein is shown in Fig. 1B. The affinity of the first ligand to bind is given by any of three site binding constants, k1 with or without coefficients c0 and c1. The site constant coefficients will differ in cases where, for example, isomerized subunits have distinct binding attributes prior to binding (cf. half- or third-site mechanisms [8,10,11] or the conformational coupling of energetics [37]) or where the protein is heteroligomeric. The second ligand may be presented with multiple binding sites of varying affinities depending on which subunit was bound first. Thus, the second binding step is composed of six possible site constant values, where variation in k2 is captured by the five coefficients c2 to c6. The third ligand binds to one of three possible protomers, with site constant k3 modified by coefficients c7 and c8 to describe these multiple forms; the end result of each process is the identical triply liganded species. Because the change in chemical potential of any of the six paths from unliganded to triply liganded is identical, the product of the equilibrium constants for one path is equal to that of any other path. The complete system can be described by 10 parameters: ET, LT, site constants k1 to k3, and coefficients c0 to c4. The values of coefficients c5 to c8 are defined by the following relationships:
The relationships between aggregate (Ki) and site constants (ki) for a trimeric protein were obtained by deriving Eq. (16) using each kind of constant and then equating coefficients (Eqs. (11)–(13)):
| (11) |
| (12) |
| (13) |
where
The mass conservation relationships for the trimeric system are given by Eqs. (14) and (15):
| (14) |
| (15) |
The system of equations (Eqs. (6), (7) and (10)–(15)) can be rearranged, resulting in a quartic polynomial in L (Eq. (16)):
| (16) |
where
The solution of this quartic equation yields L (see Supplementary material), which is then used to determine the equilibrium concentrations of all other species in terms of the constant parameters (Eqs. (17)–(20):
| (17) |
| (18) |
| (19) |
| (20) |
The L ≈ LT approximation
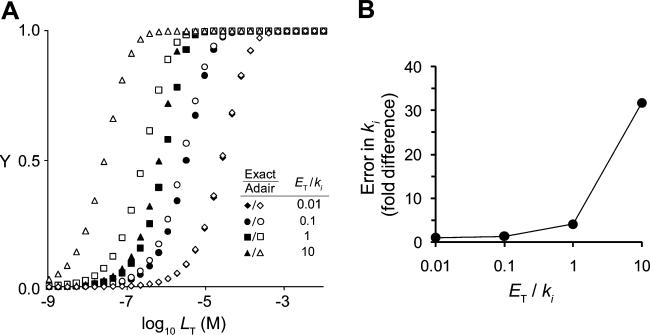
The Adair equation describes solution equilibria for cooperative binding to multi-subunit proteins (Eq. (3), dimer; Eq. (4), trimer). This equation can be rearranged, using mass conservation equations, into a polynomial in L (Eq. S5 in Supplementary material, dimer; Eq. (16), trimer) that can be solved to determine the equilibrium concentrations of species as a function of ET, LT, and ki values (Eqs. S6–S8 in Supplementary material, dimer; Eqs. (17)–(20), trimer). To demonstrate how the equilibrium distributions predicted by the Adair equation deviate from exact distributions (given by the analytical solutions) as L deviates from LT, distributions were simulated for a noncooperative trimer at four different ET/ki ratios (0.01–10). ET was held fixed (1.0 μM), and ki values were decreased in 10-fold increments from 100 μM to 100 nM. The results, given as fraction protein saturated (Y) versus concentration LT, are presented in Fig. 2A. At ET/ki = 10, the concentration of LT in the vicinity of ki is much greater than that of ET, the L = LT approximation holds well, and the two methods agree. However, as ET/ki increases, the bound ligand concentration becomes significant relative to LT when LT ≈ ki and the approximation begins to fail. As this happens, the Adair equation predicts saturation at erroneously low LT concentrations. For example, when ET/ki = 1, the ki values estimated by fitting fractional saturation to the Adair equation are more than 3-fold higher than the true ki and invoke 4-fold cooperativity for the third binding step where none exists. As can be seen in Fig. 2B, the fold difference in the Ki values predicted by the Adair and exact methods is significant when ET/ki ≈ 1 and increases sharply above this value. Thus, in situations where dissociation constants are comparable to the protein concentrations needed to observe signal, or in complex mixtures where affinities are high and protein concentrations are not known, the exact solutions are a far more accurate and reliable means of analyzing binding data.
Fig.2.
Comparison of exact and approximate models of fractional saturation versus LT for a homotrimeric protein with no cooperativity. (A) Fractional saturation of enzyme with ligand was calculated using the exact model (filled symbols) or the Adair equation assuming L = LT (open symbols) for a noncooperative homotrimeric enzyme (1.0 μM trimer) with values of the site dissociation constants (k1 = k2 = k3) set to 100 μM (◆), 10 μM (●), 1 μM (■), or 0.1 μM (▲). (B) Deviation in estimated ki value as a function of the ratio ET/ki when using the Adair equation and assuming L = LT.
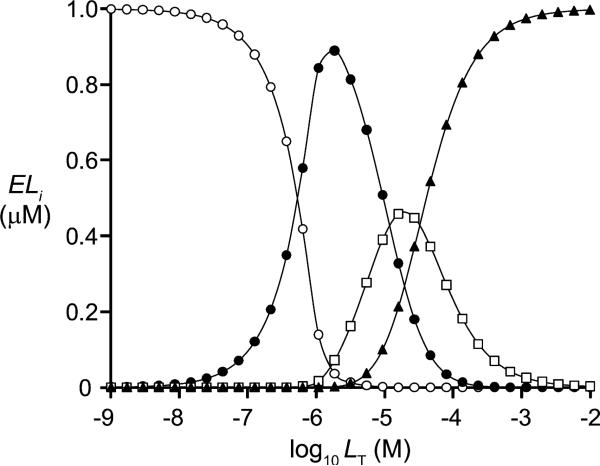
The solution to the quartic equation provides a simple, virtually errorless means of simulating equilibrium distributions of species in complex binding scenarios that involve a single type of ligand. As such, it can be useful in optimizing experimental conditions. It is often of interest to maximize the concentration of a particular enzyme form, so that the properties of that species can be studied, or to understand the concentration dependence of a species; such dependencies can be used to test for the existence of a putative complex and/or to validate a given model. As an example, consider the LT dependence of the species of a trimer in a scenario where ligand binding at the high-affinity site results in a 100-fold negative cooperativity at the unoccupied sites and binding of the second and third ligands is independent (Fig. 3). The model clearly demonstrates how LT can be used to optimize, isolate, or otherwise control the level of a particular species. Notably, the behavior of systems in which successive ligand binding events do not contribute equally to the measured signal is readily simulated using the roots of the quartic equation by simply applying a scaling factor for each enzyme form and binding constant (see below); treating data in this way allows untransformed data to be fit directly without altering the error structure associated with the dataset.
Fig.3.
Calculated concentrations of enzyme species for a trimeric protein with negative cooperativity as a function of LT. The ELi species, where i = 0 (○), 1 (●), 2 (■), or 3 (▲), were calculated for a homotrimeric protein (1.0 μM trimer) in which binding of one ligand causes 100-fold negative cooperativity at both of the other subunits and binding of the second and third ligands is independent. k1 = 0.1 μM; k2 = k3 = 10 μM.
The Excel worksheets
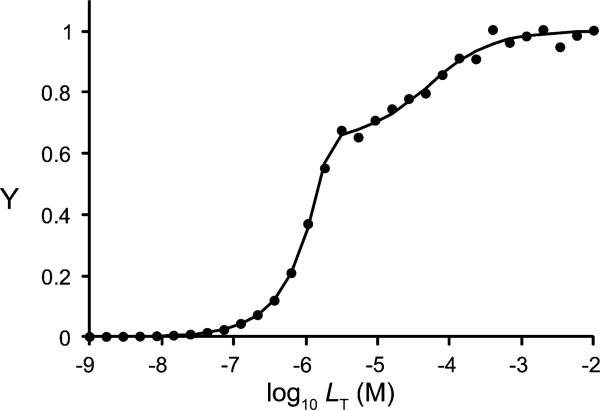
Excel worksheets designed to simulate and/or least-squares fit homotropic ligand binding data for allosteric dimers and trimers are provided in the Supplementary material. As an example, these worksheets were used to simulate binding data for a negatively cooperative trimeric protein and to least-squares fit the resulting output (Fig. 4). ki values were chosen such that the affinities of the second and third ligands were 10- and 1000-fold weaker, respectively, than that of the first ligand (i.e., k2 = 10 × k1; k3 = 1000 × k1). The fractional saturation (Y) values were calculated with ±2% random error. The resulting best-fit ki estimates were within 7% of the true values. The worksheets can also treat models where the signals that report binding differ as each subunit becomes occupied.
Fig.4.
Simulation of cooperative binding to a trimeric protein with negative cooperativity. Data were generated in silico based on parameters ET = 1 μM dimer, k1 = 0.01 μM, k2 = 0.1 μM, and k3 = 10 μM with ±2% random error. Line represents least-squares fit of the data. k1 = 0.01 μM; k2 = 0.107 μM; k3 = 9.39 μM.
Application to spectroscopic methods
Ligand binding is frequently monitored by spectral changes in the protein (e.g., absorbance, fluorescence, or magnetic resonance) across a range of ligand concentrations [1,38]. It is frequently assumed that the signal associated with the binding of a ligand to a given protomer is independent of ligand occupancy at the distal sites. The analytical method readily accommodates situations where bound species contribute different intensities to that signal. In this case, each protein species is assigned a relative signal value (Qi), which is analogous to the quantum yield in fluorescence. The signal intensity of the solution at a given concentration of protein and ligand (I) relative to that of the unliganded protein (I0) is equal to the fraction of bound protein, where each species is weighted by its Qi value (Eq. (21)):
| (21) |
Q0 (free protein) is defined as unity, Qi is equal to the I/I0 value for the species ELi, and Qn (fully liganded protein of n subunits) is equal to I/I0 at saturation. In the simplest case, where each ligand binding event contributes equally to the change in signal, the intermediate Qi values are proportional to ligand occupancy (Eq. (22)):
| (22) |
When the intermediate Qi values diverge from the proportional values, least-squares fitting may be used to estimate them if ki values are known. Conversely, if preliminary experiments can establish Qi values, these can be taken into account when fitting for ki. In this way, spectroscopically silent steps may be accounted for in the model. As an example, cytochrome P450 3A4, an enzyme that metabolizes more than one-third of common drugs, exhibits cooperative homotropic binding of up to three ligands (e.g., testosterone), where each enzyme form ELi catalyzes the reaction at a different rate and exhibits an altered spin state of the heme iron [13]. Electron paramagnetic resonance experiments that report on the spin state require enzyme concentrations much greater than Kd, thereby precluding use of the Adair equation in analysis [29]. The method presented here allows both kinetic and spectral data to be fit (simultaneously if desired) to parameters that provide a detailed description of the system, including the heterogeneity and interaction of the binding sites as well as differential properties of each enzyme form. Finally, spectroscopic signals coming from the ligand may be monitored instead of protein; this modality may be treated by substituting L for E and LT for ET in Eq. (21).
Conclusions
Equations describing the exact concentrations of ligand and protein species at equilibrium as a function of their total concentrations and dissociation constants have been presented for the dimeric and trimeric cases. The equations provide a simple means of calculating the distribution of species in complex allosteric systems and of fitting ligand binding data to LT rather than assuming L = LT. Removing this assumption can significantly enhance accuracy of the fit estimates. The method is general in that it takes into account positive and negative cooperativity at each step and allows discrete signal contributions from each of the enzyme forms.
Supplementary Material
Acknowledgment
This work was supported by the National Institutes of Health (NIH, R01 GM054469).
Footnotes
Appendix A. Supplementary data
Supplementary data associated with this article can be found, in the online version, at doi:10.1016/j.ab.2011.12.016.
References
- 1.Ward LD. Measurement of ligand binding to proteins by fluorescence spectroscopy. Methods Enzymol. 1985;117:400–414. doi: 10.1016/s0076-6879(85)17024-2. [DOI] [PubMed] [Google Scholar]
- 2.Pattnaik P. Surface plasmon resonance. Applications in understanding receptor–ligand interaction. Appl. Biochem. Biotechnol. 2005;126:79–92. doi: 10.1385/abab:126:2:079. [DOI] [PubMed] [Google Scholar]
- 3.Freyer MW, Lewis EA. Isothermal titration calorimetry: experimental design, data analysis, and probing macromolecule/ligand binding and kinetic interactions. Methods Cell Biol. 2008;84:79–113. doi: 10.1016/S0091-679X(07)84004-0. [DOI] [PubMed] [Google Scholar]
- 4.Bylund DB, Toews ML. Radioligand binding methods: practical guide and tips. Am. J. Physiol. 1993;265:L421–L429. doi: 10.1152/ajplung.1993.265.5.L421. [DOI] [PubMed] [Google Scholar]
- 5.Bardsley WG, Wyman J. Concerning the thermodynamic definition and graphical manifestations of positive and negative co-operativity. J. Theor. Biol. 1978;72:373–376. doi: 10.1016/0022-5193(78)90097-8. [DOI] [PubMed] [Google Scholar]
- 6.Cornish-Bowden A, Koshland DE., Jr. Diagnostic uses of the Hill (Logit and Nernst) plots. J. Mol. Biol. 1975;95:201–212. doi: 10.1016/0022-2836(75)90390-3. [DOI] [PubMed] [Google Scholar]
- 7.Franco R, Casado V, Cortes A, Ferrada C, Mallol J, Woods A, Lluis C, Canela EI, Ferre S. Basic concepts in G-protein-coupled receptor homo- and heterodimerization. Sci. World J. 2007;7:48–57. doi: 10.1100/tsw.2007.197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sun M, Leyh TS. The human estrogen sulfotransferase: a half-site reactive enzyme. Biochemistry. 2010;49:4779–4785. doi: 10.1021/bi902190r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kumaran S, Yi H, Krishnan HB, Jez JM. Assembly of the cysteine synthase complex and the regulatory role of protein–protein interactions. J. Biol. Chem. 2009;284:10268–10275. doi: 10.1074/jbc.M900154200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Alander J, Lengqvist J, Holm PJ, Svensson R, Gerbaux P, Heuvel RH, Hebert H, Griffiths WJ, Armstrong RN, Morgenstern R. Microsomal glutathione transferase 1 exhibits one-third-of-the-sites-reactivity towards glutathione. Arch. Biochem. Biophys. 2009;487:42–48. doi: 10.1016/j.abb.2009.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chojnowski G, Breer K, Narczyk M, Wielgus-Kutrowska B, Czapinska H, Hashimoto M, Hikishima S, Yokomatsu T, Bochtler M, Girstun A, Staron K, Bzowska A. 1.45 Å resolution crystal structure of recombinant PNP in complex with a pM multisubstrate analogue inhibitor bearing one feature of the postulated transition state. Biochem. Biophys. Res. Commun. 2010;391:703–708. doi: 10.1016/j.bbrc.2009.11.124. [DOI] [PubMed] [Google Scholar]
- 12.Ducati RG, Santos DS, Basso LA. Substrate specificity and kinetic mechanism of purine nucleoside phosphorylase from Mycobacterium tuberculosis. Arch. Biochem. Biophys. 2009;486:155–164. doi: 10.1016/j.abb.2009.04.011. [DOI] [PubMed] [Google Scholar]
- 13.Denisov IG, Frank DJ, Sligar SG. Cooperative properties of cytochromes P450. Pharmacol. Ther. 2009;124:151–167. doi: 10.1016/j.pharmthera.2009.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Seeger MA, Diederichs K, Eicher T, Brandstatter L, Schiefner A, Verrey F, Pos KM. The AcrB efflux pump: conformational cycling and peristalsis lead to multidrug resistance. Curr. Drug Targets. 2008;9:729–749. doi: 10.2174/138945008785747789. [DOI] [PubMed] [Google Scholar]
- 15.Tokaji Z. Dimeric-like kinetic cooperativity of the bacteriorhodopsin molecules in purple membranes. Biophys. J. 1993;65:1130–1134. doi: 10.1016/S0006-3495(93)81165-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sohn J, Grant RA, Sauer RT. Allostery is an intrinsic property of the protease domain of DegS: implications for enzyme function and evolution. J. Biol. Chem. 2010;285:34039–34047. doi: 10.1074/jbc.M110.135541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hill AV. The combinations of haemoglobin with oxygen and with carbon monoxide. Biochem. J. 1913;7:471–480. doi: 10.1042/bj0070471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Weiss JN. The Hill equation revisited: uses and misuses. FASEB J. 1997;11:835–841. [PubMed] [Google Scholar]
- 19.Adair GS. The hemoglobin system: VI. The oxygen dissociation curve of hemoglobin. J. Biol. Chem. 1925;63:529. [Google Scholar]
- 20.Abel NH. Beweis der Unmöglichkeit Algebraische Gleichungen von höheren Graden als dem vierten allgemein aufzulösen. J. Reine Angew. Math. 1826;1:65–84. [Google Scholar]
- 21.Cardano G, Witmer TR. Ars Magna or the Rules of Algebra. Dover, New York: 1993. (Original work published 1514) [Google Scholar]
- 22.Descartes R, Smith DE, Latham ML. La Geometrie or the Geometry of Rene Descartes. Dover, New York: 1954. (Original work published 1637) [Google Scholar]
- 23.Manders K. Algebra in Roth, Faulhaber, and Descartes. Hist. Math. 2006;33:184–209. [Google Scholar]
- 24.Wang ZX. An exact mathematical expression for describing competitive binding of two different ligands to a protein molecule. FEBS Lett. 1995;360:111–114. doi: 10.1016/0014-5793(95)00062-e. [DOI] [PubMed] [Google Scholar]
- 25.Sigurskjold BW. Exact analysis of competition ligand binding by displacement isothermal titration calorimetry. Anal. Biochem. 2000;277:260–266. doi: 10.1006/abio.1999.4402. [DOI] [PubMed] [Google Scholar]
- 26.Mack ET, Perez-Castillejos R, Suo Z, Whitesides GM. Exact analysis of ligand-induced dimerization of monomeric receptors. Anal. Chem. 2008;80:5550–5555. doi: 10.1021/ac800578w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Braun PD, Wandless TJ. Quantitative analyses of bifunctional molecules. Biochemistry. 2004;43:5406–5413. doi: 10.1021/bi035839g. [DOI] [PubMed] [Google Scholar]
- 28.Zuber E, Mathis G, Flandrois JP. Homogeneous two-site immunometric assay kinetics as a theoretical tool for data analysis. Anal. Biochem. 1997;251:79–88. doi: 10.1006/abio.1997.2243. [DOI] [PubMed] [Google Scholar]
- 29.Roberts AG, Campbell AP, Atkins WM. The thermodynamic landscape of testosterone binding to cytochrome P450 3A4: ligand binding and spin state equilibria. Biochemistry. 2005;44:1353–1366. doi: 10.1021/bi0481390. [DOI] [PubMed] [Google Scholar]
- 30.Varshavsky AD, Birnbaum DT, Beals JM, Saxberg BE. Global stochastic optimization in hierarchical modeling of ligand/protein binding profiles. Kybernetes. 1996;29:452–472. [Google Scholar]
- 31.Monod J, Wyman J, Changeux JP. On the nature of allosteric transitions: a plausible model. J. Mol. Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 32.Koshland DE, Jr., Nemethy G, Filmer D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry. 1966;5:365–385. doi: 10.1021/bi00865a047. [DOI] [PubMed] [Google Scholar]
- 33.Eigen M. New looks and outlooks on physical enzymology. Q. Rev. Biophys. 1968;1:3–33. doi: 10.1017/s0033583500000445. [DOI] [PubMed] [Google Scholar]
- 34.Karpen JW, Ruiz M. Ion channels: does each subunit do something on its own? Trends Biochem Sci. 2002;27:402–409. doi: 10.1016/s0968-0004(02)02124-2. [DOI] [PubMed] [Google Scholar]
- 35.Klotz IM, Hunston DL. Protein interactions with small molecules: Relationships between stoichiometric binding constants, site binding constants, and empirical binding parameters. J. Biol. Chem. 1975;250:3001–3009. [PubMed] [Google Scholar]
- 36.Hammes GG, Wu CW. Kinetics of allosteric enzymes. Annu. Rev. Biophys. Bioeng. 1974;3:1–33. doi: 10.1146/annurev.bb.03.060174.000245. [DOI] [PubMed] [Google Scholar]
- 37.von Ballmoos C, Wiedenmann A, Dimroth P. Essentials for ATP synthesis by F1F0 ATP synthases. Annu. Rev. Biochem. 2009;78:649–672. doi: 10.1146/annurev.biochem.78.081307.104803. [DOI] [PubMed] [Google Scholar]
- 38.Wemmer DE, Williams PG. Use of nuclear magnetic resonance in probing ligand–macromolecule interactions. Methods Enzymol. 1994;239:739–767. doi: 10.1016/s0076-6879(94)39028-2. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.