jPopGen Suite: population genetic analysis of DNA polymorphism from nucleotide sequences with errors

Summary

1. Next-generation sequencing (NGS) is being increasingly used in ecological and evolutionary studies. Though promising, NGS is known to be error-prone. Sequencing error can cause significant bias for population genetic analysis of a sequence sample.

2. We present jPopGen Suite, an integrated tool for population genetic analysis of DNA polymorphisms from nucleotide sequences. It is specially designed for data with a non-negligible error rate, although it serves well for “error-free” data. It implements several methods for estimating the population mutation rate, population growth rate, and conducting neutrality tests.

3. jPopGen Suite facilitates the population genetic analysis of NGS data in various applications, and is freely available for non-commercial users at http://sites.google.com/site/jpopgen/.

1 Introduction

The advance of next-generation sequencing (NGS) technologies has helped researchers to conduct various genetic studies efficiently in terms of both time and cost. Wider application of these technologies in ecological and evolutionary studies is expected in the near future. One disadvantage associated with these new sequencers is that their error rates are typically tenfold higher than that of Sanger sequencing (Shendure and Ji, 2008). Sequencing error can cause significant bias for population genetic analysis of a sequence sample. Given a random sample from a population, artificial polymorphisms caused by sequencing error will skew both the number and frequency spectrum of the observed SNPs. This will further skew any estimations or test statistics based on the number and/or frequency spectrum of the SNPs (Johnson and Slatkin, 2008; Achaz, 2008). The problem will be even more prominent with increased sample size because the number of sequencing errors increases linearly with sample size while that of true mutations increases slower (Liu et al., 2009, 2010).

There have been several new methods proposed to estimate population genetic parameters and test the hypothesis of strict neutrality using DNA sequences with errors (e.g. Achaz, 2008, 2009; Johnson and Slatkin, 2006, 2008, 2009; Liu et al., 2009, 2010; Hellmann et al., 2008; Knudsen and Miyamoto, 2007, 2009; Lynch, 2009). Targeting population genetic analysis of error-prone NGS data, jPopGen Suite implements some of these new methods along with several widely used methods designed for “error-free” data.

2 Platform, interface and file format

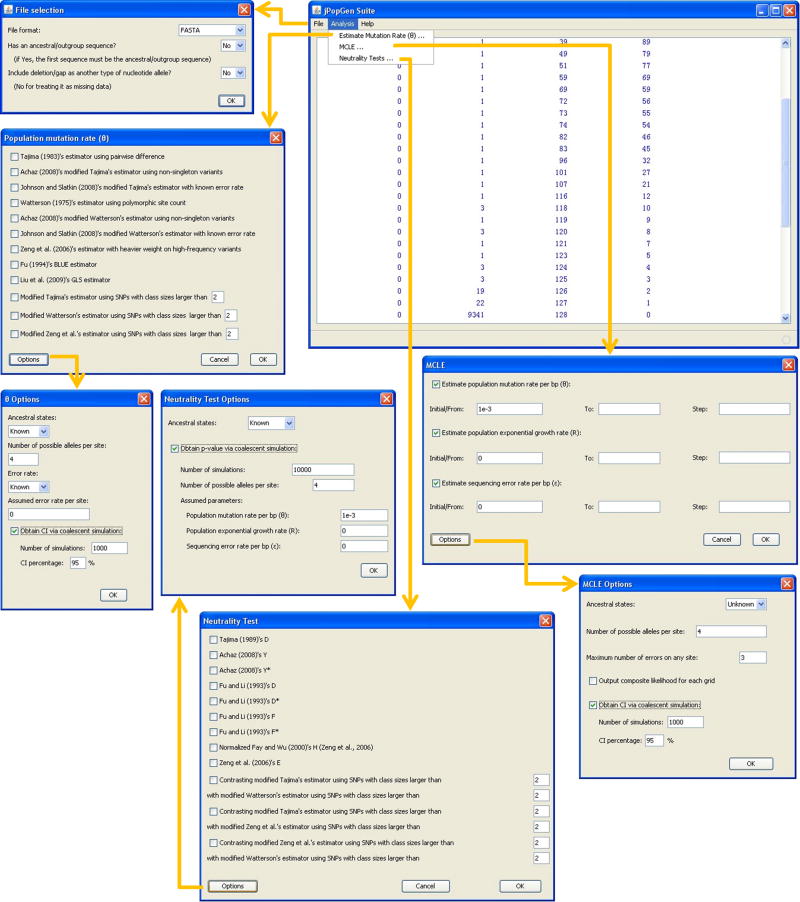
jPopGen Suite is written in Java, which enables it to run cross-platform on a wide range of computers, as long as a proper Java Runtime Environment is installed. It uses a menu-driven graphic user interface (GUI) to specify all parameter settings and conduct all integrated analyses (Fig. 1). In addition to the GUI, the full functionality of the suite can be accessed through a command line interface, which facilitates a “batch mode” for analyzing large data sets.

Fig 1.

The major graphic user interfaces of jPopGen Suite.

The default input file format is a summary of the SNP frequency spectrum (SFS) with each row describing the observed number of a particular SNP configuration (numbers of major/ancestral alleles, minor/derived alleles and missing data). The ancestral alleles of the polymorphic sites can be either known (unfolded data) or unknown (folded data). Additionally, jPopGen Suite supports the direct input of sequence data files in PHYLIP, ALN (ClustalW2), or FASTA format.

3 Analysis methods implemented

3.1 Estimating population parameters

Thirteen methods are implemented to estimate the population mutation rate θ (θ=4Nμ, where N is the effective population size and μ is the mutation rate per sequence per generation), assuming a constant population size. Among them four methods are for “error-free” data: Tajima’s (Tajima, 1983) estimator based on pairwise difference between two sequences (θ_π), Watterson’s (Watterson, 1975) estimator based on the number of polymorphic sites (θ_S), Fu’s (Fu, 1994) best linear unbiased estimators (BLUEs) for unfolded and folded data and Zeng et al.’s (Zeng et al., 2006) estimator for unfolded data (θ_L). Three methods are designed for sequences with assumed known sequencing error rate: Johnson and Slatkin’s (Johnson and Slatkin, 2008) modified θ_π estimator and θ_S estimator, and Liu et al.’s (Liu et al., 2009) generalized least square (GLS) estimators with known sequencing error rate for unfolded and folded data. The remaining six methods are for data with unknown sequencing error rate: Achaz’s (Achaz, 2008) modified θ_π and θ_S based on non-singleton variants, Liu et al.’s (Liu et al., 2009) GLS estimators based on non-singleton variants, and modified θ_π, θ_S and θ_L based on variants with minor allele count larger than a user specified number m (n-1>m≥0, where n is the number of sequences in the sample), denoted as θ_πm, θ_Sm and θ_Lm, respectively. That is,

$$\begin{array}{lll}{\theta }_{\pi m}& =& \frac{2}{\left(n-m-1\right)\left(n-m\right)}\sum _{i=m+1}^{n-1}i\left(n-i\right){\xi }_i\\ {\theta }_{\mathit{Sm}}& =& \left(\sum _{i=m+1}^{n-1}{\xi }_i\right)/\left(\sum _{i=m+1}^{n-1}\frac{1}{i}\right)\\ {\theta }_{\mathit{Lm}}& =& \frac{1}{\left(n-m-1\right)}\sum _{i=m+1}^{n-1}i{\xi }_i,\end{array}$$

for unfolded data, and

$$\begin{array}{lll}{\theta }_{\pi m}& =& \frac{2}{n\left(n-2m-1\right)}\sum _{i=m+1}^{n-m-1}i\left(n-i\right){\xi }_i\\ {\theta }_{\mathit{Sm}}& =& \left(\sum _{i=m+1}^{n-m-1}{\xi }_i\right)/\left(\sum _{i=m+1}^{n-m-1}\frac{1}{i}\right),\end{array}$$

for folded data, where ξ_i is the number of segregating sites on which the derived allele occurs i times in the sample.

jPopGen Suite implements Liu et al.’s (Liu et al., 2010) maximum composite likelihood estimators (MCLEs) to estimate the population mutation rate θ, population exponential growth rate R, and sequencing error rate ε, simultaneously. In a population exponential growth model, N(t)=N(0)exp(-rt), where N(t) is the effective population size t generations before the current time (generation 0), and the scaled population growth rate R is defined as R=2N(0)r. An error model assumes that there are n_a (n_a≥2) types of alleles at a nucleotide site, and when a sequencing error occurs on an allele, the allele has an equal probability 1/(n_a-1) to change to another type of allele. A grid search algorithm is used to estimate the three parameters.

Confidence intervals of the θ estimators and MCLEs can be inferred via coalescent simulation.

3.2 Testing the hypothesis of strict neutrality

Twelve methods are implemented for the neutrality test: Tajima’s (Tajima, 1989) D test, Achaz’s (Achaz, 2008) Y and Y* tests, Fu and Li’s (Fu and Li, 1993) D, D*, F and F* tests (correctly normalized according to Achaz, 2009), normalized Fay and Wu’s (Fay and Wu, 2000) H test (Zeng et al., 2006), Zeng et al.’s (Zeng et al., 2006) E test, and three new tests via contrasting θ_πm with θ_Sm, θ_πm with θ_Lm, and θ_Lm with θ_Sm, respectively. These three new test statistics are calculated as

$$T=\left[\left({\theta }_1-{\theta }_2\right)-\overline{E}\left({\theta }_1-{\theta }_2\right)\right]/\sqrt{\overline{\mathrm{Var}}\left({\theta }_1-{\theta }_2\right)},$$

where θ₁ and θ₂ are two different θ estimators, Ē(θ₁−θ₂) and Var̅(θ₁−θ₂) are the empirical mean and variance of θ₁-θ₂, obtained via coalescent simulation (e.g. Hudson, 2002).

Coalescent simulation is also used to estimate the p-values or significance levels of the tests. One unique feature of this tool is that the sequencing error model and the population exponential growth model are incorporated into the null model. The user can specify the known or estimated population mutation rate θ, sequencing error rate ε and population exponential growth rate R for the simulation. This is particularly important for conducting the neutrality tests when sequencing errors and population growth cannot be ignored, because both may significantly skew the null distributions of the test statistics, and therefore increase the type I error rate (Johnson and Slatkin, 2008; Achaz, 2008).

4. Suggested usage

Unless constant population size can be assumed, MCLE is recommended for the first-round analysis for estimating the population mutation rate θ, the sequencing error rate ε and the population exponential growth rate R. Using coalescent simulation, the confidence interval of the above estimations can be inferred. If ε or/and R are not significantly different to 0, then θ estimators assuming constant population size or/and no sequencing errors then can be applied for more accurate estimation of θ. We generally recommend Liu et al.’s (Liu et al., 2009) GLS estimators or Fu’s (Fu, 1994) BLUE estimators for that purpose.

The selection of neutrality tests also depends on the estimated error rate. If the sequencing errors cannot be ignored, Achaz’s (Achaz, 2008) Y and Y* tests or the three new tests via contrasting θ_πm with θ_Sm, θ_πm with θ_Lm, and θ_Lm with θ_Sm, respectively, are recommended. Otherwise, the remaining seven traditional tests can be selected based on their testing power under different alternative hypotheses.