A SPARSE CONDITIONAL GAUSSIAN GRAPHICAL MODEL FOR ANALYSIS OF GENETICAL GENOMICS DATA

Abstract

Genetical genomics experiments have now been routinely conducted to measure both the genetic markers and gene expression data on the same subjects. The gene expression levels are often treated as quantitative traits and are subject to standard genetic analysis in order to identify the gene expression quantitative loci (eQTL). However, the genetic architecture for many gene expressions may be complex, and poorly estimated genetic architecture may compromise the inferences of the dependency structures of the genes at the transcriptional level. In this paper, we introduce a sparse conditional Gaussian graphical model for studying the conditional independent relationships among a set of gene expressions adjusting for possible genetic effects where the gene expressions are modeled with seemingly unrelated regressions. We present an efficient coordinate descent algorithm to obtain the penalized estimation of both the regression coefficients and sparse concentration matrix. The corresponding graph can be used to determine the conditional independence among a group of genes while adjusting for shared genetic effects. Simulation experiments and asymptotic convergence rates and sparsistency are used to justify our proposed methods. By sparsistency, we mean the property that all parameters that are zero are actually estimated as zero with probability tending to one. We apply our methods to the analysis of a yeast eQTL data set and demonstrate that the conditional Gaussian graphical model leads to more interpretable gene network than standard Gaussian graphical model based on gene expression data alone.

1. Introduction

Genetical genomics experiments have now been routinely conducted to measure both the genetic variants and gene expression data on the same subjects. Such data have provided important insights into gene expression regulations in both model organisms and humans (Brem and Kruglyak, 2005; Schadt et al., 2003; Cheung and Spielman, 2002). Gene expression levels are treated as quantitative traits and are subject to standard genetic analysis in order to identify the gene expression quantitative loci (eQTL). However, the genetic architecture for many gene expressions may be complex due to possible multiple genetic effects and gene-gene interactions, and poorly estimated genetic architecture may compromise the inferences of the dependency structures of genes at the transcriptional level (Neto et al., 2010). For a given gene, typical analysis of such eQTL data is to identify the genetic loci or single nucleotide polymorphisms (SNPs) that are linked or associated with the expression level of this gene. Depending on the locations of the eQTLs or the SNPs, they are often classified as distal trans-linked loci or proximal cis-linked loci (Kendzioski and Wang, 2003; Kendzioski et al., 2006). Although such a single gene analysis can be effective in identifying the associated genetic variants, gene expressions of many genes are in fact highly correlated due to either shared genetic variants or other unmeasured common regulators. One important biological problem is to study the conditional independence among these genes at the expression level.

eQTL data provide important information about gene regulation and have been employed to infer regulatory relationships among genes (Zhu et al., 2004; Bing and Hoeschele, 2005; Chen et al, 2007). Gene expression data have been used for inferring the genetic regulatory networks, for example, in the framework of Gaussian graphical models (GGM) (Schafer and Strimmer, 2005; Segal et al., 2005; Li and Gui, 2006; Peng et al., 2009). Graphical models use graphs to represent dependencies among stochastic variables. In particular, the GGM assumes that the multivariate vector follows a multivariate normal distribution with a particular structure of the inverse of the covariance matrix, called the concentration matrix. For such Gaussian graphical models, it is usually assumed that the patterns of variation in expression for a given gene can be predicted by those of a small subset of other genes. This assumption leads to sparsity (i.e., many zeros) in the concentration matrix and reduces the problem to well-known neighborhood selection or covariance selection problems (Dempster, 1972; Meinshausen and Bühlmann, 2006). In such a concentration graph modeling framework, the key idea is to use partial correlation as a measure of the independence of any two genes, rendering it straightforward to distinguish direct from indirect interactions. Due to high-dimensionality of the problem, regularization methods have been developed to estimate the sparse concentration matrix where a sparsity penalty function such as the L₁ penalty or SCAD penalty is often used on the concentration matrix (Li and Gui, 2006; Friedman et al., 2008; Fan et al., 2009). Among these methods, the coordinate descent algorithm of Friedman et al. (2008), named glasso, provides a computationally efficient method for performing the Lasso-regularized estimation of the sparse concentration matrix.

Although the standard GGMs can be used to infer the conditional dependency structures using gene expression data alone from eQTL experiments, such models ignore the effects of genetic variants on the means of the expressions, which can compromise the estimate of the concentration matrix, leading to both false positive and false negative identifications of the edges of the Gaussian graphs. For example, if two genes are both regulated by the same genetic variants, at the gene expression level, there should not be any dependency of these two genes. However, without adjusting for the genetic effects on gene expressions, a link between these two genes is likely to be inferred. For eQTL data, we are interested in identifying the conditional dependency among a set of genes after removing the effects from shared regulations by the markers. Such a graph can truly reflect gene regulation at the expression level.

In this paper, we introduce a sparse conditional Gaussian graphical model (cGGM) that simultaneously identifies the genetic variants associated with gene expressions and constructs a sparse Gaussian graphical model based on eQTL data. Different from the standard GGMs that assume constant means, the cGGM allows the means to depend on covariates or genetic markers. We consider a set of regressions of gene expression in which both regression coefficients and the error concentration matrix have many zeros. Zeros in regression coefficients arise when each gene expression only depends on a very small set of genetic markers; zeros in the concentration matrix arise since the gene regulatory network and therefore the corresponding concentration matrix is sparse. This approach is similar in spirit to the seemingly unrelated regression (SUR) model of Zellner (1962) in order to improve the estimation efficiency of the effects of genetic variants on gene expression by considering the residual correlations of the gene expression of many genes. In analysis of eQTL data, we expect sparseness in both the regression coefficients and also the concentration matrix. We propose to develop a regularized estimation procedure to simultaneously select the SNPs associated with gene expression levels and to estimate the sparse concentration matrix. Different from the original SUR model of Zellner (1962) that focuses on improving the estimation efficiency of the regression coefficients, we focus more on estimating the sparse concentration matrix adjusting for the effects of the SNPs on mean expression levels. We develop an efficient coordinate descent algorithm to obtain the penalized estimates and present the asymptotic results to justify our estimates.

In the next sections, we first present the formulation of the cGGM for both the mean gene expression levels and the concentration matrix. We then present an efficient coordinate descent algorithm to perform the regularized estimation of the regression coefficients and concentration matrix. Simulation experiments and asymptotic theory are used to justify our proposed methods. We apply the methods to an analysis of a yeast eQTL data set. We conclude the paper with a brief discussion. All the proofs are given in the online Supplemental Material.

2. The Sparse cGGM and Penalized Likelihood Estimation

2.1. The sparse conditional Gaussian graphical model

Suppose we have n independent observations from a population of a vector (y′, x′), where y is a p × 1 random vector of gene expression levels of p genes and x is a q × 1 vector of the numerically-coded SNP genotype data for q SNPs. Furthermore, suppose that conditioning on x, y follows a multivariate normal distribution,

$$\mathbf{y}\mid \mathbf{x}~\mathcal{N}(\mathrm{\Gamma }\mathbf{x},\mathrm{\sum }),$$ (1)

where Γ is a p × q coefficient matrix for the means and the covariance matrix Σ does not depend on x. We are interested in both the effects of the SNPs on gene expressions Γ and the conditional independence structure of y adjusting for the effects of x, that is, the Gaussian graphical model for y = (y₁, · · ·, y_p) conditional on x. In applications of gene expression data analysis, we are more interested in the concentration matrix Θ = Σ⁻¹ after their shared genetic regulators are accounted for. It has a nice interpretation in the Gaussian graphical model, as the (i, j)-element is directly related to the partial correlation between the ith and jth components of y after their potential joint genetic regulators are adjusted. In the Gaussian graphical model with undirected graph (V, E), vertices V correspond to components of the vector y and edges E = {e_ij, 1 ≤ i, j ≤ p} indicate the conditional dependence among different components of y. The edge e_ij between y_i and y_j exists if and only if θ_ij ≠ 0, where θ_ij is the (i, j)-element of Θ. We emphasize that in the graph representation of the random variable y, the nodes include only the genes and the markers are not part of the graph. We call this the sparse conditional Gaussian graph model (cGGM) of the genes. Hence, of particular interest is to identify zero entries in the concentration matrix. Note that instead of assuming a constant mean as in the standard GGM, model (1) allows heterogeneous means.

In eQTL experiments, each row of Γ and the concentration matrix Θ are expected to be sparse and our goal is to simultaneously learn the Gaussian graphical model as defined by the Θ matrix and to identify the genetic variants associated with gene expressions Γ based on n independent observations of ( ${\mathbf{y}}_i^{\prime },{\mathbf{x}}_i^{\prime }$), i = 1, · · ·, n. From now on, we use y_i to denote the vector of gene expression levels of the p genes and x_i to denote the vector of the genotype codes of the q SNPs for the ith observation unless otherwise specified. Finally, let $\mathbf{X}=({\mathbf{x}}_1^{\prime },\cdots ,{\mathbf{x}}_n^{\prime })$ be genotype matrix and $\overline{\mathbf{x}}=1/n{\sum }_{i=1}^n{\mathbf{x}}_i$

2.2. Penalized likelihood estimation

Suppose that we have n independent observation ( ${\mathbf{y}}_i^{\prime },{\mathbf{x}}_i^{\prime }$) from the cGGM (1). Let ${\mathbf{C}}_Y=1/n{\sum }_{i=1}^n{\mathbf{y}}_i{\mathbf{y}}_i^{\prime },{\mathbf{C}}_{YX}=1/n{\sum }_{i=1}^n{\mathbf{y}}_i{\mathbf{x}}_i^{\prime }$ and ${\mathbf{C}}_X=1/n{\sum }_{i=1}^n{\mathbf{x}}_i{\mathbf{x}}_i^{\prime }$. Then the negative of the logarithm of the likelihood function corresponding to the cGGM model can be written as

$$l(\mathrm{\Xi })=-logdet\mathrm{\Theta }+tr\left\{{\mathbf{C}}_Y\mathrm{\Theta }-{\mathbf{C}}_{YX}{\mathrm{\Gamma }}^{\prime }\mathrm{\Theta }-\mathrm{\Gamma }{\mathbf{C}}_{YX}^{\prime }\mathrm{\Theta }+\mathrm{\Gamma }{\mathbf{C}}_X{\mathrm{\Gamma }}^{\prime }\mathrm{\Theta }\right\},$$

where Ξ = (Θ, Γ) represents the associated parameters in the cGGM.

The Hessian matrix of the negative log-likelihood function l(Ξ) is

$$Hl(\mathrm{\Xi })=\left(\begin{array}{cc}{\mathrm{\Theta }}^{-1}\otimes {\mathrm{\Theta }}^{-1}& -2{\mathbf{C}}_{YX}\otimes I_p+2(\mathrm{\Gamma }{\mathbf{C}}_X)\otimes I_p\\ -2{\mathbf{C}}_{YX}^{\prime }\otimes I_p+2({\mathbf{C}}_X{\mathrm{\Gamma }}^{\prime })\otimes I_p& 2{\mathbf{C}}_X\otimes \mathrm{\Theta }\end{array}\right).$$

(see Proposition 1 in Supplementary Material, Section 3). In addition, l(Ξ) is a bi-convex function of Γ and Θ. In words, this means that for any fixed Θ, l(Ξ) is a convex function of Γ, and for any Γ, l(Ξ) is a convex function of Θ. When n > max(p, q), the global minimizer of l(Ξ) is given by

$$\{\begin{array}{ll}{\stackrel{\sim }{\mathrm{\Theta }}}^{-1}=\hfill & {\mathbf{C}}_Y-{\mathbf{C}}_{YX}{\mathbf{C}}_X^{-1}{\mathbf{C}}_{YX}^{\prime },\hfill \\ \stackrel{\sim }{\mathrm{\Gamma }}=\hfill & {\mathbf{C}}_{YX}{\mathbf{C}}_X^{-1}.\hfill \end{array}$$

Under the penalized likelihood framework, the estimate of the Γ and Σ in model (1) is the solution to the following optimization problem,

$$min\left\{pl(\mathrm{\Xi })\equiv -logdet\mathrm{\Theta }+tr({\mathbf{S}}_{\mathrm{\Gamma }}\mathrm{\Theta })+\lambda \sum _{s,t}{\mathit{pen}}_1({\gamma }_{st})\rho \sum _{t,t^{\prime }}{\mathit{pen}}_2({\theta }_{{tt}^{\prime }})\right\},$$ (2)

where pen₁(·) and pen₂(·) denote the generic penalty functions, γ_st is the stth element of the Γ matrix and θ_tt′ is the tt′th element of the Θ matrix, and

$$\begin{array}{l}{\mathbf{S}}_{\mathrm{\Gamma }}=\frac{1}{n}\sum _{i=1}^n({\mathbf{y}}_i-\mathrm{\Gamma }{\mathbf{x}}_i){({\mathbf{y}}_i-\mathrm{\Gamma }{\mathbf{x}}_i)}^{\prime }\\ ={\mathbf{C}}_Y-{\mathbf{C}}_{YX}{\mathrm{\Gamma }}^{\prime }-\mathrm{\Gamma }{\mathbf{C}}_{YX}^{\prime }+\mathrm{\Gamma }{\mathbf{C}}_X{\mathrm{\Gamma }}^{\prime }.\end{array}$$

Here ρ and λ are the two tuning parameters that control the sparsity of the sparse cGGM. We consider in this paper both the Lasso or L₁ penalty function pen(x) = |x| (Tibshirani, 1996) and the adaptive Lasso penalty function pen(x) = |x|/|x̃|^γ for some γ > 0 and any consistent estimate of x, denoted by x̃ (Zou, 2007). In this paper we use γ = 0.5.

2.3. An efficient coordinate descent algorithm for the sparse cGGM

We present an algorithm for the optimization problem (2) with Lasso penalty function for pen₁(·) and pen₂(·). A similar algorithm can be developed for the adaptive Lasso penalty with simple modifications. Under this penalty function, the objective function is then

$$max\left\{logdet\mathrm{\Theta }-tr({\mathbf{S}}_{\mathrm{\Gamma }}\mathrm{\Theta })-\lambda {\left|\right|\mathrm{\Gamma }\left|\right|}_1-\rho {\left|\right|\mathrm{\Theta }\left|\right|}_1\right\}.$$ (3)

The subgradient equation for maximization of the log-likelihood (3) with respect to Θ is

$${\mathrm{\Theta }}^{-1}-{\mathbf{S}}_{\mathrm{\Gamma }}-\rho \mathrm{\Lambda }=0,$$ (4)

where Λ_ij ∈ sgn(Θ_ij). If Γ is known, Banerjee et al. (2008) and Friedman et al. (2008) have cast the optimization problem (3) as a block-wise coordinate descent algorithm, which can be formulated as p iterative Lasso problems. Before we proceed, we first introduce some notations to better represent the algorithm. Let W be the estimate of Σ. We partition W and S_Γ as

$$\mathbf{W}=\left(\begin{array}{cc}{\mathbf{W}}_{11}& w_{12}\\ w_{12}^{\top }& w_{22}\end{array}\right),{\mathbf{S}}_{\mathrm{\Gamma }}=\left(\begin{array}{cc}{\mathbf{S}}_{11}& s_{12}\\ s_{12}^{\top }& s_{22}\end{array}\right).$$

Banerjee et al. (2008) show that the solution for w₁₂ satisfies

$$w_{12}={\text{argmin}}_y(y^T{W}_{11}^{-1}y:{\left|\right|y-s_{12}\left|\right|}_{\infty }\le \rho ),$$

which by convex duality is equivalent to solving the dual problem

$$\widehat{\beta }={\text{argmin}}_{\beta }\left(\frac{1}{2}{\left|\right|{\mathbf{W}}_{11}^{1/2}\beta -b\left|\right|}^2+\rho {\left|\right|\beta \left|\right|}_1\right),$$ (5)

where $b={\mathbf{W}}_{11}^{-1/2}{s}_{12}$. Then the solution for w₁₂ can be obtained via the solution of the Lasso problem and through the relation w₁₂ = W₁₁β. The estimate for Θ can also be updated in this block-wise manner very efficiently through the relationship WΘ = I (Friedman et al., 2008).

After we finish an updating cycle for Θ, we can proceed to update the estimate of Γ. Since the object function of our penalized log-likelihood is quadratic in Γ given Θ, we can use a direct coordinate descent algorithm to get the penalized estimate of Γ. For the (i, j)th entry of Γ, γ_ij, note that for an arbitrary q × p matrix A, $\partial tr(\mathrm{\Gamma }A)/\partial {\gamma }_{ij}=a_{ji}=e_j^{\prime }{\mathbf{A}e}_i$ where e_j and e_i are the corresponding base vector with q and p dimensions. So the derivative of the penalized log-likelihood function (3)with respect to γ_ij is

$$2e_j^{\prime }({\mathbf{C}}_X{\mathrm{\Gamma }}^{\prime }\mathrm{\Theta })e_i+\lambda \mathit{sgn}({\gamma }_{ij})-2e_j^{\prime }({\mathbf{C}}_{YX}^{\prime }\mathrm{\Theta })e_i,$$ (6)

where function sgn is defined as

$$\mathit{sgn}(t)=\{\begin{array}{l}1,\text{if}t>0,\hfill \\ 0,\text{if}t=0,\text{and}\hfill \\ -1,\text{if}t<0.\hfill \end{array}$$

Setting the equation (6) to zero, we get the updating formula for γ_ij:

$${\widehat{\gamma }}_{ij}=\mathit{sgn}(g_{ij})\frac{{(\mid g_{ij}\mid -\lambda )}_{+}}{2(e_j^{\prime }{\mathbf{C}}_X{e}_j)(e_i^{\prime }\mathrm{\Theta }{e}_i)},$$ (7)

where $g_{ij}=2\{e_j^{\prime }({\mathbf{C}}_{YX}^{\prime }\mathrm{\Theta })e_i+(e_j^{\prime }{\mathbf{C}}_X{e}_j)(e_i^{\prime }\mathrm{\Theta }{e}_i){\stackrel{\sim }{\gamma }}_{ij}-e_j^{\prime }({\mathbf{C}}_X{\stackrel{\sim }{\mathrm{\Gamma }}}^{\prime }\mathrm{\Theta })e_i\}$ and Γ̃, γ̃_ij are the estimates in the last step of the iteration.

Taking these two updating steps together, we have the following coordinate descent-based regularization algorithm to fit the sparse cGGM:

The Coordinate Descent Algorithm for the sparse cGGM

1. Start with $\mathrm{\Gamma }={\mathbf{C}}_{YX}{\mathbf{C}}_X^{-1}$ and $\mathbf{W}={\mathbf{C}}_Y-{\mathbf{C}}_{YX}{\mathbf{C}}_X^{-1}{\mathbf{C}}_{YX}^{\prime }+\rho I$. If C_X is not invertible, use Γ = 0 and W = C_Y + ρI instead.

2. For each j = 1, 2, · · ·, p, solve the Lasso problem (5) under the current estimate of Γ. Fill in the corresponding row and column of W using w₁₂ = W₁₁β̂. Update β̂.

3. For each i = 1, 2, · · ·, p, and j = 1, 2, · · ·, q update each entry γ̂_ij in Γ̂ using the formula (7), under the current estimate for Θ.

4. Repeat step 2 and step 3 until convergence.

5. Output the estimate β̂, Ŵ and Γ̂.

The adaptive version of the algorithm can be derived in the same steps with adaptive penalty parameters and is omitted here. Note that when Γ = 0, this algorithm simply reduces to the glasso or the adaptive glasso (aglasso) algorithm of Friedman et al. (2008). A similar algorithm was used in Rothman et al. (2010) for sparse multivariate regressions. Proposition 2 in the Supplementary Material proves that the above iterative algorithm for minimizing pl(Ξ) with respective to Γ and Θ converges to a stationary point of pl(Ξ).

While the iterative algorithm reaches a stationary point of pl(Ξ), it is not guaranteed to reach the global minimum. Since the objective function of the optimization problem (2) is not always convex in (Γ, Θ), it is convex in either Γ or Θ with the other fixed. There are potentially many stationary points due to the high-dimensional nature of the parameter space. We also note a few straightforward properties of the iterative procedure, namely that each iteration monotonically decreases the penalized negative log-likelihood and the order of minimization is unimportant. Finally, the computational complexity of this algorithm is O(pq) plus the complexity of the glasso.

2.4. Tuning parameter selection

The tuning parameters ρ and λ in the penalized likelihood formulation (2) determine the sparsity of the cGGM and have to be tuned. Since we focus on estimating the sparse precision matrix and the sparse regression coefficients, we use the Bayesian information criterion (BIC) to choose these two parameters. The BIC is defined as

$$\mathit{BIC}(\widehat{\mathrm{\Theta }},\widehat{\mathrm{\Gamma }})=-nlog(\mid \widehat{\mathrm{\Theta }}\mid )+n\text{tr}(\widehat{\mathrm{\Theta }}{S}_{\widehat{\mathrm{\Gamma }}})+log(n)(s_n/2+p_n+k_n),$$

where p_n is the dimension of y, s_n is the number of non-zero off-diagonal elements of β̂ and k_n is the number of non-zero elements of Γ̂. The BIC has been shown to perform well for selecting the tuning parameter of the penalized likelihood estimator (Wang et al., 2007) and has been applied for tuning parameter selection for GGMs (Peng et al., 2009).

3. Theoretical Properties

Sections 4–5 in the Supplementary Materials state and prove theoretical properties of the proposed penalized estimates of the sparse cGGM: its asymptotic distribution, the oracle properties when p and q are fixed as n → ∞ and the convergence rates and sparsistency of the estimators when p = p_n and q = q_n diverge as n → ∞. By sparsistency, we mean the property that all parameters that are zero are actually estimated as zero with probability tending to one (Lam and Fan, 2009).

We observe that the asymptotic bias for β̂ is at the same rate as Lam and Fan (2009) for sparse GGMs, which is (p_n + s_n)/n multiplied by a logarithm factor log p_n, and goes to zero as long as (p_n + s_n)/n is at a rate of O{(log p_n)^−k} with some k > 1. The total square errors for Γ̂ are at least of rate k_n/n since each of the k_n nonzero elements can be estimated with rate n^−1/2. The price we pay for high-dimensionality is a logarithmic factor log(p_nq_n). The estimate Γ̂ is consistent as long as k_n/n is at a rate of O{(log p_n + log q_n)^−l} with some l > 1.

4. Monte Carlo Simulations

In this section we present results from Monte Carlo simulations to examine the performance of the proposed estimates and to compare it with the glasso procedure for estimating the Gaussian graphical models using only the gene expression data. We also compare the cGGM with a modified version of the neighborhood selection procedure of Meinshausen and Bühlmann (2006), where each gene is regressed on other genes and also the genetic markers using the Lasso regression, and a link is defined between gene i and j if gene i is selected for gene j and gene j is also selected by gene i. We call this procedure the multiple Lasso (mLasso). Note that the mLasso does not provide an estimate of the concentration matrix. For adaptive procedures, the MLEs of both the regression coefficients and the concentration matrix were used for the weights when p < n and q < n. For each simulated data set, we chose the tuning parameters ρ and λ based on the BIC.

To compare the performance of different estimators for the concentration matrix, we used the quadratic loss function

$$\text{LOSS}(\mathrm{\Theta },\widehat{\mathrm{\Theta }})=tr{({\mathrm{\Theta }}^{-1}\widehat{\mathrm{\Theta }}-I)}^2,$$

where β̂ is an estimate of the true concentration matrix Θ. We also compared ||Δ||_∞, |||Δ|||_∞, ||Δ|| and ||Δ||_F, where Δ = Θ − β̂ is the difference between the true concentration matrix and its estimate, ||A|| = max{||Ax||/||x||, x ∈ R^p, x ≠ 0} is the operator or spectral norm of a matrix A, ||A||_∞ is the element-wise l_∞ norm of a matrix A, ${\left|\right|\left|A\right|\left|\right|}_{\infty }={max}_{1\le i\le p}{\sum }_{j=1}^q\mid a_{ij}\mid$ for A = (a_ij)_p×q is the matrix l_∞ norm of a matrix A, and ||A||_F is the Frobenius norm, which is the square-root of the sum of the squares of the entries of A. In order to compare how different methods recover the true graphical structures, we considered the Hamming distance between the estimated and the true concentration matrix, defined as DIST(Θ, β̂) = Σ_i;j |I(θij = 0) − I(θ̂_ij ≠ 0)|, where θ_ij is the (i, j)-th entry of Θ and I(·) is the indicator function. Finally, we considered the specificity(SPE), sensitivity(SEN) and Matthews correlation coefficient(MCC) scores, which are defined as follows:

$$\begin{array}{c}\text{SPE}=\frac{TN}{TN+FP},\text{SEN}=\frac{TP}{TP+FN},\\ \text{MCC}=\frac{TP\times TN-FP\times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}},\end{array}$$

where TP, TN, FP and FN are the numbers of true positives, true negatives, false positives and false negatives in identifying the non-zero elements in the concentration matrix. Here we consider the non-zero entry in a sparse concentration matrix as “positive.”

4.1. Models for concentration matrix and generation of data

In the following simulations, we considered a general sparse concentration matrix, where we randomly generated a link (i.e., non-zero elements in the concentration matrix, indicated by δ_ij) between variables i and j with a success probability proportional to 1/p. Similar to the simulation setup of Li and Gui (2006), Fan et al. (2009) and Peng et al. (2009), for each link, the corresponding entry in the concentration matrix is generated uniformly over [−1, −0.5]∪[0.5, 1]. Then for each row, every entry except the diagonal one is divided by the sum of the absolute value of the off-diagonal entries multiplied by 1.5. Finally the matrix is symmetrized and the diagonal entries are fixed at 1. To generate the p × q coefficient matrix Γ = (γ_ij), we first generated a p×q sparse indicator matrix Δ = (δ_ij), where δ_ij = 1 with a probability proportional to 1/q. If γ_ij = 1, we generated γ_ij from Unif ([v_m, 1] ∪ [−1, −v_m]), where v_m is the minimum absolute non-zero value of Θ generated.

After Γ and Θ were generated, we generated the marker genotypes X = (X₁, · · ·, X_q) by assuming $X_i~\text{Bernoulli}(1,\frac{1}{2})$, for i = 1, · · ·, q. Finally, given x, we generated y the multivariate normal distribution Y |X ~ 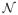(Γ X, Σ). For a given model and a given simulation, we generated a dataset of n i.i.d. random vectors (X, Y). The simulations were repeated 50 times.

4.2. Simulation results when p < n and q < n

We first consider the setting when the sample size n is larger than the number of genes p and the number of genetic markers q. In particular, the following three models were considered:

• Model 1

  (p, q, n)=(100, 100, 250), where pr(θ_ij ≠ 0)=2/p, pr(Γ_ij ≠ 0)=3/q;

• Model 2

  (p, q, n)=(50, 50, 250), where pr(θ_ij ≠ 0)=2/p, pr(Γ_ij ≠ 0)=4/q;

• Model 3

  (p, q, n)=(25, 10, 250), where pr(θ_ij ≠ 0)=2/p, pr(Γ_ij ≠ 0)=3.5/q.

We present the simulation results in Table 1. Clearly, cGGM provided better estimates (in terms of the defined LOSS function and the four metrics of “closeness” of the estimated and true matrices) of the concentration matrix over glasso for all three models considered in all measurements. This is expected since glasso assumes a constant mean of the multivariate vector, which is not a misspecified model. We also observed that the adaptive cGGM and adaptive glasso both resulted in better estimates of the concentration matrix, although the improvements were minimal. This may be due to the fact that the MLEs of the concentration matrix when p is relatively large do not provide very informative weights in the L₁ penalty functions.

Table 1.

Comparison of the performances of the cGGM, adaptive cGGM (acGGM), graphical Lasso (glasso), adaptive graphical Lasso (aglasso) and a modified neighborhood selection procedure using multiple Lasso (mLasso) for Models 1 – 3 when p < n based on 50 replications, where n is the sample size, p is the number of genes and q is the number of markers. For each measurement, mean is given based on 50 replications. Simulation standard errors are given in Supplemental Material.

Method	Estimation of Θ					Graph Selection
	LOSS	||Δ||∞	|||Δ|||∞	||Δ||	||Δ||F	DIST	SPE	SEN	MCC
	Model 1: (p, q, n)=(100,100,250), pr(θij ≠ 0)=2/p, pr(Γij ≠ 0)=3/q
cGGM	10.73	0.33	1.17	0.67	3.18	279.56	0.99	0.48	0.56
acGGM	10.29	0.31	1.17	0.66	3.01	313.48	0.99	0.42	0.50
glasso	19.17	0.69	1.89	1.12	5.19	596.12	0.97	0.24	0.21
aglasso	17.93	0.69	1.89	1.11	4.98	541.32	0.97	0.32	0.28
mLasso	-	-	-	-	-	309.50	0.99	0.38	0.48
	Model 2: (p, q, n)=(50, 50, 250), pr(θij ≠ 0)=2/p, pr(Γij ≠ 0)=4/q
cGGM	5.15	0.37	1.30	0.72	2.36	106.88	0.98	0.69	0.66
acGGM	4.62	0.29	1.14	0.63	1.97	83.20	0.99	0.66	0.71
glasso	13.95	0.75	2.12	1.20	4.57	391.84	0.87	0.37	0.18
aglasso	13.15	0.74	2.11	1.19	4.4	389.00	0.87	0.49	0.25
mLasso	-	-	-	-	-	185.68	0.95	0.60	0.48
	Model 3: (p, q, n)=(25, 10, 250), pr(θij ≠ 0)=2/p, pr(Γij ≠ 0)=3.5/q
cGGM	1.70	0.24	0.90	0.52	1.21	67.08	0.91	0.76	0.62
acGGM	1.58	0.22	0.87	0.49	1.12	56.36	0.94	0.72	0.65
glasso	5.97	0.65	1.99	1.12	2.77	315.84	0.43	0.73	0.12
aglasso	6.05	0.65	1.98	1.12	2.78	264.30	0.54	0.65	0.14
mLasso	-	-	-	-	-	111.28	0.84	0.68	0.44

In terms of graph structure selection, we first observed that different values of the tuning parameter ρ for the penalty on the mean parameters resulted in different identifications of the non-zero elements in the concentration matrix, indicating that the regression parameters in the means indeed had effects on estimating the concentration matrix. Table 1 shows that for all three models, the cGGM or the adaptive cGGM resulted in higher sensitivities, specificities and MCCs than the glasso or the adaptive glasso. We observed that glasso often resulted in much denser graphs than the real graphs. This is partially due to the fact that some of the links identified by glasso can be explained by shared common genetic variants. By assuming constant means, in order to compensate for the model misspecification, glasso tends to identify many non-zero elements in the concentration matrix and result in larger Hamming distance between the estimate and the true concentration matrix. The results indicate that by simultaneously considering the effects of the covariates on the means, we can reduce both false positives and false negatives in identifying the non-zero elements of the concentration matrix.

The modified neighborhood selection procedure using multiple Lasso accounts for the genetic effects in modeling the relationship among the genes. It performed better than glasso or adaptive glasso in graph structure selection, but worse than the cGGM or the adaptive cGGM. This procedure, however, did not provide an estimate of the concentration matrix.

4.3. Simulation results when p > n

In this Section, we consider the setting when p > n and simulate data from the following three models with values of n, p and q specified as:

• Model 4

  (p, q, n)=(1000, 200, 250), pr(Θ_ij ≠ 0)=1.5/p, pr(Γ_ij ≠ 0)=20/q;

• Model 5

  (p, q, n)=(800, 200, 250), pr(Θ_ij ≠ 0)= 1.5/p, pr(Γ_ij ≠ 0)=25/q;

• Model 6

  (p, q, n)=(400, 200, 150), pr(Θ_ij ≠ 0)= 2.5/p, pr(Γ_ij ≠ 0)=20/q.

Note that for all three models, the graph structure is very sparse due to the large number of genes considered.

Since in this setting we did not have consistent estimates of Γ or Ω, we did not consider the adaptive cGGM or adaptive glasso in our comparisons. Instead, we compared the performance of cGGM, glasso, and the modified neighborhood selection procedure using multiple Lasso in terms of estimation of the concentration matrix and graph structure selection. The performances over 50 replications are reported in Table 2 for the optimal tuning parameters chosen by the BICs. For all three models, we observed much improved estimates of the concentration matrix from the proposed cGGM as reflected by both smaller L₂ loss functions and different norms of the difference between the true and estimated concentration matrices. The mLasso procedure did not provide estimates of the concentration matrix.

Table 2.

Comparison of the performances of the cGGM, the graphical Lasso (glasso) and a modified neighbor selection using multiple lasso(mLasso) Model 4~ Model 6 when p > n based on 50 replications, where n is the sample size, p is the number of genes and q is the number of markers. For each measurement, mean is given based on 50 replications. Simulation standard errors are given in Supplemental Material.

Method	Estimation of Θ					Graph Selection
	LOSS	||Δ||∞	|||Δ|||∞	||Δ||	||Δ||F	DIST	SPE	SEN	MCC
	Model 4: (p, q, n)=(1000, 200, 250), pr(Θij ≠ 0) =1.5/p, pr(Γij ≠ 0)=20/q
cGGM	164.22	0.59	1.81	0.97	13.48	2414.28	1.00	0.31	0.47
glasso	257.12	0.71	2.86	1.31	19.82	23746.98	0.98	0.08	0.02
mLasso	-	-	-	-	-	3886.96	1.00	0.12	0.16
	Model 5: (p, q, n)=(800, 200, 250), pr(Θij ≠ 0) = 1.5/p, pr(Γij ≠ 0)=25/q
cGGM	142.30	0.75	2.30	1.20	12.82	2341.28	1.00	0.21	0.34
glasso	219.33	0.76	2.97	1.40	18.39	20871.44	0.97	0.07	0.02
mLasso	-	-	-	-	-	23750.04	0.96	0.61	0.19
	Model 6: (p, q, n)=(400, 200, 250), pr(Θij ≠ 0)=2.5/p, pr(Γij ≠ 0)=20/q
cGGM	48.73	0.44	1.55	0.77	6.86	2044.52	1.00	0.05	0.21
glasso	87.32	0.69	2.72	1.22	11.01	9258.92	0.95	0.03	−0.01
mLasso	-	-	-	-	-	2967.30	0.99	0.08	0.10

In terms of graph structure selection, since glasso does not adjust for potential effects of genetic markers on gene expressions, it resulted in many wrong identifications and much lower sensitivities and smaller MCCs than the cGGM. Compared to the modified neighborhood selection using multiple Lasso, estimates from the cGGM have smaller Hamming distance and larger MCC than mLasso. In general, we observed that when p is larger than the sample size, the sensitivities from all three procedures are much lower than the settings when the sample size is larger. For Models 5 and 6, mLasso gave higher sensitivities but lower specificities than cGGM or glasso. This indicates that recovering the graph structure in a high-dimensional setting is statistically difficult. However, the specificities are in general very high, agreeing with our theoretical sparsistency result of the estimates.

5. Analysis of Yeast eQTL Data

To demonstrate the proposed methods, we present results from the analysis of a data set generated by Brem and Kruglyak (2005). In this experiment, 112 yeast segregants, one from each tetrad, were grown from a cross involving parental strains BY4716 and wild isolate RM11-1a. RNA was isolated and cDNA was hybridized to microarrays in the presence of the same BY reference material. Each array assayed 6,216 yeast genes. Genotyping was performed using GeneChip Yeast Genome S98 microarrays on all 112 F₁ segregants. These 112 segregants were individually genotyped at 2,956 marker positions. Since many of these markers are in high linkage disequilibrium, we combined the markers into 585 blocks where the markers within a block differed by at most 1 sample. For each block, we chose the marker that had the least number of missing values as the representative marker.

Due to small sample size and limited perturbation to the biological system, it is not possible to construct a gene network for all 6,216 genes. We instead focused our analysis on two sets of genes that are biologically relevant: the first set of 54 genes that belong to the yeast MAPK signaling pathway provided by the KEGG database (Kanehisa et al., 2010), another set of 1,207 genes of the protein-protein interaction (PPI) network obtained from a previously compiled set by Steffen et al. (2002) combined with protein physical interactions deposited in Munich Information center for Protein Sequences (MIPS). Since the available eQTL data are based on observational data, given limited sample size and limited perturbation to the cells from the genotypes, it is statistically not feasible to learn directed graph structures among these genes. Instead, for each of these two data sets, our goal is to construct a conditional independent network among these genes at the expression levels based on the sparse conditional Gaussian graphical model in order to remove the false links by conditioning on the genetic marker information. Such graphs can be interpreted as a projection of true signaling or protein interaction network into the gene space (Brazhnik et al., 2002; Kontos, 2009).

5.1. Results from the cGGM analysis of 54 MAPK pathway genes

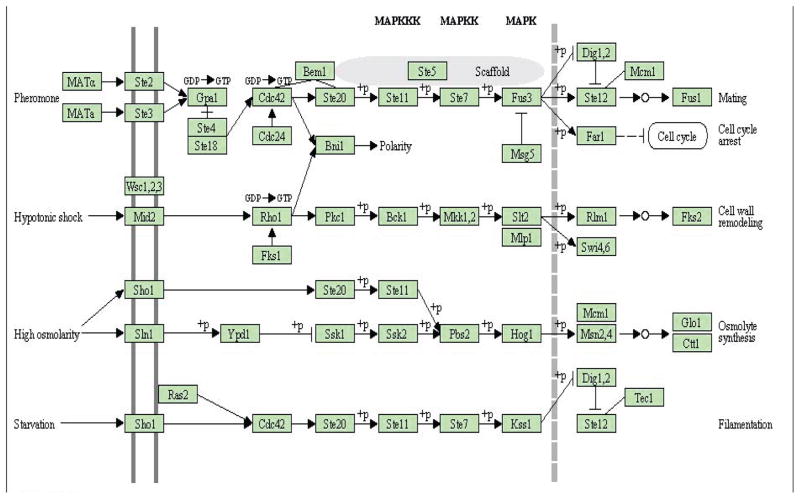
The yeast genome encodes multiple MAP kinase orthologs, where Fus3 mediates cellular response to peptide pheromones, Kss1 permits adjustment to nutrient-limiting conditions and Hog1 is necessary for survival under hyperosmotic conditions. Lastly, Slt2/Mpk1 is required for repair of injuries to the cell wall. A schematic plot of this pathway is presented in Figure 1. Note that this graph only presents our current knowledge about the MAPK signaling pathway. Since several genes such as Ste20, Ste12 and Ste7 appear at multiple nodes, this graph cannot be treated as the “true graph” for evaluating or comparing different methods. In addition, although some of the links are directed, this graph does not meet the statistical definition of either directed or undirected graph. Rather than trying to recover the MAPK pathway structure, we chose this set of 54 genes on the MAPK pathway to make sure that these genes are potentially dependent at the expression level.

Fig 1.

The yeast MAPK pathway from the KEGG database http://www.genome.jp/kegg/pathway/sce/sce04011.html

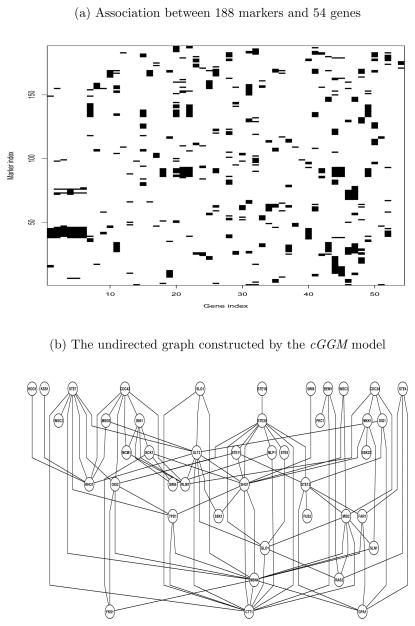
For each of the 54 genes, we first performed a linear regression analysis for gene expression level using each of the 585 markers and selected those markers with a p-value of 0.01 or smaller. We observed a total of 839 such associations between the 585 markers and 54 genes, indicating strong effects of genetic variants on expression levels. We further selected 188 markers associated with the gene expression levels of at least two out of the 54 genes, resulting in a total of 702 such associations. In addition, many genes are associated with multiple markers (see Figure 2(a)). This indicates that many pairs of genes are regulated by some common genetic variants, which when not taken into account, can lead to false links of genes at the expression level.

Fig 2.

Analysis of yeast MAPK pathway. (a) Association between 188 markers and 54 genes in the MAPK pathway based on simple regression analysis. Black color indicates significant association at p-value< 0.01. (b) The undirected graph of 43 genes constructed based on the cGGM.

We applied our proposed cGGM on this set of 54 genes and 188 markers and used the BIC to choose the tuning parameters. The BIC selected λ = 0.28 and ρ = 0.54. With these tuning parameters, the cGGM procedure selected 188 non-zero elements of the concentration matrix and therefore 94 links among these 54 genes. In addition, under the cGGM model, 677 elements of the regression coefficients Γ are not zero, indicating the SNPs have important effects on the gene expression levels of these genes. The numbers of SNPs associated with the gene expressions range from 0 to 17 with a mean number of 4. Figure 2(b) shows the undirected graph for 43 linked genes on the MAPK pathway based on the estimated sparse concentration matrix from the cGGM. This undirected graph constructed based on the cGGM can indeed recover lots of links among the 54 genes on this pathway. For example, the kinase Fus3 is linked to its downstream genes Dig1, Ste12 and Fus1. The cGGM model also recovered most of the links to Ste20, including Bni1, Ste11, Ste12, Ste5 and Ste7. Ste20 is also linked to Cdc42 through Bni1. Clearly, most of the links in the upper part of the MAPK signaling pathway were recovered by cGGM. This part of the pathway mediates cellular response to peptide pheromones. Similarly, the kinase Slt2/Mpk1 is linked to its downstream genes Swi4 and Rlm1. Three other genes on this second layer of the pathway, Fks1, Rho1 and Bck1, are also closed linked. These linked genes are related to cell response to hypotonic shock.

As a comparison, we applied the glasso to the gene expression of these 54 genes without adjusting the effects of genetic markers on gene expressions and summarize the results in Table 3. The optimal tuning parameter λ = 0.145 was selected based on the BIC, which resulted in selection of 341 edges among the 54 genes (i.e., 682 non-zero elements of the concentration matrix), including all 94 links selected by the cGGM. The difference of the estimated graph structures between the cGGM and glasso can be at least partially explained by the genetic variants associated with the expression levels of multiple genes. Among these 247 edges that were identified by only the glasso, 41 pairs of genes were associated with at least one genetic variant. The cGGM adjusted the genetic effects on gene expression and therefore did not identify these edges at the expression levels. Another reason is that the glasso assumes a constant mean vector for gene expression, which clearly misspecified the model and led to the selection of more links.

Table 3.

Comparison of the links identified by the cGGM, modified neighborhood selection using multiple Lasso (mLasso), the graphical Lasso (glasso) for the genes of the MAPK pathway and genes of the protein-protein interaction (PPI) network. Shown in the table is the number of links that were identified by the procedure indexed by row but were not identified by the procedure indexed by column due to sharing of at least one common

	cGGM	mLasso
	MAPK pathway (PPI network)
cGGM	-	0 (0)
mLasso	10 (218)	-
glasso	41 (1569)	2 (66)

We also compared the graph identified by the modified neighborhood selection procedure of using multiple Lasso. Specifically, each gene was regressed on all other genes and 188 markers using the Lasso. Again, the BIC was used for selecting the tuning parameter. This procedure identified a total of 45 links among the 54 genes. In addition, a total of 33 associations between the SNPs and gene expressions were identified. Among these 45 links, 36 were identified by the cGGM and 45 were identified by glasso.

Table 4 shows a summary of the degrees of the graphs estimated by these three procedures. It is clear that glasso resulted in a much denser graph than the neighborhood selection and cGGM, and the mLasso tends to select few links.

Table 4.

Summary of degrees of the graphs constructed by three different methods: cGGM, the graphical Lasso (glasso) and a modified neighborhood selection using multiple Lasso (mLasso), for the genes of the MAPK pathway and genes of the protein-protein interaction (PPI) network.

Method	MAPK pathway				PPI network
	Min	Max	Mean	Median	Min	Max	Mean	Median
cGGM	0	11	3.48	3	0	57	19.94	21
glasso	5	19	12.63	13	5	60	31.46	32
mLasso	0	6	1.67	1	0	12	3.18	3

5.2. Results from the cGGM analysis of 1207 genes on yeast PPI network

We next applied the cGGM to the yeast protein-protein interaction network data obtained from a previously compiled set by Steffen et al. (2002) combined with protein physical interactions deposited in MIPS. We further selected 1,207 genes with variance greater than 0.05. Based on the most recent yeast protein-protein interaction database BioGRID (Stark et al., 2011), there are a total of 7,619 links among these 1,207 genes. The BIC chose λ = 0.34 and ρ = 0.43, which resulted in selection of 12,036 links out of a total of 727,821 possible links, which gives a sparsity of 1.65%. Results from comparisons with the two other procedures are shown in Table 3. The glasso without adjusting for the effects of genetic markers resulted in a total of 18,987 edges with an optimal tuning parameter λ = 0.22. There were 9,854 links that were selected by both procedures. Again glasso selected a lot more links than the cGGM, among the links that were identified by the glasso only, 1,569 pairs are associated with at least one common genetic marker (see Table 3), further explaining that some of the links identified by gene expression data alone can be due to shared comment genetic variants.

The modified neighborhood selection procedure mLasso identified only 1,917 edges with λ = 0.42, out of which 1,750 were identified by the cGGM and 1,916 were identified by the glasso. There was a common set of 1,749 links that were identified by all three procedures. A summary of the degrees of the graphs estimated by these three procedures is given in Table 4. We observe that the glasso gave a much denser graph than the other two procedures, agreeing with what we observed in simulation studies.

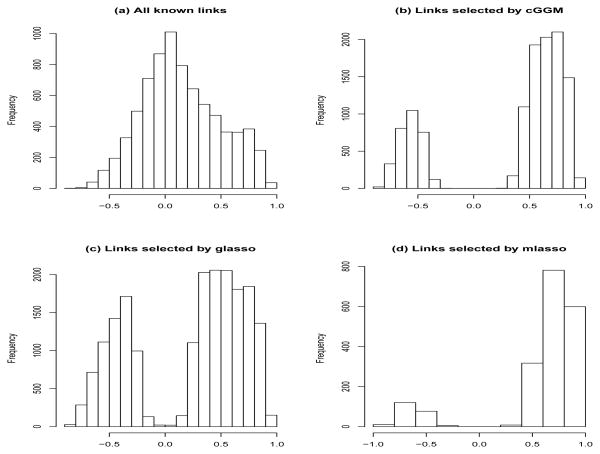
If we treat the PPI of the BioGRID database as the true network among these genes, the true positive rate from cGGM, glasso and the modified neighborhood selection procedure was 0.067, 0.071 and 0.019, respectively, and the false positive rate was 0.016, 0.026 and 0.0025, respectively. The MCC score from cGGM, glasso and the modified neighborhood selection procedure was 0.041, 0.030 and 0.033, respectively. One reason for having low true positive rates is that many of the protein-protein interactions cannot be reflected at the gene expression level. Figure 3(a) shows the histogram of the correlations of genes that are linked on the BioGRID PPI network, indicating that many linked gene pairs have very small marginal correlations. The Gaussian graphical models are not able to recover these links. Figure 3 plots (b) – (d) show the marginal correlations of the genes pairs that were identified by cGGM, glasso and mGlasso, clearly indicating that the linked genes identified by the cGGM have higher marginal correlations. In contrast, some linked genes identified by glasso have quite small marginal correlations. Another reason is that the PPI represents the marginal pair-wise interactions among the proteins rather than the conditional interactions.

Fig 3.

Histograms of marginal correlations for pairs of linked genes based on BioGRID (a) and linked genes identified by cGGM (b), glasso (c) and a modified neighborhood selection procedure (mLasso) (d).

6. Conclusions and Discussion

We have presented a sparse conditional Gaussian graphical model for estimating the sparse gene expression network based on eQTL data in order to account for genetic effects on gene expressions. Since genetic variants are associated with expression levels of many genes, it is important to consider such heterogeneity in estimating the gene expression networks using the Gaussian graphical models. We have demonstrated by simulation studies that the proposed sparse cGGM can estimate the underlying gene expression networks more accurately than the standard GGM. For the yeast eQTL data set we analyzed, the standard Gaussian graphical model without adjusting for possible genetic effects on gene expressions identified many possible false links that result in very dense graphs and make the interpretation of the resulting networks difficult. On the other hand, our proposed cGGM resulted in a much sparser and biologically more interpretable network. We expect similarly good performance on data from other published sources, such as from Schadt et al. (2003) and Cheung and Spielman (2002).

Due to the limits of the gene expression data, one should not expect to recover completely the true signaling networks since many dependencies among these genes can be observed only at the protein or metabolite level. In any global biochemical network such signaling network or protein interaction network, genes do not interact directly with other genes; instead, gene induction or repression occurs through the activation of certain proteins, which are products of certain genes (Brazhnik et al., 2002; Kontos, 2009). Similarly, gene transcription can also be affected by protein-metabolite complexes. Despite these limitations of the gene expression, it is still useful to abstract the actions of proteins and metabolites and represent genes acting on other genes in a gene network (Kontos, 2009). This gene network is what we aim to learn based on the proposed cGGM. As we observed from our analysis of the yeast eQTL data, such graphs or gene networks constructed from the cGGM can indeed explain the data and provide certain biological insights into gene interactions. Such graphs can be interpreted as a projection of true signaling or protein interaction network into the gene space (Brazhnik et al., 2002; Kontos, 2009).

We have focused in this paper on estimating the sparse conditional Gaussian graphical model for gene expression data by adjusting for the genetic effects on gene expressions. However, we expect that by explicitly modeling the covariance structure among the gene expressions, we should also improve the identification of the genetic variants associated with the gene expressions (Rothman et al., 2010). This is in fact the original motivation of the SUR models proposed by Zellner (1962). It would be interesting to investigate theoretically as to how modeling the concentration matrix can lead to improvement in estimation and identification of the genetic variants associated with the gene expression traits.

We used the Gaussian graphical models for studying the conditional independence among genes at the transcriptional level. Such undirected graphs do not provide information on causal dependency. Data from genetic genomics experiments have been proposed to construct the gene networks represented by directed causal graphs. For example, Liu et al. (2008) and Bing and Hoeschele (2005) used structural equation modeling and a genetic algorithm to construct causal genetic networks among genetic loci and gene expressions. Neto et al. (2009) developed an efficient Markov chain Monte Carlo algorithm for joint inference of causal network and genetic architecture for correlated phenotypes. Although genetical genomics data can indeed provide opportunity for inferring the causal networks at the transcriptional level, these causal graphical model-based approach can often only handle a small number of transcripts because the number of possible directed graphs is super-exponential in the number of genes considered (Chickering et al., 2004). Regularization methods may provide alternative approaches to joint modeling of genetic effects on gene expressions and causal graphs among genes at the expression level.