EPR/ENDOR, Mössbauer, and Quantum Chemical Investigation of Di-iron Complexes Mimicking the Active Oxidized State of [FeFe] Hydrogenase

Abstract

Understanding the catalytic process of the heterolytic splitting and formation of molecular hydrogen is one of the key topics for the development of a future hydrogen economy. With an interest in elucidating the enzymatic mechanism of the [Fe₂(S₂C₂H₄NH)(CN)₂(CO)₂(µ-CO)] active center uniquely found in the [FeFe]-hydrogenases, we present a detailed spectroscopic and theoretical analysis of its inorganic model [Fe₂(S₂X)(CO)₃(dppv)(PMe₃)]⁺ in two forms with S₂X = ethanedithiolate (1edt) and azadithiolate (1adt) (dppv =cis-1,2-bis(diphenylphosphino)ethylene). These complexes represent models for the oxidized mixed-valent Fe(I)Fe(II) state analogous to the active oxidized "H_ox" state of the native H-cluster. For both complexes, the ³¹P hyperfine (HF) interactions were determined by pulse EPR and ENDOR methods. For 1edt, the ⁵⁷Fe parameters were measured by ESEEM and Mössbauer spectroscopy, while for 1adt ¹⁴N and selected ¹H couplings could be obtained by ENDOR and HYSCORE. The spin density was found to be predominantly localized on the Fe(dppv) site. This spin distribution is different from the H-cluster where both the spin and charge density are delocalized over the two Fe centers. This difference is attributed to the influence of “native” cubane subcluster that is lacking in the inorganic models. The degree and character of the unpaired spin delocalization was found to vary from 1edt, with an abiological dithiolate, to 1adt, which features the authentic cofactor. For 1adt, we find two ¹⁴N signals, which are indicative for two possible isomers of the azadithiolate, demonstrating its high flexibility. All interaction parameters were also evaluated through density functional theory calculations at various levels.

INTRODUCTION

The most efficient method of storing energy is within a chemical bond. Molecular dihydrogen is touted as promising vessel for the storage of energy accumulated from renewable resources because of its low molecular weight and strong H–H single bond.^1–3 Nature has engineered hydrogenase enzymes that promote the (reversible) heterolytic formation of dihydrogen from two protons and two electrons, i.e.

$${\mathrm{H}}_2\leftrightarrows {\mathrm{H}}^{-}+{\mathrm{H}}^{+}\leftrightarrows 2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-1,4,5}.$$ (1)

Three classes of hydrogenases have been distinguished based on their active site metal constituents: [FeFe], [NiFe] and [Fe].^1,6

The active center of [FeFe] hydrogenases, the “H-cluster”, is a complex 6Fe-cluster consisting of a “classical” four cysteine ligated [4Fe-4S] cluster appended to a catalytically active [2Fe] subcluster via a protein Cys-S ligand (see figure 1).^7,8 Both iron centers are coordinated by CO and CN⁻ ligands that stabilize low oxidation and spin states.^9,10 The two Fe ions are connected by a dithiolate bridge, whose central atom has sparked considerable debate since the available crystallographic data have insufficient resolution to discriminate O, C or N. ^11,12 Convincing evidence for nitrogen as a central atom has been obtained from an extensive pulse electron paramagnetic resonance (EPR) study of the H-cluster. ¹² It has been proposed that this moiety might serve as a well-positioned base for relaying protons to and from the iron center.^11–14

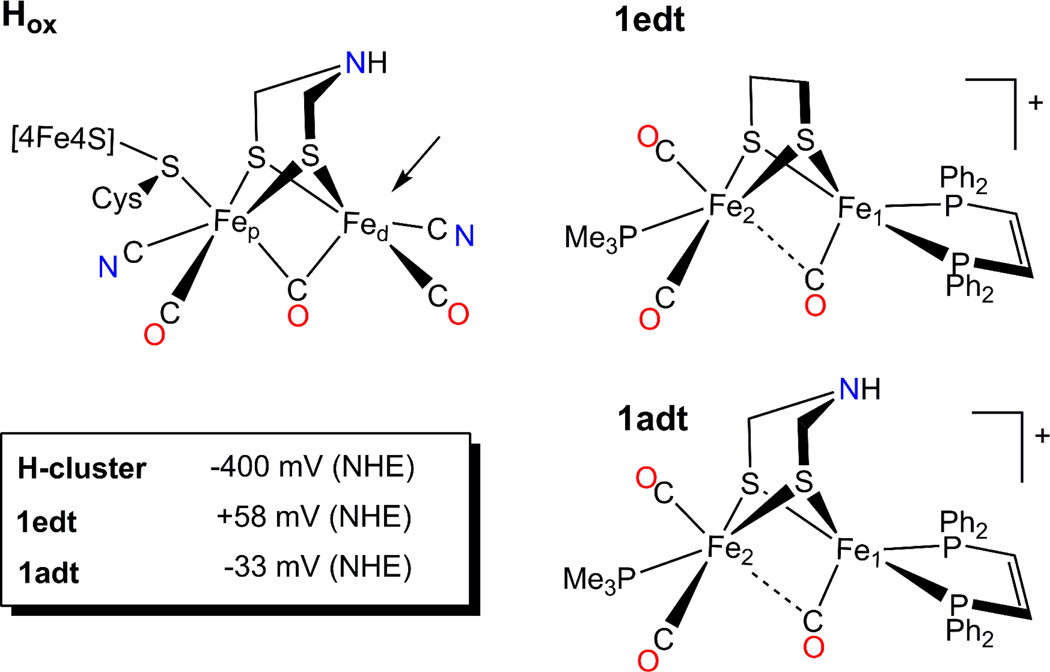
Figure 1.

Schematic representation of the H-cluster in the H_ox state and model compounds used in this study. An Arrow points to the vacant apical site on the distal Fe, which in the case of the enzyme, is the site for binding H₂. Insert: midpoint potentials for the H_red/H_ox and [Fe₂(SX)₂]^0/+ redox transition for the H-cluster and the models 1edt and 1adt, correspondingly. For the H-cluster it is specified for pH 8 ¹⁵ in Tris buffer with KCl electrolyte, for the model compounds the E₀ values are given for [(C₄H₉)₄N]PF₆ electrolyte in CH₂Cl₂ ²² and values are converted from vs Fc^0/+ to vs NHE scale by using E₀(Fc^0/+) = +0.528 vs NHE estimation.

Two catalytically relevant states of the H-cluster have been experimentally identified thus far.^1,10,15 The active oxidized state, "H_ox", is characterized by a formal 2+ charge on the cubane subunit and a Fe(I)-Fe(II) configuration of the [2Fe] sub-cluster (Figure 1). This state is believed to be the entry point of the catalytic cycle. Whether this state directly participates in the catalytic cycle or is merely a "ready" state depends on whether the exchangeable coordination site on the distal Fe is vacant (see figure 1). There is an indication that water completes the coordination sphere in this state, which must dissociate to permit substrate binding^16–18 (see below for the discussion of this ligation). Under reducing conditions e.g. provided by a hydrogen atmosphere or upon addition of a mild reductant the H_ox state converts into the so-called reduced state “H_red” which is EPR silent. Based on spectroscopic evidence, the valency of the binuclear subcluster is best characterized by Fe_p(I)-Fe_d(I),^19,20 although Fe_p(II)-Fe_d(0) is another conceivable assignment based on the study of model compounds.²¹ In the H_red state the [4Fe-4S]_H subcluster remains oxidized (formally Fe(II)₂Fe(III)₂).

Recently, we have provided evidence for another possible stable intermediate.²⁰ In this new state, the [4Fe-4S] presumably exists in the reduced Fe(II)₃Fe(III) state. As it allows to store a second electron upon heterolytic splitting it is likely that during the catalytic cycle the H-cluster passes through this state.

The catalytically pertinent [2Fe] subcluster can be viewed as a semiclassical diiron complex embedded in the protein pocket as only the Cys-S of the cubane unit tethers the site covalently to the protein superstructure. Because the diiron center is so lightly attached to the protein, it has proven a tempting target for synthetic modeling studies directed toward developing artificial hydrogen conversion systems.^2,3 However, to date only few of the published model compounds show significant conversion of protons to H₂; the majority of cases requiring a substantial over-potential (i.e. the deviation of the mid-point potential from the ones observed for native systems). ^3,23

These deficiencies of current synthetic models are likely to arise from differences in the electronic structure between these models and the active site. Specifically, we have shown that the electronic structure of the native [2Fe] cluster is strongly affected by the presence of the [4Fe-4S] subcluster;¹⁹ it is highly likely that this coupling is crucial for fine-tuning the electronic structure and thus the catalytic activity. Moreover, the pendant base, i.e. the bridging azadithiolate cofactor, might play an important role acting as a relay for proton transfer.^{1,12–14,22,24,25} Understanding these aspects will provide important insight into the mechanisms of H₂ activating catalysts, ultimately underpinning the development of efficient synthetic catalysts. To date, however, our understanding of the electronic structure of the catalytically active part of the H-cluster is rather limited. Model compounds mimicking the [2Fe] site provide a convenient means to study this part of the active center separately from the cubane moiety.

Recently, we conducted a study of {2Fe3S} model compounds closely resembling the CO-inhibited oxidized state of the H-cluster, in which a CO ligand occupies the substrate binding site.^26,27 The electronic structure of these models features a strong delocalization of the spin density over both iron centers as well as some ligands. In contrast, our previous studies of the [FeFe] hydrogenase from D. desulfuricans indicated the spin density is localized on the proximal Fe in the H_ox-CO state.^19,28 This discrepancy was the first hint that the [4Fe-4S] subcluster significantly affects the electronic structure of the [2Fe] subcluster, despite the identical coordination sphere in the model and the enzyme.

In this work we present the first detailed EPR and Mössbauer study to elucidate the ground state electronic structure of biomimetic models resembling the dinuclear part of the active H_ox state of the H-cluster (Figure 1). Here we focus on the [Fe₂(S₂X)(CO)₃(dppv)(PMe₃)] series of compounds, where dppv = cis-1,2-bis(diphenylphosphino)ethylene. In this class, the bridging dithiolate ligand can be varied considerably (X = (CH₂)₂; (CH₂)₂CH₂; (CH₂)₂NH; (CH₂)₂O; (CH₂)₂NCH₂C₆H₅). Although their redox processes are still far from the H₂/H⁺ equilibrium potential (about −410 mV vs. NHE at pH 7), they nonetheless provide an accessible Fe(I)-Fe(II) mixed-valent analogue of the “native” H_ox state.

Two variants are studied, namely 1edt: X = (SCH₂)₂ and 1adt: X = (SCH₂)₂NH (Figure 1). The structural properties of 1edt have been well characterized in previous studies using various methods.^29–31 X-band continuous wave (CW) EPR spectra, showing an almost axial signal with a distinct 1:2:1 pattern originating from two equivalent ³¹P nuclei of dppv, suggested the unpaired spin was confined to Fe₁ (coordinated by the dppv ligand) and hence formulated as Fe₂(II)-Fe₁(I). However, this result differed markedly from the fully delocalized description of the “native” H_ox state of the H-cluster.¹⁹ This difference is analogous to the one found for the H_ox-CO state and the corresponding {2Fe3S} model compounds. ^26,27

The EPR spectrum of 1adt is quite similar to that of 1edt suggesting their electronic structures are similar as well. The deviation in the principal g-values must be a consequence of introducing an amine group into the dithiolate bridge. A similar picture emerges from the IR spectroscopic analysis of these compounds. The CO-stretching IR bands differ for the two compounds (1edt: ν_CO = 2015, 1962, 1887 cm⁻¹; 1adt: ν_CO = 2013, 1956, 1901 cm⁻¹).³²

In this work we examine the impact of the amine functionalized bridge on the distribution of spin density in the Fe(II)-Fe(I) state, and therein elucidate the ground state electronic structures of 1edt and 1adt. The aforementioned catalytic properties are then contrasted with the native enzyme whose electronic structure of the H_ox state has been previously examined by an extensive multifrequency EPR approach.¹²

Additionally, the present study investigates the applicability of density functional theory (DFT) to these model compounds. Although DFT methods are widely used for the investigation of [2Fe] low valent constructs³³ their performance was not yet fully tested against EPR data. Recently we have demonstrated that a hybrid functional in conjunction with moderately large basis sets afforded reasonable estimates of the experimental spin-Hamiltonian parameters of the H_ox-CO mimicks.^26,27 However, the present case is somewhat different because of the presumably localized nature of the spin density. It remains unclear whether DFT is suitable to track the impact of nuanced modifications to the second coordination sphere. In this work we use the obtained experimental data to address these points for the first time. The results of the theoretical studies were then also used to obtain further insight into the electronic properties of the studied models.

MATERIALS AND METHODS

EPR Spectroscopy

EPR measurements were performed on a setup based on Bruker ELEXSYS E 580 X- and Q-band spectrometers as described earlier.^19,28 For Q-band measurements we used a slightly overcoupled cylindrical TE011 homebuilt resonator.³⁴

W-band ESEEM and HYSCORE measurements were performed on a Bruker ELEXSYS E 680 FT EPR W-band spectrometer with a helium flow cryostat and a variable-temperature TeraFlex Bruker resonator. The 84 GHz internal local oscillator source used for the W-band up/down converting unit was modified to achieve improved phase stability. The W-band bridge provided 300 mW output power. This setup allowed 24 ns as minimum length of the π/2 pulse using a critically coupled resonator.

The pulse sequences used in this work can be found in supplementary information (Figure S1). Conventional Q-band pulse ENDOR spectra were obtained using stochastic data acquisition³⁵ with one shot per point with t_mix = 5 µs. Variable mixing time ENDOR experiments were performed using the standard Davies and Mims ENDOR sequences in linear scan mode recording 20 – 50 shots per point. In all cases the shot repetition time was set to achieve an unsaturated ESE signal.

Pulse EPR data were simulated using home-written routines utilizing a conventional spin-Hamiltonian approach in the high field approximation as previously detailed.²⁶ In all simulations, the orientation selection was calculated accounting for the two strongly coupled ³¹P nuclei. The ¹⁴N quadrupole coupling constant was accounted for by the quadrupole coupling parameter (K), and asymmetry parameter (η):

$$K=2P_Z=\frac{e^2\mathit{\text{qQ}}}{4I(2I-1)h}=\frac{e^2\mathit{\text{qQ}}}{4h},\eta =\frac{P_x-P_y}{P_z}$$ (2)

where P_x, P_y and P_z are the principal components of the traceless quadrupole tensor (|P_x|≤|P_y|≤|P_z|) and I is the nuclear spin.

Mössbauer Spectroscopy

Mössbauer spectra were recorded on an alternating constant acceleration spectrometer. The minimum experimental line width was 0.24 mm/s (full-width at half maximum). The sample temperature was maintained constant either in an Oxford Variox or an Oxford Mössbauer-Spectromag cryostat. The latter is a split-pair conducting magnet system for applying fields of up to 8 T to the samples that can be kept at temperatures in the range 1.5 – 250 K. The field at the sample is perpendicular to the γ beam. Isomer shifts are quoted relative to metallic iron at 300 K. Mössbauer spectra were simulated with a home-written spin Hamiltonian program based on the usual nuclear Hamiltonian formalism.³⁶

DFT Calculations

All calculations were performed using the ORCA 2.8 software package³⁷ within the spin-unrestricted formalism. Geometry optimizations utilized the BP86 functional^38,39 in concert with Ahlrichs triple-ζ valence basis set with three sets of polarization functions (TZVPP) on all atoms including the hydrogen atoms.⁴⁰ The Ahlrichs (2df,2pd) polarization functions were obtained from the TurboMole basis set library under ftp.chemie.unikarlsruhe. de/pub/basen. The resolution of identity (RI) was used with the standard TZV/J expansion basis, as implemented in ORCA.

Calculations of spin-Hamiltonian parameters were performed using the three-parameter Becke–Lee–Yang–Parr (B3LYP) functional^41,42 with the Wachters basis set⁴³ on the irons and the TZVPP basis set on all other atoms. The calculated ⁵⁷Fe hyperfine coupling constants were obtained including second order spin-orbit coupling contribution. The calculated ⁵⁷Fe isomer shifts (δ) have been calibrated to the applied settings following previously published procedures.^44,45 The calibration ρ(0) values were obtained using the geometries presented by Romelt et al.⁴⁶ Correlation between the experimental isomer shifts δ (mm/s)⁴⁶ and calculated ρ(0) (a.u.⁻³) follow the linear response δ = 0.1181 – 0.3821(ρ (0) − 11614), where 11614 a.u.⁻³ has been added for convenience (see Supporting Information).

Single point energy calculations were obtained from both geometry optimization and spin-Hamiltonian calculations. However, since the differences in energies between different conformers are consistent between different types of calculations, here we only present those from the latter ones.

Synthesis of ⁵⁷Fe -Labeled Compounds

[⁵⁷Fe₂(S₂C₂H₄)(CO)₆]

This compound was prepared according to literature methods using isotopically enriched anhydrous FeCl₂.^31,47 A solution of FeCl₂ (0.26 g, 2.0 mmol) in 45 mL of acetone was treated with 1 atm of CO for 10 min. To the resulting yellow solution was added NEt₃ (0.30 mL, 22.0 mmol), changing the color to blue/grey. To this mixture was added H₂S₂C₂H₄ (0.1 mL, 10.6 mmol) generating a dark brown solution. The mixture was stirred for 15 minutes, at which point Zn powder (0.120 g, 1.9 mmol) was added. After 18 h, the red solution was filtered through a Celite plug, then dried in vacuo. The solid was reconstituted in CH₂Cl₂, and filtered through a silica plug. The solvent was stripped under vacuum and the residue extracted into hexane, and chromatographed on a plug of silica with hexane as eluent. Two bands were observed; the desired product as a large red band that eluted first, and a small pink band that was discarded. A small amount of brown insoluble material remained at the top of the column. The product fraction was dried in vacuo affording red crystals. Yield: 0.480 g (30%). This product was spectroscopically identical (¹H NMR, IR) to the non-enriched material.

[⁵⁷Fe₂(S₂C₂H₄)(CO)₄(dppv)]

Following published methods,³⁰ a slurry of 38% enriched [⁵⁷Fe₂(S₂C₂H₄)(CO)₆] (0.260 g, 7.2 mmol) and dppv (0.270 g, 6.8 mmol) in 10 mL of MeCN was treated with Me₃NO (0.065 g, 8.7 mmol), resulting in vigorous bubbling and a darkening of the solution. After 3 h, the supernatant was filtered off, and remaining precipitate was repeatedly recrystallized from CH₂Cl₂ by addition of five volumes of hexane until the supernatant was clear. Yield: 0.344 g (67%).

[⁵⁷Fe₂(S₂C₂H₄)(CO)₃(dppv)(PMe₃)]

This compound was prepared according to the literature recipe.⁴⁷ IR and ¹H NMR spectra of the product were identical to the non-enriched form. ³¹P NMR (CD₂Cl₂): 95 (d, J_Fe-P =53 Hz), 18 (d, J_Fe-P = 47 Hz).

Sample Preparation

Synthesis of reduced versions of 1edt and 1adt followed the published procedures with minor modifications.^31,32 These compounds were dissolved in toluene to a final concentration of 2 – 4 mM, treated with 1 equivalent of Fc(BArF₄) and stirred vigorously for 30 minutes under an inert atmosphere. Then the resulting material was transferred to quartz EPR tubes or Mössbauer teflon caps and frozen in liquid nitrogen.

RESULTS

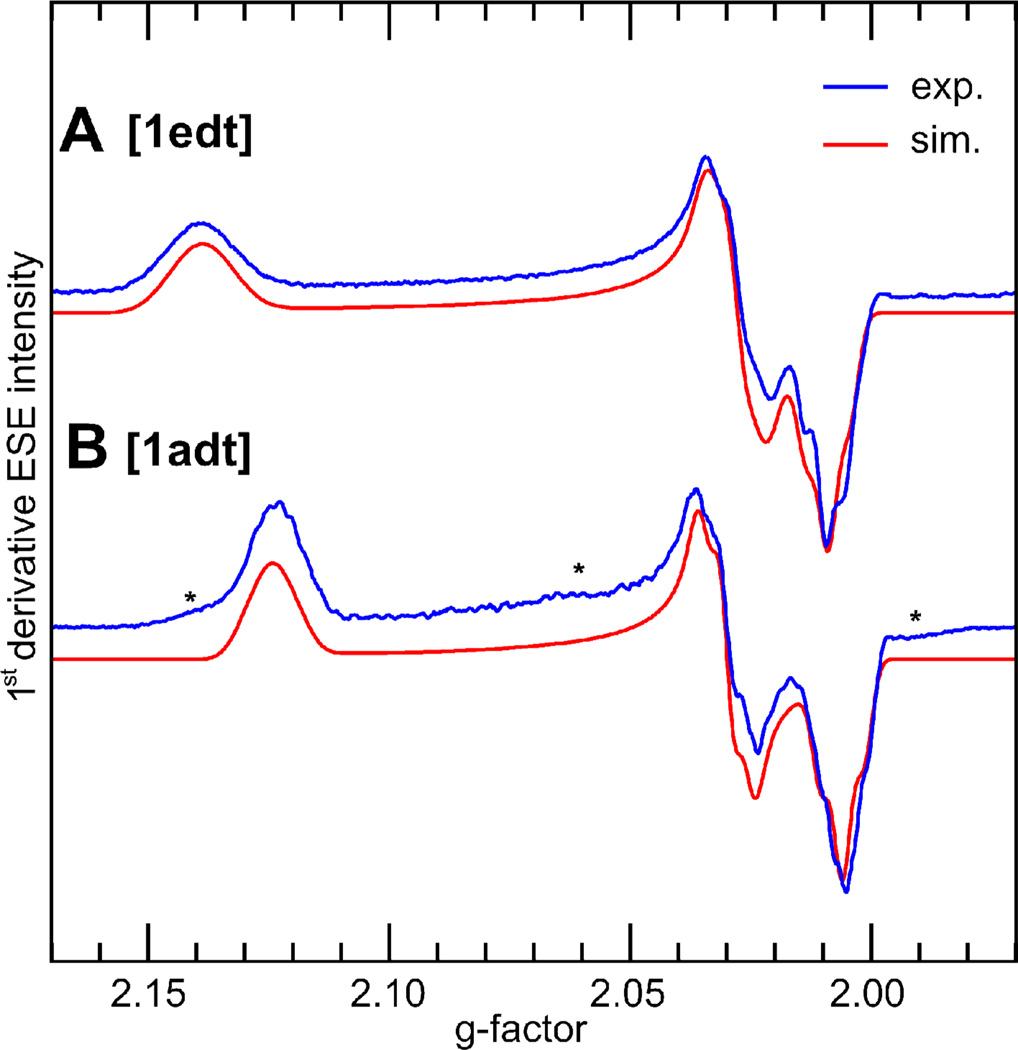
Figure 2 shows EPR spectra of 1edt and 1adt, obtained by 2 pulse-ESE detected EPR at Q-band. Both samples show signals consistent with the presence of one dominant species. The [1:2:1] splitting patterns observed at X-band originating from two presumably equivalent ³¹P nuclei of the dppv ligand³¹ are washed out at Q-band because of the increased linewidth, however, the principal g-values are more clearly resolved. The 1edt model shows a larger anisotropy and a smaller rhombicity of the g-matrix (g = 2.009, 2.028, 2.139), whereas the 1adt is more rhombic but less anisotropic (g = 2.006, 2.030, 2.124). However, as the g-matrix of both complexes is rather axial, it is apparent that both compounds have similar electronic structures that are only modestly influenced by the bridge alteration.

Figure 2.

First derivative (pseudomodulated) Q-band two pulse echo-detected EPR spectra (blue) of frozen solutions of 1edt (A) and 1adt (B) and corresponding simulations (red) using principal g-values: A g^1edt=(2.009, 2.028, 2.139), B g^1adt=(2.006, 2.030, 2.124). Experimental conditions: T = 20 K, ν_mw = 33.8560 GHz (A), 33.918 GHz (B), τ= 340 ns. The asterisks on B indicate minor contaminations of unknown origin.

1. Spectroscopic Results on 1edt

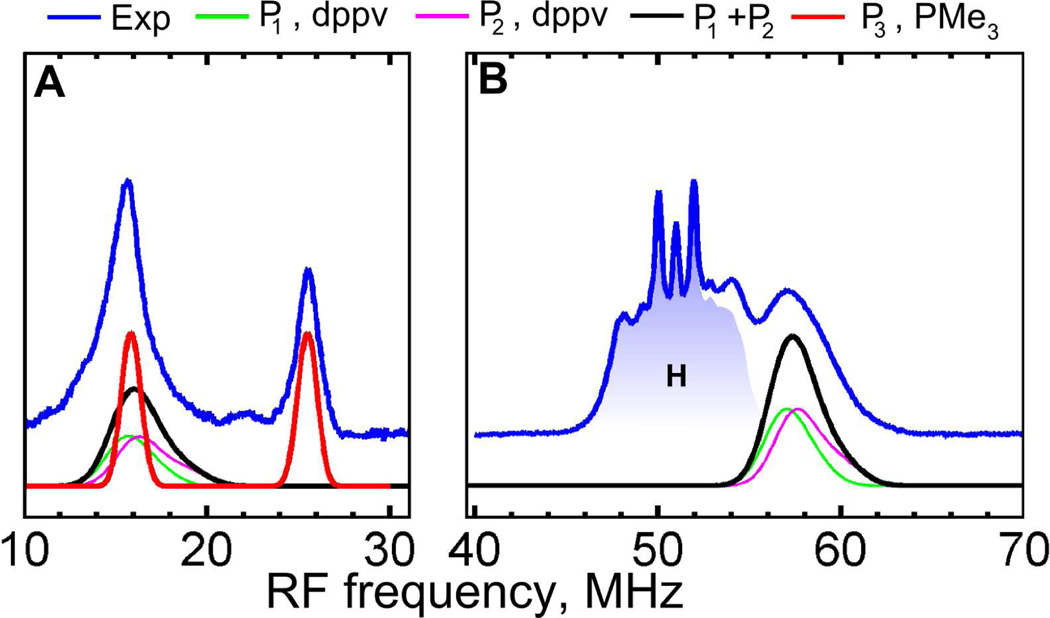
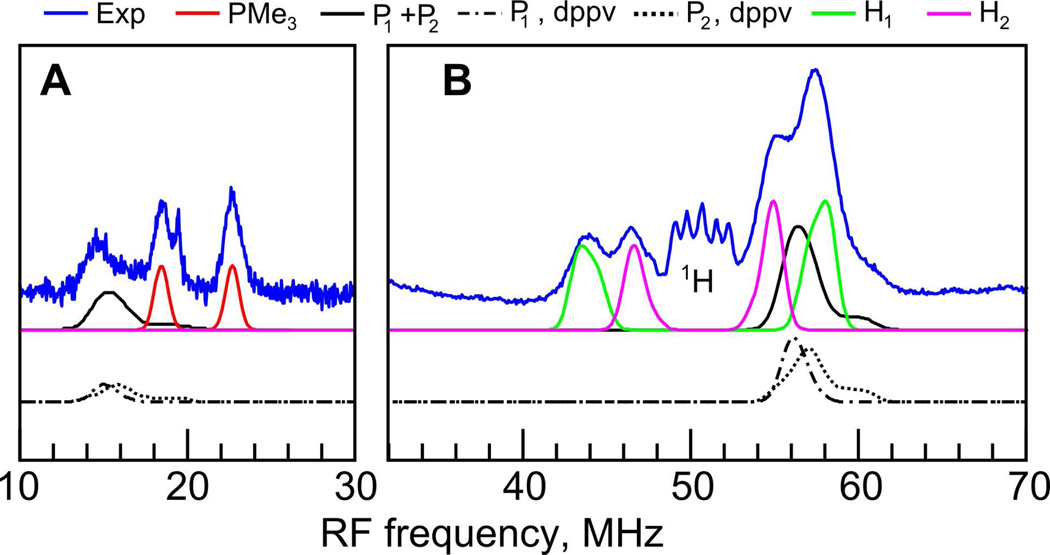
Although the two strong ³¹P hyperfine interactions can already be partially resolved in CW EPR, these interactions were also probed using orientation-selected pulse ENDOR measurements. Q-band Davies ENDOR spectroscopy revealed two different sets of ³¹P signals (Figure 3). One set corresponds to two strongly coupled ³¹P nuclei of the dppv ligand consistent with the splitting observed previously in the X-band CW EPR spectra.³¹ The best fit to the field dependent ENDOR signals was achieved assuming two slightly different ³¹P HF couplings: A(P₁) = (−72, −71, −80) MHz, A(P₂) = (−73, −72, −85) MHz. In the lower frequency region we have detected another doublet, centered at the Larmor frequency of ³¹P (ν_31P = 20.664 MHz at 1197.8 mT), which has been assigned to a weakly coupled ³¹P nucleus, A = (9.5, 11.0, 8.5) MHz. Results of the simulations of these spectra are summarized in Table 1. Since this ³¹P HF coupling is much smaller than those from the dppv ligand, we conclude that it originates from the PMe₃ ligand at the second iron (Fe₂), indicating some delocalization of the spin density to this site.

Figure 3.

Q-band Davies ENDOR spectra (blue) of 1edt measured at T = 20K and 1197.8 mT. Simulations were performed using P_1,2,3 parameters from Table 1. The ¹H ENDOR region is shaded blue for clarity. Experimental conditions: A, t_RF = 35 µs; ν_mw = 33.8708 GHz; t_inv = 200ns. B, t_RF = 5.5 µs; ν_mw = 33.8708 GHz; t_inv = 80 ns; see also Figure S2 in SI for complete field dependence.

Table 1.

Principal HFI tensor values (MHz) for 1edt and 1adt obtained from simulations of experimental spectra.

Nucleus (assignment)	Ax	Ay	Az	Aa)iso	Euler angles (deg)
					α	β	γ
1edt
31P1 (dppv)	−72	−71	−80	−74.3	0	30	0
31P2 (dppv)	−73	−72	−85	−76.6	0	30	0
31P3 (PMe3)	−9.5	−11.0	−8.5	−9.7	0	40	0
57Fe (Fe1)	−12.0	+16.6	−29.5	−8.3	10	10	0
57Fe (Fe2)	−3.0	−1.0	+0.5	−1.16	0	15	20
1adt
31P1 (dppv)	−70	−71	−78	−73.0	0	30	0
31P2 (dppv)	−69	−72	−85	−75.3	0	30	0
31P (PMe3)	−4.3	−4.5	−3	−3.90	0	30	0
14N1b)	+5.4	+3.7	+3.0	+4.0	10	25	0
14N2b)	+0.0	+0.0	+3.5	+1.17	30	60	0
1H1	+11.1	+15.8	+13.5	+13.4	40	30	0
1H2	+5.0	+8.5	+10.5	+8.0	30	30	0

^a)A_iso = (A_x + A_y + A_z)/3

^b)sign of the HF coupling is assumed based on DFT calculations (vide infra).

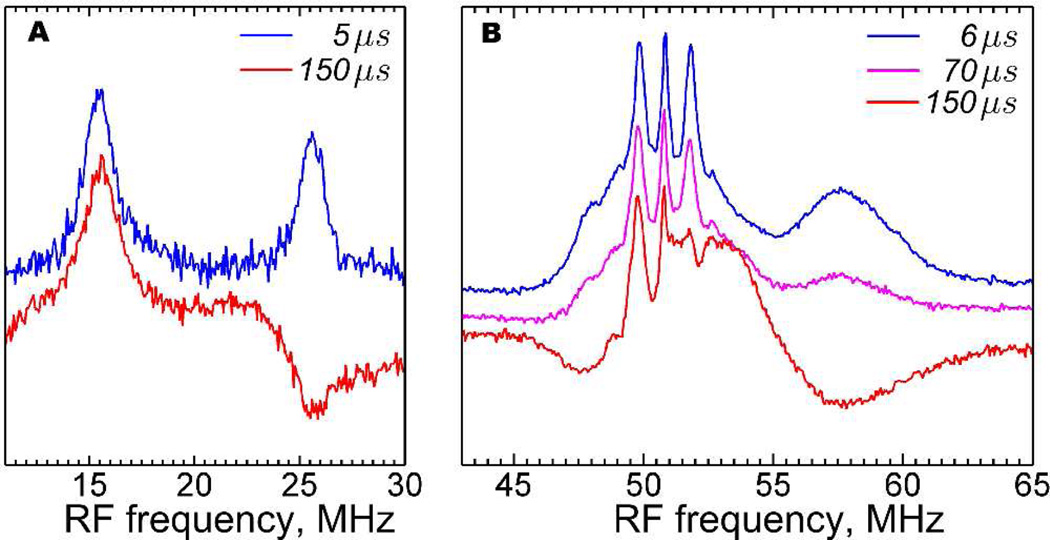
As will become apparent below, the sign of this small ³¹P HF coupling plays an important role in understanding the orientation of the PMe₃ ligand. To resolve the sign of this HF coupling we employed variable mixing time (VMT) ENDOR.^48,49 In this method the sign of the HC coupling in question can be directly read out from the polarization of the ENDOR signal upon increasing the delay time between the RF pulse and the detection sequence, t_mix (Figure S1), due to longitudinal electron spin relaxation. As can be seen from Figure 4, even at relatively high temperatures (25 K), we have observed an almost completely polarized Q-band ENDOR spectrum when t_mix exceeds 100 µs.

Figure 4.

Q-band VMT (Davies) ENDOR of 1edt measured for various t_mix delay times (see SI) at maximum absorption of the EPR spectrum (g_y). Both low (A) and high (B) frequency ENDOR signals show a clear dependence on t_mix delay times (indicated in the figure). Experimental conditions: A, T = 25 K; t_RF = 20 µs; ν_mw = 33.8269 GHz; B₀ = 1192.3 mT; t_inv = 100 ns. B, T = 25 K; t_RF = 7 µs; ν_mw = 33.8865 GHz; B₀ = 1194.4 mT; t_inv = 80 ns.

For S = ½ and I = ½, the frequency of the ENDOR resonances is given by

$${\mathrm{\nu }}_{\mathrm{\alpha }(\mathrm{\beta })}=|-g_{\mathrm{n}}{\mathrm{\beta }}_{\mathrm{n}}{\mathrm{B}}_0+(-)\mathrm{A}/2|$$ (3)

where g_n = nuclear g-value, β_n = nuclear magneton, B₀ = strength of magnetic field, A = the orientation-dependent HF coupling constant. Assignment of the ENDOR signals to a specific M_S manifold (α or β) enables the direct determination of the absolute sign of A. As follows from the description of VMT ENDOR experiments,^48–50 at sufficiently long delay time between the RF pulse and the detection (see Supporting Information for the pulse sequence), t_mix ≥ T_1e, the ENDOR signal from the M_S =−½ (β-manifold) remains positive, while the M_S = +½ (α-manifold) signal decreases relative to the other signal and even changes its sign. Considering g_n values for ³¹P and ¹ H nuclei are positive a positive A would result in ν_α < ν_L = |g_nβ_nB₀| and ν_β > ν_L (see equation 3). In this case, the lower frequency component of the ENDOR doublet (i.e. ν_α) would be affected. However, in our experiment (Figure 4A) the opposite situation was observed indicating that ν_α > ν_L. Thus A(³¹P, PMe₃) is negative. Despite being unable to simultaneously observe α-and β-manifold signals we can conclude that the ³¹P(dppv) hyperfine couplings similarly have negative signs as the high frequency component of the ENDOR signal clearly decreases and becomes negative with increasing t_mix (Figure 4). In this experiment, a polarization of the ¹H signals has also been detected; however no definite assignment could be ascertained from the overlapping signals.

Although the observation of the weakly coupled ³¹P nucleus indicates some degree of spin delocalization on to Fe₂, more direct insight into the electronic structure for these model compounds is obtained by a study of the iron centers themselves. Investigating the electronic environment of Fe atoms in coordination complexes and protein samples is routinely compromised by the absence of a nuclear spin of sufficient abundance. Naturally occurring ⁵⁷Fe (I =½) has a meager 2.2% abundance, so isotropic enrichment is necessary. In this project we benefit from the recently developed methods for the ⁵⁷Fe enrichment of 1edt.⁴⁷ By a combination of Mössbauer and pulse EPR spectroscopic methods to these highly enriched samples, we obtained the ⁵⁷Fe HF coupling constants with high accuracy.

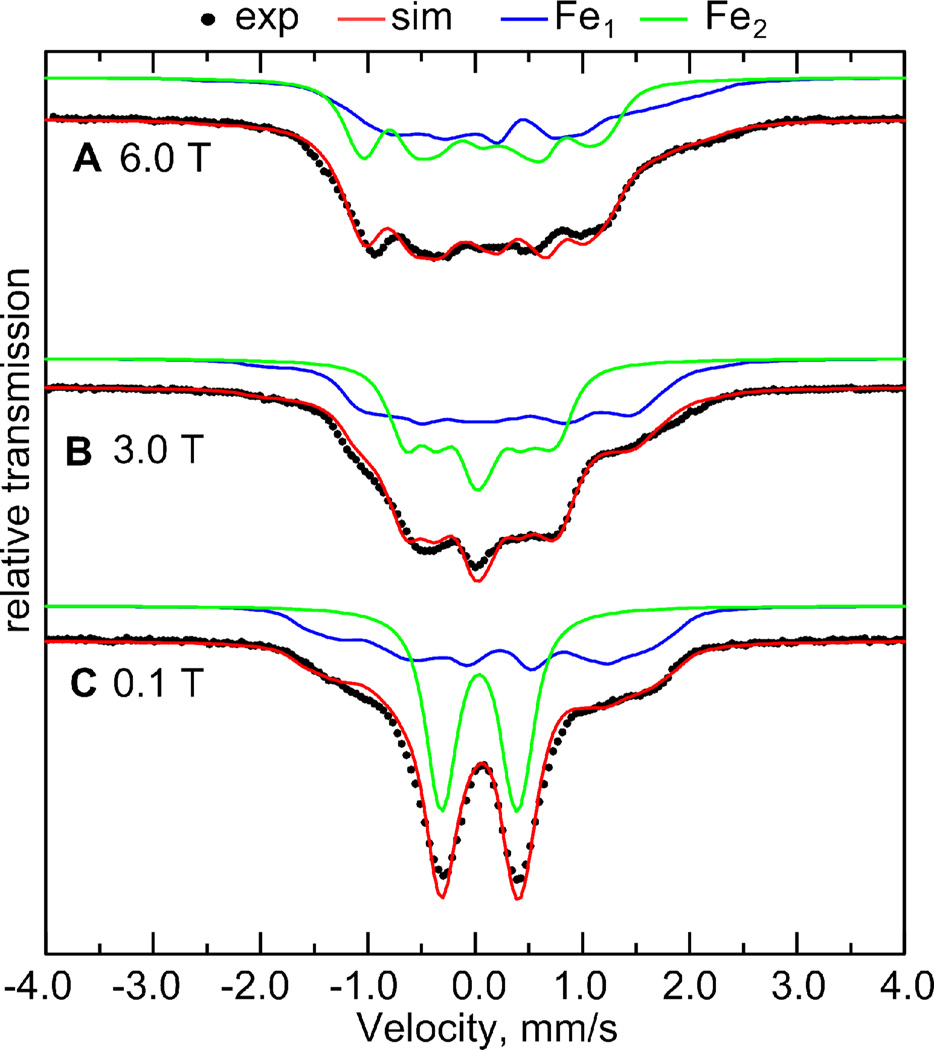
Applied field ⁵⁷Fe Mössbauer spectra of 1edt measured at 4.2 K consist of two signals corresponding to the two Fe sites in the complex (Figure 5). One of the signals at 0.1 T represents a typical quadrupole doublet with HF coupling well hidden under the line width, thus indicating relatively weak ⁵⁷Fe HFI. The other contributing signal has a rather complex and broad shape even at low magnetic fields. The overall width of this signal remains invariant with increasing magnetic field. The spectral profile of this signal remains unchanged at 1.8 K eliminating the possibility for a strong relaxation case that could also result in considerable broadening of the spectra. We therefore conclude that this second contributor is subject to a relatively large and very anisotropic ⁵⁷Fe HF tensor.

Figure 5.

Mössbauer spectra of the fully ⁵⁷Fe enriched 1edt measured at three magnetic field strengths at a temperature of 4.2 K (black) and respective simulations (red) accounting for two contributing ⁵⁷Fe nuclei: Fe₁ (blue) and Fe₂ (green) with parameters presented in Tables 1 and 2.

Due to the complexity of the signal at all measured magnetic fields, no unique set of Mössbauer parameters could be unambiguously extracted. To increase the number of constraints and thus obtain a unique set of spin-Hamiltonian parameters, additional pulse EPR experiments were conducted on the ⁵⁷Fe labeled 1edt sample.

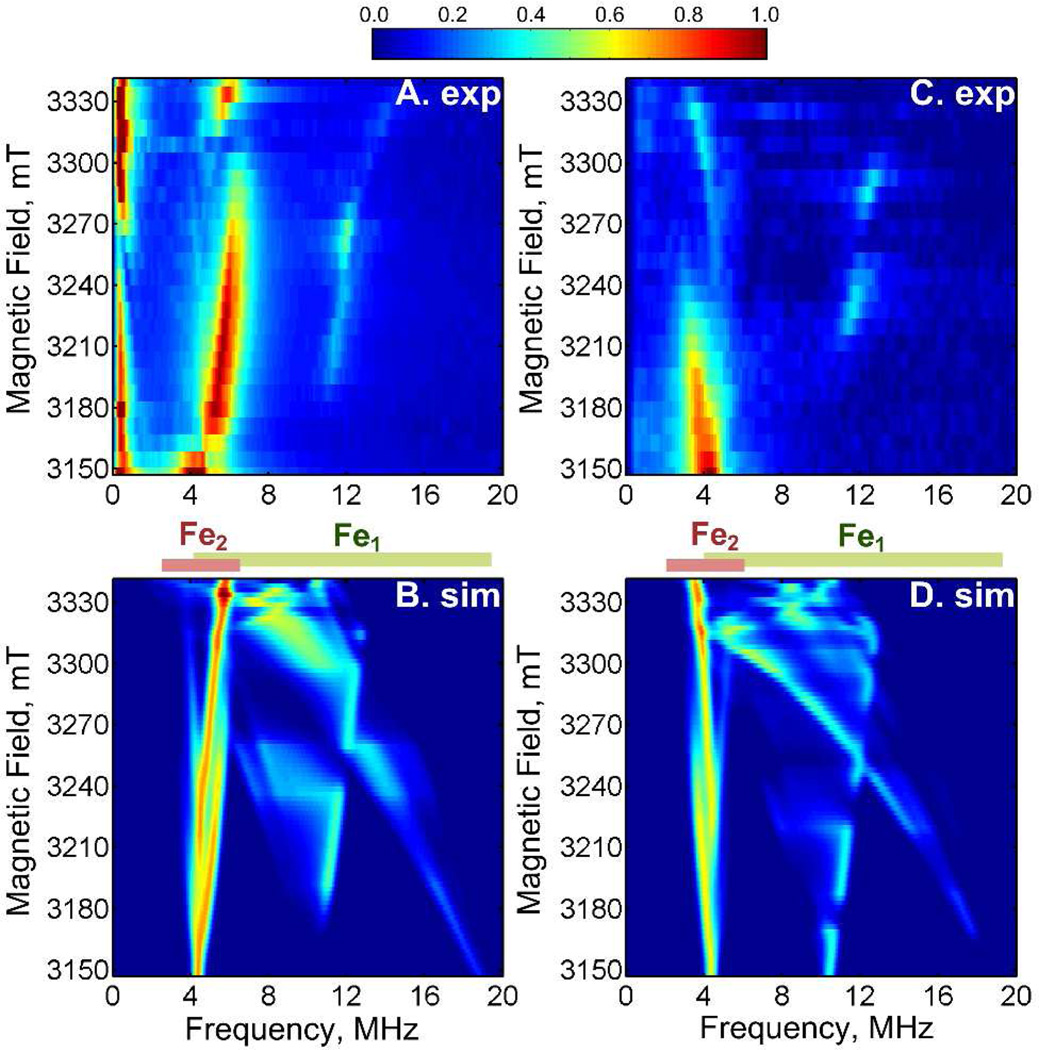
The simulations exhibited in Figure 5 were obtained from a simultaneous fit of both Fe nuclei with the inclusion of fixed coupling parameters obtained from high-frequency ESEEM and HYSCORE data (vide infra). The ⁵⁷Fe-labeled 1edt samples show distinct signals in the low frequency region of the Q- and W-band ESEEM spectra (Figure 6,7) that are consistent with a weakly coupled ⁵⁷Fe nucleus. Better resolution was obtained from HYSCORE measurements at Q-band frequency. The noticeable field dependence of these ⁵⁷Fe signals indicates a very anisotropic character of the HF coupling. The simulation could be performed using one set of parameters with a good fit to the experimental spectra (Figure 7). To corroborate these assignments we have also performed these HYSCORE experiments at W-band frequency (see Supporting Information). The resulting ⁵⁷Fe parameters match the Q-band data completely.

Figure 6.

Experimental (A–D) Q-band HYSCORE spectra of 1edt measured at the indicated field positions, and corresponding simulations (E–H) that account for one ⁵⁷Fe HF coupling (A(Fe₂), Table 1). Experimental conditions: T = 20 K; τ = 420 n; ν_mw = 33.8883 GHz; t(π/2) = 40 ns; ΔT_1,2 = 52 ns.

Figure 7.

W-band 3-pulse ESEEM spectra as function of the applied magnetic field B₀ of ⁵⁷Fe-enriched 1edt, measured at two different τ-values: 164 ns (A) and 288 ns (C), together with the respective simulations (B, D) accounting for two contributing ⁵⁷Fe HF couplings (Table 1). Experimental conditions: T = 10 K; τ = 164 ns; ν_mw = 94.0928 GHz; t(π/2) = 24 ns; ΔT = 12 ns. The color coding of the signal relative intensity is represented by the color bar.

Concerning the second ⁵⁷Fe signal, as in the case of the Mössbauer data, the high frequency W-band ESEEM signals cannot be fit with a unique set of parameters. However, as Mössbauer and pulse EPR data impose different constraints, a simultaneous simulation of all the data (Q/W-band ESEEM and HYSCORE and Mössbauer) yielded a unique set of parameters of two ⁵⁷Fe HF couplings. Figures 6 – 7 include simulations obtained from this process. It is worth noting that this approach also allowed the identification of the sign of each ⁵⁷Fe HF coupling despite their pronounced anisotropy.

The ⁵⁷Fe HF coupling constants are consistent with the weakly coupled ⁵⁷Fe signals resolved in Mössbauer experiments. The W-band ESEEM spectra at selected field positions showed additional signals that could be attributed to a second strongly coupled ⁵⁷Fe nucleus. Figure 7 shows two field dependent series of 3-pulse ESEEM spectra obtained for two different τ-values. Based on these experiments, we can confirm that the spin density is predominantly located at Fe₁. However, as indicated by the presence of weakly coupled ⁵⁷Fe and ³¹P nuclei, about 5 – 10% of the spin is found on Fe₂. Table 1 summarizes the ⁵⁷Fe and ³¹P HF coupling parameters. Table 2 shows ⁵⁷Fe Mössbauer-specific parameters, extracted from the spectra.

Table 2.

⁵⁷Fe Quarupole and Isomer Shift Parameters obtained from Mössbauer Data for 1edt.

Nucleus	ΔEQ (mm/s)	η	δ (mm/s)	Euler Angles (deg.)
				A	β	γ
57Fe (Fe1)	−0.58(3)	+0.90(10)	+0.20(1)	20	60	0
57Fe (Fe2)	+0.70(3)	+0.92(10)	+0.04(1)	0	−10	0

2. Spectroscopic Results on 1adt

To assess the impact of a nitrogen atom in the dithiolate bridge (azadithiolate), we have pursued similar EPR investigations of 1adt (Figure 1). Q-band ENDOR spectra of 1adt displayed in Figure 8 were more intricate than those of its 1edt counterpart (Figure 3). Aside from the strongly coupled ³¹P signals, a distinct set of ¹H signals was observed (Figure 8B). The pattern with a splitting in the range 10 – 15 MHz remained centered at the ¹H Larmor frequency and unperturbed by variation in the magnetic field indicating a mostly isotropic HF coupling (Table 1). Tentatively, we attribute the observed ¹H signals to the methylene and/or amine protons of the azadithiolate moiety. This assignment is supported by DFT calculations, presented in the following section. Additional structure at the high frequency side of the proton range reveals ³¹P signals, most clearly seen at the lowest measured magnetic field position (Figure 8B). These arise from two signals from either inequivalent nuclei of the dppv ligand or the presence of two isomeric forms of the complex.

Figure 8.

Q-band ENDOR spectra of 1adt measured at 20 K and field position 1192.8 mT (g_y). Low frequency spectra (A) were recorded using the refocused Mims ENDOR sequence with τ = 108 ns and t(π/2) = 16 ns, whereas the high frequency part (B) was recorded using Davies ENDOR, t_inv = 44 ns (suppressing matrix ¹H signals), t(π/2) = 16 ns, τ = 400 ns. Simulations were performed using the HF coupling constants listed in Table 1. See also Figure S3 in SI for complete field dependence.

In the low frequency region, the doublet at the ³¹P Larmor frequency is assigned to the weakly coupled PMe₃ ligand (Figure 8A). Its field dependence (see Figure S3 in supplementary information) showed this coupling to be mostly isotropic. It is interesting to note that this ³¹P HF coupling is significantly smaller in magnitude than for 1edt.

From Q-band VMT (Davies) ENDOR experiments of 1adt (Figure S4) we conclude that all ³¹P signals (from PMe₃ and dppv) correspond to negative HF couplings, as for 1edt. Conversely, the polarization pattern of the ¹H signals in Figure S4 identify the strongly coupled ¹H HF couplings as positive. Despite the lack of viable synthetic access to ⁵⁷Fe enriched variants of 1adt that precludes similar ⁵⁷Fe Mössbauer and EPR studies as conducted on enriched 1edt, it is nevertheless apparent from the ³¹P(PMe₃) HF couplings that the electronic structure of 1adt is distinct from that of 1edt.

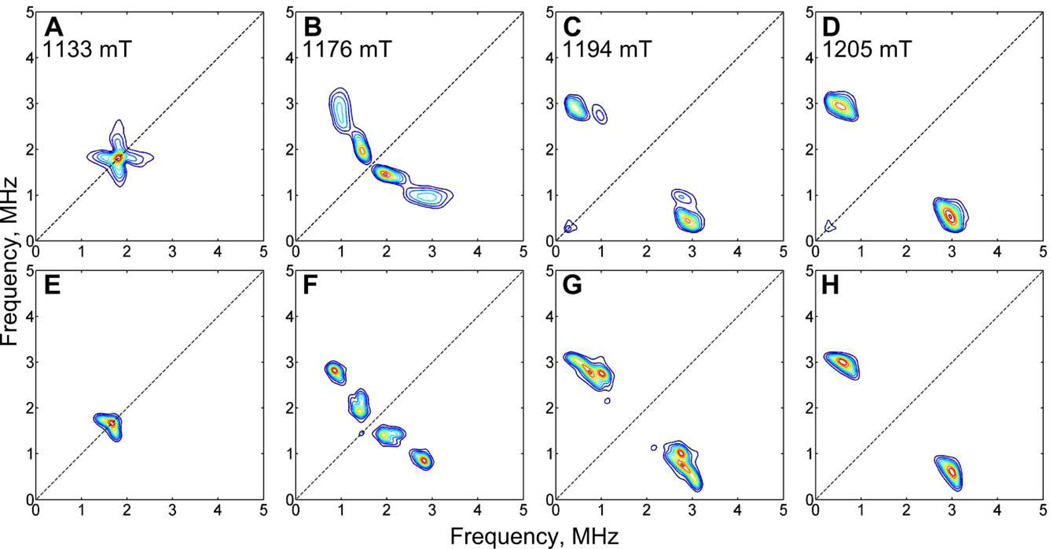
A combination of ESEEM and HYSCORE measurements enabled the determination of the HF and quadrupole coupling constants of the ¹⁴N atom in the azadithiolate ligand as it is the only nitrogen in the system. However, the observed X-band HYSCORE spectra (Figures 9, S6) reveal rather complex ¹⁴N signals. The majority of the signals in the (++) quadrant can be attributed to a single ¹⁴N nucleus. Since the ridges in the HYSCORE spectra change considerably with the position of the magnetic field (Figure S6) we assume a highly anisotropic ¹⁴N HF coupling. Closer examination of the spectra reveals additional signals that are most prominent in HYSCORE measurements with relatively short τ-values. These signals have a weaker magnetic field dependence and are attributed to a predominantly isotropic HF coupling.

Figure 9.

X-band HYSCORE spectra of 1adt (top) and corresponding simulations (bottom) accounting for two independent ¹⁴N signals that correspond to two isomeric forms of the amine group (see also Figure S6). Experimental parameters: B₀ = 342.5 mT; T = 20 K; ν_mw = 9.720 GHz; t(π/2) = 8 ns; τ = 86 ns. For clarity the presented spectra are cropped to the low frequency range, neglecting the ¹H signals. Asterisks denote instrumental artifacts.

Additional Q-band HYSCORE measurements produced two sets of signals as well (see Supporting Information). Spectral simulations depicted in Figure 9 yielded two distinct sets of ¹⁴N HF parameters (Table 1). This observation can only be rationalized by attributing each HF coupling to one of two isomers of 1adt, presumably arising from a bridge flip (eq 4). The almost identical magnitude of the quadrupole coupling for the observed ¹⁴N signals corroborates this assignment (Table 3).

Table 3.

¹⁴N Quadrupole Parameters obtained from X-band HYSCORE Analysis of 1adt.

	K(MHz)	η	Euler Angles (deg.)
			α	β	γ
14N1	1.12(1)	+0.20(5)	10	20	0
14N2	1.15(1)	0.00(10)	0	70	0

(4)

Although the geometry of the amine ligand in the model is presumably identical to that of the H-cluster, the measured ¹⁴N quadrupole coupling in 1adt is ~10% smaller than the one observed in the native enzyme (K(1adt) = 1.12/1.15 MHz versus K(H_ox) = 1.23 MHz).¹² We believe that this difference stems from the absence of neighboring protein residues that affect the site symmetry of the nitrogen atom in the enzyme.

3. Quantum chemical study of 1edt and 1adt

Previous studies of inorganic models of the H_ox-CO state, [Fe₂(µ-CO)(CO)₃(CN)₂(dithiolate)]¹⁻ (where dithiolate = {MeSCH₂C(Me)(CH₂S)₂} (2)²⁶ or {MeS(CH₂)₂N(CH₂S)₂} (3)²⁷) produced calculated values in good agreement with the physical observables. However, while 2 and 3 show a highly delocalized spin density, the present compounds evidently produce a highly localized spin distribution.³¹

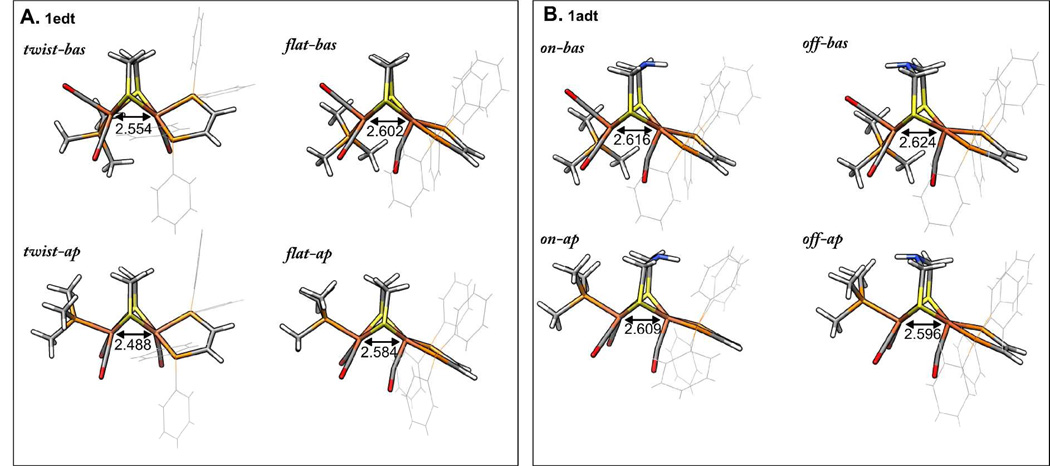
Based on geometry optimizations and earlier studies,^29,31 two principal geometric configurations of the ligands about Fe₁ in 1edt are considered: (i) dithiolate and dppv ligands form a square-pyramidal arrangement with a semi-bridging position of the CO-ligand (designated as "flat"), and (ii) twisted arrangement of the dppv ligand with respect to the dithiolate bridge and CO in a terminal basal position and henceforth referred to as "twist" (Figure 10). For each of these two arrangements, two positions of the PMe₃ ligand at Fe₂ being apical (“ap”) or basal (“bas”) with respect to the dithiolate bridge are critical to the degree of spin delocalization in the molecule. An earlier X-ray crystallographic study of the reduced variant of 1edt revealed an apical position of this ligand²⁹. However, it should be noted that the conditions for sample preparation as well as the measuring conditions are different in the current case. As the formation of the crystal implies a tight packing of molecules, lattice forces might as well favor a different isomer. Hence, in this analysis we consider the four geometric alternatives shown in Figure 10A. Following the previous approach for 2 and 3, i.e. spin unrestricted B3LYP-DFT calculations with all-electron valence triple-ζ basis sets (TZVP), the ³¹P HF coupling constants for 1edt and 1adt were nicely reproduced. However, the correspondence between the experimental and computed ⁵⁷Fe HF coupling constants was less favorable. This situation did not improve using alternative popular hybrid functionals such as PBE0 and TPSSh nor by including a dielectric continuum.

Figure 10.

Geometry optimized isomers of 1edt (A) and 1adt (B). Fe₁-Fe₂ distances are indicated in Å. "bas"/"ap" stands for basal or apical position of the PMe₃ ligand, respectively. "flat"/"twist" stands for flat (square-pyramidal) configuration of dithiolate and dppv ligands and twisted configuration. "on"/"off" indicate the position of the amine with respect to the dppv ligand.

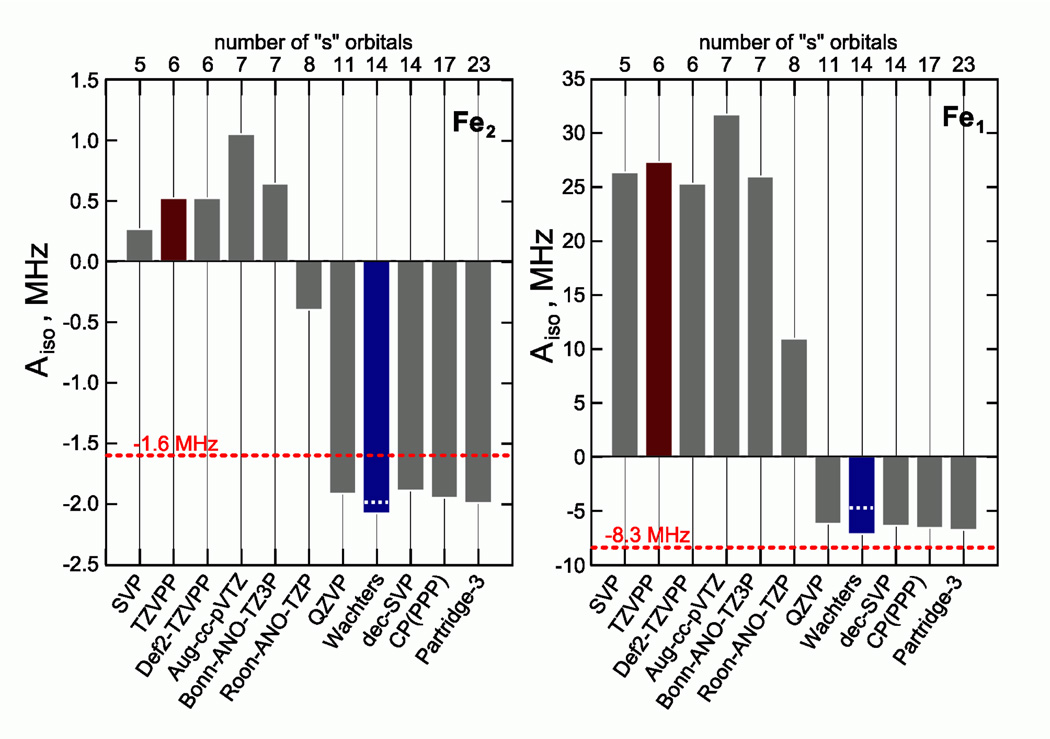
The calculated ⁵⁷Fe _Aiso values were found to be strongly affected by the basis set. Figure 11 presents the variation in ⁵⁷Fe A_iso values with the different basis sets used. TZVPP was maintained for all other atoms, having no substantial impact on the ⁵⁷Fe HF coupling constants. Surprisingly, we observed that depending on the flexibility of the core region of the iron basis sets the results fall into two distinct categories. The only exception is the rather large Atomic Natural Orbital (ANO) basis set Roos-ANO-TZP.⁵¹ Illustrative of the overall sensitivity of the computed HF values to the basis set is the finding that a decontraction of a relatively small basis set SVP (indicated as "dec-SVP") leads to a completely different result, which is in fact much closer to the experiment.

Figure 11.

⁵⁷Fe A_iso coupling constants of 1edt_flat-bas as calculated using various basis sets (see Supporting Information for detailed description) in conjunction with the B3LYP functional and TZVPP basis set on all other atoms not taking into account second order spin orbit coupling contributions. The red dashed lines indicate the experimentally obtained values from Table 1. Brown and blue bars identify TZVPP and Wachters basis sets, respectively. The white dashed lines in the blue bars indicate spin-orbit coupling corrections to the isotropic hyperfine coupling.

Overall, the “Wachters” basis set ⁴³ was preferred for computing the EPR and Mössbauer parameters; the data for 1edt are given in Table 4. For calculations in vacuo, the energy differences between the various structures were found to be relatively small (<6 kcal/mol). Nevertheless, as expected based on the structural differences, the "flat" and "twist" conformations differ considerably in the spin density distribution (see supporting information, Figure S10). In the "flat" case, the spin density is predominantly localized on Fe₁, while it is delocalized over both Fe₁ and Fe₂ in the twisted isomers. The two classes of isomers also differ dramatically with respect to the electric field gradient constant on Fe₁. Given that a substantial quadrupole splitting is computed for the twisted isomers, we infer that only "flat" isomers are present in the measured samples in accord with the experimental quadrupole splitting.

Table 4.

Comparison of experimental and calculated parameters for 1edt

	twist-ap	twist-bas	flat-ap	flat-bas	exp
ΔE, kcal/mol	5.73	5.76	2.03	0.00	-
57Fe, Fe1a)
Aiso (MHz)	−0.55	+0.97	−4.59	−4.74	−8.30
Adip (MHz)	+11.14	+9.64	+15.97	+16.58	+12.45
Arh	+0.68	+0.99	+0.46	+0.35	+ 0.70
ΔEQ (mm/s)b)	+1.47	−1.17	−0.41	−0.49	−0.58
η	0.87	0.87	0.91	0.97	0.90
δ (mm/s)c)	+0.15	+0.14	+0.17	+0.16	+0.20
Mulliken	0.7448	0.7023	0.9740	1.0189
57Fe, Fe2a)
Aiso (MHz)	−0.57	0.55	−2.25	−1.99	−1.16
Adip (MHz)	+5.77	+7.17	+2.02	+1.43	+0.90
Arh (MHz)	+0.64	+0.79	+0.30	+0.23	+0.82
ΔEQ (mm/s)b)	+0.70	−0.59	+0.67	+0.80	+0.70
η	0.99	0.69	0.52	0.48	0.92
δ (mm/s)c)	−0.03	−0.01	+0.01	+0.01	+0.04
Mulliken	0.3946	0.4178	0.1147	0.0797
31P(dppv), Aiso (MHz)
P1	−66.85	−60.13	−85.17	−82.29	−74.3
P2	−60.78	−58.69	−84.39	−85.70	−76.6
31P(PMe3), Aiso (MHz)
P3	+8.15	−40.22	+6.10	−11.91	−9.70

^a)A_iso - isotropic part, A_dip - magnitude of the anisotropic part, A_rh - rhombicity of anisotropic part, i.e. degree of deviation from axial character as such: A = A_iso + A_dip[−1+A_rh, −1−A_rh, 2]

^b)As the asymmetry parameter is almost 100% the sign of ΔE_Q does not have a physical meaning

^c)δ = 0.1181 − 0.3821 (ρ (0) − 11614), see Materials and Methods.

Although the calculated magnitude of the ³¹P HF coupling of the PMe₃ ligand is similar in the apical and basal conformations, its sign switches. This difference can be understood by considering that the spin density resides in a d_z²-like orbital at Fe₂ and therefore the sign is positive for the position of the ligand along the axial direction of the d_z² orbital (apical isomer) and negative in the equatorial plane of d_z² orbital (basal isomer). Based on the sign determination using VMT ENDOR measurements, we conclude that the PMe₃ ligand in 1edt is in the basal position. Although the crystal structure of 1edt (as its BF₄⁻ salt) shows an apical PMe₃ in the solid, the structure of a related Fe₂(pdt)(CO)₄(Imes)(PMe₃)]PF₆ features basal PMe3 on Fe₂⁵². Our assignment is further corroborated by the fact that the "flat-bas" isomer has the lowest calculated single-point energy be it by only 2 kcal/mol ³¹. Moreover, the spin density distribution mapped by DFT for the "flat-bas" isomer, with the unpaired electron essentially localized in a d_z²-like orbital of Fe₁ with minimal delocalization to the other iron site, best matches the experiment. Knowing that we can reproduce the general electronic structure using DFT methods, we can now compare data for the 1edt and 1adt variants.

For 1adt, we include two possible arrangements of the azadithiolate ligand as an additional degree of freedom. We will call the orientation of the amine facing the dppv ligand as "on", and the orientation to the other side as "off". We found that the overall electronic structure was insensitive to the orientation of the amine proton. In all cases examined, the amine proton projects toward the metal core as this afforded the most stable geometry. Additionally, we disregarded the "twist" isomer since the overall similarity in the EPR spectra of 1edt and 1adt implies that the "flat" isomer is dominant. Selecting only the “flat” arrangement for the dppv ligand, four isomers remain to be considered for 1adt as depicted in Figure 10B.

We noticed that the position of the amine perturbs the arrangement of the dppv phenyl substituents; projection of the NH group into this space results in a minor tilt of the dppv ligand, which could explain the slight inequivalence of the two ³¹P(dppv) hyperfine couplings. If the amine is flipped in the opposing direction, it affects the position of the PMe₃ ligand when this is in the apical position. Hence, the "off-ap" isomer has the highest calculated single-point energy. As was the case for 1edt the negative sign of the PMe₃ ³¹P HF coupling corresponds to a basal orientation of this ligand for 1adt.

Concerning the orientation of the amine, the two experimentally extracted sets of ¹⁴N HF coupling constants match the ones calculated for the “on” and “off” positions. If the nitrogen points towards the dppv ligand (and is closer to the spin density "cloud" near Fe) a large HF coupling constant is encountered. A much smaller ¹⁴N HF coupling constant is obtained when the amine is pointing to the other side. Interestingly, only in the "off" isomers are the methylene protons of the dithiolate bridge (but not the amine proton) calculated to have relatively large HF couplings (Table 5). The sign of these ¹H HF coupling matches the experimental assignment. We therefore conclude that the two isomers of 1adt detected in our experiments are "on-bas" and "off-bas".

Table 5.

Comparison of experimental and calculated parameters for 1adt.

	on-ap	on-bas	off-ap	off-bas	expc)
ΔE, kcal/mol	2.79	0.00	4.16	0.32	-
14N(adt)a)
Aiso (MHz)	+3.92	+2.91	+0.59	+0.83	+4.00 /+ 1.17
Adip (MHz)	+0.21	+0.22	+0.66	+0.72	+0.68 /+ 1.17
Arh	+0.34	+0.24	+0.03	+0.03	+0.51 /+ 0.0
K (MHz)	−1.24	−1.25	−1.24	−1.22	1.12 / 1.15
η	0.09	0.07	0.07	0.11	0.20 / 0.0
31P(dppv), Aiso (MHz)
P1	−88.27	−83.85	−86.23	−82.08	−73.0
P2	−92.01	−88.30	−86.22	−87.38	−75.3
31P(PMe3), Aiso (MHz)
P3	+8.39	−9.61	+9.59	−6.67	−3.90
1H(adt) Aiso (MHz)b)
H1	+2.68	+1.37	+7.05	+4.95	+8.30
H2	+1.95	+1.78	+7.07	+7.67	+13.50
H3	−1.30	−0.81	−0.87	−1.19	-
H4	−1.32	−0.77	−1.07	−1.00	-
1H(NH), Aiso (MHz)
H5	−0.60	−0.41	−1.07	−0.92	-

^a)A_iso - isotropic part of HF coupling, A_dip - magnitude of the anisotropic part, A_rh - rhombicity of anisotropic part, i.e. degree of deviation from axial character as such: A = A_iso+ A_dip[−1+A_rh, − 1−A_rh, 2].

^b)For assignment of ¹H HFCs, see Figure S11

^c)If no sign is given it is not determined experimentally.

Comparing the calculated values for these isomers with the experimental data we notice that the ¹H and ¹⁴N HF coupling constants are considerably underestimated while the ³¹P HF coupling for the PMe₃ ligand is highly overestimated. While for 1edt the calculated ³¹P HF couplings matched very well with the experimental results, the changes induced by the amino group in the bridging ligand, i.e. a reduction of spin density at Fe₁ with concomitant increase on the dithiolate bridge, were not as clearly reproduced in the calculations. However, the HOMO is indeed more distributed towards the dithiolate bridge in 1adt than in 1edt (Figure S10).

DISCUSSION

DFT accuracy

DFT calculations have reproduced the salient electronic structural features of the two models, 1edt and 1adt quite well. The calculated single-point energy differences between the various isomers are consistent with the experimental observations. The spin density was found to be localized on the five-coordinated Fe₁ site with some delocalization toward the six-coordinated Fe₂ site. A satisfactory agreement was also found for the ⁵⁷Fe Mössbauer parameters. Conversely, the calculated values of the ⁵⁷Fe HF coupling constants are strongly influenced by the flexibility of the basis set. This is not unexpected, but surprisingly, the dependence is not monotonic. Instead, two quite distinct cases were obtained with respect to the ⁵⁷Fe isotropic HF coupling constant for 1edt. This apparently relates to two potential minima solutions that could be reached depending on the basis set core functions. This is a rather important finding since ⁵⁷Fe data provide critical insight into the electronic structure of diiron compounds and their reproducibility by DFT is crucial. Nevertheless, the analysis yields a logical trend: a larger basis set provides more accurate results. To verify, whether the same holds for the previously published models of the H_ox-CO state (2), we performed test calculations at the B3LYP level. Similarly, two different cases for the ⁵⁷Fe HF coupling could be achieved depending on the basis set (see Supporting Information). Quite interestingly, the completely opposite scenario arises, i.e. a smaller basis set provides a better fit to the experimental data than a large one. For 2, the original standard contracted SVP basis set gives a very satisfactory agreement (see supporting information, Figure S9). Therefore, we conclude that despite the fact that the used methods can indeed reproduce the EPR parameters reasonably well, the DFT methods lack predictive power and for each state of the system the basis sets should be “tailored” to fit the experimental data. It remains to be seen if this problem is inherent to the DFT method or if further theoretical developments in DFT might come up with strategies to alleviate or circumvent this “bi-stability” effect.

A more subtle problem lies in the fact that the DFT methods did not identify electronic structural dissimilarities between 1edt and 1adt. According to the calculated spin Hamiltonian parameters, the electronic structures of these two compounds are virtually identical while experimentally there are obvious distinctions.

1edt vs. 1adt

Although a spin localized structure is adopted by both variants, subtleties in this distribution are evident in the spectroscopic analysis. From ⁵⁷Fe HF couplings in 1edt, about 10% of the spin density is dispersed on Fe₂ which commutes with a substantial ³¹P HF coupling constant of the PMe₃ ligand. Upon insertion of an amine the electronic structure changes. The ³¹P (PMe₃) A_iso coupling decreases by a factor of three, attended by a loss of spin density from that ligand. We can exclude a conformational change from basal to apical because the sign of the HF coupling is retained. Furthermore the EPR spectrum of 1adt is less anisotropic and more rhombic, corresponding to a modification of the frontier molecular orbital composition. The similar ³¹P HF coupling of the dppv ligand underscores a nearly identical spin population on Fe₁ in 1edt and 1adt. Interestingly, the ¹H ENDOR spectra resolve strongly coupled methylene protons on the azadithiolate bridge in contrast to the case of 1edt, where the methylene protons are much more weakly coupled. The PMe₃ ³¹P hyperfine interaction in 1adt is only one third of that in 1edt. This would suggest that the azadithiolate bridge perturbs the charge distribution in the diiron core resulting in a decrease of the spin population on Fe₂ and a concomitant increase of the spin population on the dithiolate bridge. This accounts for the variation in electronic properties of the two dithiolates without amending the geometry. The steric and electronic impact of the amine functionality in the dithiolate bridge is expressed in the composition of the MOs in the Fe₂S₂ unit, and consistent with the ease with which 1adt can be reduced.³¹ Additionally, preliminary calculations suggested that the S–C bonding is affected by interactions with the nitrogen lone pair via the so-called anomeric effect, leading to enhanced coupling of the heteroatom with the Fe₂S₂ core.⁵³

Comparison of 1adt with the H-cluster in the H_ox state

From the experimental and theoretical analysis, we conclude that the spin density in both studied variants is predominantly localized on Fe₁ with a moderate delocalization towards Fe₂. Thus it is clear that the models can be classed as Fe₁(I)-Fe₂(II) mixed valence compounds. This situation contrasts the previously studied model compounds 2 and 3 that resemble the H_ox-CO state, where the spin density is fully delocalized and integer oxidation states were not appropriate.²⁶ Thus, with saturation of the ligand environment on Fe₁ (i.e. binding of an additional CO ligand), the character of the unpaired spin density changes from localized to delocalized. An analogous trend was identified in the native H-cluster, wherein the spin density distribution was also found to shift towards the proximal iron upon CO inhibition of the H_ox state. However, there is a very significant difference between the actual spin distributions in the models and native system. In contrast to the model systems, the delocalized picture has been observed in the H_ox state and a localized one in the H_ox-CO state.

As previously detailed the electronic structure of the oxidized states of the H-cluster is heavily influenced by intercluster Heisenberg exchange interactions.^19,26 However, accounting for a Heisenberg spin-spin exchange mechanism alone seems insufficient to account for the discrepancy between the H_ox state and its inorganic mimic, 1adt. Moreover, the exchange interaction is approximately 3–4 times weaker than in the H_ox-CO state and therefore the [4Fe-4S] cluster presumably has a minimal impact of the [2Fe] center. Contrarily, the DFT computed HOMO for the diiron unit is strikingly similar to those obtained for our model complexes,^12,18 and therefore we expect to see a localized spin density for the H_ox state. There could be several reasons for this discrepancy:

1. The coordination geometry of the H_ox state may deviate from the depiction given in Figure 1 owing to the inclusion of water in the vacant (sixth) coordination site of Fe_d, as inferred from crystallographic data of [FeFe] hydrogenase from Clostridium pasteurianum ⁷ and its recent refinement ¹⁷. In recent DFT studies the presence of such a molecule has been shown to significantly affect the electronic structure ^12,18. However, since the authors specify the use of the reductant dithionite in the crystallization buffer it is doubtful that under these conditions the H_ox state is dominant in the crystal. Moreover, low temperature illumination experiments argue against the presence of water at the vacant site (see arrow in Figure 1). Below 60 K, the external CO ligand can be photodissociated, regenerating the H_ox state, as indicated by IR and EPR measurements.^10,15,54,55 Such a conversion argues against binding water at the same site. It is worth noting that the CO-photodissociation was observed even at 8 K. Taking into consideration the compact arrangement of amino acids about the open coordination site, dissociation of a CO ligand and instantaneous binding of a water ligand would require substantial motional freedom of the protein matrix which is clearly unrealistic at these temperatures. Thus, it is very likely that no ligand is present at the sixth coordination site of the distal iron in the H_ox state.

2. The interaction with the surrounding protein environment may have a substantial effect on the electronic structure of the H-cluster. Our recent DFT calculations showed a surprisingly small influence of the protein matrix on the spin distribution in the H-cluster,¹⁸ though Szilagyi et al. reported the opposite effect on the spin populations by including key acid residues.⁵⁶ Unfortunately, these results raise more questions about the reliability of such calculations on spin-exchange coupled Fe-cofactors such as the H-cluster. However, as the bi-nuclear cluster is a "dangling" unit with only one covalent bond to the protein (i.e. the Cys-S bridge between the 2Fe and 4Fe4S subclusters) the protein matrix is expected to exert only a minor influence on the electronic structure of the H-cluster. Nonetheless, the influence of the protein on the electronic structure of the active site remains an important area of investigation.

3. The distinctive electronic interaction between the [2Fe] and [4Fe-4S] subclusters seems to be the most likely explanation for the differences between the model systems and the H-cluster. It clearly transcends a simple Heisenberg exchange approximation, as this would not result in a redistribution of the spin density in the bi-nuclear subcluster.^57,58 Increasing the exchange interaction merely attenuates the observable spin population of the [2Fe] subcluster, and the Heisenberg approach cannot accommodate alternative mechanisms such as double exchange. It would be interesting to study this phenomenon in more detail in model complexes featuring a second redox center thus mimicking the intracluster interaction in the H-cluster.

The properties of the amine in the dithiolate bridge is a further variable to consider in this system. It is apparent from the experimental data that two conformations of the adt ligand are probable, highlighting the flexibility of this bridge. A similar conclusion resulted from DFT calculations of the H-cluster,¹⁷ where this flexibility may be pivotal in modulating catalytic rates as it relays protons during turnover. A recently synthesized family of [Ni(diphosphine)₂] catalysts exploit the flexibility of the pendant base throughout the catalytic cycle.²⁵

CONCLUSIONS

A detailed EPR and Mössbauer study of two structural di-iron models for the H_ox state of the H-cluster is presented. The spectroscopic data indicate that the ligand environment of the 1edt and 1adt models is characterized by a “flat” (dppv) and “basal” (PMe₃) configuration, which geometrically parallels the H-cluster. While the H_ox state of the H-cluster shows a delocalized spin density, the 1edt and 1adt are appropriately formulated as mixed-valent Fe₂(II)-Fe₁(I) pairs with the spin predominantly found on Fe₁ (in a d_z²-like orbital). Inserting an amine into the dithiolate bridging ligand, i.e. going from 1edt to 1adt, pushes spin density away from Fe₂ towards the adt ligand accompanied by large HF couplings of the methylene protons and a measureable hyperfine and quadrupole interaction of the ¹⁴N at the apex of the bridge. The adt ligand exhibits conformational flexibility leading to two configurations (“on” and “off”). DFT calculations corroborate the general picture derived from the experimental data. The ligand HF interactions (³¹P, ¹H, ¹⁴N) are well reproduced, but the properties calculated for the iron core, i.e. the ⁵⁷Fe HF interactions, are highly dependent on the chosen basis set. Finally, the calculated spin-density distribution was found to be essentially the same for 1edt and 1adt, which is not evident in the experiment.

This study provides valuable insight into the electronic and structural properties of the presented model systems. The differences between the resolved spectroscopic parameters of 1edt and 1adt and those obtained for the H-cluster underscore the difficulty in reproducing the precise electronic environment programmed into the native system with all parts playing an important role in tuning this efficient hydrogen catalyst for the best performance.