Abstract
This work is a computational study based on a new detailed metabolic network model comprising well-mixed compartments representing separate cytosol and mitochondria of astrocytes, glutamatergic and gamma aminobutyric acid (GABA)ergic neurons, communicating through an extracellular space compartment and fed by arterial blood flow. Our steady-state analysis assumes statistical mass balance of both carbons and amino groups. The study is based on Bayesian flux balance analysis, which uses Markov chain Monte Carlo sampling techniques and provides a quantitative description of steady states when the two exchangers aspartate-glutamate carrier (AGC1) and oxoglutarate carrier (OGC) in the malate-aspartate shuttle in astrocyte are not in equilibrium, as recent studies suggest. It also highlights the importance of anaplerotic reactions, pyruvate carboxylase in astrocyte and malic enzyme in neurons, for neurotransmitter synthesis and recycling. The model is unbiased with respect to the glucose partitioning between cell types, and shows that determining the partitioning cannot be done by stoichiometric constraints alone. Furthermore, the intercellular lactate trafficking is found to depend directly on glucose partitioning, suggesting that a steady state may support different scenarios. At inhibitory steady state, characterized by high rate of GABA release, there is elevated oxidative activity in astrocyte, not in response to specific energetic needs.
Keywords: energy metabolism, glucose, lactate, mathematical modeling, neuronal-glial interaction
Introduction
Computational models of brain energy metabolism focus on the interplay of neurons and astrocytes, which encompasses the glucose partitioning, lactate trafficking, and neurotransmitter cycling to properly account for the energetic needs as well as the mass balance. In spite of increasing evidence of the central role of gamma aminobutyric acid (GABA) metabolism in numerous brain conditions, models and studies including GABAergic neurons are relatively few, and they focus mostly on GABA synthesis and the role of glutamine as a precursor (Waagepetersen et al, 1998; Patel et al, 2005; Bak et al, 2006, 2007; Yang et al, 2007; Leke et al, 2008). The balance of amino groups, central to the recycling of neurotransmitters, has often been treated separately from the carbon balance (Waagepetersen et al, 2007).
Traditionally, brain energy metabolism models have considered pairwise interactions of astrocytes and either glutamatergic neurons (Gruetter et al, 2001; Aubert and Costalat, 2005; Simpson et al, 2007; Occhipinti et al, 2009; Cloutier et al, 2009; DiNuzzo et al, 2010) or GABAergic neurons (Occhipinti et al, 2010). Since astrocytes communicate with both glutamatergic and GABAergic neurons, it is plausible that their role changes depending on the prominence of either excitatory or inhibitory neurotransmitter release. Moreover, since the synthesis of neurotransmitters relies on amino group transfer, it is reasonable to expect that the latter has a role in neuroenergetics, too.
The search for an explanation of a mismatch between cerebral oxygen uptake during neuronal activity expected from stoichiometric considerations and experimentally measured values led to questioning the role of glucose as preferred substrate initiating a debate which has continued over the past 15 years (Pellerin and Magistretti, 1994, 2003; Gjedde et al, 2002; Chih and Roberts, 2003; Jolivet et al, 2010; Mangia et al, 2011), in the course of which the importance of astrocytes in brain energy metabolism became more evident. Recently, Hertz et al (2007) emphasized high oxidative rate in astrocytes, confirmed by numerous experimental studies. Keeping track of the amino group balance is necessary to fully account for the neurotransmitter synthesis and recycling. A recent article (Pardo et al, 2011) and its commentary (Hertz, 2011) raised the question of stoichiometric equilibrium in a neuron/astrocyte complex when the aspartate-glutamate carrier (AGC1/aralar) portion of the malate-aspartate shuttle (MAS) in astrocyte is weakly expressed. The tight interplay of energy metabolism and neurotransmitter cycling calls for more complete models, including both inhibitory and excitatory activity. Adding more cell types and balance conditions would make the models quickly grow intractable without sophisticated computational tools.
This study proposes a steady-state model of a neurovascular unit comprising astrocyte, glutamatergic, and GABAergic neurons, equipped with the metabolic details necessary to follow the transformation of metabolites and intermediates at steady state when both carbons and amino groups are balanced. The flux balance analyses are performed within the computational statistical framework introduced in Calvetti and Somersalo (2006), using the Metabolica software (Heino et al, 2010), available online at http://filer.case.edu/dxc57/Software/. The statistical approach acknowledges the possibility of a vast variety of feasible steady states, and seeks to map them all by extensive sampling. Thus, the methodology is in line with the commonly accepted idea that biological systems need to be able to adjust to different sustainable equilibrium states.
One of our main findings is that stoichiometric balance can be attained with incomplete MAS in the astrocyte, as proposed by Pardo et al (2011). Moreover, we show that the balance is possible with or without the aspartate shuttle to astrocytes. We identify the source of possible aspartate to be the GABAergic, not the glutamatergic neurons, which prefer to uptake aspartate, if available. Pyruvate recycling is found to have a pivotal role for the balancing of malate in the MAS in astrocyte, with a significant average flux of pyruvate carboxylase (PC) in human awake steady state (AS), in agreement with Gruetter et al (2001). During excitatory activity, oxidative metabolism in glutamatergic neurons is much higher than in the other two cell types and directly proportional to the rate of glutamate efflux into extracellular space (ECS). During inhibitory steady state (IS), astrocyte exhibits the highest rate of oxidative metabolism, in agreement with what was observed with the simpler model in Occhipinti et al (2010). This oxidative activity is a consequence of mass balance only, not in response to any direct energetic expense. As in Occhipinti et al (2010), we find that the role of malic enzyme (ME) in GABAergic neuron is central for GABA cycling. Finally, we show that stoichiometry alone does not determine glucose partitioning, from which the direction and intensity of the lactate shuttle ensues. Thus, at steady state, neurons may act as lactate producers or consumers depending on the rate at which they uptake glucose. Mitochondial processes related to the tricarboxylic acid (TCA) cycle are related to the rate of the transport of reducing equivalents and the rate at which pyruvate crosses the membrane, not by the pathway through which it was produced, with higher activity of lactate dehydrogenase compensating for steady state with lower glycolytic activity and vice versa.
Materials and methods
The present work proposes a new steady-state model for human neurovascular unit, which modifies and extends the two models that we recently proposed for the astrocyte-glutamatergic neuron (Occhipinti et al, 2009) and the astrocyte-GABAergic neuron cellular complex (Occhipinti et al, 2010). The model comprises a three-cell complex, each one subdivided into cytosol and mitochondria, where astrocytes, glutamatergic, and GABAergic neurons interact through a common ECS. In addition to the carbon balancing, the new model follows the metabolic fate of ammonia (NH4+) and the intercellular traffic of different amino group donors.
The new model is explored using statistical sampling techniques to find all possible steady states that the system with given input constraints can attain. Although stoichiometry is based on molecular and cellular considerations, the analysis is based on macroscopic mean fluxes, and assumes a well-mixed compartment model without the resolution to distinguish between presynaptic and postsynaptic neurons, or axons and soma. The steady-state analysis does not provide concentration information, nor can it account for partial volume information; instead, it provides a distribution of reaction fluxes and transport rates. All rates are scaled to correspond to a volume of 1 g brain tissue, and input values correspond to human brain.
An Eight Compartment Model of Cerebral Energy Metabolism
The model comprises separate cytosol and mitochondrial compartments for astrocytes, glutamatergic, and GABAergic neurons, and separate blood and ECS compartments. Each cell type is equipped with detailed glycolytic pathway in cytosol, TCA cycle and oxidative phosphorylation in mitochondria, complete MAS and mitochondrial ME (Hassel, 2001) in neuron; in astrocyte, ME is located in cytosol (Kurz et al, 1993). Furthermore, the activity of AGC1 portion of the MAS is weakly expressed in astrocytes (Pardo et al, 2011), a feature that is taken into account as explained later on. Pyruvate carboxylase is included in mitochondria of astrocytes only (Yu et al, 1983).
Neurotransmitters released in the ECS by glutamatergic and GABAergic neurons are completely taken up by astrocytes, where GABA is catabolized to the TCA cycle intermediate succinate via GABA transaminase and succinate semialdehyde dehydrogenase (Bak et al, 2006), while glutamate is transformed into glutamine by cytosolic astrocyte-specific enzyme glutamine synthetase. During transamination of GABA, alpha-ketoglutarate (αKG) can be converted to glutamate, then to glutamine by the glutamine synthetase. The release of glutamine into the ECS by astrocytes and its uptake by neurons close the glutamate/glutamine cycle and the GABA/glutamine cycle between astrocytes and the respective neurons. Net values of fluxes are considered, and possible reuptake of neurotransmitters is not separately included in the model.
In both neurons and astrocytes, GABA is oxidized to succinate by mitochondrial GABA transaminase followed by succinate semialdehyde dehydrogenase (Berkich et al, 2007) through the GABA shunt, which bypasses two TCA cycle reactions. Our model includes glutamate decarboxylase in neurons only, whereas GABA transaminase and succinate semialdehyde dehydrogenase are present in mitochondria of all cell types. The bidirectional reaction glutamate dehydrogenase has been included in the mitochondria of each cell.
Astrocytes uptake glucose, oxygen, glutamate, and GABA from ECS where they efflux carbon dioxide and glutamine: no a priori preferred direction is assigned for the trafficking of lactate, acknowledging the capacity of each cell type to either release or uptake lactate from ECS.
The energetic cost of excitatory neurotransmission is accounted for by means of a virtual vesicular subcompartment for glutamate and a related reaction, Glu+α × ATP → Gluves+α × ADP+α × Pi, which expresses the process of packing glutamate into a vesicle to be effluxed into ECS. Since the present model does not differentiate between presynaptic and postsynaptic neurons, we also lump into this reaction the energetic cost of membrane depolarization, extrusion of Ca2+ and Na+ entering through N-methyl D-aspartate (NMDA) and non-NMDA channels using a stoichiometry α=25 (see Occhipinti et al, 2009 for motivation), yielding a lower ATP count than suggested in the rodent study of Attwell and Laughlin (2001) (∼140,000 ATP molecules/glutamate vesicle, or 35 ATP/glutamate, assuming 4,000 molecules/vesicle). The metabolic pathway for the GABAergic neurons, as in Occhipinti et al (2010), includes similarly a ficticious reaction GABA+β × ATP → GABAves+β × ADP+β × Pi where we set β=7.8 in agreement with experimental findings (Hyder et al, 2006; Gjedde et al, 2002) that the GABA-glutamine cycle requires ∼21% of the full ATP production (38 molecules). The energetic cost of astrocytic neurotransmitter recycling pertaining glutamine synthethase and Na+/H+ extrusion after ion cotransport with glutamate is assessed at ∼2 ATP/glutamate (Attwell and Laughlin, 2001). The stoichiometry for GABA recycling may yield an unrealistically low energetic cost for astrocyte functions, since experimental data suggest that astrocytes use from 15% to >25% of brain energy (Lebon et al, 2002; Gjedde et al, 2002; Hertz et al, 2007), with part of the energy going toward K+ clean-up and calcium signaling not explicitly accounted for in the model. We compensate for the underestimation by enabling the cells to use energy for activities not explicitly described in the model by including an unspecified ATP hydrolysis.
Extracellular space is assumed to be a well-mixed compartment where the efflux and uptake of glutamate and GABA occur. The blood compartment is modeled as a well-mixed convective compartment, the input being the arteriovenous concentration differences for glucose and lactate, arterial concentrations for oxygen and carbon dioxide and the activation-dependent blood flow. A list of the biochemical reactions and crossmembrane transports considered in the model is provided in Table 1. Note that, unless otherwise specified, each reaction occurs in all three cell types, leading to a system with ∼150 fluxes.
Table 1. List of the reactions and transports across compartments included in the model.
| Reactions in cytosol | Reactions in mitochondria |
|---|---|
| GLC+ATP → G6P+ADP | AKG+NH4+NADH → GLU+NAD+ |
| G6P+ATP → 2 × GA3P+ADP | OAA+GLU → Asp+AKG(MAS) |
| GA3P+Pi+NAD+ → BPG+NADH | AKG+NH4+NADH → GLU+NAD+ |
| BPG+2 × ADP → PYR+2 × ATP | PYR+CO2+ATP → OAA+ADP+Pia |
| PYR+NADH → LAC+NAD+ | ACoA+OAA → CIT+CoA |
| ATP → ADP+Pi | CIT+NAD+ → αKG+NADH+CO2 |
| OAA+NADH → MAL+NAD+(MAS) | αKG+CoA+NAD+ → SCoA+NADH+CO2 |
| Asp+αKG → OAA+Glu(MAS) | SCoA+Pi+ADP → SUC+CoA+ATP |
| MAL+NADP → PYR+CO2a | SUC+NAD+ → FUM+NADH |
| GLUPacked → GLUa | FUM → MAL |
| GLU+NH4+ATP → Gln+ADP+Pia | MAL+NAD+ → OAA+NADH |
| GLU+25 × ATP → GLUPacked+25 × ADP+25 × Pib | GABAPacked → GABA |
| Gln → GLU+NH4b | GABA+αKG → SSA+GLU |
| GABApacked → GABAa | SSA+NAD+ → SUC+NADH |
| GABA+7.8 × ATP → GABAPacked+7.8 × ADP+7.8 × Pic | PYR+CO2+NADH → MAL+NAD+b,c |
| O2+6 × ADP+6 × Pi+2 × NADH → 6 × ATP+2 × NAD+ | |
| Multicompartment reactions | |
| MAL → αKGa,b,c | αKG → MALa,b,c |
| GLU → Aspa,b,c | Asp → GLUa,b,c |
| Transports | |
| Blood to ECS | ECS to blood |
| GLC | LAC |
| O2 | CO2 |
| Asp | Asp |
| NH4 | NH4 |
| ECS to cytosol | Cytosol to ECS |
| GLC | CO2 |
| O2 | LAC |
| LAC | Asp |
| Asp | GLUb |
| GLUa | GABAc |
| GABAa | Glna |
| NH4 | NH4 |
| Cytosol to mitochondria | Mitochondria to cytosol |
| PYR | ATP |
| ADP | CO2 |
| Pi | MAL |
| O2 | |
| NH4 | |
ACoA, acetyl-coenzyme A; ADP, adenosine diphosphate; αKG, alpha ketoglutarate; Asp, aspartate; ATP, adenosine triphosphate; BPG, bisphosphoglycerate; CIT, citrate; CoA, coenzyme A; CO2, carbon dioxide; FUM, fumarate; GABA, gamma aminobutyric acid; GA3P, glyceraldehyde 3-phosphate; GLC, glucose; Gln, glutamine; GLU, glutamate, G6P, glucose 6-phosphate; LAC, lactate; MAL, malate; NADH, nicotinamide adenine dinucleotide (reduced form); NAD+, nicotinamide adenine dinucleotide; NH4, ammonium; OAA, oxaloacetate; O2, oxygen; Pi, inorganic phosphate; SCoA, succinol coenzyme A; SSA, succinic semialdehyde; SUC, succinate; ECS, extracellular space.
In astrocyte.
In glutamatergic neuron.
In GABAergic neuron.
(MAS) Part of malate-aspartate shuttle.
To Every Cell According to Its Metabolic Needs
The input for the model is specified in terms of mean net glucose supply and lactate output in the blood compartment, as well as maximum availability of oxygen. Moreover, a target mean output flux of either excitatory or inhibitory neurotransmitter (glutamate/GABA) is assigned. Rather than supply driven, as most models in the literature, this model is demand driven in the sense that no a priori decision concerning glucose partitioning or oxygen uptake is made. This leaves it up to the metabolic needs of the cell compartments to determine the partitioning, thus allowing us to find all possible steady states in an unbiased way, not just those that correspond to prescribed substrate partitionings.
Bayesian Flux Balance Analysis
The steady-state analysis is based on the Bayesian flux balance analysis paradigm proposed in Heino et al (2007) and used to study the energetics of excitation (Occhipinti et al, 2009) and inhibition (Occhipinti et al, 2010) with simpler models. In agreement with the principles of Bayesian flux balance analysis, the mass balance conditions are interpreted as virtual measurements of the vanishing rates of change of concentrations, a low variance Gaussian error representing possible small deviations from the putative mass balance implied by the steady-state assumption, while constraints (e.g., positivity for irreversible reaction fluxes) are treated as prior information about the unknown fluxes. The posterior distribution of the vector containing the fluxes is explored via a Markov chain Monte Carlo sampler, which generates an ensemble of flux vectors distributed accordingly. The samples represent all possible steady or near steady states. The mean over the ensemble is a flux vector that may be used to summarize the steady-state distribution, at the cost of hiding variability of individual fluxes and correlations between components; for more details, we refer to Heino et al (2007). The full sample would provide a much more complete description of the predictions of the model, but poses a challenge when it comes to extracting pertinent information. The public domain Matlab package Metabolica for the analysis of metabolic networks (Heino et al, 2010) was used to obtain all of our computed results.
The Markov chain Monte Carlo methods become computer intensive as the number of unknowns increases, although there is no definite formula connecting computational burden and dimensionality. In the current application, the number of unknowns is ∼150. The sampler in Metabolica is designed to take into account the structure of the underlying probability density to keep the sampling times manageable even for significantly larger problems with the same structure. Naturally, with increasing number of mutually correlated unknowns, the interpretation of the sample data becomes more challenging.
Results
Excitatory activities in the form of action potential propagation are associated with the release of glutamate by glutamatergic neurons in the synaptic cleft, while inhibitory activities are associated with the release of GABA by GABAergic neurons. In the present model, the ECS compartment accounts also for the synaptic cleft. In kinetic studies, where concentrations count, a further subcompartmentation is more appropriate (Calvetti and Somersalo, 2010). We consider three different steady states, characterized by the type and rate at which the pertinent neurotransmitter, glutamate or GABA, is effluxed into the synaptic cleft: AS characterized by a rate of glutamate efflux of 0.30 μmol/g per minute, excitatory steady state (ES) where the rate of efflux of glutamate is 0.45 μmol/g per minute, and IS characterized by a rate of GABA efflux of 0.13 μmol/g per minute. Each state is simulated by specifying a Gaussian prior probability density for the pertinent neurotransmitter efflux from neuron to ECS with the prior mean equal to the target value. The blood flow is adjusted to correspond to a physiologically reasonable value. The remaining reaction fluxes and transport rates assess themselves as needed for the system to reach equilibrium.
Since we have no a priori reason to expect any one of the balance equations to be more off equilibrium than any other, we assume a zero mean and standard deviation (error bar) of 0.005 μmol/g per minute for all rates of change of substrates and intermediates in every compartment. The input for the model consists of the means and standard deviations of arteriovenous concentration differences of glucose and lactate, and the mean arterial concentrations and standard deviations of oxygen and carbon dioxide, the latter broadly intended so as to include carbonic acid and bicarbonate. The input values are listed in Table 2. For each of the three steady states, we generate an ensemble of 100,000 vectors using the variant of the Gibbs Markov chain Monte Carlo sampler implemented in Metabolica. Each vector in the ensemble represents a possible near steady-state realization with a corresponding relative posterior probability of occurrence. Below, we review the key findings based on the model.
Table 2. Top: Some average values reaction fluxes and transport rates in awake state, compute from 100,000 samples. Bottom: Input values for the simulations and mean results of a 100,000 steady states.
| Input | Awake | Excited | Inhibited |
|---|---|---|---|
| Blood flow | 0.55 | 0.75 | 0.55 |
| Oxygen arterial concentration | 9.3 | 9.3 | 9.3 |
| Carbon dioxide concentration | 23 | 23 | 23 |
| Glucose AV difference | 0.54 | 0.54 | 0.54 |
| Lactate AV difference | −0.18 | −0.18 | −0.18 |
| Reaction/transport |
Astrocyte |
Glutamatergic |
GABAergic |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Awake | Excited | Inhibited | Awake | Excited | Inhibited | Awake | Excited | Inhibited | |
| Glycolytic pyruvate | 0.22 | 0.28 | 0.29 | 0.28 | 0.37 | 0.31 | 0.22 | 0.27 | 0.30 |
| LDH (Pyr) | −0.11 | 0.17 | 0.00 | −0.16 | 0.25 | −0.09 | −0.14 | −0.19 | −0.03 |
| TCA | 0.12 | 0.12 | 0.30 | 0.41 | 0.60 | 0.29 | 0.14 | 0.13 | 0.21 |
| PC | 0.11 | 0.11 | 0.25 | — | — | — | — | — | — |
| Malic enzyme (c) | 0.12 | 0.12 | 0.35 | — | — | — | — | — | — |
| Malic enzyme (m) | — | — | — | ∼0 | ∼0 | ∼0 | 0.02 | 0.03 | 0.13 |
| PDH | 0.15 | 0.15 | 0.33 | 0.45 | 0.64 | 0.13 | 0.05 | 0.05 | 0.13 |
| OGC | 0.13 | 0.14 | 0.31 | 0.44 | 0.66 | 0.21 | 0.08 | 0.08 | 0.27 |
| AGC1 | 0.07* | 0.07* | 0.07* | 0.39 | 0.59 | 0.28 | 0.19 | 0.19 | 0.46 |
| OxPhos | 0.34 | 0.35 | 0.89 | 1.29 | 1.86 | 0.76 | 0.30 | 0.28 | 0.13 |
| GDA | — | — | — | 0.19 | 0.25 | 0.14 | 0.10 | 0.10 | 0.23 |
| GABA shunt | — | — | — | 0.19 | 0.25 | 0.14 | 0.07 | 0.07 | 0.10 |
| Glutamate efflux (net) | −0.30* | 0.45* | −0.11 | 0.30* | 0.45* | 0.11 | — | — | |
| GABA release (net) | −0.03 | −0.03 | −0.13 | — | — | — | 0.03 | 0.03 | 0.13* |
| Glutamine uptake (net) | −0.36 | −0.52 | −0.36 | 0.25 | 0.41 | 0.18 | 0.11 | 0.11 | 0.18 |
| Aspartate uptake (net) | 0.04 | 0.04 | 0.22 | 0.05 | 0.04 | −0.06 | −0.011 | 0.04 | −0.18 |
AGC, aspartate-glutamate carrier; AV, arteriovenous; GABA, gamma aminobutyric acid; GDA, glutamic decarboxylase; LDH, lactate dehydrogenase; OGC, oxoglutarate carrier; OxPhos, oxidative phosphorylation; PC, pyruvate carboxylase; PDH, pyruvate dehydrogenase; TCA, tricarboxylic acid.
All flux values are in μmol/g per minute. The TCA cycle rate is obtained from the flux of the FUM → MAL reaction. *indicates values that are entered as prior input values.
Anaplerotic Reactions
Anaplerotic reactions, ME in neurons and PC in astrocyte, have a central role, as they replenish the TCA cycle pool and therefore enable glutamate and GABA synthesis. In all experiments, ME activity in glutamatergic neuron is insignificant. In GABAergic neuron in excitatory activity (AS and ES), ME flux settles at 0.02 to 0.03 μmol/g per minute in the direction of malate formation, while in inhibitory activity (IS), the level is 0.12 μmol/g per minute. This points to a central role of ME in GABA cycling. The model supports a sustained pyruvate recycling activity in astrocytes, with values for the cytosolic ME (toward puryvate) and PC mean fluxes in the range of 0.12 and 0.11 μmol/g per minute, respectively, in both excitatory states, and 0.31 and 0.21 μmol/g per minute, respectively, during IS. The PC values concur with nuclear magnetic resonance spectroscopy data of Öz et al (2004), although the present study confirms an increase of PC in response to inhibitory, but not to excitatory activity.
Malate-Aspartate Shuttle and Neurotransmitter Cycling
Malate-aspartate shuttle is tightly related to neurotransmitter synthesis and recycling. A recent article (Pardo et al, 2011) showed that the glutamate/aspartate exchanger AGC1 (aralar) expresses itself predominantly in neurons, while the complementary malate/αKG exchanger oxoglutarate carrier (OGC) is active both in neurons and in astrocytes. The imbalance between the two exchangers in astrocytes raises a question of how astrocytes deal with the resulting aspartate deficiency, or equivalently, surplus αKG production in the cytosol. The present analysis suggests that the two exchangers may be imbalanced in neurons, too. Pardo et al (2011) suggest that astrocytes replenish the aspartate pool by uptaking aspartate of neuronal origin from the ECS. A related commentary (Hertz, 2011) questions the proposed mechanism raising three main points. First, aspartate is an excitatory neurotransmitter and therefore unsuitable as intercellular amino group donor; second, traffic of aspartate would impoverish the glutamate pool in neurons; third, stoichiometric problems would ensue in neurons.
Our statistical approach is particularly suited for a quantitative analysis of the suggestion of Pardo et al (2011) as well as the points raised by Hertz (2011). Moreover, since Metabolica provides a sample of all possible steady states, it is possible to restrict the analysis to a subsample with no aspartate uptake by astrocytes to test if a steady state without aspartate replenishment is possible without assuming a delayed enrichment of the aspartate pool as suggested by Hertz (2011).
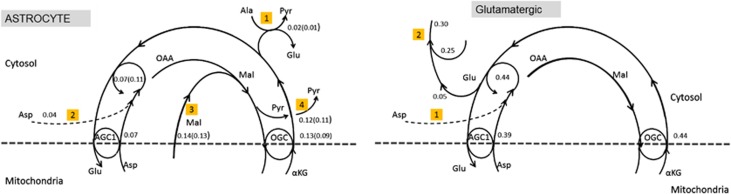
The analysis here is restricted to awake state. We consider first the cytosol of astrocytes with AGC1 activity suppressed to a target value 0.07 μmol/g per minute, corresponding to 10% of the total AGC1 activity in the cell complex, in line with the 7% activity reported in the literature (Pardo et al, 2011; Hertz, 2008). As expected, the OGC activity settles to a higher steady-state level, the mean value being 0.13 μmol/g per minute over the whole sample with no restrictions on aspartate traffic, and 0.09 μmol/g per minute over the subsample with aspartate shuttle suppressed. The imbalance leads to an excess of αKG compared with aspartate for maintaining a steady state of the transaminase αKG+Asp → OAA+Glu. When the aspartate transfer is enabled, the alanine-pyruvate shuttle settles around 0.02 μmol/g per minute. With suppressed aspartate traffic, this is exactly the difference needed to balance the MAS. When the aspartate shuttle is enabled, it settles around 0.04 μmol/g per minute, thus balancing the transaminase. The excess oxaloacetate hydrogenates to malate, which is either transported into mitochondria by OGC, or becomes pyruvate via the cytosolic ME. The model predicts a mean level of 0.11 μmol/g per minute of ME in the suppressed aspartate transport scenario, and 0.12 μmol/g per minute when the transport is present. The pertinent metabolic pathway with the mean flux values can be found in Figure 1.
Figure 1.
Left: A schematics of the cytosol portion of the malate-aspartate shuttle (MAS) in astrocyte with the values of the mean reaction fluxes and transport rates in μmol/g per minute during awake steady state (AS). The flux values in parentheses refer to the case when there is no aspartate uptake from extracellular space (ECS). The imbalance between aspartate-glutamate carrier (AGC1)/aralar and oxoglutarate carrier (OGC) is compensated by the alanine-pyruvate shuttle (pathway 1), the optional aspartate uptake (pathway 2), and malate transport from mitochondria (pathway 3) and malic enzyme (pathway 4). Right: A schematics of the cytosol portion of the MAS in glutamatergic neurons with the values of the mean reaction fluxes and transport rates in μmol/g per minute during awake steady state (AS). The uptake of aspartate (pathway 1) replenishes the aspartate pool, balancing the aspartate-glutamate transaminase. The excess glutamate contributes to the neurotransmitter cycle (pathway 2), replenishing the pool originating from the glutamine-glutamate metabolism. αKG, α-ketoglutarate; OAA, oxaloacetate.
It is of interest to trace the origin of the aspartate in the ECS. Our model assigns all aspartate production to GABAergic neurons, with mean flux 0.11 to 0.12 μmol/g per minute, of which a part goes to blood with the rate 0.02 μmol/g per minute. The uptake of aspartate by glutamatergic neurons varies from 0.05 to 0.1 μmol/g per minute, depending on whether the aspartate uptake by astrocytes is enabled or not. In the GABAergic neuron, the MAS exchanger rates are 0.08 and 0.19 μmol/g per minute for OGC and AGC1, respectively. The cytosolic equilibrium is attained because glutamine is uptaken from the ECS and further metabolized to glutamate at the rate of 0.11 μmol/g per minute, enough to compensate the aspartate efflux. Because the glutamate pool in the GABAergic cytosol feeds both the aspartate efflux and the GABA synthesis, it is incorrect to conclude that the glutamine does not participate in the GABA synthesis as a precursor, although part of the GABA originates from the ME of the GABAergic neuron, as shown in Occhipinti et al (2010). In fact, numerical simulations with suppressed ME in astrocyte lead to ill-balanced samples (data not shown here), indicating that ME is essential for balanced inhibition.
In contrast, the ME in glutamatergic neuron is consistently not active, confirming the commonly accepted view that replenishment of the glutamate/glutamine pool in glutamatergic neuron relies on astrocyte activity. In glutamatergic neurons, too, the AGC1 activity is lower than the OGC activity, 0.39 μmol/g per minute compared with 0.44 μmol/g per minute. The aspartate uptake at the rate 0.05 μmol/g per minute equilibrates the transaminase producing glutamate, thus accomplishing the metabolism from glutamine to glutamate, going at the rate of 0.25 μmol/g per minute, so that the net glutamate production reaches the glutamate efflux rate of 0.3 μmol/g per minute. This is summarized schematically in Figure 1.
While the target mean efflux rates of the neutrotransmitter characterizing the steady state is specified as input, the efflux of the complementary neurotransmitter is not a priori given, and it is allowed to settle as needed to reach stoichiometric equilibrium. Our results support a small release of GABA at an average rate of 0.03 μmol/g per minute both during the AS and ES, while in the IS there is an efflux of glutamate by the glutamatergic neuron at an average rate of 0.07 μmol/g per minute. Observe that the spontaneous GABA release corresponds to the level of ME activity in GABAergic neurons. It is tempting to conclude that the GABA synthesis is completely due to ME activity. However, this is an oversimplification that would contradict experimental evidence for external glutamine participating in the GABA synthesis (Yang et al, 2007; Patel et al, 2005).
During excitatory activation, most, but not all glutamate originates from the astrocyte generated glutamine. In the awake state, 0.05 μmol/g per minute of the total of 0.3 μmol/g per minute glutamate efflux is transaminased from αKG in neuron's cytosol. In the excited state, 0.04 μmol/g per minute of the total 0.45 μmol/g per minute arises from αKG. This finding is not in conflict with the commonly accepted opinion that glutamatergic neuron does not synthesize glutamate de novo. In fact, the only possible anaplerotic reaction, ME, is practically inactive in glutamatergic neuron, and the extra glutamate can be traced back to the uptake of aspartate that is recycled through the MAS.
Glucose Partitioning and Lactate Traffic
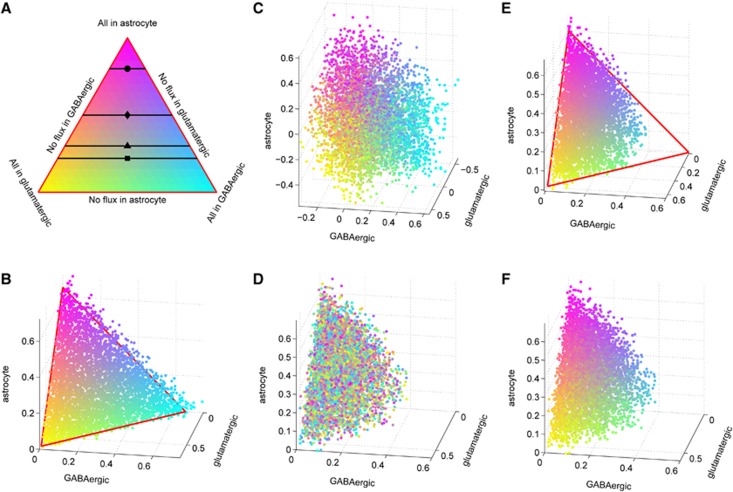
One of the key results of our analysis is that specifying the stoichiometry together with the type and level of neuronal activity are not enough to determine glucose partitioning between the three cell types. We produce a three-dimensional scatter plot of the 100,000 glucose uptake vectors, interpreting the three uptake rates (JGlc,ECS → glu)j, (JGlc,ECS → GABA)j, and (JGlc,ECS → ast)j in each sample configuration j, 1⩽j⩽100,000, as coordinates of a point in a three space. Figure 2B shows the three-dimensional scatter plot of the glucose uptake rates that fills a triangle in the positive coordinate octant, indicating that any linear combination with constant sum is a stoichiometrically possible steady state. The points are color coded according to their position in the triangle, with the interpretation for the color code given in Figure 2A. The color coding can be used to investigate the correlation between glucose partitioning and various other reaction fluxes and transport rates by associating with each flux sample vector the color determined by its glucose uptake pattern. The corresponding three-dimensional plot of the lactate uptake/release patterns, (JLac, ECS → glu)j, (JLac,ECS → GABA)j, and (JLac,ECS → ast)j, with the coloring inherited from the glucose uptake is shown in Figure 2C. The organization of the color scheme confirms that the glucose partitioning determines the lactate trafficking pattern, up to small stochastic fluctuations. Glucose uptake patterns, however, do not determine mitochondrial reactions that are dependent on the rate at which pyruvate crosses the membrane, regardless of whether it was generated glycolytically in the same cell or hydrogenased from exogenous lactate by lactate dehydrogenase. The three-dimensional scatter plot of the rates of oxidative phosphorhylation displayed in Figure 2D does not show any chromatic coherence, indicating a lack of direct causality from glucose partitioning. However, the oxidative activity is correlated with the difference between twice the glucose uptake and lactate efflux, since this difference is proportional to the cytosolic NAD+ production, which is coupled with the redox balance in mitochondria (Figures 2E and 2F).
Figure 2.
(A) A color-coded three-dimensional scatter plot of twice the rates of glucose uptake from extracellular space (ECS) in μmol/g per minute in the three cells from the computed sample, colored as follows: vectors where glucose is taken up by GABAergic neurons are cyan, by astrocytes are magenta, and by glutamatergic neurons are yellow, and the color coding of each point in the triangle defined by these three extreme cases is determined as a convex combination of these basic colors. The horizontal lines indicate different literature values of glucose partitioning: Gjedde (2007) (•), Jolivet et al (2010) (⧫), Mangia et al (2011) (▴), Simpson et al (2007), and DiNuzzo et al (2010) (▪). (B) A color-coded scatter plot of the three vectors indicating the glucose uptake in μmol/g per minute from ECS of the three cell types computed from a sample corresponding to the awake steady state. (C) Three-dimensional (3D) scatter plot of lactate efflux rate in μmol/g per minute from each cell type colored according to the glucose uptake. (D) 3D scatter plot of oxidative phosphorylation fluxes in μmol/g per minute, with color coding based on glucose partitioning. The unorganized color distribution of the scatter plot shows that the rate of oxidative activity in each cell type does not depend directly on glucose partitioning. (E) 3D scatter plot of the difference between glycolytic pyruvate production and lactate dehydrogenase in μmol/g per minute. The assignment of the color follows the rule in panel A. (F) 3D scatter plot of oxidative phosphorylation fluxes in μmol/g per minute, with color coding based on (E). The organization shows that oxidative metabolism is correlated with difference between glycolytic pyruvate production and lactate dehydrogenase. GABA, gamma aminobutyric acid.
Glucose Oxidation Versus Neurotransmitter Cycling
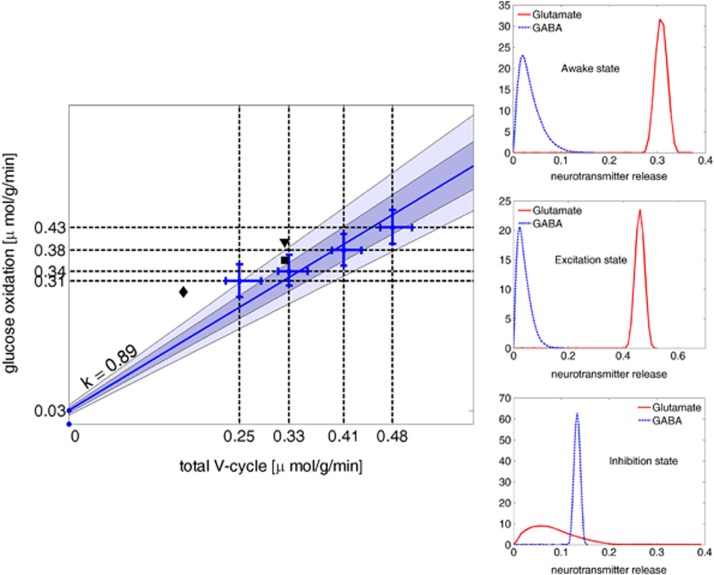
The results support a strong correlation between oxygen consumption and energetic cost of neurotransmitter cycling, although, in agreement with Occhipinti et al (2010), the GABA recycling during IS triggers a higher TCA cycle activity in astrocytes than may be expected. The relationship between the aggregate glucose oxidation flux in the three cell types and aggregate neurotransmitter cycling rates for different activation levels is illustrated by the plot in Figure 3. Following Hyder et al (2006), the glucose oxidation rate is computed as half the sum of the TCA cycle rate at the level of FUM → MAL, of glutamatergic neurons, GABAergic neurons, and astrocytes, and the neurotransmitter cycling rate is the aggregate of glutamate and GABA release. Figure 3 indicates the best linear fit through the median values of glucose oxidation over 100,000 steady-state configurations for each of several glutamatergic activity levels, and 96th and 68th percentile envelopes (lighter and darker shading, respectively). Literature values for human brain (Gruetter et al, 2001; Lebon et al, 2002; Shen et al, 1999), also marked in the figure, are slighly higher than our model would predict. The results are also qualitatively in line with the rodent studies in Sibson et al (1998) and Hyder et al (2006). Figure 3 shows also the histograms of the rates of neurotransmitters release. The histograms corresponding to the spontaneous release indicate that a steady state with no release of the complementary neurotransmitter is stoichiometrically highly improbable.
Figure 3.
Left: The plot shows the correlation between the rate of glucose oxidation, computed as one half of the sum of the tricarboxylic acid (TCA) cycle rates in the three cell types, and the rate of neurotransmitter cycling, intended as the sum of the rates of efflux in extracellular space (ECS) of glutamate and GABA from glutamatergic and GABAergic neurons, respectively. The round dots with relative horizontal and vertical error bars correspond to the medians and 68th percentiles around them of the samples of 100,000 steady states including Gaussian priors for the efflux of glutamate with mean values of 0.22, 0.30, 0.38, and 0.45 μmol/g per minute, and standard deviation 0.001 μmol/g per minute. Most of the horizontal error bar is due to the variability in GABA efflux, whereas the efflux of glutamate is tightly clustered around its mean value. The regression line that best fits the median points has equation y=0.89x+0.03. The lighter shade around it marks the 96th percentile, and the darker shade marks the 68th percentile. The values reported by Shen et al (1999) (▪), Gruetter et al (2001) (⧫), and by Lebon et al (2002) (▾), reported also in the graph, are in good agreement with the predictions of our model. Right: Histograms of the rate of release of glutamate (continuous curve) and GABA (dashed curve) in μmol/g per minute, in the three different steady states. The Gaussian shape of the distribution of the efflux rate of the neurotransmitter characterizing the steady state is a consequence of our entering the target values in the form of a Gaussian prior. The distribution of the rate of spontaneous release of GABA in AS and ES indicates that it is possible to have steady states with no GABA release at all, although some release of GABA appears more likely. In inhibitory steady state, the distribution of rates of glutamate release, widely distributed between 0 and 0.02, indicates that no release of glutamate is very unlikely. GABA, gamma aminobutyric acid; ES, excitatory steady state; AS, awake steady state.
Oxygen Partitioning
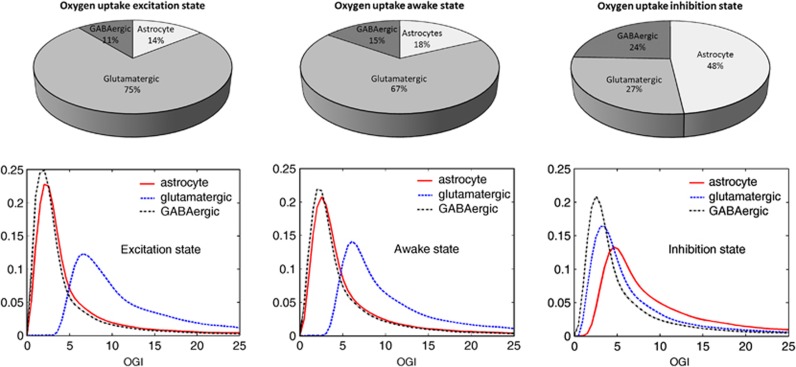
The sample mean of oxygen partitioning among the three cell types in the three different steady states is summarized by the pie charts in Figure 4, top row. In AS and ES, >80% of the oxygen is taken up by neurons, the glutamatergic neurons accounting for 75% (ES) and 67% (AS). This is in agreement with the understanding that neurons are the major sites of oxidative rephosphorylation of ATP (Gjedde, 2007). Oxygen partitioning during IS follows a different pattern, with almost one half of the oxygen uptaken by astrocytes, which are the sites of significant oxidative metabolism coupled to an elevated TCA cycle activity sustained by the anaplerotic contribution of succinic semialdehyde synthetized from GABA.
Figure 4.
Top row: average oxygen partitioning among the three cell types in the three different steady states, each computed from a sample of 100,000 configurations. In the two steady states, ES and AS, characterized by assigning a target rate of glutamate efflux, glutamatergic neurons uptake the majority of oxygen, 75% of the total in ES and 67% in AS, with the remaining almost equally split between astrocytes and GABAergic neurons. This is in agreement with the understanding that neurons are the major sites of oxidative rephosphorylation of ATP (Gjedde, 2007). In inhibitory steady state, the largest uptake of oxygen, 45%, is by astrocyte, in agreement with Hertz et al (2007) and Öz et al (2004), who reported a sustained astrocytic oxidative activity. Bottom row: histograms of oxygen glucose index (OGI) for each cell type in the three steady states. The OGI values for each cell type, which are the ratios of oxygen to glucose uptake, are computed from a 100,000 sample for each steady-state configuration. In ES, the OGI distribution in neuron can be up to 20 times higher than in astrocyte, in accordance with Gjedde (2007). GABA, gamma aminobutyric acid; ES, excitatory steady state; AS, awake steady state.
To complete the picture of the relative oxygen consumption and the fueling of the oxidative metabolism in different cell types, we calculate for each cell type the oxygen glucose index (OGI), intended as the ratio of oxygen uptake over glucose uptake. The OGI values less than six mean that the cell uptakes glucose more than it uses in oxidative metabolism, pointing toward nonoxidative metabolism, while values more than six indicate a net uptake of fuel other than glucose, mostly lactate, for oxidative metabolism. The OGI histograms presented in Figure 4B show that at ES and AS the OGI in glutamatergic neuron is strongly biased toward values in excess of six, while the OGI distributions for astrocyte and GABAergic neuron are concentrated at values much smaller than six. The left panel shows that OGI in glutamatergic neuron can be up to 20 times than in astrocyte, in accordance with Gjedde (2007).
Inhibitory steady state (right panel) shows a significant increase in OGI values for astrocyte, while overall OGI values for GABAergic neuron are smallest.
Discussion
The quantitative analysis of the neurotransmitter recycling pathways indicate that, as pointed out by McKenna (2007), the picture of GABA and glutamate synthesis is more complicated that usually understood, and underlines the qualitative difference between glutamatergic and GABAergic neurons. In particular, the imbalanced MAS exchangers are hard to analyze without a computational tool that indicates how the mass balancing needs to be done without jeopardizing the redox balancing.
The energetic cost of excitation is typically measured in terms of additional ATP required, which may go toward (1) the conversion of glutamate into glutamine by glutamine synthetase in astrocytes; (2) packing and releasing glutamate in presynaptic neurons; (3) depolarization to bring the membrane potential up to firing level; and (4) Na+ extrusion after the propagation of action potential in postsynaptic neurons (Attwell and Laughlin, 2001). Less obvious are the energetic costs related to the postactivation extracellular K+ clearance (Hertz et al, 2007), astrocytic glutamate signaling (Volterra and Meldolesi, 2005), and to maintain mass balance when GABA is released. Gamma aminobutyric acid is now recognized as potentially having a role no less important than glutamate in different afferent and efferent brain functions (Gjedde et al, 2002). The difficulty, common to all mathematical models, to correctly assess the cost of inhibition and excitation is amplified by the fine compartmentation that we have introduced, the role of astrocytes, which changes depending on the specifications of the steady state, and the multiple routing options for glutamate, GABA and their precursor, glutamine. The present study corroborates the results in Occhipinti et al (2010), pointing toward an elevated energy metabolism of inhibition, due to increased TCA activity in astrocyte in connection with GABA cycling.
In contrast to some of the existing computational models, the present model does not include the mass balance equations for the ions Na+, K+, and Ca+2. By following the cotransport stoichiometry and the induced energetic cost (Attwell and Laughlin, 2001), the ion balance could be coupled to glutamate recycling. The cotransport stoichiometry of GABA recycling is less studied in the literature and, as pointed out in Hertz et al (2007), the Na+ stoichiometry accounts for only a fraction of energetic cost in astrocytes. For these reasons, in the present model the activation state is not controlled in terms of Na+ flux as, e.g., in Aubert and Costalat (2005) but rather by specifying a target value for the relevant neurotransmitter release, augmented with a nonspecific ATP hydrolysis flux that the methodology automatically adjusts to match the stoichiometric balance.
Glucose partitioning among different cell types is tightly coupled with the question of the role of lactate as a substrate of oxidative metabolism. The present analysis confirms that stoichiometry alone does not determine the glucose partitioning, and furthermore, the direction of lactate trafficking between neurons and astrocytes under steady state is completely determined by the glucose partitioning. This indeterminacy leaves open the possibility for several scenarios, including a variety of simultaneous different trafficking patterns in the tissue. Due to physiological differences between different parts of the cells, including variations in mitochondrial density or transporter density in the membranes, and variations in substrate availability due to proximity of capillaries, it is likely that assuming one single oxidative pattern for all cells may be too simplistic, and a sampling-based picture with an ensemble of possible equilibria is closer to reality. The present analysis does not exclude the presence of physiological constraints not included in the stoichiometry that may be favorable to one or another pattern, and adding such constraints may restrict the sample. The different computational models that support one or another direction of lactate trafficking (see the Discussion in Jolivet et al, 2010, followed by Mangia et al, 2011) differ significantly in the assumed capacity of glucose uptake of different cell types. Therefore, while realizing the difference between dynamic and steady-state models, the present analysis gives a basis for understanding seemingly conflicting conclusions concerning the role of lactate.
Oxygen uptake is determined by the type and level of neuronal activity, but according to the present analysis, not by the glucose partitioning, since one can add the same constant flux to both glucose uptake and lactate efflux without affecting the redox balance. The increase in blood flow at high excitation is paired with an overwhelming dominance (75%) in oxygen uptake by glutamatergic neurons, whose markedly oxidative metabolism supplies the needed ATP production. The much lower oxygen uptake by astrocytes and GABAergic neurons, whose combined rates add up to one fourth to one third of the uptake rate by glutamatergic neuron, is in agreement with the lower energy demands. More puzzling is the partition of oxygen uptake at high inhibition, with nearly half of it (48%) going into astrocytes, where the elevated rate of oxidative metabolism is not a response to any stoichiometrically specified energetic cost. A closer examination of the metabolic activity in astrocyte in inhibitory state indicates that, due to its role in GABA cycling, some pathways, oxidative phosphorylation among them, may be activated to regenerate mitochondrial NAD+. The oxidative activity of astrocytes predicted by our model at IS is in line with published experimental results (Lebon et al, 2002; Hertz et al, 2007). The amount of increase in oxidative metabolism in astrocytes in IS remains to be validated experimentally: for the time being, this is underlining, once more, the metabolic complexity of inhibition. The oxidative activity of astrocytes and the consistent and significant presence of ME and PC activities are in line with the experimental findings in Öz et al (2004). The elevated rate of oxidative phosphorylation in astrocytes and in GABAergic neurons results in an excess production of ATP, compared with what is needed to meet the energetic needs of neurotransmitter cycling. Consequently, a relatively high rate of unspecified ATP hydrolysis flux to attain steady state ensues. Assuming that brain is energetically efficient, an interesting question which arises is if there are processes not described by the present model, comporting added energetic costs which could be met by the excess ATP production such as potassium clearing and astrocytic calcium signaling, or whether there is an uncoupling mechanism and a mitochondrial H+ leak, whereby changes in blood flow rate would be motivated by cooling needs.
Acknowledgments
The authors thank Dr Gerald Dienel and Dr Albert Gjedde for valuable suggestions and advise.
The authors declare no conflict of interest.
Footnotes
The work of ES was partly supported by the National Science Foundation grant DMS 1016183.
References
- Attwell D, Laughlin SB. An energy budget for signaling in the grey matter of the brain. J Cereb Blood Flow Metab. 2001;21:1133–1145. doi: 10.1097/00004647-200110000-00001. [DOI] [PubMed] [Google Scholar]
- Aubert A, Costalat R. Interaction between astrocytes and neurons studied using a mathematical model of compartmentalized energy metabolism. J Cereb Blood Flow Metab. 2005;25:1476–1490. doi: 10.1038/sj.jcbfm.9600144. [DOI] [PubMed] [Google Scholar]
- Bak LK, Schousboe A, Waagepetersen HS. The glutamate/GABA-glutamine cycle: aspects of transport, neurotransmitter homeostasis and ammonia transfer. J Neurochem. 2006;98:641–653. doi: 10.1111/j.1471-4159.2006.03913.x. [DOI] [PubMed] [Google Scholar]
- Bak LK, Waagepetersen HS, Melo TM, Schousboe A, Sonnewald U. Complex glutamate labeling from [U-13C]glucose or [U-13C]lactate in co-cultures of cerebellar neurons and astrocytes. Neurochem Res. 2007;32:671–680. doi: 10.1007/s11064-006-9161-4. [DOI] [PubMed] [Google Scholar]
- Berkich DA, Ola MS, Cole J, Sweatt AJ, Hutson SM, LaNoue KF. Mitochondrial transport proteins of the brain. J Neurosci Res. 2007;85:3367–3377. doi: 10.1002/jnr.21500. [DOI] [PubMed] [Google Scholar]
- Calvetti D, Somersalo E. Large scale statistical parameter estimation in complex systems with an application to metabolic models. Multiscale Model Simul. 2006;5:1333–1366. [Google Scholar]
- Calvetti D, Somersalo E. Dynamic activation model for a glutamatergic neurovascular unit. J Theor Biol. 2010;274:12–29. doi: 10.1016/j.jtbi.2010.12.007. [DOI] [PubMed] [Google Scholar]
- Chih C-P, Roberts EL., Jr Energy substrates for neurons during neuronal activation: a critical review of the astrocyte-neuron lactate shuttle hypothesis. J Cereb Blood Flow Metab. 2003;23:1263–1281. doi: 10.1097/01.WCB.0000081369.51727.6F. [DOI] [PubMed] [Google Scholar]
- Cloutier M, Bolger FB, Lowry JP, Wellstead P. An integrative dynamic model of brain energy metabolism using in vivo neurochemical measurements. J Comput Neurosci. 2009;27:391–414. doi: 10.1007/s10827-009-0152-8. [DOI] [PubMed] [Google Scholar]
- DiNuzzo M, Mangia S, Maraviglia B, Giove F. Changes in glucose uptake rather than lactate shuttle take center stage in subserving neuroenergetics: evidence from mathematical modeling. J Cereb Blood Flow Metab. 2010;30:586–602. doi: 10.1038/jcbfm.2009.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gjedde A, Marrett S, Vafaee M. Oxidative and nonoxidative metabolism of excited neurons and astrocytes. J Cereb Blood Flow Metab. 2002;22:1–14. doi: 10.1097/00004647-200201000-00001. [DOI] [PubMed] [Google Scholar]
- Gjedde A.2007Coupling of brain function to metabolism: evaluation of energy requirements Handbook of Neurochemistry and Molecular Neurobiology3rd ed. (Lajtha A, ed),Springer Verlag; Berlin [Google Scholar]
- Gruetter R, Seaquist ER, Ugurbil K. A mathematical model of compartmentalized neurotransmitter metabolism in the human brain. Am J Physiol Endocrinol Metab. 2001;281:E100–E112. doi: 10.1152/ajpendo.2001.281.1.E100. [DOI] [PubMed] [Google Scholar]
- Hassel B. Carboxylation and anaplerosis in neurons and glia. Mol Neurobiol. 2001;22:21–40. doi: 10.1385/MN:22:1-3:021. [DOI] [PubMed] [Google Scholar]
- Heino J, Calvetti D, Somersalo E. Metabolica: a statistical research tool for analyzing metabolic networks. Comput Methods Programs Biomed. 2010;97:151–167. doi: 10.1016/j.cmpb.2009.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heino J, Tunyan K, Calvetti D, Somersalo E. Bayesian flux balance analysis applied to a skeletal muscle metabolic model. J Theor Biol. 2007;248:91–110. doi: 10.1016/j.jtbi.2007.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertz L. Brain glutamine synthesis requires neuronal aspartate: a commentary. J Cereb Blood Flow Metab. 2011;31:384–387. doi: 10.1038/jcbfm.2010.199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertz L. Bioenergetics of cerebral ischemia: a cellular perspective. Neuropharmacology. 2008;55:289–309. doi: 10.1016/j.neuropharm.2008.05.023. [DOI] [PubMed] [Google Scholar]
- Hertz L, Peng L, Dienel GA. Energy metabolism in astrocytes: high rate of oxidative metabolism and spatiotemporal dependence on glycolysis/glycogenolysis. J Cereb Blood Flow Metab. 2007;27:219–249. doi: 10.1038/sj.jcbfm.9600343. [DOI] [PubMed] [Google Scholar]
- Hyder F, Patel AB, Gjedde A, Rothman DL, Behar KL, Shulman RG. Neuronal-glial glucose oxidation and glutamatergic-GABAergic function. J Cereb Blood Flow Metab. 2006;26:865–877. doi: 10.1038/sj.jcbfm.9600263. [DOI] [PubMed] [Google Scholar]
- Jolivet R, Allaman I, Pellerin L, Magistretti PJ, Weber B. Comment on recent modeling studies of astrocyte-neuron metabolic interactions. J Cereb Blood Flow Metab. 2010;30:1982–1986. doi: 10.1038/jcbfm.2010.132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurz GM, Wiesinger H, Hamprecht B. Purification of cytosolic malic enzyme from bovine brain, generation of monoclonal antibodies, and immunocytochemical localization of the enzyme in glial cells of neural primary cultures. J Neurochem. 1993;60:1467–1474. doi: 10.1111/j.1471-4159.1993.tb03309.x. [DOI] [PubMed] [Google Scholar]
- Lebon V, Petersen KF, Cline GW, Shen J, Mason GF, Dufour S, Behar KL, Shulman GI, Rothman DL. Astroglial contribution to brain energy metabolism in humans revealed by 13C nuclear magnetic resonance spectroscopy: elucidation of the dominant pathway for neurotransmitter glutamate repletion and measurement of astrocytic oxidative metabolism. J Neurosci. 2002;22:1523–1531. doi: 10.1523/JNEUROSCI.22-05-01523.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leke R, Bak LK, Schousboe A, Waagepetersen HS. Demonstration of neuron-glia transfer of precursors for GABA biosynthesis in a co-culture system of dissociated mouse cerebral cortex. Neurochem Res. 2008;33:2629–2635. doi: 10.1007/s11064-008-9814-6. [DOI] [PubMed] [Google Scholar]
- Mangia S, DiNuzzo M, Giove F, Carruthers A, Simpson IA, Vannucci SJ. Response to ‘comment on recent modeling studies of astrocyte-neuron metabolic interactions': much ado about nothing. J Cereb Blood Flow Metab. 2011;31:1346–1353. doi: 10.1038/jcbfm.2011.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKenna MC. The glutamate-glutamine cycle is not stoichiometric: fates of glutamate in brain. J Neurosci Res. 2007;85:3347–3358. doi: 10.1002/jnr.21444. [DOI] [PubMed] [Google Scholar]
- Occhipinti R, Somersalo E, Calvetti D. Astrocytes as the glucose shunt for glutamatergic neurons at high activity: an in silico study. J Neurophysiol. 2009;101:2528–2538. doi: 10.1152/jn.90377.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Occhipinti R, Somersalo E, Calvetti D. Energetics of inhibition: insights with a computational model of the human GABAergic neuron-astrocyte cellular complex. Cereb Blood Flow Metab. 2010;30:1834–1846. doi: 10.1038/jcbfm.2010.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Öz G, Berkich D, Henry PG, Xu Y, LaNoue K, Hutson S, Gruetter R. Neuroglial metabolism in the awake rat brain:CO2 fixation increases with brain activity. J Neurosci. 2004;50:11273–11279. doi: 10.1523/JNEUROSCI.3564-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardo B, Rodrigues TB, Contreras L, Garzón M, llorente-Folch I, Kobayashi K, Saheki T, Cerdan S, Satrústegui J. Brain glutamine synthesis requires neuronal-born aspartate as amino donor for glial glutamate formation. J Cereb Blood Flow Metab. 2011;31:90–101. doi: 10.1038/jcbfm.2010.146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel AB, de Graaf RA, Mason GF, Rothman GDL, Shulman RG, Behar KL. The contribution of GABA to glutamate/glutamine cycling and energy metabolism in the rat cortex in vivo. Proc Natl Acad Sci USA. 2005;102:5588–5593. doi: 10.1073/pnas.0501703102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pellerin L, Magistretti P. Glutamate uptake into astrocytes stimulates aerobic glycolysis: a mechanism coupling neuronal activity to glucose utilization. Proc Natl Acad Sci USA. 1994;91:10625–10629. doi: 10.1073/pnas.91.22.10625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pellerin L, Magistretti P. Food for thought: challenging the dogmas. J Cereb Blood Flow Metab. 2003;23:1282–1286. doi: 10.1097/01.WCB.0000096064.12129.3D. [DOI] [PubMed] [Google Scholar]
- Shen J, Peterson KF, Behar KL, Brown P, Nixon TW, Mason GF, Petroff OA, Shulman GI, Shulman RG, Rothman DL. Determination of the rate of the glutamate/glutamine cycle in human brain by in vivo13C NMR. Proc Natl Acad Sci USA. 1999;96:8235–8240. doi: 10.1073/pnas.96.14.8235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sibson N, Dhankhar A, Mason G, Rothman D, Behar K, Shulman R. Stoichiometric coupling of brain glucose metabolism and glutamatergic neuronal activity. Proc Natl Acad Sci USA. 1998;95:316–321. doi: 10.1073/pnas.95.1.316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson IA, Carruthers A, Vannucci SJ. Supply and demand in cerebral energy metabolism: the role of nutrient transporters. J Cereb Blood Flow Metab. 2007;27:1766–1791. doi: 10.1038/sj.jcbfm.9600521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volterra A, Meldolesi J. Astrocytes, from brain glue to communication elements: the revolution continues. Nat Rev Neurosci. 2005;6:626–640. doi: 10.1038/nrn1722. [DOI] [PubMed] [Google Scholar]
- Waagepetersen HS, Bakken IJ, Larsson OM, Sonnewald U, Schousboe A. Metabolism of lactate in cultured GABAergic neurons studied by 13C nuclear magnetic resonance spectroscopy. J Cereb Blood Flow Metab. 1998;18:109–117. doi: 10.1097/00004647-199801000-00011. [DOI] [PubMed] [Google Scholar]
- Waagepetersen HS, Sonnewald U, Schousboe A.2007Glutamine, glutamate and GABA: metabolic aspects Handbook of Neurochemistry and Molecular Neurobiology3rd ed. (Lajtha A, ed),Springer Verlag; Berlin [Google Scholar]
- Yang J, Li SS, Bacher J, Shen J. Quantification of cortical GABA-glutamine cycling rate using in vivo magnetic resonance signal of [2-13C]GABA derived from glia-specific substrate [2-13C]acetate. Neurochem Int. 2007;50:371–378. doi: 10.1016/j.neuint.2006.09.011. [DOI] [PubMed] [Google Scholar]
- Yu AC, Drejer J, Hertz L, Schousboe A. Pyruvate carboxylase activity in primary cultures of astrocytes and neurons. J Neurochem. 1983;41:1484–1487. doi: 10.1111/j.1471-4159.1983.tb00849.x. [DOI] [PubMed] [Google Scholar]