Abstract
Influenza viruses transcribe and replicate their negative-sense RNA genome inside the nucleus of host cells via three viral RNA species. In the course of an infection, these RNAs show distinct dynamics, suggesting that differential regulation takes place. To investigate this regulation in a systematic way, we developed a mathematical model of influenza virus infection at the level of a single mammalian cell. It accounts for key steps of the viral life cycle, from virus entry to progeny virion release, while focusing in particular on the molecular mechanisms that control viral transcription and replication. We therefore explicitly consider the nuclear export of viral genome copies (vRNPs) and a recent hypothesis proposing that replicative intermediates (cRNA) are stabilized by the viral polymerase complex and the nucleoprotein (NP). Together, both mechanisms allow the model to capture a variety of published data sets at an unprecedented level of detail. Our findings provide theoretical support for an early regulation of replication by cRNA stabilization. However, they also suggest that the matrix protein 1 (M1) controls viral RNA levels in the late phase of infection as part of its role during the nuclear export of viral genome copies. Moreover, simulations show an accumulation of viral proteins and RNA toward the end of infection, indicating that transport processes or budding limits virion release. Thus, our mathematical model provides an ideal platform for a systematic and quantitative evaluation of influenza virus replication and its complex regulation.
INTRODUCTION
Influenza A viruses are enveloped, single-stranded RNA viruses with a segmented genome comprising eight viral RNAs (vRNAs) of negative polarity (33). Generally, these vRNAs form viral ribonucleoproteins (vRNPs) by associating with the viral RNA-dependent RNA polymerase complex (RdRp), consisting of three subunits (PB1, PB2, and PA), and with multiple monomers of the viral nucleoprotein (NP). To replicate, an infectious virus particle or virion, which contains a complete set of eight vRNPs (43), enters a host cell and hijacks its biosynthetic machinery to accomplish viral protein and RNA synthesis and to assemble progeny virions, a process referred to as the viral life cycle.
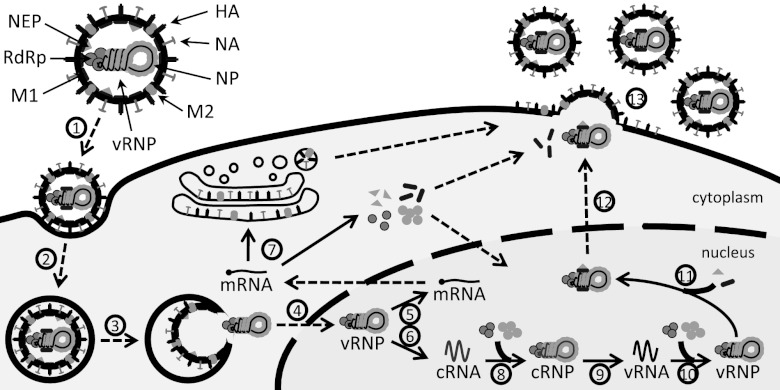
The life cycle of influenza viruses (Fig. 1) begins when virions bind to sialic acid residues on the cell surface, allowing them to enter the host cell via receptor-mediated endocytosis (37). Once inside the cell, the virus is trafficked through the endosomal network until acidification in late endosomes triggers the fusion of the viral envelope with the endosomal membrane. At the same time, vRNPs undergo uncoating, i.e., dissociate from matrix protein 1 (M1), which enables their release into the cytoplasm and import into the nucleus (9, 36). Unlike most other RNA viruses, the influenza virus replicates inside the nucleus of host cells. There, each vRNP acts as an independent functional unit that directs the synthesis of two positive-sense RNAs by using its vRNA as a template. First, viral messenger RNAs (mRNAs) are transcribed through a mechanism primed by capped RNA fragments that are cleaved from host pre-mRNAs. Since viral transcription terminates upstream of the vRNA 5′ end, the resulting mRNAs are incomplete copies of the genome and thus cannot serve as the templates for replication. Hence, a second positive-strand, full-length RNA is synthesized, the cRNA. In contrast to mRNA transcription, the replication of cRNAs is achieved via de novo initiation. Nascent cRNAs are encapsidated by newly synthesized NP and viral polymerases, leading to the formation of cRNPs. Similarly, de novo-initiated synthesis from cRNPs generates vRNAs, which form progeny vRNPs. For incorporation into new virions, vRNPs have to leave the nucleus during the late phase of infection. Binding of M1 and of the nuclear export protein (NEP) thus mediates their export (1, 35, 45). Cytoplasmic vRNPs then travel to the plasma membrane, where virus assembly and budding take place.
Fig 1.
Scheme of the influenza virus life cycle. For the sake of simplicity, only one vRNP in a virus particle is depicted, and nonstructural proteins are omitted. Solid arrows represent synthesis or protein binding. Dashed arrows indicate transport processes. Different steps are assigned by numbers (see the text for details): 1, attachment; 2, endocytosis; 3, fusion in late endosomes; 4, nuclear import; 5, transcription; 6, replication (cRNA synthesis); 7, protein translation; 8, cRNA encapsidation; 9, replication (vRNA synthesis); 10, vRNA encapsidation; 11, M1 and NEP binding; 12, nuclear export; and 13, virus assembly and budding.
The regulation of viral RNA synthesis and especially the mechanism which controls whether vRNPs engage in the transcription of viral mRNAs or the replication of cRNAs is a matter of controversy. Early studies of virus-infected cells showed that replication requires an initial round of transcription and viral protein expression (22). It has since been well established that the NP protein in particular is an essential factor for cRNA accumulation (6, 38, 47). Based on these findings, NP was proposed to cause a switch in the activity of vRNPs from early transcription to late replication by interacting with the vRNA template or the viral polymerase (reviewed in reference 47). Other viral or host factors as well as small viral RNAs (22- to 27-nucleotide [nt] fragments of the vRNAs) also have been proposed to contribute to this switch (reviewed in reference 49). However, the so-called switching hypothesis was recently challenged by in vitro experiments showing full-length cRNA synthesis in the absence of free NP (58). The authors concluded that vRNPs may produce both mRNA and cRNA from an early time point, but cRNA is degraded by host nucleases unless NP and viral polymerases stabilize it (61). Hence, NP would not induce a switch but merely act as a cofactor during cRNA encapsidation. This hypothesis is consistent with other observations showing that the relative rate of genome replication is independent of the abundance of NP (40), and that the RNA-binding activity of NP is necessary for cRNA accumulation (62). However, definite proof is still lacking. Besides the differential regulation of mRNA and cRNA synthesis during the early phase of infection, both species cease to accumulate toward the late phase. In contrast, vRNAs are continuously synthesized (21, 31, 53). This implies distinct control mechanisms for positive- and negative-strand RNA synthesis. Although the molecular basis for this control is uncertain, nuclear export could be involved, since vRNPs, which leave the nucleus, act as templates for mRNA and cRNA, while cRNPs, which remain nuclear, synthesize vRNA. The nuclear export of vRNPs depends on their interaction with M1 proteins (35), and in a cell-free system M1 also inhibited the activity of vRNPs (20, 64, 69). It was thus proposed that M1 binding inactivates progeny vRNPs, and that these inactivated vRNPs can leave the nucleus (reviewed in reference 41). Therefore, M1 proteins may regulate viral RNA synthesis as part of their role during nuclear export.
To elucidate the regulation of influenza virus RNA synthesis in a systematic way, we propose a mathematical model of the viral life cycle. In the past, modeling has provided valuable insights into the intracellular replication of eukaryotic viruses (10, 11, 23, 34, 48). For influenza virus, such a model was previously developed by our group to assess the amount of cellular resources that are consumed by virus replication during cell culture-based vaccine production (55). However, this model was based on qualitative observations and literature parameters, and due to its size and the lack of data, it was not possible to validate the simulations against experiments. We therefore refined the approach by reducing the original set of equations and used a variety of data sets from the literature to identify key parameters of virus infection. We also considered cRNA stabilization and a more detailed description of nuclear export to investigate how these mechanisms affect the dynamics of viral RNA synthesis. In the following, we first introduce our mathematical framework before focusing on the predictions for virus entry and the transition from transcription to replication. We then highlight how M1 proteins affect viral RNA synthesis, and eventually we combine all aspects to draw conclusions about virus particle release.
MATERIALS AND METHODS
The main features of influenza virus replication are shown in Fig. 1 and provide the basis for our model. In the following paragraphs, we derive a set of ordinary differential equations that describe virus entry, viral replication, transcription and protein synthesis, and virus release.
Virus entry.
First, virions bind to membrane receptors and enter the cell via receptor-mediated endocytosis. Nunes-Correia et al. proposed a kinetic model for these processes including two different binding sites, high-affinity and low-affinity sites, which might correspond to sialic acid-containing ligands and less specific interactions, respectively (44). We make minor modifications to this model to account for the infection of a single cell and add an equation for virions in early endosomes.
| (1) |
| (2) |
| (3) |
| (4) |
where VEx, VnAtt, and VEn are the numbers of virions in the extracellular medium, virions attached to binding sites of type n (hi, high affinity; lo, low affinity), and virions in early endosomes, respectively. Here, VEx corresponds to the multiplicity of infection (MOI), i.e., the number of infectious virus particles per cell. These virions attach with rate knAtt to free binding sites Bn, of which there are Bntot in total. By calculating Bn from the conservation equation (equation 2), we follow the formalism of Nunes-Correia and coworkers (44). Note that this implies a fast recycling of receptors as binding sites become vacant when virions enter the cell. Also, in this notation each virion occupies one binding site that may correspond to multiple receptors, as virus-cell binding involves multivalent bond formation (18). Once attached, virions can either dissociate from the cell with rate knDis, which follows directly from the equilibrium constant, knEq, or enter the cell with the endocytosis rate, kEn (equation 3). We assume that kEn is the same for both binding sites, as did Nunes-Correia and coworkers. Fusion of virions in endosomes occurs with rate kFus, which includes the trafficking and acidification of early endosomes as well as the fusion of the viral envelope with the endosomal membrane. It has been shown that only a fraction of virions penetrate into the cytoplasm, while others presumably fail to fuse (32, 35). We therefore introduce the fraction of fusion-competent virions, FFus, and calculate the degradation rate of virions in lysosomes, kVenDeg, accordingly. For model fits to experimental data on fusion, the total number of fused virions can be obtained by integrating kFusVEn over time.
Viral replication.
Following fusion, influenza viruses release parental vRNPs into the cytoplasm. These vRNPs enter the nucleus (9, 36), where they start synthesizing mRNA and, according to the stabilization hypothesis, also cRNA (58). However, nascent cRNA may be rapidly degraded by cellular nucleases unless it is stabilized in cRNP complexes (61). We assume that vRNP formation stabilizes nascent vRNA in a similar fashion. For the majority of vRNAs and cRNAs, different genome segments show similar levels throughout an infection (21, 31). Hence, we do not explicitly distinguish between individual segments but rather consider their total number per cell. For obtaining the abundance of an arbitrary segment, these numbers can be divided by eight, which we did when fitting the model to measurements of individual genome segments. Later in infection, M1 and NEP proteins enter the nucleus and trigger the nuclear export of vRNPs (1, 45). Since M1 binding to vRNPs inhibits their transcriptase activity (20, 64, 69), M1-vRNP complexes in the model are no longer available as the templates for RNA synthesis. Thus, virus replication is described by the following equations.
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
Each fused virion releases a complete set of eight vRNPs into the cytoplasm (Vpcyt), which enter the nucleus with rate kImp (5). Nuclear vRNPs (Vpnuc) then synthesize mRNA, which is described in the next paragraph, and cRNA (RC) with rate kCSyn (equation 7). Similarly, the synthesis of vRNA (RV) with rate kVSyn is directed by cRNPs (Cp) (equation 8). We assume that both types of nascent RNA are degraded by nucleases with rate kRDeg or bind to viral polymerases (PRdRp) with rate kRdRpBind. The resulting complexes of the viral polymerase with cRNA (RRdRpC) or vRNA (RRdRpV) are only partially stabilized and thus degraded with the rate kRRdrpDeg, which is lower than that of nascent RNA. Binding of NP (PNP) with rate kNPBind then leads to cRNP and vRNP formation, respectively. We assume that RNPs decay at a low rate, kRnpDeg, as the RNA in vRNPs is still sensitive to digestion in the presence of an excess of RNases (12). Note that this decay was omitted for incoming cytoplasmic vRNPs (equation 5). During the late phase of infection, M1 proteins (PM1Bind) can bind to vRNPs with rate kM1Bind to form M1-vRNP complexes in the nucleus (VpM1nuc). Subsequent association of NEP (PNEP) facilitates the nuclear export, which is combined in the rate kExp, assuming that the actual transport process is fast. Cytoplasmic NEP-M1-vRNP complexes (VpM1cyt) are then transported to the plasma membrane where virus budding takes place. We lump all processes of virus assembly and budding into the virus release rate, rRel, which is described later.
Viral transcription and protein synthesis.
Viral transcription takes place in the nucleus, whereas translation occurs at cytoplasmic ribosomes. However, since it has been shown that the nuclear export of mRNAs is fast (15), we assume that newly synthesized mRNAs are readily available for translation. In contrast to vRNA and cRNA, our model explicitly accounts for the mRNAs of different genome segments, since measurements reveal significant differences in their levels during infection (21, 31). Protein synthesis in simulations is directly proportional to these mRNA levels, as has been found experimentally (26). For simplicity, we only consider the net production of all structural proteins, neglecting their degradation, and assume that protein amounts in different cellular compartments are in equilibrium. As more data become available, these assumptions can be dropped in favor of a more complex model. Equations for mRNAs and proteins are the following.
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
where RiM and Pj are the numbers of mRNAs of segment i and of proteins of type j, respectively. Experiments of Hatada et al. show a negative correlation between the length of an mRNA and its level, i.e., smaller mRNAs are more abundant (21). Because we assume that all mRNAs are degraded with the same rate, kMDeg, we use a length-dependent mRNA synthesis rate, kMSyn, and scale it with Li, denoting the length of segment i's unspliced mRNA (equation 14). This is in agreement with a transcription mechanism in which only the resident polymerase complex of a vRNP synthesizes mRNAs in cis (27) and elongation is the rate-limiting step. We divided Vpnuc by 8, as only this fraction of vRNPs encodes a specific genome segment and its mRNA. To increase protein translation, multiple ribosomes can bind to a single mRNA, forming polysomes. This is considered by using the length-dependent translation rate, kPSyn (56), and the average distance between two adjacent ribosomes on an mRNA, DRib (4). Hence, protein production is proportional to the speed with which ribosomes cover the distance (DRib). New viral polymerases (PRdRp) form from the three subunits with rate kRdRp and bind to vRNAs and cRNAs with rate kRdRpBind (equation 18). Measurements show that the number of polymerases in one virus particle (NPRdRp) is greater than the eight polymerases in a complete set of vRNPs (33). Therefore, the remaining amount is assumed to leave the cell during budding. Similar terms are considered for NP, M1, and NEP, with NPj denoting the number of proteins of type j in one virion. To calculate the amount of NP, M1, and NEP bound in one NEP-M1-vRNP complex, we use the average length of a vRNA (LV) and the number of nucleotides bound by one protein, NNPnuc, NM1nuc (63), and NNEPnuc. The surface proteins hemagglutinin (PHA), neuraminidase (PNA), and matrix protein 2 (PM2) only decrease due to budding. We consider the splicing of mRNAs from segments 7 and 8 by introducing the factors FSpl7 and FSpl8 (50), which represent the fraction of mRNAs that encode M2 and NEP, respectively.
Virus release.
When vRNPs and viral proteins reach the plasma membrane, progeny virions are assembled and released from the cell. Since the precise mechanism is still not well understood (25), we do not model budding in detail but rather use a simple description:
| (25) |
where VRel is the number of progeny virions released from a cell. It has been shown that vRNPs assume a 7 + 1 configuration, which along with other evidence supports a specific packaging mechanism of the viral genome (25). The formation of a complex containing the eight genome segments would involve multiple intersegments interactions (17) and may therefore be a kinetic bottleneck. Hence, the overall rate of virus release, rRel, in our model is proportional the amount of cytoplasmic vRNPs and to the virus release rate, kRel. Viral protein levels are assumed to scale this rate by multiplication of Michaelis-Menten-like terms, which depend on the abundance of each protein j in one virion NPj (33). Here, enough proteins for KVRel virions must be present to reach half the maximal release rate. We assume that progeny virions do not reinfect the same cell. This is in agreement with the observation that neuraminidase expression on the cell surface cleaves sialic acid and limits superinfection (24).
For all steps of the virus life cycle, we assume that cellular resources, like amino acids, nucleotides, and ribosomes, as well as other host factors are abundant and do not limit replication, an assumption which has been used by several previous authors for other viruses (10, 16, 23) and which is in agreement with theoretical results for influenza virus (55).
Computation.
We solved equations 1 to 25 numerically using the CVODE routine from SUNDIALS (8) on a Linux-based system. All model parameters and initial conditions can be found in Tables A1 and A2 in the appendix. Model files and experiments were handled with the Systems Biology Toolbox 2 (51) for MatLab (version 7.5.0 R2007b). We estimated parameters using the fSSm algorithm for stochastic global optimization (13). To assess parameter uncertainties, confidence intervals were calculated were possible using a bootstrap method (28). For data sets where no measurement errors are available, the model's local sensitivity is provided instead. We calculate this sensitivity by following the approach of Gutenkunst et al. (19), who quantified the change in model output in response to parameter perturbations using an averaged least-squares formula. However, in contrast to their implementation, we perturb each parameter by 1% around its estimated value and only consider the change in model species that were measured at the time points of their measurement. Hence, this local sensitivity shows how much a given parameter affects simulation results compared to the available measurements, which indicates how accurate the parameter estimates are. In this regard, small sensitivities correspond to large variations.
RESULTS
Virus entry.
To model the binding of influenza virus particles to the cell surface, we followed the work of Nunes-Correia et al. and used their parameters for the adsorption of virions to MDCK cells (44). However, in their study the attachment rates were only measured at 4 and 20°C. To obtain these rates at 37°C, we tuned our model such that equilibrium of binding is reached after 20 min, as observed experimentally at this temperature (44). The resulting simulations show the same virus binding in steady state as the model of Nunes-Correia et al. and fit their data equally well (data not shown). After having bound to the plasma membrane, virus particles enter the cell via endocytosis, and a fraction of these particles accomplish fusion with the membrane of late endosomes. We determined the fraction of fusion-competent virions and the rates for endocytosis and fusion by fitting data of R18 labeling experiments (Fig. 2A) conducted by Stegmann et al. (57). Table 1 summarizes the obtained parameters. The first fusion events occur within 5 min after adsorption, with most fusion-competent virions escaping late endosomes within 80 min. However, half of the adsorbed virions fail to fuse and are degraded in lysosomes. According to the local sensitivity (Table 1), the model output heavily depends on the fraction of fusion-competent virions, FFus, indicating that R18 labeling experiments can yield accurate estimates of this parameter. Using the parameters shown in Table 1, we can infer the dynamics of virus entry during an infection (Fig. 2B). Following the observations of Nunes-Correia et al. (44), virion binding sites on the cell surface in our model are abundant and do not become depleted by endocytosis. Hence, all extracellular virus particles (VEx) can enter the cell, which requires approximately 1 h. The number of virus particles in endosomes peaks around 20 min postinfection and decreases subsequently due to the depletion of virions in the medium. After about 90 min, half of the parental vRNPs have entered the nucleus, where they start synthesizing viral RNAs while the rest is degraded in lysosomes.
Fig 2.
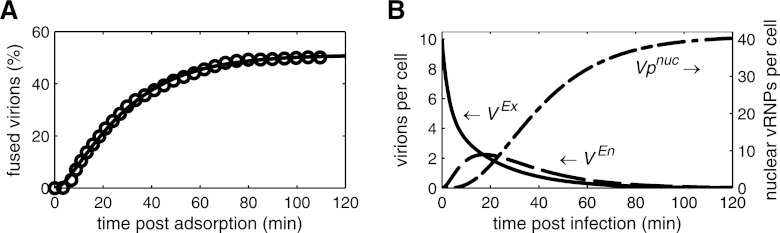
Dynamics of virus entry. Lines represent simulation results. (A) Model fit to data (circles) for the fusion of R18-labeled influenza virus (strain NIB26) with endosomes in MDCK cells modified from those of Stegmann et al. (57). In brief, virus was added to MDCK cells at 0°C for 1 h to allow for virus adsorption, cells were washed, and warm buffer (37°C) was added. The percentage of fused out of total cell-associated virions is shown. (B) Simulated amounts of extracellular virions in the medium (VEx), virions in endosomes (VEn), and vRNPs in the nucleus (Vpnuc) for infection at an MOI of 10, neglecting viral protein synthesis and vRNP degradation.
Table 1.
Parameter estimates for virus entry
| Rate constant | Value | Local sensitivity (%) |
|---|---|---|
| FFus | 0.51 | 0.44 |
| khiAtt | 8.09 · 10−2 (sites · h)−1 | 3.06 · 10−4 |
| kloAtt | 4.55 · 10−2 (sites · h)−1 | 4.36 · 10−6 |
| kEn | 4.8 h−1 | 4.46 · 10−2 |
| kFus | 3.21 h−1 | 1.32 · 10−2 |
Transition from transcription to replication.
Early experiments demonstrated that during infection, vRNPs first synthesize mRNA, whereas cRNA accumulation occurs only after the de novo synthesis of viral proteins (22). Vreede et al. proposed that this transition from transcription to replication occurs because nascent cRNAs are degraded by cellular nucleases unless viral polymerases and NP protect it from degradation (61). We included this hypothesis in our model and used two published studies for parameter estimation (58, 61). These works provide time courses of vRNA, cRNA, and mRNA levels under various experimental conditions measured by semiquantitative NA gene-specific primer extension analysis. To use these data for modeling, we conducted a densitometric analysis and quantified the intensity of each RNA signal. We then normalized these values to the corresponding vRNA signal (at the same time point), which Vreede et al. assumed to be constant during their experiments. This yielded the relative mRNA and cRNA levels per molecule of vRNA.
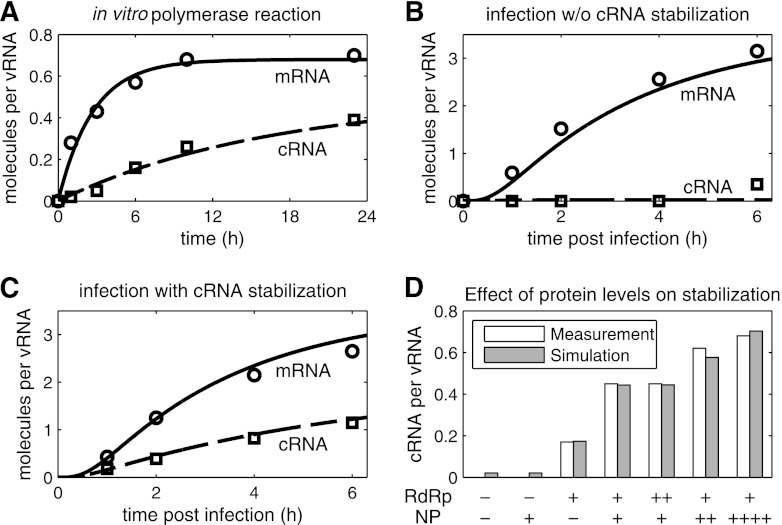
One key observation is that virion-derived vRNPs synthesize both mRNA and cRNA in vitro, i.e., in the absence of de novo-synthesized viral proteins and cellular nucleases (58). Our model can resemble this experiment (Fig. 3A) and allows for the estimation of kinetic parameters. As expected in the absence of nucleases, we find a low degradation rate of cRNA (kRDeg in Table 2). Here, kRDeg most likely corresponds to decomposition processes, suggesting a high stability of cRNA under in vitro conditions. In contrast, parameter estimation yields a high rate for mRNA degradation (kMDeg), which results from the observation that mRNA levels reach steady state after 12 h (Fig. 3A). However, kMDeg might be biased by the assumption that mRNA synthesis is constant throughout the experiment. This might not be the case due to the loss of enzymatic activity or depletion of precursors, such as cap sources, which would also yield constant mRNA levels but at a much lower degradation rate.
Fig 3.
Simulation of cRNA stabilization hypothesis. Experiments yielding NA gene-specific mRNA (○) and cRNA levels (□) were conducted by Vreede et al. using primer extension analysis (58, 61). We obtained relative RNA levels from these studies by densitometric analysis and normalized each data point to the constant vRNA signal. (A) Fit to data of an in vitro polymerase assay using virion-derived vRNPs (58). (B and C) Model fit to infection of 293T cells with influenza A/WSN/33 at an MOI of 5 (58). In brief, protein synthesis during infection was inhibited, and plasmids expressing NP, PA, and PB2 (B) or NP, PA, PB2, and PB1a (C) were transfected prior to infection. (D) Same as panel C, except that various amounts of plasmids expressing PA, PB2, PB1a (RdRp), NP, or empty vector (−) were transfected prior to infection. Bars represent the cRNA level at 2 hpi. PB1a, catalytically inactive mutant PB1-D445A/D446A which forms polymerase complexes that do not synthesize viral RNAs but stabilize cRNA.
Table 2.
Parameter estimates for the transition to genome replication
| Rate constant | Valuee |
Local sensitivity (%) |
||
|---|---|---|---|---|
| In vitroa | Cell cultureb | In vitro | Cell culture | |
| kNPBind | 3.01 · 10−4 | 7.16 · 10−3 | ||
| kRdRpBind | 1c | 6.62 · 10−7 | ||
| kMDeg | 0.37 | 0.33 | 0.13 | 1.37 · 10−2 |
| kRDeg | 0.06 | 36.36 | 1.76 · 10−2 | 1.21 · 10−5 |
| kRRdRpDeg | 4.25 | 1.16 · 10−2 | ||
| kCSyn | 0.03 | 0.76 | 8.78 · 10−2 | 5.31 · 10−2 |
| kMSyn | 0.21d | 0.96d | 0.18 | 8 · 10−2 |
Model fit is presented in Fig. 3A.
Model fit is presented in Fig. 3B to D.
Since polymerase binding is at saturation in experiments, we can only estimate the lower bound of this rate.
For better comparison, the synthesis rate of an mRNA of average length is shown. In the model, transcription is proportional to the actual length of each segment's mRNA using a length-specific synthesis rate of 350 nt · h−1 (in vitro) and 1,630 nt · h−1 (cell culture).
Values for kNPBind and kRdRpBind are given in (molecules · h)−1, and the other constants are given in h−1.
To approach the in vivo situation, we next examined infection experiments in 293T cells from the literature (61). In these experiments, cellular protein synthesis was inhibited, which prevents the production of viral proteins and, hence, should abolish cRNA stabilization. To rescue cRNA accumulation, Vreede et al. expressed four viral proteins in different combinations prior to infection: wild-type NP, PA, PB2, and a mutant PB1 (PB1a, containing D445A/D446A mutation). A trimeric polymerase complex which contains PB1a is catalytically inactive but binding competent and thus cannot synthesize viral RNAs yet still stabilize cRNA (61). For parameter estimation, we fitted all infection data sets simultaneously (Fig. 3B to D) using the same parameters, and we chose initial conditions according to the experimental setup (see Table A2 in the appendix for details). Figure 3B shows a scenario in which NP is present but no complete viral polymerase complexes are formed (in experiments only NP, PA, and PB2 were transfected). Consequently, cRNA is rapidly degraded in the simulation and cannot be detected by primer extension analysis. According to Vreede et al., the elevated cRNA signal at 6 h postinfection (hpi) can be attributed to a minor breakthrough of protein synthesis inhibition (61) and therefore is not reflected by the model. Note that in contrast to the in vitro experiment, cRNA degradation occurs with a high rate in cells (kRDeg in Table 2). This rate has to compensate for the constant cRNA synthesis by vRNPs. However, for high degradation rates, which are required to reflect the complete absence of cRNA, the model becomes increasingly insensitive. Hence, separate experiments are necessary to exactly quantify this rate. In the presence of NP and all polymerase subunits, stabilization can rescue the cRNA signal from this degradation in the experiment and in the model (Fig. 3C). The stabilization of cRNA by catalytically inactive polymerases should not affect mRNA transcription. Hence, simulated mRNA levels in Fig. 3B and C are the same and correspond well to the averages from these two independent biological experiments. In Fig. 3D, we show how different amounts of preexpressed proteins affect cRNA stabilization in our model and in the literature. In the absence of viral polymerases, simulations show very low cRNA levels regardless of whether NP is transfected (Fig. 3D, columns 1 and 2). This residual amount occurs because vRNPs constantly synthesize cRNA and degradation rates are finite. However, such low levels may be below the detection limit of primer extension analysis. The addition of polymerases in the absence of NP results in the partial stabilization of cRNA (Fig. 3D, column 3). To capture this observation in the model, RdRp-cRNA complexes have to be formed that have degradation rates lower than that of free cRNA (compare kRDeg and kRRdrpDeg in Table 2). When polymerases and NP are expressed together, cRNA accumulation is rescued substantially (Fig. 3D, column 4). Furthermore, experiments and the model show that transfecting increasing amounts of polymerases does not yield higher cRNA levels, whereas an increase in NP levels enhances stabilization. Hence, in these experiments, polymerase binding is at saturation, suggesting a high affinity to cRNA. In contrast, the binding of preexpressed NP is the rate-limiting step of cRNA stabilization. Overall, simulations are in good agreement with the measured dynamics of cRNA and mRNA accumulation and also capture qualitative observations at different protein concentrations.
Inhibition of vRNP activity and nuclear export.
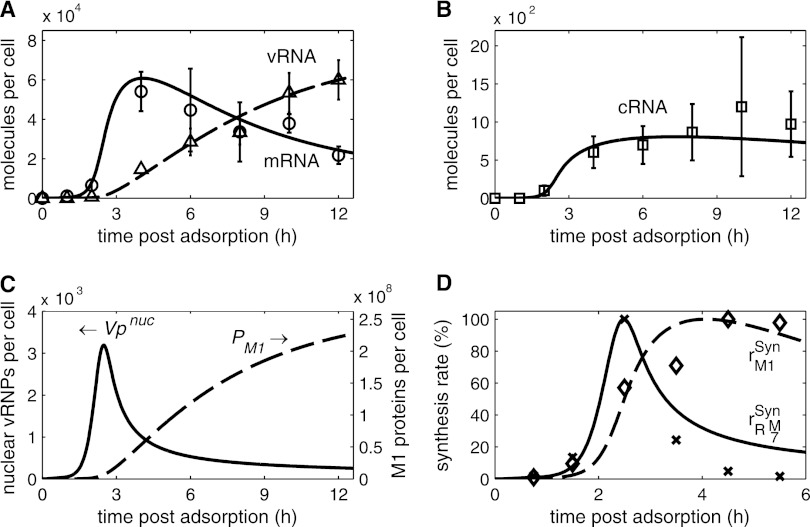
In the late phase of infection, vRNPs leave the nucleus to travel to the plasma membrane, where they are incorporated into new virus particles. Based on experimental observations, two viral proteins control nuclear export in our model: the M1 protein, which initially binds to vRNPs and renders them inactive for RNA synthesis (20, 64, 69), and NEP, which subsequently facilitates transport (1, 45). We examined whether this mechanism, in combination with cRNA stabilization, captures the viral RNA dynamics during infection. Figure 4A and B show a model fit to quantitative real-time reverse transcription-PCR (RT-PCR) data of intracellular mRNA, cRNA, and vRNA levels in infected MDCK cells obtained by Kawakami et al. (31). Viral mRNA starts to accumulate within the first hour postinfection, reaching a distinct peak at approximately 3.5 to 4 hpi (Fig. 4A). Later in infection, mRNA levels decline in the measurements and the simulation. For cRNAs, we find an increase in abundance from 1.5 hpi onwards (Fig. 4B). Again, accumulation slows down during later stages, and the cRNA level in the model eventually falls slightly toward the end of infection. Consequently, viral genome replication starts 1.5 to 2 hpi and persists throughout infection, but it levels off from 6 hpi onwards. These dynamics are in general agreement with other experiments using different influenza virus strains and cell lines (15, 21, 53, 62).
Fig 4.
Viral RNA synthesis during infection. (A and B) Model fit to vRNA (Δ), mRNA (○), and cRNA (□) levels of segment 5 (encoding NP) during an infection of MDCK cells with influenza A/WSN/33 at an MOI of 10 after 1 h of virus adsorption at 4°C. Data were determined by Kawakami et al. using strand-specific real-time RT-PCR (31). (C) Model prediction for the accumulation of M1 proteins (PM1) and vRNPs engaged in RNA synthesis (Vpnuc). (D) Comparison of model fit in panels A and B to data of Shapiro et al. for the synthesis rates of M1 proteins (◇) and mRNAs (×) of segment 7 (encoding M proteins) (53). In brief, BHK-21 cells were infected with influenza virus (WSN strain) at an MOI of 10 to 20, and virus was allowed to adsorb for 1 h at 4°C. Protein and mRNA levels were determined by pulse-chase experiments. In simulations, rM1Syn and rRM7Syn are the synthesis rates of M1 proteins (first term in equation 20) and of mRNAs of segment 7 (first term in equation 14, with i = 7), respectively. Data points and simulations are given as percentages of their maximums.
In the proposed model, the shutdown of mRNA and cRNA synthesis between 3.5 and 4 hpi depends primarily on the inhibition of vRNP activity by M1 proteins. To explore this in more detail, we used the simulations in Fig. 4A and B to infer the dynamics of M1 protein levels (Fig. 4C). M1 proteins begin to accumulate 2 hpi and subsequently bind to vRNPs in the nucleus. Therefore, the number of active vRNPs starts to decrease 2.5 hpi. However, some vRNPs remain active and continue to produce RNAs at low levels even late in infection. For cRNA, this residual synthesis is nearly in equilibrium with the degradation (Fig. 4B), since cRNAs are stabilized in cRNP complexes. In contrast, mRNA degradation outweighs synthesis at late time points (Fig. 4A). The relationship between the synthesis of M1 and of mRNA has been observed previously in qualitative (69) and dynamic experiments (53). The latter work is of special interest, since Shapiro et al. measured M1 protein and mRNA synthesis rates. Intriguingly, our model can resemble these dynamics without further parameter optimization, although the measurements were conducted in BHK-21 cells (Fig. 4D). As found by Shapiro et al., simulations show that the mRNA synthesis rate is maximal at 2.5 hpi (preceding the peak in the mRNA level shown in Fig. 4A). Its decrease coincides with the onset of M1 production. However, experiments show a complete shutdown of mRNA production, which contrasts with model predictions. However, this too might be related to the sensitivity of the experimental approach. In summary, simulation results suggest that the binding of M1 proteins to vRNPs for subsequent nuclear export causes a selective inhibition of positive-strand RNA synthesis during the late phase of infection.
Table 3 presents the parameters estimated from the data in Fig. 4A and B. Note that this data set was obtained in MDCK cells, whereas the cRNA stabilization experiments, on which Table 2 is based, were conducted in 293T cells. Hence, we reestimated the RNA synthesis rates and found that mRNA production especially is faster in MDCK cells (compare kMSyn in Tables 2 and 3). This difference might be cell line dependent or may arise due to the quality of the data sets. In particular, it has to be taken into account that the experiments in 293T cells were assayed by primer extension analysis, yielding only relative RNA levels, while the real-time RT-PCR measurements in infected MDCK cells allowed a direct quantification. The latter data set should enable more accurate estimations. For these experiments, we also find that the rate of vRNA synthesis is significantly higher than that observed for cRNA.
Table 3.
Parameter estimates for viral RNA synthesis during late infection
| Rate constantd | Value | Confidence intervala |
|---|---|---|
| kM1Bind | 1.39 · 10−6 | (0.5–3) · 10−6 |
| kRnpDeg | 0.09 | 0b–0.19 |
| kCSyn | 1.38 | 0.53–2.99 |
| kMSyn | 147c | 47–239 |
| kVSyn | 13.86 | 5.73–23.71 |
Quantiles Q0.025 and Q0.975 of 3,000 bootstrap iterations performed according to Joshi et al. (28).
Estimates reached a lower parameter bound of 9 · 10−4.
Synthesis rate of an mRNA of average length (Table 2) using a length-specific rate of 2.5 · 105 nt · h−1.
kM1Bind is given in (molecules · h)−1, and the other constants are given in h−1.
Progeny virion release.
Considering the accumulation of vRNAs toward the end of infection, we were interested in what factor(s) limits the amount of virions that are released by an infected cell. Our infection experiments showed that an average MDCK cell infected with influenza A/WSN/33 produces up to 104 progeny virions (data not shown). We tuned the virus release rate in our model such that the simulations reflect this average virus yield. Interestingly, protein loss due to releasing this amount of particles does not deplete the intracellular levels of viral polymerases M1 and NP (Fig. 5A) or of the other viral proteins (data not shown). The differences in simulated protein abundance seen in Fig. 5A arise for two reasons: budding virions contain different amounts of each protein, and mRNA levels in the model are higher for smaller genome segments, which is in agreement with Hatada et al. (21). Simulations also show that the level of vRNPs in the cytoplasm increases throughout infection (Fig. 5B), as has been observed for the vRNA level in experiments (Fig. 4A). Hence, modeling suggests that no single viral component limits the formation of progeny virions. Furthermore, Fig. 5B indicates that the first virus particles are released 3 to 4 hpi, and that more virions leave the cell at late time points due to the accumulation of cytoplasmic vRNPs and other viral components.
Fig 5.
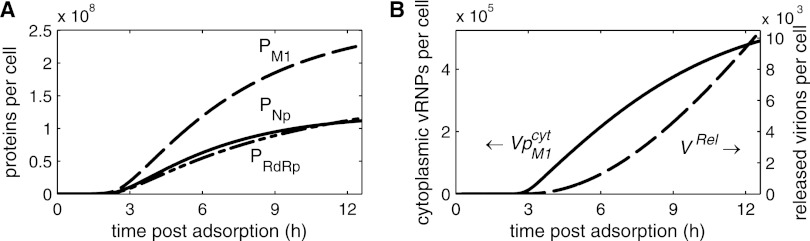
Dynamics of virus release. (A) Model prediction for the levels of M1 (PM1), NP (PNP), and viral polymerase complexes (PRdRp) based on the model fit shown in Fig. 4. (B) Level of cytoplasmic vRNPs (VpM1cyt) and cumulative amount of released progeny virions (VRel) for the simulation presented in Fig. 4.
DISCUSSION
We integrated key experimental results published by various research groups during the last 2 decades to derive a kinetic model of influenza virus replication in a mammalian cell. In contrast to previous theoretical studies, this model captures qualitative and quantitative measurements of virus entry, the transition from transcription to replication, and viral RNA levels in a single coherent framework. We used it to explore how influenza viruses regulate their life cycle and what consequence this regulation has for the dynamics of viral RNA synthesis.
Previous studies of virus entry have found virion-containing endosomes as early as 5 min after adsorption (37, 68), while uncoating occurs between 5 and 90 min (32, 36, 57). Our model is consistent with these results and allowed us to investigate the dynamics of virus entry in detail. In simulations, vRNPs accumulate in the nucleus between 13 and 90 min, which is in good agreement with immunocytochemistry of incoming NP (36). Intriguingly, virus uptake in experiments and simulations ceases thereafter. Modeling suggests that this is due to the depletion of extracellular virions. However, in infected cell culture, free virions can be found even after the entry phase (37). We thus speculate that only the virus particles in the vicinity of cells get depleted, whereas diffusion limits the transport of virions in the bulk of medium. In this case, the number of extracellular virions in our model corresponds to the number of infectious particles in close proximity to cells. Alternatively, or additionally, internalization and removal of sialic-acid containing receptors could restrict virus entry later in infection (24). Such a scenario would not be reflected in the current framework, since we adopted a binding model which implies fast receptor recycling (44). Overall, virus entry requires approximately 25 min, after which the first vRNPs reach the nucleus in experiments (36). This delay is in agreement with the observed onset of mRNA accumulation in our model, indicating that vRNPs directly begin transcription once in the nucleus.
To account for the transition from transcription to genome replication, we implemented the stabilization of cRNAs in our model and analyzed experimental data that led to this hypothesis. The model can capture these observations successfully but requires several key features to do so. For instance, to reflect low cRNA levels in the absence of viral proteins, the degradation rate of nascent cRNAs in cells has to be high enough to compensate for replication. In fact, estimation yields a significantly higher rate for infection experiments than that found in the cell-free system. Hence, cRNAs seem to be stable in vitro, whereas in cells efficient degradation takes place. It would be interesting to determine whether cellular nucleases allow for such high degradation rates. To reflect experiments that show a partial stabilization of cRNAs by viral polymerases, the model requires that cRNA encapsidation occurs via a two-step process. Initially, the rapid binding of polymerases produces RdRp-cRNA complexes, which are less susceptible to degradation than free cRNA. Stable cRNPs then are formed by NP binding. Confirming this two-step mechanism and characterizing the stability of the RdRp-cRNA intermediates thus would provide further evidence for the stabilization hypothesis. Encapsidation in two successive steps would also explain why NPs alone do not stabilize cRNA in experiments. However, NP was shown to bind RNA with high affinity in an unspecific manner (reviewed in reference 47). To be consistent with the cRNA stabilization model, NP-cRNA complexes should be susceptible to degradation. Studying whether that is the case and, if so, why polymerases are necessary for stabilization may provide further insights into the proposed mechanism. Finally, the increase in cRNA levels in response to increasing NP concentrations suggests that NP binding is the rate-limiting step of encapsidation. Whether this is a general feature or only holds true for the experimental conditions used by Vreede et al. remains to be determined. Taken together, however, these features enable our model to capture the cRNA stabilization hypothesis and the transition from transcription to replication. However, as a variety of other regulatory mechanisms were proposed, alternative models are under investigation. In future studies, the application of model discrimination techniques and their combination with model-based experimental design may allow us to validate or invalidate the competing hypotheses.
The shutdown of mRNA synthesis constitutes the second widely accepted regulation of influenza virus replication. Early evidence suggested that this step is part of the switch to genome replication (reviewed in reference 47), such that NP biases vRNPs toward replication instead of transcription; i.e., an increase in replication would be at the expense of transcription. However, our simulations show that there is no immediate shutdown of transcription but rather a sustained period of time where mRNA and cRNA are both synthesized. In the model, this allows for an accumulation of transcriptionally active progeny vRNPs which support the rapid increase in mRNA and cRNA levels between 1 and 3.5 hpi. Parental vRNPs alone could not sustain such an increase and the high mRNA levels observed in experiments. Instead of an early shutdown, we find that transcription inhibition coincides with the accumulation of M1 proteins, which marks the onset of nuclear export during the late phase of infection. According to the model, the inactivation of vRNPs by M1 binding affects both positive-strand RNAs around 4 hpi, leading to a decrease in the mRNA level and a roughly constant amount of cRNAs. In contrast, the accumulation of vRNAs continues unhindered. These dynamics were also observed in several independent experiments (21, 31, 54, 62). Hence, we proposed that M1 proteins regulate viral RNAs during the late phase of infection by interacting with vRNPs and inhibiting positive-strand RNA synthesis. In support of this, experiments in which a model cRNA or vRNA (containing a chloramphenicol acetyltransferase [CAT] gene flanked by the noncoding sequence of segment 8) was expressed in the presence of viral polymerases and NP, but not M1, showed an accumulation of all three viral RNA species but no shutdown of RNA synthesis (40). Inhibition by M1 thus could stop mRNA and cRNA production when both levels are sufficient to sustain the synthesis of viral proteins and genomic RNAs. Indeed, when cells were infected with a virus carrying a mutant M1 protein impaired in its binding to vRNPs, intracellular vRNA levels increased by 250% (66), indicating a lack of negative regulation. One could argue that this increase was due to the retention of viral genome copies in the cell because nuclear export and, therefore, budding were impaired. However, in our model, even a complete block of budding would only increase vRNA levels by roughly 10% as infected cells produce significantly more viral genomes than are incorporated into progeny virions. Hence, it seems that M1 proteins provide a negative feedback that directs vRNPs toward nuclear export, which prevents excessive RNA production in favor of budding. Finally, the export of vRNPs itself may contribute to this regulation, as two independent studies found an increase in nuclear cRNA levels in the presence of export inhibitors (7, 67).
In the present work, we focused solely on the regulation of virus replication by viral proteins, supported by in vitro experiments showing that capped RNA-primed transcription and de novo-initiated replication from short RNA templates occur in the absence of cellular proteins (42). In fact, we demonstrated that by considering the encapsidation of viral RNAs and the export of vRNPs alone, simulations can capture the dynamics of viral RNAs during infection. However, previous studies have also identified a variety of host factors that are required for efficient viral RNA synthesis in cells (reviewed in reference 65). For instance, the minichromosome maintenance complex (MCM) stimulates cRNA initiation (29, 30), and RAF-2p48 (also designated UAP56, NPI-5, and Bat1), a cellular splicing factor, acts as a chaperon for NP during RNA encapsidation (39). Also, the activity of cellular RNA polymerase II (Pol II) is crucial for viral mRNA synthesis (reviewed in reference 3). However, to directly regulate the dynamics of virus replication, such factors would have to change in abundance or activity. Otherwise, host factors would provide an admittedly essential but constant influence while the viral factors with which they interact exercise control. Indeed, for MCM and RAF-2p48, such interactions were found with the PA subunit and NP, respectively (30, 46), which are both prime candidates for viral regulators. Host factors providing such constant influence can be omitted from mathematical models. For cellular Pol II, in contrast, degradation has been reported to occur from 6 hpi onwards, and it has been suggested that this contributes to the shutdown of viral mRNA synthesis (59). We did not implement this mechanism due to the lack of quantitative data on Pol II dynamics. However, it may explain why our model overestimates the transcription rate at late time points (Fig. 4D). In the same study, the authors find that the association of Pol II and viral polymerases peaks 3 hpi and declines thereafter, much like the amount of synthetically active vRNPs in our model. Based on these observations, we hypothesize that M1 and NEP binding, which start 3 hpi, impair the association of viral and cellular RNA polymerases in preparation for nuclear export. Later in infection, the degradation of Pol II would then further reduce the rate of mRNA synthesis.
Our simulations of a complete infection cycle support previous experimental findings showing that vRNA accumulates throughout infection (21, 31, 60). Thus, the drain of vRNPs by virus release does not deplete viral genome copies in the cell. Moreover, modeling suggests that the same applies for viral proteins. Experimentally, protein synthesis was found to proceed unhindered even at late times postinfection (26), and for M1, the most abundant component in a virus particle, accumulation in cells was shown even 24 hpi despite significant virus release (66). Similarly, strong M1 and NP fluorescence could be detected by flow cytometry at late times postinfection (52). Hence, it seems that the abundance of viral components is sufficient to release more virus particles, and that other processes constitute a bottleneck. Candidates could be the formation of a complex containing all eight genome segments or the transport of vRNPs to the plasma membrane. In favor of this hypothesis, vRNPs were shown to accumulate in the perinuclear region around the microtubule-organizing centers at intermediate times postinfection (2, 14). Furthermore, for late time points, vRNPs accumulate at the plasma membrane (14), indicating that budding also is a limiting step.
By using the proposed model to analyze quantitative data on vRNA and cRNA levels, we estimated that the synthesis rate of vRNA is 10 times higher than that of cRNA. Previous works have suggested that vRNA is produced in trans by soluble polymerases (27), whereas cRNAs are synthesized in cis by the polymerase present in a vRNP (29, 58). It thus is tempting to speculate that up to 10 soluble polymerases are involved in vRNA production from one cRNP. Alternatively, structural differences in the promoter region of vRNAs and cRNAs may influence the efficiency with which synthesis is initiated (49), affecting this estimate.
In summary, we have developed a quantitative mathematical model of the influenza virus life cycle. It explicitly accounts for the stabilization of viral RNAs through their encapsidation by polymerases and NP and for the role of M1 and NEP during vRNP export from the nucleus. Unlike previous approaches, the proposed model structure combines a wide variety of experimental data sets in a consistent way and captures the time courses and levels of all three viral RNAs during infection. Hence, the model provides an ideal basis for studying virus replication and its numerous proposed regulators. Ultimately, such models will allow us to integrate our current knowledge into a systematic framework and will support the design of new experiments to deepen our understanding of influenza virus replication and its regulation.
ACKNOWLEDGMENT
We thank Markus Rehberg for helpful discussions and for comments on the manuscript.
APPENDIX
The parameters used for the simulation of influenza virus replication (Table A1) and the initial conditions and parameter changes used to fit experiments and generate figures (Table A2) are provided here.
Table A1.
List of parameters used for the simulation of influenza virus replication
| Parameter | Description | Value | Source, reference, or comment |
|---|---|---|---|
| Bhitot | No. of high-affinity binding sites | 150 sites | 44 |
| Blotot | No. of low-affinity binding sites | 1,000 sites | 44 |
| DRib | Distance between two adjacent ribosomes | 160 nt | 4 |
| FFus | Fraction of fusion-competent virions | 0.51 | Expt in Fig. 2A |
| FSp17 | Fraction of M2-encoding mRNAs | 0.02 | Based on ration of M2 to M1 |
| FSp18 | Fraction of NEP-encoding mRNAs | 0.125 | 50 |
| khiAtt | Attachment to high-affinity binding sites | 8.09 · 10−2 sites−1 · h−1 | Adjusted to data in reference 44 |
| kloAtt | Attachment to low-affinity binding sites | 4.55 · 10−2 sites−1 · h−1 | Adjusted to data in reference 44 |
| kM1Bind | Binding of M1 to nuclear vRNPs | 1.39 · 10−6 molecule−1 · h−1 | Expt in Fig. 4A and B |
| kNPBind | Binding of NP to RdRp-RNA complexes | 3.01 · 10−4 molecule−1 · h−1 | Expt in Fig. 3B-D |
| kRdRpBind | Binding of RdRp complexes to RNA | 1 molecule−1 · h−1 | Expt in Fig. 3B-D |
| kMDeg | Degradation of mRNA | 0.33 h−1 | Expt in Fig. 3B-D |
| kRDeg | Degradation of nascent cRNA/vRNA | 36.36 h−1 | Expt in Fig. 3B-D |
| kRnpDeg | Degradation of RNPs | 0.09 h−1 | Expt in Fig. 4A and B |
| kRRdRpDeg | Degradation of RdRp-RNA complexes | 4.25 h−1 | Expt in Fig. 3B-D |
| kEn | Endocytosis | 4.8 h−1 | Expt in Fig. 2A |
| khiEq | Equilibrium constant of high-affinity sites | 1.13 · 10−2 site−1 | 44 |
| kloEq | Equilibrium constant of low-affinity sites | 8.33 · 10−5 site−1 | 44 |
| kExp | NEP binding and nuclear export | 1 · 10−6 molecule−1 · h−1 | Adjusted to data from reference 2 |
| kFus | Fusion with endosomes | 3.21 h−1 | Expt in Fig. 2A |
| kImp | Nuclear import | 6 h−1 | 5 |
| kRdRp | Formation of RdRp complexes | 1 molecule−2 · h−1 | Rapid complex formation |
| kRel | Virus release | 3.7 · 10−3 virions · molecule−1 · h−1 | Cell releases 104 virions in 12 h |
| kCSyn | cRNA synthesis | 1.38 h−1 | Expt in Fig. 4A and B |
| kMSyn | mRNA synthesis | 2.5 · 10−5 nt · h−1 | Expt in Fig. 4A and B |
| kPSyn | Protein synthesis | 64,800 nt · h−1 | 56 |
| kVSyn | vRNA synthesis | 13.86 h−1 | Expt in Fig. 4A and B |
| KVRel | Influence of proteins on virus release | 10 virions | Adjusted |
| L1 | Length of segment 1's mRNA | 2,320 nt | 33 |
| L2 | Length of segment 2's mRNA | 2,320 nt | 33 |
| L3 | Length of segment 3's mRNA | 2,211 nt | 33 |
| L4 | Length of segment 4's mRNA | 1,757 nt | 33 |
| L5 | Length of segment 5's mRNA | 1,540 nt | 33 |
| L6 | Length of segment 6's mRNA | 1,392 nt | 33 |
| L7 | Length of segment 7's unspliced mRNA | 1,005 nt | 33 |
| L8 | Length of segment 8's unspliced mRNA | 868 nt | 33 |
| LV | Average length of a vRNA | 1,700 nt | Based on reference 33 |
| NPRdRP | No. of RdRp complexes in a virion | 45 molecules · virion−1 | 33 |
| NPHA | No. of HA molecules in a virion | 500 molecules · virion−1 | 33 |
| NPNP | No. of NP molecules in a virion | 1,000 molecules · virion−1 | 33 |
| NPNA | No. of NA molecules in a virion | 100 molecules · virion−1 | 33 |
| NPM1 | No. of M1 molecules in a virion | 3,000 molecules · virion−1 | 33 |
| NPM2 | No. of M2 molecules in a virion | 40 molecules · virion−1 | 33 |
| NPNEP | No. of NEP molecules in a virion | 165 molecules · virion−1 | 33 |
| NM1nuc | Nucleotides bound by one M1 molecule | 200 nt | 63 |
| NNEPNuc | Nucleotides bound by one NEP molecule | 1,700 nt | Adjusted to data in reference 47 |
| NNPnuc | Nucleotides bound by one NP molecule | 24 nt | 47 |
Table A2.
Initial conditions and parameter changes (compared to Table A1) used to fit experiments and generate figures
| Simulation | Non-zero initial conditions | Parameter changes |
|---|---|---|
| Fusion (Fig. 2A) | VhiAtt = 100 | |
| Virus entry (Fig. 2B) | VEx = 10 | kRnpDeg = 0, kPSyn = 0 |
| In vitro polymerase reaction (Fig. 3A) | Vpnuc = 8 | kMDeg = 0.37, kRDeg = 0.06, kRnpDeg = 0, kCSyn = 0.03, kMSyn = 350, kPSyn = 0, |
| Infection without cRNA stabilization (Fig. 3B) | VhiAtt = 5, PNP = 1 · 104, PPB2 = 1 · 104 | FFus = 1, kRnpDeg = 0, khiEq = 1 ⋅ 108, kCSyn = 0.76, kMSyn = 1, 630kPSyn = 0, kVSyn = 0, |
| Infection with cRNA stabilization (Fig. 3C) | VhiAtt = 5, PNP = 1 · 104, PRdRp = 1 · 104 | Same as for Fig. 3B |
| Effect of protein levels on stabilization (Fig. 3D) | VhiAtt = 5, PNP = n · 104, PRdRp = n · 104, n = [0, 1, 2, 4] = [−, +, ++, ++++] | Same as for Fig. 3B |
| Virus replication (Fig. 4 and 5) | VhiAtt = 10 | khiEq = 1 ⋅108 |
aAs Vreede et al. assumed that the vRNA signal is constant in their experiments, we omit vRNP degradation. However, degradation of cRNPs still occurs, with rate = 0.09 in these simulations.
bAs for Fig. 3B, the degradation of vRNPs was omitted whereas cRNPs are degraded with = 0.98.
Footnotes
Published ahead of print 16 May 2012
REFERENCES
- 1. Akarsu H, et al. 2003. Crystal structure of the M1 protein-binding domain of the influenza A virus nuclear export protein (NEP/NS2). EMBO J. 22:4646–4655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Amorim MJ, et al. 2011. A Rab11 and microtubule dependent mechanism for cytoplasmic transport of influenza A virus vRNA. J. Virol. 85:4143–4156 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Amorim MJ, Digard P. 2006. Influenza A virus and the cell nucleus. Vaccine 24:6651–6655 [DOI] [PubMed] [Google Scholar]
- 4. Arava Y, et al. 2003. Genome-wide analysis of mRNA translation profiles in Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. U. S. A. 100:3889–3894 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Babcock HP, Chen C, Zhuang X. 2004. Using single-particle tracking to study nuclear trafficking of viral genes. Biophys. J. 87:2749–2758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Beaton AR, Krug RM. 1986. Transcription antitermination during influenza viral template RNA synthesis requires the nucleocapsid protein and the absence of a 5′ capped end. Proc. Natl. Acad. Sci. U. S. A. 83:6282–6286 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Chase GP, et al. 2011. Influenza virus ribonucleoprotein complexes gain preferential access to cellular export machinery through chromatin targeting. PLoS Pathog. 7:e1002187 doi:10.1371/journal.ppat.1002187 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Cohen SD, Hindmarsh AC. 1996. CVODE, a stiff/nonstiff ODE solver in C. Computers Phys. 10:138–143 [Google Scholar]
- 9. Cros JF, Palese P. 2003. Trafficking of viral genomic RNA into and out of the nucleus: influenza, Thogoto and Borna disease viruses. Virus Res. 95:3–12 [DOI] [PubMed] [Google Scholar]
- 10. Dahari H, Ribeiro RM, Rice CM, Perelson AS. 2007. Mathematical modeling of subgenomic hepatitis C virus replication in Huh-7 cells. J. Virol. 81:750–760 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Dee KU, Shuler ML. 1997. A mathematical model of the trafficking of acid-dependent enveloped viruses: application to the binding, uptake, and nuclear accumulation of baculovirus. Biotechnol. Bioeng. 54:468–490 [DOI] [PubMed] [Google Scholar]
- 12. Duesberg PH. 1969. Distinct subunits of the ribonucleoprotein of influenza virus. J. Mol. Biol. 42:485–499 [DOI] [PubMed] [Google Scholar]
- 13. Egea JA, Rodriguez-Fernandez M, Banga JR, Marti R. 2007. Scatter search for chemical and bio-process optimization. J. Global Optim. 37:481–503 [Google Scholar]
- 14. Eisfeld AJ, Kawakami E, Watanabe T, Neumann G, Kawaoka Y. 2011. RAB11A is essential for influenza genome transport to the plasma membrane. J. Virol. 85:6117–6126 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Enami M, Fukuda R, Ishihama A. 1985. Transcription and replication of eight RNA segments of influenza virus. Virology 142:68–77 [DOI] [PubMed] [Google Scholar]
- 16. Endy D, Kong D, Yin J. 1997. Intracellular kinetics of a growing virus: a genetically structured simulation for bacteriophage T7. Biotechnol. Bioeng. 55:375–389 [DOI] [PubMed] [Google Scholar]
- 17. Fournier E, et al. 2012. A supramolecular assembly formed by influenza A virus genomic RNA segments. Nucleic Acids Res. 40:2197–2209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Glick GD, Toogood PL, Wiley DC, Skehel JJ, Knowles JR. 1991. Ligand recognition by influenza virus. The binding of bivalent sialosides. J. Biol. Chem. 266:23660–23669 [PubMed] [Google Scholar]
- 19. Gutenkunst RN, et al. 2007. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 3:1871–1878 doi:10.1371/journal.pcbi.0030189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Hankins RW, Nagata K, Kato A, Ishihama A. 1990. Mechanism of influenza virus transcription inhibition by matrix (M1) protein. Res. Virol. 141:305–314 [DOI] [PubMed] [Google Scholar]
- 21. Hatada E, Hasegawa M, Mukaigawa J, Shimizu K, Fukuda R. 1989. Control of influenza virus gene expression: quantitative analysis of each viral RNA species in infected cells. J. Biochem. 105:537–546 [DOI] [PubMed] [Google Scholar]
- 22. Hay AJ, Lomniczi B, Bellamy AR, Skehel JJ. 1977. Transcription of the influenza virus genome. Virology 83:337–355 [DOI] [PubMed] [Google Scholar]
- 23. Hensel SC, Rawlings JB, Yin J. 2009. Stochastic kinetic modeling of vesicular stomatitis virus intracellular growth. Bull. Math Biol. 71:1671–1692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Huang I-C, et al. 2008. Influenza A virus neuraminidase limits viral superinfection. J. Virol. 82:4834–4843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Hutchinson EC, von Kirchbach JC, Gog JR, Digard P. 2010. Genome packaging in influenza A virus. J. Gen. Virol. 91:313–328 [DOI] [PubMed] [Google Scholar]
- 26. Inglis SC, Mahy BW. 1979. Polypeptides specified by the influenza virus genome. 3. Control of synthesis in infected cells. Virology 95:154–164 [DOI] [PubMed] [Google Scholar]
- 27. Jorba N, Coloma R, OrtíN J. 2009. Genetic trans-complementation establishes a new model for influenza virus RNA transcription and replication. PLoS Pathog. 5:e1000462 doi:10.1371/journal.ppat.1000462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Joshi M, Seidel-Morgenstern A, Kremling A. 2006. Exploiting the bootstrap method for quantifying parameter confidence intervals in dynamical systems. Metab. Eng. 8:447–455 [DOI] [PubMed] [Google Scholar]
- 29. Kawaguchi A, Momose F, Nagata K. 2011. Replication-coupled and host factor-mediated encapsidation of the influenza virus genome by viral nucleoprotein. J. Virol. 85:6197–6204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Kawaguchi A, Nagata K. 2007. De novo replication of the influenza virus RNA genome is regulated by DNA replicative helicase, MCM. EMBO J. 26:4566–4575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Kawakami E, et al. 2011. Strand-specific real-time RT-PCR for distinguishing influenza vRNA, cRNA, and mRNA. J. Virol. Methods 173:1–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Koff WC, Knight V. 1979. Inhibition of influenza virus uncoating by rimantadine hydrochloride. J. Virol. 31:261–263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Lamb RA, Krug RM. 2001. Orthomyxoviridae: the viruses and their replication, p 1487–1531 Fields virology, 4th ed In Knipe DM, Howley PM. (ed), Fields virology, 4th ed Lippincott Williams & Wilkins, Philadelphia, PA [Google Scholar]
- 34. Lim K-I, Lang T, Lam V, Yin J. 2006. Model-based design of growth-attenuated viruses. PLoS Comput. Biol. 2:e116 doi:10.1371/journal.pcbi.0020116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Martin K, Helenius A. 1991. Nuclear transport of influenza virus ribonucleoproteins: the viral matrix protein (M1) promotes export and inhibits import. Cell 67:117–130 [DOI] [PubMed] [Google Scholar]
- 36. Martin K, Helenius A. 1991. Transport of incoming influenza virus nucleocapsids into the nucleus. J. Virol. 65:232–244 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Matlin KS, Reggio H, Helenius A, Simons K. 1981. Infectious entry pathway of influenza virus in a canine kidney cell line. J. Cell Biol. 91:601–613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Medcalf L, Poole E, Elton D, Digard P. 1999. Temperature-sensitive lesions in two influenza A viruses defective for replicative transcription disrupt RNA binding by the nucleoprotein. J. Virol. 73:7349–7356 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Momose F, et al. 2001. Cellular splicing factor RAF-2p48/NPI-5/BAT1/UAP56 interacts with the influenza virus nucleoprotein and enhances viral RNA synthesis. J. Virol. 75:1899–1908 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Mullin AE, Dalton RM, Amorim MJ, Elton D, Digard P. 2004. Increased amounts of the influenza virus nucleoprotein do not promote higher levels of viral genome replication. J. Gen. Virol. 85:3689–3698 [DOI] [PubMed] [Google Scholar]
- 41. Nayak DP, Hui EK-W. 2002. Assembly and morphogenesis of influenza viruses. Recent Res. Dev. Virol. 4:35–54 [Google Scholar]
- 42. Newcomb LL, et al. 2009. Interaction of the influenza a virus nucleocapsid protein with the viral RNA polymerase potentiates unprimed viral RNA replication. J. Virol. 83:29–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Noda T, et al. 2006. Architecture of ribonucleoprotein complexes in influenza A virus particles. Nature 439:490–492 [DOI] [PubMed] [Google Scholar]
- 44. Nunes-Correia I, Ramalho-Santos J, Nir S, de Lima MCP. 1999. Interactions of influenza virus with cultured cells: detailed kinetic modeling of binding and endocytosis. Biochemistry 38:1095–1101 [DOI] [PubMed] [Google Scholar]
- 45. O'Neill RE, Talon J, Palese P. 1998. The influenza virus NEP (NS2 protein) mediates the nuclear export of viral ribonucleoproteins. EMBO J. 17:288–296 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Palese P, Wang P, Wolff T, O'Neill RE. 1997. Host-viral protein-protein interactions in influenza virus replication, Molecular aspects of host-pathogen interaction, p 327–340 In McCrae MA, et al., Molecular aspects of host-pathogen interaction. Cambridge University Press, Cambridge, United Kingdom [Google Scholar]
- 47. Portela A, Digard P. 2002. The influenza virus nucleoprotein: a multifunctional RNA-binding protein pivotal to virus replication. J. Gen. Virol. 83:723–734 [DOI] [PubMed] [Google Scholar]
- 48. Reddy B, Yin J. 1999. Quantitative intracellular kinetics of HIV type 1. AIDS Res. Hum. Retrovir. 15:273–283 [DOI] [PubMed] [Google Scholar]
- 49. Resa-Infante P, Jorba N, Coloma R, Ortin J. 2011. The influenza virus RNA synthesis machine: advances in its structure and function. RNA Biol. 8:207–215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Robb NC, Jackson D, Vreede FT, Fodor E. 2010. Splicing of influenza A virus NS1 mRNA is independent of the viral NS1 protein. J. Gen. Virol. 91:2331–2340 [DOI] [PubMed] [Google Scholar]
- 51. Schmidt H, Jirstrand M. 2006. Systems biology toolbox for MATLAB: a computational platform for research in systems biology. Bioinformatics 22:514–515 [DOI] [PubMed] [Google Scholar]
- 52. Schulze-Horsel J, Genzel Y, Reichl U. 2008. Flow cytometric monitoring of influenza A virus infection in MDCK cells during vaccine production. BMC Biotechnol. 8:45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Shapiro GI, Gurney T, Krug RM. 1987. Influenza virus gene expression: control mechanisms at early and late times of infection and nuclear-cytoplasmic transport of virus-specific RNAs. J. Virol. 61:764–773 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Shapiro GI, Krug RM. 1988. Influenza virus RNA replication in vitro: synthesis of viral template RNAs and virion RNAs in the absence of an added primer. J. Virol. 62:2285–2290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Sidorenko Y, Reichl U. 2004. Structured model of influenza virus replication in MDCK cells. Biotechnol. Bioeng. 88:1–14 [DOI] [PubMed] [Google Scholar]
- 56. Spirin AS. 1986. Ribosome structure and protein biosynthesis. Benjamin/Cummings Pub. Co., Advanced Book Program, Menlo Park, CA [Google Scholar]
- 57. Stegmann T, et al. 1993. Evaluation of viral membrane fusion assays. Comparison of the octadecylrhodamine dequenching assay with the pyrene excimer assay. Biochemistry 32:11330–11337 [DOI] [PubMed] [Google Scholar]
- 58. Vreede FT, Brownlee GG. 2007. Influenza virion-derived viral ribonucleoproteins synthesize both mRNA and cRNA in vitro. J. Virol. 81:2196–2204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Vreede FT, Chan AY, Sharps J, Fodor E. 2010. Mechanisms and functional implications of the degradation of host RNA polymerase II in influenza virus infected cells. Virology 396:125–134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Vreede FT, Fodor E. 2010. The role of the influenza virus RNA polymerase in host shut-off. Virulence 1:436–439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Vreede FT, Jung TE, Brownlee GG. 2004. Model suggesting that replication of influenza virus is regulated by stabilization of replicative intermediates. J. Virol. 78:9568–9572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Vreede FT, Ng AK-L, Shaw P-C, Fodor E. 2011. Stabilisation of influenza virus replication intermediates is dependent on the RNA-binding but not the homo-oligomerisation activity of the viral nucleoprotein. J. Virol. 85:12073–12078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Wakefield L, Brownlee GG. 1989. RNA-binding properties of influenza A virus matrix protein M1. Nucleic Acids Res. 17:8569–8580 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Watanabe K, Handa H, Mizumoto K, Nagata K. 1996. Mechanism for inhibition of influenza virus RNA polymerase activity by matrix protein. J. Virol. 70:241–247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Watanabe T, Watanabe S, Kawaoka Y. 2010. Cellular networks involved in the influenza virus life cycle. Cell Host Microbe 7:427–439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Wu C-Y, Jeng K-S, Lai MM-C. 2011. The SUMOylation of matrix M1 protein modulates the assembly and morphogenesis of influenza A virus. J. Virol. 85:6618–6628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Wu M-S, et al. 2011. Mechanism of action of the suppression of influenza virus replication by Ko-Ken Tang through inhibition of the phosphatidylinositol 3-kinase/Akt signaling pathway and viral RNP nuclear export. J. Ethnopharmacol. 134:614–623 [DOI] [PubMed] [Google Scholar]
- 68. Yoshimura A, et al. 1982. Infectious cell entry mechanism of influenza virus. J. Virol. 43:284–293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Zvonarjev AY, Ghendon YZ. 1980. Influence of membrane (M) protein on influenza A virus virion transcriptase activity in vitro and its susceptibility to rimantadine. J. Virol. 33:583–586 [DOI] [PMC free article] [PubMed] [Google Scholar]