Cascaded systems analysis of noise and detectability in dual-energy cone-beam CT

Abstract

Purpose: Dual-energy computed tomography and dual-energy cone-beam computed tomography (DE-CBCT) are promising modalities for applications ranging from vascular to breast, renal, hepatic, and musculoskeletal imaging. Accordingly, the optimization of imaging techniques for such applications would benefit significantly from a general theoretical description of image quality that properly incorporates factors of acquisition, reconstruction, and tissue decomposition in DE tomography. This work reports a cascaded systems analysis model that includes the Poisson statistics of x rays (quantum noise), detector model (flat-panel detectors), anatomical background, image reconstruction (filtered backprojection), DE decomposition (weighted subtraction), and simple observer models to yield a task-based framework for DE technique optimization.

Methods: The theoretical framework extends previous modeling of DE projection radiography and CBCT. Signal and noise transfer characteristics are propagated through physical and mathematical stages of image formation and reconstruction. Dual-energy decomposition was modeled according to weighted subtraction of low- and high-energy images to yield the 3D DE noise-power spectrum (NPS) and noise-equivalent quanta (NEQ), which, in combination with observer models and the imaging task, yields the dual-energy detectability index (d^′). Model calculations were validated with NPS and NEQ measurements from an experimental imaging bench simulating the geometry of a dedicated musculoskeletal extremities scanner. Imaging techniques, including kVp pair and dose allocation, were optimized using d^′ as an objective function for three example imaging tasks: (1) kidney stone discrimination; (2) iodine vs bone in a uniform, soft-tissue background; and (3) soft tissue tumor detection on power-law anatomical background.

Results: Theoretical calculations of DE NPS and NEQ demonstrated good agreement with experimental measurements over a broad range of imaging conditions. Optimization results suggest a lower fraction of total dose imparted by the low-energy acquisition, a finding consistent with previous literature. The selection of optimal kVp pair reveals the combined effect of both quantum noise and contrast in the kidney stone discrimination and soft-tissue tumor detection tasks, whereas the K-edge effect of iodine was the dominant factor in determining kVp pairs in the iodine vs bone task. The soft-tissue tumor task illustrated the benefit of dual-energy imaging in eliminating anatomical background noise and improving detectability beyond that achievable by single-energy scans.

Conclusions: This work established a task-based theoretical framework that is predictive of DE image quality. The model can be utilized in optimizing a broad range of parameters in image acquisition, reconstruction, and decomposition, providing a useful tool for maximizing DE-CBCT image quality and reducing dose.

INTRODUCTION

Dual-energy computed tomography (DE-CT) and dual-energy cone-beam computed tomography (DE-CBCT) provide numerous potential advantages over conventional single-energy CT, most importantly in providing superior contrast by selectively combining low-energy (LE) and high-energy (HE) image data (projections or reconstructions) in decomposition of various materials in the 3D image. Weighted subtraction of 3D reconstructions exploits the attenuation and scatter characteristics of materials at different energies, thereby differentiating materials that may be indistinguishable in single-energy CT—for example, in kidney stone characterization and distinguishing iodinated vessels in bone.^{1, 2, 3} In contrast-enhanced imaging (e.g., iodine-enhanced angiography, renal, or liver imaging), DE-CT is frequently acquired at energies straddling the K-edge of the contrast agent (e.g., 33 keV for iodine), thus allowing separation of contrast-enhanced structures from other dense materials (e.g., bone) that may confound visualization.^{4, 5} More complex DE decomposition algorithms can begin to transcend the traditional contrast mechanism of linear attenuation coefficients through the discrimination of tissue composition in terms of effective atomic number, electron density, basis material densities, etc.^{1, 6, 7, 8, 9, 10} In addition to improved contrast, DE-CT or DE-CBCT could potentially achieve more accurate beam hardening correction in projection-based decomposition^{6, 11} and reduction of radiation dose in contrast-enhanced imaging by producing a virtual noncontrast image that in some scenarios can preclude a precontrast scan.¹²

Dual-energy CT has shown promise in a wide spectrum of clinical applications,^{13, 14, 15, 16} raising the need for imaging performance optimization to knowledgably guide applications with respect to radiation dose, image noise, and the imaging task. In addition to the parameters that govern imaging performance in single-energy CT (e.g., kVp, mAs, detector performance, system geometry, etc.), DE imaging introduces additional factors that significantly affect image quality (e.g., the selection of kVp pair, application of added filtration, dose allocation between the high- and low-energy scan, and choice of noise reduction filters and decomposition algorithms). Current methods of technique optimization rely primarily on physical experimentation and iteration across the numerous relevant parameters. Such experimentation involves acquisition of DE images at permutations of kVp pair, dose allocation, filter material and/or thickness, and analysis in terms of basic performance metrics such as contrast, noise, and contrast-to-noise ratio (CNR).^{17, 18, 19} Due to the vast parameter space that needs to be taken into consideration, an accurate theoretical framework that is predictive of DE-CT image quality would greatly benefit such efforts in providing an efficient, rigorous, and more complete examination of the parameters of interest (potentially beyond the experimental limits of existing scanner technologies).

Toward this end, early work derived closed-form expressions of image noise associated with common DE-CT decomposition algorithms and used such expressions to elucidate several fundamental principles in DE-CT imaging techniques. Alvarez et al.⁶ described the image noise in the projection-based estimates of Compton and photoelectric contributions to linear attenuation coefficient, and in a later work, showed that linear combinations of such estimates at an optimized display energy may form a spectral shift artifact-free image that contains the same quantum noise as a single-energy image at the same total dose²⁰—a result proven experimentally by Kalender et al.⁹ Kelcz et al.¹⁰ developed an equivalent decomposition method for estimating the densities of two materials and demonstrated the noise advantage of the two-kVp technique (where high- and low-energy images are acquired at two different energies) compared to the two-crystal technique (where both images are acquired simultaneously with two crystal layers—the first crystal forming the low-energy image and the second the high-energy image). An abundance of related work also investigated the noise characteristics of particular DE decomposition algorithms.^{1, 7, 8, 21, 22} The work reported below presents a theoretical model for reconstruction-based DE-CBCT decomposition that incorporates the detector model in the noise description, and defines DE image quality in relation to the imaging task. Based on previous modeling of DE projection radiography and CBCT,^{23, 24, 25, 26} the cascaded systems analysis framework accommodates general characteristics of imaging techniques (kVp pair, filtration, and dose allocation), the imaging chain (detector type, additive noise, etc.), and decomposition algorithm (weighted subtraction and noise reduction parameters). Analytical forms for the DE-CBCT performance metrics such as the noise-power spectrum (NPS), modulation transfer function (MTF), and noise-equivalent quanta (NEQ) are derived, allowing description of image quality with respect to a given imaging task in terms of the detectability index (d^′), which has previously shown reasonable correspondence with human observer performance for a broad range of imaging conditions and simple imaging tasks.²⁷

As detailed below, the work first presents the cascaded systems model extended to reconstruction-based DE-CT or DE-CBCT [the latter emphasizing a flat-panel detector (FPD) in the imaging chain], then validates the accuracy of the model by comparing theoretically calculated DE NPS and NEQ with experimental measurements. The utility of the model is demonstrated in example optimization of DE acquisition parameters (dose allocation and kVp pairs) in relation to specific imaging tasks using detectability index as the objective function. The results below are restricted to analysis of the 3D NPS and NEQ near the central axial plane (ignoring effects of the Fourier “null cone”/cone-beam artifact for a circular source-detector orbit²⁸) and assumes “local” stationarity of the first- and second-order image statistics²⁹—i.e., invariance of the NPS within a limited (central) region of the volumetric image.

METHODS

Reconstruction-based dual-energy image decomposition

The most common form of reconstruction-based (also called “image-based”) DE image decomposition involves a weighted subtraction of the high- and low-energy 3D image reconstructions

$$I^{\mathrm{DE}}=I^{\mathrm{HE}}-w{I}^{\mathrm{LE}},$$ (1)

where I^DE, I^HE, and I^LE denote the dual-energy, HE, and LE CBCT reconstructions, respectively. The tissue cancellation factor w is a scalar broadly defined to reduce the signal value (attenuation coefficient or HU) of one material, M₁, to the same intensity as another material, M₂, effectively “canceling” M₁ from the DE image. Assuming perfect cancellation (i.e., ignoring effects of x-ray scatter, spatial variation of x-ray energy throughout the object, etc.), we have

$${\mu }_{M_1}^{\mathrm{DE}}={\mu }_{M_2}^{\mathrm{DE}}={\mu }_{M_1}^{\mathrm{HE}}-w{\mu }_{M_1}^{\mathrm{LE}}={\mu }_{M_2}^{\mathrm{HE}}-w{\mu }_{M_2}^{\mathrm{LE}}$$ (2a)

yielding w as the ratio of the difference in effective linear attenuation coefficients (μ₁ and μ₂) of the two materials (M₁ and M₂) in the high-energy image to that in the low-energy image

$$w=\frac{{\mu }_{M_1}^{\mathrm{HE}}-{\mu }_{M_2}^{\mathrm{HE}}}{{\mu }_{M_1}^{\mathrm{LE}}-{\mu }_{M_2}^{\mathrm{LE}}}.$$ (2b)

The effective attenuation coefficients, μ, are computed using linear attenuation coefficients provided in ICRU Report No. 33 (Ref. ³⁰) and a polychromatic beam model generated from Spektr.³¹

Variants of the simple weighted subtraction algorithm have been reported in literature, e.g., applying weighting factors to both the high- and low-energy images. A bit of arithmetic reveals that signal and noise are scaled equivalently in such forms, and the detectability index (below) is unaffected by the form of (linear) weighting factors applied if the same material is being canceled. Alternatively, w may be freely varied for manual adjustment of the contrast between structures of interest and the background [e.g., to account for effects of scatter, beam hardening, or other reconstruction artifacts, or varied in this study to demonstrate the effect of material cancellation on image quality (Fig. 5)], exposing w as a parameter that may be adjusted as simply as the window and level. Results below pertain to the single-parameter, weighted subtraction DE decomposition algorithm given in Eq. 1.

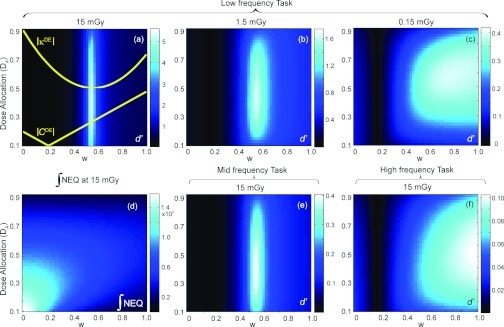
Figure 5.

Detectability index computed as a function of w and A for a low-frequency detection task at (a) 15 mGy, (b) 1.5 mGy, and (c) 0.15 mGy, and for (e) a midfrequency task and (f) a high-frequency task at 15 mGy. The integral of the quantum noise NEQ [Eq. 5] at 15 mGy is plotted in (d). Superimposed on (a) are plots of the absolute values of dual-energy contrast between a breast tumor and fibroglandular tissue, |C^DE|, and the dual-energy anatomical “clutter” magnitude, |κ^DE|. A clear optimum in d^′ is observed in (a) at w = ∼0.6 where κ^DE is reduced to 0 (i.e., cancellation of background clutter). As dose is lowered or the spatial frequency content of the tasks increases, canceling anatomical noise becomes less important, and the DE contrast eventually becomes the dominant factor in driving d^′.

Cascaded systems analysis of DE-CBCT

Previous work derived the Fourier-domain imaging performance metrics within the general framework of cascaded systems analysis³² for a variety of imaging modalities including cone-beam CT,^{26, 33} DE projection radiography,²³ and tomosynthesis.³⁴ Such modeling has demonstrated agreement with experimentally measured NPS and NEQ, with broad utility in detector design, technique optimization, and system development.^{33, 35, 36, 37}

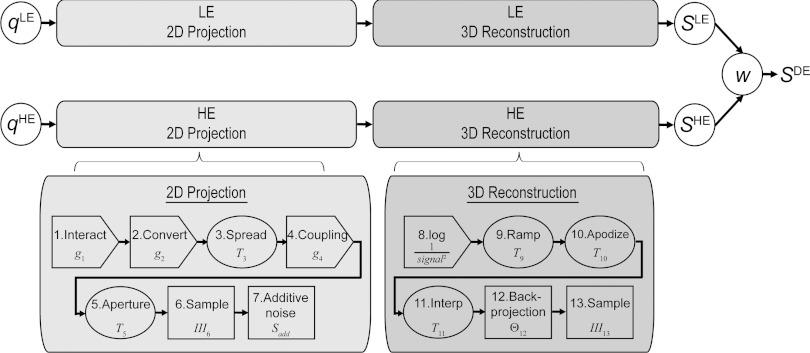
The cascaded systems model for CBCT consists of stages describing the physical processes in the 2D imaging chain and 3D reconstruction process, quantifying the propagation of signal and noise characteristics in terms of fluence, MTF, NPS, and NEQ. As shown in Fig. 1, stages 1–7 describe the physical processes of 2D projection formation (for both the LE and HE image) including x-ray interaction, photon spreading, sampling in the FPD, and electronics noise. Stages 8–13 describe the mathematical process of filtered backprojection, including reconstruction filters, 3D backprojection, and sampling. Previous work derived the closed-form relation for the stochastic noise-power spectrum (quantum and electronics noise) of a CBCT reconstruction as^{26, 38}

$$\begin{array}{ccc}\hfill S& =& \frac{\left({\overline{q}}_0{a}_{pd}^4{\overline{g}}_1{\overline{g}}_2{\overline{g}}_4\left(1+{\overline{g}}_4{P}_K{T}_3^2\right)T_5^2**II{I}_6+S_{add}\right)}{{\left({\overline{q}}_0{a}_{pd}^2{\overline{g}}_1{\overline{g}}_2{\overline{g}}_4\right)}^2}\hfill \\ & & \times T_9^2{T}_{10}^2{T}_{11}^2\frac{1}{M^2}{\Theta }_{12}^2***II{I}_{13},\hfill \end{array}$$ (3)

where ${\overline{g}}_i$ denotes the amplification (or loss) associated with gain stages (e.g., quantum detection efficiency, scintillator gain, and conversion efficiency), T_i is the transfer function for spatial spreading (e.g., MTF describing stochastic blur or integration by pixel apertures), S_add is the additive electronic noise, and Θ is the backprojection operator. The model has demonstrated close agreement with experimental measurements of both objective Fourier-domain metrics (NPS and NEQ) (Refs. ²⁶ and ³⁸) and human observer performance.²⁷ In all results below, cascaded systems model parameters associated with a FPD in combination with a 250 mg/cm² CsI:Tl scintillator (including gain, MTF, and Swank factor) were adapted from previous work.^{23, 24, 26, 39}

Figure 1.

Schematic diagram for cascaded systems analysis of reconstruction-based DE-CBCT. The 2D projection imaging chain (LE or HE) is characterized by seven stages ranging from x-ray interaction in the detector to 2D sampling and readout with additive electronic noise. The 3D reconstruction process is characterized by six algorithmic steps ranging from the logarithm to 3D backprojection and sampling. The DE decomposition step indicated by w combines the low- and high-energy reconstruction NPS (S^LE and S^HE) into the DE NPS (S^DE).

The separate models for DE decomposition and 3D reconstruction naturally combine in a general form for reconstruction-based DE-CBCT. As illustrated in Fig. 1, the DE decomposition step is incorporated following the reconstruction stages. Analogous to the form derived in Richard et al.,²³ the DE NPS, S^DE, is given by

$$S^{\mathrm{DE}}=S^{\mathrm{HE}}+w^2{S}^{\mathrm{LE}},$$ (4)

where S^HE and S^LE are the HE and LE energy NPS from Eq. 3. Frequency dependence of S and T [(f_x, f_y, f_z)] is omitted for conciseness. Similar to the single-energy NPS, the units of the 3D DE NPS, S^DE, is μ²mm³, where μ denotes the 3D DE image signal [i.e., the linear combination of single-energy linear attenuation coefficients according to Eq. 1] with units mm⁻¹.

The dual-energy NEQ can be defined based on DE NPS and MTF in a manner similar to the single-energy NEQ

$${\mathrm{NEQ}}^{\mathrm{DE}}=\pi f\frac{T^2}{S^{\mathrm{DE}}},$$ (5)

where T is the system MTF, assumed to be equal for the low-, high-, and dual-energy cases for simplicity.

The NEQ can be extended to account for the influence of anatomical background in diminishing task performance by including the background (“clutter”) power spectrum, denoted S_B, in the denominator as an additional noise term, yielding the “generalized” NEQ.⁴⁰ In anatomical sites such as the breast and lung, S_B is frequently characterized by the power-law relationship

$$S_B=\frac{\kappa }{\left(a{f}^{\beta }\right)}$$ (6)

where the exponent β describes the degree of correlation (clumpiness), a is a unity scale factor of units mm⁻¹, and κ is the magnitude of the background power spectrum, carrying the same units as S_B, μ²mm³.^{41, 42}

A similar expression can be written for the generalized NEQ of DE-CBCT as

$${\mathrm{NEQ}}^{\mathrm{DE}}=\pi f\frac{T^2}{S^{\mathrm{DE}}+S_B^{\mathrm{DE}}·T^2},$$ (7)

where $S_B^{\mathrm{DE}}$ is the dual-energy anatomical power spectrum (in the object domain). The weighted subtraction decomposition does not change the magnitude of β from a single-energy reconstruction but does affect κ in a manner proportional to the square of the contrast between the two materials that constitute the power-law pattern.³³ For example in DE breast imaging, where the contrast of endogenous fibroglandular, adipose, and tumor tissues are modified by decomposition, the factor κ^DE is proportional to the square of the contrast between fibroglandular and adipose tissue in the DE image. Selection of κ and β is detailed below.

Experimental validation of 3D dual-energy NPS and NEQ

Imaging performance metrics (e.g., NPS and NEQ) computed from the cascaded systems analysis model were validated against measurements from an experimental imaging bench consisting of: (1) an x-ray tube (DU693 in EA10 housing, Dunlee, Aurora, IL) with 14° anode angle and 0.8 mm focal spot size; (2) a PaxScan 4030CB flat-panel detector (Varian Imaging Products, Palo Alto, CA) with 2048 × 1536 pixels at 0.194 mm pixel pitch and ∼250 mg/cm² CsI:Tl scintillator; and (3) a motion control system (Compumotor 6k8, Parker Hannifin, Cleveland, OH) that operates a central rotation stage and allows precise positioning of the source and detector. The system geometry was set to that approximating a dedicated extremities scanner³⁶ with 43.3 cm source-to-axis distance and 55.4 cm source-to-detector distance. Acquisitions were performed with the FPD operated in 2 × 2 binning mode with a pixel size of 0.388 mm.

Low- and high-energy images were acquired over energy ranges of 60–90 kVp and 90–130 kVp, respectively, based on generator limitations and typical imaging techniques for DE-CBCT applications. Additional filtration was held fixed to 5 mm Al and 0.3 mm Cu for the low-energy dataset, and 0.3 mm Cu and 0.5 mm Ag for the high-energy dataset. Previous work identified such added filtration as near optimal for DE projection imaging,³⁷ and application of the theoretical model to optimize filtration specifically for 3D DE-CBCT is the subject of future work. In particular, the addition of 0.5 mm Ag to the high-energy beam has been shown to provide optimal separation between low- and high-energy spectra. Imaging techniques (mAs) were selected to deliver an approximately equal dose of 7.5 (±0.39) mGy at each kVp, with absolute dose measured using a 0.6 cm³ active volume ionization chamber (Accu-Pro 9096, RadCal, Monrovia, CA) at the center of a 16 cm diameter acrylic CTDI phantom.

To minimize scatter and beam-hardening artifacts in the image data, NPS measurements were performed in reconstructions of air with a 22.8 mm of Al placed in the beam to simulate attenuation through a uniform object (equivalent to ∼85 mm water in a 90 kVp beam filtered with 5 mm Al and 0.3 mm Cu). This method is equivalent to measuring NPS from a uniform object, e.g., a water cylinder, but with improved stationarity in the first and second-order statistics. Images were reconstructed from 360 projections acquired over 360° using 3D filtered-backprojection with a Hann apodization filter at an isotropic voxel size of 0.3 mm.

Dual-energy images were decomposed from LE and HE reconstructions according to Eq. 1. The tissue cancellation factor w was allowed to vary arbitrarily for the purposes of model validation. Two single-energy CBCT scans were acquired at each energy, allowing two DE images to be reconstructed at each energy pair. Subtraction of the 3D images provided detrending of background shading (e.g., heel effect, cupping artifact, etc.) prior to analysis of the NPS. Thirty nonoverlapping volumes of interest (VOIs) of size 53 × 53 × 53 voxels or 15.9 × 15.9 × 15.9 mm³ were placed at a constant distance from the center of reconstruction within each difference image. The “local” NPS was calculated as the ensemble average of the square of the Fourier transform of each realization, denoted as ΔVOI^DE

$$\begin{array}{ccc}& & {\mathrm{NPS}}^{\mathrm{DE}}\left(f_x,f_y,f_z\right)\hfill \\ & & =\frac{1}{2}\frac{b_x{b}_y{b}_z}{N_x{N}_y{N}_z}⟨|\mathrm{FT}\left(\Delta {\mathrm{VOI}}^{\mathrm{DE}}\left(x,y,z\right)\right){|}^2⟩,\hfill \end{array}$$ (8)

where b_i and N_i are the voxel size (0.3 mm) and extent (53 voxels) of each VOI in the ith direction, respectively. The factor of 1/2 accounts for the amplification of noise resulting from the subtraction detrending process. The statistical error in the NPS estimation was reported as the standard deviation across the ensemble of VOIs at each spatial frequency, divided by the square root of the number of VOIs in the measurement.

Detectability index as an objective function

Fourier descriptors of MTF, NPS, and NEQ have been widely used in the assessment and optimization of imaging systems. Such physical metrics in themselves, however, reveal little information as to how human observers perform in relation to a given imaging task. As a simple extension of such objective metrics, previous work applied task-based detectability index to the analysis of DE projection radiography, CBCT, and tomosynthesis by combining simple observer models and imaging tasks with the NEQ.^{26, 27, 43} Such models have been validated in comparison to human observer performance for a variety of idealized imaging tasks, providing a simple yet powerful framework that bridges the gap between objective Fourier-domain metrics and human observers.^{27, 44} Considering the linear weighted subtraction in DE-CBCT decomposition, a straightforward extension of the single-energy detectability index yields its DE analogue

$$d{\prime }_{\mathrm{DE}}^2=\int \int \int \frac{{(T^{\mathrm{DE}}·W_{\mathrm{Task}})}^2}{S^{\mathrm{DE}}+S_B^{\mathrm{DE}}·T^{\mathrm{DE}2}}d{f}_{x}d{f}_{y}d{f}_z,$$ (9)

where T ^DE denotes the DE system MTF, which was assumed to be equal to the high- and low-energy MTF. The term W_Task is the Fourier domain task function,⁴⁵ defined as the difference of the two hypotheses in a binary decision task, namely, “signal-present” versus “signal-absent” (or “background-only”) for a detection task, and “signal A” versus “signal B” for an A versus B discrimination task. The “signal-absent” hypothesis corresponds to the Fourier transform of the background, which may either be uniform (e.g., in air) or structured (e.g., power-law anatomical background in the breast or lung). The “signal-present” hypothesis, on the other hand, is given by the Fourier transform of the object function (e.g., a sphere) on the background and carries magnitude equal to the contrast between the signal and the background. For reconstruction-based DE-CBCT, similar definitions apply, with the hypotheses weighted by the DE contrast (C ^DE) which, following Eq. 1, is a linear combination of the contrast in high-energy (C ^HE) and low-energy (C ^LE) images

$$C^{\mathrm{DE}}=C^{\mathrm{HE}}-w{C}^{\mathrm{LE}}.$$ (10)

The detectability index shown in Eq. 9 corresponds to the prewhitening observer model, where the observer is assumed to be able to fully decorrelate 3D noise characteristics. Alternatively, the 3D nonprewhitening observer filters the noise with a detection template in the form of the expected signal

$$\begin{array}{c}\hfill d{\prime }_{\mathrm{DE}}^2=\frac{{\left[\int \int \int {(T^{\mathrm{DE}}·W_{\mathrm{Task}})}^{2}d{f}_{x}d{f}_{y}d{f}_z\right]}^2}{\int \int \int \left(S^{\mathrm{DE}}+S_B^{\mathrm{DE}}·T^{\mathrm{DE}2}\right)·{(T^{\mathrm{DE}}·W_{\mathrm{Task}})}^{2}d{f}_{x}d{f}_{y}d{f}_z}.\end{array}$$ (11)

Compared to the prewhitening observer, the nonprewhitening model has been shown to give better agreement with human observers.^{27, 46}

The detectability index as written in Eqs. 9, 11 corresponds to the 3D detectability index in which the observer is able to fully interrogate volumetric information. The extent to which such a simple formulation corresponds to observers dynamically scrolling slices or interpreting multiple slices at once is the subject of ongoing research in image perception. The 3D detectability index can also be defined in analogous forms pertaining to a single slice through the reconstruction (called the “slice” detectability index), where the “signal” (numerator) and “noise” (denominator) are, respectively, integrated along the direction orthogonal to the slice. The results below are presented in terms of the 3D detectability index in order to capture the fully volumetric signal and noise characteristics without limiting results to a particular plane of visualization. More complex forms of observer models (e.g., with eye filters and internal noise, channelized Hotelling observer models, etc.^{27, 46, 47}) can be incorporated into the cascaded systems model and are the subject of future work.

Optimization of DE-CBCT imaging techniques

Example calculations were performed to demonstrate the utility of detectability index as an objective function for optimizing imaging techniques and decomposition parameters, including the tissue cancellation factor (w), dose allocation (A), and kVp pairs. The tissue cancellation factor w was chosen to “cancel” a particular material relative to another, giving w as a function of kVp pairs. The detectability index was then calculated as a function of both the dose allocation factor (i.e., the fraction of dose imparted by the LE acquisition, ranging from 0 to 1) and the kVp pair, and the peak detectability d^′ (A, kVp^LE, kVp^HE) identified the optimum combination of A and kVp. Calculations assumed a nominal total dose (HE plus LE scans) of 15 mGy. The object was assumed to be equivalent to 15 cm of water. The same filtration was used as that in the experiments described in Sec. 2C (5 mm Al and 0.3 mm Cu for low-energy, and 0.3 mm Cu and 0.5 mm Ag for high-energy acquisition). Electronics noise in the simulation was taken as 7000 electrons based on measurements from Yang et al.⁴⁸

Three idealized imaging tasks were computed based on a variety of potential DE imaging applications as detailed in the following three subsections.

Identification of kidney stone composition

A kidney stone differentiation task was formulated assuming two minerals commonly found in renal calculi, brushite (CaHPO₄·2H₂O), and calcium phosphate Ca₃(PO₄)₂.⁴⁹ The linear attenuation coefficient of each was calculated from the respective elemental composition and density (brushite: 2.33 g/cm³, calcium phosphate: 3.14 g/cm³). Dual-energy decomposition was set to cancel brushite to the same intensity as a soft tissue (ICRU-44) (Ref. ⁵⁰) background. The resulting contrast between brushite (or equivalently soft tissue) and calcium phosphate was taken as the DE contrast, C^DE. The detectability index was computed for a low-to-mid frequency detection task consisting of a 1.5 mm radius sphere

$$W_{\mathrm{Task}}=\mathrm{FT}\left\{C^{\mathrm{DE}}·\mathrm{H}\left[r^2-\left(x^2+y^2+z^2\right)\right]\right\},$$ (12)

where H is the heavyside step function and r = 1.5 mm.

Iodine-enhanced vessel versus bone

A vessel-in-bone task was computed to simulate a common application of contrast-enhanced angiography in which iodine-enhanced vessels need to be distinguished from surrounding bone. The tissue cancellation factor was chosen to cancel cortical bone to the same intensity as soft tissue, leaving an iodine-enhanced vessel. The dual-energy contrast was calculated as iodine (10 mg/ml) versus bone (or equivalently soft tissue). This amounts to a detection task in the DE image. For simplicity, the directional dependence of the vessel was ignored and a symmetrical 3D midfrequency imaging task was defined directly in the Fourier domain as the difference between two Gaussians

$$\begin{array}{ccc}\hfill W_{\mathrm{Task}}& =& C^{\mathrm{DE}}·\left[\exp \left(-\frac{f_x^2+f_y^2+f_z^2}{2{\sigma }_1^2}\right)\right.\hfill \\ & & \left.-\exp \left(-\frac{f_x^2+f_y^2+f_z^2}{2{\sigma }_2^2}\right)\right],\hfill \end{array}$$ (13)

where σ₁ = 0.3 mm⁻¹ and σ₂ = 0.2 mm⁻¹.

Soft-tissue tumor detection in anatomical background

A generic soft-tissue tumor detection task was modeled assuming a tumor embedded in a power-law cluttered anatomical background. Pertinent tissues include the tumor and the two materials constituting the power-law pattern. Dual-energy contrast was therefore modeled as the signal difference between the tumor and the background material closer in attenuation coefficient to the tumor. Results below are shown for a breast tumor detection task on a fibroglandular and adipose tissue background. Other tasks that can be modeled within a similar framework (the subject of future work) include detection of a lung nodule in a lung tissue and air background, detection of a sarcoma in a muscle and adipose background, etc.

The linear attenuation coefficient of breast tumor was taken from Johns and Yaffe for infiltrating ductal carcinoma⁵¹

$${\mu }_{\mathrm{tumor}}=0.0343{\mu }_{\mathrm{Al}}+0.8411{\mu }_{\mathrm{lu}},$$ (14)

where μ_Al and μ_lu are the linear attenuation coefficients of aluminum and lucite [polymethyl methacrylate (PMMA)], respectively. The dual-energy contrast was taken as the difference in signal levels between breast tumor and fibroglandular tissue.

The anatomical background noise was characterized by the power-law relationship described in Sec. 2B, with β equal to 3 (consistent with power spectrum measurements from the breast by many authors^{52, 53} and expected of 3D self-similar “fractal” structure⁵⁴).The value of κ for anatomical background in the breast was estimated using the relationship $\kappa \approx \lambda {({\mu }_{\mathrm{fibroglandular}}^{\mathrm{DE}}-{\mu }_{\mathrm{adipose}}^{\mathrm{DE}})}^2$, i.e., κ was assumed to be proportional to the square of the contrast between adipose and fibroglandular tissue. The proportionality constant λ was found from previous measurements in a lung phantom⁵⁵ and a sphere phantom,⁵⁴ both yielding similar values of λ (∼0.0079 mm³).

The nominal imaging task for the tumor detection task consisted of a low-frequency 3 mm Gaussian function defined in the spatial domain and imaged at a total dose of 15 mGy. To illustrate the benefit of tissue cancellation, w was allowed to vary from 0 to 1 instead of being held fixed as in the previous two tasks described in Secs. 2E1, 2E2. The total dose and the frequency content of the tasks were also varied to illustrate the impact of C^DE, S^DE, and $S_B^{\mathrm{DE}}$ on detectability. Two additional dose levels were investigated, 1.5 and 0.15 mGy, spanning three orders of magnitude to examine the low-dose limits of detectability and illustrate tradeoffs between quantum noise and anatomical clutter as imaging conditions transition from an anatomical noise limited regime to a quantum noise limited regime. Two additional imaging task included: (1) a low-mid frequency task defined as a 1.5 mm radius sphere, and (2) a high-frequency task modeled as the difference between two Gaussian tasks defined in the frequency domain following Eq. 13 with σ₁ = 0.9 mm⁻¹ and σ₂ = 0.8 mm⁻¹.

RESULTS

Comparison of theoretical and experimental NPS and NEQ

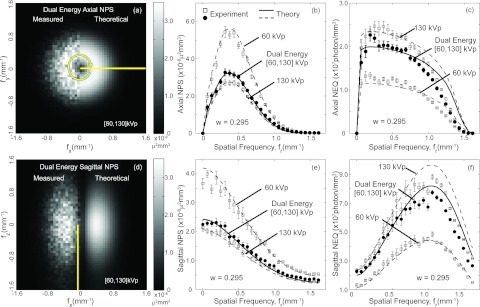
Figure 2 shows example DE NPS [Figs. 2a, 2b, 2d, 2e] and NEQ [Figs. 2c, 2f] for the [60, 130] kVp pair DE image. The profiles in Figs. 2b, 2c are the radial average calculated from the axial plane of the 3D NPS^DE and NEQ^DE, respectively. The sagittal profiles in Figs. 2e, 2f represent the angular average of line profiles taken four samples away from the origin of the f_z axis, i.e., f_z = 0.249 mm⁻¹. The NPS and NEQ from single-energy reconstructions are also plotted as dashed lines on the corresponding graphs for comparison. Error bars depict the standard deviation of measurements from all VOIs. The tissue cancellation factor w was set to 0.295, resulting in a NPS^DE with magnitude intermediate to that of the high- and low-energy. The magnitude of NPS^DE could be greater than both the high- and low-energy NPS, depending on the choice of w but will always be greater than the high-energy NPS as evident from Eq. 4.

Figure 2.

Comparison of theoretical and measured NPS and NEQ from the [60, 130] kVp DE image and the associated single-energy images. The top row shows results in the axial (f_x, f_y) plane. An axial slice through the 3D NPS^DE is shown in (a). The radial average of the 3D NPS and 3D NEQ for this axial plane are displayed in (b) and (c). The bottom row shows the sagittal (f_x, f_z) plane. A slice through the 3D NPS in the sagittal plane is shown in (d). Sagittal profiles of the single-energy and dual-energy NPS and NEQ are plotted in (e) and (f) as angular average of line profiles taken at a fixed radius (f_z = 0.249 mm⁻¹) from the f_z axis. Theoretical predictions are shown as curves, whereas experimental results are shown as individual data points for (b), (c), (e), and (f). Reasonable agreement between theory and experiment was observed for both the single-energy and dual-energy results.

Theoretical calculations of both single- and dual-energy NPS and NEQ are in reasonable agreement with experimental measurements. A slight discrepancy is observed in the NEQ tails at spatial frequency above ∼0.7 mm⁻¹ where measurements exhibit a steeper decline than theory. The discrepancy is attributed to two possible sources of error. First, a slight underestimate of the tails of the MTF causes a slight underestimate of the NPS tails, which is in turn amplified in the NEQ since it enters in the denominator. Second, there are a variety of possible noise sources in the imaging/reconstruction system that may not be exactly accounted for in the model, including small discrepancies in the spectral model, electronic noise, and aliasing artifacts. Small errors in such factors may appear as subtle discrepancies in the NPS tails but are magnified in the high-frequency NEQ. Furthermore, a slightly larger discrepancy is observed in the sagittal NEQ along the f_z axis [Fig. 2f] where samples are selected closer to the region of the cone-beam artifact (null cone).

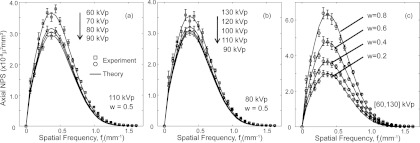
Figure 3 presents axial NPS^DE for a wide range of energy combinations at: (a) fixed high-energy at 110 kVp and low-energy ranging from 60 to 90 kVp and (b) fixed low-energy at 80 kVp at high-energy ranging from 90 to 130 kVp. A constant tissue cancellation factor (w = 0.5) was used in DE decomposition for purposes of illustration. Experimental results were plotted as individual data points for the [60, 110] and [90, 110] kVp pairs on Fig. 3a and the [80, 90] and [80, 130] kVp pairs on Fig. 3b. Figure 3c plots the axial NPS^DE for the [60, 130] kVp image at varying levels of w. The measured NPS exhibit a fairly typical level of experimental error (standard deviation in measured spectral estimates), and theoretical results demonstrate fairly good correspondence and fall within the error bars of most experimental data points. Other kVp combinations and w values were also examined and similar levels of agreement were observed. The general trend of NPS as a function of kVp is consistent with the behavior of single-energy imaging and is characteristic of the filters applied. In Fig. 3a, the NPS is seen to decrease with increasing low-energy kVp. For an incident x-ray fluence imparting the same dose to the center of the object, the total fluence to the detector after attenuation by the object increases with beam energy, therefore decreasing the NPS. Conversely, in Fig. 3b, where the low-energy kVp is kept constant, the DE NPS generally increases with high-energy kVp due to the introduction of the Ag filter which decreases the fluence to the detector beyond a certain kVp (∼80 kVp in this case). This effect, in conjunction with decreased quantum detection efficiency [$\overline{\mathrm{g}}$₁ in Eq. 3], results in NPS increasing with kVp.

Figure 3.

Comparison of theoretical and experimental DE NPS for a range of experimental conditions. (a) Fixed high-energy beam, and varied low-energy beam for a constant tissue cancellation factor w = 0.5. (b) Fixed low-energy beam, and varied high-energy beam, also for a constant tissue cancellation factor w = 0.5. (c) Varying levels of w at fixed low- and high-energy beams (60 and 130 kVp).

Detectability index

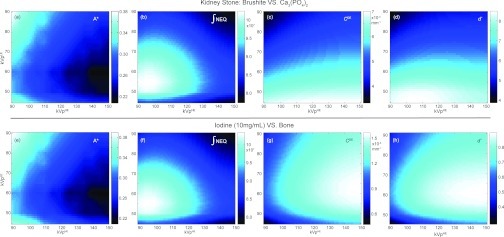
The optimization results for the brushite vs calcium phosphate kidney stone discrimination task are plotted in Figs. 4a, 4b, 4c, 4d as a function of kVp pairs (high-energy kVp, kVp^HE, and low-energy kVp, kVp^LE). As described in Sec. 2E1, the tissue cancellation factor w was chosen to cancel brushite to a soft-tissue background and has intrinsic energy dependence as well. Figure 4a plots the optimal dose allocation factor, A*, identified as the dose allocation, A, that maximizes detectability at each kVp pair. Some interesting trends were observed: for a fixed kVp^LE, A* decreases with higher kVp^HE as more dose is required to compensate for increased noise and decreased detective quantum efficiency (DQE) in the high-energy image; on the other hand, for a fixed kVp^HE, A* decreases with higher kVp^LE as the low-energy image becomes less noisy [Fig. 3a] as a result of increased transmission through the object; furthermore, as kVp^LE further increases, A* increases again due to a higher tissue cancellation factor w giving a higher weight on the low-energy image. For all kVp pairs, A* was found to be less than 0.5, indicating that more dose should be allocated to the high-energy image compared to the low-energy image. Figure 4b plots the integral of the 3D NEQ along the f_x, f_y, and f_z directions, which essentially reflects the d^′ of a task that has fixed C^DE for all energy pairs and is equally weighted in all spatial frequencies (i.e., a delta function detection task). The trend of the integral of NEQ can be explained in a similar way as that of A*: NEQ is optimized at low kVp^HE due to low NPS, and at intermediate or low kVp^LE depending on the tradeoff between decreasing NPS and increasing w. Figure 4c shows the DE contrast between brushite and calcium phosphate at different kVp pairs which follows naturally from the monotonically decreasing attenuation characteristics of the two materials. Detectability index plotted in Fig. 4d was calculated using the energy-dependent A* shown in Fig. 4a. The maximum d^′ identifies the optimal kVp pair at [45,105], with a corresponding A* of 0.32. The optimal kVp selection is driven by both the NEQ and contrast, as seen by the “blending” of optima from Figs. 4b and (c).

Figure 4.

Optimization results for a kidney stone discrimination task and an iodine vs bone discrimination task. (a) and (e): The optimal dose allocation factor, A*, identified as the dose allocation that maximizes d^′ at each kVp pair. (b) and (f): Integral of the 3D NEQ (irrespective of task) demonstrates similar trends despite different values of w and A*. (c) and (g): The dual-energy contrast of brushite vs calcium phosphate and iodine vs bone, respectively, with (g) reflecting the K-edge of iodine at 33 keV (i.e., ∼65 kVp). (d) and (h): Detectability index as a function of kVp pair calculated using the optimal dose allocation, A*, shown in (a) and (e), respectively. The detectability index of the kidney stone discrimination task (d) shows the combined effect of NEQ (b) and contrast (c), whereas that of the iodine vs bone task (h) is mainly driven by contrast (g).

Similar results are shown for the iodine vs bone discrimination task in Figs. 4e, 4f, 4g, 4h. The optimal dose allocation factors for both tasks show similar trends as the previous task as a function of kVp pairs and are less than 0.5 for all energy combinations. The integral of NEQ shows similar trends as well despite the different w and A* used in the calculations. In contrast to the kidney stone discrimination task, Fig. 4g presents a low-energy optimum at 65 kVp that reflects the K-edge effect of iodine, which consequently results in an optimal kVp selection mainly influenced by the contrast term [Fig. 4h].

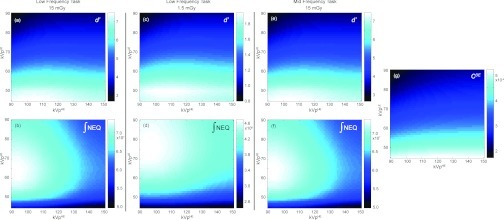
Figure 5 shows detectability index computed for the breast tumor detection task in the presence of anatomical background noise. The effects of tissue cancellation factor w and dose allocation factor (A) on d^′ are examined for three levels of total dose [(a) 15 mGy, (b) 1.5 mGy, and (c) 0.15 mGy] and three imaging tasks [(a) low-, (e) mid-, and (f) high-frequency] as described in Sec. 2E3. The absolute value of the magnitude of the DE anatomical background power spectrum, |κ^DE|, and the DE contrast modeled as the signal difference between breast tumor and fibroglandular tissue, |C^DE|, are superimposed on Fig. 5a. Figure 5d plots the integral of the 3D quantum noise NEQ. The energy pair is fixed at 60 and 120 kVp. The results for other energy pairs support similar conclusions (but are not shown for reasons of brevity).

For the low-frequency task at 15 mGy [Fig. 5a], the maximum d^′ is achieved at w ≈ 0.6, where the signal value of fibroglandular tissue is canceled to the same intensity as adipose tissue (w = 0.58), resulting in a minimum in [|κ^DE|. As the total dose decreases, the peak at w = 0.58 becomes less pronounced. As the total dose reduces by orders of magnitude to 0.15 mGy, anatomical noise is superceded by quantum noise, and cancellation of anatomical background no longer results in improved performance. Instead, d^′ is quantum noise limited and exhibits the combined effects of |C^DE| and quantum noise NEQ [Fig. 5d], as evident in: (i) the valley at w ≈ 0.2, consistent with the point at which |C^DE| reaches 0; and (ii) the peaks at A ≈ 0.4–0.6 observed at w > ∼0.5, consistent with trends in the integral of the NEQ [Fig. 5d]. Variation of the frequency content of the imaging tasks yields similar results. The influence of anatomical noise becomes less severe as the frequency content of the imaging tasks extends beyond the low-frequency region dominated by anatomical noise. For the high-frequency task, performance is quantum noise limited even at high doses. Such behavior is reminiscent of similar tradeoffs in single-energy tomosynthesis and CBCT.

The integral of the NEQ at 15 mGy plotted in Fig. 5d is representative of similar trends at other dose levels. As expected, the dose allocation that maximizes NEQ at each w is seen to increase with w, demonstrating that more doses needs to be imparted by the low-energy image as its decomposition weight increases. This trend is also reflected in the detectability index calculations in Fig. 5a–(c), (e)–(f). When w = 0 (i.e., for a single high-energy image) the NEQ decreases monotonically as A increases (i.e., as the dose allocated to the high-energy image decreases). At higher values of w, the NEQ [vertical profiles in Fig. 5d] exhibits an optimum at intermediate values of A since low and high extremes of A result in high NPS in the low-energy and high-energy images, respectively.

Optimization of kVp pairs for the breast tumor detection task are shown in Fig. 6. The detectability index computed as a function of kVp pair is plotted along with the integral of the NEQ for three conditions: (1) the low-frequency task at 15 mGy [Figs. 6a, 6b]; (2) the low-frequency task at 1.5 mGy [Figs. 6c, 6d]; and (3) the midfrequency task at 15 mGy [[Fig. 6e, 6f]. Note that the NEQ in Fig. 6b and (f) is computed with the optimal dose allocation, A*, for the respective tasks. The DE contrast modeled as the signal difference between the tumor and the fibroglandular tissue is included in Fig. 6g for reference. Based on the optimization results from Fig. 5, w was chosen to cancel fibroglandular to adipose tissue, thereby reducing anatomical noise to zero. The optimal dose allocation factor exhibits similar trends as the previous two tasks (Fig. 4) and is not shown for brevity. Similar to the kidney stone discrimination task, the detectability index is affected by both the NEQ and DE contrast, which can be appreciated through the “blending” of optima from the corresponding figures. As the total dose is reduced, the integral of NEQ exhibits an optimum at a higher kVp^LE due to the stronger influence of quantum noise, consequently moving the optimal kVp selection from [65, 90] kVp at 15 mGy [Fig. 6a] to [75, 90] kVp at 1.5 mGy [Fig. 6c]. As the frequency content of the tasks is varied, however, the optimal kVp selection remains for the most part unchanged [Fig. 6e].

Figure 6.

Detectability index and integral of the NEQ computed for a low-frequency task at 15 mGy [(a) and (b)], a low-frequency task at 1.5 mGy [(c) and (d)], and a midfrequency task at 15 mGy [(e) and (f)]. Dual-energy contrast between the tumor and fibroglandular tissue in the DE image is plotted in (g). The optimal kVp selection demonstrates a combined effect of NEQ and DE contrast, and is affected by total dose more than the frequency content of the task.

DISCUSSION AND CONCLUSIONS

This work reported a cascaded systems model for DE-CBCT based on 3D filtered backprojection and reconstruction-based decomposition. Fourier-domain imaging performance metrics such as the NPS^DE and NEQ^DE were derived from the model and validated against measurements from an experimental CBCT imaging bench across a broad range of imaging techniques and decomposition parameters. The dual-energy detectability index was derived from such Fourier metrics for a variety of imaging tasks, including renal stone discrimination, iodinated vessel-bone discrimination, and soft tissue tumor detection in anatomical clutter. The detectability index provided an objective function in the optimization of DE imaging parameters including the tissue cancellation factor (w), dose allocation factor (A), and kVp pair.

For all tasks investigated, the optimal dose allocation factor was found to be below 0.5, indicating that more dose should be allocated to the high-energy image. The endogenous breast tumor detection task illustrated the benefit of dual-energy imaging in eliminating anatomical background clutter and improving detectability beyond traditional single-energy scans. Tradeoffs reminiscent of single-energy tomosynthesis in the battle between quantum and anatomical noise are also revealed—namely, that dual-energy imaging is most beneficial for low-frequency tasks and dose levels above the quantum-limited regime. The calculations also indicated that optimal kVp selection is dependent on total dose levels more than the spatial frequency content of the imaging tasks at a constant tissue cancellation factor. The kidney stone discrimination task exemplified the application of dual-energy imaging in discerning two materials with similar attenuation coefficients not possible in single-energy reconstructions. For both of these tasks, the optimal kVp selection was found to follow a combined effect of both NEQ (quantum noise) and DE contrast (tissue cancellation). Therefore, in these cases, optimizing imaging techniques based on noise or contrast alone is not sufficient, and a fuller appreciation of NEQ in relation to the imaging task was important to identifying the optima. The iodine vs bone task demonstrated the situation in which a material of interest exhibited a strong K-edge effect that resulted in a sharp contrast profile within the energy range of interest; therefore, the optimal kVp selection in this case was mainly contrast-driven.

Assumptions implicit in this work are significant and consistent with previous application of cascaded systems analysis of Fourier metrology in DE and CBCT imaging performance. These include the assumption of linearity and shift-invariance intrinsic to linear systems analysis. Furthermore, perfect tissue cancellation was assumed with the weighted subtraction algorithm, and the effects of x-ray scatter, spatial variation of x-ray energy as a result of attenuation through the object, etc., were ignored. Moreover, the present study focuses on the weighted subtraction algorithm for material decomposition, which is limited in the extent to which it provides quantitative measure of material composition. More complex decomposition algorithms, such as basis material decomposition either in the reconstruction or projection domain, could offer quantitative information of materials and beam-hardening artifact reduction.¹¹ Modeling and optimization of such algorithms within the general framework is subject of future work. A straightforward extension of the model to linear noise reduction algorithms that further improve image quality and reduce dose is also underway.⁵⁶