Discrete RNA libraries from pseudo-torsional space

Abstract

The discovery that RNA molecules can fold into complex structures and carry out diverse cellular roles has led to interest in developing tools for modeling RNA tertiary structure. While significant progress has been made in establishing that the RNA backbone is rotameric, few libraries of discrete conformations specifically for use in RNA modeling have been validated. Here, we present six libraries of discrete RNA conformations based on a simplified pseudo-torsional notation of the RNA backbone, comparable to phi and psi in the protein backbone. We evaluate the ability of each library to represent single nucleotide backbone conformations and we show how individual library fragments can be assembled into dinucleotides that are consistent with established RNA backbone descriptors spanning from sugar to sugar. We then use each library to build all-atom models of 20 test folds and we show how the composition of a fragment library can limit model quality. Despite the limitations inherent in using discretized libraries, we find that several hundred discrete fragments can rebuild RNA folds up to 174 nucleotides in length with atomic-level accuracy (<1.5Å RMSD). We anticipate the libraries presented here could easily be incorporated into RNA structural modeling, analysis, or refinement tools.

INTRODUCTION

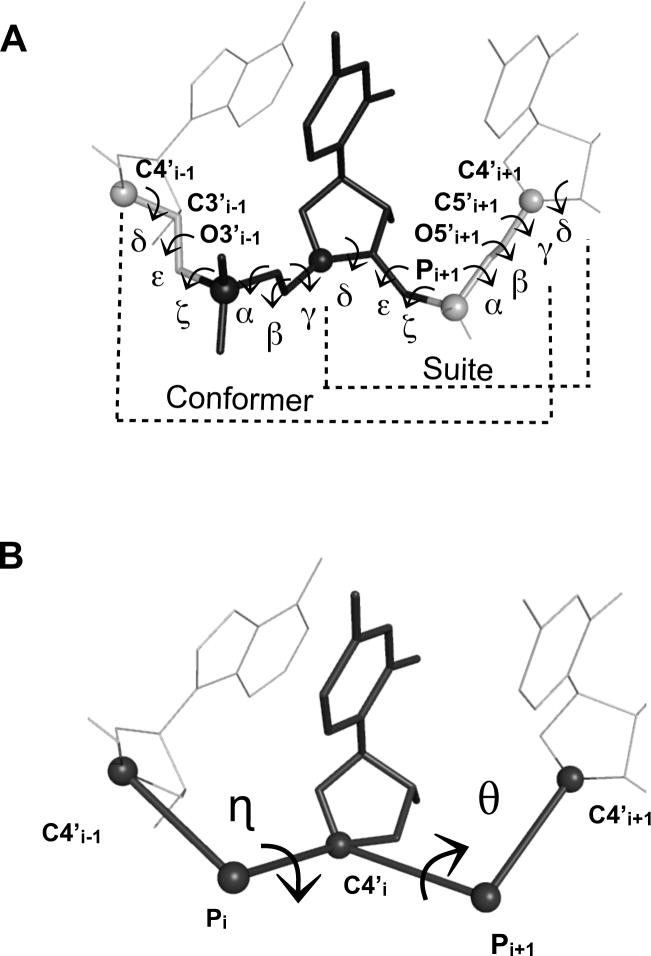
The cellular role of RNA is now known to extend far beyond simple transfer of genetic information to include catalysis, molecular recognition, and genetic control ¹. Thus, RNA can act as a folded macromolecule with striking parallels to proteins ². Knowledge of RNA 3D structure can therefore be critical for understanding the structural mechanisms involved in RNA conformational changes, ligand and protein binding, and catalysis. Despite the growing interest in RNA tertiary structure, the development and success of computational tools for RNA structural modeling has lagged behind the counterpart tools for proteins. This is in part due to the difficulty in determining experimental RNA structures with sufficiently high resolution, and is in part due to the complexity inherent in the six torsional degrees of freedom within the RNA backbone of each nucleotide (Figure 1A). In the last two decades, the number, diversity, and quality of solved RNA structures has grown tremendously and this has allowed the structural features of the RNA backbone ^{3; 4; 5; 6; 7; 8} and bases ^{9; 10} to be analyzed in great detail.

Figure 1. Using pseudo-torsions to reduce RNA backbone dimensionality.

(A) A nucleotide, with its six standard backbone torsions labeled, is depicted in black stick atoms. A suite, which spans from sugar to sugar and comprises 7 torsions is also denoted. Atoms defined to be part of a filtered fragment, which include the O3’ , C3’ and C4’ atoms of the preceding nucleotide and the P, O5’, C5’ and C4’ atoms of the following nucleotide, are also shown in stick. (B) Two pseudo-torsions (black arrows) per filtered fragment are created by forming pseudo-bonds between consecutive C4' and phosphorus atoms along the RNA backbone (black lines and spheres, respectively). The two resulting pseudo-torsions are named eta, η [C4'_i-1,P_i,C4'_i,P_i+1] and theta, θ, [P_i,C4'_i,P_i+1,C4'_i+1].

Recently, several groups identified rotameric backbone conformations that occur repeatedly within RNA structures ^{5; 6; 7; 8}. Rotameric conformations have long been observed for the torsion angles of small molecules, as well as for the torsions of the protein backbone ¹¹ and side chains ¹². The discovery that protein side-chains have strong torsional preferences led to the development of protein rotamer libraries that have been used with great success in molecular modeling for prediction and design^{13; 14} or structural validation¹⁵. Initially, protein rotamer libraries consisted of a limited number of idealized side-chain conformations that were understood to represent local minima on the potential energy surface ^{16; 17}. However, several studies suggested that early rotamer libraries were incomplete and, as a result, expanded protein rotamer libraries were developed that consisted of hundreds, or even thousands, of side-chain conformations ^{18; 19; 20; 21}. The conformations within these libraries typically consisted of side-chains taken directly from high-resolution crystal structures and therefore did not always correspond to local energy minima. Nevertheless, the larger rotamer libraries were shown to be superior to earlier libraries in achieving accuracy in protein modeling ^{18; 19; 20; 21}.

A consensus RNA backbone rotamer library of 46 conformations was recently published that incorporates and builds upon several earlier RNA rotamer libraries ^{5; 6; 7}. While the consensus library represents a significant achievement in terms of quantitatively describing RNA backbone structure, incorporating the consensus library into modeling tools that build RNA structure may present a unique challenge. This is because each rotameric backbone state is defined in terms a new unit of RNA structure, termed a “suite” (Figure 1A) ^{7; 8}. A “suite” consists of seven backbone torsions (δ, ε ,ζ, α, β, γ and δ and spans two nucleotide sugars (Figure 1A). The suite notation is straightforward to use for structure quality assessment ²². However, because each suite both begins and ends with a sugar ring, assembling individual suites into larger RNA structures can be difficult. Whereas two traditional nucleotides can be joined at a single phosphate atom, joining two suites requires that they overlap completely by one sugar ring. Therefore, a minimization protocol would need to resolve any potentially differing sugar conformations resulting from overlapping suites. While a local minimization step could be incorporated into rotamer based modeling tools, doing so could undercut advantages in computational speed that normally would be gained from using a purely rotamer based approach.

To date, no finite list of representatives of the 46 suites within the consensus rotamer set has been published. Thus, to use the suite notation during modeling building, a protocol is needed to select among the many different possible conformations that could simultaneously satisfy the ranges of seven backbone torsions involved in each of the consensus suites. Keating and Pyle recently illustrated the only technique available thus far to combine suites during model building. Their protocol requires that a backbone trace is known in advance and then uses coordinate minimization to generate suite conformations compatible with the pre-existing backbone trace ²³. In this work, we provide an alternative approach to using the consensus set during model building. Specifically, we present several discrete libraries of RNA conformations that are easy to combine and do not require coordinate minimization or a pre-existing backbone trace. The libraries we present should be ideal for use in de novo modeling tools that employ pair-wise decomposable energy functions or require discrete rotamers. However, they could also be useful as a starting point for modeling approaches that employ conformational minimization.

Instead of a rotamer set, most tools that model RNA employ either a coarse-grained modeling approach or make use of large databases of RNA fragments (for a review, see ²⁴). In coarse-grained modeling, low-resolution models are generated by representing each nucleotide in a highly reduced form, typically as one or more spheres ^{25; 26; 27}. Coarse-grained modeling can afford large advantages in speed, especially for modeling larger RNA folds ^{25; 26; 27}. However a second round of computational prediction is required to produce all-atom models from coarse-grained traces ²⁸. In contrast, all-atom RNA models are often built using either groups of base pairs ^{29; 30} or three-nucleotide long fragments taken from a single ribosomal subunit structure ³¹. Fragment based structure assembly has successfully generated models of small and medium sized RNA molecules with backbone accuracies of 2 to 10 Angstroms ^{29; 30; 31}. However, it is currently unknown what limitations these fragment libraries currently have. It is possible that some fragment libraries may over-represent certain RNA structural features, such as helical regions, but completely lack appropriate representatives for others.

In this work, we aim to develop libraries of discrete conformations (“filtered fragment libraries”) that exhaustively span RNA conformational space, are easy to assemble without implementation of minimization protocols, and are consistent with those already identified using the more comprehensive suite notation. To generate the filtered fragment sets, we use a pseudo-torsional notation that mimics the phi-psi notation of the protein backbone ^{32; 33; 34}. To form the pseudo-torsions, consecutive RNA backbone C4’ and phosphate atoms are linked with virtual bonds (Figure 1B). This creates two pseudo-torsions per RNA nucleotide: η [C4’_i-1,P_i,C4’_i,P_i+1] and θ [P_i,C4’i,P_i+1,C4’ _i+1] (arrows in Figure 1B). The RNA pseudo-torsion nomenclature might be ideal for generating libraries of RNA conformations for several reasons. First, nucleotides with similar η and θ values are often found within the same units of tertiary structure ³² and these values can be used to identify known or novel structural motifs within existing RNA structures ^{35; 36}. Second, small motifs of RNA, such as the GNRA tetra-loop, can be rebuilt with high accuracy by replacing native nucleotides in silico with non-tetraloop nucleotides that have similar pseudo-torsions ³³. Finally, when nucleotide pseudo-torsions are plotted in two-dimensional space, their associated RNA backbone conformations appear to cluster ^{32; 33}. Importantly, the clustering of nucleotide pseudo-torsions in two-dimensions has recently been shown to correspond to the clusters of the RNA backbone suites observed in seven-dimensions ²³.

The accuracy of protein modeling had generally improved after expanded rotamer libraries were introduced ^{18; 19; 20; 21}. Thus, we created six libraries of RNA filtered fragments that varied in size from small (~70 fragments) to large (~500 fragments) and then we examined how the accuracy of RNA modeling depended on the choice of library used. The various libraries were constructed by using the pseudo-torsional notation to select representatives directly from a dataset of high quality crystallographic structures with η and θ values spaced every 60º, 30º, 20º, 15º, 10º, or 5º. While each library was created using a coarse-grained approach based on only two atoms per nucleotide (C4’ and P, see Figure 1), each individual library conformation retained all-atom detail. As the word rotamer is typically reserved for ideal conformations located at the bottom of a local energy minimum, we refer to the members of each of the libraries of discrete RNA conformations as “filtered fragments”.

Here, we first briefly describe the features of the six libraries, and then we present methodological rules for connecting the fragments into dinucleotides that are consistent with the previously published suite nomenclature. We evaluate the performance of each library at modeling single nucleotides, dinucleotides, and entire RNA folds and we find that the modeling accuracy at all structural levels is dependent on the filtered fragment library used. Importantly, we find fewer than several hundred well chosen fragments are sufficient to build models of RNA folds with atomic-level accuracy. These sets of pseudo-torsion based libraries are small enough to ensure speed and efficiency for modeling tools, but large enough to model RNA folds with high accuracy. Thus we anticipate the pseudo-torsion based libraries will be of use in the future for a wide variety of modeling applications.

RESULTS

Generation of Filtered Libraries of Pseudo-Torsional Fragments

The same dataset of 171, high quality, crystallographic structures that was used to identify clusters of RNA backbone torsions in 7-dimensions ⁷ (“RNA05”; see Methods) was also used to generate the pseudo-torsion based libraries. As in ⁷, we eliminated from the dataset nucleotides with high atomic b-factors or residues with steric clashes (see Methods). Further, to ensure that only the highest quality nucleotides were included within the libraries, we removed nucleotides that had poorly-defined sugar puckers or that lacked all necessary pseudo-torsional atoms (see Figure 1A and Methods).

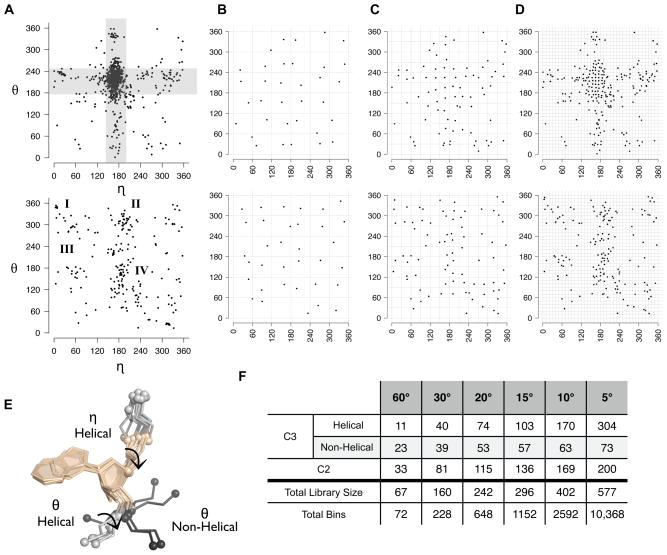
Once the dataset of high quality filtered nucleotides was created, we first surveyed the range of pseudo-torsions present by measuring the η and θ values of each filtered nucleotide (see Methods and Figure 1B) and plotting these values against each other in a 2-D, Ramachandran-like, scatter plot (Figure 2A). In keeping with precedent set in other studies ^{32; 33}, nucleotides were first grouped by sugar pucker (see Methods) and two η- θ plots were created: one η- θ plot for nucleotides with C3’-endo sugar pucker (Figure 2A, top) and a second plot for nucleotides with C2’-endo (Figure2A, bottom) sugar pucker.

Figure 2. Using pseudo-torsions to generate filtered fragment libraries.

(A) Pseudo-torsions were measured for a dataset of quality filtered RNA nucleotides (see Methods) and plotted in a Ramachandran-like manner. Pseudo-torsions are shown for C3’-endo (A, top) and C2-endo (A, bottom) nucleotides separately. Horizontal and vertical grey bars depict ranges of eta (150<η<190) and theta (190<θ<260) associated with nucleotides in a helical conformation. Clusters of nucleotides previously associated with kink-turn and π-turn motifs, asymmetrical internal loops, or S1 and S2 motifs are denoted by I, II, and III, respectively (A, bottom)²⁹. The cluster of nucleotides denoted as IV includes the 5’-halves of adenosine platforms as well as the second position of π-turns and Ω-turns (A, bottom)²⁹. (B-D) Filtered fragment libraries were generated by binning pseudo-torsional space, separated by sugar pucker, at varying degrees and selecting the single RNA extended nucleotide with pseudo-torsions closest to the center of each bin. Construction of the 60º (B, blue dots), 30º (C, green dots) and 10º (D, brown dots) libraries are shown. (E) Example C3’-endo fragment representatives, taken from the 10º library. All fragments have a helical η torsion, but differ in whether their θ torsion is helical or non-helical. Note the base placement of the central nucleotide is often similar for all fragments shown, regardless of pseudo-torsions. All atoms required to define each fragment’s pseudo-torsions, are depicted in grey stick form and the C4’ and P atoms defining the fragment pseudo-bonds are shown as spheres. (F) The total size of each of the six libraries created by pseudo-torsional binning, as well as the relative number of fragments helical in ηor θ are given. For reference, the number of pseudo-torsional bins created by each grid is also given.

Not surprisingly, the η-θ plots of the filtered RNA05 dataset were remarkably similar to η-θ plots observed in an early analysis of pseudo-torsions within a small set of 52 structures ³². Most notably, a large number of C3’-endo nucleotides had η- θ values within a very narrow range that was previously associated with the helical A-form of RNA ^{32; 33} (Figure 2A, grey regions; 150 < η <190; 190 < θ < 240). The η- θ plots of the filtered RNA05 dataset were also roughly the same as η- θ plots generated after applying an automated clustering algorithm to a larger set of approximately 7000 unfiltered crystallographic nucleotides ³³. Interestingly, the regions of scatter removed by automatically clustering nucleotides based on the similarity of their η- θ values ³³ appeared similar to the regions of scatter removed by quality filtering the RNA05 nucleotides to eliminate steric clashes, to have low b-factors, and to have well-defined pseudo-torsions and sugar pucker (see Methods and Suppl. Figure 1).

We next sought to create libraries of nucleotides with pseudo-torsions that spanned, or completely covered, the range of observed η- θ values. A previous study identified 11 pseudo-torsional based clusters by using standard clustering techniques ³³. However, we employed a non-clustering based methodology that allowed us to systematically generate libraries that varied in size but also ensured that representatives of all 11 previously observed clusters were included in each filtered fragment library. Specifically, we chose to bin the two filtered η- θ plots at one of six different resolutions (60º, 30º, 20º, 15º, 10º, or 5º) and selected from each resolution of bins the single nucleotide closest to the center of each bin (Figure 2B-D; see also Methods). If a bin was unpopulated, no nucleotide was selected. In such a manner, one “ideal” representative was chosen from each bin and taken to be representative of all other nucleotides within the same bin.

This binning process created six libraries that ranged in size from 67 to 577 (Figure 2F). Because almost every 60º and 30º bin was populated (Figure 2B-C), the 60° and 30° libraries contained filtered fragments with fairly uniformly spaced η-θ values (Figure 2F). In contrast, when the η-θ plots were binned at 20° or finer, many bins were located within the empty regions of the η-θ plots, which were unpopulated (Figure 2D). As a result, the 20°, 15°, 10° and 5° libraries were significantly smaller in size than expected from the total number of bins (Figure 2F). Further, a large number of the nucleotides within the 20°, 15°, 10° or 5° bins were located within the helical η-θ region (Figure 2D). As a result, the largest four libraries did not have evenly spaced η-θ values, but instead were biased towards helical conformations (Figure 2D, 2F). As an example, Figure 2D illustrates the selection of nucleotides using a 10° bin size and Figure 2E shows ten filtered fragments, each with helical η but varying θ, selected after binning at 10°. Note that each fragment consists of the backbone and base coordinates of a single selected nucleotide (Figure 2E, wheat atoms), as well as the coordinates of all the atoms involved in defining the selected nucleotide’s pseudo-torsions (Figure 2E, grey atoms). By saving the atoms that define the η and θ values of each library fragment, the pseudo-torsions of each fragment can be directly used during model building.

Filtered fragment library accuracy: Modeling the backbone and bases of individual nucleotides

To build accurate models of RNA folds, a filtered fragment library must reproduce structural features that are found within individual nucleotides. As a first test of each library, we thus asked how accurately the filtered fragments within each library could reproduce the backbone coordinates of each of the 8,466 individual nucleotide conformations within the original unfiltered RNA05 dataset (see Methods). To do so, we aligned the backbone atoms of every fragment within each library to the corresponding backbone atoms of every nucleotide in the RNA05 dataset and noted the RMSD over all the backbone fragment atoms, including those defining its η and θ values. We then used the backbone RMSD calculations to determine which of the library fragments was the most structurally similar to each individual RNA05 nucleotide.

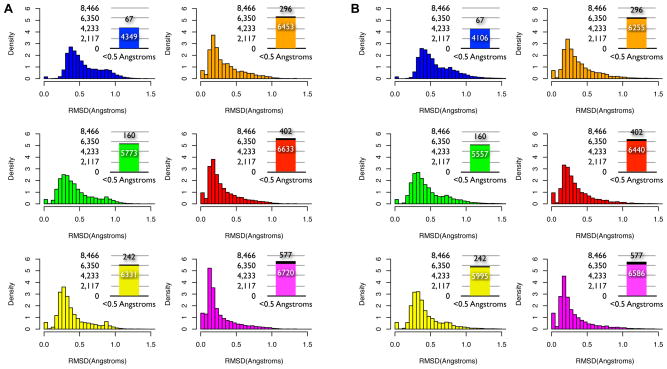
We evaluated the ability of each library to represent the diversity of backbone conformations within the RNA05 dataset by counting how many nucleotides had a library fragment with a backbone RMSD within 1Å or 0.5Å. Regardless of which filtered fragment library was examined, the majority of RNA05 nucleotides had a library fragment within 1Å backbone RMSD (Figure 3A). However, the six libraries differed in the number of nucleotides with a library fragment within 0.5Å backbone RMSD (Figure 3A, inset). For example, the 60° library modeled the backbone coordinates of approximately 50% (4349/8466) of the nucleotides to within an accuracy of 0.5Å, while the 30° library reproduced the backbone coordinates of 68% (5773/8466) of the nucleotides to within 0.5Å (Figure 3A, blue and green). In this case, a small increase in library size of only approximately 100 fragments resulted in a large increase in the number of nucleotides modeled to within 0.5Å accuracy. The shift towards modeling more RNA05 nucleotides with increased backbone accuracy continued for the remaining libraries. Impressively, all four libraries binned at 20° or finer were able to cover or “mimic” the backbone structure of 75% to 80% of the RNA05 nucleotides to within 0.5Å (Figure 3, yellow, orange, brown and magenta). This level of structural accuracy in modeling individual nucleotides is comparable to that typically calculated for many protein side-chain rotamer libraries ^{18; 19}.

Figure 3. Coverage of individual RNA05 nucleotides by pseudo-torsional fragment libraries.

(A) The backbone atoms of 8,466 individual RNA05 nucleotides were aligned with the backbone atoms of every filtered fragment within a library and the fragment with the lowest backbone RMSD was noted. The histograms show the distribution of backbone RMSD values determined between the library fragments and each of the 8,466 nucleotides and the insets show the number of RNA05 nucleotides that had a filtered library fragment with backbone RMSD of 0.5 Å or less. RNA05 nucleotides that were themselves members of the fragment library, and thus had 0 Å backbone RMSD, are shown in the inset in black. Results for each of six libraries are color coded as follows: 60º (blue), 30º (green), 20º (yellow), 15º (orange), 10º (brown) and 5º (magenta) (B) All heavy atoms of 8,466 individual RNA05 nucleotides were aligned with all heavy atoms of every fragment within a library and the filtered fragment with the lowest all-atom RMSD was noted. If needed, the base of each filtered fragment was computationally mutated to match that of the RNA05 nucleotide prior to the all-atom alignment. The histograms show the distribution of all-atom RMSD values determined between the library of filtered fragments and each of the 8,466 nucleotides. The insets show the number of RNA05 nucleotides that had a library fragment with an all-atom RMSD of 0.5 Å or less. RNA05 nucleotides that were themselves members of the fragment library, and thus had 0 Å backbone RMSD, are shown in the inset in black. Libraries are color-coded as in (A).

We next evaluated how accurately each library could reproduce the full coordinates of all of the unfiltered RNA05 nucleotides, including each nucleotide’s base. To compute all-atom RMSDs, we computationally mutated the base of each filtered fragment to match that of each RNA05 nucleotide prior to aligning all heavy atoms (see Methods). The library fragment with the minimum all-atom RMSD to each nucleotide was then noted. Surprisingly, the accuracy of the library fragments in modeling the dataset of nucleotides in all-atom detail was very similar to the accuracy previously observed for modeling only the backbone atoms of each nucleotide. Even when the base atoms were included, each of the filtered fragment libraries modeled the majority of nucleotides to within 1Å accuracy. Further, the largest four libraries modeled 70-78% of nucleotides to within 0.5Å accuracy (Figure 3B). Often, the filtered fragment that “best fit” the coordinates of an entire nucleotide when calculating all-atom RMSD was the same library fragment that “best fit” the nucleotide when only backbone RMSD coordinates had been considered (Suppl. Figure 2). These results suggest that when a library fragment accurately models the backbone atoms of a nucleotide, the base atoms of the nucleotide will often be modeled accurately as well.

Pseudo-torsional guided assembly of filtered fragments into in silico dinucleotides

We next asked whether the filtered fragments within each library could be assembled into physically realistic dinucleotides. Assembling two single nucleotides into a dinucleotide requires choosing how to place one nucleotide with respect to another. While a large number of dinucleotide conformations could theoretically be formed from a pair of individual nucleotides, we chose to orient and assemble individual library fragments into dinucleotides by using their pseudo-torsions as a guide (Figure 4A).

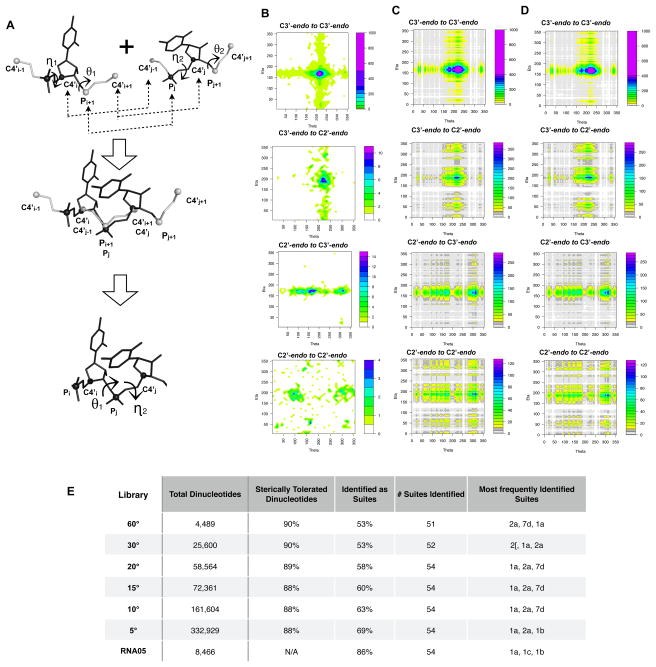
Figure 4. Assembly of pseudo-torsional fragments into dinucleotides.

(A) The nucleotides (black atoms) of any two filtered fragments can be connected into dinucleotides by using the extended pseudo-torsional atoms (grey atoms) to guide assembly by orienting one nucleotide relative to another (A, top). The last three atoms involved in the θ torsion of the first fragment [C4 _i, P_i+1, C4 _i+1] are aligned with the first three atoms involved in the torsion of the second fragment [C4’ _j-1, P_j, C4 _j] (A, middle). To connect the two fragments at the adjoining phosphate, a small translation was performed such that the overlapping phosphate atoms of the two fragments had identical coordinates. After attachment, the overlapping atoms used in the alignment (grey atoms) are removed and discarded. The connectivity of a dinucleotide can be represented in shorthand by the combination of θ-ηtorsions formed (A, bottom). If a longer stretch of RNA is desired, the last three extended atoms of the end fragment can be retained and used to add an additional fragment. (B-C) The frequency of θ- η torsions within two-nucleotides stretches of the RNA05 dataset (B) and the frequency of θ- η torsions within in silico dinucleotides assembled from the 10º library (C) are shown, color coded to the scales, in (B) and (C), respectively. Dinucleotides from the 10º library determined to have steric clashes via overlap of van der Waals radii (scaled by 60%, see Methods) are excluded from the plots in D. (E) For each filtered fragment library (column 1), the total number of dinucleotides generated (column 2), the percentage of dinucleotides determined to be free of serious atomic overlaps (column 3) and the percentage of dinucleotides identified by Suitename as a rotameric suite (column 4) are given. The total number, of out 54, of suites identified within the dinucleotides generated from each library (column 5) and the most frequently identified suites (column 6) are also given.

Specifically, dinucleotides were formed from two individual fragments by aligning three of the atoms involved in defining the θ torsion of one fragment with three of the atoms involved in defining the η torsion of a second fragment (see Figure 4A and Methods). In order to form a contiguous dinucleotide, the aligned pseudo-torsion atoms were joined at the phosphate atom, and all pseudo-torsional atoms were removed (see Figure 4B and Methods). However, for building structures longer than dinucleotides (see Modeling RNA Folds section), the pseudo-torsional atoms at the ends of a joined dinucleotide can remain and be used to guide attachment of the next incoming fragment. As a shorthand, we refer to each assembled dinucleotide by its θ-η value (red arrows in Figure 4A, bottom).

We evaluated whether assembling filtered fragments into dinucleotides based on their pseudo-torsions built realistic two-nucleotide conformations in the following manner. To begin, we created a library of dinucleotides from each fragment library by connecting, pair-wise, every combination of individual fragments in silico using the three-step assembly protocol. We then noted the θ- η value of every dinucleotide assembled in silico. To survey the connectivity of the in silico dinucleotides, we separated the dinucleotides by sugar pucker and plotted how frequently each pair of θ- η values occurred within the set of in silico dinucleotides (Figure 4C). We observed that a large number of dinucleotides with helical conformations connecting individual C3’-endo nucleotides had been formed in silico (Figure 4C; note C3’-endo sugars with 190 < θ < 240 or 150 < η <190). This trend was especially prevalent for the dinucleotides assembled from the 20º, 15º, 10º and 5º libraries (Suppl. Figure 3). As these four libraries contained a relatively large number of individual fragments with C3’-endo helical conformations (Figure 2F), this bias towards helical dinucleotide connectivities was not too surprising. We then compared the frequency of the in silico dinucleotide θ- η values (Figure 4C) to the frequency of the θ- η values calculated for two-nucleotide stretches within the dataset of RNA05 structures (Figure 4B). A similar strong bias towards connecting nucleotides with helical C3’-endo pseudo-torsions occurred within the experimental structures. We note that there is intrinsically no reason for this bias towards C3’-endo connectivity. Rather it is just a consequence of the population of filtered fragments selected to be within each library. Nevertheless, we conclude that assembling individual library fragments by using their pseudo-torsions as a guide results in dinucleotide orientations that largely mimic those observed within crystallographic structures.

While we observed that the in silico dinucleotides had orientations that largely mimic those seen experimentally, there was no guarantee per-se that the in silico dinucleotide conformations were physically realistic and free of steric overlaps. To address this, we next checked to see whether each in silico dinucleotide contained steric clashes by measuring overlap of van der Waals radii for each pair of atoms (see Methods; van der Waals radii were scaled by 60% due to the discrete nature of the fragments being assembled). After the dinucleotides identified to have serious clashes were removed from the exhaustive set (approximately 10% to 12%; Figure 4E) and the combinations of θ- η torsions of the remaining dinucleotides were re-plotted (Figure 4D), we observed that the pattern of θ- η frequencies appeared virtually unchanged (compare Figure 4C and Figure 4D). We thus conclude that the majority of the time, when two arbitrary fragments are assembled into a dinucleotide using their respective pseudo-torsions the conformation that results will be physically realistic.

Comparison of in silico dinucleotides and rotameric suites

Ideally, any library of discrete RNA conformations should include representatives of each of the previously identified backbone rotameric states ⁸. The two sugars within each in silico dinucleotide constitute one RNA suite (see Figure 1A). Based on this information, we were able to determine whether each set of in silico dinucleotides contained all of the previously published rotamer suites. To do so, we used the program Suitename ⁸ to calculate which suite, in 7 dimensional space, was most closely identified with each dinucleotide assembled in silico. We performed this calculation only for dinucleotides that had already been determined by van der Waals overlap to be free of steric clashes.

Most, but not all, of the consensus rotamer suites were identified within the dinucleotides generated in silico from the 60o and 30o libraries (46 published suites + 8 “wannabe” suites; see Figure 4E and Suppl. Figure 4). In contrast, all consensus suite conformations were observed repeatedly within the dinucleotides assembled from the libraries binned at finer resolution (Figure 4E; Suppl. Figure 4). Unsurprisingly, the most frequently generated suite type from the 20º, 15º, 10º and 5º libraries was suite 1a, which is the suite most closely associated with the helical A-form of RNA (Figure 4E; Suppl. Figure 4). While most in silico dinucleotides had torsions consistent with one of the established rotamer suites, each library also generated dinucleotide conformations that were considered non-rotamer outliers (Figure 4E). This trend occurred less often for the larger, more extensive filtered fragment libraries. Backbone conformations identified as outliers by Suitename also occur within crystallographic structures and within the original, unfiltered RNA05 dataset, approximately 14% of the RNA conformations could not be identified by Suitename to be associated with any consensus rotamer suite (Figure 4E). Thus while the majority of dinucleotide conformations generated from the filtered fragment libraries are suite-like, other dinucleotide fragment conformations may represent previously unidentified suites or contain torsional values that lie just outside a traditional suite.

Deriving a “lower-limit” estimate of model quality: Modeling RNA Folds

Thus far we have found the libraries binned at 20º or finer to be superior in reproducing the coordinates of individual nucleotides and generating dinucleotides compatible with the rotameric suites. We next subjected the filtered fragment libraries to a more rigorous modeling test: could the fragments within each library be used to build realistic, accurate models of known RNA folds of varying lengths?

To address this question, we developed a protocol to model any arbitrary target RNA fold as accurately as possible and provide a best-case (or “lower-limit”) estimate of model RMSD that could be expected from each filtered fragment library. Briefly, the protocol uses a Monte Carlo simulation to grow an RNA chain, one fragment at a time, by: (1) sampling all fragments at each nucleotide position, mutating the base of each fragment to match that of the target fold being built; (2) calculating the backbone RMSD after aligning the growing chain to the target structure for each sampled fragment; (3) selecting fragments by the backbone RMSD of the growing chain according to a Metropolis criterion (see Figure 4A for illustration of assembly and Methods for details). Physically realistic folds were built by performing excluded volume calculations during sampling and rejecting fragments that caused atomic overlaps (see Methods). However, the use of any other energy function terms was avoided, as using such terms might introduce potentially negative bias. We found that a Metropolis Monte Carlo sampling strategy produced models with lower backbone RMSD than naively selecting, at each assembly step, the single clash-free fragment yielding the lowest backbone RMSD to the target fold (data not shown).

It is important to note that the strategy we employed did not use any information about the original positioning of the crystallographic bases during model building. Instead, for each starting crystal structure, the bases were removed, and only the coordinates of crystallographic backbone were used to guide rebuilding the fold from each set of discrete library fragments.

Pseudo-Torsional Libraries Can Model RNA Folds with Atomic-Level Accuracy

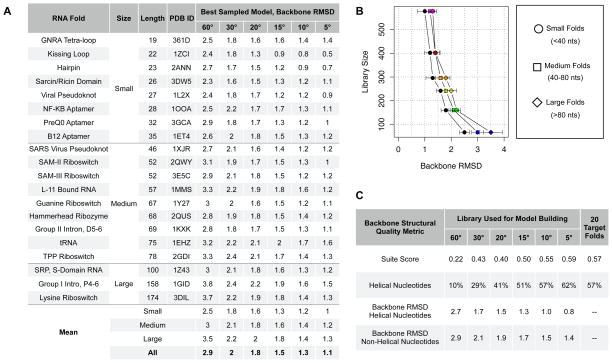
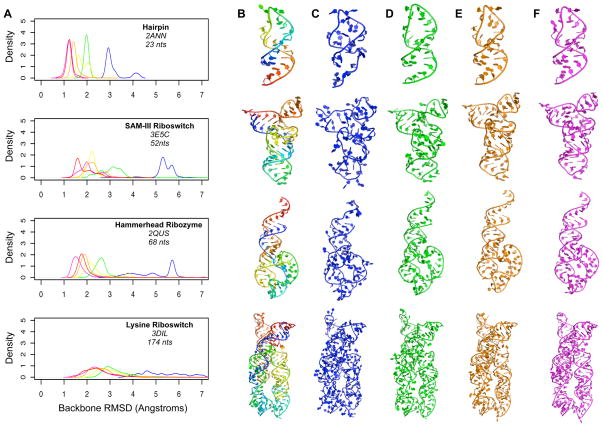
We selected twenty RNA folds that ranged in size and complexity from simple hairpins to complex ribozymes (Figure 6A) and used the “lower-limit” protocol in conjunction with each filtered fragment library to rebuild each fold 1000 times (Figure 5A). For the libraries binned every 60 or 30 degrees, sampling of low RMSD structures was often poor (2-6 Ångstroms; Figure 5A, blue and green curves). Further, even though every step of model assembly was directly guided by backbone RMSD, the best models generated by the 60º and 30º libraries were only in the 2–4 Ångstrom range (Figure 6A). This agrees with the overall poor coverage found for these libraries at the nucleotide level. The other four libraries consistently sampled low backbone RMSD models (1-4 Ångstroms; Figure 5A, yellow, orange, brown and magenta curves). The backbone RMSD of the best-sampled models improved as library binning became finer and finer (Figure 6A) and the 15°, 10° and 5° libraries consistently produced models with atomic-level accuracy (<1.5 Å backbone RMSD; Figure 6A, Figure 5C-F). As each of the filtered fragment libraries varied in its ability to accurately model the crystallographic target folds, we conclude that the quality of fragments used in RNA modeling can limit the accuracy with which RNA models can be built.

Figure 6. Estimate of the backbone model quality for six pseudo-torsional filtered fragment libraries.

(A) Twenty RNA folds (column 1; PDB identifier column 4) of varying length (columns 2-3) were modeled using one of six filtered fragment libraries (columns 5-10). For each fold, 1000 models were generated from each filtered fragment library by an RMSD guided Monte Carlo building protocol (see Methods) and the model with the best backbone RMSD is reported in columns 5-10. The last four rows give the mean backbone RMSD for models assembled by each filtered fragment library for the twenty targets grouped by size, as well as averaged over all 20 targets independent of size. (B) The relationship between library size and model quality as given in (A) is plotted. Average backbone RMSD values for models generated from each library are plotted separately into small (B, circles), medium (B, squares) and large (B, diamonds) folds. For consistency with other Figures, each of the six libraries are also coded: 60º, blue, 30º, green, 20º, yellow, 15º, orange, 10º, brown, and 5º, magenta. (C) The backbone quality of the best model generated from each library was evaluated based on variety of other structural metrics, including the overall suiteness score, as given by suitename (C, 1^st row) and the total number of nucleotides identified by suitename as helical (C, 2^nd row). The comparable value of each structural metric is given for the 20 crystallographic targets in the last column. The backbone RMSD of helical (suite 1a) and non-helical nucleotides is given in the 3^rd and 4^th rows, respectively.

Figure 5. Assembly of pseudo-torsional filtered fragments into RNA folds.

(A) The distribution of backbone RMSD values observed for 1000 models assembled from each of six filtered fragment libraries are shown the four RNA target folds. The folds shown range in size from 27 to 158 nucleotides and the distributions are color coded as follows: 60º, blue, 30º, green, 20º, yellow, 15º, orange, 10º, brown, and 5º, magenta. (B-F) The native fold for each of the four targets (B, rainbow coloring), as well as for the best model observed for each target from the 60º (C, blue), 30º (D, green), 15º (E, orange) and 5º (F, magenta) libraries, are shown in cartoon format. Backbone RMSD values for each model to the targets are given in Figure 6 and all-atom RMSD values are given in Figure 7 and Supplementary Table 3.

Surprisingly, we found no large differences in the accuracy with which each library was able to model small, medium and large RNA folds (Figure 6A-B). The one exception to this finding was the 60º library, which generated relatively poor quality models overall, regardless of size (see standard deviation bars in Figure 6B). While the filtered fragment libraries modeled large and small RNA folds with approximately the same accuracy, there was often a significant variation in the RMSD of the models produced by the Monte Carlo protocol for large folds (Figure 5A, 3DIL). This was reflected both in a significant broadening of the 1000 RMSD values sampled by the Monte Carlo protocol (see Figure 5A, 3DIL), as well as the speed with which the best observed fold among the 1000 was sampled (data not shown). Because of this, we conclude that even if a library contains fragments capable of generating a high quality model, increased structural sampling may be needed to produce accurate models of longer RNA folds.

Evaluating Model Folds Using Other Backbone Metrics: Suiteness and Helicity

The backbone quality of the models generated from each filtered fragment library was also evaluated by two other non-RMSD based metrics. First, we used Suitename to calculate the overall “suite score” for the original twenty targets as well as for the models of each target fold (Figure 6C, 1^st row). Briefly, the “suite score” reflects how many suites within a structure have backbone torsions consistent with one of the previously identified rotameric suites. Again, models built from the 60º, 30º, and 20º degree libraries performed poorly, with their average “suite score” indicating only 22% - 40% of the model nucleotides to be suite-like (Figure 6C, 1^st row). In contrast, the average “suite score” of models generated from all other libraries was almost identical to that of the original dataset (Figure 6C, 1^st row). In a few cases, the suite score of a crystallographic target was dramatically improved when the fold was rebuilt using library fragments (see Suppl. Table 2 and Discussion).

Perhaps the most simple and defining characteristic of RNA folds is that they contain a high percentage of helical nucleotides. Thus, we also determined whether the models and target folds had a similar number of helical nucleotides. To do so, we again used the program Suitename ⁸ and determined how many nucleotides within each target and model were identified as the helical, 1a suite. Only 10%–40% of the nucleotides within the twenty best models built from the 60º, 30º, and 20º libraries were identified as helical (Figure 6C, 2^nd row). These percentages were far less than the 57% of nucleotides identified as helical within the twenty crystallographic folds (Figure 6C, 2^nd row). In contrast, the 15º, 10º, and 5º libraries consistently rebuilt the target folds into RNA models with an average percent of helical nucleotides close to the original dataset (51%–62% as compared to 57%, Figure 6C, 2 row). After examining the helical 1a suite, we asked whether corresponding nucleotide positions for models and targets had identical suite conformations over the entire set of 54 conformers (see Methods). Suites within the 60º models rarely matched that of the target fold (out of 966 suites, 115 suites had identical conformers and 29 were near-identical). In contrast, >80% of suites within the 5º models were identical to that of their target folds (out of 966 suites, 727 suites had identical conformers and 72 suites were near-identical). These findings are in general agreement with the results previously described for evaluating modeling accuracy for each library based on backbone RMSD.

Evaluating the RNA models in all-atom detail: All-atom RMSD

Base pairing and positioning often play a fundamental role in most computational tools that model RNA de novo. However, the “lower-limit” protocol selects fragments during model building using only backbone RMSD and ignores the location of all base atoms, except to disallow fragments whose base atoms result in steric clashes. Thus it was possible that the backbone coordinates of “lower-limit” models were accurate but that the individual bases coordinates were not.

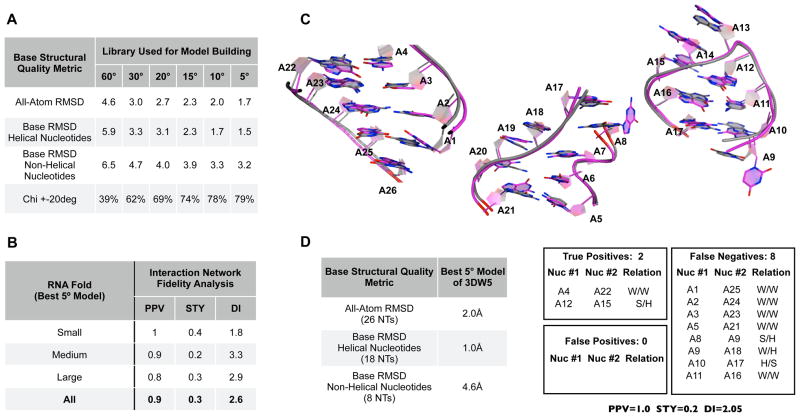
To check whether the models built from each library using a backbone-based RMSD approach had accurate base placement, we first calculated the all-atom RMSD of the twenty best models from each of the libraries to their targets (Figure 7A, 1^st row). All-atom RMSD values correlated strongly with the backbone RMSD values and, in most cases, were approximately 0.6–0.7Å greater (Suppl. Table 3). The 60º library produced structures with relatively poor all-atom RMSD values (4.6 Å; Figure 7A, 1^st row) while the all-atom models generated by the 5º library were surprisingly accurate (1.7 Å; Figure 7A, 1^st row). We also examined whether the models had any systematic differences in structural quality at helical and non-helical regions. To do so, we aligned each of the best models to its target using all backbone atoms and then, using this fixed alignment, we calculated the all-atom RMSD over all helical (e.g. suite 1a) and non-helical nucleotides separately. We observed that helical regions were modeled more accurately than the non-helical regions (Figure 7A, 2^nd and 4^th rows; 5º model mean accuracy 1.2Å and 2.3Å, respectively; see also Suppl. Table 4). This difference in accuracy appeared largely due to base placement: base atoms within helical regions of the 5º models were located, over average, 1.5Å away from their position in the target fold while the base atoms within non-helical regions of the same models were located much farther away on average (3.2Å, Figure 7A, 3^rd and 5^th rows). The “lower-limit” protocol had ensured that fragments with near ideal backbone RMSD had been selected during model building for both helical and non-helical regions alike. Thus, the RMSD of base atoms within non-helical regions such as loops and junctions may be somewhat limited by the current base conformations within the 5º library.

Figure 7. Estimate of the base model quality for six pseudo-torsional filtered fragment libraries: All-atom RMSD and hydrogen bond network fidelity.

(A) The average all-atom RMSD over the best twenty models generated from each library is given in the 1^st row. The average all-atom RMSD values, after finding the optimal alignment between each model and target based on backbone atoms, is given separately for helical (2^nd row) and non-helical (4^th row) nucleotides. The average all-atom RMSD values over only base atoms is given in the 3^rd and 5^th rows for helical and non-helical nucleotides, respectively. The last row gives the percent of all nucleotides within the models determined to have chi torsions within 20º of their targets. (B) Interaction network fidelity (INF) analysis was performed between each of the best 5º models of the twenty RNA test folds. Results for specificity, PPV=tp/(tp+fp), and sensitivity, STY=tp/(tp+fn), are given in the 2^nd and 3^rd columns, respectively. The last column reports the deformation index, or DI=RMSD/INF. Interactions were calculated as the intersection of pairings detected by RNAView and MC-annotate and results were averaged over all folds based on their size (e.g. small, medium, or large). (C) The crystal structure of test fold 3DW5 (grey) is shown aligned with the backbone of its best 5º model (magenta). All twenty-six nucleotides are shown within the three panels. (D) The all-atom RMSD, as well as the RMSD of the helical and non-helical base atoms, of 3DW5 aligned to its best 5º model are given in rows 1-3 of the table. The box regions denote the interaction network fidelity (INF) analysis. Base pairs are denoted using numbering identical to panel (C).

Evaluating the RNA models in all-atom detail: Base orientation and base pairing

In addition to RMSD, we also evaluated the accuracy of base positioning within the models built by each library using two other metrics. First, we identified the number of nucleotides within each of the models that had chi angles within 20º of the native nucleotide at the same chain position. Correct base placement, as measured by chi angle, showed steady improvements as the filtered fragment libraries grew larger and the bin resolution grew finer. Using this metric, the 60º library performed poorly and positioned only approximately 40% (468/1207) of bases positioned within 20º of their targets (Figure 7A, 6^th row). In contrast, the models generated using the 5° library had almost 80% (959/1207) of nucleotides placed in a correct base orientation (Figure 7A, 6^th row). Achieving such a high level of accurate base placement, despite the lack of enforcing any criteria to favor base orientation during model building other than sterics, might be surprising. However, accurate base placement based on pseudo-torsional information alone has been observed before ^{23; 33; 36}.

Placement of side chains within 20º is a standard often used for protein side-chain modeling ²⁰. However, it is not clear whether this level of accuracy would be sufficient to observe hydrogen-bonding patterns among RNA base pairs. We thus used two freely available annotation programs (RNAView and MC-annotate ³⁷, (see Methods) to calculate, for each target and each 5º model, how many canonical Watson-Crick pairs (G-C and A-U) and how many other “non-Watson Crick” hydrogen bond pairs ⁹ were present (Figure 7C-D; Suppl. Table 5). As in ³⁷, we used the intersection of the paired interactions reported by both annotation tools.

RNAView and MC-annotate both found instances of all 12 combinations of orientations between the Watson-Crick, Hoogsteen, and sugar “faces” of nucleotide bases ⁹ within the 5º models (data not shown). Importantly, whenever the two annotation tools agreed that a base pair was present within the 5º models, the identical base pairing was almost found within the target (high sensitivity, as reported by PPV values in Figure 7B). In contrast, many pairings found within the target fold were not detected in the 5º models (low specificity, as reported by STY values in Figure 7B). Upon examining the annotation results in greater detail, we observed that the two tools often found widely differing sets of hydrogen bonding interactions within the 5º models. For instance, within the 5º models, almost 65% of the base pairing identified by MC-annotate and almost 45% of base pairings identified by RNAView were disregarded because they did not intersect (data not shown). Figure 7C-D demonstrates one example where both annotation tools failed to agree on base pairings within a model, even though the base atoms of the model were located very close to the base atoms of the target (model and target colored magenta and grey, respectively). This failure to detect hydrogen bonding within helical regions of the 5º models was a common occurrence, despite the fact that the RMSD of the base atoms within such regions was typically low (1.5Å on average; Figure 7A, 3^rd row). Thus while the criteria commonly employed by tools such as RNAView and MC-annotate may be reliable for detecting hydrogen bonding patterns in crystal structures, the same criteria may also fail to detect pairings in models that contain bases with close to, but not ideal, geometry.

Despite the large number of false negatives within the 5º models, we nevertheless calculated the deformation index (DI) for all twenty targets. The DI is a measure that accounts for both base pairing interactions and RMSD (defined as √(PPV*STV)/RMSD ³⁷). Over all twenty targets, the average DI value was 2.6 (Figure 7B, last column). As a comparison, several of the structures within the test-set (1KXK, 1XJR and 2QUS) were recently modeled using both MC-Fold and FARNA ³⁸. Despite having poor RMSD overall (ranging from 9–15Å), both the MC-Fold and FARNA models nevertheless had notably high specificity and sensitivity values (PPV>0.8 and STY>0.6) ³⁸. Thus DI values in these three modeling cases were far higher than those reported here for the “lower-limit” models and ranged from approximately 14–20.

DISCUSSION

In this study, we used a pseudo-torsional notation of the RNA backbone to generate six filtered libraries of discrete fragments. We also presented a methodology for assembling the individual filtered fragments into larger structures using each fragment’s pseudo-torsional values as a guide. We found that accuracy in modeling individual nucleotides, dinucleotides, and entire RNA folds consistently improved as the libraries grew in size and more thoroughly covered pseudo-torsional space. The largest four libraries modeled most individual nucleotides to within 0.5Å, reproduced all the previously described rotamer suites, and built RNA folds with sub-atomic accuracy. Consequently, these libraries should be useful for numerous modeling applications including de novo structural modeling, structure analysis or crystallographic refinement.

LESSONS LEARNED FROM “LOWER-LIMIT” MODEL ASSEMBLY

Use of discrete libraries inherently limits modeling accuracy

Building all-atom models of RNA folds using backbone RMSD as a guide is not an approach that can be directly incorporated into modeling folds de novo. Nevertheless certain lessons can be learned that are applicable to de novo modeling strategies. First, almost all RNA tertiary modeling tools build models out of discrete pieces of RNA structure, most commonly either RNA fragments ³¹ or cyclic nucleotides ²⁹. However, the extent to which using different sets of RNA pieces limits modeling accuracy is not tested explicitly. Twenty years ago, an early test of nucleotide-based sampling determined that approximately 30 discrete conformations could rebuild tRNA to an accuracy of 3.1Å ^{39; 40}. This result is consistent with our finding that the 60º library of 67 filtered fragments builds models with an accuracy of 2-3Å. However, since this initial work ³⁹, few or no tests have been performed to indicate the range of modeling accuracy that can be expected from any given library of RNA conformations.

The model building protocol we used here is guided by RMSD and lacks energetic terms. Thus, we could assume that when models were poorly built, or had high RMSD to the target fold, the errors were not due to scoring. Further, the libraries we tested were small and this allowed us to use a model building protocol to perform exhaustive sampling at each point in the assembly protocol (e.g. at each step of the assembly protocol, every fragment in the library was tested and scored based on its RMSD to the target). Under these conditions, we were able to directly study how library quality can affect modeling accuracy. While we found that the use of discrete fragments during modeling especially limits accuracy when libraries are small, we found that even the largest libraries we tested imposed some limitations on modeling accuracy.

Filtered fragment libraries can build large and small folds with comparable accuracy

Despite the limitations inherent in using discrete fragments, the RMSD based building protocol showed that discrete libraries are capable of rebuilding both small and large RNA folds with approximately equal accuracy. Our “lower-limit” protocol builds models using an RMSD-based approach and thus eliminates any errors that might be introduced by use of a scoring function. Thus, we conclude that if an appropriate library of RNA conformations is used with near-perfect sampling, there should be no inherent difference in modeling large and small folds. In contrast, large RNA folds are often modeled with far worse accuracy than small hairpins and folds in de novo modeling ^{31; 38}. A similar phenomenon is observed when building random models of RNA: the mean RMSD of a random model has been shown to increase with RNA chain length ⁴¹. We were unable to use our building protocol to directly test the accuracy of other published RNA fragment libraries for building larger RNA folds. However, most of the fragment libraries currently in use are quite large, and likely contain a large diversity of RNA conformations. Thus the difficulties in de novo modeling of larger folds, as compared with smaller folds, likely results from insufficiencies in either sampling or scoring and not the quality of the RNA fragment libraries being used. With respect to sampling, we observed that, even when using RMSD to the target as a guide to sample fragments, rebuilding larger RNA folds to the same modeling accuracy as smaller RNA folds often required increased sampling. Small structural differences in the fragments selected when building larger RNA folds may more easily propagate through an entire structure, causing the models generated for larger RNA folds to vary more widely in their overall backbone RMSDs. We conclude that a similar increased sampling of larger RNA folds might also be necessary for accurately modeling large RNA folds de novo.

The backbone conformations and base orientations of filtered library fragments are linked

Perhaps the most striking result of this study was that we observed a strong correlation between the backbone orientations of the library fragments and their base orientations. The result that correct base orientation can be ascertained from backbone coordinates is not new, but has also been observed during semi-automated crystallographic model building using pseudo-torsions ²³. Here we show that selecting a library of fragments based on their backbone η and θ values and assembling these fragments based on their backbone RMSD to a target fold can generate models that accurately reproduce both the all-atom coordinates of individual nucleotides (Figure 3B) as well as entire RNA folds (Figure 6–7; Suppl. Table 3).

The all-atom models built in this study were not sampled using a base-centric approach with stringent hydrogen bonding criteria. As a result, the hydrogen bonding network analysis did not detect all native base pairing interactions within the models (Figure 7C-D). However, we found that weakening the structural constraints by introducing an increased kT value produced models with higher quality backbones overall. Indeed, enforcing perfect base planarity or strict hydrogen bonding at an early stage of modeling is likely to limit overall de novo modeling accuracy. This may be especially true in cases where slight deviations from strict hydrogen bonding criteria could result in the correct placement of the correlated backbone atoms. Certainly at later stages of modeling, one would fix inaccuracies introduced by using a discrete set of fragments and correct base placement to conform to stricter hydrogen boding criteria.

Finally, we note that a correlation between base orientation and the η and θ backbone torsions has been observed before ^{23; 33; 36}. In contrast, a similar correlation between base orientation and the standard six backbone torsions was not observed ³³. Thus the strong correlation we observe between correct backbone conformation and base orientation may be a property unique to using pseudo-torsion based fragments.

ADVANTAGES OF USING PSEUDO-TORSION FRAGMENT LIBRARIES

Selecting libraries for modeling accuracy

One advantage of the methodology presented here is that a library of appropriate size and structural resolution can be selected for the modeling task at hand. Many classification schemes have produced small sets of less than 100 RNA conformations ^{3; 8; 39; 42}. Our results show that using rigid sets of this size should be appropriate for building RNA models in the range of 2-4 Å RMSD. For instance, the 60º library developed in this work contains approximately 70 fragments and was able to build models with accuracies of 2.5 to 4Å backbone RMSD. This result is consistent with the 3.1Å accuracy noted for building tRNA with 30 discrete conformations ^{39; 40}. However, as illustrated by the work of K. Keating²³, atomic-level accuracies (e.g. <1.5Å) may be obtained from libraries of this size if a coordinate minimization step is included into the building process.

In agreement with this idea, many all-atom structural modeling tools use large libraries of RNA structural fragments that can contain hundreds or even thousands of conformations ^{29; 31}. However, our results suggest that 300 to 500 well-chosen fragments are sufficient to build RNA models with accuracies of 1.5Å backbone RMSD or better. Thus tools using libraries significantly larger than this could gain an increase in modeling speed without making a large sacrifice in modeling accuracy by selecting an appropriately sized fragment set.

Focused library sampling using pseudo-torsion based fragments

Several tools for modeling RNA incorporate experimental data or secondary structure predictions ^{27; 30}. Such tools might enjoy an additional advantage by using pseudo-torsion filtered fragment libraries. Nucleotides involved in helical regions, tetra-loops, pi loops and other diverse structural motifs have been shown to have η and θ values within well-defined ranges ^{33; 36}. Thus, only the subset of library fragments within these pseudo-torsion ranges may need to be sampled in order to model such regions. Such a strategy of focused sampling could bias simulations towards favorable conformations while, at the same time, increasing computational speed. While some tools, such as MC-SYM, currently catalog structural pieces of RNA as belonging to particular structural motifs ²⁹, the pseudo-torsion based libraries we present here could extend this idea to the single nucleotide level.

Likewise, generating all-atom models of medium and large sized RNAs still remains a computational challenge, in part due to limitations imposed by conformational sampling. As a result, coarse-grained models are often first produced for larger RNAs and, if desired, all-atom detail is added later in a separate prediction step using the coarse-grained backbone trace as a guide ²⁸. Fragment libraries have already been employed in generating all-atom models from coarse-grained backbone traces with good success ²⁸. However, the pseudo-torsion based filtered fragment libraries are smaller in overall size relative to fragment libraries and they provide the advantages of focused sampling based on structural motifs mentioned above. Additionally, if the pseudo-torsions of a coarse-grained model can be directly measured, then these values could be used to directly guide fragment selection. A similar approach, in which pseudo-torsions are measured from an electron density backbone trace and used to guide all-atom crystallographic model building, has recently been published ²³.

Rebuilding models with increased rotamericity

One final advantage of using the pseudo-torsion libraries we present is that they were generated from the same high-quality dataset, RNA05, that was originally used to determine the consensus set of rotamer suites ⁸. As a result, crystallographic folds that contained poor suite conformations or overall poor suite scores could be rebuilt using library fragments into almost identical folds with improved scores. For example, two crystallographic folds in the rebuilding test set, 361D and 1Z43, originally contained a large number of dinucleotide suites identified as outliers, or non-rotameric (11/19 and 53/112 suites, respectively). When each of these folds was rebuilt using the filtered fragments from the 5º library, the new models contained notably fewer non-rotameric suites (3/19 and 4/112, respectively, for 361D and 1Z43). We thus anticipate that using the pseudo-torsional fragment libraries in crystallographic or de novo modeling applications could improve the quality of the modeled backbone.

Finally, we note that the quality of the filtered fragment libraries we present here are dependent on the quality of the initial dataset, RNA05, from which they were generated. Thus as the quality of the dataset gets better, the quality of the fragment libraries will likely also improve. A new dataset of high quality RNA structures, RNA09, has recently been made available (http://kinemage.biochem.duke.edu/databases/rnadb.php) and it would be of interest to compare fragment libraries generated from this dataset with those published here using RNA05. Preliminary results suggest that libraries generated from the newer RNA09 dataset would be slightly larger, but largely overlap with the RNA05 libraries (Suppl. Fig 6).

COMPARISON OF PSEUDO-TORSION FRAGMENT LIBRARIES TO SEMI-AUTOMATED MODEL BUILDING WITH CONSENSUS CONFORMERS

Importantly, the libraries we have presented are not the only approach to incorporating the structural diversity of the consensus conformers into model building. For building RNA folds de novo, the discrete sets presented in this work can be easily assembled and do not require coordinate minimization. However, if a backbone trace has been already been generated, the semi-automated approach of Keating and Pyle can use the consensus suites and coordinate minimization to build an all-atom model²³. For the one test case that overlapped between the two methodologies (the guanine riboswitch), the accuracy between the two methods appeared to be comparable (1.1Å backbone RMSD for the 5º library, as reported in this work; most backbone atoms to within 0.9Å of their crystallographic coordinates, as reported in ²³). Thus both approaches appear suitable for rebuilding known backbones, including rebuilding those backbones with increased rotamericity.

CONCLUSIONS

To summarize, we have presented six filtered libraries of pseudo-torsional fragments and validated their ability to reproduce the structural features of RNA at the level of individual nucleotides, dinucleotides, and in the building of entire RNA folds. Importantly, the fragments are easy to assemble and can be classified, using their pseudo-torsions, into helical and non-helical RNA conformations. Because we have shown the filtered fragment libraries are capable of building high quality, all-atom models, we anticipate they should be useful for a variety of modeling applications including de novo RNA structure prediction and design, as well as in RNA structure analysis and refinement.

MATERIALS AND METHODS

Selection of RNA Structural Dataset

Filtered fragment libraries were generated by taking coordinates directly from the RNA Database 2005 (RNA05, http://Kinemage.biochem.duke.edu/databases/rnadb.phb) ⁷. The RNA05 dataset is hand-curated and consists of 171 RNA coordinate files (9482 nucleotides total) of resolution ≤ 3.0 Ångstroms.

Application of Quality Filters

Prior to selection of fragments, quality filters were applied to each coordinate file in RNA05 on a nucleotide-by-nucleotide basis as follows. First, the tool PROBE ⁴³ was used to check each RNA structure for steric clashes by flagging nucleotides containing any single atom with greater than 0.4 Ångstroms van der Waals radii overlap with any other atom. In order to be as strict as possible, both intra- and inter- chain overlaps of >0.4Å were taken into account. Nucleotides passing the steric clash quality filter were then subjected to a second round of quality filtering and excluded from consideration if any heavy-atom (backbone or base) within the nucleotide contained a b-factor> 60. Finally, nucleotides containing alternative conformations were excluded. Quality filtering removed 6018 nucleotides from the starting dataset, leaving a total of 3464.

Preparation of RNA Structural Dataset

Only nucleotides containing a 2' hydroxyl and base identity of A, C, G, or U were considered and modified bases were not used for this analysis. All non-RNA molecules, waters, heteroatoms and duplicate copies of RNA had been already removed within the previously published dataset. Hydrogens, which had previously been added to each structure, were removed from the RNA05 dataset.

Measurement of Nucleotide Sugar Pucker and Pseudo-Torsions

Sugar pucker was determined for each RNA05 nucleotide by using a combination of two separate criteria. First, the standard backbone torsion delta (C5’, C4’, C3’, O3’] was calculated for each nucleotide using DANGLE ⁴³. Next, the perpendicular distance between the glycosidic bond of each nucleotide and the following phosphate was calculated using a perl script (e.g. the base-phosphate perpendicular distance) ^{23; 44}. Nucleotides were then defined as having a C3’-endo sugar pucker if their delta values were 84º ± 30º and their base-phosphate perpendicular values > 2.9 Ångstroms. Likewise, nucleotides were defined to have C2’-endo sugar pucker if their delta values were 147º ± 30º and their base-phosphate perpendicular distances were ≤ 2.9 Ångstroms. 838 RNA05 nucleotides had delta values or base-phosphate perpendicular distances outside of these ranges and were discarded.

The backbone pseudo-torsions eta [η: C4’_i-1, P_i, C4’_i, P_i+1] and theta [θ: P_i, C4’_i, P_i+1, C4’_i+1] were measured for each quality-filtered RNA05 nucleotide determined to have a well-defined sugar pucker using the program DANGLE ⁴³. Nucleotides at the beginning or end of a structure, as well as nucleotides directly preceding or following a chain break, were excluded from analysis because both pseudo-torsions could not be measured. Nucleotides were also excluded from analysis if the nucleotide immediately preceding (used in defining η) or following (used in defining θ) failed to meet all filtering criteria. In all, pseudo-torsions were recorded for 1780 nucleotides (1562 and 218 for C3’-endo and C2’-endo, respectively).

In developing a semi-automated approach for crystallographic model building²³, a new pseudo-torsional notation of C1’ -P and η’ /θ’ was introduced. While this new notation has some advantages in generating all-atom detail from backbone traces of electron density, defined structural motifs have not yet been correlated with η’ /θ’ values. In contrast, structural motifs have been well characterized using the original η/ θ notation, allowing for the possibility to bias library sampling towards desired motifs (see “Focused library sampling” section above). Thus, in this work we have chosen to generate discrete fragment sets using the original C4’-P and η/ θ notation.

Selection of Filtered Fragments

To create filtered fragment libraries, individual RNA05 nucleotides were selected based on their measured pseudo-torsions as follows. First, 2-dimensional pseudo-torsional space was partitioned uniformly at six varying degrees, 60º, 30º, 20º, 15º, 10º and 5º. The partitioning was repeated independently for each C2’ and C3’-endo sugar pucker. Next, for each partitioning, we calculated the η-θ values for the center of each (η_{bin_center} and θ_{bin_center}). Finally, a perl script was used to search the list of quality-filtered RNA05 nucleotides for the single instance of correct sugar pucker with pseudo-torsional values closest (as measured by Euclidean distance, d) to the bin center. If the bin was empty and did not contain a quality filtered nucleotide, no fragment was added to the library. The Euclidean distance (d) between the pseudo-torsion values of the bin center (η_{bin_center}, θ_{bin_center}) and the pseudo-torsion values of every nucleotide within the bin (η, θ) was calculated as follows: $\text{d}=\sqrt{[{(\eta {}_{\text{bin}\_\text{center}}-\eta )}^2+{({\theta }_{\text{bin}\_\text{center}}-\theta )}^2]}$.

The crystallographic coordinates of each RNA05 nucleotide that best represented a pseudo-torsional bin were recorded and included in the appropriate filtered fragment library. The backbone coordinates defining the η and θ of the selected RNA05 nucleotides (grey atoms, Fig. 1A) were also recorded and added to the library. Fragment bond lengths and angles were assumed rigid and neither the backbone nor the glycosidic bond lengths or angles were modified from those found in the original RNA05 nucleotide. The distribution of standard torsions (α, β, γ, δ, ε, ζ and χ) for each of the six libraries mimicked that of the entire RNA05 dataset (Suppl. Fig. 5).

Fragment Attachment

Two fragments (i and j) can be attached at a single phosphate using pseudo-torsions as follows. First, the last three atoms involved in defining the θ pseudo-torsion of fragment i, (C4’_i, P_i+1, C4’_i+1, Fig. 4A) are aligned to the first three atoms defining the η pseudo-torsion of fragment j (C4’_j-1, P_j, C4’_j, Fig. 4A). This alignment will bring the phosphates P_i+1and P_j into very close proximity. In order to ensure direct connectivity between the two fragments, the coordinates of the phosphate atom of fragment j were then translated, if necessary, to overlap exactly the coordinates of the phosphate of fragment i. To form a dinucleotide, all overlapping and non-overlapping atoms involved in defining the pseudo-torsions of both fragments can be removed (Fig. 4A). If attachment of additional fragments is desired, as is the case when building an entire RNA fold, the atoms involved in defining the θ pseudo-torsion of fragment j can be retained and used to guide the attachment of an additional fragment to the end of a growing RNA chain. All alignments and translations were performed using the Biopython SVDSuperimposer and all fragment backbone and base bond lengths and angles remained fixed during fragment attachment (see also “RMSD Calculations”).

Steric Exclusion Calculations

In order to build physically realistic dinucleotides and folds, excluded volume calculations were performed after attaching one fragment to another. Attachments that resulted in steric overlaps were rejected. For generation of dinucleotides, excluded volume calculations were computed pair-wise over all atoms (backbone and base) between the two joined nucleotides except the atoms directly connected by the intervening phosphate (e.g. the O3’ of the first nucleotide with the O1P, O2P, and O5’ atoms of the 2nd nucleotide). For building of RNA folds, excluded volume calculation were also performed pair-wise over all the atoms (backbone and base) of nucleotides that “neighbored” the added fragment, where neighboring nucleotides were defined to be those having a phosphate-phosphate distance to the added fragment of less than 20Å.

For each set of atom pairs, the distance between the two atoms, in Ångstroms, was compared to the sum of the van der Walls radii of the same two atoms. If the distance between any two atoms was found to be less than their summed van der Waals radii, scaled by 60%, then a steric overlap was considered to occur. The scaling of radii by 60% was used to allow for the discrete nature of the fragments being assembled. The van der Waals radii used for calculations were as follows: carbon, 1.7Å, oxygen, 1.52Å, phosphorous, 1.8Å and nitrogen, 1.55Å.

For building of dinucleotides, if a steric clash occurred due to the presence of a purine base, the purine base was mutated in silico to a pyrimidine and the excluded volume calculations were repeated to check whether the clash had been resolved. During the mutation process, the glyscosidic bond angle of the base was left unchanged (see “Sequence Mutation Protocol”) For rebuilding target RNA folds, the base of each fragment was computationally mutated, if needed, to the sequence identical to the target fold being modeled prior to excluded volume calculations.

Sequence Mutation Protocol

A reference file, consisting of a single representative set of atomic coordinates for each RNA base type (1ET4.pdb: A203, G207, C211 and U215), was used to mutate a fragment base to match any arbitrary target sequence. The mutation protocol left all fragment sugar atoms fixed, but replaced the original fragment base coordinates with the desired mutant base coordinates within the reference file as follows. First, BioPython’s SVD based Superimposer (see “RMSD Calculations”) was used to align the reference base with the fragment base using three of the four atoms involved in the chi torsion of each base: purine [C1’, N9, C4] or pyrimidine [C1’,N1,C2]. Next, the reference base coordinates were translated, if needed, such that the reference base N1/N9 atom coordinates exactly matched those of the original fragment base N1/N9 atom coordinates. The old base coordinates were then replaced with the reference base coordinates. The chi angles of reference bases attached via the above method of superposition followed by translation were typically within 1 degree of those measured for the original fragment base.

RMSD Calculations

All superpositions and root mean squared deviation (RMSD) calculations were calculated using the Bio.SVDSuperimposer module of BioPython, which implements a singular value decomposition superposition algorithm based on ⁴⁵. Backbone RMSD values were calculated over all heavy-atoms in the sugar phosphate backbone (e.g. P, O1P, O2P, O5’, C5’, C4’, O4’, C3’, O3’, C2’, O2’, C1’). All-atom RMSD values were calculated (after mutation of fragment bases to match target structure, as necessary) over all non-heavy atoms.

Model Building Protocol

We developed a model building protocol that aims to rebuild a “target” RNA fold with the lowest possible backbone root mean squared deviation (RMSD). The protocol uses filtered library fragments and builds a model of a target fold in a step-wise fashion. The first fragment in the model is the single fragment within a library having the smallest heavy-atom backbone RMSD to the first nucleotide in the target fold. The base of this first fragment is computationally mutated to match the target sequence (see “Sequence Mutation Protocol”) and all atoms defining the fragment’s η pseudo-torsion are then removed (grey atoms in Figure 1A). To grow the chain by one nucleotide, every fragment in the library is attached to the first, one at a time in a randomly selected order. After attachment, the backbone RMSD of the entire chain built thus far to the target fold is calculated and compared with the chain backbone RMSD calculated for the last attached fragment. If the backbone RMSD of the most recently attached fragment is lower than previously observed, or if the score passes the Metropolis criterion (P_accept = min (1,e^−ΔRMSD/KT), the fragment nucleotide base was mutated to match the target sequence (see “Sequence Mutation Protocol) and checked for steric clashes with other atoms of growing chain (see “Steric Exclusion Calculations”). If the fragment is found to be clash-free, its chain RMSD value is recorded as the new best observed so far and used for comparison with later fragments.

Chain growth continued in this manner until all but the last nucleotide in the target RNA fold had been modeled. The last fragment, as with the first fragment, is selected without the Monte Carlo criterion (e.g. the single clash-free fragment with lowest backbone RMSD was chosen), and the atoms defining the θ pseudo-torsion of the last added central nucleotide (grey atoms, Figure 1A) are removed. Occasionally, after attempting to attach all fragments in a library to the end of a growing chain, no clash-free fragment was found. In such cases, chain growth was stopped, and a new Monte Carlo chain building simulation was begun. This phenomenon was initially observed when we attempted to build models without using the Monte Carlo criterion (e.g. at each chain growth step, the clash-free fragment with best score was selected deterministically). For each target fold, we used this protocol to build 500 model folds using a KT=0.001 and to build 500 model folds using a KT=0.005. Each Monte Carlo simulation was performed on a single computing node of the Yale computing cluster, which had eight 2.66 GHz Intel Xenon cores and 16 GB RAM. The computational time required to build each target fold depended on the size of the target, as well as the size of the library (Suppl. Fig. 7). Small folds (<40 NTs) were typically built in less than fifteen minutes while medium folds (40–80 NTs) were built in fifteen to forty-five minutes. In contrast, large structures (>80 NTs) were built in one to three hours (Suppl. Fig. 7).

Model building test set

To test model building accuracy using each filtered fragment library, twenty RNA crystallographic structures were selected (Figures 6-7). Each of the twenty structures was contiguous over its entire length (e.g. structures with chain breaks were not considered) and the mean structural resolution over all structures was 2.3Å (resolutions varied from 1.0 to 3.0Å). Each fold was classified based on its chain length as either small (19 to 35 nucleotides), medium (46-78 nucleotides) or large (100 nucleotides or more).

The structures within the test-set were diverse and included the tRNA fold, aptamers, riboswitches, and the P4-P6 domain of the group I intron. The majority of test-set were either solved post-2005 and had no comparable representative within the RNA05 dataset (Suppl. Table 1; 3DIL, 2GDI, 3E5C, 2QWY, 3GCA, 2ANN, 1ZCI, and 361D) or did not contribute fragments to any of the six libraries (Suppl. Table 1; 1OOA, 1XJR, and 1KXK). During analysis of the test-set (Figures 5-7), no significant differences were found between the modeling accuracy of the structures that had originally been contained within RNA05 and those that were unique.

Evaluation of modeled suite conformations

We examined twenty targets that contained a total of 1207 suites. For each target, the percentage of suites that were modeled correctly was determined as follows. First, the program Suitename⁸ was used to classify all conformers within a target and model. The classifications were then compared on a suite-by-suite basis. If a corresponding nucleotide position was classified as having the same suite in both the target and model, then it was labeled as “identical”. Corresponding nucleotide positions classified as having helical (1a) or helical-like (1m, 1L, &a, 1c or 1f) conformers in both the target and model were labeled as “near-identical”. Nucleotides that Suitename triaged (106 suites over all twenty targets) or determined to be outliers (135 suites over all twenty targets) were disregarded.

Evaluation of Base Pairing

The RNA interaction network fidelity between models and target folds was calculated using two freely available annotation tools from MC-Pipeline http://www.major.iric.ca/MC-Pipeline/): RNAView and MC-SYM ^{37; 38}. For both the model and the target structure, the network fidelity calculation was calculated by determining the intersection of the base pairing types detailed in ⁹. Stacking was not considered in the network fidelity calculation.

Availability

All six filtered fragment libraries, as well as code to build dinucleotides, are freely available at http://www.pylelab.org/software/index.html.

Highlights.

• We validate six libraries of conformations for use in RNA modeling

• Each library models individual RNA nucleotides to within 1Å

• Library fragments can be assembled into dinucleotides that are rotameric

• Some libraries can model RNA structure with atomic-level accuracy (<1.5Å)

• Libraries are made available for RNA structural modeling, analysis, or refinement