EFFICIENT CONSTRUCTION OF DISORDERED PROTEIN ENSEMBLES IN A BAYESIAN FRAMEWORK WITH OPTIMAL SELECTION OF CONFORMATIONS

Abstract

Constructing an accurate model for the thermally accessible states of an Intrinsically Disordered Protein (IDP) is a fundamental problem in structural biology. This problem requires one to consider a large number of conformations in order to ensure that the model adequately represents the range of structures that the protein can adopt. Typically, one samples a wide range of structures in an attempt to obtain an ensemble that agrees with some pre-specified set of experimental data. However, models that contain more structures than the available experimental restraints are problematic as the large number of degrees of freedom in the ensemble leads to considerable uncertainty in the final model. We introduce a computationally efficient algorithm called Variational Bayesian Weighting with Structure Selection (VBWSS) for constructing a model for the ensemble of an IDP that contains a minimal number of conformations and, simultaneously, provides estimates for the uncertainty in properties calculated from the model. The algorithm is validated using reference ensembles and applied to construct an ensemble for the 140-residue IDP, monomeric α-synuclein.

1. Introduction

Intrinsically Disordered Proteins (IDPs) are a class of polypeptides that populate diverse ensembles of conformations under physiological conditions.^{1, 2} It is believed that a number of IDPs play a critical role in the development of neurodegenerative disorders including Alzheimer’s and Parkinson’s – diseases that affect millions of people each year.^{3, 4} As a result, gaining an understanding of the conformational properties of these proteins is an important task, which could pave the way for the discovery of new therapeutics through structure based drug design.⁵

A model for the ensemble of an IDP consists of a set of structures S = {s₁,…, s_n} and a set of weights w⃗ = {w₁,…, w_n}, where w_i corresponds to the equilibrium probability of conformation s_i. Typically, these structures and weights are chosen so that averages calculated from the ensemble agree with experimental observations;^{2, 6, 7} for example, so that the radius of gyration calculated from the ensemble is similar to its experimentally determined value. Previous studies have shown that agreement with experimental observations is not sufficient to ensure that an ensemble is accurate, because there may be many different ways of choosing the structures and weights to achieve a good fit to the experimental data.^{8, 9} Therefore, it is important to develop methods that can quantify the amount of uncertainty associated with a model of an IDP ensemble.

We previously developed an algorithm, called Bayesian Weighting (BW), that uses Bayesian inference to construct an ensemble for an IDP that agrees with experimental observations, while simultaneously estimating the uncertainty associated with this model.⁸ The BW method calculates a ‘posterior’ probability distribution over all ways of weighting the structures in a pre-specified conformational library. Point estimates and error bars for various properties of the ensemble can be computed by calculating an average over this probability distribution. An important feature of the algorithm is that it provides a built-in error check in the form of an uncertainty parameter, or posterior uncertainty, which is related to the error in the estimated population weights. Our previous study suggests that this uncertainty parameter is a metric that assesses model correctness.⁸ When the uncertainty parameter is 0, one can be relatively sure that the model is correct. By contrast, a value of 1 suggests that the ensemble is inaccurate and values calculated from the ensemble will be associated with very large confidence intervals.

Of course, the quality of the structural library will also affect the accuracy of the resulting ensemble. The structural library must be diverse enough to capture the states populated by the IDP, but if it is too large then the problem will be under-restrained, leading to a large posterior uncertainty. One way to overcome this problem is to use variable selection techniques to identify an optimal subset of conformations from within a larger structural library.¹⁰ Such an algorithm might begin by estimating the population weights using a large conformational library and iteratively discarding lowly weighted conformations to improve the ensemble. In practice, performing this type of structure selection algorithm within a fully Bayesian framework would be computationally intractable because BW uses Monte Carlo methods to estimate the weights, and these calculations can take a long time to converge; therefore, we introduce an approximate algorithm called Variational Bayesian Weighting and Structure Selection (VBWSS) that can perform the calculations quite rapidly – providing a decrease in computational time of roughly 4 orders of magnitude compared to BW. In this work we describe the VBWSS method and validate the approach using ‘reference’ ensembles. Lastly we use the method to characterize the ensemble of the intrinsically disordered protein, α-synuclein (αS).

2. Theory

2.1. Optimal Structure Selection

When constructing an ensemble for an IDP, it is necessary to use a structural library that is diverse enough to cover the entire range of accessible conformations. However, increasing the size of this library adds degrees of freedom to the model making the problem more underdetermined. In our prior work, we described a method for calculating a posterior distribution that assigns a probability to each possible choice of weights as a way of quantifying uncertainty in the ensemble.⁸ The posterior probability density function (PDF) is calculated using Bayes’ theorem:⁸

$$f_{\vec{W}|\vec{M},S}(\vec{w}|\vec{m},S)=\frac{f_{\vec{M}|\vec{W},S}(\vec{m}|\vec{w},S)f_{\vec{W}|\mathrm{S}}(\vec{w}|S)}{f_{\vec{M}|S}(\vec{m}|S)}$$ (1)

where $S={\{s_i\}}_{i=1}^n$ denotes the set of structures, $\vec{w}={\{w_i\}}_{i=1}^n$ denotes the set of population weights, $\vec{m}={\{m_i\}}_{i=1}^k$ denotes the set of k experimental measurements. To calculate eq. (1) we must specify a likelihood function, f_{M⃗|W⃗, S} (m⃗|w⃗, S), and a prior distribution, f_W⃗|S (w⃗|S). The normalizing constant, or marginal likelihood (ML), is given by f_M⃗|S (m⃗|S) = ∫ f_M⃗|W⃗,S (m⃗|w⃗,S) f_W⃗|S (w⃗|S) dw⃗. The specific forms for each of these terms will be given in section 2.2. Using eq. (1), the Bayesian estimate for the weight of structure s_i is:

$$w_i^B\equiv {\displaystyle \int }{w}_i{f}_{\vec{W}|\vec{M},S}(\vec{w}|\vec{m},S)d\vec{w}$$ (2)

It may be possible to obtain a diverse ensemble that has a low uncertainty by considering different subsets, S ⊆ ℤ, of a heterogeneous structural library, ℤ, with n conformations.

In order to use Bayesian variable selection techniques to identify an optimal set of conformations, S^* ⊆ ℤ, we have to specify an a priori probability for each subset of structures. If we do not have a priori knowledge to guide this choice, it is reasonable to assume that every possible subset is equally probable; i.e., f_S (S) ∝ 1, where f_S (S) is the probability of subset S. In this case, the posterior probability for a subset of conformations is:

$$f_{S|\vec{M}}(S|\vec{m})\propto f_{\vec{M}|S}(\vec{m}|S)$$ (3)

where $\vec{w}={\{w_i\}}_{i=1}^l$ is the vector of weights for the subset S ⊆ ℤ that contains l ≤ n structures. Therefore, the optimal subset of structures is obtained by maximizing the ML, f_M⃗|S (m⃗|S). Note that it is usually not tractable to search through all subsets of structures, because the number of possibilities may very large. Instead, we begin with the entire structural library, where the weights are estimated using eq. (2) and the ML is calculated. Then, the lowest weighted structure is thrown out if its estimated weight is below a cutoff, w_cut. The weights of the remaining structures are then recalculated along with the new value of the ML and, again, the lowest weighted structure is discarded if its weight is below w_cut. The algorithm repeats this process until either the ML converges or all of the weights are greater than w_cut. The set of structures that had the largest value of the ML is chosen for the final ensemble. In what follows, we develop a variational BW, or VBW, method to facilitate efficient calculation of the weights at each step.

2.2. Variational Bayesian Weighting

At each iteration of the algorithm, after a set of structures has been chosen, an approximation to the ML can be calculated efficiently using ‘variational’ Bayesian inference.¹¹ As stated above, the ML is proportional to the criterion for selecting a set of structures. In addition, by maximizing an approximate form of the ML we can arrive at an optimal set of weights for the structural subset under consideration. In variational Bayesian inference, the posterior PDF given by eq. (1) is approximated with a simpler PDF that allows one to easily calculate quantities of interest.¹¹ Since we are interested in vectors of weights that are positive and sum to one, we choose our simple distribution to be a Dirichlet distribution with PDF:¹²

$$g(\vec{w}|\vec{\alpha },S)=\frac{\mathrm{\Gamma }({\alpha }_0)}{{\displaystyle {\sum }_{i=1}^n}\mathrm{\Gamma }({\alpha }_i)}{\displaystyle {\prod }_{i=1}^l}{w}_i^{{\alpha }_i-1}$$ (4)

where Г(·) is the gamma function, ${\{{\alpha }_i>0\}}_{i=1}^l$ are parameters of the distribution and ${\alpha }_0={\displaystyle {\sum }_{i=1}^l}{\alpha }_i$ . Using this distribution, we can calculate a lower bound on the logarithm of the ML as follows:¹³

$$\text{log }{f}_{\vec{M}}(\vec{m}|S)\ge {\displaystyle \int }g(\vec{w}|\vec{\alpha },S)\text{log }\left\{\frac{f_{\vec{M}|\vec{W}}(\vec{m}|\vec{w},S)f_{\vec{W}|S}(\vec{w}|S)}{g(\vec{w}|\vec{\alpha },S)}\right\}d\vec{w}\equiv -L(\vec{\alpha }|S)$$ (5)

We note that our overall goal is to maximize the ML; however, since equation (5) provides a lower bound for the ML, we instead maximize −L(α⃗|S), or equivalently minimize L(α⃗|S). Furthermore, it is easy to show that L(α⃗|S) is equal (up to an additive constant) to the Kullback-Leibler (KL) distance¹⁴ between g (w⃗|α⃗, S) and f_{W⃗|M⃗, S} (w⃗|m⃗, S). Therefore, by finding the set of parameters that minimizes L(α⃗|S) we also obtain an approximation to f_{W⃗|M⃗, S} (w⃗|m⃗, S).

The feature that makes the VBW algorithm computationally efficient is that the objective function can be obtained in closed-form for a suitable choice of prior distribution. Thus, one can apply a standard minimization protocol to find the set of parameters that minimize L(α⃗|S). Before sketching the derivation, we need to define all of the terms in eq. (1).

We denote the current set of structures under consideration as $S={\{s_i\}}_{i=1}^l$ and presume that we have a set of experimental measurements, $\vec{m}={\{m_i\}}_{i=1}^k$ , which have experimental errors ${\left\{{\epsilon }_i^{\text{exp}}\right\}}_{i=1}^k$ . We assume that it is possible to calculate the i^th experimental observable in the j^th conformation, denoted as m̂_ij, with an accuracy ${\epsilon }_i^{\mathit{\text{pre}}}$ . For example, if the Cα chemical shift for the first structure is calculated using SHIFTX, then ${\epsilon }_1^{\mathit{\text{pre}}}$ denotes the error reported for the calculation of a Cα chemical shift using SHIFTX, which is approximately 0.98 ppm.¹⁵ The total uncertainty that results from experimental error and inaccurate prediction algorithms is defined as ${\epsilon }_i=\sqrt{{\left({\epsilon }_i^{\text{exp}}\right)}^2+{\left({\epsilon }_i^{\mathit{\text{pre}}}\right)}^2}$ . We assume that the likelihood function for each experimental measurement follows a Gaussian distribution, such that the total likelihood function (assuming that the measurements are independent) can be written as follows:

$$f_{\vec{M}|\vec{W},S}(\vec{m}|\vec{w},S)={\displaystyle {\prod }_{i=1}^k}\left(\frac{1}{{\epsilon }_i\sqrt{2\pi }}\right)\text{exp }\{-{\displaystyle {\sum }_{i=1}^k}\frac{1}{2{\epsilon }_i^2}{(m_i-{\displaystyle {\sum }_{j=1}^l}{\mathrm{m̂}}_{\mathit{\text{ij}}}{w}_j)}^2\}$$ (6)

Finally, for the prior distribution, f_W⃗|S (w⃗|S), we choose a Dirichlet distribution with PDF:

$$f_{\vec{W}|S}(\vec{w}|S)=\frac{\mathrm{\Gamma }(n/2)}{n\mathrm{\Gamma }(1/2)}{\displaystyle {\prod }_{i=1}^l}{w}_i^{-1/2}$$ (7)

This choice of prior is a type of Jeffreys’ distribution – a class of non-informative prior distributions that are widely used in Bayesian inference.¹⁶

Beginning with the definition of L(α⃗|S) in eq. (5), we can rewrite the objective function as:

$$L(\vec{\alpha }|S)={\displaystyle \int }g(\vec{w}|\vec{\alpha },S)\text{log}\frac{g(\vec{w}|\vec{\alpha },S)}{f_{\vec{W}|S}(\vec{w}|S)}d\vec{w}-{\displaystyle \int }g(\vec{w}|\vec{\alpha },S)\text{log }{f}_{\vec{M}|\vec{W},S}(\vec{m}|\vec{w},S)d\vec{w}$$ (8)

The first term is the KL distance between two Dirichlet distributions, i.e. the variational and the prior distributions, and has been previously reported.¹⁷ The second term is given by:

$$-{\displaystyle \int }g(\vec{w}|\vec{\alpha },S)\text{log }{f}_{\vec{M}|\vec{W},S}(\vec{m}|\vec{w},S)d\vec{w}={\displaystyle {\sum }_{i=1}^k}\frac{1}{2{\epsilon }_i^2}{\displaystyle \int }g(\vec{w}|\vec{\alpha },S){\left(m_i-{\displaystyle {\sum }_{j=1}^l}{\mathrm{m̂}}_{\mathit{\text{ij}}}{w}_j\right)}^{2}d\vec{w}+C$$ (9)

where C is a constant that depends on the experimental errors. The integral in eq. (9) can be calculated exactly giving an analytical expression for eq. (8):

$$\begin{gathered} L(\vec{\alpha }|S)=\text{log}\frac{\mathrm{\Gamma }({\alpha }_0)}{\mathrm{\Gamma }(l/2)}+{\displaystyle \sum _{i=1}^l}\text{log}\frac{\mathrm{\Gamma }(1/2)}{\mathrm{\Gamma }({\alpha }_i)}+{\displaystyle \sum _{i=1}^l}({\alpha }_i-1/2)\{\psi ({\alpha }_i)-\psi ({\alpha }_0)\} \\ +\frac{1}{2}{\displaystyle \sum _{i=1}^k}{\epsilon }_i^{-2}{\left(m_i-\frac{1}{{\alpha }_0}{\displaystyle \sum _{j=1}^l}{\mathrm{m̂}}_{\mathit{\text{ij}}}{\alpha }_j\right)}^2+\frac{1}{2}{\displaystyle \sum _{i=1}^l}{\displaystyle \sum _{j=1}^l}\left({\displaystyle \sum _{l=1}^k}\frac{{\mathrm{m̂}}_{\mathit{\text{li}}}{\mathrm{m̂}}_{\mathit{\text{lj}}}}{{\epsilon }_l^2}\right)\frac{{\alpha }_i({\alpha }_0-{\alpha }_i){\delta }_{\mathit{\text{ij}}}-{\alpha }_i{\alpha }_j(1-{\delta }_{\mathit{\text{ij}}})}{{\alpha }_0^2({\alpha }_0+1)} \end{gathered}$$ (10)

where δ_ij is the Kronecker delta function, ψ (·) is the digamma function and the constant from eq. (9) has been neglected because constant terms do not play a role in function minimization.

Finally, suppose that we have used an optimization algorithm to identify the set of parameters, ${\{{\mathrm{\alpha ̂}}_i\}}_{i=1}^l$ , that minimizes L(α⃗|S) for the current set of conformations. The estimates for the population weights are given by the simple formula $w_i^B={\mathrm{\alpha ̂}}_i/{\displaystyle {\sum }_{j=1}^l}{\mathrm{\alpha ̂}}_j$ .

2.3. Variational Bayes with Structure Selection

The Variational Bayesian Weighting with Structure Selection (VBWSS) algorithm is:

1. Initialize the set of conformations to the entire structural library, i.e. set S = ℤ.

2. Use simulated annealing to find the set of parameters that minimizes L(α⃗|S).

3. Remove the lowest weighted structure if it has $w_i^B<w_{\mathit{\text{cut}}}$ and go to step 4, else go to step 5.

4. If L(α⃗|S) has not improved for 10 iterations go to step 5, else return to step 2.

5. Exit the algorithm and return the set of structures and parameters that produced the smallest value of L(α⃗|S).

The simulated annealing algorithm in step 2 used a Gaussian cooling schedule T(t) = T(0)exp(−(5t)²), where t is the fraction of steps completed. For the first iteration with the entire structural library, the number of steps was set to 100 · n and the initial temperature was set to T(0) = 2. Since each iteration of the structure selection algorithm involves throwing out a lowly weighted structure, we reasoned that the set of parameters identified in iteration j should be reasonable guess for the parameters for iteration j+1. Thus, each iteration after the first was initialized using the parameters identified in the previous iteration and run for 50 · l steps beginning from a temperature of T(0) = 1. The step size was optimized during a short equilibration period at the start of each iteration to target a 50% acceptance ratio at T = 1.

2.3. Approximate Confidence Intervals

The variational approximation to the posterior PDF can be used to calculate confidence intervals (CI) for parameters of the ensemble using a simple analytical approximation. Here, we suppose that our final set of conformations is $S={\{s_i\}}_{i=1}^l$ and the corresponding set of variational parameters is ${\{{\mathrm{\alpha ̂}}_i\}}_{i=1}^l$ . Again, we define ${\mathrm{\alpha ̂}}_0={\displaystyle {\sum }_{i=1}^l}{\mathrm{\alpha ̂}}_i$ . As an example, suppose that we are interested in estimating the ensemble average distance between two atoms in the protein. The distance between the two atoms in the i^th structure is D_i. The Bayesian point estimate for the ensemble averaged distance is $\langle D\rangle ={\mathrm{\alpha ̂}}_0^1{\displaystyle {\sum }_{i=1}^l}{D}_i{\mathrm{\alpha ̂}}_i$ and the variance in the ensemble averaged distance is $\text{var}[D]={\mathrm{\alpha ̂}}_0^{-2}{({\mathrm{\alpha ̂}}_0+1)}^{-1}{\displaystyle {\sum }_{i=1}^l}{\displaystyle {\sum }_{j=1}^l}{D}_i{D}_j({\mathrm{\alpha ̂}}_i{\mathrm{\alpha ̂}}_0{\delta }_{\mathit{\text{ij}}}-{\mathrm{\alpha ̂}}_i{\mathrm{\alpha ̂}}_j)$ , which comes from the formula for the variance of a linear combination and the covariance matrix of a Dirichlet distribution.¹² Thus, an approximate 95% CI can be calculated using $\langle D\rangle \pm 1.96\sqrt{\text{var}[D]}$ ; the 1.96 is the number of standard deviations of a Gaussian distribution that corresponds to a 95% CI.¹²

3. Results and Discussion

3.1. Validation with Reference Ensembles

The ultimate goal of the VBWSS algorithm is to construct an accurate, parsimonious representation for the conformational ensemble of an IDP using a minimum amount of computational effort while, simultaneously, estimating the uncertainty in the resulting model. Thus, there are a number of criteria by which the algorithm must be judged. First, we will address the 2 most important criteria: that the algorithm provides a means for accurately modeling conformational ensembles and for estimating their uncertainties. To address these questions, and to choose the weight threshold for structure selection, we used the method of reference ensembles.

A reference ensemble is a pre-defined ‘truth’ for which both the set of conformations and their weights are known. The same 20 reference ensembles that were used to validate the previously reported BW algorithm were also used in this study to facilitate a comparison between BW and the new VBWSS algorithm.⁸ To review, each of the reference ensembles consisted of a set of 95 conformations for the small peptide, met-enkephalin, and a set of weights. The different sets of weights were chosen so that the reference ensembles had different amounts of entropy. Backbone NMR chemical shifts were calculated for each reference ensemble using SHIFTX and were randomly perturbed by 0.1 ppm to model experimental uncertainty.¹⁵

The ensembles were compared by measuring the distances between the vectors of weights. For the measure of distance, we used the Jensen-Shannon divergence (JSD), which ranges from 0 to 1 for identical and maximally different vectors of weights, respectively, and is given by:^{18, 19}

$${\mathrm{\Omega }}^2({\vec{w}}^{(1)},{\vec{w}}^{(2)})=\frac{1}{2}{\displaystyle {\sum }_{i=1}^n}{w}_i^{(1)}{\text{ log}}_2\left(\frac{2w_i^{(1)}}{w_i^{(1)}+w_i^{(2)}}\right)+\frac{1}{2}{\displaystyle {\sum }_{i=1}^n}{w}_i^{(2)}{\text{ log}}_2\left(\frac{2w_i^{(2)}}{w_i^{(1)}+w_i^{(2)}}\right)$$ (11)

For VBWSS, if a structure was not included in the ensemble then its weight was set equal to zero. The square root of the JSD can also be used to quantify the uncertainty in an ensemble by calculating the expected distance from the point estimate for the weights.⁸ It was shown previously that such an estimate ${\sigma }_{{\vec{w}}^B}=\sqrt{{\displaystyle \int }{\mathrm{\Omega }}^2(\vec{w},{\vec{w}}^B)f_{\vec{W}|\vec{M},S}(\vec{w}|\vec{m},S)d\vec{w}}$ , was strongly correlated to the distance between the ‘true’ weights of a reference ensemble and the estimated weights, w⃗^B. This is an important feature of BW because it provides a built-in error check on the accuracy of the ensemble. To ensure that this feature was preserved in VBWSS, the weight cutoff for structure selection was chosen to maximize the correlation between σ_w⃗^B and Ω(w⃗^T, w⃗^B) for the 20 reference ensembles, yielding a value of w_cut = 0.004; this value of w_cut was used throughout the rest of the analysis.

A comparison of the accuracy of the VBWSS and BW algorithms on the 20 reference ensembles is shown in Fig. 1. As shown in Fig. 1A, the estimates for the weights obtained from the VBWSS algorithm are similar in accuracy to those obtained from BW. In addition, the correlation between the uncertainty estimate, σ_w⃗^B, and the actual error in the estimated weights, Ω(w⃗^T, w⃗^B), obtained from VBWSS is R = 0.9. The error in the weights is related to σ_w⃗^B by Ω(w⃗^T, w⃗^B) ≈ 1.54 · σ_w⃗^B Thus, VBWSS obtained a similar level of accuracy as BW and maintained the ability to quantify the uncertainty in the ensemble.

Figure 1.

(A) The error between the true and estimated weights for the 20 reference ensembles. The solid and dashed lines indicate VBWSS and BW, respectively. The ensembles are ordered by increasing entropy. (B) The correlation (R = 0.9) between σ_w⃗^B and Ω(w⃗^T, w⃗^B) obtained from VBWSS. The best fit, y = 1.54 x, is shown as a dashed line.

It is also important to ensure that CIs calculated from VBWSS provide reasonable estimates of the errors in parameters of the ensemble. We assessed this feature of the algorithm by comparing ensemble averaged inter-atomic distances calculated from the VBWSS ensembles to their corresponding values in the reference ensembles. The approximate formula for a CI defined in section 2.4 should be fairly accurate if, on average, (〈D〉 − D_ref)² ≈ var[D]; here, D_ref is the ensemble average value of the distance calculated from the reference ensemble. In practice, we found that the standard deviation, calculated using VBWSS was too small, which is a problem that is known to affect variational approximations in Bayesian inference. To correct for the bias in the estimation of the standard deviations from VBWSS, we determined an empirical equation, $\langle D\rangle \pm 1.96·\lambda ·\sqrt{\text{var}[D]}$ , that gave the CIs for the inter-atomic distances approximately 95% coverage frequency of their reference ensemble values. The best fit value was λ ≈ 1.54, which was used for subsequent calculations of CIs.

3.2. α-Synuclein Ensemble

αS is one of the most studied members of the IDP family. This 140 residue protein has been implicated in the pathology of a family of diseases known as synuclepathies.²⁰ The most common among these is Parkinson’s disease, a neurodegenerative disorder characterized by intracellular aggregates known as Lewy bodies and the loss of dopaminergic neurons.²¹ While the exact relation between the aggregates and neuronal death remains a subject of debate, understanding the nature of the unfolded protein and its ability to aggregate may prove crucial to the design of new therapies. Furthermore, although it has been suggested that αS adopts a tetrameric structure with considerable helical content in the native cell environment²², the formation of aggregates likely involves the dissociation of these tetramers into disordered monomers that can form aggregates rich in cross-beta structure²². Consequently, there is still a need to understand the structure of the unfolded form of the disordered monomeric form of αS because such data may provide insights into the aggregation process.

We applied the VBWSS algorithm to a previously generated structural library of αS that was created by pruning a large sample of ~10⁵ structures to a representative library of 299 conformations. The exact same set of experimental measurements which was used to generate the BW ensemble was used here to generate the VBWSS ensemble. More specifically, we used C, Cα, Cβ and N chemical shifts,²³ N-H RDCs²⁴ and the radius of gyration from SAXS experiments²⁵ along with the calculated values of chemical shifts using SHIFTX,¹⁵ RDC using PALES²⁶ and radius of gyration through CHARMM.²⁷ RDCs predicted from PALES are frequently scaled to account for uncertainty in predicting the magnitude of alignment.⁸ Here, the predicted RDCs were scaled by 0.25, which was found using a simple grid search to minimize the VBW objective function.

We found that the VBW algorithm was extremely efficient compared to the BW algorithm. The VBW algorithm (without structure selection) took less than 30 seconds, compared to approximately 2 weeks for BW, running in parallel on eight 2.4 GHz Intel Xeon processors – a decrease in computational time of roughly 4 orders of magnitude. The increased computational efficiency of the variational approximation more than made up for the increase in computational effort due to structure selection, with the total VBWSS algorithm taking less than 30 minutes.

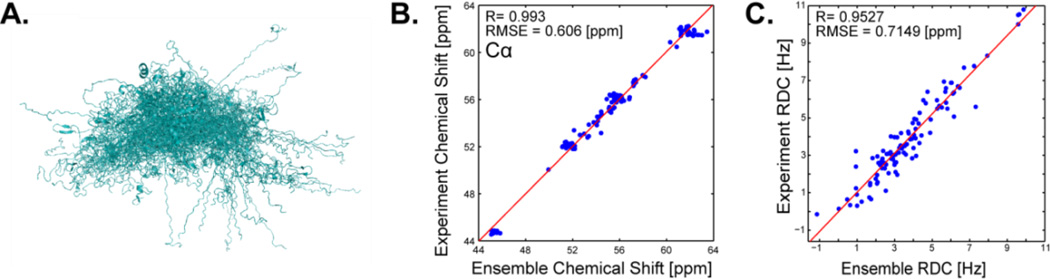
Structure selection reduced the ensemble size from 299 to 78 non-zero weighted conformations, as shown in Fig 2A. The VBWSS ensemble also fits the experimental data well (Figs. 2B–C). In addition, the calculated ensemble average value of the radius of gyration was 40.4Å with a 95% CI of [39.2–41.6]Å compared to the experimental value of 40±2Å.²⁵

Figure 2.

αS VBWSS algorithm. (A) Alignment of non-zero weighted structures. (B) Agreement of calculated and experimental Cα chemical shifts. (C) Agreement of calculated and experimental RDCs.

We cross validated our ensemble by comparing inter-residue distances obtained from a recently published FRET experiment described in Grupi et al²⁸ (Table 1). Our calculated 95% CIs for the ensemble average distances, measured between the Cα atoms, are in good agreement with the corresponding experimentally determined values. It is important to note, that we made no explicit use of any inter-residue distance data in the ensemble generation procedure.

Table 1.

Cross validation through inter-residue distances

Probe pair	Experiment [Å]	Ensemble [Å]
18,26	15.1	16.5–17.8
26,39	21.8	20.2–22.7
4,18	16.9	17.9–19.9
18,39	29.4	30.0–33.6
4,26	33.6	27.9–31.2
66,90	29.6	36.5–40.1
39,66	40.1	40.2–44.5
4,39	43.0	39.5–44.3

One of the most interesting features of αS is its ability to form aggregates that contain cross-beta structure under the right set of experimental conditions.²⁹ Because the formation of αS aggregates was shown to be involved in the pathology of Parkinson’s disease, it is of great interest to gain further knowledge about aggregation prone conformations within the disordered state. It was previously found that the minimal toxic aggregating segment is located in the NAC region of the protein, residues 68–78 or in reference to the NAC, NAC(8–18).³⁰ Therefore, we focused on assessing regions with aggregation propensity within the ensemble. Because structures that place the segment in an extended and solvent exposed orientation may be aggregation-prone, we calculated the percentage solvent accessible surface area (%SASA) of the NAC(8–18) segment using CHARMM²⁷ and the secondary structure content of each structure in the ensemble. Percentage solvent accessible surface area was calculated by dividing the SASA values for N-C-Cα atoms by the SASA values of these atoms in a fully extended conformation. Results of this analysis are shown in Fig 4. Similar analysis can be found in Ullman & Stultz.³¹

Figure 4.

Aggregation propensity in the ensemble. Colors represent the weight of each of structure. The star denotes a structure, shown to the right, with a relatively high weight.

We found that approximately 12% (8–15% is the 95% CI) of the structures have the NAC(8–18) segment in an extended (more than 3 extended residues) and solvent exposed (%SASA>40) orientation. These results are similar to those found using the BW algorithm³¹ and suggest that the ensemble of αS contains conformations that can readily form toxic, beta-sheet rich aggregates.

4. Conclusions

Constructing an ensemble for an IDP is a difficult task that requires reliable methods for estimating parameters from the ensemble and their associated uncertainties. Here, we introduced an algorithm for selecting an optimal set of conformations and implemented a variational approximation to the BW algorithm that provides a decrease in computational time of roughly 4 orders of magnitude. The two methods were combined in the VBWSS algorithm, which provides a computationally efficient method for constructing IDP ensembles. The VBWSS algorithm was validated using reference ensembles, and was found to produce a similar level of accuracy as the BW algorithm. In addition, accurate estimates for the uncertainties in characteristics of the ensemble can be calculated from VBWSS using simple formulas.

In general, proteins with a larger amount of disorder result in VBWSS ensembles with a larger amount of uncertainty, all other things being equal. Nevertheless, certain characteristics of the ensemble may be well defined even when the other aspects are highly uncertain. This highlights the importance of using confidence intervals to make inferences about ensemble characteristics.

We applied the VBWSS algorithm to construct an ensemble for αS and found that the ensemble agrees very well with experimental data. In addition to a dramatic decrease in computational time over BW, the VBWSS resulted in an improved fit to some experimental data. The BW algorithm obtains optimal structure weights for a given set of conformations while VBWSS obtains an optimal set of weights as well as an optimal set of conformations that fit the existing set of experimental data. Given this extra degree of freedom, it is not surprising that, at least in the case of α-synuclein, VBWSS obtains slightly better fits to the experimental data. In addition, we were able to reproduce experimentally measured inter-residue distances that were not included as restraints in the algorithm. The ensemble suggests that αS populates aggregation prone conformations in the disordered state. These results illustrate that the VBWSS algorithm provides an efficient, and accurate, method for constructing models of IDP ensembles.