Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Sep 1.
Published in final edited form as: Biosystems. 2012 May 14;109(3):412–419. doi: 10.1016/j.biosystems.2012.05.001

On Integrating Experimental and Theoretical Models to Determine Physical Mechanisms of Morphogenesis

Victor D Varner a,*, Larry A Taber a,✉
PMCID: PMC3423499  NIHMSID: NIHMS388485  PMID: 22612907

Abstract

Researchers in developmental biology are increasingly recognizing the value of theoretical models in studies of morphogenesis. However, creating and testing realistic quantitative models for morphogenetic processes can be an extremely challenging task. The focus of this paper is on models for the mechanics of morphogenesis. Models for these problems often must include large changes in geometry, leading to highly nonlinear problems with the possibility of multiple solutions that must be sorted out using experimental data. Here, we illustrate our approach to these problems using the specific example of head fold formation in the early chick embryo. The interplay between experimental and theoretical results is emphasized throughout, as the model is gradually refined. Some of the limitations inherent in theoretical/computational modeling of biological systems are also discussed.

Keywords: development, biomechanics, mechanobiology, computational models, head fold, chick embryo

1. Introduction

In a well-known quote, the statistician George E.P. Box stated, “essentially, all models are wrong, but some are useful” (Box and Draper, 1987). These words ring especially true for problems in the mechanics of morphogenesis, which often involve complex three-dimensional changes in form driven by multiple cellular and extracellular mechanisms. For such highly nonlinear systems, physical intuition can be misleading, and theoretical models have proven to be useful for interpreting experimental results (Clausi and Brodland, 1993; Conte et al., 2008; Davidson et al., 1995; Manoussaki et al., 1996; Ramasubramanian et al., 2008; Savin et al., 2011; Taber, 2008). Consequently, computational modeling of morphogenesis has become increasing popular during the past few decades.

Investigators readily acknowledge that theoretical models contain inherent limitations and must be tested to the extent possible using experimental data. However, it is important to recognize that fully validating a model is not possible (Oreskes et al., 1994). Regardless of the number of tests a given model may pass, it always is possible that results from a future experiment will contradict a numerical prediction. Hence, predictions provided by models, particularly those for biological systems, always must be considered cautiously.

For several reasons, developing and testing theoretical models for morphogenesis is a particularly challenging endeavor. First, experimental results can be highly variable between species, between individual organisms of a given species, at different stages of development for a single organism, and sometimes even for consecutive measurements on the same subject. The dynamic nature of morphogenesis amplifies these difficulties, as time-dependent data are needed. Thus, attaining precise quantitative agreement between theory and experiment is generally not feasible. Second, experimental perturbations used to test model predictions may trigger an adaptive response through a mechanism not included in the model. While the ability to adapt to changing conditions is vital for robust embryonic development, it makes the challenge facing both modelers and experimentalists all the more daunting. Third, biological systems typically contain enormous numbers of unknown parameters, many of which cannot be measured directly. Hence, even the most sophisticated model is at best only a rough approximation of the actual system.

The trick in developing theoretical models is to determine which parameters and mechanisms are most relevant and which can safely be neglected. This makes modeling of biological systems something of an art. In our opinion, it is best to begin with relatively simple models and add complexities in a sequential manner. This strategy is used here. However, motivated in part by ever more powerful computers, the trend today seems to be moving toward including more complexity at the outset. Although more complex models may be more realistic, the more complicated the model, the more difficult it is to gain insight into fundamental behavior.

The purpose of this paper is to show how experiments and computational modeling can be integrated to determine the physical mechanisms underlying a relatively complex morphogenetic process. For illustration, we consider the problem of head fold (HF) formation in the chick embryo. The HF is the first major 3-D structure to form during development, and we treat this problem as a case study to explore the aforementioned issues. Recently, we used modeling and experiments to propose a physical mechanism for HF morphogenesis (Varner et al., 2010). During the course of this study, however, our model continuously evolved as it was tested against new data. While intermediate (i.e., negative) model results can be instructive, they are rarely, if ever, published (Oreskes et al., 1994). Here, therefore, we trace this iterative theoretical-experimental process over the course of an individual study, include some of the salient intermediate results, and discuss broader implications for modeling the mechanics of morphogenesis.

2. Background

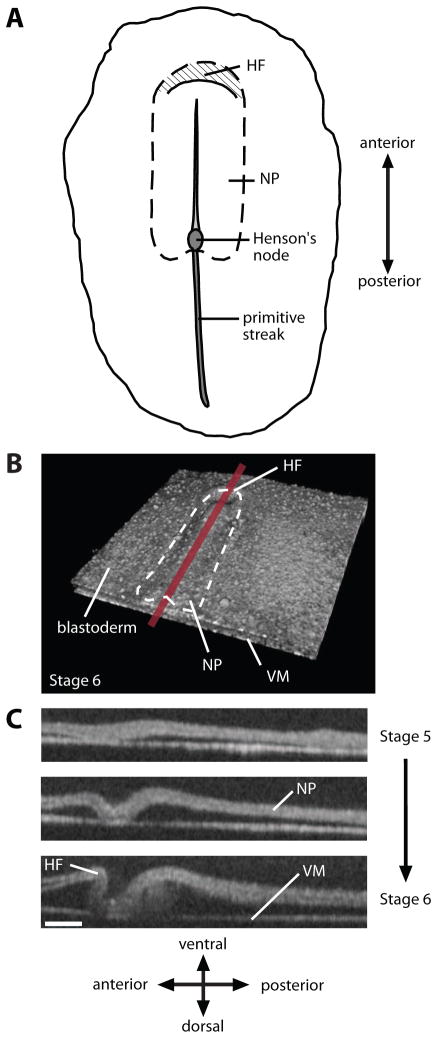
During the first day of a 21-day incubation period in the chick embryo, the blastoderm is a relatively flat disk composed of three germ layers (endoderm, mesoderm, and ectoderm) (Patten, 1971). After about 24 hours of incubation, the HF arises as a crescent-shaped fold at the anterior end of the thickened neural plate (NP) (Fig. 1). The HF is a crucial morphogenetic process, as it simultaneously initiates heart, brain, and foregut development (Bellairs, 1953b; Bellairs and Osmond, 2005; Lillie, 1952; Moore et al., 2000; Oostra et al., 2007; Schoenwolf and Smith, 2000)

Figure 1. Morphology of early chick embryo.

Figure 1

Open in a new tab

(A) Ventral schematic view of HH stage-7 embryo. Crescent-shaped head fold (HF) forms at the anterior end of the neural plate (NP). (B) 3D OCT reconstruction of HH stage-6 embryo. (VM: vitelline membrane) (C) Midline sections during HF formation (HH stages 5–6). From Varner et al. (2010).

Since the HF is one of the first observable landmarks to form during development, it naturally caught the attention of embryologists. Balfour (1881) described the avian HF as a “tucking in” of the blastoderm, a description which may suggest active folding of the tissue. A few years later, Shore and Pickering (1889) proposed instead that differential growth drives HF morphogenesis. Specifically, they postulated that the NP grows faster than the surrounding tissue, forcing the blastoderm to buckle into a crescent-shaped fold. These authors also speculated that mechanical contact with the vitelline membrane (VM) plays a role in shaping the HF.

Many decades later, Stalsberg and DeHaan (1968), building on work by Bellairs (1953a, b), suggested a different buckling mechanism. They proposed that regression of Henson’s node (see Fig. 1A) pulls the embryonic region downward, causing the blastoderm to buckle and roll over the fixed anterior border of the NP to produce the HF. Although all of these hypotheses may seem plausible, none had been tested directly in developing embryos.

As mentioned above, we recently used a combination of computational modeling and experiments to explore the HF problem (Varner et al., 2010). As new data were acquired, the model continually evolved. The following paragraphs describe the sequence of events during this study.

3. Model 1: Buckling Driven by Notochord Elongation

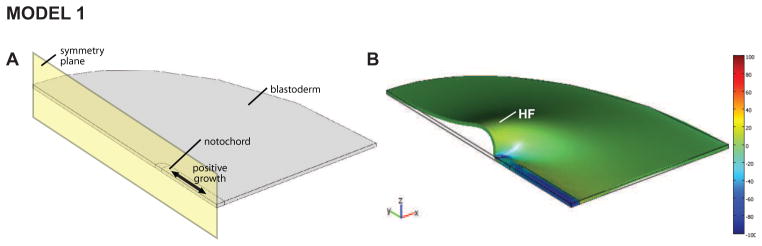
Our first model for HF formation is based on a relatively simple idea. The notochord is a relatively stiff rod embedded in the embryo just ventral to the neural tube, extending between Hensen’s node and the primitive HF region (Fig. 1A). As the HF forms, the notochord elongates and Hensen’s node migrates posteriorly. Investigators long have speculated that this structure plays a mechanical role in morphogenesis (Adams et al., 1990), and we postulated that it pushes against the HF region, causing it to buckle into a crescent-shaped fold.

To test whether this mechanism can generate the correct physical shape, we created a finite-element model consisting of a semicircular plate (blastoderm) with an embedded rod (notochord) (Fig. 2A). The edges of the plate are fixed, with symmetry assumed relative to the embryo midline. When longitudinal growth is specified in the notochord, a crescent-shaped fold resembling the HF develops at the anterior end of the rod (Fig. 2B). While this result had seemed promising, the shape of the HF midline cross section is not correct. In addition, we tested the basic idea experimentally by cutting the neural plate laterally between the notochord and the prospective HF region. During subsequent incubation a HF developed, suggesting that the notochord does not play a major role in this process (Varner et al., 2010). Thus, although this proposed mechanism may have seemed reasonable initially, further study apparently has ruled it out.

Figure 2. Model 1 gives incorrect HF shape.

Figure 2

Open in a new tab

(A) Model geometry in initial configuration. The notochord is a relatively stiff bar embedded in the blastoderm. (B) Longitudinal growth of notochord causes crescent shaped head fold (HF) to form, but cross-sectional shape is not realistic (see Fig. 1C).

4. Model 2: Convergent Extension, Cell Wedging, and Epidermal Shaping

Next, we developed a model to test a new hypothesis based on previous ideas, as well as results provided by more recent studies. Here, NP elongation essentially replaces notochord elongation, consistent with speculation by the Shore and Pickering (1889). Moreover, as shown below, proper HF shape also requires forces caused by cell wedging, active in-plane shape changes anterior to the HF, and contact with the VM. Rather presciently, the potential importance of the VM also was mentioned by Shore and Pickering (1889).

4.1. Model 2a: First approximation

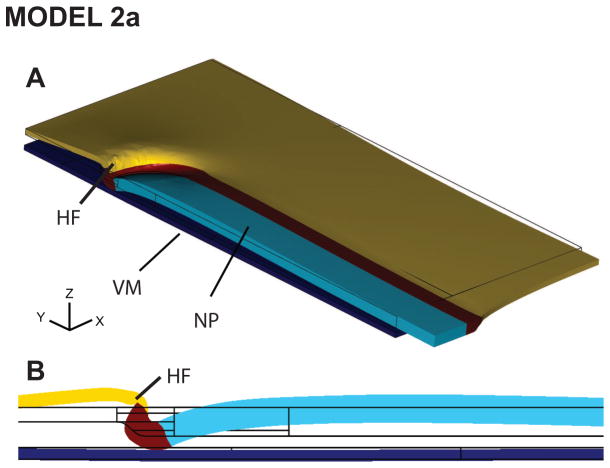
During our initial study of this hypothesis, we developed a model that includes two sets of driving forces. The first is generated by the morphogenetic process known as convergent extension, which causes the NP to elongate axially and shorten laterally in the chick embryo (Colas and Schoenwolf, 2001b; Ezin et al., 2009; Smith and Schoenwolf, 1997). Studies have shown that convergent extension occurs through a combination of cell intercalation (Ezin et al., 2009; Schoenwolf and Alvarez, 1989) and coordinated cell division (Sausedo et al., 1997).

The second driving force is cell wedging in and near the region of contact with the VM (Lawson et al., 2001) (Fig. 4D), whereby epithelial cells actively transform from cuboidal to wedge shaped. The biophysical mechanisms that cause these changes in cell shape are unknown, but they likely are intrinsic to the HF cells themselves (Moury and Schoenwolf, 1995) and may include interkinetic nuclear migration (Schenk et al., 2009; Smith and Schoenwolf, 1988) or laminin-dependent basal constriction (Gutzman et al., 2008).

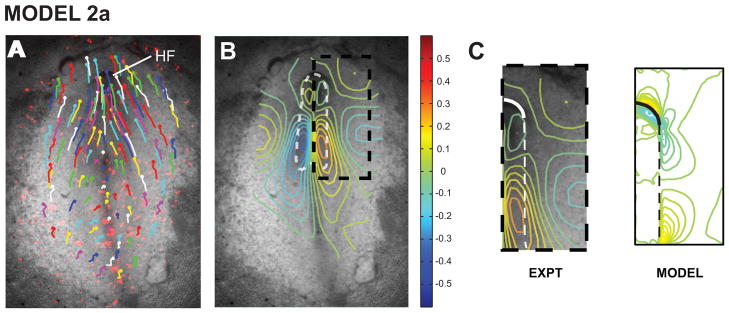
Figure 4. Model 2a includes convergent extension and cell wedging only: yields correct head fold shape.

Figure 4

Open in a new tab

(A) Viewed in 3D, the deformed model geometry has a characteristically crescent-shaped HF. (B) Midline section shows reasonable agreement in HF shape between model and experiment (compare to Fig. 1C, stage 6).

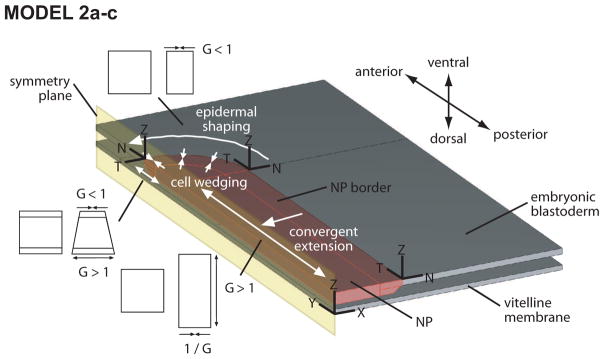
Based on these considerations, the model consists of two parallel membranes (plates) separated by a narrow gap (Fig. 3). The upper plate represents the blastoderm, with the neural plate being a relatively thick rectangular region with a rounded anterior end. The lower plate represents the vitelline membrane. The analysis includes frictionless contact between these layers. Pseudoelastic material properties were estimated from microindentation tests and assumed to be isotropic, with the NP modulus being ten times higher than that of the surrounding ectoderm and the VM modulus ten times higher than the NP modulus.

Figure 3. Schematic of models 2a–c.

Figure 3

Open in a new tab

Model consists of blastoderm and vitelline membrane separated by a narrow space. Geometry is symmetric relative to embryonic midline, and frictionless mechanical contact between layers is assumed. Driving forces consist of cell wedging along the anterior border of the neural plate (NP), convergent extension in the NP, and active epidermal shaping (shortening) anterior to NP. These morphogenetic forces are simulated by regionally specifying the growth G as shown (G > 1 and G < 1 give active extension and contraction, repectively). In models 2a–c, the NP is rectangular in shape with a rounded anterior end.

Driving forces are simulated using the continuum growth theory of Rodriguez et al. (1994), which has been used in other morphomechanical simulations (Munoz et al., 2007; Taber, 2001, 2009). A detailed discussion of this theory is beyond the scope of this paper, but briefly the theory is based on the idea that the total deformation can be decomposed locally into a active component due to growth (or contraction) and a passive component due to stress. In the model, convergent extension in the NP is simulated by positive axial growth and negative lateral growth with the surface area held constant. For local cell wedging, positive and negative growth, respectively, are specified on the lower and upper surfaces of the blastoderm. Further details are provided in Varner et al. (2010).

During the simulation, the blastoderm layer is first stretched equibiaxially (consistent with experimental data (Varner et al., 2010)), and then both driving forces are turned on. The model produces a crescent shaped fold that resembles the actual HF, both in three dimensions and in midline section (Fig. 4).

Remark 1

Like many problems in morphogenesis, it is possible (even likely) that other combinations of driving forces could produce similar HF geometry, i.e., the solution is not unique. Consequently, matching morphology may not be a sufficient test for a given model. Other types of data may be needed.

4.2. Model 2b: Refine material properties for realistic shear strains

To further test model 2a, we measured morphogenetic strain distributions, which were computed from the spatial coordinates of ectodermal labels tracked during HF formation (Fig. 5A,B). All strain components are relatively symmetric about the midline (Varner et al., 2010), and the model captures many of the main characteristics of the normal (extensional) strains in both the axial and lateral directions (not shown). However, whereas the experimental shear strain is continuous across the boundary between the NP and adjacent ectoderm, the model yields a discontinuity in shear (Fig. 5C). This discontinuity stems from the assumption of stiffer material properties in the NP. As a consequence of this assumption, the NP is more resistant to shearing by the interfacial shear force than the adjacent tissue.

Figure 5. Model 2a yields incorrect shear strain distributions.

Figure 5

Open in a new tab

(A) Tracking tissue labels gives displacement field at HH stage 6+ relative to stage 5+. (B) Shear strain field computed from displacement field. (C) Boxed region in panel B. Experimental shear strains are continuous across neural plate border (dashed line), contrary to model results. Panels A and B are from Varner et al. (2010).

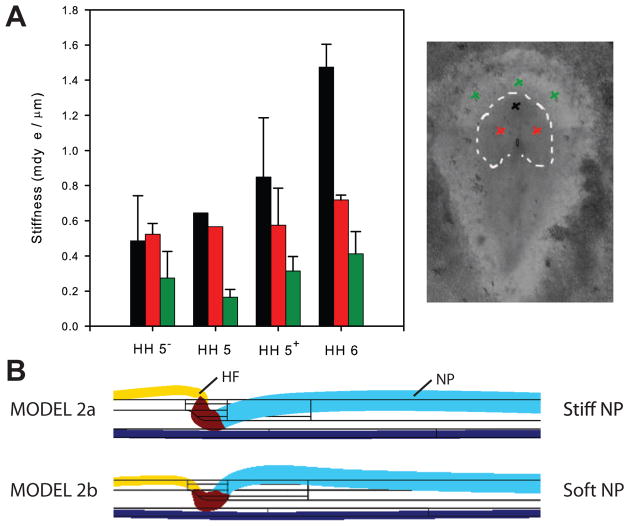
One way for the shear strain to be continuous across the border would be if the material modulus within the NP is lower than in the adjacent ectoderm. To examine this possibility, we used microindentation tests to determine the material properties at various locations during HF formation (Fig. 6A). When differences in membrane thickness are taken into account, these data indicate that the modulus in the NP is approximately half that in the surrounding tissue (Varner et al., 2010).

Figure 6. Model 2b includes regional differences in material properties: correct shear strains but wrong HF shape.

Figure 6

Open in a new tab

(A) Indentation stiffness in various regions of blastoderm. Head fold (black) is stiffest region, followed by neural plate (red) and neighboring ectoderm (green). Stiffnesses generally increase during HF development. Analysis accounting for regional differences in membrane thickness suggests that the modulus of the neural plate (NP) is about half that of the surrounding ectoderm. (B) Although shear strains agree better with experimental data (not shown), softer NP in model 2b produces less realistic HF shape than model 2a.

With this adjustment in properties, model 2b yields a roughly continuous shear stress distribution (not shown), in agreement our experimental data. However, the predicted shape of the HF is no longer realistic, as the structurally weaker NP now bends upward as it pushes against the HF (Fig. 6B). This result led us back to the literature.

4.3. Model 2c: Include epidermal shaping for realistic HF shape

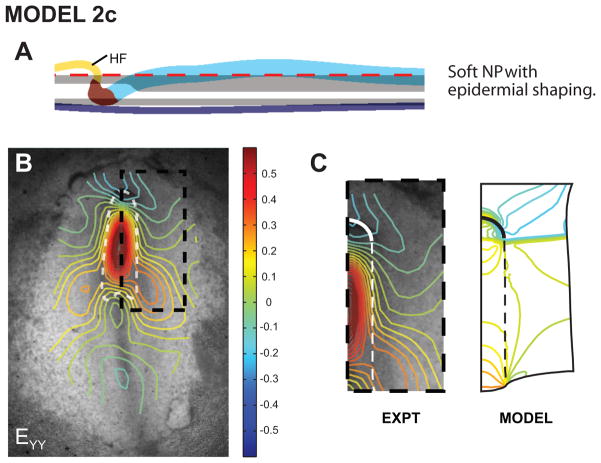
A third driving force is suggested by the study of Moury and Schoenwolf (1995), who excised a piece of ectoderm from the region anterior to the HF region. When cultured, this tissue shortened in the lateral direction. We reasoned that in-plane stresses generated by such shortening within an arch-shaped region above the HF would push the HF posteriorly as it generates tension and tends to straighten. Indeed, when this behavior is included (model 2c), the HF again acquires the correct shape (Fig. 7A). Moreover, the predicted shear (Exy) and lateral normal strain (Exx) distributions are now reasonable (not shown), but we noticed an inconsistency with the axial strain (Eyy). While the Exy data contain a single peak near the center of the NP, model 2c gives a peak at each end of the NP (Fig. 7B).

Figure 7. Model 2c includes anterior ectodermal shaping: correct HF shape and shear strains, but incorrect longitudinal strains.

Figure 7

Open in a new tab

(A) HF shape agrees reasonably well with experiment (see Fig. 1C, stage 6). (B) Longitudinal strain distributions. (C) Boxed region in panel B. Model strains have two peaks in NP, contrary to experimental data. Panel B is from Varner et al. (2010).

4.4. Model 2d: Refine NP geometry for realistic normal strains and stresses

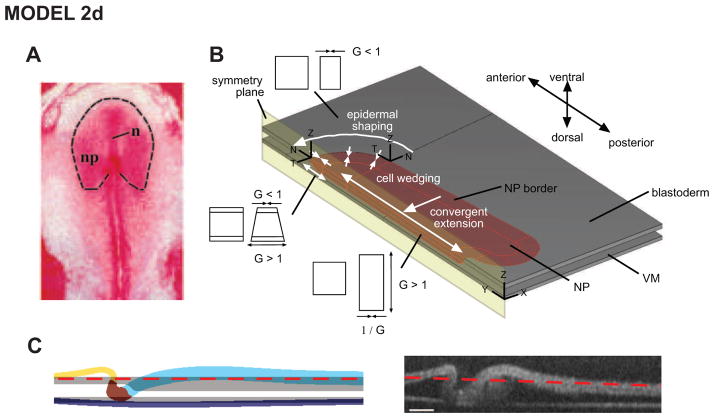
We next considered several ways to improve the strain distributions given by the model. For example, it may be possible to obtain better agreement by including regional variations in material properties within the NP, but this is not supported by our stiffness measurements. One thing we had not yet considered was to make the NP geometry more realistic, as its shape actually resembles a bell more than a rectangle (Fig. 8A).

Figure 8. Model 2d includes realistic NP geometry: correct HF shape.

Figure 8

Open in a new tab

(A) NP has characteristic bell shape (from Colas and Schoenwolf (2001a)). (B) Undeformed model geometry with realistic NP shape. (C) Deformed model HF shape agrees well with experimental shape. Panels B and C are from Varner et al. (2010).

With this adjustment, the model yields reasonably good qualitative agreement in HF morphology (Fig. 8B,C), as well as all strain components (Varner et al., 2010). In particular, the model now gives a single peak for Eyy within the NP. However, the location of the predicted peak is shifted posteriorly, strain magnitudes are relatively small compared to the experimental measurements, and the model does not capture the lateral gradient in Exx outside the NP (Varner et al., 2010). Hence, there is room for further improvement.

Remark 2

Even when a theoretical model yields accurate strain patterns, stress distributions still may be highly inaccurate. Consider, for example, a bar held at a fixed length. If the bar is passive and unstretched, both stress and strain will be zero. However, if the bar actively contracts in the axial direction, the observed and computed total strain would remain at zero, but tensile stress would be generated in the bar.

With this in mind, stress distributions were estimated using a micopipette to punch circular holes in the embryo. The size and shape of the hole relative to the pipette cross section characterizes the state of stress at a particular location. An acute increase in wound size indicates tension, while a decrease in size indicates compression. Moreover, if the material is isotropic, an elliptical wound indicates anisotropic stress, with the greatest tensile stress being in the direction of the major axis (Varner and Taber, 2010). In our experiments, all holes were nearly circular and of roughly equal size before HF formation began (Varner et al., 2010), suggesting that the blasoderm is initially in a state of approximately uniform equibiaxial tension. During HF formation, the stresses became markedly inhomogeneous, with tension developing outside the NP and compression inside this region. Stress distributions given by the model are consistent with this pattern (Varner et al., 2010), lending further support to this model.

5. Using Perturbations to Test Model Predictions

Thus far, we have shown how experimental data from normal embryos can be used to develop and refine a theoretical model for morphogenesis. But the real test is whether the model can predict the effects of various morphogenetic perturbations. In other words, can the model predict abnormal as well as normal development?

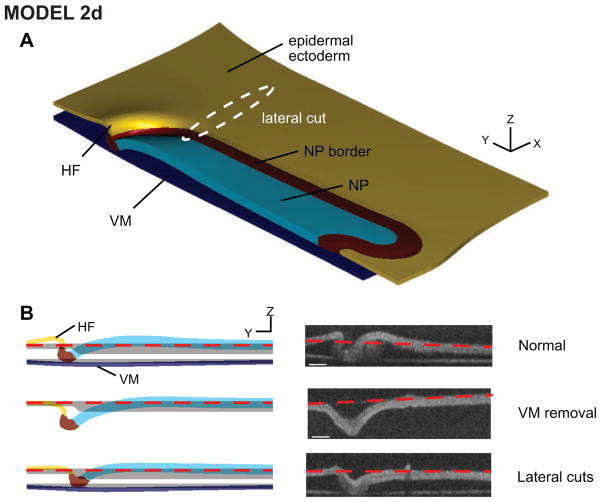
The predictive capacity of a model can be tested using genetics, drugs, or tissue dissection to alter morphogenetic forces (Martin et al., 2010; Ramasubramanian et al., 2008; Sherrard et al., 2010). For the HF problem, we cultured embryos subjected to two types of mechanical perturbation (Varner et al., 2010). First, we removed the VM at stage HH5, before the onset of HF formation. By stage 6, an abnormal v-shaped fold formed (Fig. 9B, middle row). Second, we cut through the blastoderm on either side of the already-formed HF to relieve the stresses in these regions, and the HF gradually unfurled and became v-shaped within a few hours (Fig. 9B, bottom row). These experiments were simulated in the model while keeping all parameters unchanged. In both cases, although there were some slight discrepancies with the VM removal experiment, the model predicted approximately the correct shapes of the abnormal fold and the NP (Fig. 9).

Figure 9. Model 2d predicts perturbed behavior.

Figure 9

Open in a new tab

Simulating perturbations (vitelline membrane removal and local dissections lateral to the head fold) yields abnormally shaped head folds similar to experimental morphologies. From Varner et al. (2010).

Taken together, all of these results provide relatively strong evidence supporting the combination of HF mechanisms embodied in model 2d.

6. Discussion

In this paper, we have used the head fold formation problem to illustrate how experimental and theoretical models can be integrated to gain a better understanding of morphomechanical processes. Our suggested strategy consists of the following steps:

  1. Beginning with a relatively simple model, determine parameter values for normal morphogenesis.

  2. Test the model using as many different types of experimental data as possible. Matching global morphology is generally not enough; comparing regional stress and strain distributions is crucial.

  3. Refine the model until it captures at least qualitatively the fundamental trends in the data.

  4. Test the ability of the model to predict the outcome of experimental perturbations. If necessary, refine the model further.

If the model passes all of these tests, then it likely captures at least some essential elements of the actual system, and parameter sensitivity studies can be used to help gauge model robustness by determining how variations in parameter values affect its overall behavior (Anderson et al., 2007; Valentin and Humphrey, 2009). The model then can be considered useful, although it still is wrong (Box and Draper, 1987; Oreskes et al., 1994).

Both professional engineering societies and theorists alike have stressed the importance of the verification and validation procedure in computational modeling (Anderson et al., 2007; Valentin and Humphrey, 2009). Verification typically refers to the process by which one determines that the mathematical equations in a model are solved accurately, while validation, which is emphasized in the present paper, deals with how well the mathematical model approximates reality (Anderson et al., 2007). This nomenclature, however, is not used consistently in the literature (e.g., Oreskes et al. (1994) use the term verification to refer to the process described above as validation), so readers should use care when they encounter these terms in their reading. Again, modelers should remain mindful that no computational model, no matter how thoroughly tested, can ever be fully validated. Instead, verification and validation help build confidence that the model captures some aspects of the real system.

While our final model captures the main features of HF formation, there is room for further improvement. It is possible that better agreement can be obtained, for example, by including more precise regional variations in material properties and active forces, but this would require additional experiments. In refining a computer model, one must consider what more can be gained in view of the relatively large variability that occurs naturally between even normal embryos (von Dassow and Davidson, 2007). It seems that predicting morphogenesis is inherently probabilistic, similar to quantum mechanics and theories of material failure (Taber, 2009).

It also is important to recognize the limitations in using a continuum theory to model morphodynamics. Continuum mechanics is based on the assumption that deformations of interest occur at length scales sufficiently greater than that of the discrete microscopic structure. In a tissue-level continuum simulation, therefore, individual cells are not modeled explicitly. To include cell-level behavior, some multiscale models have been proposed for certain problems in morphogenesis (Brodland, 2002; Chen and Brodland, 2008; Davidson et al., 2010; Odell et al., 1981; Taber, 1995). In general, these models include the deformation of individual cells, but cytoskeletal details are lumped into equivalent cellular forces. Developing multiscale models from the molecular to tissue levels is an enormously daunting task, especially for biological systems (Engler et al., 2009), although important recent progress has been made (Nova et al., 2010; Sander et al., 2009).

For these and other reasons, we feel that models for morphogenetic processes are a long way from being reliable predictors of developmental defects, although they may be somewhat useful for assessing probabilities. Ultimately, these models will need to include genetic, chemical, and mechanical factors, as well as feedback and interactions between these factors. Future models also will need to integrate molecular mechanisms with tissue-level behavior. Researchers now are beginning to study these aspects, both experimentally and theoretically (Beloussov, 1998; Farge, 2003; Fernandez-Gonzalez et al., 2009; Gjorevski and Nelson, 2010; Kornikova et al., 2010; Martin et al., 2010; Nerurkar et al., 2006; Pouille et al., 2009; Taber, 2008, 2009). Clearly, much remains to be done in this extremely challenging field.

Acknowledgments

This work was supported by grants R01 GM075200, R01 HL083393, and R01 NS70918 from the National Institutes of Health (LAT), as well as grant 09PRE2060795 from the American Heart Association (VDV).

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Contributor Information

Victor D. Varner, Email: vdv@princeton.edu.

Larry A. Taber, Email: lat@wustl.edu.

References

  1. Adams DS, Keller R, Koehl MA. The mechanics of notochord elongation, straightening and stiffening in the embryo of Xenopus laevis. Development. 1990;110:115–130. doi: 10.1242/dev.110.1.115. [DOI] [PubMed] [Google Scholar]
  2. Anderson AE, Ellis BJ, Weiss JA. Verification, validation and sensitivity studies in computational biomechanics. Comput Methods Biomech Biomed Engin. 2007;10:171–184. doi: 10.1080/10255840601160484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Balfour FM. A treatise on comparative embryology. MacMillan and Co; London: 1881. [Google Scholar]
  4. Bellairs R. Studies on the development of the foregut in the chick blastoderm. 1 The presumptive foregut area. J Embryol Exp Morph. 1953a;1:115–124. [Google Scholar]
  5. Bellairs R. Studies on the development of the foregut in the chick blastoderm: 2. The morphogenetic movements. J Embryol Exp Morphol. 1953b;1:369–385. [Google Scholar]
  6. Bellairs R, Osmond M. The atlas of chick development. Elsevier Academic; London: 2005. [Google Scholar]
  7. Beloussov LV. The Dynamic Architecture of a Developing Organism: An Interdisciplinary Approach to the Development of Organisms. Kluwer Dordrecht; the Netherlands: 1998. [Google Scholar]
  8. Box GEP, Draper NR. Empirical model-building and response surfaces. Wiley; New York: 1987. [Google Scholar]
  9. Brodland GW. The Differential Interfacial Tension Hypothesis (DITH): a comprehensive theory for the self-rearrangement of embryonic cells and tissues. J Biomech Eng. 2002;124:188–197. doi: 10.1115/1.1449491. [DOI] [PubMed] [Google Scholar]
  10. Chen X, Brodland GW. Multi-scale finite element modeling allows the mechanics of amphibian neurulation to be elucidated. Phys Biol. 2008;5:15003. doi: 10.1088/1478-3975/5/1/015003. [DOI] [PubMed] [Google Scholar]
  11. Clausi DA, Brodland GW. Mechanical Evaluation of Theories of Neurulation Using Computer Simulations. Development. 1993;118:1013–1023. [Google Scholar]
  12. Colas JF, Schoenwolf GC. Towards a cellular and molecular understanding of neurulation. Dev Dyn. 2001a;221:117–145. doi: 10.1002/dvdy.1144. [DOI] [PubMed] [Google Scholar]
  13. Colas JF, Schoenwolf GC. Towards a cellular and molecular understanding of neurulation. Dev Dyn. 2001b;221:117–145. doi: 10.1002/dvdy.1144. [DOI] [PubMed] [Google Scholar]
  14. Conte V, Munoz JJ, Miodownik M. A 3D finite element model of ventral furrow invagination in the Drosophila melanogaster embryo. J Mech Behav Biomed Mater. 2008;1:188–198. doi: 10.1016/j.jmbbm.2007.10.002. [DOI] [PubMed] [Google Scholar]
  15. Davidson LA, Joshi SD, Kim HY, von Dassow M, Zhang L, Zhou J. Emergent morphogenesis: elastic mechanics of a self-deforming tissue. J Biomech. 2010;43:63–70. doi: 10.1016/j.jbiomech.2009.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Davidson LA, Koehl MA, Keller R, Oster GF. How do sea urchins invaginate? Using biomechanics to distinguish between mechanisms of primary invagination. Development. 1995;121:2005–2018. doi: 10.1242/dev.121.7.2005. [DOI] [PubMed] [Google Scholar]
  17. Engler AJ, Humbert PO, Wehrle-Haller B, Weaver VM. Multiscale modeling of form and function. Science. 2009;324:208–212. doi: 10.1126/science.1170107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ezin AM, Fraser SE, Bronner-Fraser M. Fate map and morphogenesis of presumptive neural crest and dorsal neural tube. Developmental Biology. 2009;330:221–236. doi: 10.1016/j.ydbio.2009.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Farge E. Mechanical induction of Twist in the Drosophila foregut/stomodeal primordium. Curr Biol. 2003;13:1365–1377. doi: 10.1016/s0960-9822(03)00576-1. [DOI] [PubMed] [Google Scholar]
  20. Fernandez-Gonzalez R, Simoes Sde M, Roper JC, Eaton S, Zallen JA. Myosin II dynamics are regulated by tension in intercalating cells. Dev Cell. 2009;17:736–743. doi: 10.1016/j.devcel.2009.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gjorevski N, Nelson CM. Endogenous patterns of mechanical stress are required for branching morphogenesis. Integr Biol (Camb) 2010;2:424–434. doi: 10.1039/c0ib00040j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Gutzman JH, Graeden EG, Lowery LA, Holley HS, Sive H. Formation of the zebrafish midbrain-hindbrain boundary constriction requires laminin-dependent basal constriction. Mech Dev. 2008;125:974–983. doi: 10.1016/j.mod.2008.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kornikova ES, Troshina TG, Kremnyov SV, Beloussov LV. Neuro-mesodermal patterns in artificially deformed embryonic explants: a role for mechanogeometry in tissue differentiation. Dev Dyn. 2010;239:885–896. doi: 10.1002/dvdy.22238. [DOI] [PubMed] [Google Scholar]
  24. Lawson A, Anderson H, Schoenwolf GC. Cellular mechanisms of neural fold formation and morphogenesis in the chick embryo. Anat Rec. 2001;262:153–168. doi: 10.1002/1097-0185(20010201)262:2<153::AID-AR1021>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
  25. Lillie FR. Development of the chick, an introduction to embryology. 3. Holt; New York: 1952. [Google Scholar]
  26. Manoussaki D, Lubkin SR, Vernon RB, Murray JD. A Mechanical Model for the Formation of Vascular Networks In Vitro. Acta Biotheoretica. 1996;44:271–282. doi: 10.1007/BF00046533. [DOI] [PubMed] [Google Scholar]
  27. Martin AC, Gelbart M, Fernandez-Gonzalez R, Kaschube M, Wieschaus EF. Integration of contractile forces during tissue invagination. J Cell Biol. 2010;188:735–749. doi: 10.1083/jcb.200910099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Moore KL, Persaud TVN, Shiota K. Color atlas of clinical embryology. 2. Saunders; Philadelphia, PA: 2000. [Google Scholar]
  29. Moury JD, Schoenwolf GC. Cooperative model of epithelial shaping and bending during avian neurulation: autonomous movements of the neural plate, autonomous movements of the epidermis, and interactions in the neural plate/epidermis transition zone. Dev Dyn. 1995;204:323–337. doi: 10.1002/aja.1002040310. [DOI] [PubMed] [Google Scholar]
  30. Munoz JJ, Barrett K, Miodownik M. A deformation gradient decomposition method for the analysis of the mechanics of morphogenesis. J Biomech. 2007;40:1372–1380. doi: 10.1016/j.jbiomech.2006.05.006. [DOI] [PubMed] [Google Scholar]
  31. Nerurkar NL, Ramasubramanian A, Taber LA. Morphogenetic adaptation of the looping embryonic heart to altered mechanical loads. Dev Dyn. 2006;235:1822–1829. doi: 10.1002/dvdy.20813. [DOI] [PubMed] [Google Scholar]
  32. Nova A, Keten S, Pugno NM, Redaelli A, Buehler MJ. Molecular and nanostructural mechanisms of deformation, strength and toughness of spider silk fibrils. Nano Lett. 2010;10:2626–2634. doi: 10.1021/nl101341w. [DOI] [PubMed] [Google Scholar]
  33. Odell GM, Oster G, Alberch P, Burnside B. The Mechanical Basis of Morphogenesis. I Epithelial Folding and Invagination. Dev Biol. 1981;85:446–462. doi: 10.1016/0012-1606(81)90276-1. [DOI] [PubMed] [Google Scholar]
  34. Oostra RJ, Steding G, Lamers WH, Moorman AF. Steding’s and Viragh’s scanning electron microscopy atlas of the developing human heart. Springer; New York ; Berlin: 2007. [Google Scholar]
  35. Oreskes N, Shrader-Frechette K, Belitz K. Verification, validation, and confirmation of numerical models in the Earth sciences. Science. 1994;263:641–646. doi: 10.1126/science.263.5147.641. [DOI] [PubMed] [Google Scholar]
  36. Patten BM. Early embryology of the chick. McGraw-Hill; New York: 1971. [Google Scholar]
  37. Pouille PA, Ahmadi P, Brunet AC, Farge E. Mechanical signals trigger Myosin II redistribution and mesoderm invagination in Drosophila embryos. Sci Signal. 2009;2:ra16. doi: 10.1126/scisignal.2000098. [DOI] [PubMed] [Google Scholar]
  38. Ramasubramanian A, Nerurkar NL, Achtien KH, Filas BA, Voronov DA, Taber LA. On modeling morphogenesis of the looping heart following mechanical perturbations. J Biomech Eng. 2008;130:061018. doi: 10.1115/1.2978990. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Rodriguez EK, Hoger A, McCulloch AD. Stress-dependent finite growth in soft elastic tissues. J Biomech. 1994;27:455–467. doi: 10.1016/0021-9290(94)90021-3. [DOI] [PubMed] [Google Scholar]
  40. Sander EA, Stylianopoulos T, Tranquillo RT, Barocas VH. Image-based multiscale modeling predicts tissue-level and network-level fiber reorganization in stretched cell-compacted collagen gels. Proc Natl Acad Sci U S A. 2009;106:17675–17680. doi: 10.1073/pnas.0903716106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sausedo RA, Smith JL, Schoenwolf GC. Role of nonrandomly oriented cell division in shaping and bending of the neural plate. J Comp Neurol. 1997;381:473–488. [PubMed] [Google Scholar]
  42. Savin T, Kurpios NA, Shyer AE, Florescu P, Liang H, Mahadevan L, Tabin CJ. On the growth and form of the gut. Nature. 2011;476:57–62. doi: 10.1038/nature10277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Schenk J, Wilsch-Brauninger M, Calegari F, Huttner WB. Myosin II is required for interkinetic nuclear migration of neural progenitors. Proc Natl Acad Sci U S A. 2009;106:16487–16492. doi: 10.1073/pnas.0908928106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Schoenwolf GC, Alvarez IS. Roles of neuroepithelial cell rearrangement and division in shaping of the avian neural plate. Development. 1989;106:427–439. doi: 10.1242/dev.106.3.427. [DOI] [PubMed] [Google Scholar]
  45. Schoenwolf GC, Smith JL. Gastrulation and Early Mesodermal Patterning in Vertebrates. Developmental Biology Protocols. 2000:113–125. doi: 10.1385/1-59259-685-1:113. [DOI] [PubMed] [Google Scholar]
  46. Sherrard K, Robin F, Lemaire P, Munro E. Sequential activation of apical and basolateral contractility drives ascidian endoderm invagination. Curr Biol. 2010;20:1499–1510. doi: 10.1016/j.cub.2010.06.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Shore TW, Pickering JW. The Proamnion and Amnion in the Chick. J Anat Physiol. 1889;24:1–21. [PMC free article] [PubMed] [Google Scholar]
  48. Smith JL, Schoenwolf GC. Role of cell-cycle in regulating neuroepithelial cell shape during bending of the chick neural plate. Cell Tissue Res. 1988;252:491–500. doi: 10.1007/BF00216636. [DOI] [PubMed] [Google Scholar]
  49. Smith JL, Schoenwolf GC. Neurulation: coming to closure. Trends Neurosci. 1997;20:510–517. doi: 10.1016/s0166-2236(97)01121-1. [DOI] [PubMed] [Google Scholar]
  50. Stalsberg H, DeHaan RL. Endodermal movements during foregut formation in the chick embryo. Developmental Biology. 1968;18:198–215. doi: 10.1016/0012-1606(68)90043-2. [DOI] [PubMed] [Google Scholar]
  51. Taber LA. Biomechanics of Growth, Remodeling, and Morphogenesis. Appl Mech Rev. 1995;48:487–545. [Google Scholar]
  52. Taber LA. Biomechanics of cardiovascular development. Ann Rev Biomed Eng. 2001;3:1–25. doi: 10.1146/annurev.bioeng.3.1.1. [DOI] [PubMed] [Google Scholar]
  53. Taber LA. Theoretical study of Beloussov’s hyper-restoration hypothesis for mechanical regulation of morphogenesis. Biomech Model Mechanobiol. 2008;7:427–441. doi: 10.1007/s10237-007-0106-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Taber LA. Towards a unified theory for morphomechanics. Phil Trans Roy Soc A Math Phys Eng Sci. 2009;367:3555–3583. doi: 10.1098/rsta.2009.0100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Valentin A, Humphrey JD. Parameter sensitivity study of a constrained mixture model of arterial growth and remodeling. J Biomech Eng. 2009;131:101006. doi: 10.1115/1.3192144. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Varner VD, Taber LA. On measuring stress distributions in epithelia. In: Garikipati K, Arruda EM, editors. IUTAM Symposium on Cellular, Molecular and Tissue Mechanics. Springer; New York: 2010. pp. 45–54. [Google Scholar]
  57. Varner VD, Voronov DA, Taber LA. Mechanics of head fold formation: investigating tissue-level forces during early development. Development. 2010;137:3801–3811. doi: 10.1242/dev.054387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. von Dassow M, Davidson LA. Variation and robustness of the mechanics of gastrulation: the role of tissue mechanical properties during morphogenesis. Birth Defects Res C Embryo Today. 2007;81:253–269. doi: 10.1002/bdrc.20108. [DOI] [PubMed] [Google Scholar]

RESOURCES