A Parallel Algorithm for Reverse Engineering of Biological Networks

Abstract

Dynamic biological systems, such as gene regulatory networks (GRNs) and protein signaling networks, are often represented as systems of ordinary differential equations. Such equations can be utilized in reverse engineering these biological networks, specifically since identifying these networks is challenging due to the cost of the necessary experiments growing with at least the square of the size of the system. Moreover, the number of possible models, proportional to the number of directed graphs connecting nodes representing the variables in the system, suffers from combinatorial explosion as the size of the system grows. Therefore, exhaustive searches for systems of nontrivial complexity are not feasible. Here we describe a practical and scalable algorithm for determining candidate network interactions based on decomposing an N-dimensional system into N one-dimensional problems. The algorithm was tested on in silico networks based on known biological GRNs. The computational complexity of the network identification is shown to increase as N² while a parallel implementation achieves essentially linear speedup with the increasing number of processing cores. For each in silico network tested, the algorithm successfully predicts a candidate network that reproduces the network dynamics. This approach dramatically reduces the computational demand required for reverse engineering GRNs and produces a wealth of exploitable information in the process. Moreover, the candidate network topologies returned by the algorithm can be used to design future experiments aimed at gathering informative data capable of further resolving the true network topology.

1 Introduction

Network identification, or reverse engineering, is an inverse problem that is usually highly underdetermined in applications in biology due to the complex interactions genetic circuits possess^1–5. Gene regulatory networks (GRNs) prove difficult to reconstruct using computational tools and high-throughput data such as microarray gene expression data⁶. This difficulty is a bottleneck in determining the causal relationships buried within high-throughput data, in part, due to overwhelming traditional methods for network identification. Thus, there exists a need for new systematic tools to aid in the identification of the underlying architecture of networks like GRNs⁷.

Initial efforts to develop reverse engineering methodologies for GRNs focused on clustering genes into hierarchical functional units based on correlations in expression profiles⁸. Of these, time-lagged correlation analysis is the most common method to infer causal relationships from time series gene expression data^9,10. Other identification methods such as genetic algorithms¹¹, neural networks¹², and Bayesian models¹³ have also been developed. Moreover, several methods have been suggested to infer GRNs from expression data using prior knowledge of the GRN, perturbation responses, and other techniques^14–17. To deal with data shortages and computational inefficiency, a method using singular value decomposition (SVD) of linear models has been developed¹⁸ and integrated with a genetic perturbation strategy to provide an experimental protocol for deducing network topology¹⁹. These methods for network reconstruction have used specific assumptions and simplifications to deal with the inherent under-determination problem of network inference. Most methods rely on linear relationships to reconstruct the network without considering any combinatorial effects, noise or time delays. As a result, these approaches fail to capture the inherent nonlinearity of the interactions and interdependencies within the network²⁰.

To capture complex dependencies (e.g. nonlinearities) in gene expression patterns, methods using general measures of dependency based on mutual information (MI) have been proposed. The simplest one, Relevance Network (RN), infers the regulatory interactions when the MI is larger than a given threshold²¹. Other methods include Algorithm for the Reconstruction of Accurate Cellular Networks (ARACNE)²², Context Likelihood of Relatedness (CLR)²³, Maximum Relevance/Minimum Redundance Network (MRNET)²⁴, and most recently, Conservative Causal Core (C3NET)²⁵. Because these methods do not give interaction direction, one has to use MI with caution in drawing biologically meaningful conclusions. Moreover, most of these methods require a significant amount of initial data which limits their usage to only the most studied gene regulatory networks.

To circumvent many of these issues, we propose a method that serves as a first step to unraveling the myriad of possible network topologies comprising GRNs. Its purpose is to produce candidate networks reconstructed from an initial perturbation data set of the mRNA profile dynamics. The approach relies on a combination of using both the linear and nonlinear relationships to account for the expected biological behavior. The linear information is extracted from gene expression profiles and used to either generate an initial seed network from which to expand or used to guide a biased search strategy during network reconstruction. The nonlinear relationships are captured using a generalized equation governing the degree of control that a set of genes have on the dynamics of a target gene. Optimal solutions for the network inference problem are difficult to obtain; it is analogous to finding a needle in a haystack. Furthermore, attempts using optimization algorithms tend to result in suboptimal solutions due to the large, non-convex solution space. Methods that can capture different possible solutions enhance the robustness of the predicted interactions and produce better approximations to the global solution^26,27. Our proposed method decomposes the problem of inferring a network of size N into N different subnetworks, where the goal is to identify the regulators of one of the genes in the network at a time. We then combine the results and get the globally optimal solution. This approach dramatically reduces the computational demand required for reverse engineering GRNs and produces a wealth of exploitable information in the process. The method can further be expanded and integrated into the design of optimal experiments.

2 Methods

Our algorithm was tested against several mock, randomly generated networks of 4, 10, 25 and 50 genes. These networks were either obtained from the DREAM database¹⁴ or designed to possess biologically relevant motifs based on the in silico DREAM networks²⁸. The networks with 4 and 25 genes were generated using these motifs. The networks of 10 genes were from the DREAM4 challenge (insilico_size10_1, insilico_size10_2 and insilico_size10_3), and the networks of 50 genes were from the DREAM3 challenge (insilico_size50_Ecoli1, insilico_size50_Ecoli2 and insilico_size50_Yeast1). Three realizations of each network size were used to gather statistical and performance information regarding the algorithms reverse engineering capabilities, versatility and scalability. For each network, gene profile data were simulated using a system of delayed differential equations approximating mRNA expression dynamics. The model is similar to that used for the DREAM challenges¹⁴. Randomly generated parameter sets were used to produce dynamically rich, yet biologically relevant profiles, which were used as input for the algorithm.

2.1 Model

The governing equation for mRNA level x_j is a mass balance:

$${\stackrel{.}{x}}_j\left(t\right)=r_j\left(t\right)-d_j{x}_j,$$ (1)

with

$$x_j\left(0\right)=x_{0j},$$ (2)

where r_j(t) is the rate that the jth gene is transcribed, d_j is a degradation rate constant and x_0j is the initial condition. Gene transcription is a complex event involving the binding of the transcriptional machinery and various regulatory proteins. Here we model this process as governed by competitive binding of activating and inhibiting transcription factors subject to cooperativity and saturation:

$$r_j\left(t\right)=r_{0j}\frac{\sum _{i\in I_{Aj}}{\left(\frac{x_i(t-\tau )}{K_{Ai,j}}\right)}^n+e_j}{1+\sum _{i\in I_{Aj}}{\left(\frac{x_i(t-\tau )}{K_{Ai,j}}\right)}^n+\sum _{i\in I_{Ij}}{\left(\frac{x_i(t-\tau )}{K_{Ii,j}}\right)}^n+e_j},$$ (3)

where I_Aj and I_Ij are the sets of indices of variables that act as activators and inhibitors of x_j production. The time delay τ accounts for a delay between mRNA transcription and translation. (Here τ is assumed a fixed parameter.) The constants K_Ai,j and K_Ii,j can be thought of as binding constants; cooperative, nonlinear binding is assumed with Hill coefficient n > 1. The constant r_0j is the maximal rate of mRNA production and e_j accounts for potential externally stimulated or constitutive transcription that is not brought about directly through the explicit model variables. We define p_j = {K_Ai,j, K_Ii,j, r_0j, e_j} as the set of all adjustable parameters pertaining to the jth subnetwork.

The adjustable model parameters are optimized using a global approach followed by local, gradient-based search. For the global optimization, a custom algorithm was used. This algorithm consists of a simple random walk in parameter space. The best parameter set obtained from the global search is then used as the starting point for the local optimization. For the local approach, MATLAB's fmincon was used with the default settings.

2.2 Network Reconstruction

The goal of our algorithm is to determine the network topology of systems such as that illustrated in Figure 1 based on measurements of model variables without any prior knowledge of the network. In this way, the algorithm serves as a means to deconvolve the complex interactions observed in dynamical data. It is designed to minimize the number of false negatives and thus is biased towards producing false positives. This approach is useful because the results generated by the algorithm can be used to design future experiments (e.g. gene knockout (KO) experiments) targeted at pruning and modifying the reconstructed network. (It is easier to remove a false positive than correct a false negative in the context of network inference.) A unique key to our algorithm's efficiency is that candidate networks associated with activation and inhibition connections to an individual gene are independently generated and tested. To do this, Equation (1) is integrated for state variable j with other variables i (≠ j) determined by a smooth interpolation of the data. This way, a subnetwork for a gene in the network is a one-dimensional problem. One-dimensional systems representing each gene can then be probed on independent processors of a distributed system, making the algorithm trivial to parallelize.

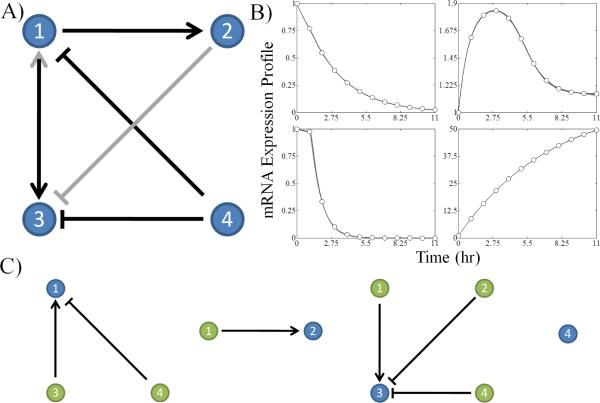
Fig. 1.

Example network results generated by the algorithm for a network of 4 genes. A) The consensus network is presented with black arrows signifying edges present in the original test network and gray edges representing false positives generated by the algorithm. The → means activation and the ⊣ means inhibition. B) The mRNA expression profiles of the subnetworks are compared with the data obtained from the test network. The gray lines are the sets of optimal subnetwork expression profiles from the ensemble of candidate subnetworks. The individual subnetworks are not necessarily identical despite their respective mRNA expression profiles being experimentally indistinguishable. C) Isolated subnetworks associated with the network decomposition are shown with the target gene displayed in blue and the regulatory genes displayed in green.

The algorithm, with overall architecture illustrated in Figure 2, works by constructing trial subnetworks to compare using kinetic data on the individual variables. This is a standard approach to reverse-engineering biological networks. Trial networks are perturbed by adding or subtracting randomly chosen network connections, and a fitness function is evaluated to determined whether or not to accept the proposed network structure. The fitness function used in the algorithm is based on a modified estimator of the likelihood of a given model explaining the data:

$$F=-(E+\alpha \ln n_p),$$ (4)

where E is the mean-squared error between model prediction and the data (given optimal parameter values) and n_p is the number of adjustable parameters. The term α lnn_p represents a penalty that is proportional to the number of structural parameters; in practice the value of α is set according to the expected mean-squared errors that provide satisfactory fits to the data. For example, when the expected mean-squared errors are small, α is also set at a relatively small value so that the fitness is not dominated by either the error or structural penalty. Since in most examples presented herein, we do not explicitly model the expected noise contribution for data sets used, we set the acceptability threshold at an extremely small value. That said, the approach is robust to noise-corrupted data when the noise is on the order of the expected biologically induced variability. To demonstrate this, we added a relative 10% Gaussian noise (N(0, 0.1)) to represent this biological variability to one of the data sets and compared the results generated from the corresponding noise-free data set. The only change made to the algorithm to address noisy data is that the threshold for determining an acceptable fit to the data and the structural penalty parameter is accordingly adjusted to populate the list of candidate subnetworks. A candidate subnetwork is defined as a subnetwork that enables simulation results to reproduce the available data.

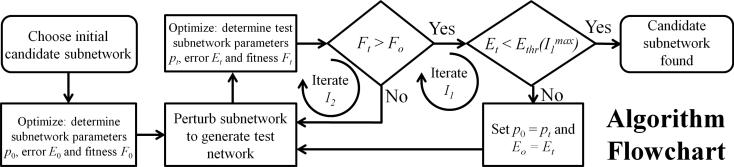
Fig. 2.

Flowchart of the algorithm. Trial subnetworks are constructed and tested against the best available subnetwork in an iterative manner. For the examples presented herein, $I_1^{max}$ and $I_2^{max}$ were set to 3 and 100, respectively. The error threshold function was defined as E_thr(I₁) = E_thr0/I₁ where E_thr0 was set to 10^–3. The value of α for the fitness function was set to 0.035. See the main text for definitions of fitness and error functions, F and E, respectively.

When searching for candidate subnetworks, trial subnetworks are tested against the current best subnetwork using two cascading iteration loops. When a trial subnetwork's fitness is greater than the current best subnetwork, it then becomes the current best subnetwork, and the search is continued until the current best subnetwork is deemed acceptable or the maximum number of iterations is met. The outer iteration loop controls the acceptability criteria while the inner iteration loop keeps track of the number of trail subnetworks tested per outer loop iteration. The acceptability criteria checks whether or not the mean-squared error of a model supported by a candidate subnetwork is sufficiently small. A subnetwork is deemed acceptable when it's mean-squared error is less than the value of the acceptability threshold, which is determined by the outer loop counter. This check prevents wasting computational resources for diminishing returns. The quality of the data determines the value of these search-based parameters, i.e. the larger the measurement uncertainty, the more lax the acceptability criteria; and the more difficult it is to find a candidate subnetwork, the higher the values attained by the loop counters. This iterative strategy is essentially an evolutionary approach to the network inference problem and provides a practical method for constructing candidate subnetworks.

Two different methods for initializing the network and two different methods for perturbing the network are employed. For non-biased initialization, the initial network is assumed to have an external activator and no other network activation or inhibition edges. The non-biased perturbation algorithm selects, with equal probability, to either add or remove an edge in the trial network at each perturbation iteration. If an edge is added, that edge is assigned to be either an activator or inhibitor, with equal probability.

The biased initialization and perturbations strategies are based on the time-lagged correlation matrix of the data:

$$C_{i,j}\left(\tau \right)=\langle (g_i\left(t\right)-{\widehat{g}}_i)(g_j(t+\tau )-{\stackrel{‒}{g}}_j\rangle ∕\sqrt{C_{i,i}\left(0\right)C_{j,j}\left(0\right)},$$ (5)

where g_i(t) is the level of the ith mRNA transcript at time t. The correlation coefficients for each column of C, represents a potential measure of the degree of influence the ith gene has on the mRNA dynamics of the jth gene after time lag τ. The gene selection probabilities are computed using their relative contribution to the sum total of the correlation coefficients. These probability intervals are computed using

$$p_{Sk}=\mid C_{k,j}\mid ∕\sum _k\mid C_{k,j}\mid \text{where}k=\{i:i\in N_D\}$$ (6)

where p_Sk is the kth element of a probability interval for selecting which gene to connect to the current network and N_D is the set of the disconnected genes.

For each gene present in the network, an ensemble of candidate subnetworks are sought until the frequency distributions of network edges (connections between genes) converges. When the subnetwork ensembles for all genes have converged, the significant connections are pooled together, and the topology for the entire GRN is generated based on a consensus.

Significant connections are based on the number of times a given connection appears in the ensemble of candidate subnetworks. When this number exceeds a certain threshold (i.e. appears in 45% of the candidate subnetworks), the connection is assumed to be significant and is stored in the consensus topology. In cases where no connection exceeds the threshold, the most frequently occurring activator and inhibitor connection are assigned in the consensus topology, as long as their respective frequencies of appearance exceeds some minimal threshold (i.e. 25%). In some cases, time-lagged mRNA expression profiles are significantly correlated with other profiles. The thresholds were set to capture most of these correlations in order to cover as many subnetwork topologies capable of supporting data-consistent simulations. This leads to dense networks in order to maximize coverage. (Coverage is defined as the percent of true edges recovered by the algorithm.) This approach enables the entire network dynamics to be reproduced when the ensemble network is simulated for the examples studied below. Future experiments can then be designed based on the consensus network topologies to shape these dense networks into their true topologies.

3 Results and Discussion

Figure 1 presents the reconstruction results generated by the algorithm from dynamical expression data simulated from a biologically inspired network of 4 genes. The algorithm is able to generate candidate subnetworks, as pictured in Figure 1C, capable of fitting the mRNA expression profiles with arbitrary accuracy, as demonstrated in Figure 1B. The algorithm successfully predicted all of the real connections, erroneously predicted two false positives (gene 3 activating gene 1 and gene 2 inhibiting gene 3) and generated zero false negatives as shown in Figure 1A. These results demonstrate the intrinsic, non-unique nature of the problem at hand. Although all the simulated trajectories pass through the data points, there is insufficient information in the data to discriminate between the candidate subnetworks returned by the algorithm. Despite this, the algorithm achieves its primary objective: to search out the topological network space and identify potential networks that produce simulations consistent with the experimental data while minimizing the number of false negatives.

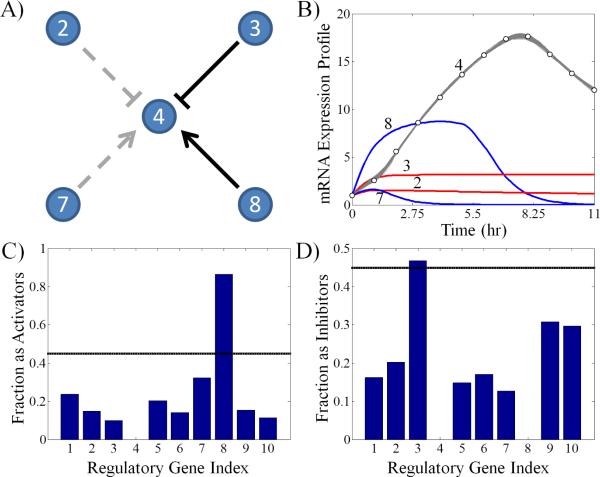
Figure 3A shows the consensus subnetwork topology associated with one gene (gene 4) in a 10 gene example. The dark lines represent connections identified by the algorithm, while the gray dashed lines are the connections present in the real network missed by the algorithm. An ensemble of 58 candidate subnetworks were needed to converge for this gene; the average number of candidate subnetworks needed for convergence was over 130 for this 10 gene network. In general, a minimum of 50 candidate subnetworks were required for subnetwork convergence in order to prevent an undersampling bias. In Figure 3B, the simulated mRNA trajectories demonstrate that despite only two of the four connections present, the subnetworks are capable of explaining the experimentally observed dynamics. Note that the mRNA trajectories were simulated using the different subnetworks from the ensemble of this gene. This further highlights the need for additional information in order to identify the connection between various genes in a regulatory network. In terms of the fraction that each gene appears as an activator or inhibitor for the target gene, it is clear that gene 8 serves as an activator and gene 3 serves as an inhibitor as shown in Figure 3C and 3D, respectively. The solid black line in the bar graphs represents the 45% cutoff value used to determine significant connections. What is not clear is the regulatory role genes 2 and 7 play in the dynamics for the target gene. Although the activation frequency for gene 7 did not make the cutoff threshold, it ranked second among the list of potential activators. Likewise, for gene 2, it appeared fourth in the list of potential inhibitors for the target gene. In cases like this, KO experiments may prove useful to identify the role these two genes play in the regulation of the target gene dynamics.

Fig. 3.

Example subnetwork results generated by the algorithm for a network of 10 genes for gene 4. A) The subnetwork topology identified by the algorithm is pictured where solid black lines represent edges recovered by the algorithm, and the gray dashed lines are edges present in the true network topology but missed by the algorithm. B) The optimal subnetwork mRNA expression profiles compared to the data for the target gene along with the interpolated mRNA expression profiles of its regulator genes are shown. Note that not all of the candidate subnetwork topologies are identical; however, they all support data consistent simulations. The numbers correspond to which profile belongs to which gene. C) and D) The fractions that these regulatory genes appear in the candidate subnetwork population as activators or inhibitors, respectively, are shown.

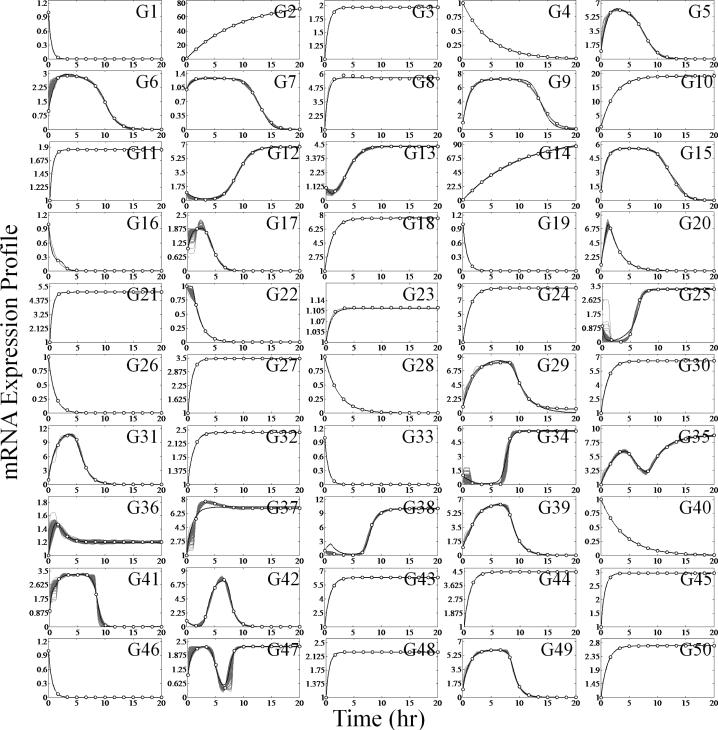
Model-based network inference algorithms must overcome the difficulty of adequately reproducing the experimental data before they can be used to deduce a candidate network topology. Moreover, as the dimension of the network increases, the likelihood of successfully fitting the experimental data significantly diminishes due to the rapidly expanding list of candidate models. Analyzing individual subnetworks versus the entire network removes this hurdle and dramatically reduces the computational burden. By decomposing the network and solving the subnetwork architecture before reconstructing the network, it then becomes possible to fit the entire dynamical data using the consensus network topology. This is demonstrated for the behavior of a 50 gene network as shown in Figure 4. Each gene profile was reproduced well when individually optimized, as shown by the gray lines. Moreover, using the consensus network, the entire network was optimized and also able to simulate the experimental data, as shown by the black lines.

Fig. 4.

Example network mRNA expression profile dynamics simulated using the consensus network topology for a network of 50 genes. The optimal parameter set was obtained using a simple gradient-based search with the initial starting point obtained from the optimal subnetwork parameter results. The gray lines correspond to the optimal subnetwork expression profiles while the black lines represents the optimal ensemble network expression profiles. Note that many of the subnetwork expression profiles are hidden by their respective network expression profile.

These results are better appreciated when focusing on the degree simplification the decomposition allows. For this example, the consensus network possessed only 859 edges of 5000 possible edges of the full network; the resulting parameter search space is effectively one sixth the dimension of the maximum parameter space. Moreover, the information obtained from the independent subnetwork optimizations was used to generate a starting point for a simple gradient-based, local optimization for the entire network. The entire parameter space was 1009-dimensional (including all kinetic constants), very large in the context of dynamical modeling, and the results demonstrate that the consensus network was able to support data-consistent simulations. If desired, it is possible to further reduce the consensus network topology and produce a minimal model capable of reproducing the experimental data with near equal fidelity. This requires removing the “weak” gene-gene interactions where a “weak” interaction is defined by the value of the binding constants (K_{Ai, j} and K_{Ii, j}). For example, the network topology of a reduced consensus network consists of only 423 edges for this example; however, the coverage drops from 50% to 37%. Although it is possible to condense the network topology, the highly underdetermined nature of the problem at hand impedes post-analysis significance testing. Specifically, the sensitivity matrix is not of full rank, and precise parameter estimation is not possible. As the goal of the algorithm is to determine putative models that can explain the data, a unique model and associate parameter set are not sought. Thus, the approach is suited to inform future experimental design. Generally, it is better to begin iterative and model-driven experiments using a network with the fewer number of false negatives at the cost of an increased false positive count. Additional data could then be used to prune the consensus network and drive down the false positive count without increasing the number of false negatives.

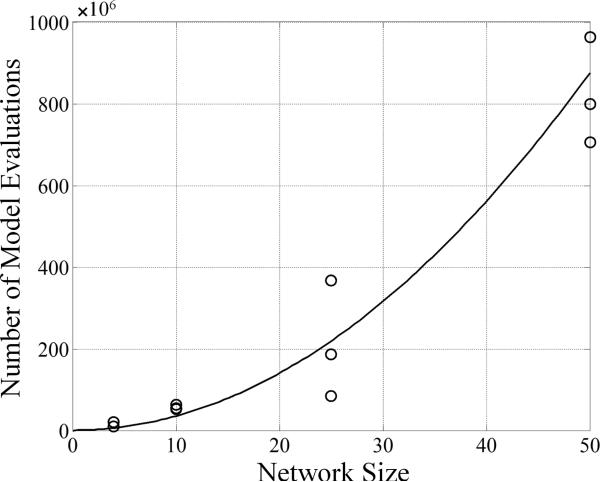
The computational demand of our approach scales with the square of the number of genes in a network. This scaling is achievable as a result of the decomposition of the entire network of size N into N subnetworks. Assuming that the chance of finding candidate subnetworks scales with N, the overall search for a consensus network scales with N². To demonstrate this property, the algorithm was tested on a series of randomly generated mock networks of varying sizes. Figure 5 shows that as the number of genes in the network is increased, the time it takes to generate the consensus network is of O(N²). (Here, every single model evaluation during the network reconstruction is reported, where the majority of computations are perfumed during the optimizations.) This manner of scaling with network size for a network inference algorithm is a substantial improvement over other inference-related algorithms, which report computational costs of at least O(N³) for deterministic model-based inference¹⁹ and at least O(N² logN) for information theory-based approaches to realistic problems^24,29. Additionally, the algorithm facilitates searching for candidate subnetworks in parallel further enhancing its capabilities.

Fig. 5.

The algorithm complexity is of O(N²). The number of model evaluations required to form the consensus network as a function of N is presented. A model evaluation is an integration from t₀ to t_end in a one-dimensional state variable space; therefore, it is assumed that each model evaluation takes approximately the same amount of computational time. The circles represent the convergence results for each of three in silico network realizations for networks consisting of 4, 10, 25 and 50 genes. The line corresponds to the equation 0.35 × 10⁶N².

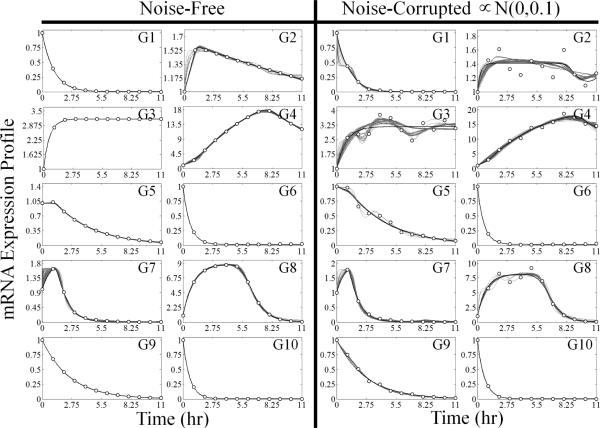
Including a biologically relevant amount of noise on top of the data does not impact the overall results, as is illustrated in Figure 6. The effect of the added noise can be seen by comparing the different subnetwork profiles for the noise-free and noise-corrupted data sets. In order to populate the list of candidate subnetworks and balance the fitness function, the acceptability threshold and structural penalty were both increased for the noisy case. Although the biased approaches were affected via differences in the time-lagged correlation coefficients, the ensemble candidate subnetwork topologies recovered by the algorithm were very similar. After applying the threshold cutoffs, the consensus networks for both the noise-free and noise-corrupted data sets were identical. Despite the same underlying network topologies supporting the model, the mRNA expression profiles were different for some genes due to the noise-corruption. Overall, the algorithm was able to generate a consensus network capable of supporting data consistent simulations regardless of the presence of biologically relevant noise levels.

Fig. 6.

The effect of 10% relative Gaussian noise (N(0, 0.1)) added on top of the data is compared to the results generated form the noise-free data for an example 10 gene network. For each case, the gray lines correspond to the optimal subnetwork expression profiles while the black lines represents the optimal ensemble network expression profiles. For the noise-free case, E_thr0 and α were kept at the values stated in the caption of Figure 2 (10^–3 and 0.035, respectively). For the noise-corrupted case, E_thr0 was set to 10^–2 and α was set to 0.35.

Table 1 lists of performance statistics for each network analyzed. It includes standard network inference metrics such as the F-score; percentage of true positives (TP), false positives (FP), false negatives (FN) relative to the maximum number of possible edges (2N²) and the coverage. The F-score equals 2pr/(p + r) and is a measure of the algorithms accuracy that includes the algorithms precision p and recall r where p = TP/(TP + FP) and r = TP/(TP + FN). As the size of the network increases, the F-score falls due to the increase in the number of false positives and false negatives; however, the growth of the false negatives with network size is mitigated as intended. Moreover, the coverage is remarkably stable towards relatively large N. Thus, the algorithm may be applied in the design of optimal experiments making the algorithm an attractive means to decipher network topology and design useful knockout and perturbation experiments.

Table 1.

Algorithm Performance Statistics

Network Size	4	10	25	50
F-score	0.86±0.04	0.76±0.04	0.61±0.01	0.70±0.08
%TP	77±8	61±5	44±1	55±9
%FP	23±7	29±3	53±1	44±9
%FN	0±0	10±3	3±0.5	1.6±0.4
Coverage	100±0	36±18	43±8	46±6

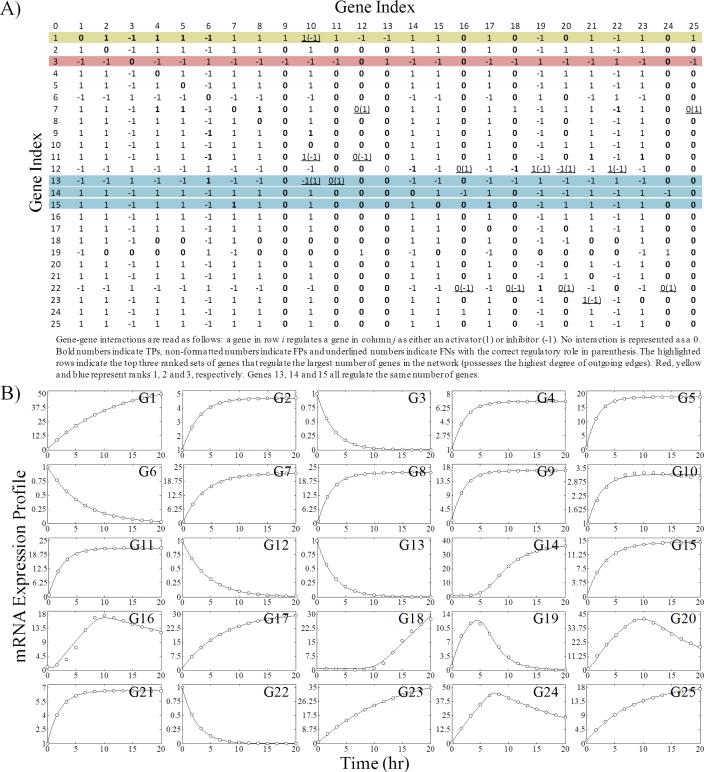
The consensus network from a 25 gene exemplar network as shown in Figure 7 is used to demonstrate how the predicted consensus networks may be used to design experiments capable of extracting useful information. Figure 7A shows the connectivity matrix for this system, where a gene in row i regulates a gene in column j. The highlighted columns represent the top ranked genes that regulate the most genes in the network (the highest degree of outgoing edges). In the context of experiment design, these top regulatory genes could be the focus of experiments aimed at validating the consensus network topology. For example, here gene 3 is the top ranked regulatory gene. This gene has no outgoing edges in the real network, but its time-lagged profile is highly correlated with other profiles in the network as seen in Figure 7B. This causes it to enter the consensus network and appear to regulate many other genes. In this case, a KO experiment would produce data enabling the removal of up to 21 FP's from the consensus network. Similarly, the other top ranked genes (genes 1, 13, 14 and 15) could be useful experimental targets to further reduce the consensus network topology. Interestingly, the consensus network topology for genes 1 and 13 each contain at least 1 FN, so the effect of removing them from the network could produce additional rich data sets capable of correcting for these FN's. Experiments could be designed based on the expansion of this list or experiments could be performed and the data fed back into the algorithm to produce a new consensus network. This process can then be repeated in the spirit of traditional model-based design of optimal experiments.

Fig. 7.

Example experiment design using the consensus network topology returned by the algorithm. A) The associated consensus connectivity matrix for an exemplar 25 gene network is presented with highlighted rows corresponding to target genes for future experiments designed to gather informative data. B) The optimal ensemble network expression profiles are presented for the corresponding network.

Evidence points to the best approach to network inference being a consensus based strategy that utilizes information obtained from a variety of methodologies^14,30,31. In our approach, each strategy outlined above was specifically designed to work together in a such complimentary manner. This consensus-based strategy is a central part of the algorithm proposed herein. Specifically, the gene-gene interactions one strategy misses may be caught by another strategy in a manner that avoids excessive computational resources. For example, the biased strategies are based on linear relationships inferred from the time-lagged correlation matrix. Using these relationships dramatically speeds up the time to identify candidate subnetworks, but these relationships can be misleading. Moreover, it is well understood that nonlinear relationships are also present in biological systems, so the biased strategies are supplemented with strategies not influenced by these potential linear relationships. The combination of these strategies allows for the most robust approach to the network inference problem.

Many investigators have found that biological GRNs are scale-free and that their connectivity is best approximated by a power-law^32,33. Our algorithm builds the candidate subnetworks in a random fashion but focused towards minimizing the false negative rate and maximizing the coverage at the expense of the false positive rate. This leads to the construction of dense consensus networks which are more characteristic of an exponential network. The algorithm may be modified to bias searches toward scale-free and power-law frameworks.

4 Conclusions

Overall, the reverse engineering algorithm presented here successfully generates plausible candidate networks capable of explaining data from biologically relevant networks based on the DREAM in-silico challenges. This model-based strategy combines both linear and non-linear methods to produce data consistent simulations. The subnetwork decomposition is responsible for the efficient computational scaling property, as well as, the ability to trivially parallelize this network inference method. Consensus networks returned by the algorithm are designed to minimize the number of false negatives, making them an attractive initial step in an iterative design process central to the design of optimal experiments paradigm. Moreover, the algorithm can be supplemented with additional experimental data to further constrain and enhance the consensus networks capable of supporting data consistent simulations.