Abstract
The Cre-recombination system has become an important tool for genetic manipulation of higher organisms and a model for site-specific DNA-recombination mechanisms employed by the λ-Int superfamily of recombinases. We report a novel quantitative approach for characterizing the probability of DNA-loop formation in solution using time-dependent ensemble Förster resonance energy transfer measurements of intra- and inter-molecular Cre-recombination kinetics. Our method uses an innovative technique for incorporating multiple covalent modifications at specific sites in covalently closed DNA. Because the mechanism of Cre recombinase does not conform to a simple kinetic scheme, we employ numerical methods to extract rate constants for fundamental steps that pertain to Cre-mediated loop closure. Cre recombination does not require accessory proteins, DNA supercoiling or particular metal-ion cofactors and is thus a highly flexible system for quantitatively analyzing DNA-loop formation in vitro and in vivo.
INTRODUCTION
Many organisms, from bacteria to vertebrates, use site-specific recombination as an efficient mechanism for generating genetic variation (1–4). Site-specific recombination differs from general recombination in that DNA is exchanged exclusively at specific sequences, either in a conservative or non-conservative manner (5). These reactions require specialized proteins to recognize the target sites and carry out the chemistry of recombination. The integration and excision of bacteriophage λ DNA into the Escherichia coli genome, mediated by the λ-integrase system (λ Int), has served as a paradigm for conservative site-specific recombination reactions (6). The Int superfamily of recombinases encompasses over 100 members (7,8), including the Flp recombinase of Saccharomyces cerevisiae (9) and the Cre recombinase from bacteriophage P1 (10). As a genetic-engineering tool, the Cre system has had profound impact on our basic understanding of biological systems and the development of useful animal models of human disease. Specifically, the ability to inactivate genes via Cre-mediated deletion activity allowed precise determination of gene functions and the creation of transgenic mice (11). In its normal biological role, Cre resolves the P1 phage genome in vivo into monomeric DNA circles, ensuring uniform partitioning of the phage genome upon host-cell division (12–14).
Like other recombinases belonging to the Int superfamily, Cre uses a catalytic tyrosine residue (Y324) in a mechanism similar to the chemistry of topoisomerase IB (15). The reaction proceeds in two stages—initial strand cleavage via a transient phosphotyrosyl intermediate is followed by exchange of one pair of DNA strands to form a stable recombinase-bound Holliday junction (HJ) (16,17). This junction is resolved by a second set of cleavage and strand-exchange steps resulting in recombinant products. The mechanism is dependent on the cooperative activity of four Cre monomers, two bound to each target site (Figure 1).
Figure 1.
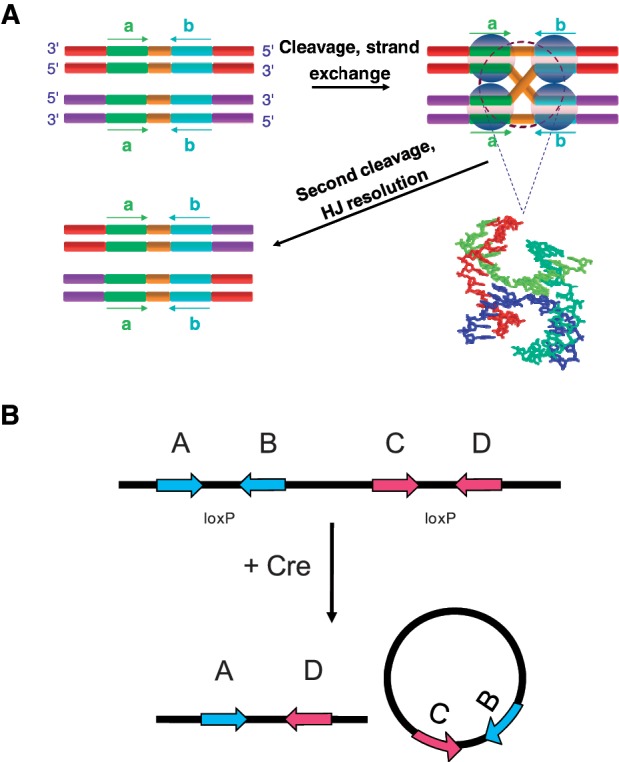
(A) Cre promotes site-specific recombination between two loxP-containing DNA sequences. The loxP target site consists of two inversely repeated, 13-bp Cre-binding sequence elements (cyan and green) that flank an 8-bp asymmetric core region (orange). Site-specific recombination occurs via ordered strand cleavage, exchange and rejoining reactions in a reversible manner. The central recombination intermediate is a Holliday junction, shown in the molecular model in a stacked-X conformation. (B) The products of intramolecular Cre recombination are determined by the orientation of loxP sites. If the target sites are directly repeated along the same DNA segment Cre mediates a deletion reaction involving the DNA segment flanked by the loxP sites.
The wild-type target site for Cre is a 34-bp DNA sequence, designated loxP, which consists of two 13-bp inverted repeats flanking an 8-bp core region (8). The loxP core sequence is non-palindromic, which confers an overall polarity on the target site and, with cis-acting loxP sites, leads to the exclusive formation of deletion products in the case of direct loxP repeats or inversion products in the case of inverse repeats (18,19). Crystallographic structures of Cre (16,20–22), Flp (23) and λ-Int (24) recombinases with various oligonucleotide substrates have been available for some time. In complexes that contain synthetic HJ intermediates, there are a number of common features, notably junctions that are nearly planar and 2-fold symmetric. These crystallographic DNA structures conform roughly to that proposed for synthetic, immobile four-way junctions under low-salt conditions (25–29). Elucidating the structure of the DNA intermediate in solution remains a major challenge due to the limited number of techniques available for characterizing such structures. Moreover, the dynamic properties of this intermediate and their relation to the overall kinetics of the reaction pathway remain unclear.
Information about the in-aqueo structure of the Cre synaptic intermediate comes mainly from topological analysis of knotted and catenated recombination products (30,31) in conjunction with scanning probe microscopy (31). Unfortunately, topological methods do not give direct structural information and microscopy techniques are potentially subject to sample-preparation artifacts. The application of fluorescence-energy transfer to this problem has not previously been reported to our knowledge, although steady-state Förster resonance energy transfer (FRET) has been used to probe the architecture of λ-int recombination intermediates (32).
Here, we describe a novel and quantitative analysis of synaptic-complex formation based on the kinetics of the recombination reaction. Our implementation of time-dependent FRET is similar to a fluorescence-based high-throughput method due to Zhang and Crothers for detecting DNA cyclization (33). Moreover, the analysis of synapsis kinetics makes use of principles similar to cyclization (34,35), but is a technique that is broadly applicable to studies of DNA-loop formation in living cells. Our method yields experimental values of the J factor, J, which can be defined as the effective concentration of one loxP recombination site in the vicinity of another when both sites are present on the same DNA molecule. In Figure 2, J can be computed from a ratio of equilibrium constants for the intra- and inter-molecular synapsis reactions that is equivalent to a quotient of fundamental rate constants. We show here that the values of J measured for both 870-bp and 3-kb DNA loops agree well with those predicted by polymer-chain statistics. The overall amplitude of the FRET signal is smaller than expected for the crystallographic structures of Cre synaptic complexes containing either duplex DNAs or Holliday-junction intermediates. This result may be attributable to restricted motions of the dyes in the synaptic intermediate and/or significant departures of the longest-lived intermediate from crystallographically observed structures.
Figure 2.
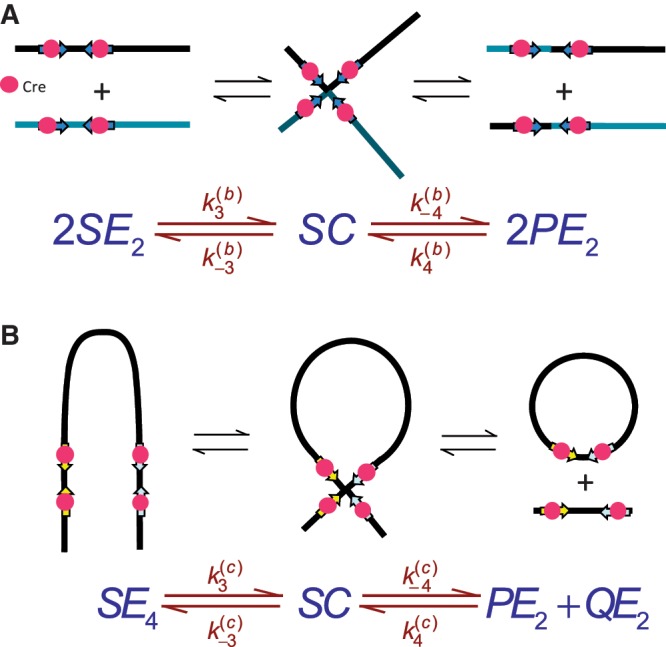
The kinetic approach used to investigate the mechanism of Cre synapsis. We measure respective sets of rate constants for site synapsis in inter- and intra-molecular recombination reactions taking place under identical conditions. (A) Intermolecular synapsis takes place between two target molecules bearing loxP sequences fully occupied by Cre protein (SE2). Formation of the synaptic complex (SC) occurs with forward and reverse rate constants 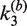 and
and 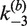 , respectively. The rate constants
, respectively. The rate constants 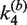 and
and 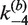 govern the ensuing resolution reaction, which leads to two Cre-saturated product DNAs (PE2). (B) Corresponding model for intramolecular recombination of a substrate DNA bearing directly repeated Cre2loxP sequences (SE4). The rate constants for the corresponding synapsis and resolution steps are
govern the ensuing resolution reaction, which leads to two Cre-saturated product DNAs (PE2). (B) Corresponding model for intramolecular recombination of a substrate DNA bearing directly repeated Cre2loxP sequences (SE4). The rate constants for the corresponding synapsis and resolution steps are 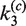 ,
, 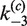 ,
,  and
and 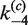 .
.
MATERIALS AND METHODS
Fluorescently labeled DNA fragments
All fluorophore-labeled deoxyoligonucleotides were purchased from IBA (Göttingen, Germany) and were purified twice by reverse-phase HPLC. For intermolecular recombination assays, labeled duplex substrates were prepared by annealing complementary oligonucleotides modified internally with ATTO 594 (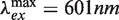 ) conjugated to a thymine at position 17 on the ‘top’ strand (TDB) or with an ATTO 647N (
) conjugated to a thymine at position 17 on the ‘top’ strand (TDB) or with an ATTO 647N (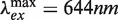 ) modification at T18 on the ‘bottom’ strand (TBA; see Supplementary Figure S1). Constructs in which neither strand was labeled (TB) or in which opposing strands were labeled with donor and acceptor (TDBA) were also prepared. The calculated Förster distance, R0, for this dye pair is 7.5 nm assuming isotropic motion of the dyes (36). Concentrations of single-stranded DNAs (ssDNA) were determined spectrophotometrically at 260 nm using a Cary 100 UV–Vis spectrophotometer according to values of the molar extinction coefficient, ε260, provided by the vendor. Duplex DNA was prepared by mixing complementary ssDNA strands at equimolar ratios in TEN50 buffer (10 mM Tris–Cl, 1 mM Na2EDTA, 50 mM NaCl, pH 8.0) and incubating the mixture in a 80°C water bath for 2 min. The bath was allowed to cool to room temperature overnight. Annealed products were analyzed by electrophoresis in a 3% agarose gel run in TBE buffer (50 mM Tris–borate, 1 mM Na2EDTA, pH 8.4) at 3 V/cm for 90 min.
) modification at T18 on the ‘bottom’ strand (TBA; see Supplementary Figure S1). Constructs in which neither strand was labeled (TB) or in which opposing strands were labeled with donor and acceptor (TDBA) were also prepared. The calculated Förster distance, R0, for this dye pair is 7.5 nm assuming isotropic motion of the dyes (36). Concentrations of single-stranded DNAs (ssDNA) were determined spectrophotometrically at 260 nm using a Cary 100 UV–Vis spectrophotometer according to values of the molar extinction coefficient, ε260, provided by the vendor. Duplex DNA was prepared by mixing complementary ssDNA strands at equimolar ratios in TEN50 buffer (10 mM Tris–Cl, 1 mM Na2EDTA, 50 mM NaCl, pH 8.0) and incubating the mixture in a 80°C water bath for 2 min. The bath was allowed to cool to room temperature overnight. Annealed products were analyzed by electrophoresis in a 3% agarose gel run in TBE buffer (50 mM Tris–borate, 1 mM Na2EDTA, pH 8.4) at 3 V/cm for 90 min.
Plasmid DNA
Unlabeled synthetic DNA fragments bearing loxP sites flanked by recognition sites for the restriction endonucleases BbvCI and BsmI were purchased as complementary oligonucleotides from IDT (Coralville, IA, USA). The presence of tandem BbvCI and BsmI sites allows for incorporation of fluorophore-labeled oligonucleotides due to vicinal nicks introduced along the same DNA strand as described below. Annealed duplexes were directionally cloned into the multi-cloning region of pGEM-5Zf(+) between SacI-PstI and NotI-SpeI sites, respectively, to generate the plasmid pCS2DloxP0, which has two directly repeated loxP sites with a center-to-center separation of 65 bp. Plasmid pCS2DloxP870 was constructed by inserting an 870-bp DNA fragment derived from the bacteriophage-λ genome between the PstI and NotI sites of pCS2DloxP0. Cloning steps were confirmed by di-dexoynucleotide sequencing. Plasmids were propagated in E. coli HB101 cells and isolated in quantity by using a Promega Wizard® Plus Megaprep purification kit (Promega Corp., Madison, WI, USA).
Fluorescently labeled plasmid DNA
Donor and acceptor fluorophores were incorporated into the plasmid according to the scheme shown in Figure 3. The purified plasmid was treated with the site-specific nicking endonucleases Nb.BbvCI and Nb.BsmI (37) (New England Biolabs, Ipswich, MA, USA) at 37 and 65°C, respectively. Progress of the nicking reaction was monitored by agarose-gel electrophoresis. ATTO 594 - and ATTO 647 N-labeled oligonucleotides (modified at T17 and T18, respectively) were then added to the multiply nicked plasmid in a 20:1 (oligonucleotide:plasmid) molar ratio, which ensures that each site of incorporation has an independent 95% probability of being labeled by its fluorophore. After annealing the mixture at 90°C for 1 min in a water bath, the bath was turned off and allowed to cool to room temperature overnight. Proteins were removed by chloroform extraction; DNA was subsequently recovered by ethanol precipitation and resuspended in TE buffer (10 mM Tris–Cl, 1 mM Na2EDTA, pH 8.0). The site-specific nicks were sealed by treatment with T4 DNA ligase (New England Biolabs, Ipswich, MA, USA) at 16°C overnight in 50 mM Tris–Cl, 10 mM MgCl2, 10 mM dithiothreitol, 1 mM ATP, 25 µg/ml BSA, 0.05% (v/v) Nonidet P-40, pH 7.8. Excess oligonucleotides were removed by spin-column chromatography on Clontech Chroma Spin-400 columns (Clontech, Mountain View, CA, USA) and the covalently closed plasmid DNA was further purified by banding on small (2-ml) CsCl–ethidium bromide gradients. Recovery of covalently closed DNA, relative to the initial mass of plasmid starting material, is 70–80%. Absolute and relative levels of incorporation of each fluorophore were determined by UV–visible absorption and fluorescence-emission spectra, respectively. The latter spectra were de-convolved using a Matlab program written in this laboratory and gave reproducible donor:acceptor ratios of 1.04 ± 0.14 with an absolute level of simultaneous incorporation of both dyes on the order of 85%.
Figure 3.
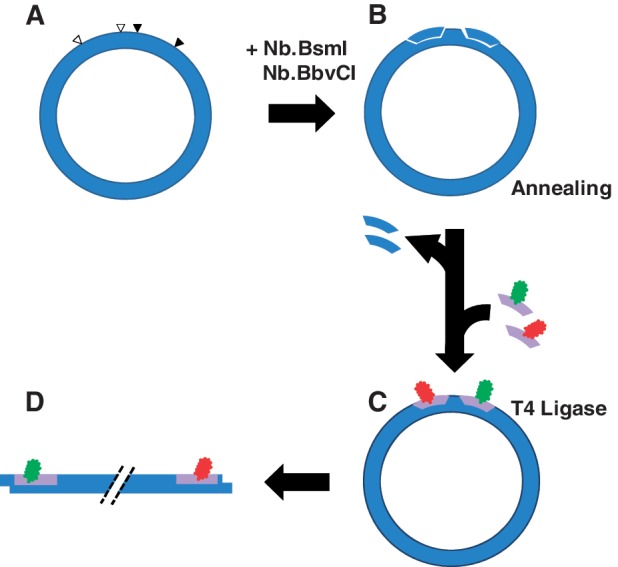
Method for generating doubly labeled plasmid DNAs. (A) We engineered novel-plasmid DNA constructs in which pairs of tandem BbvCI and BsmI restriction sites flank respective loxP sites. The minor distance between centers of the loxP sites is 65 bp. (B) Tandem nicks were generated at BbvCI and BsmI sites by treatment with mutant endonucleases Nb.BbvCI and Nb.BsmI. (C) Fluorophore labels (donor in green; acceptor in red) were incorporated by displacing the single-stranded fragments released by the tandem nicks, which were subsequently sealed with T4 DNA ligase. (D) The covalently closed plasmid was separated from residual nicked DNA and linearized by treatment with PstI.
FRET-based recombination-kinetics assays
Determination of Cre recombination activity
Cre protein was obtained from New England Biolabs (Ipswich, MA, USA) and was used without further purification. The protein provided by the vendor is of variable homogeneity, containing a mixture of full-length wild-type Cre protein and a truncated form, presumably due to limited proteolysis. The relative activities of full-length and truncated proteins are not known. Therefore, we estimated the stoichiometric concentration of active Cre protein in terms of the minimum amount of Cre per unit volume that gave measurable FRET-specific quenching of the donor dye in an intramolecular recombination assay (see below). Although this determination was made for each lot of Cre protein sourced from the vendor, we found that none of the rate constants or J values reported here depended on Cre concentration above the stoichiometric threshold.
Intermolecular-recombination assays
Time-dependent FRET measurements were carried out in a Cary Eclipse spectrofluorimeter (Agilent Technologies, Santa Clara, CA, USA) operating in Kinetics mode. The sample cuvette (nominal capacity 100 µl, Starna Cells, Atascadero, CA, USA) was thermostatted at 37°C by a Peltier-regulated circulating water bath. Equimolar mixtures of TDB and TBA duplexes were prepared in either Cre kinetics buffer [25 mM TAPS, 180 mM NaCl, 2 mM MgCl2, 2.5 mg/ml BSA, 20% (v/v) glycerol, 10% (v/v) PEG 8000, pH 8.0] or Cre core buffer (25 mM TAPS, 180 mM NaCl, 2 mM MgCl2, pH 8.0), both supplemented with 2 µg/ml linear pGEM-5Zf(+) as bulk competitor DNA. Some comments are in order regarding the unusual formulation of the kinetics buffer. This buffer composition is potentially suboptimal for intramolecular recombination, but enhances intermolecular reactions. Rigorous J-factor measurements require that the rate constants for both intra- and inter-molecular reactions be determined under identical conditions. In addition, this buffer is closely similar to that used for intramolecular recombination in (38), thereby facilitating comparison with the earlier results. Recombination was initiated by adding varying amounts of Cre with manual mixing. The dead time between addition of the protein and data collection was ∼25 s. A donor-excitation wavelength of 570 nm was used; quenching of donor emission was monitored at 625 nm with respective bandpass settings of 10 and 20 nm.
Intramolecular-recombination assays
ATTO 594/647 N doubly labeled pCS2DloxP0 and pCS2DloxP870 were linearized in the small plasmid domain between directly repeated loxP sites using PstI and NotI (New England Biolabs, Ipswich, MA, USA). These linear plasmids generate identical 3-kb looped intermediates during Cre recombination. Linearization of pCS2DloxP870 in the large domain with EcoRV and SmaI (New England Biolabs, Ipswich, MA, USA) yields a plasmid substrate that forms an 870-bp loop during synapsis. In some experiments, blunt-ended linearized plasmids were generated by treatment with T4 DNA polymerase in the presence of all four nucleoside triphosphates. Kinetics measurements were carried out under conditions identical to the intermolecular-recombination assays with the following modifications: (i) the substrate plasmid concentration was 0.5 nM, (ii) a long-pass filter with a center wavelength of 600 nm was inserted on the emission side of the optical path and (iii) competitor pGEM-5Zf(+) DNA was not added.
Confirmation of product yield via gel electrophoresis
Fluorescently labeled and unmodified pCS2DloxP0 was linearized with NotI and end labeled with α-32PdGTP using the Klenow fragment of DNA polymerase I (New England Biolabs, Ipswich, MA, USA) in NEB Buffer3. A total of 1.5 nM of each substrate was incubated with 15 nM Cre in Cre kinetics buffer at 37°C, with aliquots withdrawn at the indicated times. Reactions were terminated by heat inactivation at 65°C followed by the addition of 2.5 U of proteinase K (New England Biolabs, Ipswich, MA, USA) and further incubation at 37°C for 10 min. The aliquots from different time points were subjected to electrophoresis on 3% agarose–TBE gels, the gels dried, exposed to phosphor-image storage plates, and digital images captured using a BioRad phosphorimaging system. Bands were quantitated using ImageQuant (GE Healthcare, Piscataway, NJ) software.
Kinetics data analysis
The mechanism of Cre recombinase does not conform to a simple kinetic scheme; therefore, we employed numerical methods to extract rate constants for fundamental steps in the recombination pathway corresponding to synapse formation and dissociation. The proposed mechanisms of the both inter- and intra-molecular recombination pathways and additional information required for analysis of the time-dependent FRET signal are given in Supplementary Figures S2–S4 (see also ‘Results’ section). The inter- and intra-molecular recombination pathways share a common set of four rate constants for elementary recombinase binding and dissociation steps, 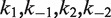 . Inter- and intra-molecular site-synapsis kinetics are characterized by the apparent rate constants,
. Inter- and intra-molecular site-synapsis kinetics are characterized by the apparent rate constants, 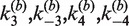 , and
, and 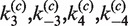 , respectively. In our analysis, we fix the parameters
, respectively. In our analysis, we fix the parameters 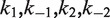 at values that were experimentally determined by Ringrose et al. (38) under reaction conditions closely similar to ours. For intermolecular FRET data, we fitted the time-dependent reduced fluorescence intensity, F(t), to five parameters:
at values that were experimentally determined by Ringrose et al. (38) under reaction conditions closely similar to ours. For intermolecular FRET data, we fitted the time-dependent reduced fluorescence intensity, F(t), to five parameters: 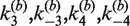 and
and 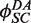 , an empirical quenching constant for the donor–acceptor pair in the synaptic complex. For intramolecular reactions, we fixed
, an empirical quenching constant for the donor–acceptor pair in the synaptic complex. For intramolecular reactions, we fixed 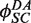 at the value obtained for the intermolecular data sets and fitted F(t) using
at the value obtained for the intermolecular data sets and fitted F(t) using 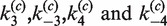 as adjustable parameters. Curve-fitting routines were implemented in Matlab and used the functions lsqcurvefit for non-linear least-squares fitting and ode15s to solve the initial-value problem for the systems of ordinary differential equations. Analysis programs are available on request.
as adjustable parameters. Curve-fitting routines were implemented in Matlab and used the functions lsqcurvefit for non-linear least-squares fitting and ode15s to solve the initial-value problem for the systems of ordinary differential equations. Analysis programs are available on request.
Monte Carlo modeling of energy-transfer efficiencies
Estimates of FRET efficiencies for structural models of Cre–loxP complexes were based on calculations of spatial locations accessible to donor and acceptor dyes. We used a Monte Carlo procedure to sample the positions of dye moieties tethered by a freely jointed chain. Distributions of the quantity
| (1) |
were computed from the dye pair-distance distributions for several crystallographic Cre–DNA complexes (36). Note that Equation (1) is based on the usual assumption of isotropic dye motions with the Förster dipole orientation factor, κ2, equal to 2/3 (39–42). The accessible volume for each dye was computed from the van der Waals surface of a protein-DNA co-crystal structure deposited in the PDB. Each of the dyes was conjugated to the C5 position of a thymine residue via a freely jointed linker chain of contour length L = 2.5 nm. The linker was divided into n identical cylindrical segments having radius Rchain = 0.1 nm and dyes were modeled as spheres of radius Rdye attached to the distal end of the linker. A value Rdye = 0.5 nm was used for both donor and acceptor, the structures of which remain proprietary; however, this value is similar to those for other dyes in the ATTO family whose structures are available. The proximal end of each tethering chain was chosen to lie uniformly on the attachment atom’s van der Waals surface. Monte Carlo-generated chains were rejected if any atom in the crystal structure overlapped with the linker or dye. Once a pre-determined number of accepted dye positions was generated for both donor and acceptor, the distribution of pair-wise donor–acceptor distances, 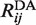 was computed. Only pair-distance data for which
was computed. Only pair-distance data for which 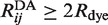 were used for calculations of the ensemble-averaged transfer efficiency, <E>, and the E-value distribution. We also computed these quantities using a uniform dye density within the maximal accessible volume for a tethered dye particle as implemented in the FRETnps Tools suite of analysis programs (43,44). Results for the uniform dye distributions are shown in Supplementary Figure S5.
were used for calculations of the ensemble-averaged transfer efficiency, <E>, and the E-value distribution. We also computed these quantities using a uniform dye density within the maximal accessible volume for a tethered dye particle as implemented in the FRETnps Tools suite of analysis programs (43,44). Results for the uniform dye distributions are shown in Supplementary Figure S5.
RESULTS
Kinetic characterization of intermolecular Cre recombination using FRET
We used bulk FRET measurements that monitor quenching of a donor dye to quantitate the rate of intermolecular Cre recombination between fluorophore-labeled loxP-bearing DNA duplexes. This method for detecting FRET was preferred over measurements of enhanced acceptor emission due to its superior signal-to-noise ratio under our conditions. We found that the minimum concentration of loxP-containing DNA fragments that supports intermolecular recombination in Cre kinetics buffer is several-fold greater than typical substrate concentrations used in intramolecular Cre reactions ([loxP] ≈ 1 nM). This behavior of the Cre intermolecular reaction is closely similar to that of ligase-mediated intermolecular joining, which requires high concentrations of DNA ends (45). Intermolecular reactions in kinetics buffer used equimolar ratios of TDB and TBA duplexes with total loxP concentrations ranging from 6.25 to 25 nM (Supplementary Figure S1). In Cre core buffer, no FRET signal was measurable at [loxP] ≤ 15 nM; thus, core buffer conditions were not used routinely for kinetic assays. Molar ratios of Cre:loxP in the reactions ranged from 2:1 to 20:1. The kinetics of intermolecular recombination were essentially independent of Cre concentration over this range, as inferred from the similarity of the fluorescence decay curves obtained at different protein:DNA ratios and also from fitted values of the apparent rate constants 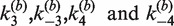 (Table 1).
(Table 1).
Table 1.
Apparent rate constants for intermolecular site synapsis
| [loxP] (nM) | [Cre] (nM) |
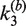 (10−3 nM−1 min−1) (±SE) (10−3 nM−1 min−1) (±SE) |
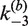 (min−1) (±SE) (min−1) (±SE) |
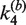 (10−3 nM−1 min−1) (±SE) (10−3 nM−1 min−1) (±SE) |
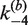 (min−1) (±SE) (min−1) (±SE) |
|---|---|---|---|---|---|
| 25 | 250 | 3.0 (±0.18) | 0.024 (±0.0018) | 0.21 (±0.024) | 0.037 (±0.0030) |
| 25 | 125 | 3.1 (±0.089) | 0.028 (±0.0019) | 0.21 (±0.049) | 0.062 (±0.0034) |
| 18 | 180 | 2.8 (±0.67) | 0.028 (±0.0028) | 0.33 (±0.098) | 0.085 (±0.0081) |
| 18 | 90 | 3.3 (±0.41) | 0.047 (±0.0097) | 0.37 (±0.029) | 0.074 (±0.016) |
| 12.5 | 125 | 3.6 (±0.31) | 0.029 (±0.0039) | 0.72 (±0.079) | 0.051 (±0.0064) |
| 12.5 | 62.5 | 3.5 (±0.31) | 0.046 (±0.0076) | 0.49 (±0.21) | 0.071 (±0.012) |
| 6.25 | 62.5 | 5.6 (±0.86) | 0.14 (±0.027) | 0.99 (±0.26) | 0.21 (±0.032) |
| 6.25 | 31.2 | 4.7 (±0.86) | 0.11 (±0.049) | 1.2 (±0.50) | 0.16 (±0.039) |
| 6.25 | 12.5 | 4.3 (±0.58) | 0.14 (±0.020) | 1.3 (±0.26) | 0.19 (±0.079) |
Values are averages of at least three independent measurements. Uncertainties in rate constants are expressed as standard errors.
In Figure 4, our experimental design monitors the recombination-mediated exchange of fluorophore-labeled strands on parental duplexes, placing donor and acceptor moieties at adjacent positions on opposing DNA strands in the product. Rate constants were obtained by fitting F(t) to a system of ordinary differential equations that describe the time-dependent concentrations of reactants, intermediates and products (Supplementary Figures S2 and S3). In the Supplementary Appendix, analysis requires knowing the extent of donor quenching in the recombination product, which we determined independently from the ratio of intrinsic donor emission signal in donor-only (TDB) duplexes versus doubly labeled (donor + acceptor) duplexes with the probes located at positions identical to those in the recombination product (TDBA). This quenching constant, 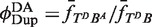 , is obtained from the ratios of quantum yields for the donor-labeled duplex in the presence and absence of acceptor. We determined
, is obtained from the ratios of quantum yields for the donor-labeled duplex in the presence and absence of acceptor. We determined 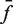 from the dependence of emission intensity at λem = 625 nm for donor-only and donor–acceptor duplexes at identical gain and bandpass settings. The value of
from the dependence of emission intensity at λem = 625 nm for donor-only and donor–acceptor duplexes at identical gain and bandpass settings. The value of 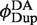 was found to be 0.01, independent of the presence and concentration of Cre protein. Thus, there is negligible quenching of donor emission due either to Cre binding or the presence of a second donor fluorophore in the synaptic complex (Supplementary Figure S4).
was found to be 0.01, independent of the presence and concentration of Cre protein. Thus, there is negligible quenching of donor emission due either to Cre binding or the presence of a second donor fluorophore in the synaptic complex (Supplementary Figure S4).
Figure 4.
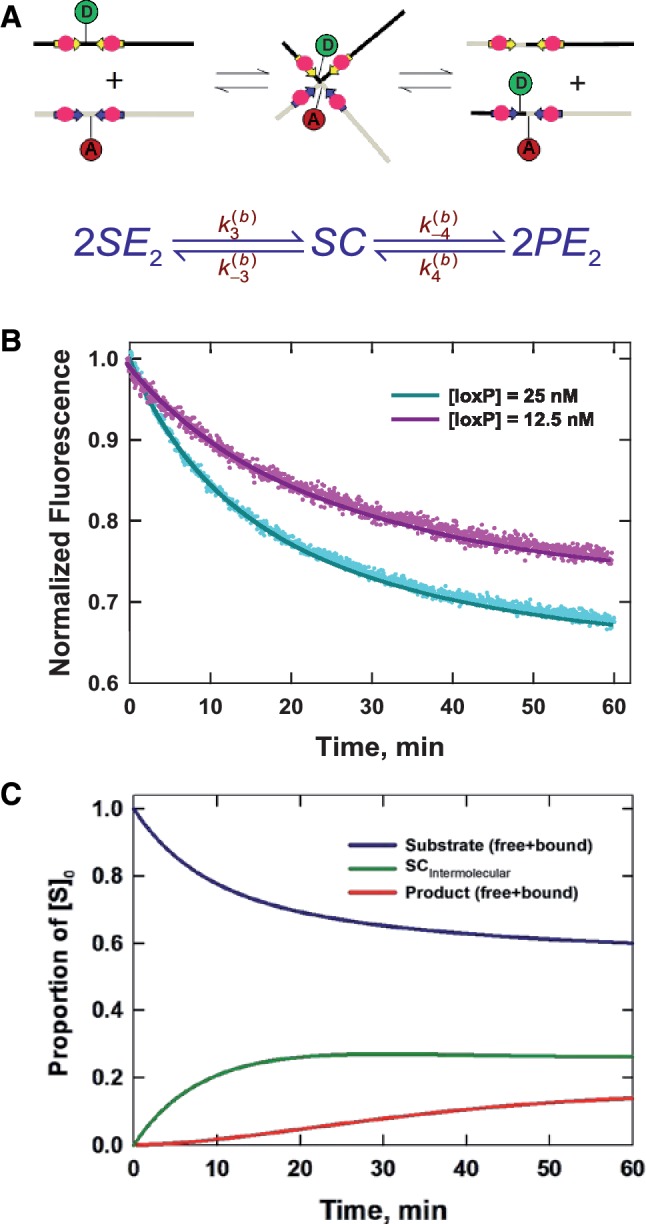
Time-dependent FRET measurements of intermolecular synapsis and recombination kinetics. (A) Recombination reactions used equimolar ratios of donor-labeled (TDB) and acceptor-labeled (TBA) duplexes in reactions having total loxP concentrations ranging from 6.25 nM to 25 nM. (B) Time-dependent fluorescence signal, F(t), which monitors recombination-mediated exchange of DNA strands via donor quenching. The recombinant product harbors donor and acceptor moieties at adjacent positions on opposing DNA strands and has a FRET efficiency of 0.99. Rate constants were obtained by fitting each set of F(t) data to the numerical solution of a system of ordinary differential equations (see Supplementary Figure S2), which describe the time-dependent concentrations of reactants, intermediates and products along the intermolecular recombination pathway. The best-fit numerical solutions are shown by solid curves; fitted values for the rate constants are given in Table 1. (C) Distribution of species (Cre-bound and unbound substrate, synaptic complex and bound and unbound product) in intermolecular recombination inferred from the values of 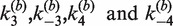 given [loxP] = 25 nM and [Cre] = 250 nM.
given [loxP] = 25 nM and [Cre] = 250 nM.
The time-dependent fluorescence of the intermolecular reaction is described very well by the single-intermediate mechanism in Figure 4B. Non-linear least-squares fitting were carried out using the numerical solutions of the corresponding system of ODEs with 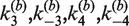 and
and 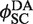 as adjustable parameters. Fitted values of
as adjustable parameters. Fitted values of 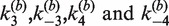 are given in Table 1; note that the value of
are given in Table 1; note that the value of 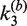 was independent of loxP concentration, whereas the measured value of
was independent of loxP concentration, whereas the measured value of 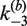 increased with decreasing [loxP] (Figure 5). Although the intermolecular reaction is not efficient when [loxP] is below 4.25 nM, a reasonable extrapolation of the rate constants can be made to lower loxP concentrations. The dependence of the intermolecular-recombination rate for low [loxP] can be important when rates of inter- and intra-molecular recombination are being compared under similar reaction conditions, discussed as follows. The apparent value of
increased with decreasing [loxP] (Figure 5). Although the intermolecular reaction is not efficient when [loxP] is below 4.25 nM, a reasonable extrapolation of the rate constants can be made to lower loxP concentrations. The dependence of the intermolecular-recombination rate for low [loxP] can be important when rates of inter- and intra-molecular recombination are being compared under similar reaction conditions, discussed as follows. The apparent value of 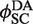 was virtually constant and equal to 0.12 ± 0.014 for all data sets, independent of [loxP] or [Cre].
was virtually constant and equal to 0.12 ± 0.014 for all data sets, independent of [loxP] or [Cre].
Figure 5.
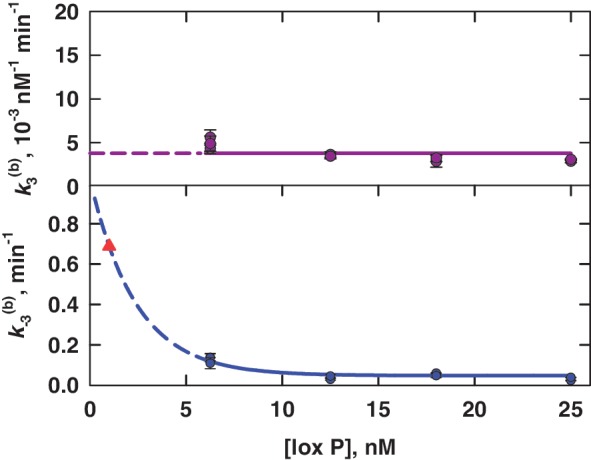
Apparent rate constants for bimolecular synapsis, 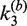 , (upper panel) and synaptic-complex dissociation,
, (upper panel) and synaptic-complex dissociation, 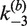 (lower panel) as functions of loxP concentration. Each data point is the average of at least three independent measurements and the error bars indicate the standard error. The horizontal line in the upper panel gives the overall average of
(lower panel) as functions of loxP concentration. Each data point is the average of at least three independent measurements and the error bars indicate the standard error. The horizontal line in the upper panel gives the overall average of 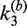 for all values of [loxP] studied; the curve in the lower panel is the fit of an exponential function to the data for
for all values of [loxP] studied; the curve in the lower panel is the fit of an exponential function to the data for 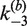 . Dashed curves are extrapolations of the [loxP] dependence to zero substrate concentration. The value of
. Dashed curves are extrapolations of the [loxP] dependence to zero substrate concentration. The value of 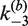 at [loxP] = 1 nM is 0.69 min−1 and is indicated by the red filled triangle; this is the value of the rate constant used to calculate J under the conditions of intramolecular recombination.
at [loxP] = 1 nM is 0.69 min−1 and is indicated by the red filled triangle; this is the value of the rate constant used to calculate J under the conditions of intramolecular recombination.
Distributions of species in the intermolecular reaction
Figure 4C shows the inferred distribution of reactants, products, and synaptic complex over the time course of a 60-min intermolecular recombination reaction for [loxP] = 25 nM given the values of 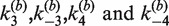 in Table 1. The yield of product is ∼15%, suggesting that most of the labeled substrate is present in the form of synaptic complex or SE2. This result explains the fact that the observed extent of donor quenching is significantly less than expected if donor-bearing DNA fragments were converted largely to products. For example, in a reaction containing 12.5 nM TDB (and 12.5 nM TBA for a total [loxP] of 25 nM), an overall extent of reaction of 50% would yield equal final concentrations of TDB and TDBA equal to 6.25 nM. The latter species is strongly quenched and contributes little to the total donor emission. Therefore, the expected emission signal reduction would also be near 50% under these conditions. However, we typically observe residual donor emission that is significantly above this value, consistent with the hypothesis that a donor-containing species with lower FRET efficiency is abundant during the entire course of the reaction.
in Table 1. The yield of product is ∼15%, suggesting that most of the labeled substrate is present in the form of synaptic complex or SE2. This result explains the fact that the observed extent of donor quenching is significantly less than expected if donor-bearing DNA fragments were converted largely to products. For example, in a reaction containing 12.5 nM TDB (and 12.5 nM TBA for a total [loxP] of 25 nM), an overall extent of reaction of 50% would yield equal final concentrations of TDB and TDBA equal to 6.25 nM. The latter species is strongly quenched and contributes little to the total donor emission. Therefore, the expected emission signal reduction would also be near 50% under these conditions. However, we typically observe residual donor emission that is significantly above this value, consistent with the hypothesis that a donor-containing species with lower FRET efficiency is abundant during the entire course of the reaction.
The apparent association equilibrium constant for the synapsis reaction (i.e. for saturated substrate SE2 forming synaptic complex) is given by the ratio 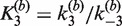 . This value is more than an order of magnitude larger than
. This value is more than an order of magnitude larger than 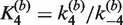 , which may suggest that the recombination mechanism involves more than one intermediate species. It is also possible that the fluorophore labels perturb the reaction differently in the forward and reverse directions, effectively breaking the symmetry of the mechanism. High stability of the Cre synaptic complex contrasts with that of Flp recombinase, which shares many biochemical and mechanistic similarities to Cre. In fact, Cre synaptic complexes can be readily isolated without chemical fixation or other stabilization steps, whereas Flp synaptic complexes require treatment with gluteraldehyde or a similar cross-linking reagent in order to be characterized or purified (31,46).
, which may suggest that the recombination mechanism involves more than one intermediate species. It is also possible that the fluorophore labels perturb the reaction differently in the forward and reverse directions, effectively breaking the symmetry of the mechanism. High stability of the Cre synaptic complex contrasts with that of Flp recombinase, which shares many biochemical and mechanistic similarities to Cre. In fact, Cre synaptic complexes can be readily isolated without chemical fixation or other stabilization steps, whereas Flp synaptic complexes require treatment with gluteraldehyde or a similar cross-linking reagent in order to be characterized or purified (31,46).
Intramolecular reaction kinetics
Detailed studies of the intramolecular reaction were facilitated by our novel fluorophore-labeling method, which places donor and acceptor modifications at specific sites in covalently closed plasmids. We investigated the intramolecular reaction using two linear plasmids that form loops of 3 kb and 870 bp on synapsis. These substrates have fluorophore-labeled loxP sites positioned near the ends of the molecule (Figure 6A). In order to avoid interference from the intermolecular reaction, intramolecular kinetics assays were carried out at substrate concentrations <2 nM ([loxP] < 4 nM), below the target-site-concentration threshold for intermolecular recombination discussed above. Post-hoc analysis of the reaction by agarose-gel electrophoresis confirmed that the yield of intermolecular-recombination products was negligible under our conditions (data not shown).
Figure 6.
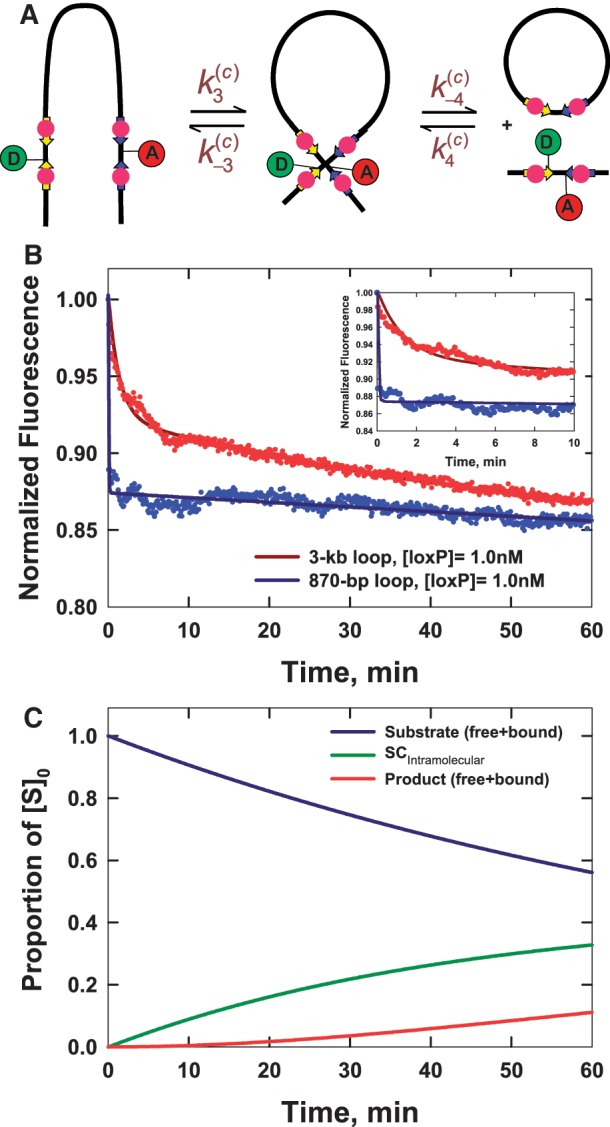
Intramolecular synapsis and recombination kinetics obtained from time-dependent FRET measurements. (A) Schematic of the intramolecular reaction carried out on a DNA fragment bearing donor- and acceptor-labeled loxP sites. (B) Fluorescence signal, F(t), which monitors donor quenching via FRET during site synapsis and recombination. Fluorescence decays are for molecules having 3-kb and 870-bp DNA loops. The positions of the donor and acceptor fluorophores in labeled product loxP sequences are the same as in Figure 4. Rate constants were obtained by fitting F(t) to a system of ordinary differential equations that describe the time-dependent concentrations of reactants, intermediates and products along the intramolecular recombination pathway (see Supplementary Figure S3). The best-fit numerical solution is given by the solid curve and corresponding rate constants are given in Table 2. Details of the fluorescence decay and the fit to the data over the first 10 min of the recombination reaction are shown in the inset. (C) Distribution of species (Cre-bound and unbound substrate, synaptic complex and bound and unbound product) in intramolecular recombination of the 3-kb loop inferred from the values of 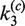 ,
, 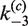 ,
, 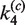 and
and 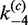 given [loxP] = 0.5 nM and [Cre] = 5 nM. Under these conditions, the asymptotic proportions of synaptic complex and recombination product are about 30 and 10%, respectively.
given [loxP] = 0.5 nM and [Cre] = 5 nM. Under these conditions, the asymptotic proportions of synaptic complex and recombination product are about 30 and 10%, respectively.
Figure 6B shows that the time-dependent FRET signals are fitted quite well by the ODE solutions for the intramolecular single-intermediate Cre-recombination pathway (Supplementary Figure S3). We fixed the value of 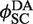 at 0.12, the best-fit value obtained from analysis of the intermolecular reaction, and treated
at 0.12, the best-fit value obtained from analysis of the intermolecular reaction, and treated 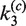 ,
, 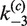 ,
, 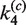 and
and 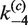 as adjustable parameters. These values are given in Table 2. FRET signals for DNA fragments having cohesive and blunt-ended termini were indistinguishable and gave the same apparent rate-constant values within experimental uncertainty.
as adjustable parameters. These values are given in Table 2. FRET signals for DNA fragments having cohesive and blunt-ended termini were indistinguishable and gave the same apparent rate-constant values within experimental uncertainty.
Table 2.
Apparent values of forward and reverse rate constants and equilibrium constant for intramolecular site synapsis
| Loop size |
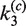 (min−1) (min−1) |
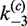 (min−1) (min−1) |
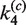 (nM−1 min−1) (nM−1 min−1) |
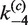 (min−1) (min−1) |
Kc |
|---|---|---|---|---|---|
| 3044 | 0.074 | 0.78 | 0.32 | 0.014 | 0.095 (±0.026) |
| 870 | 2.4 | 13 | 10 | 0.021 | 0.20 (±0.10) |
Uncertainties in Kc are reported as the standard deviation of at least three independent measurements.
The intramolecular recombination reactions showed time-dependent fluorescence signals that are qualitatively different from those observed for the intermolecular reaction (Figure 6B). There is a rapid initial decay of fluorescence emission, followed by a slower, more extended kinetic phase with little change in the fluorescence amplitude beyond 10 min. In the case of the 870-bp substrate, the initial decay phase was faster, and therefore, more difficult to characterize, than that for the 3-kb substrate. Under the reaction conditions examined, the overall amplitude of the FRET signal was quite modest, on the order of 10–15% over a 60-min reaction. We observed that the intramolecular reaction was more reproducible in Cre kinetics buffer than in core buffer, possibly because of improved protein stability. The values of the observed rate constants in the two buffer systems were identical within experimental uncertainty, thus data for reactions carried out only in Cre kinetics buffer are reported in Table 2.
Distributions of species in the intramolecular reaction
As in the intermolecular pathway, it is informative to examine the distribution of kinetic species over the course of the reaction. Figure 6C shows the time-dependent distribution of 3-kb substrate DNA present as all reactants, all products and synaptic complex using fitted values of 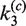 ,
, 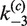 ,
, 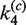 and
and 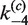 and taking the plasmid concentration equal to 0.5 nM ([loxP] = 1 nM) with low levels of excess Cre (2.5 times the stoichiometric level).
and taking the plasmid concentration equal to 0.5 nM ([loxP] = 1 nM) with low levels of excess Cre (2.5 times the stoichiometric level).
Under our conditions, the intramolecular reaction also converts only a limited fraction of substrate DNA into product. The majority of substrate is present as the SE4 intermediate (substrate DNA with Cre monomers bound at all four symmetry elements). Overall yield of product species was measured by electrophoretic analysis of end-labeled fluorophore-modified and unmodified 3-kb substrates (Figure 7). Note that actual products of the recombination reaction cannot readily be distinguished from synapsed product molecules; therefore, the gel-electrophoretic assays can potentially over-estimate the proportion of total product. The unmodified substrate gave an apparent asymptotic product yield on the order of 12%, whereas the modified substrate gave ∼8% apparent product; the latter amount is consistent with the asymptotic product distribution inferred from our kinetic analysis. These results suggest that there may be a modest effect of the fluorophores on the overall yield of the Cre reaction. Alternative locations for the conjugated fluorophores were considered; however, these were rejected due to either potential interference with Cre binding or greatly diminished FRET efficiency (see also ‘Discussion’ section).
Figure 7.
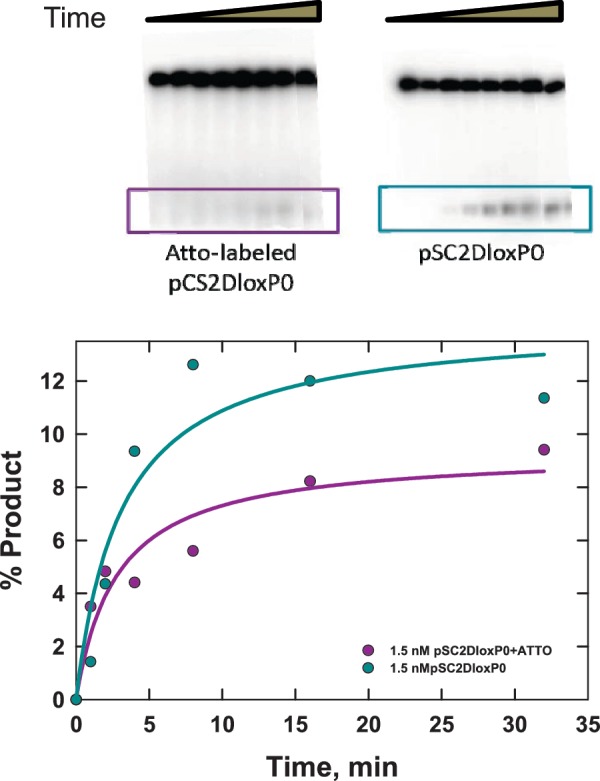
Gel-electrophoretic product assay for intramolecular Cre recombination of a linear 3-kb plasmid-DNA substrate (pCS2DloxP0). The loxP sites have been unmodified (right) or modified by conjugation of donor and acceptor fluorophores to specific T residues in the loxP core (right). Cre recombination generates ≈3-kb circular and 65-bp linear products; the latter was end labeled using 32P and quantitated by gel electrophoresis over a 32-min time course (below). The solid curves are approximate fits of an exponential function to the data and serve as a guide to the eye.
The relatively low product yield with unlabeled substrate DNA is a consequence of the Cre reaction being carried out at near-stoichiometric levels of the recombinase. Our measured levels of overall recombination are in accordance with values reported in the literature (10) for similar [Cre]:[loxP] ratios. Super-stoichiometric levels of recombinase protein (on the order of 100:1 [Cre]:[loxP]) are apparently necessary to achieve maximal levels of Cre recombination, which are in the range of 60%. However, extreme ratios of protein to DNA would be likely to have other unknown effects on DNA flexibility and folding mediated through non-specific DNA binding and/or protein-mediated aggregation.
Analysis of FRET efficiencies based on structural models for the synapse
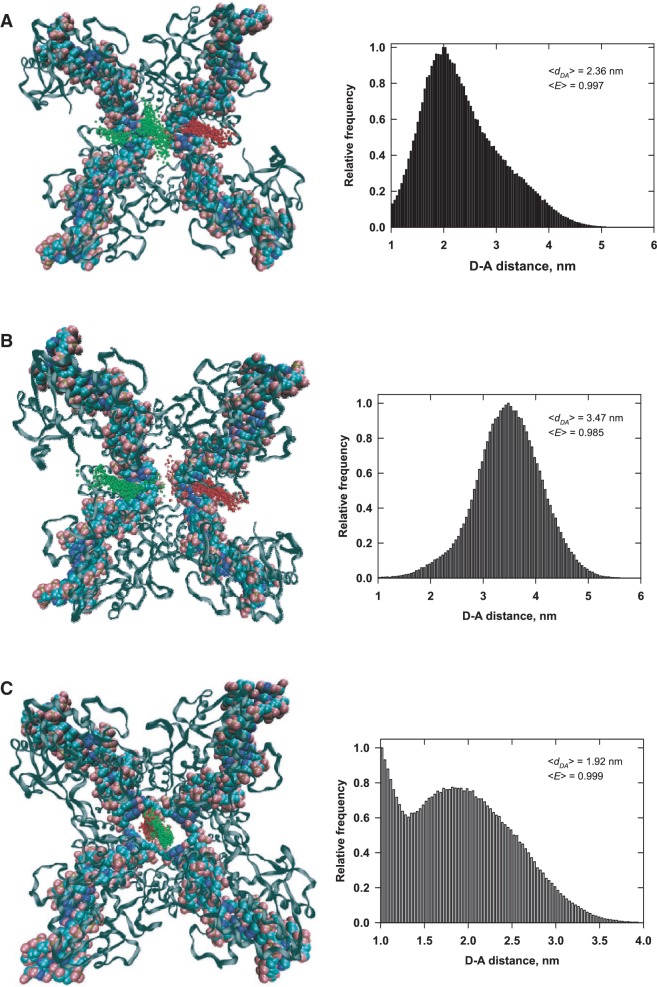
We estimated the distributions of energy-transfer efficiency, E, for static models of synaptic complexes based on the crystallographic structures of Cre bound to duplex loxP sites (21) and a loxP Holliday junction (16). Distributions of dye-pair distances were obtained by Monte Carlo sampling of the dye-accessible volume as described in the ‘Materials and Methods’ section or by a model in which the dye density was taken to be uniform within the maximum accessible volume allowed by the linker length and the van der Waals surfaces of the dyes and nucleoprotein structure. Distributions in the latter case are easier to compute, whereas those in the former case are more rigorous. Both calculations use the approximation of isotropic dye transition-moment orientations.
Distributions of dye positions in the loxP duplex synapse are shown in Figure 8. The first set of data in Figure 8A are for donor and acceptor labels in the positions expected for an anti-parallel loxP synapse, which is required for productive recombination. We generated an alternative model for the case of parallel synapsis (Figure 8B), which is mechanistically possible, but not consistent with the accepted Cre mechanism and canonically non-productive. Both of the pair-distance distributions with duplex loxP sites are markedly different from that in the Holliday-junction complex in Figure 8C. The average values of E computed by Monte Carlo simulation, <E>, are typically slightly larger than those obtained for the uniformly sampled accessible volume (see Supplementary Figure S5 in Supplementary Data). In general, the dye pair-distance distributions for the Monte Carlo and uniformly sampled models differ significantly, although the effects on average E values and the E distribution for these models are quite small. This is because <E> is heavily weighted toward small donor–acceptor pair distances and the vast majority of pair distances fall well below the Förster distance, R0, for all of the cases considered here. However, we note that all of the <E> values computed from these static models are significantly greater than the experimentally measured E value for the synaptic complex, which is 0.88.
Figure 8.
Distributions of donor–acceptor distance for three crystallographic models of the Cre-loxP synaptosome. Monte Carlo simulated donor and acceptor positions are indicated by green and red spheres, respectively. For clarity, the spheres used to mark the dye positions are significantly smaller (0.17 nm) than the dimension of the spherical dye used in the calculation. The donor–acceptor pair-distance distributions for 500 individual samples each of donor and acceptor positions are shown to the right of each model. (A) Model for an anti-parallel synapse of loxP sites generated using the PDB coordinate file 5CRX (21). (B) Model for a parallel synapse, assuming that the DNA geometry is identical to that in (A). (C) Model for a Holliday-junction intermediate, based on the PDB coordinate file 3CRX (16).
DISCUSSION
We have developed a novel approach for characterizing the rate-determining steps for inter- and intra-molecular synapsis in a site-specific recombination reaction. Our methodology uses time-dependent FRET in conjunction with numerical modeling of the recombination pathway to monitor target-site synapsis and the time-dependent yield of recombination products. The quotient of apparent equilibrium constants for the intramolecular and equivalent intermolecular reaction yields a quantity J that characterizes the thermodynamics of intramolecular loop formation. The definition 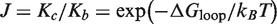 relates J to the conformational free-energy cost of forming a DNA loop of a given size and having specific boundary conditions at the loop ends. This free-energy contribution to loop formation is distinct from those associated with covalent and non-covalent DNA–DNA, protein–protein and protein–DNA interactions at the loop ends, which are assumed to be identical for the inter- and intra-molecular reactions. We also show that there is a significant difference in the experimental FRET efficiencies between the longest-lived recombination intermediate (E = 0.88) and products (E = 0.99); this fact enables us to infer the distribution of species over the course of the reaction.
relates J to the conformational free-energy cost of forming a DNA loop of a given size and having specific boundary conditions at the loop ends. This free-energy contribution to loop formation is distinct from those associated with covalent and non-covalent DNA–DNA, protein–protein and protein–DNA interactions at the loop ends, which are assumed to be identical for the inter- and intra-molecular reactions. We also show that there is a significant difference in the experimental FRET efficiencies between the longest-lived recombination intermediate (E = 0.88) and products (E = 0.99); this fact enables us to infer the distribution of species over the course of the reaction.
Site synapsis and recombination-product turnover
Our results extend the work of Ringrose et al. (38), which investigated the binding and dissociation kinetics of Cre to loxP symmetry elements and the kinetics of the intramolecular recombination reaction. Ringrose et al. conclude that Cre binds cooperatively to a single target site and forms a highly stable synaptic intermediate. However, it was not possible to measure the kinetics of site synapsis in their study, or to characterize properties of the DNA intermediate.
Our results are in general accord with Ringrose et al. to the extent that we infer a large association-equilibrium constant for the synaptic complex. On closer inspection, however, there is a significant disagreement with the previous study regarding the overall product yield of the Cre reaction. Whereas Ringrose et al. report overall yields as high as 50–60%, the results of both time-resolved FRET and electrophoretic product assays for fluorophore-labeled and unlabeled substrates in our work give actual yields of recombination products that are 4- to 5-fold lower.
There are at least two factors that could contribute to this discrepancy. One is that the assays carried out by Ringrose et al. used much higher ratios of Cre protein to loxP DNA than are present in our reactions; this has pronounced effects on product yield, as previously reported (10). We chose not to recapitulate such high ratios of Cre to DNA because of possible non-specific effects of excess protein on DNA flexibility and folding. Moreover, our results are consistent with both references (10) and (38) when adjusted for the [Cre]:[loxP] ratio. Second, the particular method of terminating recombination reactions in the electrophoretic assay used in (38) may have perturbed the instantaneous distribution of species at a particular time point. It is known that addition of detergent can alter the distribution of intermediates obtained from quenching of topoisomerase reactions (47), which involve similar chemistry.
Recombination-kinetics estimates of the probability of loop closure
Independent measurements of inter- and intra-molecular recombination rates permit quantitative determination of the probability of loop formation, the Jacobson–Stockmayer, or J factor, J (48). This probability, which is expressed in terms of concentration, is the bulk DNA-substrate concentration for which the probabilities of inter- and intra-molecular site synapsis are identical. Formally, J is a quotient of rate constants for intra- and inter-molecular synapsis, given by
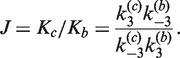 |
(2) |
Quantitative measurements of J are difficult to achieve in practice because inter- and intra-molecular reactions generally do not take place under identical conditions. The existence of a limited range of intermolecular-recombination conditions is similar to that encountered in ligase-catalyzed bimolecular-joining reactions (45), which require higher concentrations of DNA substrate than for the corresponding intramolecular reaction. Failing to take possible dependencies on substrate or enzyme concentration into account can lead to large errors in 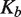 especially and hence in the absolute value of J.
especially and hence in the absolute value of J.
The most rigorous approach for obtaining absolute measurements of J is to determine individually the pairs of apparent rate constants 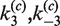 and
and 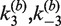 . Values of the intermolecular rate constants are corrected by extrapolation to substrate and/or protein concentrations that pertain to the intramolecular reaction conditions. We found negligible dependence of
. Values of the intermolecular rate constants are corrected by extrapolation to substrate and/or protein concentrations that pertain to the intramolecular reaction conditions. We found negligible dependence of 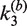 on either [loxP] or [Cre]; in the case of
on either [loxP] or [Cre]; in the case of 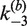 , there was no detectable dependence on [Cre], but a significant dependence on [loxP]. We took this substrate-concentration effect into account by fitting the dependence of
, there was no detectable dependence on [Cre], but a significant dependence on [loxP]. We took this substrate-concentration effect into account by fitting the dependence of 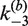 as a function of [loxP] (Figure 5). Our values of J are based on the kinetics of substrate conversion to synaptic complex and therefore not connected with the apparent values of
as a function of [loxP] (Figure 5). Our values of J are based on the kinetics of substrate conversion to synaptic complex and therefore not connected with the apparent values of 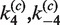 and
and 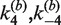 determined from the fits to the data. Indeed, the latter rate constants are less accurately determined than the other four kinetic parameters because strongly quenched product species contribute little to the total fluorescence signal.
determined from the fits to the data. Indeed, the latter rate constants are less accurately determined than the other four kinetic parameters because strongly quenched product species contribute little to the total fluorescence signal.
Using Equation 2, we obtain the values of J reported in Table 3. In Figure 9, these values are compared with the theoretical dependence of J on loop size computed using a transfer-matrix approach (49). Two sets of loop-end boundary conditions were used in the transfer-matrix calculations: cyclization of a loop with parallel ends to generate a ring and formation of a teardrop-shaped loop, equivalent to a ring with a sharp 90° bend. In both cases, the distance between loop ends is constrained to be zero, a case in which the transfer-matrix solutions for J are essentially exact. Similar calculations for chains with finite end-to-end distances are mathematically intractable and must be carried out using a different numerical approach.
Table 3.
A Comparison of experimental J-factor values from Cre recombination, Jexp, with theoretical J values, Jtheor
| Loop size (bp) | Jtheor (nM) | Jexp (nM) |
|---|---|---|
| 3044 | 20 | 18 (±4.7) |
| 870 | 55 | 37 (±18) |
Figure 9.
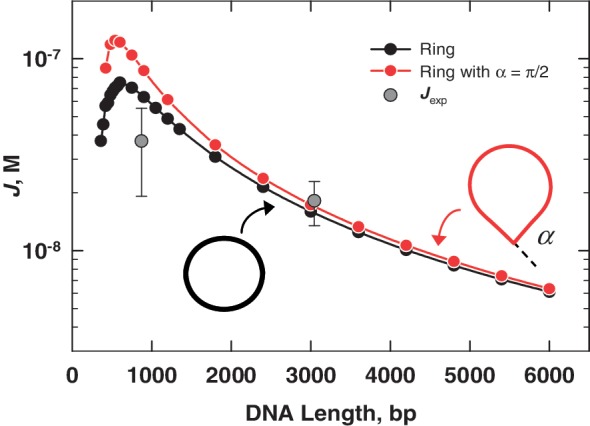
Comparison of experimental J-factor values from Cre recombination, Jexp, with theoretical J values computed using a transfer-matrix approach. The transfer-matrix calculations were done essentially as described in reference (49), with two different boundary conditions at the loop ends: parallel boundary conditions yielding a closed ring and a sharp bend, α = 90°, simulating the approximate bend angle between DNA segments in the crystallographic Holliday-junction intermediate (16,17). In both cases, the distance between loop ends is exactly equal to 0. Chain segments in the transfer-matrix model were of length 10 nm and the DNA persistence length was set to 50 nm.
In Figure 9, the experimental value of Jexp for the 3-kb looped substrate is in excellent agreement with the theoretical J value for both loop conformations. The Jexp value for the 870-bp loop falls somewhat below both theoretical curves. There is greater uncertainty associated with this measurement due, in large part, to the fact that the initial phase of the fluorescence decay is too rapid to be accurately captured in a manual mixing experiment. We note that significant modulations of J due to the helical geometry of DNA are not expected in the range of loop sizes examined here (48). These modulations are not accounted for in the transfer-matrix calculations.
Donor quenching and DNA geometry in the synaptosome
We analyzed accessible tethered-dye geometries in three prototype synapse co-crystal structures, two corresponding to paired loxP duplexes and one a Holliday-junction intermediate. These models give different donor–acceptor pair-distance distributions, but are indistinguishable in terms of their estimated average energy-transfer efficiency. In all three cases, the average donor–acceptor distance is small compared with the Förster distance, leading to negligible effects on <E>. Thus, energy-transfer measurements using the current combination of donor/acceptor positions do not allow for detailed structural characterization of DNA geometry within the synaptosome. We also investigated <E> for the same synaptic-complex models with donor and acceptor fluorophores conjugated to alternative thymine residues in the 13-bp symmetry elements or at the distal boundaries of the loxP target site. Within the symmetry elements, Monte Carlo sampling of dye locations suffered from high attrition suggesting that these positions would likely interfere with protein binding. This problem was not encountered for the thymine positions used in this work or at distal positions; however, the expected <E> for the distal cases was virtually equal to 0.
The fact that <E> is insensitive to details of synaptic-complex geometry is advantageous in the present experiments, where the value of J is the sole quantity of interest and direct effects of loop geometry on apparent E values need to be avoided. Perturbation of E by intrinsic loop geometry could occur with probes that are placed at the ends of loxP arms near the synaptosome's surface, for example. This will be the case, for instance, if the preferred geometry of a short loop affects the entry/exit angles of DNA segments in the synapse (48).
Our experimental value of E, equal to 0.88, is smaller than expected for any of the crystallographic models and can be explained in terms of several factors. A trivial possibility is that the spectral overlap between donor emission and acceptor absorption is decreased significantly in the complex, in effect reducing R0. This seems unlikely because the product duplex labeled with donor and acceptor probes gives the same E value in the presence and absence of Cre protein (see Supplementary Figure S4 in Supplementary Data). A more likely explanation is that emission anisotropy and restricted fluorophore motion have substantial effects on the apparent value of E (40,41); this would be expected for fluorophores confined to the small volume of the synaptic complex core. Our kinetic approach does not invoke absolute distance determination by FRET and therefore does not require knowledge of the anisotropy factor κ2 appearing in the Förster equation. Nevertheless, additional information about the synapse geometry is potentially available from FRET, but would require more sophisticated modeling of dye motions within the nucleoprotein complex.
We favor the view that the longest-lived intermediate DNA structure consists of an HJ because this picture is consistent with the bias in the distributions of looped geometries observed in AFM experiments as a function of site orientation (31). It has been argued previously that such conformational biases may originate from strongly favored stacked-X (50,51) or tetrahedral arrangements of target helices (31). The present FRET study was not designed to fully characterize the geometry of the recombination intermediate; however, extensions of this approach could be used in subsequent studies to reveal the dynamic nature of recombination intermediates in solution.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online: Supplementary Figures 1–5 and Supplementary Appendix.
FUNDING
The National Institutes of Health/National Science Foundation Joint Program in Mathematical Biology [DMS-0800929 from NSF to S.D.L.]. Funding for open access charge: National Science Foundation [DMS-0800929].
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Jens Michaelis for providing the MATLAB source code for FRETnps Tools. We are also grateful to Andreas Hanke for transfer-matrix results and comments on the manuscript and to Lan Ma for helpful discussions.
REFERENCES
- 1.Stark WM, Sherratt DJ, Boocock MR. Site-specific recombination by Tn3 resolvase: topological changes in the forward and reverse reactions. Cell. 1989;58:779–790. doi: 10.1016/0092-8674(89)90111-6. [DOI] [PubMed] [Google Scholar]
- 2.Lewis SM. The mechanism of V(D)J joining: lessons from molecular, immunological, and comparative analyses. Adv. Immunol. 1994;56:27–150. doi: 10.1016/s0065-2776(08)60450-2. [DOI] [PubMed] [Google Scholar]
- 3.Sherratt DJ, Arciszewska LK, Blakely G, Colloms S, Grant K, Leslie N, McCulloch R. Site-specific recombination and circular chromosome segregation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1995;347:37–42. doi: 10.1098/rstb.1995.0006. [DOI] [PubMed] [Google Scholar]
- 4.Hallet B, Sherratt DJ. Transposition and site-specific recombination: adapting DNA cut-and-paste mechanisms to a variety of genetic rearrangements. FEMS Microbiol. Rev. 1997;21:157–178. doi: 10.1111/j.1574-6976.1997.tb00349.x. [DOI] [PubMed] [Google Scholar]
- 5.Lieber MR. Site-specific recombination in the immune system. FASEB J. 1991;5:2934–2944. doi: 10.1096/fasebj.5.14.1752360. [DOI] [PubMed] [Google Scholar]
- 6.Landy A. Dynamic, structural, and regulatory aspects of lambda site-specific recombination. Annu. Rev. Biochem. 1989;58:913–949. doi: 10.1146/annurev.bi.58.070189.004405. [DOI] [PubMed] [Google Scholar]
- 7.Nunes-Duby SE, Kwon HJ, Tirumalai RS, Ellenberger T, Landy A. Similarities and differences among 105 members of the Int family of site-specific recombinases. Nucleic Acids Res. 1998;26:391–406. doi: 10.1093/nar/26.2.391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Van Duyne GD. A structural view of Cre-loxP site-specific recombination. Annu. Rev. Biophys. Biomol. Struct. 2001;30:87–104. doi: 10.1146/annurev.biophys.30.1.87. [DOI] [PubMed] [Google Scholar]
- 9.Sadowski PD. The Flp recombinase of the 2-microns plasmid of Saccharomyces cerevisiae. Prog. Nucleic Acid Res. Mol. Biol. 1995;51:53–91. [PubMed] [Google Scholar]
- 10.Abremski K, Hoess R. Bacteriophage P1 site-specific recombination. Purification and properties of the Cre recombinase protein. J. Biol. Chem. 1984;259:1509–1514. [PubMed] [Google Scholar]
- 11.Nagy A. Cre recombinase: the universal reagent for genome tailoring. Genesis. 2000;26:99–109. [PubMed] [Google Scholar]
- 12.Scott JR. Genetic studies on bacteriophage P1. Virology. 1968;36:564–574. doi: 10.1016/0042-6822(68)90188-8. [DOI] [PubMed] [Google Scholar]
- 13.Sternberg N. Demonstration and analysis of P1 site-specific recombination using lambda-P1 hybrid phages constructed in vitro. Cold Spring Harb. Symp. Quant. Biol. 1979;43(Pt 2):1143–1146. doi: 10.1101/sqb.1979.043.01.128. [DOI] [PubMed] [Google Scholar]
- 14.Sternberg N, Hamilton D, Austin S, Yarmolinsky M, Hoess R. Site-specific recombination and its role in the life cycle of bacteriophage P1. Cold Spring Harb. Symp. Quant. Biol. 1981;45(Pt 1):297–309. doi: 10.1101/sqb.1981.045.01.042. [DOI] [PubMed] [Google Scholar]
- 15.Ma CH, Kachroo AH, Macieszak A, Chen TY, Guga P, Jayaram M. Reactions of Cre with methylphosphonate DNA: similarities and contrasts with Flp and vaccinia topoisomerase. PLoS One. 2009;4:e7248. doi: 10.1371/journal.pone.0007248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gopaul DN, Guo F, Van Duyne GD. Structure of the Holliday junction intermediate in Cre-loxP site- specific recombination. EMBO J. 1998;17:4175–4187. doi: 10.1093/emboj/17.14.4175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ghosh K, Van Duyne GD. Cre-loxP biochemistry. Methods. 2002;28:374–383. doi: 10.1016/s1046-2023(02)00244-x. [DOI] [PubMed] [Google Scholar]
- 18.Hoess RH, Wierzbicki A, Abremski K. The role of the loxP spacer region in P1 site-specific recombination. Nucleic Acids Res. 1986;14:2287–2300. doi: 10.1093/nar/14.5.2287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Grainge I, Pathania S, Vologodskii A, Harshey RM, Jayaram M. Symmetric DNA sites are functionally asymmetric within Flp and Cre site-specific DNA recombination synapses. J. Mol. Biol. 2002;320:515–527. doi: 10.1016/s0022-2836(02)00517-x. [DOI] [PubMed] [Google Scholar]
- 20.Guo F, Gopaul DN, van Duyne GD. Structure of Cre recombinase complexed with DNA in a site-specific recombination synapse. Nature. 1997;389:40–46. doi: 10.1038/37925. [DOI] [PubMed] [Google Scholar]
- 21.Guo F, Gopaul DN, Van Duyne GD. Asymmetric DNA bending in the Cre-loxP site-specific recombination synapse. Proc. Natl Acad. Sci. USA. 1999;96:7143–7148. doi: 10.1073/pnas.96.13.7143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ennifar E, Meyer JE, Buchholz F, Stewart AF, Suck D. Crystal structure of a wild-type Cre recombinase-loxP synapse reveals a novel spacer conformation suggesting an alternative mechanism for DNA cleavage activation. Nucleic Acids Res. 2003;31:5449–5460. doi: 10.1093/nar/gkg732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chen Y, Narendra U, Iype EL, Cox MM, Rice AP. Crystal structure of a Flp recombinase-Holliday junction complex: assembly of an active oligomer by helix swapping. Mol. Cell. 2000;6:885–897. [PubMed] [Google Scholar]
- 24.Biswas T, Aihara H, Radman-Livaja M, Filman D, Landy A, Ellenberger T. A structural basis for allosteric control of DNA recombination by lambda integrase. Nature. 2005;435:1059–1066. doi: 10.1038/nature03657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Clegg RM, Murchie AI, Zechel A, Carlberg C, Diekmann S, Lilley DM. Fluorescence resonance energy transfer analysis of the structure of the four-way DNA junction. Biochemistry. 1992;31:4846–4856. doi: 10.1021/bi00135a016. [DOI] [PubMed] [Google Scholar]
- 26.Lilley DM, Clegg RM. The structure of the four-way junction in DNA. Annu. Rev. Biophys. Biomol. Struct. 1993;22:299–328. doi: 10.1146/annurev.bb.22.060193.001503. [DOI] [PubMed] [Google Scholar]
- 27.Clegg RM, Murchie AI, Lilley DM. The solution structure of the four-way DNA junction at low-salt conditions: a fluorescence resonance energy transfer analysis. Biophys. J. 1994;66:99–109. doi: 10.1016/S0006-3495(94)80765-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cooper JP, Hagerman PJ. Gel electrophoretic analysis of the geometry of a DNA four-way junction. J. Mol. Biol. 1987;198:711–719. doi: 10.1016/0022-2836(87)90212-9. [DOI] [PubMed] [Google Scholar]
- 29.Cooper JP, Hagerman PJ. Analysis of fluorescence energy transfer in duplex and branched DNA molecules. Biochemistry. 1990;29:9261–9268. doi: 10.1021/bi00491a022. [DOI] [PubMed] [Google Scholar]
- 30.Crisona NJ, Weinberg RL, Peter BJ, Sumners DW, Cozzarelli NR. The topological mechanism of phage lambda integrase. J. Mol. Biol. 1999;289:747–775. doi: 10.1006/jmbi.1999.2771. [DOI] [PubMed] [Google Scholar]
- 31.Vetcher AA, Lushnikov AY, Navarra-Madsen J, Scharein RG, Lyubchenko YL, Darcy IK, Levene SD. DNA topology and geometry in Flp and Cre recombination. J. Mol. Biol. 2006;357:1089–1104. doi: 10.1016/j.jmb.2006.01.037. [DOI] [PubMed] [Google Scholar]
- 32.Radman-Livaja M, Biswas T, Mierke D, Landy A. Architecture of recombination intermediates visualized by in-gel FRET of lambda integrase-Holliday junction-arm DNA complexes. Proc. Natl Acad. Sci. USA. 2005;102:3913–3920. doi: 10.1073/pnas.0500844102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhang Y, Crothers DM. High-throughput approach for detection of DNA bending and flexibility based on cyclization. Proc. Natl Acad. Sci. USA. 2003;100:3161–3166. doi: 10.1073/pnas.0530189100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shore D, Langowski J, Baldwin RL. DNA flexibility studied by covalent closure of short fragments into circles. Proc. Natl Acad. Sci. USA. 1981;78:4833–4837. doi: 10.1073/pnas.78.8.4833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Crothers DM, Drak J, Kahn JD, Levene SD. DNA bending, flexibility, and helical repeat by cyclization kinetics. Methods Enzymol. 1992;212:3–29. doi: 10.1016/0076-6879(92)12003-9. [DOI] [PubMed] [Google Scholar]
- 36.Wu P, Brand L. Resonance energy transfer: methods and applications. Anal. Biochem. 1994;218:1–13. doi: 10.1006/abio.1994.1134. [DOI] [PubMed] [Google Scholar]
- 37.Chan SH, Stoddard BL, Xu SY. Natural and engineered nicking endonucleases-from cleavage mechanism to engineering of strand-specificity. Nucleic Acids Res. 2011;39:1–18. doi: 10.1093/nar/gkq742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ringrose L, Lounnas V, Ehrlich L, Buchholz F, Wade R, Stewart AF. Comparative kinetic analysis of FLP and Cre recombinases: mathematical models for DNA binding and recombination. J. Mol. Biol. 1998;284:363–384. doi: 10.1006/jmbi.1998.2149. [DOI] [PubMed] [Google Scholar]
- 39.Dale RE, Eisinger J. Intramolecular distances determined by energy transfer. Dependence on orientational freedom of donor and acceptor. Biopolymers. 1974;13:1573–1605. [Google Scholar]
- 40.Dale RE, Eisinger J, Blumberg WE. The orientational freedom of molecular probes. The orientation factor in intramolecular energy transfer. Biophys. J. 1979;26:161–193. doi: 10.1016/S0006-3495(79)85243-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ivanov V, Li M, Mizuuchi K. Impact of emission anisotropy on fluorescence spectroscopy and FRET distance measurements. Biophys. J. 2009;97:922–929. doi: 10.1016/j.bpj.2009.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Badali D, Gradinaru CC. The effect of Brownian motion of fluorescent probes on measuring nanoscale distances by Forster resonance energy transfer. J. Chem. Phys. 2011;134:225102. doi: 10.1063/1.3598109. [DOI] [PubMed] [Google Scholar]
- 43.Muschielok A, Andrecka J, Jawhari A, Bruckner F, Cramer P, Michaelis J. A nano-positioning system for macromolecular structural analysis. Nat. Methods. 2008;5:965–971. doi: 10.1038/nmeth.1259. [DOI] [PubMed] [Google Scholar]
- 44.Muschielok A, Michaelis J. Application of the nano-positioning system to the analysis of fluorescence resonance energy transfer networks. J. Phys. Chem. B. 2011;115:11927–11937. doi: 10.1021/jp2060377. [DOI] [PubMed] [Google Scholar]
- 45.Koo HS, Drak J, Rice JA, Crothers DM. Determination of the extent of DNA bending by an adenine-thymine tract. Biochemistry. 1990;29:4227–4234. doi: 10.1021/bi00469a027. [DOI] [PubMed] [Google Scholar]
- 46.Huffman KE, Levene SD. DNA-sequence asymmetry directs the alignment of recombination sites in the FLP synaptic complex. J. Mol. Biol. 1999;286:1–13. doi: 10.1006/jmbi.1998.2468. [DOI] [PubMed] [Google Scholar]
- 47.Trask DK, Muller MT. Stabilization of type I topoisomerase-DNA covalent complexes by actinomycin D. Proc. Natl Acad. Sci. USA. 1988;85:1417–1421. doi: 10.1073/pnas.85.5.1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zhang Y, McEwen AE, Crothers DM, Levene SD. Statistical-mechanical theory of DNA looping. Biophys. J. 2006;90:1903–1912. doi: 10.1529/biophysj.105.070490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yan J, Kawamura R, Marko JF. Statistics of loop formation along double helix DNAs. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005;71:061905. doi: 10.1103/PhysRevE.71.061905. [DOI] [PubMed] [Google Scholar]
- 50.Watson J, Hays FA, Ho PS. Definitions and analysis of DNA Holliday junction geometry. Nucleic Acids Res. 2004;32:3017–3027. doi: 10.1093/nar/gkh631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.McKinney SA, Freeman AD, Lilley DM, Ha T. Observing spontaneous branch migration of Holliday junctions one step at a time. Proc. Natl Acad. Sci. USA. 2005;102:5715–5720. doi: 10.1073/pnas.0409328102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.