Summary
The replay of previously stored memories during hippocampal sharp wave ripples (SWRs) is thought to support both memory retrieval and consolidation in distributed hippocampal-neocortical circuits. Replay events consist of precisely timed sequences of spikes from CA3 and CA1 neurons that are coordinated both within and across hemispheres. The mechanism of this coordination is not understood. Here we show that during SWRs in both awake and quiescent states there are transient increases in slow gamma (20-50Hz) power and synchrony across dorsal CA3 and CA1 networks of both hemispheres. These gamma oscillations entrain CA3 and CA1 spiking. Moreover, during awake SWRs, higher levels of slow gamma synchrony are predictive of higher quality replay of past experiences. Our results indicate that CA3–CA1 gamma synchronization is a central component of awake memory replay and suggest that transient gamma synchronization serves as a clocking mechanism to enable coordinated memory reactivation across the hippocampal network.
The hippocampus is essential for encoding and consolidating episodic memories (Cohen and Eichenbaum, 1993). During exploration, subsets of CA3 and CA1 neurons are active in restricted regions of an environment, the neurons’ “place fields” (O’Keefe and Dostrovsky, 1971; O’Keefe and Nadel, 1978). This internal representation of the external world develops as animals learn about new locations (Wilson and McNaughton, 1993; Frank et al., 2004) and these learned representations are replayed during sharp-wave ripple (SWR) events. These events occur during periods of awake stillness and slow wave sleep (Wilson and McNaughton, 1994; Lee and Wilson, 2002; Foster and Wilson, 2006; Karlsson and Frank, 2009). Disruption of SWRs during sleep following learning impairs subsequent performance (Girardeau et al., 2009; Ego-Stengel and Wilson, 2010) and disruptions of awake SWRs impairs spatial learning and memory-guided decision making (Jadhav et al., 2012), indicating that hippocampal reactivation plays a central important role in memory processes.
SWRs are transient population events that originate in hippocampal area CA3 (Chrobak and Buzsaki, 1994, 1996; Sullivan et al., 2011). Broad activation of neurons in CA3 is associated with the characteristic sharp-wave recorded in CA1 stratum radiatum and results in recruitment of excitatory and inhibitory neurons in CA1, generating the fast ripple (150-250Hz) oscillation (Buzsaki, 1986; Buzsaki et al., 1992; Ylinen et al., 1995; Csicsvari et al., 2000). Memory reactivation during SWRs depends on the integrity of the CA3-CA1 network (Nakashiba et al., 2009) and SWRs often occur concurrently across hemispheres (Ylinen et al., 1995), recruiting spatially distributed neural populations. The mechanisms that support coordinated memory replay across spatially distributed neural circuits remain unclear.
Rhythmic oscillations are thought to play an important role in binding distributed cell assemblies together (Singer, 1993; Lisman, 2005), raising the possibility that ripple oscillations could coordinate memory replay. However, while SWRs occur concurrently across hemispheres, ripple oscillations are not coherent between CA3 and CA1 (Csicsvari et al., 1999; Sullivan et al., 2011) or across hemispheres (Ylinen et al., 1995). Thus, the ripple oscillation itself is an unlikely mechanism to coordinate memory replay. We investigated possible mechanisms that could support the dynamic formation of coordinated CA3 and CA1 cell assemblies during SWRs. We found a transient increase in slow gamma oscillations that was coherent across regions and hemispheres and entrained spiking. Our results suggest that this gamma rhythm serves as an internal clocking mechanism to coordinate sequential reactivation across the hippocampal network.
Results
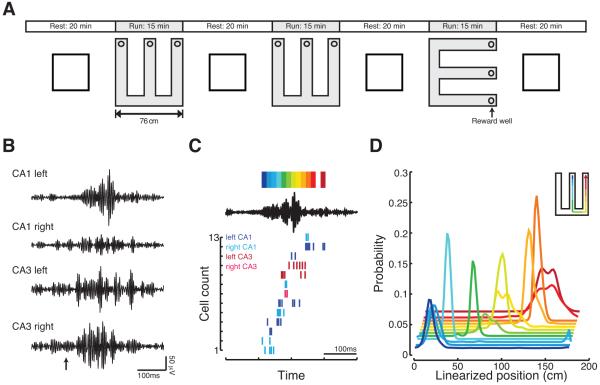
We recorded bilaterally from dorsal CA3 and CA1 stratum pyramidale in three rats as they learned a hippocampally-dependent spatial alternation task (Kim and Frank, 2009) in two initially novel W-shaped environments and during interleaved rest sessions (Karlsson and Frank, 2008, 2009) (Figure 1A; Figure S1). SWRs were detected by selecting periods when ripple power (150-250Hz) on any CA1 tetrode exceeded 3 standard deviations above the mean when animals were moving less than 4 cm/second. All results were consistent when we restricted our analyses to SWRs detected with a 5 standard deviation threshold, and CA3 and CA1 neurons were strongly phase locked to high frequency ripple oscillations recorded locally regardless of the threshold used to detect SWRs (Figure S2). Data were combined across the two W-tracks, as we observed no differences between novel and familiar environments beyond the expected increase in SWR number and amplitude during novelty (Cheng and Frank, 2008; Eschenko et al., 2008).
Figure 1.
Memory reactivation reflects the reactivation of spatially distributed neural populations. (A) Schematic of behavioral paradigm. (B) Increases in ripple power can occur concurrently across CA1 and CA3 and across hemispheres but have different structure at each recording site. Shown are filtered (150-250Hz) LFP for one SWR detected with a 6 standard deviation threshold. Arrow indicates time of SWR detection. (C) Sequential spiking of neurons during awake, remote replay of the first W-track. This SWR (same as in B) occurred when the animal was located in the second W-track. Top, the filtered (150-250Hz) LFP from left CA1 tetrode shown in B. The color bar shows the colors associated with each 15ms decoding bin. Bottom, spike rasters for all neurons with place fields in the first W-track active during the SWR. Colors indicate the region and hemisphere of each active neuron. (D) Probability distributions of decoded locations for each 15ms bin. Colors correspond to the color bar at the top of C. Inset, cartoon of the replayed trajectory. See Figures S1 and S2.
Large populations of spatially distributed neurons frequently reactivate previous experiences during SWRs. As illustrated in this example, there were concurrent increases in ripple power across spatially distributed circuits, and neurons recorded bilaterally from CA3 and CA1 were active during SWRs (Figures 1B and 1C). We used a Bayesian decoder with a uniform prior to translate the ensemble spiking of these events into probability distributions over position using place fields recorded in a previously experienced environment (Davidson et al., 2009; Karlsson and Frank, 2009) (see Experimental Procedures). In this example, the neurons with place fields near the center well fired at the beginning of the SWR whereas neurons with place fields further from the center well fired progressively later (Figure 1D; significant replay event; bootstrap resampling p<10−5). Thus, during this SWR a previously experienced behavioral trajectory was reactivated.
We consistently observed the participation of neurons from spatially distributed networks during SWRs. Across all sessions, 98% (655/667) of significant replay events included neurons from both CA1 and CA3, and 89% (589/667) included neurons from both hemispheres. As reactivation depends on the integrity of the CA3-CA1 network (Nakashiba et al., 2009) and originates within the hippocampus (Chrobak and Buzsaki, 1994, 1996; Sullivan et al., 2011), these results suggest that a spatially coherent network pattern coordinates activity across CA3 and CA1 bilaterally during SWRs.
Transient increases in slow gamma power and synchrony during awake SWRs
To determine how activity in CA3 and CA1 could be coordinated across hemispheres during SWRs we examined CA1 SWR triggered spectrograms of the local field potential (LFP) recorded in CA3 and CA1 (Figures 2A and 2B). Spectrograms were computed for 400ms before and after SWR detection using the multi-taper method (Percival and Walden, 1993; Bokil et al., 2010). As multiple SWRs can occur in trains with close temporal proximity (Davidson et al., 2009) we restricted our analysis to the first SWR of each train. Spiking during SWRs differs depending on whether the animal is awake or in a quiescent, sleep-like state (O’Neill et al., 2006; Karlsson and Frank, 2009; Dupret et al., 2010), so we examined awake and quiescent SWRs separately.
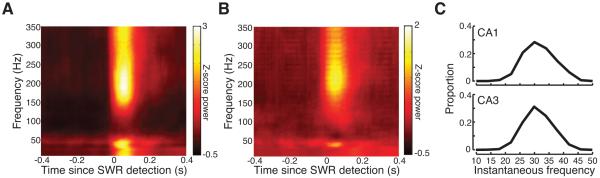
Figure 2.
Identification of a slow gamma band during SWRs. (A-B) Average SWR triggered spectrograms from (A) CA1 and (B) CA3 for one example 15-minute session on the W-track. (C) Distribution of instantaneous slow gamma frequencies shows a single peak centered at 29 Hz in both (top) CA1 and (bottom) CA3. See Figure S3.
We found that in addition to the expected increase in ripple power, there was a substantial increase in a 20-50Hz slow gamma band in both CA3 and CA1. There was also an increase low frequency power (< 20Hz) in CA1, but not in CA3 (Figure S3), likely corresponding to the sharp-wave (Buzsaki, 1986) which reflects CA3 input to CA1. To identify the slow gamma band we band-pass filtered (10-50Hz) the LFP signal during SWRs and converted the time between the peaks of the resulting signal into an estimate of instantaneous frequency. There was a unimodal distribution in both CA1 and CA3 centered at ~29Hz (Figure 2C), indicating that gamma during SWRs is unlikely to be composed of two distinct oscillators. As fewer than 2% of oscillatory cycles in the filtered 10-50 Hz signal had a frequency less than 20Hz, and as all SWRs detected had a duration >50ms, we chose to focus on 20-50Hz band to avoid conflating gamma with sharp-waves.
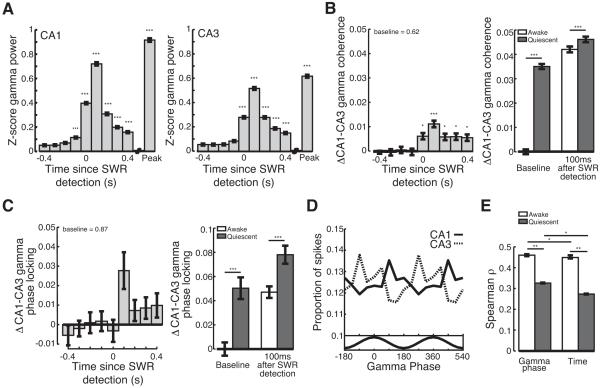
Transient increases in slow gamma power during SWRs were visible in the raw LFP traces (Figure 3A). Gamma power in both CA1 and CA3 increased substantially above baseline levels at the time of SWR detection, reached peak amplitude at the peak of the SWR, remained elevated throughout the SWR and began to decay towards baseline values after 200ms (Figure 3B; Kruskal-Wallis ANOVA, post-hoc tests; n=7653 SWRs from 74 behavioral sessions; gamma power > baseline; CA1 0-400ms, peak p<10−5; CA3 0-300ms, peak p<10−5; 400ms p<0.05; baseline = average value −450 to −400ms before SWR detection). Gamma power returned to baseline levels around the time of SWR offset (Figure S4) demonstrating that the transient increase in CA1 and CA3 gamma power is concurrent with the SWR and does not reflect a “gamma tail” (Suzuki and Smith, 1988; Bragin et al., 1995; Traub et al., 1996).
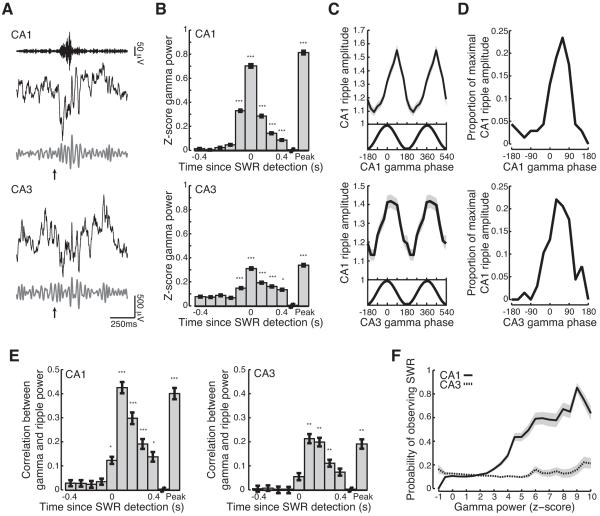
Figure 3.
Transient increase in slow gamma power during SWRs. (A) Gamma is visible in the raw LFP. Top, ripple filtered (150-250Hz) LFP recorded in CA1. Broadband (black; 1-400Hz), and slow gamma filtered (grey; 20-50Hz) LFP recorded from (top) CA1 and (bottom) CA3 for a representative SWR (same as in Figure 1B). Arrow indicates time of SWR detection. (B) Transient increase in (top) CA1 and (bottom) CA3 gamma power during SWRs. Peak is peak ripple power. All bar graphs show mean ± s.e.m. (C-D) CA1 ripple amplitude is strongly and consistently modulated by gamma phase. (C) Cross frequency coupling between slow gamma phase recorded in (top) CA1 or (bottom) CA3 and CA1 ripple amplitude for one example behavioral epoch (same session as Figures 2A and 2B). (D) Distribution of maximal CA1 ripple amplitude as a function of (top) CA1 or (bottom) CA3 slow gamma phase across all epochs. (E) Slow gamma power in (left) CA1 and (right) CA3 is correlated with CA1 ripple power on an SWR-by-SWR basis. (F) Probability of observing an SWR as a function of CA1 (solid) and CA3 (dashed) gamma power. Lines show mean, shaded regions show s.e.m. across sessions. *p<0.05; **p<0.001; ***p<10−5. See Figure S4.
We then asked how the properties of gamma and ripple oscillations covaried during SWRs. We found strong cross-frequency coupling between slow gamma phase and CA1 ripple amplitude during SWRs (Figures 3C and 3D; Rayleigh tests; relative to CA1 gamma phase p<10−5; relative to CA3 gamma phase p<10−5). CA1 ripple amplitude peaked during the early descending part of the slow gamma cycle measured in either CA1 (median angle = 50 degrees) or CA3 (median angle = 45 degrees). Thus, ripple amplitude, which is thought to reflect the activity of local inhibitory and excitatory neurons in CA1 (Buzsaki, 1986; Ylinen et al., 1995), waxes and wanes with slow gamma phase. In addition to phase-amplitude cross-frequency coupling we found strong correlations between gamma power recorded in both CA1 and CA3 and CA1 ripple power with peak correlations observed 100ms after SWR detection (Figure 3E; Kruskal-Wallis ANOVA, post-hoc tests; correlation > baseline; CA1 100-300 ms, peak p<10−5; 0, 400ms p<0.05; CA3 100-300 ms, peak p<0.001). We also noted that across all SWRs, CA1 gamma amplitude was 3.5 times greater than the ripple amplitude during SWRs (signrank test; p<10−5), demonstrating that increases in gamma power do not simply reflect temporal modulation of ripple power.
Thus, the presence of an SWR predicts a transient increase in gamma power. Next we asked whether the converse was true: are increases in gamma power predictive of the presence of an SWR? Using logistic regression, we found that gamma power in CA1 was significantly predictive of the presence of an SWR (CA1: 76% of sessions with significant GLM model p<0.05). When CA1 gamma power exceeded 5 standard deviations above its mean, there was a 50% chance that there was a concurrent SWR. This probability increased with increasing gamma power (Figure 3F). Interestingly, there was no consistent relationship between CA3 gamma power and the probability of observing an SWR (Figure 3F). These results show that gamma oscillations are a consistent feature of SWRs and they suggest that SWRs occur when CA3 gamma entrains CA1.
Does the transient increase in gamma power during SWRs reflect a neural oscillator that could promote high fidelity replay of past experience or simply a broadband power increase due to spiking activity? To address this issue we asked whether gamma was synchronized across the CA3 and CA1 networks during SWRs. We examined synchrony using two related measures, coherence and phase locking. We found a transient increase in the magnitude of CA3-CA1 gamma coherence during SWRs (Figure 4A). Across hemispheres, there was a significant increase from baseline values in CA3-CA1 gamma coherence for the 400 ms following SWR detection (Figure 4B; Kruskal-Wallis ANOVA, post-hoc tests; coherence > baseline: 0-400ms p<10−5; see also Figure S5). The transient synchronization of CA3 and CA1 during SWRs was limited to the slow gamma band. CA3-CA1 ripple coherence decreased significantly during SWRs (Figure 4C; Kruskal-Wallis ANOVA, post-hoc tests; coherence < baseline: −200, −100ms p<0.05; 0-100ms p<10−5). Furthermore, we observed no significant increase of either fast gamma (60-100Hz) (Bragin et al., 1995; Colgin et al., 2009) or “slow ripple” (100-130Hz) (Csicsvari et al., 1999) coherence, suggesting that slow gamma oscillations are uniquely suited to bind spatially distributed networks during SWRs (Figure S5).
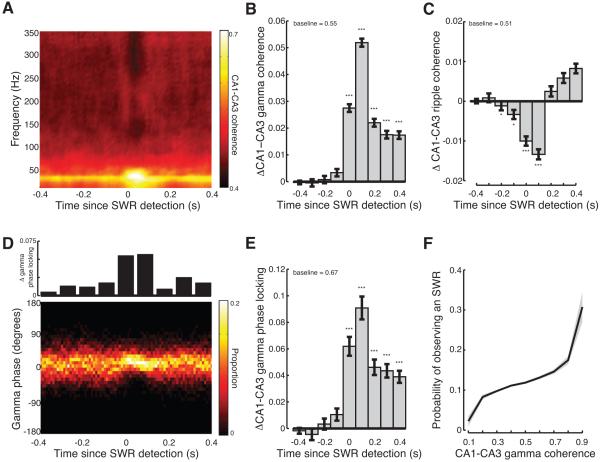
Figure 4.
Transient increase in CA3-CA1 gamma synchrony during SWRs. (A) Average magnitude of CA3-CA1 coherence relative to SWR detection for one example behavioral epoch (same session as Figures 2A and 2B). (B) Transient increase in CA3-CA1 gamma coherence across hemispheres during SWRs. Average baseline shown at top. (C) Transient decrease in CA3-CA1 ripple coherence across hemispheres during SWRs. (D) Distribution of phase offsets between CA3-CA1 gamma oscillations relative to SWR detection for one example behavioral epoch (same session as in A). Top, change in gamma phase locking from baseline. (E) Transient increase in CA3-CA1 gamma phase locking across hemispheres during SWRs. (F) Probability of observing an SWR as a function of CA1-CA3 gamma coherence. Lines show mean, shaded regions show s.e.m. across sessions. *p<0.05; **p<0.001; ***p<10−5. See Figure S5.
We next asked whether gamma oscillations during SWRs became phase locked between CA3 and CA1. Phase locking describes the extent to which the phase offsets are consistent across SWRs (see Experimental Procedures). To compute phase locking we measured the distribution of gamma phase offsets recorded in CA3 and CA1 as a function of time since SWR detection. A uniform distribution of phase offsets would have a phase locking value of 0 whereas phase locking would be 1 if there was always the same phase offset between CA3 and CA1 gamma oscillations for each SWR. As shown for an example session, the distribution of CA3 and CA1 phase offsets sharpened at the time of SWR detection and peaked ~75ms after SWR detection (Figure 4D). Across sessions there was a significant increase in gamma phase locking between CA3 and contralateral CA1 for the 400ms following SWR detection (Figure 4E; Kruskal-Wallis ANOVA, post-hoc tests; phase locking > baseline: 0-400ms p<10−5; see also Figure S5). The increase in gamma phase locking is unlikely to be due to volume conduction across hemispheres as the power of high frequency oscillations decays rapidly as a function of distance from the source (Katzner et al., 2009). These findings demonstrate that during SWRs, gamma oscillations are transiently synchronized across the spatially distributed hippocampal network.
Increases in gamma synchrony could not be attributed to decreases in measurement error associated with the transient increase in slow gamma power during SWRs. To control for this possibility we identified 200ms windows where CA1 gamma power was associated with a 40-60% chance of SWRs (Figure 3F). Coherence magnitude and phase locking were higher when an SWR was present when comparing gamma-power matched times (rank-sum tests, 2228 SWR periods, 16608 non-SWR periods; gamma power matched coherence during SWRs, 0.73±0.01 > no SWRs, 0.69±0.01 p<10−5; gamma power matched phase locking during SWRs, 0.91±0.03 > no SWR, 0.84±0.03 p<0.05). Thus increases in gamma power alone cannot account for the greater gamma coherence and phase locking we observe during SWRs.
These results demonstrate that gamma oscillations in CA3 and CA1 become transiently synchronized during SWRs. Next we asked whether gamma synchronization of CA3 and CA1 was predictive of the presence of an SWR. We found that CA3-CA1 gamma coherence was significantly predictive of the presence of an SWR (60% of sessions with significant GLM p<0.05). When CA3-CA1 gamma coherence exceeded 0.5, there was a ~10% chance that there was a concurrent SWR and this probability increased with increasing gamma power (Figure 4F).
Slow gamma modulates spiking during awake SWRs
If CA3-CA1 gamma coupling contributes to the ordered replay of past experiences then gamma oscillations should modulate spiking during SWRs. We examined spiking for CA3 (n=9,854 spikes from 312 neurons) and CA1 (n=12,720 spikes from 292 neurons) separately as a function of gamma recorded on a representative CA3 tetrode (see Experimental Procedures). As individual neurons fired sparsely during SWRs, spikes were pooled across all putative excitatory neurons. We found that spiking in both CA1 and CA3 was phase locked to CA3 gamma oscillations during SWRs (Figure 5A; Rayleigh tests; CA1 p<10−5; CA3 p<0.001). CA3 neurons fired preferentially near the peak of CA3 gamma (mean angle = 15 degrees) whereas CA1 neurons fired preferentially on the falling phase (mean angle = 112 degrees), a quarter of a cycle later. CA3 firing occurred significantly before CA1 (permutation test; p<0.001), at a timescale consistent with a monosynaptic delay of 5-10ms.
Figure 5.
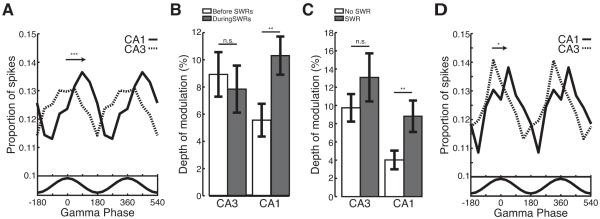
Gamma oscillations during SWRs entrain spiking in CA3 and CA1. (A) CA3 gamma oscillations modulate spiking in CA3 (dashed) and CA1 (solid). Arrow denotes difference in CA3 and CA1 mean phase. Bottom, average filtered gamma trace. (B) CA1, but not CA3, shows an increase in modulation depth during SWRs (grey) relative to the 500ms preceding (white). (C) Modulation depth during gamma power matched times with (grey) and without (white) an SWRs. (D) CA3 gamma oscillations modulate the first spike fired by CA3 (dashed) and CA1 (solid) neurons. Arrow denotes difference in CA3 and CA1 mean phase. Bottom, average filtered gamma trace. *p<0.05; **p<0.001; ***p<10−5.
We then asked whether the transient increase in gamma power and coupling we observed during SWRs was associated with a transient increase in gamma modulation of spiking. We found that CA1 spiking showed twice as much modulation by CA3 gamma during SWRs as compared to the preceding 500ms (Figure 5B; bootstrap re-sampling; depth of modulation during SWRs > preceding p<0.001). Interestingly, there was no change in the depth of modulation for CA3. The increase in modulation during SWRs for CA1 was also observed when we examined CA1 spiking relative to gamma oscillations recorded on the local tetrode (bootstrap resampling; depth of modulation during SWRs, 8% > preceding, 3% p<0.01).
The transient increase in CA1 gamma modulation during SWRs could not be explained by increases in gamma power alone. We compared the depth of modulation for spikes occurring during gamma-power matched times with and without an SWR. The depth of the gamma modulation in CA1 was twice as large when an SWR was present as compared to gamma-power matched times without an SWR (Figure 5C; bootstrap resampling; depth of modulation during SWRs, 8% > no SWRs, 4% p<0.001). There was no significant change in the depth of modulation for CA3 (Figure 5C; bootstrap re-sampling; depth of modulation during SWRs, 12% > no SWRs, 10% p>0.2). These results indicate that during SWRs there is a transient increase in gamma coupling between CA3 and CA1 and this synchrony between regions entrains spiking in hippocampal output area CA1. These results are particularly striking as previous work reported minimal modulation of CA1 spiking by CA3 gamma outside of SWRs (Csicsvari et al., 2003).
During SWRs, neurons in CA3 and CA1 frequently fire in the context of multi-spike bursts (Buzsaki, 1986; Csicsvari et al., 2000), suggesting that gamma may modulate the onset of bursting. Gamma modulation was even more pronounced in CA3 when we restricted our analysis to the first spike fired by a neuron during each SWR (Figure 5D; n=4,889 spikes from 312 neurons; Rayleigh test; mean angle = −5 degrees p<0.01; bootstrap re-sampling; depth of modulation first spike, 12% > all spikes, 8% p<0.05). The first spikes of CA1 neurons (n=5,620 spikes from 292 neurons) were also significantly phase locked, with spikes most likely to occur within a quarter cycle of the CA3 peak (Rayleigh test; mean angle = 54 degrees p<0.01). The preferred phases of firing for the first spikes emitted by CA3 and CA1 neurons were no different than the phase of firing observed in the 500ms preceding SWRs (permutation test; phase of firing before SWRs vs. first spike during SWRs; CA1 p>0.5; CA3 p>0.1). These results suggest that gamma oscillations modulate the onset of bursting in CA3, which in turn drives bursting in CA1.
Slow gamma could coordinate reactivation of stored memories
The reactivation of sequences of place cells that encode previous experiences is an important feature of SWR activity (Lee and Wilson, 2002; Foster and Wilson, 2006; Karlsson and Frank, 2009). As experimentalists, we can decode memory replay by imposing an external clock and dividing each replay event into fixed sized bins. However, the hippocampus does not have access to this external clock, so the mechanisms that coordinate memory replay must reflect internal processes that maintain precisely timed sequential neural activity across hundreds of milliseconds.
We hypothesized that gamma oscillations during SWRs serve as an internal clocking mechanism to bind distributed cell assemblies together and pace the sequential reactivation of stored memories. If gamma oscillations serve as an internal clock to coordinate replay, then two conditions must be met. First, given that we can decode replay events using a precise external clock, the variability in gamma frequency (Atallah and Scanziani, 2009) must be relatively small. Indeed, we found that there was a strong correlation between the relative timing of spikes as measured by an external clock or by the phase of gamma (Figure 6A; Spearman correlation, ρ=0.98). Second, when gamma is less well correlated with the external clock, as occurs with longer time lags, gamma oscillations should describe the sequential structure of neural activity during SWRs as well or better than an external clock.
Figure 6.
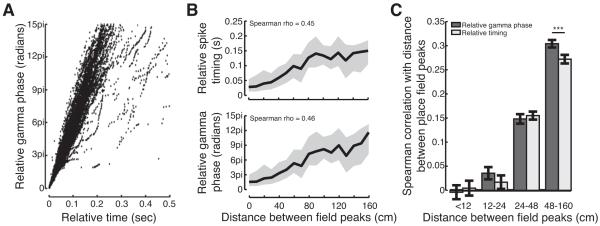
Slow gamma oscillations could provide an internal clock for memory reactivation. (A) Relative timing and relative gamma phase are strongly correlated. Each point represents the inter-spike time or phase interval between pairs of cells that fired during SWRs. (B) The relative (top) timing and (bottom) gamma phases of spikes fired by neurons during SWRs is related to the distances between their place fields. Lines show means, shaded regions show interquartile ranges. (C) Correlation between place field distance and relative gamma phase or spike timing varies as a function of distance between place field peaks. ***p<10−5.
We therefore asked whether gamma oscillations provide a consistent internal clock for replay events. During memory reactivation, pairs of cells that have place fields close together in space fire in close temporal proximity whereas pairs of cells that have place fields far apart fire at longer intervals (Figure 6B)(Karlsson and Frank, 2009). Thus, a key test of our hypothesis is that the temporal separation between spikes during SWRs, measured as a function of gamma phase, should be predictive of the distances between the cells’ place fields, and that this relationship should be as good as or better than the relationship for externally defined time. Consistent with this possibility, when we examined pair-wise reactivation of a previously experienced environment we found that distance between place field peaks was slightly more correlated with relative gamma phase, measured across multiple cycles, than relative spike timing (Figure 6B; bootstrap re-sampling; Spearman ρ gamma = 0.46 > Spearman ρ time = 0.45 p<0.05).
Internally measured gamma and externally defined times become less correlated at long time lags, so differences in gamma and externally defined time are most apparent for reactivation of neurons with place fields far apart in space. We divided cell pairs into four equally sized groups based on distance between place cell peaks and found that relative gamma phase was more strongly correlated with distance than the relative time of spikes as measured by an external clock for cell pairs with place fields farthest apart (Figure 6C; bootstrap re-sampling; Spearman ρ gamma > time; p<10−5). The low correlations for nearby place fields (<24cm apart) may result from gamma modulation of spiking as during SWRs nearby place cells fired on the same gamma cycle 75% of the time. These results indicate that gamma is slightly better than an external, experimenter-defined clock and could serve to pace the coordinated reactivation of neurons during SWRs. Given that a gamma-based clock is available to the hippocampal network but the external, experimenter-defined clock is not, these results strongly suggest that the mechanisms that give rise to gamma rhythms regulate the sequential replay of past experience during SWRs.
Next we asked whether the strength of gamma synchrony was related to the presence of sequential replay. We reasoned greater gamma synchronization of the CA3 and CA1 network during SWRs would result in enhanced coordinated sequential reactivation across the spatially distributed network. We used a Bayesian decoder to assess the quality of sequential replay during SWRs. We computed two related measures: R2 which is a goodness-of-fit measure of the relationship between the temporal order of firing in the SWR and the associated decoded position in space, and a p-value which assesses the likelihood of observing the R2 value given the observed spikes (Figure S6) (Davidson et al., 2009; Karlsson and Frank, 2009).
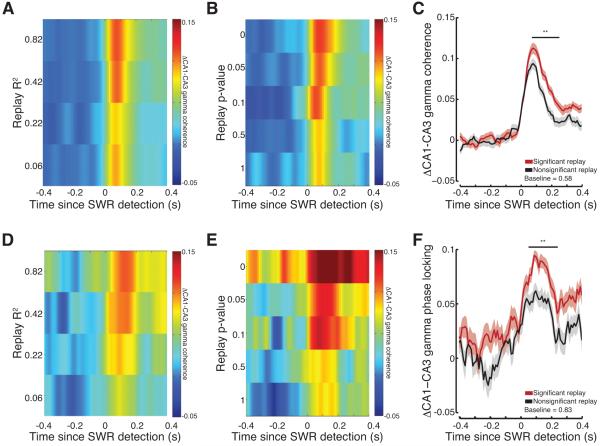
CA3-CA1 gamma coherence varied as a function of replay quality, with high quality (higher R2; Figure 7A) and more significant (lower p-value; Figure 7B) replay events displaying the strongest levels of gamma coherence following SWR detection. The magnitude and the duration of gamma coherence appeared to decrease for lower quality (lower R2) and less significant replay events (higher p-value). We then compared CA3-CA1 gamma coherence for significant (p<0.05; n=454 SWRs) and non-significant (p>0.05; n=477 SWRs) candidate SWRs. Gamma coherence was significantly greater for significant as compared to non-significant candidate SWRs for the 50-300ms following SWR detection (Figure 7C; permutation test; significant > non-significant p<0.001). Similarly, increases in CA3-CA1 gamma phase locking were predictive of the quality of memory replay. Highly significant replay events showed the largest increase in phase locking for the longest duration. In contrast, less sequential and non-significant candidate events showed the smallest increase in phase locking for the shortest duration (Figures 7D and 7E). CA3-CA1 gamma phase locking was significantly different for significant and non-significant candidate SWRs for the 50-250ms after SWR detection (Figure 7F; permutation test; significant > non-significant p<0.001).
Figure 7.
Significant memory replay is associated with stronger CA3-CA1 gamma synchrony. (A-B) CA3-CA1 gamma coherence varies as a function of replay (A) R2 and (B) p-value. (C) Gamma coherence for significant (red) as compared to non-significant (black) candidate events. Lines show means, shaded regions show s.e.m. across candidate events, line at top denotes significant differences. Average baseline shown at bottom. (D-E) CA3-CA1 gamma phase locking varies as a function of replay (D) R2 and (E) p-value. (F) Gamma phase locking for significant as compared to non-significant candidate events. **p<0.001. See Figure S6 and S7.
The increase in gamma coherence and phase locking observed for significant as compared to non-significant SWRs persisted when we controlled for gamma power, SWR magnitude, SWR duration, the number of spikes in each event and the number of cells participating in each event (Figure S7). Finally, we noted that awake replay has been reported both during SWRs (Foster and Wilson, 2006; Diba and Buzsaki, 2007; Davidson et al., 2009; Karlsson and Frank, 2009; Gupta et al., 2010) and during periods associated with theta rhythmicity (Johnson and Redish, 2007), which occurs during attentive behaviors and movement. We therefore asked whether the events we examined included a subset with high theta power, as might be expected if there were two distinct types of replay events. As theta is thought to reflect a relatively long duration state of hippocampal information processing and the sharp-wave in each SWR has power in the 6-12 Hz theta band (Buzsaki, 1986), we examined theta power during the 400ms before SWR detection. There was a unimodal distribution of theta power during this period, suggesting that all of the events we examined occurred in a similar network state (Figure S7). Finally, neither theta power nor theta coherence in the 400 ms before each SWR was related to replay quality (Spearman correlation; replay p-value vs. theta power; CA1: ρ= −0.06, p>0.1; CA3: ρ=0.01, p>0.5; replay p-value vs. theta coherence; ρ= −0.03, p >0.4).
Slow gamma oscillations during quiescent SWRs
SWRs are prevalent during slow wave sleep and when animals are at rest. We have previously shown that reactivation occurring during quiescent SWRs tends to be a less faithful recapitulation of stored memories than activity during awake SWRs (Karlsson and Frank, 2009). We therefore asked how gamma oscillations during quiescent SWRs, defined as SWRs that occurred in the rest box when animals had been still for >60s, differed from gamma seen during awake SWRs. Quiescent SWRs were accompanied by transient increases in gamma power in CA1 and CA3 (Figure 8A; Kruskal-Wallis ANOVA, post-hoc tests; power > baseline; CA1: −100 - 400ms, peak p<10−5; CA3: 0-400ms, peak p<10−5). Furthermore, gamma power in both CA1 and CA3 was significantly predictive of the presence of an SWR during rest sessions (Figure S8). There was a small but significant increase in CA3-CA1 gamma coherence during quiescent SWRs (Figure 8B; Kruskal-Wallis ANOVA, post-hoc tests; coherence > baseline; 100ms p<10−5; 0, 200-400ms p<0.05) that was significantly predictive of SWR occurrence (Figure S8), but there was no consistent increase in gamma phase locking (Figure 8C).
Figure 8.
Slow gamma during quiescent SWRs. (A) Transient increase in (left) CA1 and (right) CA3 gamma power during quiescent SWRs. Peak is peak ripple power. (B-C) CA3-CA1 gamma (B) coherence and (C) phase locking during quiescent SWRs. Average baseline value shown at top. Right, awake (white) and quiescent (grey) gamma (B) coherence and (C) phase locking during baseline and 100ms following SWR detection relative to mean awake baseline levels. (D) Gamma modulates spiking in CA3 (dashed) and CA1 (solid) during quiescent SWRs. Bottom, average filtered gamma trace. (E) Correlation between place field distance and relative gamma phase or spike timing for awake (white) and quiescent (grey) SWRs. *p<0.05; **p< 0.001; ***p<10−5. See Figure S8.
The smaller increase in gamma synchrony during quiescent SWRs could be explained in large part by an increase in baseline synchrony during quiescence. The baseline gamma coherence and phase locking were higher during quiescent SWRs (Figures 8B and 8C; rank sum test; baseline quiescent > awake; coherence p<10−5; phase locking p<10−5). Furthermore, while gamma synchrony reached a slightly higher level during quiescent SWRs as compared to awake SWRs (Figures 8B and 8C; rank sum tests; quiescent > awake 100ms following SWR; coherence p<10−5; phase locking p<10−5), the higher baseline synchrony means that SWR associated increases reflected a smaller change than seen during awake periods.
Gamma modulation of spiking and replay during quiescent SWRs
Do gamma oscillations clock the replay of previous experiences when animals are at rest? The spiking of putative excitatory neurons in both CA1 (n=11,794 spikes from 375 neurons) and CA3 (n=8,249 spikes from 391 neurons) was significantly phase locked to gamma oscillations during quiescent SWRs (Figure 8D; Rayleigh tests; CA1 p<0.01; CA3 p<0.01). However, there was less modulation of CA1 and CA3 spiking during quiescent SWRs as compared to awake SWRs (bootstrap re-sampling; CA1 p<0.01; CA3 p<0.05). Furthermore, there was no significant difference in the modulation of either CA3 or CA1 spiking during SWRs as compared to the 500ms preceding SWR detection. Thus, although CA3 gamma oscillations modulate CA3 and CA1 spiking throughout quiescent states, gamma modulation during quiescence is never as large as observed during awake SWRs.
We then asked whether gamma could serve as an internal clock for quiescent memory replay. As previously reported (Karlsson and Frank, 2009), we found lower correlations between place field location and relative spike timing during quiescent SWRs than observed during waking SWRs (Figure 8E; permutation test; Spearman ρ awake > quiescent p<0.001). Nonetheless, relative gamma phase was more correlated with distance between place field peaks than the relative spike timing (Figure 8E; bootstrap re-sampling; Spearman ρ = gamma > time p<0.05). Thus, as we observed for awake SWRs, gamma oscillations during quiescent SWRs coherently modulates the hippocampal circuit and could act as an internal clock to synchronize the replay of stored memories. Finally we asked whether the strength of gamma synchrony during quiescent SWRs in the rest session was correlated with the presence of replay. In contrast to our results for awake SWRs, we found no significant relationship between the increase in gamma synchrony during quiescent SWRs and the presence of significant replay (permutation test; significant > non-significant SWRs; coherence, p>0.2; phase locking, p>0.2). This may be a result of the smaller increases in gamma synchrony during quiescent SWRs and the overall lower fidelity of quiescent replay.
Discussion
We examined SWRs in awake and quiescent states and found a prominent and consistent increase in slow gamma power. During SWRs, gamma oscillations in CA3 and CA1 became more coherent both within and across hemispheres, indicating a transient synchronization of the entire dorsal hippocampal network. CA3 and CA1 neurons were phase locked to a common gamma rhythm during SWRs and gamma phase was a good descriptor of pair-wise reactivation. Further, during awake SWRs, higher levels of gamma synchrony between CA3 and CA1 were associated with high fidelity replay of past experience. These results suggest that gamma oscillations maintain the temporal organization of spiking during the reactivation of stored memories in the hippocampal network.
Our results also revealed differences between awake and quiescent SWRs that may be related to the lower fidelity of replay seen during quiescence (Karlsson and Frank, 2009; Dupret et al., 2010). There were smaller increases in gamma synchrony during quiescent SWRs, a difference that could be largely attributed to the higher baseline levels of synchrony. Further, as compared to awake SWRs, spiking was less modulated by gamma oscillations during quiescent SWRs and we found no clear relationship between gamma synchrony and the fidelity of quiescent replay. These findings indicate that transitions from relatively uncoupled to highly coupled network states could be important for high fidelity memory replay.
Our results are consistent with previous studies of slow gamma oscillations occurring outside of SWRs. Theoretical work has shown that gamma rhythms are well suited to synchronize networks with relatively low conduction delays (Kopell et al., 2000). Gamma rhythms have also been shown to improve information transmission in cortical networks (Sohal et al., 2009), consistent with our observation that gamma synchrony correlates with the presence of significant awake replay. Previous studies of gamma in the hippocampus have largely focused on gamma in the context of the theta rhythm (Bragin et al., 1995; Jensen and Lisman, 1996; Chrobak and Buzsaki, 1998; Lisman and Otmakhova, 2001; Csicsvari et al., 2003; Montgomery and Buzsaki, 2007; Montgomery et al., 2008; Colgin et al., 2009). However, our results demonstrate that in addition to being present during theta, slow gamma oscillations are prominent during SWRs, which occur most often when animals are still and theta is less prevalent (Buzsaki et al., 1983). Furthermore, CA3 gamma only weakly entrains CA1 spiking during theta states (Csicsvari et al., 2003), suggesting that SWRs are a period of unusually strong coupling of these networks.
What functions could gamma oscillations support? Spiking during awake SWRs is predictive of subsequent memory performance (Dupret et al., 2010) and we have shown that awake SWRs support spatial learning and memory-guided decision-making (Jadhav et al., 2012). The strong gamma synchrony during awake memory replay provides a new connection between replay and previous studies linking gamma oscillations to memory encoding (Fell et al., 2003; Osipova et al., 2006; Jutras et al., 2009; Tort et al., 2009; Fell and Axmacher, 2011) and retrieval (Lisman and Otmakhova, 2001; Montgomery and Buzsaki, 2007). In particular, one model proposed that gamma rhythms seen during awake exploration and theta are well suited to clock the retrieval of sequential memories in the hippocampus (Lisman and Otmakhova, 2001). Consistent with that idea, more recent work has demonstrated that CA3-CA1 gamma coherence is enhanced during movement through a part of a maze where animals had to make memory-guided decisions (Montgomery and Buzsaki, 2007). Similarly, CA3 gamma is prevalent at times associated with vicarious trial and error activity (Johnson and Redish, 2007). Furthermore, the slow gamma oscillation that we found to be enhanced during SWRs has previously been shown to couple CA3 and CA1 during theta (Colgin et al., 2009). When viewed in this context, our results strongly suggest that there is a specific pattern of enhanced CA3-CA1 gamma power and synchrony that is a consistent signature of awake memory retrieval in the hippocampal network, both when animals are still and when they are exploring. Slow gamma oscillations are well suited to promote accurate retrieval of sequential memories and may also contribute to the entrainment of neurons in downstream regions such as entorhinal or prefrontal cortex (Peyrache et al., 2011).
Our findings also suggest a prominent role for fast-spiking interneurons in memory reactivation. Interneurons that express the calcium-binding protein parvalbumin play an important role in the generation of cortical and hippocampal gamma oscillations (Bartos et al., 2007; Tukker et al., 2007; Cardin et al., 2009; Sohal et al., 2009) and have also been shown to be active during SWRs in vivo (Klausberger et al., 2003). Similar mechanisms may support gamma oscillations that occur during both in the context of theta and SWRs. Intriguingly, selective suppression of parvalbumin positive interneurons in the mouse hippocampus results in a working memory deficit (Murray et al., 2011). We would predict that the synchronization of the CA3 and CA1 networks was impaired in these animals, leading to a selective deficit in their ability to generate sequential memory replay.
The link between gamma and memory replay in the hippocampus complements a broad array of studies linking enhanced gamma synchrony to information processing, object recognition, sensory processing, top-down control, and attention (Womelsdorf et al., 2007; Cardin et al., 2009; Jutras et al., 2009; Sohal et al., 2009; Fell and Axmacher, 2011). These studies showed that enhanced gamma power and synchrony are associated with better sensory processing for external stimuli. Our results link gamma to internally generated patterns of activity that can be independent of sensory input, and suggest that gamma synchrony across the hippocampus plays a central role in the coordinated reactivation of stored memories.
Experimental Procedures
Distinct analyses of the data used in this study and the associated methods have been presented previously (Karlsson and Frank, 2008, 2009).
Data collection
Three male Long-Evans rats (500-600g) were food deprived to no less than 85% of their baseline weight and pre-trained to run on a linear track for liquid reward. Animals were implanted with a microdrive containing 30 independently movable tetrodes targeting anatomically connected regions of CA3 and CA1 bilaterally (Karlsson and Frank, 2008, 2009). At the end of data collection electrolytic lesions were made and electrode locations were identified histologically.
On each recording day, animals performed two or three 15 minute run sessions in W-track environments with interleaved 20-minute rest sessions. The first W-track was introduced either 6 (n = 2) or 3 (n = 1) days before animals were introduced to the second W-track (Figure S1). Rats were rewarded for performing a continuous alternation task (Frank et al., 2000; Karlsson and Frank, 2008, 2009).
Data were collected using an NSpike system (L.M.F. and J. MacArthur, Harvard Instrumentation Design Laboratory). Following recording, the rat’s position was reconstructed from video based on the locations of infrared diodes. Spike data were recorded relative to a reference tetrode located in the corpus callosum, sampled at 30KHz, digitally filtered between 600Hz and 6KHz (2 pole Bessel for high and low pass), and threshold crossing events were saved to disk. Local field potentials were recorded relative to a ground screw located above the cerebellum, sampled at 1.5KHz, and digitally filtered between 0.5Hz and 400Hz. Individual units were identified by clustering spikes using peak amplitude and spike width (MatClust, M.P.K.).
Analysis
Analyses were carried out using custom software written in Matlab (Mathworks) and the Chronux toolbox (http://www.cronux.org). All results were consistent across individual animals. SWRs were identified on the basis of peaks in the LFP recorded from tetrodes in the CA1 stratum pyramidale. CA1 stratum pyramidale tetrodes were identified using post-mortem histology and the presence of at least 2 putative excitatory neurons. The raw LFP data was band pass filtered between 150-250Hz and the SWR envelope was calculated using the Hilbert transform and smoothed with a Gaussian (4ms standard deviation). SWR events were identified as times when the smoothed envelope exceeded 3 standard deviations above the mean for at least 15ms. The entire SWR event was defined as including times immediately before and after that prolonged threshold crossing event during which the envelope exceeded the mean (Cheng and Frank, 2008). Concurrent activity in CA1 and CA3 was extracted during these periods for analysis. Analyses of awake SWRs were restricted to when the animal was moving less than 4cm/s in either of the two W-tracks and quiescent SWRs to times when the animal was had been immobile for at least one minute in the rest box. We excluded any SWRs that occurred in a one second window following detection of another SWR so that no SWRs occurred during the baseline period.
Gamma power
SWR triggered spectrograms were computed using the multi-taper method. 100ms non-overlapping temporal bins were used to compute all spectral analyses except where noted. A z-score was computed for each frequency band using the mean and standard deviation of the power calculated across the entire behavioral session for each tetrode. For each 100ms bin, we obtained a normalized measure of power for each frequency band in units of standard deviations from the mean. For illustration in figures, power was computed using 100ms sliding windows with a 10ms step size. To quantify the increase in gamma power during SWRs, the z-scored power in the gamma band (20-50Hz) was averaged across all CA1 or CA3 tetrodes such that for each SWR there was an average z-scored gamma trace. Baseline was defined as values between 450 and 400ms before SWR detection. To compute the instantaneous frequency of slow gamma oscillations during SWRs we filtered the LFP during SWRs using a bandpass filter (10-50Hz), took the Hilbert transform, detected the peaks of the resulting signal, and took the reciprocal of the time difference between peaks. To determine the relationship between gamma phase and ripple amplitude we estimated gamma phase at each time using the Hilbert transform and asked how the ripple envelope varied as a function of gamma phase. For each session we identified the gamma phase with the maximal ripple amplitude. To compute the correlation between gamma and ripple power, we took the Spearman correlation between the average ripple power in CA1 and CA1 or CA3 gamma power for each behavioral session and compared the correlation coefficient in 100ms intervals to baseline values.
Generalized Linear Model
We used a generalized linear model with a logistic link function to determine whether gamma was predictive of the presence of an SWR. Either the average gamma power across CA1 or CA3 tetrodes or the gamma coherence between the CA1 and CA3 tetrodes with the maximum number of cells was computed across the entire behavioral session in 200ms temporal bins. For each bin we also determined whether or not an SWR was observed. Gamma power or coherence was said to predict the occurrence of an SWR for behavioral sessions with significant coefficients for the gamma regression term. To illustrate the relationship between either gamma power or coherence and the occurrence of an SWR, we binned gamma power or coherence and then computed the proportion of 200ms bins that had an SWR.
Gamma synchrony
SWR triggered coherence was computed for all CA3-CA1 tetrode pairs. To quantify the magnitude of gamma coherence during SWRs, we computed the absolute value of the average coherence in the gamma band across all CA3-CA1 tetrode pairs. To quantify gamma phase locking during SWRs, the phase of coherence for the gamma band was averaged across all CA3-CA1 tetrode pairs for each SWR. Thus, each SWR contributed a single value for each 100ms temporal bin relative to SWR detection. We combined values across SWRs to obtain a distribution of gamma phase offsets in each bin. The angular variance of this distribution was taken as a measure of phase locking for each session.
Spiking modulation by gamma oscillations
Putative interneurons were identified on the basis of spike width and average firing rate (Ranck, 1973; Fox and Ranck, 1981; Frank et al., 2000) and were excluded from all analyses. Gamma phase was measured on the CA3 tetrode with the largest number of isolated cells by band pass filtering (20-50Hz) the local field potential, performing the Hilbert transform on the filtered signal, and extracting the phase component. Spikes that occurred during an SWR were identified and the gamma phase at the time of the spike was assigned. Spikes were pooled across neurons recorded in each region. The depth of modulation was defined as the difference between the peak and the trough of the spiking distribution divided by the sum of the peak and the trough of the spiking distribution.
Pair-wise reactivation
As in our previous work (Karlsson and Frank, 2009), for every pair of place fields we measured the linear distance between the place field peaks as the shortest path between the peak firing rate locations. We also measured the absolute value of both the time and gamma phase from each reference spike for one cell to all spikes from the other cell. For this analysis, gamma phase was measured on the CA3 tetrode with the most cells. Note that the pairs of spikes were often compared across multiple cycles of gamma. In the large majority of cases the Hilbert Transform yielded a continuous estimate of phase throughout the entire SWR. In the rare cases where there was a phase slip, we held phase constant throughout the slip. We then computed the Spearman’s correlation between linear distance and either relative spike timing or gamma phase to determine how strongly these measures co-varied. To determine the relationship between place field distance and correlation with gamma phase and spike timing, we divided the data into roughly four equally sized groups based on the distance between place field peaks. We then computed the Spearman’s correlation between linear distance and either relative spike timing or gamma phase for each group. For quiescent SWRs, we used place fields recorded during the preceding behavioral session for pair-wise decoding.
Decoding
To measure place field locations, we calculated an occupancy-normalized linearized place field for each cell using 2-cm bins and smoothed with a 4-cm standard deviation Gaussian curve. SWRs were excluded. A peak rate of 3Hz or greater was required for a cell to be considered a place cell. Candidate replay events were defined as SWRs during which at least five place cells fired at least one spike each. We determined the sequential representation of position during a candidate replay event using a simple Bayesian decoder that has been described in detail before (Karlsson and Frank, 2009). Briefly, each event was divided into 15ms bins and for each bin with at least one spike we calculated the spatial probability distribution using an uninformative prior.
To determine whether the temporal sequence of decoded spatial probability distributions was a significant memory replay we compared the regression of spatial locations with temporal bin to 10,000 regressions in which the order of the bins was shuffled. The P value for each candidate event was defined as the proportion of the shuffled R2 values that was greater than the R2 value of the actual event, and an event with p<0.05 was considered to be significant. Decoding was done with templates for both the animal’s current W-track and where applicable, the previously experienced W-track environment, in order to minimize false negatives.
The R2 and the p-value are correlated measures (Spearman ρ = −0.78). We focused on the p-value measurement to quantify the improvement in coherence associated with significant replay events, although our results were similar when examined as a function of R2 values. To ask how gamma phase locking and coherence varied as a function of replay significance, we computed the phase locking and average coherence across significant and non-significant events. We used a permutation test to determine when the difference between significant and non-significant candidate events was significant. We compared the measured difference to the difference computed on 1,000 permutations of the p-value associated with each candidate event.
Supplementary Material
Acknowledgments
We thank members of the Frank laboratory, V. Sohal, S. Leutgeb, P. Janak, M. Brainard, and P. Sabes for comments on the manuscript. This work was supported by an NSF graduate research fellowship to M.F.C., the John Merck Scholars Program, and the U.S. National Institutes of Health research grants RO1MH080283, RO1MH090188, and F31093067.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Atallah BV, Scanziani M. Instantaneous modulation of gamma oscillation frequency by balancing excitation with inhibition. Neuron. 2009;62:566–577. doi: 10.1016/j.neuron.2009.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat Rev Neurosci. 2007;8:45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
- Bokil H, Andrews P, Kulkarni JE, Mehta S, Mitra PP. Chronux: a platform for analyzing neural signals. J Neurosci Methods. 2010;192:146–151. doi: 10.1016/j.jneumeth.2010.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bragin A, Jando G, Nadasdy Z, Hetke J, Wise K, Buzsaki G. Gamma (40-100 Hz) oscillation in the hippocampus of the behaving rat. Journal of Neuroscience. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G. Hippocampal sharp waves: their origin and significance. Brain Res. 1986;398:242–252. doi: 10.1016/0006-8993(86)91483-6. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Horvath Z, Urioste R, Hetke J, Wise K. High-frequency network oscillation in the hippocampus. Science. 1992;256:1025–1027. doi: 10.1126/science.1589772. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Leung LW, Vanderwolf CH. Cellular bases of hippocampal EEG in the behaving rat. Brain Res. 1983;287:139–171. doi: 10.1016/0165-0173(83)90037-1. [DOI] [PubMed] [Google Scholar]
- Cardin JA, Carlen M, Meletis K, Knoblich U, Zhang F, Deisseroth K, Tsai LH, Moore CI. Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature. 2009;459:663–667. doi: 10.1038/nature08002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng S, Frank LM. New experiences enhance coordinated neural activity in the hippocampus. Neuron. 2008;57:303–313. doi: 10.1016/j.neuron.2007.11.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chrobak JJ, Buzsaki G. Selective activation of deep layer (V-VI) retrohippocampal cortical neurons during hippocampal sharp waves in the behaving rat. Journal of Neuroscience. 1994;14:6160–6170. doi: 10.1523/JNEUROSCI.14-10-06160.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chrobak JJ, Buzsaki G. High-frequency oscillations in the output networks of the hippocampal-entorhinal axis of the freely behaving rat. Journal of Neuroscience. 1996;16:3056–3066. doi: 10.1523/JNEUROSCI.16-09-03056.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chrobak JJ, Buzsaki G. Gamma oscillations in the entorhinal cortex of the freely behaving rat. Journal of Neuroscience. 1998;18:388–398. doi: 10.1523/JNEUROSCI.18-01-00388.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen NJ, Eichenbaum H. Memory, Amnesia, and the Hippocampal System. M.I.T. Press; Cambridge, MA: 1993. [Google Scholar]
- Colgin LL, Denninger T, Fyhn M, Hafting T, Bonnevie T, Jensen O, Moser MB, Moser EI. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;19:462, 353–357. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
- Csicsvari J, Hirase H, Czurko A, Mamiya A, Buzsaki G. Fast Network Oscillations in the Hippocampal CA1 Region of the Behaving Rat. Journal of Neuroscience. 1999;19:RC20. doi: 10.1523/JNEUROSCI.19-16-j0001.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csicsvari J, Hirase H, Mamiya A, Buzsaki G. Ensemble patterns of hippocampal CA3-CA1 neurons during sharp wave-associated population events. Neuron. 2000;28:585–594. doi: 10.1016/s0896-6273(00)00135-5. [DOI] [PubMed] [Google Scholar]
- Csicsvari J, Jamieson B, Wise KD, Buzsaki G. Mechanisms of gamma oscillations in the hippocampus of the behaving rat. Neuron. 2003;37:311–322. doi: 10.1016/s0896-6273(02)01169-8. [DOI] [PubMed] [Google Scholar]
- Davidson TJ, Kloosterman F, Wilson MA. Hippocampal replay of extended experience. Neuron. 2009;63:497–507. doi: 10.1016/j.neuron.2009.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diba K, Buzsaki G. Forward and reverse hippocampal place-cell sequences during ripples. Nat.Neurosci. 2007;10:1241–1242. doi: 10.1038/nn1961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupret D, O’Neill J, Pleydell-Bouverie B, Csicsvari J. The reorganization and reactivation of hippocampal maps predict spatial memory performance. Nat.Neurosci. 2010;13:995–1002. doi: 10.1038/nn.2599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ego-Stengel V, Wilson MA. Disruption of ripple-associated hippocampal activity during rest impairs spatial learning in the rat. Hippocampus. 2010;20:1–10. doi: 10.1002/hipo.20707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eschenko O, Ramadan W, Molle M, Born J, Sara SJ. Sustained increase in hippocampal sharp-wave ripple activity during slow-wave sleep after learning. Learn.Mem. 2008;15:222–228. doi: 10.1101/lm.726008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fell J, Axmacher N. The role of phase synchronization in memory processes. Nat Rev Neurosci. 2011;12:105–118. doi: 10.1038/nrn2979. [DOI] [PubMed] [Google Scholar]
- Fell J, Klaver P, Elfadil H, Schaller C, Elger CE, Fernandez G. Rhinal-hippocampal theta coherence during declarative memory formation: interaction with gamma synchronization? Eur J Neurosci. 2003;17:1082–1088. doi: 10.1046/j.1460-9568.2003.02522.x. [DOI] [PubMed] [Google Scholar]
- Foster DJ, Wilson MA. Reverse replay of behavioural sequences in hippocampal place cells during the awake state. Nature. 2006;440:680–683. doi: 10.1038/nature04587. [DOI] [PubMed] [Google Scholar]
- Fox SE, Ranck JB., Jr. Electrophysiological characteristics of hippocampal complex-spike cells and theta cells. Exp.Brain Res. 1981;41:399–410. doi: 10.1007/BF00238898. [DOI] [PubMed] [Google Scholar]
- Frank LM, Brown EN, Wilson MA. Trajectory encoding in the hippocampus and entorhinal cortex. Neuron. 2000;27:169–178. doi: 10.1016/s0896-6273(00)00018-0. [DOI] [PubMed] [Google Scholar]
- Frank LM, Stanley GB, Brown EN. Hippocampal plasticity across multiple days of exposure to novel environments. Journal of Neuroscience. 2004;24:7681–7689. doi: 10.1523/JNEUROSCI.1958-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girardeau G, Benchenane K, Wiener SI, Buzsaki G, Zugaro MB. Selective suppression of hippocampal ripples impairs spatial memory. Nat.Neurosci. 2009;12:1222–1223. doi: 10.1038/nn.2384. [DOI] [PubMed] [Google Scholar]
- Gupta AS, van der Meer MA, Touretzky DS, Redish AD. Hippocampal replay is not a simple function of experience. Neuron. 2010;65:695–705. doi: 10.1016/j.neuron.2010.01.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jadhav SP, Kemere C, German PW, Frank LM. Awake Hippocampal Sharp-Wave Ripples Support Spatial Memory. Science. 2012 doi: 10.1126/science.1217230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen O, Lisman JE. Theta/gamma networks with slow NMDA channels learn sequences and encode episodic memory: role of NMDA channels in recall. Learn.Mem. 1996;3:264–278. doi: 10.1101/lm.3.2-3.264. [DOI] [PubMed] [Google Scholar]
- Johnson A, Redish AD. Neural ensembles in CA3 transiently encode paths forward of the animal at a decision point. Journal of Neuroscience. 2007;27:12176–12189. doi: 10.1523/JNEUROSCI.3761-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jutras MJ, Fries P, Buffalo EA. Gamma-band synchronization in the macaque hippocampus and memory formation. Journal of Neuroscience. 2009;29:12521–12531. doi: 10.1523/JNEUROSCI.0640-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlsson MP, Frank LM. Network Dynamics Underlying the Formation of Sparse, Informative Representations in the Hippocampus. Journal of Neuroscience. 2008;28:14271–14281. doi: 10.1523/JNEUROSCI.4261-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlsson MP, Frank LM. Awake replay of remote experiences in the hippocampus. Nat.Neurosci. 2009;12:913–918. doi: 10.1038/nn.2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzner S, Nauhaus I, Benucci A, Bonin V, Ringach DL, Carandini M. Local origin of field potentials in visual cortex. Neuron. 2009;61:35–41. doi: 10.1016/j.neuron.2008.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SM, Frank LM. Hippocampal lesions impair rapid learning of a continuous spatial alternation task. PLoS.ONE. 2009;4:e5494. doi: 10.1371/journal.pone.0005494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klausberger T, Magill PJ, Marton LF, Roberts JD, Cobden PM, Buzsaki G, Somogyi P. Brain-state- and cell-type-specific firing of hippocampal interneurons in vivo. Nature. 2003;20:421, 844–848. doi: 10.1038/nature01374. [DOI] [PubMed] [Google Scholar]
- Kopell N, Ermentrout GB, Whittington MA, Traub RD. Gamma rhythms and beta rhythms have different synchronization properties. Proc Natl Acad Sci U S A. 2000;97:1867–1872. doi: 10.1073/pnas.97.4.1867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee AK, Wilson MA. Memory of sequential experience in the hippocampus during slow wave sleep. Neuron. 2002;36:1183–1194. doi: 10.1016/s0896-6273(02)01096-6. [DOI] [PubMed] [Google Scholar]
- Lisman J. The theta/gamma discrete phase code occuring during the hippocampal phase precession may be a more general brain coding scheme. Hippocampus. 2005;15:913–922. doi: 10.1002/hipo.20121. [DOI] [PubMed] [Google Scholar]
- Lisman JE, Otmakhova NA. Storage, recall, and novelty detection of sequences by the hippocampus: elaborating on the SOCRATIC model to account for normal and aberrant effects of dopamine. Hippocampus. 2001;11:551–568. doi: 10.1002/hipo.1071. [DOI] [PubMed] [Google Scholar]
- Montgomery SM, Buzsaki G. Gamma oscillations dynamically couple hippocampal CA3 and CA1 regions during memory task performance. Proc Natl Acad Sci U S A. 2007;104:14495–14500. doi: 10.1073/pnas.0701826104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montgomery SM, Sirota A, Buzsaki G. Theta and gamma coordination of hippocampal networks during waking and rapid eye movement sleep. J Neurosci. 2008;28:6731–6741. doi: 10.1523/JNEUROSCI.1227-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray AJ, Sauer JF, Riedel G, McClure C, Ansel L, Cheyne L, Bartos M, Wisden W, Wulff P. Parvalbumin-positive CA1 interneurons are required for spatial working but not for reference memory. Nat Neurosci. 2011;14:297–299. doi: 10.1038/nn.2751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakashiba T, Buhl DL, McHugh TJ, Tonegawa S. Hippocampal CA3 output is crucial for ripple-associated reactivation and consolidation of memory. Neuron. 2009;62:781–787. doi: 10.1016/j.neuron.2009.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Keefe J, Dostrovsky J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971;34:171–175. doi: 10.1016/0006-8993(71)90358-1. [DOI] [PubMed] [Google Scholar]
- O’Keefe J, Nadel L. The hippocampus as a cognitive map. Oxford University Press; London: 1978. [Google Scholar]
- O’Neill J, Senior T, Csicsvari J. Place-selective firing of CA1 pyramidal cells during sharp wave/ripple network patterns in exploratory behavior. Neuron. 2006;49:143–155. doi: 10.1016/j.neuron.2005.10.037. [DOI] [PubMed] [Google Scholar]
- Osipova D, Takashima A, Oostenveld R, Fernandez G, Maris E, Jensen O. Theta and gamma oscillations predict encoding and retrieval of declarative memory. J Neurosci. 2006;26:7523–7531. doi: 10.1523/JNEUROSCI.1948-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Percival DB, Walden AT. Spectral analysis for physical applications: multitaper and conventional univariate techniques. Cambridge University Press; Cambridge; New York, NY, USA: 1993. [Google Scholar]
- Peyrache A, Battaglia FP, Destexhe A. Inhibition recruitment in prefrontal cortex during sleep spindles and gating of hippocampal inputs. Proc Natl Acad Sci U S A. 2011;108:17207–17212. doi: 10.1073/pnas.1103612108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranck JB., Jr. Studies on single neurons in dorsal hippocampal formation and septum in unrestrained rats. I. Behavioral correlates and firing repertoires. Exp.Neurol. 1973;41:461–531. doi: 10.1016/0014-4886(73)90290-2. [DOI] [PubMed] [Google Scholar]
- Singer W. Synchronization of cortical activity and its putative role in information processing and learning. Annu.Rev.Physiol. 1993;55:349–74. 349–374. doi: 10.1146/annurev.ph.55.030193.002025. [DOI] [PubMed] [Google Scholar]
- Sohal VS, Zhang F, Yizhar O, Deisseroth K. Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature. 2009;459:698–702. doi: 10.1038/nature07991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan D, Csicsvari J, Mizuseki K, Montgomery S, Diba K, Buzsaki G. Relationships between Hippocampal Sharp Waves, Ripples, and Fast Gamma Oscillation: Influence of Dentate and Entorhinal Cortical Activity. J Neurosci. 2011;31:8605–8616. doi: 10.1523/JNEUROSCI.0294-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki SS, Smith GK. Spontaneous EEG spikes in the normal hippocampus. II. Relations to synchronous burst discharges. Electroencephalogr Clin Neurophysiol. 1988;69:532–540. doi: 10.1016/0013-4694(88)90165-4. [DOI] [PubMed] [Google Scholar]
- Tort AB, Komorowski RW, Manns JR, Kopell NJ, Eichenbaum H. Theta-gamma coupling increases during the learning of item-context associations. Proc Natl Acad Sci U S A. 2009;106:20942–20947. doi: 10.1073/pnas.0911331106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traub RD, Whittington MA, Colling SB, Buzsaki G, Jefferys JG. Analysis of gamma rhythms in the rat hippocampus in vitro and in vivo. J.Physiol.(Lond.) 1996;493:471–484. doi: 10.1113/jphysiol.1996.sp021397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tukker JJ, Fuentealba P, Hartwich K, Somogyi P, Klausberger T. Cell type-specific tuning of hippocampal interneuron firing during gamma oscillations in vivo. J Neurosci. 2007;27:8184–8189. doi: 10.1523/JNEUROSCI.1685-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson MA, McNaughton BL. Dynamics of the hippocampal ensemble code for space. Science. 1993;261:1055–1058. doi: 10.1126/science.8351520. [DOI] [PubMed] [Google Scholar]
- Wilson MA, McNaughton BL. Reactivation of hippocampal ensemble memories during sleep. Science. 1994;265:676–679. doi: 10.1126/science.8036517. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W, Desimone R, Engel AK, Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
- Ylinen A, Bragin A, Nadasdy Z, Jando G, Szabo I, Sik A, Buzsaki G. Sharp wave-associated high-frequency oscillation (200 Hz) in the intact hippocampus: network and intracellular mechanisms. Journal of Neuroscience. 1995;15:30–46. doi: 10.1523/JNEUROSCI.15-01-00030.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.