Anatomical basis of variation in mesophyll resistance in eastern Australian sclerophylls: news of a long and winding path

Abstract

In sclerophylls, photosynthesis is particularly strongly limited by mesophyll diffusion resistance from substomatal cavities to chloroplasts (r _m), but the controls on diffusion limits by integral leaf variables such as leaf thickness, density, and dry mass per unit area and by the individual steps along the diffusion pathway are imperfectly understood. To gain insight into the determinants of r _m in leaves with varying structure, the full CO₂ physical diffusion pathway was analysed in 32 Australian species sampled from sites contrasting in soil nutrients and rainfall, and having leaf structures from mesophytic to strongly sclerophyllous. r _m was estimated based on combined measurements of gas exchange and chlorophyll fluorescence. In addition, r _m was modelled on the basis of detailed anatomical measurements to separate the importance of different serial resistances affecting CO₂ diffusion into chloroplasts. The strongest sources of variation in r _m were S _c/S, the exposed surface area of chloroplasts per unit leaf area, and mesophyll cell wall thickness, t _cw. The strong correlation of r _m with t _cw could not be explained by cell wall thickness alone, and most likely arose from a further effect of cell wall porosity. The CO₂ drawdown from intercellular spaces to chloroplasts was positively correlated with t _cw, suggesting enhanced diffusional limitations in leaves with thicker cell walls. Leaf thickness and density were poorly correlated with S _c/S, indicating that widely varying combinations of leaf anatomical traits occur at given values of leaf integrated traits, and suggesting that detailed anatomical studies are needed to predict r _m for any given species.

Introduction

Leaf photosynthesis is determined by biochemical limitations (photosynthetic capacity) and diffusion limitations, including stomatal resistance and CO₂ diffusion resistance from sub-stomatal cavities to the carboxylating enzyme, Rubisco, in the chloroplasts (so-called ‘mesophyll diffusion resistance’) (Flexas et al., 2008, 2012; Terashima et al., 2006, 2011). The concept of mesophyll resistance (r _m, see Table 1 for symbol definitions) can be described as follows. After entering the leaf through the stomata, CO₂ faces a relatively long and tortuous pathway through gas and liquid phases before it finally reaches the carboxylating enzyme Rubisco. First, CO₂ must diffuse through the intercellular airspaces to a mesophyll cell surfaces adjacent to the airspace to enable free access for the CO₂. Gas diffusion in the liquid phase is slow, therefore CO₂ is most likely to enter the cell where the chloroplast directly abuts the cell wall (Terashima et al., 2006, 2011). This process could be greatly enhanced if the cell walls were fully lined with chloroplasts, a condition that in practice is rare (Terashima et al., 2006). CO₂ dissolves in the water-filled pores of the cell wall (Evans et al., 2009) and diffuses across the cell wall. Diffusion across cell walls is slow if the walls are lignified and porosity is low, and/or if the walls are thick. Diffusion through the cytoplasmic layer between the cell wall and the chloroplast is fast if chloroplasts are closely appressed to the cell walls. Chloroplasts are relatively thick organelles, and diffusion through the chloroplast could potentially be one of the most limiting steps in CO₂ physical diffusion, unless most Rubisco were located close to the chloroplast inner envelope membrane (Tosens et al., 2012) or carbonic anhydrase operated close to Rubisco to enhance the apparent diffusion gradient (Terashima et al., 2011).

Table 1.

Symbols and units used

Variable	Definition	Unit
A	Net assimilation rate	µmol m–2 s–1
C c	CO2 concentration in chloroplasts	µmol mol–1
C i	CO2 concentration in intercellular airspace	µmol mol–1
C i–C c	CO2 drawdown from intercellular airspace to chloroplasts	µmol mol–1
D a	Diffusion coefficient for CO2 in the gas phase	m2 s–1
d leaf	Leaf density	g cm–3
D w	Aqueous phase diffusion coefficient for CO2	m2 s–1
f ias	Fraction of mesophyll occupied by intercellular airspace	Dimensionless
f pal	Fraction of mesophyll cell volume comprised of palisade tissue	Dimensionless
H/(RT k)	Henry′s law constant	Dimensionless
∆L ias	Effective diffusion path length in the gas-phase	m
L mes	Total length of chloroplasts facing the intercellular airspace	m
L mes	Total length of mesophyll cells facing the intercellular airspace	m
p i	Effective porosity in the given part of the diffusion pathway	Dimensionless
Q	Incident quantum flux density	µmol m–2 s–1
R	Gas constant	Pa m3 K–1 mol–1
	Mesophyll resistance of exposed chloroplast surface area per unit of leaf area	m2chlor s mol–1
r cellular	Cellular resistance, sum of r cw, r pl, r cyt, r env, and r str	s m–1
R d	Dark respiration rate	µmol m–2 s–1
r cw	Cell wall resistance	s m–1
r pl	Plasma membrane resistance	s m–1
r cyt	Cytoplasm resistance	s m–1
r env	Chloroplast envelope resistance	s m–1
r str	Stroma resistance	s m–1
r gas	Gas phase resistance	s m–1
r liq	Liquid phase resistance	s m–1
r m	Mesophyll diffusion resistance	m2 s mol–1
S c/S	Chloroplast surface area exposed to intercellular airspace
	per unit of leaf area	m2 m–2
s mes	Cross-sectional surface area of mesophyll cells in micrograph	m2
s pal	Cross-sectional area of palisade mesophyll cells in micrograph	m2
s s	Cross-sectional area of mesophyll cells in micrograph	m2
S c,pal/S	S c/S for palisade mesophyll	%
S c,spon/S	S c/S for spongy mesophyll	%
S c/S mes	Ratio of exposed chloroplast to mesophyll surface areas	Dimensionless
S mes/S	Surface area of mesophyll cells exposed to airspace per unit of leaf area	m2 m–2
t chlor	Chloroplast thickness	µm
t cw	Cell wall thickness	µm
T k	Absolute temperature	K
t leaf	Leaf thickness	mm
t mes	Mesophyll thickness	mm
W	Width of the section measured	m
γ	Curvature correction factor	Dimensionless
γf,i	Proportional reduction of diffusion conductance in the cytosol and in the stroma compared with free diffusion in water	Dimensionless
	Diffusion path tortuosity	m m–1
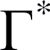
	Hypothetical CO2 compensation point without R d	µmol mol–1
ΦPSII	Effective quantum yield of PSII	Dimensionless
ξ	Leaf absorptance	Dimensionless
ε	Fraction of electrons absorbed by PSII	Dimensionless

All of these anatomical features pose partial resistances for CO₂ diffusion and contribute to the total mesophyll resistance. Slower CO₂ diffusion through the mesophyll causes larger CO₂ concentration gradients between the stroma and intercellular airspaces, C _i–C _c (Niinemets and Sack, 2006; Warren, 2008; Niinemets et al., 2009c). Ignoring the fact that CO₂ concentration in chloroplasts (C _c) is often lower than the CO₂ concentration in substomatal cavities (C _i) leads to the underestimation of Rubisco-related photosynthetic parameters (Flexas et al., 2006a., 2007; Niinemets et al., 2009a) and biased respiration rate calculations (Ayub et al., 2011). Although this is now quite widely recognized, r _m is still generally ignored in large-scale carbon gain models due to our lack of knowledge about why it varies among species, and how best to model it (Warren, 2008; Niinemets et al., 2009c).

The gas-phase pathway is longer than the liquid-phase pathway but gas diffusion in the liquid phase is approximately 10 000-fold slower (Evans et al., 1994; Terashima et al., 2006). Gas-phase resistance is thought to be negligible in thin and porous mesophytic leaves (Terashima et al., 2006; Flexas et al., 2008). Further, it has been demonstrated that gas-phase resistance is lower than liquid-phase resistance in thick, densely-packed, hypostomatous sclerophyll leaves (Syvertsen et al., 1995; Piel et al., 2002). Therefore, it is largely agreed that the main limitations to CO₂ diffusion are in the liquid phase (Flexas et al., 2009; Terashima et al., 2006, 2011).

Only a limited number of studies have analysed r _m together with its direct structural correlates. In some studies (Loreto et al., 1992; Evans et al., 1994; Tosens et al., 2012), a strong negative relationship has been reported between r _m and the area of exposed chloroplast surface per unit of leaf surface area, S _c/S. However, in others, no relationship has been found between S _c/S and r _m (Kogami et al., 2001; Gorton et al., 2003). On the other hand, a strong positive relationship between cell wall thickness and r _m was reported by Hassiotou et al. (2010). Overall, the information about the aqueous-phase structural determinants of r _m is conflicting and largely missing (Flexas et al., 2008; Warren, 2008; Evans et al., 2009).

CO₂ diffusion across the mesophyll is particularly slow in structurally robust leaves, (Niinemets and Sack, 2006; Flexas et al., 2008; Niinemets et al., 2009c, 2011). Because of stronger mesophyll diffusion limitations, evergreen sclerophylls are less sensitive to variations in stomatal openness (Niinemets et al., 2011); therefore, r _m is an important factor affecting photosynthetic performance in those species (Warren and Adams, 2006; Niinemets and Sack, 2006). Strong positive correlations between CO₂ drawdown from substomatal cavities to chloroplasts (a measure of CO₂ diffusion limitation of photosynthesis) and leaf dry mass per unit area (LMA; a measure of leaf robustness) have been observed across the species worldwide (Niinemets et al., 2009c), including Australian sclerophylls (Niinemets et al., 2009b). In the current study, 32 Australian sclerophyll species were examined for anatomical restrictions to CO₂ diffusion. The central aim was to identify and quantify the main sources of variation in r _m in these species. The data were fitted to the diffusion model of Niinemets and Reichstein (2003a) to unravel the importance of various components of the CO₂ diffusion pathway from substomatal cavities to Rubisco in the chloroplasts. In addition, the influence of anatomical traits on r _m was quantified and C _i–C _c calculated from gas exchange measurements. Finally, we turn to the question of what features of leaves are conducive to high chloroplast exposed areas per unit surface area, this being one of the two leading dimensions determining total mesophyll resistance. All acronyms used are defined in Table 1.

Materials and methods

Study sites and species

The field measurements were conducted in April 2006 as described in detail by Niinemets et al. (2009b). In brief, plant material for gas-exchange measurements and foliage chemical and structural analyses was sampled from healthy individuals of 32 Australian evergreen tree and shrub species. Sampling was primarily spread across four sites (HRHN, high rain, high nutrients; HRLN, high rain, low nutrients; LRHN, low rain, high nutrients; LRLN, low rain, low nutrients) selected in native forests and shrublands near Sydney, Australia (see Table 2 for species sampled at each site). The open- or closed-forest vegetation supported at each site is characterized by broad-leaved canopy trees (e.g. Eucalyptus spp., Corymbia spp., Syncarpia glomulifera), with a mix of broad-leaved, needle-leaved, and microphyllous species in the understorey. To get a broader range of leaf structures and photosynthetic capacities, additional samples for five species were taken from Macquarie University campus (MQ; Table 2). In all cases, mature individuals were used. All species, except Acacia spp., possessed true mature leaves. Acacia spp. possessed foliage phyllodes that are analogues of broad leaves. It is noted that important structural changes occur in leaves upon transition from the juvenile to the mature leaf form and upon replacement of juvenile foliage by phyllodes in Acacia species (Ullmann, 1989; Groom et al., 1997). Ontogenetic modifications in leaf form are also associated with alterations in leaf anatomy and mesophyll diffusion conductance (Mullin et al., 2009; Steppe et al., 2011). Such modifications constitute a potentially highly important source of species differentiation among different habitats during ontogeny, but such modifications were not studied here. Further details about sites, species, and sampling procedures can be found in Niinemets et al. (2009b).

Table 2.

Average thickness of key anatomical traits determining cellular resistance for the 32 study species from five sites

Species	Sitea	Component thickness (µm)
		Chloroplasts	Cell walls	Cytosol
Acacia longifolia	MQ	1.50	0.300	0.138
Acacia myrtifolia	HRLN	1.50	0.262	0.103
Acacia suaveolens	HRLN	1.65	0.367	0.162
Angophora hispida	HRLN	1.46	0.378	0.152
Astrotrichia floccosa	HRHN	1.71	0.330	0.132
Banksia aemula	LRLN	1.29	0.350	0.143
Banksia integrifolia	MQ	1.88	0.300	0.140
Banksia marginata	HRLN	1.30	0.388	0.111
Banksia oblongifolia	HRLN	1.36	0.380	0.141
Banksia robur	MQ	1.80	0.283	0.141
Banksia serrata	MQ	1.60	0.388	0.140
Banksia serrata	HRLN	1.57	0.380	0.142
Banksia spinulosa	LRHN	1.41	0.380	0.142
Eriostemon australasius	HRLN	1.59	0.321	0.142
Eucalyptus fibrosa	LRHN	1.28	0.374	0.143
Eucalyptus haemastoma	LRHN	1.67	0.367	0.090
Eucalyptus sclerophylla	LRLN	1.28	0.420	0.129
Eucalyptus umbra	HRHN	1.43	0.410	0.130
Grevillea speciosa	HRLN	1.74	0.335	0.142
Hakea dactyloides	HRLN	1.32	0.408	0.140
Lambertia formosa	HRHN	1.73	0.300	0.140
Lambertia formosa	HRLN	1.58	0.395	0.150
Macadamia ternifolia	MQ	1.34	0.342	0.141
Macrozamia communis	HRHN	1.88	0.263	0.150
Macrozamia spiralis	LRHN	1.44	0.373	0.140
Notolea longifolia	HRHN	1.37	0.365	0.130
Persoonia lanceolata	HRLN	1.59	0.325	0.142
Persoonia laurina	LRLN	1.61	0.310	0.141
Persoonia laurina	LRHN	1.44	0.331	0.143
Persoonia levis	HRLN	1.66	0.300	0.142
Pittosporum undulatum	MQ	1.83	0.281	0.145
Polyscias sambucifolia	MQ	1.80	0.252	0.150
Syncarpia glomulifera	HRHN	1.87	0.290	0.140
Synoum glandulosum	HRHN	1.57	0.278	0.135
Xylomelum pyriforme	HRHN	1.56	0.340	0.139

a HRHN, higher rain, high nutrients; MQ, Macquarie University campus (also higher rain); HRLN, higher rain, low nutrients; LRHN, lower rain, high nutrients; LRLN, lower rain, low nutrients. High rainfall sites experience c. 1220mm annual rainfall, low rainfall sites c. 800mm (climate data from the Australian Bureau of Meteorology; further site details given by Niinemets et al., 2009b).

Measurement protocols and determination ofdiffusion limits of photosynthesis

The detailed measurement protocol is reported in Niinemets et al. (2009b). In brief, terminal branches were cut under water in the field in morning hours during high air humidity, transported to the laboratory and stabilized under dim light of 50–100 µmol m^–2 s^–1 and at 22 °C for 1–2 d to ensure the full hydration of branches and stable stomatal conductance during gas exchange measurements. Preliminary experiments demonstrated that while the stomatal conductance was relatively high immediately after branch sampling, the stomatal conductance rapidly declined during photosynthesis measurements conducted right after branch sampling. By contrast, stomatal conductances were high and stable in preconditioned branches (Niinemets et al., 2005, 2009b).

CO₂ response curves of net assimilation and steady-state fluorescence were measured with a Li-6400 gas-exchange system equipped with a Li-6400-40 Leaf Chamber Fluorometer (Li-Cor, Inc., Lincoln, Nebraska, USA) at a leaf temperature of 25 °C and incident quantum flux density of 1000 µmol m^–2 s^–1. All gas-exchange rates were corrected for water vapour and CO₂ diffusion according to Rodeghiero et al. (2007). Gas-exchange rates and chlorophyll fluorescence measurements were used to determine the mesophyll diffusion resistance (r _m; see Table 1 for the units and abbreviations used in this study) from substomatal cavities to chloroplasts according to the variable electron transport rate method of Harley et al. (1992):

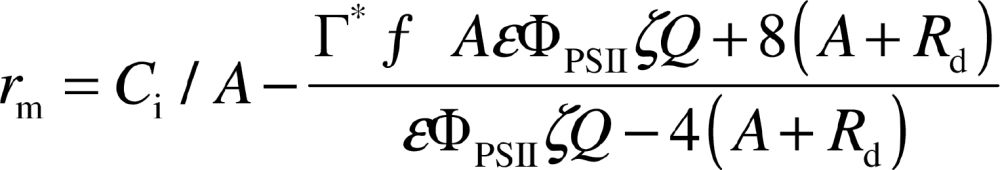(1)

where A is the net assimilation rate, C _i is the CO₂ concentration in substomatal cavities, R _d is the rate of non-photorespiratory respiration, Γ* is the hypothetical CO₂ compensation point without R _d (42.9 µmol mol^–1 at 25 °C) derived in vivo by Bernacchi et al. (2001). Q is the incident quantum flux density, Φ_PSII is the effective quantum yield of PSII, ξŀ is the leaf absorptance determined separately by an integrated sphere (Niinemets et al., 2009b), and ε is the fraction of electrons absorbed by PSII (taken as 0.5). The values of r _m were calculated for measurements of net assimilation rate over the C _i range of 150–350 µmol mol^–1, and the average value of r _m was determined for each leaf. Over this range, r _m estimations are almost independent of C _i (Flexas et al., 2007).

Light and electron microscopy

Small leaf discs around 5.8mm in diameter were removed from the leaves used for gas exchange measurements. Care was taken to avoid big leaf vessels. The leaf sections were infiltrated in a syringe with the fixative 2% glutaric aldehyde in 0.1M cacodylate buffer (pH=7.4), and post-fixed in 2% buffered osmium tetroxide at 22 °C for 2h. The samples were further dehydrated for 0.5h at 22 °C in an ethanol series and embedded in a LR White resin for an hour at 22 °C. Leaf sections of 1 µm for light microscopy, and ultrathin sections of 70nm for transmission electron microscopy (TEM) were made with Reichert–Jung ultra-cut ultra microtome (Leica, Vienna, Austria). The light microscope sections were stained with Toluidine blue and viewed in brightfield at magnifications of ×10 and ×40 by an Olympus BX 50 compound microscope, and photographed with a Scion CFW-1310 colour digital camera. The ultrathin sections were stained with lead citrate and viewed at magnifications of ×1800–×14000 by a Philips CM10 TEM microscope (Philips, Eindhoven, The Netherlands), and photographed with an Olympus-SIS Megaview digital camera.

Mesophyll surface area exposed to intercellular airspace per unit leaf area, S _mes/S, and S _c/S (chloroplast area facing the outer surface of exposed mesophyll cell walls per unit leaf area) were calculated from light and TEM micrographs (magnification ×4200) following the method of Syvertsen et al. (1995). Thus, S _mes/S, is given as:

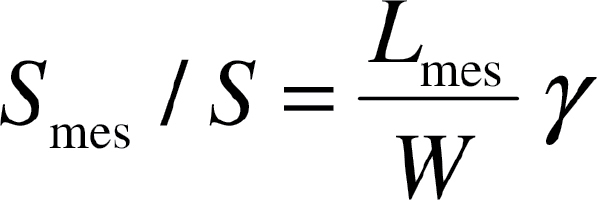, (2)

where W is the width of the section measured, L _mes is the total length of mesophyll cells facing the intercellular airspace, and γ is the curvature correction factor that depends on the shape of the cells (Evans et al., 1994) and was obtained as a weighted average for palisade and spongy mesophyll. Analogously, S _c/S, was calculated as:

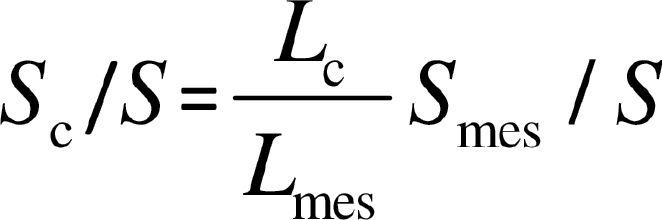, (3)

where L _c is the total length of chloroplast surface area facing the intercellular airspace in the section.

The fraction of intercellular airspace (f _ias) was determined as:

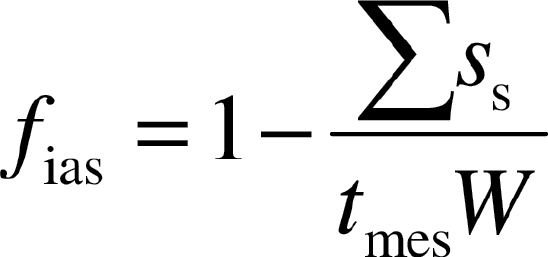(4)

where t _mes is the mesophyll thickness between the two epidermal layers and Σs _s is the sum of the cross-sectional areas of mesophyll cells.

The fraction of mesophyll cell volume comprised of palisade tissue (f _pal) was determined as:

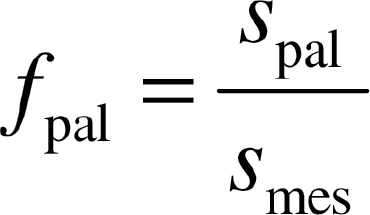(5)

where s _pal is the cross-sectional area of cell surfaces that is palisade and s _mes is the cross sectional surface area of mesophyll cells.

Cell wall thickness (t _cw), cytoplasm thickness (t _cyt), and chloroplast thickness (t _chlor) were directly measured from TEM micrographs at a magnification of ×14 000. For a given section, all characteristics were determined at least in three different fields of view, and at least three different sections were analysed.

A model for calculation of internal mesophyll diffusion resistance

Values of S _c/S were used to calculate the mesophyll diffusion resistance of exposed chloroplast surface area 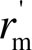(r _m S _c/S) as is common in studies of mesophyll diffusion limitations of photosynthesis (Evans et al., 2009; Terashima et al., 2006, 2011). 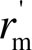is an appropriate variable in the correlative relationships with individual components of the diffusion pathway. A quantitative one-dimensional within-leaf gas diffusion model was applied to gain an insight into the partial determinants of mesophyll diffusion resistance from substomatal cavities to chloroplasts (for the full details of the model see Niinemets and Reichstein, 2003a; Tosens et al., 2012). In the model, the total mesophyll resistance (gas-phase equivalent), r _m, is separated between gas-phase resistance from substomatal cavities to the outer surface of cell walls (r _gas) and gas-phase equivalent liquid-phase resistance from the outer surface of cell walls to the chloroplasts (r _liq) (Evans et al., 1994; Niinemets and Reichstein, 2003a, b):

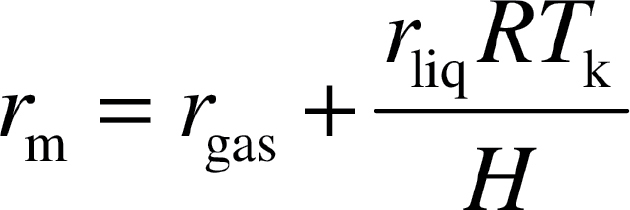(6)

where H is the Henry’s law constant (Pa m³ mol^–1), R is the gas constant (Pa m³ K^–1 mol^–1) and T _k is the absolute temperature (K). H/(RT _k) is the dimensionless form of Henry’s law constant (gas/liquid phase partition coefficient) that is needed to convert, r _liq, a resistance in the liquid phase to gas-phase equivalent resistance. At 25 °C used in our study for gas-exchange measurements, H/(RT _k) for CO₂ is 1.2 (Dodds et al., 1956; Umbreit et al., 1972).

Gas-phase diffusion depends on the fraction of mesophyll volume occupied by intercellular airspace (f _ias, m³ m^–3) and the effective diffusion path length in the gas-phase (ΔL _ias) (Syvertsen et al., 1995) as:

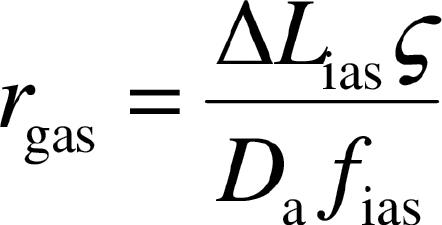(7)

where 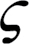is the diffusion path tortuosity (m m^–1) and D _a (m² s^–1) is the diffusion coefficient for CO₂ in the gas-phase (1.51^×10^-5 m² s^–1 at 25 °C). ΔL _ias was approximated by half of the mesophyll thickness (Niinemets and Reichstein, 2003a). An estimate of 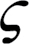can be obtained from paradermal and transverse leaf sections (Terashima et al., 1995), but its estimation is laborious and relatively imprecise due to varying geometry of leaf cells, making it difficult to discern the sites where air passages are blocked. In addition, 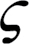may also vary with environmental conditions. A fixed value of 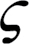of 1.57 m m^–1 was used, as previously employed by Syvertsen et al. (1995) and Niinemets and Reichstein (2003a).

A total liquid phase resistance is given as the sum of the serial resistances:

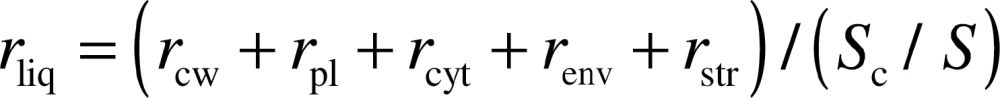(8)

where the partial resistances are: r _cw for cell wall, r _pl for plasmalemma, r _cyt for cytosol, r _env for the chloroplast envelope, and r _str for the chloroplast stroma. r _cellular was defined further as the sum of r _cw+r _pl+r _cyt+r _env+r _str. Liquid phase resistance r _liq is lower if there is a broad pathway into mesophyll cell walls facing the chloroplasts (S _c/S), but higher if r _cellular is high along a unit cross-section of that pathway. Accordingly, the contributions of pathway breadth S _c/S relative to r _cellular were visualized by plotting log₁₀ [(S _c/S)^–1] against log₁₀ r _cellular.

The cell wall, cytosol, and stroma resistances (r _i) are given by a general equation (Nobel, 1991):

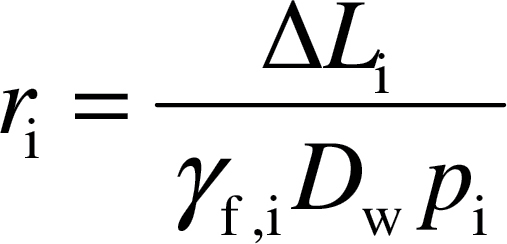(9)

where ΔL _i (m) is the diffusion path length and p _i (m³ m^–3) is the effective porosity in the given part of the diffusion pathway, D _w is the aqueous phase diffusion coefficient for CO₂ (1.790×10^–9 m² s^–1 at 25 °C) and the dimensionless factor γ _f,i accounts for the decrease of diffusion conductance in the cytosol and in the stroma compared with free diffusion in water (Weisiger, 1998). The values of γ _f,i used were 1 for cell walls and 0.294 for the cytosol and stroma (Niinemets and Reichstein, 2003a). The diffusion pathlength was taken as equal to the cell wall thickness for r _cw, the average distance between the chloroplasts and cell wall for r _cyt, and half of the chloroplast thickness for r _str (Tosens et al., 2012). Although carbonic anhydrase could potentially affect r _str in non-steady-state conditions (Evans et al., 2009; Terashima et al., 2011), the evidence of the involvement of carbonic anhydrase in determining r _str is currently equivocal and was not considered in the current study to avoid additional assumptions [see Discussion and Tosens et al. (2012) for further discussion].

Effective porosity, p _i, was taken as 1 for r _cyt and r _str. Initially, a constant value of 0.05 was applied for the porosity of cell walls (Terashima et al., 2006). However, as there is evidence that effective porosity decreases with increasing thickness of the cell walls (Evans et al., 2009), a least squared iterative analysis was used instead, varying the p _i of the cell wall to get the best fit (highest r ²) between the measured and modelled r _m values. Best fit was obtained by varying p _i linearly from 0.095 at the lowest cell wall thickness of 0.252 µm to 0.040 at the maximum cell wall thickness of 0.420 µm. This method is referred to as the variable p _i approach.

CO₂ diffusion resistance through the plasma membrane (r _pl) and chloroplast envelope membranes and (r _env) cannot be estimated from micrographs. In addition, the CO₂ diffusion rate through membranes can be modified by aquaporins (Flexas et al., 2006b, 2012; Hanba et al., 2004). However, it has been suggested that CO₂ permeability through lipid bilayers is high, on the order of 0.03 m s^–1, and therefore aquaporins have only a minor impact on CO₂ permeability (Missner et al., 2008). By contrast, it was suggested by Boron et al. (2011) that membrane permeability can be two orders of magnitude less and aquaporins play a key role in membrane permeability. As suggested in the review of Evans et al. (2009), aquaporins could limit 30% of the lipid-phase diffusion resistance at most. Membrane permeability can be estimated from CO₂ lipid-phase solubility using structure–function relationships as suggested by Niinemets and Reichstein (2003a), but information of the lipid-phase solubility of CO₂ is limited. Due to incomplete information about CO₂ diffusion through biological membranes, a constant value of 0.0035 m s^–1 for both r _pl and r _env was used in the present study, as had been successfully employed by Evans et al. (1994) and Tosens et al. (2012).

Results

Performance of the anatomical model of mesophyll diffusion resistance

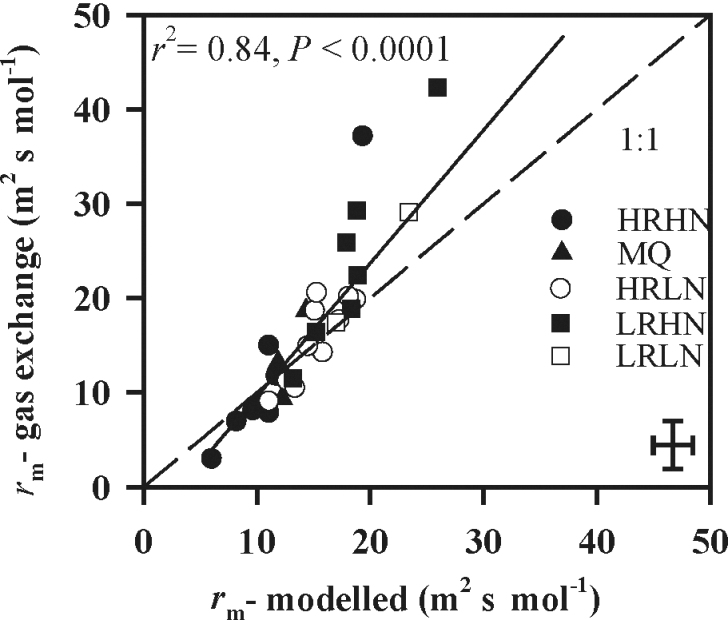
The species-mean estimates of r _m calculated from anatomical measurements were tightly correlated with the estimates obtained from coupled gas-exchange/fluorescence measurements (Fig. 1, r ²=0.84, P <0.0001). This indicates that equations 6–9 provide a reasonable assessment of relative contributions of different leaf anatomical features to mesophyll resistance. The estimates made from anatomy tended to overestimate mesophyll resistance in low-resistance species and underestimate it in high-resistance species. The average (±SE) discrepancy between modeled and measured r _m was 15.6±0.03%.

Fig. 1.

Correlation between mesophyll diffusion resistance determined from combined gas-exchange and chlorophyll fluorescence measurements (equation 1, r _m, gas exchange) and mesophyll resistance calculated from anatomical data (equations 6–9, r _m, modelled). Data were fitted by linear regression. The error bars in the lower right corner indicate the maximum size of standard errors across species. HRHN, higher rain, high nutrients; MQ, Macquarie University campus; HRLN, higher rain, low nutrients; LRHN, lower rain, high nutrients; LRLN, lower rain, low nutrients. See Table 2 for studied species and site information.

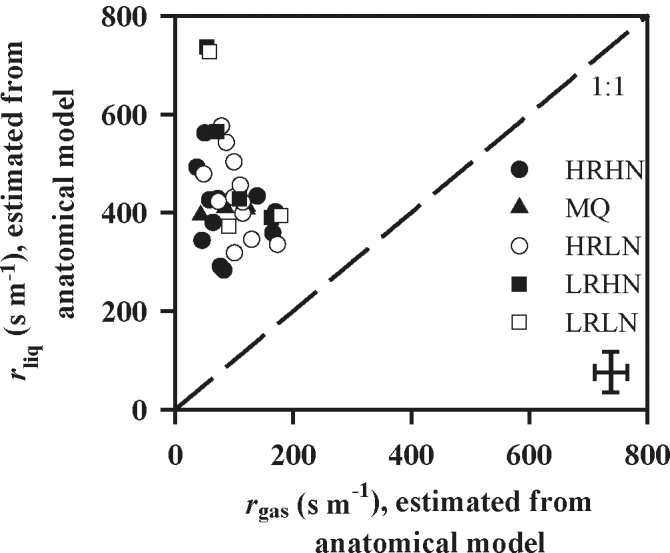
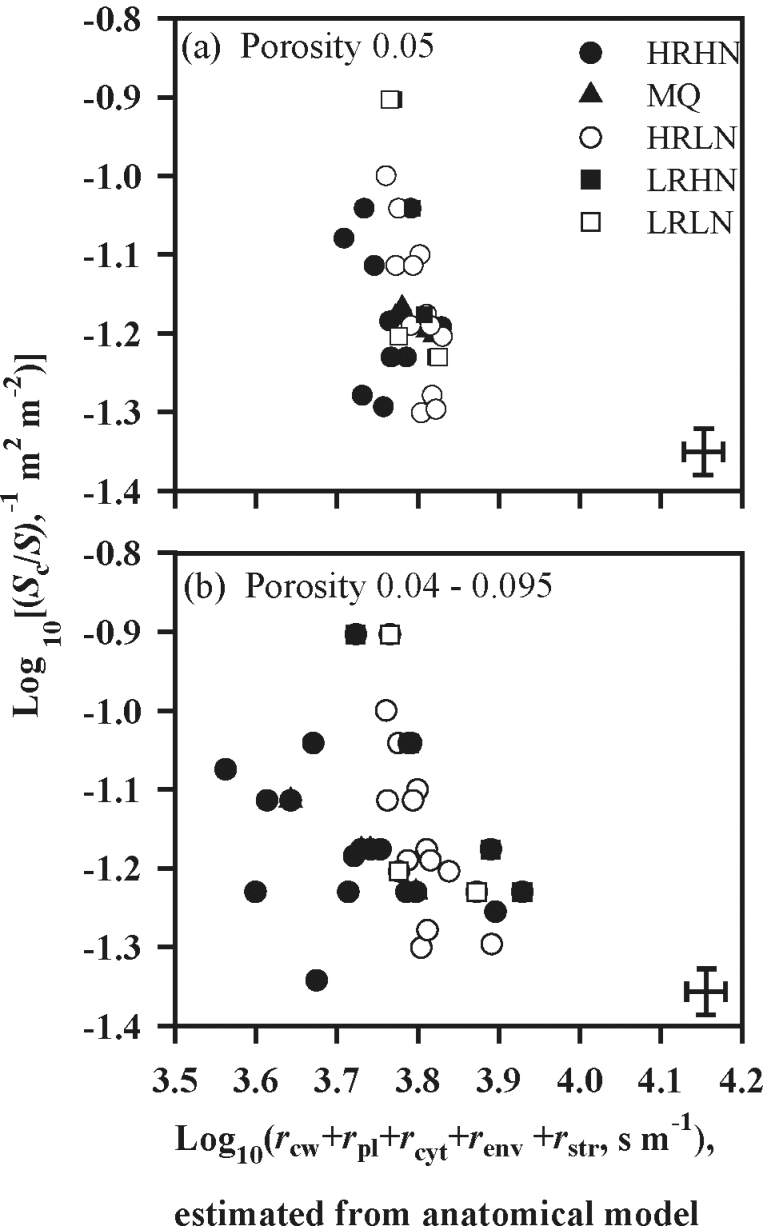
Estimated liquid-phase resistance was consistently larger than gas-phase resistance_, and varied more widely (Fig. 2). Most values of r _liq fell in the range of 250–600 s m^–1 compared with 40–180 s m^–1 for r _gas. Consequently, differences in r _m between species arose mainly from variations of the components of r _liq. Plotting log₁₀[(S _c/S)^–1] against log₁₀ r _cellular to separate the contributions of the components of r _liq demonstrated that the variation in (S _c/S)^–1 spanned about 0.5 log₁₀ units (i.e. c. 3-fold; Fig. 3a). The sum of resistances along a unit cross-section of the pathway as estimated by equations 6–9 varied rather narrowly, by about 0.1 log₁₀ units (Fig. 3a). Chloroplasts represent potentially the longest diffusion path in the liquid phase (Table 2). Nevertheless, the largest contribution to r _cellular resulted from cell walls, being more than 50% in all species (Table 3). These values were estimated assuming a constant cell wall porosity of 0.05 in all species. However, when the porosity of cell walls was assumed to decrease with increasing the thickness of cell walls as described in the Materials and methods, r _cellular was predicted to be at least as important as S _c/S in determining the variation in r _m across the species (Fig. 3b).

Fig. 2.

Relationship between the CO₂ diffusion resistance in liquid (r _liq) and gas phase (r _gas). r _liq is the sum of partial cellular resistances in cell wall (r _cw), plasmalemma (r _pl), cytosol between cell wall and chloroplast (r _cyt), chloroplast envelope (r _env), and chloroplast stroma (r _str) multiplied by the inverse of chloroplast exposed to total leaf surface area ratio (S _c/S)^–1: (r _cw+r _pl+r _cyt+r _env+r _str)/(S _c/S). In the r _liq calculations, we assumed a mesophyll cell wall porosity of 0.05 for all species. Representation of symbols and error bars as in Fig. 1.

Fig. 3.

Relationship between the inverse of chloroplastsurface area exposed to intercellular airspace per unit leaf area (S _c/S)^–1, and the sum of individual cellular resistances [(r _cw+r _pl+r _cyt+r _env+r _str)]. Both axes are log-transformed. Log (liquid-phase resistance) is the sum of these two log-components, Log[(S _c/S)^–1] and Log(r _cw+r _pl+r _cyt+r _env+r _str) and increasestowards the upper right corner. The sum of serial liquid-phase resistances was calculated assuming a constant mesophyllcell wall porosity of 0.05 for all species (a), or assumingvariable porosity of mesophyll cell walls, with porosity rangingfrom 0.040 to 0.095, decreasing with increasing depth of cellwall (b). A constant value of 0.0035 m s^–1 was assigned toboth r _pl and r _env. Symbols and error bars as in Fig. 1.

Table 3.

Contribution of different components of cellular resistance to the total cellular resistance, estimated from the anatomical model for the 32 study species from five sites*1

A constant mesophyll cell wall porosity of 0.05 was assumed for all species.

Species	Sitea	Contribution to total cellular resistance (%)
		Stroma	Cell walls	Cytosol	Membranesb
Acacia longifolia	HRHN	30.7	55.5	4.3	9.2
Acacia myrtifolia	HRLN	26.2	59.5	5.0	9.2
Acacia suaveolens	HRLN	24.0	62.6	4.7	8.7
Angophora hispida	HRLN	21.8	66.3	2.9	9.0
Astrotrichia floccosa	HRHN	27.8	57.2	3.8	11.2
Banksia aemula	LRLN	20.5	65.4	4.5	9.6
Banksia integrifolia	MQ	29.9	56.1	4.5	9.6
Banksia marginata	HRLN	19.5	68.2	3.3	9.0
Banksia oblongifolia	HRLN	20.3	66.6	4.2	9.0
Banksia robur	MQ	30.3	55.1	4.7	10.0
Banksia serrata	MQ	22.7	64.8	4.0	8.7
Banksia serrata	HRLN	22.7	64.5	4.1	8.7
Banksia spinulosa	LRHN	20.8	66.1	4.2	8.9
Eriostemon australasius	HRLN	25.4	60.4	4.5	9.6
Eucalyptus fibrosa	LRHN	18.0	69.0	4.1	8.6
Eucalyptus haemastoma	LRHN	29.9	55.9	3.3	10.9
Eucalyptus sclerophylla	LRLN	18.1	69.9	3.4	8.6
Eucalyptus umbra	HRHN	20.1	67.8	3.7	8.5
Grevillea speciosa	HRLN	20.5	60.0	4.3	9.2
Hakea dactyloides	HRLN	18.9	68.5	4.0	8.6
Lambertia formosa	HRHN	28.1	57.5	4.6	9.8
Lambertia formosa	HRLN	22.2	65.1	4.2	8.5
Macadamia ternifolia	MQ	21.4	64.4	4.5	9.7
Macrozamia communis	HRHN	32.0	52.6	5.1	10.3
Macrozamia spiralis	LRHN	19.6	67.0	4.3	9.2
Notolea longifolia	HRHN	21.0	65.8	4.0	9.2
Persoonia lanceolata	HRLN	25.2	60.7	4.5	9.6
Persoonia laurina	LRLN	26.3	59.3	4.6	9.8
Persoonia laurina	LRHN	23.2	62.6	4.6	9.7
Persoonia levis	HRLN	27.3	58.1	4.7	9.9
Pittosporum undulatum	MQ	30.4	54.8	4.8	10.0
Polyscias sambucifolia	MQ	31.7	52.4	5.3	10.6
Syncarpia glomulifera	HRHN	30.3	55.3	4.5	9.8
Synoum glandulosum	HRHN	27.5	57.2	4.7	10.6
Xylomelum pyriforme	HRHN	24.2	62.1	4.3	9.4

a Site codes as in Table 2.

b Membrane contribution is determined by the permeabilities of plasmalemma and chloroplast envelope membranes. These permeabilities were fixed at a constant value of 0.0035 m s^–1 for all species. However, the contribution of membrane permeabilities to total cellular resistance varies due to the variation in numerical values for the other components of the diffusion pathway.

Mesophyll cell wall as an important contributor to mesophyll resistance

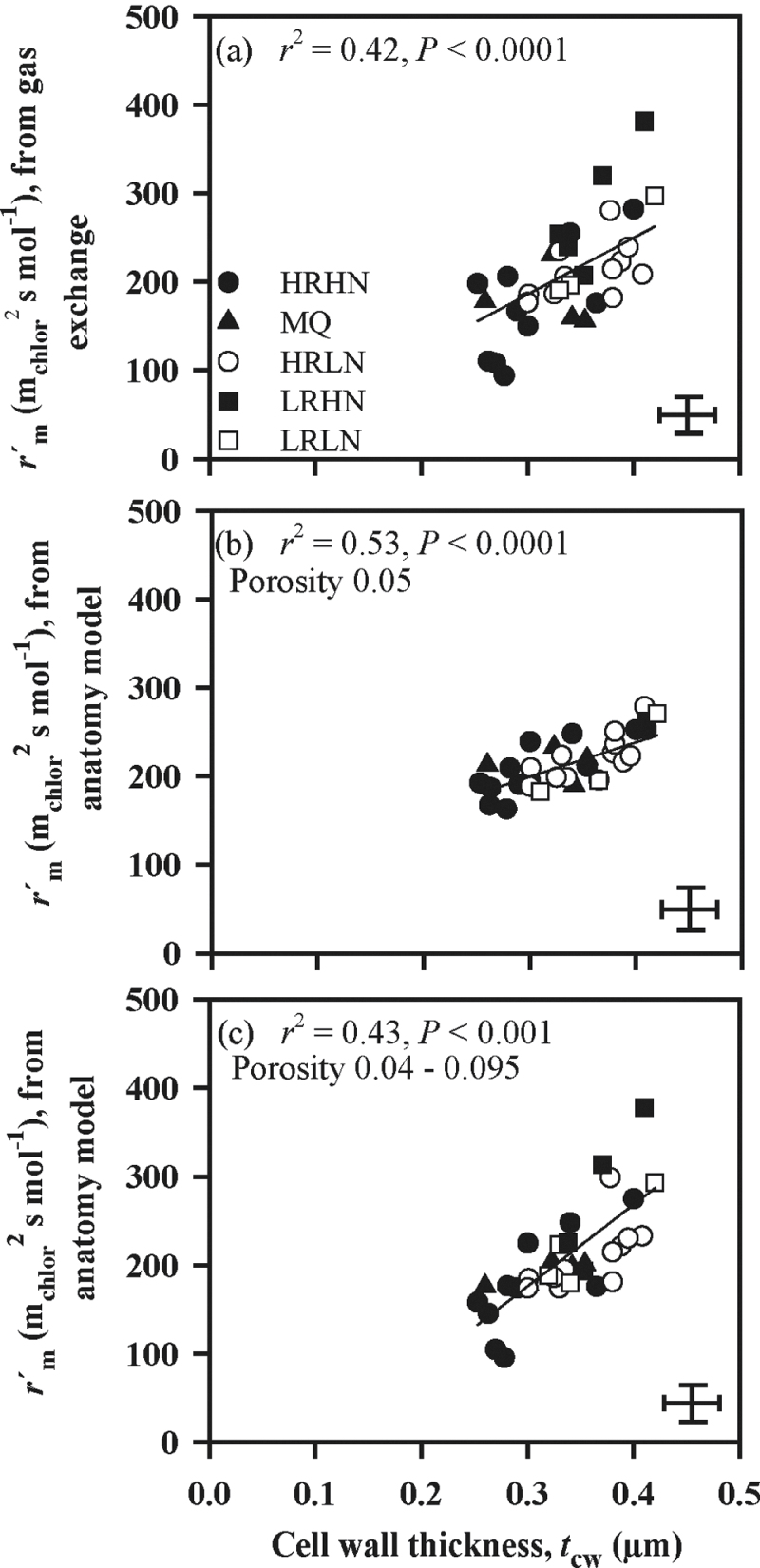
Mesophyll cell wall thickness was a strong predictor of interspecific variation in mesophyll resistance per unit of exposed chloroplast surface (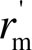, Fig. 4a). By contrast, variation in 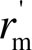calculated from anatomy (Fig. 4b) was only about as large as expected from the direct influence of cell wall thickness on resistance. Mesophyll cell wall porosity was treated initially as a constant of 0.05 in these calculations. When the porosity was assumed to decrease with increasing cell wall thickness (as in Fig. 3b), the consequence of the assumption of variable porosity was that the wall resistance varied across species considerably more widely than wall thickness per se – approximately 5-fold more (Fig. 4a, 4c).

Fig. 4.

Correlations between mesophyll resistance per unit exposed chloroplast surface area, 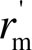and cell wall thickness (t _cw) for 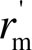estimates derived from gas-exchange measurements (a) and modelled using anatomical data, either assuming a constant mesophyll cell wall porosity of 0.05 for all species (b) or varying the porosity (p _i) between 0.040 to 0.095 across species (c). In the latter case, the best fit was obtained by varying p _i linearly from 0.095 at the lowest cell wall thickness of 0.252 µm to 0.040 at the maximum cell wall thickness of 0.420 µm. Representation of symbols and error bars as in Fig. 1.

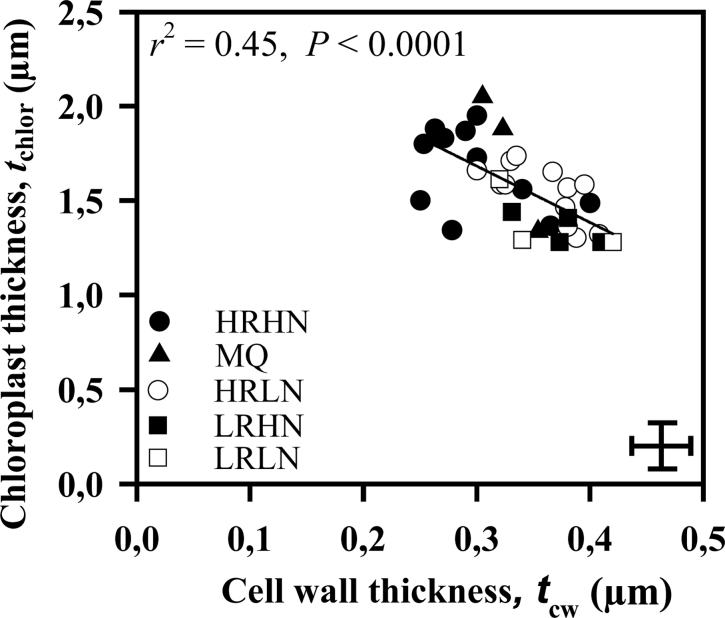
Comparing Fig. 3b with Fig. 3a, the species from the high-rain high-nutrient site tended to be separate from the other species, towards lower r _cellular. They tended to have distinctly thinner mesophyll cell walls (Table 4), and the implications of that difference for wall resistance were amplified when porosity was assumed to be higher in thin-walled species. Chloroplast thickness and t _cw tended to co-vary in such a way that species with thick cell walls tended to have thinner chloroplasts adjacent to them (Fig. 5).

Table 4.

Average (±SE) cell wall thickness (t _cw) and chloroplast surface area exposed to intercellular airspace per unit leaf area (S _c/S) in four contrasting environments

Means with the same letter are not significantly different (P >0.05). Only the species sampled from natural sites were included. The low rain, low nutrient site was not included in the statistical analysis due to limited sample size.

Site	t cw (µm)	S c/S (m2 m–2)
High rain, high nutrient	0.322±0.030 a	15.3±1.0 a
High rain, low nutrient	0.356±0.012 b	13.4±1.0 a
Low rain, high nutrient	0.365±0.034 b	15.0±1.3 a
Low rain, low nutrient	0.360±0.033	13.7±1.1

Fig. 5.

The relationship between cell wall thickness, t _cw, and chloroplast thickness, t _chlor across the species. Data were fitted by linear regression. Symbols and error bars as in Fig. 1.

Structural limitations to r _m measured in the field

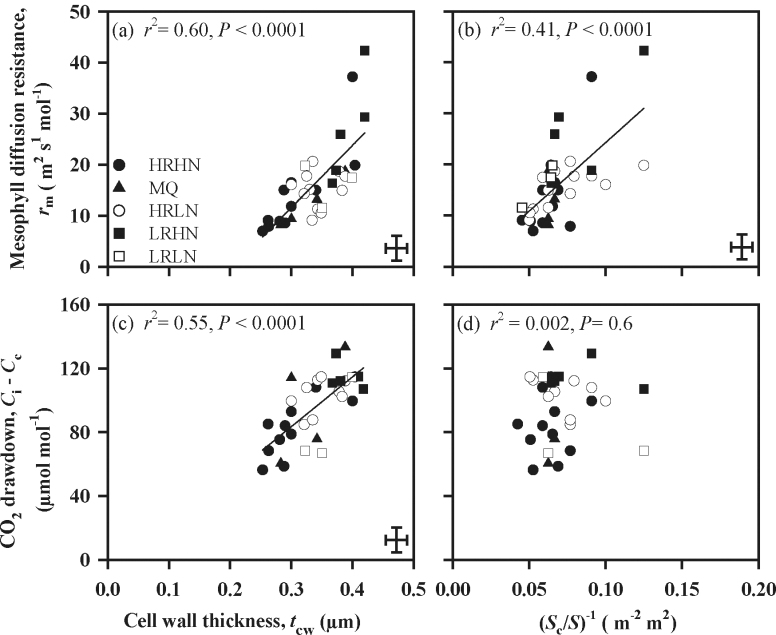
As expected, given the above results from model predictions, variation in t _cw and S _c/S predicted a considerable portion of that in r _m measured via gas exchange (Fig. 6a, 6b). The estimated CO₂ concentration drawdown from the internal airspace into the chloroplast (C _i–C _c) was well correlated with mesophyll cell wall thickness (Fig. 6c) but unrelated to S _c/S (Fig. 6d).

Fig. 6.

Mesophyll resistance (r _m, (a, b) and CO₂ drawdown from intercellular airspace to chloroplasts (C _i–C _c, (c, d)) in relation to (a, c) mesophyll cell wall thickness, t _cw, and (b, d) chloroplast surface area exposed to intercellular airspace per unit leaf area (S _c/S). The data were fitted by linear regression. The symbols and error bars as in Fig. 1.

How Australian sclerophylls increase S _c/S

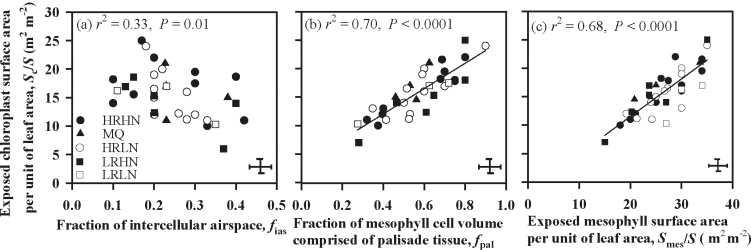
Finally, we turn to the anatomical features which lead to a highly exposed chloroplast area per unit surface area of the leaf (this being one of the two leading influences on total mesophyll resistance). S _c/S did not increase with the depth of the leaf lamina nor with the depth of mesophyll (see Supplementary Fig. S1a, b at JXB online). S _c/S and f _ias were negatively correlated (Fig. 7a).

Fig. 7.

Correlations of chloroplast surface area exposed to intercellular airspace per unit leaf area, S _c/S, (a) the fraction of mesophyll occupied by intercellular airspace, f _ias; (b) the fraction of mesophyll cell volume in palisade tissue, f _pal; and (c) mesophyll surface area exposed to intercellular airspace per unit leaf area, S _mes/S. The data were fitted by linear regressions. Data presentation and error bars as in Fig. 1.

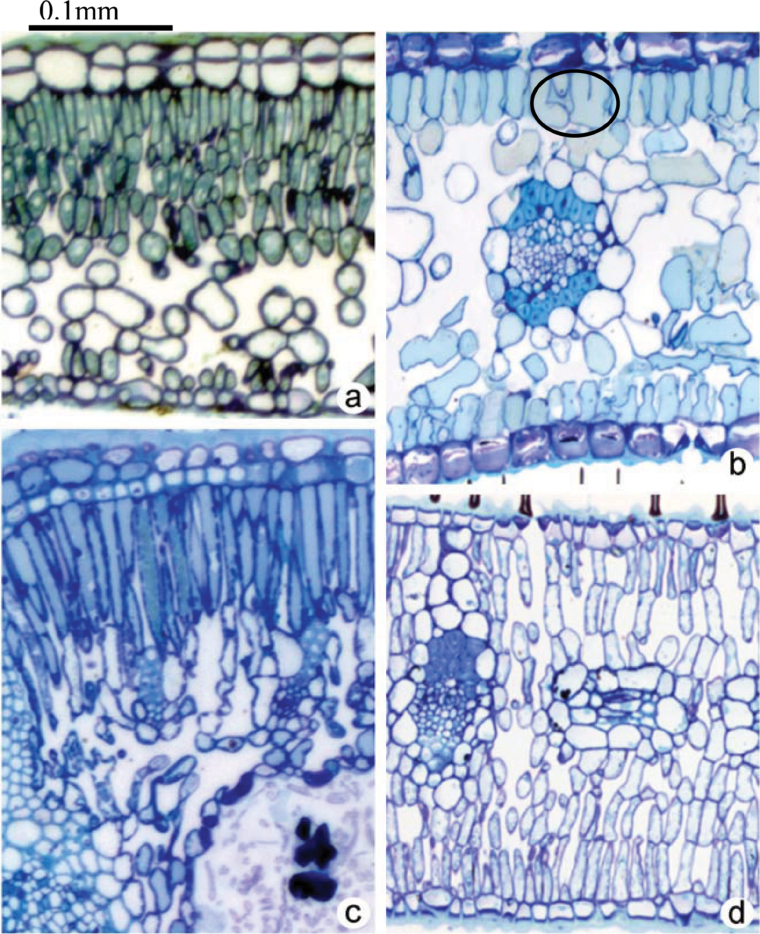
The most important source of variation across species with regard to the exposed mesophyll cell surface, and hence in the exposed chloroplast surface, proved to be the fraction of mesophyll contributed by the palisade tissue (Fig. 7b). There seemed to be several factors contributing to this. First, although two-dimensional sections often give the impression that the palisade mesophyll is closely packed, in fact, many of its cell surfaces are adjacent to airspaces. Second, the proportion of cell surface occupied by exposed chloroplasts tended to be greater in palisade than in spongy tissue (data not shown). Third, the elongated shape of palisade cells means that they have more cell surface per volume than do spongy mesophyll cells. Fourth, palisade cells were quite small in many of the species studied here, which also increases the amount of cell surface per volume occupied. These tendencies are shown in Fig. 8a–d (transverse anatomical sections from selected species). Further, c. 50–90% of S _c/S was controlled by palisade compared with spongy mesophyll among the study species (see Supplementary Table S1 at JXB online). As might be expected, the area of chloroplasts adjacent to airspaces was strongly correlated with the area of mesophyll cell surface adjacent to airspaces (Fig. 7c).

Fig. 8.

Representative light micrographs of leaf transverse sections demonstrating the strategies in Australian species to reduce mesophyll resistance by increasing S _mes/S and S _c/S. (a) Stacked layers of small palisade cells in Pittosporum undulatum; (b) armed cells in Persoonia lanceolata leaf (inside the circle); (c) mesophyll cell elongation in Banksia integrifolia; and (d) multiple layers of palisade cells in the lower and upper leaf sides in Eucalyptus haemastoma. The sections were stained with Toluidine blue and the photos are taken at magnification of ×10.

Discussion

Diffusion model of mesophyll resistance

The correspondence between r _m data from the anatomical model and gas exchange measurements (r ²=0.84) can be considered good given that there are various uncertainties inherent to both measurement and modelling approaches (e.g. in gas exchange methods the assumptions concerning the fraction of light absorbed by PSII; Pons et al., 2009). As argued above, in our view, the approach outlined in equations 6–9 allows for a trustworthy assessment of the relative contributions of different anatomical features to overall mesophyll resistance.

In our model, r _m is divided between two components, r _gas and r _liq (equation 6). r _gas increases with decreasing f _ias and increases with increasing leaf thickness, while r _liq increases with increasing the length of composite parts of the diffusion pathway and decreases with increasing S _c/S that determines the number of parallel diffusion pathways into the cells (Terashima et al., 2006). Because gas diffusion in the liquid phase is c. 10 000-fold slower than in the gas phase, the bulk of diffusional limitations is in the liquid phase (Syvertsen et al., 1995; Piel et al., 2002; Terashima et al., 2006). Our study across Australian sclerophyll species supports the idea that r _gas is negligible compared with r _liq. Furthermore, r _liq varied more among species than did r _gas (Fig. 2). In the liquid phase, variation in (S _c/S)^–1 was greater than that in r _cellular, at least when cell wall porosity was assumed to be invariant (Fig. 3a).

It has been assumed that membranes of all species are similarly permeable to CO₂ and a constant permeability value suggested by Evans et al. (1994) was used. Under this assumption membranes contributed c. 8–11% of the total r _cellular (Table 3). It has been suggested that CO₂ diffusion through membranes is regulated by aquaporins (Hanba et al., 2004; Flexas et al., 2006b; Terashima et al., 2006, 2011). Primarily, aquaporins have been associated with short-term fluctuations in r _m, for example, if plants are suddenly exposed to extreme drought (Terashima et al., 2011), and it has been suggested that membrane permeability can be reduced by as much as two orders of magnitude (Boron et al., 2011), while other studies suggest that the role of aquaporin is minor (Missner et al., 2008; and the discussion in Flexas et al., 2012). The debate over the role of aquaporins has clearly not yet settled, but, in our study, a satisfactory agreement between modelled and measured r _m was achieved by ignoring the possible interspecific variations in lipid phase resistance.

It was found that most chloroplasts were positioned close to cell walls, with only a very thin layer of cytosol in between. Cytoplasm thickness varied little among species and, on average, it accounted for c. 3–5% of the total liquid phase resistance (Table 3). Gillon and Yakir (2001) proposed that r _str is primarily controlled by carbonic anhydrase (CA) activity in the chloroplast. They suggested that CA activity is increasingly important to facilitate CO₂ diffusion in species with thick cell walls such as evergreen sclerophylls (Gillon and Yakir, 2001). At the normal cytosolic pH of 7.5, cytosolic CA should be sufficiently active to ensure the fast interconversion of CO₂ and bicarbonate. However, to date, there is little evidence that variation in cytosolic CA significantly influences r _m (Terashima et al., 2006). In addition, the studies of Price et al. (1994) and Williams et al. (1996) with genetic transformants with low chloroplastic CA, indicated a minor effect of chloroplastic CA levels on photosynthetic performance. The results presented here suggested that r _str is controlled by the length of the physical CO₂ diffusion path in chloroplasts. This importance of chloroplast thickness is also indirectly supported by the fact that species with thicker mesophyll cell walls had thinner chloroplasts adjacent to these cell walls. Therefore, species with high cell wall resistance might be under particularly strong evolutionary selection to reduce r _str by minimizing the diffusion path length in chloroplasts.

Overall, the correspondence between measured and modelled estimates of diffusion resistance is striking (Fig. 1), and provides encouraging evidence that the principal processes governing interspecific variation in r _m were captured by the model. More complex 3D models have been developed (Aalto and Juurola, 2002; Tholen and Zhu, 2011), and such models probably have greater predictive capacity. However, parameterization of such models is currently highly time-consuming and the parameterizations are not general such that we feel that a simple 1D model as used here is more practical for interspecific comparisons where a large number of species needs to be examined.

Mesophyll cell wall as an important contributor to mesophyll resistance

The relationship between t _cw and mesophyll resistance calculated per unit of S _c/S was steeper than the observed variation in cell wall thickness could have been capable of producing according to equations 6–9 with the cell wall porosity at a constant value of 0.05, as we initially treated it (Fig. 4a, 4b). This steeper response probably reflects a variation in a model variable that has considerable influence on r _m, and that was taken as a constant in the initial analyses. Consider first the possibility that such a variable occurred in equations 6–9 and was measured for different species. For example, cell wall thickness might have been correlated with low S _c/S increasing mesophyll resistance by narrowing the pathway into cells or with a low fraction of intercellular airspace increasing gas-phase resistance. But, in both cases, the variable would have influenced the estimate of mesophyll resistance made from anatomical measurements through equations 6–9, and that estimate would have been correlated with mesophyll cell wall thickness in the same manner as the mesophyll resistance measured through gas exchange, shown in Fig. 4a. However, the mesophyll resistance calculated from anatomy (Fig. 4b) was much more weakly correlated with cell wall thickness, the relationship being only about as strong as expected from the direct influence of cell wall thickness on resistance.

It follows, therefore, that the extra variable correlated with cell wall thickness and it was not treated as a variable in the calculation by equations 6–9. The likeliest candidate is the porosity of the walls of mesophyll cells. Initially this was treated as a constant of 0.05 in the calculations described above, which resulted in reasonable total mesophyll resistance values across species. However, if wall porosity varied substantially and was correlated with wall thickness, this could account for the stronger effect of cell walls on liquid phase resistance (Fig. 4a, 4b). The resistance imposed by cell walls depends on cell wall porosity, the tortuosity of pores, and cell wall thickness. Values for cell wall porosity and tortuosity of the pores are poorly known (Evans et al., 2009); for example, porosities suggested in the literature include 0.05, 0.07, 0.1 or 0.3 (Evans et al., 2009; Nobel, 1991; Terashima et al., 2006). It was noted by Terashima et al. (2006) that cell wall porosity might vary considerably across species, and that r _cw would become an important factor determining internal diffusion resistance at porosities below 0.1. When porosity was modelled as varying from 0.040 to 0.095 and as being negatively correlated with cell wall thickness, then cell wall thickness contributed to variation in 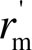as much as that observed (Fig. 4). The effect of assuming porosity varying in conjunction with cell wall thickness was to make wall resistance at least as important as S _c/S as a source of variation across species in determining mesophyll resistance (Figs. 3,4).

It is emphasized that the linear decline of mesophyll cell wall porosity with cell wall thickness used in our calculations is hypothetical and should not be interpreted as a measured relationship. There are no direct measurements of cell wall porosity, and it remains logically possible that the discrepancy between Fig. 4a and 4b could be resolved by a correlation between cell wall thickness and some other trait that increased resistance. Nevertheless, our provisional opinion is that the most biologically plausible explanation is for thicker cell walls to be more lignified and have less pore volume per unit depth.

Structural limitations to photosynthesis measured in the field

According to our model calculations, and to our results (Fig. 6a, 6b), there are two main sources of variation in r _m across Australian sclerophyll species: t _cw and S _c/S.

Previously, a strong negative relationship between r _m and S _c/S in annual species with thin cell walls has been demonstrated by Evans et al. (1994), whereas the correlation was far weaker among forest tree species with thicker mesophyll cell walls (Terashima et al., 2006), as also seen here. No effect of S _c/S on r _m was shown by Kogami et al. (2001). The cause of such a difference between studies is probably higher t _cw in evergreen and some deciduous species (Terashima et al., 2006). Here, HRLN and LRHN species had significantly thicker cell walls (Table 3) and, consequently, had generally higher r _m per (S _c/S)^–1 (Fig. 4). This suggests that the negative effect of a longer diffusion pathway dominates over the positive effect of high S _c/S in species with thicker mesophyll cell walls.

Since r _m varies widely across Australian sclerophyll species and it is higher in leaves with thicker cell walls, the question arises to what extent photosynthesis is limited by r _m. It has been suggested that the degree to which photosynthesis is limited by structure is approximately invariant across species (Evans and Loreto, 2002). However, a number of subsequent studies have demonstrated that C _i–C _c does, in fact, vary among species (Warren, 2008); for example, it is generally higher in high LMA leaves with robust structure (Niinemets et al., 2005; Niinemets and Sack, 2006), and in leaves with thicker cell walls (current study). By contrast, C _c varied little among the five Banksia species studied by Hassiotou et al. (2009). Yet, just as here, there was a strong negative relationship between g _m (r _m=1/g _m) and t _cw. Overall, these results collectively suggest that in Australian sclerophyll species photosynthesis is more limited by r _m in leaves with thicker cell walls.

Integrative trait LMA fails to predict r _m across broad sample of species

Flexas et al. (2008) drew an upper boundary of r _m versus LMA relationship that increased linearly with increasing LMA. The trend, when extrapolated, predicts an infinite r _m at an LMA of about 250g m^–2 _. However, in Australian sclerophylls, r _m and C _i–C _c were in the same range as those in other broad-leaved evergreen sclerophyll species, although Australian sclerophyll leaves possess somewhat greater LMA values (Niinemets et al., 2009b; Hassiotou et al., 2010).

According to Syvertsen et al. (1995); Hanba et al. (1999, 2001), Miyazawa and Terashima (2001); Terashima et al. (2001, 2006), and Tosens et al. (2012), t _cw varies from 0.2–0.3 µm in deciduous species and from 0.3–0.5 µm in evergreen species, whereas S _c/S varies from 8–23 m² m^–2. Anatomical measurements from this study indicate that, in these highly sclerophyllous species S _c/S and t _cw are in the same range as reported for other sclerophylls and deciduous tree species (accordingly, 8–22 m² m^–2 and 0.252–0.420 µm, see also Tables 2 and 4). Similarly, Hassiotou et al. (2010) reported t _cw values from approximately 0.23–0.43 µm in Banksia species. Although r _m often correlates with the integrative trait LMA (Niinemets et al., 2009c), Australian species are outliers in the general LMA and r _m relationship (Hassiotou et al., 2009; Niinemets et al., 2009b). While, in other sclerophylls, thick-walled mesophyll is distributed uniformly between the epidermal layers, in Australian sclerophylls (e.g. Proteaceae) there is characteristically a heterogeneous distribution of thick-walled sclerenchyma and mesophyll islands, where the individual mesophyll cell does not necessarily have thick cell walls (Jordan et al., 2005; Niinemets et al., 2009b).

How Australian sclerophyll leaves increase S _c/S

According to the model predictions, one of the most important sources of variation in r _m was S _c/S. That led us to the question of what features of leaves are conducive to exposing large areas of chloroplast at the cell surfaces per unit surface area of the leaf. It is commonly assumed that increased t _leaf reflects both higher S _c/S as well as S _mes/S (Hanba et al., 2002, Terashima et al., 2006), and across annuals and deciduous species this relationship does indeed seem to hold (Evans et al., 1994; Hanba et al., 1999; Terashima et al., 2006; Tosens et al., 2012). However, across the woody sclerophyll species studied in this work, S _c/S did not correlate with leaf (or mesophyll) thickness (see Supplementary Fig. S1a, b at JXB online). Similarly, Slaton and Smith (2002) analysed species across a wide range of genera and did not find a positive correlation between S _mes/S and t _mes.

Thick leaves have been considered disadvantageous because of increased gas phase resistance (Parkhurst, 1994; Terashima et al., 2001). In the leaves of Hakea dactyloides (Proteaceae) the thickest in this study, r _gas contributed 30% of r _m. Presumably thick-leaved sclerophyll species would most benefit from minimizing gas phase resistance as much as possible and organizing their mesophyll to that end. For example, S _c/S can be increased (Terashima et al., 2011) by having several layers of small palisade cells (Figs 8a, 8d), by having armed type cells (Fig. 8b, shown within the circle (as noted by Terashima et al., 2011, armed cells having lobes help to increase S _c/S) or by cell elongation (Fig. 8c). The palisade cells were small in most of the species studied here (Fig. 8a, 8b, 8d). Out of these strategies, only cell elongation might require a simultaneous increase in leaf thickness, but otherwise it is just a matter of mesophyll architecture. By having small-celled leaves can decrease gas phase resistance and simultaneously increase S _c/S (Terashima et al., 2006). Hassiotou et al. (2010) reported a positive correlation between the length of palisade cells and leaf thickness in Banksia species. In our study the fraction of mesophyll composed of palisade varied from 50–90% (see Supplementary Table S1 at JXB online). This fraction was positively correlated with S _c/S (Fig. 7b), indicating that palisade tissue did importantly contribute to S _c/S.

The intercellular airspace volume fraction correlated negatively with S _c/S, indicating that many of the species studied tended to pack their mesophyll tightly and leave just sufficient airspace adjacent to the cell walls for CO₂ dissolution. This contrasts with the positive correlation between the fraction of intercellular air spaces and S _c/S reported for tobacco (Evans et al., 1994). As expected, species in our study with high S _mes/S also had higher S _c/S (Fig. 7c). This positive relationship has also been reported by Hanba et al. (2001) and Terashima et al. (2006).

Often it is assumed that higher t _leaf reflects higher S _c/S (Hanba et al., 1999; Terashima et al., 2011). Our data call into question such postulations. Considered across a wide range of species, there was no relationship between S _c/S and leaf (or mesophyll) thickness.

Conclusions

Although advanced three-dimensional models of mesophyll resistance have been developed, parameterizing these models is complicated and laborious for a large number of species, as studied here. Further, the predictive power of these models has not yet been tested across species. Overall, our calculations demonstrate that r _m can be successfully predicted from a simple 1-dimensional model which assumes that r _m is determined by key structural leaf anatomical traits that determine the diffusion pathway length.

The two strongest sources of variation across species in total mesophyll resistance are the components of liquid phase resistance: S _c/S, the area of chloroplast exposed at the mesophyll cell surfaces per unit surface area of the leaf, and cell wall resistance. These data demonstrate that structural limitations to photosynthesis are more enhanced in leaves with thicker cell walls. As explained above, the steep relationship of liquid phase resistance with cell wall thickness can not be explained by cell wall thickness alone and most likely arises from a further effect of cell wall porosity varying with cell wall thickness. Overall, these data demonstrate that, across the broad sample of species possessing various structural foliage adaptation mechanisms to cope with adverse environmental conditions, simple integrative traits such as LMA alone fail to predict r _m.

Supplementary data

Supplementary data can be found at JXB online.

Supplementary Table S1. Contribution (%) of exposed mesophyll surface area per unit of leaf area (S _c/S) that was controlled by palisade mesophyll (S _c,pal/S) compared with spongy mesophyll (S _c,spon/S), for the study species from five sites.

Supplementary Fig. S1. Correlations of chloroplast surface area exposed to intercellular airspace per unit leaf area, S _c/S, with (a) leaf thickness, t _leaf, and (b) mesophyll thickness, t _mes.