Competing Risks Regression for Stratified Data

Summary

For competing risks data, the Fine–Gray proportional hazards model for subdistribution has gained popularity for its convenience in directly assessing the effect of covariates on the cumulative incidence function. However, in many important applications, proportional hazards may not be satisfied, including multicenter clinical trials, where the baseline subdistribution hazards may not be common due to varying patient populations. In this article, we consider a stratified competing risks regression, to allow the baseline hazard to vary across levels of the stratification covariate. According to the relative size of the number of strata and strata sizes, two stratification regimes are considered. Using partial likelihood and weighting techniques, we obtain consistent estimators of regression parameters. The corresponding asymptotic properties and resulting inferences are provided for the two regimes separately. Data from a breast cancer clinical trial and from a bone marrow transplantation registry illustrate the potential utility of the stratified Fine–Gray model.

1. Introduction

Competing risks data arise when subjects may fail from several distinct types including disease and nondisease related causes. The observed data consist of a failure time and a failure type. In this setting, the cumulative incidence (also referred to as the subdistribution) may be of prime interest as it quantifies the absolute risks of different failure types. The focus of this article is evaluating covariate effects on the cumulative incidence across levels of a stratifying variable using the popular Fine–Gray regression model.

To compare the cumulative incidence of a particular type of failure among different groups, Gray developed a class of K-sample tests based on weighted averages of the subdistribution hazards for that particular failure type of interest (Gray, 1988). Pepe (1991) proposed a nonparametric two sample test for group effects. No covariates other than the group factor can be considered in these tests. A semiparametric proportional hazards model was proposed by Fine and Gray (1999) to assess the effect of covariates or prognostic factors on the cumulative incidence function. The Fine–Gray model captures the cause-specific failure probabilities after adjusting for patient-specific risks and provides a way to directly examine the influence of risk factors on the absolute risks. Alternative models and methods of estimation for cumulative incidence regression have been studied in, for example, Klein and Andersen (2005); Scheike and Zhang (2008); and Scheike, Zhang, and Gerds (2008), including nonproportional hazards models and goodness-of-fit methods for assessing the proportional hazards assumption. In this article, we focus on a simple extension of the Fine–Gray model, which is currently the most widely used cumulative incidence regression methodology in practice, adapting techniques that are widely employed with proportional hazards modeling under independent censoring.

In real applications, the proportional subdistribution hazards assumption may not hold for certain covariates. In these scenarios, naive application of the Fine–Gray model, either omitting such covariates or including them assuming they satisfy the proportional hazards assumption, could lead to biased estimation and tests, and potential loss of power. We propose a stratified Fine–Gray model that adjusts for such discrete factors, without estimating their effects on the sub-distribution hazard. The main idea is to allow the baseline hazard function to vary across levels of stratification variables.

In classical survival analysis, stratifying is a common data analytic strategy. For instance, in proportional hazards regression with independent censoring, there are frequently important factors, the different levels of which produce hazard functions that differ markedly from proportionality. Stratification on these factors may yield a simpler and more flexible analysis than modeling interactions parametrically with functions of time defined through time-dependent covariates (Kalbfleisch and Prentice, 2002). Notably, stratification is a standard approach to account for varying patient populations such as in multicenter clinical trials, where baseline hazards vary across centers (Therneau and Grambsch, 2000). Both Splus and SAS statistical software offer the strata option in fitting the Cox (1972) regression model, but these functions may not be suitable for the Fine–Gray model.

We consider two typical data sets that exhibit different stratification regimes where cumulative incidence is a primary endpoint. We say data are regularly stratified if there are a small number of large groups (strata) and that data are highly stratified if the number of groups (strata) is large compared to the strata sizes.

Clinical trial E1178 conducted by the Eastern Cooperative Oncology Group compared 2 years of treatments tamoxifen therapy to placebo in elderly (⩾ age 65) breast cancer patients with positive auxiliary nodes. The cumulative incidence of breast cancer recurrence is of great interest. Nonproportional hazards of the treatment effect has previously been observed using time-dependent covariates (Fine and Gray, 1999), suggesting stratification on treatment when testing effects of other risk factors. Within each treatment arm, there are a large number of patients, as with regularly stratified data.

A bone marrow transplant registry is maintained by the European Blood and Marrow Transplant Group. The primary endpoint is time from graft to first occurrence of acute or chronic graft-versus-host-disease (GvHD) whereas death and relapse (free of GvHD) are the competing events. This is a multicenter design. Katsahian et al. (2006) proposed a frailty model for the subdistribution hazard to assess the heterogeneity across clusters and to incorporate such an effect when testing other risk factors. A stratified competing risks regression can be applied here to account for correlation within center due to unobserved center effects without estimating those effects. The number of centers is much larger than the number of patients from each center, yielding highly stratified data.

Existing work on the cumulative incidence function for clustered and/or stratified data includes, but is not limited to modified nonparametric Gray type tests (Chen et al., 2008), mixed proportional hazards models (Katsahian et al., 2006), and introducing interactions using time-dependent covariates to the Fine-Gray (1999) model. The modified tests focus on formally testing group effects, which limits the introduction of continuous covariates and the quantification of covariate effects. The mixed proportional hazards model is a frailty regression model tailored to competing risks data. Although the approach seems promising, the statistical properties of the resulting analysis are unclear (Katsahian et al., 2006). Moreover, if the main goal is to investigate covariate effects, introducing a dependence parameter in modeling the joint distribution within each cluster does not seem to have much advantage. Stratified (Gross and Huber, 1987) and marginal proportional hazards approaches (Lee, Wei, and Amato, 1992) have been advocated for such scenarios with independent censoring. Such models avoid introducing time-dependent covariates to capture cluster effects, simplifying the explanation of the noncluster covariate effects.

In Section 2, we introduce the stratified Fine–Gray model. In Section 3, we discuss partial likelihood inferences for the stratified model in the absence of independent censoring, along with inverse weighting estimation equations, which permit additional independent censoring. Inferential issues are presented in Section 4, with results for the two stratification regimes in separate subsections. Prediction of the cumulative incidence is discussed in Section 5. Section 6 discusses some simulation studies, with the analysis of the two motivating data sets following in Section 7. We conclude with a few remarks. Technical details are included in the Web Appendices.

2. Data and Model

Let T, C be the failure and censoring times, ε ∈ {1,…, m} be the cause of failure, and Z be a I × 1 vector of covariates. For right censored data, one observes {X = T ≤ C, Δ = I(T ≤ C), Δε, Z}, where a ∧ b = min(a, b). Here, as in Fine and Gray (1999), we permit Z to include time-varying covariates that are known, deterministic functions of time and time-independent covariates, and hence are fully observed. In the sequel, we suppress the dependence on time, when there is no loss of clarity. We are interested in assessing the effect of covariates on the cumulative incidence function for failure from cause 1, conditional on the covariates: F₁(t; Z) ≡ Pr(T ≤ t, ε = 1|Z). We assume (T, ε, Z) and C are independent given Z; assumptions for the dependence of C on stratum are described below.

Fine and Gray (1999) proposed a proportional hazards model for the subdistribution hazard λ₁(t;Z) = dF₁(t; Z)/{1 − F₁(t; Z)}. The model relates the covariates with λ₁(·) for independent and identically distributed (i.i.d.) observations {X_i, Δ_i, Δ_iε_i, Z_i}_{i=1,…, n} by ${\lambda }_1\left(t;{\mathbf{\text{Z}}}_i\right)={\lambda }_{10}\left(t\right)exp\left({\mathit{\text{β}}}_0^{\prime }{\mathbf{\text{Z}}}_i\right)$, where λ₁₀(·) is an unspecified, nonnegative function denoting the baseline subdistribution hazard when covariate Z = 0; β₀ is a l × 1 vector of unknown regression parameters.

The goal of our study is to introduce stratification to the Fine–Gray model. With stratification, we observe {X_ki, Δ_ki, Δ_kiε_ki, Z_ki}_{k=1,…,s;i=1,…,nk}, where k denotes the stratum, i denotes the subject within strata, and ${\sum }_{k=1}^s{n}_k=n$. For regularly stratified data, we assume i.i.d. observations within strata, whereas for highly stratified data, we will assume that information observed within a cluster is i.i.d. across strata; see condition 3 in Web Appendix A. When appropriate, the n observations can be denoted using single index: {X_l, Δ_l, Δ_lε_l, Z_l, K_l}_l=1,…,n, where K = k ∈ {1,…,s} gives the stratification information. We define the cumulative incidence function for stratum k as F_1k(t; Z) ≡ Pr(T ≤ t, ε = 1 | Z, K = k). Correspondingly, the proportional hazards specification for the subdistribution hazard for kth stratum λ_1k (t; Z) = dF_1k (t; Z)/{1 − F_1k (t; Z)} is

$${\lambda }_{1k}\left(t;{\mathbf{\text{Z}}}_{ki}\right)={\lambda }_{1k0}\left(t\right)exp\left({\mathit{\text{β}}}_0^{\prime }{\mathbf{\text{Z}}}_{ki}\right),$$ (1)

where λ_1k0 is the baseline subdistribution hazard in stratum k(= 1,…, s) and β₀ is the regression coefficient, which is assumed common to all strata. An important point is that no assumptions are made about the relationships between the baseline hazard functions.

3. Estimation

The estimation procedure is adapted from Fine and Gray (1999). The data are said to be complete when failure time T and failure cause ε are observed for all individuals; the data are censoring complete (CC) when the failure time is right censored but potential censoring time C is always observed. Starting from a modification of the partial likelihood for the subdistribution for complete or CC data, we then extend the estimation equation to classical right censored data.

3.1 Complete and Censoring Complete Data

With complete data, the risk set at time of failure of the ith subject in the kth stratum is R_ki = {i′ : (T_ki′ ≥ T_ki) ∪ (T_ki′ ≤ T_ki ∩ ε_ki′ ≠ 1)}. When the data are CC, the associated risk set is modified to R_ki = {i′ : (T_ki′ ∧ C_ki′ ≥ T_ki) ∪ (T_ki′ ≤ T_ki ∩ ε_ki′ ≠ 1 ∩ C_ki′ ≥ T_ki)}. We will detail the derivation of the partial likselihood approach for the CC data, because the complete data are special cases of the CC data by letting the censoring times be larger than the maximum failure time.

Let N_ki = I(T_ki ≤ t, ε_ki = 1) and Y_ki(t) = 1 − N_ki(t−) denote the counting process and risk process for the complete data, respectively. When the data are CC, the risk process is modified to $Y_{ki}^{\ast }\left(t\right)=I\left(C_{ki}\ge t\right)Y_{ki}\left(t\right)$. Applying the partial likelihood approach to λ_1k (t | Z), we obtain the corresponding partial likelihood

$$L^{\ast }\left(\beta \right)=\prod _{k=1}^s\prod _{i=1}^{n_k}{\left\{\frac{e^{{\mathit{\text{β}}}^{\prime }{\mathbf{\text{Z}}}_{ki}\left(X_{ki}\right)}}{\sum _{i=1}^{n_k}{Y}_{k{i}^{\prime }}^{\ast }\left(X_{ki}\right)e^{{\mathit{\text{β}}}^{\prime }{\mathbf{\text{Z}}}_{k{i}^{\prime }}\left(X_{ki}\right)}}\right\}}^{{\Delta }_{ki}I\left({\varepsilon }_{ki}=1\right)}=\prod _{k=1}^s\prod _{i=1}^{n_k}{\left\{\frac{e^{{\mathit{\text{β}}}^{\prime }{\mathbf{\text{Z}}}_{ki}\left(X_{ki}\right)}}{n_k{\mathbf{\text{S}}}_k^{\left(0\right)}\left(\mathit{\text{β}},X_{ki}\right)}\right\}}^{{\Delta }_{ki}I\left({\varepsilon }_{ki}=1\right)},$$

where

$${\mathbf{\text{S}}}_k^{\left(p\right)}\left(\mathit{\text{β}},t\right)=n_k^{-1}\sum _{i=1}^{n_k}{Y}_{ki}^{\ast }\left(t\right){\mathbf{\text{Z}}}_{ki}{\left(t\right)}^{\otimes p}{e}^{{\mathit{\text{β}}}^{\prime }{\mathbf{\text{Z}}}_{ki}\left(t\right)},p=0,1,2,$$

with a^⊗0 = 1, a^⊗1 = a, and a^⊗2 = aa^T. Differentiating the log partial likelihood in β yield the following estimating equation:

$${\mathit{\text{U}}}_1^{\ast }\left(\mathit{\beta },t\right)=\sum _{k=1}^s\sum _{i=1}^{n_k}{\int }_0^t\left\{{\mathbf{\text{Z}}}_{ki}\left(u\right)-{\overline{\text{Z}}}_k\left(\mathit{\text{β}},u\right)\right\}I\left(C_{ki}\ge u\right)d{N}_{ki}\left(u\right)$$ (2)

Where ${\overline{\mathbf{\text{Z}}}}_k\left(\mathit{\text{β}},t\right)={\mathit{\text{S}}}_k^{\left(1\right)}\left(\mathit{\beta },t\right)/{\mathit{\text{S}}}_k^{\left(0\right)}\left(\mathit{\text{β}},t\right)$. The estimator β̂, which maximizes L*(β) may be obtained as a solution to ${\mathbf{U}}_1^{\ast }\left(\mathit{\text{β}},\tau \right)=0$.

3.2 Weighted Estimating Equation for Right Censored Data

When classical right censoring is present, we can adapt inverse probability of censoring weighting techniques (Robins and Rotnitzky, 1992) to construct an unbiased estimating function, as proposed by Fine and Gray (1999). Let G(·) be the survival function of the censoring variable with highly stratified data and G_k(·) be the survival function of the censoring variable in the kth stratum with the regular stratification. The implicit weight I(C_ki ≥ t) with the CC data is replaced by w_ki(t) = I(C_ki ≥ T_ki ∧ t)G_k (t)/G_k (X_ki ∧ t), where G_k (t) = Pr(C_ki ≥ t), i = 1,…, n_k, for each k with regularly stratified data, assuming the censoring distribution is stratum dependent. For highly stratified data, the replacement would be w_ki (t) = I(C_ki ≥ T_ki ∧ t)G(t)/G(X_ki ∧ t), and G(t) = Pr(C_ki ≥ t), k = 1,…, s; i = 1,…, n_k, assuming random vectors (n_k, C_k1,…, C_knk) are i.i.d. across k, but allow the dependence in the censoring times in a given stratum. That is, arbitrary dependence among C_k1,…, C_knk would be allowed.

The difference in the assumptions for the two data regimes has to do with the consistency of the potential estimator of the censoring time distribution. For regularly stratified data, the size of each stratum goes to infinity. We can afford to allow for the dependence between censoring time C and strata K. Therefore, G_k(·) is used. If strata sizes are finite, we cannot consistently estimate the censoring distribution in each strata. Information must be pooled across strata via the assumption of a single G, as is employed with highly stratified data.

Because the distribution of the censoring random variable is unknown in either stratification regime, G_k(·)(G(·)) needs to be estimated: Ĝ_k(·), the Kaplan–Meier estimate of the survival function of the censoring random variable in the kth stratum is used with regular stratification and Ĝ(·), the Kaplan–Meier estimate of the survival function of the censoring random variable, is used with highly stratified data. Only patients from the kth stratum are used in the calculation of ŵ_ki(t) for regularly stratified data because the stratum sizes go to infinity. In contrast, for highly stratified data, patients from all strata are used in Ĝ.

The estimated weights are ŵ_ki (t) = I(C_ki ≥ T_ki ∧ t)Ĝ_k(t)/Ĝ_k (X_ki ∧ t) or ŵ_ki (t) = I(C_ki ≥ T_ki ∧ t)Ĝ(t)/Ĝ(X_ki ∧ t) such that ŵ_ki(t) → w_ki(t) as n → ∞ for both stratification schemes. That is,

$${\widehat{w}}_{ki}\left(t\right)=\{\begin{array}{ll}0\hfill & \mathrm{\text{if}}\mathrm{\text{right}}\mathrm{\text{censored}}\hfill \\ {\stackrel{⌢}{G}}_k\left(t|X_{ki}\right)\mathrm{\text{or}}\stackrel{⌢}{G}\left(t|X_{ki}\right)\hfill & \mathrm{\text{if}}\mathrm{\text{failed}}\hfill \\ 1\hfill & \mathrm{\text{otherwise}}.\hfill \end{array}$$

The resulting weighted score function is:

$$U_1\left(\mathit{\text{β}},t\right)=\sum _{k=1}^s\sum _{i=1}^{n_k}{\int }_0^t\left\{Z_{ki}\left(u\right)-\frac{\sum _{i^{\prime }=1}^{n_k}{\stackrel{⌢}{w}}_{k{i}^{\prime }}\left(u\right)Y_{k{i}^{\prime }}\left(u\right)Z_{k{i}^{\prime }}\left(u\right)e^{{\mathit{\text{β}}}^{\prime }{Z}_{k{i}^{\prime }}\left(u\right)}}{\sum _{i^{\prime }=1}^{n_k}{\stackrel{⌢}{w}}_{k{i}^{\prime }}\left(u\right)Y_{k{i}^{\prime }}\left(u\right)e^{{\mathit{\text{β}}}^{\prime }{Z}_{k{i}^{\prime }}\left(u\right)}}\right\}$$

$${\stackrel{⌢}{w}}_{k{i}^{\prime }}\left(u\right)d{N}_{ki}\left(u\right)=\sum _{k=1}^s\sum _{i=1}^{n_k}{\int }_0^t\left\{{\mathbf{\text{Z}}}_{ki}\left(u\right)-{\stackrel{⌢}{\mathbf{\text{Z}}}}_k\left(\mathit{\text{β}},u\right)\right\}{\stackrel{⌢}{w}}_{ki}\left(u\right)d{N}_{ki}\left(u\right),$$ (3)

where ${\widehat{\text{S}}}_k^{\left(p\right)}\left(\mathit{\text{β}},t\right)=n_k^{-1}{\sum }_{i=1}^{n_k}{\widehat{w}}_{ki}\left(t\right)Y_{ki}\left(t\right){\mathbf{\text{Z}}}_{ki}{\left(t\right)}^{\otimes p}{e}^{{\mathit{\text{β}}}^{\prime }{\mathbf{\text{Z}}}_{ki}\left(t\right)}$, ${\widehat{\mathbf{\text{Z}}}}_k\left(\mathit{\text{β}},t\right)={\widehat{S}}_k^{\left(1\right)}\left(\mathit{\text{β}},t\right)/{\widehat{S}}_k^{\left(0\right)}\left(\mathit{\text{β}},t\right),p=0,1,2$. The estimator of β̂ is obtained by zeroing the estimating equation (3).

4. Inference

In this section, we consider the asymptotic properties of the estimators for different data regimes. In each case, the consistency of β̂ comes first. Then the asymptotic normality of $n^{-\frac{1}{2}}{\mathit{\text{U}}}_1^{\ast }\left({\mathit{\text{β}}}_0,\tau \right)$ or $n^{-\frac{1}{2}}{\mathit{\text{U}}}_1\left({\mathit{\text{β}}}_0,\tau \right)$ is shown. Asymptotic normality of ${\mathit{\text{n}}}^{\frac{1}{2}}\left(\widehat{\mathit{\text{β}}}-{\mathit{\text{β}}}_0\right)$ is obtained by Taylor series approximation and the first two results. Variance estimation follows.

4.1 Regularly Stratified Data

In this scenario, the number of strata s is finite. When n → ∞, n_k → ∞, for each k = 1,…, s.

We start from the CC data. Under the regularity conditions stated in Web Appendix A, we can show that β̂ is consistent by adapting the consistency result of β̂ in Andersen and Gill (1982). Then by Taylor series expansion and the consistency of $\mathit{\text{β}}^,n^{\frac{1}{2}}\left(\widehat{\mathit{\text{β}}}-{\mathit{\text{β}}}_0\right)\approx {\mathbf{\Omega }}_r^{-1}\left\{n^{-\frac{1}{2}}{\mathit{\text{U}}}_1^{\ast }\left({\mathit{\text{β}}}_0,\tau \right)\right\}$, where Ω_r is the limit of the negative of the partial derivative matrix of the score function ${\mathit{\text{U}}}_1^{\ast }\left(\mathit{\text{β}},\mathit{\tau }\right)$ evaluated at β₀. Clearly, ${\mathit{\text{U}}}_1^{\ast }\left(\mathit{\text{β}},t\right)={\sum }_{k=1}^s{\mathit{\text{U}}}_{1k}^{\ast }\left(\mathit{\text{β}},t\right)$, where each component ${\mathit{\text{U}}}_{1k}^{\ast }\left(\mathit{\text{β}},t\right)={\sum }_{i=1}^{n_k}{\int }_0^t\left\{{\mathbf{\text{Z}}}_{ki}\left(u\right)-{\overline{\mathbf{\text{Z}}}}_k\left(\mathit{\text{β}},u\right)\right\}I\left(C_{ki}\ge u\right)d{N}_{ki}\left(u\right)$ and by Fine and Gray (1999), as $n_k\to \infty ,n_k^{-\frac{1}{2}}{\mathit{\text{U}}}_{1k}^{\ast }\left({\mathit{\text{β}}}_0,\tau \right)\stackrel{D}{\to }N\left(0,{\mathbf{\Omega }}_{rk}\right)$ with

$${\mathbf{\Omega }}_{rk}={\int }_0^{\tau }\left\{s_k^{\left(2\right)}\left({\mathit{\text{β}}}_0,t\right)/s_k^{\left(0\right)}\left({\mathit{\text{β}}}_0,t\right)-e_k{\left({\mathit{\text{β}}}_0,t\right)}^{\otimes 2}\right\}\times s_k^{\left(0\right)}\left({\mathit{\text{β}}}_0,t\right){\lambda }_{0k}\left(t\right)dt,$$

where $s_k^{\left(p\right)}\left(\mathit{\text{β}},t\right)={lim}_{nk\to \infty }{n}_k^{-1}{\sum }_{i=1}^{n_k}{Y}_{ki}^{\ast }\left(t\right){\mathbf{\text{Z}}}_{ki}{\left(t\right)}^{\otimes p}{e}^{{\mathit{\text{β}}}^{\prime }{\mathbf{\text{Z}}}_{ki}}$, and $e_k\left(\mathit{\text{β}},t\right)=s_k^{\left(1\right)}\left(\mathit{\text{β}},t\right)/s_k^{\left(0\right)}\left(\mathit{\text{β}},t\right),p=0,1,2$. It follows that ${\sum }_{k=1}^s{\pi }_k{\mathbf{\Omega }}_{rk}={\mathbf{\Omega }}_r$, Where p_k = n_k/n → π_k. Thus, as $n\to \infty ,n^{-\frac{1}{2}}{\mathit{\text{U}}}_1^{\ast }\left({\mathit{\text{β}}}_0,\tau \right)={\sum }_{i=1}^s{p}_k^{\frac{1}{2}}{n}_k^{-\frac{1}{2}}{\mathit{\text{U}}}_{1k}^{\ast }\left({\mathit{\text{β}}}_0,\tau \right)\stackrel{D}{\to }N\left(0,{\mathbf{\Omega }}_r\right)$. Hence, $n^{-\frac{1}{2}}\left(\widehat{\mathit{\text{β}}}-{\mathit{\text{β}}}_0\right)\stackrel{D}{\to }N\left(0,{\mathbf{\Omega }}_r^{-1}\right)$.

A consistent estimate of the covariance matrix for the regression coefficients can be obtained by replacing the unknown quantities with their observed values. We have

$${\stackrel{⌢}{\mathbf{\Omega }}}_r=\frac{1}{n}\sum _{k=1}^s\sum _{i=1}^{n_k}{\Delta }_{ki}I\left({\varepsilon }_{ki}=1\right)\times \left[\frac{{\mathit{\text{S}}}_k^{\left(2\right)}\left(\stackrel{⌢}{\mathit{\text{β}}},X_{ki}\right)}{{\mathit{\text{S}}}_k^{\left(0\right)}\left(\stackrel{⌢}{\mathit{\text{β}}},X_{ki}\right)}-{\left\{\frac{{\mathit{\text{S}}}_k^{\left(1\right)}\left(\stackrel{⌢}{\mathit{\text{β}}},X_{ki}\right)}{{\mathit{\text{S}}}_k^{\left(0\right)}\left(\stackrel{⌢}{\mathit{\text{β}}},X_{ki}\right)}\right\}}^{\otimes 2}\right].$$

When the data are right censored, by applying results of weighted score function for incomplete data (Fine and Gray, 1999) to each component of ${\mathit{\text{U}}}_1\left(\mathit{\text{β}},t\right):{\mathit{\text{U}}}_{1k}\left(\mathit{\text{β}},t\right)={\sum }_{i=1}^{n_k}{\int }_0^t\left\{{\mathbf{\text{Z}}}_{ki}\left(u\right)-{\widehat{\mathbf{\text{Z}}}}_k\left(\mathit{\text{β}},u\right)\right\}{\widehat{w}}_{ki}\left(u\right)d{N}_{ki}\left(u\right)$, the asymptotic properties for right censored stratified data may be established. One may show that as $n\to \infty ,n^{-1}\left\{{\mathit{\text{U}}}_1\left(\mathit{\text{β}},\tau \right)-{\mathit{\text{U}}}_1^{\ast }\left(\mathit{\text{β}},\tau \right)\right\}={\sum }_{i=1}^s{p}_k{n}_k^{-1}\left\{{\mathit{\text{U}}}_{1k}\left(\mathit{\text{β}},\tau \right)-{\mathit{\text{U}}}_{1k}^{\ast }\left(\mathit{\text{β}},\tau \right)\right\}$ goes in probability to 0 uniformly for β in a compact neighborhood of β₀. Therefore, β̂, the solution to U₁(β, τ) = 0 is consistent for β₀. Furthermore, for each $n_k^{-\frac{1}{2}}{\mathit{\text{U}}}_{1k}\left({\mathit{\text{β}}}_0,\tau \right)\stackrel{D}{\to }N\left(0,{\sum }_{rk}\right)$, where Σ_rk = E{(η_ki + ψ_ki)^⊗2}. The details of η_ki and ψ_ki for each k are omitted here because they are identical to η_i and ψ_i in Fine and Gray (1999), with the added subscript k. Because U_1k are independent, $n^{-\frac{1}{2}}{\mathit{\text{U}}}_1\left({\mathit{\text{β}}}_0,\tau \right)={\sum }_{k=1}^s{p}^{\frac{1}{2}}{n}_k^{-\frac{1}{2}}{\mathit{\text{U}}}_{1k}\left({\mathit{\text{β}}}_0,\tau \right)$ is asymptotically normally distributed as N(0,Σ_r), where ${\sum }_r={\sum }_{k=1}^s{\pi }_k{\sum }_{rk}$. Similar to CC data, $n^{\frac{1}{2}}\left(\widehat{\mathit{\text{β}}}-{\mathit{\text{β}}}_0\right)\approx {\mathbf{\Omega }}_r^{-1}\left\{n^{-\frac{1}{2}}{\mathit{\text{U}}}_1\left({\mathit{\text{β}}}_0,\tau \right)\right\}$, where ${\mathbf{\Omega }}_{\mathit{\text{r}}}^{-1}$ has the same form as the variance in the CC case. Hence, the distribution of ${\mathit{\text{n}}}^{\frac{1}{2}}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)$ is asymptotically normal with covariance matrix ${\mathbf{\Omega }}_r^{-1}{\sum }_r{\mathbf{\Omega }}_r^{-1}$.

To estimate the covariance matrix for the regression coefficients, we need to find a consistent estimator of Ω_r and Σ_r. The estimator of Ω_r is Ω̂_r with ${\widehat{\mathit{\text{S}}}}_k^{\left(p\right)}$ replacing ${\mathit{\text{S}}}_k^{\left(p\right)}$ for each k, p = 0, 1, 2. Each component of Σ_r, Σ_rk can be estimated with the empirical covariance matrix ${\widehat{\sum }}_{rk}=n_k^{-1}{\sum }_i{\left({\widehat{\eta }}_{ki}+{\widehat{\psi }}_{ki}\right)}^{\otimes 2}$. For brevity, we do not show the details of η̂_ki and ψ̂_ki, which can be obtained by adding subscript k to η̂_i and ψ̂_i in Fine and Gray (1999). Therefore, the distribution of ${\mathit{\text{n}}}^{\frac{1}{2}}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)$ can be approximated by a normal distribution with variance $n{\left\{{\sum }_{k=1}^{\mathit{\text{S}}}{n}_k{\widehat{\mathbf{\Omega }}}_{rk}\right\}}^{-1}\left\{{\sum }_{k=1}^{\mathit{\text{S}}}{n}_k{\widehat{\sum }}_{rk}\right\}{\left\{{\sum }_{k=1}^{\mathit{\text{S}}}{n}_k{\widehat{\mathbf{\Omega }}}_{rk}\right\}}^{-1}$.

4.2 Highly Stratified Data

In this scenario, the strata size n_k is finite, k = 1,…, s, s → ∞ as n → ∞.

As in the regularly stratified data, we consider the CC situation first. In Web Appendix B, we show β̂ is consistent under regularity conditions listed in Web Appendix A. We can further show asymptotic normality of $n^{-\frac{1}{2}}{\mathit{\text{U}}}_1^{\ast }\left({\mathit{\beta }}_0,\tau \right)$ as follows. Because $M_{ki}^{\ast }\left(\mathit{\beta },t\right)={\int }_0^{t}I\left(C_{ki}\ge u\right)d{N}_{ki}\left(t\right)-{\int }_0^t{Y}_{ki}^{\ast }\left(u\right){\lambda }_{k0}\left(u\right)e^{{\mathit{\beta }}^{\prime }{\mathbf{\text{Z}}}_{ki}\left(u\right)}du$ is a martingale for CC data filtration $F^{\ast }\left(t\right)=\sigma \left\{I\left(C_{ki}\ge u\right),I\left(C_{ki}\ge u\right)N_{ki}\left(u\right),Y_{ki}^{\ast }\left(u\right),Z_{ki}\left(u\right),u\le t,k=1,\dots ,s;i=1,\dots ,n\right\}$ (Fine and Gray, 1999), we can reexpress ${\mathit{\text{U}}}_1^{\ast }\left(\mathit{\beta },\mathit{\text{t}}\right)$ as a martingale-type estimation equation:

$${\mathit{\text{U}}}_1^{\ast }\left(\mathit{\beta },t\right)=\sum _{k=1}^{\mathit{\text{S}}}\sum _{i=1}^{n_k}{\int }_0^t\left\{{\mathbf{\text{Z}}}_{ki}\left(u\right)-{\overline{\mathbf{\text{Z}}}}_k\left(\mathit{\beta },u\right)\right\}d{M}_{ki}^{\ast }\left(\mathit{\beta },u\right).$$

Applying the martingale central limit theorem (Rebolledo, 1980), ${\mathit{\text{n}}}^{-\frac{1}{2}}{\mathit{\text{U}}}_1^{\ast }\left({\mathit{\beta }}_0,\cdot \right)$ converges in distribution to a continuous Gaussian process. At time $t=\tau ,n^{-\frac{1}{2}}{\mathit{\text{U}}}_1^{\ast }\left({\mathit{\beta }}_0,\tau \right)\stackrel{p}{\to }N\left(0,{\mathbf{\Omega }}_h\right)$, where

$${\mathbf{\Omega }}_h=\underset{n\to \infty }{lim}{n}^{-1}\sum _{k=1}^{\mathit{\text{S}}}\mathbf{\text{E}}\left[\sum _{k=1}^{n_k}{\int }_0^{\tau }{\left\{{\mathbf{\text{Z}}}_{ki}\left(u\right)-{\overline{\mathbf{\text{Z}}}}_k\left({\mathit{\beta }}_0,u\right)\right\}}^{\otimes 2}\times Y_{ki}^{\ast }\left(u\right)e^{{{\mathit{\beta }}^{\prime }}_0{\mathbf{\text{Z}}}_{ki}\left(u\right)}{\lambda }_{k0}\left(u\right)du\right].$$ (4)

Some algebra proves that equation (4) satisfies

$${\mathbf{\Omega }}_h=\underset{n\to \infty }{lim}{n}^{-1}\sum _{k=1}^{\mathit{\text{S}}}\mathbf{\text{E}}\left[\sum _{i=1}^{n_k}{\int }_0^{\tau }{\left\{{\mathbf{\text{Z}}}_{ki}\left(u\right)-{\overline{\mathbf{\text{Z}}}}_k\left({\mathit{\beta }}_0,u\right)\right\}}^{\otimes 2}\times Y_{ki}^{\ast }\left(u\right)e^{{{\mathit{\beta }}^{\prime }}_0{\mathbf{\text{Z}}}_{ki}\left(u\right)}\frac{d{\overline{N}}_k\left(u\right)}{{\mathit{\text{S}}}_k^{\left(0\right)}\left({\mathit{\beta }}_0,u\right)}\right].$$

Similar to the regularly stratified data, Ω_h is equal to the limit of the negative of the partial derivative matrix of the score function evaluated at β₀. In addition, $n^{\frac{1}{2}}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)\approx {\mathbf{\Omega }}_h^{-1}\left\{n^{-\frac{1}{2}}{\mathit{\text{U}}}_1^{\ast }\left({\mathit{\beta }}_0,\tau \right)\right\}$. Thus, $n^{-\frac{1}{2}}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)\stackrel{D}{\to }N\left(0,{\mathbf{\Omega }}_h^{-1}\right)$. Note that m̄Ω_h equals to I defined in condition (4) of Web Appendix A, where m̄ is the average strata size as n → ∞.

Replacing the unknown quantities in Ω_h with their observed values gives

$${\widehat{\mathbf{\Omega }}}_h=\frac{1}{n}\sum _{k=1}^{\mathit{\text{S}}}\sum _{i=1}^{n_k}{\Delta }_{ki}I\left({\varepsilon }_{ki}=1\right)\times \left[\frac{{\mathit{\text{S}}}_k^{\left(2\right)}\left(\widehat{\mathit{\beta }},X_{ki}\right)}{{\mathit{\text{S}}}_k^{\left(0\right)}\left(\widehat{\mathit{\beta }},X_{ki}\right)}-{\left\{\frac{{\mathit{\text{S}}}_k^{\left(1\right)}\left(\widehat{\mathit{\beta }},X_{ki}\right)}{{\mathit{\text{S}}}_k^{\left(0\right)}\left(\widehat{\mathit{\beta }},X_{ki}\right)}\right\}}^{\otimes 2}\right],$$

an analogous formulation to that for Ω̂_r.

When the data are right censored, β̂ is consistent as shown in Web Appendix C.1. We also establish that $n^{\frac{1}{2}}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)\approx {\stackrel{\sim }{\mathbf{\Omega }}}_h^{-1}\left\{n^{-\frac{1}{2}}{\mathit{\text{U}}}_1\left({\mathit{\beta }}_0,\tau \right)\right\}$, where

$${\stackrel{\sim }{\mathbf{\Omega }}}_h=\underset{n\to \infty }{lim}{n}^{-1}\sum _{k=1}^{\mathit{\text{S}}}\mathbf{\text{E}}\left[\sum _{i=1}^{n_k}{\int }_0^{\tau }{\left\{{\mathbf{\text{Z}}}_{ki}\left(u\right)-{\stackrel{\sim }{\mathbf{\text{Z}}}}_k\left({\mathit{\beta }}_0,u\right)\right\}}^{\otimes 2}\times w_{ki}\left(u\right)Y_{ki}\left(u\right)e^{{{\mathit{\beta }}^{\prime }}_0{\mathbf{\text{Z}}}_{ki}\left(u\right)}\frac{d{\overline{N}}_k\left(u\right)}{{\stackrel{\sim }{\mathit{\text{S}}}}_k^{\left(0\right)}\left({\mathit{\beta }}_0,u\right)}\right].$$

We show in Web Appendix C.2 that ${\mathit{\text{S}}}^{-\frac{1}{2}}\mathit{\text{U}}\left({\mathit{\beta }}_0,\tau \right)={\mathit{\text{S}}}^{-\frac{1}{2}}{\sum }_{k=1}^{\mathit{\text{S}}}\left({\eta }_k+{\psi }_k\right)+o_p\left(1\right)$ is asymptotically normal with co-variance matrix Σ_h = E{(η_k + ψ_k)(η_k + ψ_k)^T}, where

$${\psi }_k=\sum _{i=1}^{n_k}{\int }_0^{\infty }\mathbf{\text{q}}\left(y\right)/\left\{\overline{m}\pi \left(y\right)\right\}d{M}_{ki}^c\left(y\right),$$

$${\eta }_k=\sum _{i=1}^{n_k}{\int }_0^t\left\{{\mathbf{\text{Z}}}_{ki}\left(u\right)-{\stackrel{\sim }{\mathbf{\text{Z}}}}_k\left({\mathit{\beta }}_0,u\right)\right\}{w}_{ki}\left(u\right)d{N}_{ki}\left(u\right),$$

$$\pi \left(y\right)=\underset{n\to \infty }{lim}\frac{1}{n}\sum _{i=1}^{n}I\left(X_t\ge y\right),$$

$$\mathbf{\text{q}}\left(y\right)=\mathbf{\text{E}}\left[\sum _{i=1}^{n_k}\sum _{j=1}^{n_k}{\int }_0^t{A}_{kj}\left({\mathit{\beta }}_0,u\right)\times I\left(X_{kj}<y\le u\right)w_{kj}\left(u\right)d{N}_{ki}\left(u\right)\right],$$

, and

$$A_{kj}\left({\mathit{\beta }}_0,u\right)=\frac{Y_{kj}\left(u\right)e^{{{\mathit{\beta }}^{\prime }}_0{\mathbf{\text{Z}}}_{kj}\left(t\right)}}{n{\stackrel{\sim }{\mathit{\text{S}}}}_k^{\left(0\right)}\left({\mathit{\beta }}_0,u\right)}\times \left\{{\mathbf{\text{Z}}}_{kj}\left(u\right)-{\stackrel{\sim }{\mathbf{\text{Z}}}}_k\left({\mathit{\beta }}_0,u\right)\right\}.$$

Here, Z˜_k(β₀,·) is Ẑ_k(β₀,·) with ŵ_ki(·) being replaced by w_ki(·), and $M_{ki}^c(\cdot )$ is the martingale associated with the censoring process.

It follows that ${\mathit{\text{n}}}^{\frac{1}{2}}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)$ is asymptotically normal with covariance matrix ${\stackrel{\sim }{\mathbf{\Omega }}}_h^{-1}\left({\overline{m}}^{-1}{\sum }_h\right){\stackrel{\sim }{\mathbf{\Omega }}}_h^{-1}$.

The estimator of Ω˜_h is Ω̂_h with ${\widehat{\mathit{\text{S}}}}_k^{\left(p\right)}$ replacing ${\mathit{\text{S}}}_k^{\left(p\right)}$ for all k and p as in the regularly stratified case. The inner matrix in the variance, Σ_h, can be estimated empirically by $1/\mathit{\text{S}}{\sum }_{k=1}^{\mathit{\text{S}}}{\left({\widehat{\eta }}_k+{\widehat{\psi }}_k\right)}^{\otimes 2}$, where

$${\widehat{\eta }}_k=\sum _{i=1}^{n_k}{\int }_0^{\infty }\left\{{\mathbf{\text{Z}}}_{ki}\left(u\right)-{\widehat{\mathbf{\text{Z}}}}_k\left(\widehat{\mathit{\beta }},u\right)\right\}{\widehat{w}}_{ki}\left(u\right)d{N}_{ki}\left(\widehat{\mathit{\beta }},u\right),$$

$${\widehat{\psi }}_k=\sum _{i=1}^{n_k}{\int }_0^{\infty }\widehat{\text{Q}}\left(\widehat{\beta },y\right){\left\{\sum _{l=1}^{n}I\left(X_l\ge y\right)/s\right\}}^{-1}d{\widehat{M}}_{ki}^c\left(y\right),$$

$${\widehat{M}}^c\left(y\right)=I\left(X\le y,\Delta =0\right)-{\int }_0^{y}I\left(X\ge t\right)d{\widehat{\wedge }}^c\left(t\right),$$

$${\widehat{\wedge }}^c\left(t\right)={\int }_0^t{\left\{\sum _{l=1}^{n}I\left(X\ge y\right)\right\}}^{-1}\sum _{l=1}^{n}dI\left(X\le u,\Delta =0\right),$$

$$\widehat{Q}\left(\widehat{\mathit{\beta }},y\right)={\mathit{\text{s}}}^{-1}\sum _{k=1}^{\mathit{\text{S}}}\sum _{i=1}^{n_k}\sum _{j=1}^{n_k}{\int }_0^{\infty }{\widehat{A}}_{kj}\left(\widehat{\mathit{\beta }},u\right)I\left(X_{kj}<y\le u\right)\times {\widehat{w}}_{kj}\left(u\right){\widehat{w}}_{ki}\left(u\right)d{N}_{ki}\left(u\right),$$

and Â_kj is defined analogous to A_kj with Z˜ replaced by Ẑ and S˜ replace by Ŝ.

This variance estimator can be unstable in small sample sizes, owing to variability in Ĝ in the tails and the small within cluster sample sizes. As an alternative, bootstrap variance estimation is introduced for highly stratified right censored data. Adapting the simple bootstrap sampling for censored data (Efron, 1981), we have the following scheme:

1. Draw a bootstrap sample by independently sampling s times with replacement from the s strata. This corresponds to drawing repeated from the empirical distribution of the strata, which puts equal mass, 1/s, on each stratum;

2. Let data* represent this artificial data set, calculate β̂*;

3. Independently repeat the above steps B times, obtaining B regression coefficient estimates, denoted ${\widehat{\mathit{\beta }}}_i^{\ast },i=1,\dots ,B$;

4. Calculate the sample standard deviation of the ${\widehat{\mathit{\beta }}}_i^{\ast },i=1,\dots ,B$, and use this as an estimate of the standard error of β̂.

This resampling approach is valid under the assumption that data within cluster are i.i.d. across clusters.

5. Predicting Cumulative Incidence

To predict cumulative incidence at time t for a patient with covariates Z = z, we need an estimator of the baseline cumulative subdistribution hazard. This estimator can be obtained using a variation of Breslow's (1974) estimator for regularly stratified data, but is infeasible for highly stratified data due to finite strata sizes. In this section, we will briefly discuss the estimators of the cumulative subdistribution hazard for regularly stratified data and the associated cumulative incidence estimators for individuals with certain covariate values.

With CC data, for each stratum k, the Breslow type estimator is

$${\widehat{\wedge }}_{k0}^{\ast }\left(t\right)=\frac{1}{n_k}\sum _{i=1}^{n_k}{\int }_0^t\frac{1}{{\mathit{\text{S}}}_k^{\left(0\right)}\left(\widehat{\mathit{\beta }},u\right)}|\left(C_{ki}\ge u\right)d{N}_{ki}\left(u\right),k=1,\dots ,\mathit{\text{s}},$$

where β̂ is defined in Section 4. Thus, the cumulative subdistribution hazard for a patient with covariates Z = z at time t is estimated by

$${\widehat{\Lambda }}_k^{\ast }\left(t,\mathbf{\text{z}}\right)={\int }_0^{t}exp\left\{{\widehat{\mathit{\beta }}}^{\prime }\left(u\right)\right\}d{\widehat{\Lambda }}_{ki}\left(u\right)=\frac{1}{n_k}\sum _{i=1}^{n_k}{\int }_0^t\frac{exp\left\{{\widehat{\mathit{\beta }}}^{\prime }\mathbf{\text{z}}\left(u\right)\right\}}{{\mathit{\text{S}}}_k^{\left(0\right)}\left(\widehat{\mathit{\beta }},u\right)}|\left(C_{ki}\ge u\right)d{N}_{ki}\left(u\right),k=1,\dots ,\mathit{\text{s}}.$$

When the data are right censored, our estimator of the baseline cumulative subdistribution hazard for stratum k is

$${\widehat{\Lambda }}_{k0}\left(t\right)=\frac{1}{n_k}\sum _{i=1}^{n_k}{\int }_0^t\frac{{\widehat{w}}_{ki}\left(u\right)}{{\widehat{\mathit{\text{S}}}}_k^{\left(0\right)}\left(\widehat{\mathit{\beta }},u\right)}d{N}_{ki}\left(u\right).$$ (5)

This is essentially the Breslow estimator, after incorporating the inverse probability of censoring weights to account for independent right censoring. The corresponding cumulative subdistribution hazard is estimated by

$${\widehat{\Lambda }}_k\left(t,\mathbf{\text{z}}\right)=\frac{1}{n_k}\sum _{i=1}^{n_k}{\int }_0^t\frac{exp\left\{{\widehat{\mathit{\beta }}}^{\prime }\mathbf{\text{z}}\left(u\right)\right\}}{{\widehat{\mathit{\text{S}}}}_k^{\left(0\right)}\left(\widehat{\mathit{\beta }},u\right)}{\widehat{w}}_{ki}\left(u\right)d{N}_{ki}\left(u\right),k=1,\dots ,\mathit{\text{s}}.$$

Now that we have obtained the estimators of the cumulative subdistribution hazards at time t for a patient with covariates z, we can predict the cumulative incidence by ${\widehat{F}}_{1k}\left(t,\mathbf{\text{z}}\right)=1-exp\left\{-{\widehat{\Lambda }}_k^{\ast }\left(t,\mathbf{\text{z}}\right)\right\}$ for CC data, or F̂_1k (t, z) = 1 − exp{−Λ̂_k (t, z)} for right censored data. Confidence intervals and bands for ${\widehat{F}}_{1k}\left(t,\mathbf{\text{z}}\right),{\widehat{\Lambda }}_k^{\ast }(t,\mathbf{\text{z}}\text{or}{\widehat{\Lambda }}_k\left(t,\mathbf{\text{z}}\right)$ can be constructed along the lines of Fine and Gray (1999). They are easily obtained by adding stratum information k to the earlier results. The details are omitted.

As stated previously, we are not able to predict cumulative incidence using highly stratified data. We can only evaluate the effect of risk factors on the cumulative incidence.

6. Simulation Experiments

Numerical investigations were conducted to assess the performance of the proposed weighted estimation approach. We compared the estimators from the stratified weighted score function (3) to the stratified censoring complete (CCS) estimators (described in Section 3.1) and the CC estimators (described in Section 3.2 of Fine and Gray, 1999). The objective is to assess potential biases in ignoring the stratification information when naively using the unstratified analyses versus the stratified analyses, which appropriately account for such stratification.

In all sets of simulations, data were generated repeatedly 1000 times. Within each replicate, we employed the algorithm used by Fine and Gray (1999) to generate the data for each stratum. Two competing risks were considered. The subdistribution for type 1 failure was given by $F_{1k}(t;\mathbf{\text{Z}}=Pr(T_{ki}\le t,{\varepsilon }_{ki}=1|{\mathbf{\text{Z}}}_{ki}=1-{\left\{1-p+p{e}^{-{\rho }_{k}t\gamma k}\right\}}^{exp\left({{\mathit{\beta }}^{\prime }}_1{\mathbf{\text{Z}}}_{ki}\right)}$, which is a weibull mixture with mass 1 − p at ∞ when Z_ki = 0, and uses the proportional subdistribution hazards for nonzero covariate values. The subdistribution for type 2 failure was then obtained by taking Pr(ε_ki = 2 | Z_ki) = 1 − Pr(ε_ki = 1 | Z_ki) and using an exponential distribution with rate $exp\left({{\mathit{\beta }}^{\prime }}_2{\mathbf{\text{Z}}}_{ki}\right)$ for Pr(T_ki ≤ t| ε_ki = 2, Z_ki). Censoring times were generated from the uniform [a,b] distribution.

6.1 Simulation of Regularly Stratified Data

We present two sets of simulations to demonstrate the performance of the weighted estimation function when the number of strata is fixed. In both sets of simulations, we considered 3 strata; covariates are i.i.d. given stratum; (ρ₁, ρ₂, ρ₃) = (1,.3,2), (γ₁, γ₂, γ₃) = (.5,2,1); and p = 0.6.

First, we generated data by assuming the true parameter values (β₁,β₂) to be (0, −0.5) for normal covariates, which have unit variance and varying means of 0, 1, or 2; and assuming (β₁,β₂) to be (0, 1) for Bernoulli covariates with means of .3, .5, or .7 for the three strata, respectively. Censoring times were generated from a uniform [a,b] distribution with a and b being specified to reach the targeted percentage of censored observations. We used two different percentages of censoring for each. Table 1 gives the empirical sizes of CC, CCS, and stratified weighted (WS) score tests for sample sizes of 100, 250, 500, and 1000 at the nominal level of 0.05. As the sample size increases, the empirical size of the unstratified test (CC) deviates substantially from the nominal level, especially for the normal covariates. The stratified weighted tests and the CCS tests both achieve close to the nominal level.

Table 1. Comparison of empirical sizes of tests from CC, CCS, weighted stratified (WS) estimating equations (regularly stratified data).

Z	[a,b]	n	s	cen	β1	CC	CCS	WS
Normal	[∞, ∞]	100	3	0	0	0.075	0.048	0.060
		250	3	0	0	0.081	0.059	0.058
		500	3	0	0	0.123	0.055	0.058
		1000	3	0	0	0.143	0.051	0.055
Normal	[0, 1.7]	100	3	0.55	0	0.089	0.059	0.071
		250	3	0.55	0	0.099	0.054	0.057
		500	3	0.54	0	0.251	0.047	0.045
		1000	3	0.55	0	0.340	0.052	0.052
Bernoulli	[∞, ∞]	100	3	0	0	0.061	0.045	0.052
		250	3	0	0	0.071	0.043	0.045
		500	3	0	0	0.078	0.048	0.050
		1000	3	0	0	0.106	0.045	0.046
Bernoulli	[0.5, 1.5]	100	3	0.36	0	0.056	0.043	0.052
		250	3	0.36	0	0.062	0.056	0.057
		500	3	0.34	0	0.104	0.051	0.051
		1000	3	0.35	0	0.178	0.052	0.050

Next, we changed (β₁,β₂) to (0.5, −0.5) for normal covariates; and (1,1) for Bernoulli covariates, keeping other items unchanged. The sample size was 250 for each replicate. Table 2 gives E(β̂₁), estimated with the average of the β̂₁ from the 1000 replicates; var(β̂₁), estimated with the empirical variance of β̂₁; and E(var̂), the average of the variance estimators of β̂₁. As expected, the performances of the two stratified approaches are better than the unstratified approach, which exhibits substantial bias. Both of the stratified approaches gave very similar results, with small biases and similar variances.

Table 2. Comparison of parameter estimates from CC, CCS, stratified weighted (WS) estimating equations (regularly stratified data).

Z	[a,b]	cen	Eq.	β1	β̂1	var(β̂1)	E(var̂1)
Normal	[∞, ∞]	0	CC	0.5	0.551	0.005	0.004
			CCS	0.5	0.504	0.007	0.006
			WS	0.5	0.504	0.007	0.006
Normal	[0.5, 1.5]	0.37	CC	0.5	0.533	0.007	0.006
			CCS	0.5	0.498	0.010	0.010
			WS	0.5	0.498	0.010	0.010
Bernoulli	[∞, ∞]	0	CC	1	1.027	0.023	0.024
			CCS	1	1.003	0.025	0.026
			WS	1	1.003	0.025	0.026
Bernoulli	[0, 1.7]	0.44	CC	1	0.942	0.045	0.043
			CCS	1	0.990	0.052	0.050
			WS	1	0.989	0.050	0.048

6.2 Simulation for Highly Stratified Data

We assumed that the number of strata was 50; the strata sizes were uniformly distributed from {3,4,5}; (ρ₁,…, ρ_k,…, ρ₅₀) = (0.1,…, 0.1k,…, 5), (γ₁,…,γ_k,…,γ₅₀) = (5,…, 5 −0.1k,…, 0.1); and p = 0.6. The covariates were two dimensional. The first component was independently distributed as a normal or Bernoulli covariate. The mean of the distributions was strata dependent with three levels as in the regularly stratified case. The second component was i.i.d. uniformly distributed independent of strata. We considered the true parameter values to be (β₁₁,β₁₂,β₂₁,β₂₂) = (0, 1, −0.5, .5) and (β₁₁,β₁₂,β₂₁,β₂₂) = (1, 1, −0.5, .5), respectively.

Table 3 gives the results for β₁₁ and β₁₂ for the various approaches. The weighted stratified (WS) approach for right censored data and the CCS approach produce very similar and precise estimators of the parameters and their variances, for both β₁₁ and β₁₂. For right censored data, both the model based plug-in (WSh) and bootstrap (WSb) variance estimators (E(var̂)) are provided for the weighted estimating equation. They have correlations of between 96% and 98% in the four settings. The former leads to slightly lower empirical coverage than the latter, although both methods, as well as CCS inferences, have coverages which are close (within 0.02) to the nominal level. In contrast, the approach without stratification (CC) provides biased results and coverages that are greatly reduced. When β₁₁ = 0,β̂₁₁ departs substantially from the truth; when β₁₁ = 1,β̂₁₂ and β₁₂ are very discrepant.

Table 3. Comparison of parameter estimates from CC, CCS, stratified weighted (WSh for plug-in variance estimator and WSb for bootstrap variance estimator) estimating equations (highly stratified data).

					E(β̂)1		var(β̂)		E(var̂)		coveragê
Z11	[a, b]	Percentage censored	β1		β11	β12	β11	β12	β11	β12	β11	β12
Normal	[0.5, 1.5]	.27	(0,1)	CC	.287	.911	.006	.119	.005	.103	.019	.927
				CCS	.005	.992	.017	.205	.016	.194	.946	.945
				WSh	.008	.990	.016	.198	.015	.184	.941	.942
				WSb	.008	.990	.016	.198	.016	.201	.951	.952
Normal	[0, 1.5]	.28	(1,1)	CC	1.009	.507	.010	.110	.008	.101	.934	.645
				CCS	1.042	1.055	.046	.295	.039	.283	.937	.952
				WSh	1.041	1.050	.045	.286	.037	.267	.931	.948
				WSb	1.041	1.050	.045	.286	.043	.302	.950	.960
Binary	[0, 1.7]	.37	(0,1)	CC	.385	.884	.039	.125	.040	.123	.521	.938
				CCS	−.003	1.048	.101	.275	.093	.259	.943	.941
				WSh	.004	1.039	.095	.261	.088	.247	.939	.937
				WSb	.004	1.039	.095	.261	.099	.280	.953	.953
Binary	[0, 1.2]	.41	(0,1)	CC	1.239	.650	.046	.132	.047	.119	.833	.805
				CCS	1.033	1.038	.135	.314	.120	.288	.944	.949
				WSh	1.037	1.034	.132	.307	.117	.280	.938	.936
				WSb	1.037	1.034	.132	.307	.165	.320	.964	.941

Wsh & WSb differ only in the variance computation, whereas the estimates are the same.

7. Real Data Examples

7.1 The Eastern Cooperative Oncology Group Study

In this study, there were 167 eligible patients. Of the 82 patients on placebo, 59 had breast cancer recurrence, 19 died without recurrence, and 4 were censored; of the 85 patients on tamoxifen, 42 had breast cancer recurrence, 23 died without recurrence, and 20 were censored. In addition to treatment group to be considered, there were three prognostic factors: number of positive nodes, tumor size, and age at treatment. We were interested in the cumulative incidence function of breast cancer recurrence for the two treatment groups with the competing event being death without recurrence.

The data were previously analyzed by Fine and Gray (1999). The model they suggested for breast cancer recurrence allows the subdistribution hazards ratio of treatment to be quadratic in time due to substantial lack of fit in the proportional subdistribution hazards model. The other covariates were considered in the analysis in the form of linear proportional hazards terms, which did not suggest lack of fit.

Based on the above, we considered model (1) with covariates for ith patient in kth group Z_ki = (Z_1ki, Z_2ki, Z_3ki) = (log(nodes),tumor size, age)_ki, where k =1, 2 denotes the treatment group (1 for placebo and 2 for tamoxifen); i = 1,…, 82 for k = 1; i = 1,…, 85 for k = 2. Instead of being a covariate, treatment was a stratification variable. The estimated coefficients and standard errors for this model, as well as those from Fine and Gray's analysis are displayed in Table 4. The coefficient estimates and standard errors of the 3 covariates from the two models agree. The log of the number of nodes and the tumor size are significant for the subdistribution of the breast cancer recurrence, whereas age is insignificant.

Table 4. Estimation of coefficients and standard errors in models for breast cancer recurrence.

	Fine and Gray			Stratified regression
	β̂	se(β̂)	p	β̂	se(β̂)	p
Log(nodes)	.274	.111	.014	.272	.111	.014
Tumorsize	.109	.040	.007	.107	.040	.007
Age	−.037	.028	.180	−.036	.027	.190
Treatment	−2.035	.644	.002	–	–	–
Treatment × t	.857	.334	.010	–	–	–
Treatment × t2	−.086	.034	.013	–	–	–

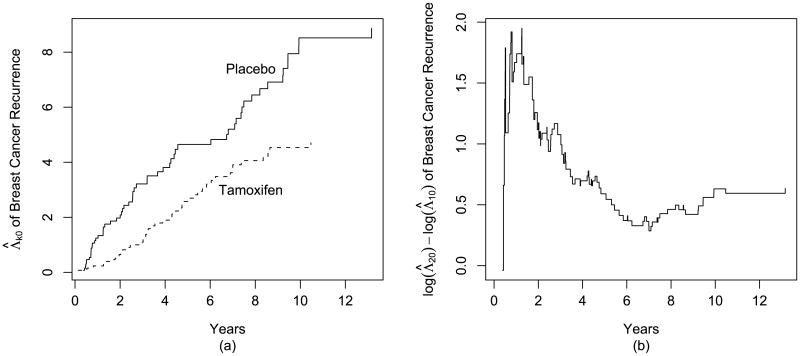
Using the estimators described in Section 5, we are able to compare the estimated baseline cumulative subdistribution hazards for the two treatment groups when covariates Z = 0. Figure 1a depicts the estimated baseline cumulative subdistribution hazards of breast cancer recurrence for each group using our stratified competing risk regression model described above. Figure 1b gives the log of the ratio of baseline cumulative subdistribution hazards. The nonconstancy of the curve in Figure 1b is clear evidence of nonproportionality of the subdistribution hazards of treatment. One could argue that interpreting the treatment effect is more intuitive using such plots, as opposed to fitting more complex models with time-dependent covariates to capture the nonproportional treatment effect.

Figure 1.

Estimated baseline cumulative subdistribution hazards for tamoxifen (k = 1) and placebo groups (k = 2).

7.2 Acute Myeloid Leukemia Data

The data arise from an ongoing registry by the European Blood and Marrow Transplant Group. The event of interest was the time from graft to the first occurrence of either acute GvHD grade 2 or chronic GvHD. Death and relapse without GvHD are the competing causes of failure. Katsahian et al. (2006) proposed a frailty model for the subdistribution hazard to test the prognostic factors while adjusting for the center effect. A subset of the data was used in their frailty model analyses, with the reference date being 1 January 2002 as well as the following inclusion criteria for patients: (1) received either genoidentical or matched unrelated donor (MUD) stem cell transplant; (2) were more than 16 years old at time of transplant; (3) had acute myeloid leukemia in first complete remission; (4) received a transplant between 1 January 1994 and 31 December 2004; and (5) did not receive reduced intensity regimen nor T cell depleted transplant. Centers with only one patient enrolled were excluded. A total of 1022 patients from 121 clusters was analyzed.

In our analysis, we used the same registry, but with data extracted up to July 2008, while maintaining the inclusion criteria from Katsahian et al. (2006). The median follow-up was 1250 days, comprised of patients still alive without relapse and disease. Thus, we have a total of 2952 patients from 244 centers, with 1385 GvHD events and 629 competing causes of failure observed. The median patients per center was 6. About 1/3 of centers had only two or three patients.

Because the patient populations are remarkably different across centers, which was evident from Katsahian et al. (2006), we consider the highly stratified Fine–Gray model (1), stratifying on center. The four covariates are specified as in Katsahian et al. (2006). Let Z_ki = (Z_1ki, Z_2ki, Z_3ki, Z_4ki) for the ith subject in the kth center, where k = 1,…, 244; i = 1,…, i_k; and i_k = 2,…, 92. Here, Z_1ki = I(female donor to male recipient match), Z_2ki = I(source of stem cells is peripheral blood), Z_3ki =I(French-American-British [FAB] classification of acute myeloid leukemia is M5, M6, or M7), and Z_4ki = I(type of transplant is matched unrelated donor). We first considered univariate models (1), similarly to Katsahian et al. (2006), followed by a multiple covariate analysis. Unstratified Fine–Gray models were also applied.

The coefficient estimates are reported in Table 5. In all cases, sex matching between donor and recipient (female donor to male recipient versus others) is a significant prognostic factor in the subdistribution hazard of GvHD occurrence, whereas the other three factors are not significant. Despite similar overall conclusions from the unstratified and stratified analysis, attention needs to be paid to some of the covariate estimates. For source of stem cells (peripheral blood or bone marrow), the coefficient estimates from the two approaches have opposite sign, suggesting an interaction between stem cell transplants and centers. We note that the univariate model (called simple stratified regression) and the model with multiple covariates (called multiple stratified regression) give very similar results from both an unstratified and stratified approach. This suggests that there is modest confounding of the covariate effects under consideration by heterogeneity across centers.

Table 5. Estimation of coefficients and standard errors in models for acute GvHD or chronic GvHD occurrence.

	Unstratified				Stratified
	Simple		Multiple		Simple		Multiple
	β̂	p	β̂	p	β̂	p	β̂	p
Female to male versus others	.363(.060)	<.01	.368(.063)	<.01	.343(.073)	<.01	.372(.075)	<.01
PBSC versus BMT	−.051(.054)	.35	−.060(.057)	.29	.076(.075)	.31	.060(.084)	.48
FAB M5, M6, M7 versus others	.089(.067)	.19	.099(.069)	.15	.109(.063)	.08	.109(.066)	.10
Matched unrelated donor versus genoidentical	.049(.081)	.54	.086(.087)	.33	.119(.116)	.33	.120(.122)	.34

PBSC = peripheral blood stem cells; BMT = bone marrow transplant.

8. Concluding Remarks

Recently, Ruan and Gray (2008) proposed a generic Kaplan– Meier multiple imputation method that recovers the missing potential censoring information for the analysis of cumulative incidence functions using standard analysis, which can potentially be applied in the setting of stratified analysis. Although the methods performed well empirically, the statistical properties of the approach were not established. Such imputation-based procedures have not been used very often in survival settings, in part because of the ad hoc nature of the resulting inferences and a lack of understanding regarding when such inferences are valid. A goal of this article was to develop rigorous methodology for stratified Fine–Gray models, similar to that for stratified Cox models for independently censored data.

We proposed both bootstrap and plug-in formulas to obtain variance estimators for the highly stratified situation. The closed form variance estimator does not require estimation of the baseline hazard in each stratum, unlike for regularly stratified data and the original Fine and Gray (1999) model. This is accomplished by employing an alternative derivation of the influence function, which is not applicable in the other settings. In the simulation studies, we find that with realistic sample sizes, the bootstrap variance estimator slightly outperforms the closed form estimator. General bootstrap theory should be valid with highly stratified data, assuming the data within cluster (including cluster size) are i.i.d. across strata. A rigorous proof would entail more careful consideration of the regularity conditions.

There are alternative modeling strategies to tackle the same inferential problem. In our applications, the covariate effects are of primary interest, with the correlations within clusters serving as a nuisance. For situations where the correlations are of genuine interest, the random effects model introduced by Katsahian et al. (2006) might be of greater utility, where the frailty is introduced on the stratum level hazard. Scheike et al. (2010) proposed a closely related frailty model, which implies a semiparametric additive model for the marginal cumulative incidence function. Another possibility is to model the covariate effects unconditionally on stratum, without specifying the correlation structure. The model proposed by Chen et al. (2008) assumes common baseline subdistribution hazards within strata but different subdistribution hazards across covariate groups instead of across strata. The goal is to test the equivalence of such hazards nonparametrically in the two sample set-up, adjusting for correlations within clusters. Such marginal approaches require further development to accommodate general regression models. This work is beyond the scope of the current article but merits further research.

The implementation of the proposed methodology may, in some cases, be carried out using existing software. For complete censored competing risks data, one can perform a stratified Cox regression analysis of a modified data set where individuals observed to fail from causes other than the cause of interest (say 1) are given a censored observation at the time of the observed censoring time (Andersen, Abildstrom, and Rosthøj, 2002). The R function for standard Cox regression, COXPH with the option STRATA, can be applied to this modified data set. For censored competing risks data, we have designed a R function stratified competing risks regression (CRRS) for the weighted estimating equation procedures described in Section 4; see Supplementary Materials.