Abstract
One great challenge of genomic research is to efficiently and accurately identify complex gene regulatory networks. The development of high-throughput technologies provides numerous experimental data such as DNA sequences, protein sequence, and RNA expression profiles makes it possible to study interactions and regulations among genes or other substance in an organism. However, it is crucial to make inference of genetic regulatory networks from gene expression profiles and protein interaction data for systems biology. This study will develop a new approach to reconstruct time delay Boolean networks as a tool for exploring biological pathways. In the inference strategy, we will compare all pairs of input genes in those basic relationships by their corresponding 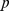 -scores for every output gene. Then, we will combine those consistent relationships to reveal the most probable relationship and reconstruct the genetic network. Specifically, we will prove that
-scores for every output gene. Then, we will combine those consistent relationships to reveal the most probable relationship and reconstruct the genetic network. Specifically, we will prove that 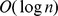 state transition pairs are sufficient and necessary to reconstruct the time delay Boolean network of
state transition pairs are sufficient and necessary to reconstruct the time delay Boolean network of  nodes with high accuracy if the number of input genes to each gene is bounded. We also have implemented this method on simulated and empirical yeast gene expression data sets. The test results show that this proposed method is extensible for realistic networks.
nodes with high accuracy if the number of input genes to each gene is bounded. We also have implemented this method on simulated and empirical yeast gene expression data sets. The test results show that this proposed method is extensible for realistic networks.
Introduction
In order to understand complex biological networks and pathways, we need to investigate global structures instead of individual behaviors since there are interactions and associations between genes. Due to the invention of high throughput technology, genome-wide expression profiles can be measured simultaneously [1]. However, it is still a great challenge to identify complex biological networks from genome-wide data because the number of gene interactions is huge [2]. In recent years, there has been a significant progress in research concerning genetic network models and network reconstruction problems.
Clustering and dimension reduction are important methods for grouping genes that have similar expression profiles [3], [4]. In the framework of clustering, it is important to define the degree of similarity between genes. By the method of clustering, we can group genes that have similar expressions. However, we still cannot find the causal relationship between genes. Hence, apart from the relationship of similarity, we will also have to consider another causal relationship between genes.
There have been many methods proposed in the literature to tackle the problem of genetic regulatory network reconstruction. For instance, the steady state approach have been used to model gene regulatory networks [5]. In addition, the Bayesian network model is an important technique that has been studied extensively in the past two decades [6]–[11]. A Bayesian network is a directed acyclic graph (DAG) comprised of two components. The first component is comprised of nodes that correspond to a set of variables and a set of directed edges between variables with Markov properties. The second component describes a conditional distribution for each variable given its parents in the graph. Recently, Bayesian network models have been applied to analyze microarray expression and biological data [12]–[15]. However, Bayesian network algorithms have limitations when dealing with large-scale gene regulatory networks because of their complex modeling structure [16]. Although algorithms for reconstructing Bayesian networks have already been developed [17], [18], the algorithms’ computational costs remain a concern for the searching of all potential network structures on the genome-wide expression data.
Therefore, we are considering a simpler model: Boolean networks, which have been studied extensively in a variety of contexts. Boolean networks [19], [20] can effectively explain the dynamic behaviors of living systems. Moreover, for large-scale gene regulatory networks, Kim et al. [21] have used Boolean network with chi-square test on the yeast cell cycle microarray gene expression data sets. The chaos and attractors of Boolean network are also discussed widely from the aspect of power spectrum [22]–[24]. Recently, Boolean network also have been used as a discrete model for the lac operon [25].
Boolean networks were originally introduced by Kauffman, and received attention in the studies of gene regulatory networks because of their simple structures [26]. In a Boolean network model, nodes represent the gene expression states. The status of a gene is quantized to one of the two states: on or off, representing a gene as active or inactive respectively. The wiring of rules between nodes in the graph represents a functional link between genes and determines the expressions of target genes after giving a series of input genes. Under the structure of Boolean networks, the target gene is determined by a set of genes with specific rules. For each gene, if the indegree (i.e., the number of input genes to each gene) is bounded by a constant 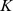 , only
, only 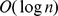 pairs of state transition are necessary and sufficient to reconstruct the original network with
pairs of state transition are necessary and sufficient to reconstruct the original network with  nodes [27], [28]. However, Boolean networks have been criticized for their deterministic nature. The assumption that every affected gene would be expressed immediately at the next time step may be unsound.
nodes [27], [28]. However, Boolean networks have been criticized for their deterministic nature. The assumption that every affected gene would be expressed immediately at the next time step may be unsound.
Another point of view of constructing genetic network is to focus on the indication the pairwise relationships between genes. Most of the works is to find the gene-pairs with similarity relationship [29]–[33]. The similarity of a gene-pair represents the two genes with the same expression or opposite expression. In 2005, Li and Lu proposed directed acyclic Boolean network and the statistical reconstruction method of SPAN to infer the pair wise relations of every element [34]. The proposed method can reconstruct Boolean networks from noisy array data by assigning an s-p-score for every pair of genes. In the study, they proposed another relationship between two genes: relationship of prerequisite under the Boolean network model. If gene 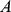 is a prerequisite for gene
is a prerequisite for gene 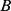 , then the “on” status of gene
, then the “on” status of gene 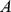 is necessary for the “on” status of gene
is necessary for the “on” status of gene 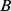 . Boolean implication network, with the similar aspect, investigated all Boolean implication between pairs of gene for large scale genome microarray datasets [35]. Following the model, Wang et al.[36] proposed a two step counting approach for constructing biological pathways with Boolean network. However, most of these methods only consider pair wise relationship in order to decrease the time complexity. Therefore, if the structure of network is a combination of a set of genes to affect another gene, the algorithms will lose some information and rules in the genetic network reconstruction.
. Boolean implication network, with the similar aspect, investigated all Boolean implication between pairs of gene for large scale genome microarray datasets [35]. Following the model, Wang et al.[36] proposed a two step counting approach for constructing biological pathways with Boolean network. However, most of these methods only consider pair wise relationship in order to decrease the time complexity. Therefore, if the structure of network is a combination of a set of genes to affect another gene, the algorithms will lose some information and rules in the genetic network reconstruction.
In this study, we will consider a much more generalized model by combining the structure of the above two models. If a Boolean function with one or several genes is a prerequisite for a target gene, then the induction of the Boolean function with input genes is necessary for the expression of the target gene. Hence, the target will be influenced by the Boolean function with several input genes. However, the induction of the Boolean function may not activate the target gene immediately, but at a future time. Therefore, the target gene may not have been influenced right now and we will treat these relationships as time delay affection. In this study, we will infuse these additional relationships for more generalized systems.
Boolean Network
Boolean networks were introduced by Kauffman (1969) forty years ago to represent genetic regulatory networks. First, we will review the definition of a Boolean network. A Boolean network 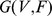 is a directed graph consisting of two components: a set of nodes
is a directed graph consisting of two components: a set of nodes 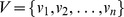 that corresponds to genes, and a list of Boolean functions
that corresponds to genes, and a list of Boolean functions 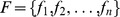 that corresponds to the rule of interaction and combination of several genes. For every node
that corresponds to the rule of interaction and combination of several genes. For every node  , its expression is simplified to two levels: on and off, representing a gene as active or inactive. For every Boolean function
, its expression is simplified to two levels: on and off, representing a gene as active or inactive. For every Boolean function 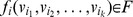 ,
, 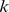 specified input nodes
specified input nodes 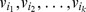 are assigned to the node
are assigned to the node 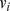 in the graph and represent the rules of regulatory mechanisms between genes. The expression of a gene is determined by the expression of the gene directly affecting it with a Boolean function. Therefore, the state of each node
in the graph and represent the rules of regulatory mechanisms between genes. The expression of a gene is determined by the expression of the gene directly affecting it with a Boolean function. Therefore, the state of each node  is determined by the Boolean function
is determined by the Boolean function 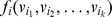 .
.
For each node 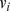 , the gene expression state at time
, the gene expression state at time  is assumed to take either 0 (not-expressed) or 1 (expressed) and is expressed as
is assumed to take either 0 (not-expressed) or 1 (expressed) and is expressed as 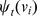 . In a Boolean network, every gene expression profile at time
. In a Boolean network, every gene expression profile at time 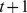 is completely determined by the expression profile of a set of genes
is completely determined by the expression profile of a set of genes 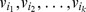 at time
at time  and the corresponding Boolean function
and the corresponding Boolean function 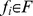 . That is, we can write
. That is, we can write 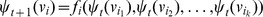 .
.
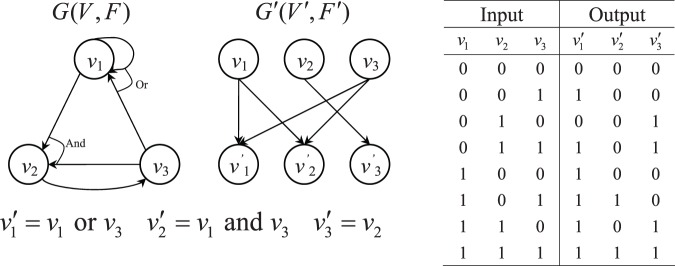
For convenience, we converted the Boolean network 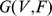 to the wiring diagram
to the wiring diagram 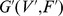 (See Figure 1) [37]. For each node
(See Figure 1) [37]. For each node  , suppose
, suppose 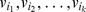 are the input nodes assigned to
are the input nodes assigned to 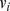 . Then we construct an additional node
. Then we construct an additional node 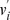 and connected the edge from
and connected the edge from 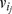 to
to 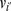 for each
for each 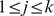 . That is, the set of
. That is, the set of  represents the gene expression profile at time
represents the gene expression profile at time  and the set of
and the set of  corresponds to the gene expression profile at time
corresponds to the gene expression profile at time 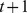 . Hence we can treat the set of
. Hence we can treat the set of  as the input values and the set of
as the input values and the set of  as the corresponding output values. Therefore, the output values of
as the corresponding output values. Therefore, the output values of  are determined by
are determined by 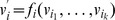 .
.
Figure 1. Boolean network G(V,F), wiring diagram G′(V′,F′) and its input/output.
The Structure of Time Delay Boolean Network
In the previous subsection, we found that given the values of the node (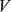 ) at time
) at time  , the expressions at time
, the expressions at time 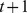 will be updated immediately by specific Boolean function (
will be updated immediately by specific Boolean function (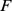 ). That is, for every gene
). That is, for every gene  , if the expression profile of a set of genes
, if the expression profile of a set of genes 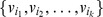 at time
at time  and the corresponding Boolean function
and the corresponding Boolean function 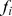 is observed, the gene expression of
is observed, the gene expression of 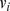 at time
at time 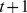 is determined by
is determined by 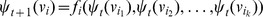 . However, in real genetic regulatory situations, the deterministic system has been criticized due to the existence of misclassification error and noise. In addition, some of the gene expression may result in time delay when the gene is influenced by one or several input genes. That is, the induction of Boolean function may not activate the target gene immediately, but in the future. Hence, it would have been much more flexible to use a non-deterministic network system. In this subsection, we will consider two relationships between the Boolean function and the target gene instead of the deterministic relation.
. However, in real genetic regulatory situations, the deterministic system has been criticized due to the existence of misclassification error and noise. In addition, some of the gene expression may result in time delay when the gene is influenced by one or several input genes. That is, the induction of Boolean function may not activate the target gene immediately, but in the future. Hence, it would have been much more flexible to use a non-deterministic network system. In this subsection, we will consider two relationships between the Boolean function and the target gene instead of the deterministic relation.
First, we will introduce the structure of time delay Boolean networks. Suppose there are  elements,
elements, 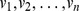 in a Boolean network. For any elements
in a Boolean network. For any elements 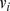 with specific Boolean function
with specific Boolean function 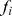 , we have two kinds of pair wise relationship: prerequisite and similarity. We say that a Boolean function
, we have two kinds of pair wise relationship: prerequisite and similarity. We say that a Boolean function 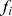 with specific
with specific 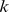 input genes
input genes 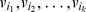 at time
at time  is the prerequisite for the target gene
is the prerequisite for the target gene 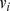 at time
at time 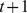 , if the on-status of Boolean function at time t is necessary for the on-status of gene
, if the on-status of Boolean function at time t is necessary for the on-status of gene 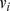 at time
at time 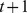 . This relationship is denoted by
. This relationship is denoted by 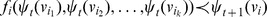 . In other words, if the Boolean function
. In other words, if the Boolean function 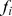 is not active at time
is not active at time  , gene
, gene 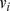 will be inactive at time
will be inactive at time 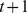 . If it does not cause confusion, we will omit the notation of
. If it does not cause confusion, we will omit the notation of 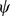 and input genes as denoted by
and input genes as denoted by 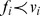 . Moreover, for every gene
. Moreover, for every gene 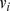 , we use
, we use 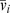 as its dual (from 0 to 1, or from 1 to 0) in this paper. Therefore, for any Boolean function and target gene with a prerequisite relationship there are a total of two possible relationships:
as its dual (from 0 to 1, or from 1 to 0) in this paper. Therefore, for any Boolean function and target gene with a prerequisite relationship there are a total of two possible relationships: 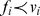 and
and 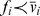 . In this model, we do not consider the situation of a dual of Boolean function prerequisite to the target gene, that is
. In this model, we do not consider the situation of a dual of Boolean function prerequisite to the target gene, that is 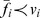 and
and 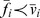 . Since for any Boolean function whose dual is a prerequisite to the target gene, there must exist another Boolean function that is a prerequisite to the target gene. For instance, if
. Since for any Boolean function whose dual is a prerequisite to the target gene, there must exist another Boolean function that is a prerequisite to the target gene. For instance, if 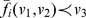 , where
, where 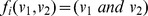 , then
, then 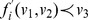 , where
, where 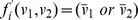 . Therefore, for the prerequisite relationship, we only consider the Boolean function that is a prerequisite to target gene and the dual of target gene.
. Therefore, for the prerequisite relationship, we only consider the Boolean function that is a prerequisite to target gene and the dual of target gene.
The other type of relationship between Boolean function and target gene is similarity. We say that the Boolean function 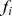 and target gene
and target gene 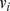 are similar if the status of the Boolean function and the status of the target gene are in the same expression, and we denoted this by fi∼vi. In the same way, we do not consider the situation of Boolean function similar to the dual of target gene such as fi∼
are similar if the status of the Boolean function and the status of the target gene are in the same expression, and we denoted this by fi∼vi. In the same way, we do not consider the situation of Boolean function similar to the dual of target gene such as fi∼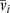 in this study. Since if there is one Boolean function that is similar to the dual of target gene, there must exist another Boolean function that is similar to the target gene.
in this study. Since if there is one Boolean function that is similar to the dual of target gene, there must exist another Boolean function that is similar to the target gene.
In the diagram, if a Boolean function 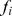 is a prerequisite to
is a prerequisite to 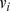 , we draw a directed arrow from the vertex
, we draw a directed arrow from the vertex 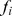 to
to 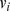 and if
and if 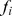 is similar to
is similar to 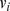 , we use an undirected line to connect
, we use an undirected line to connect 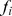 and
and 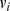 .
.
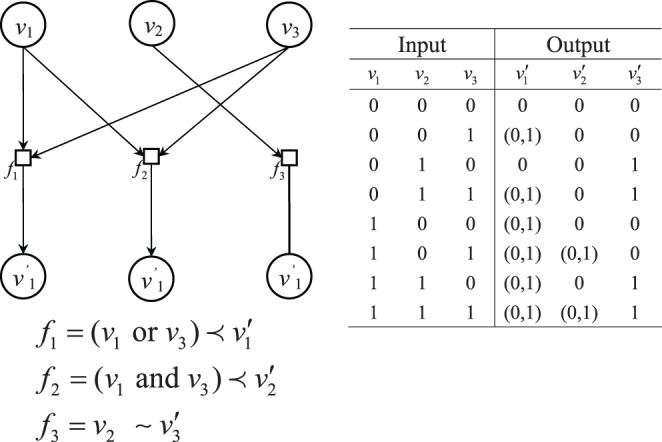
In the model of time delay Boolean network we proposed, the output of the gene expression is not completely determined by the input state and Boolean function. The output expression may have more than one possible result in the time delay Boolean network. We illustrate the above construction by an example in Figure 2. It has three elements, one similarity and two prerequisite relationships. The possible outputs for every input state are listed in the right part of the graph. If we knew the network structure, some of the inputs would have more than one possible output expression in the time delay Boolean network.
Figure 2. One example of time delay Boolean network and its input/output.
Methods
Identification Algorithm
First, we only consider Boolean networks in which the maximum number of input genes is bounded by a constant 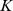 for every target gene, because it has been proven that the number of profiles required grows exponentially if
for every target gene, because it has been proven that the number of profiles required grows exponentially if 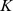 is not bounded [38]. For simplicity, we only show algorithms for the case of
is not bounded [38]. For simplicity, we only show algorithms for the case of 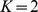 . However, the algorithm can be intuitively generalized to any
. However, the algorithm can be intuitively generalized to any 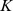 in a straightforward way. For the inference of genetic network, we need to clarify the following questions for each target gene.
in a straightforward way. For the inference of genetic network, we need to clarify the following questions for each target gene.
Which input genes will affect the target gene?
What kind of Boolean functions will be used for combining those input genes?
What kind of relationship exists between the Boolean function and the target gene?
In this subsection, we propose an algorithm to clarify the above questions. The algorithm below is conceptually very simple since it simply uses output Boolean functions with input genes and relationships with target genes that are consistent with the data. First, for each output gene expression at time 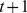 such as
such as 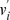 , we consider all the pairs of elements in
, we consider all the pairs of elements in 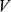 at time
at time  , for instance
, for instance 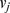 and
and 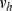 . Then we count the eight incidents of (
. Then we count the eight incidents of (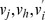 ) being (0,0,0), (0,0,1),
) being (0,0,0), (0,0,1),  , (1,1,1) from the sample and arrange them in a
, (1,1,1) from the sample and arrange them in a 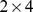 table; see the left part of Table 1. We mark a cell “+” if the count is positive and mark it “0” otherwise.
table; see the left part of Table 1. We mark a cell “+” if the count is positive and mark it “0” otherwise.
Table 1. Count and probabilities table for 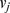 ,
, 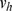 and
and 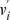 assuming no misclassification error.
assuming no misclassification error.
| v′i/vjvh | 00 | 01 | 10 | 11 | v′i/vjvh | 00 | 01 | 10 | 11 |
| 0 | m 000 | m 010 | m 100 | m 110 | 0 | q 000 | q 010 | q 100 | q 110 |
| 1 | m 001 | m 011 | m 101 | m 111 | 1 | q 001 | q 011 | q 101 | q 111 |
For detecting whether there exists a Boolean function which is a prerequisite to the target gene, we will compare the 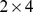 output table with the left four basic relationships in Table 2. We consider the basic relationships to be consistent with the output table if the position of 0 cell in the basic relationships is also 0 in the output table. By comparing the output table with the four basic relationships, we can find relationships that are consistent with the output tables. If there is more than one relationship that is consistent with the output tables, we would use the Boolean logic gate “and” to combine the Boolean function and transfer the result to another Boolean function. Hence, the final Boolean function is the prerequisite to the target gene. Similarly, by comparing the
output table with the left four basic relationships in Table 2. We consider the basic relationships to be consistent with the output table if the position of 0 cell in the basic relationships is also 0 in the output table. By comparing the output table with the four basic relationships, we can find relationships that are consistent with the output tables. If there is more than one relationship that is consistent with the output tables, we would use the Boolean logic gate “and” to combine the Boolean function and transfer the result to another Boolean function. Hence, the final Boolean function is the prerequisite to the target gene. Similarly, by comparing the 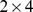 output table with the right four basic relations in Table 2, we could get another Boolean function which is the prerequisite to the dual of target gene.
output table with the right four basic relations in Table 2, we could get another Boolean function which is the prerequisite to the dual of target gene.
Table 2. Count profiles for the basic eight relationships without misclassification error.
(vj or vh) v′i
v′i
|
(vj or vh)
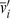
|
||||||||
| v′i/vjvh | 00 | 01 | 10 | 11 | v′i/vjvh | 00 | 01 | 10 | 11 |
| 0 | + | + | + | + | 0 | 0 | + | + | + |
| 1 | 0 | + | + | + | 1 | + | + | + | + |
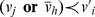
|
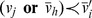
|
||||||||

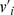 / / |
00 | 01 | 10 | 11 |
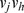
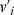 / / |
00 | 01 | 10 | 11 |
| 0 | + | + | + | + | 0 | + | 0 | + | + |
| 1 | + | 0 | + | + | 1 | + | + | + | + |
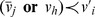
|
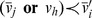
|
||||||||
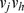
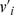 / / |
00 | 01 | 10 | 11 |
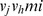
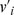 / / |
00 | 01 | 10 | 11 |
| 0 | + | + | + | + | 0 | + | + | 0 | + |
| 1 | + | + | 0 | + | 1 | + | + | + | + |
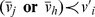
|
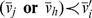
|
||||||||
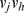
 / / |
00 | 01 | 10 | 11 |
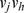
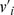 / / |
00 | 01 | 10 | 11 |
| 0 | + | + | + | + | 0 | + | + | + | 0 |
| 1 | + | + | + | 0 | 1 | + | + | + | + |
Moreover, if only one Boolean function occurred in above relationship, that is, if there is only one Boolean function that is the prerequisite to the target gene or the dual of target gene, we will treat that relationship as our final relationship between the Boolean function and the target gene. However, if both of the two prerequisite relationships happened (i.e. 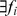 and
and 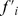
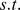
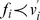 and
and 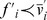 ), we need to check whether these two relationships are in conflict. If the dual of
), we need to check whether these two relationships are in conflict. If the dual of 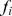 is equivalent to
is equivalent to 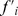 , our conclusion for inference will be that
, our conclusion for inference will be that 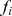 is similar to the target gene (that is,
is similar to the target gene (that is, 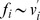 ); otherwise, we will treat it as if there is no relationship between the input genes and the target gene because we did not gather enough information to judge true relationships between
); otherwise, we will treat it as if there is no relationship between the input genes and the target gene because we did not gather enough information to judge true relationships between 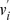 and (
and (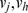 ) at this moment. By the above identification procedure, we can find the corresponding input genes, Boolean function and their relationship for every target gene.
) at this moment. By the above identification procedure, we can find the corresponding input genes, Boolean function and their relationship for every target gene.
Identification Algorithm with Noisy Array
In previous subsection, we discussed an identification method for data without noise. In this section we will consider the situation of noisy array data. We assume that every element in the entry of (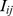 ,
, 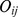 ),
), 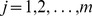 switches to its reverse status with a misclassification probability
switches to its reverse status with a misclassification probability 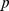 independently; that is
independently; that is
| (1) |
| (2) |
Thus, the observed array (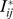 ,
, 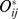 ) contains misclassification error. Our goal is to reconstruct time delay Boolean network from noisy array of binary data (
) contains misclassification error. Our goal is to reconstruct time delay Boolean network from noisy array of binary data (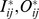 ).
).
Similar to section 2, we assume that the maximum number of input genes is bounded by 2 for every target gene. We treat the data in the 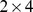 table as a multinomial distribution with eight cells whose probabilities are
table as a multinomial distribution with eight cells whose probabilities are 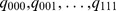 as shown in the right part of Table 1, where
as shown in the right part of Table 1, where 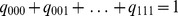 . Similarly, we extract the data with misclassification error for every output gene and each pair of input genes as the
. Similarly, we extract the data with misclassification error for every output gene and each pair of input genes as the 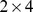 table. Now the observed data
table. Now the observed data 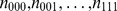 are not generated from the multinomial
are not generated from the multinomial 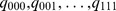 , but from another multinomial
, but from another multinomial 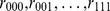 as shown in Table 3, where
as shown in Table 3, where 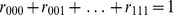 .
.
Table 3. Count and probabilities table for 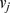 ,
, 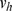 and
and 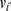 with misclassification error.
with misclassification error.
| v′i/vjvh | 00 | 01 | 10 | 11 | v′i/vjvh | 00 | 01 | 10 | 11 |
| 0 | n 000 | n 010 | n 100 | n 110 | 0 | r 000 | r 010 | r 100 | r 110 |
| 1 | n 001 | n 011 | n 101 | n 111 | 1 | r 001 | r 011 | r 101 | r 111 |
Because of the misclassification error, a portion of the samples of 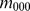 may change to the other seven cells. We use the notations of
may change to the other seven cells. We use the notations of 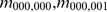 ,
, 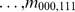 to represent the counts of eight cells changed from
to represent the counts of eight cells changed from 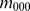 . Analogous notations are defined for
. Analogous notations are defined for 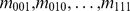 . The splitting is shown in Table 4. Consequently, the generated probabilities (
. The splitting is shown in Table 4. Consequently, the generated probabilities (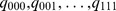 ) are calculated as follows:
) are calculated as follows: 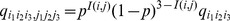 , where
, where 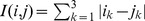 . Here, we adopt the notation
. Here, we adopt the notation 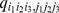 analogous to
analogous to 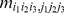 . The above parameters and splits are shown in Table 4. In the table, it is easy to find that the correspondence between two sets of counts and probabilities is the following:
. The above parameters and splits are shown in Table 4. In the table, it is easy to find that the correspondence between two sets of counts and probabilities is the following:
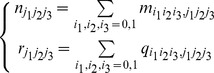 |
| (3) |
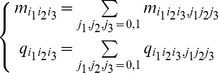 |
Table 4. Splitting counts caused by misclassification error.
| v′i/vjvh | 00 | 01 | 10 | 11 | ||||
| m 000,000 | m 000,001 | m 010,000 | m 010,001 | m 100,000 | m 100,001 | m 110,000 | m 110,001 | |
| 0 | m 000,010 | m 000,011 | m 010,010 | m 010,011 | m 100,010 | m 100,011 | m 110,010 | m 110,011 |
| m 000,100 | m 000,101 | m 010,100 | m 010,101 | m 100,100 | m 100,101 | m 110,100 | m 110,101 | |
| m 000,110 | m 000,111 | m 010,110 | m 010,111 | m 100,110 | m 100,111 | m 110,110 | m 110,111 | |
| m 001,000 | m 001,001 | m 011,000 | m 011,001 | m 101,000 | m 101,001 | m 111,000 | m 111,001 | |
| 1 | m 001,010 | m 001,011 | m 011,010 | m 011,011 | m 101,010 | m 101,011 | m 111,010 | m 111,011 |
| m 001,100 | m 001,101 | m 011,100 | m 011,101 | m 101,100 | m 101,101 | m 111,100 | m 111,101 | |
| m 001,110 | m 001,111 | m 011,110 | m 011,111 | m 101,110 | m 101,111 | m 111,110 | m 111,111 | |
For the complete data 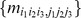 , the log-likelihood is given by
, the log-likelihood is given by
| (4) |
where 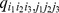 are those splitting probabilities. Since the complete data
are those splitting probabilities. Since the complete data 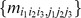 are not observable, we use the EM algorithm to maximize the log-likelihood. In the E-step, the splitting counts of complete data
are not observable, we use the EM algorithm to maximize the log-likelihood. In the E-step, the splitting counts of complete data 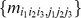 are evaluated by the conditional expectations using the current values of the parameters by the following formula
are evaluated by the conditional expectations using the current values of the parameters by the following formula
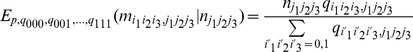 |
(5) |
where 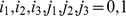 . One probabilities of
. One probabilities of 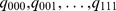 are zero in those different hypotheses specified in Table 5. In the M-step, we maximize the conditional expectation of the log-likelihood for the complete data to obtain the maximum likelihood estimates (MLEs) of the parameters. According to the MLEs, we can compute the
are zero in those different hypotheses specified in Table 5. In the M-step, we maximize the conditional expectation of the log-likelihood for the complete data to obtain the maximum likelihood estimates (MLEs) of the parameters. According to the MLEs, we can compute the 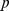 -score for every pair of input genes and target gene, which are obtained by estimating for the misclassification probability under every prerequisite relationship.
-score for every pair of input genes and target gene, which are obtained by estimating for the misclassification probability under every prerequisite relationship.
Table 5. The eight basic relationships and their probabilistic hypotheses and 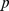 -scores.
-scores.
| Relation | Hypothesis | Scores |
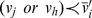
|
q000 = 0 |
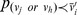
|
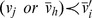
|
q010 = 0 |
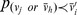
|
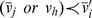
|
q100 = 0 |
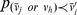
|
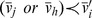
|
q110 = 0 |
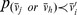
|
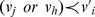
|
q001 = 0 |
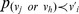
|
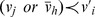
|
q011 = 0 |
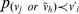
|
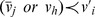
|
q101 = 0 |
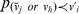
|
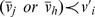
|
q111 = 0 |
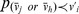
|
For the first step, we would like to determine the most probable relationships between every pair of input genes and one output gene. Next, we find the most probable Boolean function with pair input genes for every output gene and select candidate pairs of input genes and output gene for the watch list. Finally, we reconstruct a time delay Boolean network by integrating the relationship of those genes selected.
For one output gene 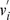 and a pair of input genes
and a pair of input genes 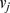 and
and 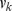 , we define the
, we define the 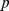 -scores
-scores 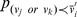 ,
, 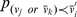 ,
, 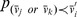 ,
, 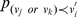 ,
, 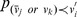 ,
, 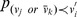 ,
, 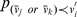 are, respectively, the maximum likelihood estimates of p under the triangular model:
are, respectively, the maximum likelihood estimates of p under the triangular model: 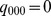 ,
, 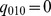 ,
, 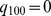 ,
, 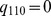 ,
, 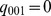 ,
, 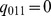 ,
, 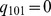 ,
, 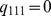 .
.
According to the EM algorithm described above, we can evaluate the 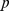 -score for every output gene. We use the MLE
-score for every output gene. We use the MLE 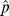 to measure how well each hypothesis fits: the smaller the score is, the more likely that the corresponding hypothesis could be true.
to measure how well each hypothesis fits: the smaller the score is, the more likely that the corresponding hypothesis could be true.
If the samples are generated from a time delay Boolean network, 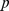 -score are quite useful for the discovery of true relationships. Here we can consider the maximum compatibility criterion: to choose the maximum threshold value so that the selected relationships contain no conflicts [34]. We collect those relationships whose
-score are quite useful for the discovery of true relationships. Here we can consider the maximum compatibility criterion: to choose the maximum threshold value so that the selected relationships contain no conflicts [34]. We collect those relationships whose 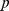 -scores are smaller than a threshold. Known biological results are helpful for the determination of a threshold. For example, if we know the relationship
-scores are smaller than a threshold. Known biological results are helpful for the determination of a threshold. For example, if we know the relationship 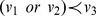 is true, then the
is true, then the 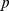 -scores smaller than
-scores smaller than 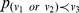 should be in our watch list. As more relationships are included in the watch list, the more likely we are to observe incompatible ones. In general, we can choose the threshold that allows the maximum number of relationships with no conflicting relationships. Next we will demonstrate the method by illustration examples.
should be in our watch list. As more relationships are included in the watch list, the more likely we are to observe incompatible ones. In general, we can choose the threshold that allows the maximum number of relationships with no conflicting relationships. Next we will demonstrate the method by illustration examples.
Results and Discussion
Theoretical Results
First, we will analyze the number of input/output pairs required for the network reconstruction of time delay Boolean network to be unique. The theoretical results of classical Boolean networks only consider the similar relationship [27], [38], [39]. The following results prove the theoretical results time delay Boolean networks that has a more flexible structure and consider both similar and prerequisite relationship.
Proposition 1
For all subsets of
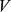 with
with
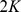 genes,
if all assignments (i.e.,
genes,
if all assignments (i.e.,
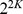 assignments)
of Boolean values appear in input expression patterns and all of its possible output expression patterns of the target gene are present, the identification of genetic network is determined to be unique, if it exists.
assignments)
of Boolean values appear in input expression patterns and all of its possible output expression patterns of the target gene are present, the identification of genetic network is determined to be unique, if it exists.
(Proof) Let  be any gene in
be any gene in 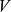 and suppose
and suppose  is controlled by a Boolean function
is controlled by a Boolean function  with similarity or prerequisite relationship (i.e.,
with similarity or prerequisite relationship (i.e., 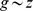 or
or 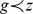 ). If the Boolean function
). If the Boolean function 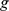 is similar to
is similar to  , the case is proved for the classical Boolean networks in Akutsu et al. (1998). Next, we consider the case of Boolean function
, the case is proved for the classical Boolean networks in Akutsu et al. (1998). Next, we consider the case of Boolean function 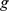 as a prerequisite to
as a prerequisite to  . In this case, there must exist a specific input value
. In this case, there must exist a specific input value  for
for  such that
such that  have two possible values 0 and 1. Hence, any other genes would not control
have two possible values 0 and 1. Hence, any other genes would not control  because all assignments of Boolean values are appearance. Let us illustrate the above statement by the example for the case of
because all assignments of Boolean values are appearance. Let us illustrate the above statement by the example for the case of 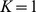 and
and 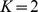 . If
. If 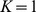 and
and  , when the input of
, when the input of  is 1, the outcome of
is 1, the outcome of  being both 0 and 1 will appearance. Therefore, given the input of
being both 0 and 1 will appearance. Therefore, given the input of 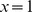 , the outcome of
, the outcome of  is not deterministic no matter the value of any other gene
is not deterministic no matter the value of any other gene 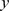 is 1 or 0. Hence, any other gene
is 1 or 0. Hence, any other gene 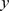 would not affect gene
would not affect gene  . If
. If 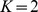 and
and 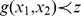 for some Boolean function
for some Boolean function 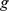 , there must exist an input
, there must exist an input 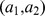 such that
such that 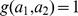 . Then, for any other pair of gene
. Then, for any other pair of gene 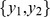 where
where 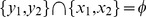 , the outcome of
, the outcome of  is not deterministic for any input of
is not deterministic for any input of 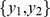 , if the input of
, if the input of  is
is 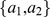 . In a case of
. In a case of 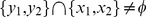 , we can prove that gene
, we can prove that gene 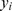 which does not belong to
which does not belong to 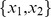 would not affect the gene
would not affect the gene  in a similar way.
in a similar way.
Proposition 2
The probability that one sub-assignment with all of its possible results in the target gene does not appear among m random input expression pattern is at most
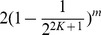 .
.
(Proof) For any fixed set of nodes 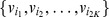 , the probability that a sub-assignment
, the probability that a sub-assignment  does not appear in one random input expression pattern is
does not appear in one random input expression pattern is 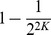 . Thus, among the
. Thus, among the  random input expressions, the probability that
random input expressions, the probability that  appears is
appears is  times is equal to
times is equal to 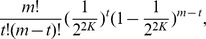 where
where 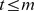 . In addition, the probability that all of the possible results in the target gene does not appear among
. In addition, the probability that all of the possible results in the target gene does not appear among  times input is smaller than
times input is smaller than 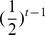 for
for 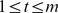 and equal to 1 for
and equal to 1 for  . Hence the probability that one sub-assignment and all of its possible results does not appear among
. Hence the probability that one sub-assignment and all of its possible results does not appear among  random input expression is smaller than
random input expression is smaller than 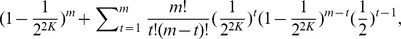 and this can be bounded by
and this can be bounded by 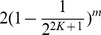 by an algebra calculation.
by an algebra calculation.
Next we prove the main theorem.
Theorem 1
For the identification of one time delay Boolean network of n nodes with maximum indegree
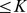 ,
, 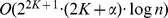 uniformly and randomly sampled input patterns are sufficient for exact inference with probability at least
uniformly and randomly sampled input patterns are sufficient for exact inference with probability at least
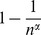 .
.
(Proof) We consider the probability that the condition of Proposition 1 is not satisfied under  random input expression patterns.
random input expression patterns.
By Proposition 2, the probability that  with all of its possible results in the target gene does not appear among the
with all of its possible results in the target gene does not appear among the  random input expression patterns is bounded by
random input expression patterns is bounded by 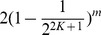 for any fixed set of nodes
for any fixed set of nodes 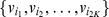 . Since the number of combinations of
. Since the number of combinations of 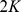 nodes from a set of
nodes from a set of  possibilities is bounded by
possibilities is bounded by 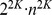 , the probability that the condition of Proposition 1 is not satisfied is at most
, the probability that the condition of Proposition 1 is not satisfied is at most 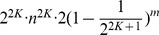 . It is not difficult to see that
. It is not difficult to see that 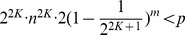 holds for
holds for 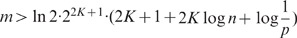 . Hence, we obtain the theorem by letting the non-identification probability
. Hence, we obtain the theorem by letting the non-identification probability 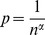 .
.
Next we develop an information theoretic lower bound on the number of input/output pairs needed for the identification of a time delay Boolean network.
Theorem 2
If the maximum indegree
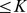 , at least
, at least
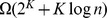 input/output pairs are required for the identification of a time delay Boolean network in the worst case.
input/output pairs are required for the identification of a time delay Boolean network in the worst case.
(Proof) The number of time delay Boolean networks is given by all the possible combination of Boolean function with 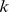 nodes from a set of
nodes from a set of  possibilities with all possible relations between Boolean functions with target node. Since there are
possibilities with all possible relations between Boolean functions with target node. Since there are 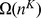 possible combinations of input nodes,
possible combinations of input nodes, 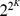 possible Boolean functions and 3 possible relations between Boolean function with each node, there are
possible Boolean functions and 3 possible relations between Boolean function with each node, there are 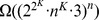 Boolean networks whose maximum indegree is at most
Boolean networks whose maximum indegree is at most 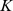 . On the other hand, there are at most
. On the other hand, there are at most 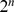 possible output patterns with one input expression pattern. Therefore,
possible output patterns with one input expression pattern. Therefore, 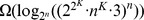 which is the same as
which is the same as 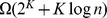 input/output pairs are required in the worst case.
input/output pairs are required in the worst case.
Example with Simulation and Real Data
We will illustrate our method by the example described in Figure 2. For the pair of samples consist of three elements list in the right part of Figure 2, we uniformly generated 100 input samples and their corresponding possible output samples with misclassification probability 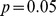 . For the prerequisite relationship, if the status of Boolean function with input genes is on, then we allow the output value to have equal probability of on or off. The data can be arranged as input/output sample similar to that obtained from the microarray data with time. Namely, the input of each sample can represent the gene expression at time
. For the prerequisite relationship, if the status of Boolean function with input genes is on, then we allow the output value to have equal probability of on or off. The data can be arranged as input/output sample similar to that obtained from the microarray data with time. Namely, the input of each sample can represent the gene expression at time  and the output can represent the gene expression at time
and the output can represent the gene expression at time 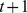 . For each pair of input and output genes, we compute the 8 basic
. For each pair of input and output genes, we compute the 8 basic 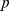 -scores that represent the 8 basic hypotheses in Table 5 for all of pair input genes and output genes. After the calculation, the simulation results of every
-scores that represent the 8 basic hypotheses in Table 5 for all of pair input genes and output genes. After the calculation, the simulation results of every 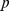 -score are listed in Table 6.
-score are listed in Table 6.
Table 6. By the time delay Boolean network in Figure 1, we generate 100 samples with p = 0.05.
| Samples | Hypotheses | Relation | ||||||||
| Input Output | q000 = 0 | q010 = 0 | q100 = 0 | q110 = 0 | q001 = 0 | q011 = 0 | q101 = 0 | q111 = 0 | ||
| v 1,v 2 | v 1 ′ | 0.493 | 0.418 | 0.273 | 0.379 | 0.148 | 0.178 | 0.372 | 0.343 | |
| v 1,v 3 | v 1 ′ | 0.438 | 0.147 | 0.248 | 0.222 | 0.016 | 0.245 | 0.182 | 0.241 | (v
1
or v
3) v′
1
v′
1
|
| v 2,v 3 | v 1 ′ | 0.318 | 0.260 | 0.571 | 0.214 | 0.189 | 0.293 | 0.138 | 0.374 | |
| v 1,v 2 | v 2 ′ | 0.326 | 0.300 | 0.304 | 0.297 | 0.091 | 0.092 | 0.232 | 0.209 | |
| v 1,v 3 | v 2 ′ | 0.338 | 0.216 | 0.349 | 0.197 | 0.039 | 0.069 | 0.038 | 0.243 | (v
1
and v
3) v′2
v′2
|
| v 2,v 3 | v 2 ′ | 0.326 | 0.253 | 0.390 | 0.174 | 0.052 | 0.141 | 0.017 | 0.169 | |
| v 1,v 2 | v 3 ′ | 0.211 | 0.011 | 0.355 | 0.029 | 0.040 | 0.228 | 0.011 | 0.294 | |
| v 1,v 3 | v 3 ′ | 0.338 | 0.290 | 0.402 | 0.734 | 0.669 | 0.291 | 0.379 | 0.360 | v 2∼v′3 |
| v 2,v 3 | v 3 ′ | 0.247 | 0.312 | 0.030 | 0.011 | 0.039 | 0.011 | 0.283 | 0.241 | |
Beside the example with 3 elements, in order to shows the superiority of the proposed method can be applied to a larger network, a more comprehensive example with a larger network is given in Figure S1.
Next, we have to decide the threshold for choosing the relations. When we increase the threshold of the 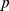 -score, the relations whose
-score, the relations whose 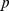 -score are smaller than the threshold will be chosen. Moreover, when the number is 0.138, the conflict occurs, since we have
-score are smaller than the threshold will be chosen. Moreover, when the number is 0.138, the conflict occurs, since we have 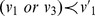 and
and 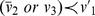 . However, in our model, there are at most two genes that would affect an output gene. Therefore, we can choose 0.138 as our threshold and include relations whose
. However, in our model, there are at most two genes that would affect an output gene. Therefore, we can choose 0.138 as our threshold and include relations whose 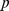 -score is smaller than the threshold. By these procedures, we can reconstruct the time delay Boolean network identical to Figure 2.
-score is smaller than the threshold. By these procedures, we can reconstruct the time delay Boolean network identical to Figure 2.
In the area of gene regulatory network study, Schuller has summarized regulatory cis-acting elements of structural genes of the nonfermentative metabolism and described the molecular interactions among general regulators and pathway-specific factors [40]. In the gene regulation of gluconeogenesis by Sip4 and Cat8 pathway, the carbon source control could be identified for the regulator Cat8; see (Figure 6) in Schuller [40]. In this study, we apply our proposed approach to explore the expression profiles and show some exploratory result on the Cat8 pathway.
In order to demonstrate the effectiveness of reconstruction, we use the microarray expression dataset of yeast Saccharomyces cerevisiae produced by DeRisi et al. [1] and Spellman et al. [41]. In total, the data is comprised of 41 experiments after filtering out experiments with missing values. By these experimental microarray data sets, we can use our proposed method to reconstruct the biological pathway and the genetic regulation network result is shown in Figure 3. The result is consistent with the genetic network in the literature. That is, the restraint of Mig1 or activation of Snf1 is a prerequisite for the decreasing of Cat8. Moreover, the restraint of Snf1 or Cat8 is a prerequisite for the decreasing of Mls1. However, the negative similarity between Snf1 and Mig1 is undetectable in our current model.
Figure 3. Network reconstruct from the expression data of yeast Saccharomyces cerevisiae.
Conclusions
In this paper, we have introduced the model of time delay Boolean network that generalizes the Boolean network model in order to cope with dependencies that have two kinds of relationships: similarity and prerequisite. The approach for reconstruction of genetic network inference from gene expression data relies on the assumption that the expression of a gene is likely to be controlled by a relatively small number (say 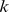 ) of genes. Also, some bounds on the size of data required for the identification of the time delay Boolean networks under constant of indegree are stated and discussed. Moreover, the algorithm of the network reconstruction from noisy array data is developed.
) of genes. Also, some bounds on the size of data required for the identification of the time delay Boolean networks under constant of indegree are stated and discussed. Moreover, the algorithm of the network reconstruction from noisy array data is developed.
One characteristic of a Boolean network is that all the variables in the graph are binary. If the data we observed is continuous or quantized to have more than two levels, we need to discretize them. For microarray data, the ratios of expression level would be one possible approach of discretization. That is, we can treat the gene as on (active) if the log-ratio of its expression is larger than zero. We treat it as off (inactive) otherwise. In general, biological background knowledge will be helpful for setting thresholds for discretizaion. On the other hand, if the samples are obtained from a time course, then we can consider the gene as on or off by detecting whether the gene is either increasing or decreasing with time.
The work in progress is aimed at evaluating the effectiveness of the described approach for inferring genetic networks from biological gene expression time series data. Besides that, implementation on some other real biological data is also an important task.
For the implement of the network reconstruction algorithm, the greatest complexity is the computation of 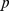 -score for each of the
-score for each of the 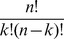 input elements and
input elements and  output elements, where
output elements, where  is the number of elements and
is the number of elements and 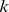 is the number of indegree. It is an iterative algorithm to compute the MLE for the
is the number of indegree. It is an iterative algorithm to compute the MLE for the 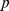 -scores by EM procedure while the common practice is to set an upper bound for iterations in numerical implementation. Consequently, this keeps the
-scores by EM procedure while the common practice is to set an upper bound for iterations in numerical implementation. Consequently, this keeps the 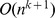 complexity for the computation of MLE. In addition, the sorting algorithm for the
complexity for the computation of MLE. In addition, the sorting algorithm for the 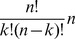 data cost
data cost 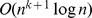 in terms of time. Hence, the overall time complexity for the network reconstruction is
in terms of time. Hence, the overall time complexity for the network reconstruction is 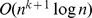 for this algorithm.
for this algorithm.
Supporting Information
An example of genetic network with 8 nodes.
(PDF)
Acknowledgments
We thank the editor and reviewers for their constructive comments.
Funding Statement
The authors acknowledge support from the National Science Council, National Center for Theoretical Sciences, Shing-Tung Yau Center, and Center of Mathematical Modeling and Scientic Computing at the National Chiao Tung University in Taiwan. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. DeRisi JL, Iyer VR, Brown PO (1997) Exploring the metabolic and genetic control of gene expression on a genomic scale. Science 278: 680–686. [DOI] [PubMed] [Google Scholar]
- 2. Bornholdt S (2005) Less is more in modeling large genetic networks. Science 310: 449–451. [DOI] [PubMed] [Google Scholar]
- 3. Eisen MB, Spellman PT, Brown PO, Botstein D (1998) Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci U S A 95: 14863–14868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Tzeng J, Lu HH-S, Li WH (2008) Multidimensional scaling for large genomic data sets. BMC Bioinformatics 9: 179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Rawool S, Venkatesh K (2007) Steady state approach to model gene regulatory networks–simulation of microarray experiments. Biosystems 90: 636–655. [DOI] [PubMed] [Google Scholar]
- 6.Jensen FV (1996) An introduction to Bayesian networks. London: University College London Press.
- 7.Jensen FV (2001) Bayesian networks and decision graphs. New York: Springer.
- 8. Moler EJ, Radisky DC, Mian IS (2000) Integrating naive bayes models and external knowledge to examine copper and iron homeostasis in s. cerevisiae. Physiol Genomics 4: 127–135. [DOI] [PubMed] [Google Scholar]
- 9.Pearl J (1988) Probabilistic reasoning in intelligent systems: networks of plausible inference. San Mateo: Morgan Kaufmann.
- 10. Needham C, Bradford J, Bulpitt A, Westhead D (2007) A primer on learning in Bayesian networks for computational biology. PLoS Comput Biol 3: e129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Reynolds S, Käll L, Riffle M, Bilmes J, Noble W (2008) Transmembrane topology and signal peptide prediction using dynamic Bayesian networks. PLoS Computational Biology 4: e1000213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Friedman N, Linial M, Nachman I, Pe’er D (2000) Using bayesian networks to analyze expression data. Journal of Computational Biology 7: 601–620. [DOI] [PubMed] [Google Scholar]
- 13. Imoto S, Higuchi T, Goto T, Tashiro K, Kuhara S, et al. (2004) Combining microarrays and biological knowledge for estimating gene networks via bayesian networks. Journal of Bioinformatics and Computational Biology 2: 77–98. [DOI] [PubMed] [Google Scholar]
- 14. Scharfe C, Lu HH-S, Neuenburg JK, Allen EA, Li GC, Klopstock T, Cowan TM, Enns GM, Davis RW (2009) Mapping gene associations in human mitochondria using clinical disease phenotypes. PLoS Computational Biology 5: e1000374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Liu T, Sung W, Mittal A (2006) Learning gene network using time-delayed bayesian network. International Journal of Artificial Intelligence Tools 15: 353–370. [Google Scholar]
- 16.Friedman N, Nachman I, Pe’er D (1999) Learning bayesian network structure from massive datasets: the sparse candidate algorithm. In: Proceedings of the Fifteenth conference on Uncertainty in artificial intelligence. 206–215.
- 17. Heckerman D, Geiger D, Chickering DM (1995) Learning bayesian networks: the combination of knowledge and statistical data. Machine Learning 20: 197–243. [Google Scholar]
- 18. Balakrishnan S, Madigan D (2006) A one-pass sequential Monte Carlo method for Bayesian analysis of massive datasets. Bayesian Analysis 1: 345–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Huang S (1999) Gene expression profiling, genetic networks and cellular states: An integrating concept for tumorigenesis and drug discovery. Journal of Molecular Medicine 77: 469–480. [DOI] [PubMed] [Google Scholar]
- 20. Shmulevich I, Gluhovsky I, Hashimoto RF, Dougherty ER, Zhang W (2003) Steady-state analysis of genetic regulatory networks modelled by probabilistic Boolean networks. Comparative and Functional Genomics 4: 601–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Kim H, Lee JK, Park T (2007) Boolean networks using the chi-square test for inferring large-scale gene regulatory networks. BMC Bioinformatics 8: 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Zhang R, de SCavalcante HLD, Gao Z, Gauthier DJ, Socolar JES, et al. (2009) Boolean chaos. Phys Rev E 80: 045202. [DOI] [PubMed] [Google Scholar]
- 23. Socolar JES, Kauffman SA (2003) Scaling in ordered and critical random Boolean networks. Physical Review Letters 90: 68702. [DOI] [PubMed] [Google Scholar]
- 24. Dealy S, Kauffman SA, Socolar JES (2005) Modeling pathways of differentiation in genetic regulatory networks with boolean networks: Research articles. Complex 11: 52–60. [Google Scholar]
- 25. Veliz-Cuba A, Stigler B (2011) Boolean models can explain bistability in the lac operon. Journal of Computational Biology 18: 783–794. [DOI] [PubMed] [Google Scholar]
- 26. Kauffman SA (1969) Metabolic stability and epigenesis in randomly constructed genetic nets. Journal of Theoretical Biology 22: 437–467. [DOI] [PubMed] [Google Scholar]
- 27.Akutsu T, Miyano S (1999) Identification of genetic networks from a small number of gene expression patterns under the boolean network model. Proc Pacific Symposium on Biocomputing : 17–28. [DOI] [PubMed]
- 28.Ideker T, Thorsson V, Karp R (2000) Discovery of regulatory interactions through perturbation: inference and experimental design. Proc Pacific Symposium on Biocomputing : 302–313. [DOI] [PubMed]
- 29. Allocco DJ, Kohane IS, Butte AJ (2004) Quantifying the relationship between co-expression, coregulation and gene function. BMC Bioinformatics 5: 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Bosl WJ (2007) Systems biology by the rules: hybrid intelligent systems for pathway modeling and discovery. BMC Systems Biology 1: 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Jordan IK, Marino-Ramirez L, Wolf YI, Koonin EV (2004) Conservation and coevolution in the scale-free human gene coexpression network. Molecular Biology and Evolution 21: 2058–2070. [DOI] [PubMed] [Google Scholar]
- 32. Lee HK, Hsu AK, Sajdak J, Qin J, Pavlidis P (2004) Coexpression analysis of human genes across many microarray data sets. Genome Research 14: 1085–1094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Opgen-Rhein R, Strimmer K (2007) From correlation to causation networks: a simple approximate learning algorithm and its application to high-dimensional plant gene expression data. BMC Systems Biology 1: 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Li LM, Lu HH-S (2005) Explore biological pathways from noisy array data by directed acyclic boolean networks. Journal of Computational Biology 12: 170–185. [DOI] [PubMed] [Google Scholar]
- 35. Sahoo D, Dill D, Gentles A, Tibshirani R, Plevritis S (2008) Boolean implication networks derived from large scale, whole genome microarray datasets. Genome Biology 9: R157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Wang H, Lu HH-S, Chueh TH (2011) Constructing biological pathway by a two-step counting approach. Plos one 6: e20074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Somogyi R, Sniegoski CA (1996) Modeling the complexity of genetic networks: Understanding multigene and pleiotropic regulation. Complexity 1: 45–63. [Google Scholar]
- 38.Akutsu T, Kuhara S, Maruyama O, Miyano S (1998) Identification of gene regulatory networks by strategic gene disruptions and gene overexpression. Proc 9th ACM-SIAM Symp Discrete Algorithms: 695–702.
- 39. Akutsu T, Kuhara S, Maruyama O, Miyano S (2003) Identification of genetic networks by strategic gene disruptions and gene overexpressions under a boolean model. Theoretical Computer Science 298: 235–251. [Google Scholar]
- 40. Schuller HJ (2003) Transcriptional control of nonfermentative metabolism in the yeast saccharomyces cerevisiae. Current Genetics 43: 139–160. [DOI] [PubMed] [Google Scholar]
- 41. Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, et al. (1998) Comprehensive identification of cell cycle-regulated genes of the yeast saccharomyces cerevisiae by microarray hybridization. Molecular Biology of Cell 9: 3273–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
An example of genetic network with 8 nodes.
(PDF)