Double-robust semiparametric estimator for differences in restricted mean lifetimes in observational studies

Summary

Restricted mean lifetime is often of direct interest in epidemiologic studies involving censored survival times. Differences in this quantity can be used as a basis for comparing several groups. For example, transplant surgeons, nephrologists and of course patients are interested in comparing post-transplant lifetimes among various types of kidney transplants in order to assist in clinical decision-making. As the factor of interest is not randomized, covariate adjustment is needed in order to account for imbalances in confounding factors. In this report, we use semiparametric theory to develop an estimator for differences in restricted mean lifetimes while accounting for confounding factors. The proposed method involves building working models for the time-to-event and coarsening mechanism (i.e., group assignment and censoring). We show that the proposed estimator possesses the double robust property; i.e., when either the time-to-event or coarsening process is modeled correctly, the estimator is consistent and asymptotically normal. Simulation studies are conducted to assess its finite-sample performance and the method is applied to national kidney transplant data.

1. Introduction

It is often of interest in biomedical studies to compare groups of subjects with respect to their survival time. In almost all cases, the study’s observation period may conclude before all subjects have experienced the event of interest, resulting in censored data. In observational studies, lack of randomization requires that the groups of interest be compared in a manner which accounts for the possibility that the group-specific adjustment covariate distributions may be different. Proportional hazards regression (Cox, 1972) has become the dominant method of survival analysis in settings where covariate adjustment is needed. In the application of the Cox model, groups may be contrasted through the hazard ratio, provided that the group-specific hazard functions are proportional. If proportionality fails, the ‘overall’ hazard ratios estimated by a Cox model with time-constant group effects will have an awkward interpretation, as identified by Struthers and Kalbfleisch (1986). Moreover, investigators are often more interested in contrasts among mean survival times than ratios of hazards. Since the baseline hazard is handled non-parametrically, restricted mean lifetime is often estimated when Cox regression is employed, and several methods have been proposed for this purpose (e.g., Karrison, 1987; Zucker, 1998; Chen and Tsiatis, 2001).

If one wished to compare group-specific restricted mean survival time, two general approaches could be employed. In the first, differences in restricted mean lifetime are estimated via directly modeling the relationship of survival time with covariates, then explicitly averaging across the fitted values from such models for each treatment (Karrison, 1987; Zucker, 1998; Chen and Tsiatis, 2001). Zhang and Schaubel (2011) developed methods for comparison of group-specific restricted mean lifetimes in the presence of dependent censoring based on this general idea. A second possibility would be to use Inverse Probability of Treatment Weighting (Hubbard, van der Laan, and Robins, 1999; Wei, 2008) to essentially equalize the adjustment covariate distribution across groups; in this case, the probability of receiving treatment conditional on covariates is modeled. Covariates operate as confounding factors when they affect both survival time and treatment assignment. The two aforementioned methods lead to valid inference, under appropriate conditions regarding censoring, because each of them eliminates confounding by tackling one of the two pathways. With respect to censoring, the first approach requires that survival time and censoring time are independent conditional on treatment and baseline covariates; whereas the second approach requires the more restrictive conditional independence assumption given treatment only. Both assumptions can be relaxed if the relationship of censoring and covariates is further modeled, as in Zhang and Schaubel (2011). If censoring has been appropriately accounted for, either by exploiting its conditional independence or through modeling, each of the first and second methods leads to consistent and asymptotically normal estimators of treatment-specific restricted mean lifetimes (and, hence, between-treatment differences therein) under correct specification of the regression models for survival time or treatment assignment probability, respectively.

Restricted mean lifetime is a very meaningful quantity in the solid organ transplant setting. For example, a kidney transplant is typically not going to last the remainder of the transplant recipient’s life, particularly if the deceased organ donor was older than the recipient. This makes restricted mean lifetime a more useful quantity than mean survival time itself. Consider a study of simultaneous kidney-pancreas (SPK) transplant recipients. Pancreas transplantation is risky and controversial, and its merits are not universally accepted by nephrologists. A useful way to evaluate the benefit receiving a pancreas (in addition to a kidney) is to compare outcomes between SPK and kidney-alone (KA) recipients. Since the majority of SPK recipients are Type I diabetics, it makes sense to restrict attention to this subgroup of patients. Typically for SPK patients, the pancreas is transplanted along with the kidney in an attempt to, in a sense, ‘cure’ the diabetes. However, the surgery is considerably more complicated, meaning that survival may actually end up being lower for SPK than KA patients, despite the potential benefits of successful pancreas transplantation. As described in the preceding paragraph, one could compare SPK and KA transplantation with respect to average restricted mean lifetime by either modeling post-transplant survival times, or by modeling the probability that a pancreas is received. Since it is possible for at least one of the two models to be incorrect, it would be preferable to use a method that requires the correctness of only one model.

In this article, we propose a method which adjusts for confounding factors by modeling covariate effects on each of survival time, treatment assignment and censoring. The method is developed from the perspective where the treatment assignment and censoring are viewed as a coarsening (generalization of missing data) process, and will be explained in Section 3. The benefit of modeling both the death hazard and coarsening process is that valid inference on causal parameters is obtained when either one of two processes are modeled correctly; i.e., either the model for survival time is correct, or the models for both treatment assignment and censoring are correct. Such a property has been termed double-robustness by several previous authors who developed analogous methods in other contexts; e.g., Scharfstein, Rotnitzky, and Robins (1999); Robins, Rotnitzky and van der Laan (2000); van der Laan and Robins (2003), Lunceford and Davidian (2004) and Bang and Robins (2005).

The remainder of the article is organized as follows. In Section 2, we set up the requisite notation and state the required assumptions. We describe the proposed double-robust method in Section 3. Asymptotic results are provided in Section 4, with their applicability to finite samples assessed through simulation in Section 5. The proposed method is then applied in Section 6 to compare simultaneous kidney-pancreas and kidney-alone transplants using data from the Scientific Registry of Transplant Recipients. The article concludes with some remarks in Section 7.

2. Notation and Assumptions

In this section we set up the requisite notation. Let A denote the treatment group, which is not randomized, and for simplicity of presentation we assume there are only two treatment groups to be compared (A = 0, 1); extension to situations with more than two groups can be accomplished, as we discuss later. We let T denote survival time, which is subject to right censoring, C. We assume that T and C are independent given A and baseline covariates Z, denoted by T⫫C|(A, Z), where ⫫ denotes “independent of”. We let U = min(T, C) and Δ = I(T ≤ C). Since A is not randomized, imbalances in baseline covariates may exist between the two groups. Elements of the Z vector which affect both A assignment and T are referred to as confounders and require adjustment in order for comparisons between the A = 1 and A = 0 groups to be valid. In a study with n subjects, the observed data may be summarized by {A_i, U_i, Δ_i, Z_i}, assumed to be independent and identically distributed across subjects i = 1, …, n.

Treatment groups are to be compared in terms of restricted mean lifetime up to time L, min(T, L). In particular, interest focuses on the comparison of average survival time up to time L under two specific scenarios: (i) the treatment is applied to the entire population, in which case A_i = 1 for all i = 1, …, n (ii) the treatment is applied to no member of the population, such that A_i = 0 for i = 1, …, n. The causal parameter of interest may be defined in terms of potential outcomes; as studied, for example, by Rubin (1974, 1978) in the general causal inference setting and by Chen and Tsiatis (2001) in the context of censored data. Let T^j (j=0,1) denote the potential (or counterfactual) lifetime of a randomly selected subject from the population under study if, possibly contrary to fact, s/he received treatment A = j. Therefore, there is a two-dimensional potential outcome (T⁰, T¹) corresponding to each subject. The treatment-specific difference in restricted mean lifetime is defined as δ = E{min(T¹, L)} − E{min(T⁰, L)}; which is equal to ${\int }_0^L\{S_1(t)-S_0(t)\}dt$, where S_j(t) represents the survival function of T ^j. We set μ_j = E{min(T^j, L)}. Since μ_j represents a population mean, a natural estimator would be $n^{-1}{\sum }_{i=1}^{n}min(T_i^j,L)$, with an estimator for δ defined accordingly. However, such estimators cannot be implemented in practice because potential outcomes $T_i^0$ and $T_i^1$ can never be simultaneously observed for subject i, even if there were no censoring. That is, for a subject who actually receives A_i = j, the observed lifetime T_i is equal to her/his potential lifetime $T_i^j$, with $T_i^{1-j}$ then being missing. Since subjects who receive A = j are not a random sample of the population, the sample average of restricted lifetimes across subjects who actually receive A = j does not consistently estimate μ_j and, consequently, differences in such sample averages do not consistently estimate the causal parameter of interest, δ. Specifically, $n_j^{-1}{\sum }_{i=1}^n{A}_{ij}min(T_i^j,L)$ and $n_1^{-1}{\sum }_{i=1}^n{A}_{i1}min(T_i^1,L)-n_0^{-1}{\sum }_{i=1}^n{A}_{i0}min(T_i^0,L)$, where A_ij = I(A_i = _j), j = 0,1 and $n_j={\sum }_{i=1}^n{A}_{ij}$, do not consistently estimate μ_j or δ, respectively, in the presence of confounders.

Valid inference is possible when all confounders are captured in the data; i.e., there are no unmeasured confounders. Formally, this assumption can be stated as (T¹, T⁰)⫫A|Z, which can be interpreted as the assignment of A being random, conditional on Z. Under this assumption, P(T > t|A = j, Z) = P(T^j > t|A = j, Z) = P(T^j > t|Z), which we denote by S_j(t|Z), where the first equality is because T = T^j if A = j and the second equality is due to the no unmeasured confounders assumption. As S_j(t) = E_Z{S_j(t|Z)}, it is straightforward that $\delta ={\int }_0^L{E}_Z\{S_1(t\mid \mathit{Z})-S_0(t\mid \mathit{Z})\}dt$, where the expectation E_Z is taken with respect to the marginal distribution of Z. This assumption allows us to represent the causal parameter, defined in terms of potential outcomes (T¹, T⁰), as a function of observed variates. Generally, the no-unmeasured-confounders assumption is essential to carrying out valid inference pertaining to the counterfactual variates using only the observed data.

3. Proposed Method

We propose a method based on semiparametric theory, for which the estimators are valid under the frequently employed assumption that T⫫C|(A, Z). The resulting estimator possesses the so-called double robustness property. Before introducing the proposed method, we explain its motivation and its relationship to existing methods.

3.1 Motivation and connection to existing methods

First, let us assume that, contrary to fact, treatment A = j was applied to the entire population. Suppose in addition, for the time being, that survival and censoring times were independent given treatment; i.e., T⫫C|A. Under such assumptions, a natural estimator for μ_j would then be ${\int }_0^{L}exp\{-{\widehat{\mathrm{\Lambda }}}_j^{★}(t)\}dt$, where

$${\widehat{\mathrm{\Lambda }}}_j^{★}(t)={\int }_0^t\frac{{\sum }_{i=1}^n{dN}_i(u)}{{\sum }_{i=1}^n{Y}_i(u)},$$

is the Nelson-Aalen estimator for Λ_j(t), the marginal cumulative hazard function of T ^j, with N_i(t) = I(U_i ≤ t, Δ_i = 1) and Y_i(t) = I(U_i ≥ t) denoting the death counting process and at-risk process, respectively. The estimator ${\widehat{\mathrm{\Lambda }}}_j^{★}(t)$ or, equivalently, $d{\widehat{\mathrm{\Lambda }}}_j^{★}(t)$ can be viewed as the solution to the following estimating equation,

$$\sum _{i=1}^n\{{dN}_i(t)-Y_i(t)d{\mathrm{\Lambda }}_j(t)\}=0,$$

which is an unbiased estimating equation in the setting where all subjects receive treatment A = j. In reality, not everyone in the population receives treatment j and, when confounders exist, treatment-specific Nelson-Aalen estimators do not consistently estimate Λ_j(t) for j =0, 1.

It is well established that, under the no-unmeasured-confounders assumption specified previously, Inverse Probability of Treatment Weighted (IPTW) estimating equations lead to consistent estimators (Robins et. al., 1994; Lunceford and Davidian, 2004; Tsiatis, 2006). IPTW estimating equations are developed from the perspective of missing data problems; i.e., the treatment indicator A_ij may be viewed as a missingness indicator for the counterfactual outcome $T_i^j$ (A_ij = 1 if $T_i^j$ is observed and A_ij = 0 if $T_i^j$ is missing). Tsiatis (2006; Chapter 7) discusses how to construct Inverse Probability Weighted (IPW) estimating equations for general cases. Specifically, for estimating dΛ_j(t), assuming again that T ⫫C|A, the IPTW estimating equation is given by

$$\sum _{i=1}^n{w}_{ij}(\widehat{\mathit{\theta }})\{{dN}_i(t)-Y_i(t)d{\mathrm{\Lambda }}_j(t)\}=0,$$ (1)

where w_ij(θ̂) = A_ij/p_ij(θ̂) and p_ij(θ̂) estimates P(A_ij = 1|Z_i), modeled through a parametric model (e.g., logistic regression) with parameter θ. Solving this equation leads to the inverse probability of treatment weighted estimator proposed by Wei (2008),

$${\widehat{\mathrm{\Lambda }}}_j^{\mathit{inv}}(t)={\int }_0^t\frac{{\sum }_{i=1}^n{w}_{ij}(\widehat{\mathit{\theta }}){dN}_i(u)}{{\sum }_{i=1}^n{w}_{ij}(\widehat{\mathit{\theta }})Y_i(u)}.$$ (2)

Under the assumption that T⫫C|A, if the assumed model for P(A_ij = 1|Z_i) is correct, then ${\widehat{\mathrm{\Lambda }}}_j^{\mathit{inv}}(t)$ is consistent for Λ_j(t). If not, then (2) fails to be consistent for Λ_j(t), even if treatment assignment is modeled correctly.

In most observational studies, the assumption that T⫫C|A is too restrictive. A more realistic assumption would be that T⫫C|(A, Z), which is the setting we consider in developing the proposed estimator.

3.2 Coarsened data

The IPTW estimating equation was developed from the perspective of missing data problems. Thus far, the missingness we have considered pertains to subject i having missing experience with respect to the group to which the subject does not belong. Let us now consider a broader view of missingnes, in particular, the more general concept of coarsening (Heitjan and Rubin, 1991; Gill, van der Laan and Robins, 1997; Tsiatis, 2006). In the case of missing data, some components of the full data are not observed for some subjects. More generally, in the case of coarsened data, one observes a many-to-one function of the full data for some of the subjects in the sample and different many-to-one functions may be observed for different subjects. Specific to our setting, the full data that one would like to observe are coarsened due to treatment assignment and censoring. In the context of estimating μ_j, the full data that one would like to observe is ( $T_i^j$, Z_i), i = 1, …, n. When A_ij = 0, $T_i^j$ is completely missing and, for subject i, one observes Z_i, which is a many-to-one function of the full data. When A_ij = 1 and $C_i=t<T_i^j$, the many-to-one function that one observes is { $I(T_i^j\ge t)$, Z_i}. The coarsening mechanism in our case is of a special form, known as monotone coarsening (Tsiatis, 2006; Chapter 8), which generalizes the notion of monotone missingness. The observed data for subject i is in the most coarsened form when A_ij = 0, less coarsened when A_ij = 1 and $C_i=t_1<T_i^j$, and even less coarsened when A_ij = 1 and $C_i=t_2<T_i^j$, t₁ < t₂, and not coarsened at all when A_ij = 1 and $C_i\ge T_i^j$. In summary, coarsening prevents one from observing the full data that one would like to observe and in our setting, the full data, $T_i^j$, i = 1, …, n, are subject to coarsening at time t = 0, due to treatment assignment, and at any time t > 0 thereafter, due to censoring.

Using the IPW principle, one can inverse weight an unbiased estimating function based on full data by the probability of observing the complete case (not being coarsened), i.e., the probability of assigning to treatment j and not being censored by t. The IPW estimating equation for dΛ_j(t) based on the observed data is

$$\sum _{i=1}^n{w}_{ij}(\widehat{\mathit{\theta }})e^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(t)}{\kappa }_i(t){dM}_i^T(t;d{\mathrm{\Lambda }}_j)\equiv \sum _{i=1}^n{w}_{ij}(\widehat{\mathit{\theta }})e^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(t)}\{{dN}_i(t)-Y_i(t)d{\mathrm{\Lambda }}_j(t)\}=0,$$ (3)

where κ_i(t) = I(C_i ≥ T_i or C_i ≥ t), ${dM}_i^T(t;d{\mathrm{\Lambda }}_j)={dN}_i^T(t)-Y_i^T(t)d{\mathrm{\Lambda }}_j(t),N_i^T(t)=I(T_i\le t),Y_i^T(t)=I(T_i\ge t)$, with ${\mathrm{\Lambda }}_{ij}^C(t)$ denoting the cumulative conditional hazard function of C at t given (Z_i, A_i = j). Note that we utilize κ_i(t) defined above, as opposed to I(C_i ≥ T_i), since the more explicit formulation is useful in the asymptotic derivations given in the Web Appendix. The key difference between (3) and (1) is that (3) is weighted by the estimated inverse of the probability of remaining uncensored, $e^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(t)}$. In (1), such additional weighting is unnecessary under the assumption that T⫫C|A.

3.3 Proposed double-robust method

The IPW estimating equation can be augmented in such a way that the resulting estimator is double robust (Scharfstein, Rotnitzky, and Robins, 1999; Tsiatis, 2006). In the case of monotone coarsening, a double robust estimating equation can be written in closed form, as discussed in detail in Tsiatis (2006, Chapter 10). Using similar principles, we construct a double robust estimator for dΛ_j(t) by augmenting (3) as follows,

$$\sum _{i=1}^n[w_{ij}(\widehat{\mathit{\theta }})e^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(t)}{\kappa }_i(t){dM}_i^T(t;d{\mathrm{\Lambda }}_j)+{\mathcal{A}}_{ij}(t)]=0,$$ (4)

where the augmentation term is defined as

$${\mathcal{A}}_{ij}(t)=\{1-w_{ij}(\widehat{\mathit{\theta }})\}E\{{dM}_i^T(t;d{\mathrm{\Lambda }}_j)\mid A_{ij}=1,{\mathit{Z}}_i\}+w_{ij}(\widehat{\mathit{\theta }}){\int }_0^{t}E\{{dM}_i^T(u;d{\mathrm{\Lambda }}_j)\mid A_{ij}=1,{\mathit{Z}}_i,U_i\ge u\}{e}^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(u)}{d\widehat{M}}_{ij}^C(u),$$

with ${d\widehat{M}}_{ij}^C(u)={dN}_{ij}^C(u)-Y_{ij}(u)d{\widehat{\mathrm{\Lambda }}}_{ij}^C(u)$ and $N_{ij}^C(t)=A_{ij}I(U_i\le t,{\mathrm{\Delta }}_i=0)$. The resulting estimator for dΛ_j(t) is double robust in the sense that it will be consistent if either the models corresponding to the weight (product of the inverse of probabilities of treatment assignment and censoring) or the model corresponding to $E\{{dM}_i^T(t;d{\mathrm{\Lambda }}_j)\mid {\mathit{Z}}_i,A_{ij}=1\}$ are correctly specified. Solving this equation leads to the following estimator for Λ_j(t),

$${\int }_0^t\frac{{\sum }_{i=1}^n\{w_{ij}(\widehat{\mathit{\theta }})e^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(t)}{dN}_i(u)+{\mathcal{A}}_{ij}^N(u)\}}{{\sum }_{i=1}^n\{w_{ij}(\widehat{\mathit{\theta }})e^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(t)}{Y}_i(u)+{\mathcal{A}}_{ij}^N(u)\}},$$

where we specify

$$\begin{array}{l}{\mathcal{A}}_{ij}^N(u)=\{1-w_{ij}(\widehat{\mathit{\theta }})\}E\{{dN}_i^T(u)\mid {\mathit{Z}}_i,A_{ij}=1\}+{\widehat{w}}_{ij}(\widehat{\mathit{\theta }}){\int }_0^{t}E\{{dN}_i^T(u)\mid A_{ij}=1,{\mathit{Z}}_i,U_i\ge u\}{e}^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(u)}{d\widehat{M}}_{ij}^C(u)\\ {\mathcal{A}}_{ij}^Y(u)=\{1-w_{ij}(\widehat{\mathit{\theta }})\}E\{Y_i^T(u)\mid {\mathit{Z}}_i,A_{ij}=1\}+w_{ij}(\widehat{\mathit{\theta }}){\int }_0^{t}E\{Y_i^T(u)\mid A_{ij}=1,{\mathit{Z}}_i,U_i\ge u\}{e}^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(u)}{d\widehat{M}}_{ij}^C(u).\end{array}$$

In practice, the expectations need to be replaced by their empirical counterparts. The fact that $N_i^T(t)$ and $Y_i^T(t)$ are functions of T_i suggests modeling T_i as a function of the factors which potentially affect it, namely A_i and Z_i.

In the next subsection, we describe in detail the proposed method and why it exhibits the double robust property.

3.4 Assumed models and proposed estimator

In our proposed method, we build working models for (i) survival time T given A and Z, (ii) treatment A given covariates Z, and (iii) censoring C given A and Z. Specifically, for each treatment A = 0, 1, we assume a proportional hazards model (Cox, 1972, 1975),

$${\lambda }_{ij}(t)\equiv \lambda (t\mid A_i=j,{\mathit{Z}}_i)={\lambda }_{0j}(t)\text{exp}({\mathit{\beta }}_j^T{\mathit{Z}}_i),j=0,1,$$ (5)

where λ(t|A_i = j, Z_i) is the conditional hazard function given Z_i and [A_i = j] and λ_0j(t) is an unspecified treatment-specific baseline hazard function. Estimators for β_j and ${\mathrm{\Lambda }}_{0j}(t)={\int }_0^t{\lambda }_{0j}(u)du$ can be obtained by the maximum partial likelihood (PL) estimator, β̂_j, and the Breslow (1972) estimator, Λ̂_0j(t), respectively. Defining the counting process by N_ij(t) = A_ijI(U_i ≤ t, Δ_i = 1) and the at-risk process by Y_ij(t) = A_ijI(U_i ≥ t), β̂_j is the solution to the estimating equation

$$\sum _{i=1}^n{\int }_0^{\tau }\{{\mathit{Z}}_i-\frac{{\sum }_{i=1}^n{\mathit{Z}}_{i}exp({\mathit{\beta }}_j^T{\mathit{Z}}_i)Y_{ij}(t)}{{\sum }_{i=1}^{n}exp({\mathit{\beta }}_j^T{\mathit{Z}}_i)Y_{ij}(t)}\}{dN}_{ij}(t)=0,j=0,1$$

where τ satisfies P(U ≥ τ) > 0 and, in practice, can be set to the maximum observation time; while the Breslow estimator for Λ_0j is defined as

$${\widehat{\mathrm{\Lambda }}}_{0j}(t)={\int }_0^t\frac{{\sum }_{i=1}^n{dN}_{ij}(t)}{{\sum }_{i=1}^{n}exp({\widehat{\mathit{\beta }}}_j{\mathit{Z}}_i)Y_{ij}(t)}j=0,1.$$

Finally, estimators for ${\mathrm{\Lambda }}_{ij}(t)={\int }_0^t{\lambda }_{ij}(u)du$ can be obtained by Λ̂_ij(t) = exp(β̂_jZ_i)Λ̂_0j(t). If model (5) is correct, then β̂_j and Λ̂_0j consistently estimate β_j and Λ_0j, respectively. Otherwise, β̂_j and Λ̂_0j will not converge to their respective targets but, under suitable regularity conditions (listed in the Web Appendix) will converge in probability to well-defined limits (Struthers and Kalbfleisch, 1986; Lin and Wei, 1989) which we denote by ${\mathit{\beta }}_j^{\ast }$ and ${\mathrm{\Lambda }}_{0j}^{\ast }(t)$, respectively. For notational convenience, we also define ${\mathrm{\Lambda }}_{ij}^{\ast }(t)=exp({\mathit{\beta }}_j^{\ast }{\mathit{Z}}_i){\mathrm{\Lambda }}_{0j}^{\ast }(t)$.

We also assume that treatment assignment is governed by the following logistic model,

$$\text{logit}\{P(A_i=1\mid {\mathit{Z}}_i)\}={\mathit{\theta }}^T{\mathit{X}}_i,$$ (6)

where X_i is a vector made up of (possibly transformed) elements of Z_i and an intercept. Inference on model (6) can be made through maximum likelihood, with the maximum likelihood estimator for θ, θ̂, solving the estimating equation,

$$\sum _{i=1}^n{\mathit{X}}_i\{A_i-\text{expit}({\mathit{\theta }}^T{\mathit{X}}_i)\}=0,$$ (7)

where expit(u) = exp(u)/{1 + exp(u)}. If model (6) is correct, then θ̂ consistently estimates the true parameter, θ. Otherwise, under suitable regularity conditions (listed in the Web Appendix), θ̂ converges to a limit, denoted θ^*, which need not equal θ. We define p_ij(θ) = expit{(−1)^j+1θ^TX_i}, which equals the probability of receiving treatment A = j when the assumed model is correct.

With respect to censoring, for each treatment A = 0, 1, we assume a proportional hazards model,

$${\lambda }_{ij}^C(t)\equiv {\lambda }^C(t\mid A_i=j,{\mathit{Z}}_i)={\lambda }_{0j}^C(t)exp({\mathit{\alpha }}_j^T{\mathit{Z}}_i^C),j=0,1,$$ (8)

where λ^C(t|A_i = j, Z_i) is the conditional hazard function of C_i given Z_i and [A_i = j], ${\lambda }_{0j}^C(t)$ is an unspecified treatment-specific baseline hazard function of C_i, and ${\mathit{Z}}_i^C$ is a vector made up of elements of Z_i with a superscript C indicating that the vector may be different from that in model (5). As described previously, estimators for α_j and ${\mathrm{\Lambda }}_{0j}^C(t)={\int }_0^t{\lambda }_{0j}^C(u)du$ can be obtained by the maximum PL estimator and the Breslow estimator, respectively, denoted by α̂_j and ${\widehat{\mathrm{\Lambda }}}_{0j}^C(t)$. Estimators for ${\mathrm{\Lambda }}_{ij}^C(t)$ can be obtained by ${\widehat{\mathrm{\Lambda }}}_{ij}^C(t)=exp({\widehat{\mathit{\alpha }}}_j^T{\mathit{Z}}_i^C){\widehat{\mathrm{\Lambda }}}_{0j}^C(t)$. Similarly, if model (8) is correct, α̂_j and ${\widehat{\mathrm{\Lambda }}}_{0j}^C(t)$ consistently estimate α_j and ${\mathrm{\Lambda }}_{0j}^C(t)$, respectively; otherwise, under suitable regularity conditions (see Web Appendix), convergence is instead to limits ${\mathit{\alpha }}_j^{\ast }$ and ${\mathrm{\Lambda }}_{0j}^{C\ast }(t)$. We define ${\mathrm{\Lambda }}_{ij}^{C\ast }(t)=exp({\mathit{\alpha }}_j^{\ast T}{\mathit{Z}}_i^C){\mathrm{\Lambda }}_{0j}^{C\ast }(t)$.

The proposed estimator for Λ_j(t) is given by

$${\widehat{\mathrm{\Lambda }}}_j(t){\int }_0^t\frac{n^{-1}{\sum }_{i=1}^n[w_{ij}(\widehat{\mathit{\theta }})e^{{\widehat{\mathrm{\Lambda }}}_j^C(u)}{dN}_{ij}(u)+e^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}d{\widehat{\mathrm{\Lambda }}}_{ij}(u)\{1-w_{ij}(\widehat{\mathit{\theta }}){\widehat{G}}_{ij}(u)\}]}{n^{-1}{\sum }_{i=1}^n[w_{ij}(\widehat{\mathit{\theta }})e^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(u)}{Y}_{ij}(u)+e^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}\{1-w_{ij}(\widehat{\mathit{\theta }}){\widehat{G}}_{ij}(u)\}]},$$ (9)

where ${\widehat{G}}_{ij}(u)=1-{\int }_0^u{e}^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(s)+{\widehat{\mathrm{\Lambda }}}_{ij}(s)}{d\widehat{M}}_{ij}^C(s)$. Consequently, one can estimate S_j(t) by Ŝ_j(t) = e^−Λ̂_j(t) and μ_j by ${\widehat{\mu }}_j={\int }_0^L{\widehat{S}}_j(u)du$. Finally, the proposed estimator for δ is given by δ̂ = μ̂₁ − μ̂₀. The proposed estimators for μ_j and δ are consistent and asymptotically normal when (i) the working model (5) is correct or (ii) the working models (6) and (8) are both correct.

The proposed estimator for Λ_j(t) in (9) differs from the IPTW estimator of Wei (2008), from (2), in two ways. First, the weight in (2) is the inverse of the probability of treatment assignment, while the weight in (9) is also comprised of the inverse probability remaining uncensored. Second, there are additional terms in the numerator, $n^{-1}{\sum }_{i=1}^n\left[e^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}d{\widehat{\mathrm{\Lambda }}}_{ij}(u)\{1-w_{ij}(\widehat{\mathit{\theta }}){\widehat{G}}_{ij}(u)\}\right]$, and denominator, $n^{-1}{\sum }_{i=1}^n\left[e^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}\{1-w_{ij}(\widehat{\mathit{\theta }}){\widehat{G}}_{ij}(u)\}\right]$, which we refer to as augmentation terms. From this perspective, the proposed estimator may be viewed as an augmented IPW estimator (Tsiatis, 2006).

When the models for treatment assignment and censoring are both correctly specified, w_ij(θ̂) converges in probability w_ij(θ) ≡ A_ij/p_ij(θ), and $e^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(u)}$ converges to $e^{{\mathrm{\Lambda }}_{ij}^C(u)}$. Then, using an iterated conditional expectation argument by first conditioning on Z_i or (A_i = j, Z_i), the augmentation term in the denominator converges in probability to 0 since

$$\begin{array}{l}{n}^{-1}\sum _{i=1}^n\left[e^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}\left\{1-w_{ij}(\widehat{\mathit{\theta }})+w_{ij}(\widehat{\mathit{\theta }}){\int }_0^u{e}^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(s)+{\widehat{\mathrm{\Lambda }}}_{ij}(s)}{d\widehat{M}}_{ij}^C(s)\right\}\right]\\ \stackrel{p}{\to }E[e^{-{\mathrm{\Lambda }}_{ij}^{\ast }(u)}\{1-w_{ij}(\mathit{\theta })\}]+E\left\{e^{-{\mathrm{\Lambda }}_{ij}^{\ast }(u)}{w}_{ij}(\mathit{\theta }){\int }_0^u{e}^{{\mathrm{\Lambda }}_{ij}^C(s)+{\mathrm{\Lambda }}_{ij}^{\ast }(s)}{dM}_{ij}^C(s)\right\}\\ =E\left\{e^{-{\mathrm{\Lambda }}_{ij}^{\ast }(u)}\left[1-E\{\frac{A_{ij}}{p_{ij}(\mathit{\theta })}\mid {\mathit{Z}}_i\}\right]\right\}+E\left[e^{-{\mathrm{\Lambda }}_{ij}^{\ast }(u)}{w}_{ij}(\mathit{\theta })E\left\{{\int }_0^u{e}^{{\mathrm{\Lambda }}_{ij}^C(s)+{\mathrm{\Lambda }}_{ij}^{\ast }(s)}{dM}_{ij}^C(s)|A_i=j,{\mathit{Z}}_i\right\}\right],\\ =0,\end{array}$$

where ${dM}_{ij}^C(s)={dN}_{ij}^C(s)-Y_{ij}(s)d{\mathrm{\Lambda }}_{ij}^C(s)$ is a martingale increment when the model for C is correctly specified. Similarly, iterating conditional expectations, the augmentation term from the numerator also converges in probability to zero under the same conditions. Therefore, even if the assumed hazard function model for T is incorrect, when the assumed models for treatment probability and censoring are correct, we would expect that the proposed estimator converges to the same limit as the IPW estimator, the consistency of which can be understood intuitively. Under the same conditions, the proposed estimator for Λ_j(t) is consistent; hence the consistency of S_j(t) and δ.

The consistency of the proposed estimator when the model for survival time is correct but the model for treatment probability or censoring is possibly incorrect is less obvious. The proposed estimator can be rewritten as

$${\int }_0^t\frac{n^{-1}{\sum }_{i=1}^n[e^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}d{\widehat{\mathrm{\Lambda }}}_{ij}(u)+\{w_{ij}(\widehat{\mathit{\theta }})e^{{\widehat{\mathrm{\Lambda }}}_j^C(u)}{\kappa }_i(u){dN}_i^T-e^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}d{\widehat{\mathrm{\Lambda }}}_{ij}(u)w_{ij}(\widehat{\mathit{\theta }}){\widehat{G}}_{ij}(u)\}]}{n^{-1}{\sum }_{i=1}^n[e^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}+\{w_{ij}(\widehat{\mathit{\theta }})e^{{\widehat{\mathrm{\Lambda }}}_{ij}^C(u)}{\kappa }_i(u)Y_i^T(u)-e^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}{w}_{ij}(\widehat{\mathit{\theta }}){\widehat{G}}_{ij}(u)\}]},$$ (10)

which can be shown to be consistent for Λ_j(t) if λ_ij(t) is modeled correctly by (5). To see this, note the first term of the denominator, $n^{-1}{\sum }_{i=1}^n{e}^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}$, converges to S_j(u), while the first term of the numerator, $n^{-1}{\sum }_{i=1}^n{e}^{-{\widehat{\mathrm{\Lambda }}}_{ij}(u)}d{\widehat{\mathrm{\Lambda }}}_{ij}(u)$, converges to −dS_j(u). In addition, it can be shown that the second term in the numerator and the second term in the denominator of (10) converge in probability to 0 if model (5) is correct (details presented in Web Appendix). These results collectively imply that Λ̂_j(t) would then converge in probability to Λ_j(t). Therefore, even if the model for treatment probability or censoring is incorrect, our proposed estimator for δ is consistent, as long as the model for survival time is correct.

Arguments in the above two paragraphs heuristically explain why the proposed method is expected to possess the so-called double-robustness property; detailed theoretical properties of the proposed method are presented in the next section.

4. Asymptotic Properties

In this section, we list the large sample properties of the proposed estimators. To begin, it is convenient to introduce the following notation:

$$\begin{array}{l}{\mathit{R}}_j^{(d)}(t;\mathit{\beta })=n^{-1}\sum _{i=1}^n{Y}_{ij}(t){\mathit{Z}}_i^{\otimes d}exp({\mathit{\beta }}^T{\mathit{Z}}_i),{\mathit{r}}_j^{(d)}(t;\mathit{\beta })=E\{{\mathit{R}}_j^{(d)}(t;\mathit{\beta })\},\\ {\overline{\mathit{Z}}}_j(t;\mathit{\beta })=\frac{{\mathit{R}}_j^{(1)}(t;\mathit{\beta })}{R_j^{(0)}(t;\mathit{\beta })},{\overline{\mathit{z}}}_j(t;\mathit{\beta })=\frac{{\mathit{r}}_j^{(1)}(t;\mathit{\beta })}{r_j^{(0)}(t;\mathit{\beta })},\\ {\mathbf{\Omega }}_j(\mathit{\beta })={\int }_0^{\lambda }\left\{\frac{{\mathit{r}}_j^{(2)}(t;\mathit{\beta })}{r_j^{(0)}(t;\mathit{\beta })}-{\overline{\mathit{z}}}_j{(t;\mathit{\beta })}^{\otimes 2}\right\}E\{Y_{ij}(t){\lambda }_{ij}(t)\}dt,\\ \text{and}\mathit{V}(\mathit{\theta })=E\left[\frac{exp({\mathit{\theta }}^T\mathit{X}){\mathit{X}}^{\otimes 2}}{{\{1+exp({\mathit{\theta }}^T\mathit{X})\}}^2}\right],\end{array}$$

for d = 0, 1, 2, where for a column vector a, a^⊗2 = aa^T, a^⊗1 = a, and a^⊗0 = 1. In addition, parallel to the notation defined above, we define a set of notation, with either superscript or subscript C, that will be used in proofs related to censoring C; specifically, ${\mathit{R}}_{Cj}^{(d)}(t;\mathit{\alpha }),{\mathit{r}}_{Cj}^{(d)}(t;\mathit{\alpha }),{\overline{\mathit{Z}}}_j^C(t;\mathit{\alpha }),{\overline{z}}_j^C(t;\mathit{\alpha })$, Ω_Cj(α) are defined similarly as above except that Z_i, β, λ_ij(t), N_ij(t), Λ_0j are replaced by ${\mathit{Z}}_i^C$, α, ${\lambda }_{ij}^C(t),N_{ij}^C(t),{\mathrm{\Lambda }}_{0j}^C$ accordingly.

We assume a set of regularity conditions, listed in the Web Appendix, in the proof of consistency and asymptotic normality of the proposed estimators. Before introducing the main theorem, we list some pertinent results from the existing literature. Under the assumed regularity conditions, Lin and Wei (1989) show that β̂_j converges in probability to ${\mathit{\beta }}_j^{\ast }$, and that β̂_j is asymptotically normal with $n^{\frac{1}{2}}({\widehat{\mathit{\beta }}}_j-{\mathit{\beta }}_j^{\ast })={\mathbf{\Omega }}_j^{-1}({\mathit{\beta }}_j^{\ast })n^{-\frac{1}{2}}{\sum }_{i=1}^n{\mathit{U}}_{ij}({\mathit{\beta }}_j^{\ast })+o_p(1)$, where

$$\begin{array}{l}{\mathit{U}}_{ij}({\mathit{\beta }}_j^{\ast })={\int }_0^{\tau }\{{\mathit{Z}}_i-{\overline{\mathit{z}}}_j(t;{\mathit{\beta }}_j^{\ast })\}{dM}_{ij}^{\ast }(t),\\ \text{with}d{\mathrm{\Lambda }}_{0j}^{\ast }(t)=\frac{E\{{dN}_{ij}(t)\}}{{r_j^{(0)}}_j(t;{\mathit{\beta }}^{\ast })},d{\mathrm{\Lambda }}_{ij}^{\ast }(t)=exp({\mathit{\beta }}_j^{\ast T}{\mathit{Z}}_i)d{\mathrm{\Lambda }}_{0j}^{\ast }(t),\\ \text{and}{dM}_{ij}^{\ast }(t)={dN}_{ij}(t)-Y_{ij}(t)d{\mathrm{\Lambda }}_{ij}^{\ast }(t).\end{array}$$

We can then show (see Web Appendix) that Λ̂_ij(t) converges in probability to ${\mathrm{\Lambda }}_{ij}^{\ast }(t)$ and that

$$n^{\frac{1}{2}}\{{\widehat{\mathrm{\Lambda }}}_{ij}(t)-{\mathrm{\Lambda }}_{ij}^{\ast }(t)\}={\mathit{K}}_{ij}^T(t;{\mathit{\beta }}_j^{\ast }){\mathbf{\Omega }}_i^{-1}({\mathit{\beta }}_j^{\ast })n^{-\frac{1}{2}}\sum _{i=1}^n{\mathit{U}}_{ij}({\mathit{\beta }}_j^{\ast })+e^{{\mathit{\beta }}_j^{\ast T}{\mathit{Z}}_i}{n}^{-\frac{1}{2}}\sum _{i=1}^n{\int }_0^t\frac{{dM}_{ij}^{\ast }(u)}{r_j^{(0)}(u;{\mathit{\beta }}_j^{\ast })}$$

plus a term that converges in probability to zero, where ${\mathit{K}}_{ij}(t;{\mathit{\beta }}_j^{\ast })={\int }_0^t\{{\mathit{Z}}_i-{\overline{\mathit{z}}}_j(u;{\mathit{\beta }}_j^{\ast })\}d{\mathrm{\Lambda }}_{ij}^{\ast }(u)$. Similar results hold for α̂_j and ${\widehat{\mathrm{\Lambda }}}_{ij}^C(t)$ in the model for censoring. In addition, θ̂, converges in probability to θ^* and θ̂ is asymptotically normal with $n^{\frac{1}{2}}(\widehat{\mathit{\theta }}-{\mathit{\theta }}^{\ast })={\mathit{V}}^{-1}({\mathit{\theta }}^{\ast })n^{-\frac{1}{2}}{\sum }_{i=1}^n{\mathit{X}}_i\{A_i-\text{expit}({\mathit{\theta }}^{\ast T}{\mathit{X}}_i)\}+o_p(1)$; see Zeng and Chen (2009). When model (5) is correct, ${\mathit{\beta }}_j^{\ast }$ and ${\mathrm{\Lambda }}_{ij}^{\ast }(t)$ are equal to their respective true underlying target values, β_j and Λ_ij(t). Similarly, θ^* = θ when model (6) is correct.

The asymptotic properties of the proposed estimators for μ_j and δ are summarized by the following theorem.

Theorem 1

Under conditions (a) – (h) listed in the Web Appendix, as n → ∞, if the working model specified in (5) or the working models in (6) and (8) are correct, then μ̂_j converges in probability to μ_j and $n^{\frac{1}{2}}({\widehat{\mu }}_j-{\mu }_j)$ is asymptotically normal with mean zero and variance $E({\phi }_{ij}^2)$, where ${\phi }_{ij}=-{\int }_0^L{S}_j(u){\varphi }_{ij}(u)du$,

$$\begin{array}{l}{\varphi }_{ij}(t)={\mathit{B}}_j^T(t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast }){\mathit{V}}^{-1}({\mathit{\theta }}^{\ast }){\mathit{X}}_i\{A_{ij}-p_{ij}({\mathit{\theta }}^{\ast })\}\\ +{\mathit{F}}_j^T(t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast }){\mathbf{\Omega }}_j^{-1}({\mathit{\beta }}_j^{\ast }){\mathit{U}}_{ij}({\mathit{\beta }}_j^{\ast })+{\int }_0^t{J}_j(u,t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast })\frac{{dM}_{ij}^{\ast }(u)}{r_j^{(0)}(u;{\mathit{\beta }}_j^{\ast })}\\ +{\mathit{P}}_j^T(t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast }){\mathbf{\Omega }}_{Cj}^{-1}({\mathit{\alpha }}_j^{\ast }){\mathit{U}}_{ij}^C({\mathit{\alpha }}_j^{\ast })+{\int }_0^t{H}_j(u,t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast })\frac{{dM}_{ij}^{C\ast }(u)}{r_{Cj}^{(0)}(u;{\mathit{\alpha }}_j^{\ast }\}}\\ +{\int }_0^t\frac{w_{ij}({\mathit{\theta }}^{\ast })e^{{\mathrm{\Lambda }}_{ij}^{C\ast }(u)}{dM}_{ij}^{†}(u)+\{1-w_{ij}({\mathit{\theta }}^{\ast })G_{ij}(u)\}{e}^{-{\mathrm{\Lambda }}_{ij}^{\ast }(u)}\{d{\mathrm{\Lambda }}_{ij}^{\ast }(u)-d{\mathrm{\Lambda }}_j(u)\}}{D_j(u;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast })}\end{array}$$

and ${dM}_{ij}^{†}(u)={dN}_{ij}(u)-Y_{ij}(u)d{\mathrm{\Lambda }}_j(u)$, with ${\mathit{B}}_j(t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast }),{\mathit{F}}_j(t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast }),J_j(u,t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast }),{\mathit{P}}_j(t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast }),H_j(u,t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast })$, G_ij(u) and $D_j(u;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast })$ defined in the Web Appendix. In addition, under the same conditions, δ̂ converges in probability to δ and $n^{\frac{1}{2}}(\widehat{\delta }-\delta )$ is asymptotically normal with mean zero and variance E(φ_i1 − φ_i0)².

The above theorem is stated without explicitly assuming which working model is correctly specified; i.e., model for the survival time, or for the coarsening mechanism. When one or all of the working models are correct, some of the terms in ϕ_ij(t) and, correspondingly, in φ_ij are identically zero, depending on which model is correct. For example, using iterated conditional expectation arguments, we may show that if the model (5) is correct, then ${\mathit{B}}_j(t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast })$ is equal to zero, and if the models for coarsening mechanism (6) and (8) are true, then ${\mathit{F}}_j(t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast })$ and $J_j(u,t;{\mathit{\theta }}^{\ast },{\mathit{\beta }}_j^{\ast },{\mathit{\alpha }}_j^{\ast })$ are identically zero. In the implementation of the proposed method, one models both survival time and coarsening mechanism, hoping that at least one of the modeling procedures is correct and therefore considerably increasing the chance of valid inference for the true causal parameters. As one does not know which working model is correct, to estimate variance of the proposed estimators, all terms in ϕ_ij(t) must be computed, even though some components are actually zero. Due its complexity, a direct plug-in estimator of the asymptotic variance is rather involved and would accumulate a substantial amount of estimation error. Therefore, we suggest estimating the variance of the proposed estimator by bootstrapping instead. In our simulations, we used a standard nonparametric bootstrap, where one draws bootstrap samples from (A_i, U_i, Δ_i, Z_i), i = 1, …, n with equal probability and with replacement. An alternative is the weighted bootstrap of Kosorok, Lee, and Fine (2004), which we do not evaluate in this report. SAS code for implementing the proposed methods is available at http://www-personal.umich.edu/~mzhangst/.

5. Simulation Studies

We carried out simulation studies to evaluate the finite sample properties of the proposed method. All reported results are based on 1000 Monte Carlo data sets, each with a sample size of n = 600 or n = 300. Variances of all estimators are estimated by a bootstrap procedure which used 50 bootstrap replicates.

For each Monte Carlo data set, we generated data as follows. First, we generated a baseline covariate vector, Z = {Z₁, Z₂, Z₃}^T as multivariate normal with mean zero, unit variance, corr(Z₁, Z₃) = 0.2 and all other pairwise correlations equal to 0. To be consistent with the assumed regularity conditions, we truncated each component of Z at −4 and 4. The treatment indicator, A, was then generated as Bernoulli with parameter expit(−0.5Z₁ − 0.5Z₂). In order for the elements of Z to serve as confounders, each should also be predictive of the survival time. As such, we generated T from an exponential distribution with parameter exp(−2.5−1.5Z₁ − Z₂ − 0.7Z₃) for treatment A = 0 and exp(−3 − Z₁ − 0.9Z₂ − Z₃) for A = 1. Finally, censoring time C was generated as exponential with parameter exp(−5+Z₁ +1.2Z₂) for treatment A = 0 and exp(−4.5 − 0.2Z₁ − 0.7Z₂) for A = 1, which lead to approximately 28% censoring.

In addition to the proposed method, we evaluated three other methods. The first is the method of Chen and Tsiatis (2001), where one builds treatment-specific Cox models for T given Z. The second is the IPTW method of Wei (2008), wherein one instead builds a regression model for A given Z. The third method is that of Hubbard et al (1999), which involves building working models for each of T, A and C given Z and, like our method, is double robust. The key difference between our proposed estimator and that of Hubbard et al (1999) is that the latter involves estimating the survival function directly, in contrast with our method which does so indirectly through the cumulative hazard. In a sense, our method can be viewed as a double robust extension of the Nelson-Aalen method to account for non-random treatment assignment and conditionally-independent censoring. The Hubbard et al (1999) method corresponds to an extension of the survival function estimator obtained as a sample average of the number of subjects at risk, weighted by the inverse probability of not being censored.

We considered each of the four estimators in settings where the required assumptions hold, and when they fail. Specifically, for the T|A, Z model used in the proposed, Chen and Tsiatis (2001) and Hubbard et al (1999) methods, the correct model was fitted using covariates (Z₁, Z₂, Z₃), while the incorrect model was fitted using (Z₁, Z₃). For the A|Z model used in the proposed, Wei (2008) and Hubbard et al (1999) methods, the correct model was fitted using (Z₁, Z₂), while the incorrect model was fitted using Z₁ only. For the C|A, Z model used in the proposed and Hubbard et al (1999) methods, the correct model was fitted using (Z₁, Z₂), while the incorrect model using Z₂ only.

Results for estimating μ₁ and δ based on data with a sample size of n = 600 are reported in Table 1 and Table 2, respectively, with L set to 10 and 20. Additional results with n = 300 are reported in the Web Appendix. The proposed estimators appear to be approximately unbiased for the true parameters under all scenarios in which either the survival time or the coarsening mechanism are modeled correctly. Moreover, the 95% coverage probabilities approximately achieve the nominal level. Such results are consistent with the purported double-robust property of the proposed method. Estimators using the method of Hubbard et al (1999) behave similarly to the proposed method. However, they appear to have larger bias for estimating both μ₀ and μ₁, especially when sample size is small (see Web Appendix). In contrast, the estimators of Chen and Tsiatis (2001) and Wei (2008) perform well when the corresponding assumed model is correct, but with large biases observed if the assumed model is incorrect.

Table 1.

Estimation of restricted mean lifetime with sample size n = 600 and restriction time L = 10. T, Z, C: indicate whether the model for T, Z, or C, respectively, is true or false. Bias is the Monte Carlo Bias; ESD is the Monte Carlo standard deviation of estimates; ASE is the Monte Carlo average of estimated standard errors; CP is the coverage probability of nominal 95% Wald confidence intervals.

Method	T	Z	C	BIAS	ESD	ASE	CP	BIAS	ESD	ASE	CP
				μ̂0 (μ0=5.978)				μ̂1 (μ1=6.949)				δ̂ = μ̂1 − μ̂0 (δ=0.871)
Proposed	T	T	T	0.010	0.199	0.201	0.934	0.003	0.201	0.191	0.929	−0.008	0.217	0.218	0.947
	T	F	F	0.020	0.199	0.201	0.931	−0.002	0.201	0.191	0.929	−0.021	0.217	0.218	0.949
	F	T	T	0.010	0.205	0.224	0.947	0.002	0.204	0.204	0.946	−0.007	0.228	0.266	0.970
	F	F	F	0.408	0.211	0.214	0.496	−0.298	0.219	0.205	0.689	−0.706	0.261	0.260	0.217
Hubbard et al	T	T	T	0.026	0.199	0.204	0.935	0.029	0.201	0.191	0.927	0.003	0.218	0.222	0.950
	T	F	F	0.038	0.199	0.201	0.932	0.028	0.201	0.191	0.928	−0.010	0.217	0.218	0.945
	F	T	T	0.027	0.207	0.227	0.947	0.028	0.205	0.205	0.940	0.001	0.229	0.269	0.970
	F	F	F	0.437	0.211	0.215	0.434	−0.272	0.219	0.206	0.724	−0.708	0.262	0.260	0.212
IPTW		T		−0.101	0.221	0.268	0.964	0.034	0.212	0.226	0.962	0.135	0.251	0.351	0.976
		F		0.259	0.220	0.251	0.838	−0.269	0.227	0.229	0.790	−0.528	0.280	0.340	0.683
Chen & Tsiatis	T			0.012	0.195	0.196	0.940	0.006	0.195	0.184	0.928	−0.006	0.208	0.207	0.946
	F			0.290	0.207	0.212	0.717	−0.335	0.211	0.201	0.603	−0.624	0.254	0.253	0.318

Table 2.

Estimation of restricted mean lifetime with sample size n = 600 and restriction time L = 20. Entries as in Table 1.

Method	T	Z	C	BIAS	ESD	ASE	CP	BIAS	ESD	ASE	CP
				μ̂0 (μ0=9.806)				μ̂1 (μ1=11.488)				δ̂ = μ̂1 − μ̂0 (δ=1.682)
Proposed	T	T	T	0.017	0.391	0.406	0.953	0.018	0.426	0.411	0.944	0.002	0.442	0.450	0.941
	T	F	F	0.039	0.402	0.408	0.953	0.011	0.426	0.409	0.936	−0.029	0.452	0.450	0.943
	F	T	T	0.010	0.399	0.446	0.966	0.019	0.437	0.443	0.950	0.009	0.461	0.549	0.972
	F	F	F	0.838	0.474	0.451	0.519	−0.675	0.459	0.434	0.648	−1.513	0.580	0.546	0.200
Hubbard et al	T	T	T	0.022	0.395	0.419	0.955	0.073	0.427	0.413	0.940	0.051	0.447	0.464	0.951
	T	F	F	0.068	0.397	0.409	0.955	0.070	0.427	0.410	0.937	0.002	0.447	0.451	0.945
	F	T	T	0.019	0.404	0.456	0.972	0.073	0.437	0.446	0.947	0.055	0.466	0.560	0.975
	F	F	F	0.891	0.482	0.459	0.481	−0.622	0.460	0.436	0.699	−1.513	0.586	0.554	0.200
IPTW		T		−0.415	0.423	0.516	0.896	0.131	0.458	0.508	0.962	0.545	0.516	0.726	0.944
		F		0.273	0.441	0.505	0.948	−0.569	0.477	0.495	0.796	−0.842	0.577	0.708	0.830
Chen & Tsiatis	T			0.024	0.387	0.392	0.950	0.022	0.412	0.398	0.942	−0.002	0.418	0.424	0.957
	F			0.431	0.412	0.425	0.827	−0.669	0.439	0.424	0.639	−1.099	0.512	0.517	0.454

6. Application

We applied the proposed method to compare restricted mean post-transplant lifetime between simultaneous pancreas-kidney (SPK) and kidney-alone (KA) transplant recipients. We restricted the study population to Type-I diabetics since the majority of SPK patients are in this category.

Data were obtained from the Scientific Registry of Transplant Recipients (SRTR), a nationwide solid organ transplant registry. The study population consisted of deceased-donor kidney transplant recipients who were transplanted at age ≥18 during 2000–2008. Only primary kidney transplant patients were eligible, with repeat transplants excluded. We included 6,054 SPK and 7,513 KA transplants. Follow-up began at the date of transplant. The event of interest was graft failure, defined as the minimum time of death or when repeat kidney transplantation occurred. Patients were censored at loss to follow-up or at the end of the observation period (December 31, 2008). Adjustment covariates included age at transplant, gender, race, blood type, pre-transplant time on dialysis and donor age. All of the adjustment covariates are significant at the level of 0.05 in the fitted model for treatment assignment. In the fitted models for survival, age at transplant, blood type, time on dialysis and donor age are predictive of survival for SPK transplant subjects, and age at transplant, time on dialysis and donor age are predictive for KA transplant subjects. We set the restriction time to L=5 years, reflecting the amount of available follow-up.

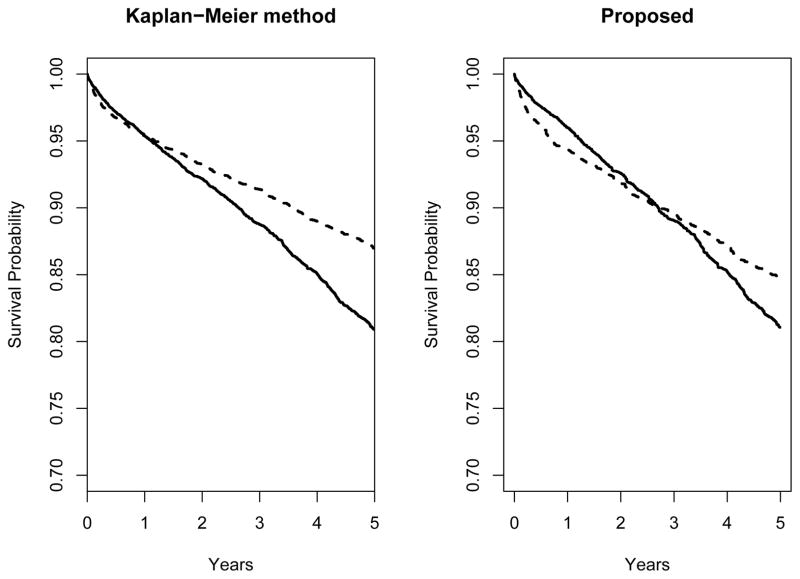
In Figure 1, we plot average survival curves for SPK and KA transplant patients estimated using the proposed double-robust method; for comparison, survival curves from Kaplan-Meier method are also plotted. Using the proposed double-robust method, average survival is initially greater for the KA group. However, survival is estimated to be equal by approximately the t =2.5 year point, and is greater for SPK patients thereafter. If one eyeballs the area under each of the survival curves, they appear to be approximately equal. Note that the considerable non-proportionality of the SPK and KA hazard functions would invalidate an analysis based on a proportional hazards model using an indicator for SPK.

Figure 1.

Average survival probability for simultaneous pancreas-kidney (SPK; A_i=1; dashed line) and kidney-alone (KA; A_i=0; solid line) transplant recipients

To compare restricted mean lifetime, we applied (i) the proposed method, which utilizes working Cox models for post-transplant survival and censoring and a logistic model for the SPK probability (ii) the method of Wei (2008), which requires only a model for SPK probability (iii) the Chen and Tsiatis (2001) method, which uses Cox models for post-transplant survival. Variance for the proposed estimator is estimated by bootstrap using 100 bootstrap replicates. Results are listed in Table 3. Mean 5-year post-transplant lifetimes were very similar for SPK and KA transplant recipients, with the difference being comfortably non-significant for all three methods. For example, based on the proposed method, SPK live, on average, for δ̂ = 0.012 years (i.e., 4.4 days) longer than KA recipients, out of first 5 post-transplant years. In addition to being non-significant (p =0.69), this difference is not at all important clinically. Both the SPK and KA groups live an average of 4.5 years out of the first 5 post-transplant, which would be considered excellent. Based on our analysis, relative to the receipt of a kidney alone, the additional transplantation of a pancreas (i.e., in addition to a kidney) did not extend mean survival time among Type I diabetics; at least not based on the first 5 post-transplant years.

Table 3.

Five-year restricted mean lifetime for simultaneous pancreas-kidney (SPK; A_i=1) and kidney-alone (KA; A_i=0) transplant recipients.

Method	μ̂1	$\widehat{SE}({\widehat{\mu }}_1)$	μ̂0	$\widehat{SE}({\widehat{\mu }}_0)$	δ̂	$\widehat{SE}(\widehat{\delta })$	p
Proposed	4.54	0.024	4.53	0.017	0.012	0.031	0.69
IPTW	4.55	0.023	4.54	0.017	0.0098	0.030	0.74
Chen & Tsiatis	4.56	0.022	4.55	0.014	0.0097	0.027	0.72

Results are very similar across the three methods, implying that both the logistic and Cox models appear to be correct. To be more specific, the Cox model assumed by the Chen and Tsiatis (2001) method was not mis-specified to the extent that relaxing the assumption of its correctness made any meaningful difference; similar statements apply to the logistic model.

7. Discussion

We propose a semiparametric double-robust estimator of the difference in treatment-specific restricted mean survival time. The proposed method uses working models for the coarsening mechanism (treatment assignment and censoring) and the death hazard, but is consistent if either coarsening mechanism or death hazard are modeled correctly. Asymptotic properties of the proposed estimator are derived and shown through simulation to be applicable to finite samples. The method is applied to national kidney transplant data.

In this report, we focused on the setting of two treatment groups. The proposed method can be extended to settings with more than two groups. Suppose there are K treatment groups to be compared and that A_i takes values from 1, …, K. We are interested in estimating μ_j for j = 1, …, K, and comparisons between groups can be carried out by estimating their pairwise differences. In considering the estimation of μ_j, recall that the proposed method is developed from the point of view that the full data is possibly coarsened by treatment assignment and censoring. For each treatment j = 1, …, K, the full data corresponding to estimating μ_j is (T ^j, Z_i), i = 1, …, n, which may be coarsened at time t = 0 if A_ij = 0 and at time t > 0 if A_ij = 1 and $C_i=t<T_i^j$. Since this is a direct extension of the set-up described previously, Λ_j(t) and μ_j can be estimated using the proposed methods, except that the regression model for A_i needs to accommodate a response with > 2 categories (e.g., a generalized logit model), with the estimation of P(A_ij = 1|Z_i) modified accordingly.

Through the proposed method (and existing methods), we demonstrate that Type-I diabetic simultaneous pancreas-kidney (SPK) transplant recipients had almost identical 5-year restricted mean lifetime to kidney-alone (KA) transplant recipients. This would appear to be a fairly negative statement about the value of SPK among Type-I diabetic patients with end-stage renal disease. Two considerations are important. First, since the data are observational, there is always the potential for unmeasured covariates to induce bias. Such bias, in this case, would strongly favor the KA group. For example, although both groups consisted of Type I diabetics, there is the possibility that KA patients tended to have more a manageable degree of diabetes such that pancreas transplantation was not indicated. Second, since survival was greater for the SKP group from t=2.5 years onward, it is possible that greater restricted mean lifetime could be observed in the SPK group if a data set implying a longer restriction time (e.g., L=10 years) were used.

8. Supplementary Materials

A Web Appendix, referenced in Section 4, is available with this paper at the Biometrics website on Wiley Online Library.