Tuning of EAG K⁺ channel inactivation: Molecular determinants of amplification by mutations and a small molecule

Abstract

Ether-à-go-go (EAG) and EAG-related gene (ERG) K⁺ channels are close homologues but differ markedly in their gating properties. ERG1 channels are characterized by rapid and extensive C-type inactivation, whereas mammalian EAG1 channels were previously considered noninactivating. Here, we show that human EAG1 channels exhibit an intrinsic voltage-dependent slow inactivation that is markedly enhanced in rate and extent by 1–10 µM 3-nitro-N-(4-phenoxyphenyl) benzamide, or ICA105574 (ICA). This compound was previously reported to have the opposite effect on ERG1 channels, causing an increase in current magnitude by inhibition of C-type inactivation. The voltage dependence of 2 µM ICA-induced inhibition of EAG1 current was half-maximal at −73 mV, 62 mV negative to the half-point for channel activation. This finding suggests that current inhibition by the drug is mediated by enhanced inactivation and not open-channel block, where the voltage half-points for current inhibition and channel activation are predicted to overlap, as we demonstrate for clofilium and astemizole. The mutation Y464A in the S6 segment also induced inactivation of EAG1, with a time course and voltage dependence similar to that caused by 2 µM ICA. Several Markov models were investigated to describe gating effects induced by multiple concentrations of the drug and the Y464A mutation. Models with the smallest fit error required both closed- and open-state inactivation. Unlike typical C-type inactivation, the rate of Y464A- and ICA-induced inactivation was not decreased by external tetraethylammonium or elevated [K⁺]_e. EAG1 channel inactivation introduced by Y464A was prevented by additional mutation of a nearby residue located in the S5 segment (F359A) or pore helix (L434A), suggesting a tripartite molecular model where interactions between single residues in S5, S6, and the pore helix modulate inactivation of EAG1 channels.

INTRODUCTION

Ether-à-go-go (EAG) K⁺ channels were first discovered in Drosophila melanogaster, where the behavioral mutant eag was associated with spontaneous repetitive firing in motor axons and increased transmitter release (Ganetzky and Wu, 1983). Molecular cloning revealed that eag encoded a K⁺ channel subunit (Warmke et al., 1991), and voltage-clamp studies in Xenopus laevis oocytes determined that these channels conduct a delayed rectifier K⁺ current (Brüggemann et al., 1993). A human homologue (hEAG) of Drosophila eag and a related gene (hERG, human EAG-related gene [ERG]) were later discovered by screening a human hippocampus cDNA library (Warmke and Ganetzky, 1994), and in turn, a Drosophila homologue of hERG1 was identified (Titus et al., 1997). Further cloning efforts led to the identification of additional EAG (EAG1 and EAG2) and ERG (ERG1–ERG3) genes in mammals (Gutman et al., 2003).

The physiological roles of EAG and ERG channels have been extensively studied but remain incompletely characterized. In mammals, EAG1 channels are strongly expressed in several brain regions, including olfactory bulb, hippocampus, cerebellum, and brain stem (Martin et al., 2008), but the precise physiological roles of these channels are still not clear. Increased expression of EAG1 has been linked to certain cancers and tumor cell lines, and EAG1 inhibition by blockers, antibodies, and siRNA decreases the proliferation of tumor cell lines (Hemmerlein et al., 2006; Gómez-Varela et al., 2007; Pardo and Stühmer, 2008). Drosophila erg1 channels are encoded by the seizure locus, and mutations cause a muscle paralysis associated with hyperactivity in the flight motor pathway (Titus et al., 1997). In mammals, ERG1 channels are prominently expressed in the central nervous system with functions that may overlap with EAG channels. ERG1 channels are also expressed in the heart where their physiological and pathophysiological functions have been well characterized. Cardiac ERG1 channels conduct I_Kr, the rapid delayed rectifier K⁺ current (Sanguinetti et al., 1995; Trudeau et al., 1995) that has a key role in determining duration of the plateau phase and the rate of repolarization of action potentials in cardiomyocytes. Loss of function mutations in human ERG1 prolong the action potential and cause long QT syndrome, a heart condition associated with potentially fatal cardiac arrhythmia (Curran et al., 1995; Sanguinetti et al., 1996).

Although closely related, the biophysical properties of EAG and ERG channels differ from one another. During a depolarizing voltage-clamp pulse, the rate of EAG current activation is relatively fast and exhibits a prominent Cole–Moore shift, i.e., delayed and slowed activation when currents are elicited from more negative holding potentials (V_hs) (Terlau et al., 1996; Lin and Papazian, 2007). Drosophila eag1 currents inactivate slowly (Brüggemann et al., 1993; Robertson et al., 1996), whereas time-dependent inactivation was not detected for mouse EAG1 channels expressed in Xenopus oocytes (Robertson et al., 1996). ERG1 channels activate more slowly than EAG1 and exhibit an exceptionally strong and rapid C-type inactivation (Smith et al., 1996; Spector et al., 1996). Inactivation greatly reduces net repolarizing outward current at positive transmembrane potentials, permitting the prolonged plateau phase of cardiomyocyte action potentials typical for humans and other large mammals (Sanguinetti and Tristani-Firouzi, 2006; Rosati et al., 2008).

The mechanistic and structural basis of C-type inactivation has been explored in several K⁺ channels using site-directed mutagenesis, x-ray crystallography, and molecular dynamics simulation. It has been proposed that C-type inactivation reduces K⁺ conductance via a subtle voltage-dependent change in conformation of the selectivity filter that can be preceded by a transient loss of K⁺ selectivity (López-Barneo et al., 1993; Zhou et al., 2001; Cuello et al., 2010b). C-type inactivation is slowed by elevated [K⁺]_e and extracellular TEA (Grissmer and Cahalan, 1989; Choi et al., 1991; López-Barneo et al., 1993), and mutations near the selectivity filter (e.g., S620T or S631A in human ERG type 1 [hERG1]) can greatly attenuate or eliminate this gating process (Schönherr and Heinemann, 1996; Suessbrich et al., 1997; Zou et al., 1998). Recently, several synthetic compounds have been discovered that suppress C-type inactivation of hERG1 channels and thereby cause a striking voltage-dependent increase in the magnitude of outward currents. One of these compounds, 3-nitro-N-(4-phenoxyphenyl) benzamide, or ICA105574 (ICA), shifts the half-point of hERG1 inactivation by +180 mV at a concentration of 2 µM (Gerlach et al., 2010), rivaling or surpassing the effects of inactivation-perturbing point mutations. The effects of ICA on closely related EAG1 channels have not yet been determined.

Here, we define the biophysical properties and structural determinants of human EAG gene type 1 (hEAG1) channel inactivation using site-directed mutagenesis and pharmacological modulation of channels heterologously expressed in Xenopus oocytes. We show that wild-type (WT) hEAG1 channels exhibit an intrinsic slow inactivation that reduces peak outward current amplitude by <10%. Based on the effects of ICA on the related hERG1 channel described above, we assumed that ICA would cause a minor increase in hEAG1 current magnitude consistent with removal of its subtle inactivation. Instead, we found that ICA inhibited hEAG1 in a voltage-dependent manner consistent with an enhancement of its intrinsic slow inactivation gating process. While trying to understand the molecular mechanisms of these opposite pharmacological activities of ICA, we discovered that hEAG1 inactivation was also markedly enhanced by nonconserved mutations of an aromatic residue (Tyr464) located in the S6 segment. Unlike typical C-type inactivation, the rate of Y464A- or ICA-induced inactivation was not slowed by elevated [K⁺]_e or external application of TEA. Moreover, in hERG1, the mutation of Tyr652 (equivalent to Tyr464 in hEAG1) does not appreciably alter channel inactivation. Markov models were developed that recapitulate the main features of intrinsic inactivation and its enhancement by the Y464A mutation or ICA. A homology model of the hEAG1 channel pore domain was used to identify two residues in close proximity to Tyr464: Phe359 in S5 and Leu434 in the pore helix. Inactivation of Y464A EAG1 channels was prevented by a second site mutation of either residue. Moreover, opposite to WT hEAG1 channels, but similar to WT hERG1, F359L hEAG1 channels were activated by ICA. Collectively, these findings suggest that interactions between Tyr464, Phe359, and Leu434 are crucial molecular determinants of hEAG1 channel inactivation. Similar to hEAG1 channels, inactivation of KCNQ1 channels is also subtle (only clearly revealed by examination of tail current kinetics; Tristani-Firouzi and Sanguinetti, 1998), and point mutations of residues equivalent to Tyr464 and Leu434 in hEAG1 and a residue in S5 greatly accentuate KCNQ1 inactivation (Seebohm et al., 2005). Collectively, our present and previous site-directed mutagenesis studies suggest a similar tripartite molecular model for slow inactivation of hEAG1 and KCNQ1 channels, and that although hEAG1 and hERG1 channels are highly related, they do not share a common mechanism of inactivation.

MATERIALS AND METHODS

Molecular biology

Human EAG1 (KCNH1; National Center for Biotechnology Information Reference Sequence: available from GenBank/EMBL/DDBJ under accession no. NM_002238.3) cDNA cloned into psGEMHE oocyte expression vector was provided by the late Dr. Dennis Wray. Mutations in WT hEAG1 cDNA were made using the QuikChange site-directed mutagenesis kit (Agilent Technologies) and verified by DNA sequence analyses. Plasmids were linearized by NotI, and cRNA was prepared with the mMessage mMachine T7 kit (Life Technologies). The concentration of cRNA was quantified by RiboGreen assay (Life Technologies).

Oocyte isolation and cRNA injection

The procedure used to harvest oocytes from Xenopus was approved by the University of Utah Institutional Animal Care and Use Committee. To remove oocytes, frogs were anesthetized with 0.2% tricaine methane sulfonate, and a small abdominal incision was made to remove ovarian lobes. The incision was sutured closed, and the frog was returned to its aquarium. A maximum of four surgical procedures with 1-mo intervals were performed on each frog. To isolate individual oocytes and remove their follicle cell layer, ovarian lobes were first manually dispersed with forceps, and then treated for 90–120 min with 1 mg/ml of type II collagenase (Worthington Biochemical Corp.) in Ca²⁺-free ND96 solution that contained (in mM): 96 NaCl, 2 KCl, 1 MgCl₂, and 5 HEPES, with pH adjusted to 7.6 with NaOH. Stage IV and V oocytes were injected with WT or mutant cRNA and incubated for 1–5 d at 18°C in Barth’s saline solution before use in voltage-clamp experiments. Barth’s solution contained (in mM): 88 NaCl, 2 KCl, 0.41 CaCl₂, 0.33 Ca(NO₃)₂, 1 MgSO₄, 2.4 NaHCO₃, 10 HEPES, 1 pyruvate, and 50 mg/L gentamycin, with pH adjusted to 7.4 with NaOH.

Two-electrode voltage-clamp protocols and data analysis

Ionic currents were recorded from single oocytes using a standard two-microelectrode voltage-clamp technique (Goldin, 1991; Stühmer, 1992). Oocytes were placed in a recording chamber (∼0.4-ml volume) perfused at 2 ml min⁻¹ with KCM211 solution at 22–24°C. KCM211 solution contained (in mM): 98 NaCl, 2 KCl, 1 CaCl₂, 1 MgCl₂, and 5 HEPES, with pH adjusted to 7.6 with NaOH. A GeneClamp 500 amplifier, Digidata 1322A data acquisition system, and pCLAMP 8.2 or 9.0 software (Molecular Devices) were used to produce command voltages and to record current and voltage signals. To reduce leakage of KCl from micropipettes into the oocytes, agarose-cushion microelectrodes were fabricated as described previously (Schreibmayer et al., 1994). The resistance of microelectrodes after breaking their tip and sealing with 1% agarose/3 M KCl ranged from 0.2 to 0.6 MΩ when backfilled with 3 M KCl.

For experiments with TEA (Sigma-Aldrich) or when [KCl]_e was increased, an equimolar concentration of NaCl was omitted to maintain constant osmolarity of the KCM211 solution. ICA (purchased from Sigma-Aldrich and AKos GmBH) was dissolved in dimethyl sulfoxide to prepare a 10-mM stock solution. Final [ICA] was obtained by dilution of the stock solution with KCM211 immediately before use for each experiment.

During an initial equilibration period, oocytes were voltage clamped to a V_h of −100 mV, and 1-s pulses to a test potential (V_t) of 0 mV were applied every 10 s until current magnitude reached a steady-state level. During perfusion of the recording chamber with ICA solutions, the pulse interval was lengthened to 30 s. After currents achieved a new steady-state level in the presence of ICA, the relevant voltage-clamp protocols were repeated.

To determine the voltage dependence of channel activation and inactivation, a dual-pulse protocol was used. Conditioning prepulses (V_pres) of 10-s duration to potentials ranging from −130 to +20 mV were applied in 15-mV increments from a V_h of −100 mV. After each prepulse, a 4.5-s test pulse was applied to +30 mV. Variations from this voltage-pulse protocol are described in Results and figure legends. Conductance (G) was calculated as the peak outward current in response to a prepulse (I_pre) divided by the corrected electrical driving force, as described in Eq. 1,

$$G=\frac{I_{pre}}{\text{GHK[}(V-E_K)]}=\frac{I_{pre}}{\frac{FV}{RT}\frac{\text{exp}\left(F\right(V-E_K)/RT)-1}{\text{exp}(FV/RT)-1}},$$ (1)

where E_K is the reversal potential for K⁺ flux (−96 mV in 2 mM of external K⁺), F is Faraday’s constant, R is the gas constant, and T is temperature in °K. The electrical driving force was corrected based on the Goldman–Hodgkin–Katz equation, defined as GHK[(V − E_K)] (Clay, 2009), to account for unequal K⁺ distribution in the intracellular and extracellular solution. For each oocyte, G was plotted as a function of V_pre and fitted to a Boltzmann function. The fitted curve was extrapolated to more positive potentials to estimate maximum conductance (G_max). To determine the voltage dependence of current inactivation, the peak outward current during the test pulses to +30 mV (I_max, normalized to 1.0) was plotted as a function of V_pre, and the relationship was fitted with the Boltzmann function (Eq. 2):

$$\frac{G}{G_{\max }}=\frac{1}{1+\text{exp}(-zF(V_{\text{pre}}-V_{0.5})/RT)},$$ (2)

where z is the effective valence, and V_0.5 is the potential at which the current is half-inactivated. In some experiments, adjusted I_max was estimated by fitting the currents during each test pulse with an exponential function and extrapolated to the onset of the test pulse.

Offline data analysis was performed with Clampfit 9.0 (Molecular Devices), Origin 8.2 (OriginLab), and Excel (Microsoft) software. All data are expressed as mean ± SEM (n = number of oocytes), and statistical significance was evaluated by two-way ANOVA and Tukey’s HSD test, or the Student’s t test where appropriate (P ≤ 0.05 was considered a statistically significant difference).

Biotinylation and Western blot

The Pierce cell surface protein isolation kit (Thermo Fisher Scientific) was used for biotinylation of surface proteins in oocytes. Groups of oocytes (40–50) were injected with 20 ng of WT or mutant hEAG1 cRNA and maintained for 4 d at 18°C in Barth’s saline solution. Oocytes were then incubated with 1 mg/ml of solution (Sulfo-NHS-SS-Biotin in ND96) to label membrane proteins. After 1 h at 4°C, the reaction was stopped by adding quenching solution. Oocytes were washed twice with ND96 solution and once with Tris-buffered saline, and then incubated in 500 µl of lysis buffer with protease inhibitors for 15 min. After homogenization and incubation on ice for 15 min, the buffer volume was increased to 1 ml and lysate was centrifuged at 10,000 g for 10 min. The clarified supernatant was dialyzed against NeutrAvidin Agarose beads (Thermo Fisher Scientific) for 3 h at 4°C. The beads were collected via centrifugation at 2,000 g for 1 min and washed thoroughly with lysis buffer. After the final wash, samples were eluted by heating the beads to 60°C for 20 min in SDS-PAGE loading buffer. Samples were subjected to SDS-PAGE electrophoresis and analyzed by Western blotting with a 1:1,000 dilution of rabbit anti-hEAG1 antibody (Abcam) and a 1:4,000 dilution of horseradish peroxidase–conjugated goat anti–rabbit secondary antibody (Santa Cruz Biotechnology, Inc.). Samples were also analyzed for calnexin (ER marker) with a 1:5,000 dilution of rabbit primary antibody (Abcam) and a rabbit secondary antibody (Santa Cruz Biotechnology, Inc.). GAPDH and Gβ were detected with a 1:2,000 dilution of mouse primary antibody (Abcam) and a 1:500 dilution of mouse antibody (Santa Cruz Biotechnology, Inc.), respectively, and a mouse secondary antibody (Jackson ImmunoResearch Laboratories, Inc.).

Molecular modeling

The Swiss-Model Protein Structure Modeling Server at the ExPASy website was used in the automated mode (Arnold et al., 2006) to construct a homology model of the hEAG1 channel based on the KcsA K⁺ channel structure (Protein Data Bank accession no. 1BL8) as a template. Structure diagrams were generated using PyMOL Molecular Graphics software (version 1.2.8; Schrödinger).

Markov modeling of EAG1 currents

Mathematical models of EAG1 channel currents were developed to reconstruct experimental data. The explored models differ in their topology, as depicted in Figs. 10 and S9. Each model includes a Markovian description of channel states and the Goldman–Hodgkin–Katz current equation for K⁺ current through a population of channels based on their states. In the Markov models, forward rates α and backward rates β were defined as dependent on the transmembrane voltage, V_m:

$$\alpha ={\alpha }_o{e}^{z_{\alpha }{V}_{m}F/RT}$$ (3)

$$\beta ={\beta }_o{e}^{-z_{\beta }{V}_{m}F/RT},$$ (4)

with the rates α₀ and β₀ at 0 mV, and the charges z_α and z_β. Other transition rates (α_CI0, …, α_CI3, α_OI, β_CI0, …, β_CI3, β_OI, λ, γ) had a constant value. Current conducted by EAG channels (I_EAG) was described by the Goldman–Hodgkin–Katz current equation for K⁺:

$$I_{\mathit{EAG}}=O{P}_{\mathit{EAG}}\frac{V_m F}{R T}\frac{{\left[K^{+}\right]}_i-{\left[K^{+}\right]}_e\text{exp}(-V_m F/RT)}{1-\text{exp}(-V_m F/RT)},$$ (5)

with permeability P_EAG, extracellular potassium concentration [K⁺]_e, intracellular potassium concentration [K⁺]_i, and the probability that channels are in an open state O.

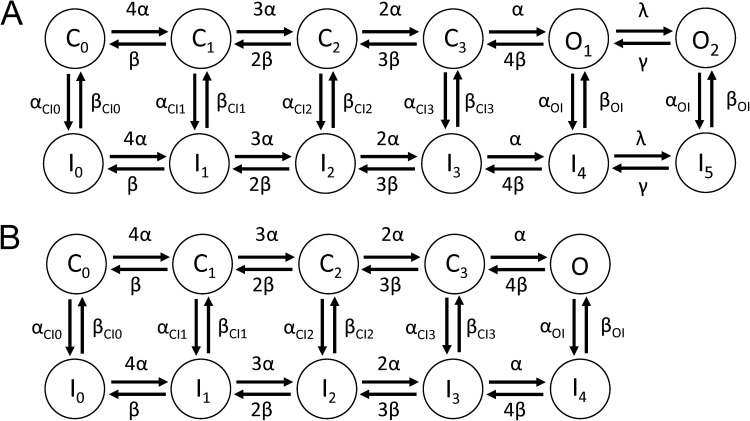
Figure 10.

Schematics of (A) 12- and (B) 10-state Markov models of EAG1 channel current.

Parameters of the Markov models were determined by numerical fitting of feature vectors extracted from experimental and simulation data, f_e and f_m, respectively. The fitting was performed for experimental data from WT hEAG1 at 0 (Control), 2, 5, and 10 µM ICA, and from Y464A hEAG1. The fit error E was defined as:

$$\text{E}=\sqrt{{\displaystyle \sum _{i=\mathrm{1\dots }n}{\left(\frac{{\Vert f_{m,i}-f_{e,i} \Vert }_2}{{\Vert f_{e,i} \Vert }_2}\right)}^2+{(1-\text{Max}{\displaystyle \sum _j{\text{C}}_j})}^2+{({\text{O}}_{Max}-\text{Max}{\displaystyle \sum _j{\text{O}}_j})}^2}},$$ (6)

with the number of features n, the Euclidean norm${\Vert \dots \Vert }_2$, the maximal closed-state probability at the end of the prepulse (−90 mV)

$$\text{Max}{\displaystyle \sum _j{\text{C}}_j},$$

the maximal open-state probability during the test pulse to +30 mV

$$\text{Max}{\displaystyle \sum _j{\text{O}}_j},$$

and a predefined maximal open-state probability O_Max. Features were measured for I_EAG at different voltages and included maxima and parameters from exponential fits. The fit error E included functions of closed and open states to select parameter sets that cause specified open probabilities at activating voltages and high probability of closed states at low voltages, respectively.

The fitting procedure was multi-scale and iterative, and it combined random perturbation and selection of parameter sets with the smallest fit error followed by their optimization. A multi-scale procedure was developed to establish estimates for initial values of the fitting parameters. A first estimate was determined by fitting to reduced data, i.e., features from current traces elicited by stepping to voltages of −130, −85, −40, and +5 mV. The estimates were used for a second fitting that used features from current traces elicited by stepping to −130, −100… +20 mV. The resulting fitting parameters were applied for a final fitting using the complete dataset. In each of these fitting procedures, the number of iterations was eight. In each iteration, 480 perturbed parameter sets were evaluated. Perturbations were initially in the range of 50–150% of the original parameter value. After each iteration, the perturbation range was decreased to a final range of 98–102%. The 48 parameter sets with the smallest fit error were optimized using the steepest descent method (Press et al., 1992) and used for the parameter set perturbation in the next step.

For the Control model, four degrees of freedom of the closed-inactivated and open-inactivated transitions were investigated. Rate coefficients α_CI0 and β_CI0 were kept identical to α_OI and β_OI, respectively. In addition, α_CI1, α_CI2, and α_CI3 were identical as were β_CI1, β_CI2, and β_CI3. For the ICA and Y464A models, linear interpolation was applied for α_CI0 and β_CI0 to α_OI and β_OI, respectively.

Simulations with the models and their parameterization were performed using Matlab R2011b (The Mathworks, Inc.). The simulations were performed with a variable order method for solution of ordinary differential equations based on numerical differentiation formulas (Matlab function ode15s). An initial time step Δt of 1 ms was chosen. Initial values of the state variables are listed in Table S1. For all models, the temperature was set at 293°K, [K⁺]_o = 2 mM and [K⁺]_i = 85 mM. All calculations were performed in double precision. Numerical fitting procedures were accelerated by using the Matlab Parallel Computing Toolbox.

Online supplemental material

Fig. S1 illustrates the slow onset of open-state inactivation of WT hEAG1 channels expressed in Xenopus oocytes. Fig. S2 shows that unlike typical C-type inactivation, elevated [K⁺]_e does not significantly alter the rate of inactivation for Y464A hEAG1 channel current. Fig. S3 compares the onset of fast inactivation for Y464A hEAG1 channel current before and after treatment of an oocyte with 1 µM ICA. Fig. S4 shows that 10 mM of external TEA reduces current magnitude but does not slow the rate of inactivation for Y464A hEAG1 channel current. Fig. S5 shows that 10 mM of external TEA does not slow the rate of ICA-induced inactivation of WT hEAG1 channel current. Fig. S6 shows a Western blot for whole cell fraction of cRNA-injected and -uninjected oocytes. Fig. S7 shows that F359A and F359A/Y464A mutant hEAG1 channels do not inactivate. Fig. S8 is a schematic representation of the five- and six-state Markov models for EAG1 channel gating. Fig. S9 presents simulated EAG1 currents using preliminary Markov models. Fig. S10 compares the rates of onset of activation and inactivation of WT hEAG1 channel currents for oocytes treated with 2 and 10 µM ICA. Table S1 lists features for model fitting and their fit errors. Table S2 presents the initial values for channel states used in different models. Table S3 lists the rate constant parameters for models of WT EAG1 channels (Control; 2, 5, and 10 µM ICA) and Y464A EAG1 channels. The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201210826/DC1.

RESULTS

Voltage-dependent inactivation of hEAG1 channels

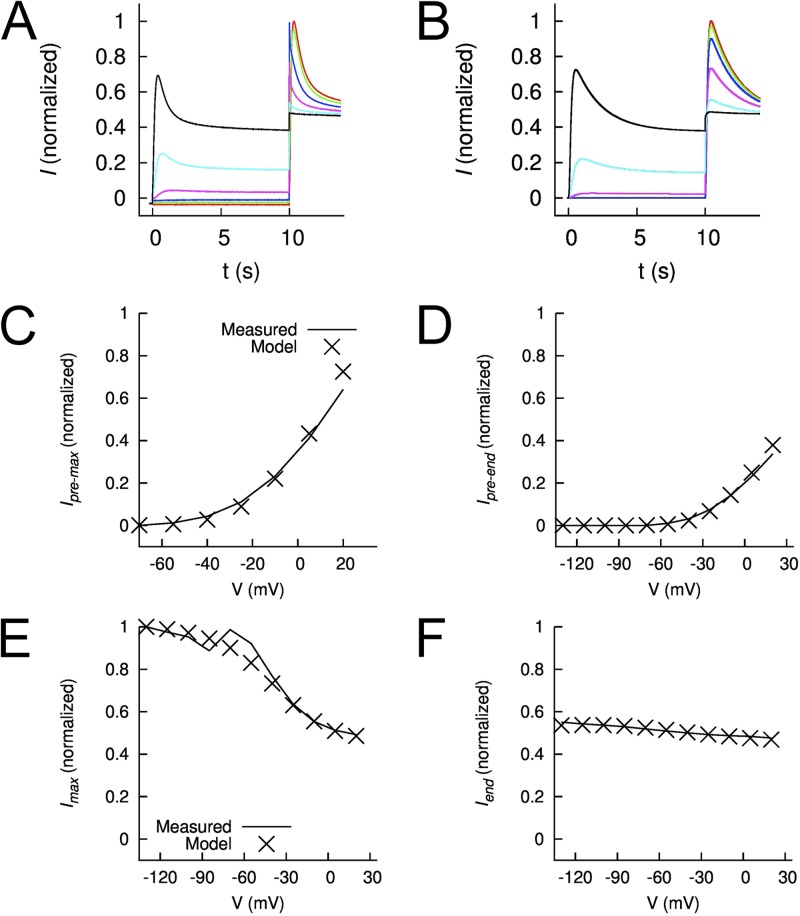
To characterize the voltage dependence of hEAG1 channel activation and inactivation, a double-pulse voltage-clamp protocol was used. V_pres of 10-s duration were applied in 15-mV increments to potentials ranging from −130 to +20 mV. After each prepulse, a test pulse was applied to +30 mV to assess channel availability. Under control conditions, hEAG1 currents activated with a V_pre ≥ −40 mV did not exhibit any time-dependent decay in magnitude (Fig. 1 A, top). However, the peak current measured at the test pulse of +30 mV (I_max) decreased progressively as a function of V_pre, indicative of voltage-dependent inactivation. The extent of inactivation was small and only reduced I_max elicited after a prepulse to +20 mV by 5–10%. The voltage dependence of hEAG1 channel inactivation determined under control conditions is plotted in Fig. 1 B (closed squares) and fitted with a Boltzmann function to determine V_0.5 (−81.4 ± 3.5 mV) and z (1.49 ± 0.32; n = 7). By comparison, the activation of hEAG1 currents (Fig. 1 B, closed diamonds) developed over a more positive range of voltage, with a threshold near −55 mV, a V_0.5 of −4.6 ± 0.7 mV, and z of 1.83 ± 0.06. Collectively, these findings indicate that hEAG1 channels inactivate from both closed and open states. Control currents shown in Fig. 1 A do not exhibit a time-dependent decay expected for open-state inactivation, probably because the onset of inactivation is very slow and of minor proportion, and overlaps with a slow component of activation. A time-dependent decay of current, consistent with very slow open-state inactivation, was only clearly evident when the test pulse to +30 mV was extended to 30 s (Fig. S1).

Figure 1.

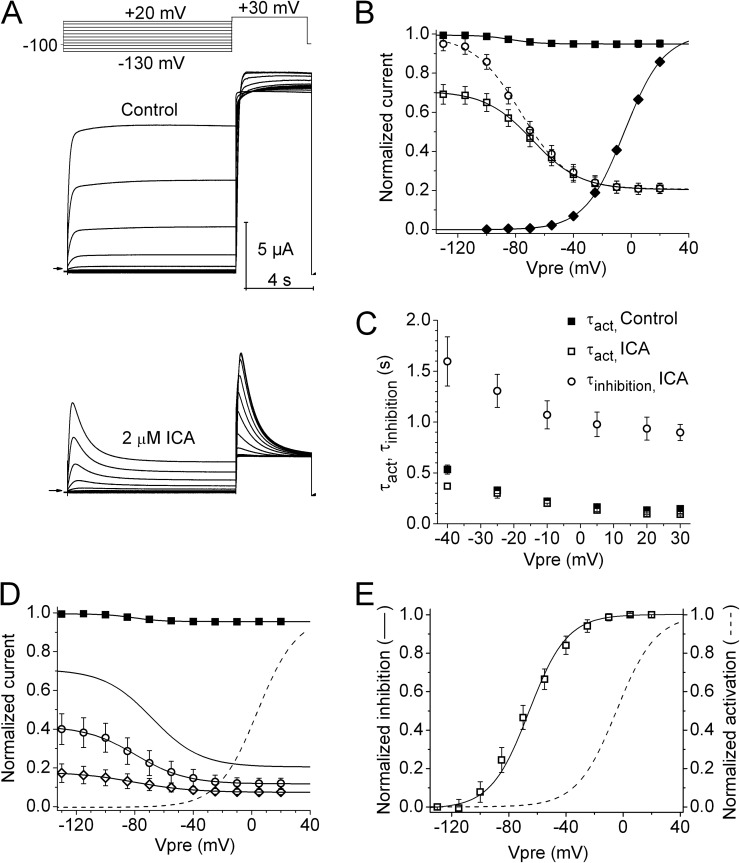
Intrinsic inactivation of hEAG1 channels is enhanced by ICA. (A) hEAG1 currents recorded before (Control, middle) and after 2 µM ICA (bottom) using the voltage-pulse protocol shown in the top. V_h was −100 mV, and V_pre was 10 s in duration and ranged from −130 to +20 mV, applied in 15-mV increments. After each V_pre, a test pulse was applied to +30 mV. Zero current level is indicated by an arrow on the bottom left of the current traces in this panel and in all other figures. (B) Voltage dependence of hEAG1 activation (control, ◆) and inactivation in the absence (■) and presence of 2 µM ICA (□). For inactivation curves, normalized I_max was plotted as a function of V_pre. For the activation curve, I_pre normalized for electrical driving force was plotted as a function of V_pre. Data (n = 7) were fitted with a Boltzmann function (curves). For control inactivation, V_0.5 = −81.4 ± 3.5 mV and z = 1.49 ± 0.32; for control activation, V_0.5 = −4.6 ± 0.7 mV and z = 1.83 ± 0.06. For inactivation in the presence of ICA, V_0.5 = −66.0 ± 4.1 mV and z = 1.15 ± 0.15. ○, extrapolated I_max in the presence of 2 µM ICA: V_0.5 = −73.3 ± 3.9 mV and z = 1.11 ± 0.16. (C) Plot of time constants for onset of activation (control, ■; 2 µM ICA, □) and inactivation (2 µM ICA, ○) during the 10-s V_pres (n = 8). (D) Voltage dependence of inactivation in the absence and presence of three concentrations of ICA. The normalized I_max–V_pre relationship for the test pulse is plotted for control (■), 2 µM ICA (solid curve; same as data plotted in B), 5 µM ICA (○), and 10 µM ICA (◇). For reference, the voltage dependence of hEAG1 activation (B) is replotted as a dashed curve. For control inactivation, V_0.5 = −82.6 ± 2.6 mV and z = 1.26 ± 0.36 (n = 16). For 5 µM ICA, V_0.5 = −80.0 ± 4.4 mV and z = 1.65 ± 0.27 (n = 5); for 10 µM ICA, V_0.5 = −89.5 ± 4.7 mV and z = 1.39 ± 0.17 (n = 7). (E) Plot of the voltage dependence of hEAG1 control activation and inactivation after 2 µM ICA. For inactivation, minimum and maximum I_max was set to 0 and 1, respectively.

Inhibition of hEAG1 current by ICA

ICA strongly inhibits inactivation and thereby increases the magnitude of hERG1 channel currents, especially at positive potentials (Gerlach et al., 2010; Garg et al., 2011). We tested the effects of this compound on hEAG1, with the expectation that it might also inhibit intrinsic inactivation and increase current magnitude. Instead, we found that ICA appeared to enhance inactivation of hEAG1. As shown in the bottom of Fig. 1 A, after a 30-min incubation with 2 µM ICA, peak currents were reduced in magnitude and exhibited further time-dependent decay during both the conditioning and test pulses. The prepulse voltage dependence of current inhibition by ICA was quantified by plotting I_max as a function of V_pre. The relationship was fitted with a Boltzmann function (Fig. 1 B, open squares) to determine V_0.5 (−66.0 ± 4.1 mV) and z (1.15 ± 0.15; n = 7). To account for the relatively rapid current inhibition compared with the slow onset of hEAG1 activation at +30 mV, the decay phase of test-pulse currents was fitted to an exponential function and an adjusted I_max was estimated by extrapolation of the exponential fit to the onset of the test pulse. The adjusted I_max was plotted as a function of V_pre (Fig. 1 B, open circles). With this adjustment, normalized I_max after the conditioning pulse to −130 mV with 2 µM ICA matched predrug I_max. The adjusted I_max–V_pre relationship had a V_0.5 of −73.3 ± 3.9 mV and a z of 1.11 ± 0.16.

To determine the effects of ICA on hEAG1 kinetics, currents recorded during the 10-s V_pres were fitted with a mono- (control) or bi-exponential (ICA) function. ICA at 2 µM did not affect the rate of fast activation of hEAG1 (Fig. 1 C, squares). The rate of ICA-induced current decay was voltage dependent, and the time constant varied from 1.6 s at −40 mV to 0.9 s at +30 mV (Fig. 1 C, open circles). Higher concentrations of ICA (5 and 10 µM) further reduced current magnitude and shifted the V_0.5 for current inhibition to more negative potentials (Fig. 1 D, open symbols). After the most negative prepulse to −130 mV, I_max was reduced by 60% with 5 µM and 83% with 10 µM ICA.

Prepulse-dependent inhibition of current by 2 µM ICA developed over a voltage range that was mostly negative to the voltage range required for channel activation (Fig. 1 E). The slopes of these relationships were similar; however, the V_0.5 for channel activation was 61 mV more positive than the V_0.5 for current inhibition. This difference suggests that ICA primarily inhibits current by altering channel gating (enhanced inactivation) as opposed to a pore block mechanism where the voltage dependence of activation and inhibition would be expected to fully overlap (Delpón et al., 1997; González et al., 2001; Lee et al., 2010). Clofilium (Gessner et al., 2004) and astemizole (García-Ferreiro et al., 2004) are two established open-channel blockers of hEAG1 channels. Therefore, we next determined and compared the voltage dependence of activation and inhibition of hEAG1 by these two drugs.

Voltage dependence of open-channel block by clofilium and astemizole

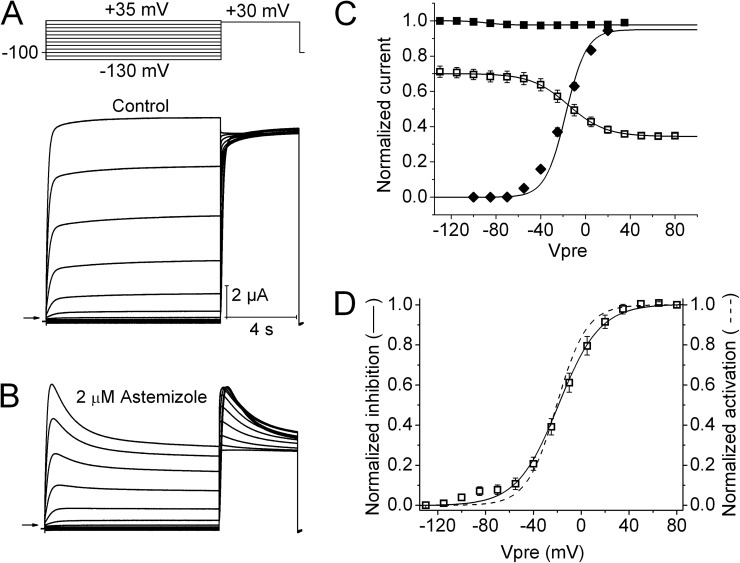
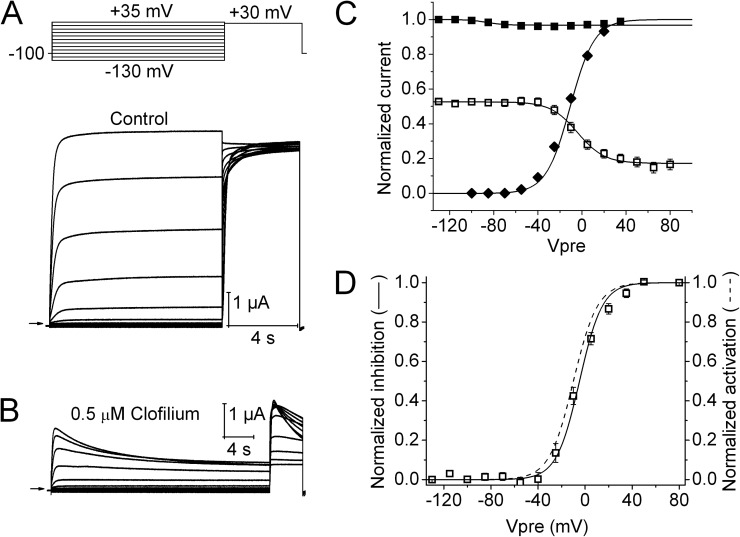
The effects of clofilium and astemizole on hEAG1 currents were examined at concentrations of 0.5 and 2 µM, respectively. Currents were elicited with a two-pulse inactivation protocol similar to that used to characterize ICA, except that the maximum V_pre was increased to +80 mV in the presence of drug. The current decay induced by astemizole during 10-s V_pres (Fig. 2, A and B) superficially resembled the effects of ICA. However, as shown in Fig. 2 C, the V_0.5 for channel block by astemizole (−15.7 ± 3.3 mV; n = 5) was similar to the V_0.5 of channel activation (−17.8 ± 1.4 mV). The voltage dependence of block was inverted and its full range was normalized from 0 to 1 (Fig. 2 D) to more clearly illustrate that the voltage dependency of these two relationships overlaps one another. Clofilium also inhibited hEAG1 currents, but the onset of block was slower (Fig. 3, A and B) when compared with astemizole. In the presence of clofilium, V_pre was increased to 30 s to account for the slower kinetics of block. The V_0.5 for current inhibition by clofilium was nearly the same (shifted +6.5 mV) as the V_0.5 of channel activation (Fig. 3, C and D). Thus, as predicted for these open-channel blockers and unlike ICA, the voltage dependence of channel activation is a direct determinant of the relative block induced by astemizole or clofilium.

Figure 2.

Voltage-dependent hEAG1 channel block by astemizole. (A) Control hEAG1 currents (bottom) elicited with voltage-pulse protocol shown in the top. V_h was −100 mV, and V_pre was 10 s in duration and ranged from −130 to +35 mV, applied in 15-mV increments. (B) Currents recorded from the same oocyte after steady-state block by 2 µM astemizole. (C) Voltage dependence of hEAG1 activation (◆) and inactivation (■) in control, and inhibition by 2 µM astemizole (□). For inactivation and inhibition curves, normalized I_max was plotted as a function of V_pre. For the activation curve, I_pre normalized for electrical driving force was plotted as a function of V_pre. Data (n = 5) were fitted with a Boltzmann function (curves). For control inactivation, V_0.5 = −88.5 ± 2.4 mV and z = 2.84 ± 0.62; for control activation, V_0.5 = −17.8 ± 1.4 mV and z = 1.84 ± 0.01. For inactivation in the presence of astemizole, V_0.5 = −15.7 ± 3.3 mV and z = 1.51 ± 0.07. (D) Comparison of the voltage dependence of hEAG1 activation (dashed curve) and block by 2 µM astemizole (□).

Figure 3.

Voltage dependence of hEAG1 channel block by clofilium. (A) Control hEAG1 currents (bottom) elicited with voltage-pulse protocol shown in the top. V_h was −100 mV, and V_pre was 10 s in duration and ranged from −130 to +35 mV, applied in 15-mV increments. (B) Currents recorded from same oocyte after steady-state block by 0.5 µM clofilium. Note that the duration of V_pre was increased to 30 s. (C) Voltage dependence of hEAG1 activation (◆) and inactivation (■) in control, and inhibition by 0.5 µM clofilium (□). For inactivation and inhibition curves, normalized I_max was plotted as a function of V_pre. For the activation curve, I_pre normalized for electrical driving force was plotted as a function of V_pre. Data (n = 5) were fitted with a Boltzmann function (curves). For control inactivation, V_0.5 = −86.7 ± 4.5 mV and z = 3.12 ± 1.21; for control activation, V_0.5 = −12.4 ± 0.8 mV and z = 2.00 ± 0.02. For inactivation in the presence of clofilium, V_0.5 = −5.2 ± 1.7 mV and z = 2.13 ± 0.13. (D) Comparison of the voltage dependence of hEAG1 activation (dashed curve) and block by 0.5 µM clofilium (□).

Mutation of Tyr464 in S6 segment enhances hEAG1 channel inactivation

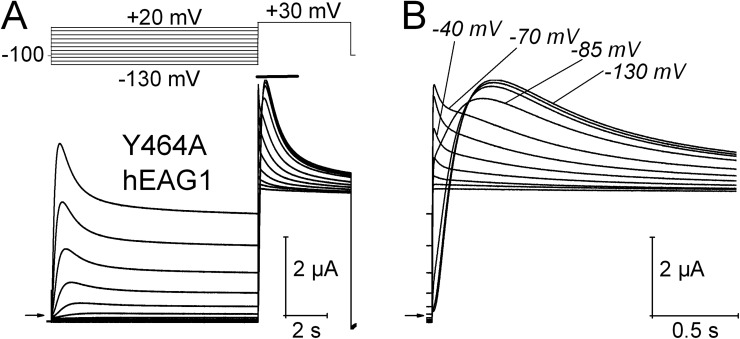
Mutation of Tyr652 in S6 of hERG1 to Ala (Y652A) does not appreciably alter the kinetics of channel activation or inactivation (Fernandez et al., 2004) but greatly attenuates the ability of ICA to inhibit inactivation (Garg et al., 2011). Thus, we wondered if the corresponding mutation in hEAG1 (Y464A) would also prevent or impact the ability of ICA to alter hEAG1 channel gating. Unexpectedly, the Y464A mutation alone was found to induce prominent voltage-dependent inactivation of hEAG1 (Fig. 4 A). Moreover, inactivation was composed of multiple components that were revealed in a V_pre-dependent manner. From a V_pre of −130 to −85 mV, current activated in response to a pulse to +30 mV exhibited fast and slow time components of inactivation, with time constants of 0.57 ± 0.02 s and 3.2 ± 0.3 s (Fig. S2; n = 5). From a V_pre of −70 mV or more positive, an additional and even faster component of inactivation was evident (Fig. 4 B). When the V_pre was −85 mV or more negative, this fast component of inactivation was masked by the slower rate of activation. In addition to a greatly enhanced inactivation, Y464A hEAG1 channels expressed poorly compared with WT channels, requiring injection of oocytes with ∼14 ng cRNA to obtain equivalent current magnitudes after 1 d of incubation as that achieved with 0.2 ng cRNA for WT channels.

Figure 4.

Y464A hEAG1 channels exhibit enhanced inactivation. (A) Voltage-pulse protocol and corresponding Y464A hEAG1 currents. (B) Test-pulse currents (during time indicated by a solid bar in A) are shown on an expanded time scale. Test currents elicited after V_pre of −130, −85, −70, and −40 mV are labeled. A fast inactivating component of current is evident when V_pre ≥ −70 mV.

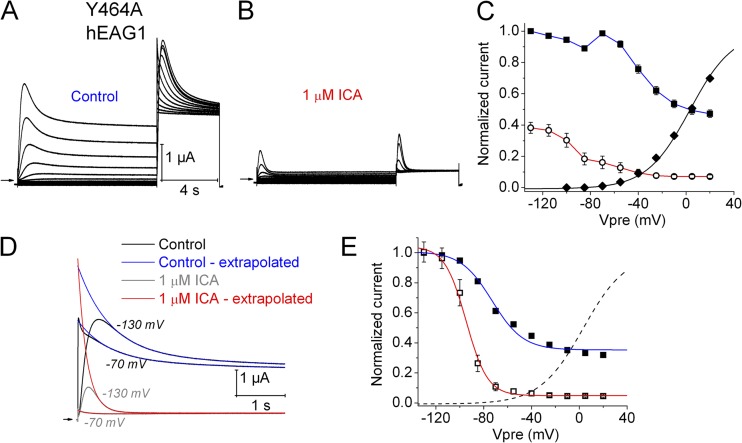
In contrast to Y652A hERG1 channels, which are insensitive to the activating effect of ICA (Garg et al., 2011), Y464A hEAG1 channels were even more sensitive to the inhibiting effect of ICA than WT channels, accelerating the rate of inactivation (Fig. S3) and causing a greater tonic inhibition of current (Fig. 5, A and B). For example, 1 µM ICA reduced I_max (V_t = +30 mV and V_h = −100 mV) by 35 ± 6% for WT channels (n = 5) versus 68 ± 4% (n = 8) for Y464A channels.

Figure 5.

Effect of 1 µM ICA on Y464A hEAG1 channel currents. (A) Control Y464A hEAG1 currents elicited with two-pulse protocol, where V_h was −100 mV and V_pre was 10 s in duration and ranged from −130 to +20 mV applied in 15-mV increments, each followed by a test pulse to +30 mV. (B) Currents recorded after steady-state inhibition of hEAG1 by 1 µM ICA. (C) Voltage dependence of activation (◆) and inactivation in the absence (■) and presence (○) of 1 µM ICA. For control activation, V_0.5 = −15.1 ± 2.1 mV and z = 1.31 ± 0.02 (n = 8). (D) Test-pulse currents recorded at +30 mV after V_pre to −130 and −70 mV during control and after 1 µM ICA. Traces were fitted with two-exponential function and extrapolated back to the start of the pulse for control (blue curves) and after 1 µM ICA (red curves). (E) Extrapolated I_max–V_pre relationships for control (■) and after 1 µM ICA (□). Dashed curve is same activation curve plotted in C. For control inactivation, V_0.5 = −73.3 ± 0.7 mV and z = 1.44 ± 0.05 (n = 8). For 1 µM ICA, V_0.5 = −94.3 ± 1.9 mV and z = 3.78 ± 0.16 (n = 8).

The voltage dependence of activation and effects of ICA on inactivation (I_max–V_pre relationship) of Y464A hEAG1 are plotted in Fig. 5 C. The V_0.5 for current activation was −15.1 ± 2.1 mV (n = 8), a potential where inactivation was nearly complete. The I_max–V_pre relationship determined under control conditions (Fig. 5 C, closed squares) and after 1 µM ICA (Fig. 5 C, open circles) deviated from the normal sigmoidal shape. A probable cause of the reduced magnitude of I_max at V_pre of less than −70 mV was the relatively slow onset of activation of channels compared with their faster rate of inactivation. To account for this effect, the slower inactivating components of test-pulse currents were fitted to an exponential function, and an adjusted I_max was estimated by extrapolation of the exponential fit to the onset of the test pulse. This fitting procedure was performed for currents recorded before and after ICA (Fig. 5 D). The voltage dependence of Y464A hEAG1 inactivation (Fig. 5 E, closed squares) was determined by fitting the adjusted I_max–V_pre relationship with a Boltzmann function (V_0.5 = −73.3 ± 0.7 mV and z = 1.44 ± 0.05). The relationship was nearly the same as that estimated for WT channels in the presence of 2 µM ICA (V_0.5 = −73.3 ± 3.9 mV and z = 1.11 ± 0.16; Fig. 1 B). However, given the uncertainties inherent with extensive extrapolation required to estimate adjusted I_max, especially in the presence of ICA (Fig. 5, D and E, open squares), the adjusted I_max–V_pre relationship plotted in Fig. 5 E should be viewed with caution. Nevertheless, it is clear that ICA greatly enhanced inactivation of Y464A channels.

Effects of external TEA and elevated [K⁺]_e on Y464A hEAG1 inactivation

The rate of C-type inactivation in Kv channels is slowed by high [K⁺]_e (López-Barneo et al., 1993). In contrast, the rate of Y464A hEAG1 channel inactivation was unaffected by elevation of [K⁺]_e from 2 to 20 mM, and slightly faster at 104 mM (Fig. S2). The rate of C-type inactivation is also slowed by external TEA (Choi et al., 1991; Smith et al., 1996). In contrast, externally applied 10 mM TEA did not slow inactivation of Y464A hEAG1, and in fact, at V_ts between 0 and +40 mV, inactivation was accelerated by TEA (Fig. S4). In addition, and similar to its effects on other Kv channels, 10 mM TEA caused a voltage-independent reduction of peak and steady-state current by ∼50% (Fig. S4). TEA also had no apparent effect on the rate of ICA-induced inactivation of WT hEAG1 channels (Fig. S5). Collectively, these findings indicate that the prominent inactivation of hEAG1 induced or enhanced by mutation (Y464A) or drug (ICA) is not mediated by a typical C-type mechanism.

Molecular determinants of Y464A-induced inactivation

To explore the structural basis of Y464A-induced inactivation in hEAG1, Tyr464 was substituted with other amino acids, including other aromatics (Phe and Trp), a hydrophilic (Ser), or several hydrophobic (Leu, Ile, Met, and Val) residues. Preliminary experiments with these mutant channels indicated that some were nonfunctional (Y464I, Y464L, Y464M, and Y464W) or expressed very poorly (Y464V). One possible explanation for the reduced or absent currents was that these mutant channels inactivated at much more negative potentials or a rate much faster than activation. It was previously reported that external Mg²⁺ slows the rate of activation of EAG channels (Terlau et al., 1996). Therefore, to accelerate channel activation and potentially unmask a fast component of inactivation, 1 mM Mg²⁺ in the KCM211 extracellular solution was replaced by Ca²⁺. In addition, V_pre was reduced to 1 s to allow us to pulse to more negative potentials without activating excessive endogenous currents.

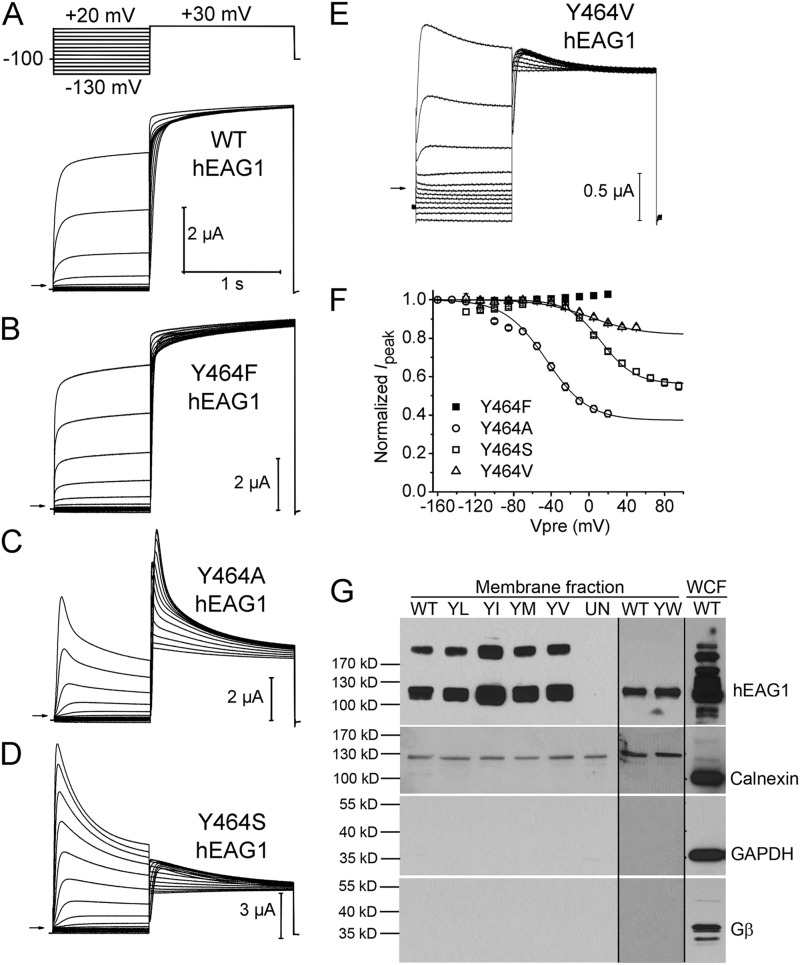
As illustrated in Fig. 6 A, WT channels activated more rapidly and displayed only minimal inactivation in the absence of external Mg²⁺. Similar to WT channels, Y464F hEAG1 channel currents were robust and exhibited minimal inactivation (Fig. 6 B). For Y464A hEAG1, the faster rate of activation associated with the absence of Mg²⁺ accentuated the fast component of inactivation (Fig. 6 C). Y464S channels exhibited prominent inactivation, albeit requiring greater depolarization (Fig. 6 D). Y464V hEAG1 also required higher depolarization to elicit a modest inactivation (Fig. 6 E). The voltage dependence of inactivation of Y464F, Y464A, Y464S, and Y464V channels measured in the absence of external Mg²⁺ is summarized in Fig. 6 F.

Figure 6.

Mutation of Tyr464 in hEAG1 has variable effects on inactivation. (A–E) WT or indicated mutant hEAG1 currents recorded from oocytes bathed in Mg²⁺-free external solution. WT currents were elicited with voltage-pulse protocol shown in the top: V_h was −100 mV and V_pre was 1 s in duration and ranged from −130 to +20 mV, applied in 15-mV increments. After each V_pre, a 1.5-s test pulse was applied to +30 mV to measure channel availability. For some mutant channels V_h and/or V_pre was varied as follows: Y464A, V_h = −130 mV and V_pre ranged from −160 to +20 mV; Y464S, V_pre ranged from −130 to +95 mV; Y464V, V_pre ranged from −130 to +50 mV. (F) Voltage dependence of inactivation for mutant hEAG1 channels (n = 4–6) as indicated. Boltzmann fits: Y464A, V_0.5 = −45.0 ± 1.3 mV and z = 1.14 ± 0.07; Y464S, V_0.5 = 13.0 ± 1.8 mV and z = 1.43 ± 0.12; Y464V, V_0.5 = 1.6 ± 12.4 mV and z = 0.96 ± 0.13. (G; top) Western blots for hEAG1 in the NeutrAvidin-captured cell surface protein fractions (membrane fraction) from a single batch of oocytes expressing WT or Tyr464 mutant channels. YL, Y464L; YI, Y464I; YM, Y464M; YV, Y464V). The hEAG1 monomer is represented by the 113-kD band; a higher band was also seen in all injected oocytes, but not in the uninjected oocytes (UN). Y464W (YW) channels and matched control (WT) channels were studied with a different batch of oocytes (less hEAG1 protein; therefore, dimer band was absent) on a different gel. For all hEAG1 constructs, each oocyte was injected with 20 ng cRNA. hEAG1 antibody showed reactivity to multiple intracellular proteins in the whole cell fraction (WCF), overlapping the 113-kD hEAG1 protein signal. Rightmost lane is for the WCF. (Bottom three panels) Western blots for calnexin, GAPDH, and Gβ from the same preparations as the top panel. Notice the absence of these three proteins in the membrane fraction.

All Tyr464 mutations other than Y464F exhibited poor or no functional expression. WT and Y464F hEAG1 channel currents activated at +20 mV were typically 5–7 µA when measured 24 h after injection of oocytes with 0.2 ng cRNA. In contrast, Y464A and Y464S mutants required larger amounts (14 ng) of cRNA to achieve similar levels of functional expression. Nonaromatic and hydrophobic substitutions had the greatest effect on expression. Y464V channels expressed at very low levels, and substitution with Trp, Leu, Ile, or Met resulted in nonfunctional channels regardless of incubation time (up to 6 d) when oocytes were injected with 14–20 ng cRNA. The Tyr464 mutations do not reduce or eliminate channel function because of protein misfolding and/or reduced trafficking to the plasma membrane, as the surface expression of the Tyr464 mutant channels determined by a biotinylation/Western blot assay was found to be similar to WT channels (Figs. 6 G and S6). These findings suggest that Tyr464 mutants (other than Y464F) conduct poorly or not at all because they are highly or permanently inactivated.

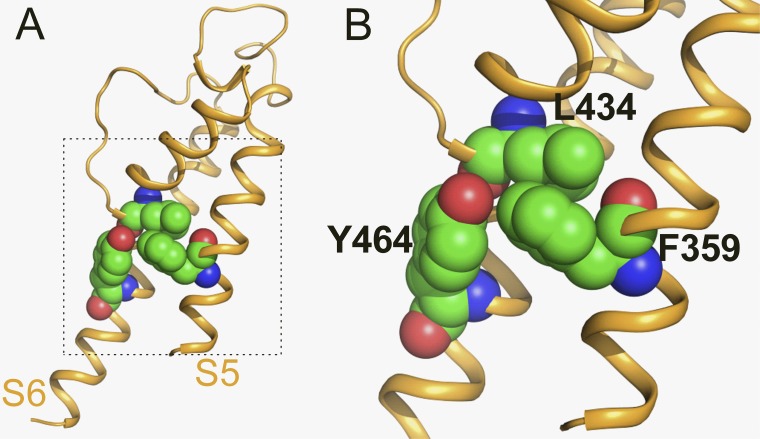
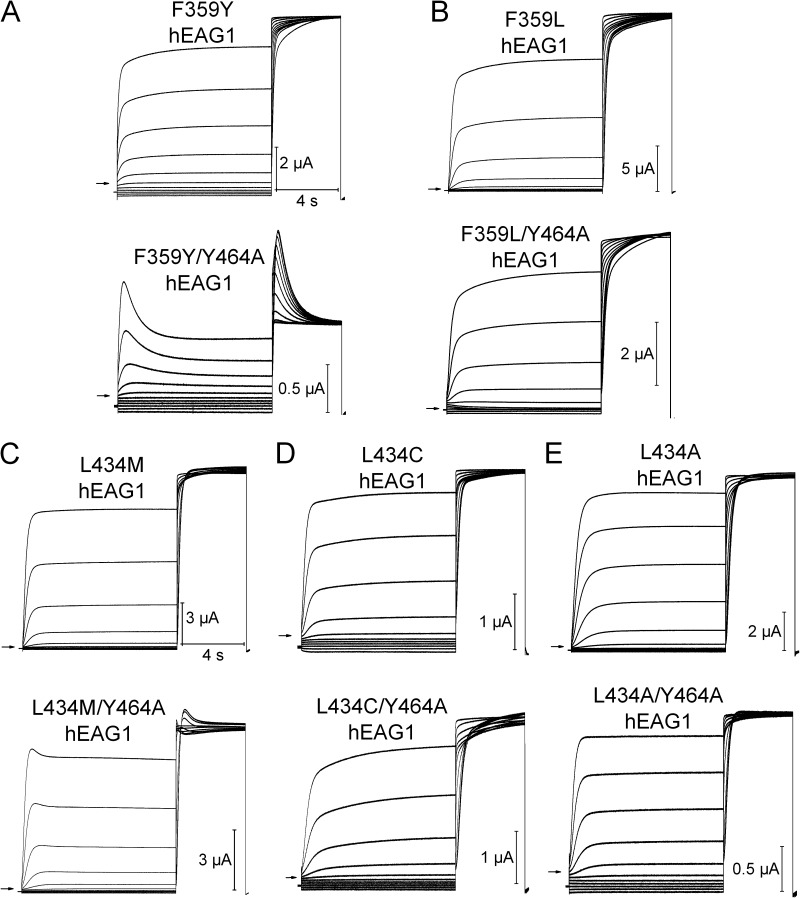
To further explore the molecular determinants of hEAG1 inactivation, we mutated residues predicted to be in close proximity to Tyr464. A homology model of the hEAG1 pore module was constructed based on the Streptomyces lividans K⁺ channel KcsA crystal structure (Protein Data Bank accession no. 1BL8). Tyr464 in hEAG1 corresponds to Phe103 in KcsA, which was reported previously to interact with the pore helix to mediate channel inactivation (Cuello et al., 2010a). The hEAG1 model predicts that the side chain of Tyr464 closely interacts with only two other residues: Leu434 in the pore helix and Phe359 in S5 of the same subunit (Fig. 7). To test the importance of these two residues in channel inactivation, each was mutated singly to smaller or less hydrophobic residues, and in combination with Y464A to assay for intragenic rescue of gating. The conservative mutation F359Y did not enhance inactivation nor did it rescue Y464A; i.e., F359Y did not prevent the Y464A-induced inactivation (Fig. 8 A). The nonconserved mutation F359L also did not enhance inactivation but suppressed Y464A-induced inactivation; i.e., the double mutation F359L/Y464A restored normal gating (Fig. 8 B). F359A also rescued Y464A gating (Fig. S7). In addition, the K⁺ selectivity of F359L/Y464A channels was reduced. After subtraction of linear leak, the reversal potential for these channels was −38.3 ± 1.4 mV (n = 7) instead of the usual −98 mV for WT or hEAG1 channels with only a single mutation. Substitution of Leu434 with Met, Cys, or Ala had no effect on inactivation (Fig. 8, C–E, top). L434M/Y464A channels exhibited minimal but faster than normal inactivation, and L434C or L434A fully rescued the gating of Y464A channels (Fig. 8 C–E, bottom). Collectively, the site-directed mutagenesis findings described above suggest a tripartite model to explain the enhanced inactivation of Tyr464 mutant channels. We propose that in WT hEAG1, Tyr464 in S6 and Phe359 in S5 strongly interact, presumably by π-stacking. When this interaction is disrupted (e.g., by mutation of Tyr464 to any residue other than Phe), Phe359 can interact with Leu434 in the pore helix to strongly enhance intrinsic voltage- and time-dependent inactivation, presumably by a conformational change in the selectivity filter that reduces ion conductance that is similar but not identical to C-type inactivation. Substitution of Tyr464 with other hydrophobic residues (Leu, Ile, Met, and Val) has an even greater disruptive effect on the selectivity filter, perhaps via direct interaction with Leu434 in the pore helix in addition to release of Phe359 from the braking action exerted through the putative π-stacking interaction with Tyr464. The π-stacking hypothesis predicts that substitution of Tyr464 with Trp, another aromatic residue, would not alter channel gating. Instead, we found that Y464W mutant channels trafficked normally to the cell surface but were nonfunctional. Trp is more bulky than Tyr or Phe, and this may prevent its π-stacking with Phe359 and/or enhance direct interaction with Leu434 to inactivate the channel similar to that proposed for the other nonaromatic hydrophobic substitutions.

Figure 7.

Homology model of the pore domain for a single hEAG1 subunit. Model used the crystal structure of KcsA (Protein Data Bank accession no. 1BL8) as a template. Lateral view (A) and close-up view (B) of a subunit with Leu434 (base of pore helix), Tyr464 (S6), and Phe359 (S5) residues shown in space fill.

Figure 8.

Intragenic rescue of Y464A-enhanced hEAG1 inactivation by a second site mutation in either Phe359 (in S5) or Leu434 (in pore helix). (A–E) Currents for indicated mutant hEAG1 channels recorded during two-pulse inactivation protocol: V_h = −100 mV, and V_pre (10 s) ranged from −130 to +20 mV, applied in 15-mV increments. A test pulse to +30 mV was applied after each V_pre. The top set of traces in each panel is for channels with indicated single mutation; the bottom set of traces shows currents for same mutation introduced into the Y464A channel. All mutations except the conserved F359Y (A, bottom) and L434M (C, bottom) rescued inactivation of Y464A. Inward currents in some traces represent unsubtracted leak currents. Based on reversal potential of time-dependent currents, only F359L/Y464A channels had reduced K⁺ selectivity. Currents shown are representative of four to six oocytes for each mutant channel.

F359L hEAG1 is activated by ICA

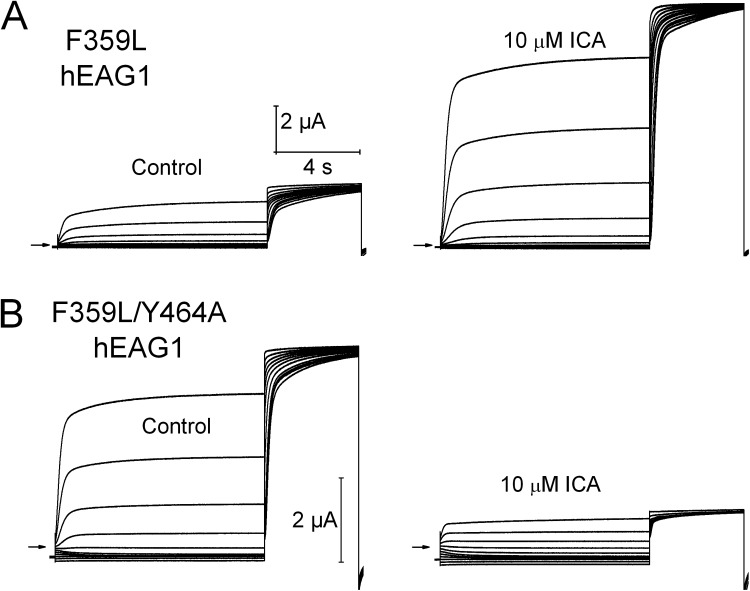
As noted above, the voltage dependence of Y464A hEAG1 inactivation is similar to that induced in WT channels by 2 µM ICA, suggesting a common underlying mechanism. To explore this possibility, we determined the effect of ICA on F359L mutant channels. F359L is one of the mutations that rescued gating of Y464A channels (Fig. 8 B), and the equivalent mutation in hERG1 (F557L) eliminated channel response to 30 µM ICA, presumably because it disrupted the drug-binding site (Garg et al., 2011). Based on its effects in hERG1, we assumed that F359L hEAG1 channels would also be insensitive to ICA. Instead, we found that ICA increased F359L hEAG1 channel currents by 5.4 ± 0.6–fold at 10 µM (n = 3) without any evident change in kinetics (Fig. 9 A). Thus, in contrast to F557L hERG1 and opposite to the effect on WT hEAG1, ICA is an agonist of F359L hEAG1 channels. The mechanism of this activity will require further study but presumably results from an increase in channel open probability, perhaps by preventing F359L hEAG1 channel transition into an absorbing inactivated state. Opposite to channels harboring only the F359L mutation, F359L/Y464A hEAG1 channel currents were inhibited by 80.4 ± 0.02% (n = 7) with 10 µM ICA (Fig. 9 B). However, unlike WT channels, F359L/Y464A hEAG1 channel currents recorded in the presence of ICA did not exhibit time-dependent decay. This finding suggests that either ICA blocks the pore of these channels or primarily enhances closed-state inactivation. Thus, ICA is an activator of F359L hEAG1 and an inhibitor of F359L/Y464A hEAG1 channels, indicating that Phe359 in S5 is required for ICA to induce open-state inactivation, as well as demonstrating that Tyr464 in S6 is required for the activator effect of ICA on F359L hEAG1 channels. The latter finding is of particular interest because we reported previously that the equivalent Tyr in hERG1 (Tyr652) is also required for ICA-mediated channel activation (Garg et al., 2011). Collectively, our present findings with hEAG1 and previous findings with hERG1 indicate that a strategically positioned Phe in S5 and a Tyr in S6 are critical determinants of ICA-induced alterations of channel inactivation.

Figure 9.

ICA activates F359L hEAG1 channels and inhibits F359L/Y464A hEAG1 channels. (A) F359L hEAG1 currents recorded under control conditions and after the application of 10 µM ICA. (B) F359L/Y464A hEAG1 currents recorded under control conditions and after the application of 10 µM ICA. In all panels, currents were elicited with two-pulse inactivation protocol: V_h = −100 mV, and V_pre (10 s) ranged from −130 to +20 mV, applied in 15-mV increments. A test pulse to +30 mV was applied after each V_pre.

Markov modeling of hEAG1 channel gating

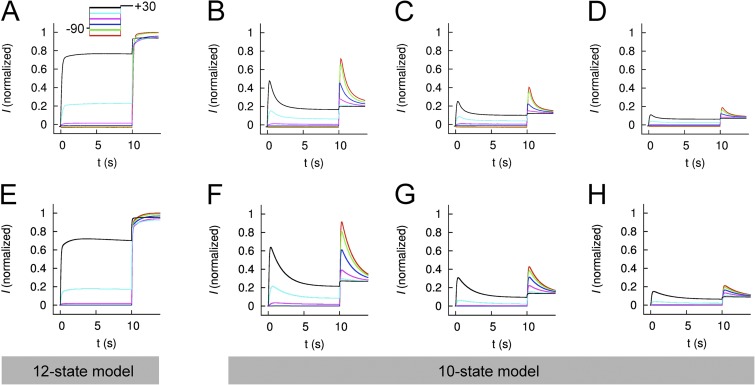
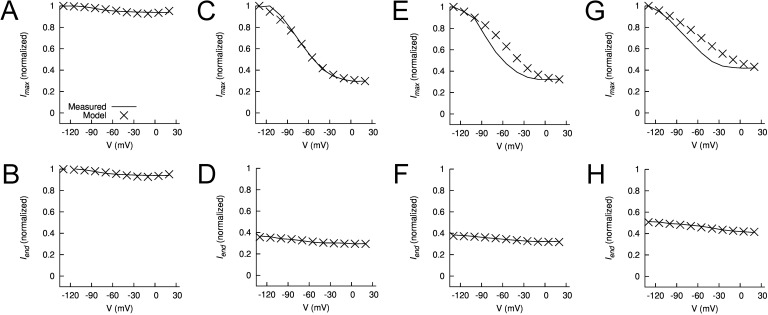
Mathematical models of WT EAG1 channel currents were developed to reconstruct experimental data. The first and simplest model considered four closed states and a single open state (Fig. S8 A). This model was able to satisfactorily reproduce I-V relationships and current kinetics during the prepulses (Fig. S9 A); however, it did not reproduce the experimentally observed V_pre-dependent differences in I_max for test pulses to +30 mV. A six-state model that included a single inactivated state coupled to the single open state (Fig. S8 A) was also unable to reconstruct differences in I_max (Fig. S9 B). We next considered 10- and 12-state models that paired an inactivated state to each closed and open state. The 12-state model featured 2 open states (Fig. 10 A); the 10-state model had a single open state (Fig. 10 B). Only the 12-state model (Fig. 11 E) accurately reproduced the slower phase of activation observed for WT hEAG1 under control conditions (Fig. 11 A). This difference is more obvious by inspection of test currents (at +30 mV) in Fig. S9 C (10-state model) and Fig. 11 E (12-state model) and reflected in the fit errors (Table 1). For the 12-state model, the errors for individual features and the rate coefficients are presented in Tables S2 and S3, respectively. The modeled magnitudes of peak and end of pulse currents under control conditions are plotted in Fig. 12 (A and B) for the prepulses and in Fig. 13 (A and B) for the test pulses and closely match the experimentally measured values. An important feature of the Control model was accentuated forward rate coefficients α_CI1, α_CI2, and α_CI3 versus forward rate coefficients α_CI0 and α_OI.

Figure 11.

Comparison of measured and modeled currents for WT hEAG1. (A–D) Currents recorded from five to eight oocytes for each condition (Control [A] or ICA at 2 [B], 5 [C], and 10 µM [D]) were averaged and normalized to their corresponding peak control current. Voltage-pulse protocol: V_h = −90 mV and V_pre (10 s) ranged from −130 to +20 mV, applied in 30-mV increments; at 10 s, a test pulse to +30 mV was applied. (E–H) Simulated EAG currents (I) for control (E, 12-state model) and in the presence of 2 (F), 5 (G), and 10 µM (H) ICA (all 10-state models).

Table 1.

Fit error E for the investigated models

Model	E 5-State	E 6-State	E 10-State	E 12-State
Control	3.894	3.892	0.421	0.271a
2 µM ICA	230.212	0.696	0.430a	0.463
5 µM ICA	981.122	1.965	1.472a	1.512
10 µM ICA	47.436	1.454	1.133a	1.154
Y464A	39.876	0.433	0.232a	0.254

^aThe smallest E for control and different ICA concentrations.

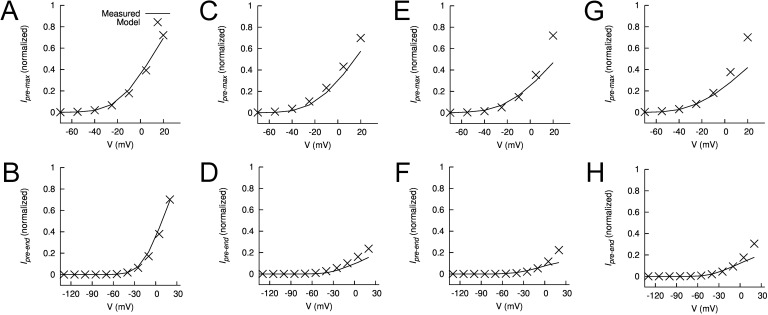
Figure 12.

Features of measured and modeled WT hEAG1 current during prepulses. (A–H) Plots of normalized maximum (I_premax) and end (I_preend) currents during the prepulse for control (A and B) in the presence of 2 (C and D), 5 (E and F), and 10 µM ICA (G and H). In each panel, experimentally measured currents (curves) are compared with modeled currents (X), all normalized to their respective I_max (peak current at V_t of +30 mV).

Figure 13.

Features of measured and modeled WT hEAG1 current during test pulses to +30 mV. (A–H) Plots of normalized maximum (I_max) and end (I_end) currents during test pulse for control (A and B) in the presence of 2 (C and D), 5 (E and F), and 10 µM ICA (G and H). In each panel, experimentally measured currents (curves) are compared with modeled currents (X), all normalized to their respective I_max.

Multiple models were considered for simulating currents measured in the presence of 2, 5, and 10 µM ICA. Parameterization of the five-state model, lacking an inactivated state, and the six-state model, with an inactivated state, was not successful (Fig. S9, D and E). We next attempted to vary only C to I and O to I transitions but keeping α₀, z_α, β₀, and z_β fixed as in the 10- and 12-state control models; however, the resulting fit error was large. The fitting was improved by using the comprehensive parameterization approach as for the control model, and a linear interpolation of rate coefficients as described in Materials and methods. Results of parameterization of the 10- and 12-state models are presented in Figs. 11 D and S8 F, respectively. The fit error was similar for the 10- and 12-state models, and both of these were smaller than the 6-state model (Tables 1 and S2). Therefore, the 10-state model was selected for further analysis of currents recorded in the presence of ICA.

The experimental data for 2, 5, and 10 µM ICA are presented in Fig. 11 (B–D) and are compared with model currents in Fig. 11 (F–H). The models reproduce the [ICA]-dependent decrease in relative current magnitude, a manifestation of enhanced inactivation. For the three ICA models, the magnitudes of peak and end of pulse currents are plotted in Fig. 12 (C–H for prepulses) and in Fig. 13 (C–H for test pulses) and adequately match the experimentally measured values. In the three ICA models, the major effects of drug compared with the Control model were faster forward rates for closed-state inactivation (α_CI1, α_CI2, and α_CI3) and the forward rate α_OI for open-state inactivation. For example, α_CI2 was increased from 0.0256 in Control to 0.257 for 2 µM ICA, whereas the backward rate (β_CI2) was only increased from 0.016 to 0.089 (Table S3).

The 10- and 12-state models were equally effective (similar fit errors; Table 1) in reproducing Y464A hEAG1 channel currents. Individual fit errors for the Y464A model are presented in Table S1. The experimentally measured Y464A currents and modeled currents are compared in Fig. 14 (A and B). The model reproduces the mutation-induced change in peak currents and enhanced inactivation (Fig. 14, C–F) but does not account for the very fast phase of inactivation measured at +30 mV after V_pre ≥ −70 mV (Figs. 4 B and 6 C). The major difference between the Y464A model and all other models was the slowed activation and deactivation rates (Table S3). In addition, compared with the Control model, the Y464A model had faster forward and backward rates for closed- and open-state inactivation. For example, α_CI2 was increased from 0.0256 (Control) to 0.168 (Y464A), and the backward rate (β_CI2) was increased from 0.016 (Control) to 0.247 (Y464A) (Table S3).

Figure 14.

Comparison of measured and modeled currents of Y464A hEAG1. (A) Currents recorded from 10 oocytes were averaged and normalized to I_max. Voltage-pulse protocol: V_h = −90 mV and V_pre (10 s) ranged from −130 to +20 mV, applied in 30-mV increments; at 10 s, a test pulse to +30 mV was applied. (B) Simulated EAG1 currents (I) for Y464A hEAG1. Features of the currents were extracted during the prepulse (C and D) and test pulse (E and F). In each panel, experimentally measured currents (curves) are compared with model currents (X), all normalized to their respective I_max.

DISCUSSION

Inactivation of EAG1 channels appears to be species dependent. Drosophila eag1 channels inactivate substantially (Brüggemann et al., 1993; Robertson et al., 1996), whereas inactivation is absent in mouse EAG1 (Robertson et al., 1996). Here, we report that human EAG1 channels exhibit a modest (5–10% reduction in current at +30 mV) and very slow voltage-dependent inactivation. Experimental data demonstrate and Markov modeling corroborates that hEAG1 channels inactivate from both closed and open states. Intrinsic inactivation was markedly enhanced by ICA, a previously described activator of hERG1 channels. Intrinsic inactivation was also enhanced by mutation of Tyr464, equivalent to a key aromatic residue previously implicated in KcsA channel inactivation (Cuello et al., 2010b). The molecular determinants for enhanced inactivation induced by ICA or the Y464A mutation may be similar and are tentatively proposed to involve interaction between three residues located in close proximity to one another in S5 (Phe359), S6 (Tyr464), and the pore helix (Leu434) in a single hEAG1 subunit.

Comparison of hEAG1 inactivation with other K⁺ channels

Several modes of inactivation have been defined in K⁺ channels, including N-, C-, P-, and U-type inactivation (Kurata and Fedida, 2006). N-type inactivation was first identified in Shaker channels and is mediated by physical occlusion of the pore by the cytoplasmic N-terminal peptide chain (Hoshi et al., 1990). After truncation of the N terminus in Shaker, a much slower C-type inactivation was revealed (Hoshi et al., 1991). C-type inactivation is mediated by a conformational change in the selectivity filter that prevents or reduces K⁺ conductance. A similar mechanism likely mediates the more rapid P-type inactivation (De Biasi et al., 1993), and thus, the lumped term “P/C-type” inactivation is often used (Chen et al., 2000). A hallmark of C-type inactivation is that its rate is slowed by extracellular TEA or an increase in [K⁺]_e (Grissmer and Cahalan, 1989; Choi et al., 1991; López-Barneo et al., 1993; Smith et al., 1996). In contrast, external TEA increases currents in channels that exhibit P-type inactivation (De Biasi et al., 1993). ERG1 channels show prominent C-type inactivation, which is sensitive to external TEA (Smith et al., 1996), [K⁺]_e (Wang et al., 1997), and to mutations of residues near the selectivity filter (Schönherr and Heinemann, 1996; Smith et al., 1996; Suessbrich et al., 1997; Zou et al., 1998). In contrast, we found that inactivation of the related hEAG1 was not slowed by external TEA or elevated [K⁺]_e. Other types of inactivation (e.g., U-type) have been described in Kv2.1, Kv3.1, Kv4, and Shaker (Jerng and Covarrubias, 1997; Klemic et al., 1998, 2001; Kurata and Fedida, 2006), where channels inactivate from the preopen and open states and are insensitive, or in some cases their rate of onset is enhanced, by extracellular TEA or elevated [K⁺]_e. Further study is required to understand how slow inactivation in hEAG1 differs or is similar to specific properties of inactivation described for other Kv channels.

Markov models of EAG

The Markov models presented here are the first quantitative description of EAG channel gating and currents. Four different model topologies were investigated using an automated stochastic optimization approach described previously for our study of hERG1 gating currents (Abbruzzese et al., 2010). This approach evaluates a far greater number of parameterizations than are normally investigated using the more common methodology of manual parameter adjustment. The approach allowed us to demonstrate that simple 5- and 6-state models were inadequate and that a 10- or 12-state model was more appropriate for description of EAG1 channels. The 10- and 12-state models featured an inactivation state paired with each closed and open state because there was no compelling reason to exclude the likelihood that channels could inactivate from any particular state. Lacking experimental evidence to the contrary and to simplify parameterization, the rate coefficients between inactivated states were identical to those of their paired closed or open states. For the control model, the best fit was obtained using two open states to account for the slow phase of activation of currents elicited from the more negative V_pre. For ICA or Y464A models, a single open-state model was as effective as a two open-state model because of the dominance of inactivation gating. There are several limitations of the models. First, some important experimental data are lacking, including single-channel conductance and kinetics, gating currents, and kinetics of drug binding. The lack of these measures limited our ability to further constrain the model and motivated our simplistic definition of parameters. Second, the analysis was constrained to four topologies; many others are possible but were not considered.

ICA enhances inactivation of hEAG1 channels

The time- and voltage-dependent inhibition of hEAG1 channel currents by ICA could result from either a direct consequence of binding to the central cavity (pore block), or indirectly by enhancing the rate and extent of intrinsic inactivation. Astemizole (García-Ferreiro et al., 2004; Gessner et al., 2004) and clofilium (Gessner et al., 2004) have been described as direct pore blockers of EAG1 channels, whereas the phenylquinazolinone HMJ-53A (Chao et al., 2008) and the natural alkaloid rhynchophylline (Chou et al., 2009) inhibit delayed rectifier K⁺ channels in neuroblastoma N2A cells by enhancing C-type inactivation. We propose that ICA is a gating modifier and not a pore blocker for several reasons. First, the voltage dependence of hEAG1 channel activation does not overlap with the voltage dependence of ICA-induced inhibition, as would be expected for an open state–dependent pore blocker. For ICA, the V_0.5 for inhibition of current was 62 mV more negative than the V_0.5 for current activation. Moreover, as relative channel activation was increased from 20 to 90%, inhibition was only increased from 77 to 79%, inconsistent with open-channel block. In contrast, for two known pore blockers, astemizole (García-Ferreiro et al., 2004) and clofilium (Gessner et al., 2004), we found that the voltage dependence for channel activation and prepulse-dependent inhibition were the same. Second, the rate of current decay (inactivation rate) was only modestly accelerated when [ICA] was increased from 2 to 10 µM, despite a great increase in tonic inhibition (Fig. S10). This finding is in contrast to the dramatic [astemizole]-dependent increased rate of time-dependent block of hEAG1 (García-Ferreiro et al., 2004) channels. Enhanced tonic inhibition caused by higher [ICA] is attributed to the trapping of channels in an absorbing inactivation state. Third, ICA exerts its activator activity in hERG1 by binding to a site outside of the central cavity, specifically to a hydrophobic-binding pocket located between S5 of one subunit and S6 of a neighboring subunit (Garg et al., 2011). Because of the high sequence homology between the pore domains of hEAG1 and hERG1, it is likely that ICA binds to a similar site in both channels. A key residue of the activator-binding site in hERG1 is Phe557; F557L channels were insensitive to ICA (Garg et al., 2011). The homologous mutation in hEAG1 (F359L) also dramatically altered drug action; instead of inhibition, ICA activated F359L hEAG1. This key Phe residue is located in S5 away from the central K⁺ conduction pathway. The side chain of Tyr464 in S6 faces the central cavity. Mutation of the corresponding residue in hERG1 (Y652A) suppresses activity of many known pore blockers, presumably because it is a key component of the binding site for these drugs (Mitcheson et al., 2000; Fernandez et al., 2004). In contrast, the mutation Y464A in hEAG1 enhanced rather than reduced current inhibition by ICA. Collectively, our present and previous findings strongly suggest that ICA does not bind to the central cavity of hEAG1. Instead, we propose that ICA modifies inactivation gating of hEAG1 by binding to the same or similar hydrophobic pocket associated with ICA-mediated suppression of inactivation in hERG1 channels.

Mechanism of intrinsic hEAG1 inactivation and its enhancement by Y464A or ICA

Slow inactivation of WT hEAG1 channels is voltage dependent and results in <10% reduction of current magnitude at positive potentials. It is difficult to ascertain whether the strong inactivation of Y464A hEAG1 channels is simply an exaggerated form of the intrinsic gating described for WT channels or is an additional and distinct mutation-induced form of inactivation. However, it is noted that the voltage dependence and rate of inactivation of Y464A hEAG1 appear superficially similar to the intrinsic gating of Drosophila eag1. Perhaps coincidently, the voltage dependence of inactivation of Y464A hEAG1 is also similar to that induced by 2 µM ICA in WT hEAG1. One difference was that Y464A hEAG1 inactivation included a very rapid component that was most evident when currents were elicited from a V_h of −70 mV or more positive. This fast component was not detectable with ICA-induced inactivation. Nonetheless, similar to ICA-induced inactivation, Y464A hEAG1 inactivation was unaffected (or slightly accelerated) by external TEA or high [K⁺]_e, implying a mechanism(s) different from C-type inactivation.

Y464A hEAG1 was more sensitive to the inhibitory effects of ICA but suppressed the ability of ICA to activate F359L hEAG1 channels. Likewise, the equivalent mutation in hERG1 (Y652A) prevented channel activation by ICA. Together, these findings suggest that this key Tyr residue may be an allosteric mediator of both the activator and the inhibitory effects of ICA on these related channels. The functional importance of Tyr464 can also be inferred from the functional consequences of mutation to residues other than Ala or Phe. Substitution of Tyr with Ser or Val enhanced inactivation but also shifted the voltage dependence to more positive potentials. Substitution with the hydrophobic residues Leu, Ile, or Met generated nonfunctional channels that were nonetheless trafficked normally to cell surface, suggesting the possibility that Y464L/I/M channels are constitutively inactivated. Mutation of the equivalent S6 residue (Phe344) in KCNQ3 channels also dramatically decreased currents while having little or no effect on surface membrane expression of channel proteins (Choveau et al., 2012a). Homology modeling of these and other mutant KCNQ3 channels was used to conclude that specific interactions between the pore helix and S6 can alter the structure of the selectivity filter to either favor or prevent K⁺ conductance (Choveau et al., 2012a,b). Thus, as discussed further below, an interaction between a specific residue in S6 and the pore helix appears to mediate inactivation in KCNQ and other K⁺ channels not directly related to EAG1.

Mutation of the residue equivalent to Tyr464 can affect inactivation gating in other Kv channels. Based on sequence alignments, Tyr464 in hEAG1 is homologous to Phe103 in KcsA, Ile470 in Shaker, and Tyr652 in hERG1 channels. Phe103 in KcsA is proposed to be involved in bidirectional coupling between the activation gate (S6 bundle crossing) and the inactivation gate (selectivity filter) (Cuello et al., 2010a). Mutation of Ile470 in Shaker or Phe103 in KcsA to smaller residues suppresses inactivation (Holmgren et al., 1997; Melishchuk and Armstrong, 2001; Cuello et al., 2010a). In Shaker, substitution of Ile470 with a Tyr induces a complex inactivation with several components that show variable sensitivity to [K⁺]_e and external TEA (Klement et al., 2008), and I470A channels have reduced inactivation (Cuello et al., 2010a). In KcsA, elegant structural studies (Cuello et al., 2010a) have shown that movement of the inner (TM2) helix associated with activation is linked with a tilting of Phe103 toward the pore helix, and via a network of H bonds among Trp67, Glu71, and Asp80 causes inactivation by destabilization of the selectivity filter. However, opposite to the effects of the mutations Y464A in hEAG1 or F344A in KCNQ3 (Choveau et al., 2012a), F103A KcsA has a reduced rate and extent of inactivation compared with WT channels (Cuello et al., 2010a). Finally, in contrast to Shaker, KcsA, KCNQ3, and hEAG1, the equivalent S6 mutation in hERG1 (Y652A) has minimal effect on inactivation gating (Fernandez et al., 2004). Thus, voltage-dependent modulation of the selectivity filter/inactivation gate by an aromatic residue or hydrophobic residue in S6 appears to apply to many, but not all, Kv channels.

The mechanisms of KCNQ1 K⁺ channel inactivation are not well understood, but a functional analysis of site-directed mutant channels and homology modeling approach was used previously to propose a tripartite model of inactivation in these channels. Specific mutations of Leu273 (S5), Val310 (pore helix), or Phe340 (S6) in KCNQ1 were found to greatly enhance intrinsic inactivation as well as alter channel deactivation (Seebohm et al., 2005). V310A and V310G KCNQ1 channels exhibited the most extensive inactivation compared with WT channels, whereas L273F also inactivated substantially, but at a much slower rate than the other two mutant channels. Further study discovered that L273F-induced inactivation differed from inactivation of WT channels, and molecular dynamic simulations suggested that slow inactivation of L273F channels may be caused by selective alteration of the conformation of selectivity filter site s1 (Gibor et al., 2007). Sequence alignment indicates that Val310 and Phe340 in KCNQ1 are equivalent to Leu434 and Tyr464 in hEAG1. Leu273 in KCNQ1 is located two helical turns above the position equivalent to Phe359 in hEAG1; in both channels, these S5 residues make direct contact with the key pore helix residue (i.e., Val310 in KCNQ1 or Leu434 in hEAG1). Thus, in two unrelated Kv channels, hEAG1 and KCNQ1, selectivity filter–mediated inactivation can be manipulated by mutation of three residues located in equivalent or similar positions in the channel subunit.

Summary

Human EAG1 channels inactivate in a slow voltage-dependent manner. The resulting changes in current magnitude are relatively minor and do not have any known physiologically relevant consequences. However, inactivation can be dramatically enhanced by ICA, a drug previously shown to have the opposite activity on hERG1 channels, or by mutation of Tyr464 located in the S6 segment at a position known to be a key determinant of inactivation in several unrelated K⁺ channels.

Our experimental data and homology modeling suggest a minimal tripartite molecular model for hEAG1 inactivation involving interactions between Tyr464 in S6, Leu434 in the pore helix, and Phe359 in S5. Rescue of hEAG1 from Y464A-enhanced inactivation by mutating either Leu434 or Phe359 to smaller residues suggests that Tyr464 normally maintains the selectivity filter in a conformation that favors ion conductance and disfavors inactivation. We propose that interaction between Tyr464 and Phe359 places a “brake” on inactivation by limiting Phe359–Leu434 interaction. Mutation of Phe359 to Ala or Leu alone does not alter inactivation gating, but these mutations can prevent Y464A-enhanced inactivation. Phe359 and Tyr464 are also key determinants of ICA-mediated enhancement of inactivation. When mutated to Leu (F359L), ICA activates hEAG1, whereas it inhibits F359L/Y464A channel currents. Further studies will be required to determine if modulation of inactivation by Y464A and ICA occurs by convergent molecular mechanisms, and whether the molecular model for selectivity filter–mediated inactivation of hEAG1 and KCNQ1 is applicable to other Kv channels.