Time course of dynamic range adaptation in the auditory nerve

Abstract

Auditory adaptation to sound-level statistics occurs as early as in the auditory nerve (AN), the first stage of neural auditory processing. In addition to firing rate adaptation characterized by a rate decrement dependent on previous spike activity, AN fibers show dynamic range adaptation, which is characterized by a shift of the rate-level function or dynamic range toward the most frequently occurring levels in a dynamic stimulus, thereby improving the precision of coding of the most common sound levels (Wen B, Wang GI, Dean I, Delgutte B. J Neurosci 29: 13797–13808, 2009). We investigated the time course of dynamic range adaptation by recording from AN fibers with a stimulus in which the sound levels periodically switch from one nonuniform level distribution to another (Dean I, Robinson BL, Harper NS, McAlpine D. J Neurosci 28: 6430–6438, 2008). Dynamic range adaptation occurred rapidly, but its exact time course was difficult to determine directly from the data because of the concomitant firing rate adaptation. To characterize the time course of dynamic range adaptation without the confound of firing rate adaptation, we developed a phenomenological “dual adaptation” model that accounts for both forms of AN adaptation. When fitted to the data, the model predicts that dynamic range adaptation occurs as rapidly as firing rate adaptation, over 100–400 ms, and the time constants of the two forms of adaptation are correlated. These findings suggest that adaptive processing in the auditory periphery in response to changes in mean sound level occurs rapidly enough to have significant impact on the coding of natural sounds.

a nearly ubiquitous mechanism across sensory systems for efficient stimulus coding in the face of fast changes in the environment is to dynamically adjust the coding strategy to changes in the stimuli. Sensory neurons adapt to changes in stimulus magnitude by varying their response properties on multiple time scales. For example, retinal ganglion cells adapt to changes in luminance over 100 ms to seconds and minutes (Yeh et al. 1996). In auditory nerve (AN) fibers, rapid, short-term, and long-term adaptation to a change in sound level occurs over a few milliseconds to seconds (Chimento and Schreiner 1991; Javel 1996; Kiang et al. 1965; Smith and Zwislocki 1975; Westerman and Smith 1984). Sensory systems also adapt to changes in a statistical property (such as mean or variance) of a dynamic stimulus by varying the input-output relation as well as the response strength (Wark et al. 2007). Such “statistical” adaptation has been observed in visual (Baccus and Meister 2002; Brenner et al. 2000; Fairhall et al. 2001), auditory (Dean et al. 2005; Nagel and Doupe 2006; Watkins and Barbour 2008; Wen et al. 2009), and somatosensory systems (Garcia-Lazaro et al. 2007; Maravall et al. 2007). How rapidly the adaptation occurs provides important indications on how sensory systems maintain efficient coding when the natural environment changes.

Dynamic range adaptation to the mean level of dynamic sound stimuli has been reported in the AN (Wen et al. 2009), the auditory midbrain (Dean et al. 2005), and the primary auditory cortex (Watkins and Barbour 2008). This form of adaptation, characterized by a shift in the operating point of a neuron's dynamic range, is distinct from classic firing rate adaptation, which is characterized by a decrement in firing rate in response to sustained stimuli (Wen et al. 2009). The time course of dynamic range adaptation must be rapid enough to keep up with changes in the acoustic environment to be functionally relevant. Dynamic range adaptation to the mean sound level in the inferior colliculus (IC) occurs rapidly, over a fraction of a second (Dean et al. 2008). We hypothesized that such adaptation occurs as rapidly in the AN as in the IC, if not more rapidly. Studying the time course of dynamic range adaptation in the AN is of particular interest because the underlying mechanisms are likely to be relatively simple at this most peripheral stage in the auditory pathway.

The goal of this work was to characterize the time course of dynamic range adaptation to changes in the mean sound level in the AN. We recorded from AN fibers in anesthetized cats, using stimuli in which sound levels were alternatively drawn from two probability distributions differing in their means (Baccus and Meister 2002; Dean et al. 2008; Fairhall et al. 2001; Kvale and Schreiner 2004; Nagel and Doupe 2006; Nouvian et al. 2006; Smirnakis et al. 1997). We further developed a phenomenological model that accounts for both forms of AN adaptation and used the model to accurately characterize the time course of dynamic range adaptation. Our model-assisted analysis shows that dynamic range adaptation is as rapid as firing rate adaptation, occurring in just a few hundreds of milliseconds.

METHODS

Neurophysiology

Methods for recording from single AN fibers in anesthetized cats were essentially the same as described by Kiang et al. (1965) and Wen et al. (2009) and were approved by the Animal Care and Use Committees of both the Massachusetts Eye and Ear Infirmary and the Massachusetts Institute of Technology. Cats were anesthetized with Nembutal (37.5 mg/kg) and urethane (100 mg/kg), with supplementary doses given as needed to maintain an areflexic state. The AN was exposed by removing the posterior portion of the skull and then retracting the cerebellum. The tympanic bullae and the middle ear cavities were opened to expose the round window. Throughout the experiment, the cat was given injections of dexamethasone (0.26 mg/kg) to alleviate brain swelling and Ringer solution (50 ml/d) to prevent dehydration. To assess cochlear function, a silver electrode was positioned near the round window to record the AN compound action potential (CAP) in response to click stimuli. Recordings were discontinued when the CAP threshold increased by more than 10 dB over the course of an experiment.

Experiments were carried out in an electrically shielded soundproof chamber. Sound was delivered to the cat's ear monaurally through a closed acoustic assembly driven by an electrodynamic speaker (Realistic 40-1377). The acoustic system was calibrated to allow accurate control over the sound pressure level at the tympanic membrane. Stimuli were generated by a 24-bit digital-to-analog converter (NI 4461) using sampling rates of either 50 or 100 kHz. Noise stimuli were digitally filtered to equalize the transfer characteristics of the acoustic system.

Spike activity was recorded with glass micropipettes filled with 2 M KCl. The electrode was inserted into the nerve and mechanically advanced using a micropositioner (Kopf 650). The electrode signal was bandpass filtered (300–3,000 Hz) and fed to a software spike detector triggering on level crossings. The spike times were recorded and saved to disk for subsequent analysis.

A click stimulus at ∼55 dB SPL was used to search for single units. Upon contact with a fiber, a frequency tuning curve was measured by an automatic tracking algorithm (Kiang et al. 1970) using 50-ms tone bursts, and the characteristic frequency (CF) was determined. The fiber's spontaneous firing rate (SR) was measured over an interval of 20 s. AN fiber responses to broadband noise were then studied as a function of stimulus level using the paradigms described below. The broadband noise was a burst of exactly reproducible Gaussian noise with bandwidth of either 25 or 50 kHz depending on the sampling rate; the same noise token was used in all neurons and all experiments. All noise bursts were 50 ms in duration, including 2-ms rise-fall times.

Stimulation Paradigms

The dynamic stimuli previously used for studying dynamic range adaptation in the IC (Dean et al. 2005), primary auditory cortex (Watkins and Barbour 2008), and AN (Wen et al. 2009) contained a high-probability region (HPR) in their stimulus level distribution. In this paradigm, the level of a continuously presented stimulus (pure tone or broadband noise) is drawn at random every 50 ms from a probability distribution containing an HPR (see Fig. 1 in Wen et al. 2009). Levels within the HPR have an 80% overall probability of occurrence, whereas levels outside the HPR have an overall probability of 20%. This “constant-HPR paradigm” was applied in 10 AN fibers using a broadband noise carrier for comparison with results obtained by applying the “switching-HPR paradigm,” described next.

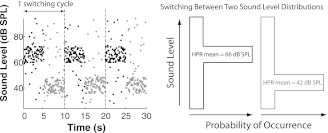
Fig. 1.

Switching-high-probability-region (HPR) stimuli. A 30-s portion of the switching-HPR stimuli comprising 3 switching cycles (left) is shown in which each dot represents a 50-ms broadband noise burst; in the first half (black dots) of each switching cycle, the sound levels of the stimulus are drawn randomly from a nonuniform level distribution (right) with the HPR centered at 1 level (66 dB SPL), whereas in the second half (gray dots), the HPR is centered at a different level (42 dB SPL). Typically, a total of 60 switching cycles, lasting 10 min, were used for measuring the time course of auditory nerve (AN) adaptation.

To study the time course of dynamic range adaptation in the AN, we used a stimulus paradigm described by Dean et al. (2008), referred to as “switching-HPR stimuli,” in which the HPR mean level alternates or switches between two different values every 5 s (Fig. 1). Such switching paradigms have been widely used in studies of statistical adaptation in sensory systems (Baccus and Meister 2002; Dean et al. 2008; Fairhall et al. 2001; Kvale and Schreiner 2004; Nagel and Doupe 2006; Nouvian et al. 2006; Smirnakis et al. 1997). Whereas our previous work (Wen et al. 2009) used both CF tones and broadband noise with a constant-HPR paradigm, only broadband Gaussian noise was used with the switching-HPR stimuli in the present work. As in the constant-HPR paradigm, each noise burst lasts 50 ms with no interstimulus silent interval. Each switching cycle lasts 10 s and comprises a first half-cycle in which 100 consecutive stimulus levels are drawn at random from a distribution with a high HPR mean level, and a second half-cycle in which 100 stimulus levels are drawn from a level distribution with a lower HPR mean level (24, 36, or 48 dB lower than the higher HPR mean level). For both level distributions, the stimulus level spans the same 66-dB range in 1-dB increments, and the overall probability for the levels within the 12-dB-wide HPR is 82% (slightly larger than the 80% probability used by Wen et al. 2009). Thus, for every three switching cycles, each level outside the HPR is presented exactly once while each HPR level is presented 20 times. Typically, a switching-HPR run consisted of 60 switching cycles and lasted for 10 min. In some fibers, we measured responses to two or more switching-HPR stimuli with different HPR mean levels.

We also measured the rate-level functions (RLFs) of AN fibers in conditions designed to minimize adaptation, the “baseline” paradigm (Dean et al. 2005; Wen et al. 2009). The sound levels of broadband noise bursts were randomly drawn from a uniform distribution spanning 75 dB in 1-dB increments. Each noise burst lasted 50 ms, with a 250-ms silent interval between successive stimuli. Typically, 10 trials were presented at each level to obtain a baseline RLF, which was used primarily to specify the saturating nonlinearity in the AN adaptation model (see Fig. 5).

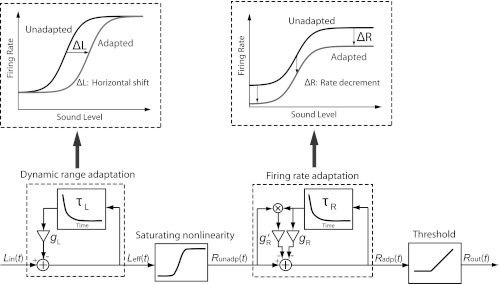
Fig. 5.

Schematic of the dual-adaptation model. The model comprises 2 adaptation modules: dynamic range adaptation and firing rate adaptation. The input to the model, L_in(t), is a time sequence of sound levels of switching-HPR stimuli (re. Fig. 1). The output of the dynamic range adaptation module is the effective level, L_eff(t), which is the difference between the original level's L_in(t) and a linearly filtered version (with time constant τ_L and gain g_L) of L_eff(t). As illustrated in the top left block, dynamic range adaptation produces a pure horizontal shift (ΔL) of the RLF. The saturating nonlinearity module, taking the form of the baseline RLF and sandwiched between the 2 adaptation modules, converts the effective levels, L_eff(t), to unadapted firing rates, R_unadp(t). The output of the firing rate adaptation module is the adapted firing rates, R_adp(t), calculated as the difference between R_unadp(t) and a linearly filtered version (with time constant τ_R and gain g_R, g′_R) of R_adp(t). As illustrated in the top right block, firing rate adaptation produces a pure firing rate decrement (ΔR), thus a vertical drop of the RLF. The threshold module half-wave rectifies R_adp(t) and yields the final firing rate output, R_out(t).

Data Analysis

For each 50-ms stimulus epoch in the switching-HPR stimulus, we counted the number of spikes over a window extending from the response latency to the end of the epoch. The latency was estimated for each fiber from peristimulus time histograms averaged across all levels in the baseline paradigm. Specifically, the latency was defined as the first peristimulus time when the firing rate was more than 4 SD over the spontaneous rate (estimated from the silent intervals between stimuli). These spike counts over 50-ms epochs constitute the raw data for all subsequent analyses. These analyses aimed at quantitatively characterizing three features of the responses to switching-HPR stimuli: 1) dynamic range shifts in the steady state, 2) the time course of average firing rate adaptation, and 3) the time course of dynamic range adaptation.

Dynamic range shifts in the steady state.

We first calculated the steady-state RLFs for each of the two level distributions characterizing a switching-HPR stimulus. Only responses from the last 3 s of each half switching cycle were included to ensure these RLFs represent a “steady state.” As in our previous study of dynamic range adaptation in the AN (Wen et al. 2009), steady-state RLFs were fit with the model of Sachs and Abbas (1974) and Winslow and Sachs (1988). The fitted steady-state RLFs were used as a reference to characterize how quickly the RLF shifts after a switch (see below). We also calculated the horizontal shift (in dB) between the midpoints of the normalized steady-state RLFs for the two half switching cycles for comparison with our earlier results using the constant-HPR paradigm (Wen et al. 2009).

Time course of average firing rate adaptation.

We measured the mean firing rate across all switching cycles as a function of time within the cycle to examine the dynamics of firing rate adaptation to the switch in level distribution. An exponential function (with additive baseline) was fit, using the least-squares method, to the time course of the mean firing rate separately for each half switching cycle. The exponential fits were used to compute rate adaptation time constants following both an upward switch in HPR mean level (from a low to a high level) and a downward switch (from a high to a low level).

Time course of dynamic range adaptation.

To characterize the time course of the shift in the operating point of the RLF that characterizes dynamic range adaptation, we only used data from sound levels within the HPR for each half switching cycle, because there were not enough stimulus trials outside the HPR to reliably estimate a complete RLF across the 66-dB range of levels with fine time resolution. The analysis consisted of three steps (see Fig. 4). First, firing rates for each of the 13 HPR levels were binned into successive 300-ms time epochs (i.e., 6 consecutive 50-ms stimulus epochs) to provide averaged rate-level data for each epoch. The outcome was 16 partial RLFs, corresponding to the HPR levels only, for each of the two 5-s half switching cycles at successive time epochs following the switch. Second, each partial RLF was fit by a straight line. The RLF shift (in dB) was approximated by the horizontal distance from the reference (the steady-state RLF preceding the switch) to the fitted line. This horizontal distance was obtained by averaging the horizontal distances between the two end points of each line. Finally, to estimate the time constant of dynamic range adaptation for each half switching cycle, an exponential was fit to the sequence of RLF shifts as a function of time (in 300-ms bins). A limitation of this analysis is that it gave a reasonable characterization of the time course of dynamic range shift only when the HPR was located in the steeply rising part of the RLF. However, we were able to overcome this limitation by using a model-assisted approach, described next.

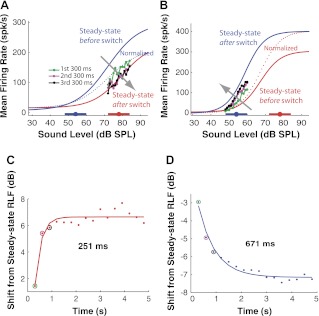
Fig. 4.

Time course of dynamic range shift in the AN. The AN fiber shown in A and C has its CF at 4.9 kHz and its spontaneous firing rate at 25.6 spk/s, whereas the fiber shown in B and D has its CF at 592 Hz and its spontaneous firing rate at 8.7 spk/s. A: evolution of RLFs with time for upward switches with HPR changing from 54 to 78 dB SPL in an AN fiber. Fitted data are represented as follows: blue line, steady-state RLF before the switch; red line, steady-state RLF after the switch; dotted blue line, pre-switch steady-state RLF (blue line) normalized to post-switch steady-state RLF (red line). Raw data are represented as follows: green line/dots, averaged HPR-region RLF for the high HPR levels of the first 300-ms epoch after the switch; magenta line/dots, HPR-region RLF of the second 300-ms after the switch; black line/dots, HPR-region RLF of the third 300-ms epoch. Fitted straight lines to the HPR-region RLF are not shown. Thick horizontal bars with filled circles along the x-axis denote the HPRs and their mean levels, respectively. The gray arrow indicates the direction of RLF evolution with time. B: same as in A but for downward switches from 78 to 54 dB SPL in a different AN fiber. C: horizontal shift of the RLF with time from the normalized steady-state RLF before the switch for consecutive 300-ms epochs for upward switches. Dots represent raw data (color-coded circles designate the results for the first three 300-ms epochs); line is fitted single exponential. The time constant is 251 ms. D: same as C but for the downward switch shown in B in which the shift has a negative sign, indicating the shift direction is opposite that for upward switches. The time constant is 671 ms.

Model

We developed a phenomenological “dual-adaptation” model to account for both forms of adaptation observed in the AN: firing rate adaptation and dynamic range adaptation. Whereas firing rate adaptation is characterized by a firing rate decrement following prior stimulation, dynamic range adaptation refers to the shift of RLF toward the mean sound level of a dynamic stimuli (Wen et al. 2009). The model contains two first-order linear filter modules, each accounting for one form of adaptation, with a saturating nonlinearity sandwiched in between (see Fig. 5). The input to the model, L_in(t), a time sequence of sound levels, is first transformed by the “dynamic range adaptation” module into effective sound levels, L_eff(t), which are then converted to unadapted firing rates, R_unadp(t), by the saturating nonlinearity (determined from the measured baseline RLF). R_unadp(t) is transformed to adapted rates, R_adp(t), via the “firing rate adaptation” module, and the output is finally half-wave rectified by the “threshold” module to prevent negative firing rates.

The dynamic range adaptation module computes the effective sound level, L_eff, using the recursive equation:

$$L_{\text{eff}}\left(t\right)=L_{\text{in}}\left(t\right)-g_{\text{L}}L{\prime }_{\text{eff}}\left(t\right)*h_{{\tau }_L}\left(t\right),$$ (1)

in which h_τL represents an exponential function with time constant τ_L, g_L is a constant gain, the asterisk indicates convolution, and L′_eff(t) = L_eff(t) − L₀ when L_eff(t) > L₀, or 0 otherwise. L₀ sets the threshold level at which the adaptation starts to operate.

The firing rate adaptation module computes the adapted firing rate, R_adp(t), as follows:

$$R_{\text{adp}}\left(t\right)=R_{\text{unadp}}\left(t\right)-g_{\text{R}}{R}_{\text{adp}}\left(t\right)*h_{{\tau }_{\text{R}}}\left(t\right)-g{\prime }_{\text{R}}{R}_{\text{unadp}}\left(t\right)\left[R_{\text{adp}}\left(t\right)*h_{{\tau }_{\text{R}}}\left(t\right)\right],$$ (2)

in which h_τR(t) represents an exponential function with time constant τ_R, and g_R and g′_R are constant gains. On the right-hand side of Eq. 2, the third term represents a firing rate-dependent feedback term, which accounts for the observation that the firing rates at low sound levels usually are reduced to zero due to adaptation while there is still room for the firing rates at high levels to decrease (Wen et al. 2009). In other words, firing rate adaptation does not show the same strength in AN fibers for low vs. high levels, and this effect is accounted for by this additional term. In all, the model has six free parameters: τ_L, g_L, L₀, τ_R, g_R, and g′_R. The model's saturating nonlinearity is completely specified by a least-squares fit to the baseline RLF using the Sachs and Abbas (1974) model and therefore introduces no additional free parameter.

We used a maximum likelihood approach to fit the dual-adaptation model to the sequence of AN firing rates in response to switching-HPR stimuli. Because the AN spike counts are approximately Poisson-distributed while the model (which is deterministic) only predicts the expected value of the spike count for each epoch, the maximum likelihood method, rather than the least-squares method, was chosen for model fitting because it takes into account the stochastic nature of the AN neural data. To this end, we computed the joint likelihood, LH_D|M, of the observed spike counts in each of the 50-ms epochs given the model parameters and found the parameter set that maximized the likelihood using the Matlab function “fminsearch.” To assess the goodness-of-fit of the model, we also computed the likelihood, LH_P|M, of a synthetic Poisson-distributed spike count sequence generated by the best-fitting model concatenated with a Poisson spike generator using the same stimulus as in the recording. Specifically, for each 50-ms stimulus epoch, a Poisson random variable was generated for the spike count using the expected value of the firing rate specified by the model. (A Poisson distribution is completely specified by its mean.) LH_P|M represents the maximum possible likelihood given the noise introduced by the Poisson-distributed spike events in AN fibers. We then computed the relative difference in log-likelihood between LH_P|M and LH_D|M, expressed as a percentage of LH_P|M, and required this relative likelihood difference to be less than 25% for the model fit to the data to be acceptable. Although somewhat arbitrary, this 25% difference criterion appeared to correspond to an acceptably good fit between the data and the model firing rates, whereas model fits with more than 25% likelihood difference showed obvious deviations from the data. Among the 46 AN recordings from which we measured both a baseline RLF and responses to switching-HPR stimuli, the model fit met this goodness-of-fit criterion in 40 recordings (87%).

RESULTS

We measured rate responses to switching-HPR broadband-noise stimuli from 30 AN fibers (51 measurements) in 8 cats with CFs ranging from 500 Hz to 20 kHz. From the firing rate data, we measured the time constants of average firing rate adaptation and, when possible, also characterized the time course of dynamic range adaptation. Because the estimated time constants of dynamic range adaptation were biased by limitations in the data, we developed a phenomenological model that captures both forms of AN adaptation and used the model to improve the time constant estimates.

Steady-State Dynamic Range Shifts

Figure 2 shows the normalized steady-state RLFs for an example AN fiber in response to switching-HPR stimuli with HPRs centered at 66 and 42 dB SPL (A) and at 78 and 54 dB SPL (B). These steady-state RLFs were obtained by taking the rates for each level occurring during the last 3 s of each half switching cycle and averaging across all switching cycles. To measure the amount of dynamic range adaptation long after a switch occurs, we normalized each steady-state RLF by its minimum and maximum so that rates range between 0 and 100%, and calculated the horizontal shift of the midpoint level, L₅₀, of the normalized RLFs (Wen et al. 2009). For this fiber, the RLF shifts by 5.6 dB when the mean HPR level switches between 66 and 42 dB SPL (Fig. 2A), resulting in a normalized shift (defined as the horizontal shift divided by the difference between the HPR mean levels) of 0.25 dB/dB. The shift is 6.1 dB for the HPR switching between 78 and 54 dB SPL (Fig. 2B), corresponding to a normalized shift of 0.30 dB/dB. Thus the normalized shifts for both switching-HPR pairs are similar, consistent with our previous finding with constant-HPR stimuli that L₅₀ increases nearly linearly with HPR mean level (Wen et al. 2009).

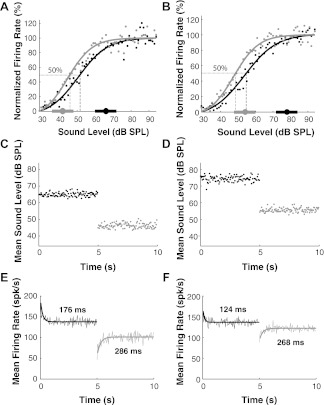
Fig. 2.

An AN fiber's firing rate responses to switching-HPR stimuli. A: normalized rate-level functions (RLFs) obtained from steady-state rate responses (the responses in the last 3 s of each half switching cycle) to the stimuli shown in C. The dynamic range shift (L₅₀ shift, the horizontal span between the dashed gray and black lines) is 5.6 dB. B: same as A but in response to the stimuli shown in D. The dynamic range shift is 6.1 dB. C: time course of the averaged sound levels across all 60 switching cycles, with the HPR mean level switching between 66 and 42 dB SPL. D: same as C but with the HPR mean switching between 78 and 45 dB SPL. E: averaged firing rate across all the switching cycles with time in response to the stimuli shown in C. F: averaged firing rate across all the switching cycles with time in response to the stimuli shown in D. This AN fiber's characteristic frequency (CF) is 841 Hz, and its spontaneous firing rate is 61 spikes/s (spk/s).

We tested whether the steady-state dynamic range shifts measured with switching-HPR stimuli are similar to those measured using constant-HPR stimuli to verify that a steady state was indeed reached 2 s after a switch. For all the 51 switching-HPR measurements, the median normalized shift was 0.25 dB/dB, which does not significantly differ from the 0.24 dB/dB median for the 27 constant-HPR measurements made with noise stimuli in the study by Wen et al. (2009) (Wilcoxon rank sum test, P = 0.70). In addition, we directly compared the dynamic range shifts in 10 fibers that were studied with both constant-HPR and switching-HPR stimuli. The comparison was made for the two HPR values for which the most data were available: 66 vs. 42 dB SPL. For these 10 AN fibers, the mean normalized shift was 0.24 dB/dB for constant-HPR stimuli compared with 0.26 dB/dB for switching-HPR stimuli; these values are not significantly different (paired t-test, P = 0.49). More importantly, the mean normalized shifts for the two types of stimuli were strongly correlated (r = 0.72, P = 0.019). Thus AN fibers appear to exhibit similar dynamic range shifts in response to constant-HPR and switching-HPR stimuli, confirming that dynamic range adaptation has reached a steady state 2 s after a switch.

Time Course of Average Firing Rate Adaptation

We expect that switching-HPR stimuli elicit both firing rate adaptation and dynamic range adaptation following each switch. Figure 2C shows the mean stimulus level averaged across all 60 cycles as a function of time within a switching cycle when the level distribution switches between a high HPR centered at 66 dB SPL and a low HPR centered at 42 dB SPL. Figure 2D shows the mean sound levels for HPR mean levels switching between 78 and 54 dB SPL. Even though the level distributions always span 66 dB, the mean levels in each half-cycle only fluctuate by about ±3 dB around the center of the HPR as a result of the averaging across switching cycles.

Figure 2, E and F, shows the time course of an AN fiber's firing rates for each 50-ms epoch averaged across all 60 switching cycles in response to the stimuli whose mean levels are shown in C and D, respectively. The time course of the mean firing rate is well fit by an exponential function for each half-cycle. In Fig. 2E, the time constant of the exponential is 176 ms for the HPR mean level switching upward from 42 to 66 dB SPL, which is shorter than the 286-ms time constant for switching downward. Similarly, in Fig. 2F, the time constant is 124 ms when switching upward from 54 to 78 dB SPL, which is shorter than 268 ms for the downward switch.

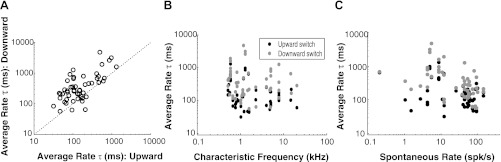
Figure 3A shows scatter plots of the time constants of average rate adaptation for upward against downward switches across 51 measurements from 30 fibers made with 4 different switching pairs (i.e., 66 vs. 42, 78 vs. 54, 78 vs. 42, and 78 vs. 30 dB SPL). In general, the time constants measured from the same fiber with different switching-HPR stimuli were similar (not shown), so all the time constants were grouped together for analysis. Although the time constants for upward and downward switches are correlated (r = 0.65, P < 0.001), the median time constant for upward switches is 131 ms, about one-half the 272-ms median time constant for downward switches (Wilcoxon rank sum test, P < 0.001). This adaptation asymmetry is also observed in the time course of AN short-term adaptation after a step increase in intensity of a short tone stimulus (Harris and Dallos 1979; Young and Sachs 1973) and in other sensory modalities including retinal ganglion cells (Hosoya et al. 2005; Smirnakis et al. 1997). The time constants of firing rate adaptation in Fig. 3A are longer than those typically reported for AN short-term adaptation (Chimento and Schreiner 1991; Harris and Dallos 1979; Westerman and Smith 1984). However, the 50-ms resolution of our analysis precluded detecting forms of adaptation occurring on very short time scales.

Fig. 3.

Characteristics of firing rate adaptation to switching-HPR stimuli for AN fiber population. A: time constants (τ) of average firing rate for upward and downward switches. Medians and 25–75% quartiles are 131 and 74–246 ms, respectively, for upward switches and 272 and 170–670 ms, respectively, for downward switches. Dotted line indicates identity (y = x). B: time constants do not show significant dependence on CF (P = 0.10 for upward switches and P = 0.42 for downward switches). C: time constants show a decreasing trend with spontaneous rate (r = −0.38, P = 0.006 for upward switches; r = −0.39, P = 0.004 for downward switches).

There is considerable variability in the time constants for both switching directions. Figure 3B shows that the time constants for both switching directions do not significantly depend on CF (upward: r = −0.23, P = 0.10; downward: r = −0.11, P = 0.42). However, the time constants do show a significant decreasing trend with increasing SRs (r = −0.38, P = 0.006 for upward switches; r = −0.39, P = 0.004 for downward switches) (Fig. 3C). This weak trend still leaves most of the variability in time constants unexplained. Although our sample contained only two data points with SRs below 1 spike/s (due to difficulties in maintaining contact between these fibers and the electrode over long periods of time), the AN fiber sample in our previous study (Wen et al. 2009) did contain a larger number of low-SR fibers, and dynamic range adaptation in these fibers was qualitatively similar to that observed in high-SR and medium-SR fibers.

Because 80% of the sound levels of an HPR stimulus are concentrated within a 12-dB narrow range, the switching-HPR stimulus resembles a noise stimulus in which the level switches between two constant values corresponding to the midpoints of each HPR (Fig. 2, C and D). We asked whether the time courses of firing rate adaptation in response to switching-HPR and switching-constant-level stimuli are also similar. We recorded the responses to constant-level switching stimuli in which the two levels matched the HPR mean levels of switching-HPR stimuli in 11 AN fibers and measured the time constants for the average rate across switching cycles. For both switching directions, the mean time constants for the two stimuli were not significantly different (2-sample t-tests: P = 0.29 for upward switches and P = 0.52 for downward switches). This similarity in rate time constants for the two stimuli suggests that the mean sound levels, rather than stimulus level dynamics, are the primary determinants of the time course of average rate adaptation in AN fibers.

Time Course of Dynamic Range Adaptation

The method illustrated in Fig. 2, E and F, for estimating the time constants of adaptation to switching-HPR stimuli confounds two phenomena: firing rate adaptation, which is characterized by a decrement in maximum rate with increasing HPR mean level, and dynamic range adaptation, manifested by a horizontal shift of RLF toward the HPR (Wen et al. 2009). To isolate dynamic range adaptation from firing rate adaptation, we would need to track the horizontal shift in normalized RLF at fine time steps over the time course of a switching cycle. Doing so proved difficult because too few stimulus trials were available at each stimulus level outside of the HPR for reliably estimating the RLF at each 50-ms time epoch of a switching cycle. We nevertheless could estimate the time course of RLF shifts for some measurements by imposing two restrictions (see methods): 1) we only used levels within the HPR, and 2) the HPR had to be located within the steeply rising portion of the RLF so that the shift would be well defined. Moreover, we combined data over 300-ms time epochs to have enough repeats to construct the RLFs within the HPR.

Figure 4 illustrates this analysis for two AN fibers using switching-HPR stimuli with HPRs centered at 78 and 54 dB SPL. The two solid lines in Fig. 4A show the model fits to the steady-state RLFs computed over the last 3 s of each half switching cycle (similar to Fig. 2, A and B, but not normalized) for one fiber. Because the 78-dB HPR, but not the 54-dB HPR, is located near the steeply rising part of the RLF, we investigated the time course of the RLF shift after the upward switch from 54 to 78 dB SPL. The pre-switch steady-state RLF (solid blue line in Fig. 4A) was used as a reference for measuring the time course of dynamic range shift after the switch. To minimize the effect of firing rate adaptation on the shift measurement, we scaled the pre-switch steady-state RLF so that it would have the same maximum and minimum rates as the post-switch steady-state RLF (solid red line in Fig. 4A), resulting in a rescaled reference RLF (dotted blue line). The HPR portions of the RLFs for the first three 300-ms time epochs following the upward switch are shown in Fig. 4A (data points connected by lines in green, magenta, and black, respectively). These partial RLFs could not be normalized because there were not enough stimulus repeats outside of the HPR to reliably estimate the minimum and maximum firing rates necessary for normalization. The partial RLF for the first 300-ms epoch after the switch (green) has already shifted substantially. By the second 300-ms epoch (magenta), the shift is nearly complete and the RLF begins to overlap with the post-switch (78 dB SPL) steady-state RLF. We used straight lines to fit the HPR portion of the RLF for each of the 16 300-ms epochs within a 5-s half switching cycle. Figure 4C shows the horizontal shift of each fitted line from the pre-switch steady-state RLF as a function of time after the switch. The shift increases monotonically to reach an asymptote at 6.3 dB and is well fit by an exponential with a time constant of 251 ms.

Figure 4, B and D, shows the time course of the shift in the HPR region of the RLF for another fiber. In this case, because the 60-dB HPR was located close to the steeply rising portion of the RLFs, we analyzed the time course of dynamic range adaptation for the downward switch from 78 to 54 dB SPL. Again, most of the dynamic range shift was complete by the second 300-ms epoch (Fig. 4B), and the time course of the shift was well fit by an exponential with a time constant of 671 ms (Fig. 4D).

Across our AN fiber sample, we were able to estimate shift time constants for 13 upward switches and 24 downward switches in which the HPR was located in the steeply rising part of the RLF. The shift time constants ranged from 130 ms to >1,000 ms with a median of 370 ms for upward switches and 605 ms for downward switches. The median shift time constant was significantly smaller for upward switches than for downward switches (Wilcoxon rank sum test, P = 0.018). This adaptation asymmetry also held for the six fibers in which we could estimate shift time constants for both upward and downward switches.

The above analysis shows that dynamic range adaptation occurs in under a second, but it has a number of limitations. First, it only characterizes dynamic range shifts in the HPR region of the RLF and is only applicable to cases (fewer than 50%) when the HPR lies in the steeply rising part of the RLF. Second, the temporal resolution of the analysis (300 ms) is coarser than that of the stimulus (50 ms), which could lead to an overestimation of the adaptation time constant. Third, although the analysis uses the normalized steady-state RLF before the switch as a reference for measuring dynamic range shifts, the HPR portions of the RLFs could not be normalized because there were not enough data outside of the HPR to reliably estimate the minimum and maximum firing rates that are necessary for normalization. This lack of normalization means that estimated time constants of dynamic range adaptation are confounded by co-occurring firing rate adaptation. In the following sections, we describe a model-assisted analysis that largely overcomes these limitations by making more efficient use of the data.

The Dual-Adaptation Model Captures Both Forms of AN Adaptation

We developed a phenomenological dual-adaptation model (Fig. 5) that captures both forms of AN adaptation to changes in mean sound level (see methods). The model consists of a cascade of two adaptation modules producing dynamic range adaptation and firing rate adaptation, respectively, with a saturating nonlinearity sandwiched in between that determines the RLF shape.

For each measurement with switching-HPR stimuli, we used the maximum likelihood method to fit the model to the entire sequence of raw firing rates (converted to spike counts) for each of the 12,000 50-ms time epochs (from a total of 60 switching cycles). Assuming a Poisson distribution of spike counts for each 50-ms epoch, we searched for the set of model parameters that maximized the joint likelihood of the neural spike counts given the model. The model was fit to 46 AN recordings for which we measured both the baseline RLF and responses to switching-HPR stimuli.

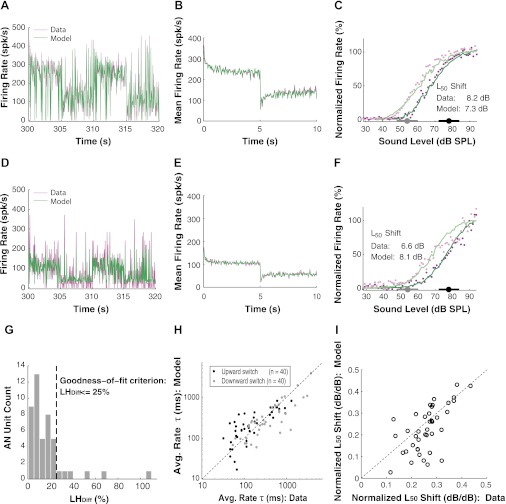
Figure 6A shows an example model fit to a 20-s segment of the measured raw firing rates for an AN fiber in response to a stimulus switching between HPR mean levels of 54 and 78 dB SPL. Qualitatively, there is an adequate agreement between the model and the neural data. Because the model is deterministic, the fluctuations in the model response reflect the changes in stimulus level occurring every 50 ms and the dynamics of the adaptation modules in the model. The AN fiber response also reflects variations in stimulus level and adaptation dynamics, as for the model, but in addition shows Poisson-like variability inherent to neural firings, which is not represented in the model. Therefore, a close match between the model responses and the single-trial AN fiber responses (e.g., in Fig. 6, A and D) should not be expected, because this amounts to comparing the mean of a random variable with a particular realization of this random variable. For this reason, we used a likelihood approach rather than conventional least squares to quantitatively assess the goodness of fit of the model to the data. Specifically, we computed the log-likelihood, LH_P|M, of an artificial spike count sequence generated by the best-fitting model with a Poisson generator and compared LH_P|M with the log-likelihood of the measured spike count sequence given the same model. LH_P|M represents the likelihood that would be obtained for Poisson spike counts if the model were exact and therefore constitutes an upper bound on the likelihood of the data. The percentage difference in log-likelihood, LH_Diff, between the actual and artificial spike count sequences was used to assess whether the model fit is reasonable considering the Poisson-like randomness of the spike counts. LH_Diff for the fiber in Fig. 6A is 5.6%, well within our 25% goodness-of-fit criterion (see methods).

Fig. 6.

Fit of the dual-adaptation model to AN fibers' responses to switching-HPR stimuli. Typical switching-HPR stimuli contained 60 switching cycles and lasted 600 s. A: an AN fiber's rate responses during a 20-s epoch (from 300 to 320 s) of the stimuli. This fiber is the same as that shown in Fig. 4, B and D. LH_Diff, the percentage difference in log-likelihood, is 5.6% for this fiber, indicating a good fit. B: the time course of the average firing rates across all 60 cycles in the model matches closely to that of the data. An exponential was fit to the responses of each half switching cycle for extracting the time constants of average rate (fitted lines not shown). C: the steady-state RLFs predicted by the model (lines) compared with those in the AN recordings (dots). For both data and model, lighter colors correspond to lower HPR and darker colors to higher HPR. The L₅₀ shift between the 2 RLFs for both the model and the data are provided. D–F: same content as A–C, respectively, but for another AN fiber. This fiber is the same as that shown in Fig. 4, A and C. G: histogram of LH_Diff for 46 AN recordings, of which the model fit meets the goodness-of-fit criterion for 40 recordings (i.e., LH_Diff ≤ 25%). H: average rate time constants predicted by the model are close to those estimated from neural data for our AN fiber population. I: the normalized L₅₀ shifts in the model are comparable with those in the data.

Figure 6B compares average firing rates for the model and the data across all 60 switching cycles for each 50-ms epoch. The model trace matches the data trace closely. As in the analysis of the neural data, an exponential was fit to the time course of model average firing rates for each half switching cycle to obtain the time constants of firing rate adaptation. Figure 6C shows the steady-state RLFs obtained from the last 3 s of each half switching cycle for both the model and the data. The L₅₀ shift in RLFs is 7.3 dB for the model, comparable to the 8.2-dB shift for the data. Thus, for this measurement, the model provides an adequate fit to both dynamic (average rate adaptation) and static (steady-state RLF) aspects of the neural data.

Figure 6, D–F, shows another example of a model fit for responses to HPR stimuli switching between 54 and 78 dB SPL. In this case, the fluctuations in the single-trial responses in Fig. 6D are much more pronounced for the data than for the model, consistent with the additional Poisson-like stochastic variability present in the data but not in the model response. This stochastic variability is more apparent in Fig. 6D than in Fig. 6A, probably because the firing rates tend to be lower in Fig. 6D, resulting in a greater coefficient of variation for a Poisson-distributed variable. The more pronounced fluctuations in Fig. 6D are reflected in LH_Diff, which was 22.6% in this case, just within our 25% goodness-of-fit criterion. Nevertheless, the time course of average firing rates across switching cycles was well fit by the model (Fig. 6E). Although the model adequately fits the steady-state RLF for the HPR centered at 78 dB SPL, it fails to capture the shape of the steady-state RLF at high levels for the HPR centered at 54 dB SPL (Fig. 6F). The L₅₀ shift of the steady-state RLFs is 8.1 dB in the model, which is slightly greater than the 6.6-dB shift in the data. The substantial difference in steady-state RLFs between the model and the data is consistent with the relatively large LH_Diff.

The distribution of LH_Diff for the model fits to all of the 46 AN measurements is shown in Fig. 6G. Only six measurements had a likelihood difference greater than 25%; in most of these cases, the poor fit may have resulted in part from relatively low spike counts (maximum firing rates below 100 spike/s). The goodness of fit for the 40 AN recordings that meet the 25% criterion is consistent with group comparisons of average rate time constants (Fig. 6H) and normalized L₅₀ shifts (Fig. 6I) between the model and the data. Across the population, the model-derived average rate time constants are strongly correlated with the time constants directly estimated from the data for both upward switches (r = 0.81, P < 0.001) and downward switches (r = 0.83, P < 0.001). Moreover, the median average rate time constants for downward switches do not significantly differ between the model (245 ms) and the data (294 ms) (Wilcoxon rank sum test, P = 0.31). This also holds for downward switches: model (207 ms) and data (113 ms) (Wilcoxon rank sum test, P = 0.13). Although this difference by a factor of two in median downward switch time constants may appear large, it is small compared with the nearly two orders of magnitude range of time constants in the data (Figs. 3A and 6H). Although for some AN fibers the normalized shifts in steady-state RLFs for the model response are smaller than the shifts in the neural data (Fig. 6I), these two shifts are well correlated across the AN fiber population (r = 0.64, P < 0.001). Also, the median normalized shift for the model (0.22 dB/dB) does not significantly differ from the median shift for the data (0.26 dB/dB) (Wilcoxon rank sum test, P = 0.12). Overall, these quantitative comparisons support the adequacy of the model in accounting for the adaptive responses of AN fibers to changes in mean sound level.

Model-Assisted Estimates of Dynamic Range Adaptation Time Constants

We used the dual-adaptation model to improve our estimates of the time course of dynamic range adaptation. Unlike the AN neural recordings, model simulations are virtually not constrained by the stimulus duration. For each of the 40 well-fit measurements, we drove the best-fitting model with a switching-HPR stimulus consisting of 4,320 cycles (12 h of stimulation), 72 times the number of cycles used in our AN experiments. The large number of switching cycles provided sufficient repeats even for sound levels outside the HPR to obtain complete RLFs with fine time resolution within a switching cycle. Importantly, the model-generated RLFs have well-defined baseline and saturation regions, allowing us normalize the RLFs to eliminate the confound of firing rate adaptation from estimates of dynamic range shifts.

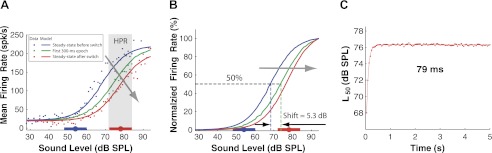
We first show that the dynamic range shifts measured from complete RLFs generated by the model can substantially differ from shifts estimated by the horizontal distance between the nonnormalized HPR portions of the RLFs in the AN data. Figure 7 shows an example for upward switches from 54 to 78 dB SPL for the same fiber as in Fig. 4, A and C. Although the model responses (solid lines) closely match the AN data (points) (Fig. 7A), the calculated RLF shift from the normalized pre-switch steady-state RLF to the first 300-ms epoch post-switch is 5.3 dB for the model (measured as the L₅₀ shift between normalized RLFs; Fig. 7B) compared with only 1.4 dB in the data (measured as the horizontal distance between the nonnormalized HPR-region RLF and the pre-switch steady-state RLF; Fig. 4, A and C). The discrepancy in the shift estimates is due to the lack of RLF normalization in the AN data imposed by the small number of stimulus repeats in the baseline and saturation regions of the RLF, which lie outside the HPR. By using normalization to eliminate the confound of firing rate adaptation, the model allows us to estimate the time course of dynamic range adaptation more accurately than is possible directly from the neural data.

Fig. 7.

The dual-adaptation AN model predicts the shift time constants with less bias. This fiber is the same as that shown in Fig. 4, A and C. A: evolution of RLFs with time for upward switches from 54 to 78 dB SPL. RLFs of the steady state before (blue) and after (red) the switch and of the first 300-ms epoch (six 50-ms epochs combined) after the switch (green) are plotted for both AN neural data (dots) and the model (lines). The model was first fitted to the fiber's responses to the switching-HPR stimuli, containing 60 switching cycles, and then run for 4,320 switching cycles to allow for extracting the time course of dynamic range adaptation. The gray arrow indicates the direction of the RLF evolution with time. B: normalized model RLFs for the steady state before the switch and the first 300-ms epoch (six 50-ms epochs combined). The RLF shift between the first 300-ms epoch and the pre-switch steady-state RLF is 5.3 dB when calculated from the model responses (measured as the L₅₀ shift between the 2 corresponding complete normalized RLFs) compared with 1.4 dB when directly estimated from the AN data (measured as the horizontal distance between the HPR-region RLFs of the first 300-ms epoch and the steady-state RLF). The gray arrow indicates the direction of the RLF shift with time. C: predicted time course of dynamic range adaptation in the model at time steps of 50 ms. Time course of dynamic range adaptation is characterized by the shift of the L₅₀ of the RLF for each consecutive 50-ms epoch. The time constant of 79 ms, extracted from the fitted exponential curve, is about one-third of the 251 ms directly estimated from neural data (see Fig. 4C).

We used model responses to characterize the time course of the dynamic range shift after a switch with a 50-ms resolution, the same as in the stimulus. Figure 7C shows the model-predicted time course of the RLF midpoint L₅₀ for upward switches from 54 to 78 dB SPL for the same AN fiber as in Fig. 4, A and C. L₅₀ rapidly approaches the steady-state L₅₀ after the switch, and the time course is well fit by an exponential with a time constant of 79 ms. This model-assisted estimate of shift time constant is three times shorter than the 251-ms time constant estimated directly from the same AN fiber's data using a coarser time resolution (Fig. 4C).

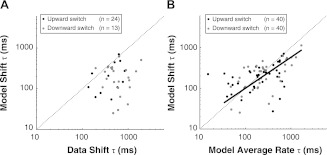
Figure 8A compares the shift time constants estimated with the help of the model and directly from the data for the recordings from which we were able to estimate the shift time course and for which the model met the goodness-of-fit criterion. Specifically, among the 40 recordings for which the model met the goodness-of-fit criterion, there were 13 recordings for upward switches and 24 recordings for downward switches for which the HPR was located within the steeply rising portion of the RLF so that the shift time course could be directly estimated from the neural data. Combining upward and downward switches, the median shift time constant estimated by the model-assisted analysis (209 ms) is significantly smaller than the median time constant directly estimated from the data (509 ms) (Wilcoxon rank sum test, P < 0.001). Importantly, this difference between model-assisted and direct estimates of shift time constants does not reflect an inability of the model to match the data (its adequacy was evaluated in Fig. 6), but rather results from biases in the time constant estimates obtained directly from the data stemming from the coarse temporal resolution (300 ms) of the analysis as well as the confound of firing rate adaptation. The model-assisted analysis overcomes these biases by generating a sufficient number of responses over the entire range of levels to apply the RLF normalization that eliminates the confound of firing rate adaptation with 50-ms time resolution. These model-assisted estimates show that the time course of dynamic range adaptation is well under 1 s, less than one-half that directly (but less accurately) estimated from the neural data.

Fig. 8.

Time constants of dynamic range adaptation estimated by the dual-adaptation AN model. A: the shift time constants of the model compared with those of the data. For upward switches, there are 13 AN fibers with which we were able to estimate the shift time course directly from neural data and the model met the goodness-of-fit criterion. For downward switches, there are 24 such fibers. B: the shift time constants predicted by the model for AN fibers with good model fitting results (n = 40) plotted against the model-predicted average rate time constant. The straight line is the fitted curve in the orthogonal least-squares sense (i.e., type II linear regression for 2 variables both dependent or having errors) for all data points with the outliers excluded (only 1 data point was excluded for which the model average time constant is smaller than 20 ms, which is well below the analysis time bin, 50 ms); the slope of the line is 0.76.

Figure 8B shows a scatter plot of model-assisted shift time constants vs. average rate time constants for the 40 AN recordings in which a good model fit was obtained. The median shift time constants were 211 ms for upward switches (25–75% percentiles: 110–268 ms) and 262 ms for downward switches (25–75% percentiles: 122–347 ms). As for average rate time constants, the median shift time constant for upward switches was significantly shorter than that for downward switches (paired t-test, P < 0.001). Combining upward and downward switches, the shift time constants are correlated with the rate time constants across the population (r = 0.72, P < 0.001). Moreover, the median shift time constant does not significantly differ from the median average rate time constant (Wilcoxon rank sum test, P = 0.29).

Although the model-assisted time constant estimates, shift or average rate, are primarily determined by the model's underlying time constants, τ_L or τ_R, of each adaptation module (Fig. 5), the two are theoretically distinct because the model's adaptation filters are placed in a feedback loop, which alters the effective time constant. Nevertheless, the shift and rate time constants derived from fits to models responses were correlated with the model's underlying time constants τ_L and τ_R, respectively (not shown).

DISCUSSION

We used switching-HPR stimuli to investigate the time course of dynamic range adaptation in the AN through both single-unit recordings in anesthetized cats and computational modeling. Although our neural recordings characterized the time course of the average firing rate across all switching cycles, they did not provide sufficient data for accurately characterizing the time course of dynamic range shifts. Using a dual-adaptation model to better characterize the time course of adaptation, we found that dynamic range adaptation occurs as rapidly as firing rate adaptation, over just a few hundred milliseconds, and that the time constants for the two forms of adaption are correlated across the AN fiber population.

Our results show that the time constants of both firing rate adaptation (Fig. 3) and dynamic range adaptation (Fig. 8B) vary over nearly two orders of magnitude across the AN fiber population. Although the time constants of firing rate adaptation depend somewhat on SR (Fig. 3C), this weak trend leaves most of the variability unexplained. This variability is surprising for AN fibers, which are thought to constitute a fairly homogeneous neural population, and such large variability in time constants has not been reported in previous studies of short-term adaptation (Chimento and Schreiner 1991; Harris and Dallos 1979; Westerman and Smith 1984). Perhaps the continuous stimulation with switching-HPR stimuli over 10 min used in the present study reveals sources of variability that play a weak role when short stimuli separated by long intervals of silence are used, as in traditional studies of adaptation.

Dynamics of Firing Rate Adaptation and Dynamic Range Adaptation

Adaptation to stimulus statistics in sensory systems seems to have two major components: one modifying the threshold or operating point of the input-output (I/O) function and another changing the gain or slope and maximum rate (Wark et al. 2007). AN adaptation to changes in mean sound level demonstrates these two components. The relationship between the two components depends on the stimulus and the system. For example, retinal neurons in both the fly and vertebrates show a rapid change in gain of their I/O function when adapting to a change in stimulus contrast, whereas the firing rate has a slower time course (Baccus and Meister 2002; Fairhall et al. 2001). In the avian auditory forebrain, the gain also changes rapidly after a change in the variance of the amplitude envelope, but changes in threshold occur more slowly and are correlated with changes in firing rate (Nagel and Doupe 2006). In the AN, the two forms of adaption seem to be more tightly related in that dynamic range adaptation and firing rate adaptation 1) occur on similar time scales, 2) have shorter time constants for upward than for downward switches, and 3) have correlated time constants across the AN fiber population, suggesting they may share a common neural mechanism.

Dual-Adaptation Model

The dual-adaptation model comprises two adaptation modules accounting for dynamic range adaptation and firing rate adaptation, respectively. This structure was suggested by the decomposition of the adaptive responses of AN fibers into a vertical rate decrement and a horizontal shift of the RLF (Gibson et al. 1985; Wen et al. 2009). As expected, eliminating the model's dynamic range adaptation module produced responses lacking RLF shifts (not shown). The model can predict rate responses to arbitrary level sequences with or without silent intervals. Because of its generality, the model structure might be applicable to neural adaptation at other stages of the auditory system and in other sensory modalities. On the other hand, this phenomenological model is not meant to reproduce the underlying mechanisms.

The adaptation mechanisms in the model are essentially linear and time invariant, with a single time constant for each adaptation module. Interestingly, the model still predicts the observed adaptation asymmetry between upward and downward switches. The exponential dynamics in the model are consistent with a report that the time constant of adaptation in IC neurons does not depend on the duration of the switching period (Dean et al. 2008). In contrast, the time constants of adaptation to a change in stimulus contrast in H1 neurons of the fly retina appear to scale proportionately to the duration of the switching period (Fairhall et al. 2001). Such a result is suggestive of power law rather than exponential dynamics (Wark et al. 2007).

A model (Zilany and Carney 2010) incorporating both power law dynamics and classic exponential processes for the synapse between inner hair cells and spiral ganglion cells has been shown to produce dynamic range shifts to changes in mean sound level that resemble those observed in the AN by Wen et al. (2009). The power law dynamics were critical because a version of the model containing only a cascade of exponential processes as in the Westerman and Smith (1988) model was unable to predict dynamic range adaptation comparable to that observed in the AN data. It is difficult to compare our model with that of Zilany and Carney because the two models are very different in their structure and purpose. Our experimental results provide detailed data about the time course of dynamic range adaptation for further testing this and other models of adaptation. Although fitting the power law adaptation model to AN responses to switching-HPR stimuli would be computationally challenging due to the model's complexity, power law dynamics do appear promising for modeling dynamic range adaptation and deserve further investigation.

Time Course of Dynamic Range Adaptation is Similar in AN and IC

Although IC neurons show stronger dynamic range adaptation to mean sound level than AN fibers (Wen et al. 2009), the time course of adaptation appears to be similar at the two sites. Both the median and the range of time constants of average rate adaptation in IC neurons (Dean et al. 2008) are very similar to those of AN fibers. In both AN and IC, adaptation occurs more rapidly to an increase than to a decrease in mean sound level.

As in our AN study, the data from IC neurons were not sufficient to accurately estimate the time course of dynamic range adaptation. Still, approximate estimates based on the shift of the HPR region of RLF show that dynamic range adaptation in IC neurons is completed within 600–900 ms of the switch (Dean et al. 2008). Our modeling results show that the shift of the HPR region of nonnormalized RLFs does not always accurately represent the dynamic range shift in AN fibers due to the confound of firing rate adaptation. This problem is likely to be even more severe for IC neurons, where the wide diversity of RLF shapes makes estimation of a horizontal shift difficult.

The time constants of firing rate adaptation tend to decrease with increasing CF in the guinea pig IC (Dean et al. 2008). Adaptation in the cat AN, however, does not show such a CF dependence (Fig. 3B). Our results are consistent with previous studies of in the AN, which did not report a CF dependence of time constants for short-term adaptation (Harris and Dallos 1979; Smith 1977; Westerman and Smith 1984). A CF dependence has been reported for the time constant of rapid adaptation in the AN (Rhode and Smith 1985; Westerman and Smith 1984), but these time constants are so short (<15 ms) relative to the 50-ms granularity of our analysis that they are unmeasurable with our paradigm. The lack of CF dependence of adaptation in the AN suggests that, besides possible interspecies differences, the CF dependence observed in the IC is established at processing stages between the AN and IC or in the IC itself. Low- and high-CF regions of the IC receive inputs from different brain stem nuclei (Oliver 1987) and also differ in their temporal coding of electric stimuli delivered through cochlear implants (Middlebrooks and Snyder 2010). These anatomic and functional differences may contribute to the CF dependence in the time course of adaptation.

Possible Mechanisms for Dynamic Range Adaptation

The rapid time course of dynamic range adaptation (100–400 ms) imposes constraints on the possible underlying mechanisms. Neurotransmitter release at the inner hair cell ribbon synapse is a particularly promising candidate mechanism because it occurs on a wide range of timescales, from several milliseconds to seconds (Nouvian et al. 2006). The fast kinetic component of exocytosis, occurring over tens of milliseconds, is associated with the depletion of the readily releasable pool and is thought to underlie AN short-term adaptation (Moser and Beutner 2000; Spassova et al. 2004). The slow kinetics components have time constants on the order of several hundred milliseconds (Nouvian et al. 2006) and thus might contribute to dynamic range adaptation. Our finding of a correlation between the time constants of firing rate adaptation and dynamic range adaptation (Fig. 8B) is consistent with an involvement of the ribbon synapse in dynamic range adaptation given the strong evidence that short-term adaptation is linked to a decrease in neurotransmitter release.

Although an involvement of the hair cell synapse in dynamic range adaptation is likely, other evidence points to a possible role of the cochlear mechanics. Stimulation of the medial olivocochlear (MOC) efferent system produces RLF shifts similar to dynamic range adaptation by reducing the gain of the cochlear amplifier (Cai and Geisler 1996; Guinan 2006). Specifically, electrical stimulation of the MOC efferents causes both a fast effect, occurring within 100 ms (Cooper and Guinan 2003), and a slow effect, occurring over 10 s (Cooper and Guinan 2003; Sridhar et al. 1995). Thus the fast effect may be too fast, and the slow effect appears too slow, to be strongly associated with AN dynamic range adaptation. On the other hand, the human MOC reflex to acoustic stimulation has a time course of 100–400 ms (Backus and Guinan 2006), which is within the range of time constants of AN dynamic range adaptation we observed. However, there may be species differences and in any case, MOC efferents effects are likely very weak in our barbiturate-anesthetized preparation (Boyev et al. 2002).

Although an involvement of the cochlear amplifier through action of the MOC system is unlikely in our anesthetized preparation, we still cannot rule out a role for the cochlear amplifier in dynamic range adaptation. Ongoing studies in our laboratory (Wen and Delgutte 2012) reveal clear differences in the amount and growth of dynamic range adaptation produced by HPR tone stimuli placed at the CF vs. well below the CF of AN fibers. This sharp frequency dependence in dynamic range adaptation seems hard to understand based on a purely synaptic mechanism. If so, there may be multiple mechanisms contributing to AN dynamic range adaptation, some occurring at the inner hair cell synapse and some mediated by the cochlear amplifier. Other possible sites for AN dynamic range adaptation include transduction channels (Vollrath et al. 2007) and postsynaptic intrinsic membrane channels, which have been shown to play a role in retinal adaptation (Kim and Rieke 2001, 2003; Weick and Demb 2011).

Functional Implications of the Rapid Time Course of Dynamic Range Adaptation

Rapid dynamic range adaptation in the auditory periphery likely contributes to the adaptive processing at higher centers of the auditory pathway. IC neurons in anesthetized ferrets shift the steep part of their rate-interaural level difference (ILD) curves to match the mean ILD of a stimulus with dynamic ILD (Dahmen et al. 2010). Although ILD adaptation is much stronger (∼1 dB/dB) than AN dynamic range adaptation (∼0.25 dB/dB), it is still likely influenced by dynamic range adaptation occurring in each monaural pathway.

Short-term firing rate adaptation by a sustained stimulus in the AN leads to a decrement in rate responses to subsequent stimuli (Harris and Dallos 1979; Smith 1977, 1979). This suppression likely contributes to psychophysical forward masking of a target preceded by a masking sound, although signal detection analysis shows that neural forward masking in the AN is small compared with psychophysical forward masking (Relkin and Pelli 1987; Relkin and Turner 1988). Our finding that the time course of AN dynamic range adaptation is similar to that of firing rate adaptation suggests that dynamic range adaptation might also play a role in forward masking. If so, we would expect a direct relation between the dynamic range shift produced by the masker and the amount of masking of the following target. It will be interesting to investigate psychophysical forward masking by HPR stimuli that induce strong dynamic range adaptation in the AN. Even if a forward masking is partly produced by dynamic range adaptation, the main contribution to psychophysical forward masking is still likely to be of central origin (Alves-Pinto et al. 2010; Nelson et al. 2009) because dynamic range adaptation is stronger in the IC than in the AN (Wen et al. 2009).

The ability to rapidly adapt to changes in mean sound level allows auditory neurons to provide more precise and efficient coding in a fast changing acoustic environment. Dean et al. (2008) showed that sound level changes in natural environments occur over tens of milliseconds to up to several seconds. Dynamic range adaptation occurring over a few hundreds of milliseconds seems fast enough to track most changes in the acoustic environment, thus allowing the auditory system to better discriminate level changes. Our results show that such rapid adaptation already occurs at the initial stage of the neural auditory pathway.

GRANTS

This work was supported by National Institute of Deafness and Other Communicative Disorders Grants R03 DC011156 (to B. Wen), R01 DC002258 (to B. Delgutte), and P30 DC005209.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: B.W., G.I.W., I.D., and B.D. conception and design of research; B.W., G.I.W., I.D., and B.D. performed experiments; B.W. analyzed data; B.W. and B.D. interpreted results of experiments; B.W. prepared figures; B.W. and B.D. drafted manuscript; B.W., G.I.W., I.D., and B.D. edited and revised manuscript; B.W., G.I.W., I.D., and B.D. approved final version of manuscript.