Dissecting sources of quantitative gene expression pattern divergence between Drosophila species

Abstract

Gene expression patterns can diverge between species due to changes in a gene’s regulatory DNA or changes in the proteins, e.g., transcription factors (TFs), that regulate the gene. We developed a modeling framework to uncover the sources of expression differences in blastoderm embryos of three Drosophila species, focusing on the regulatory circuit controlling expression of the hunchback (hb) posterior stripe. Using this framework and cellular-resolution expression measurements of hb and its regulating TFs, we found that changes in the expression patterns of hb’s TFs account for much of the expression divergence. We confirmed our predictions using transgenic D. melanogaster lines, which demonstrate that this set of orthologous cis-regulatory elements (CREs) direct similar, but not identical, expression patterns. We related expression pattern differences to sequence changes in the CRE using a calculation of the CRE’s TF binding site content. By applying this calculation in both the transgenic and endogenous contexts, we found that changes in binding site content affect sensitivity to regulating TFs and that compensatory evolution may occur in circuit components other than the CRE.

Introduction

Changes in gene expression patterns drive phenotypic change between both individuals and species (Gompel et al, 2005; McGregor et al, 2007; Wittkopp et al, 2008; Chan et al, 2010; Frankel et al, 2011). Many studies have identified dramatic gene expression changes, such as the gain or loss of an expression pattern, that underlie morphological phenotypes. Though more difficult to detect, small quantitative changes in gene expression may also lead to phenotypic variation between individuals and the evolution of new phenotypes between species (Brem et al, 2002; Wittkopp et al, 2009; Rockman et al, 2010). Indeed, quantitative variation in gene expression is pervasive within and between species, for example (Hutter et al, 2008; Nuzhdin et al, 2008; Cheung and Spielman, 2009; Muller et al, 2012). A fundamental challenge is to contextualize quantitative expression variation: what are its sources and its phenotypic consequences?

Gene expression occurs in the context of a network. The expression pattern of any given gene is dependent on the expression of its regulators. Information about the position and level of regulators is integrated by regulatory DNA, e.g., promoters, cis-regulatory elements (CREs or enhancers), and 3′ and 5′ untranslated regions (UTRs). Any part of a regulatory network can change between species, obscuring the underlying mechanism of expression pattern conservation and divergence. For example, if the expression pattern of a gene has changed, then this could be due to changes in the expression of upstream regulators or changes in any of the relevant pieces of regulatory DNA. Reciprocally, if an expression pattern is conserved, then either the expression patterns of upstream regulators and the function of regulatory DNA are conserved or changes in one component have been compensated for by changes in another.

To contextualize gene expression changes between species, it is therefore ideal to examine the expression patterns of the entire network simultaneously. Practically, there is a trade-off between measuring all network components comprehensively and measuring them in multiple cell types. Single-celled organisms are amenable to comprehensive measurements of gene expression using genome-wide techniques, i.e., RNA-seq. These types of studies have revealed widespread rewiring of transcriptional networks, even in cases where the output of the circuits is conserved, reviewed in Li and Johnson (2010). Making comprehensive measurements in animals is more technically challenging since an organism is composed of multiple cell types with distinct gene expression profiles. Genome-scale techniques are not spatially resolved, as they require whole organisms or tissues to be homogenized. Imaging techniques offer spatial resolution and are increasingly quantitative but are often limited to only a few genes. For example, in insects, comparative studies of small numbers of genes have shown both cases where gene expression patterns appear conserved in the face of changing regulatory sequence (Lukowitz et al, 1994; Ludwig et al, 2000; Wittkopp et al, 2003; Wratten et al, 2006; Hare et al, 2008a; Swanson et al, 2011) and cases where expression patterns diverge (Ludwig et al, 2005; Zinzen et al, 2006; Goltsev et al, 2007; Lott et al, 2007; Crocker et al, 2008; Fowlkes et al, 2011). Here, we pursue a strategy that is intermediate between these two extremes—simultaneous measurement of a small number of relevant network components, in multiple species, at cellular resolution.

As a model system to develop this approach, we use the conserved developmental transcriptional network that patterns the anterior-posterior axis in Drosophila embryos. This network exhibits quantitative differences in spatial and temporal expression patterns across multiple closely related species (Fowlkes et al, 2011). We recently completed a survey of gene expression in blastoderm embryos of D. yakuba (dyak) and D. pseudoobscura (dpse) (Fowlkes et al, 2011), which complements the existing data set for D. melanogaster (dmel) (Fowlkes et al, 2008). Our high-resolution imaging methods produce a gene expression atlas in which the relative expression levels for an arbitrary number of genes are mapped onto each cell in an average 3D embryo. These data are uniquely suited for identifying quantitative expression differences, as subtle differences in expression can be accurately measured. Our global analysis of these three data sets showed that individual genes differ quantitatively in their spatiotemporal gene expression patterns. However, cellular gene expression profiles, consisting of 13 genes in the anterior-posterior patterning network, are mostly conserved, implying that regulatory relationships between these genes are also largely conserved.

Here, we develop and apply a computational framework to assess the sources of expression divergence for an individual regulatory circuit in this network. We define a regulatory circuit to be the inputs and output of an individual CRE (Ben-Tabou de-Leon and Davidson, 2007). A gene can be controlled by multiple CREs, each of which controls a portion of the gene expression pattern in space and time. In this study, we define the inputs to be the regulating transcription factors (TFs) of a CRE and the output to be the portion of the expression pattern directed by the CRE. However, our general strategy can also be extended to accommodate other components of transcriptional regulatory circuits. This approach allows us to: (1) quantify the behavior of the circuit across species; (2) attribute the sources of expression divergence either to changes in the expression patterns of upstream regulators or to changes in the regulatory logic of the circuit; and (3) assess the contributions of changes in CRE sequence to the expression output.

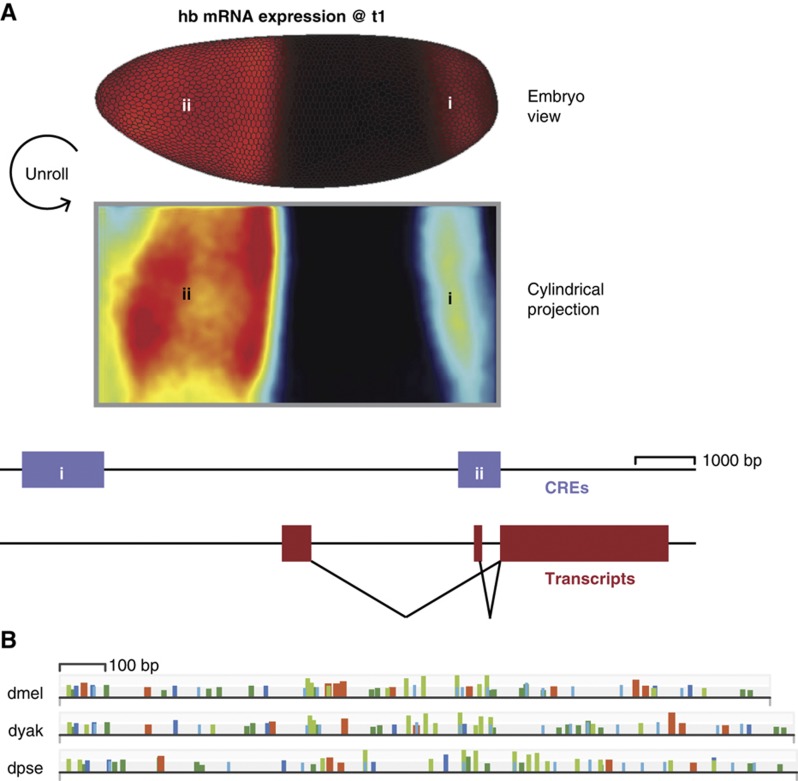
As a case study, we examine the circuit that controls the hunchback (hb) posterior stripe. hb is a widely conserved zinc-finger TF near the top of the anterior-posterior segmentation network hierarchy (Lehmann and Nüsslein-Volhard, 1987; Struhl et al, 1992; Lukowitz et al, 1994; Lynch and Desplan, 2003). hb is expressed in two regions at the blastoderm stage: a broad anterior domain, which is largely maternally controlled, and a posterior stripe, which is solely due to zygotic transcription (Figure 1A; Lehmann and Nüsslein-Volhard, 1987; Tautz et al, 1987; Schröder et al, 1988). The hb posterior stripe expression pattern varies quantitatively between dmel, dyak, and dpse (Fowlkes et al, 2011). From extensive experimental data, we know hb’s input TFs and the structure of the CREs in its locus (Jäckle et al, 1986; Casanova, 1990; Margolis et al, 1995; Kosman and Small, 1997). Like many other CREs in the network, the TF binding site content of the hb posterior stripe CRE varies significantly across these three Drosophilids (Moses et al, 2006; Kim et al, 2009), whose last common ancestor lived ∼25 million years ago (Figure 1B; Richards et al, 2005).

Figure 1.

The two spatial domains of the hb expression pattern are driven by two CREs. (A) hb is expressed in a broad anterior domain and a posterior stripe in blastoderm-age embryos. We show two views of the dmel hb mRNA expression pattern at the first time point from the dmel atlas (Fowlkes et al, 2008). On top is a rendering in a typical dorsolateral embryo view, where expression is in red with brightness proportional to level. On bottom is a cylindrical projection, where high expression is in red and low expression is in blue. In both views, anterior is to the left and dorsal is up. Below the expression patterns, we show the structure of the hb locus, with regulatory elements in purple and transcripts in red. The expression pattern is controlled by two CREs, one driving the anterior domain (ii) and one driving the posterior stripe (i). The two hb transcript isoforms are functionally identical, and both transcripts contribute to both spatial expression domains (Margolis et al, 1995). (B) The binding site content of the hb posterior stripe CRE varies between species. We plot the predicted TF binding sites of hb’s regulators in the sequences of orthologous hb posterior stripe CREs from D. melanogaster (dmel), D. yakuba (dyak), and D. pseudoobscura (dpse) (see Materials and methods). hkb sites are highlighted in orange and tll, kni, Kr, and gt sites are shown as light blue, dark blue, light green, and dark green rectangles, respectively. The height of the rectangle is proportional to binding site strength and the width of the rectangle is proportional to the length of the binding site.

Our approach is to first define an input/output function that relates the concentration of regulating TFs to the observed expression pattern in individual cells. We then assess the degree of conservation of the circuit’s input/output function by fitting the function in each of the three Drosophila species. Because these functions operate at cellular resolution, we can quantify the extent to which expression divergence is due to upstream changes in the expression patterns of regulating TFs. We validate our predictions using CRE reporter constructs in transgenic animals in which all inputs are constant and only the sequence of the CRE is changing. We also use these transgenic data to calculate the CRE sequence contribution to the input/output function without fitting additional parameters; this calculation is based on predicted TF binding sites in the set of orthologous CREs. Finally, we add this calculation of CRE sequence contribution to the input/output function in the endogenous context to assess the contribution of CRE sequence to the behavior of the native regulatory circuit.

Using this strategy, we found that there is a large degree of functional conservation in the hb posterior stripe circuit. The majority of the endogenous gene expression divergence is due to positional shifts in expression of hb’s regulators. We found that the calculated CRE sequence contribution improves the fit of the input/output function in the transgenic context. We conclude that small changes in CRE sequence do have functional consequences; they alter sensitivity to regulating TFs. This has implications for current models of CRE function, where the degree of flexibility in the arrangement of TF binding sites is a matter of debate (Crocker and Erives, 2008; Hare et al, 2008a, 2008b). We found that adding the CRE sequence contribution to the input/output function in the endogenous context leads to mixed results, implying that orthologous TFs in these species may not be functionally identical, as is widely assumed, or that compensatory evolution has occurred outside of the CRE. We discuss the implications of these results for understanding transcriptional circuit evolution with quantitative precision.

Results

There are quantitative differences in the hb expression pattern between species

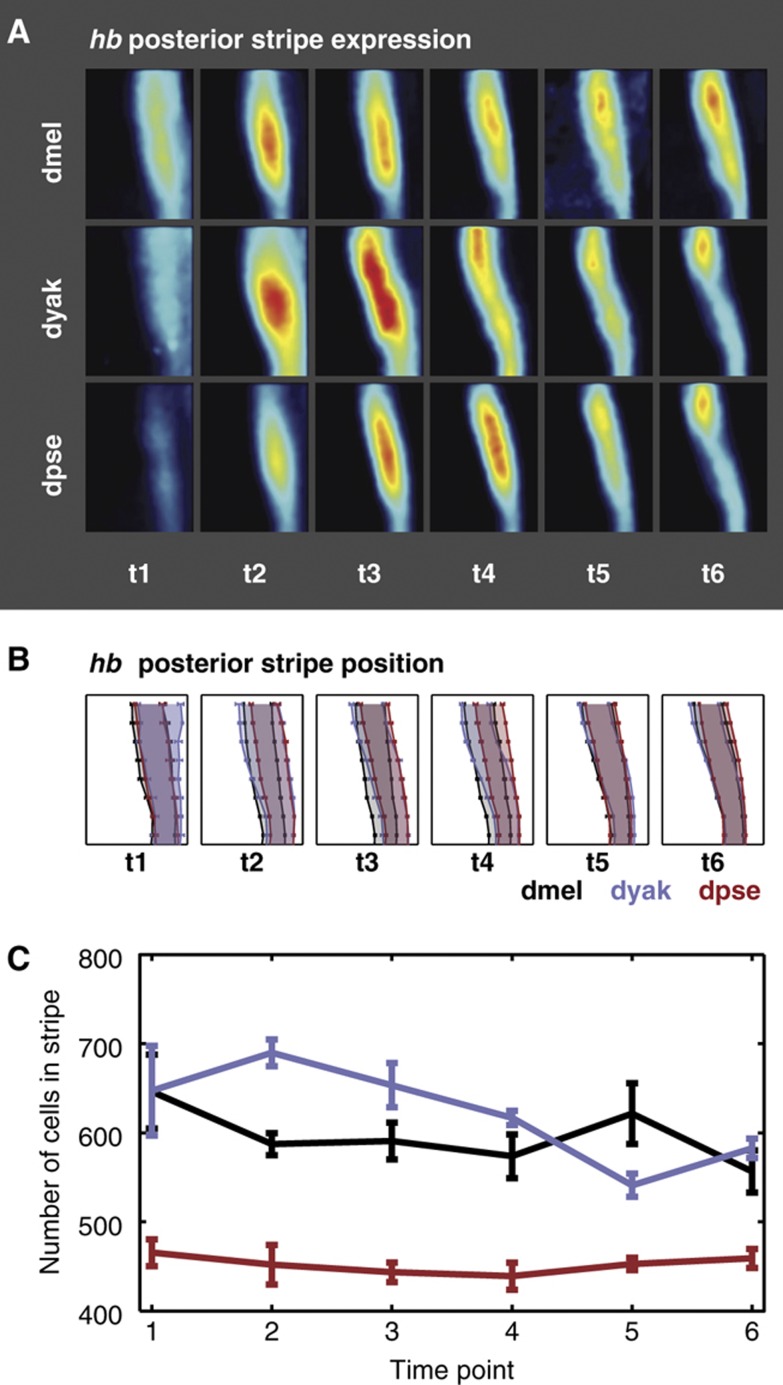
The endogenous expression pattern of hb was previously measured at cellular resolution in dmel, dyak, and dpse (Fowlkes et al, 2008, 2011; Figure 2A). Briefly, expression was visualized using RNA fluorescent in-situ hybridization against hb and a fiduciary marker (see Materials and methods). The in-situ protocol uses an amplification step to improve the signal to noise ratio. We find no evidence that this protocol results in non-linear amplification of signal (Supplementary Figure 1). The stained embryos were imaged using 2-photon laser scanning microscopy, and automated image analysis techniques were used to convert image data into PointClouds, text files that contain the spatial coordinates and expression levels of hb and the fiduciary marker in each nucleus (Luengo Hendriks et al, 2006). Each of the PointClouds was then matched to a species-specific embryo template using the fiduciary marker (Fowlkes et al, 2008). Once all the embryos are mapped onto the template, average hb expression values are calculated for each cell at each time point. Since expression can only be measured in relative units with this in-situ protocol, each gene’s expression values are normalized so that the minimum value is 0 and the 95th percentile value corresponds to 1. The resulting gene expression atlases contain the average values of hb expression derived from 5 to 29 embryos for each of six time intervals during the hour of blastoderm-stage development. The resulting gene expression patterns are qualitatively similar: each species has a hb posterior stripe, but they vary quantitatively in relative position, particularly in the earlier time points, and in the width of the stripe (Figure 2B and C).

Figure 2.

hb patterns differ between three Drosophila species. (A) The hb posterior stripe expression pattern diverges between three species. We show the average expression patterns in the posterior 36% of embryos for the endogenous hb pattern in dmel, dyak, and dpse, at six time points spanning the hour of blastoderm-stage development. The panels are oriented with the anterior end to the left and the dorsal side on the top, and the levels are indicated by the color, where black is no expression and red is high expression. The shape and dynamics of the hb posterior stripe expression pattern vary between the three species. (B) The average hb posterior stripe boundary locations vary between species at early time points. We plot the average boundary locations of the hb posterior stripe in percentage egg length. The panels are oriented in the same manner as (A). Average boundary positions are shown for dmel in black, dyak in purple, and dpse in red, for six time points. Error bars denote the standard error of the mean. (C) The average number of cells in the hb posterior stripe varies between species at all time points. We plot the average number of cells in the hb posterior stripe for dmel, dyak, and dpse for six time points. Error bars denote the standard error of the mean. dpse embryos have fewer total cells than dmel and dyak embryos. Therefore, the number of cells in the dpse hb posterior stripe is much smaller than in dyak and dmel stripes, even though its size as a fraction of egg length is similar. Source data is available for this figure in the Supplementary information.

Source data for Figure 2B ^{(9.5KB, zip)}

Source data for Figure 2C ^{(3KB, zip)}

A modeling framework to understand the origins of hb gene expression divergence between species

Many factors may cause the observed inter-species divergence in the hb expression pattern. Changes in any part of a gene’s regulatory DNA or the expression patterns of the regulatory molecules that bind this DNA can influence a gene’s expression pattern (Maston et al, 2006; Consortium et al, 2010). Given our cellular resolution data set, we are best equipped to assess the influence of spatially varying inputs on a gene’s output. We therefore restrict our considerations to hb’s input TFs and the CRE that integrates these inputs. We then separate potentially influential changes in the circuit into two categories: differences in the expression patterns of hb’s input TFs, which we call positional information, and differences in hb’s sensitivity to its inputs, which we call regulatory logic. The terms trans and cis are often used to denote these contributions to expression divergence, but we decided against these terms for two reasons. First, in studies that concern gene expression divergence, trans is often used to connote changes in TF coding sequences. Here, positional information only refers to changes in the expression pattern of the TFs. Second, our use of positional information is consistent with the definition traditionally used in developmental biology, i.e., the spatially varying expression patterns of molecules that determine cell type.

Our modeling framework is designed to disentangle the contributions of changes in positional information and regulatory logic to hb expression divergence by modeling gene expression in single cells. We first define a function that relates inputs to outputs in individual cells, Equation (1). If the change in the output expression pattern between species is due to a change in the position of an upstream regulator, i.e., a change in positional information, then we expect this function to accurately predict expression of the output based on the concentration of inputs across all cells in each species. However, the cells will occur in different locations because the spatial pattern of the inputs differs.

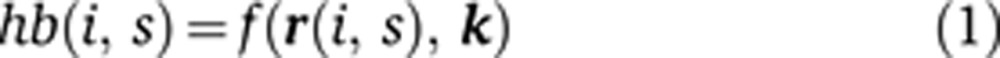Here, hb(i, s) is the measured hb gene expression level in cell i in species s, r(i, s) is a vector containing the corresponding expression levels of hb’s regulators, k is a vector consisting of coefficients describing the effect of each TF on hb, i.e., the strength of repression or activation per expression unit of the TF, and f is a function relating r and k to hb.

In contrast, if the expression difference is due to a change in regulatory logic, i.e., the circuit is responding to an upstream input differently, then we would expect a difference in the relationship of input and output concentrations. We can incorporate this into Equation (1) by including a species-specific vector k(s) to relate the levels of regulators to the level of hb. Equation (2) therefore describes the scenario in which the divergence in the hb pattern is caused by both changes in positional information and regulatory logic.

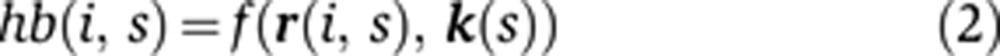Given a functional form, we call the fit of Equation (2) to each species’ own data the best fit; it is the best performance possible given that functional form. To determine whether a regulatory circuit is conserved, we can fit the function in one species using Equation (1), use those fit parameters to predict expression in the other species (we call this the applied fit), and compare the performance of the model to the best fit. If the contribution of positional information is large relative to changes in regulatory logic, then these two fits will be similar. If the contribution of positional information is small, then the best fit will be much better than the applied fit.

To implement this framework for the hb posterior stripe, we must make several choices regarding the inputs of the circuit, the use of the six time points in our data set, and the form of the function f. We chose the five primary regulators of hb’s posterior stripe defined by genetic analyses: giant, gt; huckebein, hkb; knirps, kni; Krüppel, Kr; and tailless, tll (Jäckle et al, 1986; Casanova, 1990; Margolis et al, 1995; Kosman and Small, 1997). These genes are all in gene expression atlases for dmel, dyak, and dpse (Fowlkes et al, 2008, 2011). We excluded caudal, a potential activator of hb, because caudal is not in the dpse atlas due to low level staining (Fowlkes et al, 2011). Thus, caudal’s contribution is not spatially localized in our model and is instead included in the constant term in Equation (3) (see Discussion). The time points in the atlases correspond to ∼10 min intervals. Because transcription can occur on the timescale of a few minutes (Ardehali and Lis, 2009), we assume that target expression levels can be predicted from regulators’ expression levels at the same time point and therefore use all time points to fit our function simultaneously. Adding a time delay of one 10 min time step between the inputs and outputs improved the modeling accuracy but reduced the total size of our data set. Because excluding a single time point can create a similar increase in modeling accuracy, we did not use a time delay in subsequent analyses (Supplementary Figure 2). There are many functional forms we could use for f. We first consider a simple linear form. Explicitly, Equations (1) and (2) correspond to

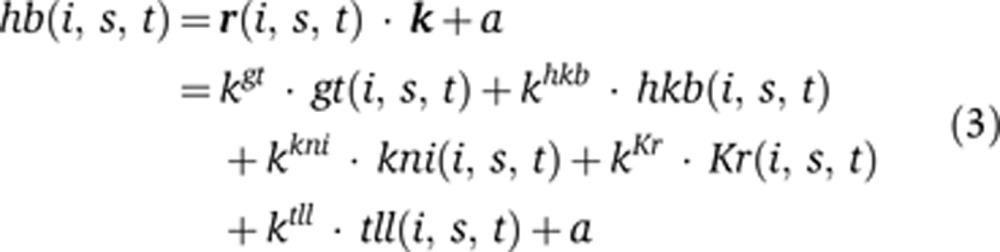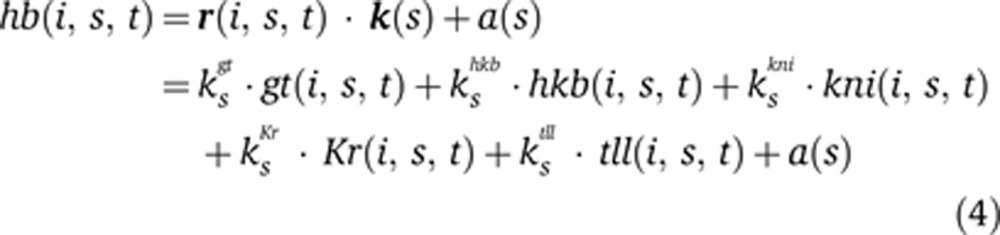The constants a and a(s) and the coefficients k and k(s) were fit using standard methods for multiple linear regression.

To evaluate the model fits, we compared the predicted levels of hb expression with the measured values using the area under a receiver operating characteristic curve (ROC AUC) (Swets, 1988). ROC curves compare the predictions from the model with the experimental data in a binary manner; this requires us to threshold both the experimental data and the predictions to score them relative to one another. Importantly, we did not threshold the data for the purpose of prediction, only for the purposes of scoring. For each cell, we determined whether hb is ‘on’ or ‘off’ in the experimental data using a different threshold for each species or transgenic line (Materials and methods). For the modeling results, we varied the threshold separating ‘on’ from ‘off’ cells. For each threshold, we calculated true positive and false positive rates, plotted these rates against each other to create the ROC curve, and calculated the area underneath it (Supplementary Figure 3). An AUC of 1 corresponds to a perfect classifier, and an AUC of 0.5 corresponds to a random classifier. We used this measure because it is not influenced by the experimental noise in ‘off’ cells and potential global changes in levels between species. Furthermore, though we find no evidence for non-linearities in our measurements (Supplementary Figure 1), the ROC AUC is not very sensitive to potential non-linearities (Supplementary information). An alternate measure of model performance (the r² value) also supports our conclusions (Supplementary Figure 4).

The majority of hb expression pattern divergence is due to changes in positional information

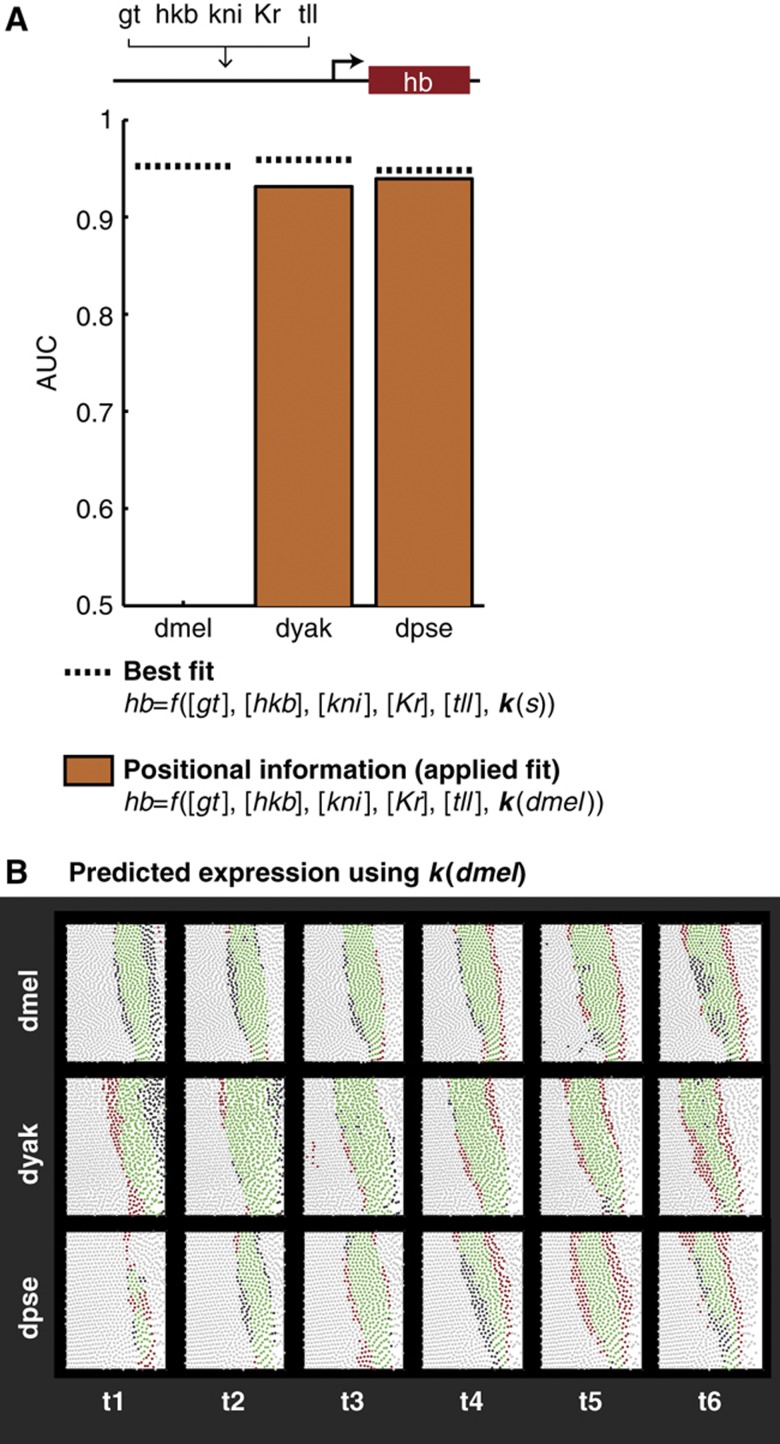
To test the capability of a linear model to recapitulate each species’ hb pattern, we fit the k(s) vector in Equation (4) using the posterior 36% of the each species’ embryo, which corresponds to the location of the endogenous dmel hb posterior stripe ±10% of the egg length. The linear model fits the endogenous hb expression in each species with AUC=0.95, 0.96, and 0.95 for dmel, dyak, and dpse, respectively (Figure 3A; P-values<0.001 using the Mann–Whitney U-test). The coefficients resulting from this fit are shown in Table I.

Figure 3.

A linear model fits endogenous hb expression patterns with high accuracy. (A) Changes in positional information account for a large portion of hb expression pattern divergence. Here, we show the results of fitting a multiple linear regression model to the endogenous hb pattern in each species (dotted line, best fit) and by fitting to dmel and applying the resulting coefficients to the hb patterns in dyak and dpse (orange bars, positional information). Performance of the model was measured using the area under the ROC curve (AUC), and the results are plotted for the species in order or increasing phylogenetic distance from dmel. (B) Differences in the hb expression pattern can be explained using a common parameter set. We show the detailed results of the positional information model, using k(dmel). For the sake of visualization, we found a threshold for each species that yielded an 80% true positive rate. This corresponds to a single point on the ROC curve that we integrated to calculate the AUC scores shown in (A). Each circle in the subpanels corresponds to a cell, with green and light gray circles corresponding to correct predictions in which the cell is on (green) or off (light gray) in the experimental data. The red and dark gray cells correspond to incorrect predictions, in which the cell is off (red) or on (dark gray) in the experimental data.

Table 1. Coefficient values resulting from the multiple linear regression to the endogenous data sets (best fit).

s	dmel	dyak	dpse
a(s)	0.483	0.569	0.429
k s hkb	−0.497	−0.293	−0.306
k s gt	−0.566	−1.05	−0.730
k s kni	−0.418	−0.913	−0.435
k s Kr	−0.429	−0.628	−0.0914
k s tll	0.170	0.0707	0.0272

To assess the contribution of changing positional information to expression pattern divergence, we compared the performance of the linear model using a single set of k values, the applied fit, to the performance using species-specific k(s), the best fit. Specifically, we fit the model in dmel, and applied the fit parameters to the other species. We found that using the dmel parameters, k(dmel), recapitulates most of the performance in dyak and dpse (AUC=0.93 and 0.94, respectively; Figure 3A; P-values<0.001 using the Mann–Whitney U-test). We also conducted an error propagation analysis to ensure that differences in the applied fits are not due to differences in measurement error between species. We find that a conservative estimate of the effect of measurement error on the AUC is smaller than the differences we interpret as significant (Supplementary information).

These results indicate that a large fraction of hb expression divergence is explained by changes in the positional information of hb’s upstream regulators. A detailed view of the model performance (Figure 3B) shows that changes in positional information cause notable differences between species, e.g., the narrow stripe at the first time point of dpse and the wide stripe at the second two time points of dyak (see columns 1–3 of Figure 3B). This result implies that the regulatory logic between hb and its regulators is largely conserved between dmel, dyak, and dpse.

Though the applied fit is an excellent predictor of hb expression, a statistical comparison shows that there is a significant difference between the best fits and applied fits for both dyak and dpse (P-values<0.001 using the Mann–Whitney U-test), indicating there is not complete conservation of the regulatory logic. We explore the contributions of sequence divergence in the orthologous CREs to these differences in later sections.

We performed several additional calculations to test the assumptions of our model. When we fit the linear model to the entire embryo at once, the performance of the model drops substantially (Supplementary Figure 5), implying that there is more than one input/output function creating the endogenous hb pattern. We expect this because there are multiple CREs in the locus. The model performance did not improve substantially upon the addition of higher order terms and is worse when any regulator is excluded (Supplementary Figure 6). Ten-fold cross-validation confirms that the model is not over-fit to the data (Supplementary Figure 7).

Transgenic experiments show the changes in regulatory logic encoded by orthologous hb posterior stripe CREs

Our model indicates that the regulatory logic of this circuit is largely conserved but exhibits quantitative differences between species. These differences could be due to changes in activity or level of input TFs or changes in the CRE, promoter, or UTRs. Indeed, all of these sequence components differ between species. We tested whether sequence variation in the hb posterior stripe CRE leads to quantitative expression differences for two reasons. First, CREs dictate the wiring of the circuit; they integrate information about the input TF concentrations to produce a particular output. Second, they are a well-characterized regulatory component of the circuit, making comparative bioinformatics analysis tractable.

We tested whether this set of orthologous CREs direct quantitatively different expression patterns by making transgenic reporters in dmel, where all inputs are identical and only the CRE sequences differ. These reporters drive the expression of lacZ. All constructs were integrated into the dmel genome at the same site (Materials and methods). We created transgenic lines for the dmel, dyak, dpse, and D. persimilis (dper) hb CREs. Because dpse and dper are closely related, we expect the expression driven by these two CREs to be more similar to each other than to dmel or dyak. This comparison gives an informal sense of the error in our experimental and analytical techniques. For each transgenic line, we measured lacZ expression levels in four or more embryos per time point (Materials and methods). We combined the data for the transgenic constructs with the existing dmel expression atlas (Fowlkes et al, 2008), resulting in a data set that includes cellular resolution measurements of both the inputs and output of each CRE. This data set allowed us to measure the input/output function of each CRE and detect quantitative differences in their regulatory logic.

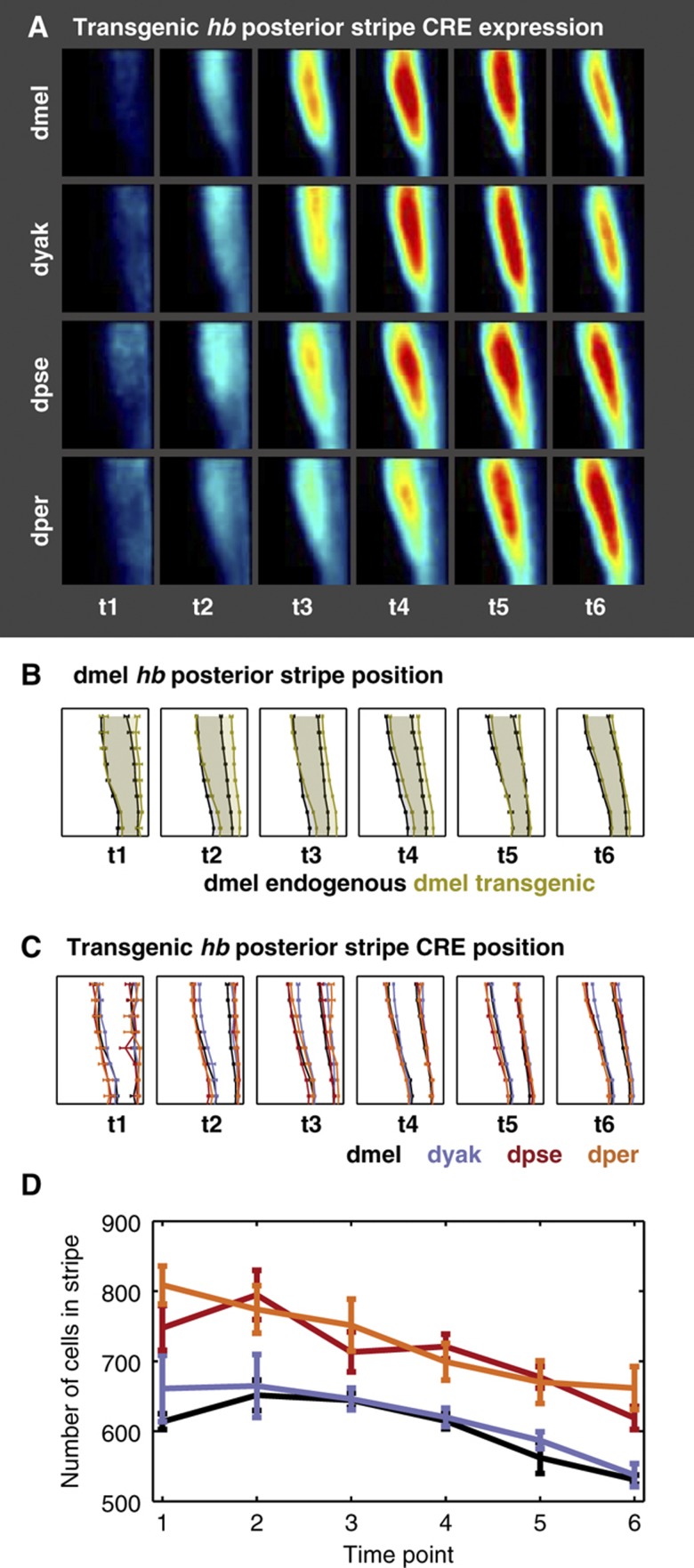
The expression patterns driven by these orthologous CREs are similar but differ quantitatively in stripe location and width (Figure 4). The orthologous CREs also drive variable amounts of expression in the anterior (Supplementary Figure 8, see Discussion). Given the common positional information, observed differences must be entirely due to sequence changes between the CREs.

Figure 4.

Orthologous CREs drive similar, but not identical expression patterns in transgenic dmel lines. (A) Expression patterns driven by orthologous hb posterior stripe CREs vary quantitatively. We show the average lacZ expression pattern in the posterior 36% of transgenic flies using the same conventions as Figure 2A. These patterns are measured in transgenic dmel lines containing the hb posterior stripe CRE from each of four species, driving a lacZ reporter. (B) The transgenic and endogenous dmel hb posterior stripe patterns are not identical. A comparison of the stripe boundary locations of the endogenous and transgenic hb posterior stripe indicate that the patterns are different, particularly at early time points. Here, we plot the average stripe boundary position for the dmel endogenous (black) and transgenic (olive) patterns, relative to total egg length, for six time points. The error bars show the standard error of the mean. (C) The transgenic hb posterior stripe boundary locations vary subtly between species. We plot the average boundary locations of the hb posterior stripe CRE in percentage egg length. Average boundary positions are shown for the dmel CRE in black, dyak in purple, and dpse in red, and dper in orange, for six time points. Error bars denote the standard error of the mean. (D) The average number of cells in the hb posterior stripe varies between some species at all time points. We plot the average number of cells in the hb posterior stripe CRE for dmel, dyak, dpse, and dper CREs for six time points. Error bars denote the standard error of the mean. This plot shows that a change in boundary position of ∼1% egg length corresponds to a change of ∼100 cells contained within the stripe. Source data is available for this figure in the Supplementary information.

Source data for Figure 4C ^{(12.6KB, zip)}

Source data for Figure 4D ^{(4KB, zip)}

We tested the effects of these sequence changes on the regulatory logic of the circuit using our computational framework. To do this, we write Equation (1) as

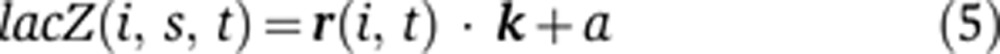where lacZ(i, s, t) is the expression value of lacZ driven by the CRE from species s in cell i at time t, r is a 1 × 5 vector of the expression values of hb’s five regulators in the corresponding cell, k is a 5 × 1 vector of coefficients describing the effect of each regulator on lacZ’s expression pattern, and a is a constant. We fit the k vector in Equation (5) to the dmel transgenic data set using the posterior 36% of the embryo.

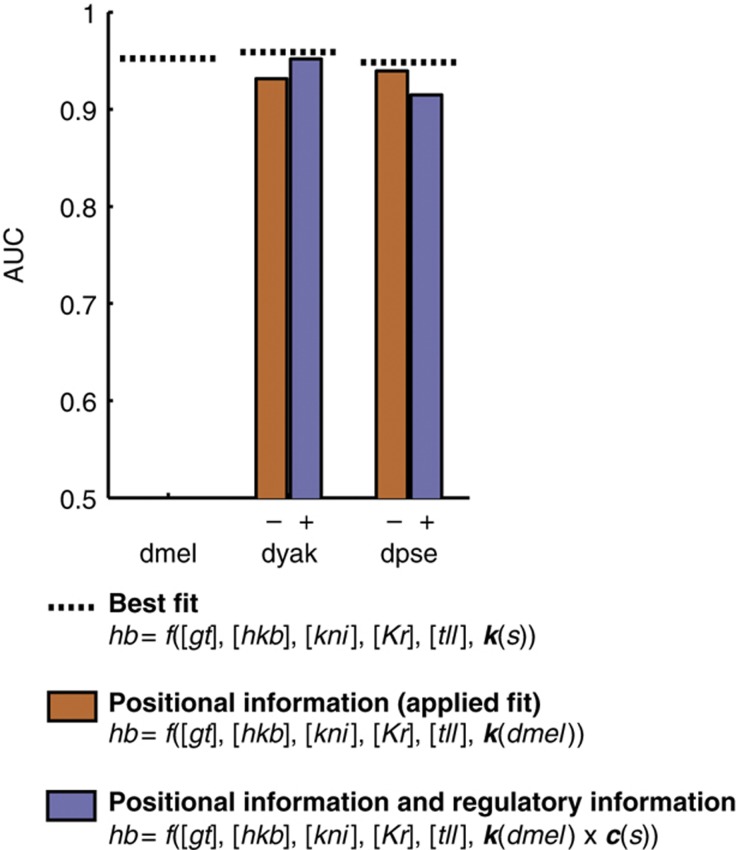
The linear model fits the dmel data with AUC=0.94 (Figure 5; P-value<0.001 using the Mann–Whitney U-test). We applied the same coefficient vector k to the other transgenic data sets without re-fitting. The range of AUCs resulting from this analysis, 0.88–0.91 (P-values<0.001 using the Mann–Whitney U-test), indicate that though largely similar, there are quantitative differences between the regulatory logic encoded by the orthologous CREs. Cross-validation showed that the linear model is not over-fit to the data (Supplementary Figure 9).

Figure 5.

The addition of sequence weights improves the fit of a linear model to the transgenic data. (A) Including CRE sequence information improves the fit of the linear model to the transgenic expression pattern. We show the results of fitting a multiple linear regression model to the transgenic line expressing lacZ under the control of the dmel hb posterior stripe CRE and applying the resulting coefficients to the other transgenic lines (orange bars, positional information). Adding a sequence weight, a scaling parameter that accounts for the differences in binding site content of the different posterior stripe CREs, improves the fit of the model to the data (purple bars, regulatory logic). (B) Sequence weights for the hb posterior stripe CRE. We plot the sequence weight for each TF and CRE, which roughly corresponds to the total binding potential for each TF along the CRE. The sequence weights are normalized so that they are 1 in dmel (black bars). (C) The addition of the sequence weight lowers the false positive predication rate. As in Figure 3, we visualize the results of the model at the 80% true positive rate. In each sub-panel, each circle corresponds to a cell, with the color indicating whether or not the model is correct. Green circles are cells that are correctly predicted to be on, light gray circles are cells that are correctly predicted to be off. Red circles are cells that are incorrectly predicted be to on, and dark gray circles are cells that are incorrectly predicted to be off. For each species, excluding dmel, we show the model performance without (−, top row) and with (+, bottom row) the sequence weight.

A simple sequence-based calculation accounts for changes in the regulatory logic encoded by orthologous CREs

In the transgenic experiments, the only possible source of regulatory logic divergence is sequence divergence in the CREs. We therefore attempted to calculate the sequence contribution to k(s) using predicted TF binding sites in the CREs.

Theoretically, k reflects a combination of each regulator’s intrinsic potency and its capacity to act on the CRE, e.g., the number and strength of its binding sites. Since all transgenics share the same dmel environment, the potency of the regulators is the same for all lines, and only their capacity to act changes. We express each element i of k(s) as

where p_i is the potency of regulator i, and c_i(s) is its capacity. We set all the values of c(dmel) to 1, so k(dmel)=p and is unchanged from the calculation done for Equation (5). To calculate c(s), which we call a ‘sequence weight,’ for the other transgenic lines, we use a formula that corresponds to the total strength of each regulator’s predicted binding sites in each CRE, normalized to the total strength in the dmel CRE (Materials and methods; Figure 5B). In principle, the sequence weight could be calculated in other ways; however, as we show below, this simple calculation is informative in our framework.

The addition of this sequence weight improves the fit of the input/output function to the data (Figure 5A and C; AUCs=0.92–0.97; comparison P-values<0.001 using the Mann–Whitney U-test). The most dramatic improvements of prediction performance are for those species that are the most diverged from dmel. Increasing the influence of gt and kni and decreasing the influence of hkb in dpse and dper allows the model to more accurately recapitulate the lacZ expression pattern, specifically the extension of the stripe further to the posterior of the embryo, where hkb is expressed. The increase in model performance indicates that these orthologous CREs differ in sensitivity to their inputs, and we conclude that sequence changes in these CREs have functional consequences.

Though simple, the sequence weight is a useful calculation for predicting the effects of sequence changes on expression output. This is notable because the improvement in fit does not require fitting any extra parameters and because the sequence weight does not include any information about the arrangement of sites relative to one another. We presume this is not because local arrangement of sites is unimportant but rather because these orthologous CREs all contain functional arrangements of binding sites. If this is true, then an alternative method for calculating the sequence weight would be necessary to assess synthetic or non-orthologous CREs.

Sequence-based calculations of regulatory logic are only effective in the endogenous context at shorter phylogenetic distances

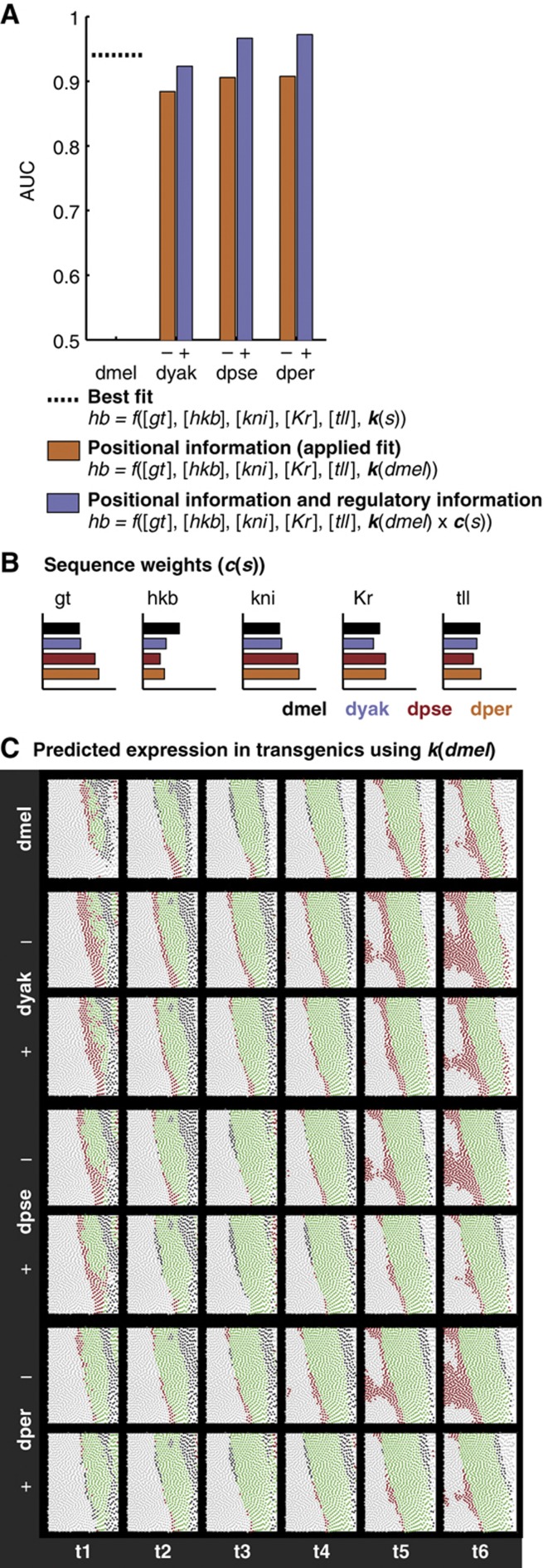
We applied the sequence weight calculation to the endogenous data sets. As explained above, k represents both the potency, p, of each TF, and its capacity to act, c, on the target. We assumed that p is conserved between species because of the high degree of coding sequence conservation of the TFs in this system. To predict binding sites in the other species, we also assumed that the DNA binding preferences determined for each dmel TF are valid for its orthologs in dyak and dpse (see Discussion). We then estimated the contribution of cis-regulatory changes by calculating c(s) as we did for the transgenic lines and multiplied these sequence weights to the corresponding values of k(dmel).

We found that the addition of the sequence weight to the predictions made using the k(dmel) parameter set improves the dyak predictions, increasing the AUC from 0.93 to 0.95, and worsens the dpse predictions, decreasing the AUC from 0.94 to 0.91 (Figure 6; comparison P-values<0.001, using the Mann–Whitney U-test). When compared with dmel, virtually all of the hb expression divergence in dyak is explained by changes in positional information and changes in regulatory logic due to sequence changes in the CRE. dpse is further diverged from dmel than dyak. Nearly all of hb expression divergence in dpse is explained by positional information. However, we cannot estimate all the changes in regulatory logic using only the sequence weight for the CRE. This is not because the sequence weight is ineffective for the dpse hb posterior stripe CRE (see transgenic results in Figure 5). Rather it may reflect the fact that many features of the locus, including other hb CREs, the promoter, and the UTRs, contribute to hb expression. These features are all presumably more diverged in dpse than in dyak as compared with dmel. Changes in these other components may overwhelm the effect of sequence changes in the hb posterior stripe CRE in the dpse endogenous context. Alternatively, dpse TFs may not be equivalent to their dmel counterparts in terms of their potency, DNA binding preferences, or absolute gene expression levels, limiting our ability to fit the model or calculate the sequence weight.

Figure 6.

The addition of the sequence weight improves endogenous dyak predictions. We show the results of fitting a multiple linear regression model to the endogenous hb pattern using a species-specific parameter vector k(s) (dotted line, best fit), the dmel parameter vector (orange bars, positional information), the dmel parameter vector and sequence weights (purple bars, regulatory information). The addition of a sequence weight improves the model fit in dyak and worsens the model fit in dpse.

Discussion

We present a method to investigate the origins of quantitative divergence in gene expression patterns. Because gene expression occurs in the context of a network, to compare any one component between species one must control for changes in other parts of the network. In the context of a single transcriptional circuit operating in a multicellular organism, we must disentangle the influences of positional information (where inputs are expressed) and regulatory logic (how inputs are interpreted). By separating these influences we were able to detect fine-scale differences in the functions of the orthologous CREs that wire this particular circuit. Our method can be applied to many such circuits and to regulatory sequences other than CREs.

Our method uses cellular resolution measurements of both the inputs and output of a transcriptional circuit in three species. We found that expression pattern divergence is largely explained by changes in the expression patterns of the input TFs. We used transgenic experiments to confirm that these orthologous CREs direct highly similar, but quantitatively distinct expression patterns. We used this transgenic data set to develop a sequence-based calculation of CRE regulatory function. Applying this calculation in the transgenic context, we showed that sequence changes in orthologous CREs alter sensitivity to their input TFs. Applying this calculation in the endogenous context, we attributed the observed expression divergence between dmel and dyak to a combination of changes in the expression patterns of regulating TFs and sequence changes in the CRE. In the context of the dmel/dpse comparison, we concluded that either (1) components in the regulatory circuit other than the input TF expression patterns and the CRE have diverged between dmel and dpse, or (2) TFs functionally diverge between these species.

A framework for contextualizing quantitative gene expression divergence

Our approach requires measuring expression in both endogenous and transgenic contexts. Endogenous expression patterns are the biologically relevant outputs of the entire transcriptional network, but they are difficult to compare across species since many parts of the network change simultaneously. In transgenic animals, the expression pattern of a reporter gene under the control of a particular regulatory element is easier to interpret, since the animals will only vary in the sequence of the test element. However, in isolation, these elements may not function as they do in the endogenous context. In fact, reporter constructs often do not recapitulate the native expression pattern precisely (discussed below). We combined these two types of measurements in a unified computational framework to assess sources of quantitative expression divergence between species. We used the endogenous measurements to fit a function relating the concentration of inputs to output for an individual transcriptional circuit and assessed the conservation of this circuit across species. We used the transgenic measurements to develop an appropriate calculation for one component of this circuit—the underlying CRE—and applied this calculation in the endogenous context to learn how it contributes to the observed expression pattern.

Quantitating sensitivity to sequence perturbation

A major unresolved question is whether there is a ‘grammar’ to the arrangement of TF binding sites in CREs: are particular binding site compositions, orders, or spacing more or less effective in the control of gene expression? The answer to this question is critical for understanding the molecular mechanism by which CREs operate and the constraints under which they evolve. Of the few CREs that have been dissected in detail (Arnosti et al, 1996; Swanson et al, 2010; Struffi et al, 2011), examples range from those with a stringent requirement for a particular arrangement of sites, e.g., the enhanceosome (Thanos and Maniatis, 1995), to examples where multiple sequence arrangements appear to be functional, e.g., the even-skipped stripe 2 enhancer (Ludwig et al, 2000; Hare et al, 2008a). Our finding that the set of orthologous hb posterior stripe CREs vary quantitatively in their function emphasizes that sensitivity to binding site arrangement is a continuous rather than a discrete property. This is consistent with previous work on neurogenic ectoderm CREs, which found that their response to inputs could be fine-tuned over evolution (Crocker et al, 2008). CREs therefore do not need to be classed as either sensitive or insensitive to sequence changes; using our computational framework, their sensitivity can be precisely quantitated in terms of their response to individual inputs.

Regulatory information may be dispersed throughout the hb locus

The pattern produced by the dmel transgenic line differs in both dynamics and shape from the endogenous dmel hb expression pattern (Figure 4B). This discordance might be due to the differences between the reporter construct and the endogenous locus: the constructs use a non-endogenous promoter; the CRE is ∼40 bp away from the promoter in the transgenic construct and ∼3000–6000, bp away in the endogenous locus; and the constructs use a reporter gene, lacZ, which may show different transcription and degradation rates compared with the hb transcript. Alternatively, the constructs may omit relevant regulatory sequence. The use of transgenic reporters is widespread (Ludwig et al, 2005; Crocker et al, 2008; Hare et al, 2008a), making these discrepancies notable, especially for studies where quantitative differences are important.

Several pieces of evidence suggest that transgenic constructs may be missing relevant regulatory sequence. First, the CREs from other species drive more expression in the anterior region than the orthologous dmel CRE in the transgenic animals (Supplementary Figure 8). This variability does not correlate with variability in anterior expression in the endogenous context (Supplementary Figure 5), implying that this additional expression is masked in the endogenous context by repressive signals located elsewhere in the hb locus. Second, the idea of dispersed regulatory information is consistent with the recent identification of ‘shadow’ enhancers, or CREs in the same locus that drive similar expression patterns, reviewed in Barolo (2012). The discovery of many shadow enhancers suggests that regulatory information is generally not limited to the classically identified CREs (Kazemian et al, 2010). In support of this view, experimental in-vivo binding measurements show that regulatory TFs often bind outside annotated CREs (Li et al, 2008), and it remains unclear why these binding events would be non-functional. In addition, scattered blocks of conservation have been found outside the annotated regulatory elements in both the eve and bric-a-brac loci (Hare et al, 2008a; Bickel et al, 2011).

A number of additional experiments may help elaborate the location and mechanism of integration of regulatory information in a locus like hb. To rule out the role of reporter construct artifacts, reporters that more closely reflect the endogenous hb locus with regard to promoter sequence, UTR sequences, and promoter-CRE spacing can be constructed. These additional sequences could also be isolated from the other species and compared in the transgenic context to determine if any of them contribute to expression differences. Our modeling framework can easily accommodate additional parameters that describe the influence of these components on the output. It will also be informative to look at the behavior of a reporter engineered into a construct that includes larger pieces of the hb locus, an experiment enabled by the availability of BAC libraries for several Drosophilids (Ejsmont et al, 2009; Song et al, 2011).

Other contributions to expression divergence

Our modeling framework allows us to separate the contributions of positional information and regulatory logic to the observed differences in hb’s expression pattern between species. Implicit in the calculation of the sequence weight is the assumption that other aspects of the network, namely the potencies of the regulators (p) and their DNA binding preferences, are conserved between species. We made this assumption based on two observations: the strong sequence conservation between orthologous TFs in these species and the similar behavior of orthologous cis-regulatory sequences in the same transgenic dmel context. However, neither of these observations tests this assumption explicitly. Though it is hard to directly measure a regulator’s potency, a data set that includes all four hb CREs in all four transgenic species environments would allow us to infer each regulator’s potency in each species. Though transgenic technology is most facile in dmel, it is possible to make transgenics in an increasing number of Drosophilids (Holtzman et al, 2010).

The high level of sequence conservation in the DNA binding domains of input TFs suggests that their DNA binding specificity is virtually identical, but our sequence weight calculation is limited by available data. We used position weight matrices (PWMs) that describe the binding preferences for dmel proteins to calculate the sequence weights for each CRE (Bergman et al, 2005). Though this calculation is technically correct for the transgenic experiments, ideally, we would use PWMs describing the binding preferences of the TFs from dmel, dyak, and dpse in the sequence weight calculations in the endogenous context. However, even if DNA binding specificities prove to be identical, changes outside of the DNA binding domain may also affect gene expression through other means, like changes in protein–protein interactions. These are harder to measure with current techniques, but are critical for a detailed understanding of the evolution of this network.

Another limitation of our method is the use of relative expression measurements. In fitting a model in a single species, absolute measurements are unnecessary because fit parameters include the effect of concentration differences between regulators. However, absolute concentrations of the same gene in different species may vary. This would manifest in two ways. First, differences in expression levels may contribute to variation in the parameter values of the ‘best fits’ for sets of orthologous regulators (see Table I). Second, when parameters fit in one species are applied to another, differences in expression level may contribute to a decrease in the ‘applied fits’. As imaging technologies improve, it is likely that obtaining absolute measures of expression will become routine and will circumvent this issue.

A simple modeling framework for comparative analysis of transcriptional circuits

We began our study with a circuit level model of the hb posterior stripe that was agnostic to sequence information. Other sequence-agnostic models of the regulatory network have been used to study other facets of the system, e.g., the topology and the manner in which canalization is achieved (Perkins et al, 2006; Manu et al, 2009). However, due to their interconnected, network level properties, these models are not suitable for determining the sources of expression divergence in a single circuit. Our model, while less detailed than these previous models, was constructed specifically to allow us to dissect the sources of quantitative expression differences between species. Given the complexity of transcriptional regulation, it is likely that no single modeling framework will be appropriate for every question (Wunderlich and DePace, 2011). We anticipate that the increase in quantitative, systematic data for transcriptional networks will be accompanied by an increase in models appropriate for different biological questions.

To account for the regulatory sequence contribution to gene expression divergence, we developed a simple measure of relative CRE sequence function. Other predictive models of Drosophila CRE function have been developed by fitting many different types of CREs simultaneously, using a thermodynamic framework (Segal et al, 2008; He et al, 2010). These studies systematically assessed the influence of cooperativity and local binding site arrangement on CRE output. However, they are not accurate enough to predict subtle quantitative differences in expression observed between closely related species, and sometimes fail to predict expression of orthologous CREs entirely. By fitting the same parameters to different types of CREs, context-dependent rules may be obscured, e.g., TFs that act as activators in one context and repressors in another appear to have average activities of zero.

Here, we take a fundamentally different approach by comparing activities of orthologous CREs from closely related species, where we can assume orthologous sequences are built using similar rules. When done systematically for many CREs, this approach may be particularly useful for discerning rules of CRE architecture. By characterizing natural sequence variants that have been filtered by evolution to be functional but differ quantitatively, we likely need to examine many fewer sequences than if we were to characterize a random collection of synthetic CREs. In support of this argument, work from Fakhouri et al (2010) has shown than synthetic CREs built from a limited number of components and designed to test the influence of local sequence arrangement can be useful for discovering specific rules about CRE architecture.

Our approach of comparing relative CRE sequence function can also be used to suggest new experiments. We can calculate the sequence weights of the hb posterior stripe CRE in other sequenced species and use them to predict expression patterns. This approach can focus time-intensive experiments on relevant subsets of CREs. We are particularly interested in CREs with pervasive sequence rearrangements and conserved output as well as those with small-scale sequence changes and divergent output.

It is notable that a linear model captures critical aspects of hb regulation. The importance of cooperativity and synergy in this system have been well documented (Simpson-Brose et al, 1994; Arnosti et al, 1996; Burz et al, 1998; He et al, 2010). Since non-linear effects can produce sharp, narrow stripes of gene expression, it is possible that they are less important for the graded expression patterns of the gap genes and are more important for the expression of sharply defined expression patterns, such as the pair-rule genes. The linear model also implies that the effects of the regulators on the output are additive in this setting, suggesting that the ‘information display’ model of CRE interpretation may be at play at this locus (Kulkarni and Arnosti, 2003). Though the linear model represents a simplification, it recapitulates known features of hb regulation. For example, Ashyraliyev et al (2009) identify the importance of hkb in setting the posterior border of hb expression. By dropping regulators from our model, both individually and in pairs, we also observe the importance of hkb in the accurate prediction of hb expression (Supplementary Figure 6).

Interpretation of coefficients

Aside from the five regulators included as inputs, there is evidence that other TFs are important for the formation of the hb posterior stripe, e.g., caudal and Zelda (Jaeger, 2011; Nien et al, 2011). We excluded both Zelda and caudal because their expression patterns have not been measured in the relevant species. Zelda is expressed in a uniform pattern in the embryo (Liang et al, 2008), so any contribution to inter-species divergence would be from changes in its level, a quantity better assessed by other experimental techniques, e.g., qPCR or quantitative western blot. In its current form, the effects of both of these activators, as well as other factors are included in the constant term in Equations (3) and (4). We calculated the sequence weight for caudal, which is 1.10 for dyak and 0.79 for dpse and dper. The constant values for dmel, dyak, and dpse are 0.4833, 0.5688, and 0.4293, respectively, which show a qualitative trend similar to that of the caudal sequence weight, providing circumstantial evidence that our interpretation of the constant term is correct.

Sources of upstream variation in the anterior-posterior patterning system

Our model does not address the sources of the positional variation of hb’s regulators, but our data set may be useful for addressing this question. One possibility is that variation in the morphology of the embryos, in terms of shape, nuclear number, and density has ramifications for the output of this patterning system. Our data set spans embryos with variation in nuclear number (species averages range from 5087±327 to 6128±348 nuclei), egg length (394±31 to 452±23 microns), and embryo surface area (143 000±12 100 to 198 000±16 000 microns²) (Fowlkes et al, 2011). A different type of model that includes morphogen behavior in this range of morphological contexts might prove useful for addressing this issue. Other possible sources of variation include translation rates, degradation rates, and post-translational modifications. These control mechanisms operate in this system (Tautz and Pfeifle, 1989; Thomsen et al, 2010; Kim et al, 2011) and could potentially be included in this framework.

Connecting regulatory sequence and function

In previous work, we measured the expression patterns of several key TFs and developed a metric to compare cellular gene expression profiles pair-wise between three species (Fowlkes et al, 2011). The cellular gene expression profile reflects the input/output relationship of many CREs operating in the system. Therefore, the expression distance metric we developed provides a global view of regulatory similarity between the three species. However, without further analysis the similarities and differences are not attributable to any particular input/output function. In this study, we undertook a detailed analysis of a particular input/output function using our comparative data. Our results are consistent with the view provided by the expression distance metric, where the cells near the hb posterior stripe were identified as having similar cellular gene expression profiles. Comparison of cellular gene expression profiles may prove to be a relatively simple and unbiased way to pinpoint conserved and divergent regulatory functions for further study.

Determining the origins of quantitative expression differences between species will advance our understanding of transcriptional regulation in two ways. First, linking sequence changes to quantitative differences in expression patterns for many CREs may identify rules governing enhancer architecture. CREs in this system have been extensively annotated using transgenic experiments (Gallo et al, 2011), functional genomic data (Consortium et al, 2010; Kvon et al, 2012), and sequence conservation (Berman et al, 2004; Sinha et al, 2004; Odenwald et al, 2005). Application of our method to other CREs in additional species is a clear future direction. Second, understanding how transcriptional circuits evolve, both in terms of their overall output and in terms of their individual components, will provide insights into how genetic changes are either amplified or buffered to influence generation of new phenotypes. Our experimental and computational approach lays the groundwork for these goals.

Materials and methods

Identification of predicted transcription binding sites

To identify predicted TF binding sites for Figure 1B, we used Patser (http://ural.wustl.edu/software.html), with a GC content of 0.406, a P-value cutoff of 0.003, and PWMs derived from Bergman et al (2005).

Creation of transgenic flies

We used the dmel hb posterior stripe CRE identified in Berman et al (2004), element hb_Hz1.4, with an ∼100 bp buffer on each side to ensure completeness (Release 5 coordinates 3R:4526471-4528036). Orthologous CREs were identified using the genome-wide alignments available in the UCSC Genome Browser (Fujita et al, 2011) and the coordinates are as follows: dyak: 3R:8589892-8591517 (Nov. 2005 assembly), dpse: 2:27088673-27090287 (Nov. 2005 assembly), and dper: super_6:2470507-2472121 (Oct. 2005 assembly). The four posterior stripe CREs were amplified from genomic DNA libraries from the sequenced lines (Drosophila Species Stock Center, https://stockcenter.ucsd.edu) using primers that contain species-specific sequences and synthetic cut sites for NotI and BglII, with the exception of the dmel posterior stripe CRE. The dmel CRE sequence contained a BglII cut site, so NotI was used on both ends. Each PCR product was digested with BglII and/or NotI and inserted into the multiple cloning site of the pBΦY vector (Hare et al, 2008a). The pBΦY vector contains the dmel eve basal promoter (2R:5866782-5866986) driving lacZ and also has the attB site necessary for site-specific integration using the ΦC31 system (Fish et al, 2007). Each plasmid was then co-injected with the ΦC31 integrase into w¹¹⁸ flies carrying the attP2 integration site (Groth et al, 2004) by Genetic Services, Inc. Transformant flies were then homozygosed.

In-situ hybridization

Whole mount in-situ hybridization was performed as described in Luengo Hendriks et al (2006). In brief, 0–4 h old embryos (25°C) were collected, dechorionated, fixed in a mixture of formaldehyde and heptane, and devitellinized in a mixture of heptane and methanol. Embryos were then post-fixed in formaldehyde and washed several times in a formamide-based hybridization buffer. The embryos were incubated at 56°C with two full-length cDNA probes, a DIG-labeled probe for the fiduciary marker, fushi tarazu (ftz), and a DNP-labeled probe for lacZ. The embryos were then successively stained using anti-DIG-HRP (anti-DIG-POD; Roche, Basil, Switzerland) and anti-DNP-HRP (Perkin-Elmer TSA-kit, Waltham, MA, USA) antibodies, using reactions with coumarin- and Cy3-tyramide (Perkin-Elmer). To stain the nuclei, embryos were treated with RNaseA and then stained with Sytox Green (Invitrogen, Carlsbad, CA, USA). The embryos were mounted in DePex (Electron Microscopy Sciences, Hatfield, PA, USA), using a bridge of #1 coverslips to preserve embryo morphology.

Image acquisition, image processing, and atlas creation

Stained and mounted embryos were imaged and processed using the methods described in Luengo Hendriks et al (2006) and Fowlkes et al (2008). Briefly, the three-dimensional image stacks of each embryo were acquired using 2-photon laser scanning microscopy on a Zeiss LSM 710 with a plan-apochromat 20 × 0.8 NA objective. Using the software described in Luengo Hendriks et al (2006), each image file was converted into a PointCloud, a text file that includes the location and levels of gene expression for each nucleus in the embryo.

Using the expression pattern of the fiduciary marker ftz, embryos were registered to a representative embryo (template) with the methods described in Fowlkes et al (2008). The registered embryos were then combined with the data from Fowlkes et al (2008) to create a gene expression atlas, a text file that contains the average expression values of hb’s five regulators and the lacZ output from each of the four transgenic lines in each cell of the embryo. The gene expression atlas includes data from 64 embryos from the dmel line, 57 embryos from the dyak line, 52 embryos from the dpse line, and 51 embryos from the dper line. Each time point average included the data from at least 4 embryos, with an average of 10 embryos per time point. These blastoderm-stage embryos were sorted into time points by visualizing them using phase contrast optics and observing the degree of membrane invagination. The six, ∼10 min time points correspond to 0–3%, 4–8%, 9–25%, 26–50%, 51–75%, and 76–100% membrane invagination and were judged by using the side of the embryo where membrane invagination is the furthest progressed.

Characterization of stripe boundary positions and size

The analysis of hb posterior stripe boundary positions and the number of cells in the stripe was done in MATLAB using the PointCloud toolbox (http://bdtnp.lbl.gov/Fly-Net/bioimaging.jsp?w=analysis). Using the stripe finding functions included in the toolbox, we located the stripes in each individual PointCloud used to construct the gene expression atlases, and we then recorded the boundary positions and number of cells located in each embryo’s stripe.

Modeling of hb posterior stripe

To carry out the modeling of the posterior stripe, MATLAB was used to implement standard multiple linear regression techniques using the glmfit command. The matrix of independent variables had a row for each cell at each time point and five columns corresponding to the relative expression levels of each of the five regulators used in the study. The dependent variable vector had an equal number of rows and one column corresponding to the level of lacZ or hb in each cell at each time point.

To calculate the ROC AUC, we calculated the ROC curve by first thresholding the experimental data. The threshold was calculated as the mode of the target expression data plus one standard deviation:

Then, one species at a time, we varied the threshold applied to the predictions of the linear model, considering all points below the threshold as an ‘off’ prediction, and all points above the threshold as an ‘on’ prediction. For each threshold, we calculated the true positive rate, i.e., the fraction of experimentally verified ‘on’ cells that are predicted correctly, and the false positive rate, i.e., the fraction of the experimentally ‘off’ cells that are predicted incorrectly. We plot the true positive rate as a function of the false positive rate and calculate the area underneath the curve using the trapezoidal rule. To calculate the statistical significance of an individual ROC AUC, we use the non-parametric Mann–Whitney U-test. To compare the values of two ROC AUCs, we use a test based on the Mann–Whitney U-test, as implemented in the StAR software (Vergara et al, 2008).

To do the 10-fold cross-validation, either the dmel endogenous or the transgenic data set was used. The data set was split into 10 roughly equal fractions. In turn, each fraction was left out of the set used to train the multiple linear regression, and then used to evaluate the resulting model.

Calculation of sequence weights

To calculate the sequence weight of a given sequence for a given TF c(s), we use the following formula

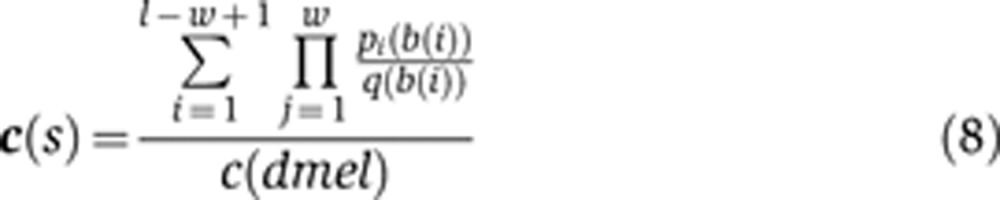Here, l is the length of the sequence being considered, w is the width of the PWM of the TF, b(i) is the base at position i of the sequence, p_j(b) is the frequency of seeing base b at position j of the PWM, and q(b) is the background frequency of base b. When multiplied by a concentration, this value is roughly proportional to the total number of TF molecules bound to a sequence, assuming the sites are not saturated (Supplementary information). To look for saturated binding sites, i.e., very strong sites that will be occupied with a high probability even at low concentrations of TF, we searched for binding sites that accounted for 50% or more of the total value of the sequence weight and found a single hkb site in the dyak posterior stripe CRE that fit this criteria. To avoid the presumably unrealistic impact of this single binding site, we thresholded its value to its 99th percentile value.

Here, we again use a background GC content=0.406 and the PWMs from Bergman et al (2005). The sequence weights we use in our model c(s) are vectors of length 5, with each entry consisting of the sequence weight for one of the five regulators. We compared the performance of these PWMs with those derived from bacterial one-hybrid (Noyes et al, 2008) and SELEX (Li et al, 2011) experiments. The qualitative performance of the model is independent of the PWM set used and is discussed in more detail in Supplementary Figure 10. We chose to use the PWMs from Bergman et al (2005) as they gave the highest performance on the transgenic lines. To calculate the sequence weights for the posterior stripe CRE, we used the sequences in our transgenic constructs.

Supplementary Material

Supplementary Material

Supplementary Figures S1-10