A Single Mutation in a Tunnel to the Active Site Changes the Mechanism and Kinetics of Product Release in Haloalkane Dehalogenase LinB

Background: Tunnel properties affect ligand passage in enzymes with buried active sites.

Results: A tunnel mutation from leucine to tryptophan changes the mechanism of bromide ion release from haloalkane dehalogenase LinB.

Conclusion: Interactions of the bromide ion with the tryptophan increase free energy barrier for its passage, causing the reaction mechanism change.

Significance: The results provide guidelines for enzyme engineering.

Abstract

Many enzymes have buried active sites. The properties of the tunnels connecting the active site with bulk solvent affect ligand binding and unbinding and also the catalytic properties. Here, we investigate ligand passage in the haloalkane dehalogenase enzyme LinB and the effect of replacing leucine by a bulky tryptophan at a tunnel-lining position. Transient kinetic experiments show that the mutation significantly slows down the rate of product release. Moreover, the mechanism of bromide ion release is changed from a one-step process in the wild type enzyme to a two-step process in the mutant. The rate constant of bromide ion release corresponds to the overall steady-state turnover rate constant, suggesting that product release became the rate-limiting step of catalysis in the mutant. We explain the experimental findings by investigating the molecular details of the process computationally. Analysis of trajectories from molecular dynamics simulations with a tunnel detection software reveals differences in the tunnels available for ligand egress. Corresponding differences are seen in simulations of product egress using a specialized enhanced sampling technique. The differences in the free energy barriers for egress of a bromide ion obtained using potential of mean force calculations are in good agreement with the differences in rates obtained from the transient kinetic experiments. Interactions of the bromide ion with the introduced tryptophan are shown to affect the free energy barrier for its passage. The study demonstrates how the mechanism of an enzymatic catalytic cycle and reaction kinetics can be engineered by modification of protein tunnels.

Introduction

The passage of small molecules through protein channels and tunnels is a phenomenon occurring in many biological processes, including passage of polar and charged species through membrane channels (1, 2), polypeptide passage through the ribosomal exit tunnel (3, 4), and ligand access into and egress from deep protein-binding sites (5–9). In enzymes, the active site is often not located on the protein surface, but it is buried and connected to the bulk solvent through tunnels that may be permanent or transient. The importance of amino acid residues that affect the size and shape of the tunnels connecting the active site and the protein surface for substrate specificity and enzymatic activity has been demonstrated for haloalkane dehalogenases (HLDs)⁷ (10–13). The large amount of structural and biochemical data available for HLDs makes this family of enzymes a good model for basic enzymology studies.

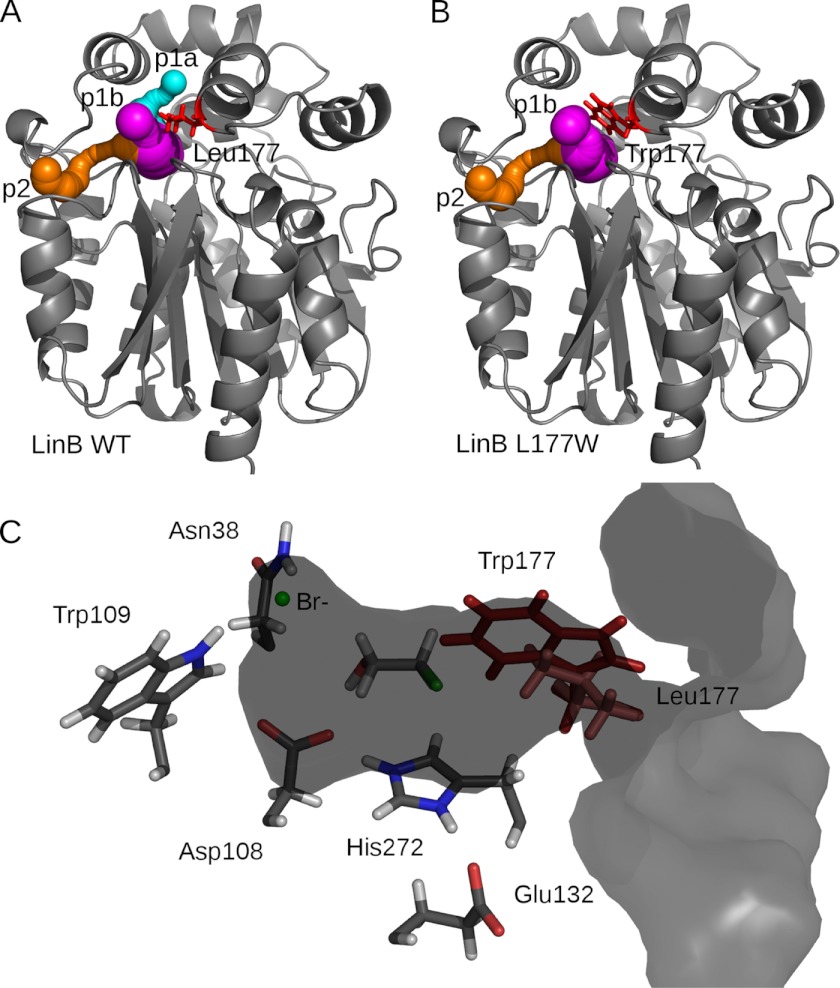
HLDs are bacterial enzymes that cleave carbon-halogen bonds by a hydrolytic mechanism leading to the formation of the corresponding alcohol, a halide ion, and a proton (14). The active site of HLDs is deeply buried between the main domain and the cap domain and is connected with the surrounding solvent by several tunnels (15) (Fig. 1A). Computer-assisted design and engineering of the tunnels in the haloalkane dehalogenase DhaA (16) from Rhodococcus rhodochrous sp. NCIMB 13064 resulted in a biocatalyst with 32-fold improved catalytic efficiency toward the toxic environmental pollutant 1,2,3-trichloropropane (12). Using transient kinetics and molecular simulations, the mutants were shown to change the rate-limiting step from the first reaction step to the product release by limiting the accessibility of the active site to water molecules and hindering product egress. Systematic engineering of a tunnel bottleneck residue in the HLD LinB from Sphingobium japonicum UT26 demonstrated the dependence of specificity and activity on the size and physico-chemical character of the tunnel (11). The modified tunnel residue, Leu-177, was selected based on a sequence alignment that identified this position as the most variable among all residues forming the active site and the tunnels. Of the 15 mutants constructed by site-directed mutagenesis with a substitution at this position, the LinB L177W mutant, which has a bulky tryptophan residue blocking one of the enzyme's main tunnels (Fig. 1B), showed the most profound changes in the substrate specificity. A dramatic decrease of activity toward the best substrate, 1,2-dibromoethane, to 7% of the wild type (LinB WT) value was observed.

FIGURE 1.

A, crystal structure of LinB WT (Protein Data Bank code 1MJ5) (gray schematic) with CAVER-calculated tunnels shown in sphere representation as follows: p1a tunnel (cyan), p1b tunnel (magenta), and p2 tunnel (orange). B, model structure of LinB L177W with tunnels, same color-coding as for LinB WT. C, LinB WT in surface representation, clipped through the active site and p1b tunnel. The catalytic residues and halide-stabilizing residues are shown in stick representation (Leu-177, light red), together with the 2-bromoethanol product docked in the active site with AutoDock 4.0 and the bromide ion. The position of the modeled Trp-177 (dark red) is shown for reference.

Here, we have performed steady-state and transient kinetics experiments to measure the equilibria and rates of product release for the LinB L177W mutant. We used the CAVER 3.0 program (17) for the analysis of the geometry of the tunnels in the protein structures of LinB WT and LinB L177W obtained using classical molecular dynamics (MD) simulations, and we compared these tunnels with product egress pathways identified using the Random Acceleration Molecular Dynamics (RAMD) (18) simulation technique, which was specifically developed to allow an unbiased simulation of ligand release from deeply buried protein-binding sites. Subsequently, we calculated the free energy profiles and identified energy barriers for the egress of a bromide ion along the preferred tunnel using the Adaptive Biasing Force (ABF) method (19, 20), which enhances the sampling during molecular dynamics simulations by applying a history-dependent bias that cancels the running estimate of the local free energy gradient. The results of the free energy calculations allow a quantitative comparison with the rates of the reaction obtained by transient kinetics experiments. To understand the molecular details of the product release process, we investigated specific interactions of the bromide ion with tunnel-lining residues. We find that the higher free energy barrier for the passage of the bromide ion in LinB L177W compared with LinB WT is caused by electrostatic interactions of the bromide ion with the tryptophan introduced at position 177.

EXPERIMENTAL PROCEDURES

Steady-state Fluorescence

The steady-state fluorescence was measured in a 1-cm quartz cuvette using a SPEX FluoroMax (SPEX Industries, Edison, NJ) fluorescence spectrometer. Fluorescence emission at 340 nm from Trp residues was observed upon excitation at 295 nm. The fluorescence of LinB WT, LinB L177W, bovine serum albumin (BSA), and N-acetyltryptophan amide (NATA) was recorded at different bromide ion concentrations ranging from 0 to 2 m.

Stopped-flow Fluorescence

The experiments were performed with the stopped-flow instrument SFM-20 (BioLogic, France) combined with a Jasco J-810 spectropolarimeter (Jasco, Japan) equipped with a xenon arc lamp with excitation at 295 nm and in an SFM-300 stopped-flow instrument (BioLogic, France) combined with MPS-200. Fluorescence emission from Trp residues was observed through a 320-nm cutoff filter supplied with the instruments. All reactions were performed at 37 °C in 100 mm glycine buffer, pH 8.6. Amplitudes and the observed rate constants of single exponential fits were determined using Origin 6.1 (OrigineLab Corp.). The dissociation constants were then evaluated from the amplitudes of fluorescence quench for the kinetically detectable phase and from the initial fluorescence value for the rapid equilibrium phase.

Preparation of Structural Models

The crystal structure of LinB WT (Protein Data Bank code 1MJ5, resolution 0.95 Å) (21) was taken as a starting point for modeling. The terminal His tag residues were removed, and atoms with alternative crystallographic positions were modeled in alternate location A. The LinB L177W structure was modeled based on the LinB WT structure using the mutagenesis wizard in PyMOL Version 1.0r2 (22), adopting the rotamer with the fewest clashes. Docking of the 2-bromoethanol product into the LinB WT structure was performed using the AutoDock 4.0 program suite (23). The docked position of 2-bromoethanol in the active site is shown in Fig. 1C. The polar and nonpolar hydrogens in the LinB WT and LinB L177W protein structures were added using WHATIF Version 5.2 (24). The Gln-152 side chain amide group was rotated 180°, and His-272 was modeled as doubly protonated, based on optimization of the hydrogen-bond network by WHATIF Version 5.2 (24) and in accordance with the MD simulations and analysis of the LinB crystal structure (21), which showed His-272 to be at least partially doubly protonated in the ligand-free form of the enzyme. The assumption is that the alcohol product leaves before the proton and the halide ion, and therefore the doubly protonated His-272 is the most relevant titration state, as suggested by experiments for the DhlA haloalkane dehalogenase (25, 26). All crystallographic water molecules not overlapping with the docked ligands were added to the complexes, and the active site chloride ion was converted to a bromide ion. The system was neutralized by the addition of 12 sodium cations. Finally, the complexes were immersed in a rectangular box of TIP3P (27) water molecules with a minimum water layer thickness of 10.0 Å. About 12,760 water molecules were added to solvate each system.

Analysis of Tunnels in Static Structures

The CAVER 3.0 beta2 (17) program was used for calculating pathways leading from the buried active site to the solvent in the LinB WT and LinB L177W. Structures containing hydrogen atoms were used, but no water molecules or ligands were present during the tunnel calculation. The non-hydrogen atoms of the structure were approximated by 12 spheres of the size of a hydrogen atom. The position of the bromide ion in the active site was defined as the initial starting point from which the tunnels to the bulk solvent were searched. The tunnel search was performed using a probe of 0.7 Å radius and a cost function exponent of 2. The identified tunnels were clustered by hierarchical average link clustering based on the pairwise distances of the tunnels computed using a linear transformation coefficient of 20 and a distance threshold of 27.

MD System Equilibration

Energy minimization and equilibration were performed with the AMBER 9 (28) software using the ff99SB force field (29). Parameters for halogenated ligands were taken from Kmunicek et al. (30). Parameters for the bromide ion were taken from Lybrand et al. (31). The equilibration protocol consisted of the following: (i) 500 steps of steepest descent energy minimization and 500 steps of conjugate gradient minimization of water molecules and ions, with the rest of the system restrained harmonically with a force constant of 500 kcal·mol⁻¹·Å⁻²; (ii) 1000 steps of steepest descent minimization and 1500 steps of conjugate gradient minimization of the whole system; (iii) gradual heating of the whole system from 0 to 300 K in 20 ps, maintaining the temperature with a Langevin thermostat and temperature coupling constant of 1.0 ps, in a constant volume periodic box. The positions of the protein and ligand atoms were maintained by weak restraints with a force constant of 10.0 kcal·mol⁻¹·Å⁻². The time step was 2 fs, and all bonds involving hydrogen atoms were constrained by using the SHAKE algorithm (32). The Particle Mesh Ewald method was used for the long range electrostatic interactions with a nonbonded cutoff of 10 Å; and (iv) 300 ps of unrestrained MD simulations at 300 K in an isothermal-isobaric (NPT) ensemble, using the same parameters as in the previous equilibration step and a constant pressure of 1.0 atm with isotropic position scaling and a pressure relaxation time of 2.0 ps.

MD Production Runs

The production runs were performed with the NAMD version 2.7b1 simulation package (33), using the same AMBER force field parameters as in the equilibration phase. The time step was 2 fs, and all bonds involving hydrogen were constrained with SHAKE. The Particle Mesh Ewald method was used to calculate Coulomb interactions. A cutoff of 10 Å was applied for nonbonded interactions, and switching functions were turned off. The simulation was propagated for 10 ns in the microcanonical (NVE) ensemble, and snapshots were gathered every 2 ps. Additionally, 10-ns production runs of the complexes of both LinB WT and LinB L177W with the bromide ion, but without any alcohol product were performed, using the same simulation parameters.

Analysis of Tunnels in MD Trajectories

CAVER 3.0 beta2 (17) was used for the calculation of tunnels in the 10-ns MD simulations of LinB WT and LinB L177W. For both systems, 5000 snapshots were analyzed. Similarly to the static structures, water molecules or ligands were removed prior to the tunnel calculation, and the non-hydrogen atoms of the structure were approximated by 12 spheres of the size of a hydrogen atom. The initial starting point of the tunnel search was first specified by LinB atoms 578, 1655, 2072, and 3242 and was automatically optimized to prevent its collision with protein atoms. The tunnel search was performed using a probe of 1 Å radius and a cost function exponent of 2. Redundant tunnels in each frame were removed using a linear transformation coefficient of 20 and a threshold of 0.5. Clustering of the tunnels identified during each simulation was performed by hierarchical average link clustering based on the pairwise distances of the tunnels computed using a linear transformation coefficient of 20 and a distance threshold of 40. Additionally, tunnels were also calculated using a probe radius of 0.7 Å to obtain a more precise estimate of the differences in the bottleneck radii of the individual tunnels.

RAMD Simulations

RAMD simulations (18) of the complexes of LinB WT and LinB L177W with 2-bromoethanol were performed in NAMD version 2.6 (33), using the RAMD 3.0 Tcl script. The starting snapshots of the systems for RAMD simulations were extracted from the production runs after 1 ns and after 2 ns of production MD. The maximum duration of each RAMD simulation was set to 1 ns; when a ligand exit event was detected, i.e. the distance between the ligand center of mass and the protein center of mass exceeded 30 Å, the simulation was halted. The RAMD parameters to be used were first tested on the LinB L177W system, the final set of parameters used for both systems containing the alcohol product, i.e. the complexes of LinB WT and LinB L177W with 2-bromoethanol were as follows: force constant, 5 kcal·mol⁻¹·Å⁻¹, and threshold distance. 0.001–0.004 Å, and force direction re-evaluation every 10 steps. Eight runs of a maximum length of 1 ns were performed for each system. RAMD simulations of bromide ion egress were performed without any alcohol product present in active site. For consistency, the same magnitude of the applied force was used (5 kcal·mol⁻¹·Å⁻¹) as for 2-bromoethanol, but due to the lower mass of the bromide ion, the threshold distance was increased to 0.005 Å to keep the number of applied RAMD force vectors in the range of approximately 10 in each run.

Analysis of MD and RAMD Simulations

The stability of the MD trajectories was assessed by plotting total energy, root mean square deviation, and radius of gyration, calculated using the Ptraj module of AMBER 9 (28), against time (data not shown). Per residue B-factors were also measured with Ptraj. The trajectories were visually inspected with VMD (Visual Molecular Dynamics) program (34). Analysis of the egress routes in RAMD was performed by analyzing the residues contacted by the ligand during egress. The annotation of the routes was based on the similarity to the tunnels observed in the crystal structure of LinB WT using CAVER (Fig. 1A).

ABF Simulations

ABF simulations of bromide ion exit from LinB WT and LinB L177W were performed using the COLVARS module of NAMD 2.7b3. In COLVARS, the reaction coordinate (RC) describing the bromide ion exit from the enzyme was defined as a collective variable, and an adaptive biasing force (20) was applied along it. The collective variable selected to define the RC was the distance of the bromide ion from the midpoint of atom ND2 of residue Asn-38 and atom NE1 of residue Trp-109 nitrogens of the halide-stabilizing residues.

To test which pathways are most likely to be sampled by the ABF method, 10 independent ABF runs were performed, using one window spanning the first half of the RC (1–15 Å) with bins of 0.25 Å and a simulation time of 2 ns in both the LinB WT and the LinB L177W systems. The distance from the nitrogens of the halide-stabilizing residues to the p1b tunnel entrance from bulk solution is about 14.5 Å in both the LinB WT and the LinB L177W. The ABF simulations were started from different snapshots of the first 1 ns of the production MD. This, together with the random assignment of initial velocities, should ensure sufficiently different starting conditions in each run.

For the calculation of the free energy profile of bromide ion egress, ABF simulations were used in which the RC was split into smaller windows of 2 Å and with a bin size of 0.2 Å to enhance the efficiency of sampling. The starting snapshots for each window were extracted from the test runs, with the bromide ion in the p1b tunnel and at the appropriate distance from the nitrogens of the halide-stabilizing residues. The RC was subsequently extended to 27 Å, taking starting snapshots from previous windows, to reach a converged free energy, as expected for the situation where the bromide ion is fully in bulk solvent, due to the inclusion of the Jacobian correction term (20). The interaction energy of the bromide ion with the protein residues and with water in each snapshot of the ABF simulations was calculated using the VMD (Visual Molecular Dynamics) program NAMD Energy plugin Version 1.4.

Free Energy Perturbation (FEP) Calculations

To compute the binding free energy of the bromide ion to the protein, FEP calculations were performed in which the bromide ion was decoupled from its binding site in LinB, from the bulk aqueous solution containing the protein and counter-ions as in the ABF calculations, and from plain water without any neutralizing counter-ions.

The starting coordinates for the decoupling of the bromide ion from the “bound state” in the LinB WT-binding site were taken from the corresponding LinB WT production MD after 1 ns of simulation. The starting coordinates for decoupling of the bromide ion from the “unbound state,” i.e. from bulk water containing the LinB enzyme and 12 sodium counter-ions, were taken from the last ABF window (25–27 Å). For the simulation of bromide ion decoupling from plain water, the bromide ion was solvated in a box of water of wall thickness 39.0 Å (creating a simulation box of the same size as that with protein), and the box was energy-minimized and equilibrated with the AMBER 10 software (35) and then propagated for 1 ns in the microcanonical (NVE) ensemble with NAMD Version 2.7b3 before the FEP calculation was started. The AMBER ff99SB force field (29) was used for all simulations.

The binding free energy of the bromide ion was calculated using the “double decoupling method” (36). The λ parameter was varied between 0 and 1 in steps of 0.1. Forward and backward runs with 10 ps equilibration and 100 ps production per step were performed, which were then combined using the simple overlap sampling method (37). To avoid the so called “end-point catastrophe,” the electrostatic interactions were not introduced before the coupling parameter λ reached a value of 0.5. Furthermore, a soft-core van der Waals radius-shifting coefficient C_shift = 5.0 was used, shifting the interatomic distances used in the Lennard-Jones potential as shown in Equation 1,

To prevent the bromide ion from leaving the binding site during decoupling at large values of λ, a flat-bottomed harmonic well potential shown in Equation 2 was applied using the Colvars module,

and

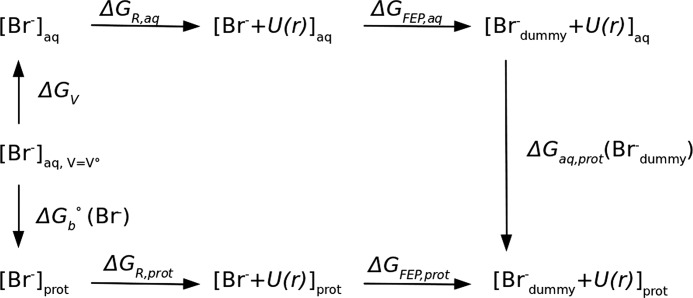
A wall constant K of 100 kcal·mol⁻¹·Å⁻² was used, with a bottom radius r₀ of 1.2 Å. For consistency, the same restraint was applied in the unbound state simulations. The bromide-binding free energy was calculated using the thermodynamic cycle given in Fig. 2.

FIGURE 2.

Thermodynamic cycle used to determine the standard free energy of binding ΔG_b⁰ of a bromide ion to LinB using the double decoupling method. ΔG_FEP is the free energy for Br⁻ decoupling obtained from the FEP simulation (Br_dummy⁻ stands for the fully decoupled, noninteracting particle); ΔG_V is the free energy for changing from the standard-state volume V⁰ to the sampled unbound volume; ΔG_R is the free energy to remove the restraining potential U(r). Subscripts aq and prot denote positions in bulk solvent environment and in at the protein-binding site, respectively.

To determine the standard free energy of binding ΔG⁰, the free energy ΔG_V for changing from the standard-state volume V⁰= 1661 ų, which corresponds to a 1 m concentration, to the sampled unbound volume and the free energy ΔG_R to remove the restraints have to be included (38, 39). The ΔG⁰ of binding can then be calculated as shown in Equation 3,

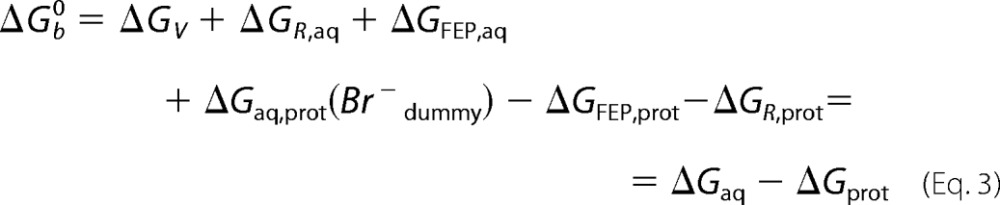where ΔG_V is the ratio of the sampled unbound volume V_u to the standard-state volume V⁰ as shown in Equation 4,

and ΔG_R is the correction due to the energetic contribution of the restraint potential U(r) felt by the decoupled particle (40) shown in Equation 5,

The volume sampled by the bromide ion in the unbound state was calculated using the VMD (Visual Molecular Dynamics) program VolMap plug-in. The ΔG_R term was calculated after completion of the simulations from the restraint potential energies for the conformations generated for the fully interacting bromide ion (λ = 1).

RESULTS

Kinetics of Bromide Ion Binding

Steady-state and transient kinetic data were collected to reveal the effect of the L177W mutation on the mechanism and the rate constant of product release. The steady-state fluorescence of LinB WT, LinB L177W, bovine serum albumin (BSA), and NATA was measured after mixing with different bromide ion concentrations (0–1500 mm). The data were fitted using a modified form of Stern-Volmer quenching Equation 6,

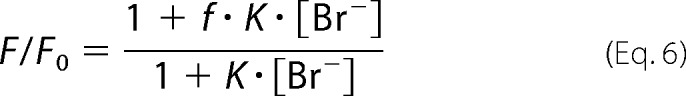where F and F₀ are fluorescence intensities in the presence and absence of bromide, respectively; and K is the quenching constant (which is the apparent association equilibrium constant of the quenching interaction between bromide and a binding site), and f is the fluorescence level of bromide-bound complex relative to the apoenzyme.

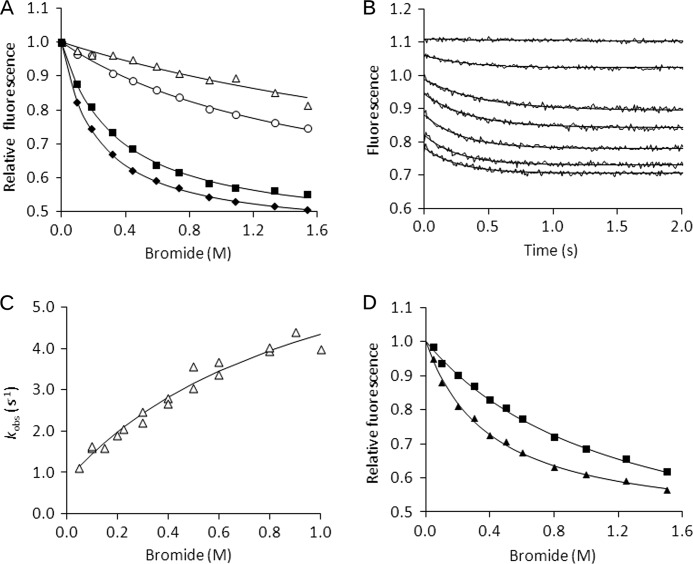
Both BSA and NATA showed nonspecific fluorescence quenching with increasing bromide ion concentration, reflecting the action of the anion as a general fluorescence quencher (Fig. 3A). The LinB WT and LinB L177W fluorescence profiles showed strong additional quenching activity, suggesting specific binding of the bromide ion to both LinB WT and LinB L177W. The resulting dissociation constants calculated from the steady-state fluorescence analysis were 350 ± 20 and 220 ± 10 mm, and the fluorescence level (f) of bromide-bound complex was 0.44 ± 0.01 and 0.43 ± 0.01 for LinB WT and LinB L177W, respectively.

FIGURE 3.

Steady-state and stopped-flow fluorescence analysis of bromide binding at 37 °C in 100 mm glycine buffer, pH 8.6. A, steady-state fluorescence of 5 μm BSA (open triangles), 20 μm NATA (open circles), 20 μm LinB WT (black squares), and 20 μm LinB L177W (black diamonds); solid lines represent the best fits obtained by using Equation 6. B, fluorescence traces obtained upon rapid mixing of 30 μm LinB L177W with bromide ion to a final concentration of 0–2 m; solid lines represent the best fits to the data by using a single exponential equation. C, dependence of observed rate constant (k_obs) of the slow kinetic phase on bromide ion concentration; solid line represents the best fit obtained by using Equation 7. D, dependence of fluorescence values on bromide ion concentration analyzed from LinB L177W stopped-flow fluorescence traces after the rapid phase (squares) and after the overall reaction (triangles), and solid lines represent the best fits obtained by using Equation 6.

The kinetics of bromide ion binding were analyzed using the stopped-flow method (Fig. 3B). The data show a significant difference in the mechanism between LinB WT and LinB L177W. The single step binding of the bromide ion to LinB WT was described previously (41), whereas LinB L177W shows two distinct binding phases that suggest a two-step mechanism of bromide ion binding (Scheme I).

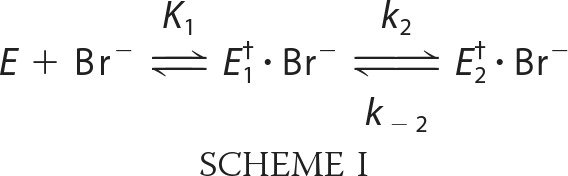The first phase reached rapid equilibrium when the fluorescence quench occurred within the dead time of the instrument (0.5–5 ms), and only the difference in initial fluorescence signal was observed. The equilibrium constant of the first step K₁ = 1 230 ± 160 mm and the fluorescence level of the bromide-bound complex f = 0.45 ± 0.05 were calculated from the dependence of the initial fluorescence quench on bromide ion concentration. The rapid equilibrium phase was followed by the second kinetic phase with a slow decay of fluorescence signal in time. The single exponentials were fitted to the fluorescence traces, and the observed rate constants and amplitudes were used for detailed kinetic analysis. The rate constants for bromide ion binding k₂ = 7.1 ± 1.3 s⁻¹ and release k₋₂ = 0.8 ± 0.2 s⁻¹ were obtained by fitting Equation 7 to the dependence of the observed rate constants on the concentration of the bromide ion (Fig. 3C).

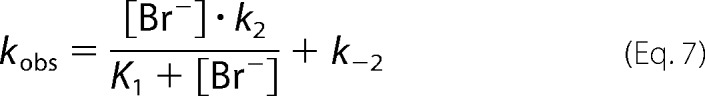Importantly, the data suggest that not only did the mechanism change but also that the rate constant of bromide release was significantly decreased by the tunnel mutation from the value of >500 s⁻¹ observed previously for the LinB WT (ΔG^‡ <14.3 kcal/mol at 310.15 K) to the value of 0.8 ± 0.2 s⁻¹ (ΔG^‡ = 18.3 kcal/mol at 310.15 K) determined for LinB L177W. The value of the equilibrium constant K₁ = 1 000 ± 400 mm calculated from Equation 7 was in good agreement with the value calculated from the initial fluorescence quench (K₁ = 1 230 ± 160 mm). The equilibrium constant for the second step was calculated from the rate constants obtained, K₂ = k₂/k_–2 = 8.9. The data on the dependence of the total stopped-flow amplitudes, the sum of the rapid and slow quench, on bromide ion concentration was fitted to Equation 6 and used for evaluation of the overall dissociation constant (Fig. 3D). The obtained value of K_d = 400 ± 40 mm is in agreement with the value calculated from the steady-state fluorescence quench experiment (K_d = 220 ± 10 mm) (Fig. 3A). It is also nearly identical to the previously reported value for binding of the bromide ion to the LinB WT enzyme with K_d = 470 ± 30 mm (41), suggesting that the mutation in the tunnel altered the mechanism and kinetics of bromide binding and release but did not affect the overall affinity. The rate and equilibrium constants for bromide binding to LinB WT and LinB L177W are summarized in Table 1.

TABLE 1.

Kinetics of bromide binding by LinB WT and LinB L177W determined at 37 °C and pH 8.6

	Kd	K1	K2	k1	k−1	k2	k−2
	mm	mm		mm−1·s−1	s−1	s−1	s−1
LinB WTa	470 ± 30			>1	>500
LinB L177W	400 ± 40	1230 ± 160	8.9	>1	>500	7.1 ± 1.3	0.8 ± 0.2

^a Data are from Prokop et al. (41).

A simple binding experiment cannot be performed with the second product of the 1,2-dibromoethane conversion, because 2-bromoethanol serves as a substrate and undergoes follow-up dehalogenation catalyzed by both LinB WT and LinB L177W. However, the multiple turnover data indicate that both binding and release of 2-bromoethanol occur in a fast single-step process, reaching rapid equilibrium, and cannot be rate-determining during the conversion of 1,2-dibromoethane either by LinB WT or by LinB L177W. The tunnel mutation caused significant effects on the mechanism and kinetics of 2-bromoethanol conversion but did not affect the kinetics of 2-bromoethanol release after the conversion of 1,2-dibromoethane (see the supplemental Appendix).

Tunnels in Static Structures

The tunnels connecting the active site with bulk solvent in LinB WT and LinB L177W were analyzed using the CAVER program (15, 17, 42), which was developed specifically for identification and visualization of tunnels in proteins with buried active sites. The current version employs a fast and accurate algorithm based on decomposition of a metric space using Voronoi diagrams and Delaunay triangulation. In LinB WT crystal structure, three important tunnels were found using CAVER as follows: the p1a tunnel, the p1b tunnel, and the p2 tunnel (Fig. 1), in accordance with the results of Petrek et al. (15). The p1a, p1b and p2 tunnels were previously (15) termed the upper tunnel, the lower tunnel, and the slot, respectively. The p1a tunnel branches off the p1b tunnel at a distance of about 6 Å from the starting point located in the active site. The distance from the starting point to the point where the p1b tunnel reaches the solvent-accessible surface of the protein is about 12 Å. The p1b and p1a tunnels identified by CAVER can thus be considered as two representations of one tunnel with an asymmetric opening (the main tunnel). The radius of the bottleneck for the p1a, p1b, and p2 tunnels was 0.9, 1.3, and 0.9 Å, respectively. In the modeled LinB L177W structure, the p1a tunnel was not found (Fig. 1B), although the p1b tunnel was slightly wider (1.4 Å) and the p2 tunnel retained its radius of 0.9 Å. All other tunnels found in these structures had a bottleneck radius equal or smaller than 0.7 Å.

Classical MD Simulations

In the 10-ns simulations with the alcohol product present in the active site, no spontaneous ligand exit was observed in either LinB WT or LinB L177W. In the simulations without alcohol product, the bromide ion started to leave its binding site near the halide-stabilizing residues after about 2.1 ns, and complete exit via the p1b tunnel was observed after about 2.8 ns of production time in the LinB WT, whereas in the simulation of LinB L177W, no exit of the bromide ion was observed in 10 ns.

Tunnels in MD Trajectories

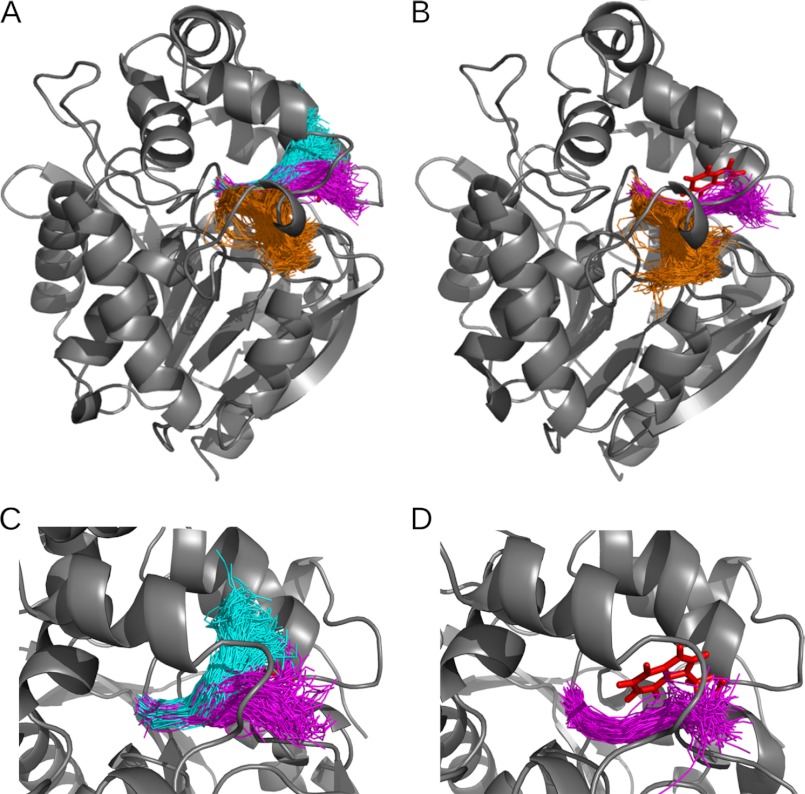
The analysis of the MD simulation snapshots of LinB WT using CAVER 3.0 (17) resulted in identification of three dominant pathways connecting the active site of the enzyme with its surface (Table 2 and Fig. 4A). Based on the classification proposed by Klvana et al. (43), two of these pathways (p1a and p1b) correspond to the p1 tunnel and the remaining one to the p2 tunnel. The p1 tunnel divides into the upper (p1a) and lower (p1b) branch approximately halfway along its length (Fig. 4), and the two branches of the p1 tunnel function as one wide and large tunnel with an asymmetric, hourglass opening, with the Leu-177 residue located at the narrowest part of the tunnel. The other potential pathways were found in <1% of the snapshots and were not analyzed further. Of all the tunnels identified in the analyzed snapshots, the p1 tunnel was by far the most frequently open (80% of the time) for the probe used, i.e. the tunnel had a bottleneck radius ≥1.0 Å. The p1 tunnel was also the widest of all tunnels (average bottleneck radius of 1.1 Å and maximum bottleneck radius of 1.9 Å). The p1a branch of the main tunnel was narrower and less frequently open than the p1b branch (48 versus 73% of the time). The second important pathway p2 was open for the probe used in only 18% of the analyzed snapshots. Compared with the p1 tunnel, it also had a narrower bottleneck (average bottleneck radius of 0.9 Å and maximum bottleneck radius of 1.6 Å).

TABLE 2.

Comparison of the characteristics of the top-ranked tunnel clusters identified in MD simulations of LinB WT and LinB L177W using the CAVER 3.0 program

Tunnel cluster	Percentage of snapshots with identified tunnela		Average bottleneck radiusb		Maximum bottleneck radiusa
	LinB WT	LinB L177W	LinB WT	LinB L177W	LinB WT	LinB L177W
	%		Å		Å
p1b	73	44	1.1	1.0	1.9	1.7
p1a	48		1.0		1.8
p1 (p1b+p1a)	80	44	1.1	1.0	1.9	1.7
p2	18	17	0.9	0.9	1.6	1.5

^a Data were calculated with a probe radius of 1.0 Å.

^b Data were calculated with a probe radius of 0.7 Å.

FIGURE 4.

Top ranked tunnel clusters identified in MD simulations of LinB WT and LinB L177W using CAVER 3.0. The tunnel cluster representing the p1b branch of the main tunnel is colored in magenta; p1a branch of the main tunnel is in cyan; and p2 tunnel is in orange. Tunnels identified in snapshots of the MD simulation are shown as tunnel center lines in one snapshot of protein conformation. Only a subset of the tunnel snapshots is shown for clarity. Other tunnel clusters (identified in less than 1% of MD snapshots) are omitted. Tunnel clusters are identified in LinB WT (A) and in LinB L177W (B). Close-up view is shown of the main tunnel (p1a and p1b) in LinB WT (C) and of the p1b branch of the main tunnel in LinB L177W (D). In LinB WT, the Leu-177 residue is hidden behind the center lines of the tunnels. In LinB L177W, the p1a branch of the main tunnel was not observed; the Trp-177 residue, which blocks the p1a tunnel, is shown in red stick representation. The figure was generated using the PyMOL visualization software.

Analogous analysis of the MD simulation of LinB L177W revealed two dominant pathways corresponding to the p1b and p2 tunnels (Table 2 and Fig. 4B). The p1a tunnel was not found, because the bulky Trp-177 residue blocks this tunnel. Similarly to the LinB WT, other pathways identified in <1% of the snapshots were not analyzed. The p1 tunnel was the most frequently open for the probe used (44% of the time) and the widest of all the tunnels. The second most important pathway p2 was open for the probe used only 17% of the time and had a narrower bottleneck (see Table 2).

Ligand Egress Pathways

To simulate ligand egress from the active site and reveal the preferred egress pathway (tunnel) for both 2-bromoethanol and bromide ion, a series of simulations using the RAMD method was performed. This method was specifically developed for identifying egress routes for ligands (18). The ligand egress may occur on millisecond or longer time scales and therefore can be too computationally demanding to observe in classical MD simulations. In RAMD, the process is sped up by applying a small, artificial, and randomly oriented force on the center of mass of the ligand that permits the ligand to find an exit tunnel without an a priori directional bias. The parameters of the applied force, however, have to be carefully chosen to avoid distortion of the structure of the protein. In summary, this technique allows potential pathways for the ligand egress to be identified but does not provide thermodynamic information.

In the RAMD simulations with 2-bromoethanol, ligand exit events were observed in seven of the eight simulations of the LinB WT and six of the eight simulations of LinB L177W (Table 3). Ligand exit was observed after at least 150 ps. At the same time, at least one simulation without 2-bromoethanol exit was obtained, suggesting the simulation parameters are reasonably balanced. In LinB WT, all tunnels were almost equally preferred by 2-bromoethanol. In LinB L177W, no exit of 2-bromoethanol through the p1a tunnel was observed, and the egress occurred more frequently (four times) through the p1b tunnel than through the p2 tunnel (two times).

TABLE 3.

Frequency of occurrence of ligand exit along the different egress pathways observed in RAMD simulations

Enzyme	Ligand	p1a	p1b	p2	Other	None	tavga	tminb	tmaxc
							ps	ps	ps
LinB WT	2-Bromoethanol	3	2	2		1	260	96	378
LinB L177W	2-Bromoethanol		4	2		2	617	288	937
LinB WT	Bromide ion	3	4	1			98	31	167
LinB L177W	Bromide ion		5	2	1		574	272	933

^a Average exit time was computed for the subset of the eight trajectories simulated for each system in which a ligand exit event was observed.

^b Minimum observed exit times for the given system are shown.

^c Maximum observed exit times for the given system are shown.

Exit of the bromide ion was observed in all simulations in both LinB WT and LinB L177W, and the p1b tunnel was the most frequent exit route in both proteins (Table 3). No exit of the bromide ion through the p1a tunnel was observed in LinB L177W. For both alcohol and bromide ion products, longer average simulation times (excluding trajectories without ligand exit) were observed for LinB L177W than LinB WT. For the bromide ion product, this difference is larger, with average simulation times about six times longer in LinB L177W than in LinB WT.

Free Energy Profiles

The energetics of the bromide ion egress were investigated using the ABF method (20). A requirement for the construction of a free energy profile is adequate sampling of the phase space along the chosen reaction coordinate (ξ). In the ABF method, this is achieved by discretizing the reaction coordinate into small bins, in which the mean force along ξ is estimated from the running ensemble average and is then canceled out by an equal and opposite biasing force. This allows the system to overcome barriers and escape from minima on the free energy landscape, and eventually it leads to uniform sampling of the chosen reaction coordinate. Nevertheless, the convergence properties of the free energy calculation depend upon the relaxation properties of the degrees of freedom other than ξ.

To test which tunnel is preferentially sampled by the ABF technique, 10 independent test runs were performed for both LinB WT and LinB L177W systems, in which the bromide ion was placed in its binding site and gradually pushed away by the applied adaptive biasing force. In both systems, the p1b tunnel was the most frequent exit route, being observed in all 10 simulations in LinB WT and in 7 out of 10 cases in LinB L177W. In LinB L177W, the other tunnel used by the bromide ion was the p2 tunnel.

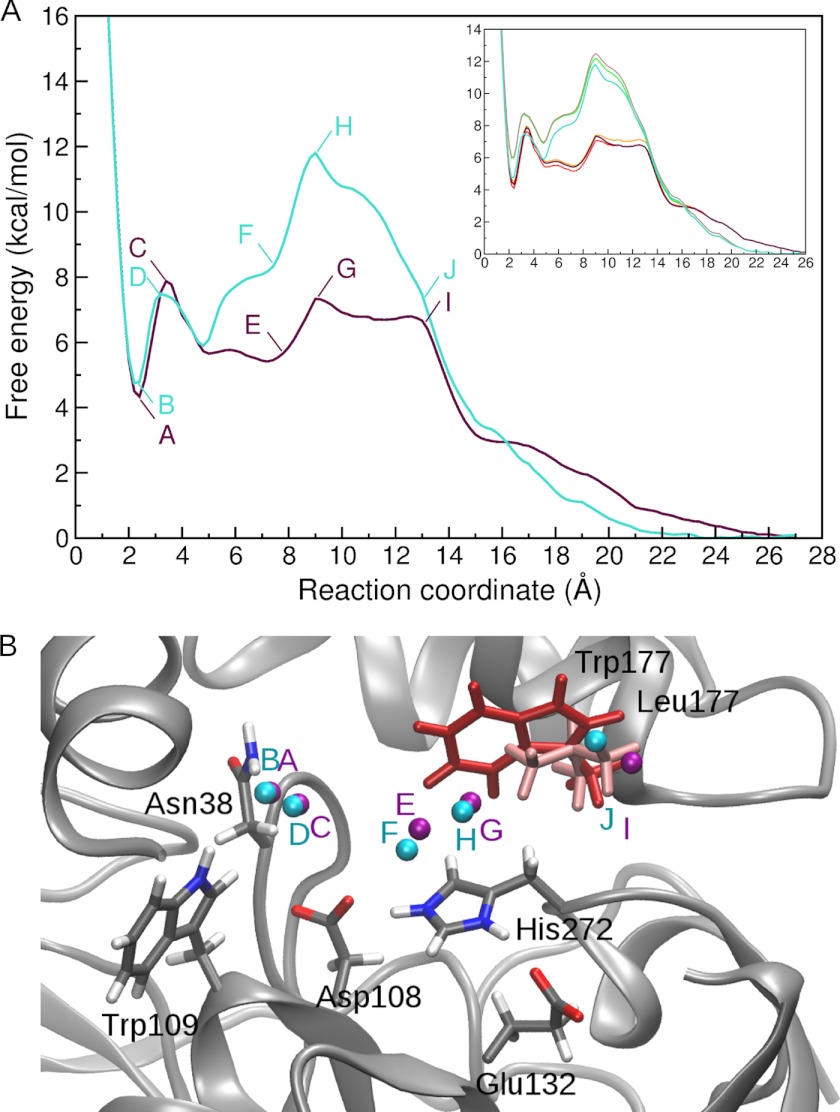
To derive the free energy profile for bromide ion egress, the ABF simulations were set up in a series of 2 Å windows with starting positions of the bromide ion along the p1b tunnel (the preferred tunnel in the test runs). For sufficient convergence of the free energy profiles, at least 90,000 samples per bin (bin size 0.2 Å) were needed (Fig. 5A, inset). In the resulting free energy profiles (Fig. 5A), a local minimum of 4.3 and 4.7 kcal/mol is present at about 2.3 Å distance from the nitrogens of the halide-stabilizing residues in the LinB WT and LinB L177W system, respectively, corresponding to the bromide ion-binding site. (The average distance of the bromide ion from the halide-stabilizing residues is 2.38 ± 0.20 and 2.33 ± 0.19 Å in the standard MD simulations without alcohol in LinB WT and LinB L177W, respectively.) In LinB WT, a maximum follows at about 3.5 Å, with a barrier of about 3.5 kcal/mol, which is the highest barrier in the free energy profile. In the LinB L177W, the highest barrier for unbinding, 11.7 kcal/mol, occurs at 9.2 Å, corresponding to a small maximum that occurs in LinB WT at the same distance.

FIGURE 5.

Free energy profiles from ABF simulations of bromide ion exit in LinB WT (purple) and LinB L177W (turquoise). Convergence of the free energy profiles with increasing number of samples per bin is shown in the inset; profiles for 70,000, 80,000, and 90,000 samples per bin are shown for LinB WT (yellow, orange, and purple, respectively) and LinB L177W (green, brown, and turquoise, respectively) (A). Position of the bromide ion in selected snapshots of ABF simulations for LinB WT (purple spheres) and LinB L177W (turquoise spheres) are shown (B). The labels indicate the corresponding position on the free energy profile. The LinB WT is shown in the starting conformation of the ABF simulations in gray schematic representation, with important residues highlighted in stick representation. The Leu-177 residue is colored light red, and the Trp-177 residue from LinB L177W is superimposed for reference and colored dark red.

Interaction Energy of the Bromide Ion with Selected Residues

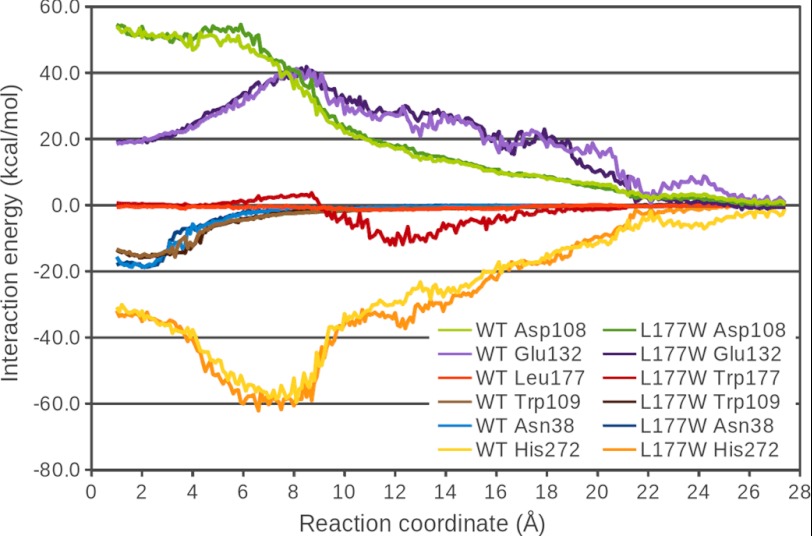
The total interaction energy of the bromide ion with important residues in the active site and along the p1 tunnel was analyzed in the ABF simulations of both LinB WT and LinB L177W (Fig. 6). These residues include the two halide-stabilizing residues, Asn-38 and Trp-109, the charged residues forming the catalytic triad, Asp-108, His-272, and Glu-132, and the mutated tunnel-lining residue Leu-177/Trp-177. As expected, the interactions of the bromide ion are dominated by the electrostatic component (data not shown) and therefore are strongest with the charged residues. The plots of their dependence on the reaction coordinate show a maximum (in absolute values) in the part of the reaction coordinate where the two charged species come closest together. This occurs for Asp-108 at about 5 Å, for His-272 at about 7 Å, and for Glu-132 at about 8.5 Å. In the halide-binding site, the overall repulsive effect of the interactions with these charged residues is compensated by attractive interactions with the polar halide-stabilizing residues Asn-38 and Trp-109, which diminish relatively quickly along the reaction coordinate (Fig. 6) and explain the sharp minimum of the free energy profile at about 2.3 Å (Fig. 5). The interaction of the bromide ion with the halide-stabilizing residues as well as with the catalytic residues is very similar in both studied systems (Fig. 6). The exception is a stronger attraction to His-272 in the region of 4–7 Å in LinB L177W, which is, however, compensated by a stronger repulsion from Asp-108. Some of the interaction energy plots for LinB WT and LinB L177W also deviate for larger values of the reaction coordinate, consistent with more difficult sampling of this region, which is reflected in relatively large standard deviations (data not shown). The most significant difference in the interaction patterns of the two enzymes is the interaction of the bromide ion with the mutated Leu-177/Trp-177 residue. In LinB WT, the interaction with Leu-177 is almost negligible (maximum attraction of −1.5 ± 0.7 kcal/mol at 11.4 Å), whereas in LinB L177W, the interaction with Trp-177 shows a repulsion in the region from about 5.5 to 8.9 Å with a maximum of 3.2 ± 0.8 kcal/mol at 8.2 Å, and then an attraction in the region from 9.0 Å onward, with a maximum attraction of −12.1 ± 1.5 kcal/mol at 11.9 Å. This can be interpreted as the interaction of the bromide ion with the dipole moment of the indole ring of Trp-177 side chain. The side chain is oriented such that at values of the reaction coordinate between 5.5 and 8.9 Å, the bromide ion is close to the negatively charged six-membered ring of the indole system, resulting in a repulsive interaction. However, at values around 12 Å, the bromide ion can interact favorably with the positively charged hydrogen on the nitrogen of the pyrrole ring.

FIGURE 6.

Total interaction energy (electrostatic and van der Waals) of the bromide ion with selected residues as a function of the bromide position along the ABF reaction coordinate.

Free Energy Perturbation Calculations

The free energy of decoupling of the bromide ion obtained from FEP calculations, together with the corresponding corrections are listed in Table 4. The unbound state is in both cases (unbound state with protein and plain water simulation) more favorable than the bound state. The difference between the two unbound state simulations is probably due to the interaction of the bromide ion with the protein and the 12 sodium counter-ions (which may also account for the slow flattening of the free energy profile of LinB WT as the reaction coordinate distance increases when the bromide ion is outside the protein, see Fig. 5A). If the plain water simulation is taken as the unbound state, then the binding free energy ΔG_b⁰ of the bromide ion to LinB WT is 7.9 ± 1.7 kcal/mol. In the case of the unbound state with protein, the binding free energy ΔG_b⁰ of bromide for LinB WT is 4.9 ± 1.8 kcal/mol, in very good agreement with the value obtained from the ABF simulations (4.3 kcal/mol). This simulation probably also corresponds better to the experimental conditions of the measurement of bromide ion affinity (protein and ions present; the experimental ΔG_b⁰ values for LinB WT and LinB L177W are −0.66 and −0.57 kcal/mol, respectively).

TABLE 4.

Calculated free energies for the decoupling of the bromide ion (in kcal·mol⁻¹)

	ΔGFEP	ΔGV	ΔGR	ΔGtot
Bound state in LinB WT	71.0 ± 1.6		0.0	71.0 ± 1.6
Unbound state (LinB WT, counter-ions)	73.9 ± 0.8	1.9	0.1	75.9 ± 0.8
Unbound state (plain water)	76.8 ± 0.6	1.8	0.3	78.9 ± 0.6

DISCUSSION

Several experimental and computational studies of enzymes with buried active sites, such as acetylcholinesterases (6, 44), haloalkane dehalogenases (12, 43), cytochromes P450 (7, 18, 45, 46), and lipases (47–50) have been performed and have underlined the importance of enzyme tunnels for catalytic activity, specificity, and enantioselectivity. Here, we report the first combined experimental and computational study of the effect of a tunnel-lining mutation on the mechanism of the biotechnologically interesting enzyme, haloalkane dehalogenase LinB.

L177W Mutation Changes the Mechanism of Bromide Ion Release and Results in Bromide Release Becoming the Rate-limiting Step of the Catalytic Cycle

We performed steady-state and transient kinetic analysis to reveal the effect of the mutation L177W on the mechanism and kinetics of product transport. The results show that the L177W tunnel mutation did not have a significant effect on the overall equilibrium binding affinity of the bromide ion to the LinB enzyme, but the mechanism and kinetics of bromide ion binding are changed significantly by the mutation. The mechanism of bromide ion binding to LinB L177W has two steps, although a single-step binding mechanism was described for LinB WT. Moreover, the L177W mutation slowed down the bromide ion transport significantly. Comparison of the rate constant 0.8 ± 0.2 s⁻¹ measured for the bromide ion release with the value of the steady-state turnover rate constant of 1,2-dibromoethane conversion (k_cat = 0.61 ± 0.02 s⁻¹) suggests that the bromide ion release became the rate-limiting step in the overall catalytic cycle of LinB L177W, although the chemical step (hydrolysis of an alkyl-enzyme intermediate) is the rate-limiting step identified in the LinB WT enzyme (41). No significant effect was observed on the kinetics of release of the second reaction product, 2-bromoethanol, upon the L177W mutation.

L177W Mutation Hinders Product Release through the p1a and p1b Tunnels

The geometry of the tunnels connecting the active site with bulk solvent was analyzed using the CAVER 3.0 program, in MD trajectories of both LinB WT and LinB L177W. Based on the geometric analysis, both branches of the p1 tunnel as well as the p2 tunnel are proposed to be relevant pathways for ligand passage in LinB WT, whereas in LinB L177W, only the p1b branch of the main tunnel and the p2 tunnel seem to be relevant. In both studied systems, the p2 tunnel seems to be significantly less preferable than the p1 tunnel.

The geometric analysis of the tunnels was complemented with simulations of ligand egress. For both reaction products, 2-bromoethanol and the bromide ion, exit through the p1a tunnel was only observed in the LinB WT enzyme, which means that the L177W mutation effectively blocked this tunnel for ligand passage. Moreover, the L177W mutation also hinders the exit through the remaining tunnels, as longer ligand exit times are observed in LinB L177W compared with LinB WT, especially for bromide ion exit. These results are in qualitative agreement with the experimental observations of the binding and unbinding rates of products obtained from the transient kinetics experiments.

In the RAMD simulations of alcohol egress (spanning up to 1 ns), no bromide ion exit event was observed. This supports our assumption that spontaneous exit of the halide ion is probably slower than the exit of the alcohol and is consistent with the classical MD simulation of Negri et al. (51), in which the 2-bromoethanol exit preceded that of the bromide ion. Based on this simulation, the authors also suggested that 2-bromoethanol leaves through the p2 tunnel and the bromide ion leaves through the p1a tunnel. Our observations, however, revealed that the tunnels cannot be ascribed to the transport of only one type of product, because the products can leave through various pathways, and that the p1 tunnel is preferred by both products over the p2 tunnel in both LinB WT and LinB L177W.

Slower Release of the Bromide Ion by LinB L177W Results from a Higher Free Energy Barrier of Bromide Ion Egress

To investigate the energetics of the binding and unbinding process of the key product, the bromide ion, and to derive the free energy profile for this process, the ABF method (19, 20) was used. The free energy profiles obtained for bromide ion passage along the p1 tunnel are in good agreement with the experimentally determined difference in the free energy barriers and differences in the binding free energies of the bromide ion to the two studied systems, but they fail to reproduce the absolute ΔG values from experiment. The calculated binding free energies of the bromide ion to LinB WT and LinB L177W are 4.3 and 4.7 kcal/mol, respectively (difference of 0.4 kcal/mol), whereas the experimental values are −0.66 and −0.57 kcal/mol, respectively (difference of 0.1 kcal/mol). Similarly, the difference in the free energy barrier for the unbinding of the bromide ion of 4.5 kcal/mol between LinB WT and the LinB L177W is in accord with experimental observations (free energy difference of >4.0 kcal/mol), although the absolute values of the ΔG are, again, not directly comparable with experimental values.

To determine whether these discrepancies in absolute ΔG values are due to force field imprecision or the ABF method employed, a series of FEP calculations was performed in which the bromide ion was decoupled from the LinB WT enzyme-binding site, from the bulk solution containing the protein and counter-ions as in the ABF calculations, and from plain water (without neutralizing counter-ions). The computed binding free energy is positive, i.e. unfavorable for both types of unbound state simulation (unbound state simulated in the presence of protein and counter-ions or in plain water), and amounts to 7.9 ± 1.7 and 4.9 ± 1.8 kcal/mol, respectively.

These results thus support the ABF calculations and show that the discrepancy between the experimentally determined ΔG and the values obtained computationally is not a matter of the ABF method or insufficient sampling but is due to imprecision of the force field used. The neglect of polarizability in the classical nonpolarizable force field used may lead to an overestimation of the ion-water dipole interactions (52). The nonpolarizable model will also affect the interactions of the ion with polarizable protein side chains, such as the halide-stabilizing residues Asn-38 and Trp-109, which in turn may be underestimated (53). Moreover, the explicit water models used in the simulations were developed to describe the bulk solvent behavior and the balance of water-water and protein-water interactions, but they may not be accurate in describing the properties of buried water molecules in protein cavities (54), especially in the presence of charged groups (55). Nevertheless, our results show that these imprecisions cancel out if we focus on the relative differences between the two studied systems, possibly due to the relatively small perturbation of the system caused by the mutation.

Higher Free Energy Barrier for Bromide Ion Passage in LinB L177W Results from Interactions of the Bromide with Trp-177

To interpret the differences in the free energy profiles for bromide ion passage in LinB WT and LinB L177W at the molecular level, the interaction energy of the bromide ion with selected residues in the binding site and along the p1 tunnel were analyzed as a function of the reaction coordinate. The differences in the interaction energy of the bromide ion can clearly explain the differences in the free energy profiles between the two LinB enzyme systems. The free energy profiles start to deviate at about 5 Å and progressively diverge from each other in the region from about 5 to 9 Å, where the interaction with the Trp-177 residue of LinB L177W is more unfavorable than the interaction with Leu-177 of LinB WT. In the region from 9 to 18 Å, where the interaction with Trp-177 is more favorable than that with Leu-177, the free energy profile of LinB L177W falls off more rapidly than that of LinB WT. Because the interactions of the bromide ion in the binding site are not perturbed by the mutation, the larger free energy barrier for bromide ion release in LinB L177W is caused by specific interactions of the bromide with the tryptophan residue introduced.

Conclusions

In recent years, it has become evident that active site properties are not the only determinant of enzyme substrate specificity and activity and that the characteristics of access tunnels play an equally important role. Therefore, analysis of the molecular properties of the access pathways and mechanisms of ligand passage is essential for the understanding of enzyme structure-function relationships. A detailed understanding of these phenomena can in turn facilitate engineering the enzyme specificity and activity; instead of targeting the highly conserved and evolutionary optimized active site, it is possible to improve enzyme catalytic properties by engineering of the entrance tunnels (12).

In this paper, we measured the kinetic parameters of ligand binding and unbinding, investigated the ligand egress pathways, and calculated the passage of products through tunnels in one of the biotechnologically important HLDs. Our results show how changes in the accessibility of the enzyme's tunnel and the modification of its physico-chemical properties by a single mutation can have a dramatic effect on the passage of ligands and thereby on the overall catalytic properties.