Rate limit of protein elastic response is tether dependent

Abstract

The elastic restoring force of tissues must be able to operate over the very wide range of loading rates experienced by living organisms. It is surprising that even the fastest events involving animal muscle tissues do not surpass a few hundred hertz. We propose that this limit is set in part by the elastic dynamics of tethered proteins extending and relaxing under a changing load. Here we study the elastic dynamics of tethered proteins using a fast force spectrometer with sub-millisecond time resolution, combined with Brownian and Molecular Dynamics simulations. We show that the act of tethering a polypeptide to an object, an inseparable part of protein elasticity in vivo and in experimental setups, greatly reduces the attempt frequency with which the protein samples its free energy. Indeed, our data shows that a tethered polypeptide can traverse its free-energy landscape with a surprisingly low effective diffusion coefficient D_eff ∼ 1,200 nm²/s. By contrast, our Molecular Dynamics simulations show that diffusion of an isolated protein under force occurs at D_eff ∼ 10⁸ nm²/s. This discrepancy is attributed to the drag force caused by the tethering object. From the physiological time scales of tissue elasticity, we calculate that tethered elastic proteins equilibrate in vivo with D_eff ∼ 10⁴–10⁶ nm²/s which is two to four orders magnitude smaller than the values measured for untethered proteins in bulk.

While the dynamics of proteins have been studied in detail using bulk techniques their behavior when tethered and placed under force is still poorly understood. Tissue elasticity in living organisms results from the extension and recoil of proteins that are tethered to rigid structures that move under force. For example, the giant protein titin responsible for the elasticity of muscle, is mechanically anchored to both the Z disk and the M-line of the half-sarcomere (1), responding to a mechanical perturbation by elastically changing the end-to-end length (2). Hence, it is likely that one of the limiting factors in the physiological activity of a muscle fiber is ultimately determined by the dynamics of the elastic recoil of an extended and tethered polypeptide. Hummingbirds flip their wings by up to 80 Hz, and insects up to 800 Hz (3). It is interesting here to consider that the fastest muscle-driven wing beat rates never surpass a kilohertz (3). Other types of physiological activities also appear to be capped at a similar time scale. For example, salamanders can shoot and fully extend their tongues out in less than 7 ms in order to catch flying prey (4). Throughout these physiological activities it is essential that the extending polypeptide remains elastic. If at any time the speed of the muscle motion exceeded the relaxation time of the polypeptide, the muscle will cease to be elastic, greatly affecting its ability to provide a restoring force, and to store energy. For example, a significant part of the turkey’s stride results from energy stored in the passive elasticity of muscle (5). In light of these observations, it is interesting to determine the extent to which these physiological limits can be explained in terms of the diffusional dynamics of the tethered extending polypeptides.

The elasticity of a polypeptide is typically modeled using either the worm-like-chain (WLC) (6, 7) or the freely-jointed-chain models of polymer elasticity (2), where the dynamics of equilibration is assumed to be instantaneous compared to the physiological time scales. This assumption can be justified given that bulk studies of untethered proteins using Förster resonance energy transfer (FRET) probes have conclusively measured the diffusional dynamics of single polypeptides and shown that freely diffusing proteins equilibrate with a very fast diffusion coefficient of D ∼ 10⁷–10⁸ nm²/s (8–11). It is therefore not surprising that some theoretical studies modeling the elastic behavior of proteins use the values of D measured from untethered protein in bulk (12, 13).

A recent attempt was made to measure the internal friction of extended proteins tethered to Atomic Force Microscope (AFM) cantilevers (14, 15). Although these experiments had a limited time resolution (> 10 ms), the authors made an effort to subtract the contributions made by the cantilever in order to get an estimate of the protein’s internal friction. These experiments estimated an internal friction at 100 pN, predicting values of D ∼ 10³ nm²/s for the tethered protein, which is five orders of magnitude smaller than those measured by FRET experiments. Other authors have used force spectroscopy techniques to measure the elastic dynamics of tethered polypeptides resulting in values of D ∼ 10²–10⁴ nm²/s (16–18). As a consequence, some theoretical work of proteins under force used very low values of D ∼ 1,200 nm²/s (19, 20) to match the results obtained from force spectroscopy. Similarly, a value of approximately 10⁴ nm²/s was needed to explain the dynamics of riboswitches tethered onto optical tweezers beads (21). Thus, the diffusional dynamics of a protein estimated from bulk techniques and from force spectroscopy techniques are very disparate.

It is surprising that these contradictory results have not been questioned before. In spite of its importance for understanding tissue elasticity, the effect of tethering on the internal dynamics of a protein is still not understood. We probe the elasticity of single extended polypeptides in the submillisecond range using a fast force-spectrometer, which provides a 20-fold improvement in time resolution, in combination with Brownian dynamics and Molecular Dynamics simulations (MD). MD simulations suggest that diffusion of an isolated protein under force occur on a very fast time scale (D ∼ 10⁸ nm²/s), in agreement with FRET measurements. These simulations were done by applying force to a single atom in the terminal end of the protein and measuring the resulting changes in length (22). However, freely diffusing polypeptides measured in bulk are far from representing the physics of elastic proteins such as titin, which by definition must always be tethered to larger structures that move in conjunction. Here we demonstrate that the large slowing down of the diffusional dynamics of a protein as measured in AFM experiments is due to the drag force exerted by the object to which it is tethered. We therefore suggest that the slow dynamics probed in force spectroscopy is an inherent property of tethering a protein to a solid object, of widespread significance for understanding the dynamics of tissue elasticity.

Results and Discussion

The advent of force-clamp spectroscopy has made it possible to probe the dynamics of single proteins extending and relaxing under a well defined force (23). This approach now permits a direct study of the relaxation times of a polypeptide under a rapid load change. However, the published response times of the feedback in force spectrometers ranges from 5–10 ms for fast AFMs (23) and up to approximately 100 ms for optical tweezers instruments (24). Although the current instrumentation can comfortably measure the kinetics of protein unfolding and refolding, it is far too slow to probe the recoil dynamics of a stretched polypeptide under force. The main limitations have been the frequency response of the piezoelectric actuators and of the cantilevers used in the AFM instruments. Here we built a new force-clamp apparatus (Fig. 1A) that makes use of a fast piezoelectric actuator (> 300 kHz) and small Olympus cantilevers with resonant frequencies > 10 kHz. The set-up can settle the applied force within approximately 150 μs (see SI Text).

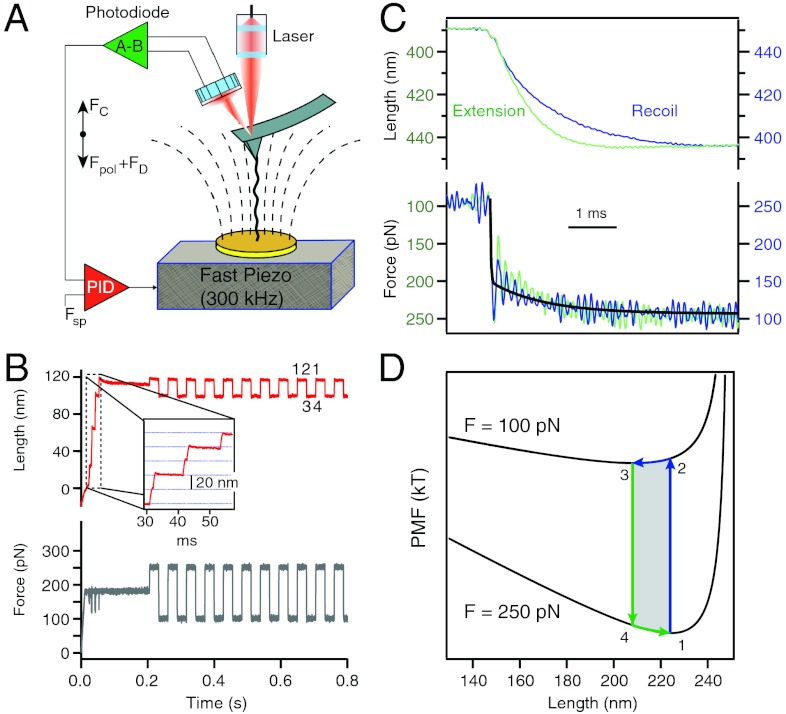
Fig. 1.

Experimental design for time resolved measurements of the recoil dynamics of an extended polypeptide. (A) Schematic diagram of the force-clamp apparatus. A single polypeptide is extended between a high-speed cantilever (Olympus biolever) and a piezoelectric actuator with a high resonant frequency (300 kHz, Physik Instrumente PL-055.30). A well-tuned PID amplifier adjusts the piezoelectric actuator so as to keep the force on the polypeptide at the set point value (F_sp). Under force clamp conditions, F_c = F_pol + F_D, where F_c is the force applied by the cantilever, F_pol is the elastic force produced by the molecule and F_D is the flow drag force (dashed lines) from the motion of the piezoelectric actuator. (B) Typical experimental trace of the end-to-end length corresponding to the force protocol on the lower box. The inset shows a staircase of ubiquitin unfolding events (stars) measured at 180 pN providing a strong fingerprint for a single polypeptide and measures its initial length. The extended polypeptide is then repeatedly cycled between 250 pN and 100 pN in order to collect many trajectories (7 < n < 30) until the molecule detaches. (C) Example of a recoil trajectory (blue) obtained by averaging eight consecutive recoil trajectories. The averaged force trace shows a step (250 pN down to 100 pN) with a half time of approximately 33 μs, which is more than 10 times shorter than the relaxation time constant of the polypeptide measured to be approximately 1.11 ms. After recoil, the corresponding extension (green trace) is much faster with a time constant of approximately 0.68 ms. The force traces are superimposable. (D) Potential of mean force of a 250 nm long polymer calculated at two pulling forces of 250 pN and 100 pN, using the WLC model of polymer elasticity (lower box). The figure highlights the physics of our experimental design. The polypeptide starts extended at 250 pN (1) and then it is abruptly relaxed to 100 pN (2) where it recoils down to its new minimum (3), then it is switched back to the high force (4) where it extends to the PMF minimum at 250 pN (1).

Our experimental design consists of first unfolding and extending a single ubiquitin polyprotein at a force of 180 pN, resulting in a series of step increases in length of approximately 20 nm (23). This staircase uniquely identifies the ubiquitin protein and also verifies that force is applied to a single polypeptide chain (Fig. 1B). Once a poly-ubiquitin protein is fully extended, the polypeptide was repeatedly cycled between 250 pN and 100 pN in order to measure the relaxation and extension dynamics (Fig. 1B). At these high forces, the polypeptide always remains highly extended. We averaged and merged all the repeating cycles of recoil and reextension such that we obtained a smoothed recoil (blue) and extension (green) trace (Fig. 1C; top traces). A similar procedure was used to average and merge the force steps over the same trace (Fig. 1C; bottom traces). The response time achieved by the new force clamp instrumentation is shown in Fig. 1C, where approximately 70% of the command force settles with a time constant of approximately 20 μs. The residual creep in the force settles more slowly with a time constant of 1.1 ms. The observed oscillations are due to the main resonant mode of the system, as the instrument approaches the limit of its operating bandwidth (approximately 7 kHz). Crucially, the polypeptide relaxes more slowly than the force with an exponential time course with a time constant of τ = 1.17 ms. The polypeptide reextends with a faster time course (τ = 0.68 ms), while the averaged force traces appear identical. Our protocol cycles an extended polypeptide between two well defined regions of the potential of mean force (PMF), calculated from the WLC model of polymer elasticity and the applied force (25, 26) (Fig. 1D; 1–4). The PMF slope is steeper at the higher force of 250 pN (4 to 1 in Fig. 1D), which causes a faster rate of extension when compared to the rate of recoil at 100 pN (2 to 3 in Fig. 1D). This asymmetry suggests that our recordings are reporting on the underlying PMF of the polypeptide, in the millisecond time scale, as also illustrated by our MD simulations (see below).

In Fig. 2A we fit single exponentials to recoil trajectories measured at 100 pN and extension trajectories measured at 250 pN. The polypeptides can be of very different contour lengths, L_c, due to the varying length of the polyproteins that are picked up by the AFM cantilever. Thus, we can measure the relaxation time constant, τ, as a function of the contour length of the polypeptide for both types of trajectories (Fig. 2B). The results show that the value of τ grows linearly with L_c, for both the recoil and extension trajectories, albeit with very different slopes (filled circles and triangles respectively; Fig. 2B). The linear dependency of τ vs. L_c can be explained by the scaling of the PMF with the contour length of the polypeptide, where the distance between minima at 250 pN and 100 pN (ΔL; inset of Fig. 2B), increases linearly with the contour length. These measurements clearly indicate that the extended polypeptide equilibrates at each new force by sampling its PMF.

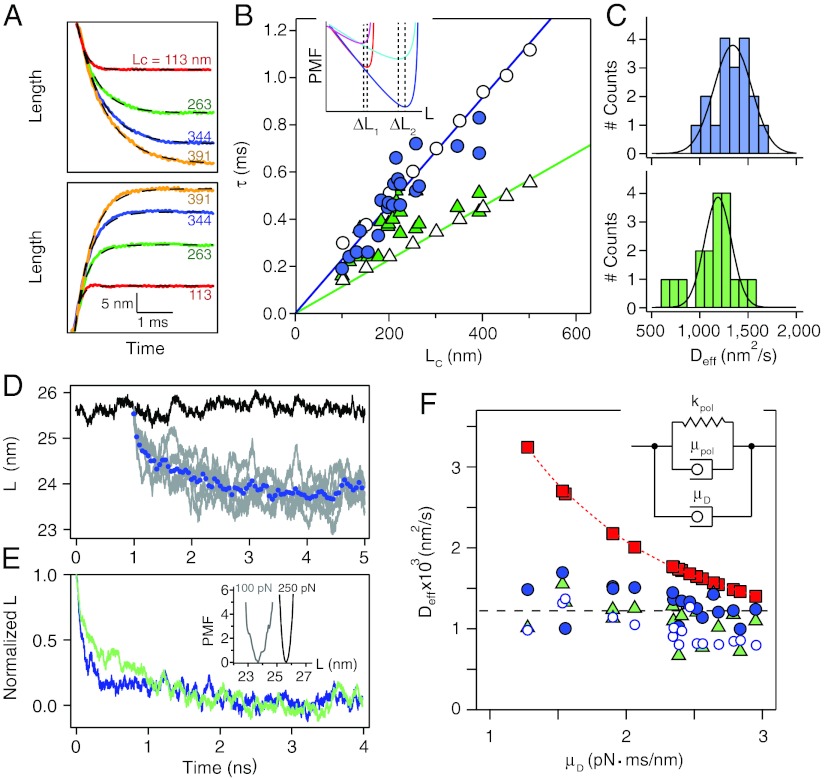
Fig. 2.

Time constants and diffusion coefficients from extension and recoil traces of single polypeptides. (A) A series of four different recoil (upper box) and extension (lower box) trajectories measured from extended polypeptides of different contour lengths L_C (as labeled; 113 nm, 263 nm, 344 nm, and 391 nm). The data were fit with a single exponential to measure the value of the relaxation time constant, τ, (dashed lines). (B) Relaxation (filled circles) and extension (filled triangles) time constants, τ, as a function of the contour length of the polypeptide L_c. The asymmetry of the potential shown in Fig. 1D, results into very different values of τ for the extension and recoil, as shown in Fig. 1B. The linear contour length dependency of τ is readily reproduced by Brownian dynamics simulations using the potential shown in Fig. 1D and the values of D_eff measured from these data (open circles and triangles). The linear dependency of D_eff on L_c results from that of the total travel (ΔL) on L_c (inset). (C) Histograms of values for D_eff measured from the recoil (top box) and extension (bottom box) traces shown in Fig. 2A. (D and E) MD simulations of the end-to-end length as a function of time for ubiquitin maintained at a constant force of 250 pN (D; black curve); relaxation after force is quenched from 250 pN to 100 pN (D; grey curves) and averaged over five such trajectories (D; blue dots). Even if each of the time-origins of each trajectory differs, we make them coincide in the plot for clarity. (E) Normalized recoil (green curve) and extension (blue curve) averaged over five trajectories. The inset shows the PMF along the end-to-end distance at 100 pN (gray curve) and 250 pN (black curve). Both curves are shifted so that their minimum is 0. (F) Plot of the measured values of D_eff (circles from recoils; triangles from extensions) as a function of the viscoelastic drag, μ_D, measured from each cantilever. The upper squares show the values of D_max = k_BT/μ_D, marking the upper limit of D measured for each cantilever. We attribute the difference between D_eff and D_max to the noninstantaneous force step of the force-clamp apparatus. The open circles show the values of D_eff measured from BD simulations that include the time course of the force-step for each experiment. The inset portrays a simplified mechanical representation of the principal contributions to the forces of an extending polypeptide during these experiments. The Voigt model representing the polypeptide (k_pol, μ_pol) is in parallel with the drag (μ_D) generated by the motion of the piezoelectric actuator, giving μ_eff = μ_pol + μ_D.

Here we examine whether simple Brownian dynamics based on the PMF predicted by the WLC model can account for the time scales of relaxation of the extended polypeptides as they adjust to a new force. The time course of the end-to-end length of a model polypeptide is calculated by solving the stochastic equation of motion:

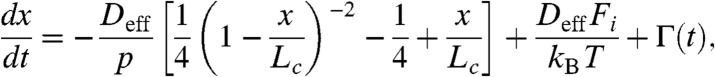[1]

where x(t) is the one-dimensional end-to-end reaction coordinate, D_eff is the effective diffusion coefficient, p is the persistence length set to 0.4 nm, F_i is the applied force, k_B is Boltzmann’s constant, T is the absolute temperature, and Γ(t) is white noise with 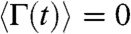and correlation time 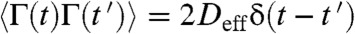. We completed a set of simulations where the force was switched between 250 pN and 100 pN and the contour length L_c was varied from 100 nm to 500 nm. We fitted single exponentials to the simulated extensions and relaxations and measured the resulting time constants (open triangles and circles respectively; Fig. 2B). Simulations using a fixed value of D_eff = 1,226 nm²/s (see below), matched the observed trends in our data, readily reproducing the difference in time constants between relaxation and extension and their linear growth with contour length (Fig. 2B). We also estimated the value of D_eff directly from each relaxation trace with a simple high force approximated solution to Eq. 1 as

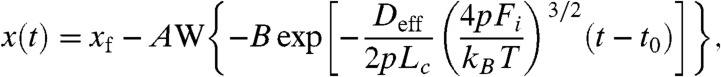[2]

where W is the Lambert W function which is defined to be the multivalued inverse of the function z = W(z)e^W(z) (27), x_f is the final protein length after the relaxation, A and B are fitting parameters, and t₀ is the time at which the force was changed. Fits of Eq. 2 to the relaxation data shown in Fig. 2A gave a distribution of D_eff values for both types of relaxation (Fig. 2C). The fitted values indicates a mean of 1,317 ± 197 nm²/s for the recoil and 1,135 ± 234 nm²/s for the extension traces, giving an average value of approximately 1,226 nm²/s, which was used in the simulations of Fig. 2B. Our observations support the view that a tethered polypeptide samples its PMF with a diffusion coefficient of D_eff ∼ 10³ nm²/s, which is in surprisingly close agreement with previous measurements using tethered proteins (14–18).

The measured values of D_eff for tethered polypeptides are 4–5 orders of magnitude smaller than those measured from studies of polypeptides in bulk using FRET techniques (8–11). Indeed, if we use a value of D_eff ∼ 10⁸ nm²/s in our Brownian dynamics simulations, the resulting relaxation times are in the nanosecond time scale, far from those observed experimentally. Nevertheless, it could be argued that diffusion of an extended protein under force is a much slower process than the diffusion of unfolded proteins in solution as studied by FRET. To gain more insight into these discrepancies, we did all-atom MD simulations in explicit solvent of ubiquitin relaxation under force (see SI Text for details). When kept under a constant force of 250 pN, the protein is fully extended and its end-to-end distance fluctuates around an average value of L = 25.5 nm (Fig. 2D, black trace). At given moment along this trajectory, we quenched the force to a lower value of 100 pN while monitoring the relaxation of L (Fig. 2D, gray traces). These trajectories, starting from different initial configurations, were averaged to recover an average profile (Fig. 2D, blue points). It is clear that L relaxes on a nanosecond time scale, in stark contrast with the millisecond relaxation observed by our experiments, before it fluctuates around a new average value of L = 23.7 nm at 100 pN. Importantly, we checked that L does not further decay during a much longer simulation of 30 ns. Fitting these two lengths with the WLC predictions gives a contour length L_c = 28.4 nm and a persistence length p = 0.38 nm, in agreement with values usually measured experimentally (28, 29), suggesting that the full relaxation of the end-to-end distance was being reached.

We then explored the reverse scenario where the protein equilibrated at 100 pN is pulled at a constant force of 250 pN. The renormalized average of several such traces allowed direct comparison with the normalized recoil profile (Fig. 2E). The slower relaxation compared to the extension shows that AFM experiments and MD simulations are probing the same PMF. For both forces, the PMF extracted from the end-to-end distributions of equilibrium simulations further proves this point. The PMF at 250 pN is significantly stiffer than that at 100 pN, in agreement with the WLC predictions (Fig. 1D) and explains why the extension (i.e., motion along the 250 pN free energy surface) is faster than relaxation (motion along the 100 pN free-energy surface).

Independently from these extension/relaxation simulations, we estimated the diffusion coefficient along the end-to-end distance close to the minimum of each free-energy basin (see SI Text for details). The obtained values are D_pol = (5.3 ± 1.4)·10⁸ nm²/s for L = 23.7 nm and F = 100 pN, and D_pol = (4.2 ± 1.1)·10⁸ nm²/s for L = 25.5 nm and F = 250 pN. The obtained values are in close agreement with those measured in FRET experiments, but 5 to 6 orders of magnitude larger than those measured in our AFM experiments. Even if our method to estimate D_pol may suffer from uncertainties and other force fields may lead to some differences in the measured time scale, these factors cannot in any case explain the 6 order of magnitude difference with our experiments.

In order to understand these important discrepancies we must first consider the various contributions to the value of D_eff in a protein placed under force. In the simulations, the force is directly applied to one extremity of the protein while the other is being fixed. From an experimental point of view, application of a mechanical force to a polypeptide always must involve the tethering of the polypeptide to a macroscopic object. Motion of the polypeptide is thus intimately tied to motion of the object. Any attempt of the polypeptide to move along the end-to-end length reaction coordinate of the PMF must also displace the object to which the protein is tethered. In our case, the polypeptide is tethered to an AFM cantilever and to a large gold covered surface. Thus, any change in the end-to-end length of the polypeptide must also result in drag generated between the moving surfaces (Fig. 1A). A simplified representation of these combined elements is shown in the inset of Fig. 2F, where the extended polypeptide is represented as a Voigt model with an elastic constant k_pol and an internal friction of μ_pol. The polypeptide is placed in parallel with the drag caused by the motion of the tethered objects μ_D, so that friction forces are simply additive. We measured the drag force on a cantilever without attached proteins by simply touching the surface and then rapidly moving it away from the cantilever. These measurements gave a drag of 2.3 pN·ms/nm. We also measured the drag in each individual experiment after the protein detached from the cantilever and the surface started to rapidly move away (see SI Text). From these measurements we obtained an average value of 2.3 ± 0.5 pN·ms/nm. We plot the measured values of D_eff as a function of μ_D for the individual experiments and observe that D_eff has a weak dependence on the drag forces (Fig. 2F). If drag forces were the sole limiting factor affecting the motion of the polypeptide, we would expect the values of D_eff to rise rapidly as drag is reduced, varying as 1/μ_D, which is not the case here. However, as it is apparent in Fig. 1C even in the best cases the force step applied to the polypeptide is far from approaching an ideal Heaviside step. Brownian dynamics simulations using the actual measured raw force traces readily reproduce our data. Fitting Eq. 2 to the resulting relaxation traces recovers the values of D_eff measured experimentally (open circles; Fig. 2F).

Thus, it is possible to conclude that despite the considerable improvements in the time resolution of our instrumentation the surprisingly low values of D_eff measured using force spectroscopy are still dominated by the drag resulting from the motion of the objects to which the polypeptide is tethered. While in our case these objects are the AFM cantilever and a gold-coated glass coverslide, such drag is an obligatory result of the elasticity of tethered polypeptides, a configuration that is widespread in biology. It is difficult to know the magnitude of the drag forces acting on the individual proteins of intact elastic tissues. However, if we consider the biological bandwidth of 800 Hz as the limit of protein elasticity, we can make some educated guesses of the biological drag coefficients and compare them with those measured in this work.

In order to estimate the drag in biological tissues, we examine the limits to the bandwidth of elastic tissues using a simple model as shown in Fig. 3. We use Brownian dynamics (with D = 1,300 nm²/s) to measure the effect of a small sinusoidal force (10 pN, peak to peak) on the extension dynamics of a prototypical tethered protein (L_c = 30 nm), as a function of the perturbation frequency, f (Fig. 3A). We analyze these traces using standard lock-in detection to measure the output signal components; the in-phase and the out-of-phase amplitudes of the elastic response (triangles and circles in the lower left inset of Fig. 3B). Fitting with the corresponding real and imaginary parts of the mechanical impedance of a Kelvin-Voigt model (solid lines), 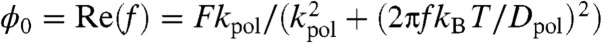and results in a perfect fit. The output power of the polypeptide oscillations calculated in dB as 10· log(Amp²(f)/Amp²(0)) is shown in Fig. 3B (triangles), where 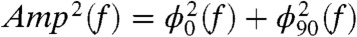. Fitting the data with 10· log(1/(1 + (2πfk_BT/k_polD_pol)²)) returned values of D_pol = 1,313 nm²/s and k_pol = 1.31 pN/nm (solid lines; Fig. 3B). Khatri, et al introduced an elegant expression for a frictional WLC elasticity constant k_wlc = 4/L_c·(p/k_BT)^1/2·F^3/2 (15). Substituting for the values of L_c, F, and p used in our simulations we calculate k_pol = 1.31 pN/nm in good agreement with our Voigt model fits. However, a Voigt model serves only as a first approximation given that real polypeptides possess multiple relaxation times.

Fig. 3.

Bandwidth of an extended polypeptide. (A) Brownian dynamics computes the length of a 30 nm long polypeptide placed under a 10 pN sinusoidal load of varying frequency, f, using the measured value of D_pol = 1,300 nm²/s. The figure shows polypeptide responses at two different frequencies (25 Hz, and 250 Hz). (B) We use lock-in detection to measure the in-phase (ϕ₀, triangles) and the out-of phase (ϕ₉₀, circles) components of the elastic response of the polypeptide as a function of the load frequency, f. The solid lines (inset), correspond to the real (triangles) and imaginary (circles) parts of the mechanical impedance of a Kelvin-Voigt model (inset), fitted to the data. From ϕ₀ and ϕ₉₀ we calculate power as a function of frequency for the polypeptide (triangles). The solid line fits the Kelvin-Voigt model to the data returning values of D_pol = 1,313 nm²/s and k_pol = 1.31 pN/nm. The arrow shows the -3 dB point, giving a bandwidth of 66 Hz. These measurements show that the elasticity of a polypeptide-based material is band-limited to a few hundred Hertz, in good agreement with broadly observed animal behavior.

From these considerations we can now establish the concept of elastic bandwidth. As shown in Fig. 3B, the power output follows the typical Lorentzian function of a low-pass filter. We define the corner frequency of the elastic response as being the frequency at which the power decreased by -3 dB, with respect to the power measured at zero frequency. For the simulations shown in Fig. 3A, the elastic bandwidth is 66 Hz. The half power frequency can also be straightforwardly calculated from the above considerations as;

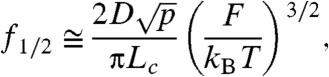[3]

where the elastic bandwidth of a polypeptide grows linearly with D. It is interesting to consider the consequences of Eq. 3. For example, simplifying the complex muscle titin protein to a polypeptide with L_c = 300 nm, p = 0.6 nm and at F = 4 pN (2) and assuming f_1/2 ∼ 50 Hz (hummingbird) (3), we calculate a value of D_eff ∼ 10⁴ nm²/s. For the same titin protein operating at the limits of insect motion at f_1/2 ∼ 800 Hz would give values of D_eff ∼ 10⁶ nm²/s. Our estimate of the speed limit of a tethered protein in vivo is much larger than that measured in our experimental system but still at least two orders of magnitude smaller than the values obtained by FRET and MD simulations. It is clear that the diffusional constants measured for polypeptides in solution do not apply to tethered polypeptides, and that extended polypeptides sample their PMF with values of D_eff that are unique to each system and cannot be generalized.

Fig. 4 summarizes the consequences of tethering a polypeptide to an object in order to establish an elastic system. As described before, the basic PMF for a polypeptide contains an attractive potential that acts mostly at short extensions combined with the potential of the WLC which rapidly becomes dominant as the polypeptide extends (25, 26). At zero force, the PMF is downhill towards the collapsed state. Application of a constant force perturbation modifies the PMF creating an entropic barrier at relatively high extensions that can trap the collapsing polypeptide for some time, before it proceeds downhill towards the fully collapsed state (25, 26, 30). The dynamics of extended polypeptides responding to a change in the force will be determined, to a large extent, by the value of D_eff. Molecules tethered to AFM cantilevers such as those used in our work will move along their PMF with values of D_eff ∼ 10³ nm²/s (1; Fig. 4), which readily explain our earlier observations (30, 31). It is interesting to consider that the value of D_eff also affects barrier-crossing events. Indeed, transition state theory predicts that the attempt frequency for barrier-crossing events is given by D_effω₀ω_B/2π, where ω₀ and ω_B represent the curvatures of the PMF before the barrier and at the transition state (32). Thus, the kinetics of barrier crossing events that change the end-to-end length [e.g., (2); Fig. 4] will be greatly affected by tethering. An example of such barrier is the entropic barrier created by the force, which crosses over long distances along the PMF (Fig. 4) (30). In this case, the kinetics of barrier crossing will be greatly affected by drag and by the resulting D_eff. By contrast, barrier crossing events that do not significantly change the end-to-end length of the molecule will be unaffected by the drag of the tethered objects. Indeed, the mechanical unfolding of ubiquitin which only has to extend by approximately 0.25 nm to cross the unfolding barrier (23) shows a very high attempt frequency (33).

Fig. 4.

Effect of tethering on the dynamics of an extending polypeptide. The act of tethering a polypeptide to an object (top inset) is an essential step in constructing an elastic system and introduces drag (μ_D; bottom inset) in parallel with the molecule (k_pol, μ_pol). Polypeptide PMF’s calculated at F = 0 and F = 12 pN (25). Any motion of the polypeptide along its PMF will cause drag from the tethered objects, greatly affecting its kinetics both for simple diffusion (1) or for barrier crossing events that significantly change the end-to-end length of the molecule (2).

Our observations of the effects of tethering on the value of D_eff apply to extended polypeptides where the internal friction of the molecule does not seem to play a significant role. However, under conditions where the internal friction of a polypeptide may become dominant, for example in collapsed molten globule states (34), the effects of tethering should be minimal. Furthermore, although the dynamics of a polypeptide takes place in more than one dimension, the effects of tether-drag will be mostly along the pulling coordinate. Other instruments such as optical tweezers and magnetic tweezers, which tether polypeptides to beads, will also show a substantial amount of drag giving different values of D_eff for different bead sizes. Extended polypeptides probed by different instruments will show different dynamics depending of the values of D_eff that result from tethering the polypeptide in each unique configuration. Thus, it is important that the drag is characterized in each instrumental configuration, and that its effects are understood and taken into account when analyzing force-spectroscopy data of extended molecules. Most importantly, the dynamics of a molecule whose kinetics is dominated by the drag of the objects to which it is tethered cannot be extrapolated to that of an untethered freely diffusing molecule in bulk. This conclusion is of wide significance for the understanding of the dynamics of numerous proteins that are tethered and under force in vivo.

Materials and Methods

Details about protein engineering and purification, experimental setup, and Brownian dynamics and MD simulations are provided in the SI Text.