Human DNA Polymerase ι Utilizes Different Nucleotide Incorporation Mechanisms Dependent upon the Template Base

Abstract

Human DNA polymerase ι (Polι) is a member of the Y family of DNA polymerases involved in translesion DNA synthesis. Polι is highly unusual in that it possesses a high fidelity on template A, but has an unprecedented low fidelity on template T, preferring to misincorporate a G instead of an A. To understand the mechanisms of nucleotide incorporation opposite different template bases by Polι, we have carried out pre-steady-state kinetic analyses of nucleotide incorporation opposite templates A and T. These analyses have revealed that opposite template A, the correct nucleotide is preferred because it is bound tighter and is incorporated faster than the incorrect nucleotides. Opposite template T, however, the correct and incorrect nucleotides are incorporated at very similar rates, and interestingly, the greater efficiency of G misincorporation relative to A incorporation opposite T arises predominantly from the tighter binding of G. Based on these results, we propose that the incipient base pair is accommodated differently in the active site of Polι dependent upon the template base and that when T is the templating base, Polι accommodates the wobble base pair better than the Watson-Crick base pair.

Replicative DNA polymerases synthesize DNA with high fidelity, and because of their intolerance of distortions in the DNA geometry, they are blocked at DNA lesions (4, 5). The DNA polymerases belonging to the Y family, on the other hand, are low-fidelity enzymes with the ability to replicate through DNA lesions. Humans possess three Y family DNA polymerases (Pols)—Polη, Polκ, and Polι—and in addition, they have Rev1, which displays specificity for incorporating a C opposite template G. Polη from both yeast and humans synthesizes DNA with a low fidelity, misincorporating nucleotides with frequencies of ∼10⁻² to 10⁻³ (11, 14, 19). The fidelity of Polκ is somewhat better than that of Polη, because it misincorporates nucleotides with frequencies of ∼10⁻³ to 10⁻⁴ (9, 16).

In contrast to Polη and Polκ, which exhibit nearly similar efficiencies and fidelities of nucleotide incorporation opposite each of the four template bases, Polι incorporates nucleotides opposite the various template bases with very different efficiencies and fidelities (7, 10, 18, 23). Polι is most efficient at incorporating the correct nucleotide T opposite template A, and it also exhibits the highest fidelity opposite this template base, misincorporating nucleotides with frequencies of ∼10⁻⁴ to 10⁻⁵. Opposite templates G and C, Polι exhibits a significant reduction in the efficiency of correct nucleotide incorporation, and opposite both these template bases, it misincorporates nucleotides with frequencies of ∼10⁻¹ to 10⁻². Polι exhibits the lowest efficiency for incorporating the correct nucleotide A opposite template T, and opposite this template base, it synthesizes DNA with an unprecedented low fidelity; in particular, it misincorporates a G with an ∼10-fold-higher efficiency than it incorporates an A.

While the steady-state kinetic analyses used in the measurements of efficiencies and fidelities of Polι and other related polymerases noted above provide accurate measurements of the fidelity of nucleotide incorporation, they provide little information regarding the mechanistic basis of the fidelity. Thus, in order to understand the mechanistic basis of the very different fidelities of Polι on different template residues, it was necessary to use pre-steady-state kinetic analyses. Because pre-steady-state kinetics allows one to directly measure the kinetics of nucleotide incorporation in the first enzyme turnover, with this approach, it is possible to examine the rates of the individual steps of nucleotide incorporation, which are not observable once the enzyme undergoes subsequent, steady-state turnovers (2, 8).

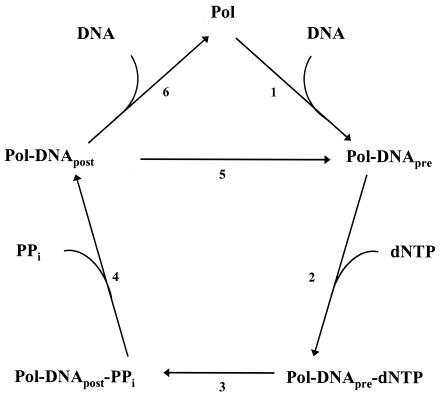
Pre-steady-state kinetic analyses have been performed on several DNA polymerases, including the Klenow fragment of Escherichia coli DNA polymerase I (12, 13), the bacteriophage T7 DNA polymerase (17, 22), mammalian DNA polymerase β (1, 21, 24), human DNA polymerase γ (6), and yeast Polη (20). From these studies, it has been concluded that the basic mechanism of nucleotide incorporation by DNA polymerases consists of at least the following steps (Fig. 1). In step 1, the polymerase binds to the DNA, forming the preinsertion polymerase-DNA binary complex. In step 2, the deoxynucleoside triphosphate (dNTP) binds to this binary complex, forming the preinsertion polymerase-DNA-dNTP ternary complex. In step 3, the phosphodiester bond is formed between the α-phosphate of the incoming dNTP and the 3′ OH at the primer terminus, forming a postinsertion polymerase-DNA-pyrophosphate complex. In step 4, pyrophosphate is released, forming the postinsertion polymerase-DNA binary complex. Then either the polymerase advances to the next template base, forming another preinsertion polymerase-DNA binary complex (step 5), or the polymerase dissociates from the DNA (step 6). Some of these steps may involve additional elementary steps, such as conformational changes within the binary or ternary complexes. For example, structural and kinetic evidence has suggested that the initial dNTP binding step (step 2) is coupled to a rapid induced-fit conformational-change step (24) and that the subsequent nucleotide incorporation step (step 3) follows a rate-limiting conformational-change step (3, 15, 20).

FIG. 1.

Minimal mechanism of DNA synthesis by DNA polymerases. Briefly, these steps are DNA binding (step 1), dNTP binding (step 2), phosphodiester bond formation (step 3), pyrophosphate release (step 4), and either advancement to the next template residue (step 5) or DNA release (step 6). The subscripts pre and post refer to the pre- and postnucleotide insertion complexes, respectively. The numbers refer to the steps described in the text.

Using pre-steady-state kinetics, here we investigate the mechanistic differences between nucleotide incorporation opposite templates A and T by Polι that are responsible for the high fidelity on template A and extremely low fidelity on template T. We found that on template A, the correct nucleotide is preferred because it binds tighter (step 2) and is incorporated faster (step 3) than the incorrect nucleotides. In contrast, opposite template T, the correct and incorrect nucleotides are incorporated at similar rates. Interestingly, the greater efficiency of G misincorporation opposite template T relative to correct A incorporation arises predominantly from the tighter binding of G opposite T in the enzyme active site. We infer from these results that the incipient base pair is accommodated differently in the active site of Polι, depending on whether A or T is the templating base, and that when the T is the templating base, the polymerase active site better accommodates the wobble base pair rather than the Watson-Crick base pair.

MATERIALS AND METHODS

DNA and nucleotide substrates.

A synthetic 25-mer oligodeoxynucleotide (5′GCCTCGCAGCCGTCCAACCAACTCA) was used as the primer strand. Two synthetic 45-mer oligodeoxynucleotides (5′GGACGGCATTGGATCGACCTTGAGTTGGTTGGACGGCTGCGAGGC and 5′GGACGGCATTGGATCGACCATGAGTTGGTTGGACGGCTGCGAGGC) were used as the template T and A strands, respectively. The primer strand (10 μM) was 5′-³²P-end labeled with polynucleotide kinase (Boehringer Mannheim) and [γ-³²P]ATP (6,000 Ci/mmol; Amersham Pharmacia) at 37°C for 1 h. The labeled primer strands were separated from unreacted [γ-³²P]ATP using a Sephadex G-25 spin column (Amersham Pharmacia). The 5′-³²P-end-labeled primer strand was annealed to the template strand in 50 mM Tris Cl (pH 7.5)-100 mM NaCl by heating to 90°C for 2 min and slowly cooling to room temperature over several hours. Annealed reactions were stored at 4°C for up to 1 week. Solutions of each dNTP (100 mM, sodium salt) were purchased from U.S. Biochemicals and stored at −70°C.

Polι purification.

Polι was overexpressed in yeast strain BJ5464 harboring plasmid pPOL114, which carries the glutathione S-transferase (GST) gene fused in frame with full-length Polι under control of the GAL PGK promoter. The GST-Polι fusion protein was purified by the same protocol previously used to purify yeast Polη (20). Following cell lysis, the GST-Polι fusion protein was bound to the glutathione Sepharose 4B matrix (Amersham Pharmacia). The Polι protein was then eluted from the matrix by treatment with PreScission protease (Amersham Pharmacia), which cleaves between the GST and Polι portions of the fusion protein, leaving full-length Polι fused to a 7-amino-acid N-terminal peptide. Protein concentrations were determined by the Bio-Rad protein assay using bovine serum albumin as a standard and by UV A₂₈₀ under denaturing conditions (8 M urea) using a molar extinction coefficient of 38,470 M⁻¹ cm⁻¹ (calculated from the amino acid composition). Both methods gave similar results. The total concentration of Polι was compared to the concentration of active Polι (see Results), and the preparation of Polι used in this study was found to be 87% active. The protein was stored in 10- to 50-μl aliquots at −70°C.

Pre-steady-state kinetics.

All polymerase reactions were measured in 25 mM TrisCl (pH 7.5), 5 mM MgCl₂, 5 mM dithiothreitol (DTT), and 10% glycerol at 22°C. The KinTek rapid chemical quench flow instrument was used to observe the incorporation of dTTP opposite template A. Preincubated Polι (130 nM final concentration) and DNA (300 nM final concentration) in the first syringe were rapidly mixed with various concentrations of dTTP (0 to 50 μM final concentration) in the second syringe and quenched with 0.3 M EDTA from the third syringe after specified time intervals (0 to 15 s). The extended primer products were separated from the unextended primer reactants on a 15% polyacrylamide sequencing gel containing 8 M urea. Gel band intensities were measured with the PhosphorImager instrument (Molecular Dynamics).

The incorporation of dGTP, dATP, and dCTP opposite template A and the incorporation of each of the four dNTPs opposite template T were slow enough to be measured without using the quench flow instrument. Initially, incorporation opposite template T was carried out under identical conditions by using the quench flow instrument. However, because the kinetics were linear under these conditions, the incorporation opposite template T were subsequently measured by hand using a final Polι concentration of 45 nM.

Data analysis.

For correct nucleotide incorporation opposite template A, the amount of product formed (P) was graphed as a function of time (t). The data were fit by nonlinear regression (Sigma Plot 7.0) to the burst equation:

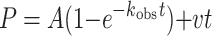(1)

where A is the amplitude of the pre-steady-state burst phase, k_obs is the observed first order rate constant for the pre-steady-state burst phase, and v is the observed rate for the linear, steady-state phase.

To determine the concentration of active Polι ([Polι]) and the dissociation constant (K_D) for the DNA binding step (K_D^DNA), the amplitude of the pre-steady-state burst phase (A) was graphed as a function of total DNA concentration, [DNA]. The data were fit by nonlinear regression to the quadratic equation:

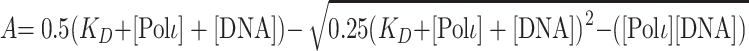(2)

To determine the K_D for the initial nucleotide binding step and the maximal first-order rate constant of nucleotide incorporation (k_pol) for correct nucleotide incorporation opposite template A, the observed first-order rate constant (k_obs) was graphed as a function of [dNTP]. The data were fit by nonlinear regression to the hyperbolic equation:

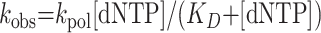(3)

For incorrect nucleotide incorporation opposite template A as well as the incorporation of all four nucleotides opposite template T, the amount of product formed was graphed as a function of time. The k_obs values were obtained by dividing the slope of the line by the active Polι concentration, and the k_obs values were graphed as a function of [dNTP]. The K_D for the initial nucleotide binding step and the k_pol for the nucleotide incorporation step were determined by fitting the data to the hyperbolic equation.

RESULTS

Human Polι synthesizes DNA with high fidelity on a template A residue, but synthesizes DNA with an unprecedented low fidelity on a template T residue. To gain a clearer understanding of the mechanistic basis of the high fidelity of Polι on some template bases and low fidelity on others, we have examined the incorporation of all four incoming dNTPs by Polι opposite template A and T residues in the first enzyme turnover (i.e., under pre-steady-state conditions).

Polι displays biphasic kinetics.

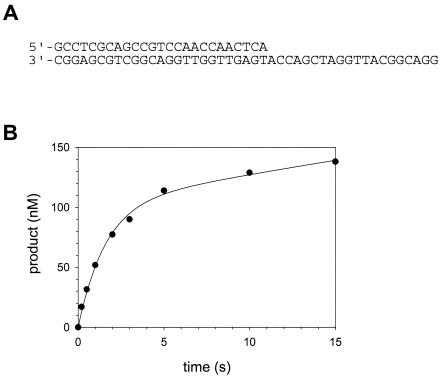
In order to examine the incorporation of nucleotides in the first enzyme turnover, we first had to determine whether or not Polι displays biphasic kinetics, also referred to as “burst kinetics.” To do this, we had to use Polι concentrations similar to those of the DNA substrate, and we had to quench the reactions after time intervals often shorter than 1 s. This required the use of the quench flow instrument. Preincubated Polι (130 nM final, active polymerase concentration [see the section “Active site titration and K_D for DNA binding”]) and the DNA substrate (300 nM final concentration) containing a template A residue (Fig. 2A) in one syringe were rapidly mixed with dTTP (50 μM final concentration) from the other syringe and quenched after various time intervals ranging from 0.2 to 15 s.

FIG. 2.

Pre-steady-state kinetics of nucleotide incorporation by Polι. (A) The DNA substrate (template A) used in this study. (B) Preincubated Polι (130 nM) and DNA (300 nM) were rapidly mixed with 50 μM dTTP for various time intervals by using a rapid chemical quench flow instrument. The amount of product formed was graphed as a function of time, and the solid line represents the best fit of the data to the burst equation with an amplitude equal to 100 ± 7 nM, a burst rate constant equal to 0.63 ± 0.07 s⁻¹, and a linear rate equal to 2.4 ± 0.6 nM/s.

The amount of product formed was graphed as a function of time (Fig. 2B), and the kinetics of T incorporation opposite a template A residue was indeed biphasic. The best fit of the data to the burst equation (see Materials and Methods) yielded a burst amplitude equal to 100 ± 7 nM, an observed burst rate constant equal to 0.63 ± 0.07 s⁻¹, and an observed linear rate constant equal to 0.018 ± 0.005 s⁻¹. Biphasic, or burst, kinetics was observed, because nucleotide incorporation was 35-fold faster in the first enzyme turnover than in subsequent enzyme turnovers. This means that the step that has an observed first-order rate constant equal to 0.018 s⁻¹ and limits the steady-state enzyme turnovers must occur following the nucleotide incorporation step (step 3, Fig. 1), which has an observed first-order rate constant equal to 0.63 s⁻¹. This steady-state rate-determining step is likely dissociation of the enzyme from the DNA substrate (step 6, Fig. 1).

Active site titration and K_D for DNA binding.

The presence of a clearly discernible pre-steady-state burst phase allowed us to directly measure the K_D for the initial nucleotide binding step (K_D^dNTP) (step 2, Fig. 1) as well as the first-order rate constant (k_pol) for the nucleotide incorporation step (step 3, Fig. 1). However, before proceeding with these measurements, we had to better define the reaction conditions for these experiments. Thus, we needed to measure the concentration of active Polι molecules and the K_D^DNA (step 1, Fig. 1). Because the amplitude of the pre-steady-state burst phase is equal to the concentration of the Polι-DNA complex at the beginning of the reaction, it is possible to determine the concentration of active Polι molecules and the K_D^DNA by looking at the variation of the pre-steady-state burst amplitude with the total concentration of the DNA substrate used (8).

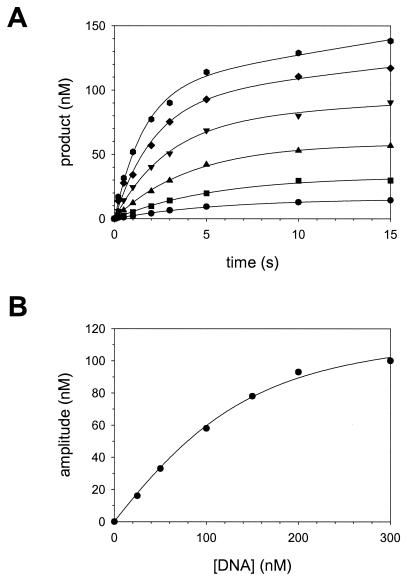
Polι (150 nM final total concentration; see Materials and Methods) was preincubated with various concentrations of the DNA substrate (25 to 300 nM final concentration) in one syringe, and reactions were initiated by rapidly mixing with dTTP (50 μM final concentration) from the other syringe. For each DNA concentration, the amount of product formed was graphed as a function of time (Fig. 3A), and the data from each plot were fit to the burst equation. The burst amplitude from each plot was then graphed as a function of DNA concentration (Fig. 3B). From the best fit of these data to the quadratic equation (see Materials and Methods), we obtained a K_D^DNA equal to 44 ± 7 nM and a concentration of active Polι molecules equal to 130 ± 10 nM. Thus, the concentration of Polι used in this study was 87% active, and all other experiments were corrected for the concentration of active Polι.

FIG. 3.

Determination of active Polι concentration and the K_D for the DNA binding step (K_D^DNA). (A) Polι (130 nM) was preincubated with various concentrations of DNA (•, 25 nM; ▪, 50 nM; ▴, 100 nM; ▾, 150 nM; ♦, 200 nM; and , 300 nM), and the reactions were initiated by rapid mixing with 50 μM dTTP. The amount of product formed was graphed as a function of time, and the solid lines represent the best fits of these data to the burst equation. (B) The burst amplitudes from these fits were graphed as a function of DNA concentration, and the solid line represents the best fit of the data to the quadratic equation with a concentration of active Polι equal to 130 ± 10 nM and a K_D^DNA equal to 44 ± 7 nM.

Mechanism of correct nucleotide incorporation opposite template A.

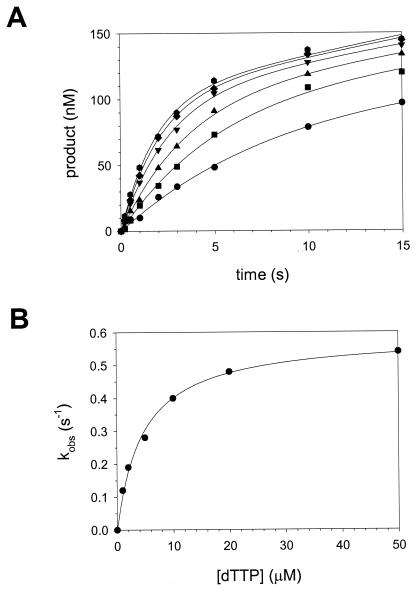
We next determined the K_D^dNTP for the initial nucleotide binding step (step 2, Fig. 1) and the first-order rate constant k_pol for the nucleotide incorporation step (step 3, Fig. 1) in the case of correct nucleotide T incorporation opposite a template A residue. Polι (130 nM) was preincubated with DNA (300 nM) in one syringe and mixed with various concentrations of dTTP (1 to 50 μM) from the other syringe. For each dTTP concentration, the amount of product formed was plotted as a function of time (Fig. 4A), and the data in each plot were fit to the burst equation. The observed pre-steady-state burst rate constant (k_obs) was then graphed as a function of dTTP concentration (Fig. 4B), and the data were fit to the equation describing a hyperbola (see Materials and Methods). The average K_D^dNTP for the initial nucleotide binding step (step 2, Fig. 1) was 4.9 μM, and the average first-order rate constant, k_pol, for the nucleotide incorporation step (step 3, Fig. 1) was 0.63 s⁻¹ (Table 1).

FIG. 4.

Kinetics of incorporation of the correct nucleotide opposite a template A residue by Polι. (A) Polι (130 nM) was preincubated with DNA (300 nM), and the reactions were initiated by rapid mixing with various concentrations of dTTP (•, 1 μM; ▪, 2 μM; ▴, 5 μM; ▾, 10 μM; ♦, 20 μM; and , 50 μM). The amount of product formed was graphed as a function of time, and the solid lines represent the best fits of these data to the burst equation. (B) The burst rate constants from these fits were graphed as a function of dTTP concentration, and the solid line represents the best fit of the data to the hyperbolic equation with a k_pol equal to 0.59 ± 0.02 s⁻¹ and a K_D^dTTP equal to 4.7 ± 0.4 μM.

TABLE 1.

Nucleotide incorporation by Polι on template A

Nucleotide · template	kpol (s−1)a	KD (μM)a	kpol/KD (μM−1 s−1)	kpol/kpolb	KD/KDc	Fidelityd
dGTP · A	0.0037 ± 0.0001	470 ± 50	7.9 × 10−6	170	96	16,000
dATP · A	0.013 ± 0.002	200 ± 50	1.6 × 10−4	48	41	810
dTTP · A	0.63 ± 0.06	4.9 ± 0.2	0.13
dCTP · A	0.0019 ± 0.0001	280 ± 10	6.8 × 10−6	330	57	19,000

^aThe k_pol and K_D values represent the averages and standard errors from three independent determinations.

^bCalculated by k_pol for dTTP·A divided by k_pol for dNTP·A.

^cCalculated by K_D for dNTP·A divided by K_D for dTTP·A.

^dCalculated by k_pol/K_D for dTTP·A divided by k_pol/K_D for dNTP·A.

Mechanism of incorrect nucleotide incorporation opposite template A.

To better understand the mechanistic basis of the moderate fidelity of Polι on the template A residue, we next determined the K_D^dNTP and k_pol values for incorrect nucleotide incorporation opposite the template A base. Because of the slower rate of nucleotide incorporation with the incorrect nucleotides, it was possible to do these experiments without the assistance of the quench flow instrument. Polι (130 nM) and DNA (300 nM) were mixed with various concentrations of dGTP, dATP, or dCTP (50 to 2000 μM) for various time points ranging from 15 to 90 s. The amount of product formed varied linearly with time, and no pre-steady-state burst phase was observed in any of these reactions. This indicates that nucleotide incorporation in the first enzyme turnover occurs at the same rate as incorporation in the subsequent enzyme turnovers. Thus, the nucleotide incorporation step (step 3, Fig. 1) has now become rate limiting in the steady state.

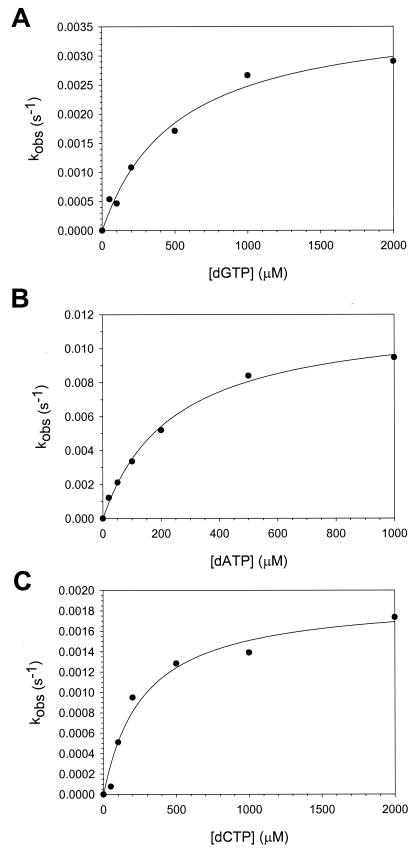
For each dNTP concentration, we plotted the amount of product formed versus time and calculated the observed first-order rate constant, k_obs, for nucleotide incorporation from the slope of each line. The k_obs was then graphed as a function of dNTP concentration (Fig. 5), and from the best fit of these data to the hyperbolic equation, we obtained K_D^dNTP and k_pol values for incorrect nucleotide binding and incorporation, respectively, opposite template A. The average K_D^dNTP values for the incorrect nucleotides ranged from 200 to 470 μM, and the average k_pol values for the incorrect nucleotides ranged from 0.0019 to 0.013 s⁻¹ (Table 1).

FIG. 5.

Kinetics of incorporation of the incorrect nucleotides opposite a template A residue by Polι. (A) Polι (130 nM), DNA (300 nM), and dGTP (0 to 2000 μM) were reacted for various time intervals, and the linear rate constants of nucleotide incorporation were graphed as a function of dGTP concentration. The solid line represents the best fit of the data to the hyperbolic equation with a k_pol equal to 0.0038 ± 0.0003 s⁻¹ and a K_D^dGTP equal to 520 ± 110 μM. (B) Polι (130 nM), DNA (300 nM), and dATP (0 to 1000 μM) were reacted for various time intervals, and the linear rate constants of nucleotide incorporation were graphed as a function of dATP concentration. The solid line represents the best fit of the data to the hyperbolic equation with a k_pol equal to 0.012 ± 0.001 s⁻¹ and a K_D^dATP equal to 240 ± 20 μM. (C) Polι (130 nM), DNA (300 nM), and dCTP (0 to 2000 μM) were reacted for various time intervals, and the linear rate constants of nucleotide incorporation were graphed as a function of dCTP concentration. The solid line represents the best fit of the data to the hyperbolic equation with a k_pol equal to 0.0019 ± 0.0002 s⁻¹ and a K_D^dCTP equal to 280 ± 70 μM.

Mechanism of nucleotide incorporation opposite template T.

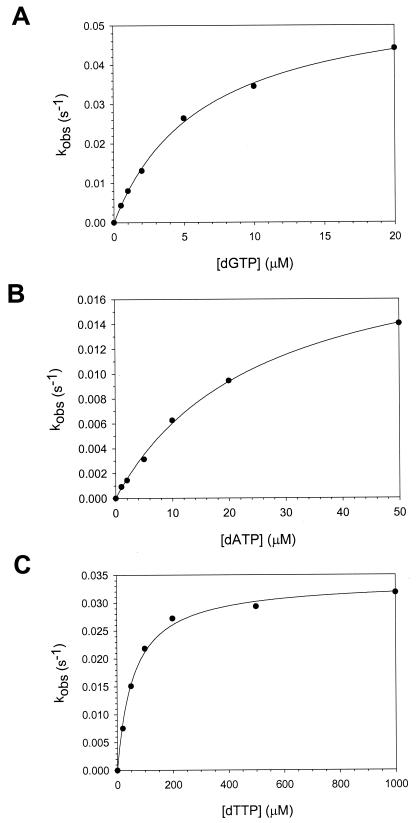
To better understand the mechanistic basis of the extremely low fidelity of Polι on template T residues, we determined the K_D^dNTP and k_pol values for nucleotide incorporation opposite this templating base. As was the case for incorrect nucleotide incorporation opposite template A, nucleotide incorporation—both correct and incorrect—was slow enough to perform these experiments by hand, and the amount of product formed varied linearly with time in the case of G, A, and T incorporation. We were unable to observe the incorporation of C opposite the template T residue under any of the conditions tested. The k_obs was then graphed as a function of dNTP concentration (Fig. 6), and from the best fit of these data to the hyperbolic equation, we obtained K_D^dNTP values for correct and incorrect nucleotide binding opposite a template T and k_pol values for subsequent nucleotide incorporation. The average K_D^dNTP value for dGTP binding was 5.7 μM, while the K_D^dNTP values for dATP and dTTP were 46 and 61 μM, respectively (Table 2). The average k_pol values for the nucleotide incorporation opposite template T ranged from 0.029 to 0.054 s⁻¹ (Table 2).

FIG. 6.

Kinetics of incorporation of nucleotides opposite a template T residue by Polι. (A) Polι (43 nM), DNA (300 nM), and dGTP (0 to 20 μM) were reacted for various time intervals, and the linear rate constants of nucleotide incorporation were graphed as a function of dGTP concnetration. The solid line represents the best fit of the data to the hyperbolic equation with a k_pol equal to 0.058 ± 0.002 s⁻¹ and a K_D^dGTP equal to 6.4 ± 0.4 μM. (B) Polι (43 nM), DNA (300 nM), and dATP (0 to 50 μM) were reacted for various time intervals, and the linear rate constants of nucleotide incorporation were graphed as a function of dATP concentration. The solid line represents the best fit of the data to the hyperbolic equation with a k_pol equal to 0.021 ± 0.001 s⁻¹ and a K_D^dATP equal to 25 ± 2 μM. (C) Polι (43 nM), DNA (300 nM), and dTTP (0 to 1,000 μM) were reacted for various time intervals, and the linear rate constants of nucleotide incorporation were graphed as a function of dTTP concentration. The solid line represents the best fit of the data to the hyperbolic equation with a k_pol equal to 0.034 ± 0.001 s⁻¹ and a K_D^dTTP equal to 60 ± 5 μM.

TABLE 2.

Nucleotide incorporation by Polι on template T

Nucleotide · template	kpol (s−1)a	KD (μM)a	kpol/KD (μM−1 s−1)	kpol/kpolb	KD/KDc	Fidelityd
dGTP · T	0.054 ± 0.004	5.7 ± 0.7	9.5 × 10−3	0.54	0.12	0.07
dATP · T	0.029 ± 0.005	46 ± 15	6.3 × 10−4
dTTP · T	0.032 ± 0.002	61 ± 5	5.2 × 10−4	0.91	1.3	1.2
dCTP · T	NDe	ND

^aThe k_pol and K_D values represent the averages and standard errors from three independent determinations.

^bCalculated by k_pol for dATP·T divided by k_pol for dNTP·T.

^cCalculated by K_D for dNTP·T divided by K_D for dATP·T.

^dCalculated by k_pol/K_D for dATP·T divided by k_pol/K_D for dNTP·T.

^eND, no detectable incorporation observed.

DISCUSSION

One remarkable feature of DNA polymerases is that their specificity for the incoming nucleotide changes dramatically depending on the template base present in their active site. For virtually all polymerases, there is a strong preference for incorporating the nucleotide that forms the correct Watson-Crick base pair with the template base. Moreover, the catalytic efficiencies with which any given polymerase forms the 4 possible correct bp are approximately the same. Polι is an exception to these rules.

Polι incorporates the correct nucleotide opposite template A with an efficiency of several hundred to several thousand fold greater than that opposite template T, while the efficiency of correct nucleotide incorporation opposite templates G and C is intermediate between these extremes. The fidelity of nucleotide incorporation opposite the different template residues varies in a similar manner. The fidelity of Polι is high opposite template A, with error frequencies of 10⁻⁴ to 10⁻⁵. Opposite templates G and C, Polι has a relatively low fidelity, with error frequencies ranging from 10⁻¹ to 10⁻². Polι has an unprecedented low fidelity opposite template T, with error frequencies ranging from 10⁺¹ to 10⁻¹. The fidelity opposite template T is so poor that Polι preferentially inserts the incorrect G ∼10-fold more efficiently than the correct A (7, 10, 18, 23). These efficiencies and error frequencies of Polι in the presence of each template residue were previously determined by using steady-state kinetics. However, while steady-state kinetics allows one to accurately quantify the efficiency and fidelity of nucleotide incorporation, it provides little information about the mechanistic basis of the efficiency and fidelity. Pre-steady-state kinetics, in contrast, allows one to directly examine the contributions of the individual steps of the nucleotide incorporation reaction to the efficiency and fidelity of the reaction. Thus, to understand the mechanistic differences when various template bases are present in the active site of Polι, we examined the pre-steady-state kinetics of the incorporation of all four incoming nucleotides opposite template A and template T residues.

Mechanistic basis of the high fidelity of Polι opposite template A.

A comparison of the K_D^dNTP values for the correct and incorrect nucleotides opposite template A indicates that the correct nucleotide binds the polymerase-DNA binary complex with a 40- to 100-fold-higher affinity than the incorrect nucleotides. Assuming an arbitrary nucleotide concentration of 100 μM, this would correspond to changes in the ΔG associated with binding the correct versus the incorrect nucleotide (ΔΔG) of 2.2 to 2.7 kcal/mol. From a comparison of the k_pol values for the incorporation of correct and incorrect nucleotides opposite template A, we find that when the correct nucleotide is bound, it is incorporated 50 to several hundred times faster than when the incorrect nucleotide is bound. This corresponds to changes in the free energy of activation when bound to the correct versus the incorrect nucleotide (ΔΔG^‡) of 2.2 to 3.4 kcal/mol. Thus, the enzyme binds the transition state of the elementary step corresponding to k_pol, be it the chemical step of phosphodiester bond formation or a conformational change step immediately preceding and limiting chemistry, better when T is bound opposite template A than when the incorrect nucleotides are bound opposite A. From these observations, we conclude that opposite a template A residue, Polι maintains a relatively high fidelity because of its selectivity for the correct nucleotide at both the initial nucleotide binding step (step 2, Fig. 1) and at the subsequent nucleotide incorporation step (step 3, Fig. 1).

Mechanistic basis of the low fidelity of Polι opposite template T.

Opposite template T, we find that the correct nucleotide A does not bind the polymerase-DNA binary complex any better than the incorrect nucleotide T. In fact, the ΔΔG for binding A versus T opposite template T is less than 0.2 kcal/mol. What is even more surprising is that the incorrect nucleotide G binds opposite template T with an eightfold-better affinity than does A, which corresponds to a ΔΔG of −1.2 kcal/mol. This indicates that Polι binds the ground state of the incipient G-T wobble pair somewhat tighter than the A-T Watson-Crick pair. From a comparison of the k_pol values for the correct and incorrect nucleotides, we find that once bound to the polymerase-DNA complex, the three nucleotides A, G, and T are incorporated at similar rates, and the ΔG^‡ values for the incorporation of these different nucleotides differ by less than 0.4 kcal/mol. We note that Polι is very poor at incorporating a C opposite template T, and it remains unclear how the polymerase discriminates so well against this incorrect base pair.

Comparison of nucleotide incorporation opposite templates A and T.

The incorporation of a correct T opposite template A differs dramatically from the incorporation of a correct A opposite template T. When T is the templating base, the K_D^dNTP for the correct nucleotide increases by a factor of 10 compared to the K_D^dNTP for the correct nucleotide when A is the templating base. The change in the ΔG associated with binding T opposite A versus binding A opposite T (ΔΔG) is 1.3 kcal/mol. Thus, the presence of T as the template base interferes with the ability of Polι to bind the correct incoming nucleotide in the ground state. Similarly, when T is the template base, the k_pol for the correct nucleotide incorporation step decreases 20-fold compared to when A is the template base. This corresponds to a ΔΔG^‡ for incorporating T bound opposite template A versus A bound opposite template T of 1.8 kcal/mol. This means that Polι does not stabilize the transition state of the correct nucleotide incorporation step to the same degree with template T as it does with template A.

Interestingly, for the misincorporation of G opposite template T, the initial nucleotide binding step is remarkably similar to that of the T incorporation opposite template A. A comparison of K_D^dNTP values shows that Polι binds a G when T is the template with the same affinity as it binds T when A is the template; the ΔG values in these two cases differ by less than 0.1 kcal/mol. Thus, with respect to the initial nucleotide binding step (step 2, Fig. 1), no differences are observed between the binding affinity of an incorrect G opposite T and the binding of a correct T opposite A. A comparison of the k_pol values indicates that upon nucleotide binding, the G opposite a template T is incorporated 12-fold slower than the incorporation of a T opposite template A, and this corresponds to a ΔΔG^‡ for incorporating T bound opposite A versus G bound opposite T of 1.4 kcal/mol. Thus, despite nearly the same affinity for binding the T-A and G-T base pairs in the ground state, Polι does not stabilize the transition state of the nucleotide incorporation step (step 3, Fig. 1) to the same degree with G-T base pair as it does with the T-A base pair.

Structural basis for the unusual specificity of Polι.

Although an understanding of the observed nucleotide incorporation specificities at the structural level awaits the structures of Polι in ternary complexes with several different incipient base pairs, based on the pre-steady-state kinetics reported here, we can make some predictions about the interactions of the enzyme with different incipient base pairs. Our results suggest that the incipient base pair is accommodated differently in the active site of Polι, depending on whether an A or a T is the template base. Because the K_D^dNTP is lower for binding the correct nucleotide T opposite template A than it is for binding the incorrect nucleotides, Polι must bind the incipient base pair in the ground state for the correct incoming nucleotide T opposite template A better than the incorrect nucleotides. That would suggest that when A is the template base, the enzyme stabilizes the cannonical Watson-Crick base pairing geometry by making more close contacts with the T-A base pair than with the three possible mispairs.

In contrast, the K_D^dNTP is lower for binding the incorrect nucleotide G opposite template T than it is for binding the correct nucleotide A. This implies that Polι binds the ground state for the G-T mispair better than the A-T base pair, suggesting that when T is the template base, the enzyme better accommodates the G-T wobble base pairing geometry than the Watson-Crick base pairing geometry. Furthermore, the fact that the K_D^dNTP for binding G opposite T is the same as for binding T opposite A implies that Polι must bind the ground state for the G-T mispair with nearly the same affinity as the T-A base pair. These results predict that in the ternary complexes of the T-A base pair and G-T mispair, the enzyme makes similar close contacts with the ground state of the incipient base pair in these seemingly very different cases.