Automated Tracing of Filaments in 3D Electron Tomography Reconstructions using Sculptor and Situs

Abstract

The molecular graphics program Sculptor and the command-line suite Situs are software packages for the integration of biophysical data across spatial resolution scales. Herein, we provide an overview of recently developed tools relevant to cryo-electron tomography (cryo-ET), with an emphasis on functionality supported by Situs 2.7 and Sculptor 2.1. We describe a work flow for automatically segmenting filaments in cryo-ET maps including denoising, local normalization, feature detection, and tracing. Tomograms of cellular actin networks exhibit both cross-linked and bundled filament densities. Such filamentous regions in cryo-ET data sets can then be segmented using a stochastic template-based search, VolTrac. The approach combines a genetic algorithm and a bidirectional expansion with a tabu search strategy to localize and characterize filamentous regions. The automated filament segmentation by VolTrac compares well to a manual one performed by expert users, and it allows an efficient and reproducible analysis of large data sets. The software is free, open source, and can be used on Linux, Macintosh or Windows computers.

1. Introduction

Situs is a widely used modeling package of command-line tools, originally developed for the interpretation of low-resolution electron microscopy density maps (Wriggers et al., 1999; Wriggers, 2010). Sculptor is a molecular graphics visualization program based in part on fast Situs algorithms that can be explored in real time (Birmanns and Wriggers, 2003; Birmanns et al., 2011). Both packages play important (and complementary) bridging roles between high-resolution atomic structures and lower-resolution structural data from other experimental sources. We recently began to focus on applications in cryo-electron tomography (cryo-ET; Baumeister 2002), an important but particularly challenging application field in structural biology due to the currently limited resolution (4–5 nm) and high noise present in the 3D reconstructions (Medalia et al., 2002; Frangakis and Förster, 2004).

To allow for a meaningful and reproducible analysis of cryo-tomograms, it is necessary to separate features of interest from the background. This process is referred to as “segmentation” and is currently mostly performed manually by assigning a label to pixels sharing the visual characteristics of the feature of interest. For a tomographic stack of images, the corresponding contours of these labels can then be used to reconstruct the 3D shape of the feature of interest. This procedure often relies on non-objective user-dependent selection and tracing steps. Given the enormous amounts of information present in tomographic reconstructions, it is virtually impossible to perform a complete segmentation based on visual inspection of the tomogram. For a statistically sound analysis of this information, a robust automated segmentation approach is needed that is also capable of detecting small-scale features. Depending on the quality of the tomographic data, these features are usually hard to recognize and can be easily overlooked, especially if they have orientations perpendicular to the plane of a tomographic slice. This is particularly true for the filaments in cryo-ET tomograms of cellular actin networks studied in this paper.

In this report, we describe a software implementation for the reconstruction of actin filaments from 3D tomography maps comprising the following steps:

1. Two denoising filters are described which reduce high-frequency noise artifacts and which facilitate the desired segmentation of features. Herein, we compared the performances of a linear Gaussian-weighted averaging filter and of a nonlinear Digital Paths Supervised Variance (DPSV) denoising filter.

2. A Gaussian-weighted local normalization is applied to cryo-ET maps prior to any analysis. Such normalization is beneficial because it enhances the appearance of structural features and equalizes any uneven density distributions across experimental cryo-ET maps.

3. Two map editing tools, polygon-clipping and a multi-point floodfill, are described which facilitate filament tracing by masking out non-filamentous density regions such as the cell membrane, extracellular space, ribosomes and storage vesicles.

4. Cryo-ET reconstructions suffer from incomplete sampling of the Fourier space, resulting in anisotropic resolution and degradation of image quality in the reconstructed tomogram along the direction of the optical axis. We corrected for these effects in real space by implementing resolution anisotropy and an orientation-dependent attenuation of filament intensities.

5. VolTrac (Volume Tracer) was originally developed for detecting alpha-helices (Rusu and Wriggers, 2012), but it was modified here to annotate filamentous actin networks in cryo-ET reconstructions. The VolTrac method combines a genetic algorithm (GA) for quasi-continuous sampling with a bidirectional expansion for following filament curvature and length.

6. The resulting predictions are compared to subjective expert annotations of filaments.

In the following sections below we explain the six steps and apply them to the detection of actin networks in Dictyostelium discoideum cells. Actin polymerization powers the formation of different types of cellular actin networks (Pollard and Borisy, 2003), such as finger-like extensions of the cell membrane, referred to as filopodia. Filopodia are characterized by a central core of bundled actin filaments. Their backbone consists of shorter actin filaments, which are aligned in parallel or obliquely to the filopod’s axis (Medalia et al., 2007). A D. discoideum filopodium dataset (Medalia et al., 2007) is used for visualization purposes in sections 3–6, whereas a sub-volume containing cross-linked actin filaments (Rigort et al., 2012) is used for validation in section 7. We conclude the paper with a discussion of implementation details, limitations, and future work in section 8.

2. Denoising 3D Tomography Reconstructions

Frozen-hydrated biological specimens are highly sensitive to ionizing radiation. Therefore, in cryo-ET, the cumulative electron dose must be minimized and distributed between images to avoid radiation damage-related structural changes within the vitrified sample. As a consequence of this electron dose fractionation, and due to the low contrast of ice-embedded specimens, the signal-to-noise ratio (SNR) in 3D reconstructions is very low. Therefore, careful noise reduction is essential prior to the extraction of biologically relevant information (Frangakis and Hegerl, 2001). Ideally, a denoising algorithm preserves as much of the signal as possible while reducing the noise to a sufficiently low level (Stoschek and Hegerl, 1997). Efficient denoising approaches allow the preservation of information for a subsequent analysis by means of manual or automated segmentation techniques. A number of methods have been described that demonstrate the value of denoising approaches in 2D and 3D datasets (for an overview, see Narasimha et al., 2008).

The size of the actin filaments in this work (7 nm or about 4 voxels diameter) limits the amount of denoising that can be applied to the corresponding cryo-ET maps. In a first approach to denoising we have implemented a linear Gaussian averaging with sigma-1D of 1.912 nm (see Suppl. Data 1). In the application of sections 6 and 7 this sigma-1D value corresponds to one voxel, and the full width of the averaging kernel is 5 voxels. As an alternative to Gaussian averaging, we have also implemented a non-linear DPSV filter in a cubic mask of 5 voxel width using digital paths of length 2. The DPSV filter uses local variance information to control noise in a locally adaptive manner (Szczepanski et al., 2004; Smolka, 2008). We have adapted the DPSV filter to cryo-ET maps (Suppl. Data 1) and compared its performance to Gaussian averaging using an HIV virion map (Briggs et al., 2007) as example. Aided by a supervised classification of digital paths based on a discriminant analysis, the DPSV filter preserves more details than the Gaussian (Suppl. Data 1: Suppl. Fig. 3). However, Gaussian and DPSV have similar denoising properties (Suppl. Data 1: Suppl. Fig. 2) and perform similarly well in the filament tracing applications below. Since the results in the following do not sensitively depend on the type of denoising filter, all Figures in this paper are based on the conventional Gaussian averaging, whereas DPSV results are mentioned as needed.

In Sculptor version 2.1, the denoising filters can be applied to a map via the menus “Volume” → “Gaussian” or “DPSV Filter” (entering parameters in the pop-up dialog box; Gaussian parameters are sigma-1D and the truncation limit; see Supplementary Data 1 for DPSV parameters). In Situs version 2.7 a separate command-line utility volfltr was implemented for DPSV. The Gaussian averaging can be selected in Situs 2.7 as a command line option of the voltrac program.

3. Local Normalization of Map Density

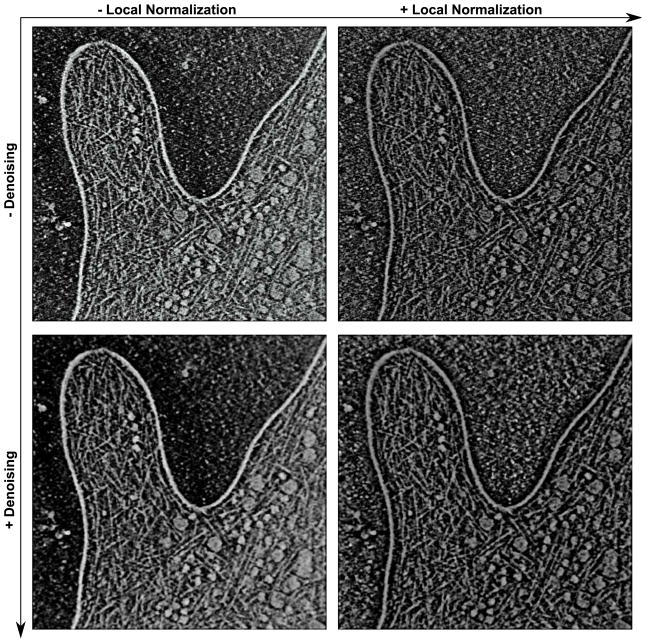
Cryo-ET volumes can suffer from uneven density levels across the map due to uneven specimen or ice thickness, or due to missing directions in the backprojection. Figure 1 shows a reconstruction of a D. discoideum filopodium (Medalia et al., 2007). Upon inspection of the density isolevels of the filaments in the raw data (upper left in Fig. 1), a subtle increase in density from the lower left to the upper right was observed. Therefore, to normalize the features across the map, a Gaussian-weighted local normalization was applied.

Figure 1.

Visual comparison of filter performance using the large D. discoideum filopodium dataset. The panels depict the central 2D slice in the presence and absence of local normalization and denoising. The raw filopodium reconstruction was generated based on original recordings as described by Medalia et al. (2007), with the map inverted (background black and at zero), such that features are white and positive. The voxel size of the (two times binned) map is 1.62 nm, twice that of the unbinned recordings. The binned map was cropped to the filopodium data, resulting in a final map size of 512 × 512 × 106 voxels. The local normalization filter has a spatial extent σ_W = 11.5 voxel units. The Gaussian-weighted average (applied before local normalization) uses a sigma-1D of 1.92 nm (see Suppl. Data 1) for consistency with the validation dataset used in sections 6 and 7. The molecular graphics in all Figures were generated with Sculptor (Birmanns et al., 2011).

For each voxel r, the average $\overline{{\rho }_{et}(\mathbf{r})}$ and the standard deviation σ(ρ_et(r)) of the densities were computed by using Gaussian weights in the local neighborhood. The parameter σ_W defined the spatial extent of the Gaussian. For the two maps presented here, σ_W approximately equals 19 nm, resulting in a smooth variation of the average and standard deviation. The locally normalized densities were then computed according to the formula (Rusu and Wriggers, 2012)

$${\rho }_{et}^{/}(\mathbf{r})=\frac{{\rho }_{et}(\mathbf{r})-\overline{{\rho }_{et}(\mathbf{r})}}{\sigma ({\rho }_{et}(\mathbf{r}))},$$ (1)

where ρ_et(r) is the original density at voxel r and ${\rho }_{et}^{/}(\mathbf{r})$ represents the locally normalized density. In Sculptor version 2.1, the local normalization can be applied to a map via the menus “Volume” → “Local Normalization” (entering σ_W in the pop-up dialog box). In Situs version 2.7, the local normalization can be selected as a command line option of the voltrac program.

The local normalization will amplify any exterior noise, so an application together with the denoising filter is synergistic. The effect of local normalization is shown in Figure 1, both in the absence and presence of a subsequent denoising. The resulting filtered volume (right panels) exhibits a more uniform distribution of density, and the filter enhances the appearance of rod-like features used in subsequent analysis. No particular physical meaning is attributed to the locally normalized densities.

4. Segmentation of Non-Filamentous Densities

The filopodium dataset shown in Figure 1 exhibits non-filamentous high-density features that were removed in a series of pre-processing steps.

First, the extracellular space (outside the membrane) was masked by polygon clipping using the established Situs tool voledit. This step involved an interactive tracing of the membrane in the specimen (X,Y) plane and the application of polygon-clipping to all Z sections. The masked density was removed (subtracted) from the map.

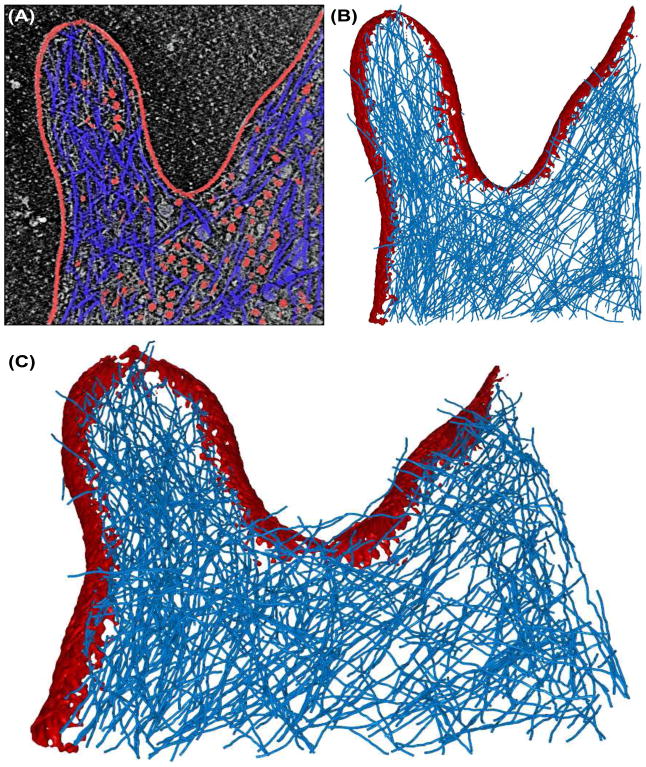
Second, the cell membrane itself was segmented and removed from the map using the established “floodfill” strategy. The original approach initiates the segmentation from a given starting position (user defined) and extracts all the contiguous voxels in the neighborhood with intensities above a given threshold (user defined; here we chose the mean map density level). In Situs, floodfill can be applied within voledit in combination with voldiff map subtraction. In Sculptor, standard floodfill can be applied to a map via the menus “Volume” → “Floodfill”, or directly by right clicking on the desired voxel in “Map Explorer”. Figure 2A,B shows in red the segmented cell membrane.

Figure 2.

Filament detection in the filopodium dataset. Membrane regions and globular densities (segmented out before filament tracing) are shown in red, and VolTrac filament tracing results (actin network) are shown as blue translation centers of the bidirectional expansion (see section 6). (A) Central 2D slice of the raw data. (B) 3D iso-surface rendering of the 3D reconstruction with membrane and non-filamentous densities segmented (see section 4). (C) Segmented membrane and predicted actin network in tilted 3D perspective. Masking, segmentation of non-filamentous densities (parameters for multi-point floodfill: sigma-1D: 2 voxels; threshold: 0.52; number of points: 300), denoising and local normalization were applied prior to tracing of the filaments (see text). For map details and filter parameters, see the caption of Fig. 1.

Third, globular densities in the cytoplasm, which presumably correspond to ribosomes and other macro-molecular complexes (red in Fig. 2A,B), were segmented and subtracted by a novel multi-point floodfill approach in Sculptor 2.1. Multi-point floodfill was implemented to extract not only one (as in the original floodfill) but several regions automatically. The approach uses a denoised version of the map to automatically set the starting positions based on density maxima. The multi-point floodfill sorts the (denoised) input map by decreasing density values. Then the approach initiates consecutive floodfill operations starting with the highest density and going down the list of values. The approach ensures that a new floodfill does not start in a region that was already segmented in a previous iteration.

In Sculptor version 2.1, multi-point floodfill can be applied to a map via the menus “Volume” → “Multi Point Floodfill”, entering the following parameters:

• the sigma-1D of a Gaussian averaging filter that will be applied to the original map for denoising purposes,

• the number of times to start flood fill, and

• the threshold value.

It is straightforward to refine the three parameters interactively in the molecular graphics program. In the applications described below we started the interactive exploration with default values for sigma-1D (2 voxels) and for the threshold (mean map density). For the number of start points one would typically start with a small number and increase it if more results are desired. The main advantage of this approach is that it returns a manageable (i.e. relatively small) number of segmentations compared to exhaustive segmentation algorithms such as the watershed transform (Volkmann, 2002). One limitation is that the use of a global threshold value for the entire map may not result in ideal segmentations if there are density variations across the map. Therefore we applied multi-point floodfill after the local normalization described in section 3.

5. Correction for Missing Fourier Information in Real Space

Cryo-ET reconstructions suffer from incomplete sampling of the Fourier space. The filopodium tomograms used in this work were recorded with single-axis tilt about the Y-axis, resulting in a ‘wedge’ of missing Fourier information in the Z-direction (Penczek and Frank, 2006). The missing wedge in Fourier space corresponds to anisotropic, object-dependent artifacts in the real space reconstruction.

For small spherical features there is an elongation in the Z-direction (optical axis) which can be interpreted as lowered resolution (Radermacher, 1988) relative to the specimen (X,Y) plane. This elongation in Z-direction is easily corrected. In the current implementation we support a user-defined elongation factor following the approach taken earlier in the Situs colores tool (Chacón and Wriggers, 2002): The anisotropy is imposed by an initial compression of the map (interpolation) and by a final decompression of the results in Z-direction. The algorithm wrapped inside the compression thus remains isotropic. The elongation depends on the size of the wedge and can be computed theoretically (Radermacher, 1992) or observed by visual inspection of the map. Here, we used an empirical elongation factor of 2 which is close to the theoretical value for a ±60° single axis tilt.

In addition, there is an orientation-dependent degradation of density of extended objects such as filaments. Let a pair of angles (φ, θ) describe the orientation (Rigort et al., 2012): φ is the azimuth angle between the tilt axis (Y-axis) and the filament projected onto the specimen (X,Y) plane, whereas θ is the altitude angle between a filament and the specimen plane. For θ=90° filaments are parallel to the optical axis and the equator of the filament transform will lie within the (X,Y)-plane, unaffected by the missing wedge. For smaller θ < 90° there will be some degradation of densities as the filament transform enters the missing wedge. This leads to relatively strong filament densities in Z-direction that would bias the tracing described in the next section towards large θ angles. To correct for this θ-dependent bias we modulate the densities with a correction factor λ + (1 + λ)cos²(θ), where λ is an attenuation parameter that can be set empirically after inspecting the orientation-dependent filament densities. (The empirical assignment is necessary due to the local normalization partially equilibrating the original densities.) In this work we use a value of λ = 0.75 which was set after inspecting density values of the locally normalized maps.

We did not attempt to explicitly correct for a φ-dependent degradation of density in this work (in addition to any implicit φ-dependent correction afforded by local normalization). For angles φ = 90°, θ < 30° the equator of the filament transform will lie within the missing wedge and the filaments disappear, hence a correction is not possible. It is understood that such orientations are not detectable by the tracing algorithm described in the following section.

6. Segmentation of Filamentous Density

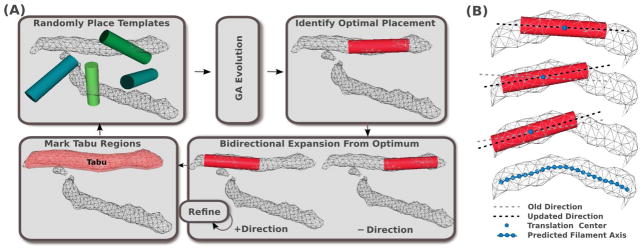
The work flow of VolTrac, as applied to filament detection in cryo-ET, is shown in Figure 4. In Sculptor version 2.1 the filament detection can be applied to a map via the menus “Docking” → “Volume Tracer” (entering parameters described below in the pop-up dialog box). Here, we give an abridged overview of the procedure relevant for cryo-ET; for more details, see (Rusu and Wriggers, 2012).

Figure 4.

(A) Filament segmentation work flow using VolTrac (Rusu and Wriggers, 2012): A random initial population of cylindrical templates evolves for several GA generations. The best scoring template is then used for the bidirectional expansion. The annotated region is included in the tabu list. A new GA run is executed, starting from new random distributions. (B) During the bidirectional expansion, the axis of the template is updated, allowing the template to follow the curvature of the filamentous density. The predicted filament is described by the translation centers obtained in the bidirectional expansion. The center points can be low-pass filtered to create a mask used for segmenting the filament (see section 6).

VolTrac utilizes a genetic algorithm (GA; Goldberg 1989) to optimize randomly placed cylindrical start templates (the algorithm was adapted from the original alpha- helix detection; as in the original application, the automatically generated templates used here have no helical features). One important advantage of the GA search (Fig. 4A) is the support of a quasi-continuous representation of translations and rotations that are updated by the typical mutation and crossover operators (Rusu and Birmanns, 2010) to maximize the ‘fitness’ score, the cross-correlation with the density. For the cryo-ET application, we used the standard GA parameters (Rusu and Wriggers, 2012), except a template cylinder radius of 2.4 nm and a length of 50 nm were used. In general, these template size parameters should be adjusted by the user based on the filament dimensions. For example, one can create a few cylinder templates with different radii and check the overlap with the filament (the radius should be slightly smaller than the actual filament radius, which is approximately 3 nm in the case of actin). The code is robust, so it works even if the radius is not perfectly matched.

The template with the highest cross-correlation usually covers part of a filament region, aligned with its main axis, but it does not capture the full length of the filament or its curvature (Fig. 4A). Therefore, a bidirectional expansion is performed, using templates that measure half of the radius and length of the GA templates (1.2 nm and 25 nm, respectively), to trace the filament axis (Fig. 4B). Expansion proceeds until the score at the current position falls below a user-defined percentage of the initial score. Here, we used a 75% threshold. There is a tradeoff between the length of the detected filaments and the effect of noise (Rusu and Wriggers, 2012), so this threshold must be determined empirically. In single particle cryo-EM applications, we found suitable scores for the detection of alpha-helices in the range of 50–70% (Rusu and Wriggers, 2012).

Once a filament is characterized by the bidirectional expansion, it is appended to the tabu list and eliminated from further exploration (Fig. 4A). A tabu region is defined by a user-defined radius about each translation center of the filament (Fig. 4B). The radius should be of the order of the map resolution. Here, it was set to 6.0 nm (which approximately corresponds to the nominal resolution of the filopodium data). The algorithm proceeds by eliminating tabu regions from the search until it converges (or is stopped), and a list of filaments ranked by correlation-weighted length is returned (Rusu and Wriggers, 2012). In the case of cryo-ET, we ignored this ranking. The coordinates of the final filaments can be stored and used for further processing.

Note that the tabu regions are not actually subtracted from the map. In the GA evolution, if individuals enter a tabu region (which is, of course, possible due to the mutation or crossover), their fitness is set to zero, resulting in their termination. In addition, the random start initialization will place all individuals outside the tabu regions.

Figure 2 shows the results of VolTrac applied to the D. discoideum filopodium map (Medalia et al., 2007). The blue filaments in Figure 2 are the traces resulting from the bidirectional expansion center points. As expected, the traces are largely contained in the intra-cellular region, but the membrane has weaker density in the top slices of the map and is not fully removed by multipoint flood fill (we cropped the map very conservatively). VolTrac catches such noise by over expanding filaments into the weaker membrane density. We show the original, raw results in Figure 2, although it would be easy to manually edit the traces which are saved as PDB files.

To segment the actual filament densities the traces can be spread out to the full width of the filaments using floodfill, as described above. Alternatively, a mask can be created for isolating the densities. The center points can be spread out to a radius larger than the filament radius and thresholded to create a binary mask that can then be multiplied by the original map. This sequence of steps can be accomplished by the Situs tools pdb2vol (for applying a point-spread function), voledit (for binary thresholding), and volmult (for map multiplication). Equivalent steps can also be taken via Sculptor’s Lua scripting language (see the online PDF manual for details).

7. Comparison with Expert Annotations

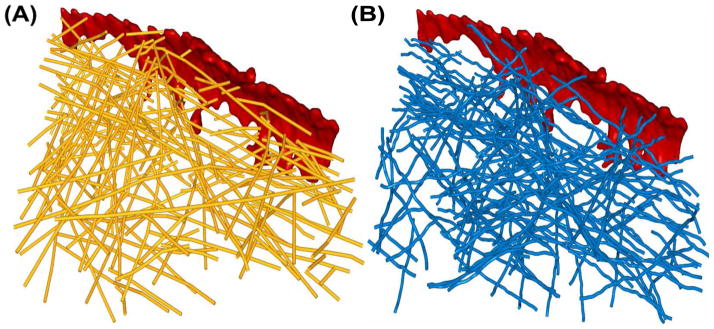
A validation of the automated filament segmentation can be attempted using manual assignments. In a recent paper (Rigort et al., 2012) a sub-volume, from a tomogram showing a membrane protrusion region, was annotated by three different expert users. Figure 3A shows the union of the manual segmentation sets performed by the experts and Figure 3B shows the result of an automated segmentation. The union of the manual sets was chosen because the three expert sets formed smaller subsets of our prediction with few false positives, indicating that the experts were fairly conservative in their annotation. This union of the three sets was also used by Rigort et al. (2012) in their validation.

Figure 3.

Validation of filament detection in a smaller sub-volume of the filopodium (Rigort et al., 2012). (A) Expert-annotated actin filament center points (Rigort et al., 2012) shown in yellow. (B) VolTrac filament tracing results shown as blue translation centers of the bidirectional expansion. Membrane regions are shown in red, and the actin networks are shown as point traces. The voxel size is 1.912 nm and the total map size is 200 × 200 × 71 voxels. The local normalization filter has a spatial extent σ_W = 10 voxel units. The Gaussian-weighted average (applied before local normalization) uses a sigma-1D of 1 voxel unit. The parameters for multi-point floodfill were: sigma-1D: 2 voxels; threshold: 0.475; number of points: 20. The data used in this Figure are available online in Suppl. Data 2-6.

We performed automated tracings using parameters given in the caption of Fig. 3 for both Gaussian- and DPSV-filtered maps (see section 2). All volumetric maps and both automatic and manual filament traces of this section are available in the online supplementary material (Suppl. Data 2-6).

For the Gaussian-filtered maps, 70% of the VolTrac predictions correspond to expert annotated filaments, and 59% of the expert annotated filaments where detected by VolTrac. For DPSV-filtered maps, 67% of automatic predictions correspond to manual predictions, and 57% of manual predictions were detected by VolTrac. This comparison of manual and automated segmentations will yield only an estimate of the reliability, since the true coverage of the specimen by actin filaments and the effect of human bias are unknown. However, we note that the Gaussian-filtered performance numbers agree well with the values stated by Rigort et al. (2012) using their tracing algorithm (79% of their automatic predictions corresponded to manual predictions, and 60% of manual predictions were detected by the algorithm). Hence we can state that our method performs similarly to Rigort et al. (2012), with slightly more false positives returned by our calculations owing to minor differences in coverage between the algorithms.

8. Conclusions

We have described a work flow for automatically segmenting filaments in cryo-ET maps including denoising, local normalization, feature detection, and tracing, and we adapted an exhaustive template-based search, VolTrac, to the problem of segmentation of filamentous densities. The results show that the application of these techniques, many of which were developed earlier for single particle cryo-electron microscopy, holds much promise for 3D reconstructions obtained by cryo-ET. The software tools described in this paper allowed the automated tracking of actin filaments in tomograms of cellular actin networks. Although the biological implications were not a subject of the current study, further analysis of the results could provide insights into the mechanism of actin-driven membrane protrusion by studying, for example, the actin filament length distributions, the angles between filaments, and the molecular architecture near the membranes.

Although the bidirectional expansion cannot originate in a tabu region during the GA search, it is allowed to grow into one. This is particularly interesting in the case of actin networks, where filaments are branched (Pollard and Beltzner, 2002). In this case, the algorithm will technically detect two filaments, covering both branches of the “Y” and extending through the base, so the base will be tracked twice in such cases. We did not explore this further but the feature could be used for automatic detection of branch points.

A constraint in any adaptation is the general purpose of the original tools that needs to be maintained. VolTrac was originally devised for alpha-helix detection, but cryo-ET has specialized limitations, such as the missing Fourier space information, which will be subject of future research. In the current implementation we corrected for these effects in real space by implementing resolution anisotropy using an elongation factor-dependent interpolation, and by an orientation-dependent attenuation of filament intensities relative to the optical axis. We did not (yet) explicitly correct for any azimuthal orientation-dependent degradation of density relative to a single tilt axis because it seemed unnecessary based on comparisons with predictions by human experts (Fig. 3). In the future we plan to correct for any residual orientation-dependent variation in the filament densities. In the conceptual framework presented here (which is based on real-space densities) this would involve fitting an envelope function to locally normalized filament densities based on spherical coordinates. Such an orientation-dependent normalization will be implemented in future software releases.

Although our denoising filters acted in the spatial domain and were designed to be isotropic, we note that the DPSV filter can implicitly take directionality into account via the discriminant analysis of the paths: DPSV can distinguish between paths with noise and those without it and ideally recover density values, using only the paths that include the true signal (Suppl. Data 1). It would be worthwhile in the future to explore the use of directional path lengths or non-cubic masks in DPSV.

A useful future extension of our approach would be the tracing of other cytoskeletal filaments such as microtubules. We expect this to be straightforward in situations where microtubules form thin rod-like densities and the hollow interior is not resolved. We have also tested the tracing on cryo-ET maps of microtubules obtained at higher magnification (Cheri Hampton and Joachim Frank, unpublished data) using hollow templates. This proved more challenging, as the templates did not always find the inside of tubes but on occasion aligned with neighboring microtubules (or outside noise), resulting in unstable traces that would require manual intervention. After completion of this work a paper appeared which describes such expert feedback during an interactive tracing of microtubules (Weber et al., 2012). Our approach currently lacks a correction for microtubule-specific ‘missing wedge’ artifacts as proposed by Weber et al. (2012), which we plan to add in a future software release. But their experience agrees with our preliminary results in the sense that microtubule tracing requires expert interventions (augmented by computational approaches to reduce the manual labor involved). This can be performed most efficiently using a graphical interface afforded by a 3D visualization program.

During the stochastic optimization, VolTrac often determines high-density filaments first. Such characteristics prompted us to integrate VolTrac into the interactive graphics software Sculptor (Birmanns et al., 2011). The user can investigate the filaments on the fly as they are generated and stop the execution early to adjust parameters. The tools described in sections 2–6 were included in Sculptor version 2.1, available freely at http://sculptor.biomachina.org. Because Sculptor is primarily intended to function as an interactive graphics program (and cryo-ET maps are quite large, resulting in long calculations), it can become impractical to wait several hours for results. The computation times on a Linux workstation (Intel i7, 3.4GHz, 8 cores) for the filopodium dataset (Fig. 2; 512 × 512 × 106 voxels at two times binning) were 1 min, 10 min, 3 h, and 24 h, and the compute times for the validation dataset (Fig. 3; 200 × 200 × 71 voxels; no binning) were 10 s, 1 min, 6 min, and 73 min, for Gaussian-weighted averaging, DPSV, local normalization, and VolTrac, respectively. Therefore, we have also added full-featured command line implementations of these tools to the Situs package, version 2.7, available freely at http://situs.biomachina.org. While most tools described in this work are available in both programs, multi-point floodfill is currently supported only by Sculptor, and polygon clipping is currently supported only by the voledit program of Situs.

Supplementary Material

01

Supplementary Data 1: A PDF document with a theoretical discussion of the DPSV denoising filter.

02

Supplementary Data 2: The raw sub-volume used for validating the predictions in Figure 3 in MRC/CCP4 format.

03

Supplementary Data 3: The processed sub-volume used for VolTrac (after multi-point floodfill, polygon clipping, denoising, and local normalization) in MRC/CCP4 format.

04

Supplementary Data 4: Processing steps described in detail for Supplementary Data 3.

05

Supplementary Data 5: A PDB file with the the union of three expert-annotated actin filament center points (Rigort et al., 2012) shown in Figure 3A.

06

Supplementary Data 6: A PDB file with the VolTrac predicted actin filament center points shown in Figure 3B.