Identifying genetic marker sets associated with phenotypes via an efficient adaptive score test

Abstract

In recent years, genome-wide association studies (GWAS) and gene-expression profiling have generated a large number of valuable datasets for assessing how genetic variations are related to disease outcomes. With such datasets, it is often of interest to assess the overall effect of a set of genetic markers, assembled based on biological knowledge. Genetic marker-set analyses have been advocated as more reliable and powerful approaches compared with the traditional marginal approaches (Curtis and others, 2005. Pathways to the analysis of microarray data. TRENDS in Biotechnology 23, 429–435; Efroni and others, 2007. Identification of key processes underlying cancer phenotypes using biologic pathway analysis. PLoS One 2, 425). Procedures for testing the overall effect of a marker-set have been actively studied in recent years. For example, score tests derived under an Empirical Bayes (EB) framework (Liu and others, 2007. Semiparametric regression of multidimensional genetic pathway data: least-squares kernel machines and linear mixed models. Biometrics 63, 1079–1088; Liu and others, 2008. Estimation and testing for the effect of a genetic pathway on a disease outcome using logistic kernel machine regression via logistic mixed models. BMC bioinformatics 9, 292–2; Wu and others, 2010. Powerful SNP-set analysis for case-control genome-wide association studies. American Journal of Human Genetics 86, 929) have been proposed as powerful alternatives to the standard Rao score test (Rao, 1948. Large sample tests of statistical hypotheses concerning several parameters with applications to problems of estimation. Mathematical Proceedings of the Cambridge Philosophical Society, 44, 50–57). The advantages of these EB-based tests are most apparent when the markers are correlated, due to the reduction in the degrees of freedom. In this paper, we propose an adaptive score test which up- or down-weights the contributions from each member of the marker-set based on the Z-scores of their effects. Such an adaptive procedure gains power over the existing procedures when the signal is sparse and the correlation among the markers is weak. By combining evidence from both the EB-based score test and the adaptive test, we further construct an omnibus test that attains good power in most settings. The null distributions of the proposed test statistics can be approximated well either via simple perturbation procedures or via distributional approximations. Through extensive simulation studies, we demonstrate that the proposed procedures perform well in finite samples. We apply the tests to a breast cancer genetic study to assess the overall effect of the FGFR2 gene on breast cancer risk.

1. Introduction

With rapid advances in high throughput technology, modern genetic studies have provided datasets that can be used to identify genetic variants associated with various diseases such as cancer, auto-immune diseases, cardiovascular diseases, and psychiatric disorders (e.g. Baum and others 2007; Frayling 2007; Hunter and others 2007; Rioux and others 2007; Yeager and others 2007; Sullivan and others 2008; Wallace and others 2008). These studies, while providing valuable resources for investigating the genetic risk of diseases, impose a grand challenge in identifying important genetic variants, due to the large number of genetic markers under investigation.

The standard approach to screening for important genetic markers is based on single-marker marginal analyses, which may suffer from low power and poor reproducibility (Vo and others, 2007). The lack of power is in part attributed to the fact that multiple genetic markers may relate to the phenotype simultaneously, and most have weak or no effects. To overcome such difficulties, biological knowledge-based methods have been advocated to integrate prior information into statistical learning (Brown and others, 2000). One useful strategy is through marker-set analysis, where a set of genetic markers are assembled based on prior knowledge such as multiple variants in a gene or a pathway. The results from marker-set analysis are often more reliable, reproducible, and powerful than the results from individual marker analysis (Curtis and others, 2005; Efroni and others, 2007; Wu and others, 2010), and have attractive interpretations.

To identify marker-sets associated with disease outcomes, one may test for the overall effect of a marker-set, of dimension p, on the phenotype of interest. A convenient way to do this is via a standard p-degrees of freedom (DF) Rao score test (Rao, 1948) for the significance of the global effect. However, when p is not small, such a test may have little power, especially when the markers are correlated. One may also consider combining p-values of univariate tests to obtain an overall assessment (Zaykin and others, 2002; Lin, 2005; Nyholt, 2004; Moskvina and Schmidt, 2008). Such an approach often works well when the signal is extremely sparse, but may not be powerful when multiple markers jointly affect the outcome. To improve the power of the standard score test, modified score tests have been derived under an empirical bayes (EB) framework (Carlin and Louis, 1997) for various types of models (Thomas and others, 1992; Commenges, 1994; Goeman and others, 2005; Liu and others, 2007, 2008; Wu and others, 2010). Such modifications achieve the power gain by taking advantage of the between-marker correlation and thus reducing the effective DF of the test. However, when the true signals are sparse and/or when the markers within a set have weak correlations, these tests also suffer from a lack of power. For example, in the case–control National Cancer Institute Cancer Genetic Markers of Susceptibility (CGEMs) study (Hunter and others, 2007) to be discussed in Section 4, one is interested in studying the association between the FGFR2 gene and breast cancer risk. There are 41 typed single-nucleotide polymorphisms (SNP) in FGFR2, including those within a 30-kb region of the gene. As the number of SNPs is not small and many of these SNPs have weak linkage disequilibrium (LD), i.e. week correlation, the standard score test and the EB-based test will suffer loss of power.

To overcome these difficulties, we propose an adaptive score test procedure that incorporates the strength of the signals from the individual markers within a set. The adaptive procedure, defined in Section 2, rescales the marker values by the Z-score of an initial estimator of their association with the outcome and thus down-weights the non-informative markers. We study its theoretical distribution and provide simple procedures for approximating the null distribution of the test statistic. Our numerical studies suggest that the adaptive test performs well with respect to both empirical size and power when the true signals are relatively sparse and the markers are weakly correlated. However, when the true signals are not sparse and the correlation among the markers is high, the adaptive procedure suffers from the variability in the initial estimator and thus may perform worse compared with the EB score test. In Section 3, we derive an automatic omnibus procedure that combines information from both types of score tests. In Section 4, we examine the overall effect of the FGFR2 gene on the risk of breast cancer using the data from the CGEMS study. Findings from our numerical studies in Section 5 indicate that the omnibus test pays little price for selecting between the EB and adaptive tests. Some concluding remarks are given in Section 6.

2. Methods

2.1. Data structure and standard score tests

Suppose data consist of n independent and identically distributed random vectors, {(Y _i,V_i,U_i),i=1,…,n}, where Y _i is the response, V_i=(V _i1,…,V _ip)^T is the set of new markers under investigation, and U_i=(U_i1,…,U_ipu) represents other covariates such as confounders with U_i1=1, for the ith subject. To test the overall effect of the marker set V on the response Y conditional on U, e.g. the overall effect of the 41 SNPs in the FGFR2 gene on breast cancer risk, we consider the quasilikelihood model (McCullagh and Nelder, 1989) with

(2.1)

where 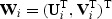, μ(⋅), and 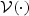are pre-specified mean and variance functions, and 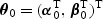is the vector of unknown effects for U and V. Common examples of model (2.1) includes linear, logistic, Gamma, and Poisson regression.

Our primary interest lies in testing whether the set of genetic markers V is associated with Y after adjusting for confounders U. That is, we aim to test the null hypothesis,

(2.2)

In standard statistical theory, score-type testing first fits the model under H₀, producing an estimate 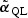that is the solution to the quasilikelihood score equation under H₀, defined as follows. Let 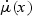be the derivative of μ(x), 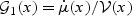and 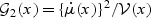. Then 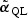solves

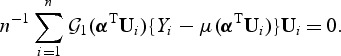(2.3)

An estimate of σ² under H₀ is

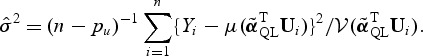(2.4)

The standardized score statistic is then defined as

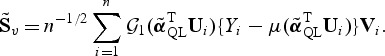(2.5)

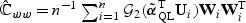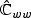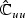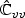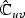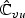There are two ways to form a test statistic based on (2.5). Let , partition with top left block p_u×p_u matrix , bottom right block p×p matrix , and non-diagonal blocks and , and 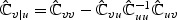. The standard score test statistic is

(2.6)

and under H₀, it is asymptotically central 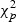. The local power of this score test is also well known (Harris and Peers, 1980; Rao, 2005). See Martinez and others (2010) for a recent explication.

The simplicity of the standard score test is convenient, but comes at potentially considerable cost because of the p-DF. In genomic applications, p is typically not small and some markers in a set have no effects. For example, there are p=41 SNPs in the FGFR2 gene. Such a large DF carries with it a potential loss of power, as we see in our simulations (Section 5).

Another way to use the score statistic (2.5) is to employ an EB framework by imposing a working assumption that the {β_0j,j=1,…,p} are independent and follow an arbitrary distribution with mean 0 and variance τ. We hence test the null hypothesis (2.2) by testing whether τ=0. The working distributional assumption, while useful for deriving a globally valid testing procedure, is not required to hold. This leads to the score test

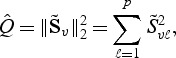(2.7)

where for any vector a, a_ℓ denotes the ℓth element of a, and ∥a∥_q denotes the L_q vector norm. These types of score test statistics have been shown previously to be powerful alternatives to the standard score test under various settings (Goeman and others, 2005; Liu and others, 2007; Kwee and others, 2008; Wu and others, 2010). The distribution of (2.7) is given in Section 2.3.

2.2. An efficient adaptive score test

As shown in the simulation Section 5, the EB-based score test (2.7) is quite powerful when the signal is not sparse. However, for settings when the signal is sparse and the markers are weakly correlated with each other, this test has limited power due to the high DF paid for the non-informative markers. To overcome such a difficulty, we propose an adaptive score statistic that incorporates information on the signal strength of each marker. Specifically, we first obtain an initial root-n consistent estimator of β₀, denoted by 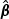. Without loss of generality, we assume that the vector of element-wise variances of 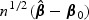, κ², can be consistently estimated by 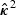. Our proposed rescaling factor is 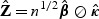, where ⊘ represents element-wise division. Here, 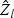is the Z-statistic for testing β_0ℓ=0, which reflects the strength of the signal β_0ℓ relative to the noise. 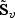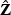The adaptive score test is then constructed by rescaling in element-wise by such that non-informative markers will be down-weighted towards zero, thus effectively eliminating these markers from the score statistic. We define our adaptive score test statistic as

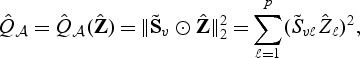(2.8)

where ⊙ denotes element-wise product. If the ℓth component 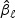of 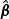is not significantly different from zero, this clearly shows that the ℓth marker plays little role in the test statistic.

For the initial estimator, one may obtain 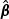as the standard quasilikelihood estimator. Specifically, let 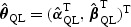be the solution to 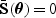, where

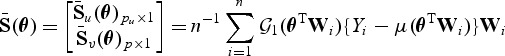(2.9)

is the quasilikelihood score equation under the alternative. A simple choice for the variance estimator of 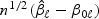is

(2.10)

where 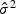could be estimated under H₀ as in (2.4), 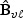is the ℓth row vector of 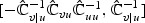and 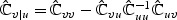. Then one may let 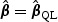and 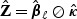in the adaptive score test (2.8), where .

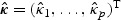When p is not small and the signals are moderate or weak, 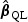may have large variation and thus may lead to power loss for the test rescaled with . To overcome such difficulties, we propose to improve the power by considering a ridge penalized quasilikelihood (PQL) estimator 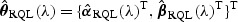, where 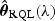is the solution to 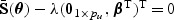, and λ is a tuning parameter with λ→λ₀≥0. The estimator 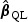corresponds to the maximum PQL estimator under the random effects model 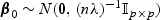(Green, 1987; Breslow and Clayton, 1993). In practice, one may choose an optimal 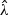based on procedures such as generalized cross-validation. The adaptive score test (2.8) may also be constructed based on 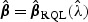along with the variance estimators 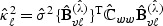, where 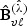is the ℓth row vector of .

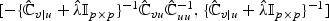2.3. Distribution of the test statistic under the null and under the local alternative

In the Appendix of the supplementary material available at Biostatistics online, we derive the distributions of the test statistics (2.7)–(2.8) under H₀ and more generally under the local alternative H_1n:β₀=n^−1/2b₀. Define

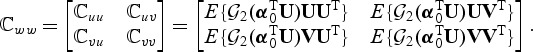(2.11)

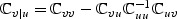, z₀=b₀⊘κ, and 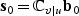. Furthermore, let ε_w denote a  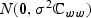random vector, 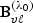and A_vℓ, respectively, denote the ℓ^th row of 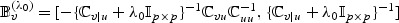and 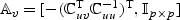. Then 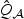converges to

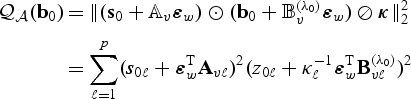(2.12)

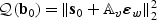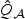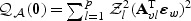in distribution. The same arguments as given in the Appendix of the supplementary material available at Biostatistics online can be used to show that under H_1n, the EB-score test statistic (2.7) converges in distribution to . Under H₀, b₀=0 and thus in (2.8) and in (2.7) converge in distribution to and 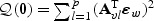, respectively, where .

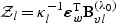2.4. Implementation

In general, it is straightforward to approximate the null distribution of in (2.8) via perturbation by repeatedly generating realizations of 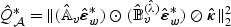, where 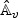and 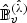are defined by replacing 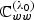with its empirical counterpart, and where 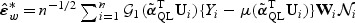and 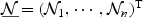is a vector of independent N(0,1) random variables. This is because asymptotically, the distribution of 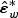given the observed data and the unconditional distribution of ε_w are asymptotically the same. Mimicking the Satterthwaite approximation, we find that in our numerical studies, the null distribution of 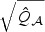can be well approximated by a rescaled χ² distribution, i.e. 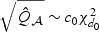. The scale parameter c₀ and the degrees of freedom d₀ can be estimated by matching the first two moments of 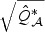. Similarly, the null distribution of the standard score test in (2.7) can be approximated by .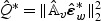

2.5. Theoretical differences between the tests

Some insight as to the difference between our adaptive test and the ordinary score test can be gained by considering the case that there are no additional confounders, so that U=1 and λ₀=0. In this case, 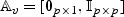, , 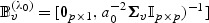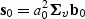and 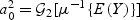, where Σ_v=var(V). Since E(V)=0, 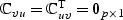. Thus 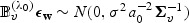and 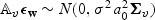. Now, let 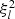denote the lth diagonal element of 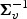, , 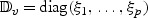write 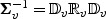and let 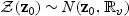. It follows that 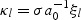and 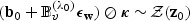. Therefore, we may simplify the distribution of 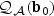as

Furthermore, if V is uncorrelated, then 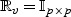, 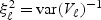and 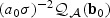are equivalent to 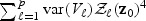. On the other hand, the distribution of (2.7) scaled by (a₀σ)⁻² can be written as 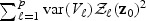. Thus, for the orthogonal case, asymptotically, the EB score statistic is a weighted sum of p independent 1-DF χ² random variables with non-centrality parameters 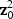; whereas the adaptive score statistic is a weighted sum of p-independent squared 1-DF χ² random variables with non-centrality parameters .

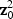3. An efficient adaptive omnibus test

3.1. Theoretical local power calculations

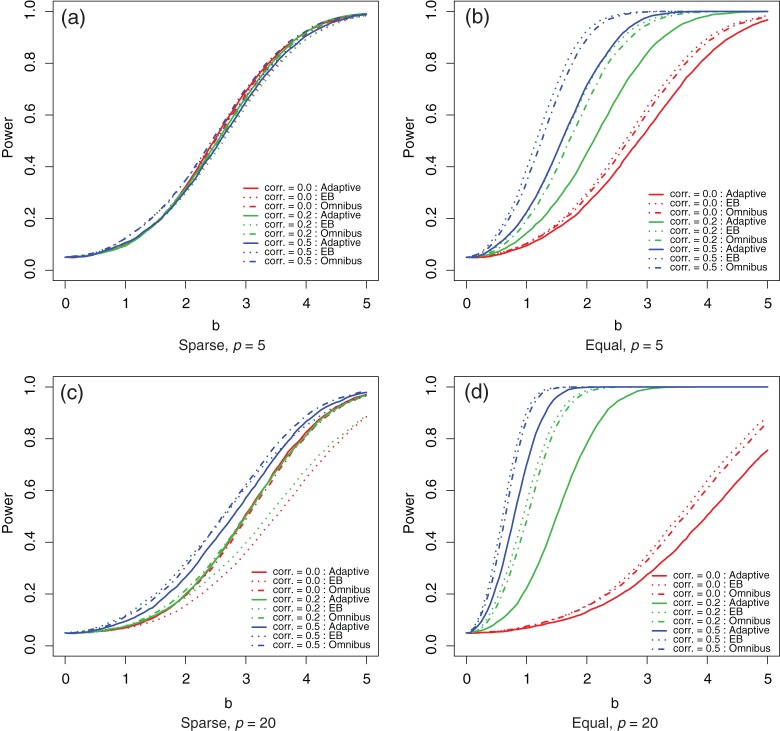
To compare the performance of the EB score test and the adaptive test, we consider the simple setting of linear regression with σ²=1, U=1 for an intercept and V is multivariate normal with mean zero, unit variance, and a common correlation ρ. In Figure 1, we present the power curves under the local alternative for ρ=0.0,0.2 and 0.5 for two extreme settings: (i) when signals are sparse with b₀=(b,0,…,0)^T and (ii) when all covariates contribute equally with 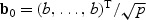. It appears that the adaptive procedure outperforms the EB score test under the sparse setting, but the phenomenon is reversed for the setting where the signals are equally contributed from all p covariates. The relative performance of the adaptive and EB score test procedures also varies with the correlation ρ. The lower the correlation is, the more advantage the adaptive procedure has.

Figure 1.

Theoretical power curve for the adaptive (solid curves), EB-score (dotted curves), and omnibus combining and 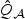(dot dashed curves) tests under local alternatives with various levels of correlations (corr.): 0.0 (thin gray curves); 0.2 (black curves); and 0.5 (thick gray curves).

3.2. Omnibus test and implementation

In general, the relative performance of the EB-based score test and the adaptive procedure depends on the sparsity of b₀ and the between-marker correlation. In practice, without prior information on these factors, it is unclear which procedure should be chosen for a given dataset. To overcome this difficulty, we propose to automatically combine evidence between the EB score test and the adaptive test by taking the minimum p-value and comparing to its null counterpart. 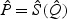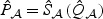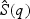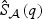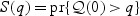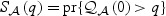Specifically, let and be the respective p-values based on the EB score test and the adaptive score test, where and are estimators of and , respectively. Then the omnibus test is based on the minimum p-value, 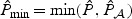which converges in distribution to 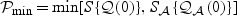under H₀. Our simulation studies in Section 5 indicate that the omnibus test pays a relatively low price with respect to power for utilizing two tests. Our theoretical power analysis under the aforementioned two settings also supports this finding as shown in Figure 1.

In practice, the null distribution of 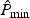can be approximated easily via perturbation methods. Let 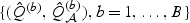denote B perturbed realization of 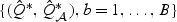, where for each b, 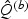and are perturbed with the same set of independent normal vector . Then the null distribution of 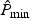can be approximated by the empirical distribution of 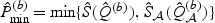across b=1,…,B, where 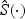and 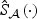are obtained by fitting rescaled χ² distributions to 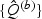and 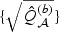. When 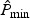is very small, it may be challenging to obtain its p-value using resampling, because a large B would be required to ensure adequate approximation. For such settings, we propose to approximate the null distribution of 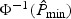using a normal mixture. Specifically, we fit a ν₀-population normal mixture, 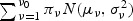, to 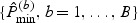and obtain maximum likelihood estimates for {(π_ν,μ_ν,σ_ν),ν=1,…,ν₀}, denoted by 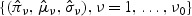. Then the p-value can be estimated by 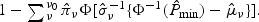Through our empirical studies, we find that this approximation works well and hence could be useful when aiming to control for low type I error rates. Similar strategies could be used to approximate the distribution of 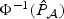to improve the χ² approximation, especially for the tail probabilities. Here, the number of components ν₀ can be either pre-specified or chosen adaptively using criteria such as BIC. In practice, we find that ν₀=3 works well for approximating the distribution of .

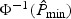4. Example: the FGFR2 gene for the risk of breast cancer

We applied our proposed procedures to assess the association between the FGFR2 gene and the risk of sporadic postmenopausal breast cancer using the genome-wide association studies (GWAS) data of the Nurses’ Health Study, which was part of the aforementioned CGEMS study (Hunter and others, 2007). Using the Illumina HumanHap500 array, this study initially genotyped 1183 women with postmenopausal invasive breast cancer and 1185 individually matched controls. Data for analysis consist of 1091 cases and 1110 controls with complete information. Among the loci reported as potentially associated with breast cancer in Hunter and others (2007) include several SNPs in FGFR2 or its intron 2. Here, we examine the overall effect of the FGFR2 gene, consisting of 41 typed SNPs, including those within the 30-kb region of the gene, on the risk of breast cancer. The analysis adjusted for age group, hormone usage, age at menarche, and the first 4 eigenvectors generated from EIGENSTRAT principal components analysis (Price and others, 2006) to account for population stratification.

We first fit the data with marginal logistic regression models with one SNP at a time adjusting for these covariates. The log odds ratio estimates along with their 95% confidence intervals obtained from the 41 marginal models are shown in Supplementary material, Figure S1 (see supplementary material available at Biostatistics online). Out of these 41 SNPs, 14 SNPs have marginal p-value < 0.05 and 3 SNPs, rs2420946, rs1219648, rs2981579, with p-value <10⁻⁵. The SNP rs1219648 has been previously shown to be highly associated with increased risk of breast cancer while both rs2420946 and rs2981579 are in high LD with rs1219648 (Hunter and others, 2007). An experimental rationale was presented in indicating that this SNP is part of a haplotype that increases risk for ER+ breast cancer by increasing FGFR2 transcription.

To assess the overall effect of the gene, we employed the aforementioned procedures including the univariate test using the minimum of these p-values. Since this gene is highly associated with breast cancer risk, we used 100 000 perturbation samples along with the normal mixture approach to approximate the p-values. The univariate test gives an overall p-value of 4.0×10⁻⁵. On the other hand, our adaptive test gives a p-value of 4.3×10⁻⁸, the EB score test a similar p-value of 7.2×10⁻⁷ while the the standard p-DF score test has no power in detecting the signal with a p-value of 0.12. The omnibus test combining and 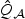yielded a p-value of 1.8×10⁻⁷ based on the normal mixture approximation. However, a larger number of perturbation samples would be required to obtain more accurate estimate of the p-value for these tests.

5. Simulation studies

5.1. Setup and null case

We conducted simulation studies to assess the performance of the proposed score test. For simplicity, we considered the setting that U=1. To mimic the GWAS setting, we generated V based on the LD structure of two genes: (i) the ASAH1 gene with high LD and (ii) the FGFR2 gene with moderate to low LD. Based on the Illumina 500 K platform, we included p=14 SNPs of the ASAH1 gene and p=31 SNPs of the FGFR2 gene, whose LD heat maps are shown in Supplementary material, Figure S2 (see supplementary material available at Biostatistics online). The response variable Y is generated from the linear regression model 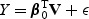with ϵ∼N(0,4) generated independent of V. For each configuration, we generated 4000 datasets to calculate the empirical size when the null hypothesis is true and 1000 datasets to calculate the empirical power when it is not. For each dataset, the resampling procedure was carried out with B=5000 and B=1000, for the null and alternative settings, respectively. We considered n=200, 500, and 1000.

As a benchmark, we also report results on the univariate test, whose significance is determined by comparing the observed minimum p-value of p univariate tests to its corresponding null distribution. For each simulated dataset, we carried out the following test procedures: (i) the p-DF score test ; (ii) the EB based score test in (2.7); (iii) adaptive score test in (2.8) rescaled with ridge initial estimator 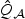; and (iv) univariate test (Uni). In addition, we consider various omnibus tests based on the minimum p-value among the two or three p-values from (ii), (iii), and (iv). Note that we considered only ridge estimators as our initial estimator, since the standard quasilikelihood estimator is unstable due to the high collinearity between the SNPs. To examine how well the χ² distribution approximates the null distribution of 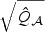and , we also provided the empirical size and power based on the approximation. We also examined the performance of the normal mixture approximation to the distribution of the omnibus test statistics as well as the distribution of 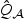. Unless noted otherwise, p-values for all other test statistics are based on the perturbation procedure, which can conveniently account for various types of correlations.

First, to examine the validity of our proposed testing procedure in finite samples, we generated data under H₀ model with β₀=0 to assess the size of the score test. As shown in Table 1, the empirical sizes of the aforementioned tests at type I error rate of 1% and 5% are summarized in Table 1. Across all the configurations, the empirical sizes are close to the nominal levels for all procedures except for the standard p-DF test, which is often overly conservative due to the correlation among the V. Furthermore, it appears that the χ²-based approximation works reasonably well in practice for approximating the distribution of 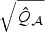at type I error rate 5%. However, it appears that at a lower error rate of 1%, the χ² approximation is slightly anti-conservative, while the normal mixture approximation appears to provide a better approximation and works well for approximating the distribution of other minimum p-value test statistics.

Table 1.

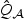Empirical sizes (in %) at target sizes of 1% and 5% for the score tests when V is simulated based on the 17 tagSNPs of the ASAH1 gene and 31 tagSNPs of the FGFR2 gene on the illumina chip. Here is the p-DF score test in (2.6), is the test (2.7), is the test at (2.8) with initial ridge estimate, “Uni” is the test that is based on the minimum p-value across p univariate tests, and min_A1,…,Ak represents the omnibus test that takes the minimum p-value of the tests based on A₁,…,A_k. The p-values are obtained via perturbation (ptb), chi-square approximation (χ²), and normal mixture approximation (Mix).

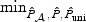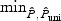n	Size	ptb	χ2	ptb	χ2	Uni	ptb	χ2	Mix	ptb	Mix	ptb	Mix	ptb	Mix
ASAH1 gene
200	1	0.3	0.2	1.1	1.3	0.8	1.1	1.6	1.3	1.1	1.2	0.9	0.8	0.9	0.8
500	1	0.4	0.3	1.0	1.4	0.8	1.1	1.5	1.3	1.0	1.1	0.7	0.7	0.8	0.8
1000	1	0.7	0.2	0.9	1.1	0.7	1.0	1.3	1.1	1.0	1.1	0.8	0.8	0.8	0.8
200	5	3.1	1.2	5.5	5.4	4.4	5.7	5.6	5.4	5.8	5.6	4.5	4.5	4.4	4.3
500	5	4.3	1.7	5.2	5.1	4.7	5.2	5.2	5.0	5.5	5.2	4.7	4.5	4.6	4.4
1000	5	3.7	1.5	4.6	4.5	4.5	5.2	5.1	4.9	5.0	4.7	4.6	4.5	4.5	4.3
FGFR2 gene
200	1	0.1	0.1	0.7	0.9	0.7	0.6	0.9	0.8	0.6	0.6	0.7	0.7	0.7	0.7
500	1	0.3	0.5	0.9	1.1	1.0	0.9	1.2	1.0	0.9	1.0	1.1	1.0	1.1	1.1
1000	1	0.6	0.6	0.8	1.0	1.0	0.9	1.3	1.0	0.7	0.7	0.9	0.9	0.9	1.0
200	5	1.7	1.8	5.1	5.2	5.2	4.3	4.4	4.2	4.4	4.2	5.1	5.0	5.1	4.8
500	5	2.8	3.1	5.0	5.1	5.2	4.9	5.0	4.7	4.7	4.5	5.2	5.0	5.2	4.8
1000	5	3.8	3.4	4.6	4.5	5.3	5.1	5.2	4.9	5.0	4.7	5.2	5.0	5.2	4.9

5.2. Power comparisons

For empirical power analyses, we let 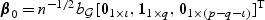, for ι=0,…,p−q, and 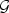indexes either ASAH1 or FGFR2. Hence ι+1 represents the starting position the causal variants, q determines the sparsity of the signal, and 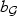reflects the strength of the signal. We consider 4 choices of q and 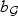: (i) dense signal q=⌈0.8p⌉, b_ASAH1=3.5, b_FGFR2=2.8; (ii) moderately sparse signal q=⌈0.5p⌉, b_ASAH1=4.1, b_FGFR2=3.5; (iii) sparse signal q=⌈0.1p⌉, b_ASAH1=7.1, b_FGFR2=5.4; and (iv) single causal variant q=1, b_ASAH1=b_FGFR2=10.6. The pattern of the results is similar across the three sample sizes and hence we present only results for n=500.

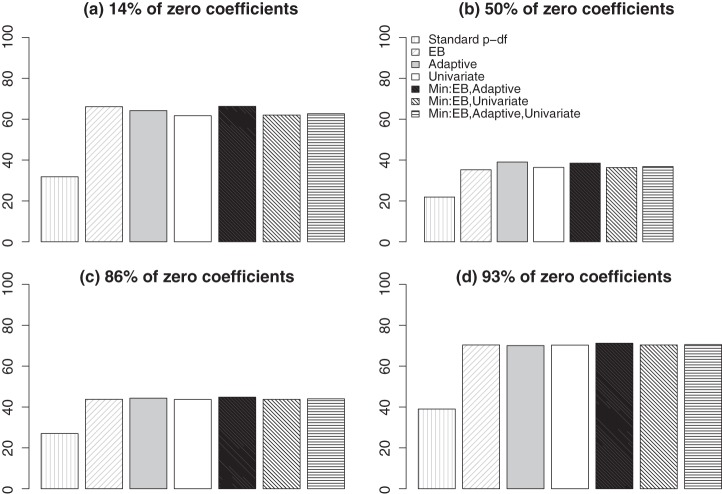
Since the SNPs in the ASAH1 gene are generally in high LD with each other, we summarize the power of the tests averaged over the entire range of ι in Figure 2. As we expect from the theoretical analysis, the EB test is the most powerful under the dense signal setting with 14% sparsity. For the sparse settings, the adaptive test is at least as powerful as other procedures. Across all settings, the standard p-DF test is the least powerful. The most robust test is the omnibus test based on 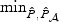, the minimum p-value from and 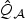, which always has power similar to the best among (a)–(d).

Figure 2.

Empirical power (in %) for various tests using the ASAH1 gene under local alternatives averaged over all the choices of ι’s. (a) q=12, b_ASAH1=3.5 (14% sparsity); (b) q=7, b_ASAH1=4.1 (50% sparsity); (c) q=2, b_ASAH1=7.1 (86% sparsity); and (d) q=1, b_ASAH1=10.6 (93% sparsity).

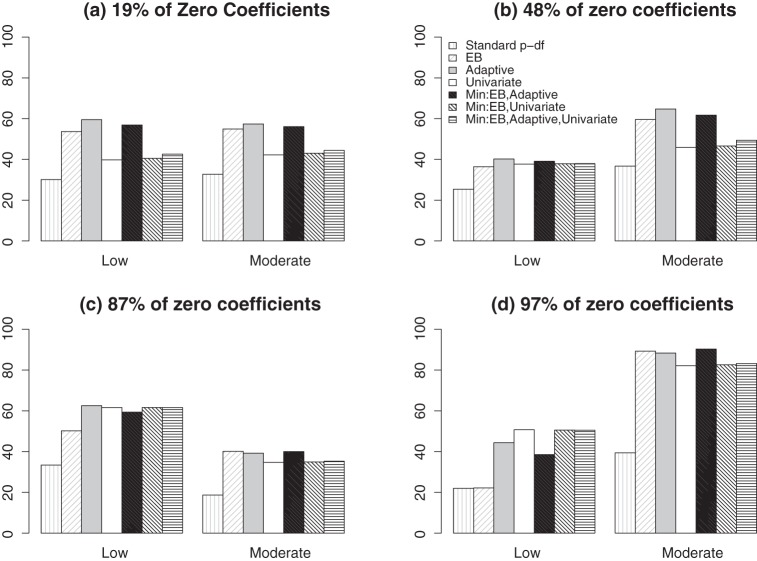
For the FGFR2 gene, the LD is generally weak among the SNPs, but the correlation structure changes over different regions. To gauge the general pattern of how the correlation might affect the test performances, we let ℘(ι) denote the average correlation between the causal and non-causal SNPs for a given ι and summarize the power by averaging over different levels of ℘(ι). In Figure 3, we present the power averaged over the set of ι with low ℘(⋅) and the set of ι with moderate ℘(⋅). When ℘(⋅) is low and the signal is moderately sparse, the adaptive test is more powerful than its competitors. For example, when the sparsity is 19%, the average power is 54% for the EB test and 60% for the adaptive test while the univariate test has a power of 40%. The univariate test is generally less powerful except when there is only a single causal variant and ℘(⋅) is low. When ℘(⋅) is moderate, the EB test and the adaptive test have more similar performances and the univariate test generally is less powerful. Similar to the results for the ASAH1 gene, the test based on 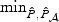almost always achieves power close to the best among (a)–(d), except for when ℘(⋅) is low with extreme sparsity. Other omnibus tests based on 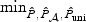and 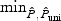can be less powerful whenever the univariate test does not work well, where 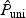denotes the p-value based on the univariate test. For example, for the FGFR2 gene with 19% sparsity and low ℘(⋅), the powers of the univariate test and the omnibus test that includes the univariate test is only ∼ 43%, while the power of 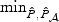is close to 57%.

Figure 3.

Empirical Power (in %) for various tests using the FGFR2 gene under local alternatives averaged over the set of ι with low ℘(⋅) (low) and the set of ι with moderate ℘(⋅) (moderate). For settings of q and b were considered: (a) q=25, b_FGFR2=3.5 (19% sparsity); (b) q=16, b_FGFR2=2.8 (48% sparsity); (c) q=4, b_FGFR2=5.4 (87% sparsity); and (d) q=1, b_FGFR2=10.6 (97% sparsity).

6. Discussions

In this paper, we proposed an adaptive score test procedure to test for the effect of a set of genetic markers, by rescaling the design matrix of the genetic markers with an initial estimator of the marker effects. When compared with the EB score test in (2.7), the adaptive test in (2.8) has higher power when the signal is sparse and the between marker correlation is low. The null distribution of 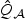can be estimated via a simple Monte-Carlo procedure. In practice, we find that the null distributions of and 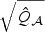can also be approximated well by skewed χ² distributions with DF, 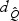and , respectively. 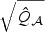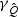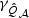Furthermore, under the local alternative, the distributions of and can be approximated by non-central χ² distributions with non-centrality parameters, and , respectively. However, providing theoretical justification for why such an approximation works well for 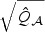is challenging and warrants further research.

The χ² approximations allow us to assess the relative performance of these two testing procedures by comparing 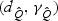to 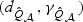under various settings. In simulation studies (results not reported) with a compound symmetry correlation structure for V with correlation ℘, we compared how ℘ and signal sparsity affect the results. The adaptive test is most effective when ℘ is low and sparsity is high, since under such settings 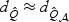but 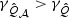. As ℘ increases, 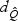decreases quickly, but 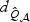remains almost constant. As the sparsity of the signal increases, 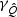decreases while 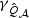increases but the magnitude of change in the non-centrality parameters appears to be slower with larger ℘, particularly for . Thus, when the correlation increases, the EB-based test gains power by maintaining low DF while the adaptive test pays the price for having higher DF, in part due to the increased difficulty in estimating β₀.

To get more intuition behind these relative performances, we consider the local alternative β₀=n^−1/2b₀ and the setting with orthogonal normal design, U=1, and σ²=1. Due to the complexity of the power functions, we focus on the setting when p is not small for the ease of approximation. One can show that 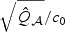is approximately χ² with

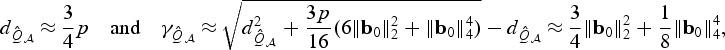while 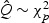and 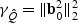, where 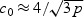. Comparing the non-sparse case with 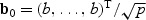to the sparse case with b₀=(b,0,…,0)^T, one finds that the EB test has the same power at these two local alternatives since 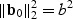in both cases. On the other hand, the adaptive test has much greater power in the sparse setting since 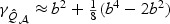for the sparse case and 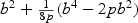in the non-sparse case. Hence when signal is sparse and b is not small, the adaptive test gains power by amplifying the strong signals, which is reflected in the increased non-centrality parameter 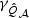. On the other hand, when signal is not sparse, b⁴−2pb² could be substantially smaller than 0 and hence leads to a power loss when compared with the EB test.

In general, the ridge-rescaled adaptive test has more power than the test rescaled by the standard quasi-likelihood estimator, especially when the correlation among the V is high. The omnibus test which combines information from both the EB-based score test and the adaptive test appears to pick out the winner with relatively little price paid for selecting the better one, at least for the settings we have examined. It will be interesting to extend the proposed procedures to accommodate the rare variants from next generation sequence studies. When the minor allele frequencies of the rare variants are too low, the proposed weight vector 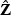based on simple initial estimators may be unstable. Alternative weights that account for rare variants and may increase power warrants further research.

As shown in the data example section, when the p-value is extremely small, it remains numerically difficult to obtain a good estimate of the tail probability for the omnibus test due to the requirement of a large number of perturbations. On the other hand, our proposed perturbation procedure would enable us to easily obtain the overall type I error-adjusted p-values when multiple marker sets are under investigation. By generating the same set of 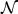for all the marker sets, one can obtain the null distribution of the minimum p-value across all marker sets and compare the observed p-value to this null distribution to estimate the adjusted p-value. For approximating the tail probabilities, we find that a normal mixture works well for approximating the distribution of the minimum p-value, both under H₀ and under the alternative.

Funding

Research was supported by grants from the National Institute of Health (R01-GM079330 to T.C.) and the National Science Foundation (DMS-0854970 to T.C.); the National Cancer Institute (R37-CA076404 and P01-CA134294 to X.L.); the National Cancer Institute (R37-CA057030 to R.J.C.) and Award Number KUS-CI-016-04, made by King Abdullah University of Science and Technology (KAUST) to R.J.C.