Abstract
In this work, we study the evolution of the susceptible individuals during the spread of an epidemic modeled by the susceptible-infected-recovered (SIR) process spreading on the top of complex networks. Using an edge-based compartmental approach and percolation tools, we find that a time-dependent quantity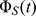 
, namely, the probability that a given neighbor of a node is susceptible at time 
, is the control parameter of a node void percolation process involving those nodes on the network not-reached by the disease. We show that there exists a critical time 
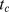above which the giant susceptible component is destroyed. As a consequence, in order to preserve a macroscopic connected fraction of the network composed by healthy individuals which guarantee its functionality, any mitigation strategy should be implemented before this critical time 
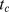. Our theoretical results are confirmed by extensive simulations of the SIR process.
Introduction
The study of epidemic spreading has been one of the most successful applications on networks science. Recent outbreaks of new influenza strains like the H1N1 [1] and the H5N5 flu or the Severe Acute Respiratory Syndrome (SARS) [2], which are characterized by a high rate of mortality and/or fast propagation velocity, motivate the development of epidemic models that capture the main features of the spread of those diseases. In particular, mathematical tools applied to model epidemics are very important since they allow to understand how a disease impact on the society, helping to develop new policies to slow down its spreading.
One of the simplest models that reproduce seasonal diseases, such as influenza, is the susceptible-infected-recovered (SIR) model [3], [4], which has been the subject of extensive theoretical and numerical research on complex networks [3]. In the SIR model the individuals can be in one of three states, susceptible, infected or recovered. In its discrete formulation [5]–[7], at each time step, infected individuals infect their susceptible neighbors with probability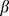 
and recover at a fixed time 
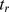since they were infected, called recovery time. According to these rules, the disease spreads on the contact network until it reaches the steady state where there are only susceptible and recovered individuals. It was found that the steady state of the SIR model can be mapped into a link percolation problem which provides a theoretical framework to study this process [6], [8]–[10]. It is known that the size of the infection, defined as the fraction of recovered individuals at the steady state, is governed by the effective probability of infection or transmissibility 
of the disease which depends on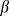 
and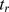 
. In the SIR model, the size of the infection is the order parameter of a second order phase transition with a critical threshold transmissibility 
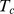. Below 
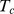the disease is an outbreak, where the infection reaches a small fraction of the population while above 
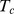an epidemic develops exactly as in a link percolation process [6], [8]–[10]. In uncorrelated infinite networks this threshold is given by 
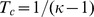[6], [11], where 
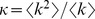is the branching factor of the network, and 
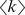and 
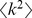are the first and the second moment, respectively, of the degree distribution 
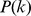. Here, 
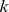is the degree or number of links that a node can have with 
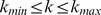. For Erdös-Rényi networks (ER), the degree distribution is 
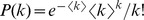and the threshold is found at 
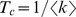. However, most of the real networks have a heterogeneous degree distribution that is better represented by a pure Scale-Free network (SF) with 
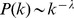, where 
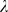measures the broadness of the distribution. In the thermodynamic limit, for SF networks with 
, 
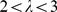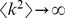and as a consequence, the critical transmissibility 
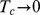which means that the epidemic spreads for any value of 
[6], [11]. However, due to finite size effects, real networks have finite critical transmisibilities.
In a recent paper, using a generating function formalism, Newman [12] showed that at the steady state of the SIR model there exists a second threshold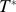 
above which the residual network composed by the biggest giant susceptible cluster that remains after a first propagation, is destroyed. From an epidemiological point of view, this implies that if a disease spreads for a second time on the residual network, it cannot become an epidemic. On the other hand, Valdez 
[13] showed that 
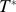is an important parameter to determine the efficiency of a mitigation or control strategy, because any strategy that decrease the transmissibility below 
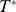, can protect a large and connected cluster of susceptible individuals. Using a percolation framework, they explained the lost of the susceptible giant cluster as a not-random node percolation process, that they called node void percolation, in which a susceptible individual corresponds to a void node in link percolation.
Even though percolation theory was very useful to describe the steady state of the SIR model on complex networks, it is still very challenging to explain the dynamics of the model to develop intervention strategies before the epidemic spreads to a large fraction of the population. To describe the dynamics of epidemic spreading on networks, recently some researchers developed differential rate equations for the SIR model that take into account the network topology. Lindquist 
[14] introduced an “effective degree” approach through a large system of ordinary differential equations. Under this approach, the nodes and their neighbors are categorized by their disease state (susceptible, infected, recovered) and each differential equation compute the evolution of the fraction of susceptible or infected nodes with a number 
and 
of infected and susceptible neighbors, respectively, with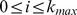 
and 
. As a result, a system with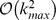 
equations needs to be solved. This approach represents accurately the evolution of the number of infected individuals, but at a high computational cost. On the other hand, Miller [15] and Miller 
[16], [17] proposed an ingenious approach to describe the evolution of a SIR process with rates by means of an edge-based compartmental model (EBCM) [15], [16] which has the advantage to describe the dynamical spreading of an epidemic with only a few equations. With these equations, the authors found accurate results for the evolution of the number of infected individuals for static and dynamic evolutive topologies like “edge swapping” and “dormant contacts” for transmissibilities above the critical threshold [16].
While most of the literature is focused on studying the evolution of the fraction of infected or susceptible individuals, it has not yet been investigated how the epidemic spread affects the evolution of the network composed by the susceptible individuals. Understanding this problem is important because the network composed by the healthy individuals is the network that sustains the functionality of a society, e.g. the economy of a region. In this paper we present a novel idea for the SIR model, based on a dynamical study of the network composed by susceptible individuals. We show that the temporal decreasing of the size of the giant susceptible cluster can be described as a dynamic void node percolation process with an instantaneous void control parameter. We find that there exists a critical time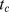 
above which the giant susceptible component overcomes a temporal second order phase transition with mean field exponents. The paper is organized as following: in Methods and Results we present the theoretical framework to derive the evolution equations. Then we study the evolution of the giant susceptible cluster and its temporal critical behavior. Finally we present our conclusions.
Methods and Results
Theoretical framework
The evolution equations of the dynamic SIR model provide the basis for analyzing theoretically novel magnitudes that could be useful for epidemiologists and authorities to plan policies to stop a disease before an epidemic develops. In the SIR model, initially, all the nodes are susceptible except for one node randomly infected, that represents the index case from which the disease spreads. The infected individual transmits the disease to susceptible neighbors with probability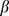 
each time unit and recovers 
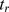time units since he was infected. For the SIR with fixed recovery time, the transmissibility is given by 
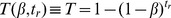[13].
In order to study the evolution of the states of the individuals in the SIR with fixed recovery time, we use the edge-based compartmental model (EBCM) [15]–[17]. The EBCM is based on a generating function formalism, widely implemented in branching and percolation process on complex networks [3], [18]–[20]. For a branching process that spreads on uncorrelated networks, such as the tree of infected individuals, two generating functions that contain the information of the topology of these networks are defined. The first one is the generating function of the node degree distribution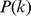 
which is given by 
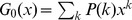. The second one is the generating function of the degree distribution of the first neighbors of a node, also called excess degree distribution 
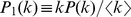, given by 
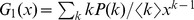. Here, 
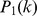is the probability to reach a neighbor of a node, following a link. It is straightforward that the mean connectivity of the nodes is 
.
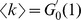Denoting the fraction of susceptible, infected and recovered individuals at time 
by 
, 
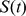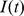and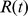 
, respectively, the EBCM approach describes the evolution of the probability that a node (which we call root node) is susceptible. In order to compute this probability, an edge is randomly chosen and a direction is given, in which the node in the target of the arrow is the root, and the base is its neighbor. Disallowing that the root infects the neighbor, 
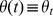is the probability that the neighbor does not transmit the disease to the root, with 
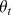given by
 |
(1) |
where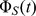 
, 
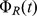and 
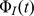are the probabilities that the neighbor is susceptible, recovered, or infected but has not transmitted yet the disease to the root. The probability that a root node with connectivity 
is susceptible is therefore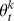 
and the fraction of susceptible nodes is 
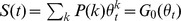. This approach simplifies the calculations, reducing the problem to finding an evolution equation for 
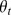, from where the evolution of 
, 
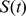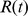and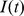 
is derived. Thus, using the EBCM approach adapted to SIR with fixed 
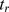(see Supporting Information Sec.1), the evolutions of 
, 
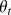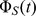and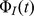 
are given by the deterministic equations
 |
(2) |
 |
(3) |
 |
(4) |
where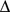 
is the discrete change of the variables between times 
and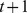 
. Eq. (2) represents the decrease of 
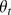when a infected neighbor transmits the disease. Eq. (3) represents the decrease of 
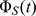when a susceptible neighbor is infected (notice that 
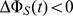). This term contributes to an increase of 
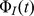in Eq. (4) where the first term represents the decrease of 
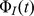when the links transmit the disease, the second term corresponds to the term of Eq. (3) mentioned above and the third term represents the decrease of 
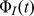due to the recovery of infected individuals.
From the above equations, the evolution of the fraction of infected individuals can be computed as
 |
(5) |
where the first term represents the fraction of new infected individuals (see Supporting Information Sec.1). The second term represents the recovery of infected individuals that have been infected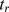 
time units ago.
These difference equations correctly describe the evolution of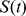 
, 
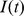and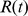 
above the criticallity for all values of 
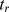and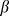 
(see Supporting Information Sec.1). In the next section, we will show that combining this approach and dynamic percolation, we can describe the time-dependent evolution of the susceptible individuals in the SIR model as a dynamic void node percolation process for any value of 
.
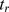Temporal percolation of susceptible individuals
In Ref. [13] it was found that the process under which the susceptible clusters size decrease can be explained with node void percolation defined below that as we will show can be related with the dynamic SIR process.
In the steady state of the SIR model an epidemic cluster is equivalent to a Leath growth process [21], [22] with a link occupancy probability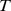 
. The Leath process on complex networks generates a single cluster that represents the infection tree for a given value of the transmission probability 
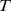. Denoting by 
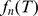the probability that a cluster reaches the 
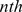generation following a link, the probability 
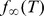that a link leads to a giant component (
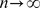) is given by [13], [22]
 |
(6) |
where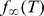 
is the solution of
 |
(7) |
As the “infectious” cluster grows from a root, generation by generation, the sizes of the void clusters, 
the nodes not reached by the disease, are reduced as in a node dilution process, since when a link is traversed a void cluster loses a node and all its edges. As a consequence, for large generations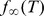 
can also be interpreted as the probability that a void cluster loses a node. However, in this kind of percolation process the void nodes are not killed at random, instead they are removed following a link. We call this type of percolation “node void percolation”. If we denote by 
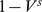the probability that a void node is removed due to the occupancy of a link, at the steady state the following relation holds
 |
(8) |
Then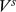 
is the probability that a void node is not removed due to the fact that the link has not been traversed. Thus, 
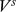is equivalent to 
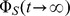because the void nodes correspond to the susceptible individuals in the steady state. As in any percolation process, there is a critical probability 
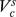at which the void network undergoes a second order phase transition. Above 
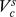a giant void component exist while at and below 
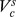void nodes belong only to finite components. In epidemic terms, this means that at 
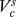only finite susceptible clusters can be reached. As a consequence, the fraction of links 
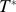needed to reach this point fulfills [13]
 |
(9) |
Therefore, from Eqs. (7) and (9) we obtain
 |
(10) |
where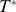 
is the solution of Eq. (10). This result shows that at the steady state, for 
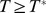, we have 
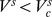and therefore the size of the giant susceptible cluster 
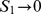[13]. Even though static percolation is a useful tool to analyze the final size of the giant component of susceptible individuals [12], it is very important to know the evolution of 
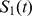, since it can be used as a criteria to begin or to increase an intervention to protect a large fraction of the susceptible population [13]. As we will show below, 
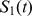can be fully related with a node void percolation process at every instant 
.
In order to describe the evolution of the size of the giant susceptible cluster, we define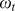 
as the probability that a neighbor of a root not connected to the giant susceptible cluster has not yet transmitted the disease to the root at time 
. This is possible if the neighbor of the root node is infected but has not yet transmitted the disease, recovered or susceptible but not connected to the giant susceptible cluster, with probabilities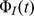 
, 
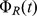and 
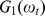respectively. Similarly to 
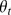(see Eq. (1)), these probabilities satisfy the relation
 |
(11) |
where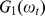 
is the generating function of the neighbor of a root not connected to the giant susceptible cluster. From Eq. (1), 
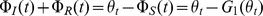. Then Eq. (11) can be rewritten as,
 |
(12) |
and the evolution of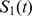 
is given by
 |
(13) |
where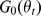 
is the total fraction of susceptible individuals and 
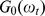is the fraction of individuals belonging to finite susceptible clusters at time 
. Notice that the dynamical Eqs. (12) and (13) are a time-dependent versions of the ones derived in Ref. [12] for the steady state (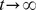
) of the SIR model. This suggests that the evolution of the giant susceptible or percolating void cluster can be thought as a temporal percolation process. Thus, the magnitudes derived for the static percolation of the susceptible individuals have a dynamical counterpart. As a result, 
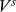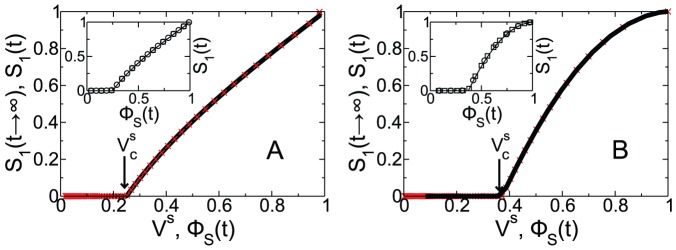
and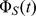 
, are equivalent not only at the steady state, but also at every instant of time. In order to show the equivalence, in Fig. 1 we show in the same plot 
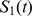as a function of 
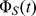, obtained from Eqs. (3)–(2) and (12)–(13), and the steady state 
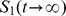as a function of 
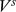[12] for ER and SF networks with the same 
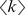and 
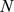for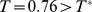 
.
Figure 1.
Equivalence between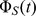 
and 
. 
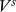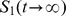as a function of 
(
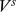) obtained in Refs. [12], [13] and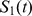 
as a function of 
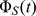(solid line) obtained from Eqs. (3)–(2) and (12)–(13) with 
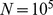and mean connectivity 4.07 in the giant component for (A) a ER network with 
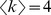and (B) SF network with 
, 
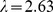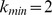and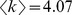 
. In the insets we show 
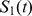as a function of 
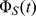from the simulations (symbols) and from Eqs. (3)–(2) and (12)–(13) (solid line) for 
(
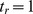) and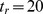 
(
). (Color online).
As we can see, the static curve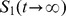 
as a function of 
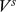is the same as 
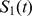as a function of 
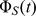and they coincide with the simulations for different values of 
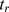which shows the equivalence between 
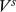and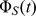 
at every instant of time and not only at the steady state (for details of the simulations see Supporting Information Sec.1). Thus our process can be explained by a dynamic percolation with an instantaneous void transmissibility 
.
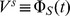With our theoretical formulation, we will show that there is a critical time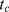 
at which the giant susceptible cluster disappears that correspond to the time at which 
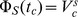. In order to prove this, notice that according to Eq. (12), 
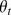and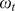 
can be thought as two points with the same image of the function 
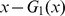. Solving this equation for the variable 
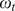above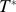 
, two solutions are found since the curve 
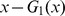is a concave function for 
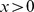as can be seen in Fig. 2. One of the solutions is the trivial one, for which 
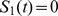, that corresponds to the maximum of the function 
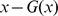at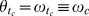 
. Then the giant susceptible cluster is destroyed at the point 
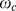which fulfills
 |
(14) |
then,
 |
(15) |
Thus when Eq. (14) is satisfied, the giant susceptible cluster disappears and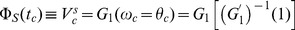 
, 
 |
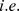
(16) |
For ER networks it is straightforward to show that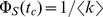 
.
Figure 2. Schematic of the behavior of Eq. (12) for .
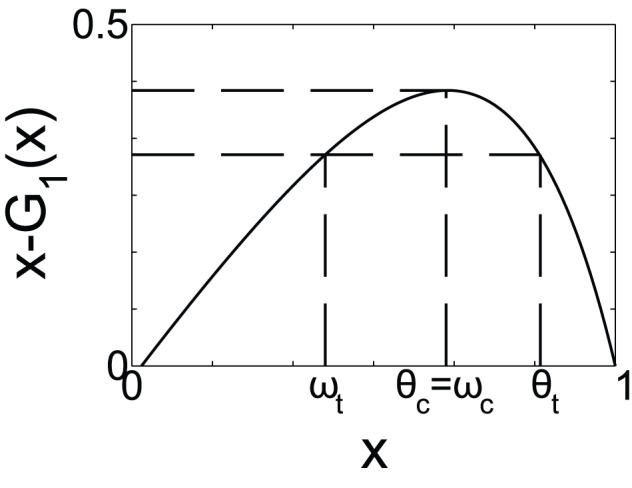
. From the initial condition 
, 
and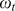 
, satisfies Eq. (12). For 
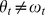we have two solutions that correspond to 
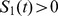. When 
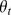reaches the maximum of the function 
, 
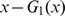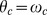, the giant susceptible component is destroyed. The dashed lines are used as a guide to show the possible solutions of Eq. (12).
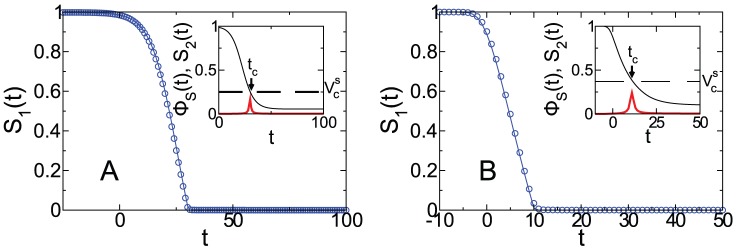
In Fig. 3 we plot the time evolution of the fraction of susceptible individuals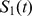 
in the susceptible giant component as a function of 
for ER and SF networks obtained from the theory and the simulations, for a transmissibility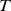 
above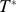 
.
Figure 3.
Time evolution of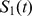 
for 
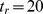and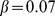 
(
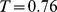) and mean connectivity 
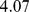in the giant component for (A) a ER network with 
(
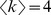) and (B) a SF networks with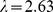 
, minimal connectivity 
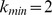and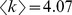 
(
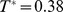). The symbols correspond to the simulations with the time shifted to 
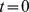when 
% of the individuals are infected, and the solid lines correspond to the theoretical solutions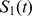 
(blue solid line) of Eqs. (12)–(13). In the insets we show the size of the second biggest susceptible cluster 
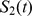(red solid line) and the evolution of 
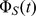(black solid line) obtained from simulations. The value of 
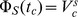(dashed line) was obtained from Eq. (16). 
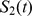has been amplified by a factor of 50 in order to show it on the same scale as the rest of the curves. The simulations are averaged over 1000 network realizations with 
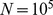. (Color online).
As shown in Fig. 3, there is an excellent agreement between the theoretical curve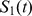 
, obtained from Eqs. (12) and (13), and the simulations which validate that percolation tools can be used to describe the time dependence of the susceptible individuals in the SIR process for 
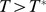. On the other hand, in the figure we can see that for 
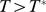, the giant susceptible cluster 
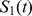is destroyed at 
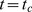which occurs exactly at 
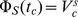(see the insets of Fig. 3). Our results show that 
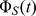can be used to determine whether a giant susceptible cluster exists at a given time. In turn, in the insets of Fig. 3 we can see that the size of the second susceptible cluster 
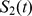has a sharp peak around 
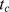, indicating that, as in static percolation, the susceptible individuals overcome a second order phase transition. However, this transition is not given by a random node percolation process. As the disease spreads through the links, the susceptible individuals are removed with probability proportional to 
, 
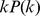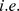, the susceptible network loses the higher degree nodes first. For this reason, the disease spreading induces a second order phase transition in the susceptible network with mean field exponents at 
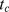(see discussion in the Supporting Information Sec.2).
An important implication of our results is that, it can be used by the health authorities to implement intervention strategies before the critical time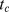 
is reached. This will allow to protect a macroscopic fraction of the network composed by healthy interconnected individuals which preserve all the topological properties characteristic of social contact networks and their functionality.
Conclusions
In this paper we introduce a temporal dynamic percolation to characterize the evolution of the susceptible individuals in a SIR model. We show using an edge-based compartmental approach and percolation tools that as the disease spreads the evolution of the susceptible network can be explained as a temporal node void percolation that can be mapped instantaneously into static percolation. We show that for transmissibilities above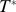 
, there exist a critical time above which the giant susceptible cluster is destroyed and the susceptible network overcomes a second order transition with mean field exponents. All our theoretical results are in excellent agreement with the simulations. Our findings are very interesting from an epidemiological point of view since the existence of a threshold time implies that when a very virulent disease reaches a small number of susceptible individuals, the authorities have only a limited time to intervene, in order to protect a big community (susceptible giant component) that has not been already reached by the epidemic, and to preserve the topological features of SF networks. Our finding on the susceptible network could be extended to other epidemics dynamics allowing to obtain a better description of the effect of diseases spreading on social and technological networks.
Supporting Information
(PDF) Supporting Information.
(PDF)
Acknowledgments
The authors gratefully thanks to Erik M. Volz for a useful private communication and to the anonymous reviewer for his/her deep reading of our paper and his/her helpful comments. This work is part of a research project of UNMdP and FONCyT (Pict 0293/2008).
Funding Statement
No current external funding sources for this study.
References
- 1. Bajardi P, Poletto C, Ramasco JJ, Tizzoni M, Colizza V, et al. (2011) Human mobility networks, travel restrictions, and the global spread of 2009 h1n1 pandemic. PLoS ONE 6: e16591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Colizza V, Barrat A, Barthelemy M, Vespignani A (2007) Predictability and epidemic pathways in global outbreaks of infectious diseases: the SARS case study. BMC Medicine 5: 34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D (2006) Complex networks: Structure and dynamics. Physics Reports 424: 175–308. [Google Scholar]
- 4.Anderson RM, May RM (1992) Infectious Diseases of Humans: Dynamics and Control. Oxford University Press, Oxford.
- 5. Lagorio C, Migueles M, Braunstein L, López E, Macri P (2009) Effects of epidemic threshold definition on disease spread statistics. Physica A: Statistical Mechanics and its Applications 388: 755–763. [Google Scholar]
- 6. Newman MEJ (2002) Spread of epidemic disease on networks. Phys Rev E 66: 016128. [DOI] [PubMed] [Google Scholar]
- 7. Parshani R, Carmi S, Havlin S (2010) Epidemic threshold for the susceptible-infectious-susceptible model on random networks. Phys Rev Lett 104: 258701. [DOI] [PubMed] [Google Scholar]
- 8. Grassberger P (1983) On the critical behavior of the general epidemic process and dynamical percolation. Math Biosci 63: 157–172. [Google Scholar]
- 9. Miller JC (2007) Epidemic size and probability in populations with heterogeneous infectivity and susceptibility. Phys Rev E 76: 010101. [DOI] [PubMed] [Google Scholar]
- 10. Kenah E, Robins JM (2007) Second look at the spread of epidemics on networks. Phys Rev E 76: 036113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Cohen R, Erez K, ben Avraham D, Havlin S (2000) Resilience of the internet to random breakdowns. Phys Rev Lett 85: 4626–4628. [DOI] [PubMed] [Google Scholar]
- 12. Newman MEJ (2005) Threshold effects for two pathogens spreading on a network. Phys Rev Lett 95: 108701. [DOI] [PubMed] [Google Scholar]
- 13. Valdez LD, Macri PA, Braunstein LA (2012) Intermittent social distancing strategy for epidemic control. Phys Rev E 85: 036108. [DOI] [PubMed] [Google Scholar]
- 14. Lindquist J, Ma J, van den Driessche P, Willeboordse F (2011) Effective degree network disease models. Journal of Mathematical Biology 62: 143–164. [DOI] [PubMed] [Google Scholar]
- 15. Miller JC (2011) A note on a paper by Erik Volz: SIR dynamics in random networks. Journal of Mathematical Biology 62: 349–358. [DOI] [PubMed] [Google Scholar]
- 16. Miller JC, Slim AC, Volz EM (2011) Edge-based compartmental modelling for infectious disease spread. Journal of The Royal Society Interface 9: 890–906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Volz EM (2008) SIR dynamics in random networks with heterogeneous connectivity. Journal of Mathematical Biology 56: 293–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Dorogovtsev SN, Goltsev AV, Mendes JFF (2008) Critical phenomena in complex networks. Rev Mod Phys 80: 1275–1335. [Google Scholar]
- 19. Newman MEJ, Strogatz SH, Watts DJ (2001) Random graphs with arbitrary degree distributions and their applications. Phys Rev E 64: 026118. [DOI] [PubMed] [Google Scholar]
- 20. Newman MEJ, Jensen I, Ziff RM (2002) Percolation and epidemics in a two-dimensional small world. Phys Rev E 65: 021904. [DOI] [PubMed] [Google Scholar]
- 21. Leath P (1976) Cluster size and boundary distribution near percolation threshold. Phys Rev B 14: 5046. [Google Scholar]
- 22. Braunstein LA, Wu Z, Chen Y, Buldyrev SV, Kalisky T, et al. (2007) Optimal path and minimal spanning trees in random weighted networks. I J Bifurcation and Chaos 17: 2215–2255. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF) Supporting Information.
(PDF)