The SENSE-Isomorphism Theoretical Image Voxel Estimation (SENSE-ITIVE) Model for Reconstruction and Observing Statistical Properties of Reconstruction Operators

Abstract

The acquisition of sub-sampled data from an array of receiver coils has become a common means of reducing data acquisition time in MRI. Of the various techniques used in parallel MRI, SENSitivity Encoding (SENSE) is one of the most common, making use of a complex-valued weighted least squares estimation to unfold the aliased images. It was recently shown in Bruce et al. [Magn. Reson. Imag. 29(2011):1267–1287] that when the SENSE model is represented in terms of a real-valued isomorphism, it assumes a skew-symmetric covariance between receiver coils, as well as an identity covariance structure between voxels. In this manuscript, we show that not only is the skew-symmetric coil covariance unlike that of real data, but the estimated covariance structure between voxels over a time series of experimental data is not an identity matrix. As such, a new model, entitled SENSE-ITIVE, is described with both revised coil and voxel covariance structures. Both the SENSE and SENSE-ITIVE models are represented in terms of real-valued isomorphisms, allowing for a statistical analysis of reconstructed voxel means, variances, and correlations resulting from the use of different coil and voxel covariance structures used in the reconstruction processes to be conducted. It is shown through both theoretical and experimental illustrations that the miss-specification of the coil and voxel covariance structures in the SENSE model results in a lower standard deviation in each voxel of the reconstructed images, and thus an artificial increase in SNR, compared to the standard deviation and SNR of the SENSE-ITIVE model where both the coil and voxel covariances are appropriately accounted for. It is also shown that there are differences in the correlations induced by the reconstruction operations of both models, and consequently there are differences in the correlations estimated throughout the course of reconstructed time series. These differences in correlations could result in meaningful differences in interpretation of results.

1. Introduction

The fundamental basis for image formation in magnetic resonance imaging (MRI) is the discovery that the spatial information of an object can be Fourier encoded in the resonance spectrum by a magnetic field gradient [1, 2]. Fourier encoded by magnetic field gradients, the complex-valued spatial frequencies are not measured instantaneously, but rather individually in a serial fashion, resulting in a long acquisition time for the spatial frequencies for a volume of images. As such, the measurement of sub-sampled spatial frequencies with multiple receiver coils, in parallel[3], has become a popular means of reducing image acquisition time.

The basis of parallel MRI is such that an array of receiver coils are used to acquire spatial frequencies for reduced field-of-view (FOV) images concurrently, which are combined into a single full FOV image using a technique such as SENSitivity Encoding (SENSE) [4]. The SENSE model has become a very popular parallel image reconstruction technique as it does not have strict restrictions on the layout of receiver coils, and the reduction in time achieved by sub-sampling the spatial frequencies reduces the requirements on issues such as breath holding in cardiac imaging [5]. However, the advantage gained in reducing acquisition time by sub-sampling spatial frequencies has a reciprocal effect on the time and difficulty faced in reconstructing the sub-sampled data.

When the AMMUST (A Mathematical Model for Understanding the Statistical effects) framework for analyzing reconstruction and pre-processing operators in [6] was adapted to represent the SENSE reconstruction model in terms of a real-valued isomorphism in [7], it was found that when represented in this way, that the complex-valued normal distribution assumed in the noise between receiver coils imposes a skew-symmetric coil covariance structure. However, when estimated from two different experimental data sets, it is shown that this assumption is miss-specified. It is also generally assumed in the literature that there is an identity covariance structure between the aliased voxels in each of the coil images. This assumption is also shown to be miss-specified, as there is a non-identity voxel covariance structure when estimated directly from experimental data. With both the coil and voxel covariance structures shown to be inappropriately defined when represented in terms of a real-valued isomorphism, we propose a new image reconstruction model, entitled SENSE-Image Theoretical Isomorphism Voxel Estimation (SENSE-ITIVE), which uses both a mathematically correct covariance structure between receiver coils and a non-identity voxel covariance structure, both observed in real data.

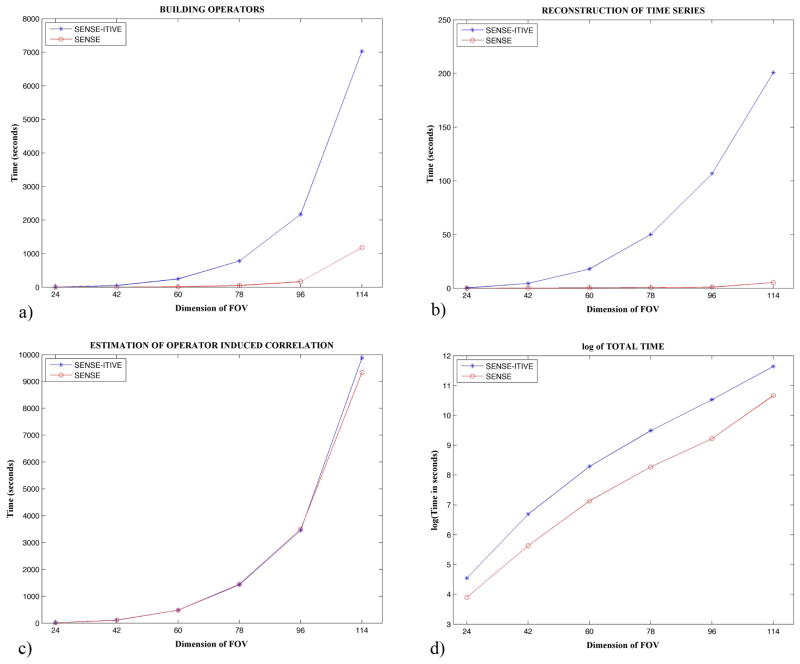
Comparisons between the SENSE and SENSE-ITIVE models are theoretically illustrated on a time series with 490 scans (TRs) of 96×96 constant circle and Shepp-Logan phantom data, generated with covariance structures between coils and voxels similar to that of experimental data. The reconstruction techniques and statistical analysis undertaken in the theoretical illustration are then carried across to experimentally acquired spherical phantom and human subject fMRI data. A real-valued isomorphism representation of the complex-valued coil covariance matrix, as well as the covariance structure between voxels, is estimated from an experimental time series of 490 scans of a spherical phantom, and an experimental time series of resting state scans with a human subject. The time series of data acquisitions in each data set are reconstructed by both models, after which a statistical analysis is performed comparing the effects that the miss-specified coil and voxel covariance structures in the SENSE model have on voxel means, covariances, and correlations. As the results of the study conducted in this manuscript are most significant in functional connectivity studies, lower resolution 96×96 images were used in both the theoretical and experimental illustrations.

The implementation of a real-valued isomorphism in [7] showed that the mapping, or “unfolding,” of aliased voxels from the receiver coil images into a single combined image induces a correlation between the aliased voxels from each “fold.” While the SENSE-ITIVE model itself does not address this issue, a comparison of the correlations induced by the SENSE and SENSE-ITIVE reconstruction operators illustrates the effects of miss-specified coil and voxel covariance structures. As presented in [7], the implementation of image smoothing amplifies the correlation induced between aliased voxels by the SENSE image reconstruction operators, and thus image smoothing by means of a Gaussian kernel is applied in both the theoretical and experimental illustrations.

2. Theory

2.1 Linear Framework

The derivation in [8] that allows for the complex-valued inverse Fourier transformation to be represented in terms of a real-valued isomorphism is the basis on which a statistical analysis of the linear operations commonly performed in image reconstruction can be performed. The mathematical formalism of image reconstruction by [8] was generalized by [6] to make use of a Cartesian linear image reconstruction, and was further extended in [7] to accommodate sub-sampled data from multiple receiver coils and represent the SENSE model as a linear operator. Traditionally, the sub-sampling of data occurs by omitting lines of k-space in the Phase Encoding (PE) direction, although the framework and principle can be applied for any direction. In this Cartesian framework, the subscript y denotes the PE direction (i.e. bottom-top), while the subscript x denotes the frequency encode direction (i.e. left-right). For an acceleration factor (also commonly known as a reduction factor), A, a receiver coil would only acquire every A^th line of k-space in the PE direction. Thus, a sub-sampled matrix of spatial frequencies for coil l, F_lC, where l = [1,2, …, N_C], would be of dimensions (p_y/A)×p_x. In a real-valued isomorphism, a reconstructed complex-valued aliased image from each coil, in vector form, y_l, is represented as a product of a 2D inverse Fourier transformation operator [8], Ω, with the observed sub-sampled complex-valued k-space spatial frequencies in vector form, f_l, as

$$y_l=\mathrm{\Omega }{f}_l.$$ (1)

If F_lC is a (p_y/A)×p_x matrix of sub-sampled two-dimensional complex-valued spatial frequencies, then the vector of observed k-space spatial frequencies, f_l, in Eq. (1) are formed by stacking the p_xp_y/A real spatial frequencies on top of the p_xp_y/A imaginary spatial frequencies

$$f_l=\mathit{vec}(Re(F_{lC}^T),Im(F_{lC}^T)),$$ (2)

where vec(·) is a vectorization operator that stacks the columns of its matrix argument, Re(·) denotes the real part, and Im(·)denotes the imaginary part. Similarly to the observed k-space data, if the complex-valued reconstructed image is of dimensions (p_y/A)×p_x, then the reconstructed image vector will consist of p_xp_y/A real reconstructed image values stacked above p_xp_y/A imaginary reconstructed image values, resulting in a reconstructed image vector y of dimensions 2p_xp_y/A×1.

To reconstruct sub-sampled complex-valued spatial frequencies from an array of N_C receiver coils, the vectorization in Eq. (2) is applied to each of the N_C sub-sampled spatial frequency matrices, which are in turn concatenated into a single vector, f, with alternating real and imaginary components. The Ω operation, which can be adjusted to account for intra-acquisition decay and magnetic field inhomogeneities acquired in the k-space signal [6, 9] if T₂* or ΔB maps can be obtained, is applied to all N_C coils at once by

$$y=(I_{N_C}\otimes \mathrm{\Omega })f.$$ (3)

The Kronecker product, ⊗, in Eq. (3) multiplies every element of the identity matrix I_NC by the entire matrix Ω, generating a block diagonal inverse Fourier reconstruction operator that reconstructs the sub-sampled spatial frequencies from each coil into reduced FOV aliased coil image vectors. The reconstructed aliased coil image vectors produced by Eq. (3),

$$y=\mathit{vec}(Re(y_l^T),Im(y_l^T))$$ (4)

are stored in a vector comprised of the sub-vectors of reconstructed images from the l= [1,2,.., N_C] coils, with the real reconstructed aliased image values of each coil stacked upon the corresponding imaginary reconstructed aliased image values.

As described in [7], the vector of reconstructed aliased voxel values from each coil, y_l, needs to be permuted to being ordered by voxel, rather than by coil, such that the SENSE unfolding operation can be performed on each of the aliased voxels. A complex permutation, P_C, is thus applied resulting in a vector with sub-vectors of length 2N_C with the N_C real aliased voxel values stacked upon the N_C imaginary aliased voxel values corresponding to each of the N_C receiver coils. For even acceleration factors, it was also shown in [7] that a Fourier transform shift permutation, P_S, needs to be applied such that the unfolding process performed by the SENSE model results in a centered image. The vector of aliased voxel values, a, ordered by voxel and shifted according to the choice of acceleration factor A, is thus

$$a=P_S{P}_C(I_{N_C}\otimes \mathrm{\Omega })f.$$ (5)

2.2 The SENSE Isomorphism

The SENSE model makes use of a complex-valued weighted least squares estimation process in un-aliasing the A voxel values in each of the N_C aliased coil images. In the SENSE model, an aliased voxel j=[1,2,…rp], where rp denotes the total number of aliased voxels in each reduced FOV coil image, is comprised of a complex-valued vector a_jC = a_jR + ia_jI with N_C voxel measurements from the sub-sampled spatial frequencies from each coil, that are derived by

$$a_{jC}=S_{jC}{v}_{jC}+{\epsilon }_{jC}.$$ (6)

In Eq. (6), S_jC = S_jR + iS_jI is a complex-valued sensitivity matrix, of dimension N_C×A, derived from the fully sampled complex-valued coil image sensitivity matrix, v_jC = v_jR + iv_jI is a vector of length A containing the complex-valued un-aliased scalar voxel values, and ε_jC = ε_jR + iε_jI is the complex-valued additive measurement noise vector of length N_C. It is generally assumed that the complex-valued measurement noise, ε_C, is derived from the complex-valued normal distribution [10] given by

$$f({\epsilon }_{jC})={(2\pi )}^{-N_C}{\mid {\mathrm{\Psi }}_C\mid }^{-1/2}exp\left(-\frac{1}{2}{\epsilon }_{jC}^H{\mathrm{\Psi }}_C^{-1}{\epsilon }_{jC}\right),$$ (7)

where Ψ_C = Ψ_R + iΨ_I is the complex-valued coil covariance matrix and H denotes the Hermitian, or conjugate transpose. After a transformation of variables, to represent Eq. (7) in terms of the aliased voxel values, a_jC, it can be shown that the least squares estimate of the complex-valued true scalar voxel values is

$$v_{jC}={(S_{jC}^H{\mathrm{\Psi }}_C^{-1}{S}_{jC})}^{-1}{S}_{jC}^H{\mathrm{\Psi }}_C^{-1}{a}_{jC}.$$ (8)

As the additive measurement noise, derived from the complex-valued normal distribution

$${\epsilon }_{jC}~CN(0,{\mathrm{\Psi }}_C)$$

provides the covariance between the coils in the SENSE model, when represented as a real-valued isomorphism,

$${\epsilon }_j~N\left(0,\left[\begin{array}{cc}{\mathrm{\Psi }}_R& -{\mathrm{\Psi }}_I\\ {\mathrm{\Psi }}_I& {\mathrm{\Psi }}_R\end{array}\right]\right),$$

the complex coil covariance matrix, Ψ_C, in terms of a real-valued isomorphism, as used in the SENSE model, is expressed as

$${\mathrm{\Psi }}_{SE}=\left[\begin{array}{cc}{\mathrm{\Psi }}_R& -{\mathrm{\Psi }}_I\\ {\mathrm{\Psi }}_I& {\mathrm{\Psi }}_R\end{array}\right].$$ (9)

It is of note that the covariance structure presented in Eq. (9) is skew symmetric, assuming that the real-by-real and imaginary-by-imaginary covariances are equivalent to the real-by-real covariance. In addition, it is assumed that the real-by-imaginary covariance between coils is the negative of the imaginary-by-real covariance between coils, which is equivalent to the imaginary-by-imaginary covariance. It will be shown when estimated from experimental data that this is not the case and that the covariance in Eq. (9) is miss-specified, requiring the true covariance structure to be rearranged to accommodate the skew-symmetric structure. If Eq. (6) is expressed as a real-valued isomorphism

$$a_j=S_j{v}_j+{\epsilon }_j,$$ (10)

where a_j = (a^T_jR,a^T_jI)^T is a vector of the N_C real aliased voxel measurements stacked upon the N_C imaginary aliased voxel measurements, ε_j= (ε^T_jR,ε^T_jI)^T is a vector of the N_C real parts of the complex-valued additive noise stacked upon the N_C imaginary parts, and v_j = (v^T_jR,v^T_jI)^T is a vector of the A un-aliased real voxel values stacked upon the A un-aliased imaginary voxel values. The un-aliased scalar voxel values, v_j, in Eq. (10) are derived from a real-valued representation of the complex-valued sensitivity matrix

$$S_j=\left[\begin{array}{cc}{S}_{jR}& -S_{jI}\\ S_{jI}& S_{jR}\end{array}\right],$$

where S_jR and S_jI are the real and imaginary sensitivities for voxel j respectively. Eq. (8) can thus be represented in terms of a real-valued isomorphism as

$${\left[\begin{array}{c}{v}_{jR}\\ v_{jI}\end{array}\right]}_{SE}={\left({\left[\begin{array}{cc}{S}_{jR}& -S_{jI}\\ S_{jI}& S_{jR}\end{array}\right]}^T{\left[\begin{array}{cc}{\mathrm{\Psi }}_R& -{\mathrm{\Psi }}_I\\ {\mathrm{\Psi }}_I& {\mathrm{\Psi }}_R\end{array}\right]}^{-1}\left[\begin{array}{cc}{S}_{jR}& -S_{jI}\\ S_{jI}& S_{jR}\end{array}\right]\right)}^{-1}{\left[\begin{array}{cc}{S}_{jR}& -S_{jI}\\ S_{jI}& S_{jR}\end{array}\right]}^T{\left[\begin{array}{cc}{\mathrm{\Psi }}_R& -{\mathrm{\Psi }}_I\\ {\mathrm{\Psi }}_I& {\mathrm{\Psi }}_R\end{array}\right]}^{-1}\left[\begin{array}{c}{a}_{jR}\\ a_{jI}\end{array}\right]$$

or

$$v_{\mathit{jSE}}={(S_j^T{\mathrm{\Psi }}_{SE}^{-1}{S}_j)}^{-1}{S}_j^T{\mathrm{\Psi }}_{SE}^{-1}{a}_j$$ (11)

where S_j is of dimension 2N_C×2A, Ψ_SE is of dimension 2N_C×2N_C, and the vector of voxel measurements a is of dimension 2N_C×1. Thus, the isomorphism in Eq. (11) yields an image space vector, v_j, of dimension 2A×1 that is comprised of the A real voxel values stacked upon the A imaginary voxel values. These A values correspond to the A folds that are formed via under-sampling the data in k-space by a factor of A. It can be shown that the estimated complex-valued un-aliased single combined image voxel values in Eq. (8) is mathematically equivalent to the estimated real and imaginary isomorphism vector of un-aliased single combined image voxel value in Eq. (11).

In order to carry out the SENSE isomorphism using the linear framework, Eq. (11) is rewritten as

$$v_{SE}=U_{SE}a,$$ (12)

where the SENSE unfolding matrix U_SE is block diagonal with the j^th block for aliased voxel j

$$U_{\mathit{SEj}}={(S_j^T{\mathrm{\Psi }}_{SE}^{-1}{S}_j)}^{-1}{S}_j^T{\mathrm{\Psi }}_{SE}^{-1},$$

and a is the vector of aliased voxel values described in Eq. (5). Provided with the array of fully sampled coil sensitivities, a coil sensitivity matrix, S, can be constructed by placing the 2N_C×2A coil sensitivities, S_j, corresponding to each aliased voxel, j, along the diagonal of a block diagonal matrix. Assuming an identity covariance structure between voxels, and that each voxel shares the same coil covariance structure, the covariance structure used in the weighted least squares estimation in the SENSE model is constructed using the Kronecker product I_rp⊗Ψ_SE. With the block diagonal coil sensitivity and coil covariance matrices, a block diagonal SENSE unfolding operator in Eq. (12), U_SE, is constructed by using the matrix representation of Eq. (11) as

$$U_{SE}=\left(S^T{\left(I_{rp}\otimes {\mathrm{\Psi }}_{SE}\right)}^{-1}S\right)S^T{\left(I_{rp}\otimes {\mathrm{\Psi }}_{SE}\right)}^{-1}.$$ (13)

The operator U_SE will “unfold” the N_C real and N_C imaginary voxel values in all rp aliased voxels from the N_C coils into A real and A imaginary voxel values for each of A folds

$$v_{SE}=U_{SE}{P}_S{P}_C\left(I_{N_C}\otimes \mathrm{\Omega }\right)f.$$

As described in [7], a final permutation, P_U, is necessary to reorder the un-aliased real and imaginary image values in v_SE from being ordered by voxel to being ordered by fold, and then from being ordered by fold to ordered by row, resulting in a vector of all real un-aliased image values stacked upon all imaginary un-aliased image values

$$y_{SE}=P_U{U}_{SE}{P}_S{P}_C\left(I_{N_C}\otimes \mathrm{\Omega }\right)f.$$ (14)

2.3 The SENSE-ITIVE model

As will be illustrated with experimental data, when the covariance between coils is estimated from a time series of experimental data, there is a real-by-real, imaginary-by-imaginary, real-by-imaginary, and an imaginary-by-real covariance between coils

$${\mathrm{\Psi }}_{SI}=\left[\begin{array}{cc}{\mathrm{\Psi }}_{RR}& {\mathrm{\Psi }}_{RI}\\ {\mathrm{\Psi }}_{RI}^T& {\mathrm{\Psi }}_{II}\end{array}\right].$$ (15)

As the estimated covariance between coils is symmetric, the real-by-imaginary covariance structure is simply the transpose of the imaginary-by-real covariance. It is important to note that although derived from the multivariate normal distribution of coil measurements, the skew-symmetric SENSE coil covariance matrix in Eq. (9) cannot be expressed in this fashion, unless all elements in Ψ_SE are zero. The SENSE coil covariance structure, Ψ_SE, is therefore miss-specified, requiring a rearrangement of the structure in Eq. (15) such that the format in Eq. (9) can be accommodated.

In general, the SENSE model is applied on a voxel-by-voxel basis, thus assuming an identity covariance structure between voxels, and that all voxels use the same covariance structure between coils. It will be shown when the covariance structure is estimated between voxels over a time series of images that there is a non-identity voxel covariance structure, ϒ. Given the miss-specification in both the SENSE coil covariance structure in Eq. (9) and the covariance between voxels in Eq. (13), consider a new model, entitled the SENSE-Image Theoretical Isomorphism Voxel Estimation (SENSE-ITIVE), that makes use of a covariance structure between coils like that in Eq. (15) and a non-identity voxel covariance, as estimated from the data. The SENSE-ITIVE unfolding operation utilized in un-aliasing the vector of aliased voxels in Eq. (5) is thus

$$U_{SI}=\left(S^T{\left(\mathrm{\Upsilon }\otimes {\mathrm{\Psi }}_{SI}\right)}^{-1}S\right)S^T{\left(\mathrm{\Upsilon }\otimes {\mathrm{\Psi }}_{SI}\right)}^{-1}.$$ (16)

With an estimated non-identity voxel covariance, ϒ, the SENSE-ITIVE unfolding matrix is not a block diagonal matrix, like that of the SENSE unfolding operator in Eq. (13), but rather a full matrix. Therefore, to implement a non-identity voxel covariance structure, like that estimated from real data, it is necessary to make use of a linear isomorphism such as the one in this manuscript.

As the coil and voxel covariance structures assumed in the unfolding operation in Eq. (16) are the only differences to that of the SENSE model, the remainder of the operations remain the same, and thus a vector of un-aliased voxel values, y_SI, derived from a vector of sub-sampled spatial frequencies from N_C receiver coils, f, is expressed as

$$y_{SI}=P_U{U}_{SI}{P}_S{P}_C\left(I_{N_C}\otimes \mathrm{\Omega }\right)f.$$ (17)

In addition to the SENSE (SE) and SENSE-ITIVE (SI) reconstruction operations performed in Eqs. (14) and (17), supplementary pre-processing operators, such as apodization or a gridding operator for non-Cartesian acquisitions, ink-space [6], O_K, and image space post-processing operators, such as image smoothing, O_I, can be incorporated into both models as

$$y_{SE/SI}=O_I{P}_U{U}_{SE/SI}{P}_S{P}_C\left(I_{N_C}\otimes \mathrm{\Omega }{O}_K\right)f.$$ (18)

Operators O_I, and O_K are treated as identity in this study unless stated otherwise. All operators used to reconstruct the acquired k-space signal in the SENSE and SENSE-ITIVE models in Eq. (18) can be combined into a single operator for each model as

$$O_{SE}=O_I{P}_U{U}_{SE}{P}_S{P}_C\left(I_{N_C}\otimes \mathrm{\Omega }{O}_K\right)$$ (19)

and

$$O_{SI}=O_I{P}_U{U}_{SI}{P}_S{P}_C\left(I_{N_C}\otimes \mathrm{\Omega }{O}_K\right)$$ (20)

respectively.

Provided with a non-identity voxel covariance ϒ, the covariance structure of the k-space data, acquired from receiver coils, with a coil covariance of Ψ is defined to be

$$\mathrm{\Gamma }=\frac{p_x{p}_y}{A}\left(\mathrm{\Psi }\otimes \mathrm{\Upsilon }\right).$$

The covariance induced by the reconstruction operators from the SENSE (SE) and SENSE-ITIVE (SI) models can be evaluated as

$${\mathrm{\sum }}_{SE/SI}=cov(y_{SE/SI})=O_{SE/SI}\mathrm{\Gamma }{O}_{SE/SI}^T.$$

If the k-space covariance matrix Γ is assumed to be identity, the covariance induced purely by the SENSE and SENSE-ITIVE operators reduces to

$${\mathrm{\sum }}_{SE/SI}=O_{SE/SI}{O}_{SE/SI}^T.$$ (21)

It was illustrated in [7] that the resulting covariance matrix Σ_SE/SI is not proportional to an identity covariance matrix, a result purely from reconstruction and processing operations. This leads to a nonidentity correlation, and hence induced correlation between voxels by the SENSE reconstruction operations in Eq. (21). It will be seen when comparing the use of a mathematically correct coil covariance combined with a non-identity voxel covariance estimated from the data, as assumed in the SENSE-ITIVE model, that the correlation induced between the previously aliased voxels by the reconstruction operators in Eq. (21) is unlike that of the SENSE model, where both the coil and voxel covariance structures are miss-specified.

2.4 SENSE and SENSE-ITIVE Geometry Factor

In order to perform the matrix inverse in the weighted least squares estimation utilized in both the SENSE and SENSE-ITIVE models, it is necessary for N_C to be greater than the acceleration factor A. If this is not the case, it results in an underdetermined system of equations and thus poorly conditioned unfolding matrices in Eqs. (13) and (16). It is common practice for the geometry factor (g-factor) to be used as a means of quantifying the level of noise amplification between the receiver coils in the array, and describes how well aliased voxels will be unfolded given the choice of coil geometry in image reconstruction [11, 12]. Like the SENSE and SENSE-ITIVE unfolding operations, the geometry factor for the SENSE and SENSE-ITIVE models can be represented in terms of a real-valued isomorphism as

$$g_{SE}=\sqrt{\mathit{diag}\left[{\left(S^T{\left(\mathrm{\Upsilon }\otimes {\mathrm{\Psi }}_{SE}\right)}^{-1}S\right)}^{-1}\right]\mathit{diag}\left[\left(S^T{\left(\mathrm{\Upsilon }\otimes {\mathrm{\Psi }}_{SE}\right)}^{-1}S\right)\right]}$$ (22)

and

$$g_{SI}=\sqrt{\mathit{diag}\left[{\left(S^T{\left(\mathrm{\Upsilon }\otimes {\mathrm{\Psi }}_{SI}\right)}^{-1}S\right)}^{-1}\right]\mathit{diag}\left[\left(S^T{\left(\mathrm{\Upsilon }\otimes {\mathrm{\Psi }}_{SI}\right)}^{-1}S\right)\right]}$$ (23)

where the operator diag(·) forms a vector listing the diagonal elements of its matrix argument. The two vectors formed by the diag(·) operator in both (22) and (23) are multiplied on an element by element basis, resulting in vectors g_SE and g_SI are of length p_xp_y, and ordered by voxel. The vectors can thus be unfolded by the same unfolding permutation, P_U, as used in Eq. (14), and finally reshaped into g-factor matrices by un-stacking the columns and transposing. It can be shown that the SENSE and SENSE-ITIVE coil covariance structures as well as the non-identity voxel covariance structure, ϒ, are non-singular, and thus when multiplied by their respective inverse matrices produce an identity matrix. As such, if the matrix inverses are carried out in Eqs. (22) and (23), in conjunction with the non-singular nature of the coil and voxel covariance structures and properties of Kronecker products, that the g-factor for SENSE and SENSE-ITIVE are equivalent. Therefore, for a given coil geometry, the condition of the 2N_C ×2A voxel sensitivity matrices, S, is the same for both the SENSE and SENSE-ITIVE models, as defined by the g-factor. It is by this definition of the g-factor that it is necessary to have a acceleration factor, A, that is neither equivalent nor larger than the number of coils, N_C, such that the numerical condition of the matrix inverse utilized in the SENSE and SENSE-ITIVE least squares estimations is preserved.

3. Theoretical Illustration

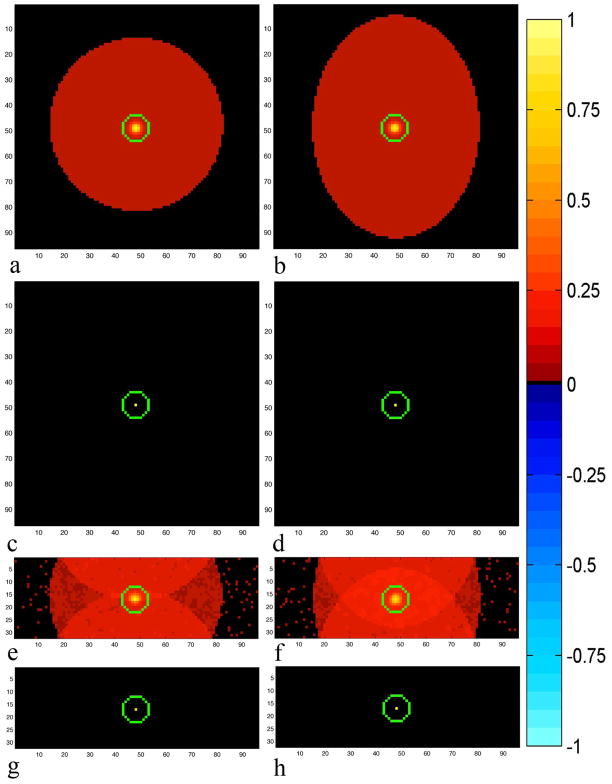
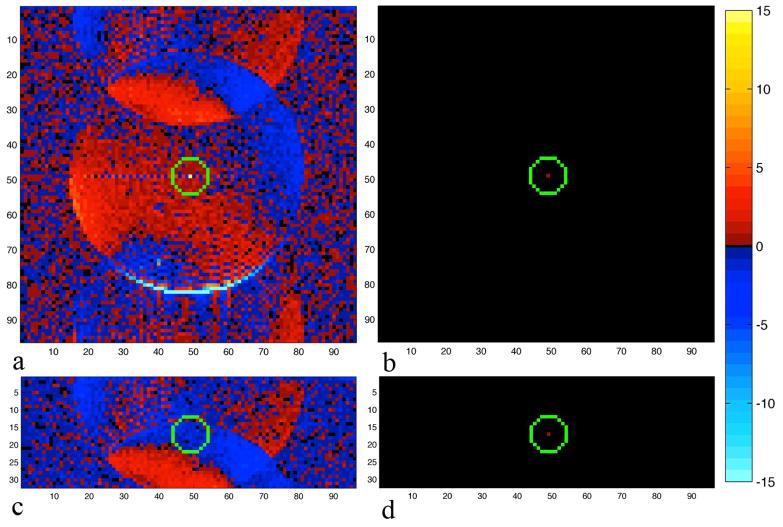
To theoretically illustrate the differences between the SENSE and SENSE-ITIVE models, two time series of 490 images with a 96×96 FOV for N_C=4 coils were created using a noiseless circle and Shepp-Logan phantom to respectively simulate the spherical phantom and human subject data sets in the experimental illustration. For the Shepp-Logan phantom, the outer rim of the phantom was set to 2.5, the upper oval within the phantom was set to 1.875, the left and right inner ovals were set to zero, with the remainder of the area within the phantom set to 0.5. These modifications of the standard Shepp-Logan phantom were chosen to match the maximum and minimum values of the unsmoothed human subject magnitude, while the circle was set to 2.5 throughout to match the maximum un-smoothed spherical phantom magnitude. The noiseless circle and Shepp-Logan phantom were combined with theoretical coil sensitivity profiles [7], a circular coil covariance similar to that of experimental data and a voxel covariance structure that is assumed to be identity between voxels outside of the circle/phantom and a Gaussian kernel with a full width at half maximum (FWHM) of three voxels. The sensitivity profiles for the four coils were generated by multiplying the noiseless circle and Shepp-Logan phantoms with Gaussian kernels, with a FWHM of 25 voxels, that were centered along the four edges of the full FOV images. These profiles therefore had a zero magnitude in space around the circle and phantom, and a zero phase throughout. The height of the Gaussian kernel in the voxel-covariance structure was set to 1 with the kernel tapering to 0.1 everywhere within the circle and phantom, resulting in a profile of the covariance structure similar shape to that of the real data. The originally induced full FOV voxel covariance structure about the center voxel for the circle and Shepp-Logan phantom data sets are illustrated in Figs. 1a and 1b, respectively with green circles placed around the center voxel.

Figure 1.

Correlation about the center voxel a) used in generating the circle data set, b) used in generating the Shepp-Logan phantom data set, c-d) assumed by the SENSE model for full FOV image reconstruction, e) reduced FOV estimated voxel correlation from circle time series, f) reduced FOV estimated voxel correlation from Shepp-Logan phantom time series, g-h) reduced FOV identity correlation assumed by the SENSE model.

For each TR in the two image time series, a matrix of coil images, Y_t, where t varies from 1 to 490, was constructed by

$$Y_t=M+E_t,$$ (24)

where M is a 2N_C×p_xp_y matrix with the first N_C rows corresponding to the N_C real noiseless coil images, in vector form, and the second N_C rows corresponding to the imaginary noiseless coil images, which are initially zero. The noise matrix E_t is also of dimension 2N_C×p_xp_y and generated with matrix normal or Kronecker product covariance structure [13] by

$$E_t=P_{\mathrm{\Psi }}{z}_t{Q}_{\mathrm{\Upsilon }}$$

where P_Ψ is the first unitary matrix in the singular value decomposition (SVD) of

$$\mathrm{\Psi }=P_{\mathrm{\Psi }}{\mathrm{\sum }}_{\mathrm{\Psi }}{Q}_{\mathrm{\Psi }}^T,$$

Q is the second unitary matrix in the SVD of

$$\mathrm{\Upsilon }=P_{\mathrm{\Upsilon }}{\mathrm{\sum }}_{\mathrm{\Upsilon }}{Q}_{\mathrm{\Upsilon }}^T,$$

and z_t is a random matrix variable with elements drawn from the standard normal distribution. In this illustration, a circular covariance, similar to that estimated from the experimental data sets, was assumed between coils with

$${\mathrm{\Psi }}_R={\mathrm{\Psi }}_I={\psi }^2\left[\begin{array}{cccc}1& 0.24& 0.17& 0.24\\ 0.24& 1& 0.24& 0.17\\ 0.17& 0.24& 1& 0.24\\ 0.24& 0.17& 0.24& 1\end{array}\right],{\mathrm{\Psi }}_{RI}={\psi }^2\left[\begin{array}{cccc}-0.0091& -0.0042& 0.0004& -0.0042\\ -0.0042& -0.0091& -0.0042& 0.0004\\ 0.0004& -0.0042& -0.0091& -0.0042\\ -0.0042& 0.0004& -0.0042& -0.0091\end{array}\right]$$

and ${\mathrm{\Psi }}_{IR}={\mathrm{\Psi }}_{RI}^T$. A standard deviation of ψ=0.02was used for both the circle and Shepp-Logan phantom to further scale the coil covariance, Ψ, of each data set to more closely resemble the corresponding coil covariance matrices from the spherical phantom and human subject experimental data sets. For each of the 490 TRs, the matrix Y_t in Eq. (24) is thus comprised of N_C row vectors corresponding to the real simulated coil images stacked upon N_C row vectors of the imaginary simulated coil images.

To simulate sub-sampling, each of the rows in Y_t were reshaped into matrices, by stacking columns and transposing, and Fourier transformed into k-space, where lines were discarded in the PE direction for an acceleration factor A=3. A vector of sub-sampled spatial frequencies for each TR, f_t, as described in Eq. (1) was constructed by vectorizing the real and imaginary components of the spatial frequencies for each of the N_C=4 coils, and stacking them by the same means described in Eq. (4).

3.1 Estimated Coil Covariance and Voxel Covariance Structures

To replicate the procedure to be used in the experimental illustration, the coil and voxel covariances were estimated from both time series of images using the estimation procedure outlined in Appendix A. For each TR, the 2N_C×2N_C real-valued isomorphism representation of the complex coil-covariance matrix was evaluated from the observed aliased voxel values, a_t, by

$$cov(a_t)=cov(P_S{P}_C(I_{N_C}\otimes \mathrm{\Omega })f_t)=\mathrm{\sum }.$$

As assumed by the SENSE model, there is an identity covariance between voxels in the first iteration of the coil and voxel covariance estimation process, illustrated in Figs. 1c and 1d for a full FOV voxel covariance, and Figs. 1g and 1h for a reduced FOV voxel covariance about the center voxel, indicated by green circles, for the circle and Shepp-Logan phantom data sets respectively. Each voxel in the reduced FOV therefore shares the same coil covariance structure, allowing the estimated coil covariance matrix to be expressed as

$$\mathrm{\sum }=I_{rp}\otimes \mathrm{\Psi }.$$ (25)

If this first estimate of the coil covariance, Ψ̂, is partitioned into NC×NC real-valued quadrants as

$$\widehat{\mathrm{\Psi }}=\left[\begin{array}{cc}{\mathrm{\Psi }}_1& {\mathrm{\Psi }}_2\\ {\mathrm{\Psi }}_3& {\mathrm{\Psi }}_4\end{array}\right],$$ (26)

it will be of the form ${\mathrm{\Psi }}_3={\mathrm{\Psi }}_2^{\text{T}}$ and Ψ₁ ≈ Ψ₄, as this was the structure of the covariance assumed in generating the data. Assuming the imposed skew-symmetric coil covariance structure in the SENSE model, the estimated coil covariance in Eq. (25) would be reordered into

$$\widehat{\mathrm{\Psi }}=\left[\begin{array}{cc}{\mathrm{\Psi }}_1& -{\mathrm{\Psi }}_4\\ {\mathrm{\Psi }}_4& {\mathrm{\Psi }}_1\end{array}\right],$$ (27)

replacing Ψ₂ and Ψ₃ with −Ψ₄ and Ψ₄ respectively. This skew-symmetric reordering of the first coil covariance in Eq. (27) is thus used as Ψ_SE in the SENSE unfolding operation in Eq. (13). As the SENSE-ITIVE model makes use of the non-identity covariance between voxels, this initial estimation of the coil covariance in Eq. (26) cannot be used. The estimation process in Appendix A is carried out estimating the coil and voxel covariance matrices until convergence is attained. In this illustration, six iterations were performed, at which point both coil and voxel covariance structures did not differ much from one iteration to the next. If the coil covariance of the final iteration, Ψ̃, is again partitioned into N_C×N_C real-valued quadrants as

$$\stackrel{\sim }{\mathrm{\Psi }}=\left[\begin{array}{cc}{\stackrel{\sim }{\mathrm{\Psi }}}_1& {\stackrel{\sim }{\mathrm{\Psi }}}_2\\ {\stackrel{\sim }{\mathrm{\Psi }}}_3& {\stackrel{\sim }{\mathrm{\Psi }}}_4\end{array}\right],$$ (28)

it will again be of the form ${\stackrel{\sim }{\mathrm{\Psi }}}_2={\stackrel{\sim }{\mathrm{\Psi }}}_4^{\text{T}}$ and Ψ̃₁ ≈ Ψ̃₄. After the final iteration, the estimated voxel covariance structure, ϒ̃, is no longer identity, and the final estimation of the coil covariance in Eq. (27) is used as Ψ_SE in the SENSE-ITIVE unfolding operation in Eq. (16). The final estimations of the voxel correlation about the center voxel are illustrated in Figs. 1e and 1f for the reduced FOV circle and Shepp-Logan phantom data sets respectively.

3.2 Image Reconstruction and Statistical Analysis of Theoretically Generated Data

The 490 vectors of spatial frequencies, f_t, were then reconstructed with the SENSE and SENSE-ITIVE models using Eqs. (19) and (20) respectively. It was shown in [7] that the implementation of image smoothing amplifies the effects of the correlation induced between voxels by the SENSE image reconstruction operators. As such, the post-processing operations, O_I, in Eqs. (19) and (20) are a smoothing operation, S_m, which applies a Gaussian smoothing kernel with a FWHM of three voxels to the real and imaginary parts of each voxel in the reconstructed images. The SENSE and SENSE-ITIVE operators for reconstructing k-space data are thus

$$O_{SE/SI}=S_m{P}_U{U}_{SE/SI}{P}_S{P}_C\left(I_{N_C}\otimes \mathrm{\Omega }{O}_k\right).$$ (29)

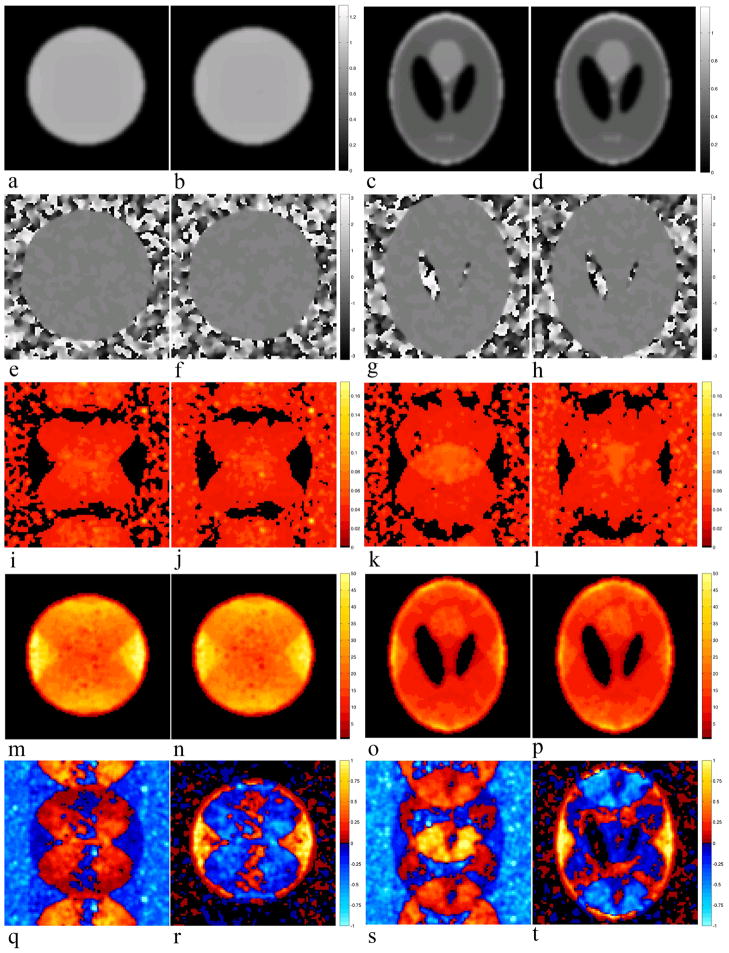
The magnitude and phase of the complex mean reconstructed images for the circle and Shepp-Logan phantom data sets are illustrated in Figs. 2a–2h for the SENSE and SENSE-ITIVE models. It can be seen for both the circle magnitude reconstructed images in Figs. 2a and 2b and the Shepp-Logan magnitude reconstructed images in Figs. 2c and 2d are very similar for the SENSE and SENSE-ITIVE models respectively, with differences only on the order of 10⁻². The mean phase images for the circle in Figs. 2e and 2f are also very similar for the two models, with only minor noticeable differences in empty space. Minor differences in the phase are also noted between the two models in the inner ovals of the Shepp-Logan phantom in Figs. 2g and 2h for SENSE and SENSE-ITIVE respectively where the magnitude is close to zero.

Figure 2.

a)SENSE (SE) circle mean magnitude, b) SENSE-ITIVE (SI) circle mean Magnitude, c)SE Shepp-Logan Phantom (SLP) mean magnitude, d) SI SLP mean Magnitude, e) SE circle mean Phase, f) SI circle mean phase, g) SE SLP mean Phase, h) SI SLP mean phase, i) SE circle standard deviation, j) SI circle standard deviation, k) SE SLP standard deviation, l) SI SLP standard deviation, m) SE circle SNR, and n) SI circle SNR images, o) SE SLP SNR, p) SI SLP SNR images, q) normalized difference SE-SI standard deviation of circle, r) normalized difference SE-SI SNR of circle, s) normalized difference SE-SI standard deviation of SLP, and t) normalized difference SE-SI SNR of SLP. Smoothing (Sm) was applied with a Gaussian kernel with a FWHM of 3 voxels.

The difference between the SENSE and SENSE-ITIVE models becomes more distinct when the standard deviation, and in turn signal-to-noise ratio (SNR) are examined. The standard deviations illustrated for the circle and Shepp-Logan phantom data sets are illustrated in Figs. 2i and 2k for the SENSE model and in Figs. 2j and 2l for the SENSE-ITIVE model. As the reconstructed data is complex-valued, the real and imaginary variances, ${\sigma }_R^2$, and ${\sigma }_I^2$, were estimated separately, averaged and converted to a standard deviation by taking the square root. To further illustrate the differences between the two models, the SENSE-ITIVE standard deviation in Figs. 2j and 2l were subtracted from the corresponding SENSE standard deviations in Figs. 2i and 2k. These difference images, presented in Figs. 2q and 2s for the circle and Shepp-Logan phantom respectively, were threshold to one tenth of the original standard deviation and normalized to being on a scale between −1 and 1.

Within these standard deviation difference images, there are three regions to consider. The first region is defined by the areas in space on the left and right of the circle and phantom in which the standard deviation of the SENSE-ITIVE model is greater than that of the SENSE model, as indicated by the lighter blue regions in Figs. 2q and 2s. The second region is on the left and right within the circle and phantom in which there was no previous aliasing, where the SENSE-ITIVE model again appears to have a slightly greater standard deviation to that of the SENSE model. The third region to consider is the remainder of the circle and phantom as well as the areas in space above and below the circle and phantom in which aliasing previously occurred. It is evident in these aliased regions that the SENSE model has a higher standard deviation to that of SENSE-ITIVE model. With SNR evaluated as (mean magnitude)/(standard deviation) in each voxel, the increased standard deviation in the SENSE model within the areas that were previously aliased results in a lower SNR in Figs. 2m and 2o by comparison to the SENSE-ITIVE model in Figs. 2n and 2p with a higher SNR. This difference is most evident in the blue regions of Figs. 2r and 2t where the SNR of the SENSE-ITIVE model was subtracted from the SNR of the SENSE model, threshold to one tenth the scale of the original SNR values, and normalized to being on a scale between −1 and 1. The difference in the SNR in space in Figs. 2r and 2t appears to be close to zero as the region outside the circle and phantom is close enough to zero in the magnitude of both models that the SNR becomes virtually zero in turn. In the un-aliased portion of the circle and phantom, the SENSE model appears to have an increased SNR to that of the SENSE-ITIVE model. The use of a miss-specified coil and voxel covariance structure assumed by the SENSE model therefore only appears to have a theoretical advantage over the SENSE-ITIVE model, in which the coil and voxel covariance structures are estimated from the data, in the areas in which there is no aliasing within the object.

Correlations are presented about the center voxel estimated over the time series, and compared to the operator-induced correlation about the center voxel using Eq. (21). To observe the correlation induced purely by the SENSE and SENSE-IVITE operators in Eq. (29), correlation induced between voxels is derived by

$$\text{corr}({\mathrm{\sum }}_{SE/SI})=D_O^{-1/2}(O_{SE/SI}{O^T}_{SE/SI})D_O^{-1/2},$$ (30)

where D_O=diag(O_SE/SIO^T_SE/SI)is a diagonal matrix of the variances from the diagonal of the covariance matrix Σ_SE/SI= O_SE/SIO^T_SE/SI and the −1/2 superscript denotes that the diagonal elements are square rooted and inverted. The real-valued isomorphism correlation matrix produced by Eq. (30) can be partitioned into quadrants as

$$\text{corr}({\mathrm{\sum }}_{SE/SI})=\left[\begin{array}{cc}RR& RI\\ IR& II\end{array}\right],$$

where any row, j, of each quadrant denotes the correlation between voxel j and all other voxels in the reconstructed image for the respective complex denomination. The correlation about voxel j can be generated by dividing the j^th row of corr(Σ_SE/SI) into p_x vectors of 1×p_y, each of which denoting a column of the reconstructed image, stacking the row vectors into a matrix, and finally transposing. Given that magnitude-only data has become the gold standard in image analysis, a magnitude-squared analysis is undertaken in this study as it can be shown that the correlation between magnitude-squared data is asymptotically equivalent to the correlation between magnitude data [6]. Although the correlation can be observed about any voxel in the full FOV images, the correlations observed in this study will all be about the center voxel for consistency. A small green circle is placed about the center voxel of the three folds, corresponding to the choice of acceleration factor A=3, to draw the readers eye to correlations above a threshold of 0.15 between the center voxel and the corresponding voxels previously aliased with the center voxel in the center of the upper and lower folds.

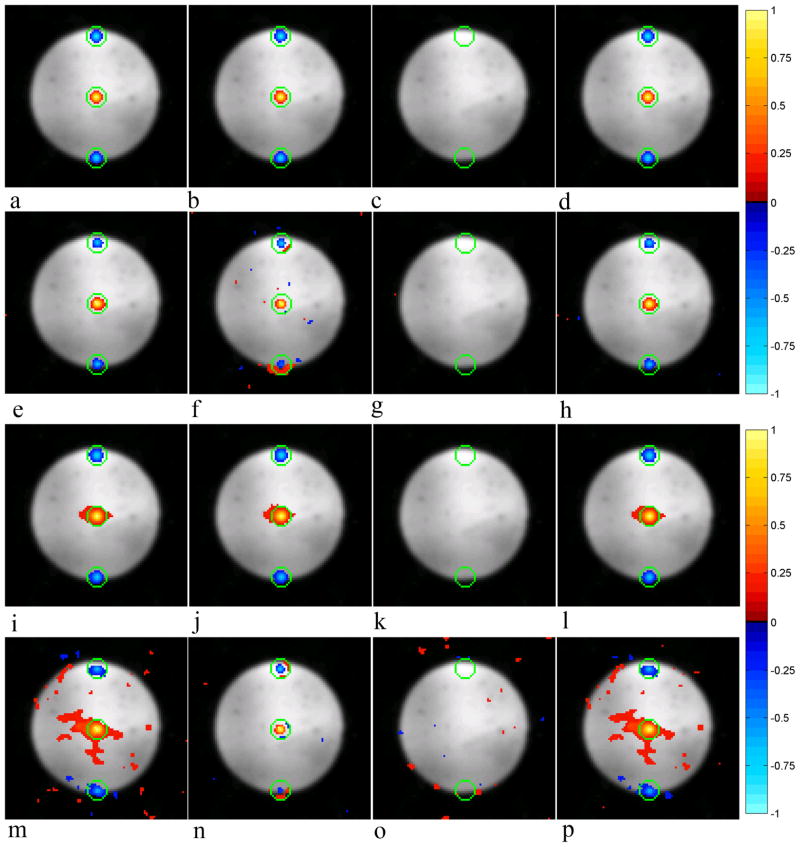
The real, imaginary, real/imaginary, and magnitude-squared operator induced correlations about the center voxel, derived using Eq. (30), along with the correlations about the center voxel estimated from the reconstructed time series of the circle data set are presented in Fig. 3 for both the SENSE and SENSE-ITIVE models. As illustrated in [7], the application of image smoothing results in clusters of voxels correlated with one another, rather than individual voxels. It can be seen in the real, imaginary and magnitude-squared operator induced correlations for the SENSE model in Figs. 3a, 3b, and 3d as well as the corresponding correlations for the SENSE-ITIVE model in Figs. 3i, 3j and 3l that the center voxel shows a positive correlation with a circular cluster of voxels in the center of the image as well as a negative correlation with a cluster of voxels in the center of the upper and lower folds. While the sign of these correlations is the same for both models, it is of note that the SENSE-ITIVE model, which makes use of a more mathematically accurate coil covariance structure as well as an estimated non-identity voxel covariance structure, induces slightly larger clusters of voxels in the center of the upper, lower, and center folds. The operator induced correlations between the real and imaginary components (real/imaginary) are presented in Figs. 3c and 3k for the SENSE and SENSE-ITIVE models respectively. It can be seen that the center voxel has a very low correlation with a small cluster of voxels in the upper fold for both models, and it is of note that there is no correlation induced in the center voxel itself by either model. The correlation between the imaginary and real is not presented in this manuscript as it is simply the transpose of the correlation between the real and imaginary.

Figure 3.

A comparison between a) SENSE (SE) real, b) SE imaginary, c) SE real/imaginary, d) SE magnitude-squared operator induced correlation about the center voxel, and e) SE real, f) SE imaginary, g) SE real/imaginary, h) SE magnitude-squared estimated correlation about the center voxel over the time series of the circle with, i) SENSE-ITIVE (SI) real, j) SI imaginary, k) SI real/imaginary, and l) SI magnitude-squared operator induced correlation about the center voxel and m) SI real, n) SI imaginary, o) SI real/imaginary, and p) SI magnitude-squared estimated correlation about the center voxel over the time series of the circle. Correlations presented with a threshold of 0.15 for operators with an identity estimated voxel covariance structure assumed. Smoothing was applied with a Gaussian kernel with a FWHM of 3 voxels.

Although the size of the clusters of voxels in the middle region of the upper, lower and center folds correlated with the center voxel estimated over the time series in Figs. 3e–3h for the SENSE model and Figs. 3m–3p for the SENSE-ITIVE model vary in size and shape, it is important to note that there are clearly clusters of correlated voxels with the sign and position as the clusters of correlated voxels induced by the operators. The cluster of correlated voxels in the center of the FOV is larger for the SENSE model in the real, imaginary, and magnitude-squared correlations in Figs. 3e, 3f, and 3h than that of the SENSE-ITIVE model in Figs. 3m, 3n, and 3p, contrary to the behavior in the corresponding operator induced correlations. Despite the increased size of the operator induced correlations of the SENSE-ITIVE model in Figs. 3i, 3j, and 3l, it would appear that neglecting to incorporate a more accurate voxel covariance structure in the SENSE model results in an increased spread of correlations estimated over the time series in Figs. 3e–3h to that of the SENSE-ITIVE model in Figs. 3m–3p. In the real/imaginary correlations estimated for the SENSE model in Fig. 3g, the correlations in all three folds appear to be larger than those in the SENSE-ITIVE model in Fig. 3o. It is important to note that in all correlations estimated about the center voxel throughout the time series, it is the weaker correlations that vary in shape between models, while the size of the clusters of stronger correlation in the center of each fold more closely resemble the clusters of correlated voxels induced by the respective reconstruction operators of both models.

The real, imaginary, real/imaginary, and magnitude-squared operator induced correlations about the center voxel, derived using Eq. (30), along with the correlations about the center voxel estimated throughout the reconstructed time series of the Shepp-Logan phantom data set are presented in Fig. 4 for both the SENSE and SENSE-ITIVE models. The general behavior of the real, imaginary, and magnitude-squared operator induced voxels correlated with the center voxel as a result of the SENSE model in Figs. 4a, 4b, and 4d and the SENSE-ITIVE model in Figs. 4i, 4j, and 4l are not unlike the corresponding operator induced correlations of the circle data set, presented in Fig. 3. A significant difference, however, is noted between the correlations observed throughout the circle and Shepp-Logan phantom time series. In the real, imaginary, and magnitude-squared correlations estimated about the center voxel, one can see an oval shaped cluster of correlated voxels in the center of each fold for the SENSE model in Figs. 4e, 4f, and 4h, while the estimated SENSE-ITIVE correlations in Figs. 4m, 4n, and 4p are smaller and more circular in shape. The shape of the correlations observed in the SENSE model are consistent with the shape of the region in the center of the previously reduced FOV coil images where there is the most overlap of the phantom as well as the center of the reduced FOV voxel covariance structure estimated for the Shepp-Logan phantom data set in Fig. 1f. As the Shepp-Logan phantom occupies more of a full FOV image than the circle, there will be a considerably larger overlap of high signal within the aliased images for the Shepp-Logan phantom than in the aliased images for the circle. With a larger overlap in the aliased images, it is therefore to be expected that there will be a larger correlation in the previously aliased regions of the reconstructed images. As the size of these correlations is reduced in the SENSE-ITIVE model in Figs. 4m, 4n, and 4p, where the non-identity voxel covariance in Fig. 1f is incorporated into the reconstruction, it is evident that the miss-specified voxel covariance structure in the SENSE model does not appropriately account for this overlap of aliased voxel values, resulting in an increased spread of correlation throughout the reconstructed images. In the magnitude squared correlations in Figs. 4h and 4p, both models show a zero correlation within the inner ovals where the magnitude, and in turn SNR, are both zero.

Figure 4.

A comparison between a) SENSE (SE) real, b) SE imaginary, c) SE real/imaginary, d) SE magnitude-squared operator induced correlation about the center voxel, and e) SE real, f) SE imaginary, g) SE real/imaginary, h) SE magnitude-squared estimated correlation about the center voxel over the time series of the Shepp-Logan Phantom with, i) SENSE-ITIVE (SI) real, j) SI imaginary, k) SI real/imaginary, and l) SI magnitude-squared operator induced correlation about the center voxel and m) SI real, n) SI imaginary, o) SI real/imaginary, and p) SI magnitude-squared estimated correlation about the center voxel over the time series of the Shepp-Logan Phantom. Correlations presented with a threshold of 0.15 for operators with an identity estimated voxel covariance structure assumed. Smoothing was applied with a Gaussian kernel with a FWHM of 3 voxels.

While all of the clusters in the real, imaginary, real/imaginary, and magnitude-squared estimated time series correlations for both the circle and Shepp-Logan phantom data sets reconstructed by the SENSE and SENSE-ITIVE models appear to change in shape and size, it is of note that the areas of strongest correlation are still in the center of each fold. While the correlations in this study are presented for acceleration factors of A=3, it is therefore to be expected that these correlations would be even stronger and more spread out throughout the image if a higher reduction factor were used. As stated in [7], this could have serious functional connectivity implications should one draw conclusions as to where these correlations stem from without a prior understanding of the correlations induced by image reconstruction operators such as SENSE and SENSE-ITIVE.

4. Experimental Application and Analysis

To further illustrate the difference between the SENSE and SENSE-ITIVE models, two sets of data were acquired from an array of 8 receiver coils with a 3.0 T General Electric Signa LX magnetic resonance imager. The first set of data was of a spherical agar phantom, while the second set was a series of non-task images of a human subject. Both data sets were comprised of nine 2.5 mm thick axial slices that are 96×96 in dimension for a 24 cm FOV, with the phase encoding direction oriented as anterior to posterior (bottom-top in images). In functional connectivity MRI, images are acquired over time and statements are made about the correlations between voxels or regions. The methodology described here is applicable to matrix sizes larger than the 96×96 one illustrated here. However, it is rare to have matrix sizes larger than 96×96 in fMRI. Acquired for a series of 510 TRs, the data sets had a repetition time(TR) of 1 s, an echo time(TE) of 42.8 ms, an effective echo spacing of 768 ms, a flip angle of 45°, and an acquisition bandwidth of 125 kHz. The first 20 TRs were discarded to account for T₁ effects and because the echo time had been varied (in the human data), resulting in 490 TRs that were all acquired under the same conditions. All of the remaining 490 images from coils 1, 3, 5, and 7 were used in estimating both the sensitivity maps and the coil and voxel covariances, from N_C=4 equally spaced coils, to be used in image reconstruction. Sub-sampling was simulated for an acceleration factor of A=3 by deleting lines of k-space in each of the fully acquired coil images in the PE direction.

Both the spherical phantom data and the human subject data were acquired with a custom Echo Planar Imaging (EPI) pulse sequence and reconstructed using locally developed image reconstruction software. The centerline of k-space for each receiver coil was acquired with three navigator echoes in order to estimate the error in the center frequency and group delay offsets between the odd and even k-space lines [6]. As EPI techniques are susceptible to dynamic fluctuations in the homogeneities of the main magnetic field from factors such as respiration and out of field motion, the global, temporal phase structure was corrected in both data sets after unfolding to account for field shifts associated with gradient heating and radio frequency phase variation [9]. Additionally, to account for drift in the gradients, a plane was fit to and subtracted from the phase of each image for each coil in the time series using the technique outlined in [14]. This procedure effectively eliminates the ripple effect, noted in the human subject phase in Fig. 10 of [7], from the correlation images in Fig. 11 of [7].

Traditionally, the raw coil sensitivity maps would be derived by normalizing the surface coil sensitivities in each voxel by the corresponding body coil sensitivities [11]. As a body coil was not utilized for either of the scans, the raw coil sensitivity maps were thus normalized by dividing the coil sensitivities by an average of the coil sensitivities in each voxel. Alternatively, a square root of the sum of squares of the coil sensitivities in each voxel could be used [11, 12]. However, little difference was observed between the root sum of squares sensitivity map and the simple complex average, and thus the simple complex average sensitivity maps were used in this study as they provide both magnitude and phase images, when the root sum of squares sensitivities do not have a phase. Magnitude and phase images are necessary to utilize all of the data in a complex-valued time series model [15, 16].

4.1 Phantom Data

To bridge the gap between the theoretical illustration in Section 3 and the application to the human subject data to follow, a spherical agar phantom was scanned. Unlike a human subject, the phantom is not prone to respiratory movement or physiological effects, and thus provides a good baseline for experimental observations. Coil sensitivity maps were estimated using a simple complex average over the time series of spherical phantom coil images, while coil covariances and voxel covariances were estimated from the time series using the estimation process outlined in Appendix A. An analysis is performed on the statistical properties of reconstructed images both with a skew-symmetric coil covariance combined with an identity voxel covariance, as assumed by the SENSE model, and then with a coil and voxel covariance estimated directly from the data, consistent with the SENSE-ITIVE model. Voxel means and variances are observed through reconstructed magnitude, phase, standard deviation, and SNR images. The correlation between voxels throughout the time series are estimated and illustrated about the center voxel. These correlations are compared to the operator induced correlations from the respective models using the estimated sensitivity maps, coil covariance structure, and voxel covariance structure, presented on a magnitude image for the respective model.

4.1.1 Estimated Coil Covariance and Voxel Covariance Structures

The coil and voxel covariance structures to be used in the reconstruction of the spherical phantom data set were estimated via the estimation procedure outlined in Appendix A. Provided with an identity covariance between voxels in the first iteration, the initial estimation of the coil covariance structure is denoted Ψ̂. To gain a better understanding of the covariance structure between coils, an average covariance was formed by partitioning Ψ̂ into N_C×N_C real-valued quadrants as in Eq. (26), and taking the mean of the diagonals of each quadrant. As an array of 4 coils was used, the main diagonal of the coil covariance represents the coil of interest, the second and fourth supra and sub diagonals correspond to the neighboring coils, and the third supra and sub diagonals correspond to the opposite coil. This averaged covariance structure was then transformed into the correlation matrix in Table 1 by

Table 1.

Averaged coil correlation estimated from data assuming an Identity voxel covariance

1	0.3405	0.2438	0.3405	−0.0239	−0.0134	−0.0037	−0.0134
0.3405	1	0.3405	0.2438	−0.0134	−0.0239	−0.0134	−0.0037
0.2438	0.3405	1	0.3405	−0.0037	−0.0134	−0.0239	−0.0134
0.3405	0.2438	0.3405	1	−0.0134	−0.0037	−0.0134	−0.0239
−0.0239	−0.0134	−0.0037	−0.0134	1	0.5198	0.2248	0.5198
−0.0134	−0.0239	−0.0134	−0.0037	0.5198	1	0.5198	0.2248
−0.0037	−0.0134	−0.0239	−0.0134	0.2248	0.5198	1	0.5198
−0.0134	−0.0037	−0.0134	−0.0239	0.5198	0.2248	0.5198	1

$$\text{corr}(\mathrm{\Psi })={D_{\mathrm{\Psi }}}^{-1/2}\mathrm{\Psi }{D_{\mathrm{\Psi }}}^{-1/2},$$

where D_Ψ is a diagonal matrix of the variances from the diagonals of Ψ̂, and the superscript −1/2 denotes the reciprocal of the square root of D_Ψ.

When comparing the different quadrants of the correlation structure in Table 1, it can be seen that Ψ₃ = Ψ₂^T and Ψ₁ ≈ Ψ₄, just as in the SENSE-ITIVE model introduced in Eq. (15) of this manuscript, where Ψ_RI=Ψ_IR^T and Ψ_R = Ψ_I. Upon closer inspection of the real and imaginary components of the coil correlation in Table 1, one can see that the correlation between the coils along the main diagonals and their neighbors follow a circular structure (as was used in the theoretical illustration). To accommodate the skew-symmetric coil covariance structure estimated with an identity voxel covariance in the SENSE model, the coil correlation in Table 1 was reordered into the skew-symmetric coil covariance structure in Eq. (27), as presented in Table 2, and then used in the SENSE unfolding operation in Eq. (13).

Table 2.

Skew-symmetric re-organization of coil correlation in Table 1, as assumed by the SENSE model

1	0.3405	0.2438	0.3405	−1	−0.5198	−0.2248	−0.5198
0.3405	1	0.3405	0.2438	−0.5198	−1	−0.5198	−0.2248
0.2438	0.3405	1	0.3405	−0.2248	−0.5198	−1	−0.5198
0.3405	0.2438	0.3405	1	−0.5198	−0.2248	−0.5198	−1
1	0.5198	0.2248	0.5198	1	0.3405	0.2438	0.3405
0.5198	1	0.5198	0.2248	0.3405	1	0.3405	0.2438
0.2248	0.5198	1	0.5198	0.2438	0.3405	1	0.3405
0.5198	0.2248	0.5198	1	0.3405	0.2438	0.3405	1

The estimation process in Appendix A was carried out for 6 iterations, estimating the coil and voxel covariance structures to be used in the SENSE-ITIVE model until both Ψ̃ and ϒ̃ did not vary much from one iteration to the next. The final estimation of the coil correlation, Ψ̃, is listed in Table 3. Again, if the correlation in Table 3 were divided into quadrants such as in Eq. (28), one can see that ${\stackrel{\sim }{\mathrm{\Psi }}}_2={\stackrel{\sim }{\mathrm{\Psi }}}_3^{\text{T}}$ and Ψ̃₁ ≈ Ψ̃₄ as assumed by the SENSE-ITIVE model in Eq. (15), and used in the SENSE-ITIVE unfolding operation in Eq. (16).

Table 3.

Averaged coil correlation estimated from data assuming a non-Identity voxel covariance

1	0.2995	0.186	0.2995	−0.0047	0.0037	0.0128	0.0037
0.2995	1	0.2995	0.186	0.0037	−0.0047	0.0037	0.0128
0.186	0.2995	1	0.2995	0.0128	0.0037	−0.0047	0.0037
0.2995	0.186	0.2995	1	0.0037	0.0128	0.0037	−0.0047
−0.0047	0.0037	0.0128	0.0037	1	0.5717	0.358	0.5717
0.0037	−0.0047	0.0037	0.0128	0.5717	1	0.5717	0.358
0.0128	0.0037	−0.0047	0.0037	0.358	0.5717	1	0.5717
0.0037	0.0128	0.0037	−0.0047	0.5717	0.358	0.5717	1

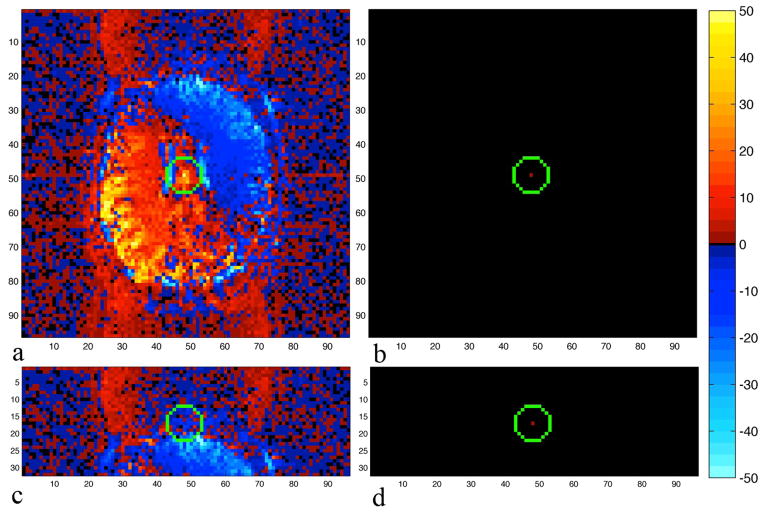
To observe the covariance structure estimated over the time series between voxels, the row of the estimated voxel covariance, ϒ̃, corresponding to the voxel of interest is reshaped into a matrix, by unstacking rows. The covariance about the center voxel for acceleration factors A=1 and A=3 are illustrated for the estimated non-identity voxel covariance in Figs. 5a and 5c, and for an identity voxel covariance in Figs. 5b and 5d, where the center voxel in each image in Fig. 5 is indicated with a green circle. The apparent aliasing noted in Fig. 5a is a result of Nyquist ghosting that has not been completely removed. It is clearly evident that the assumption made in the SENSE model that there is an identity covariance between voxels in Fig. 5b and 5d is unlike that estimated from the experimental time series in Figs. 5a and 5c. In reconstructing the time series of aliased coil images, the reduced FOV identity voxel covariance in Fig. 5d is thus used in the SENSE model, while the estimated reduced FOV voxel covariance in Fig. 5c is used in the SENSE-ITIVE model.

Figure 5.

Spherical phantom voxel correlation estimated about center voxel for a) full FOV and c) reduced FOV with an acceleration factor of A=3. By contrast, the identity voxel correlation about the center voxel assumed by the SENSE model for b) full FOV and d) reduced FOV with an acceleration factor of A=3.

4.1.2 Image Reconstruction and Statistical Analysis of Spherical Phantom Data

As noted in [7], the incorporation of image smoothing, as is common practice in fMRI, amplifies the correlations and effects of the image reconstruction operators. As such, a Gaussian smoothing kernel with a FWHM of three voxels was applied to each of the reconstructed images in the time series for both models. Once the time series was reconstructed, the mean, standard deviation, SNR, and correlation were evaluated in each voxel.

The magnitude and phase of the mean complex-valued images over the 490 images of the time series reconstructed by the SENSE model are presented in Figs. 6a and 6c, and in Figs. 6b and 6d for the SENSE-ITIVE. While both the magnitude and phase images appear very similar in nature, there are very minor differences between the two models in empty space and in the regions above and below the phantom in the phase images in Figs. 6c and 6d. These regions are present as a result of a combination of aliasing and Nyquist ghosting that has not been completely removed, leading to minor differences in these regions between the two models.

Figure 6.

a)SENSE (SE) mean magnitude, b) SENSE-ITIVE (SI) mean magnitude, c) SE mean phase, d) SI mean phase, e) SE standard deviation, f) SI standard deviation, g) SE SNR, h) SI SNR, i) normalized difference SE-SI standard deviation, and j) normalized difference SE-SI SNR images from real phantom data. Smoothing (Sm) was applied with a Gaussian kernel with a FWHM of 3 voxels.

Observing the standard deviation within each voxel over the time series in Figs. 6e and 6f for the SENSE and SENSE-ITIVE models respectively, one can see that there is a lower standard deviation both in the area surrounding the phantom and within the phantom itself for the SENSE model than that of the SENSE-ITIVE model. This is most apparent in Fig. 6i, where the standard deviation of the SENSE-ITIVE model in Fig. 6f is subtracted from the standard deviation of the SENSE model in Fig. 6e, threshold to one-tenth the standard deviation in Figs. 6e and 6f, and normalized to being on a scale from −1 to 1. In Fig. 6i, it is evident that the SENSE model only exhibits a higher standard deviation in areas where aliasing once occurred above, below, and within the phantom itself. In both models, the areas of lowest standard deviation are within the centers of the upper and lower folds where aliasing occurred and in the sides of the phantom in the center fold where no aliasing occurred. As SNR is evaluated as (mean magnitude)/(standard deviation) in each voxel, the lower standard deviation in the SENSE model gives rise to a higher SNR in these regions, as presented in Fig. 6g, and a slightly increased SNR within the phantom itself to that of the SENSE-ITIVE model in Fig. 6h. This is most evident in the yellow regions of Fig. 6j, where of the SNR of the SENSE-ITIVE model in Fig. 6h is subtracted from the SNR of the SENSE model in Fig. 6g, threshold to one-tenth the SNR in Figs. 6g and 6h, and normalized to being on a scale from −1 to 1. Seeing as the SENSE model does not appropriately represent the covariance between either voxels or coils, the residual effects of aliasing may be miss-represented, leading to a seemingly artificial increase in SNR, as it is within these aliased regions in the phantom that the difference between the SNR of the SENSE and SENSE-ITIVE models appears to be the greatest. As this artificial increase in SNR noted in the SENSE model is observed in the three areas in which the most overlap occurred in the aliased images, should an acceleration factor higher than A=3 be used, one would expect the SNR to be over-estimated even more if the covariance structure between voxels is not appropriately accounted for.

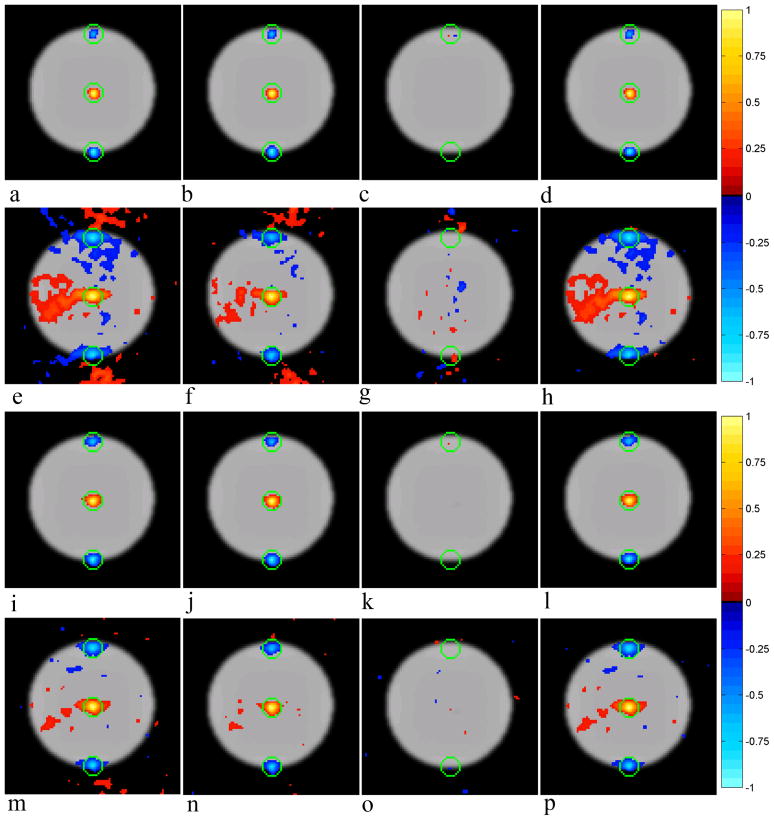
The theoretical correlations induced about the center voxel from Eqs. 19 and 20 for the spherical phantom purely by the SENSE and SENSE-ITIVE reconstruction operators, derived by Eq. (30), are presented in Figs. 7a–7d and 7i–7l respectively, while the correlations estimated throughout the time series of reconstructed images are presented about the center voxel in Figs. 7e–7h for the SENSE model and in Figs. 7m–7p for the SENSE-ITIVE model. All correlation images are presented with a threshold of 0.15, and superimposed on top of a magnitude underlay for the respective models. In all images of Fig. 7, green circles have been placed about the center voxel of the upper, lower, and middle folds to remind the reader of the previously aliased voxels in the center of the three folds. The real, imaginary, and magnitude-squared operator induced correlations about the center voxel for the SENSE model in Figs. 7a, 7b, and 7d closely resemble those in the theoretical illustration in Figs. 3a, 3b, and 3d while the SENSE-ITIVE correlations in Figs. 7i, 7j, and 7l appear to be slightly larger in the center voxel and are no longer confined to a small circular cluster in the center of each fold as they were in the theoretical illustration in Figs. 3i, 3j, and 3l. Both the SENSE and SENSE-ITIVE operator induced real/imaginary correlations about the center voxel in Figs. 7c and 7k have noabove threshold correlated clusters of voxels in the center of the upper, lower or center folds. It is of note that the shape of the clusters of operator induced correlated voxels in the SENSE-ITIVE model are larger than those of their theoretical counterparts in Fig. 3. The fact that these clusters are larger for the SENSE-ITIVE model than that of the SENSE model is consistent with what was observed in the theoretical illustration, and would suggest that the inclusion of a more accurate voxel covariance structure will more accurately represent the correlation structure inherent in the data.

Figure 7.

A comparison between a) SENSE (SE) real, b) SE imaginary, c) SE real/imaginary, d) SE magnitude-squared operator induced correlation about the center voxel, and e) SE real, f) SE imaginary, g) SE real/imaginary, h) SE magnitude-squared estimated correlation about the center voxel over the time series of the Spherical Phantom with, i) SENSE-ITIVE (SI) real, j) SI imaginary, k) SI real/imaginary, and l) SI magnitude-squared operator induced correlation about the center voxel and m) SI real, n) SI imaginary, o) SI real/imaginary, and p) SI magnitude-squared estimated correlation about the center voxel over the time series of the Spherical Phantom. Correlations presented with a threshold of 0.15 for operators with an identity estimated voxel covariance structure assumed. Smoothing was applied with a Gaussian kernel with a FWHM of 3 voxels.

Without the physiologic effects and the issues that arise with movement in human subject data sets, the correlations estimated throughout the time series for the spherical phantom data set provide an excellent means of observing the degree to which operator induced correlations affect the overall correlation structure of the data. The real, imaginary, real/imaginary and magnitude squared correlations estimated about the center voxel throughout the time series for the SENSE model presented in Figs. 7e–7h appear remarkably similar to the corresponding operator induced correlations of the SENSE model in Figs. 7a– 7d. It is interesting to note that while the real and magnitude squared correlations estimated over the theoretical time series reconstructed by the SENSE model in Figs. 3e and 3h exhibited slightly larger clusters of induced correlations about the center voxel than the corresponding SENSE-ITIVE correlations in Figs. 3m and 3o, the correlations estimated throughout the time series of spherical phantom images reconstructed by the SENSE-ITIVE model in Figs. 7m and 7p display a larger positive correlation in the center of the image to the SENSE model in Figs. 7e and 7h. Upon observation of the full FOV voxel covariance structure in Fig. 5a, it is apparent that there is Nyquist ghosting that has not been entirely removed from the spherical phantom data set. While the Nyquist ghost above and below the phantom is not a part of the phantom itself, there is clearly a non-zero signal in these regions. This will have the same effect as for a larger object in terms of the amount of overlapping signal in the aliased images, and consequently a larger correlation structure becomes evident in the SENSE-ITIVE reconstructed time series in Figs. 7m and 7p as a more accurate voxel covariance structure is used. While the imaginary estimated correlation for the SENSE model in Fig. 3f also showed a larger correlation in the center of the image, the imaginary correlation in Fig. 7f estimated about the center voxel for the spherical phantom shows a small circular cluster of positively correlated voxels instead. Unlike the real/imaginary correlation estimated in the SENSE reconstructed images in Fig. 7g, the estimated real/imaginary correlation in the SENSE-ITIVE reconstructed images show a minor scattering of non-zero correlations throughout the image in Fig. 7o.

The fact that the correlations estimated throughout the time series exhibit a structure very similar to the operator induced correlations in both the SENSE and SENSE-ITIVE models indicates that the correlations estimated over the time series could prove very misleading in functional connectivity studies. For magnitude squared correlations in particular, which are asymptotically equivalent to the gold standard magnitude used in most studies today [6], if one did not account for operator induced correlations, one could easily, and mistakenly, assume that there is a strong positive correlation between the center, anterior, and posterior regions of the phantom. Using the SENSE model, with a miss-specified coil and voxel covariance structure, the correlation estimated throughout the time series is not as accurately represented as it is in the SENSE-ITIVE model, in which the covariance between coils and voxels is estimated from the data set and used in the reconstruction process.

As the acceleration factor of A=3 was selected for this study, there are three clusters of voxels correlated with the center voxel. Should one for instance increase the number of coils to N_C=8 and the acceleration factor to A=6, the number of folds would double from that of this study, and thus the number of operator induced clusters of voxels correlated with the center voxel would increase to 6 in turn. (This result can be generalized to a larger number of coils and a larger acceleration factor and thus a larger number of clusters of voxels.) These correlations could have even more serious functional connectivity implications as they would make one easily conclude that the center voxel is correlated with a cluster of voxels in the center of each of the 6 folds, when in fact they are merely a byproduct of the voxel mapping scheme used in the SENSE and SENSE-ITIVE models.

4.2 Human Subject Data

Unlike a static spherical phantom, data acquired for a human subject is prone to respiratory movement and physiological effects. Coil sensitivity maps, coil covariances and voxel covariances were estimated from the time series of human subject images by the same means to that of the phantom data set. The SENSE model again assumes a skew-symmetric coil covariance structure and an identity covariance between voxels and therefore made use of the re-arranged coil covariance structure in Eq. (27), estimated from the first iteration of the estimation process in Appendix A. The coil and voxel covariance structures of the SENSE-ITIVE model were estimated by allowing the estimation to run for six iterations, at which point neither covariance structure varied much from one iteration to the next.

4.2.1 Image Reconstruction and Statistical Analysis of Human Subject Data

As with the theoretical illustration and phantom data sets, a Gaussian smoothing kernel with a FWHM of three voxels was applied to each of the reconstructed images in the time series for both models. Provided with estimates of the coil and voxel covariance structures for both models from the human subject data, each of the 490 images in the time series were reconstructed by the respective models, after which an analysis was performed on the means, standard deviation, SNR, and correlation in each voxel over the time series. The estimated voxel correlation about the center voxel, indicated by a green circle, for a full FOV reconstruction of the human subject data set is presented in Fig. 8a with the identity voxel covariance about the center voxel for a full FOV assumed by the SENSE model in Fig. 8b. The apparent aliasing noted above and below the brain in Fig. 8a is a result of Nyquist ghosting that has not been completely removed. The corresponding reduced FOV voxel correlations about the center voxel are presented in Figs. 8c and 8d for the SENSE-ITIVE and SENSE models, respectively. As with the spherical phantom illustration, it is evident that the correlation about the center voxel is not identity, as assumed by the SENSE model. In reconstructing the time series of aliased coil images for the human subject, the reduced FOV identity voxel covariance in Fig. 8d is therefore used in the SENSE model, while the estimated reduced FOV voxel covariance in Fig. 8c is used in the SENSE-ITIVE model.

Figure 8.

Human subject voxel correlation estimated about center voxel for a) full FOV and c) reduced FOV with an acceleration factor of A=3. By contrast, the identity voxel correlation about the center voxel assumed by the SENSE model for b) full FOV and d) reduced FOV with an acceleration factor of A=3.

The magnitude and phase of the mean complex-valued images over the 490 images of the time series of human subject data reconstructed by the SENSE model are presented in Figs. 9a and 9c, and in Figs. 9b and 9d for the SENSE-ITIVE As in the spherical phantom data set, it is difficult to distinguish the difference between the mean magnitude and phase of each model, despite numerical differences. The mean phase images for the SENSE and SENSE-ITIVE models in Figs. 9c and 9d only exhibit minor differences between the two models in the space surrounding the brain, particularly in the regions above and below the brain where both aliasing and Nyquist ghosting previously occurred.

Figure 9.

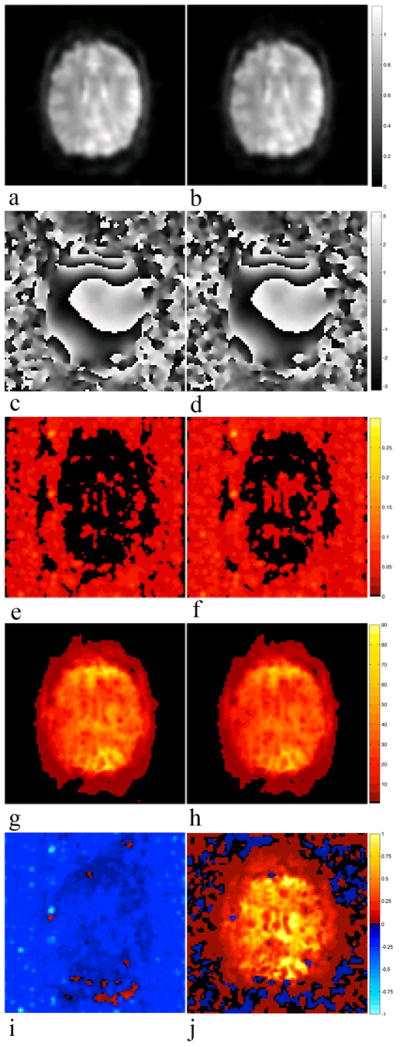
a)SENSE (SE) mean magnitude, b) SENSE-ITIVE (SI) mean magnitude, c) SE mean phase, d) SI mean phase, e) SE standard deviation, f) SI standard deviation, g) SE SNR, h) SI SNR, i) normalized difference SE-SI standard deviation, and j) normalized difference SE-SI SNR images from human subject data set. Smoothing (Sm) was applied with a Gaussian kernel with a FWHM of 3 voxels.

Similar to the spherical phantom illustration, the standard deviation of the SENSE model in Fig. 9e appears to be slightly lower in space and within the brain to that of the SENSE-ITIVE model in Fig. 9f. This is most apparent in Fig. 9i, where the standard deviation of the SENSE-ITIVE model in Fig. 9f is subtracted from the standard deviation of the SENSE model in Fig. 9e, threshold to one-tenth the standard deviation in Figs. 9e and 9f, and normalized to being on a scale from −1 to 1. It is evident in Fig. 9i that the only regions in which the standard deviation of the SENSE model is greatest is in the lower portion of the brain, as well as in the aliased regions above and below the brain. As such, the SNR, defined to be (mean magnitude)/(standard deviation) in each voxel, is greater throughout the brain for the SENSE model in Fig. 9g than that of the SENSE-ITIVE model in Fig. 9h. This is most evident in yellow regions within the brain of Fig. 9j, where of the SNR of the SENSE-ITIVE model in Fig. 9h is subtracted from the SNR of the SENSE model in Fig. 9g, threshold to one-tenth the SNR in Figs. 9g and 9h, and normalized to being on a scale from −1 to 1.

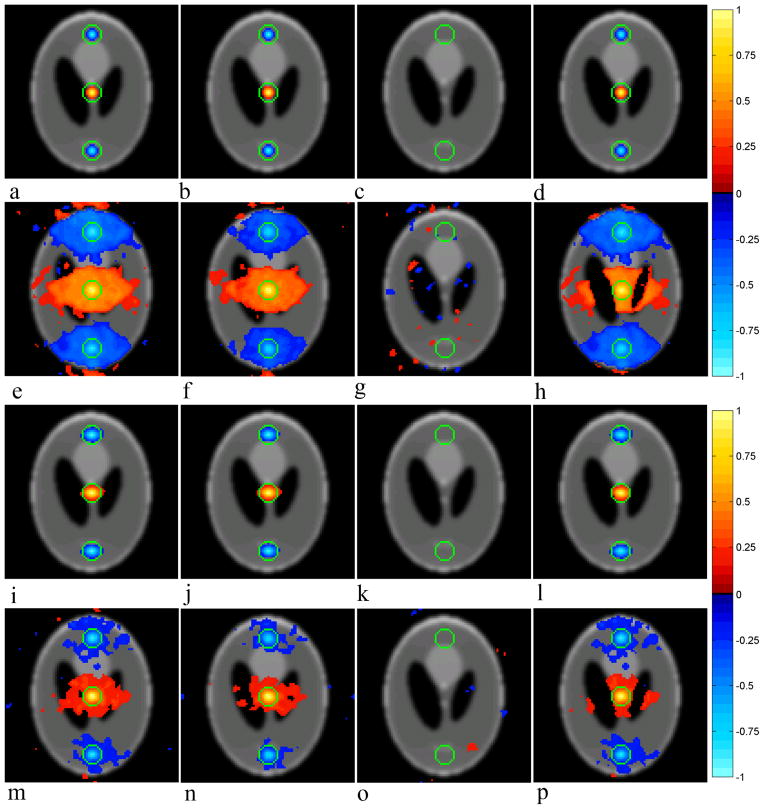
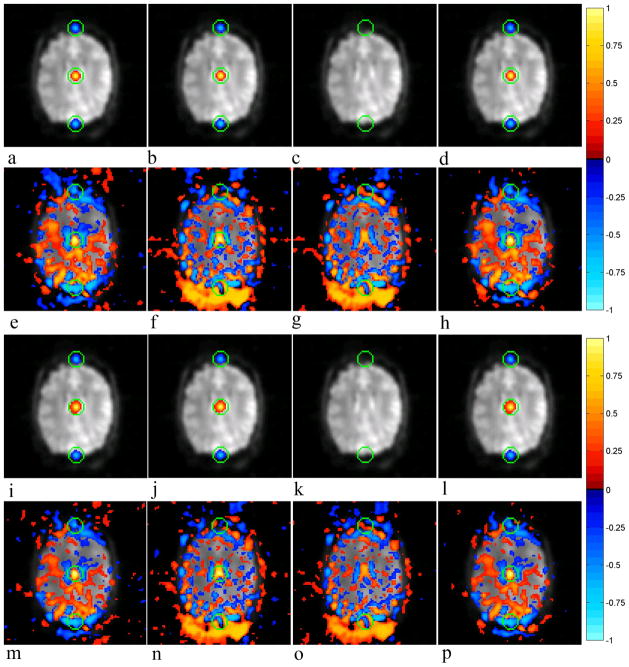
The theoretical correlations induced about the center voxel for the human subject purely by the SENSE and SENSE-ITIVE reconstruction operators are presented in Figs. 10a–10d and 10i–10l respectively, while the correlations estimated throughout the time series of reconstructed images are presented about the center voxel in Figs. 10e–10h for the SENSE model and in Figs. 10m–10p for the SENSE-ITIVE model. It is of note that the estimated correlations of the time series reconstructed with the SENSE model in Figs. 10e–10h are effectively the same as the estimated correlation images in Figs. 11 in [7], in which the ripple effect was noted due to shifts in the gradients that had not been accounted for using the phase adjustment in [14]. All correlation images are presented with a threshold of 0.15, and superimposed on top of a magnitude underlay for the respective models, with green circles placed about the center voxel of the upper, lower, and middle folds to remind the reader of the previously aliased voxels in the center of the three folds. The brain presented in the human subject data set occupies a smaller proportion of the full FOV images than the spherical phantom. As such, there is less overlap of the brain in the aliased images and thus unlike the spherical phantomdata sets. With less overlap, the operator induced correlations about the center voxel for both the SENSE and SENSE-ITIVE models are very similar in the case of the human subject data set to those illustrated in the theoretical illustration in Fig. 4. The real, imaginary and magnitude-squared operator induced correlations for the SENSE model in Figs. 10a, 10b, and 10d and for the SENSE-ITIVE model in Figs. 10i, 10j, and 10l have a cluster of voxels positively correlated with the center voxel in the center of the FOV and a negatively correlated cluster of voxels in the center of the upper and lower folds, and are all confined to within the area defined by the green circles. These clusters are in general very slightly larger for the SENSE-ITIVE model than they are for the SENSE model, although not as large as those observed for the SENSE-ITIVE model in the spherical phantom data set in Figs. 7i, 7j, and 7l. The real/imaginary induced correlation images about the center voxel in Figs. 10c and 10k do not show any clusters of correlated voxels for either of the models.

Figure 10.

A comparison between a) SENSE (SE) real, b) SE imaginary, c) SE real/imaginary, d) SE magnitude-squared operator induced correlation about the center voxel, and e) SE real, f) SE imaginary, g) SE real/imaginary, h) SE magnitude-squared estimated correlation about the center voxel over the time series of the Human Subject with, i) SENSE-ITIVE (SI) real, j) SI imaginary, k) SI real/imaginary, and l) SI magnitude-squared operator induced correlation about the center voxel and m) SI real, n) SI imaginary, o) SI real/imaginary, and p) SI magnitude-squared estimated correlation about the center voxel over the time series of the Human Subject. Correlations presented with a threshold of 0.15 for operators with an identity estimated voxel covariance structure assumed. Smoothing was applied with a Gaussian kernel with a FWHM of 3 voxels.

In the correlations estimated throughout the time series of images reconstructed by both the SENSE and SENSE-ITIVE models, one can observe negative clusters of voxels, correlated to the center voxel, in the upper and lower folds of the real and magnitude squared correlation images in Figs. 10e and 10h for the SENSE model, and Figs. 10m and 10p for the SENSE-ITIVE model, with positive clusters of correlated voxels in the center. These correlations directly align with the corresponding operator-induced correlations in Figs. 10a and 10d for the SENSE model and Figs. 10i and 10l for the SENSE-ITIVE model. Although the operator induced correlations of both models exhibited negative imaginary correlations in the upper and lower folds with a positive imaginary correlation in the center fold in Figs. 10b and 10j, it is primarily the positive correlation in the center fold that is apparent in the estimated imaginary correlations for the human subject in Figs. 10f and 10n for the SENSE and SENSE-ITIVE models respectively. Additionally, while there was no noticeable real/imaginary induced correlation for either model in Figs. 10c and 10k, there is clearly a non-zero real/imaginary correlation estimated from the SENSE and SENSE-ITIVE reconstructed images in Figs. 10g and 10o respectively, that appears similar in nature to the imaginary correlations in Figs. 10f and 10n. While the estimated correlations for both models appear very similar in nature in the human subject data set, upon close observation one can see that the correlations of the SENSE model are slightly greater than those of the SENSE-ITIVE model, as noted in the theoretical illustration in Fig. 4. This increased correlation of the SENSE model is most likely a result of an inappropriate representation of the estimated voxel covariance structure presented in Fig. 8c. These correlations could have serious functional connectivity implications as one could mistakenly conclude that the clusters of correlated voxels in the center of the three folds possess a correlation of a biological origin without realizing the artificial source of the correlation.

Discussion

The mathematical framework outlined in [6] and [8] that allows image reconstruction operators to be expressed as matrices, and thus used to determine the statistical effects that each operator induces on the mean, covariance, and correlation of the data to be reconstructed, was expanded upon in [7] to represent the SENSE image reconstruction process as a linear isomorphism. It has been shown that when represented in terms of a real-valued isomorphism, the skew-symmetric coil covariance and identity voxel covariance structures, assumed by the SENSE model, are inappropriately defined when compared to the covariance structures estimated from both spherical phantom and human subject data sets. As such, a model that adjusts the SENSE model to account for both of these miss-specifications, entitled SENSE-ITIVE, has been proposed. The SENSE-ITIVE model uses a more mathematically correct coil covariance structure in conjunction with an estimated voxel covariance structure.

To illustrate the effects of using different coil and voxel covariance structures, a two part theoretical illustration was presented with a time series of constant circle and Shepp-Logan phantom images. Both time series were generated using a theoretical circular coil covariance structure similar to that in real data and a Gaussian voxel covariance structure, scaled and modified to mimic the real data. It was shown that the correlation induced about the center voxel by the SENSE image reconstruction operators was slightly less than that of the SENSE-ITIVE model, but the SENSE model illustrated an increase in standard deviation as well as the correlation estimated over the time series in the areas of previously aliased voxels. This increase in standard deviation was in turn marked by a decrease in the SNR within the circle and phantom in all regions where voxels were once aliased due to the sub-sampling process. The SENSE model was thus shown to have a theoretical advantage over the SENSE-ITIVE model, in terms of SNR, only in regions where aliasing was minimal.

The validity of the covariance adjustments made to the SENSE model with the SENSE-ITIVE model have been verified with experimental data, for both a spherical phantom and a human subject, acquired from a 3.0 T GE Signa LX magnetic resonance imager. The coil covariance used in the SENSE model was derived in the first iteration of the coil and voxel estimation process in which an identity voxel covariance structure was assumed. This covariance was then reordered to match the skew-symmetric coil covariance in the SENSE model. The estimation process of the coil and voxel covariance structures in both the human subject and spherical phantom data sets were carried out until both the coil and voxel covariance structures did not vary much from one iteration to the next. At this stage, the estimated covariance structures between coils and voxels were used in the SENSE-ITIVE model, without being rearranged to being skew-symmetric as in the SENSE model.

Both data sets were reconstructed using the SENSE and SENSE-ITIVE reconstruction operators, with image smoothing applied after reconstruction. In both data sets, both models showed similar behavior in mean magnitude and phase images. The standard deviation within both the spherical phantom and brain appeared to be lower for the SENSE model. This was unlike that of the theoretical illustration, giving the SENSE model an artificial increase in the SNR of the experimental data sets as a result of the miss-specified coil and voxel covariance structures.

The correlations induced by the image reconstruction operators were shown to be consistent in both the spherical phantom and human subject data sets with the theoretical illustration for both models, with the exception of the SENSE-ITIVE model showing slightly larger clusters of correlated voxels in the spherical phantom data set. In the spherical phantom data set, there was a clear resemblance between the operator induced correlations and those estimated over the time series. This operator-induced correlation could have serious implications in functional connectivity studies, as one would mistakenly conclude that there is a correlation between the center voxel and a cluster of voxels in the anterior and posterior regions of the brain, when in fact it is merely a consequence of using a reconstruction model that incorporates a voxel-mapping scheme, such as SENSE and SENSE-ITIVE.

It is of note that the study outlined in this manuscript addresses only the assumptions made in the SENSE model introduced in [4]. While many improvements have been made to the original SENSE model with the advent of techniques such as Compressed Sensing [17], these improvements are beyond the scope of this study. However, it is important to note that irrespective of the parallel image reconstruction model used, when sub-sampled data is used to generate missing information in either the image or spatial frequency domain, a correlation is induced between voxels as a result of the image reconstruction process.

Traditionally, the image reconstruction process in the SENSE model is performed on a voxel-by-voxel basis. However, in order to make use of both the more accurate representation of the coil and voxel covariance structures, it is necessary to use a linear isomorphism, such as the one outlined in both [7] and this manuscript, where all voxels are reconstructed at once. The only disadvantage of such a procedure is the computational requirements that the linear operators utilize. The times (in seconds) required for a PC with dual quad-core processors and 24 Gb of RAM to generate the SENSE and SENSE-ITIVE operators, reconstruct a time series with 490 TRs on N_C=4 coils, sub-sampled with A=3, and estimate the operator induced correlations are illustrated in Figs. 11a, 11b, and 11c respectively for images of size 24, 42, 60, 78, 96, and 114. It is evident in Fig. 11a that incorporating a non-identity voxel covariance structure into the SENSE-ITIVE model requires more time to build the reconstruction operators than for the SENSE model, where an identity covariance is used. Likewise, it is apparent in Fig. 11b that the reconstruction of the time series for SENSE is faster than for SENSE-ITIVE. The times in Fig. 11b are to be expected since the SENSE operators are sparse while the SENSE-ITIVE operators are not, and thus the time for the multiplication of a matrix and a vector is decreased. It was found, however, that for a larger FOV, the use of a sparse representation of the SENSE operators becomes inefficient when the operator induced correlation matrix is determined, and thus a full representation of the operators were used. As the SENSE and SENSE-ITIVE operators are of the same dimension, it is therefore to be expected that the times for estimating the operator induced correlations will be equivalent, as shown in Fig. 11c. The apparent exponential increase in time with the size of the image to be reconstructed for the processes in Figs. 11a, 11b, and 11c is confirmed in Fig. 11d, where the log of the total time for the SENSE and SENSE-ITIVE programs to be run appears linear.

Figure 11.

Computation times, in seconds, for a) building the SENSE and SENSE-ITIVE reconstruction operators for images of size 24, 42, 60, 78, 96, and 114 with N_C=4 coils, subsampled by A=3, b) reconstructing a time series of 490 TRs, c) estimating the operator induced correlation. The log of the total time shown to be linear in d).

To improve upon the times in Fig. 11, it would be most beneficial if both sparse matrices were used wherever possible and parallel matrix multiplication techniques, such as PUMMA [18] and SUMMA [19], are employed. Despite these computational requirements, however, the benefits of using a linear framework, such as the one in [6] and [7], allows for an analysis to be performed on the statistical implications of the image reconstruction operations. It has been illustrated that this is of particular importance when operators that perform a mapping of data from multiple receiver coils to multiple folds to un-alias an aliased image, such as in the SENSE and SENSE-ITIVE models, are used.

Appendix A. Voxel and Coil Covariance Estimation

Provided with a time series of N_TR complex-valued, aliased, k-space arrays of dimension p_x×p_y/A, the covariance structure between voxels and the covariance between coils can be estimated in an iterative fashion. Let V denote a p_xp_y/A×2N_C×N_TR real-valued array comprised of the N_C real and N_C imaginary vectorized components of the image-space images from the N_C coils in each TR. From the 3D array V, the mean can be taken in the third dimension to estimate the mean image, V̄. With an initial assumption that the covariance between voxels, ϒ, is identity, the coil covariance Ψ is assumed to be equivalent in each voxel as Γ= I_rp⊗Ψ. Thus, the coil covariance can be estimated as

$$\widehat{\mathrm{\Psi }}=\frac{1}{N_{TR}\ast rp}\sum _{t=1}^{N_{TR}}{\left(V_t-\overline{V}\right)}^T{I_{rp}}^{-1}\left(V_t-\overline{V}\right),$$

where rp denotes the total number of voxels in the p_x×p_y/A aliased images. This initial estimate of the coil covariance structure can then be used to estimate a covariance between all voxels, ϒ̂, in the aliased coil images as

$$\widehat{\mathrm{\Upsilon }}=\frac{1}{N_{TR}\ast N_C}\sum _{t=1}^{N_{TR}}\left(V_t-\overline{V}\right){\widehat{\mathrm{\Psi }}}^{-1}{\left(V_t-\overline{V}\right)}^T.$$

At this stage, the voxel covariance matrix can be translated into a correlation matrix, as there is little difference in the reconstruction and induced operator correlations. With this estimate of the voxel covariance, the coil covariance structure can be re-estimated in the second iteration to account for the covariance between voxels as

$$\stackrel{\sim }{\mathrm{\Psi }}=\frac{1}{N_{TR}\ast rp}\sum _{t=1}^{N_{TR}}{\left(V_t-\overline{V}\right)}^T{\widehat{\mathrm{\Upsilon }}}^{-1}\left(V_t-\overline{V}\right).$$

Similarly, the covariance structure between voxels can be re-estimated provided with the updated coil covariance

$$\stackrel{\sim }{\mathrm{\Upsilon }}=\frac{1}{N_{TR}\ast N_C}\sum _{t=1}^{N_{TR}}\left(V_t-\overline{V}\right){\stackrel{\sim }{\mathrm{\Psi }}}^{-1}{\left(V_t-\overline{V}\right)}^T.$$

This iterative process can be repeated until a desired level of convergence criteria is met for both the coil and voxel covariance structures. In this study, convergence was determined by the iteration in which both the voxel and coil covariance structures were of full rank. The final covariance between the voxels of the aliased images from the array of receiver coils is denoted

$$\stackrel{\sim }{\mathrm{\Gamma }}=\stackrel{\sim }{\mathrm{\Psi }}\otimes \stackrel{\sim }{\mathrm{\Upsilon }}.$$