One-Electron Oxidation of Neutral Sugar Radicals of 2′-Deoxyguanosine and 2′-Deoxythymidine: A Density Functional Theory (DFT) Study

Abstract

One electron oxidation of neutral sugar radicals has recently been suggested to lead to important intermediates in the DNA damage process culminating in DNA strand breaks. In this work, we investigate sugar radicals in a DNA model system to understand the energetics of sugar radical formation and oxidation. The geometries of neutral sugar radicals C_1′^•, C_2′^•, C_3′^•, C_4′^• and C_5′^• of 2′-deoxyguanosine (dG) and 2′-deoxythymidine (dT) were optimized in the gas phase and in solution using the B3LYP and ωB97x functionals and 6-31++G(D) basis set. Their corresponding cations (C_1′⁺, C_2′⁺, C_3′⁺, C_4′⁺ and C_5′⁺) were generated by removing an electron (one-electron oxidation) from the neutral sugar radicals and their geometries were also optimized using the same methods and basis set. The calculation predicts the relative stabilities of the neutral sugar radicals in the order C_1′^• > C_4′^• > C_5′^• > C_3′^• > C_2′^•, respectively. Of the neutral sugar radicals, C_1′^• has the lowest vertical ionization potential (IP^vert) ca. 6.33 eV in the gas phase and 4.71 eV in solution. C_2′^• has the highest IP^vert ca. 8.02 eV in the gas phase and the resultant C_2′ cation is predicted to undergo a barrierless hydride transfer from the C_1′ site to produce the C_1′ cation. One electron oxidation of C_2′^• in dG is predicted to result in a low lying triplet state consisting of G^+• and C_2′^•. The 5′,8-cyclo-2′-deoxyguanosin-7-yl radical formed by intramolecular bonding between C_5′^• and C₈ of guanine transfers spin density from C_5′ site to guanine and this structure has IP^vert 6.25 eV and 5.48 eV in the gas phase and in solution.

Introduction

The effects of ionizing radiation on DNA have been intensively investigated owing to the fact that DNA is the main target for biological important damage. Initially, radiation randomly ionizes each component of DNA and its surrounding, i.e., bases, sugar (deoxyribose), phosphate and waters producing highly reactive ion radical species.^1–12 The specific mechanisms of formation and reaction of these transient radical intermediates is of fundamental interest to understand the extent of DNA damage and related consequences. For example, the irradiation of DNA by a high-energy Argon ion-beam (high linear energy transfer (LET) radiation) produced a far greater yield of neutral sugar radicals than ion radicals in the track core. Since these sugar radicals were formed in the track core, where excitations and ionizations are in proximity, it was proposed that excited-state cation radicals could be the direct precursors of the neutral sugar radicals.^13,14 Based on this hypothesis, the radical cations of nucleosides, nucleotides and DNA and RNA oligomers were excited using UV-visible light to produce neutral sugar radicals which were further characterized by the ESR (electron spin resonance) experiment as C_1′^•, C_3′^• and C_5′^• sugar radicals.^15–23 This hypothesis was also supported by the excited state calculations of the radical cations of deoxyribonucleosides and several single-stranded dinucleosides.^17–19,23 C_5′^• sugar radical formation from one-electron oxidized 2′-deoxyguanosine (2′-dG^•+) by proton coupled hole transfer (PCHT) was proposed using theoretical calculations.²⁴ Using EPR/ENDOR sugar radicals at each of the carbon sites have been shown to result from direct radiation damage of nucleosides and nucleotides in the solid state.^{25, 26}

In the indirect effect of radiation, radicals are produced by the radiolysis of the water surrounding DNA which reacts with DNA. The most important of these radicals is the hydroxyl radical (OH^•). which readily reacts with DNA bases and the sugar phosphate backbone to produce base and sugar radicals.^{1,27,28,29,30–33} The dominant reaction of OH^• is the addition reaction at C₄, C₅ and C₈ atoms of purines and C₅ and C₆ atoms of pyrimidines.^34–38 OH^• reacts with the sugar moiety by hydrogen abstraction and produce C_1′^•, C_2′^•, C_3′^•, C_4′^• and C_5′^• sugar radicals. The rate of the hydrogen abstraction reaction by OH^• from different sites of the sugar unit depends on the accessibility of the sugar hydrogen atoms to the solvent and the proposed order is H5′ > H4′ > H3′ ≈ H2′ ≈ H1′.^30–33 However, in several studies C_1′^• sugar radical formation was observed predominantly.^39–44 For example, Bernhard and coworkers^39–40 report C_1′^• in abundance from X-irradiated DNA samples in aqueous solution or as a film which is supported by work done by Greenberg and coworkers.^41–42 The relative stability of the different sugar radicals have been calculated by several workers^45–49 and the order is generally found to be C_1′^• > C_4′^• > C_5′^• > C_3′^• > C_2′^•.

Carbon centered neutral sugar radicals in DNA/RNA are known to lead to base release, strand breaks or cross-link formation.^50–58 It has also been reported that sugar radicals may be the locus for further oxidation by several chemical species.^{27,28,30–33,50–60} In fact double oxidation events have been suggested that involve first oxidation of the sugar to form the sugar radical with a second subsequent oxidation of the sugar radical to form a non radical damage site. These non radical double oxidized sugars are suggested to result in DNA strand breaks and are thus suggested to be important intermediates in DNA damage processes. In this context, the study of the ionization potential of these sugar radicals are of both chemical and biological interest.

Our goal in this work is to test the hypotheses put forward by Bernhard and coworkers²⁶ to account for the fact that stand breaks in DNA were found to be more abundant than sugar radicals trapped at low temperatures. They proposed that one electron oxidation of sugar radicals by one electron oxidized DNA bases leads to non radical damage that results in DNA strand breaks. Our present work gives the energetics of the first step in the process, i.e., one electron oxidation of the sugar radicals of two model systems 2′-deoxyguanosine and 2′-deoxythymidine. The oxidation is found to be favorable for most of the sugar radical species but shows there would be a DNA base dependence for certain sugar radical oxidations. Most intriguing is our prediction that oxidation of the C2′ radical of dG leads to a low lying triplet state consisting of G^+• and C₂′•.

Method of Calculations

In this work we employ both the B3LYP and ωB97x methods. B3LYP has been found to be an excellent and cost effective choice for calculating various molecular properties of DNA bases in neutral and radical states.^5,61–73 The ωB97x functional, recently developed from the group of Head-Gordon²⁹, is also a good choice to describe the ionization energies of molecules. Therefore, in the present study both methods are employed to calculate the ionization potentials of sugar radicals of 2′-deoxyguanosine and 2′deoxythymindine.

The geometries of the sugar radicals (C_1′^•, C_2′^•, C_3′^•, C_4′^• and C_5′^•) of 2′-deoxyguanosine and 2′-deoxythymidine in the gas phase and in solution were fully optimized using the B3LYP/6-31++G(d) and ωB97x/6-31++G(d) methods. The geometries of one-electron oxidized sugar radicals (C_1′⁺, C_2′⁺, C_3′⁺, C_4′⁺ and C_5′⁺) were optimized using the same methods and basis set in the gas phase and in solution by considering the corresponding optimized geometries of the sugar radicals as input. The effect of bulk aqueous solution was modeled through the use of the self-consistent reaction field and the integral equation formalism polarized continuum model (IEFPCM) having dielectric constant ε = 78.4 as implemented in the Gaussian 09 program.⁷⁵ All the calculations were performed using the Gaussian09 suite of programs.⁷⁵ GaussView molecular modeling software⁷⁶ was used to plot the spin density distribution around the molecule and JMOL molecular modeling software was used to draw the molecular structures.⁷⁷

Results and Discussion

(a) Suitability of the method

We considered DNA/RNA bases (adenine (A), guanine (G), cytosine (C), thymine (T) and uracil (U)) and deoxyribose (sugar) moiety as test cases and calculated their vertical and adiabatic ionization potentials (IPs) using the B3LYP/6-31++G(d) method. The calculated IPs by the B3LYP/6-31++G(d) method were compared with the available experimental estimates of the IPs of theses bases and sugar, see Table 1. This test is necessary to establish the reliability of the chosen method because, to the best of our knowledge, the IPs of sugar radicals have not been determined experimentally. The IPs of DNA bases have been extensively studied using ab initio and DFT methods and well documented in the literature.^7,8,78–81 In Table 1, we compared our B3LYP/6-31++G(d) calculated IP values with experiment for method suitability purpose only and for more details see recent reviews.^7,8,79 From Table 1, we found that the vertical and adiabatic IP (IP^vert and IP^adia) of A, G, C, T and U are in good agreement with the experimental IP values.^82,83 The maximum difference between theory and experiment for IP^vert is 0.27 eV and for IP^adia is 0.21 eV, respectively, see Table 1. Very recently, using tunable vacuum ultraviolet (VUV) synchrotron radiation coupled to an effusive thermal source the ionization energy (AIE) of deoxyribose (sugar) gas phase has reported to be 9.1(±0.05) eV⁸⁴ in the pyranose form. However, the structure of furanose is appropriate for modeling the structure of deoxyribose (sugar) in DNA, thus, we calculated the vertical and adiabatic IPs of furanose using the B3LYP/6-31++G(d) method and the values are IP^vert (9.61 eV) and IP^adia (8.93 eV), respectively. The corresponding values calculated using the ωB97x/cc-pVTZ method in ref. 84 are 10.06 eV and 9.05 eV, respectively, see Table 1. Identical calculations for the pyranose form gave 9.6 and 8.8 eV, respectively.⁸⁴ In our calculation, we also considered deoxyribose (sugar) moiety with NH₂ substitution at the C_1′ site (see Figure S1 in the supporting information (SI)) and calculated the IPs using the B3LYP/6-31++G(d) and ωB97x/cc-pVTZ methods, see Table 1. As pointed out above in comparison to experiment the B3LYP/6-31++G(d) values are found to be good estimates.

Table 1.

B3LYP/6-31++G(d) and ωB97x/6-31++G(d) calculated vertical and adiabatic ionization potentials (IPs) in eV of DNA/RNA bases, furanose and deoxyribose (sugar).

Molecule	B3LYP/6-31++G(d)		Experimenta		ωB97x/6-31++G(d)
	IPvert	IPadia	IPvert	IPadia	IPvert	IPadia
Guanine	7.99	7.64	8.24	7.77	8.14 (8.00)e	7.71 (7.57)e
Adenine	8.24	8.05	8.44	8.26	8.42 (8.32)e	8.16 (8.05)e
Thymine	8.98	8.74	9.14	8.87	9.13 (9.05)e	8.81 (8.76)e
Cytosine	8.67	8.56	8.94	8.68	8.86 (8.78)e	8.74 (8.65)e
Uracil	9.45	9.24	9.50	9.32	9.60 (9.50)e	9.30 (9.21)e
Furanose	9.61	8.93	-	(ca. 9.3)b	10.18 (10.06)c	9.24 (9.05)c
1′-NH2- furanosed	8.66	8.04	-	-	9.02 (8.97)e	8.21 (8.17)e

^aRefs. 35, 36.

^bAn experimental value for only the α-pyranose form (9.1 eV IP^adia) has been reported, Ref. 84. Calculations in Ref.84 suggest the furanose IP^adia will 0.2 eV higher or 9.3 eV.

^cCalculated using the ωB97x/cc-pVTZ method, Ref. 84.

^dSee Figure S1 in the supporting information.

^eCalculated using the ωB97x/cc-pVTZ method.

The ωB97x/6-31++G(d) method was also used to calculate the ionization potentials of the test cases presented in Table 1, we find that the combination of ωB97x functional with 6-31++G(d) basis set provides the “best estimate” of the ionization potentials. The calculated IPs by the ωB97x/6-31++G(d) method are in close agreement with the experimental IPs values having maximum difference of less than 0.1 eV, see Table 1. Since the B3LYP/6-31++G(d) method is also able to give good estimates of the IPs of molecules we employ both methods to estimate the IPs of sugar radicals of 2′-deoxyguanosine and 2′-deoxythymidine.

(b) Geometries and relative stabilities

The B3LYP/6-31++G(d) optimized geometries of sugar radicals (C_1′^•, C_2′^•, C_3′^•, C_4′^• and C_5′^•) of 2′-deoxyguanosine and their corresponding cations (one-electron oxidized sugar radicals) in the gas phase and in solution are presented in Figures S2 and S3 in the SI. From the calculation it is evident that the optimized geometries of sugar radicals in the gas phase are similar to those optimized using the PCM model for solution effects. On the formation of C_1′ radical a significant conformational change occurs at C_1′ site of the sugar ring. The C_1′ atom which was non-planar (the sum of the three angles (N9-C_1′-O + O-C_1′-C_2′ + C_2′-C_1′-N9) is ca. 329 deg.) in the 2′-deoxyguanosine (see Figure S1 in the SI) becomes quite planar in gas phase and the sum of the corresponding angle is ca. 349 deg. In C_2′ radical, C_2′ atom becomes completely planar and the sum of the angles centering C_2′ atom is ca. 360 deg. In C_3′, C_4′ and C_5′ radicals the sum of the angles centering the C_3′, C_4′ and C_5′ atoms are 345 deg., 357 and 353 deg., respectively. Thus, on radical formation the C_2′, C_4′ and C_5′ radicals become planar while C_1′ and C_3′ radicals have small non-planarity. The B3LYP/6-31++G(d) calculation predicts the relative stability of the sugar radicals in the order C_1′^• > C_4′^• > C_5′^• > C_3′^• > C_2′^• which is in agreement with the earlier studies. On one-electron oxidation, large structural changes, mainly, in the sugar moiety are taking place. Cross-linking between C_2′ and C₈ (guanine) atoms was found on the formation of C_2′ cation in the gas phase, however, in solution this cross-link is absent and O_3′ atom makes bond with the C_2′ atom, see Figure S3 in the SI. C_4′ and C_5′ cations show sugar ring fragmentation in the gas phase, see Figure S3 in the SI. The cross-link formation or sugar ring fragmentation is not unusual and has been found experimentally.^27,28,33 C_1′ and C_3′ cations were found to retain their parent neutral sugar radical structure and radical site becomes planar, i.e., the sum of the angles centering C_1′ and C_3′ atoms is 360 deg., see Figures S2 and S3 in the SI. Except for C_2′⁺, the optimization of C_1′⁺, C_3′⁺, C_4′⁺ and C_5′⁺ in solution are found to retain their parent sugar radical structure, Figure S2 and S3 in the SI. The relative vertical stabilities of the cations in the gas phase and in solution follow the order C_1′⁺ > C_4′⁺ > C_5′⁺ > C_3′⁺ > C_2′⁺.

The ωB97x/6-31++G(d) calculated geometries of sugar radicals and their cations in the gas phase and in solution are given in Figures S4 and S5 in the SI. The optimized geometries by the ωB97x/6-31++G(d) method are in close agreement with those optimized using the B3LYP/6-31++G(d) method. The ωB97x/6-31++G(d) method also shows that on radical formation the sugar radical sites become planar and the sum of the angles centering the C_1′, C_2′, C_3′, C_4′ and C_5′ radical sites are 347, 360, 343, 354 and 352 deg., respectively, and on cation formation the corresponding angles are 360, 357, 360, 360 and 358 degs, respectively. The optimization of the cations (C_1′⁺, C_2′⁺, C_3′⁺, C_4′⁺, C_5′⁺) by the ωB97x/6-31++G(d) method in gas phase shows that C_1′ and C_3′ cations retain their parent sugar radical structure. However, C_2′, C_4′ and C_5′ cations show bond formation between O_3′ and C_2′ atoms of sugar ring in C_2′⁺ and C_1′-O bond dissociation in C4_′⁺ and C_5′⁺. The optimization of cations in the solution using the PCM model retain their parent radical structure except for C_2′⁺ which shows O_3′ and C_2′ bond formation as found in the gas phase, see Figures S4 and S5 in the SI.

(c) Spin density distribution and ionization potentials

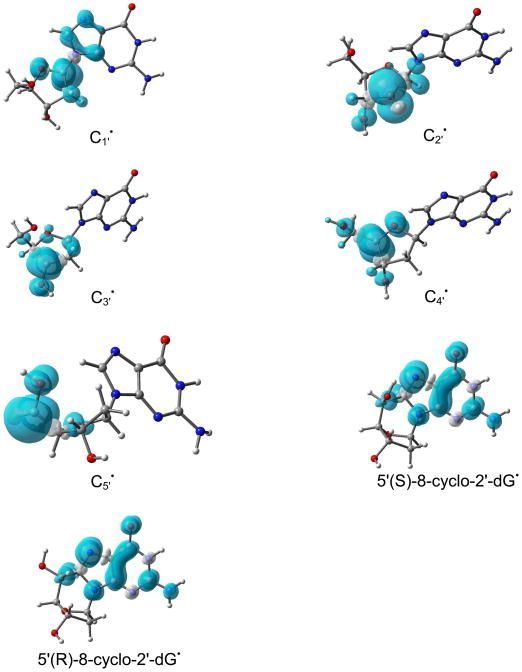
The B3LYP/6-31++G(d) calculated Mulliken spin density distributions in sugar radicals from 2′dexoyguanosine are shown in Figure 1. In supporting information the calculated atomic spin densities at each atom and the isotropic hyperfine coupling constants are given (Table S2). The spin density distribution of a molecule provides the distribution of the odd electron within the molecule and is usually in close accord with the singly occupied molecular orbital (SOMO). In our calculation, both the methods (B3LYP/6-31++G(d) and ωB97x/6-31++G(d)) showed that for C_2′ and C_5′ radicals the spin and SOMO distributions differ with each other. In these two cases (C_2′ and C_5′ radicals), the spin was localized on the C_2′/C_5′ atom while the SOMO was localized on the guanine base. This was observed for C_2′ radical by the B3LYP method and for C_2′ and C_5′ radicals by the ωB97x method. This discrepancy is often found to occur when two portions of a radical have energetically near equal IPs that are not well coupled electronically in the half filled orbital. This issue was overcome by the use of restricted open shell method for these two cases; however, little difference (< 0.05 eV) in IP between the restricted and unrestricted calculations was found (Table 2). For the C_1′ radical, the most of the spin density (> 90 %) is located on the C_1′ atom with a small delocalization on C5, C8 and N7 atoms of guanine, see Figure 1. Likewise in C_2′ to C_5′ radicals, the spin density are localized on the single carbon site of the sugar ring. Thus, the present calculation suggests that further oxidation would be from the radical sites of these carbon-centered sugar radicals. Our theoretical predictions are further supported by several experiments that suggest the formation of carbon-centered sugar cations. Using quantitative kinetic measurements, the mechanism of C_1′ radical oxidation of 2′-deoxyuridin-1′-yl radical has been explored in detail.⁵⁸ The C_1′ radical reacts with O₂ to form peroxyl radical with rate constant 1 × 10⁹ M⁻¹ s⁻¹ which release O₂⁻ with rate constant 1.5 × 10⁴ s⁻¹ to produce C_1′ cation. The further reaction of C_1′⁺ with water produces 2′-deoxyribonolactone as shown below.^27,58

Figure 1.

B3LYP/6-31++G(d) calculated Mulliken spin density distribution in sugar radicals (dG(C1′•) – dG(C5′•)) and in 5′,8-cyclo-2′-deoxyguanosin-7-yl radical in their two diastereoisomeric forms. Spin densities were calculated with 0.002 electron/bohr³.

Table 2.

B3LYP/6-31++G(d) and ωB97x/6-31++G(d) calculated vertical and adiabatic ionization potentials (IPs) in eV of neutral sugar radicals of 2′-deoxyguanosine (dG) in gas phase and in aqueous solution.

Sugar radical of dG	B3LYP/6-31++G(d)				ωB97x/6-31++G(d)
	Gas phase		Aqueous phasea		Gas phase		Aqueous phasea
	IPvert	IPadia	IPvert	IPadia	IPvert	IPadia	IPvert	IPadia
dG(C1′•)	6.33	5.34	4.71	3.82	6.56	5.33	4.97	3.83
dG(C2′•)	8.02b	c	6.41	c	8.71b	c	6.75	c
dG(C3′•)	7.28	6.44	5.29	4.31	7.65	6.47	5.43	4.29
dG(C4′•)	7.17	c	5.31	4.33	7.44	c	5.43	4.33
dG(C5′•)	7.50	6.86	5.44	4.63	7.97	6.84	5.52	4.67

^aCalculated using IEFPCM model with ε = 78.38.

^bRestricted open shell B3LYP/6-31++G(d) and ωB97x/6-31++G(d) calculated values are 7.98 eV and 8.66 eV, respectively.

^cOptimized structures underwent significant rearrangements that did not correspond to their parent sugar radical structure, see Figures in the SI.

In addition the formation of C_2′ radical and its cation C_2′⁺ were experimentally observed from the photoreaction of 2′-iododeoxyuridine by Sugiyama et al.⁸⁵ and C_1′⁺ was produced by the 1′, 2′-shift of C_1′-H to C_2′. The oxidation of C_4′ radical to give C_4′⁺ by bleomycin/Fe²⁺/O₂ complex has been supported by the experiments of Stubbe et al.⁸⁶ and Giese and coworkers.⁸⁷ The chemistry of C_5′ radical proceeds as: (i) formation of cross-link between C_5′ and C8 atoms of purines with reaction rate constant (k_c = 1.6 × 10⁵ s⁻¹). and (ii) The formation of C_5′⁺ by the oxidation reaction with K₃Fe(CN)₆ and the rate constant of the reaction was reported to be ca. 10⁹ M⁻¹ s^−1.27,88

The B3LYP/6-31++G(D) and ωB97x/6-31++G(D) calculated ionization potentials of sugar radicals of 2′-deoxyguanosine in gas phase and in solution are presented in Table 2. From Table 2, it is evident that C_1′ radical has the lowest vertical ionization potential in the gas phase and in solution and the calculated values are gas phase (solution) 6.33(4.71) eV by the B3LYP/6-31++G(d) and 6.56(4.97) eV by the ωB97x/6-31++G(d). For dG(C_2′) radical, the restricted B3LYP/6-31++G(d) and ωB97x/6-31++G(d) calculations give the gas phase vertical IP as 7.98 eV and 8.66 eV, respectively, which is highest among all the considered radicals, see Table 2. For this case, we found that vertical triplet state of dG(C_2′⁺) is more stable than the vertical singlet state of dG(C_2′⁺), discussed later.

Thus, the present calculation predicts that C_1′^• is the most probable site for oxidation followed by C_3′^•, C_4′^• and C_5′^•. The vertical ionization potential of C_2′^• in gas phase is 8.02 – 8.71 eV and thus it is the most difficult to oxidize. The IP of C_2′^• is also comparable to the IPs of guanine (7.99 – 8.14 eV) and adenine (8.24 – 8.42 eV), see Table 1, and thus the ionization of purines in comparison to C_2′^• may be favored. The ionized C_2′^• radical (C_2′⁺) is experimentally found to be highly reactive⁸⁵ which is confirmed by our calculation as discussed in the next section. The vertical gas phase ionization potentials (IP^vert) of C_1′^•, C_2′^•, C_3′^•, C_4′^• and C_5′^• lie in the order C_1′^• < C_4′^• ≈ C_3′^• < C_5′^• < C_2′^•, see Table 2. The calculated adiabatic IPs of C_1′^•, C_3′^• and C_5′^• are quite low in solution and they lie in the range 3.82 eV – 4.67 eV, see Table 2

A small delocalization of spin on N9, C4, C8 and N7 atoms of guanine is seen from the spin density distribution maps (Figure 1) of C_1′ radical and suggests that guanine may influence the IP of this sugar radical and perhaps others. Since guanine has the lowest IP and thymine has the highest IP of all the bases, comparing 2′-deoxythymidine with 2′-deoxyguanosine should provide a good test of the effect of the base on the IP of the sugar radicals. The calculated vertical and adiabatic IPs of 2′-deoxythymidine in the gas phase and in solution by the B3LYP and ωB97x methods are presented in Table 3. From Table 3, we see that IP of the sugar radicals of 2′-deoxythymidine are generally only slightly higher than the IPs of sugar radicals of 2′-deoxyguanosine, see Table 2. This small effect is reflected in the small delocalization of spin found for the C_1′ radical in dT (Figure S9) which is similar to that found for the C_1′ radical in dG (Figure 1). The dT(C_1′^•) has the lowest and dT(C_2′^•) has the highest IP as found for the other two cases (Tables 2 and T1 in the SI). The high reactivity of dT(C_2′⁺) is also evidenced. The optimization of dT(C_2′⁺) by both the methods show rearrangement that transfers the thymine base from C_1′ to C_2′ through N1-C2 bond formation in the gas phase, see Figure S6 in the SI. In solution, however, a barrierless hydrogen atom transfer from C_3′ to C_2′ occurs resulting in C_3′⁺, see Figure S7 in the SI. This reaction, i.e., the formation of dT(C_3′⁺) from dT(C_2′⁺) through 1, 2-shift of C_3′-H to the C_2′ carbocation, has been proposed from experimental studies for dU(C_3′⁺) formation from dU(C_2′⁺) via 1, 2-shift of C_3′-H to the C_2′ carbocation.⁸⁵

Table 3.

B3LYP/6-31++G(d) and ωB97x/6-31++G(d) calculated vertical and adiabatic ionization potentials (IPs) in eV of neutral sugar radicals of 2′-deoxythymidine in gas phase and in aqueous solution. See Figure S6 and S7 in the SI.

	B3LYP/6-31++G(d)				ωB97x/6-31++G(d)
Sugar radical	Gas phase		Aqueous phasea		Gas phase		Aqueous phasea
	IPvert	IPadia	IPvert	IPadia	IPvert	IPadia	IPvert	IPadia
dT(C1′•)	6.59	5.60	4.83	3.85	6.90	5.60	5.20	3.85
dT(C2′•)	8.43	-	6.50	-	8.83	-	6.69	-
dT(C3′•)	7.38	6.56	5.26	4.37	7.70	6.22	5.38	4.34
dT(C4′•)	7.65	-	5.42	-	7.94	-	5.53	4.44
dT(C5′•)	7.77	-	5.32	4.55	8.07	-	5.43	4.61

^aCalculated using IEFPCM model with ε = 78.38.

We note that we also considered another model by replacing the guanine base with NH₂ group at the C_1′ atom of the sugar ring, see Figure S1 and Table T1 along with discussion in the SI. This was less informative as the NH₂ group actually lowered the IPs more than the guanine.

(d) 1′, 2′-hydride shift of C_1′-H to C_2′ in C_2′⁺ singlet state

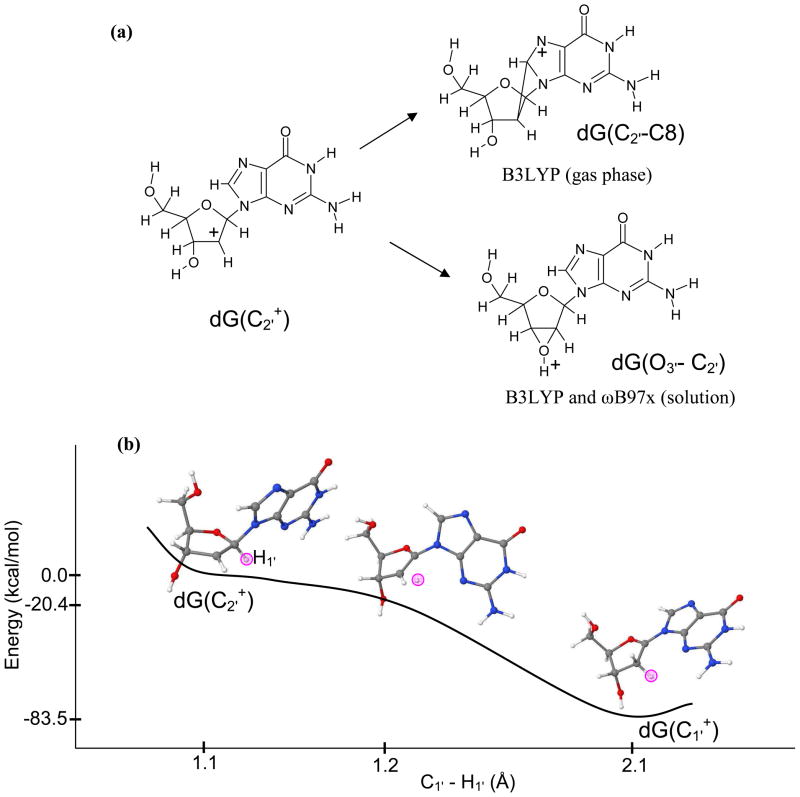
As we mentioned that C_2′^• has the highest IP among all the sugar radicals considered in the present study and its cation is highly reactive. The full optimization of C_2′⁺ by the B3LYP method in its singlet state results in a cross-link between C8(guanine) and C_2′ of sugar ring in the gas phase and bond formation between O_3′ and C_2′ atoms in solution which is obtained by both B3LYP and ωB97x methods, see Figure 2(a). The O_3′ and C_2′ bonding is not possible in DNA because O_3′ is rigidly attached to the phosphate group. This bonding is also absent in the optimized radical structure, therefore, we optimized the C_2′⁺ structure in the gas phase and in solution by constraining the O_3′- C_3′- C_2′- C_1′ as present in C_2′^•. This constrained optimization by the ωB97x/6-31++G(d) shows a barrierless transformation of C_2′⁺ to C_1′⁺ by hydride transfer, see Figure 2(b). Our calculation supports the experimental observation of the formation of C_1′⁺ from C_2′⁺ by the 1′, 2′-shift of C_1′-H to C_2′ by Sugiyama et al.⁸⁵ The B3LYP/6-31++G(d) method shows the cross-linking of C8(Guanine) and C_2′ in the solution. This calculation clearly provide evidence that C_2′⁺ is a very short lived species if formed and is highly reactive and able to oxidize C_1′ or the purine base.

Figure 2.

(a) Full optimization of dG(C_2′⁺) in its singlet state resulted in a cross-link between C_2′ ⁻C8 by the B3LYP/6-31++G(d) in the gas phase and O_3′ ⁻C_2′ bond formation in solution (PCM) by the B3LYP/6-31++G(d) and ωB97x/6-31++G(d). (b) The ωB97x/6-31++G(d) constrained optimization of dG(C_2′⁺) produced dG(C_1′⁺) through H_1′ hydride transfer from C_1′ to C_2′ in solution using PCM model. Reaction proceeds barrierless in the gas phase and in solution. The pink circle shows the position of the transferring H_1′ atom during the reaction. Energies and distances shown are not to the scale.

(e) C_2′⁺ Triplet State in dG(C_2′⁺)

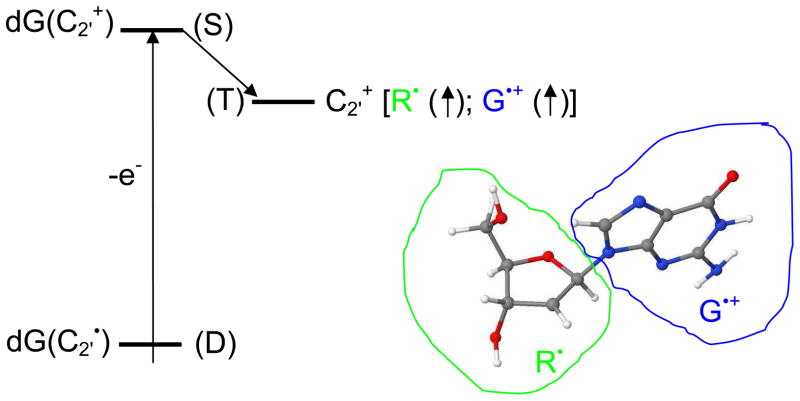
Another interesting aspect of dG(C_2′⁺) is that the vertical triplet state (T) lies lower in energy than the singlet state (S) as calculated by both the ωB97x/6-31++G(d) and B3LYP/6-31++G(d) methods (See Figure 3). This is a consequence of the low IP of G which transfers an electron to the C_2′ site and is therefore not expected for dT(C_2′⁺). In the triplet state spins (shown by upward arrows in Figure 3) are localized on guanine (G) and at C_2′ in the deoxyribose (R) effectively making a diradical. Thus, after intersystem crossing to the triplet state the reactivity of dG(C_2′⁺) would be determined by the diradical nature of the intermediate. The formation of dG(C_1′⁺) and the dG(C_2′-C8)+ might be explained by hydrogen atom shift and radical-radical reaction, respectively.

Figure 3.

Schematic diagram of the vertical ionization of C_2′^• of 2′-deoxyguanosine in doublet (D) state. The vertical triplet state (T) is lower in energy than the singlet (S) state of dG(C_2′⁺) as calculated by both the ωB97x/6-31++G(d) and B3LYP/6-31++G(d) methods. In the triplet state spins (shown by upward arrows) are localized on guanine (G) and deoxyribose (R) making a diradical.

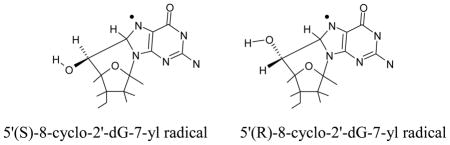
(e) Cyclization of C_5′ and C8

The cyclization of C_5′ and C8 has been observed experimentally.^50,51 The underlying mechanism of this cyclization is the initial formation of the C_5′ radical which binds with C8 atom of guanine or adenine with cyclization rate constant of 1.6 × 10⁵ s⁻¹. The cyclic radical structure has two diastereoisomeric forms: (i) 5′ (S),8-cyclo-2′-deoxyguanosin-7-yl and (ii) 5′ (R),8-cyclo-2′-deoxyguanosin-7-yl. Using the B3LYP/6-31++G(d) and ωB97x/6-31++G(d) methods, we optimized the geometries of these two isomers in their radical and cation states. Our structural optimization showed that the sugar ring of these cyclic structures adopt the O-exo conformation (Figure S8 in the SI) as found in earlier studies using NMR spectroscopy⁸⁹ and theory.^90,91 The calculated spin density distribution of these two isomers in their radical state are shown in Figure 1. From Figure 1, it is clearly evident that spin density in these isomers resides mainly on the guanine base. Thus, on cyclization spin density is transferred from C_5′ site to the guanine in these two isomers. The calculated IPs of these two isomers in the gas phase and in solution lie in the range ca. 4.3 eV – 6.3 eV, see Table 4. From the IP values, it is inferred that these cyclic radical structures in DNA would undergo electron transfer to one electron oxidized bases in DNA.

Table 4.

B3LYP/6-31++G(d) and ωB97x/6-31++G(d) calculated vertical and adiabatic ionization potentials in eV of 5′,8-cyclo-2′-deoxyguanosin-7-yl radical in gas phase and in aqueous solution.

5′,8-cyclo-2′-deoxyguanosin-7-yl radical	B3LYP/6-31++G(d)				ωB97x/6-31++G(d)
	Gas phase		Aqueous phasea		Gas phase		Aqueous phasea
	IPvert	IPadia	IPvert	IPadia	IPvert	IPadia	IPvert	IPadia
5′ (S)	6.34	5.89	4.66	4.31	6.38	5.85	4.70	4.29
5′ (R)	6.25	5.90	4.58	4.29	6.33	5.88	4.64	4.28

^aCalculated using IEFPCM model with ε = 78.38.

Conclusions

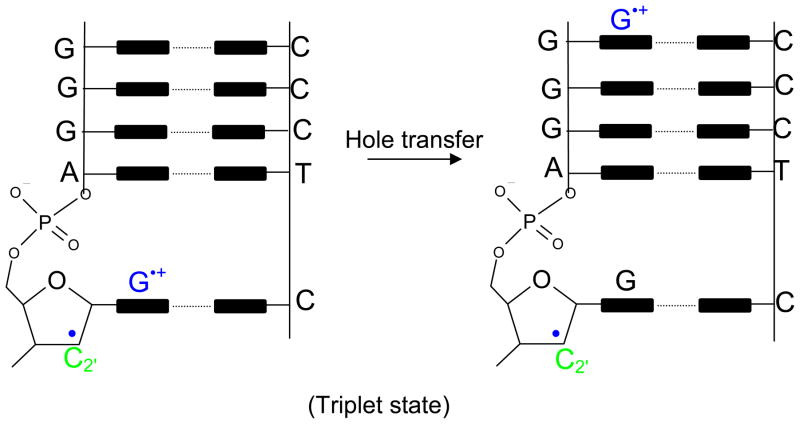
From the present study, we found that each of the neutral sugar radicals (except for C_2′) have lower IPs than the DNA bases and thus can be a locus for oxidation. C_1′ radical has the lowest ionization potential (6.33 eV IP^vert) while C_2′ radical has the highest ionization potential (8.02 eV IP^vert). Our calculations predict that not only is the C_2′ radical far more difficult to be oxidize than the other sugar radicals, its cation (C_2′⁺) is highly reactive and undergoes barrierless hydride transfer from C_1′ or C_3′ resulting in the formation of C_1′⁺ and C_3′⁺. This reaction has been found experimentally by Sugiyama et al.⁸⁵ Another intriguing feature is that for dG(C_2′⁺) the triplet state lies lower and it is a diradical in nature with spin localizing on both the base and the sugar, see Figure 3. This theoretical finding is considered significant and the triplet (diradical) should live long enough for “hole” transfer to neighboring bases or sites of lower ionization potential to take place as shown in the schematic diagram in Figure 4. This theoretical prediction needs experimental verification. Thus, the overall conclusion for C_2′⁺, we have, is that it is a very reactive species and different reaction paths are possible as explained above.

Figure 4.

Proposed schematic of possible hole transfer in the triplet state of dG(C_2′⁺) after one electron oxidation of dG(C_2′^•)

The calculated IP of the sugar radicals by both methods employed, B3LYP and ωB97x, are in close agreement particularly the adiabatic ionization potentials. Except for C_2′^•, the B3LYP/6-31++G(d) calculated vertical ionization potential values of C_1′^•, C_3′^•, C_4′^• and C_5′^• are slightly less than the likely more reliable ωB97x/6-31++G(d) values, see Tables 2, 3 and T1 in the SI. Both the methods are found to be suitable for the calculation of the ionization potentials of molecules. The reactivity of the dG(C_2′⁺) to produce dG(C_1′⁺) by hydride transfer is well reproduced by the ωB97x/6-31++G(d) method, see Figure 2(b). The B3LYP/6-31++G(d) method readily predicts the experimentally observed cross-linking between C_2′ and C8. For dT(C_2′⁺) both the methods show d(C_3′⁺) formation by barrierless hydride transfer from C_3′ to C_2′ in solution (Figure S7 in the SI) which is observed experimentally.⁸⁵ The C_5′ sugar radical is formed in significant amounts by radiation⁹² and is known to undergo facile attack at C8 in guanine to produce a cyclized species, the 5′,8-cyclo-2′-deoxyguanosin-7-yl radical in two diastereoisomeric (R) and (S) forms.^50,51 The ionization potentials of these radicals (Table 4) are relatively low 6.25 eV – 6.28 eV (gas phase IP^vert) and 4.58 eV – 4.70 eV (solution IP^vert) and in keeping with these low IPs these cross-links in DNA are readily further oxidized to form the diamagnetic products, i.e., 5′,8-cyclo-2′-deoxyguanosine isomers.

Scheme 1.

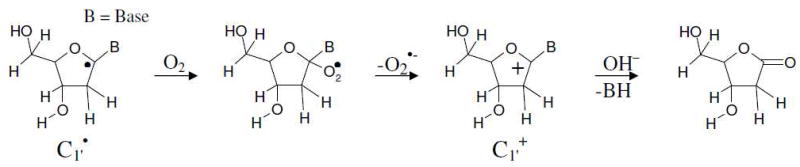
Reaction of C_1′^• with oxygen to form the cation and its reaction with water to form the 2′deoxyribonolactone