Abstract
Most kinetic measurements of the partial reactions of Na+,K+-ATPase have been conducted on enzyme from mammalian kidney. Here we present a kinetic model that is based on the available equilibrium and kinetic parameters of purified kidney enzyme, and allows predictions of its steady-state turnover and pump current in intact cells as a function of ion and ATP concentrations and the membrane voltage. Using this model, we calculated the expected dependence of the pump current on voltage and extracellular Na+ concentration. The simulations indicate a lower voltage dependence at negative potentials of the kidney enzyme in comparison with heart muscle Na+,K+-ATPase, in agreement with experimental results. The voltage dependence is enhanced at high extracellular Na+ concentrations. This effect can be explained by a voltage-dependent depopulation of extracellular K+ ion binding sites on the E2P state and an increase in the proportion of enzyme in the E1P(Na+)3 state in the steady state. This causes a decrease in the effective rate constant for occlusion of K+ by the E2P state and hence a drop in turnover. Around a membrane potential of zero, negligible voltage dependence is observed because the voltage-independent E2(K+)2 → E1 + 2K+ transition is the major rate-determining step.
Introduction
The Na+,K+-ATPase is a crucial enzyme in animal physiology. It is responsible for maintaining Na+ and K+ electrochemical potential gradients across the plasma membranes of all multicellular animal species. These gradients are essential for the maintenance of cell volume and for a variety of physiological processes, including nerve, muscle, and kidney function.
The mechanism of the enzyme's complete reaction cycle is generally described by the Albers-Post formalism. A simplified version of this cycle is shown in Fig. 1. Much information has been gathered on the kinetics of the partial reactions of this cycle. However, this information was gained from studies of a small number of purified enzyme systems. This is because, in comparison with ion channels, individual ion pumps such as the Na+,K+-ATPase produce a relatively low ion flux across the membrane. Therefore, measurements of ion pump activity, particularly partial reactions, have been limited to tissues in which the Na+,K+-ATPase naturally occurs at a very high level of expression. By far the most commonly studied source of Na+,K+-ATPase has been mammalian kidney, for which Jørgensen (1,2) developed a purification procedure in the 1970s. Of course, investigators have gained a great amount of valuable information regarding the transport modes of Na+,K+-ATPase from ion flux measurements carried out using red blood cells or resealed red cell ghosts (3,4). However, as pointed out by Kaplan (5), the low expression level of the enzyme in human red blood cells (∼250 copies per cell) limits the scope of partial-reaction kinetic studies in this system.
Figure 1.
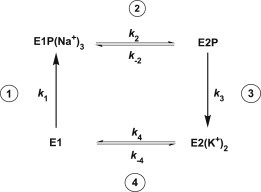
Simplified representation of the Albers-Post scheme describing the Na+,K+-ATPase catalytic cycle. Step 1: Binding of three Na+ ions from the cytoplasm, phosphorylation by ATP, and occlusion of Na+ within the protein. Step 2: Conformational change of the phosphorylated protein releasing the Na+ ions to the extracellular medium. Step 3: Binding of two K+ ions from the extracellular medium, occlusion of K+ within the protein, and dephosphorylation. Step 4: Conformational change of the unphosphorylated protein releasing K+ ions to the cytoplasm.
In a less complicated world, kinetic and thermodynamic data obtained from studies of Na+,K+-ATPase in one animal species or one tissue would be valid for all other species and tissues. Unfortunately for the researcher, this seems not to be the case. Recently, it was shown that Na+,K+-ATPase from pig kidney is significantly more thermally stable than that derived from shark rectal gland (6), and that the two enzymes display significant differences in their kinetics, i.e., different rate-determining steps (7). This is despite the fact that these two enzymes have very similar amino acid sequences and three-dimensional structures (8–10). The amino acid sequences of the α-subunits of both enzymes show 87% identity. In the case of the smaller β- and γ-subunits, the sequence identities are 66% and 23%, respectively (6). Via experiments in which both enzymes were independently reconstituted into synthetic lipid vesicles, Hansen et al. (6) recently showed that that the bulk properties of the lipid membrane are not responsible for the difference in the thermal stabilities of pig and shark enzymes, and they suggested that it may be due to relatively few differences in the enzyme's overall sequence.
In this work, we compare the Na+,K+-ATPases of mammalian heart and kidney. It has already been established that the kinetics of a related enzyme, the sarcoplasmic reticulum Ca2+-ATPase, differ significantly between skeletal muscle and heart muscle (11). It has been shown that in skeletal muscle, ion pumping is stimulated by ATP binding to an allosteric site on a phosphorylated form of the enzyme, whereas in cardiac muscle ATP accelerates ion pumping by binding to a nonphosphorylated form of the enzyme. If such major differences occur in the Ca2+-ATPase mechanism between different tissues, the Na+,K+-ATPase may also display significant differences. Therien and Blostein (12) reported in 1999 that the Na+,K+-ATPase of heart tissue possesses a somewhat higher degree of K+/Na+ antagonism at its cytoplasmic face in comparison with the Na+,K+-ATPase of kidney, i.e., K+ more effectively competes with Na+ for binding to the E1 state in the heart. However, this may not be the only difference. Gadsby and Nakao (13) also reported that the maximum turnover rate of the Na+,K+-ATPase in heart muscle cells is only about half that of Na+,K+-ATPase from kidney at a similar temperature. Significant kinetic differences also exist between the Na+,K+-ATPase of kidney and that of red blood cells. For example, at 0°C the Na+,K+-ATPase phosphoenzyme of red blood cells is insensitive to the addition of K+ ions and is rapidly dephosphorylated by ADP, whereas at higher temperatures it is dephosphorylated by both K+ and ADP (14,15). This difference in behavior at different temperatures is not observed in the kidney enzyme (16–18).
Because of the large amount of data that have been gathered on the partial reactions of the kidney enzyme, it is now possible to reconstruct the kinetics of its entire reaction cycle and make predictions regarding its steady-state behavior under different experimental conditions. Here, we present a mathematical model that allows such predictions, and we compare the predictions of the kidney-based model with experimental results obtained for the Na+,K+-ATPase in heart muscle cells via the whole-cell patch-clamp technique. For this comparison, we concentrated on two well-established observations made on heart muscle cells: the significant inhibition of pump current by inside-negative membrane potentials (13), and the significant inhibition of pump current by high concentrations of extracellular Na+ (up to 150 mM) observed at negative holding potentials (19). Our comparison indicates that there could well be significant differences in the kinetic behavior of heart and kidney Na+,K+-ATPase, in particular with respect to their voltage dependence. These differences are most likely due to the different levels of expression of isoforms of the Na+,K+-ATPase's major catalytic α-subunit. In the kidney enzyme, the α1 isoform constitutes >99% of the expression of the α-subunit (20); however, results from Gao et al. (21) indicate that in cardiac myocytes the α1 subunit is expressed to 82%, with 18% of the α-subunits being expressed as the α2 isoform.
Materials and Methods
Pump current simulations
We performed computer simulations of the steady-state pump current observed experimentally via the whole-cell patch-clamp technique using the commercially available program Berkeley Madonna 8.0 and the variable step-size Rosenbrock integration method for stiff systems of differential equations. The simulations yielded the time course of the concentration of each enzyme intermediate involved and the outward current (i.e., the number of elementary charges transported per pump molecule per second). For the purposes of simulations of the steady-state current, each enzyme intermediate was normalized to a unitary concentration and the enzyme was arbitrarily assumed to be totally in the E1 state initially. Each simulation was then carried out until the distribution between the different enzyme states no longer changed and the outward current reached a constant value.
In simulations of transient kinetic data, before simulating the time course of the current transients caused by any sudden change in the experimental conditions (e.g., Na+ concentration or membrane voltage), we calculated the initial steady-state distribution of the enzyme between the E1, E1P(Na+)3, E2P, and E2(K+)2 states by performing a simulation, as described in the previous paragraph, in which the enzyme was assumed to be totally in the E1 state initially. The simulation was carried out until the distribution between the various enzyme states no longer changed. This distribution was then used as a starting condition for the simulation of concentration-jump or voltage-jump experiments.
Results
Kinetic model
Under experimental conditions in which inorganic phosphate and ADP are absent, the complex Albers-Post cycle describing the partial reactions of Na+,K+-ATPase can be reduced to the simpler four-state model shown in Fig. 1. Here, E1P(Na+)3 and E2(K+)2 represent occluded states of the protein, i.e., states in which the respective ions are enclosed within the protein and have no direct access to either the cytoplasm or the extracellular fluid. In contrast, E1 and E2P represent states in which the ion-binding sites have access to the cytoplasm and the extracellular fluid, respectively. In the case of the occluded states, E1P(Na+)3 and E2(K+)2, no exchange of the occluded ions with either the cytoplasm or the extracellular fluid is possible. However, in the case of the nonoccluded states, we assume that rapid exchange of Na+ and K+ between the binding sites and either the cytoplasm or the extracellular fluid can occur. Thus, in the case of the E2P state, we assume that there is a rapid exchange of Na+ ions and K+ ions between the extracellular fluid and two of the ion transport binding sites. It has been well established that the stoichiometry of the Na+,K+-ATPase is 3Na+/2K+/ATP. Therefore, one of the ion-binding sites is considered to be completely specific for Na+, whereas Na+ or K+ can both bind with differing affinities to the other two. Therefore, ion binding to E2P can be treated as a series of coupled equilibria, as shown in Fig. 2. An analogous scheme can be drawn for the E1 state.
Figure 2.
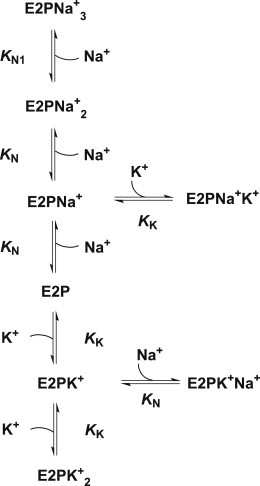
Scheme describing the coupled equilibria of Na+ and K+ binding to the E2P conformation of the enzyme. The model assumes competition between Na+ and K+ at two of the transport sites with dissociation constants KN and KK, respectively, and one specific Na+ transport site with a dissociation constant KN1.
In the four-state model of Fig. 1, therefore, we show only the major rate-determining steps of the enzyme cycle explicitly. In our computer model (see Appendix), we only include differential rate equations for the E1, E1P(Na+)3, E2, and E2(K+)2 states because we consider ion binding to E1 and E2P to be very rapid, such that the binding reactions to these two states relax instantaneously on the timescale of the four rate-determining steps, i.e., ion binding reactions are treated as equilibria. Thus, the four reactions whose kinetics are explicitly included in the model in sequence starting from E1 are as follows:
-
1.
Phosphorylation of the enzyme by ATP and simultaneous occlusion of three Na+ ions within the protein.
-
2.
Conformational change of phosphorylated enzyme involving a deocclusion of Na+ and opening of the binding sites to the extracellular fluid (and its reverse reaction).
-
3.
Occlusion of two K+ ions within the phosphorylated enzyme, stimulating a dephosphorylation of the protein.
-
4.
Conformational change of unphosphorylated enzyme involving a deocclusion of K+ and opening of the binding sites to the cytoplasm (and its reverse reaction).
Oka et al. (22) used a similar four-state model, also assuming rapid equilibria for ion and ATP binding, to model the steady-state activity of cardiac Na+,K+-ATPase. However, the mathematical procedure used here to determine the steady-state activity is very different from that used by Oka et al. (22), who calculated the pump current analytically by applying the King-Altman method (23), in which the steady-state turnover of the enzyme is directly calculated from the observed rate constants of all the reaction steps. Here we used a numerical procedure (see Materials and Methods) that also allows the kinetics of transient changes in steady-state pump current to be simulated.
In the model, we consider that each of the four rate-determining reactions only reaches its maximum observable rate constant when the reactant state is fully saturated by the appropriate substrates. For example, the maximum rate constant for phosphorylation, k1, is only achieved when the enzyme is fully saturated with three Na+ ions and ATP. Although it does not explicitly appear in Fig. 1, the model assumes that high-affinity binding of ATP to E1 is required to stimulate the reactions E1 → E1P(Na+)3 and E1 → E2(K+)2. Low-affinity binding of ATP to the E2 state is also assumed to stimulate the reaction E2(K+)2 → E1. As in the case of Na+ and K+ binding, ATP binding is also treated in the model as a rapid equilibrium.
This simple kinetic model excludes a number of partial reactions that experimentally are known to occur. Thus, the model does not take into account ADP-stimulated dephosphorylation of E1P(Na+)3, Pi-stimulated phosphorylation of E2, dephosphorylation of E2P in the absence of occluded K+, or conformational changes of unphosphorylated enzyme in the absence of bound ATP. However, under conditions of physiological levels of Na+, K+, and ATP in the cytoplasm and the absence of any added inorganic phosphate or ADP, these reactions are either effectively suppressed or their rate constants are negligible in comparison with those of the four major reactions shown in Fig. 1. Therefore, we consider that at this stage, the extra complexity that the model would gain by including these reactions is not warranted.
In addition to differential rate equations for each of the four major enzyme states, to complete the model we included differential rate equations to describe the transient current across the membrane. Because the enzyme pumps three Na+ ions out of the cell in exchange for two K+ ions in, there is a net transport of one positive charge out. In our model, we assume that ion-binding reactions are rapid equilibria. Therefore, when the enzyme is actively pumping both Na+ and K+, the release of two Na+ ions to the extracellular fluid will immediately be neutralized by the uptake of two K+ ions. Similarly, in the cytoplasm, when two K+ ions are released, this will be immediately neutralized by the uptake of two Na+ ions. Therefore, the rate of change of the outward current at any point in time can be described by the rate of release of one Na+ ion from the E2P state, which is given by the rate of conversion of E1P(Na+)3 to E2P minus the rate of the backward reaction (see Appendix, Eq. A15). This is an important difference from our previously published kinetic model (24), which only allows steady-state currents to be estimated from the steady-state rate of phosphate production.
A final important point regarding the construction of the model is the incorporation of voltage dependence. In patch-clamp measurements, it is possible to control the transmembrane voltage accurately. This has a significant influence on the kinetics of the charge-transporting (electrogenic) partial reactions of the enzyme. Therefore, this also needs to be included in the model. This can be done by multiplying the rate or equilibrium constants of all the electrogenic reactions by Boltzmann factors, i.e., exp(aFVm/RT) (see Appendix, Eqs. A9–A14). Here F is the Faraday constant, Vm is the total transmembrane potential difference, R is the ideal gas constant, T is the absolute temperature, and a is termed a dielectric coefficient and is the fraction of the total membrane potential difference that influences the electrogenic reaction concerned. It is sometimes approximated as the fractional distance across the membrane over which an ion is transported during an electrogenic reaction (25,26). Because there is a net transport of one positive charge due to ion pumping, if one proceeds around the Na+,K+-ATPase cycle in the normal physiological direction, the dielectric coefficients of all of the electrogenic reactions must add up to +1. The values of the dielectric coefficients we used in our model are based on values estimated in previous voltage-jump studies (27–29). Values of all the rate and equilibrium constants used in the simulations, as well as the values of the dielectric coefficients, are given in Table 1. All of the rate and equilibrium constants were derived from measurements on mammalian kidney Na+,K+-ATPase.
Table 1.
Values of the rate constants, equilibrium constants, and dielectric coefficients of the four-state model used for the simulations shown in Figs. 3–5
| Parameter | Reaction | Value | Reference |
|---|---|---|---|
| k1 | E1→E1P(Na+)3 | 200 s−1 | (37) |
| k2,V=0 | E1P(Na+)3 → E2P | 225 s−1 | (40) |
| k-2,V=0 | E2P → E1P(Na+)3 | 401 s−1 | (40) |
| k3,V=0 | E2P → E2(K+)2 | 342 s−1 | (7) |
| k4max | E2(K+)2 → E1 | 90 s−1 | (44) |
| k4min | E2(K+)2 → E1 | 11 s−1 | (45) |
| k-4 | E1 → E2(K+)2 | 550 s−1 | (51) |
| KN1i,V=0 | E1Na+3 ↔ E1Na+2 + Na+ | 1.8 mM | (37) |
| KNi | Microscopic dissociation constant for the first two Na+ ions from E1 | 8 mM | (37) |
| KN1o,V=0 | E2PNa+3 ↔ E2PNa+2 + Na+ | 100 mM | (35) |
| KNo,V=0 | Microscopic dissociation constant for the last two Na+ ions from E2P | 400 mM | (40) |
| KKi | Microscopic dissociation constant for two K+ ions from E1 | 10 mM | (12) |
| KKo | Microscopic dissociation constant for 2K+ from E2P | 1.33 mM | (38) |
| KA1 | E1ATP ↔ E1 + ATP | 8 μM | (37) |
| KA2 | E2(K+)2ATP ↔ E2(K+)2 + ATP | 71 μM | (37) |
| a(KN1i) | E1Na+3 ↔ E1Na+2 + Na+ | −0.25 | (52) |
| a(k2) | E1P(Na+)3 → E2P | +0.1 | (35) |
| a(k−2) | E2P → E1P(Na+)3 | −0.1 | (35) |
| a(KN1o) | E2PNa+3 ↔ E2PNa+2 + Na+ | +0.65 | (27,34,35) |
| a(KNo) | Dissociation of the last two Na+ ions from E2P | +0.37∗ | |
| a(k3) | E2P → E2(K+)2 | −0.37 | (53) |
This value was chosen to balance the dielectric coefficient of −0.37 determined by Rakowski et al. (53) for extracellular K+ binding and yield on overall transfer of one positive charge into the extracellular medium.
Simulations of the expected kinetic behavior of kidney Na+,K+-ATPase
Simulations of the expected dependence of the pump current, Ip, per pump molecule on the extracellular Na+ concentration and the total transmembrane potential difference, Vm, based on the Albers-Post model and the kinetic parameters given in Table 1 for mammalian kidney enzyme are shown in Fig. 3. For comparison, experimental results of Nakao and Gadsby (19) regarding the dependence of Ip for heart muscle Na+,K+-ATPase on both the extracellular Na+ and Vm are also reproduced. The experimental results indicate that for heart muscle Na+,K+-ATPase there is a significant positive slope in the I/V curve at negative membrane potentials, which becomes more pronounced as the extracellular Na+ concentration increases, i.e., at large negative membrane potentials, Ip increases with increasing Vm. The effect saturates as one moves to positive membrane potentials, at which point Ip becomes virtually voltage independent.
Figure 3.
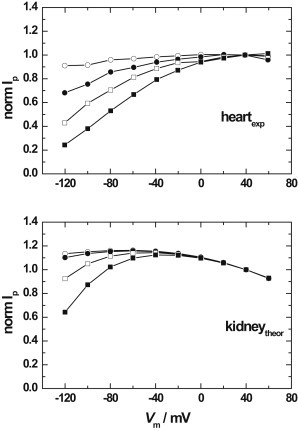
Dependence of the Na+,K+-ATPase current-voltage relationship (I/V curve) on the extracellular Na+ concentration. Symbols correspond to the following Na+ concentrations: 1.5 mM (○), 50 mM (●), 100 mM (□), and 150 mM (■). The solid lines between the points have simply been drawn to aid the eye of the reader. Upper curve: Experimental results for guinea pig heart ventricular myocytes, obtained via the whole-cell patch-clamp technique, reproduced from Fig. 3 of Nakao and Gadsby (19). The pump current, Ip, of each curve has been normalized to the value obtained at a holding potential of + 40 mV. The experimental conditions were [Na+]cyt = 50 mM, [K+]cyt = 0 mM, [K+]ext = 5.4 mM, [ATP]cyt = 10 mM, T = 36°C. Lower curve: Computer simulations of the expected I/V curve for mammalian kidney Na+,K+-ATPase pump current based on the kinetic and equilibrium parameters given in Table 1 and the Albers-Post scheme described by Figs. 1 and 2. The ion concentrations, ATP concentration, and temperature used for the simulations were the same as for the upper curve.
In comparison, the predicted behavior of kidney Na+,K+-ATPase is different in some respects. At negative holding potentials, there is still a positive slope of the I/V curve and the magnitude of the slope is still more pronounced at high extracellular Na+ concentrations, but the magnitude of the drop in pump current in going from 1.5 to 150 mM extracellular Na+ is significantly smaller. For example, at 150 mM extracellular Na+ and −120 mV, the normalized Ip drops to ∼0.6, whereas for the heart enzyme, Ip drops experimentally to ∼0.2. The other difference between the experimental heart results and the simulated kidney results is that the kidney results predict a slight negative slope in the I/V curve at positive potentials, which is independent of the extracellular Na+ concentration, in contrast to an apparent saturation in the pump current at positive potentials in the case of the heart results. If all of the experimental parameters used in the simulations are correct, this result indicates that heart and kidney Na+,K+-ATPases must have some slightly different kinetic or equilibrium parameters, at least with respect to at least one of the partial reactions that determines the overall pump turnover, i.e., the rate-determining steps, the steps leading into rate-determining steps, or the degree of charge displacement associated with the transport charge of these steps.
Voltage-jump transient simulation
To demonstrate the applicability of the model for reproducing the results of transient kinetic experiments, we carried out simulations in which the membrane voltage was rapidly changed from −120 mV to 0 mV. This corresponds to the experimental procedure used by Gadsby et al. (30) on the Na+,K+-ATPase in squid giant axons. However, voltage-jump experiments of this type have also been conducted on the Na+,K+-ATPase in cardiac myocytes and Xenopus oocytes in addition to squid giant axons (27–31).
A voltage-jump simulation using the kinetic and equilibrium parameters given in Table 1 is shown in Fig. 4 (upper panel). In accord with the experimental conditions used by Gadsby et al. (30), the ion and ATP concentrations used were [Na+]o = 25 mM. [Na+]i = 80 mM, [K+]o = [K+]i = 0 mM and [ATP] = 5 mM. In the absence of any intracellular ADP or extracellular K+, the enzyme can be assumed, both before and after the voltage jump, to be distributed totally between the E1P(Na+)3 state and the E2P states (occupied by zero, one, two, or three Na+ ions). Before the voltage jump from −120 to 0 mV occurs, the simulation indicates that 56% of the enzyme should be in the E1P(Na+)3 state and 44% should be in E2P states. After the voltage jump, the final distribution at the end of the voltage transient becomes 0.2% in the E1P(Na+)3 state and 99.8% in E2P states. This significant redistribution of the enzyme from E1P(Na+)3 to E2P is accompanied by the release of Na+ from the specific Na+ ion binding site. Therefore, the voltage jump is associated with a rapid rise in the outward current transient as the Na+ ions are released to the extracellular fluid, and a slower decay back to zero current because movement of the enzyme around its catalytic cycle past the E2P state in the absence of extracellular K+ is inhibited (see Fig. 4, upper panel). The decay back to zero current is exponential, with a relaxation time of 4 ms. This value is controlled predominantly by the reciprocal of the rate constant for the E1P(Na+)3 → E2P transition at 0 mV of 225 s−1 (see Table 1). This simulated result is in good agreement with the slowest current transient observed by Gadsby et al. (30) with a time constant of 1–10 ms, which they also attributed to the release of occluded Na+ from the enzyme as a consequence of the E1P(Na+)3 → E2P transition. Gadsby et al. (30) also observed two faster but smaller-amplitude transients, which they attributed to the release from E2P of the two Na+ ions bound to the nonspecific sites, i.e., E2PNa+2 → E2PNa+ + Na+ and E2PNa+ → E2P + Na+. These two transients had time constants of 0.2–0.5 ms and ≤28 μs. These two faster transients were not reproduced by the simulations, because the model assumes that ion binding to and release from the E2P state are rapid equilibria on the timescale of the four reactions explicitly included in the model (see Figs. 1 and 2). To reproduce these smaller rapid transients, the model would have to be extended to explicitly include the kinetics of ion binding. Thus, the model as it stands is applicable to the simulation of transients from the millisecond time range and beyond, but cannot be applied to simulations into the submillisecond range. The ability of the model to reproduce current transients arises because of its basis on the numerical integration of differential rate equations. This is a significant advantage of this approach over a fully analytical one, such as that used in the model of Oka et al. (22), which can only be used to calculate steady-state currents.
Figure 4.
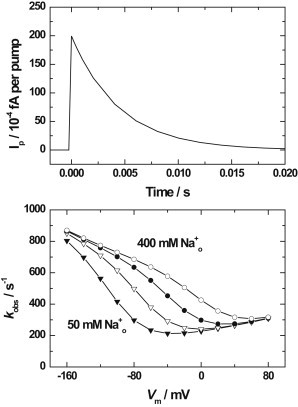
Simulation of a voltage-jump transient. The initial conditions were [Na+]cyt = 80 mM, [Na+]ext = 25 mM, [K+]cyt = [K+]ext = 0 mM, [ATP]cyt = 5 mM, Vm = −120 mV, T = 22°C, as in the experiments of Gadsby et al. (30). At time = 0, the membrane voltage was jumped to 0 mV. The current transient is attributed to the voltage-dependent release of Na+ from the E2P state, which is rate-limited by the E1P(Na+)3 → E2PNa+3 transition.
The lower panel of Fig. 4 presents the results of calculations of the expected observed rate constant, kobs (i.e., the reciprocal of the time constant), of the decaying phase of the voltage-jump transient and its dependence on both the final transmembrane voltage and the extracellular Na+ concentration. Using the values given for the kidney enzyme in Table 1, the value of kobs can be calculated directly from the following equation:
| (1) |
where f(3Nao) is the fraction of enzyme in the E2P state with three Na+ ions bound, and k2 and k-2 are respectively the voltage-dependent forward and backward rate constants of the E1P(Na+)3 → E2P transition (see Eqs. A10 and A11 in the Appendix). The simulated results show a significant increase in kobs as the extracellular Na+ concentration increases and as the membrane potential becomes more negative. Both of these effects can be explained by an increase in occupation of sites on E2P by Na+ ions, which increases the value of the term f(3Nao) in Eq. 1 and hence causes kobs to increase. At positive membrane potentials, there is a smaller increase in kobs with increasing membrane potential. This effect can be explained by the relatively small voltage dependence of k2 (see Eq. A10). Qualitatively similar behavior to that shown in Fig. 4 was experimentally observed by Holmgren et al. (29) in measurements on the Na+,K+-ATPase of squid giant axons. The only noteworthy difference between our calculations and the experimental results of Holmgren et al. (29) is the range of kobs values. The measurements showed a saturating value of ∼1400 s−1 at negative potentials and a minimum value of ∼100 s−1, whereas the calculations indicate a saturating value of ∼900 s−1 at negative potentials and a minimum value of ∼200 s−1. These differences must be due to different magnitudes of the rate constants k2,V=0 and k-2,V=0 for the kidney and squid enzymes.
Na+,K+-ATPase regulation
Because the Na+,K+-ATPase plays such a crucial role in animal physiology, it must adapt to changing cellular conditions and physiological stimuli (32), and therefore its activity must be regulated. In principle, membrane proteins can be regulated by changes in the level of their expression, changes in delivery and incorporation into the membrane, or post-translational modifications to their structure that change the activity of the protein itself. Such modifications are termed acute mechanisms of regulation because they are fast-acting in comparison with changes in expression level. Both phosphorylation and glutathionylation have been suggested as possible acute regulatory mechanisms. Recently, Massey et al. (33) reported that in the kidney, a differential regulatory phosphorylation of the Na+,K+-ATPase occurs depending on the enzyme's conformational state. Liu et al. (34) found that the β-subunit of Na+,K+-ATPase in the heart undergoes glutathionylation, also depending on the pump's conformational state. These results suggest that any shift in the enzyme's distribution between different conformational states could influence its propensity toward regulatory post-translational modification. A possible physiological mechanism that could shift the enzyme's conformational distribution is an increase in the cytoplasmic Na+ concentration. This would occur transiently in nerve and muscle cells at the onset of an action potential as a normal part of their physiological activity. Sustained increases in the cytoplasmic Na+ concentration level are observed in red blood cells in certain hereditary blood conditions, i.e., spherocytosis and elliptocytosis, in which the plasma membrane has a higher than normal ion permeability. The cytoplasmic Na+ level influences the enzyme's conformational distribution because it is not saturating under normal physiological conditions for most cells, and the phosphorylation of the enzyme by ATP, which is dependent on cytoplasmic Na+ binding, is a major rate-determining step of the enzyme's pump cycle (24). The kinetic model presented here allows the time course and magnitude of any shifts in the enzyme's conformational equilibrium to be calculated. To demonstrate this, we simulated the time courses of the population of enzyme in the states E1, E2, E1P, and E2P after a sudden jump in the cytoplasmic Na+ concentration from a normal physiological level of 15 mM to a concentration of 150 mM (see Fig. 5).
Figure 5.
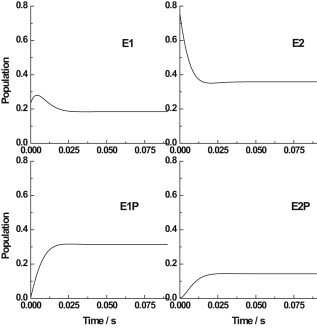
Simulations of the time courses of the relative populations of the Na+,K+-ATPase in the conformational states E1, E2, E1P, and E2P after a jump in the cytoplasmic Na+ concentration from 15 to 150 mM. All other conditions ([Na+]ext = 140 mM, [K+]cyt = 120 mM, [K+]ext = 4 mM, [ATP]cyt = 3 mM, Vm = −80 mV, T = 24°C) were held constant. The simulations were based on the kinetic and equilibrium parameters given in Table 1.
Overall, the simulations predict that an increase in the cytoplasmic Na+ concentration should be accompanied by increases in the populations of phosphorylated states (E1P and E2P) at the expense of the population of unphosphorylated states (particularly E2). The E1 state shows an initial transient increase in its population due to the shift in the E1/E2 distribution in favor of the Na+-selective E1 state, which is followed by a drop in its population. At the initial cytoplasmic Na+ concentration of 15 mM, the enzyme is almost entirely in unphosphorylated states (76% in E2 and 19% in E1). This is because at this concentration, the slowest steps of the pump cycle are the transition E2(K+)2 → E1 + 2K+ and the phosphorylation step E1Na+3 + ATP → E1P(Na+)3 + ADP. Hence, the enzyme accumulates in the states, leading into the major rate-determining steps, E1Na+3 and E2(K+)2. However, after the cytoplasmic Na+ concentration jumps to 150 mM, the effective rate constant for the phosphorylation reaction dramatically increases because of the increase in level of saturation of the ion-binding sites on E1 by cytoplasmic Na+. With the phosphorylation reaction no longer contributing so strongly to the rate determination of the cycle, the level of enzyme in the phosphorylated states increases significantly (i.e., 31% in E1P and 14% in E2P from 0.4% and 0.2% initially).
The simulations shown in Figs. 4 and 5 demonstrate that the model is capable of predicting conformational distribution changes due to both voltage and concentration jumps, which could potentially be used to rationalize changes in conformationally dependent regulatory modifications to the pump.
Discussion
The Na+,K+-ATPase is an electrogenic ion pump, i.e., it carries out a net transport of charge across the plasma membrane. This is due to its stoichiometry under normal physiological conditions of three Na+ ions transported out of the cell and two K+ ions transported into the cell during each turnover. Because the Na+,K+-ATPase transports net charge across the membrane, its activity must in principle be dependent on the electrical membrane potential. However, whether or not a voltage dependence of its activity is apparent over physiologically relevant membrane potentials (i.e., ∼−80 to +60 mV in the case of the heart) depends on how strongly the charge transporting steps influence the overall turnover of the enzyme. A significant voltage dependence of the enzyme's steady-state activity will only be apparent when either the charge-transporting steps themselves are rate-determining steps of the cycle or the charge-transporting steps influence the population of an enzyme intermediate that is a reactant leading into a rate-determining step.
The simulations presented in Fig. 3, based on kinetic and equilibrium parameters derived from mammalian kidney enzyme, indicate that for the kidney Na+,K+-ATPase, a lower degree of voltage dependence would be expected across the membrane potential range of 0 to −120 mV from that observed experimentally for heart muscle Na+,K+-ATPase (13,19) (see Fig. 3). This suggests some differences in the kinetic or equilibrium parameters of the heart and kidney enzymes.
However, Oka et al. (22) recently reported simulations that showed a very different result. These authors also carried out simulations based on kidney data, but they found a strong voltage dependence and extracellular Na+ concentration dependence identical to that measured in heart cells (13,19). The decisive difference between the simulations of Oka et al. (22) and those presented here lies in the values of the rate constants used. The major charge-transporting step of the Na+,K+-ATPase is widely accepted to be the release of the first Na+ to the extracellular medium, which is rate-limited by the E1P → E2P transition (27,29,30,35). Increasingly negative membrane potentials would cause Na+ from the extracellular medium to rebind to the E2P state, driving the enzyme back toward the E1P(Na+)3 state. Whether this effect has a major influence on the overall turnover depends on the forward and backward rate constants of the E1P → E2P reaction. In their model, Oka et al. (22) chose values of 80 s−1 and 8 s−1 at 37°C (or 31 s−1 and 3.1 s−1 at 20°C) for the forward and backward rate constants, respectively. This makes the E1P → E2P reaction the slowest forward reaction of their entire kinetic model, i.e., the major rate-determining step of their cycle. If the charge-transporting step of the cycle is simultaneously the major rate-determining step of the cycle, it is to be expected that under these conditions significant voltage dependence would be predicted.
However, a large body of experimental evidence from various studies indicates that the E1P → E2P transition is not a major rate-determining step of the kidney enzyme (36–40). All of these studies indicate a rate constant for the E1P → E2P transition of ≥200 s−1 at 24°C. Also, for heart muscle Na+,K+-ATPase, the E1P → E2P transition has been shown to be a fast reaction. Lu et al. (41) estimated a rate constant for the heart enzyme in the range of 300–900 s−1. On the basis of their data, Gadsby and Nakao (13) also came to the conclusion that the major voltage-sensitive step of the heart Na+,K+-ATPase is not rate-limiting; rather, the voltage-sensitive step controls the concentration of the enzyme intermediate entering the rate-limiting step. Therefore, it would appear that the good agreement in voltage dependence and extracellular Na+ dependence between the simulations of Oka et al. (22) and the measurements of Gadsby and Nakao (13) is simply fortuitous, because the simulations were based on an artificially low rate parameter. In fact, Oka et al. (22) stated that the rate constants they used may require revision.
For mammalian kidney Na+,K+-ATPase, it is widely accepted that under saturating conditions of all substrates and no membrane potential, the major rate-determining step is the E2 → E1 transition (see Fig. 1) and its associated release of K+ to the cytoplasm (42–45). Experiments on solid supported membranes have shown that this reaction does not involve any significant charge transport (46). This being the case, one would not expect any major voltage dependence of the activity of mammalian kidney Na+,K+-ATPase when no electrical potential is applied across the membrane (i.e., at Vm = 0), which was the condition under which the rate constant for the E2 → E1 transition was determined (42–45). This is what the simulations in Fig. 3 show. The experimental measurements on the heart enzyme (see Fig. 3) also show no significant voltage dependence (i.e., an approximately zero slope of the I/V curve) around 0 mV. This would be consistent with the E2 → E1 transition also being the major rate-determining step of the heart enzyme around 0 mV.
However, both the experimental heart enzyme results and, to a lesser degree, the simulations of kidney enzyme show a significant dependence of the pump current on the extracellular Na+ concentration (see Fig. 3). If the observed extracellular Na+ concentration dependence is not due to a rate-limiting E1P → E2P transition or to any other rate-limiting charge-transporting step, then Gadsby and Nakao (13) must be correct in suggesting that a reaction directly following the charge-transporting step must become rate-limiting at negative potentials. The reaction immediately following the release of Na+ from the E2P state is the occlusion of K+ from the extracellular medium. As far as we are aware, no direct measurements on the rate constant of this reaction for the heart enzyme have been made. For the pig kidney enzyme, the reaction is fast when the E2P state is completely saturated with K+, with a rate constant of ∼340 s−1 at 24°C (7). However, this reaction could contribute significantly to rate limitation at negative potentials because a negative potential would promote electrogenic Na+ binding to the E2P state and shift the E1P/E2P distribution back toward the E1P(Na+)3 state. The consequent depletion in population of the E2PK+2 state would decrease the effective rate constant of K+ occlusion by E2P, leading to a possible decrease in the pump turnover.
Whether this effect does in fact cause a decrease in turnover depends on the rate constants of the individual reaction steps. For the kidney enzyme, using the parameters given in Table 1, the simulations shown in Fig. 3 indicate that it does. The simulations carried out at 150 mM extracellular Na+ and −120 mV yield a degree of occupation of the E2P state by two K+ ions of 0.093. This is in comparison with a value of 0.634 at 1.5 mM Na+ and −120 mV. Thus, the higher Na+ concentration causes a dramatic decrease in the occupation of the E2P state by two K+ ions. Taking into account the voltage of −120 mV via Eq. 14, one can then calculate an apparent rate constant for K+ occlusion by the E2P state. Thus, multiplying the value of k3 at zero membrane potential of 342 s−1 by 0.093 and the Boltzmann factor shows that the apparent rate constant reduces to a value of 169 s−1. This is not far above the slowest rate constant in the cycle, i.e., that for the E2 → E1 transition of 90 s−1 (k4). Thus, the voltage-induced drop in occupation of E2P by K+ would be expected to make K+ occlusion by E2P a significant contributor to rate determination at negative potentials. In contrast, at 1.5 mM extracellular Na+ and −120 mV, if one does the same calculation, one arrives at an apparent rate constant for K+ occlusion by E2P of 1151 s−1. This is so far above the rate constant for the E2 → E1 transition that one would not expect any significant contribution of K+ occlusion by E2P to the rate limitation of the overall pump turnover. This accounts for the very low dependence of the pump current on voltage at low extracellular Na+ concentrations.
A possible explanation for the differences between the behavior of the heart enzyme and that predicted by the simulations for the kidney enzyme is that the two enzymes are composed of different isoforms. In the kidney, the major catalytic subunit of the enzyme is present predominantly as the α1 isoform (20), whereas in heart muscle both the α1 and α2 isoforms are present (21,47). Horisberger and Kharoubi-Hess (48) found that when the α1 subunit was expressed together with the β1 subunit in Xenopus oocytes, it displayed a smaller voltage dependence at negative potentials than the α2 subunit when expressed with β1. They did not coexpress any FXYD proteins together with the α- and β-subunits. In agreement with the results of Horisberger and Kharoubi-Hess (48), Apell and Bersch (49) found very little voltage dependence of the activity of the α1β1 form of the enzyme over the membrane potential range of −100 to 0 mV when they reconstituted it from rabbit kidney into synthetic lipid vesicles. Thus, it seems to be the case that the difference in the I/V behaviors of the heart and kidney most likely arises from intrinsic structural differences in the α-subunit and different degrees of expression of the α-isoforms in heart and kidney tissues. Horisberger and Kharoubi-Hess (48) also found that the α2 isoform of the enzyme had a slightly lower apparent affinity for K+ ions than the α1 isoform. This is further supported by the results of Segall et al. (50), who reported that the α2 isoform favors more strongly the Na+-stabilized E1 state over the K+-stabilized E2 state. On the basis of kinetic studies on α-subunit chimeras, they attributed this difference primarily to sequence differences in the N-terminal third of the α-subunit. A difference in Na+/K+ ion selectivity could be the underlying physical reason for the increased voltage dependence of the heart enzyme. A lower affinity of the E2P state for K+ ions means that Na+ can more effectively compete for occupation of the nonspecific ion sites on E2P, even at less negative potentials. This helps to drive the enzyme back toward the E1P(Na+)3 state and simultaneously reduces the degree of occupation of E2P by two K+ ions. The consequence of this is a reduced effective rate constant for K+ occlusion by E2P and hence a reduced overall turnover of the enzyme. Apart from a decrease in K+ affinity, an increase in Na+ affinity to E2P and an increase in the rate constant for the backward rate constant, E2PNa+3 → E1P(Na+)3 are also possible mechanisms by which the voltage dependence of the enzyme could be increased. Quenched-flow results obtained by Segall et al. (50) indicate that there is unlikely to be any difference in the rate constant of the forward reaction E1P(Na+)3 → E2P(Na+)3 for the heart and kidney enzymes.
The good agreement between the predictions of the model and the experimental behavior of the α1β1 enzyme gives one confidence that the model can be used to investigate the kinetics of regulation of both the kidney enzyme (as described in the Results section) and, with minor modifications, the heart enzyme. In the case of the heart enzyme, however, it would be important to bear in mind that the kinetic and equilibrium parameters used in the modeling would be apparent values, because, as described above, the expressed enzyme in that tissue consists of a mixed population of α-subunit isoforms (21,47).
Finally, it is interesting to consider the significance of the results shown in Fig. 3 within the physiological context of heart and kidney function. A typical extracellular Na+ concentration of a heart muscle cell is 150 mM (54) and a typical resting potential is ∼−80 mV. However, before each contraction, the membrane potential increases to +60 mV (the action potential) due to the influx of Na+ through voltage-sensitive Na+ channels. According to the results of Nakao and Gadsby (19), shown in the upper panel of Fig. 3, at the physiological extracellular Na+ concentration of 150 mM this increase in membrane potential alone should cause a roughly 100% increase in the pump turnover. This would be advantageous for the cell, because it would make it easier for the Na+,K+-ATPase to pump out the excess Na+ ions that had just entered via the Na+ channels during the extended plateau phase of the cardiac action potential, and thus to reestablish resting conditions before the next action potential. This voltage-dependent increase in Na+,K+-ATPase activity would further enhance the stimulation of the enzyme already expected by the increase in intracellular Na+ concentration, which under physiological conditions is not at a saturating level. A lower activity of the heart Na+,K+-ATPase under resting conditions of −80 mV also has the advantage of conserving ATP when high ion pumping rates are not essential. In the case of kidney cells, however, there are no changes in membrane potential associated with their activity. The membrane potential is always ∼−80 mV. Thus, there is no advantage for a kidney cell in possessing a voltage-dependent Na+,K+-ATPase, and a kidney cell should not suffer at all by possessing a lower voltage dependence of its Na+,K+-ATPase. Therefore, the experimental and predicted results for heart and kidney Na+,K+-ATPase shown in Fig. 3 seem to make sense in terms of the physiological function of these two types of cells.
Acknowledgments
The authors acknowledge the support and advice of the late Prof. Bob Rakowski (Ohio University, Athens, OH), particularly regarding the incorporation of voltage dependence into our kinetic modeling, and helpful discussions with Prof. Klaus Fendler (Max Planck Institute of Biophysics, Frankfurt, Germany) and Prof. Doug Yingst (Wayne State University, Detroit, MI).
H.H.R. acknowledges, with gratitude, financial support (Project Grant 633252) from the National Health and Medical Research Council (Australia). R.J.C. received financial support from the Australian Research Council (Discovery Grant DP-120103548).
Appendix: Simulation of the Steady-State Pump Current
Based on the four-state Albers-Post model of the Na+,K+-ATPase enzymatic cycle shown in Fig. 1, the following differential rate equations describe the change in concentration of all of the enzyme intermediates:
| (A1) |
| (A2) |
| (A3) |
| (A4) |
In these equations, the term f(3Nai) represents the fraction of enzyme in the E1 state occupied by three Na+ ions. Similarly, f(ATPE1) represents the fraction of enzyme in the E1 state occupied by ATP. The significance of these f-terms can be easily understood if we take the phosphorylation reaction as an example. The maximum rate constant for phosphorylation, k1, is only achieved when the E1 state of the enzyme is completely saturated by three Na+ ions and one ATP molecule. Thus, the observed rate constant, k1obs, for the reaction is given by k1 multiplied by the probability that E1 has three bound Na+ ions (= f(3Nai)) and by the probability that E1 has a bound ATP molecule (=f(ATPE1)). This simple mathematical formulation of the rates will break down at very low cytoplasmic Na+ and ATP concentrations, when second-order binding of the substrates to the enzyme becomes slower than the subsequent first-order phosphorylation and occlusion of Na+. However, under normal physiological conditions, the assumption of rapid binding equilibria, on which Eqs. A1–A4 and the four-state scheme shown in Fig. 1 are based, can be considered a good approximation.
Also appearing in Eqs. A1–A4 are the fraction of enzyme in the E2 state with ATP bound, f(ATPE2); the fraction of enzyme in the E2P state with three Na+ ions bound, f(3Nao); the fraction of enzyme in the E2P state with two K+ ions bound, f(2Ko); and the fraction of enzyme in the E1 state with two K+ ions bound, f(2Ki). In a manner similar to that described for the phosphorylation reaction, these fractions or probabilities modify the observed rate constant for each relevant reaction step, as shown in Eqs. A1–A4. Because in our model we consider all of the substrate binding reactions to be equilibria, the f-terms are determined solely by the substrate concentrations and the relevant equilibrium (or dissociation) constants of each substrate. Thus,
| (A5) |
| (A6) |
In contrast to ATP binding, the expressions for the f-terms describing Na+ and K+ binding are much more complex because here one must consider competition between two Na+ ions and two K+ ions for the same binding sites, as shown in Fig. 2. The relevant expression for Na+ binding to E2P is:
| (A7) |
An analogous expression to Eq. A7 can be written for f(3Nai), in which all of the superscript and subscript o's are replaced by i's, to indicate binding to E1 from the intracellular fluid (cytoplasm) rather than the outer medium (extracellular fluid). The relevant expression for K+ binding to E2P is:
| (A8) |
An analogous expression to Eq. A7 can also be written for f(2Ki), in which all the superscript and subscript o's are replaced by i's, to indicate binding to E1 from the cytoplasm.
Our use of the fraction of enzyme in the E2P state with three Na+ ions bound, f(3Nao), as a measure of the probability of the reverse reaction E2P → E1P(Na+)3 occurring is based on the assumption that this transition can only occur after three Na+ ions have bound to the E2P state. Experimental data indicating that this is indeed the case were recently obtained via voltage-jump measurements on the Na+,K+-ATPase of giant squid axons (25).
The effects of the transmembrane electrical potential difference V (defined as electrical potential in minus electrical potential out) are taken into account in the model by the following Boltzmann expressions:
| (A9) |
| (A10) |
| (A11) |
| (A12) |
| (A13) |
| (A14) |
where F, R, and T represent the Faraday constant, the universal gas constant, and the absolute temperature, respectively. The numerical factors preceding F in each expression are the relevant dielectric coefficients for each reaction, as given in Table 1.
Based on the model, the differential rate equation for the transient outward current due to the Na+,K+-ATPase, Ip, is given by
| (A15) |
The outward current at any point in time can be determined by numerically integrating the coupled series of differential rate equations (Eqs. A1–A4 and A15). For the purposes of this work, the simulations were carried out until Ip no longer changed. This was then taken as its steady-state value.
References
- 1.Jørgensen P.L. Purification and characterization of (Na+ + K+ )-ATPase. 3. Purification from the outer medulla of mammalian kidney after selective removal of membrane components by sodium dodecylsulphate. Biochim. Biophys. Acta. 1974;356:36–52. doi: 10.1016/0005-2736(74)90292-2. [DOI] [PubMed] [Google Scholar]
- 2.Jørgensen P.L. Isolation of (Na+ + K+)-ATPase. Methods Enzymol. 1974;32:277–290. [PubMed] [Google Scholar]
- 3.Glynn I.M. The Na+,K+-transporting adenosine triphosphatase. In: Martonosi A.N., editor. 2nd ed. Vol. 3. Plenum; New York: 1985. pp. 35–114. (The Enzymes of Biological Membranes). [Google Scholar]
- 4.Sachs J.R. Cation fluxes in the red blood cell: Na+,K+ pump. Methods Enzymol. 1989;173:80–93. doi: 10.1016/s0076-6879(89)73006-8. [DOI] [PubMed] [Google Scholar]
- 5.Kaplan J.H. Ion movements through the sodium pump. Annu. Rev. Physiol. 1985;47:535–544. doi: 10.1146/annurev.ph.47.030185.002535. [DOI] [PubMed] [Google Scholar]
- 6.Hansen A.S., Kraglund K.L., Esmann M. Bulk properties of the lipid bilayer are not essential for the thermal stability of Na,K-ATPase from shark rectal gland or pig kidney. Biochem. Biophys. Res. Commun. 2011;406:580–583. doi: 10.1016/j.bbrc.2011.02.094. [DOI] [PubMed] [Google Scholar]
- 7.Myers S.L., Cornelius F., Clarke R.J. Kinetics of K+ occlusion by the phosphoenzyme of the Na+,K+-ATPase. Biophys. J. 2011;100:70–79. doi: 10.1016/j.bpj.2010.11.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Morth J.P., Pedersen B.P., Nissen P. Crystal structure of the sodium-potassium pump. Nature. 2007;450:1043–1049. doi: 10.1038/nature06419. [DOI] [PubMed] [Google Scholar]
- 9.Shinoda T., Ogawa H., Toyoshima C. Crystal structure of the sodium-potassium pump at 2.4 A resolution. Nature. 2009;459:446–450. doi: 10.1038/nature07939. [DOI] [PubMed] [Google Scholar]
- 10.Ogawa H., Shinoda T., Toyoshima C. Crystal structure of the sodium-potassium pump (Na+,K+-ATPase) with bound potassium and ouabain. Proc. Natl. Acad. Sci. USA. 2009;106:13742–13747. doi: 10.1073/pnas.0907054106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cable M.B., Briggs F.N. Allosteric regulation of cardiac sarcoplasmic reticulum Ca-ATPase: a comparative study. Mol. Cell. Biochem. 1988;82:29–36. doi: 10.1007/BF00242512. [DOI] [PubMed] [Google Scholar]
- 12.Therien A.G., Blostein R. K+/Na+ antagonism at cytoplasmic sites of Na+-K+-ATPase: a tissue-specific mechanism of sodium pump regulation. Am. J. Physiol. 1999;277:C891–C898. doi: 10.1152/ajpcell.1999.277.5.C891. [DOI] [PubMed] [Google Scholar]
- 13.Gadsby D.C., Nakao M. Steady-state current-voltage relationship of the Na/K pump in guinea pig ventricular myocytes. J. Gen. Physiol. 1989;94:511–537. doi: 10.1085/jgp.94.3.511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Blostein R. Relationships between erythrocyte membrane phosphorylation and adenosine triphosphate hydrolysis. J. Biol. Chem. 1968;243:1957–1965. [PubMed] [Google Scholar]
- 15.Kaplan J.H., Kenney L.J. Temperature effects on sodium pump phosphoenzyme distribution in human red blood cells. J. Gen. Physiol. 1985;85:123–136. doi: 10.1085/jgp.85.1.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Post R.L., Kume S., Sen A.K. Flexibility of an active center in sodium-plus-potassium adenosine triphosphatase. J. Gen. Physiol. 1969;54:306–326. doi: 10.1085/jgp.54.1.306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.White B., Blostein R. Comparison of red cell and kidney (Na+K)-ATPase at 0°C. Biochim. Biophys. Acta. 1982;688:685–690. doi: 10.1016/0005-2736(82)90280-2. [DOI] [PubMed] [Google Scholar]
- 18.Hara Y., Nakao M. Sodium ion discharge from pig kidney Na+, K+-ATPase Na+-dependency of the E1P-E2P equilibrium in the absence of KCl. J. Biochem. 1981;90:923–931. doi: 10.1093/oxfordjournals.jbchem.a133580. [DOI] [PubMed] [Google Scholar]
- 19.Nakao M., Gadsby D.C. [Na] and [K] dependence of the Na/K pump current-voltage relationship in guinea pig ventricular myocytes. J. Gen. Physiol. 1989;94:539–565. doi: 10.1085/jgp.94.3.539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lücking K., Nielsen J.M., Jørgensen P.L. Na-K-ATPase isoform (α3, α2, α1) abundance in rat kidney estimated by competitive RT-PCR and ouabain binding. Am. J. Physiol. 1996;271:F253–F260. doi: 10.1152/ajprenal.1996.271.2.F253. [DOI] [PubMed] [Google Scholar]
- 21.Gao J., Wymore R., Baldo G.J. Isoform-specific regulation of the sodium pump by α- and β-adrenergic agonists in the guinea-pig ventricle. J. Physiol. 1999;516:377–383. doi: 10.1111/j.1469-7793.1999.0377v.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Oka C., Cha C.Y., Noma A. Characterization of the cardiac Na+/K+ pump by development of a comprehensive and mechanistic model. J. Theor. Biol. 2010;265:68–77. doi: 10.1016/j.jtbi.2010.04.028. [DOI] [PubMed] [Google Scholar]
- 23.King E.L., Altman C. A schematic method of deriving the rate laws for enzyme-catalyzed reactions. J. Phys. Chem. 1956;60:1375–1378. [Google Scholar]
- 24.Kong B.Y., Clarke R.J. Identification of potential regulatory sites of the Na+,K+-ATPase by kinetic analysis. Biochemistry. 2004;43:2241–2250. doi: 10.1021/bi0355443. [DOI] [PubMed] [Google Scholar]
- 25.Läuger P. Thermodynamic and kinetic properties of electrogenic ion pumps. Biochim. Biophys. Acta. 1984;779:307–341. doi: 10.1016/0304-4157(84)90015-7. [DOI] [PubMed] [Google Scholar]
- 26.Läuger P. A microscopic model for the current-voltage behaviour of the Na,K-pump. Eur. Biophys. J. 1986;13:309–321. [Google Scholar]
- 27.Rakowski R.F. Charge movement by the Na/K pump in Xenopus oocytes. J. Gen. Physiol. 1993;101:117–144. doi: 10.1085/jgp.101.1.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Holmgren M., Rakowski R.F. Pre-steady-state transient currents mediated by the Na/K pump in internally perfused Xenopus oocytes. Biophys. J. 1994;66:912–922. doi: 10.1016/s0006-3495(94)80867-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Holmgren M., Wagg J., Gadsby D.C. Three distinct and sequential steps in the release of sodium ions by the Na+/K+-ATPase. Nature. 2000;403:898–901. doi: 10.1038/35002599. [DOI] [PubMed] [Google Scholar]
- 30.Gadsby D.C., Bezanilla F., Holmgren M. The dynamic relationships between the three events that release individual Na+ ions from the Na+/K+-ATPase. Nat. Commun. 2012;3:669. doi: 10.1038/ncomms1673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nakao M., Gadsby D.C. Voltage dependence of Na translocation by the Na/K pump. Nature. 1986;323:628–630. doi: 10.1038/323628a0. [DOI] [PubMed] [Google Scholar]
- 32.Therien A.G., Blostein R. Mechanisms of sodium pump regulation. Am. J. Physiol. Cell Physiol. 2000;279:C541–C566. doi: 10.1152/ajpcell.2000.279.3.C541. [DOI] [PubMed] [Google Scholar]
- 33.Massey K.J., Li Q., Yingst D.R. Angiotensin II-dependent phosphorylation at Ser11/Ser18 and Ser938 shifts the E2 conformations of rat kidney Na+/K+-ATPase. Biochem. J. 2012;443:249–258. doi: 10.1042/BJ20111398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liu C.-C., Garcia A., Rasmussen H.H. Susceptibility of β1 Na+-K+ pump subunit to glutathionylation and oxidative inhibition depends on conformational state of pump. J. Biol. Chem. 2012;287:12353–12364. doi: 10.1074/jbc.M112.340893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wuddel I., Apell H.J. Electrogenicity of the sodium transport pathway in the Na,K-ATPase probed by charge-pulse experiments. Biophys. J. 1995;69:909–921. doi: 10.1016/S0006-3495(95)79965-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kane D.J., Fendler K., Clarke R.J. Stopped-flow kinetic investigations of conformational changes of pig kidney Na+,K+-ATPase. Biochemistry. 1997;36:13406–13420. doi: 10.1021/bi970598w. [DOI] [PubMed] [Google Scholar]
- 37.Clarke R.J., Kane D.J., Bamberg E. Kinetics of Na+-dependent conformational changes of rabbit kidney Na+,K+-ATPase. Biophys. J. 1998;75:1340–1353. doi: 10.1016/S0006-3495(98)74052-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kane D.J., Grell E., Clarke R.J. Dephosphorylation kinetics of pig kidney Na+,K+-ATPase. Biochemistry. 1998;37:4581–4591. doi: 10.1021/bi972813e. [DOI] [PubMed] [Google Scholar]
- 39.Geibel S., Barth A., Fendler K. P3-[2-(4-hydroxyphenyl)-2-oxo]ethyl ATP for the rapid activation of the Na+,K+-ATPase. Biophys. J. 2000;79:1346–1357. doi: 10.1016/S0006-3495(00)76387-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Babes A., Fendler K. Na+ transport, and the E1P-E2P conformational transition of the Na+/K+-ATPase. Biophys. J. 2000;79:2557–2571. doi: 10.1016/S0006-3495(00)76496-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lu C.-C., Kabakov A., Hilgemann D.W. Membrane transport mechanisms probed by capacitance measurements with megahertz voltage clamp. Proc. Natl. Acad. Sci. USA. 1995;92:11220–11224. doi: 10.1073/pnas.92.24.11220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Steinberg M., Karlish S.J.D. Studies on conformational changes in Na,K-ATPase labeled with 5-iodoacetamidofluorescein. J. Biol. Chem. 1989;264:2726–2734. [PubMed] [Google Scholar]
- 43.Pratap P.R., Palit A., Robinson J.D. Kinetics of conformational changes associated with potassium binding to and release from Na+/K+-ATPase. Biochim. Biophys. Acta. 1996;1285:203–211. doi: 10.1016/s0005-2736(96)00162-9. [DOI] [PubMed] [Google Scholar]
- 44.Lüpfert C., Grell E., Clarke R.J. Rate limitation of the Na+,K+-ATPase pump cycle. Biophys. J. 2001;81:2069–2081. doi: 10.1016/S0006-3495(01)75856-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Humphrey P.A., Lüpfert C., Clarke R.J. Mechanism of the rate-determining step of the Na+,K+-ATPase pump cycle. Biochemistry. 2002;41:9496–9507. doi: 10.1021/bi025836o. [DOI] [PubMed] [Google Scholar]
- 46.Pintschovius J., Fendler K., Bamberg E. Charge translocation by the Na+/K+-ATPase investigated on solid supported membranes: cytoplasmic cation binding and release. Biophys. J. 1999;76:827–836. doi: 10.1016/S0006-3495(99)77246-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Blanco G., Mercer R.W. Isozymes of the Na-K-ATPase: heterogeneity in structure, diversity in function. Am. J. Physiol. 1998;275:F633–F650. doi: 10.1152/ajprenal.1998.275.5.F633. [DOI] [PubMed] [Google Scholar]
- 48.Horisberger J.-D., Kharoubi-Hess S. Functional differences between α subunit isoforms of the rat Na,K-ATPase expressed in Xenopus oocytes. J. Physiol. 2002;539:669–680. doi: 10.1113/jphysiol.2001.013201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Apell H.-J., Bersch B. Na,K-ATPase in artificial lipid vesicles: potential dependent transport rates investigated by a fluorescence method. In: Skou J.C., Nørby J.G., Maunsbach A.B., Esmann M., editors. The Na+, K+-Pump, Part A: Molecular Aspects. Alan R. Liss; New York: 1988. pp. 469–476. [PubMed] [Google Scholar]
- 50.Segall L., Javaid Z.Z., Blostein R. Structural basis for α1 versus α2 isoform-distinct behavior of the Na,K-ATPase. J. Biol. Chem. 2003;278:9027–9034. doi: 10.1074/jbc.M211636200. [DOI] [PubMed] [Google Scholar]
- 51.Bugnon P., Doludda M., Merbach A.E. High-pressure stopped-flow spectrometer for kinetic studies of fast bioinorganic reactions by absorbance and fluorescence detection. In: Heremans K., editor. High-Pressure Research in the Biosciences and Biotechnology. Leuven University Press; Leuven, Belgium: 1997. pp. 143–146. [Google Scholar]
- 52.Domaszewicz W., Apell H.-J. Binding of the third Na+ ion to the cytoplasmic side of the Na,K-ATPase is electrogenic. FEBS Lett. 1999;458:241–246. doi: 10.1016/s0014-5793(99)01162-x. [DOI] [PubMed] [Google Scholar]
- 53.Rakowski R.F., Vasilets L.A., Schwarz W. A negative slope in the current-voltage relationship of the Na+/K+ pump in Xenopus oocytes produced by reduction of external [K+] J. Membr. Biol. 1991;121:177–187. doi: 10.1007/BF01870531. [DOI] [PubMed] [Google Scholar]
- 54.Darnell J., Lodish H., Baltimore D. 2nd ed. Scientific American Books; New York: 1990. Molecular Cell Biology. [Google Scholar]


