The influence of surfactant on the propagation of a semi-infinite bubble through a liquid-filled compliant channel

Abstract

We investigate the influence of a soluble surfactant on the steady-state motion of a finger of air through a compliant channel. This study provides a basic model from which to understand the fluid–structure interactions and physicochemical hydrodynamics of pulmonary airway reopening. Airway closure occurs in lung diseases such as respiratory distress syndrome and acute respiratory distress syndrome as a result of fluid accumulation and surfactant insufficiency. This results in ‘compliant collapse’ with the airway walls buckled and held in apposition by a liquid occlusion that blocks the passage of air. Airway reopening is essential to the recovery of adequate ventilation, but has been associated with ventilator-induced lung injury because of the exposure of airway epithelial cells to large interfacial flow-induced pressure gradients. Surfactant replacement is helpful in modulating this deleterious mechanical stimulus, but is limited in its effectiveness owing to slow surfactant adsorption. We investigate the effect of surfactant on micro-scale models of reopening by computationally modelling the steady two-dimensional motion of a semi-infinite bubble propagating through a liquid-filled compliant channel doped with soluble surfactant. Many dimensionless parameters affect reopening, but we primarily investigate how the reopening pressure p_b depends upon the capillary number Ca (the ratio of viscous to surface tension forces), the adsorption depth parameter λ (a bulk concentration parameter) and the bulk Péclet number Pe_b (the ratio of bulk convection to diffusion). These studies demonstrate a dependence of p_b on λ, and suggest that a critical bulk concentration must be exceeded to operate as a low-surface-tension system. Normal and tangential stress gradients remain largely unaffected by physicochemical interactions – for this reason, further biological studies are suggested that will clarify the role of wall flexibility and surfactant on the protection of the lung from atelectrauma.

1. Introduction

The goal of this paper is to investigate the influence of soluble surfactant on the migration of a semi-infinite finger of air through a compliant elastically supported channel filled with a viscous fluid. This problem is of general interest because it demonstrates complex fluid–structure and physicochemical hydrodynamic interactions that exist as the interface propagates through, and opens, the channel. Furthermore, this system may advance our understanding of the interfacial flows that exist during the removal of liquid obstructions in pulmonary airways, hereafter referred as airway reopening.

Pulmonary airways are flexible, interdependent, fluid-lined conduits that convey gas to and from the alveoli, the site of gas exchange with blood. At birth, this network is liquid-filled, and a semi-infinite bubble of air must navigate through the multiple generations of airways (~20) in order to initiate gas exchange with blood at the alveolar level. In a full-term neonate, this airway recruitment is facilitated by the existence of a sophisticated surfactant system that dynamically reduces surface tension in the lining fluid (Notter 2000).

Unfortunately, a number of disease states may prevent pulmonary airways from opening naturally or can result in liquid lining instabilities that can cause closure and collapse of extended regions of sequential airways, which is termed ‘atelectasis’. For example, airway closure is common in respiratory distress syndrome (RDS), which is related to prematurity of the surfactant system and leads to a high surface tension of the air–liquid interface; in acute respiratory distress syndrome (ARDS), which can be caused by sepsis or smoke inhalation and results in increased vascular permeability that causes pulmonary oedema and surfactant deactivation by plasma proteins; in cystic fibrosis, which results in abnormal rheological properties; and in emphysema, which is due to a loss of stiffness of the surrounding tissue. These diseases are clinically significant; for example, ARDS afflicts approximately 200 000 individuals annually in the USA and has a mortality of approximately 40 % (Rubenfeld et al. 2005). Recent papers on the phenomenon of airway closure include Gaver, Halpern & Jensen (2005), Halpern et al. (2008) and Heil, Hazel & Smith (2008).

Ventilation at low lung volumes may contribute to lung injury because of the repetitive opening and closing of airways, and the generation of large pressures required to open terminal airways. This phenomenon is known as atelectrauma (Gaver et al. 2006), and has been related to large normal stress gradients sweeping across the epithelial cell surface as a large region of a collapsed airway is reopened through a peeling motion that separates the walls of the obstructed region as a finger of air penetrates the obstruction. Furthermore, the airway topology may play a large role in the magnitude of these stresses (Jacob & Gaver 2005; Yalcin, Perry & Ghadiali 2007). While the rupture of menisci that occlude airways is beneficial in removing obstructions, the associated mechanical stresses may damage epithelial cells in the vicinity of the rupture (Huh et al. 2007).

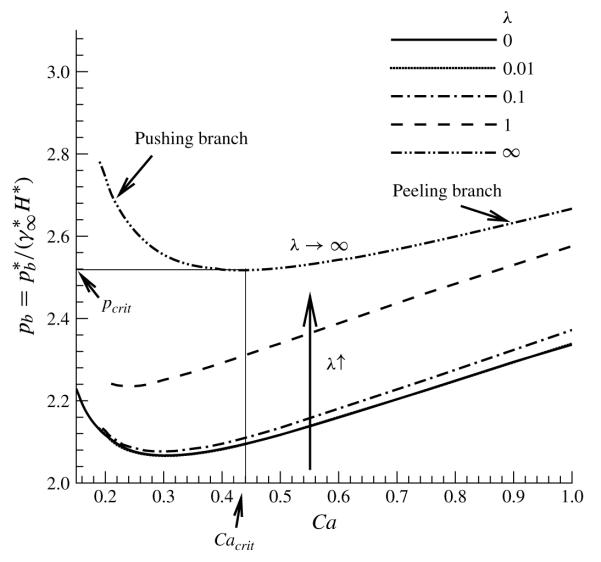
Since fluid–structure interactions and physicochemical hydrodynamics are hypothesized to contribute to atelectrauma, a number of theoretical studies have modelled this system to investigate the macro- and micro-mechanical effects related to this system. These studies commonly investigate the propagation of a semi-infinite bubble through a liquid-filled compliant channel as a model of airway reopening. Benchtop studies identified macro-scale fluid–structure interactions that may occur during airway reopening (Gaver, Samsel & Solway 1990; Perun & Gaver 1995a,b). Theoretical models have considered the steady motion of a surfactant-free system wherein a semi-infinite air bubble is driven by a bubble pressure $p_b^{\ast }$ through a liquid-filled two-dimensional channel that is supported by elastic springs and is under constant longitudinal tension, as shown in figure 1 (Gaver et al. 1996; Jensen et al. 2002; Halpern et al. 2005; Naire & Jensen 2005). These studies, which incorporate a Stokes flow approximation, predict that, for the bubble to propagate at a steady speed U*, $p_b^{\ast }$ must exceed a critical value, p_crit*, associated with a velocity $U_{\mathit{crit}}^{\ast }$. Two different types of motion were identified, as demonstrated by figure 2:

1. a slow ‘pushing branch’ for U* < $U_{\mathit{crit}}^{\ast }$, where U* decreases below $U_{\mathit{crit}}^{\ast }$ as $p_b^{\ast }$ increases above $U_{\mathit{crit}}^{\ast }$; and

2. a fast ‘peeling motion branch’ for U* > $U_{\mathit{crit}}^{\ast }$, where U* increases above $U_{\mathit{crit}}^{\ast }$ as the driving pressure $p_b^{\ast }$ increases above $p_{\mathit{crit}}^{\ast }$.

FIGURE 1.

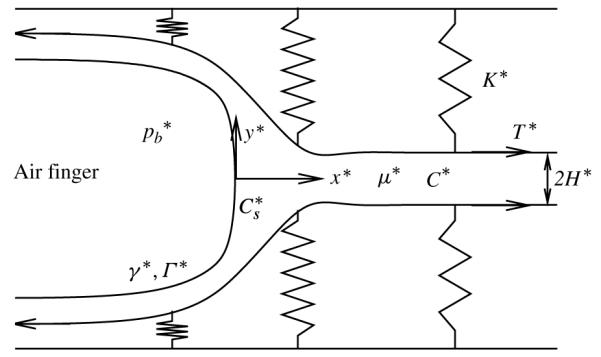
Schematic of model showing a semi-infinite bubble moving steadily from left to right due to an imposed pressure drop $p_b^{\ast }$ inflating a liquid-filled compliant channel. In this analysis, the frame of reference is fixed to the bubble tip, which provides a steady-state solution.

FIGURE 2.

Bubble pressure $p_b^{\ast }∕({\gamma }_{\infty }^{\ast }∕H^{\ast })$ versus the dimensionless bubble speed Ca for different values of the adsorption 1 depth parameter λ. Note that λ → ∞ corresponds to the surfactant-free case and λ = 0 to the bulk equilibrium limit. The values of the other parameters are η = 100, ϕ = 0.5, Pe_s = 10³, Pe_b = 50, St_a = 0.3, St_d = 0.03 and E_l = 1.

Follow-up theoretical studies have shown that fluid inertia can have an influence on the bubble and wall shapes, and for given speed U* the reopening pressure $p_b^{\ast }$ is normally higher than that obtained by Stokes flow models (Heil 2000), but the general behaviour is similar. A three-dimensional model by Hazel & Heil (2003) incorporated a more realistic airway model and allowed for buckling. This model continues to predict a two-branch behaviour.

Benchtop studies have not demonstrated the predicted two-branch behaviour (Gaver et al. 1990; Perun & Gaver 1995a,b; Juel & Heap 2007). Instead, as U* is reduced, $p_b^{\ast }$ approaches a finite value that is interpreted as a yield pressure for the system, $p_b^{\ast }{\mid }_{\text{yield}}$. Analysis by Halpern et al. (2005) predicted that the pushing branch is unstable: if the solution is given a positive pressure perturbation, the system migrates from the pushing to the peeling branch; and if a negative pressure perturbation is applied, the bubble slows down indefinitely. Recent computational studies by Hazel & Heil (2008) suggest that even a small gravitational effect can eliminate the low-pressure pushing branch due to the buoyant rise of the finger of air. In highly flexible channels, these studies showed that $p_{\mathit{crit}}^{\ast }$ ~9λ/R, which is in good agreement with experimental measurements of $p_b^{\ast }{\mid }_{\text{yield}}$.

Yap & Gaver (1998) extended the model of Gaver et al. (1996) by considering the effect of surfactant, which modifies the surface tension at the air–liquid interface. Surfactant transport is generally modelled as a two-step process wherein surfactant in the liquid phase (bulk surfactant) is transported by convection and diffusion to a region near the interface (subsurface) from which sorption with the interface occurs. In Yap & Gaver (1998), bulk surfactant transport was assumed to be much faster than the adsorption process (the bulk equilibrium limit), and therefore the bulk surfactant concentration was assumed to be constant and equal to the influx concentration. That study demonstrated significant physicochemical interactions that can lead to ‘rigidification’ of the interface, similar to that described by Stebe & Bartes-Biesel (1995). Rigid-walled systems have been used to investigate transport limitations that can exist under low bulk concentration conditions (as may occur in RDS or as a result of surfactant dilution caused by liquid filling the airspaces in ARDS), and demonstrated surfactant interactions and transport phenomena that may limit the efficacy of surfactant delivery (Ghadiali & Gaver 2000, 2001, 2003). Computational simulations that include multi-layer characteristics of an inactive surface-associated contaminant (termed ‘surfinactant’) suggest that unsteady fluid flow and transport can be used to increase the local concentrations of surfactant and thereby reduce the mechanical stress associated with reopening (Zimmer, Williams & Gaver 2005). Experiments by Pillert & Gaver (2009) demonstrated that these effects may reduce the pressure drop across the interface. Recent studies have shown that, in the presence of surfactant, temporary flow reversal can be useful in protecting cells from large-magnitude interfacial stresses (Glindmeyer, Smith & Gaver 2012). These studies are particularly relevant to overcoming transport limitations that would occur during competitive adsorption with plasma proteins, as might exist in ARDS (see Zasadzinski et al. 2010). Based upon these studies, it has been suggested that pulsatile reopening may create a ‘new paradigm’ for mechanical ventilation that could reduce the incidence of ventilator-induced lung injury (VILI) (Amin & Suki 2012).

The work of Naire & Jensen (2005) was the first to explore surfactant transport in a flexible-walled system that extends beyond the bulk equilibrium approximation. To do so, they developed a one-dimensional asymptotic model of surfactant-mediated airway reopening in a flexible axisymmetric tube model by exploiting the experimentally and theoretically derived surfactant properties and transport properties from rigid-walled experiments and theory by Ghadiali & Gaver (2000, 2003). That study predicted that the integrated effects of surface tension reduction and the relative increase of wall stiffness due to the presence of surfactants could significantly reduce the reopening pressure. Furthermore, the wall stresses were predicted to be large enough to cause cell damage, most likely through strain at the cellular scale.

Herein we present a two-dimensional computational analysis of fluid flow and surfactant transport as a finger of air propagates through a compliantly collapsed channel that is obstructed with a surfactant-doped viscous fluid. This analysis extends beyond the work of Yap & Gaver (1998) and Naire & Jensen (2005) by simulating the distributions of surfactant in both the bulk and surface phases, allowing for the prediction of the coupling between physicochemical hydrodynamics and fluid–structure interactions. Our goal is to present a general description of this system, with a focus on the role of surfactant sorption rates, diffusivity and bulk concentration on the surfactant distribution and flow fields and the resulting driving pressure and mechanical stresses at the flexible-walled boundary. While direct simulation of parameter values associated with the physiological problem was not achievable, we use the trends associated with our analysis to provide insight into the physiological problem of pulmonary airway reopening.

2. Model formulation

The reopening model considered here is similar to that described in Gaver et al. (1996), but with the inclusion of surfactant transport. We investigate the steady two-dimensional motion of a semi-infinite gas bubble that is forced at a constant bubble pressure, $p_b^{\ast }$, through a compliant channel that is liquid-filled with a fluid of viscosity μ*, as shown in figure 1. The bubble interface is located at y* = ±f* (x*) and the channel walls at y* = ±h* (x*), where (x* = 0, y* = 0) defines the location of the bubble tip. Sufficiently far ahead of the bubble, the channel collapses to a uniform width of 2H*. Surfactant molecules are present in the fluid with concentration C* (x* , y*) and along the air–liquid interface with concentration Γ* (s*), where s* is the distance along the interface, with s* = 0 defining the location of the bubble tip. Sufficiently far ahead of the bubble tip, the bulk surfactant concentration is defined as $C_0^{\ast }$. We seek steady-state solutions that exist in the bubble-tip frame of reference.

2.1. Transport equations

Here we present the dimensional surfactant transport equations, which were not featured in the constant-surface-tension reopening model of Gaver et al. (1996). Under steady conditions, the surfactant concentrations Γ*(s*) and C* (x*, y*) satisfy the following transport equations (Ghadiali & Gaver 2003):

$${\nabla }_s^{\ast }•\left(u_s^{\ast }{\Gamma }^{\ast }\widehat{t}\right)=D_s^{\ast }{\nabla }_s^{\ast 2}{\Gamma }^{\ast }+j^{\ast }$$ (2.1)

and

$${\mathit{u}}^{\ast }•{\nabla }^{\ast }{C}^{\ast }=D_b^{\ast }{\nabla }^{\ast 2}{C}^{\ast },$$ (2.2)

where ${\nabla }_s^{\ast }$ is the surface gradient, $u_s^{\ast }$ is the tangential component of the velocity along the interface, $\widehat{t}$ is the tangential vector, u* = (u*, v*) is the two-dimensional fluid velocity, j* is the flux of surfactant from the bulk to the interface, and $D_s^{\ast }$ and $D_b^{\ast }$ are the interfacial and bulk molecular diffusivities. The flux j* is described by a two-step process: (i) diffusion from the bulk to the subsurface; and (ii) adsorption/desorption from the subsurface to the interface (Ghadiali & Gaver 2003). Thus,

$$j^{\ast }=-D_b^{\ast }\left(\widehat{n}•{\nabla }^{\ast }{C}^{\ast }\right)=k_a^{\ast }{C}_s^{\ast }({\Gamma }_{\infty }^{\ast }-{\Gamma }^{\ast })-k_d^{\ast }{\Gamma }^{\ast },$$ (2.3)

where $D_a^{\ast }$ and $D_d^{\ast }$ are the adsorption and desorption coefficients, respectively, $C_s^{\ast }$ is the subsurface bulk concentration, ${\Gamma }_{\infty }^{\ast }$ is the maximum monolayer packing interfacial concentration (Krueger & Gaver 2000 ¹) and $\widehat{n}$ is the unit normal vector pointing out of the liquid.

2.2. Surfactant equation of state

We use a linear equation of state that expresses the surface tension γ* in terms of the interfacial surfactant concentration,

$${\gamma }^{\ast }={\gamma }_{\infty }^{\ast }-E^{\ast }({\Gamma }^{\ast }-{\Gamma }_{\infty }^{\ast }),$$ (2.4)

where ${\gamma }_{\infty }^{\ast }$ is the surface tension of the air–liquid interface when Γ* = Γ* and E* is the surface elasticity number. This equatin is valid for Γ* < ${\Gamma }_{\infty }^{\ast }$ and is a simplification over the more complex equations of state that are coupled to transport process and multi-layer formatio (Krueger & Gaver 2000; Ghadiali & Gaver 2003) and eliminates the singularity that exists at Γ* = ${\Gamma }_{\infty }^{\ast }$.

2.3. Dimensionless governing equations and boundary conditions

We introduce the dimensionless variables

$$\phantom{\{}\begin{array}{c}\hfill (x,y)=\frac{(x^{\ast },y^{\ast })}{H^{\ast }},(u,v)=\frac{(u^{\ast },v^{\ast })}{{\gamma }_{\infty }^{\ast }∕{\mu }^{\ast })},p=\frac{p^{\ast }}{{\gamma }_{\infty }^{\ast }∕H^{\ast }},\hfill \\ \hfill \gamma =\frac{{\gamma }^{\ast }}{{\gamma }_{\infty }^{\ast }},\Gamma =\frac{{\Gamma }^{\ast }}{{\Gamma }_{\infty }^{\ast }},c=\frac{C^{\ast }}{C_0^{\ast }},j=\frac{j^{\ast }}{{\gamma }_{\infty }^{\ast }{\Gamma }_{\infty }^{\ast }∕\left({\mu }^{\ast }{H}^{\ast }\right)}\hfill \end{array}\}$$ (2.5)

which are used to non-dimensionalize the governing equations.

We neglect the effects of fluid inertia, and so the motion of the liquid lining is governed by the Stokes and continuity equations,

$$\nabla p={\nabla }^2\mathit{u},\nabla •\mathit{u}=0,$$ (2.6)

where u = (u, v) is the dimensionless fluid velocity and p is the fluid pressure. The stress and kinematic boundary conditions at the air–liquid interface, y = f (x), are

$$\tau =\sigma •\widehat{n}=-(p_b+\gamma {\kappa }_i)\widehat{n}+\frac{\partial \gamma }{\partial s}\widehat{t},\mathit{u}•\widehat{n}=0,$$ (2.7)

where σ = –pI + ∇ u + ∇u^T is the stress tensor, ${\kappa }_i={\nabla }_s•\widehat{n}$ is the interfacial curvature, ${\nabla }_s=(\mathit{I}-\widehat{n}\widehat{n})•\nabla$ is the surface divergence vector and γ is the surface tension. The constitutive linear equation for γ , equation (2.4), becomes

$$\gamma =1-E_l(\Gamma -1)\text{for}\Gamma \ast \ast \ast 1,$$ (2.8)

where $E_l=E^{\ast }{\Gamma }_{\infty }^{\ast }∕{\gamma }_{\infty }^{\ast }$ is an elasticity number.

At the flexible1wall, y = h(x), the stress and the kinematic boundary conditions are

$$\widehat{m}•\sigma •\widehat{m}=\eta {\kappa }_{\mathit{wall}}-\varphi (h-1)m_y,u=\mathit{Ca}(m_x^2-1),v=\mathit{Ca}{m}_x{m}_y,$$ (2.9)

where $\widehat{m}=(m_x,m_y)$ is the unit normal pointing out of the fluid, ${\kappa }_{\text{wall}}={\nabla }_s•\widehat{m}$ is the wall curvature, $\eta =T^{\ast }∕{\gamma }_{\infty }^{\ast }$ is a dimensionless wall tension parameter, $\varphi =K^{\ast }{H}^{\ast 2}∕{\gamma }_{\infty }^{\ast }$ denotes a wall stiffness parameter, and $\mathit{Ca}={\mu }^{\ast }{U}_{\mathit{tip}}^{\ast }∕{\gamma }_{\infty }^{\ast }$ is the capillary number, which is a dimensionless velocity that describes the ratio of viscous forces to surface tension forces.

Along the line of symmetry, y = 0, ahead of the bubble tip:

$$\frac{\partial u}{\partial y}=0\text{and}v=0.$$ (2.10)

Sufficiently far ahead of the bubble, the film thickness tends to the collapsed channel width, and, since the normal to the wall is vertical, the velocity is solely in the horizontal direction and equal to –Ca:

$$h\left(x\right)\to 1,\mathit{u}\to (-\mathit{Ca},0)\text{as}x\to \infty .$$ (2.11)

Far upstream, in the inflated region, the boundary conditions are

$$h\left(x\right)\to p_b∕\varphi +1,f\left(x\right)\to p_b∕\varphi ,\mathit{u}\to (-\mathit{Ca},0)\text{as}x\to -\infty .$$ (2.12)

The dimensionless interfacial surfactant transport equation (2.1) becomes

$$\frac{\mathrm{d}}{\mathrm{d}s}\left(u_s\Gamma \right)=\frac{1}{{\mathit{Pe}}_s}\frac{{\mathrm{d}}^2\Gamma }{\mathrm{d}{s}^2}+j,$$ (2.13)

where ${\mathit{Pe}}_s={\gamma }_{\infty }^{\ast }{H}^{\ast }∕\left({\mu }^{\ast }{D}_s^{\ast }\right)$ is the surface Péclet number, representing the ratio of a diffusive time scale $T_D^{\ast }=H^{\ast 2}∕D_s^{\ast }$ to a convective time scale $T_C^{\ast }=H^{\ast }{\mu }^{\ast }∕{\gamma }_{\infty }^{\ast }$. From (2.3), the scaled (Langmuir) flux, j, becomes

$$j={\mathit{St}}_{\lambda }{C}_s(1-\Gamma )-{\mathit{St}}_d\Gamma ,$$ (2.14)

where ${\mathit{St}}_a=\left({\mu }^{\ast }{\Gamma }_{\infty }^{\ast }\right)k_a^{\ast }∕{\gamma }_{\infty }^{\ast }$ and ${\mathit{St}}_d=\left(H^{\ast }{\mu }^{\ast }\right)k_d^{\ast }∕{\gamma }_{\infty }^{\ast }$ are adsorption and desorption Stanton numbers, respectively, and St_λ=St_a/λ, where $\lambda =({\Gamma }_{\infty }^{\ast }∕C_0^{\ast })∕H^{\ast }=L_{\mathit{ads}}^{\ast }∕H^{\ast }$ is the dimensionless adsorption depth parameter. Note that we have elected to represent the adsorption process by the product of two dimensionless parameters: St_a represents the concentration-independent adsorption properties, and is therefore a fundamental property of the surfactant, and λ (described below) represents the concentration dependence.

The adsorption depth $L_{\mathit{ads}}^{\ast }={\Gamma }_{\infty }^{\ast }∕C_0^{\ast }$ represents the depth into a fluid layer that would contain sufficient surfactant molecules that, if brought to the surface, would saturate the interface to the maximum equilibrium surface concentration ${\Gamma }_{\infty }^{\ast }$. This depth $L_{\mathit{ads}}^{\ast }$ is derived by applying conservation of mass to a rectangular region with an interfacial cross-sectional area A* and depth $L_{\mathit{ads}}^{\ast }$. Then $L_{\mathit{ads}}^{\ast }$ is found by relating the mass of surfactant in the bulk phase $\left(C_0^{\ast }{A}^{\ast }{L}_{\mathit{ads}}^{\ast }\right)$ to the mass of surfactant that can exist at the interface purely due to adsorption $\left({\Gamma }_{\infty }^{\ast }{A}^{\ast }\right)$ (Ferri & Stebe 2000). The dimensionless adsorption depth $\lambda =L_{\mathit{ads}}^{\ast }∕H^{\ast }$ ranges from 0 to ∞, corresponding to $C_0^{\ast }\to \infty$ for λ → 0 and $C_0^{\ast }\to 0$ for λ → ∞. Thus, as λ increases to an O(1) quantity, we expect that surfactant from the upstream thin-film region will be significantly depleted by transfer from the bulk to the surface phase. We will use this concept to determine the existence of a critical surfactant concentration that is necessary to retain the system in a low-surface-tension state.

The boundary conditions on Γ are: (i) a symmetry condition at the bubble tip; and (ii) a zero flux at the upstream end:

$$\frac{\mathrm{d}\Gamma }{\mathrm{d}s}=0\text{at}s=0\text{and}\frac{\mathrm{d}\Gamma }{\mathrm{d}s}\to 0\text{as}s\to \infty .$$ (2.15)

In the bulk phase, the surfactant concentration, C(x,y), satisfies the following dimensionless convection–diffusion equation:

$$\frac{\partial }{\partial x}\left(\mathit{uC}\right)+\frac{\partial }{\partial y}\left(\mathit{vC}\right)=\frac{1}{{\mathit{Pe}}_b}\left(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2}\right).$$ (2.16)

Here ${\mathit{Pe}}_b^{\ast }={\gamma }_{\infty }^{\ast }{H}^{\ast }∕\left({\mu }^{\ast }{D}_b^{\ast }\right)$ is the bulk Péclet number. The boundary conditions for C(x, y) are: (i) the concentration is set to unity at the downstream end; (ii) no streamwise variation in the upstream film region; (iii) a zero-flux condition along the channel wall; (iv) a symmetry condition along the centreline; and (v) a flux condition between the air–liquid interface and the bulk. Thus,

$$\phantom{\{}\begin{array}{c}C\to 1\text{as}x\to \infty ,\hfill \\ \frac{\partial C}{\partial x}\to 0\text{as}x\to -\infty ,\hfill \\ \widehat{m}•\nabla C=0\text{on}y=h,\hfill \\ \frac{\partial C}{\partial y}=0\text{along}y=0\text{for}x>0,\hfill \\ \widehat{n}•\nabla C=-\lambda {\mathit{Pe}}_{b}j\text{on}y=f.\hfill \end{array}\}$$ (2.17)

2.4. Macroscopic mass balance analysis

In order to confirm the numerical accuracy of the computations, we conduct a macroscopic mass balance that yields analytical expressions for the relationship between the bulk and surface surfactant concentrations in the upstream film region as functions of the adsorption and desorption parameters. Sufficiently far behind the tip, as x → –∞, Γ → Γ_f and C → C_f. In addition, in this region the bulk and interfacial surfactants are in equilibrium, so that j = 0. Hence

$${\Gamma }_f=\frac{{\mathit{St}}_{\lambda }{C}_f}{{\mathit{St}}_{\lambda }{C}_f+{\mathit{St}}_d}.$$ (2.18)

Furthermore, global mass conservation requires that

$${\Gamma }_f^{\ast }+H^{\ast }{C}_f^{\ast }=H^{\ast }{C}_0^{\ast }.$$ (2.19)

Alternatively, in dimensionless form, this conservation equation produces a second equation involving Γ_f and C_f:

$${\Gamma }_f=\frac{1-C_f}{\lambda }.$$ (2.20)

From (2.20) and (2.18), an expression for C_f is obtained in terms of the adsorption depth parameter λ and the ratio of Stanton numbers, St_r = St_a/St_d,

$$C_f=\frac{\sqrt{{\left[\right(\lambda -1){\mathit{St}}_r+\lambda ]}^2+4\lambda {\mathit{St}}_r}-(\lambda -1){\mathit{St}}_r-\lambda }{2{\mathit{St}}_r}.$$ (2.21)

Note that, in the bulk equilibrium case, the appropriate limits are recovered, namely, lim_λ→0C_f = 1 and lim_λ→0Γ_f = 1. The expressions for Γ_f and C_f will be used to confirm the accuracy of our simulations.

3. Numerical scheme

In this section we briefly describe the iterative algorithm used to determine the bubble and wall shapes, the surfactant concentrations and the bubble pressure for a prescribed capillary number Ca, wall parameters η and ϕ and surfactant parameters Pe_s, Pe_b, St_a, St_d, λ and E_l. A description of the boundary element method (BEM) used to solve the equations for fluid motion can be found, for example, in Halpern & Gaver (1994), Gaver et al. (1996) and Halpern et al. (2005). Appendices A and B provide details of the finite volume method that is used to solve the surfactant transport equations.

Our algorithm consists of the following six main steps.

1. Specify the value of Ca and commence with an initial estimate for the bubble pressure p_b, the air-finger half-width f(x), the channel half-width h(x), the interfacial surfactant concentration Γ(s) and the bulk concentration C(x, y).

2. Compute the stress at the air–liquid interface by using (2.7) and the kinematic boundary condition along the wall by using (2.9) for use in the BEM boundary conditions.

3. Solve the BEM equations, keeping Γ(s) and C(x, y) fixed, and determine the unknown velocities on the air–liquid interface and the stress on the wall.

4. Iterate using a Newton’s method to update p_b, f (x) and h(x) until the kinematic boundary condition at the air–liquid interface, (2.7), and the normal stress condition on the wall, (2.9), are satisfied to an accuracy of 10⁻⁶.

5. Use BEM to compute the internal fluid velocity field.

6. Update Γ(s) and C(x,y) by solving (A 2) and (B 3) using the finite volume method described in appendices A and B.

   The above process is used to update p_b, f (x), h(x), Γ(s) and C(x, y), and is repeated. We monitor the following quantities between successive iterations:

   1. the maximum residual from the Newton’s method solution of h, f and p_b;
   2. the maximum relative difference in Γ ; and
   3. the maximum relative difference in C(x, y).

   Convergence is achieved once Max((i), (ii), (iii)) < 10⁻⁶. In this process, under-relaxation is used in updating all unknowns after each iteration.

4. Results and analysis of the idealized system

4.1. Parameter values

We investigate the system around the following baseline parameter values:

$$\begin{array}{c}\hfill \eta =100,\varphi =0.5,{\mathit{Pe}}_s={10}^3,{\mathit{Pe}}_b=50,{\mathit{St}}_a=0.3,\hfill \\ \hfill {\mathit{St}}_d=0.03,\lambda =1,E_l=1.\hfill \end{array}$$ (4.1)

We explore solutions near this base parameter set to determine the relationship between physicochemical hydrodynamics and fluid–structure interactions. Using the base value of E_l = 1 is equivalent to selecting ${\gamma }_0={\gamma }_0^{\ast }∕{\gamma }_{\infty }^{\ast }=2$; therefore, the surface tension for the surfactant-free system is twice the surface tension of the bulk equilibrium system.

4.2. Effect of the dimensionless velocity, Ca

Figure 2 presents the macro-scale response of the system with the bubble pressure versus bubble speed relationship for different values of the adsorption depth parameter λ. The λ → ∞ curve corresponds to a surfactant-free system, and λ 0 corresponds to the bulk equilibrium condition.

As in Gaver et al. (1996), two solution branches exist: a ‘peeling’ branch for Ca > Ca_crit, where p_b increases with Ca; and a ‘pushing’ branch for Ca < Ca_crit, where p_b increases with decreasing Ca (points defined on the λ → ∞ curve). Analysis of these branches is provided by Gaver et al. (1996), Hazel & Heill (2003) and Halpern et al. (2005). In general, for fixed Ca, p_b increases with increasing λ (corresponding to a decrease in $C_0^{\ast }$). For each λ, there is a critical value of bubble pressure, p_crit, below which there are no steady-state solutions, and p_crit increases with λ. As in Naire & Jensen (2005), we find that an increase in $C_0^{\ast }(\lambda \downarrow )$(λ ↓) reduces the reopening pressure for fixed Ca; however, the change in p_b over 0 ≤ λ≤ ∞ is much less pronounced than that predicted by their one-dimensional analysis. The difference between their model and ours is discussed in detail in § 5.4. We also show an increase in the range of stable reopening bubble pressures and speeds. The micro-scale influence of λ is discussed in greater detail below.

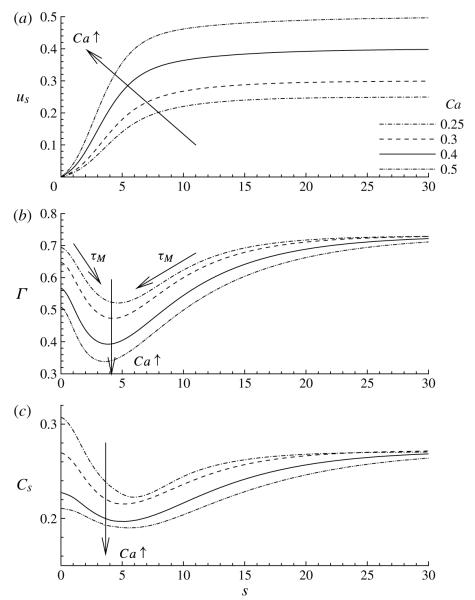
In figure 3, the surface velocity u_s, Γ and the subsurface concentration C_s are plotted as functions of the arclength s for different values of Ca. Here s = 0 defines the location of the bubble tip. Because the frame of reference is fixed to the bubble tip, u_s = 0 at s = 0, and u_s → Ca as s → ∞. In the tip region, u_s > 0, which indicates that recirculation exists at the bubble tip. This is due to Marangoni convection, which is caused by a large surfactant gradient dΓ/ds that rigidifies the interface in the tip region. Furthermore, surfactant is swept away from the bubble-tip region as Ca increases owing to increased surface convection. Arrows indicating the direction of the Marangoni stress τ_M are shown in figure 3(b). Unlike the rigid-walled model of Ghadiali & Gaver (2003), the concentrations in the film region, Γ_f and C_f, which are given by (2.20) and (2.21), are independent of Ca because the deposited film thickness is independent of Ca.

FIGURE 3.

The effect of capillary number Ca on (a) the surface velocity u_s in a frame of reference fixed to the bubble tip, (b) the surface concentration Γ and (c) the subsurface concentration C_s. The arclength s is measured along the interface, with s = 0 defining the bubble-tip location. The other parameter values are η = 100, ϕ = 0.5, Pe_s = 10³, Pe_b = 50, St_a = 0.3, St_d = 0.03, λ = 1 and E_l = 1.

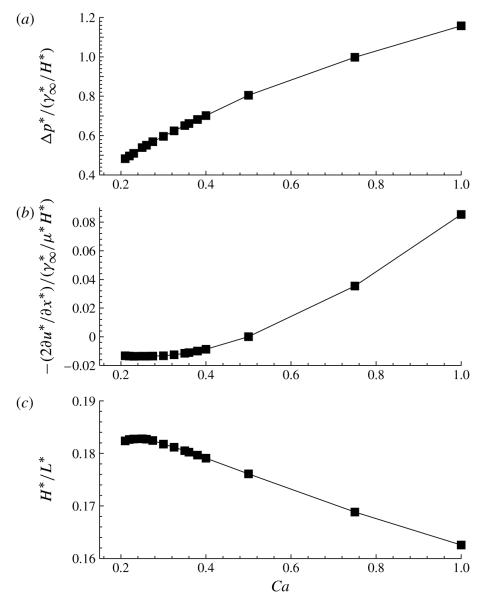
The pressure drop across the bubble tip, Δp_tip, depends on a surface tension component and a viscous component:

$${\phantom{\mid }\Delta p_{\mathit{tip}}=p_b-p(x=0)={\gamma }_{\mathit{tip}}{\kappa }_{\mathit{tip}}-2\frac{\partial u}{\partial x}\mid }_{x=0}.$$ (4.2)

Figure 4 presents the relationship between (a) the interfacial pressure drop and (b) the viscous contribution to the pressure drop as a function of Ca. Clearly, from figure 4(a,b), the surface tension contribution γ_tipk_tip dominates the local viscous effects at the tip.

FIGURE 4.

The effect of capillary number Ca on (a) the dimensionless interfacial pressure drop at the bubble tip, (b) the viscous contribution to the bubble-tip pressure drop and (c) the dimensionless fractional film thickness that is deposited on the channel wall. The other parameter values are identical to those in figure 3.

We also compute the fractional film thickness H*/L*, where 2L* is the distance between the two channel walls at the upstream end (x* → –∞). Applying (2.9) far upstream where the wall is flat, p_b = ϕ(L*/H* – 1) or H*/L* = 1/L = (p_b/ϕ + 1)⁻¹. Since H* is constant (by conservation of mass) and L* is determined by $p_b^{\ast }$, the fractional film thickness can be interpreted as the inverse channel width. Figure 4(c) shows that H*/L* decreases with increasing Ca for Ca > 0.25. This trend is in contrast to the increase in the film thickness with Ca that is observed in rigid-walled systems, further demonstrating the importance of fluid–structure interactions.

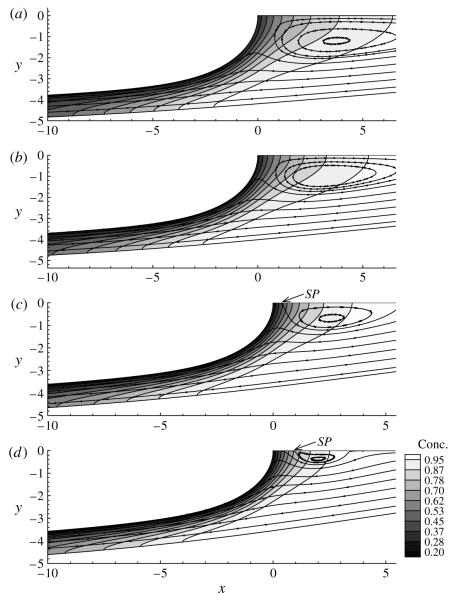
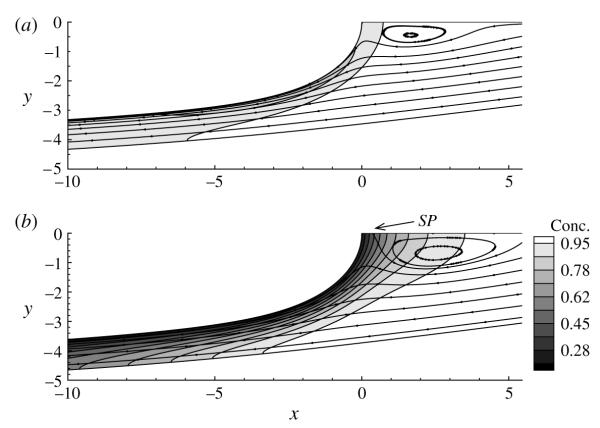
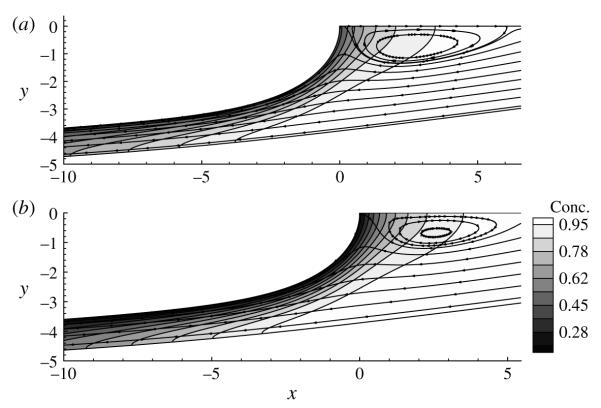
Figure 5 shows the streamlines and bulk concentration contours for a range of Ca. It is evident that, with an increase in Ca, the concentration boundary layer near the interface becomes more fully developed. Furthermore, a recirculation region is observed ahead of the bubble tip, whose size increases with decreasing Ca. This feature is similar to that encountered for the surfactant-free case (Gaver et al. 1996), with the exception that the recirculation region is not attached to the bubble tip. For Ca > 0.3, a saddle point (denoted SP) emerges along the axis of symmetry and moves away from the bubble tip, indicating the presence of a dividing streamline that separates the recirculation region from the rest of the flow. Eventually, for sufficiently large Ca, both the saddle point and the vortex disappear. In all cases shown in figure 5, the recirculation region is displaced ahead of the bubble tip, which was not evident when E_l = 0. Therefore, it is likely that this relocation is a result of Marangoni stresses that rigidify the interface, as previously explained.

FIGURE 5.

Streamlines and bulk concentration contours surrounding the bubble tip for (a) Ca = 0.25, (b) Ca = 0.3, (c) Ca = 0.4 and (d) Ca = 0.5. The other parameters are the same as those in figures 3 and 4. Here SP denotes the location of the saddle point along the axis of symmetry.

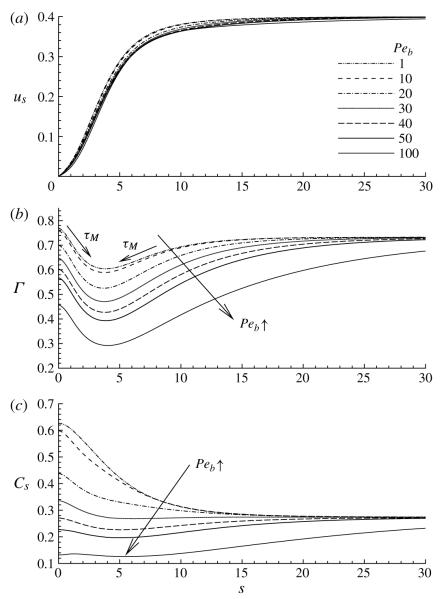
4.3. Effect of the bulk Péclet number, Pe_b

The influence of the bulk Péclet number on u_s, Γ and C_s is shown in figure 6. Since all other parameters are held constant, the change in Pe_b is equivalent to changing the bulk diffusivity. This figure demonstrates a significant decrease in C_s near the bubble tip as Pe_b increases, while the concentration in the film region is independent of Pe_b. The subsurface concentration does not vary significantly with arclength at large Pe_b, and in the neighbourhood of the bubble tip C_s is lower than the film concentration C_f, which indicates that bulk diffusion is too slow to replenish the subsurface.

FIGURE 6.

The influence of the bulk Péclet number Pe_b on (a) the surface velocity u_s, (b) the surface concentration Γ and (c) the subsurface concentration C_s. The other parameter values are: Ca = 0.4, η = 100, ϕ = 0.5, Pe_s = 10³, St_a = 0.3, St_d = 0.03, λ = 1 and E_l = 1.

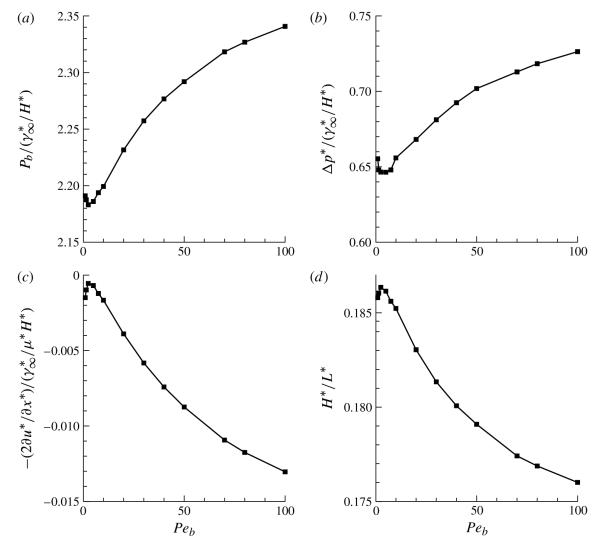
Figure 7 presents (a) the bubble pressure, (b) the interfacial pressure drop, (c) the viscous contribution of the interfacial pressure drop and (d) the proportional film thickness as functions of Pe_b. Each panel demonstrates that a low-Pe_b behaviour occurs for Pe_b < 10. For larger Pe_b, diffusion limitation induces an increase in the bubble pressure and interfacial pressure drop due to a reduction of Γ (and commensurate increase in γ). Furthermore, the fractional film thickness decreases with increasing Pe_b. While these trends continue, they are modulated with increasing Pe_b.

FIGURE 7.

The effect of the bulk Péclet number Pe_b on (a) the bubble pressure p_b, (b) the dimensionless interfacial pressure drop at the bubble tip, (c) the viscous contribution to the bubble-tip pressure drop and (d) the dimensionless fractional film thickness that is deposited on the channel wall. The other parameter values are identical to those used to generate figure 6.

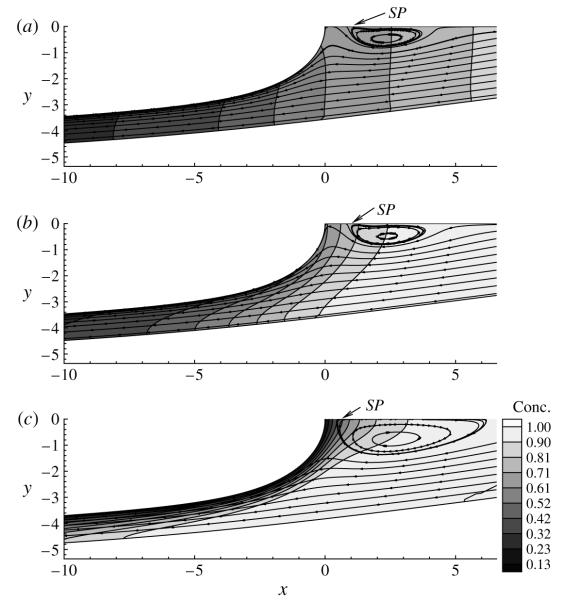
Figure 8 displays the streamlines and bulk concentration contours near the bubble for several values of Pe_b corresponding to figure 6. At small values of Pe_b (Pe_b = 1), the concentration gradients near the bubble surface are small according to (2.17), and consequently the bulk concentration is essentially a function of x, which creates a striped pattern. With increasing Pe_b (reduced bulk diffusion), the adsorption flux dominates, and a concentration boundary layer is formed along the interface. In the limit Pe_b → ∞, the outer solution to the bulk transport equation is C = constant along streamlines, with C = 1 to match the downstream bulk concentration. However, this outer solution does not satisfy the interfacial flux condition. Therefore, a thin diffusion boundary layer of thickness L_D exists where the concentration varies rapidly in the direction normal to the bubble surface $(\partial C∕\partial n=\widehat{n}•\nabla C)$. A balance of the dominant diffusion term in the direction normal to the interface and the dominant streamwise convective term yields the length scale for this diffusion boundary layer as $L_D\sim {\mathit{Pe}}_b^{-1∕2}$. For this reason, C_s decreases with increasing Pe_b (see figure 6); however, the downstream vortex drives surfactant towards the bubble tip, which results in a local maximum in Γ near s = 0, despite the fact that Marangoni stresses eliminate the converging stagnation point at the bubble tip.

FIGURE 8.

Streamlines and bulk concentration contours for (a) Pe_b = 1, (b) Pe_b = 10 and (c) Pe_b = 100. The other parameter values are the same as those used in figures 6 and 7.

4.4. Effect of the dimensionless adsorption depth, λ

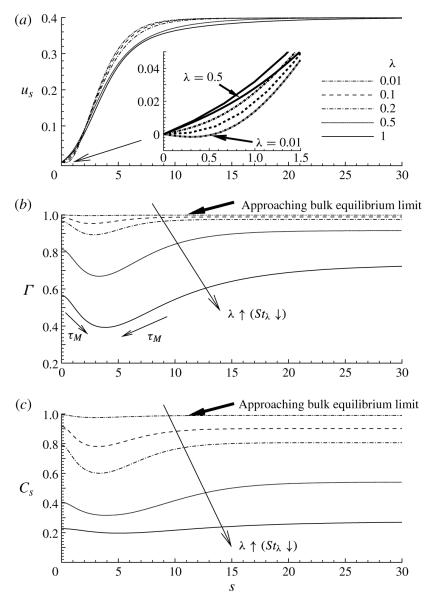
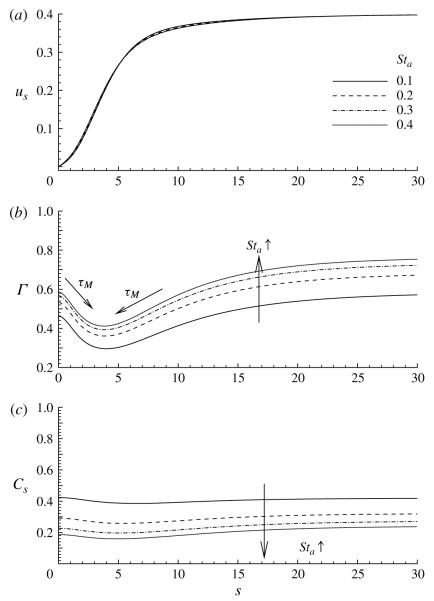
Figures 9 and 10 document the influence of the influx concentration C₀, which is investigated by varying λ. Recall that λ ≪ 1 implies that the bulk concentration is very large, and hence the depletion of surfactant from the bulk by the interface will not be significant. This behaviour is seen in figure 9(b,c), where for λ = 0.01, C_s ~ 1 and Γ ~ 1. For this particular case, the surfactant concentration at the interface is nearly uniform, and so the interface does not maintain a tangential (Marangoni) stress and is mobile. The downstream recirculation region is attached to the interface, which is evident by u_s < 0 in the tip region (see inset of figure 9a). Figure 10(a) corroborates this behaviour by demonstrating a nearly uniform bulk concentration for λ 0.1, and is consistent with the high-concentration interfacial remobilization predictions and observations (Stebe, Lin & Maldarelli 1991; Stebe & Maldarelli 1994; Stebe & Bartes-Biesel 1995).

FIGURE 9.

The effect of the adsorption depth parameter λ on (a) the surface velocity u_s, (b) the surface concentration Γ and (c) the subsurface concentration C_s. The inset in (a) shows that the surface velocity changes sign near the bubble tip for sufficiently small λ. The other parameter values are: Ca = 0.4, η = 100, ϕ = 0.5, Pe_b = 50, Pe_s = 10³, St_a = 0.3, St_d = 0.03 and E_l = 1.

FIGURE 10.

Streamlines and bulk concentration contours for (a) λ = 0.1 and (b) λ = 1. All other parameter values are the same as those in figure 9.

As λ increases, a saddle point moves along the axis of symmetry, the vortex moves away from the tip, and u_s > 0 for all s. Thus the interfacial flow at the tip opposes the downstream vortex, rigidifying the interface. However, direct convection along the interface does not drive surfactant to the tip; instead, the downstream vortex provides an influx of bulk surfactant to the tip region that induces a local maximum concentration at the tip. This behaviour is evident in figures 9(b,c) and 10(b). In addition, as λ increases, the total amount of surfactant present in the film layer decreases. For this reason, less surfactant is adsorbed to the interface, and the subsurface concentration C_s approaches an s-independent value in the thin film.

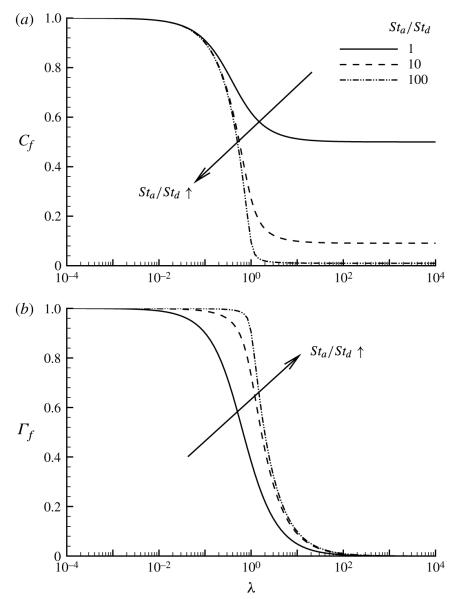
In figure 11 we explore the dependence of the thin-film concentrations on λ for three different ratios of Stanton numbers, St_r = St_a/St_d 1, 10 and 100, using (2.20) and (2.21), which were derived from the control-volume analysis given in § 2.4. The bulk equilibrium limit is obtained as λ → 0, corresponding to an infinite amount of bulk surfactant present in the system (C₀ → ∞); in this limit, both C_f → 1 and Γ_f → 1. Increasing St_r induces a more rapid adsorption from the bulk, and for a given value of λ this increases (decreases) the concentration in the thin film (bulk). The rate at which this limit is reached is reduced with decreasing St_r because of slower adsorption. Both C_f and Γ_f decrease with increasing λ, with a transition to the large-λ limit occurring when λ ~ O(1), that is, when the adsorption depth and film thickness are of comparable magnitude. In contrast, as λ → ∞, Γ_f → St_r/(λ(1 + St_r)) and C_f → (1 + St_r)⁻¹, which is a constant value (figure 11). However, it should be noted that, if λ → ∞ through a reduction in $C_0^{\ast }$, the dimensional thin-film concentration approaches zero, since $C_f^{\ast }=C_0^{\ast }{C}_f$.

FIGURE 11.

The influence of the adsorption depth parameter λ on (a) the thin-film bulk concentration C_f, (2.21), and (b) the thin-film surface concentration Γ, (2.20), for three different values of St_a/St_d.

Although it has already been revealed in figure 2 that p_b increases with increasing λ, this variation is more clearly shown for Ca = 0.4 in figure 12. This figure shows that p_b increases sigmoidally with increasing λ, with the most significant increase occurring when λ = O(1). For λ → ∞ the system operates at a constant surface tension, with ${\gamma }^{\ast }=2{\gamma }_{\infty }^{\ast }$. Therefore, calculations were conducted with a constant surface tension at Ca = μU_tip/γ* = 0.2, ϕ = KH²/γ* = 0.25 and η T/γ* = 50. This simulation is consistent with the solutions found by Gaver et al. (1996) and the analytical prediction by Jensen et al. (2002). For λ → 0 (the bulk equilibrium limit), p_b ~ 2.08, the same value as in Yap & Gaver (1998); while, as λ → ∞ (the surfactant-free limit), p_b → 2.52. Therefore, for this value of Ca, the surfactant-free driving pressure is only 20 % larger than in the bulk equilibrium case despite the fact that the surface tension has increased by 100 %. Since this prediction occurs for the bulk equilibrium limit, diffusive transport limitations can only reduce this effect further.

FIGURE 12.

Bubble pressure versus adsorption depth parameter. The other parameter values are: Ca = 0.4, η = 100, ϕ = 0.5, Pe_b = 50, Pe_s = 10³, St_a = 0.3, St_d = 0.03 and E_l = 1. The dashed line, with λ → ∞, represents the surfactant-free case, while the dotted line represents the bulk equilibrium limit.

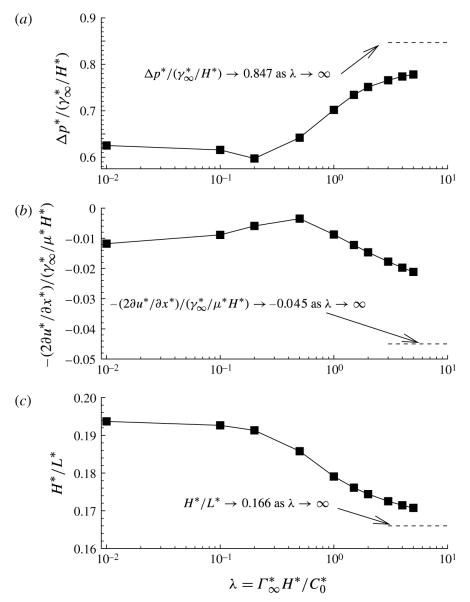
Figure 13 demonstrates how the adsorption depth affects the interfacial pressure drop (Δp) and the fractional film thickness deposited on the upstream channel wall. These demonstrate, once again, the transition from high-concentration to low-concentration behaviour that occurs with λ ~ O(1). In contrast to the p_b shown in figure 12, Δp has a local minimum near λ = 0.2, and a local maximum of the viscous contribution near λ = 0.5. As λ decreases (through an increase in C₀, for example), the fractional film thickness (H*/L* ) increases substantially, which is a reflection of the reduced p_b that leads to a decrease in the upstream channel width, L*.

FIGURE 13.

The effect of adsorption depth parameter λ on (a) the dimensionless interfacial pressure drop at the bubble tip, (b) the viscous contribution to the bubble-tip pressure drop and (c) the dimensionless fractional film thickness that is deposited on the channel wall. The other parameter values are set to: Ca = 0.4, η = 100, ϕ = 0.5, Pe_b = 50, Pe_s = 10³, St_a = 0.3, St_d = 0.03 and E_l = 1.

4.5. Effect of the dimensionless adsorption rate, St_a

Figures 14 and 15 demonstrate the influence of the adsorption Stanton number, St_a, on the flow field and surfactant distribution. In general, an increase in St_a reduces the surfactant concentration in the bulk, as it increases the concentration along the interface. The more rapid depletion of surfactant from the bulk increases the magnitude of the concentration boundary layer, as shown in figure 15. In the parameter range of this study, the interfacial velocity is weakly influenced by changes in St_a (figure 14a).

FIGURE 14.

The effect of the adsorption Stanton number St_a on (a) the surface concentration Γ and (b) the subsurface concentration C_s. The other parameter values are: Ca = 0.4, η = 100, ϕ = 0.5, Pe_b = 50, Pe_s = 10³, St_d = 0.03, E_l = 1 and λ = 1.

FIGURE 15.

The influence of St_a on the flow field and bulk concentration field: (a) St_a = 0.1 and (b) St_a = 0.4. The other parameter values are the same as those used for figure 14

4.6. Analysis of the bubble pressure, p_b

From a macroscopic momentum balance following Gaver et al. (1996, § 2.4),

$$p_b=\frac{{\gamma }_f}{L}+\frac{1}{L}{\int }_{-\infty }^{\infty }{\left({\tau }_x\right)}_{\text{wall}}\mathrm{ds},$$ (4.3)

where L is the upstream channel width; in the linear wall model used in the idealized system, L = p_b/ϕ + 1 ~ p_b/ϕ. The term γ_f/L represents the far-upstream contribution from interfacial tension, and, in a system with nearly parallel walls in the upstream region (as occurs in the pushing branch), this term is approximately equal to Δp_tip. The term (1/L) ${\int }_{-\infty }^{\infty }{\left({\tau }_x\right)}_{\text{wall}}$ ds represents the contribution from the x-component of the wall stress, which depends on the airway wall geometry and the flow field.

Asymptotic analysis shows that, to leading order,

$$p_b\sim \{\begin{array}{c}\begin{array}{cc}\varphi {\mathit{Ca}}^{-2∕3},\hfill & \hfill \text{pushing branch (Gaver et al.1996)},\hfill \\ {\eta }^{1∕6}{\varphi }^{1∕2}{\mathit{Ca}}^{1∕3},\hfill & \hfill \text{peeling branch (Jensen et al.2002)}.\hfill \end{array}\hfill \end{array}\phantom{\}}$$ (4.4)

In the pushing branch, the primary contribution comes from the viscous stress in the very long ‘inflated channel’ region downstream of the bubble tip, and so (1/L) ${\int }_{-\infty }^{\infty }{\left({\tau }_x\right)}_{\text{wall}}$ ds ≫ Δp_tip on this branch. In dimensional form,

$$p_b^{\ast }\sim \{\begin{array}{c}\begin{array}{cc}{K}^{\ast }{H}^{\ast }{\left(\frac{{\gamma }_{\infty }^{\ast }}{{\mu }^{\ast }{U}_{\mathit{tip}}^{\ast }}\right)}^{2∕3},\hfill & \hfill \text{pushing branch},\hfill \\ \beta {\left(T^{\ast }\right)}^{1∕6}{\left(K^{\ast }\right)}^{1∕2}{\left({\mu }^{\ast }{U}_{\mathit{tip}}^{\ast }\right)}^{1∕3},\hfill & \hfill \text{peeling branch,}\hfill \end{array}\hfill \end{array}\phantom{\}}$$ (4.5)

where β is a weak function of Ca when Ca ≫ 1 (Jensen et al. 2002). The analysis described by (4.3)–(4.5) provides insight into why the simulations presented in figure 12 predict only a 20 % increase in p_b with a doubling of the surface tension that occurs from λ = 0 to λ → ∞. In the pushing branch, (4.5) suggests that the doubling of surface tension could result in an increase of p_b by 60 % as a result of modified downstream viscous stresses. The peeling branch p_b is only weakly dependent on surface tension because λ ≈ 1 + h.o.t. where ‘h.o.t.’ are higher-order terms in Ca for Ca ≫ 1. Since Ca = 0.4 lies between the peeling and pushing branches, neither of these limits are entirely appropriate, but the analysis suggests that the modest increase in p_b results from fluid–structure interactions that modulate the increase in pressure due to pressure-dependent widening of the upstream (open) end of the channel (increasing L), which (a) magnifies the force that is applied to the bubble, and (b) reduces the Young–Laplace pressure drop across the air–liquid interface. In § 5 we will investigate whether this is a result of the idealized linear wall model, (2.9).

The leading-order analysis of (4.5) neglects the effects of the bubble-tip pressure drop; however, by comparing the Δp_tip (figure 4) to p_b (figure 2) at the transition between the pushing and peeling branches (Ca = 0.2), it is evident that Δp_tip provides a meaningful contribution to the total bubble pressure, since Δp_tip ~ p_b/4. The viscous contribution to Δp_tip is minuscule (figure 4); therefore, p_tip ~ λk_tip. Along the peeling branch (Ca = 1), Δp_tip ~ p_b/2; since the viscous contribution remains inconsequential (figure 4), the enhanced influence of Δp_tip over that of the pushing branch occurs because of an increased k_tip from a narrowing of the bubble tip as the wall shape becomes wedge-shaped near the meniscus front. This is described as ‘region 2’ by Jensen et al. (2002), which acts as a valve that determines the flow rate of the system. The relationship between γ_f and p_b is clear from (4.3). From (2.20) and (2.21) and figure 11 it is evident that γ_f depends only upon λ and St_r, and that a significant change in γ_f occurs when λ ~ O(1). This behaviour is also reflected by the data presented in figure 12, and leads to the prediction of a critical surfactant concentration, which is described below in § 5.2.

5. Analysis in the context of pulmonary airway reopening

The results presented above provide a detailed description of the interactions between surfactant transport, physicochemical hydrodynamics and fluid–structure interactions that exist in an idealized model of the propagation of a semi-infinite bubble through a compliant channel that is obstructed by a surfactant-doped liquid occlusion. Here we put this information in context as it relates to the physiological process of opening a pulmonary airway. We explore the validity of the simplified model and investigate model improvements that may enhance the applicability of these models to simulate segments of the pulmonary system. Our goal is to identify mechanisms that may be used to protect sensitive tissues in the lung.

5.1. Model assumptions and limitations

We selected the parameters for our base state (§ 4.1) to provide a fundamental understanding of physicochemical interactions that exist as a semi-infinite bubble progresses through a flexible-walled channel. In the present section we use this analysis to guide our understanding of the behaviour of a two-dimensional representation of a collapsed bronchial airway; however, several assumptions have been incorporated that may limit the direct applicability to the physiological system.

In the lung, the liquid lining properties are assumed to be ρ* = 1 g cm⁻³, μ* = 0.05 g (cm s)⁻¹, ${\gamma }_{\mathit{eq}}^{\ast }$ = 25 dyn cm ⁻¹, $k_a^{\ast }$ = 0.5 cm³ mg⁻¹ s⁻¹,$C_0^{\ast }$ = 1 mg ml⁻¹ and D* ≈ 10⁻⁶ cm² s⁻¹ following Ghadiali & Gaver (2000). Assuming a reopening velocity of $U_{\mathit{tip}}^{\ast }$ = 1 cm s⁻¹, we find $\mathit{Ca}={\mu }^{\ast }{U}_{\mathit{tip}}^{\ast }∕{\gamma }_{\infty }^{\ast }\sim {10}^{-3}$. However, Ca ≪ 1 is not tractable computationally, and furthermore results in flow in the ‘pushing’ branch that is unstable (Halpern et al. 2005) and unlikely to exist owing to gravity (Hazel & Heil 2008). Instead, we have investigated Ca ~ O(1) in order to replicate conditions appropriate to the peeling branch, which better represents the physiological state.

Since the convection rate was increased, the transport parameters were adjusted accordingly, so that St_λ/Ca ~ 10⁻¹, thus assuring that the surfactant adsorption rate is slower than the rate of interfacial creation. Also, St_d/St_λ ≪ 1 to ensure that desorption was slower than adsorption (Zimmer et al. 2005).

The relationship between convection and diffusion in the fluid phase is described by a Péclet number based upon the convective velocity, ${\mathit{Pe}}_b{\mid }_{\mathit{conv}}=2U_{\mathit{tip}}^{\ast }{L}^{\ast }∕D_b^{\ast }$, where 2L* is the total upstream channel width. since L* = (p_b/ϕ + 1)H*, we estimate Pe_b|_conv ~ 10⁴. Therefore, the value of the Péclet number based upon the relaxation velocity scale is

$${\mathit{Pe}}_b=\frac{{\gamma }_{\infty }^{\ast }{H}^{\ast }}{{\mu }^{\ast }{D}_b^{\ast }}=\frac{{\mathit{Pe}}_b{\mid }_{\mathit{conv}}}{2\mathit{Ca}(p_b∕\varphi +1)},$$

which provides an estimate of Pe_b ~ 10³. While simulations of Pe_b of this large magnitude are untenable because of concentration boundary layer effects that require extraordinary accuracy of the velocity field near the air–liquid interface, responses have been demonstrated for Pe_b ~ 10² and also for limiting behaviour as Pe_b → ∞, which provides insight into the transport behaviour when convection dominates diffusion, and allows the exploration of the important transport limitations associated with this system for even higher Pe_b.

The analysis of this problem neglects start-up effects, which are likely to affect the behaviour of the interface near airway bifurcations. In addition, the analysis does not include an evaluation of unsteadiness that may influence transport owing to the cyclic expansion and compression of airways that can affect the local velocity fields (Zimmer et al. 2005; Smith & Gaver 2008; Smith et al. 2012). Finally, the relationship between inertia and viscous effects is represented by Re = ρU_tipW/μ ~ 0.5. Based upon the analysis of Heil (2000), the Stokes flow representation of this problem provides a suitable demonstration of the flow properties.

5.2. Critical surfactant concentration

The influence of λ, as described by figure 12, indicates that the reopening pressure depends on the value of the dimensionless adsorption length. The minimum reopening pressure p_b occurs at large concentrations, λ → 0. However, over the range 10⁻¹ < λ < 1, a transition to a higher p_b exists. Since $\lambda \equiv {\Gamma }_{\infty }^{\ast }∕\left(C_0^{\ast }{H}^{\ast }\right)$, this result suggests that a critical surfactant concentration, $C_0^{\ast }{\mid }_{\mathit{crit}}$, must be exceeded in order to make the transition to lower reopening pressures, and that this critical concentration is in the range ${\Gamma }_{\infty }^{\ast }∕H^{\ast }<C_0^{\ast }{\mid }_{\mathit{crit}}<10{\Gamma }_{\infty }^{\ast }∕H^{\ast }$.

To estimate consider the reopening of a 1 mm one-dimensional airway with H = 2.5 μ 10⁻³ cm (5 % film thickness) and Γ_∞ = 4.>0 × 10⁻¹⁰ mol cm⁻² (Krueger & Gaver 2000). The critical bulk concentration is then estimated to be

$$0.1\mathrm{mg}{\mathrm{ml}}^{-1}<C_0^{\ast }{\mid }_{\mathit{crit}}<1\mathrm{mg}{\mathrm{ml}}^{-1}.$$ (5.1)

Despite the many approximations involved in this analysis, this result coincides with the experimental results obtained by Bilek, Dee & Gaver (2003), who showed that a bulk concentration of 1 mg ml⁻¹ of Infasurf (ONY, Inc.), a pulmonary surfactant used for surfactant replacement therapy, was sufficient to protect airway epithelial cells from damage in an experimental model of airway reopening. In addition, pulsatile motion of a bubble in a surfactant-doped solution with C = 0.1 mg ml⁻¹ within a cylindrical tube demonstrates enhanced surfactant transport, indicating that a concentration at this level is sufficient to develop surfactant enrichment through physicochemical interactions (Pillert & Gaver 2009). Recent experiments demonstrate the protective effects of C = 0.1 mg ml⁻¹, and these effects are significantly enhanced with C = 1.0 mg ml⁻¹ (Glindmeyer et al. 2012).

5.3. Micro-scale stress field

In vitro experimental studies of airway reopening have investigated the role of micro-mechanical stresses on damage to epithelial cells that line airways. These studies have correlated the normal stress gradient with cell membrane disruption that is observed to damage the cell layer in rigid-walled experiments of airway reopening (Bilek et al. 2003; Kay et al. 2004; Yalcin et al. 2007). The observed epithelial cell damage is hypothesized to be caused by the normal stress gradient migrating across the epithelial surface, which acts as a travelling wave that squeezes the cell in a fore–aft direction (similar to a rolling pin) and creates a large time-dependent transmembrane pressure that ruptures the cell membrane.

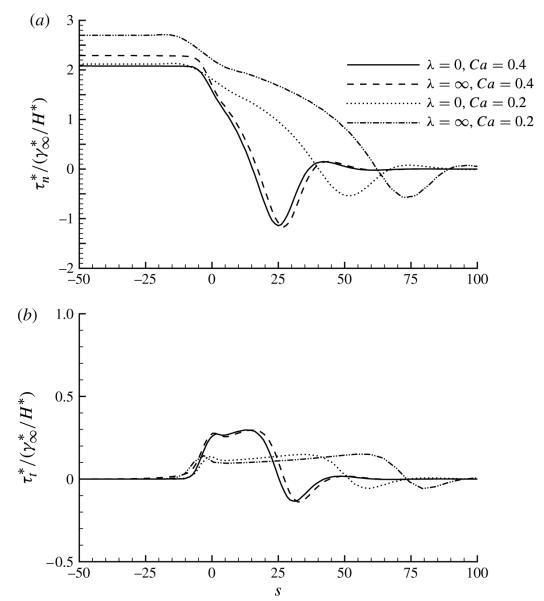
In order to examine the potential protective mechanism of surfactant in a flexible-walled model of airway reopening, in figure 16 we present (a) the normal stress (τ_n) and (b) the tangential stress (τ_t) as functions of distance along the wall, with s = 0 denoting the location of the tip, at Ca = 0.4 (peeling branch) and Ca = 0.2 (pushing branch), for λ = 0 and ∞. This figure shows that the normal stress decreases for s > 0 because of the pressure drop at the bubble tip due to surface tension. Ahead of the bubble tip, τ_n < 0 due to inward wall deflection below the wall equilibrium position. In addition, τ_t ≪ τ_n, and this figure demonstrates a downstream-directed stress in the vicinity of the tip, with an upstream-directed shear stress in the collapsed region.

FIGURE 16.

Profiles of (a) the non-dimensional wall normal stress and (b) the wall tangential stress for Ca = 0.2 and 0.4 and λ = 0 and ∞. The other parameter values are η = 100, ϕ = 0.5, Pe_b = 50, Pe_s = 10³, St_d = 0.03 and E_l = 1.

Surprisingly, for Ca = 0.4, figure 16 shows very little difference in the stress fields as a function of λ. The maximum stress gradients are not markedly modified by the existence of surfactant, and the only major difference that exists is the overall magnitude of the normal stress difference between the upstream gas phase and the downstream collapsed region, which is consistent with the p_b versus Ca relationship shown in figure 2. The very small change in p_b is also consistent with the surface-tension-independent behaviour that is predicted for the peeling branch by Jensen et al. (2002), as discussed above.

To illustrate the difference between large Ca peeling solutions and small Ca pushing solutions, figure 16 also shows the wall stresses for Ca = 0.2. Here we see that the difference in upstream-to-downstream pressure drop is magnified over the peeling case. In addition, the magnitude of the tangential stress is not affected, but both tangential and normal stresses are exerted over a slightly larger distance. However, the pressure gradient is not significantly influenced by a change in λ.

5.4. Wall model effects

In the investigation of the idealized model, it was found that there was only an approximately 20 % increase in $p_b^{\ast }$ with a 100 % increase of λ* (§ 4.4). In contrast, Naire & Jensen (2005) investigated the dependence of $p_b^{\ast }$ on the bulk concentration (their figure 4b) similar to that shown in figure 12 for three values of Ca. Along the pushing branch (Ca ~ 0.02), they found that a 150 % increase in λ* results in approximately a 400 % increase in $p_b^{\ast }$, while the peeling branch (Ca ~ 0.18) results in approximately a 250 % increase in $p_b^{\ast }$. Therefore, the predicted pressure differences were far in excess of the fractional increase in surface tension, and thus are much greater than those predicted by our two-dimensional planar analysis. We hypothesize that this effect may be due to the relative stiffening of the tube in comparison to surface tension forces, which diminishes the pressure-induced increase in L, thereby reducing the incremental increase in λ* (§ 4.6). In this section we will attempt to resolve this discrepancy by exploring the relationship between the channel compliance (‘tube law’) and the driving pressure in the system.

In addition to the relative insensitivity of $p_b^{\ast }$ on $C_0^{\ast }$, from figure 16 it is evident that the predicted magnitude of the normal stress gradient is unaffected by the surfactant concentration – and yet, experiments in rigid-geometry channels suggest that surfactant is protective because of its reduction of the normal stress gradient that sweeps across cells. We observe that the major difference between the pushing and peeling branches relates to the wall shape that exists downstream of the bubble tip (Gaver et al. 1996), and that between these two situations the gradients are significantly different. We therefore hypothesize that the linear wall equation (2.9) may be responsible for masking differences in normal stress gradients that otherwise would exist in a more physiologically relevant model of airway reopening that is based upon a nonlinear tube law.

In order to investigate the airway tube law hypothesis, we replace the linear wall model equation (2.9) with a nonlinear wall equation that is based on the tube law model developed by Lambert et al. (1982), which was adapted by Overby (1997). At the flexible wall, y = h(x), the stress condition is

$$\widehat{m}•\sigma •\widehat{m}=\eta {\kappa }_{\text{wall}}-P_{\mathit{tr}}{m}_y,$$ (5.2)

where P_tr, the transmural pressure, is given by

$$P_{\mathit{tr}}=A+\frac{B}{h^{2∕m_1}}+C{\left(\frac{1-{\lambda }_0}{1-{\lambda }_0{h}^2}\right)}^{1∕m_2}.$$ (5.3)

The value of λ₀ is tabulated by Lambert et al. (1982), with λ₀ = 0.075 for generation 13; however, the original Lambert formulation was not suitable because it introduces discontinuities in curvature at P_tr = 0. For this reason, Overby (1997) used a nonlinear least-squares regression algorithm to identify the remaining constants as A = –10.2, B = –0.012, C = 10.2, m₁ 0.63 m₂ = 6.49.

Figure 17 demonstrates this tube law and the effective tube stiffness, ϕ_eff = dP_tr/dh, which shows that the uninflated region of the channel is flaccid, but becomes increasingly stiff as the airway inflates and reaches a maximum displacement at h₀ = λ₀^−1/2. The minimum value of ϕ_eff from the nonlinear model (ϕ_eff ~ 0.3 at h = 1) is reduced from the value ϕ = 0.5 that was investigated in the linear and so this results in greater compliance near h = 1. However, the walls stiffen (ϕ_eff increases) with increasing wall displacement, especially for h > 2.5. As shown below, the average wall stiffness over the entire displacement is greater than that of the linear case – this leads to a net increase in the driving pressure over that predicted for the linear wall model.

FIGURE 17.

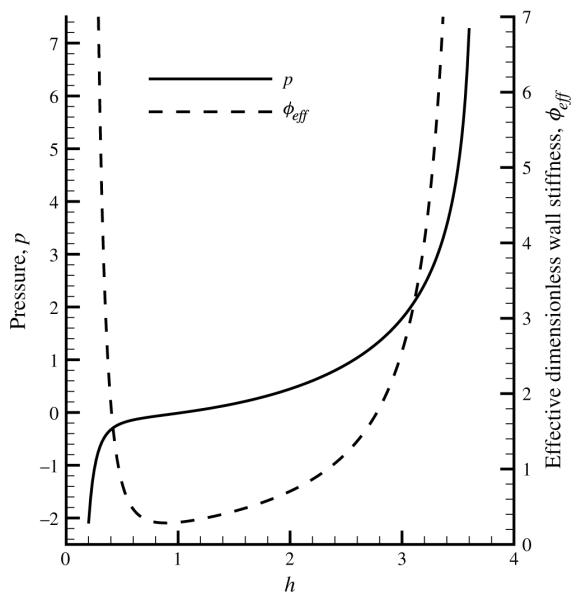
Nonlinear pressure–channel height relationship and effective stiffness, (5.2).

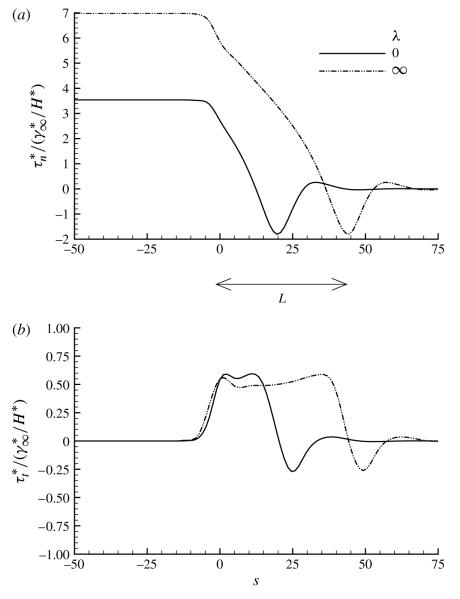
In this nonlinear model, the transition between the pushing and peeling branches occurs at a higher Ca, and the effect of wall nonlinearity is shown in figure 18 for Ca = 0.8 for λ = 0 (bulk equilibrium) and λ → ∞ (surfactant-free). This value of Ca is in the transition region between the pushing and peeling branches. It is quite clear that the inclusion of surfactant to the bulk equilibrium limit decreases the reopening pressure by approximately 50 %. Unlike the idealized linear model results, this decrease in p_b corresponds to the 50 % decrease in surface tension that would occur if λ = λ_∞. So, since the airway wall becomes increasingly stiff at high pressures, the physiological tube law decouples the upstream fluid–structure interactions by limiting the extent of the lateral deformation. This, in turn, sets the reopening pressure to be nearly proportional to the surface tension, as one would expect if the tip curvature was not modified by the surface tension. Nevertheless, the stress gradients remain insensitive to λ. These results are consistent with the predictions from the one-dimensional model by Naire & Jensen (2005), although that study demonstrated a greater change in p_b. As Ca is increased further into the peeling branch, the pressure difference between the λ = 0 and λ → ∞ cases is diminished, and both the stress-field magnitudes and gradients show little sensitivity to the surfactant concentration. The insensitivity of the stress-field magnitude is in contrast to the model results of Naire & Jensen (2005), who found a strong correlation existing in this range.

FIGURE 18.

The influence of using a nonlinear tube law, (5.2), on (a) the wall normal stress and (b) the wall tangential stress. Here Ca = 0.8, corresponding to the transition between pushing and peeling solutions. The parameter values are: Ca = 0.8, η = 100, ϕ = 0.5, Pe_b = 50, Pe_s = 10³, St_a = 0.03, St_d = 0.03 and E_l = 1.

This investigation shows that, even with the nonlinear tube law, the stress gradients remain nearly independent of the surfactant concentration, and therefore the magnitude of the normal stress gradient is largely determined by the wall deformation (see also Naire & Jensen 2005). So, as can be seen in figure 18, when the magnitude of p_b increases with increasing surface tension, the length of the travelling wave extends commmensurately. Since the length of the travelling wave is far greater than the length of a cell, the pressure gradient presented to the surface of the cell would be independent of the surface tension (i.e. surfactant concentration) and would only depend on the reopening velocity.

5.5. The relationship between model results and experimental observations

These studies bring up an interesting conundrum concerning the mechanisms responsible for surfactant protection that cannot be resolved without additional biologically based experiments that would use flexible-walled models. This issue relates to differences in the mechanical stress fields that exist in rigid and flexible-walled systems, as described below.

Rigid-walled

In rigid-walled systems (as investigated by Bilek et al. 2003; Kay et al. 2004; Yalcin et al. 2007), an increase in Ca is associated with:

1. a slight increase in the total pressure drop across the bubble tip (ΔP);

2. (b) an increase in the maximum shear stress, τ_s|_max; and

3. (c) a large decrease in the maximum pressure gradient, dP/dx|_max.

Since experiments have shown that an increase of Ca, through either an increase of velocity or an increase in viscosity, reduces the damage to the cell layer, it has been concluded that the magnitude of dP/dx|_max is likely to be the damaging mechanical stimulus. Furthermore, decreasing λ is associated with a decrease in damage, and this is consistent with a decrease in dP/dx|_max. These studies have disassociated the increase in damage with reduced velocity as being a function of the exposure time.

Flexible-walled

Our simulations of flexible-walled systems presented in this paper demonstrate the following features of the macro- and micro-scale stress fields that are associated with an increase in surfactant concentration $C_0^{\ast }$ (decrease in λ and γ ) at fixed Ca (equivalent to fixed velocity, U):

1. a decrease in p_b;

2. a small change in dP/dx|_max; and

3. (c) a reduction in the exposure time (Δt_exp ~ L/U), where L is the length of the travelling wave (see figure 18).

   Unfortunately, carefully controlled reopening experiments have not been conducted in flexible-walled biomimetic airways, and so it is not possible to draw conclusions on damage mechanisms solely from the available information. However, three possible scenarios exist.

   1. Our simulations suggest that, if the magnitude of dP/dx|_max is the damaging stimulus (as predicted from rigid models), in flexible model experiments at steady state we would expect that flexibility itself would be protective, and we would not expect to see enhanced airway protection when surfactant concentrations are increased. If this response is observed in biological studies, then enhancing wall flexibility could be instrumental in protecting an airway. Since highly oedematous airways are liquid-filled to nearly a maximum state of expansion (Hubmayr 2002), these airways are likely to behave similarly to rigid tubes. Rather than attempting to deliver surfactant to these regions, it may be more effective to reduce the level of oedema so that a flexible-walled state is developed. Clinically, this would imply that a state of ‘watchful waiting’ or ‘medical observation’ could be appropriate. In this approach, repeated testing may be performed without medical intervention until oedema is resolved. This means that airway pressures would be maintained at a low level during a period of active surveillance that could assess the liquid volume in the lung. After oedema is resolved, airway reopening would commence through increased airway pressures.

   2. In contrast, if an increase in surfactant concentration is observed to reduce the damage to epithelial cells (as in rigid-walled configurations), this suggests that the magnitude of p_b or the exposure duration (or both) are responsible for cell damage in flexible airways. This result would contradict our present understanding of damage mechanisms that have been gleaned from biological studies using rigid-walled models. In this case, it is likely that cell damage is caused by stretch-induced strains, as hypothesized by Naire & Jensen (2005). This damage mechanism would be similar to that occurring in volutrauma, but would exist only in the airways that are reopened by removal of a viscous occlusion.

   3. Alternatively, surfactant-induced reduction of damage could be a transient (albeit long-lasting) response that occurs as the system evolves to a steady state. If this is the case, the tube would fill with fluid downstream of the interface and function as a rigid tube. In this evolution, the upstream film thickness will not be fixed, and must in general be less than H in order for the downstream region to accumulate fluid. Such a decoupling of the upstream film thickness from the downstream channel width is similar to that which exists in rigid-walled reopening, and may cause dP/dx|_max to depend on the surface tension (and hence the surfactant concentration) in the system. In this situation, the transient behaviour would be consistent with the mechanistic hypotheses that have been based upon rigid-walled models.

In summary, the present analysis of fluid–structure interactions and coupled physicochemical hydrodynamics in flexible-walled airway reopening does not completely resolve issues of the protective mechanisms that may be used to reduce the incidence of pulmonary atelectrauma. As such, it is clear that more experimental evidence is necessary to establish the role of interfacial flows in atelectrauma. Nevertheless, in concert with data from the biological system, the computational simulations investigated in this paper may be used to identify the structure and magnitude of the mechanical stimuli that must be ameliorated in order to reduce the incidence of atelectrauma-based ventilator-induced lung injury.

6. Conclusions

In this study we have computationally modelled the physicochemical influence of surfactant on the reopening of a pulmonary airway by considering the steady two-dimensional motion of a semi-infinite bubble propagating through a liquid-filled compliant channel doped with surfactant. While a large number of dimensionless parameters influence the dynamics of the system, we specifically investigate the importance of the capillary number Ca (a dimensionless velocity) and the adsorption depth parameter λ (inversely related to the bulk concentration).

We find that a modification of Ca significantly impacts the concentration distribution in the tip region of the propagating bubble through a macro-scale modification of the flow structure. The dimensionless adsorption depth λ is a critical parameter in this system because it provides a description of the quantity of surfactant that must exist in the bulk in order to dynamically populate the ever-lengthening interface. In these studies we find that the system can only respond as a low-surface-tension interface if λ < λ_crit, where 0.1 < λ_crit < 1.

These studies demonstrated a surprising result that, aside from the macro-scale pressure drop in the system, the stress field was relatively insensitive to surfactant transport parameters. This result implies that the wall equation determines the nature of the stress field through fluid–structure interactions. Therefore, this study does not resolve the question of the physicochemical properties that are necessary to protect the lung from atelectrauma. As such, we propose that further biological studies are necessary to elucidate the relationship between airway wall flexibility and mechanical stress-induced damage in models of pulmonary airway reopening.

Appendix A. Interfacial surfactant concentration

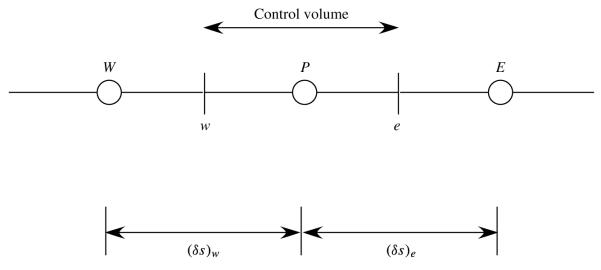
The interfacial surfactant concentration is solved on a non-uniform grid with a higher density of node points near the bubble tip. Equation (2.13) is integrated over a control volume between grid points e and w, as shown in figure 19:

$${\left(u_s\Gamma \right)}_e-{\left(u_s\Gamma \right)}_w=D_e({\Gamma }_E-{\Gamma }_P)-D_w({\Gamma }_P-{\Gamma }_W)+\delta S_P{\mathit{J}}_P,$$ (A 1)

where Γ_P is the surfactant concentration at point P, J_P is the flux at P given by (2.14), and D = 1/(Pe_sδs) is a diffusivity parameter.

FIGURE 19.

Grid used to solve interfacial surfactant concentration.

The convective terms on the left-hand side of (A 1) are approximated using Patankar’s hybrid power-law scheme (Patankar 1980). Equation (A 1) then becomes

$$a_p{\Gamma }_P=a_e{\Gamma }_E+a_w{\Gamma }_W+\delta S_P{\mathit{J}}_P,$$ (A 2)

where a_p = a_e + a_w + u_se − u_sw and

$$a_e=D_e{f}_{\mathit{PLH}}\left(\frac{u_{\mathit{se}}}{D_e}\right)+\max (-u_{\mathit{se}},0),$$ (A 3a)

$$a_w=D_w{f}_{\mathit{PLH}}\left(\frac{u_{\mathit{sw}}}{D_w}\right)+\max (u_{\mathit{sw}},0),$$ (A 3b)

and

$$f_{\mathit{PLH}}\left(a\right)=\max (0,{(1-0.1\mid a\mid )}^5).$$ (A 4)

Equation (A 2) is applied at each node point along the interface, giving rise to a tridiagonal system of linear equations that is solved using the Thomas algorithm. The boundary conditions are given by (2.15).

Appendix B. Bulk surfactant concentration

Boundary-fitted coordinates (ξ, η), where ξ = ξ(x, y) and η = η(x, y), are used to describe the grid of our domain since its boundaries do not easily line up with the usual Cartesian (x, y) coordinate system. The (ξ, η) transformations between the physical and computational domains are obtained by solving a system of Poisson equations (see e.g. Fletcher & Srinivas 1991; Thompson, Soni & Weatherill 1999).

In the (ξ, η) coordinate system, the bulk concentration equation becomes

$${\left[F^{\xi }C-\frac{1}{{\mathit{Pe}}_b}\frac{B_{11}}{\mathit{J}}{C}_{\xi }\right]}_{\xi }+{\left[F^{\eta }C-\frac{1}{{\mathit{Pe}}_b}\frac{B_{22}}{\mathit{J}}{C}_{\eta }\right]}_{\eta }=\frac{1}{{\mathit{Pe}}_b}\left[{\left(\frac{B_{12}}{\mathit{J}}{C}_{\eta }\right)}_{\xi }+{\left(\frac{B_{12}}{\mathit{J}}{C}_{\xi }\right)}_{\eta }\right],$$ (B 1)

where B = AA^T is a 2 × 2 matrix, J = det(A), F = (F^ξ, F^η) = Au and

$$\mathit{A}=\left[\begin{array}{cc}\hfill y_{\eta }\hfill & \hfill -x_{\xi }\hfill \\ \hfill -y_{\xi }\hfill & \hfill x_{\eta }\hfill \end{array}\right].$$ (B 2)

Equation (B 1) is integrated over the central cell shown in figure 20, to yield an approximation equation for the concentration at the centre, C_P:

$$-a_e{C}_E-a_w{C}_W-a_n{C}_N-a_s{C}_S+a_p{C}_P=S_c,$$ (B 3)

where a_p = a_e + a_w + a_n + a_s and

$$a_e=\frac{1}{{\mathit{Pe}}_b}{\left(\frac{B_{11}}{\mathit{J}}\right)}_e{f}_{\mathit{PLH}}\left(\frac{{\mathit{Pe}}_b{f}_e}{{(B_{11}∕\mathit{J})}_e}\right)+\max (-f_e,0),$$ (B 4a)

$$a_w=\frac{1}{{\mathit{Pe}}_b}{\left(\frac{B_{11}}{\mathit{J}}\right)}_w{f}_{\mathit{PLH}}\left(\frac{{\mathit{Pe}}_b{f}_w}{{(B_{11}∕\mathit{J})}_w}\right)+\max (f_w,0),$$ (B 4b)

$$a_n=\frac{1}{{\mathit{Pe}}_b}{\left(\frac{B_{22}}{\mathit{J}}\right)}_n{f}_{\mathit{PLH}}\left(\frac{{\mathit{Pe}}_b{f}_n}{{(B_{22}∕\mathit{J})}_n}\right)+\max (-f_n,0),$$ (B 4c)

$$a_s=\frac{1}{{\mathit{Pe}}_b}{\left(\frac{B_{22}}{\mathit{J}}\right)}_s{f}_{\mathit{PLH}}\left(\frac{{\mathit{Pe}}_b{f}_s}{{(B_{22}∕\mathit{J})}_s}\right)+\max (f_s,0)$$ (B 4d)

and

$$f_e=F_e^{\xi },f_w=F_w^{\xi },f_n=F_n^{\eta },f_s=F_s^{\eta }.$$ (B 5)

FIGURE 20.

A typical finite-volume cell used in the computation of the bulk surfactant concentration.

A similar power-law scheme is used for the convective terms of the bulk concentration equation. Sc is the integral of the source term in (B 1):

$$\begin{array}{cc}\hfill \mathit{Sc}=& \frac{1}{{\mathit{Pe}}_b}[{\left(\frac{B_{12}}{J}\right)}_e{\left(\frac{\partial C}{\partial \eta }\right)}_e-{\left(\frac{B_{12}}{J}\right)}_w{\left(\frac{\partial C}{\partial \eta }\right)}_w\phantom{]}\hfill \\ \hfill & \phantom{[}+{\left(\frac{B_{12}}{J}\right)}_n{\left(\frac{\partial C}{\partial \xi }\right)}_n-{\left(\frac{B_{12}}{J}\right)}_s{\left(\frac{\partial C}{\partial \xi }\right)}_s],\hfill \end{array}$$ (B 6)

where

$${\left(\frac{\partial C}{\partial \eta }\right)}_e=\frac{1}{4}(C_N-C_S+C_{\mathit{NE}}-C_{\mathit{SE}}),$$ (B 7a)

$${\left(\frac{\partial C}{\partial \eta }\right)}_w=\frac{1}{4}(C_N-C_S+C_{\mathit{NW}}-C_{\mathit{SW}}),$$ (B 7b)

$${\left(\frac{\partial C}{\partial \xi }\right)}_n=\frac{1}{4}(C_E-C_W+C_{\mathit{NE}}-C_{\mathit{NW}}),$$ (B 7c)

$${\left(\frac{\partial C}{\partial \xi }\right)}_s=\frac{1}{4}(C_E-C_W+C_{\mathit{SE}}-C_{\mathit{SW}}).$$ (B 7d)

The derivative boundary conditions given in (2.17) are written in the form

$$\frac{1}{{\mathit{Pe}}_b\lambda }\mathit{n}•\nabla C=j_n,$$ (B 8)

where the flux j_n is zero at the upstream end, the wall and the centreline, and is equal to j along the air–liquid interface. In the transformed coordinate system this becomes

$$\frac{B_{11}}{\mathit{J}}\frac{\partial C}{\partial \xi }+\frac{B_{12}}{\mathit{J}}\frac{\partial C}{\partial \eta }={\mathit{Pe}}_b\lambda \sqrt{B_{11}}{j}_n.$$ (B 9)

Equations (B 9) and (B 6) are then substituted into (B 3). Because (B 3) consists of a large system of sparse equations, it is solved iteratively.