Abstract
This paper considers feature selection for data classification in the presence of a huge number of irrelevant features. We propose a new feature-selection algorithm that addresses several major issues with prior work, including problems with algorithm implementation, computational complexity, and solution accuracy. The key idea is to decompose an arbitrarily complex nonlinear problem into a set of locally linear ones through local learning, and then learn feature relevance globally within the large margin framework. The proposed algorithm is based on well-established machine learning and numerical analysis techniques, without making any assumptions about the underlying data distribution. It is capable of processing many thousands of features within minutes on a personal computer while maintaining a very high accuracy that is nearly insensitive to a growing number of irrelevant features. Theoretical analyses of the algorithm’s sample complexity suggest that the algorithm has a logarithmical sample complexity with respect to the number of features. Experiments on 11 synthetic and real-world data sets demonstrate the viability of our formulation of the feature-selection problem for supervised learning and the effectiveness of our algorithm.
Index Terms: Feature selection, local learning, logistical regression, ℓ1 regularization, sample complexity
1 Introduction
HIGH throughput technologies now routinely produce large data sets characterized by unprecedented numbers of features. Accordingly, feature selection has become increasingly important in a wide range of scientific disciplines. In this paper, we consider feature selection for the purposes of data classification. An example of data classification tasks where feature selection plays a critical role is the use of oligonucleotide microarray for the identification of cancer-associated gene expression profiles of diagnostic or prognostic value [1], [2], [50]. Typically, the number of samples is less than 100, while the number of features associated with the raw data is on the order of thousands or even tens of thousands. Among this enormous number of genes, only a small fraction is likely to be relevant for cancerous tumor growth and/or spread. The abundance of irrelevant features poses serious problems for existing machine learning algorithms, and represents one of the most recalcitrant problems for their applications in oncology and other scientific disciplines dealing with copious features. Performance of most classification algorithms suffers as the number of features becomes excessively large. It has been recently observed, for example, that even support vector machine (SVM) [3]—one of the most advanced classifiers, believed to scale well with the increasing number of features—experiences a notable drop in accuracy when this number becomes sufficiently large [4], [14]. It has been proven by [5] that SVM has a worst-case sample complexity that grows at least linearly in the number of irrelevant features. In addition to defying the curse of dimensionality, eliminating irrelevant features can also reduce system complexity, processing time of data analysis, and the cost of collecting irrelevant features. In some cases, feature selection can also provide significant insights into the nature of the problem under investigation.
Feature selection for high-dimensional data is considered one of the current challenges in statistical machine learning [7]. In this paper, we propose a new feature-selection algorithm that addresses several major issues with existing methods, including their problems with algorithm implementation, computational complexity, and solution accuracy for high-dimensional data. The formulation of the proposed algorithm is based on a simple concept that a given complex problem can be more easily, yet accurately enough, analyzed by parsing it into a set of locally linear problems. Local learning allows one to capture local structure of the data, while the parameter estimation is performed globally within the large margin framework to avoid possible overfitting. The new algorithm performs remarkably well in the presence of copious irrelevant features. A large-scale experiment conducted on 11 synthetic and real-world data sets demonstrates that the algorithm is capable of processing many thousands of features within minutes on a personal computer, yet maintaining a very high accuracy that is nearly insensitive to a growing number of irrelevant features. In one simulation study where we consider Fermat’s spiral problem, our algorithm achieves a close-to-optimal solution even when the data contain one million irrelevant features.
We study the algorithm’s properties from several different angles to explain why the proposed algorithm performs well in a high-dimensional space. We show that the algorithm can be regarded as finding a feature weight vector so that the upper bound of the leave-one-out cross-validation error of a nearest-neighbor classifier in the induced feature space is minimized. By using fixed point theory, we prove that with a mild condition the proposed algorithm converges to a solution as if it had perfect prior knowledge as to which feature is relevant. We also conduct a theoretical analysis of the algorithm’s sample complexity which suggests that the algorithm has a logarithmical sample complexity with respect to the input data dimensionality. That is, the number of samples needed to maintain the same level of learning accuracy grows only logarithmically with respect to the feature dimensionality. This dependence is very weak, and matches the best known bounds proven in various feature-selection contexts [5], [6]. Although logarithmical sample complexity is not new in the literature, it holds only for linear models, whereas in our algorithm no assumptions are made about the underlying data distribution.
In this paper, we also show that the aforementioned theoretical analysis of our feature-selection algorithm may have an important theoretical implication in learning theory. Based on the proposed feature-selection algorithm, we show that it is possible to derive a new classification algorithm with a generalization error bound that grows only logarithmically in the input data dimensionality for arbitrary data distribution. This is a very encouraging result considering that a large part of machine learning research is focused on developing learning algorithms that behave gracefully when faced with the curse of dimensionality.
This paper is organized as follows: Section 2 reviews prior work, focusing on the main problems with existing methods that are addressed by our algorithm. The newly proposed feature-selection algorithm is described in Section 3. This section also presents the convergence analysis of our algorithm in Section 3.1, its computational complexity in Section 3.2, and its extension to multiclass problems in Section 3.3. Experimental evaluation is presented in Section 4. The algorithm’s sample complexity is discussed in Section 5, after which we conclude the paper by tracing back the origins of our work and pointing out major differences and improvements made here as compared to other well-known algorithms.
2 LITERATURE REVIEW
Research on feature selection has been very active in the past decade [8], [10], [11], [12], [14], [18], [19]. This section gives a brief review of existing algorithms and discusses some major issues with prior work that are addressed by our algorithm. The interested reader may refer to [8] and [9] for more details.
Existing algorithms are traditionally categorized as wrapper or filter methods, with respect to the criteria used to search for relevant features [10]. In wrapper methods, a classification algorithm is employed to evaluate the goodness of a selected feature subset, whereas in filter methods criterion functions evaluate feature subsets by their information content, typically interclass distance (e.g., Fisher score) or statistical measures (e.g., p-value of t-test), instead of optimizing the performance of any specific learning algorithm directly. Hence, filter methods are computationally much more efficient, but usually do not perform as well as wrapper methods.
One major issue with wrapper methods is their high computational complexity due to the need to train a large number of classifiers. Many heuristic algorithms (e.g., forward and backward selection [11]) have been proposed to alleviate this issue. However, due to their heuristic nature, none of them can provide any guarantee of optimality. With tens of thousands of features, which is the case in gene expression microarray data analysis, a hybrid approach is usually adopted wherein the number of features is first reduced by using a filter method and then a wrapper method is applied to the reduced feature set. Nevertheless, it still may take several hours to perform the search, depending on the classifier used in the wrapper method. To reduce complexity, in practice, a simple classifier (e.g., linear classifier) is often used to evaluate the goodness of feature subsets, and the selected features are then fed into a more complicated classifier in the subsequent data analysis. This gives rise to the issue of feature exportability—in some cases, a feature subset that is optimal for one classifier may not work well for others [8]. Another issue associated with a wrapper method is its capability of performing feature selection for multiclass problems. To a large extent this property depends on the capability of a classifier used in a wrapper method to handle multiclass problems. In many cases, a multiclass problem is first decomposed into several binary ones by using an error-correct-code method [13], [34], and then feature selection is performed for each binary problem. This strategy further increases the computational burden of a wrapper method. One issue that is rarely addressed in the literature is algorithmic implementation. Many wrapper methods require the training of a large number of classifiers and manual specification of many parameters. This makes their implementation and use rather complicated, demanding expertise in machine learning. This is probably one of the main reasons why filter methods are more popular in the biomedical community [1], [2].
It is difficult to address the aforementioned issues directly in the wrapper-method framework. To overcome this difficulty, embedded methods have recently received an increased interest (see, e.g., [4], [5], [14], [16], [17]). The interested reader may refer to [15] for an excellent review. Embedded methods incorporate feature selection into the learning process of a classifier. A feature weighting strategy is usually adopted that uses real-valued numbers, instead of binary ones, to indicate the relevance of features in a learning process. This strategy has many advantages. For example, there is no need to prespecify the number of relevant features. Also, standard optimization techniques (e.g., gradient descent) can be used to avoid a combinatorial search. Hence, embedded methods are usually computationally more tractable than wrapper methods. Still, computational complexity is a major issue when the number of features becomes excessively large. Other issues including algorithm implementation, feature exportability, and extension to multiclass problems also remain.
Some recently developed embedded algorithms can be used for large-scale feature-selection problems under certain assumptions. For example, [4], [14] propose performing feature selection directly in the SVM formulation, where the scaling factors are adjusted using the gradient of a theoretical upper bound on the error rate. RFE [16] is a well-known feature-selection method specifically designed for microarray data analysis. It works by iteratively training an SVM classifier with a current set of features, and then heuristically removing the features with small feature weights. As with wrapper methods, the structural parameters of SVM may need to be reestimated by using, for example, cross validation during iterations. Also, a linear kernel is usually used for computational reasons. ℓ1-SVM with a linear kernel [17], with a proper parameter tuning, can lead to a sparse solution where only relevant features receive nonzero weights. A similar algorithm is logistical regression with ℓ1 regulation. It has been proven by [5] that ℓ1 regularized logistical regression has a logarithmical sample complexity with respect to the number of features. However, the linearity assumption of data models in these approaches limits their applicability to general problems.
3 OUR ALGORITHM
In this section, we present a new feature-selection algorithm that addresses many issues with prior work discussed in Section 2. Let be a training data set, where xn is the nth data sample containing J features, yn is its corresponding class label, and J ≫ N. For clarity, we here consider only binary problems, while in Section 3.3, our algorithm is generalized to address multiclass problems. We first define the margin. Given a distance function, we find two nearest neighbors of each sample xn, one from the same class (called nearest hit or NH) and the other from the different class (called nearest miss or NM). The margin of xn is then computed as
| (1) |
where d(·) is a distance function. For the purposes of this paper, we use the Manhattan distance to define a sample’s margin and nearest neighbors, while other standard definitions may also be used. This margin definition is implicitly used in the well-known RELIEF algorithm [18], and first mathematically defined in [19] (using euclidean distance) for the feature-selection purpose. An intuitive interpretation of this margin is a measure as to how much the features of xn can be corrupted by noise (or how much xn can “move” in the feature space) before being misclassified. By the large margin theory [3], [20], a classifier that minimizes a margin-based error function usually generalizes well on unseen test data. One natural idea then is to scale each feature, and thus obtain a weighted feature space, parameterized by a nonnegative vector w, so that a margin-based error function in the induced feature space is minimized. The margin of xn, computed with respect to w, is given by:
| (2) |
where zn = |xn − NM(xn)| − |xn − NH(xn)| and |·| is an element-wise absolute operator. Note that ρn (w) is a linear function of w and has the same form as the sample margin of SVM, given by ρSVM (xn) = wT φ (xn), using a mapping function φ(·). An important difference, however, is that by construction the magnitude of each element of w in the above margin definition reflects the relevance of the corresponding feature in a learning process. This is not the case in SVM except when a linear kernel is used, which, however, can capture only linear discriminant information. Note that the margin thus defined requires only information about the neighborhood of xn, while no assumption is made about the underlying data distribution. This means that by local learning we can transform an arbitrary nonlinear problem into a set of locally linear ones.
The local linearization of a nonlinear problem enables us to estimate the feature weights by using a linear model that has been extensively studied in the literature. It also facilitates the mathematical analysis of the algorithm. The main problem with the above margin definition, however, is that the nearest neighbors of a given sample are unknown before learning. In the presence of many thousands of irrelevant features, the nearest neighbors defined in the original space can be completely different from those in the induced space (see Fig. 2). To account for the uncertainty in defining local information, we develop a probabilistic model where the nearest neighbors of a given sample are treated as hidden variables. Following the principles of the expectation-maximization algorithm [21], we estimate the margin by computing the expectation of ρn(w) via averaging out the hidden variables:
| (3) |
where ℳn = {i : 1 ≤ i ≤ N, yi ≠ yn}, ℋn = {i : 1 ≤ i ≤ N, yi = yn, i ≠ n}, Ei~ℳn denotes the expectation computed with respect to ℳn, and P(xi = NM(xn)|w) and P(xi = NH(xn)|w) are the probabilities of sample xi being the nearest miss or hit of xn, respectively. These probabilities are estimated via the standard kernel density estimation:
| (4) |
and
| (5) |
where k(·) is a kernel function. Specifically, we use the exponential kernel k(d) = exp(−d/σ), where the kernel width σ is an input parameter that determines the resolution at which the data are locally analyzed. Other kernel functions can also be used, and the descriptions of their properties can be found in [22].
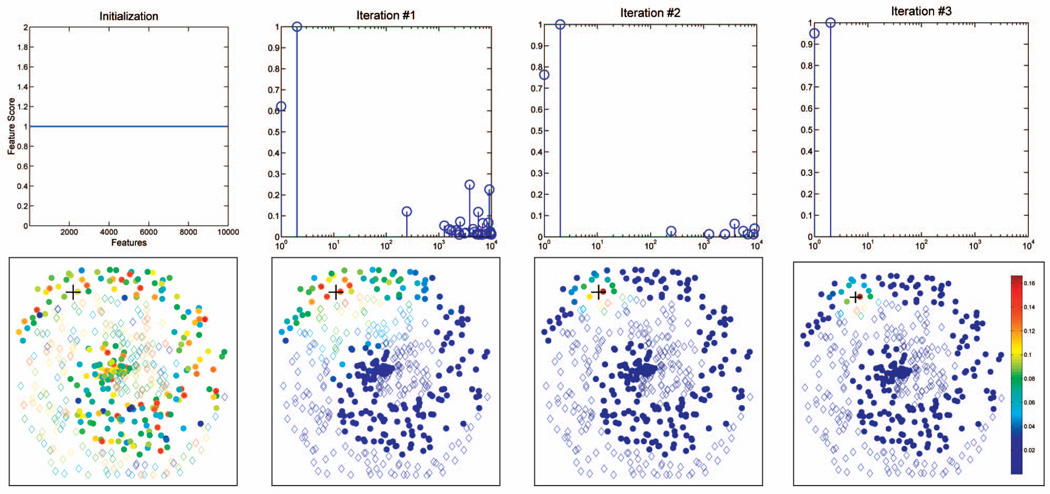
Fig. 2.
The algorithm iteratively refines the estimates of weight vector w and probabilities P(xi = NH(xn)|w) and P(xi = NM(xn)|w) until convergence. The result is obtained on the spiral data with 10,000 irrelevant features. Each sample is colored according to its probability of being the nearest miss or hit of a given sample, indicated by a black cross. The plot shows that the algorithm converges to a perfect solution in just three iterations. (The figure is better viewed electronically.)
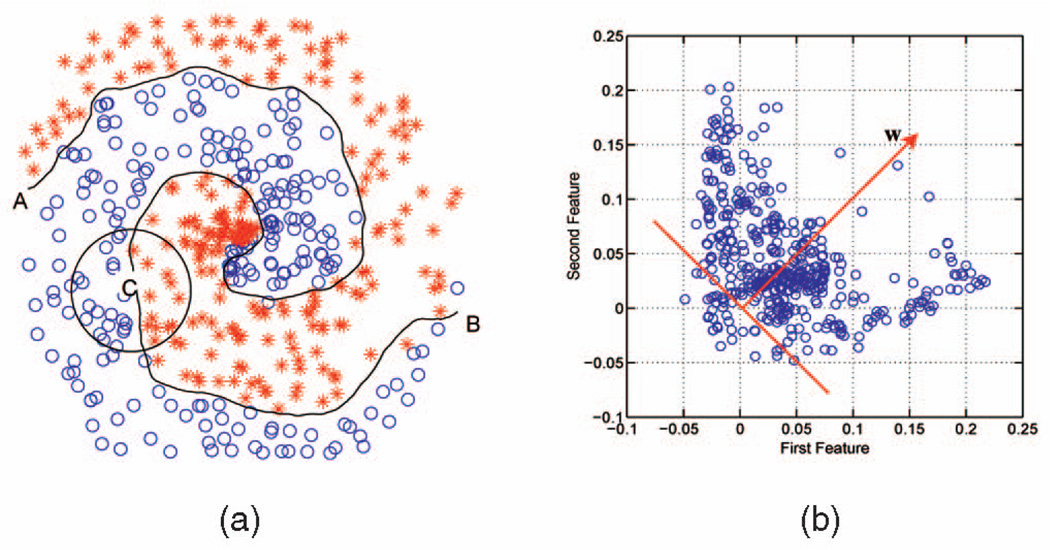
To motivate the above formulation, we consider the well-known Fermat’s problem in which two-class samples are distributed in a two-dimensional space, forming a spiral shape, as illustrated in Fig. 1a. A possible decision boundary is also plotted. If one walks from point A to B along the decision boundary, at any given point (say, point C), one would obtain a linear problem locally. One possible linear formulation is given by (3). Clearly, in this spiral problem, both features are equally important. By projecting the transformed data z̄n onto the feature weight vector w = [1, 1]T, we note that most samples have positive margins (Fig. 1b). The above arguments generally hold for arbitrary nonlinear problems for a wide range of kernel widths as long as the local linearity condition is preserved. We will demonstrate in the experiment that the algorithm’s performance is indeed robust against a specific choice of kernel width.
Fig. 1.
Fermat’s spiral problem. (a) Samples belonging to two classes are distributed in a two-dimensional space, forming a spiral shape. A possible decision boundary is also plotted. If one walks from point A to B along the decision boundary, at any given point (say, point C), one would obtain a linear problem locally. (b) By projecting the transformed data z̄n onto the direction specified by w, most samples have positive margins.
After the margins are defined, the problem of learning feature weights can be solved within the large margin framework. Two of the most popular margin formulations are SVM [3] and logistic regression [23]. Due to the nonnegative constraint on w, the SVM formulation represents a large-scale optimization problem, while the problem size cannot be reduced by transforming it into the dual domain. For computational convenience, we therefore perform the estimation in the logistic regression formulation, which leads to the following optimization problem:
| (6) |
where w ≥ 0 means that each element of w is nonnegative.
In applications with a huge amount of features, we expect that most features are irrelevant. For example, in cancer prognosis, most genes are not involved in tumor growth and/or spread [1], [2]. To encourage the sparseness, one commonly used strategy is to add an ℓ1 penalty of w to an objective function [5], [17], [24], [25], [26], [27], [28]. Accomplishing sparse solutions by introducing the ℓ1 penalty has been theoretically justified (see, for example, [29] and the references therein). With the ℓ1 penalty, we obtain the following optimization problem:
| (7) |
where λ is a parameter that controls the penalty strength and, consequently, the sparseness of the solution.
The optimization formulation (7) can also be written as:
| (8) |
In statistics, the above formulation is called nonnegative garrote [30]. For every solution to (7) obtained for a given value of λ, there is a corresponding value of β in (8) that gives the same solution. The optimization problem of (8) has an interesting interpretation: If we adopt a classification rule where xn is correctly classified if and only if margin ρ̄(w) ≥ 0 (i.e., on average, xn is closer to the patterns from the same class in the training data excluding xn than to those from the opposite class), then is the leave-one-out (LOO) classification error induced by w, where I(·) is the indicator function. Since the logistic loss function is an upper bound of the misclassification loss function, up to a difference of a constant factor, the physical meaning of our algorithm is to find a feature weight vector so that the upper bound of the LOO classification error in the induced feature space is minimized. Hence, the algorithm has two levels of regularization, i.e., the implicit LOO and explicit ℓ1 regularization. We will shortly see that this property, together with the convergence property, leads to superior performance of our algorithm in the presence of many thousands of irrelevant features. We will also see that the performance of our algorithm is largely insensitive to a specific choice of λ due to the LOO regularization.
Since z̄n implicitly depends on w through the probabilities P(xi = NH(xn)|w) and P(xi = NM(xn)|w), we use a fixed-point recursion method to solve for w. In each iteration, z̄n is first computed by using the previous estimate of w, which is then updated by solving the optimization problem (7). The iterations are carried out until convergence. It is interesting to note that though local learning is a highly nonlinear process, in each iteration we only deal with a linear problem.
For fixed z̄n, (7) is a constrained convex optimization problem. Due to the nonnegative constraint on w, it cannot be solved directly by using gradient descent. To overcome this difficulty, we reformulate the problem slightly as:
| (9) |
thus obtaining an unconstrained optimization problem. It is easy to show that, at the optimum solution, we have . The solution of v can thus be readily found through gradient descent with a simple update rule:
| (10) |
where ⨂ is the Hadamard operator and η is the learning rate determined by the standard line search. Note that the objective function of (9) is no longer a convex function, and thus a gradient descent method may find a local minimizer or a saddle point. The following theorem shows that if the initial point is properly selected, the solution obtained when the gradient vanishes is a global minimizer.
Theorem 1. Let f(x) be a strictly convex function of x ∈ IRJ and g(x) = f(y), where . If , then x+ is not a local minimizer, but a saddle point or a global minimizer of g(x). Moreover, if x+ is found through gradient descent with an initial point , then x+ is a global minimizer of g(x).
Proof. For notional simplicity, we use to denote . Also, we use A ≻ 0 and A ⪰ 0 to denote that A is a positive definite or semidefinite matrix, respectively.
We first prove that if , then x+ is either a saddle point or a global minimizer of g(x). To this end, we examine the properties of the Hessian matrix of g(x), denoted as H. Let x+) be a stationary point of g(x) satisfying:
| (11) |
The entries of H(x+) are given by
| (12) |
where δ(i, j) is the Kronecker delta function that equals 1 if i = j, and 0 otherwise. Note that some elements of x+ may be equal to zero. Thus, the elements of x+) can be grouped into two sets, and . From (11), we have . For simplicity, assume without loss of generality that the first M elements of x+) belong to S0, while the rest of the J - M elements belong to S≠0. Then, from (12), the Hessian matrix of g(x), evaluated at x+, is given by
| (13) |
where we have used the fact that ,
| (14) |
| (15) |
and
| (16) |
Since f(x) is a strictly convex function of x, we have B ≻ 0. Therefore, by Schur product theorem [51], B ⊗ C is a positive definite matrix. It follows that H(x+) ⪰ 0 if and only if A ⪰ 0.
If H(x+) is not positive semidefinite, then x+ is a saddle point. In the following, we prove that if H(x+) ⪰ 0, then x+ must be a global minimizer of g(x). Suppose opposite that, instead of x+, some x* is a global minimizer of g(x) and y* ≠ y+). Then, by Taylor’s theorem, there exists α ∈ (0; 1) such that
| (17) |
where we have used the fact that . Since f is a strictly convex function, we have and R is a positive number. Also, our initial assumption that H(x+) ⪰ 0 is equivalent to A ⪰ 0, that is, . It follows that f(y*) - f(y+) ≥ 0, where the equality holds when y* = y+). This contradicts the initial assumption that x* is a global minimizer of g(x) and y* ≠ y+). We finished the proof that a given stationary point x+ of g(x) is either a saddle point if H(x+) is not positive semidefinite or a global minimizer of g(x) if H(x+) ⪰ 0.
Next, we prove that if stationary point x+ is found via gradient descent with an initial point , then x+ is a global minimizer of g(x). Suppose that ∂g/∂x* = 0 and x* is a saddle point. Again we assume that the first M elements of x* belong to S0, while the rest of the J - M elements belong to S≠0. There exists an element i ∈ S0 so that (otherwise H(x*) ⪰ 0 and x* is a global minimizer). Due to the continuity, there exists ξ > 0 such that ∂f/∂yi < 0 for every . It follows that ∂g/∂xi = 2xi(∂f/∂yi) < 0 for . That is, is not reachable by using a gradient descent method, given by xi ← xi - η(∂g/∂xi), except when the component of the initial point x(0) is set to zero. Equivalently, the saddle point x* is not reachable via gradient decent. This concludes the proof of the theorem.
For fixed z̄n, the objective function (7) is a strictly convex function of w. Theorem 1 assures that in each iteration, via gradient descent, reaching a global optimum solution of w is guaranteed. After the feature weighting vector is found, the pairwise distances among data samples are reevaluated using the updated feature weights, and the probabilities P(xi = NM(xn)|w) and P(xj = NH(xn)|w) are recomputed using the newly obtained pairwise distances. The two steps are iterated until convergence. The implementation of the algorithm is very simple. It is coded in Matlab with less than 100 lines. Except for the line search, no other built-in functions are used. The pseudocode is presented in Algorithm 1.
Algorithm 1.
Pseudocode of the proposed feature selection algorithm.
|
Input : Data , kernel width σ, regularization parameter λ, stop criterion θ |
|
| Output: Feature weights w | |
| 1 | Initialization: Set w(0) = 1, t = 1 ; |
| 2 | repeat |
| 3 | Compute d(xn, xi|w(t−1), ∀xn, xi ∈ 𝒟 |
| 4 | Compute P(xi=NM(xn)|w(t−1)) and P(xj=NH(xn)|w(t−1)) as in (4) and (5); |
| 5 | Solve for v through gradient descent using the update rule specified in (10); |
| 6 | |
| 7 | t = t +1 ; |
| 8 | until ‖w(t) − w(t−1)‖ < θ; |
| 9 | w = w(t). |
In the following three sections, we analyze the convergence and computational complexity of our algorithm, and present its extension to multiclass problems.
3.1 Convergence Analysis
We begin by studying the asymptotic behavior of the algorithm. If σ → +∞, for every w ≥ 0, we have
| (18) |
since . On the other hand, if σ → 0, by assuming that for every xn, d(xn, xi|w) ≠ d(xn, xj|w) if i ≠ j, we have
and 0 otherwise.1 Similar asymptotic behavior holds for P(xi = NH(xn)|w). From the above analysis, it follows that for σ → +∞, the algorithm converges to a unique solution in one iteration since P(xi = NM(xn)|w) and P(xi = NH(xn)|w) are constants for any initial feature weights. On the other hand, for σ → 0, the algorithm searches for only one nearest neighbor when computing margins, and we empirically find that the algorithm may not converge. This suggests that the convergence behavior and convergence rate of the algorithm are fully controlled by the kernel width, which is formally stated in the following theorem:
Theorem 2. For the feature-selection algorithm defined in Algorithm 1, there exists σ* such that
whenever σ > σ*. Moreover, for a fixed σ > σ*, the algorithm converges to a unique solution for any nonnegative initial feature weights w(0).
We use the Banach fixed point theorem to prove the convergence theorem. We first state the fixed point theorem without proof, which can be found, for example, in [31].
Definition 1. Let 𝒰 be a subset of a normed space 𝒵 and ‖·‖ is a norm defined in 𝒵. An operator T : 𝒰 → 𝒵 is called a contraction operator if there exists a constant q ∈ [0,1] such that ‖T(x) − T(y)‖ ≤ q‖x−y‖ for every x, y ∈ 𝒰. q is called the contraction number of T. An element of a normed space 𝒵 is called a fixed point of T :𝒰 → 𝒵 if T(x) = x.
Theorem 3 (Fixed Point Theorem). Let T be a contraction operator mapping a complete subset 𝒰 of a normed space 𝒵 into itself. Then, the sequence generated as x(t+1) = T(x(t)), t = 0; 1; 2; …, with arbitrary x(0) ∈ 𝒰, converges to the unique fixed point x* of T. Moreover, the following estimation error bounds hold:
| (19) |
Proof of Theorem 2. The gist of the proof is to identify a contraction operator for the algorithm, and make sure that the conditions of Theorem 3 are met. To this end, we define 𝒫 = {p : p = [P(xi = NM(xn)|w), P(xj = NH(xn)|w)]} and 𝒲 ={w : w ∈ IRJ, ‖w‖1 ≤ β, w ≥ 0}, and specify the first step of the algorithm in a functional form as T1 :𝒲 → 𝒫, where T1(w) = p, and the second step as T2 : 𝒫 → 𝒲, where T2(p) = w. Then, the algorithm can be written as w(t) = (T2 ο T1)(w(t−1)) ≜ T(w(t−1)), where (ο) denotes functional composition and T :𝒲 → 𝒲. Since 𝒲 is a closed subset of finite-dimensional normed space IRJ (or a Banach space) and thus complete [31], T is an operator mapping complete subset 𝒲 into itself. Next, note that for σ → + ∞, the algorithm converges with one step. We have
for any w1, w2 ∈ 𝒲. Therefore, in the limit, T is a contraction operator with contraction constant q = 0, that is,
Therefore, for every ε > 0, there exists σ* such that q(σ) ≤ ε whenever σ > σ*. By setting ε < 1, the resulting operator T is a contraction operator. By the Banach fixed point theorem, our algorithm converges to a unique fixed point provided the kernel width is properly selected. The above arguments establish the convergence theorem of the algorithm.
The theorem ensures the convergence of the algorithm if the kernel width is properly selected. This is a very loose condition as our empirical results show that the algorithm always converges for a sufficiently large kernel width (see Fig. 5b). Also, the error bound in (19) tells us that the smaller the contraction number, the tighter the error bound and hence the faster the convergence rate. Our experiments suggest that a larger kernel width yields a faster convergence.
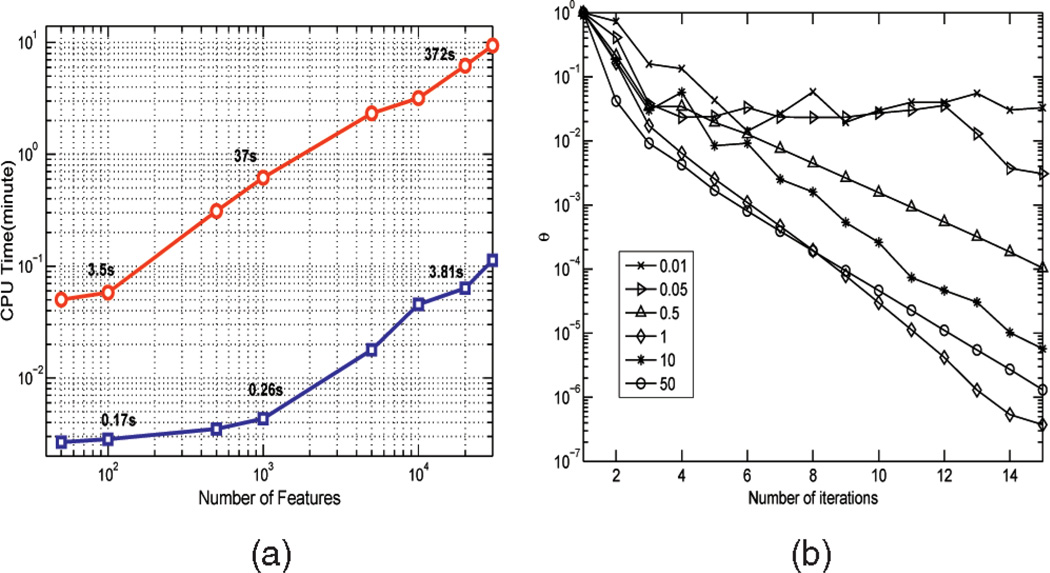
Fig. 5.
(a) The CPU time it takes our algorithm to perform feature selection on the spiral data with different numbers of irrelevant features, ranging from 50 to 30,000. The CPU time spent on solving the ℓ1 optimization problems is also reported (blue line). The plot demonstrates linear complexity with respect to the feature dimensionality. (b) Convergence analysis of our algorithm performed on the spiral data with 5,000 irrelevant features, for λ = 1 and σ ∈ {0:01; 0:05; 0:5; 1; 10; 50}. The plots present θ = ‖w(t) − w(t−1)‖2 as a function of the number of iteration steps.
Unlike many other machine learning algorithms (e.g., neural networks), the convergence and the solution of our algorithm are not affected by the initial value if the kernel width is fixed. This property has a very important consequence: Even if the initial feature weights were wrongly selected (e.g., investigators have no or false prior information) and the algorithm started computing erroneous nearest misses and hits for each sample, the theorem assures that the algorithm will eventually converge to the same solution obtained when one had perfect prior knowledge. The correctness of the proof of Theorem 2 is experimentally verified in Section 4.1.
3.2 Computational Complexity and Fast Implementation
The algorithm consists of two main parts: computing pairwise distances between samples and solving the ℓ1 optimization problem, the computational complexities of which in each iteration are 𝒪(N2J) and 𝒪(NJ), respectively. Here, J is the feature dimensionality and N is the number of samples. When N is sufficiently large (say 100), most of the CPU time is spent on the first task (see Fig. 5a). The computational complexity of our algorithm is comparable to those of RELIEF [18] and Simba [19], which are known for their computational efficiency. A close look at the update equation of v, given by (10), allows us to further reduce complexity. If some elements of v are very close to zero (say less than 10−4), the corresponding features can be eliminated from further consideration with a negligible impact on the subsequent iterations, thus providing a built-in mechanism for automatically removing irrelevant features during learning.
Our algorithm has a linear complexity with respect to the number of features. In contrast, some popular greedy search methods (e.g., forward search) require on the order of 𝒪(J2) moves in a feature space [9]. However, when the sample size becomes excessively large, it can still be computationally intensive to run our algorithm. Considerable efforts have been made over the years to improve the computational efficiency of nearest-neighbor search algorithms [32]. It is possible to use similar techniques to reduce the number of distance evaluations actually performed in our algorithm, which will be our future work.
3.3 Feature Selection for Multiclass Problems
This section considers feature selection for multiclass problems. Some existing feature-selection algorithms, originally designed for binary problems, can be naturally extended to multiclass settings, while for others the extension is not straightforward. For both embedded and wrapper methods, the extension largely depends on the capability of a classifier to handle multiclass problems [9]. In many cases, a multiclass problem is first decomposed into several binary ones by using an error-correct-code method [13], [34], and then feature selection is performed for each binary problem. This strategy further increases the computational burden of embedded and wrapper methods. Our algorithm does not suffer from this problem. A natural extension of the margin defined in (2) to multiclass problems is [34]:
| (20) |
where 𝒴 is the set of class labels, NM(c)(xn) is the nearest neighbor of xn from class c, and 𝒟c is a subset of 𝒟 containing only samples from class c. The derivation of our feature-selection algorithm for multiclass problems by using the margin defined in (20) is straightforward.
4 EXPERIMENTS
We perform a large-scale experiment on 11 synthetic and real-world data sets to demonstrate the effectiveness of the newly proposed algorithm. The experiment is performed on a desktop with Pentium 4 2.8 GHz and 2 GB RAM.
4.1 Spiral Problem
This section presents a simulation study on Fermat’s spiral problem, carefully designed to verify various properties of the algorithm, theoretically established in Section 3.1. Fermat’s spiral problem is a binary classification problem, where each class contains 230 samples distributed in a two-dimensional space, forming a spiral shape, as illustrated in Fig. 1. In addition to the first two relevant features, each sample is contaminated by a varying number of irrelevant features, where this number is set to {50, 500, 5,000, 10,000, 20,000, 30,000}. The number 30,000 far exceeds the amount of features experienced in many scientific fields. For example, human beings have about 25,000 genes, and hence nearly all gene expression microarray platforms have less than 25,000 probes. The added irrelevant features are independently sampled from zero-mean and unit-variance Gaussian distribution. Our task is to identify the first two relevant features. Note that only if these two features are used simultaneously can the two classes of the samples be well separated. Most filter and wrapper approaches perform poorly on this example since, in the former, the goodness of each feature is evaluated individually, while in the latter, the search for relevant features is performed heuristically.
Fig. 2 illustrates the dynamics of our algorithm performed on the spiral data with 10,000 irrelevant features. The algorithm iteratively refines the estimates of weight vector w and probabilities P(xi = NH(xn)|w) and P(xi = NM(xn)|w) until convergence. Each sample is colored according to its probability of being the nearest miss or hit of a given sample, indicated by a black cross. We observe that, with uniform initial feature weights, the nearest neighbors defined in the original feature space can be completely different from the true ones. The plot shows that the algorithm converges to a perfect solution in just three iterations. This example also illustrates why similarity-based learning algorithms (e.g., KNN and SVM with RBF kernel) perform poorly in the presence of copious irrelevant features. This is because the neighboring samples of a test sample provide misleading information.
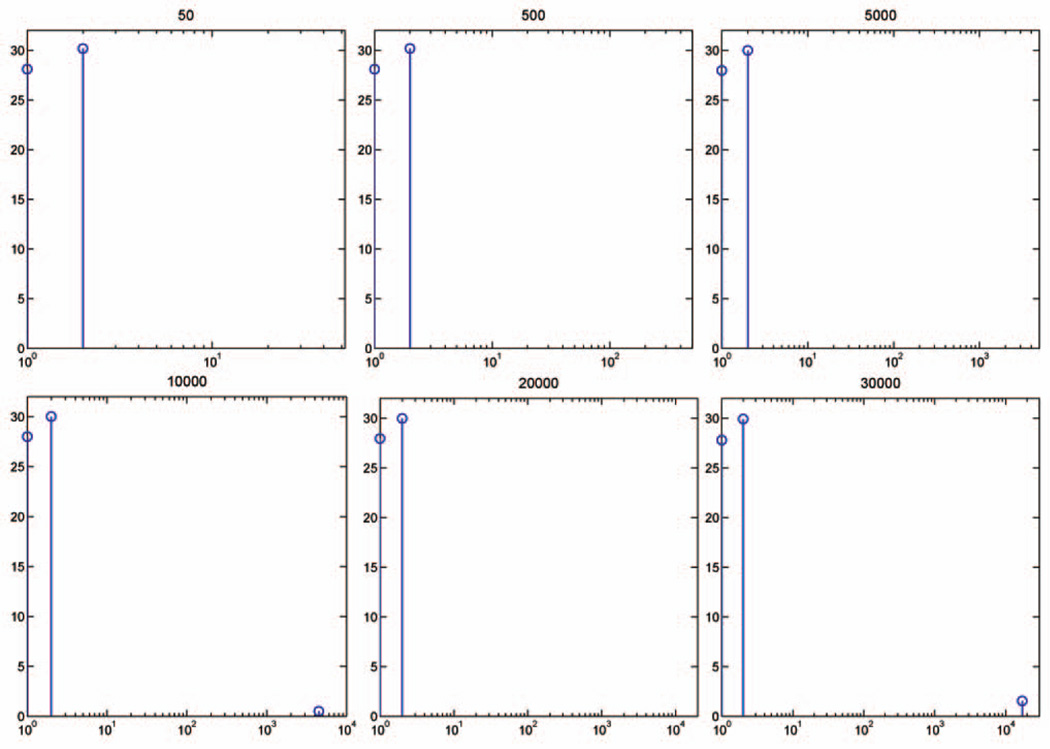
Fig. 3 presents the feature weights that our algorithm learns on the spiral data for a varying number of irrelevant features. The results are obtained for parameters σ and λ, respectively, set to 2 and 1, while the same solution holds for a wide range of other values of kernel widths and regularization parameters (insensitivity to a specific choice of these parameters will be discussed shortly). Our algorithm performs remarkably well over a wide range of feature-dimensionality values, with the same parameters. We also note that the feature weights learned are almost identical, across all feature-dimensionality values. This result is a consequence of Theorem 2, which may be explained as follows: Suppose that we have two spiral data sets with 5,000 and 10,000 irrelevant features, respectively. Also, suppose that we first perform the algorithm on the second data set and that after some iterations the algorithm finds 5,000 irrelevant features whose weights are very close to zero. Then, both problems are almost identical, except that the first problem has a uniform initial point (see line 1 of Algorithm 1) and the second one has a nonuniform initial point. By Theorem 2, the algorithm converges to the same solution for both problems. Of course, due to the randomness of irrelevant features and the finite number of iteration steps, the two solutions are slightly different. For example, in Fig. 3for the data set with 30,000 features, the algorithm selects one false feature as relevant, in addition to two relevant ones. However, the weight associated with the selected irrelevant feature is much smaller than the weights of the two relevant ones.
Fig. 3.
Feature weights learned on the spiral data set with different numbers of irrelevant features, ranging from 50 to 30,000. The y-axis represents the values of feature weights and the x-axis is the number of features, where the first two are always fixed to represent the two relevant features. Zero-valued feature weights indicate that the corresponding features are not relevant. The feature weights learned across all dimensionality are almost identical for the same input parameters.
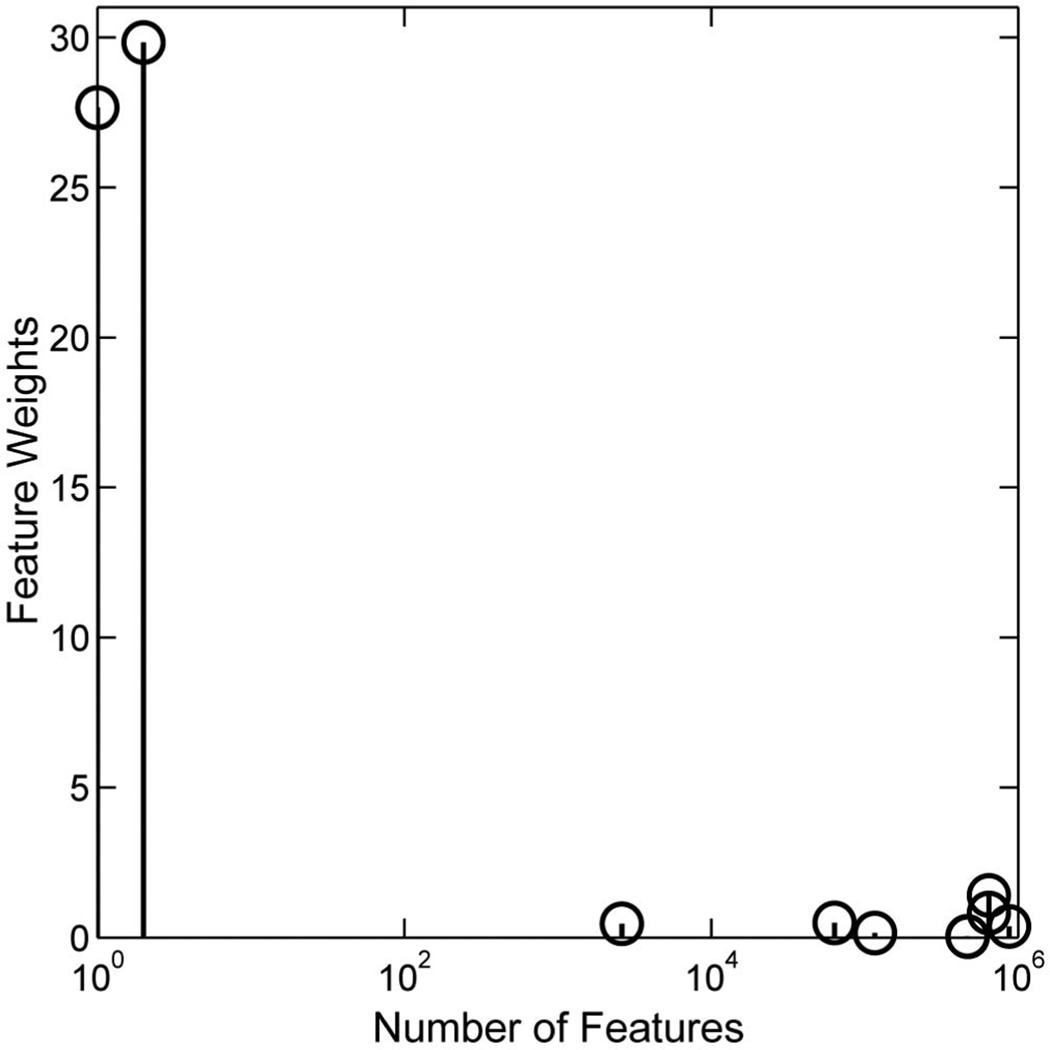
One may be interested to know how many irrelevant features can be added to the data set before the algorithm fails. To answer this question, we conduct an experiment where the number of irrelevant features is continuously increased. We find that the algorithm attains the almost identical solutions to those presented in Fig. 3 until one million irrelevant features are added (Fig. 4). The algorithm fails simply because our computer runs out of memory. This result suggests that our algorithm is capable of handling problems with an extremely large input data dimensionality, far beyond that needed in many data-analysis settings one may currently encounter. This result is very encouraging, and some theoretical analyses on the algorithm’s sample complexity are presented in Section 5 that explain in part the algorithm’s excellent performance.
Fig. 4.
Feature weights learned on the spiral data with one million features.
Our algorithm is computationally very efficient. Fig. 5a shows the CPU time it takes the algorithm to perform feature selection on the spiral data with different numbers of irrelevant features. The stopping criterion in Algorithm 1 is θ = 0:01. As can be seen from the figure, the algorithm runs for only 3.5 s for the problem with 100 features, 37 s for 1,000 features, and 372 s for 20,000 features. The computational complexity is linear with respect to the feature dimensionality. It would be difficult for most wrapper methods to compete with ours in terms of computational complexity. Depending on the classifier used to search for relevant features, it may take several hours for a wrapper method to analyze the same data set with 10,000 features, and yet there is no guarantee that the optimal solution will be reached, due to heuristic search. The CPU time spent on solving the ℓ1 optimization problems is also reported, which accounts for about 2 percent of the total CPU time.
Fig. 5b presents the convergence analysis of our algorithm on the spiral data with 5,000 irrelevant features, for λ = 1 and different kernel widths σ ∈ {0:01; 0:05; 0:5; 1; 10; 50}. We observe that the algorithm converges for a wide range of σ values, and that a larger kernel width generally yields a faster convergence. These results validate our theoretical convergence analysis, presented in Section 3.1.
The kernel width σ and the regularization parameter λ are two input parameters of the algorithm. Alternatively, they can be estimated through cross validation on training data. It is well known that cross validation may produce an estimate with a large variance. Fortunately, this does not pose a serious concern for our algorithm. In Figs. 6 and 7, we plot the feature weights learned with different kernel widths and regularization parameters. The algorithm performs well over a wide range of parameter values, always yielding the largest weights for the first two relevant features, while the other weights are significantly smaller. This suggests that the algorithm’s performance is largely insensitive to a specific choice of parameters σ and λ, which makes parameter tuning, and hence the implementation of, our algorithm easy, even for researchers outside of the machine learning community.
Fig. 6.
Feature weights learned on the spiral data with 5,000 irrelevant features, for a fixed kernel width σ = 2 and different regularization parameters λ ∈ {0:1; 0:5; 1; 1:5; 2}.
Fig. 7.
Feature weights learned on the spiral data with 5,000 irrelevant features, for a fixed regularization parameter λ = 1 and different kernel widths σ ∈ {0:1; 0:5; 1; 3; 5}.
4.2 Experiments on UCI Data
This section presents our feature-selection results obtained on seven benchmark UCI data sets [35], including banana, waveform, twonorm, thyroid, heart, diabetics, and splice. For each data set, the set of original features is augmented by 5,000 irrelevant features, independently sampled from a Gaussian distribution with zero mean and unit variance. It should be noted that some features in the original feature sets may be irrelevant or weakly relevant. Unlike the spiral data, however, this information is unknown to us a priori. The data sets are summarized in Table 1.
TABLE 1.
Summary of the Data Sets Used in the Experiment
| Dataset | Train | Test | Feature |
|---|---|---|---|
| spiral | 460 | / | 2(0 ~ 106) |
| twonorm | 120 | 7000 | 20(5000) |
| waveform | 120 | 4600 | 21(5000) |
| banana | 468 | 300 | 2(5000) |
| thyroid | 70 | 75 | 5(5000) |
| diabetics | 130 | 300 | 8(5000) |
| heart | 58 | 100 | 13(5000) |
| splice | 110 | 2175 | 60(5000) |
| prostate cancer | 102 | / | 22283 |
| breast cancer | 97 | / | 24488 |
| DLBCL | 77 | / | 5469 |
The number of irrelevant features artificially added to the original ones is indicated in the parentheses.
We compare our algorithm with five other algorithms, including the Kolmogorov-Smirnov (KS) test [4], AMS [14], RFE with a RBF kernel [16], Simba [19], and I-RELIEF [42]. As we mentioned before, our algorithm can be used for classification purposes (see (8)). The kernel width and regularization parameter thus can be estimated through 10-fold cross validation on training data, without resorting to other classifiers. The KS test is a nonparametric univariate method that determines the information content of each feature by using as a test statistic the maximum difference of the empirical distribution functions between samples of each class. AMS, along with RFE, is among the first to perform feature selection directly in the SVM formulation. The basic idea of AMS is to automatically tune the scaling parameters of a kernel by minimizing a generalization error bound. The scaling parameters can be used as the test statistic to evaluate the information content of each feature. The code is downloaded from [14]. The default settings of the algorithm are used, and the span bound is minimized. Since AMS is computationally very expensive, we apply AMS to the UCI data containing only 1,000 irrelevant features. Simba is a local-learning-based algorithm that in part motivates the development of our algorithm. One major problem with Simba is its implementation: Its objective function is characterized by many local minima. This problem is mitigated in Simba by restarting the algorithm from five different starting points. Nevertheless, the reach of a global optimal solution is not guaranteed. The codes of Simba are downloaded from [19]. The nonlinear sigmoid activation function is used. The number of passes of training data is set to 5, while the default value is 1. All other parameters use their default values. The codes of RFE are downloaded from [16]. The RBF kernel is used and the number of retained features is set to 30. It is difficult to specify the kernel width and regularization parameter of SVM used in RFE. We estimate both parameters through 10-fold cross validation by using original training data without 5,000 irrelevant features. It should be noted that in practical applications one would not have access to noise-free data. As with Simba, I-RELIEF is also a local-learning-based method. One major difference between I-RELIEF and ours is that the objective function of I-RELIEF is not directly related to the classification performance of a learning algorithm. Moreover, I-RELIEF imposes a ℓ2 constraint on feature weights, and thus cannot provide a sparse solution. During the review process, the editor suggested us to combine I-RELIEF with a back-selection strategy similar to that used in RFE. In the presence of copious irrelevant features, there is no guarantee that a useful feature has to have a weight larger than half of the other features. Consequently, as with RFE, some useful features may be eliminated during the back-selection process. The number of retained features is set to 30, and the kernel width is the same as that used in our algorithm. For notational simplicity, we refer to it as I-RELIEF/BS. Except for RFE, where the computationally intensive tasks (i.e., SVM training) is executed in C, all other algorithms are programmed in Matlab.
SVM (with RBF kernel) is used to estimate the classification errors obtained by using the features selected by each algorithm. The structural parameters of SVM are estimated through 10-fold cross validation on the original training data without 5,000 irrelevant features. To eliminate statistical variations, each algorithm is run 10 times for each data set. In each run, a data set is first randomly partitioned into a training and test data, a feature weight vector is learned, the top-ranked features are successively fed into SVM, and the minimum test error is recorded. Table 2 presents the averaged classification errors and standard deviations of each algorithm. For a rigorous comparison, a Student’s paired two-tailed t-test is also performed. The p-value of the t-test represents the probability that two sets of compared results come from distributions with a equal mean. A p-value of 0.05 is considered statistically significant. The last row of Table 2 summarizes the win/tie/loss of each algorithm when compared to ours at the 0.05 p-value level. In our algorithm, after a feature weight vector is learned, the maximum value of the feature weights is normalized to 1, and the features with weights >0:01 are considered useful. The false discovery rate (FDR), defined as the ratio between the number of artificially added, irrelevant features identified by our algorithms as useful ones and the total number of irrelevant features (i.e., 5,000), is reported in Table 2. For reference, the classification errors of SVM performed on the original data and corrupted data are also reported. From these experimental results, we have the following observations:
SVM using all features performs poorly, which is consistent with the results reported in the literature (see, for example, [4], [14]). SVM using the features identified by our algorithm performs similarly or sometimes even slightly better than SVM using the original features (e.g., heart and splice), which clearly demonstrates the effectiveness of our algorithm for the purpose of feature selection. Among the six algorithms, ours yields the best results in six out of the seven data sets. RFE is a popular method, however, nearly all of the RFE applications use a linear kernel. We observe that RFE with an RBF kernel does not perform well on data with a very high data dimensionality. This is possibly due to the poor performance of SVM in the presence of copious irrelevant features, leading to an inaccurate estimate of feature weights. We empirically find that in some cases RFE removes all of the useful features after the first iteration. Except for our algorithm, none of the competing methods perform well on the banana data.
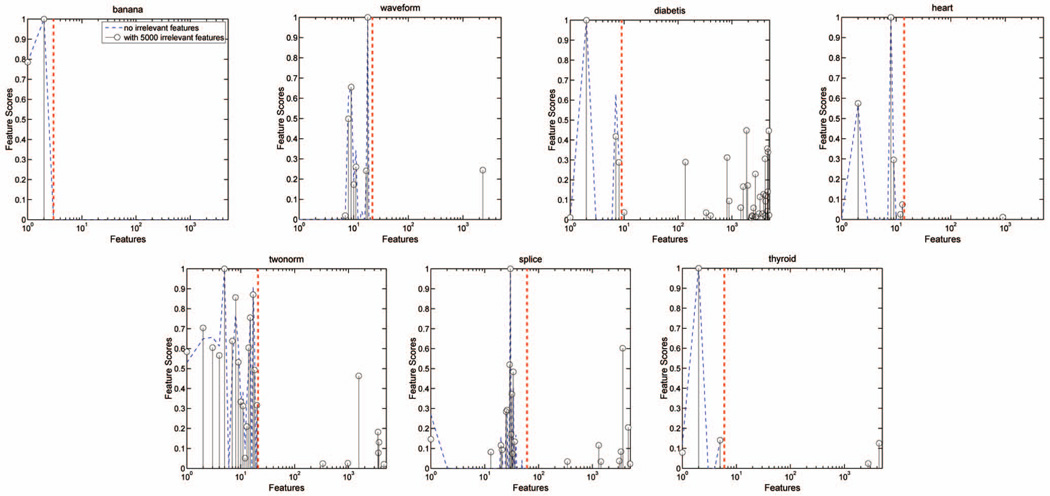
In addition to successfully identifying relevant features, our algorithm performs very well in removing irrelevant ones. The false discovery rate, averaged over the seven data sets, is only 0.19 percent. The feature weights learned on one realization of each data set are plotted in Fig. 8. Except for diabetics, our algorithm removes nearly all of the irrelevant features. For comparison, the feature weights learned using the original data are also plotted. We observe that the weights learned in the two cases are very similar, which is consistent with the result of the spiral data and the theoretical results of Section 3.1.
The CPU time of the six algorithms, averaged over the 10 runs, is presented in Table 3. In terms of computational efficiency, the KS test performs the best, ours the second, I-RELIEF/BS, RFE and Simba the third, and AMS the least efficient. On average, it takes our algorithm less than half a minute to process 5,000 features. It should be noted that the CPU time of AMS is obtained by using only 1,000 features and RFE is implemented in C, and hence the comparison is somewhat in favor of AMS and RFE.
TABLE 2.
Classification Errors and Standard Deviations (Percent) of SVM Performed on the Seven UCI Data Sets Contaminated by 5,000 Useless Features
| SVM | SVM | Our Method | I-RELIEF/BS | KS | AMS | RFE | Simba | ||
|---|---|---|---|---|---|---|---|---|---|
| Dataset | (orginal features) | (all features) | Error | FDR | (1000) | ||||
| twonorm | 2.8(0.3) | 35.0(1.0) | 4.1(0.9) | 2.2/1000 | 4.1(1.0) | 4.6(0.9) | 5.0(0.9) | 48.9(0.4) | 15.4(3.9) |
| waveform | 12.8(0.9) | 33.0(0.2) | 13.8(1.1) | 0.6/1000 | 15.4(1.6) | 14.0(1.4) | 18.1(1.9) | 40.2(2.8) | 15.8(1.0) |
| banana | 10.9(0.5) | 32.9(0.2) | 10.9(0.5) | 0/1000 | 41.9(5.2) | 32.3(4.9) | 35.3(11.0) | 32.9(0.2) | 45.0(1.9) |
| diabetics | 27.2(1.9) | 34.3(1.9) | 27.7(2.4) | 7.4/1000 | 29.9(6.0) | 27.0(2.3) | 25.6(1.5) | 42.3(4.2) | 33.3(8.2) |
| thyroid | 6.3(3.2) | 30.0(3.7) | 6.4(2.7) | 0.4/1000 | 10.1(1.8) | 16.3(9.7) | 22.8(14.9) | 29.5(3.8) | 20.5(9.0) |
| heart | 20.3(5.6) | 45.6(3.4) | 19.0(5.2) | 0.3/1000 | 20.5(6.0) | 23.1(3.5) | 23.1(4.0) | 43.3(4.6) | 20.5(5.3) |
| splice | 20.4(1.8) | 48.9(2.0) | 17.8(1.9) | 2.3/1000 | 22.0(2.2) | 23.5(1.0) | 24.6(3.0) | 48.7(0.8) | 20.1(2.6) |
| win/tie/loss | / | / | / | / | 0/3/4 | 0/4/3 | 1/0/6 | 0/0/7 | 0/2/5 |
FDR is defined as the ratio between the number of artificially added, irrelevant features identified by our algorithm as useful ones and the total number of irrelevant features (i.e., 5,000). The last row summarizes the win/loss/tie of each algorithm when compared with ours at the 0.05 p-value level.
Fig. 8.
Feature weights learned in one sample trial of the seven UCI data sets with and without 5,000 irrelevant features. The dashed red line indicates the number of original features. The weights plotted on the left side of the dashed line are associated with the original features, while those on the right are with the additional 5,000 irrelevant features. The feature weights learned in the two cases are very similar.
TABLE 3.
CPU Time Per Run (in Seconds) of Six Algorithms Performed on Seven UCI Data Sets
| Dataset | Ours | I-RELIEF/BS | KS | RFE | AMS (1000) |
Simba |
|---|---|---|---|---|---|---|
| twonorm | 24 | 24 | 0.9 | 28 | 256 | 44 |
| waveform | 9 | 37 | 1.4 | 28 | 311 | 45 |
| banana | 97 | 250 | 2.2 | 298 | 1242 | 419 |
| diabetics | 41 | 30 | 2.3 | 33 | 449 | 50 |
| thyroid | 2 | 11 | 1.4 | 12 | 91 | 17 |
| heart | 4 | 8 | 3.5 | 8 | 91 | 13 |
| splice | 24 | 34 | 1.0 | 24 | 249 | 38 |
| Average | 29 | 56 | 1.8 | 62 | 384 | 89 |
The results of AMS are obtained by using only 1,000 features.
We above use classification errors as the main criterion to compare different algorithms. Classification errors, however, may not tell the whole story. Some other criteria are worthy of mention. All of the five algorithms that we compare to our algorithm are feature weighting methods. In our experiment, the test data is used to estimate the minimum classification errors. In practical applications, without test data, one may have to use a classifier learned on training data to determine the number of features that will be used in the test stage, which requires considerable efforts on parameter tuning. In our method, the regularization parameter can be learned simultaneously within the learning process, without using any other classifiers. Our method performs back selection implicitly: When the weight of a feature is less than 10−8, the feature is eliminated from further consideration. Unlike RFE and I-RELIEF/BS, where the number of discarded features in each iteration is predefined regardless of the values of their feature weights, in our algorithm, when a feature should be removed and how many of them should be removed are all automatically determined by the algorithm. On the theoretical side, ours has a solid theoretical foundation that will be presented in Section 5, whereas it is difficult to perform a similar theoretical analysis for some algorithms we herein consider. In the next section, we conduct an experiment to demonstrate that ours is not only effective in eliminating noisy features but also redundant ones.
4.3 Experiments on Microarray Data
In this section, we demonstrate the effectiveness of our algorithm using three microarray data sets, including breast cancer [1], prostate cancer [52], and diffuse large B-cell lymphoma (DLBCL) [53]. The detailed data information is summarized in Table 1. For all three data sets, the number of genes is significantly larger than the number of samples. Another major characteristic of microarray data, unlike the UCI data we considered in the previous section, is the presence of a significant number of redundant features (or coregulated genes) since genes function in a modular fashion. It is well known that including redundant features may not improve, but may sometimes deteriorate classification performance [10]. From the clinical perspective, the examination of the expression levels of redundant genes may not improve clinical decisions but increase medical examination costs needlessly. Hence, our goal is to derive a gene signature with a minimum number of genes to achieve a highly accurate prediction performance.
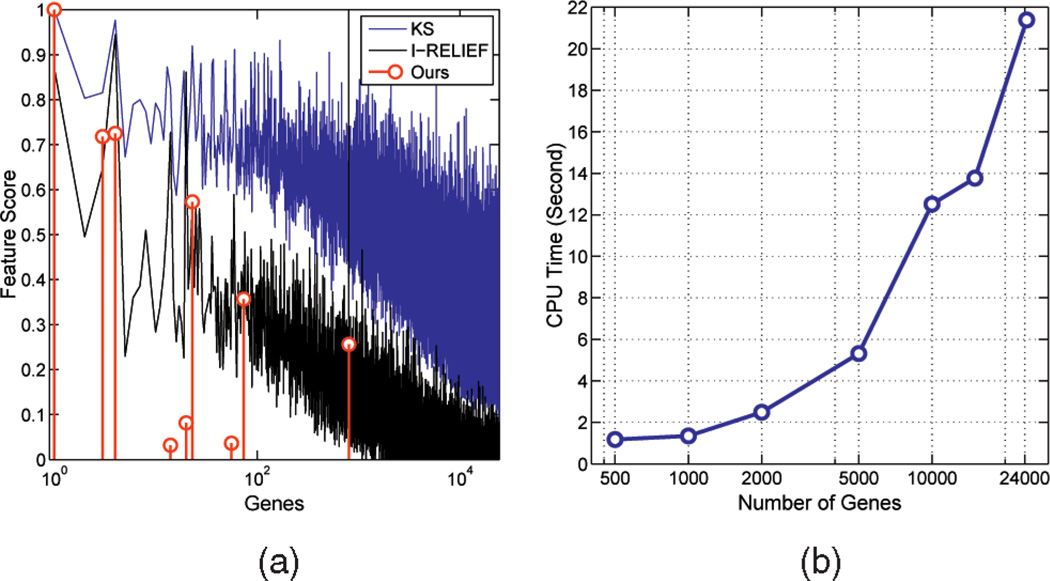
We have shown in the previous section that our algorithm significantly outperformed AMS, RFE, and Simba in terms of computational efficiency and accuracy. In this experiment, we only consider the KS test and I-RELIEF/BS, which are the two most competitive algorithms with respect to performance. For the results reported in this paper, the kernel width and regularization parameter of our algorithm are set to 5 and 1, respectively. We empirically find that the algorithm yields nearly identical prediction performance for a wide range of parameter values. The same kernel width is also used in I-RELIEF/BS. We use KNN to estimate the performance of each algorithm. We do not spend additional effort to tune the value of K, but simply set it to 3. Due to the small sample size, the leave-one-out cross validation (LOOCV) method is used. In each iteration, one sample is held out for testing and the remaining samples are used for identifying a gene signature. The genes are then ranked in a decreasing order based on their corresponding feature weights, and the 50 top-ranked genes are successively fed into a KNN classifier. The process is repeated until each sample has been tested. The classification errors are finally averaged and the best results are reported in Table 4. The number of genes at which the minimum error is attained is also recorded. Since, in each iteration of LOOCV, KNN classifies a test sample either correctly or incorrectly (i.e., 0 or 1), we are unable to perform a statistical test (e.g., t-test) to rigorously quantify the performance of each algorithm, as we did in the previous section. Nevertheless, we observe from Table 4 that our algorithm yields better prediction accuracy with a much smaller gene subset. This is because both I-RELIEF/BS and the KS test are unable to eliminate redundant features. If a gene is top ranked, its coregulated genes will also have a high ranking score. To further demonstrate this, we plot in Fig. 9a the feature weight vectors learned by the three algorithms performed on the breast cancer data. For ease of presentation, the genes presented along the x-axis are arranged based on the p-values of a t-test in a decreasing order. For example, the first gene contains the most discriminant information according to the t-test. We observe that some of the top-ranked features in the t-test are not selected in the gene signature learned by our algorithm. One possible explanation is that these excluded genes are redundant with respect to the identified gene signature.
TABLE 4.
Classification Errors (Percent) of Three Algorithms Performed on Three Microarray Data
| Dataset | Our Method | I-RELIEF/BS | KS |
|---|---|---|---|
| Prostate Cancer | 16.5 (6) | 25.3 (9) | 21.5 (13) |
| Breast Cancer | 21.7 (4) | 23.7 (28) | 27.8 (39) |
| DLBCL | 2.6 (10) | 5.2 (7) | 7.8 (23) |
The number in parentheses is the number of genes at which the minimal classification error is attained.
Fig. 9.
(a) Feature weights learned by the three algorithms performed on the breast cancer data. (b) The CPU time it takes our algorithm to identify a gene signature for the breast cancer data with a varying number of genes, ranging from 500 to 24,481.
This experiment further demonstrates the computational efficiency of our algorithm. Fig. 9b presents the CPU time it takes our feature-selection algorithm to identify a gene signature for the breast cancer data set with a varying number of genes, ranging from 500 to 24,481. It only takes about 22 seconds to process all 24,481 genes. If a filter method (e.g., t-test) is first used to reduce the feature dimensionality to, say, 2,000, as is almost always done in microarray data analysis, our algorithm runs for only about two seconds.
5 ANALYSIS OF SAMPLE COMPLEXITY
This section presents a theoretical study of our algorithm’s sample complexity. The main purpose of the analysis is to explain why the proposed algorithm performs so well for high-dimensional data, as demonstrated in the previous section. As one can see from (8), the algorithm finds a feature weight vector aimed at minimizing an empirical logistic loss. Hence, it is a learning problem and the analysis can be performed under the VC-theory framework. Specifically, we try to establish the dependence of the generalization performance of the proposed algorithm on input data dimensionality. Our study suggests that the algorithm has a logarithmical sample complexity with respect to the input feature dimensionality. We should emphasize that for many existing feature-selection algorithms (e.g., wrapper method), due to heuristic search, it would be difficult to conduct such theoretical analysis.
We begin by reviewing some basic concepts of the statistical learning theory. Let {x, y} be a pair of observation and target value, sampled from a fixed but unknown joint distribution p(x, y). In the sequel, we absorb y into x, for notation simplicity. Given a set of real-valued mapping functions ℱ = {f(x|α) : α ∈ Ω}, parameterized by α, and a loss function ℒ(f(x|α)), we are concerned with the problem of finding a parameter α to minimize the expected loss: R(α) = E[ℒ(f(x|α))] = ∫ ℒ(f(x|α))p(x)dx. In real applications, the true distribution is rarely known and one has access only to a limited number of observations XN = {x1,…, xN} independently drawn from the unknown distribution. A natural method to solve a learning problem is to find a parameter α to minimize the empirical loss: . We are interested to know how well a learning algorithm trained on a limited number of training data will perform on unseen data. This can be studied under the VC theory, which relies on the uniform convergence of the empirical loss to the expected loss. It has been proven by [36] that if the bound supα∈Ω|R(α, XN) - R(α)| is tight, then the function that minimizes the empirical loss is likely to have an expected loss that is close to the best in the function class.
A theorem, due to [37], provides an upper bound on the rate of the uniform convergence of a class of functions in terms of its covering number. Before we present the theorem, we first define the concept of covering number. The interested reader may refer to [38] and [39] for more comprehensive coverage on this subject.
Definition 2. Let ℱ = {f(x|α) : x ∈ IRJ, α ∈ Ω} be a set of real-valued function. Given N arbitrary data samples XN = {x1, … xN} ⊂ IRJ; define ℱ(XN) = {f (XN|α) = [f(x1|α);… f(xN|α)]T : α ∈ Ω}. We say that set 𝒱 = {v1, … vK} ⊂ IRN ε-covers ℱ(XN) in the p-norm if for all α there exists vk ∈ 𝒱 so that ‖f (XN|α) − vk‖p ≤ N1/pε where ‖ · ‖p is the p-norm. The covering number of ℱ(XN) in the p-norm; denoted as 𝒩p(ℱ ε XN) is the cardinality of the smallest set that ε-covers ℱ(XN). Define 𝒩p(ℱ ε N) = supXN 𝒩p(ℱ ε XN).
Theorem 4 [37]. For all ε > 0 and distribution p(x), we have
| (21) |
where
and 𝒩1 is the 1-norm covering number of function class ℒ.
In general, it is very difficult to estimate the covering number of an arbitrary function class. Some general bounds on covering numbers exist. For example, the covering number of a closed ball of radius r centered at the origin in IRJ is bounded by (4r=ε)J [40], where ε is the radius of the disks covering the ball. These bounds are usually too loose to be useful. Fortunately, there exists a tight bound for linear function class, due to [41], which can be used for estimating the covering number for our purposes. We slightly modify the theorem of [41] to include the nonnegative constraint of feature weights.
Theorem 5. Let
Then, we have
| (22) |
where ⌈x⌉ is the nearest integers of x toward infinity.
The proof of the theorem is similar to that in [41]. By using Theorems 4 and 5, we establish the following bounds for our algorithm with σ = + ∞ and σ → 0. Note that, when the kernel width goes to zero, the algorithm finds only one nearest neighbor for each pattern when computing margins, as shown in Section 3.1.
Theorem 6. Let ‖w‖1 ≤ β, w ≥ 0, x ∈ IRJ , and ‖x‖∞ ≤ 1. For the proposed algorithm, if σ = + ∞, for all ε > 0 and distribution p(x), we have
| (23) |
Proof. If σ = + ∞,
| (24) |
Hence, for a given data set XN, zn is a constant vector independent of w. Construct a data set ZN = [z1, …,zN]. It can be shown that ‖zn‖∞ ≤2. Define a class of linear functions
By Theorem 5, the covering number
From the definition of the cover number and Jensen’s inequality, we have 𝒩1 ≤𝒩2.
Now, let us consider the function class ℒ = {l(g(z)) : g ∈ 𝒢}. In the proposed algorithm, l(·) is a the logistic loss function, and l(g(z)) = log(1 + exp(−g(z))). It is proven in [39] that if l(·) is a Lipschitz function with Lipschitz constant L, then the covering number of ℒ is 𝒩1(ℒ ε, N) ≤ 𝒩1(𝒢, ε/L, N). The logistic loss function is a Lipschitz function with Lipschitz constant L = 1 [5]. Hence,
| (25) |
By using Holder’s inequality,
| (26) |
Hence,
Plugging (25) into Theorem 4, we prove the theorem.
Theorem 7. Let ‖w‖1 ≤ β, w ≥ 0, x ∈ IRJ , and ‖x‖∞ ≤ 1. For the proposed algorithm, if σ → 0, for all ε > 0 and distribution p(x), we have
| (27) |
If the number of samples is smaller than the feature dimensionality, then
| (28) |
Proof. Consider the following equation: wT|x1 − x2| = wT|x1 − x3|, which divides the parameter space into two parts, where the nearest neighbor of x1 is either x2 or x3. Assume for simplicity that there are N/2 samples in each class. There are
hyperplanes that divide the parameter space into at most N(N/2 − 1)2 + 1 parts. In each of these parts, the nearest neighbor of a given sample are the same, independent of w. For the ith part, construct a data set ZN = [z1, …, zN], where zn = |xn − NM(xn)| − |xn − NH(xn)|, and define a class of linear function
By Theorem 5, the covering number of 𝒢i is upper bounded by
and the total covering number is therefore upper bounded by
Now, by using the same arguments that prove Theorem 6, we conclude the proof of the theorem.
In the current formulation, when the kernel width goes to zero, the algorithm may not converge. However, the algorithm is not agnostic. The current formulation is based on batch learning. Although not considered in this paper, it is possible to specify an online-learning version of our algorithm that updates feature weights after seeing each sample—not the entire data set. The convergence of this online feature-selection algorithm does not depend on any specific value of the kernel width, but onthe learning rate [43].
Both Theorems 6 and 7 can be easily written into the following PAC style generalization error bounds that facilitate the sample complexity analysis.
Theorem 8. Let ‖w‖1 ≤ β, w ≥ 0, x ∈ IRJ, and ‖x‖∞ ≤ 1. For the proposed algorithm, if σ → 0, for all w and δ > 0, with probability of at least 1 − σ, the following generalization error bound holds:
| (29) |
and for σ = + ∞, a similar generalization error bound holds with a minor difference of some constants:
| (30) |
Theorem 8 can be proven by setting the right sides of (23) and (27) to δ and solving for ε.
As can be seen from (29) and (30), both generalization error bounds depend logarithmically on the feature dimensionality J. An equivalent statement of Theorem 8 is that for the obtained learning algorithms, the number of samples needed in order to maintain the same level of learning accuracy grows only logarithmically with respect to the feature dimensionality. This dependence is very weak, and matches the best known bounds proved in various feature-selection contexts.
Using the infinite kernel width in our algorithm amounts to making the linear assumption about the data model. In this case, our algorithm has a similar generalization error bound to that of ℓ1 regularized logistic regression. The main difference is that our algorithm has an implicit LOO regularization. Taking this regularization into account when deriving the error bound may lead to an even tighter bound.
A somewhat surprising result is that when the kernel width goes to zero, our algorithm also has a logarithmic sample complexity. As discussed in Section 3, if we adopt a classification rule that classifies x by the sign of its margin ρ̄(x), our algorithm can be viewed as the one-nearest-neighbor classifier (1NN). It is well known that 1NN performs poorly for high-dimensional data. Gilad-Bachrach et al. [19] prove that when feature selection is performed, the generalization error bound of 1NN depends logarithmically on the input feature dimensionality, but polynomially on the number of selected features [19, Theorem 1]. While our generalization bound in (29) is consistent with the result of [19], note, however, that our bound does not depend on the number of the selected features, but on the total size of the feature weights (i.e., ‖w‖1 bounded by β; also see (8)). This result is consistent with that of [45] that the size of the weights is more important than the size of neural networks. We perform some experiments on using our algorithm for classification purposes (i.e., classify x by the sign of its margin ρ̄(x)) on the UCI data sets contaminated by varying numbers of irrelevant features ranging from 0 to 10,000. Since the main focus of the paper is on feature selection, we report the detailed results in the supplementary data, which can be found on the Computer Society Digital Library at http://doi.ieeecomputersociety.org/10.1109/TPAMI.2009.190. As can see from Table 1S, the classification performance is largely insensitive to a growing number of irrelevant features. This result is very encouraging and indicates that it is possible to develop a new classification algorithm with a logarithmic dependence on data dimensionality without making any assumption of data distributions.
Here we only provide the sample complexity analysis for two specific kernel widths. However, it is reasonable to expect that a relatively large kernel width should improve the generalization error bound of the algorithm over that derived when the kernel width goes to zero (consider a similar case where KNN usually performs better than 1NN). The result presented in Fig. 7 shows that a large kernel width can indeed remove irrelevant features, and our empirical result obtained on the spiral data set contaminated by up to one million irrelevant features suggests that the proposed algorithm have a logarithmic sample complexity.
It is worth noting that the above analysis for a general case with an arbitrary value of kernel width is very difficult. Indeed, after decades of research, the covering number or similar techniques (i.e., Rademacher complexity and VC dimension) are only defined for a small set of functional classes. The problem of deriving generalization error bounds for arbitrary functional classes is still largely open in the machine learning community, and we do not expect that this paper can solve this open problem. However, the experimentally verified high accuracy, computational efficiency, and ease of implementation of the proposed algorithm justify its presentation to the broader community at this stage of our theoretical development.
6 DISCUSSION
We conclude this paper by tracing back the origins of this work, comparing our algorithm with some related feature-selection/weighting approaches, and summarizing the main contributions we made in this paper.
Our approach is motivated to a great extent by the ideas implemented in the RELIEF algorithm [18]. RELIEF is considered one of the most successful feature weighting algorithms due to its simplicity and effectiveness [33]. It has been long regarded as a heuristic filter method, until recently, when we mathematically proved that RELIEF is an online-learning algorithm that solves a convex optimization problem aimed at maximizing the averaged margin [42]. One major problem with RELIEF is that the nearest neighbors of a given sample are predefined in the original feature space, which typically yields erroneous nearest hits and misses in the presence of copious irrelevant features. RELIEF-F [49] mitigates this problem by searching for multiple, instead of just one, nearest neighbors when computing margins. Empirical studies have shown that RELIEF-F achieves significant performance improvement over RELIEF [49]. However, the performance of both algorithms degrades significantly with the increase of feature dimensionality. To address this problem, we recently proposed a new feature weighting algorithm referred to as I-RELIEF, which performs significantly better than RELIEF-F [42]. Similarly to the algorithm proposed in this paper, I-RELIEF employs a probabilistic model to define the local information of a given sample. However, as with all other algorithms in the RELIEF family, the objective function optimized by I-RELIEF is not directly related to the classification performance of a learning algorithm. Moreover, I-RELIEF imposes an ℓ2 constraint on feature weights, and thus is not able to remove redundant features and provide a sparse solution (see Fig. 9a). I-RELIEF does not enjoy the same theoretical properties as ours. This work is also motivated by the Simba algorithm recently proposed in [19]. Compared to RELIEF, Simba reevaluates the distances according to the learned weight vector, and thus is superior to RELIEF. One major problem, however, is that the objective function optimized by Simba is characterized by many local minima, which can be mitigated by restarting the algorithm from several initial points [19]. Also, Simba represents a constrained nonlinear optimization problem that cannot be easily solved by conventional optimization techniques. We empirically find that Simba performs very well when the number of irrelevant features is small, but may fail completely when there exist a large number of irrelevant features (see Table 2). One possible explanation is that the chance for Simba to be stuck into local minima is increased dramatically with the increased number of features.
Feature selection is closely related to distance metric learning (see, e.g., NCA [46], LMNN [47], and LFE [48]). These algorithms are also based on local learning and share the same goals as ours to reduce data dimensionality, but they completely differ in algorithmic formulations. Moreover, these algorithms are all for feature extraction and it is unclear whether they enjoy the same theoretical properties outlined in Section 5.
The proposed algorithm embraces some fundamental concepts in machine learning. It is related to SVM in the sense that both algorithms solve a nonlinear problem by first transforming it into a linear problem and then solving the linear one so that the margin is maximized. Unlike SVM, the linearization in our approach is achieved by local learning, instead of projecting the data onto a higher (possibly infinite) space, based on the concept that a given complex problem can be more easily, yet accurately enough, analyzed by parsing it into a set of locally linear ones. Local learning allows one to capture local structure of the data, while the parameter estimation is performed globally to avoid possible over-fitting. The idea of “fit locally and think globally” is also used in the well-known locally linear embedding (LLE) algorithm that approximates a complex nonlinear manifold using a set of locally linear patches [44]. LLE is an algorithm for dimensionality reduction in unsupervised learning settings, while our algorithm is for supervised learning. Another important difference between the two algorithms is that LLE is based on the assumption that nearby points in the high-dimensional space remain adjacent in the reduced low-dimensional space, which may not be true in the presence of copious irrelevant features, as shown in Fig. 2.
The main contribution of the paper is that we provided a principled way to perform feature selection for classification problems with complex data distributions and very high data dimensionality. It avoids any heuristic combinatorial search, and hence can be implemented efficiently. Unlike many existing methods, ours has a solid theoretical foundation that ensures its performance. Moreover, its implementation and parameter tuning are easy, and the extension of the algorithm to multiclass settings is straightforward. We have experimentally demonstrated that our algorithm is already capable of handling many feature-selection problems one may encounter in scientific research. Considering the increased demand for analyzing data with a large number of features in many research fields, including bioinformatics, economics, and computer vision, we expect that the work presented in this paper will make a broad impact.
Supplementary Material
Acknowledgments
The authors thank the associate editor Dr. Olivier Chapelle and three anonymous reviewers for numerous suggestions that significantly improved the quality of the paper. This work is in part supported by the Susan Komen Breast Cancer Foundation under grant No. BCTR0707587.
Biographies

Yijun Sun received two BS degrees in electrical and mechanical engineering from Shanghai Jiao Tong University, China, in 1995, and the MS and PhD degrees in electrical engineering from the University of Florida, Gainesville, in 2003 and 2004, respectively. Currently, he is a research scientist at the Interdisciplinary Center for Biotechnology Research and an affiliated faculty member in the Department of Electrical and Computer Engineering at the University of Florida. His research interests are mainly in machine learning, bioinformatics, and their applications to cancer study and microbial community analysis.

Sinisa Todorovic received the PhD degree in electrical and computer engineering at the University of Florida in 2005. He was a postdoctoral research associate at the Beckman Institute at the University of Illinois at Urbana-Champaign between 2005 and 2008. Currently, he is an assistant professor in the School of Electrical Engineering and Computer Science at Oregon State University. His research interests include computer vision and machine learning, with focus on object/activity recognition and texture analysis. His synergistic activities include: associate editor of the Image and Vision Computing Journal, program chair of the First International Workshop on Stochastic Image Grammars 2009, and reviewer for all major journals and conferences in computer vision. He was awarded the Jack Neubauer Best Paper Award by the IEEE Vehicular Technology Society in 2004, and the Outstanding Reviewer Award by the 11th IEEE International Conference on Computer Vision in 2007.

Steve Goodison received the BSc degree in biochemistry from the University of Wales in 1989. He went on to receive the PhD degree in molecular biology from Oxford University in 1993 as a Wellcome Trust Scholar. Postdoctoral studies at Oxford University included diabetes research as a Wellcome Trust fellow and in cancer research in the Department of Clinical Biochemistry. He joined the University of California, San Diego as an assistant professor in 2001, was an associate professor at the University of Florida, and is currently a professor at the M.D. Anderson Cancer Center Orlando and the University of Central Florida. His research interests are primarily cancer research, and include molecular pathology, the function of specific genes in the metastatic spread of cancer, and biomarker discovery and development for clinical diagnosis and prognosis.
Footnotes
In a degenerated case, it is possible that d(xn; xi|w) = d(xn; xj |w), which, however, is a zero-probability event provided that patterns contain some random noise. For simplicity, the degenerated case is not considered in our analysis.
Contributor Information
Yijun Sun, Email: sunyijun@biotech.ufl.edu, The Interdisciplinary Center for Biotechnology Research, University of Florida, PO Box 103622, Gainesville, FL 32610-3622..
Sinisa Todorovic, Email: sinisa@eecs.oregonstate.edu, The School of Electrical Engineering and Ccomputer Science, 2107 Kelley Engineering Center, Oregon State University, Corvallis, OR 97331..
Steve Goodison, Email: Steven.Goodison@orlandohealth.com, The Cancer Research Institute, M.D. Anderson Cancer Center-Orlando, Orlando, FL 32827..
References
- 1.van’t Veer L, et al. Gene Expression Profiling Predicts Clinical Outcome of Breast Cancer. Nature. 2002;vol. 415:530–536. doi: 10.1038/415530a. [DOI] [PubMed] [Google Scholar]
- 2.Wang Y, et al. Gene-Expression Profiles to Predict Distant Metastasis of Lymph-Node Negative Primary Breast Cancer. Lancet. 2005;vol. 365:671–679. doi: 10.1016/S0140-6736(05)17947-1. [DOI] [PubMed] [Google Scholar]
- 3.Vapnik V. Statistical Learning Theory. Wiley; 1998. [DOI] [PubMed] [Google Scholar]
- 4.Weston J, Mukherjee S, Chapelle O, Pontil M, Poggio T, Vapnik V. Feature Selection for SVMs; proc. 13th Advances in Neural Information Processing Systems; 2001. pp. 668–674. [Google Scholar]
- 5.Ng AY. Feature Selection, L1 vs. L2 Regularization, and Rotational Invariance; proc. 21st Int’l Conf. Machine Learning; 2004. pp. 78–86. [Google Scholar]
- 6.Ng AY, Jordan MI. Convergence Rates of the Voting Gibbs Classifier, with Application to Bayesian Feature Selection; proc. 18th Int’l Conf. Machine Learning; 2001. pp. 377–384. [Google Scholar]
- 7.Lafferty J, Wasserman L. Challenges in Statistical Machine Learning. Statistica Sinica. 2006;vol. 16:307–322. [Google Scholar]
- 8.Hilario M, Kalousis A. Approaches to Dimensionality Reduction in Proteomic Biomarker Studies. Briefings in Bioinformatics. 2008;vol. 9(no. 2):102–118. doi: 10.1093/bib/bbn005. [DOI] [PubMed] [Google Scholar]
- 9.Guyon I, Elisseeff A. An Introduction to Variable and Feature Selection. J. Machine Learning Research. 2003;vol. 3:1157–1182. [Google Scholar]
- 10.Kohavi R, John GH. Wrappers for Feature Subset Selection. Artificial Intelligence. 1997;vol. 97(nos. 1/2):273–324. [Google Scholar]
- 11.Pudil P, Novovicova J. Novel Methods for Subset Selection with Respect to Problem Knowledge. IEEE Intelligent Systems. 1998 Mar;vol. 13(no. 2):66–74. [Google Scholar]
- 12.Koller D, Sahami M. Toward Optimal Feature Selection; proc. 13th Int’l Conf. Machine Learning; 1996. pp. 284–292. [Google Scholar]
- 13.Dietterich TG, Bakiri G. Solving Multiclass Learning Problems via Error-Correcting Output Codes. J. Artificial Intelligence Research. 1995;vol. 2:263–286. [Google Scholar]
- 14.Chapelle O, Vapnik V, Bousquet O, Mukherjee S. Choosing Multiple Parameters for Support Vector Machines. Machine Learning. 2002;vol. 46(no. 1):131–159. [Google Scholar]
- 15.Lal TN, Chapelle O, Weston J, Elisseeff A. Embedded Methods. In: Guyon I, Gunn S, Nikravesh M, Zadeh L, editors. Feature Extraction, Foundations and Applications. Springer-Verlag; 2006. pp. 137–165. [Google Scholar]
- 16.Guyon I, Weston J, Barnhill S, Vapnik V. Gene Selection for Cancer Classification using Support Vector Machines. Machine Learning. 2002;vol. 46(nos. 1–3):389–422. [Google Scholar]
- 17.Zhu J, Rosset S, Hastie T, Tibshirani R. 1-Norm Support Vector Machines; proc. 16th Advances in Neural Information Processing Systems; 2004. [Google Scholar]
- 18.Kira K, Rendell LA. A Practical Approach to Feature Selection; proc. Ninth Int’l Conf. Machine Learning; 1992. pp. 249–256. [Google Scholar]
- 19.Gilad-Bachrach R, Navot A, Tishby N. Margin Based Feature Selection—Theory and Algorithms; proc. 21st Int’l Conf. Machine Learning; 2004. pp. 43–50. [Google Scholar]
- 20.Schapire RE, Freund Y, Bartlett PL, Lee WS. Boosting the Margin: A New Explanation for the Effectiveness of Voting Methods. Annals of Statistics. 1998;vol. 26(no. 5):1651–1686. [Google Scholar]
- 21.Dempster A, Laird N, Rubin D. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. Royal Statistical Soc., Series B. 1977;vol. 39(no. 1):1–38. [Google Scholar]
- 22.Atkeson C, Moore A, Schaal S. Locally Weighted Learning. Artificial Intelligence Rev. 1997;vol. 11(no. 15):11–73. [Google Scholar]
- 23.Bishop CM. pattern Recognition and Machine Learning. Springer; 2006. [Google Scholar]
- 24.Tibshirani R. Regression Shrinkage and Selection via the Lasso. J. Royal Statistical Soc., Series B. 1996;vol. 58(no. 1):267–288. [Google Scholar]
- 25.Park MY, Hastie T. ℓ1 Regularization Path Algorithm for Generalized Linear Models. J. Royal Statistical Soc., Series B. 2007;vol. 69(no. 4):659–677. [Google Scholar]
- 26.Meier L, van de Geer S, Buhlmann P. The Group Lasso for Logistic Regression. J. Royal Statistical Soc., Series B. 2008;vol. 70:53–71. [Google Scholar]
- 27.Roth V. The Generalized LASSO. IEEE Trans. Neural Networks. 2004 Jan;vol. 15(no. 1):16–28. doi: 10.1109/TNN.2003.809398. [DOI] [PubMed] [Google Scholar]
- 28.Rosset S. Following Curved Regularized Optimization Solution Paths; proc. 17th Advances in Neural Information Processing Systems; 2005. pp. 1153–1160. [Google Scholar]
- 29.Donoho DL, Elad M. Optimally Sparse Representations in General Nonorthogonal Dictionaries by ℓ1 Minimization. proc. Nat’l Academy of Sciences USA. 2003;vol. 100(no. 5):2197–2202. doi: 10.1073/pnas.0437847100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Breiman L. Better Subset Regression Using the Nonnegative Garrote. Technometrics. 1995;vol. 37(no. 4):373–384. [Google Scholar]
- 31.Kress R. Numerical Analysis. Springer-Verlag; 1998. [Google Scholar]
- 32.Zezula P, Amato G, Dohnal V, Batko M. Similarity Search—The Metric Space Approach. Springer; 2006. [Google Scholar]
- 33.Dietterich TG. Machine Learning Research: Four Current Directions. AI Magazine. 1997;vol. 18(no. 4):97–136. [Google Scholar]
- 34.Sun Y, Todorovic S, Li J, Wu D. Unifying Error-Correcting and Output-Code AdaBoost through the Margin Concept; proc. 22nd Int’l Conf. Machine Learning; 2005. pp. 872–879. [Google Scholar]
- 35.Asuncion A, Newman D. UCI Machine Learning Repository. 2007 [Google Scholar]
- 36.Vapnik V, Chervonenkis A. Theory of Pattern Recognition, (in Russian) Nauka; 1974. [Google Scholar]
- 37.Pollard D. Convergence of Stochastic Processes. Springer-Verlag; 1984. [Google Scholar]
- 38.Devroye L, Györfi L, Lugosi G. A Probabilistic Theory of Pattern Recognition. Springer-Verlag; 1996. [Google Scholar]
- 39.Anthony M, Bartlett PL. Neural Network Learning: Theoretical Foundations. Cambridge Univ. Press; 1999. [Google Scholar]
- 40.Cucker F, Smale S. On the Mathematical Foundations of Learning. Bull. Am. Math. Soc. 2002;vol. 39(no. 1):1–49. [Google Scholar]
- 41.Zhang T. Covering Number Bounds of Certain Regularized Linear Function Classes. J. Machine Learning Research. 2002;vol. 2:527–550. [Google Scholar]
- 42.Sun Y, Li J. Iterative RELIEF for Feature Weighting; proc. 23rd Int’l Conf. Machine Learning; 2006. pp. 913–920. [Google Scholar]
- 43.Kushner H, Yin G. Stochastic Approximation and Recursive Algorithms and Applications. Springer-Verlag; 2003. [Google Scholar]
- 44.Roweis ST, Saul LK. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science. 2000;vol. 290(no. 5500):2323–2326. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- 45.Bartlett PL. The Sample Complexity of Pattern Classification with Neural Networks: The Size of the Weights Is More Important Than the Size of the Network. IEEE Trans. Information Theory. 1998 Mar;vol. 44(no. 2):525–536. [Google Scholar]
- 46.Goldberger J, Roweis S, Hinton G, Salakhutdinov R. Neighbourhood Components Analysis; proc. 17th Advances in Neural Information Processing Systems; 2005. pp. 513–520. [Google Scholar]
- 47.Weinberger K, Blitzer J, Saul LK. Distance Metric Learning for Large Margin Nearest Neighbor Classification; proc. 18th Advances in Neural Information Processing Systems; 2006. pp. 1473–1480. [Google Scholar]
- 48.Sun Y, Wu D. A RELIEF Based Feature Extraction Algorithm; proc. Eighth SIAM Int’l Conf. Data Mining; 2008. pp. 188–195. [Google Scholar]
- 49.Kononenko I. Estimating Attributes: Analysis and Extensions of RELIEF; proc. European Conf. Machine Learning; 1994. pp. 171–182. [Google Scholar]
- 50.Sun Y, Goodison S, Li J, Liu L, Farmerie W. Improved Breast Cancer Prognosis through the Combination of Clinical and Genetic Markers. Bioinformatics. 2007;vol. 23(no. 1):30–37. doi: 10.1093/bioinformatics/btl543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Horn R, Johnson C. Matrix Analysis. Cambridge Univ. Press; 1985. [Google Scholar]
- 52.Stephenson AJ, Smith A, Kattan MW, Satagopan J, Reuter VE, Scardino PT, Gerald WL. Integration of Gene Expression Profiling and Clinical Variables to Predict Prostate Carcinoma Recurrence after Radical Prostatectomy. Cancer. 2005;vol. 104(no. 2):290–298. doi: 10.1002/cncr.21157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Shipp MA, et al. Diffuse Large B-Cell Lymphoma Outcome Prediction by Gene Expression Profiling and Supervised Machine Learning. Nature Medicine. 2002;vol. 8:68–74. doi: 10.1038/nm0102-68. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.