How mechanisms of perceptual decision-making affect the psychometric function

Abstract

Psychometric functions are often interpreted in the context of Signal Detection Theory, which emphasizes a distinction between sensory processing and non-sensory decision rules in the brain. This framework has helped to relate perceptual sensitivity to the “neurometric” sensitivity of sensory-driven neural activity. However, perceptual sensitivity, as interpreted via Signal Detection Theory, is based on not just how the brain represents relevant sensory information, but also how that information is read out to form the decision variable to which the decision rule is applied. Here we discuss recent advances in our understanding of this readout process and describe its effects on the psychometric function. In particular, we show that particular aspects of the readout process can have specific, identifiable effects on the threshold, slope, upper asymptote, time dependence, and choice dependence of psychometric functions. To illustrate these points, we emphasize studies of perceptual learning that have identified changes in the readout process that can lead to changes in these aspects of the psychometric function. We also discuss methods that have been used to distinguish contributions of the sensory representation versus its readout to psychophysical performance.

1. Introduction

Psychometric functions quantify the relationship between perceptual performance and physical properties of the stimulus (Klein, 2001). These functions are often not merely descriptive but also can be used to help infer the underlying computational processes implemented in the brain. For example, psychometric functions based on principles of Signal Detection Theory helped to discredit the idea of a sensory threshold that must be exceeded for a stimulus to have any effect on the observer. These functions instead emphasize the usefulness of distinguishing continuously variable sensory processing and a non-sensory decision rule (Green & Swets, 1966; Macmillan & Creelman, 2004). This distinction, and the underlying assumptions about distributions of signal and noise in the brain, have been central to studies relating psychophysical performance to “neurometric” analysis of neural data from single-unit recordings in monkeys and electroencephalography (EEG) and functional magnetic imaging (fMRI) in humans (Britten, Shadlen, Newsome & Movshon, 1992a; Cohen & Newsome, 2009; Cook & Maunsell, 2002; Gerdjikov, Bergner, Stüttgen, Waiblinger & Schwarz, 2010; Lee, Wehrhahn, Westheimer & Kremers, 1995; Luna, Hernández, Brody & Romo, 2005; Mountcastle, Steinmetz & Romo, 1990; Philiastides & Sajda, 2006; Stüttgen & Schwarz, 2008; Tolhurst, Movshon & Dean, 1983; Uka & DeAngelis, 2003; Vogels & Orban, 1990; Wutte, Smith, Flanagin & Wolbers, 2011).

However, these kinds of psychometric and neurometric analyses can paint an incomplete picture of sensory processing in the brain (Shadlen, Britten, Newsome & Movshon, 1996; Stüttgen, Schwarz & Jäkel, 2011). Consider, for example, a well-known study that recorded from motion-sensitive neurons in the middle temporal area (MT) of extrastriate visual cortex of monkeys performing a visual motion direction-discrimination task and found closely matching values of psychometric and neurometric sensitivity (Britten, Shadlen, Newsome & Movshon, 1992b). These neurometric functions were computed from spike counts measured from individual MT neurons during a fixed-duration motion-viewing period, using the area under the receiver-operator characteristic (“ROC”) curve to quantify how well stimulus motion could be distinguished based on the neural responses alone (Green & Swets, 1966). Critically, this analysis is based on not only the measured responses of the given neuron, but also the assumption that those responses are read out in a particular way to form the perceptual decision: as a difference between the responses of the given neuron and of its complementary “anti-neuron”. However, the real decision process in the brain involves many more neurons, different temporal dynamics, and possibly more complex readout schemes (Cohen & Newsome, 2009; Geisler & Albrecht, 1997; Pouget, Dayan & Zemel, 2003; Seung & Sompolinsky, 1993). Thus, any effective model of perceptual performance must account for both the relevant sensory representation and how that representation is read out and combined with goals, task rules, and other cognitive factors to form the perceptual decision that instructs the behavioral response.

The idea that readout plays a key role in perceptual performance has been underscored in recent years in the field of perceptual learning. Perceptual learning describes long-lasting, training-induced improvements in perceptual sensitivity (Gold & Watanabe, 2010). These improvements can reflect a diversity of underlying neural mechanisms (Ahissar, Nahum, Nelken & Hochstein, 2009; Ghose, 2004; Gilbert, Sigman & Crist, 2001; Petrov, Van Horn & Ratcliff, 2011). For some tasks, improvements in performance correspond to changes in the response properties of neurons in early sensory areas, such as primary visual, auditory, or somatosensory cortex (Maertens & Pollmann, 2005; Recanzone, Merzenich & Schreiner, 1992; Recanzone, Merzenich, Jenkins, Grajski & Dinse, 1992; Recanzone, Schreiner & Merzenich, 1993; Schoups, Vogels, Qian & Orban, 2001; Schwartz, Maquet & Frith, 2002; Yotsumoto et al., 2009; Yotsumoto, Watanabe & Sasaki, 2008). However, for other tasks, perceptual learning is accompanied by little or no changes in these early sensory areas (Ghose, Yang & Maunsell, 2002; Law & Gold, 2008). Instead, the key neural changes are thought to occur at later stages of processing, particularly those involved in using information from the sensory representation to form the perceptual decision (Dosher & Lu, 1998; Dosher & Lu, 1999; Jacobs, 2009; Law & Gold, 2008; Mollon & Danilova, 1996; Petrov, Dosher & Lu, 2005). Thus, perceptual sensitivity can be shaped by mechanisms of readout, even when the sensory representation is stable.

The goal of this article is to review how recent advances in our understanding of decision mechanisms in the brain have helped to clarify their specific roles in perceptual performance, as quantified via the psychometric function. We focus, in part, on studies of changes in decision processes related to perceptual learning, because those studies have helped to elucidate how those processes relate to perceptual performance. However, we emphasize that the relationship between decision processing and performance is not specific to perceptual learning but rather must always be considered when attempting to interpret psychophysical data in terms of the underlying brain mechanisms. To illustrate these points, we first describe the readout process that is central to forming perceptual decisions, then describe the psychometric function and show that many of its commonly measured features depend critically on the nature of this readout process, and finally discuss methods for distinguishing contributions of representation and readout on psychophysical performance.

2. Background

2.1. Representation versus readout

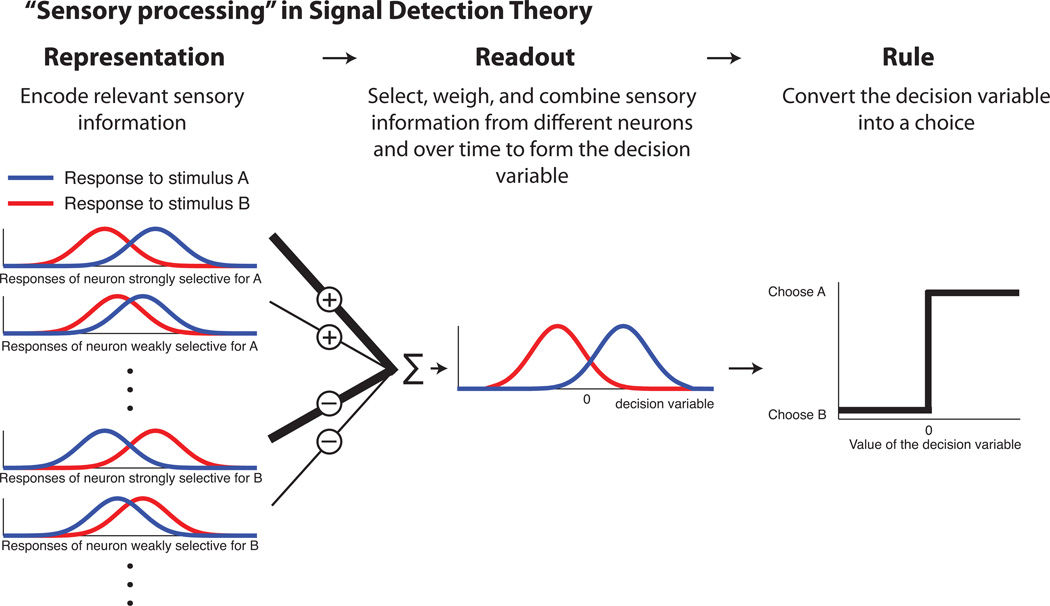
Perceptual decisions involve the detection, discrimination, or identification of sensory stimuli. These decisions require several stages of complex processing in the brain between the extraction of relevant sensory information by receptors in the periphery to generation of the appropriate motor response to indicate the decision. Here we consider two important stages that can be distinguished based on their computational roles and neural implementations (Fig. 1) (Gold & Shadlen, 2007; Schneidman, Bialek & Berry, 2003). The first is the representation, or “encoding,” of the extracted sensory information in the brain. The second is the readout, or “decoding,” of the encoded representation to form a decision variable that, when applied to a decision rule, determines the final choice (Graham, 1989).

Figure 1. The decision process.

Schematic of a 2AFC perceptual decision (is the stimulus A or B?) decomposed into three processes: 1) the representation of relevant sensory information by populations of neurons with relevant tuning properties and a variety of sensitivities to the two alternatives under consideration; 2) readout of that information to form a decision variable; and 3) application of a rule to the decision variable to generate a choice. The readout scheme illustrated here uses a simple weighted sum of the outputs of sensory neurons. To generate a decision variable whose sign can distinguish between the two alternatives, positive weights are assigned to neurons that encode one alternative, negative weights to the others. To maximize discriminability using this scheme, each weight (indicated by line thickness) is proportional to the relative sensitivity of the associated sensory neuron.

The sensory representation consists of neurons whose activity is modulated by relevant features of the sensory stimulus. This activity is driven by the sensory input and is typically not strongly modulated by the task design and other cognitive variables, although top-down processes can have effects even on sensory representations in thalamus and primary sensory cortex (Bender & Youakim, 2001; Lima, Singer & Neuenschwander, 2011; Mehta, Ulbert & Schroeder, 2000; Saalmann & Kastner, 2011). These neurons have been identified based on tuning properties that are appropriate for distinguishing between the alternatives under consideration, weak correlations between their activity and choice behavior (indicating a possible contribution to the decision variable but not the decision variable itself), and manipulations including microstimulation and inactivation that have a causal influence on perceptual performance (Parker & Newsome, 1998).

In contrast, readout reflects how information in the sensory representation is interpreted to form the decision variable that guides behavior. This process was first considered in detail in the context of peripheral nerves but soon was applied to stimulus-tuned neurons in the central nervous system (Britten et al., 1992; Hawken & Parker, 1990; Johnson, 1980; Johnson, Darian-Smith & LaMotte, 1973; Johnson, Darian-Smith, LaMotte, Johnson & Oldfield, 1979). In general, readout involves selecting relevant sensory signals, weighing their relative contributions to the decision process, and combining the weighed signals to form the decision variable. This goal-directed process, which is probably under the guidance of top-down control mechanisms, can take into account stimulus selectivity, response variability and other properties of the sensory representation to form a decision variable that maximizes the discriminability of the alternatives under consideration for the particular perceptual task (Chen, Geisler & Seidemann, 2006; Chen, Geisler & Seidemann, 2008; Geisler & Albrecht, 1997; Pouget et al., 2003; Scolari & Serences, 2010; Seung & Sompolinsky, 1993; Shadlen et al., 1996; Tanji & Hoshi, 2008).

A useful illustration of the readout process is provided by a comparison of two visual motion discrimination tasks. One, known as a “coarse” task, requires the subject to discriminate between two opposite directions of motion (i.e., 180° apart). The other, a “fine” task, requires the subject to discriminate between two nearby directions of motion (≤20° apart). Performance on both tasks depends on motion information extracted by the visual system and represented in the activity of direction-selective neurons in area MT and elsewhere (Britten et al., 1992; Celebrini & Newsome, 1994; Celebrini & Newsome, 1995; Purushothaman & Bradley, 2005; Salzman, Britten & Newsome, 1990; Salzman, Murasugi, Britten & Newsome, 1992a; Thompson & Liu, 2006). However, the most effective readout schemes for the two tasks select different subsets of neurons to form the relevant decision variables (Hol & Treue, 2001; Jazayeri & Movshon, 2007a; Law & Gold, 2009a; Purushothaman & Bradley, 2005; Regan & Beverley, 1985). Direction-tuned MT neurons have a direction-tuning width (half-width at half-height of a Gaussian tuning curve) of approximately 40° (Albright, 1984; Law & Gold, 2008). Thus, for the coarse task, the two alternative directions activate non-overlapping populations of MT neurons. Accordingly, the most informative neurons to solve the task are those tuned to the directions to be discriminated. In contrast, for the fine task, the two nearby directions tend to activate roughly the same population of MT neurons. Within that population, the most informative neurons are those tuned slightly away from the directions to be discriminated, because those neurons provide responses that differ the most for the two test directions.

Once selected, the sensory responses must also be weighed and combined into the decision variable. One conceptually simple scheme is to use a weighted sum in which neurons that encode one alternative are assigned positive weights, and neurons that encode the other alternative are assigned negative weights. The resulting decision variable represents a difference in activity between pools of neurons whose activity represents the two alternatives, as in ROC-based analyses (Fig. 2). For a one-interval task, this decision variable can be computed from the activity of separate pools of sensory neurons (or “neurons” and “antineurons”) tuned to the two alternatives. For a two-interval task, this decision variable can be computed from the activity of one pool of sensory neurons and its memory trace (Gold & Shadlen, 2007; Hernández, Zainos & Romo, 2002; Romo, Hernandez & Zainos, 2004). Under certain assumptions, the value of this kind of decision variable is proportional to the logarithm of the likelihood ratio corresponding to the two alternatives (Britten et al., 1992; Gold & Shadlen, 2001). This quantity, which is central to Signal Detection Theory and other aspects of statistical decision theory, can be compared to a criterion value to generate a final choice that will maximize the proportion of correct responses, given that decision variable (Duda & Hart, 1972; Gold & Shadlen, 2007; Green & Swets, 1966; Macmillan & Creelman, 2004).

Figure 2. Relationships between the ROC curve, yes-no detection, and 2AFC discrimination according to Signal Detection Theory.

The decision variable for yes-no detection (lower left) is compared to a criterion, the value of which (green arrows) determines the proportions of hits and false alarms, plotted as an ROC curve (top). The area under the ROC curve (shaded area) corresponds to the expected percentage of correct responses for a 2AFC discrimination task that uses as a decision variable a difference between the “detect A” and “detect B” yes-no decision variables (lower right). The optimal decision rule in this case is based simply on the sign of the decision variable (in the example shown, positive values correspond to “decide A” and negative values correspond to “decide B”). Psychophysical methods measure the ROC curve directly from behavior and then infer the underlying decision variables (Green & Swets, 1966; Macmillan & Creelman, 2004). Neurometric methods compute ROC curves from neural activity. These methods often assume that 2AFC performance equals the difference in measured activity from a single sensory neuron, corresponding to a “detect A” decision variable, and its presumed “anti-neuron,” corresponding to a “detect B” decision variable (Britten et al., 1992).

More generally, readout must appropriately select, weigh, and combine relevant sensory signals not just from different neurons, but also over time. For two-interval tasks, this time dependence is inherent to the task design, which requires readout of sequentially presented sensory input (Romo & Salinas, 2003). For both one- and two-interval designs, there is often, but not always, an additional time dependence of processing within each stimulus interval, leading to perceptual sensitivity that depends on stimulus duration (Gold & Shadlen, 2007; Uchida, Kepecs & Mainen, 2006). For some tasks, including the coarse direction-discrimination task using random-dot stimuli, this dependence on stimulus duration extends beyond the temporal integration properties of neurons in the sensory representation and instead reflect properties of the readout process (Bair & Movshon, 2004; Gold & Shadlen, 2000; Huk & Shadlen, 2005; Watamaniuk & Sekuler, 1992). This idea is central to “sequential-sampling” models of decision-making that can account for the trade-off between speed and accuracy that is common to many perceptual tasks (Gold & Shadlen, 2007; Link, 1992; Smith & Ratcliff, 2004; Wickelgren, 1977).

2.2 The psychometric function

The psychometric function describes how an observer’s decisions about the presence or identity of a stimulus depend on the value of a particular parameter of that stimulus, such as its strength or signal-to-noise ratio (Blackwell, 1952; Kingdom & Prins, 2009; Klein, 2001). Here we consider primarily functions applied to discrimination tasks that have been used in physiological experiments with monkeys that have formed much of the foundation of our knowledge of the relationship between neural activity and perceptual ability (Gold & Shadlen, 2007; Parker & Newsome, 1998). For example, the coarse and fine direction-discrimination tasks typically use a one-interval design in which a single stimulus is presented and a binary response is required, corresponding to one of two possible directions of motion (Britten et al., 1992; Purushothaman & Bradley, 2005). In contrast, a commonly used flutter-discrimination task uses a two-interval design, in which two stimuli are presented sequentially and a binary response is required, corresponding to the frequency of the second stimulus relative to the first (higher or lower) (Romo & Salinas, 2003). Although many psychologists refer to the former as “yes-no” and the latter as “two-alternative,” for simplicity we will refer to both as two-alternative forced-choice (2AFC) tasks and focus on common principles of the underlying decision process (Macmillan & Creelman, 2004; Stüttgen et al., 2011).

Many of these principles likely extend to other task designs, as well, including those involving stimulus detection. Relationships between yes-no (one-interval) detection tasks and 2AFC discrimination tasks are summarized in Fig. 2. However, there are also important differences in the underlying decision processes for the two task types. For example, computing the decision variable for a detection task can be complicated when there is temporal uncertainty about when the stimulus will appear (Gold & Shadlen, 2007; Lasley & Cohn, 1981). Moreover, the decision rule can have different effects in the two task types, including a variable guess rate in yes-no detection tasks that is fixed at 0.5 in 2AFC discrimination tasks (Green & Swets, 1966; Macmillan & Creelman, 2004; Nachmias, 1981). To avoid these complications, below we restrict our attention to 2AFC discrimination tasks, unless otherwise noted. We also avoid discussions of more complicated n-AFC tasks (for n>2), whose theoretical and neural underpinnings likely overlap with those of 2AFC tasks but are just beginning to be explored (Albantakis & Deco, 2009; Bogacz, Usher, Zhang & McClelland, 2007; Brown & Heathcote, 2008; Churchland, Kiani & Shadlen, 2008; McMillen & Holmes, 2006; Niwa & Ditterich, 2008; Usher & McClelland, 2001).

A typical 2AFC psychometric function shows the fraction of correct responses as a function of stimulus strength (Fig. 3, top). These data can be fit using a variety of sigmoid-shaped functions that describe monotonically improving accuracy, from a guess rate of 0.5 for the lowest stimulus strengths to often nearly perfect accuracy for the highest stimulus strengths. Commonly used functions include the cumulative normal, which was originally derived for toxicology analyses but is also a conveniently parameterized function that has been used in many psychophysical studies; the cumulative Weibull, including a particular variant designed to approximate a readout process known as probability summation, in which the decision variable is not a pooled signal but rather represents appropriate activation of one of several independent channels; and logistic functions, which are convenient functions to use for hypothesis testing and, under certain assumptions, represent analytical solutions to the kinds of accumulate-to-bound decision models described above (Finney, 1947; Klein, 2001; Quick, 1974; Salzman et al., 1990; Salzman et al., 1992a; Shadlen, Hanks, Churchland, Kiani & Yang, 2006; Strasburger, 2001).

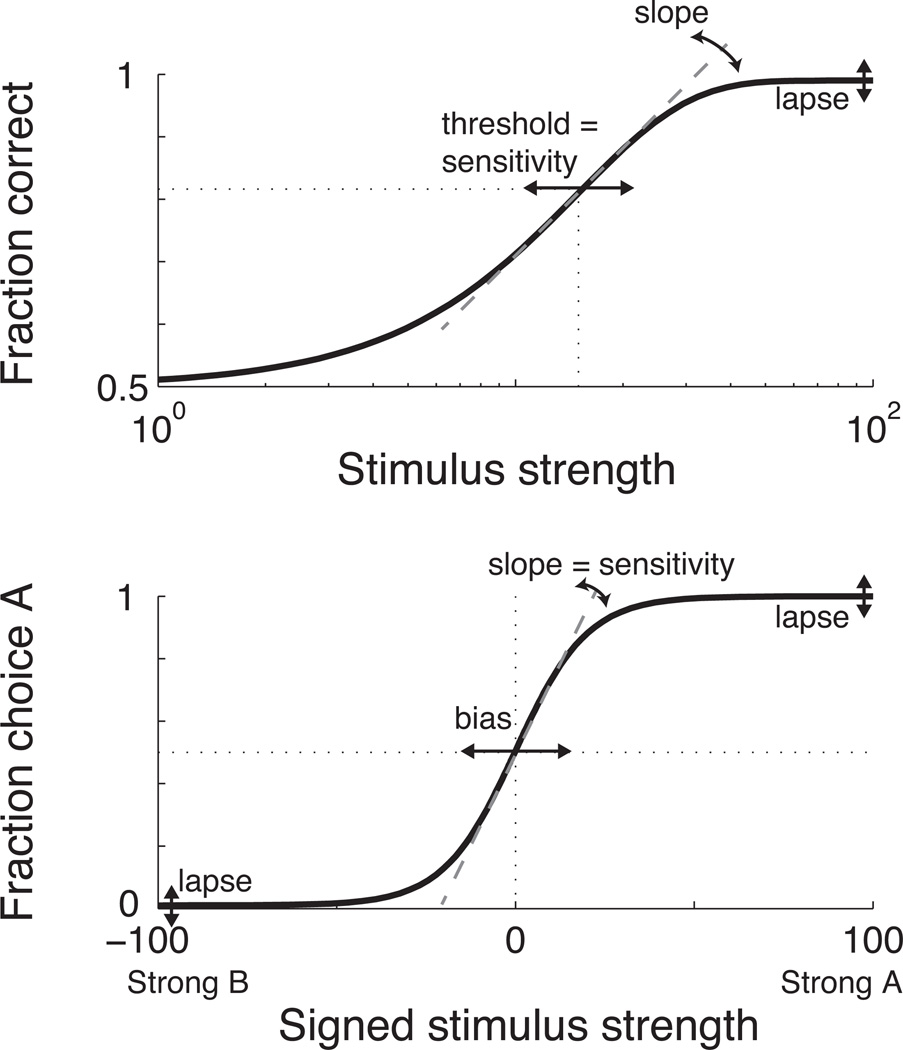
Figure 3. Features of 2AFC psychometric functions.

Top: An “accuracy” function depicting the fraction of correct responses as a function of stimulus strength, on a logarithmic abscissa in arbitrary units from 0 to 100. The function is a cumulative Weibull function with parameters α (threshold) = 15 and β (shape) = 1.4. Bottom: A “choice” function depicting the fraction of trials in which stimulus “A” was chosen as a function of signed stimulus strength, on a linear abscissa in which positive/negative values correspond to presentation of stimulus A/B. The function is a logistic function with two parameters, θ₀ (bias) = 0 and θ₁ (sensitivity) = 0.099. The functions and parameters used in both panels are similar to those reported for monkeys performing the coarse direction-discrimination task (Britten et al., 1992; Salzman et al., 1992).

These functions have different parameterizations but are typically described by a small set of key features. The horizontal position of the psychometric function describing accuracy as a function of stimulus strength represents sensitivity to the stimulus in the context of the given task. Sensitivity is typically measured as a discrimination threshold, which is the value of the stimulus parameter corresponding to a fixed percentage of correct responses. According to Signal Detection Theory, choice accuracy can be converted into a measure of perceptual sensitivity called d’ that reflects the underlying decision variable. This measure assumes that the underlying decision variable is distributed as a Gaussian with equal variances but different means for the two alternatives. It is computed as the difference in means divided by their common standard deviation (Green & Swets, 1966; Macmillan & Creelman, 2004). For a 2AFC task, d’=1 corresponds to ~76% correct responses, which is often used for measuring discrimination threshold.

The slope of the psychometric function describes changes in accuracy as a function of changes in stimulus strength. When measured at threshold, psychometric slope represents the reliability of the estimated threshold. When measured at its maximum value, equivalent to the point of inflection on the rising portion of the curve (which may or may not be where threshold was measured), psychometric slope can be useful for comparing slope and threshold estimates across studies that might have used different forms of the psychometric function or different criterion levels of performance (Strasburger, 2001).

The dependence of perceptual performance on stimulus duration can be assessed in several ways. For response-time (RT) tasks, in which the subject chooses when to stop processing the stimulus and initiate the appropriate behavioral response, psychometric functions are often accompanied by chronometric functions that describe RT as a function of stimulus strength (Luce, 1986; Meyer, Osman, Irwin & Yantis, 1988). These functions have been particularly useful for constraining fits of behavioral data to accumulate-to-bound models, in which the temporal accumulation of sensory evidence accounts for the dependence of performance on stimulus duration (Palmer, Huk & Shadlen, 2005; Ratcliff & Rouder, 1998; Shadlen et al., 2006). Time dependence can also be assessed using experimenter-controlled, variable-duration stimuli, with or without interleaved RT trials (Gold & Shadlen, 2000; Ludwig, Gilchrist, McSorley & Baddeley, 2005; Marks, 1974; Meyer, Irwin, Osman & Kounios, 1988; Watamaniuk, 1993; Watamaniuk & Sekuler, 1992). In these cases, psychometric functions can be plotted with respect to two independent variables, stimulus strength and duration, that explicitly quantify the relationship between performance and stimulus duration (Gold & Shadlen, 2000; Gold & Shadlen, 2003; Kiani, Hanks & Shadlen, 2008).

Two other features of psychometric functions are commonly interpreted in terms of non-perceptual factors but, as we describe below, under some conditions can reflects aspects of the decision variable. The upper asymptote of the psychometric function reflects the fraction of errors made for easily perceptible stimuli. The difference between this asymptote and perfect performance (i.e., all correct responses) is typically referred to as the lapse rate, because it is assumed to result from transient lapses of attention for well-trained subjects. As such, lapses are typically thought to result from brain processes that are separate from the perceptual decision. However, in principle, lapses can reflects any factor that interferes with the ability to appropriately carry out the rules of the task, such as an inappropriately designed readout. Reliable estimates of lapse rates, which require atypically large samples of performance data for easily perceptible stimuli, can be important for obtaining accurate estimates of psychometric threshold and slope (Finney, 1947; Klein, 2001; Wichmann & Hill, 2001).

The psychometric function can also reflect a propensity of the subject to choose one alternative versus the other, called a choice bias. Choice biases, which have been particularly well characterized as a form of time-order effect called an interval bias on two-interval forced-choice tasks, can lead to improper estimates of perceptual sensitivity if not diagnosed and accounted for properly (Green & Swets, 1966; Klein, 2001; Yeshurun, Carrasco & Maloney, 2008). A choice bias can be diagnosed as a horizontal shift relative to the indecision point (i.e., zero stimulus strength) in certain psychometric functions that separate the behavioral data in terms of choice (Fig. 3, bottom). For these functions, the fraction of choosing one alternative (which varies from zero to one) is plotted as a function of signed stimulus strength, with negative/positive values corresponding to each of the two alternatives. The slope of these functions is typically interpreted in terms of psychometric sensitivity, analogous to the threshold of the accuracy function. High sensitivity corresponds to a steep slope, and low sensitivity corresponds to a shallow slope. Accordingly, sensitivity can be quantified as half of the difference between the values of stimulus strength corresponding to a probability of 0.75 of choosing each of the two alternatives (Klein, 2001). Alternatively, if choice biases are present but reasonably small, sensitivity can be quantified from the accuracy function according to principles of Signal Detection Theory (that is, distinguishing sensitivity from the decision rule) by computing accuracy as the average of the z-scores of the percentage of correct responses measured for each choice, not the average of the percentage of correct responses themselves (Green & Swets, 1966; Macmillan & Creelman, 2004; Yeshurun et al., 2008).

Thus, psychometric functions for 2AFC tasks are typically characterized in terms of discrimination threshold, slope, time dependence, lapse rate, and choice bias. In the following section, we describe how these measures can be affected by decision mechanisms that read out sensory information to instruct behavioral choices.

3. Effects of readout on specific features of the psychometric function

3.1 Effects on discrimination threshold

Discrimination threshold is often used as the primary measurement of performance on psychophysical tasks, providing a quantitative answer to the basic question, “How well did the subject perform?” Its importance in psychophysics is underscored by the many techniques designed to provide a reliable estimate of its value alone, even without measuring the full psychometric function (Leek, 2001). Among its many uses, discrimination threshold is central to studies of perceptual learning. These studies, which have shown that training can cause long-lasting decreases in discrimination threshold (increases in perceptual sensitivity), have also yielded important insights into how discrimination thresholds can depend critically on both the representation and readout of sensory information in the brain.

The relationship between the response properties of sensory neurons and perceptual discrimination thresholds has been studied extensively (Parker & Newsome, 1998; Romo & Salinas, 2003). One commonly used approach characterizes the activity of individual sensory neurons in terms of an ideal-observer’s ability to use that activity to solve the associated perceptual task. This kind of analysis, like the ROC-based techniques described above (Fig. 2), can yield “neurometric” functions that can be compared directly to psychometric functions obtained under identical conditions, typically in terms of discrimination thresholds. For several examples, including neuronal activity measured in extrastriate visual cortex for certain motion tasks and in primary somatosensory cortex for a flutter-discrimination task, psychometric and neurometric discrimination thresholds can be nearly equal (Britten et al., 1992; Celebrini & Newsome, 1994; Cohen & Newsome, 2009; Cook & Maunsell, 2002; Gu, DeAngelis & Angelaki, 2007; Hernández, Zainos & Romo, 2000). An obvious implication of these kinds of studies is that psychophysical sensitivity should, at least in principle, be able to achieve the sensitivity provided by individual sensory neurons.

Consistent with these ideas, perceptual learning-related improvements in psychophysical thresholds have been linked to changes in sensory-driven responses of neurons in the sensory representation. For example, monkeys trained to discriminate the orientation of a small visual grating learn to effectively discriminate between more and more similar orientations, measured as systematic decreases in discrimination threshold. These improvements in performance are accompanied by changes in the response properties of relevant neurons in primary visual cortex that provided increasingly different responses to the test stimuli (Schoups et al., 2001). Similar results have been reported for single-unit responses in primary auditory and somatosensory cortex of monkeys and fMRI BOLD responses in primary visual cortex of humans (Maertens & Pollmann, 2005; Recanzone et al., 1992; Recanzone et al., 1992; Recanzone et al., 1993; Schwartz et al., 2002; Yotsumoto et al., 2009; Yotsumoto et al., 2008).

However, sensory signals must be read out properly to confer the lowest possible discrimination thresholds. The examples of the coarse and fine direction-discrimination tasks illustrate how proper readout can depend on the tuning properties of the sensory neurons for the parameter of interest, in those cases direction tuning width (Hol & Treue, 2001; Jazayeri & Movshon, 2007a; Law & Gold, 2009a; Purushothaman & Bradley, 2005; Regan & Beverley, 1985). Even within the subpopulations of neurons that have appropriate tuning properties for a given task, some will be more informative than others. This variability can arise from differences in baseline firing, response strength, and signal-to-noise ratios. In addition, a sensory neuron can be tuned for multiple stimulus dimensions. For example, responses of direction-tuned MT neurons to moving visual stimuli can be modulated by the disparity of the stimulus (DeAngelis & Newsome, 1999). For these neurons, task-irrelevant stimulus features could in principle influence their sensitivity for task-relevant features. Thus, the most effective readout strategies take all of these factors into account to emphasize the output of neurons whose responses are more informative under the conditions tested (Fig. 4A).

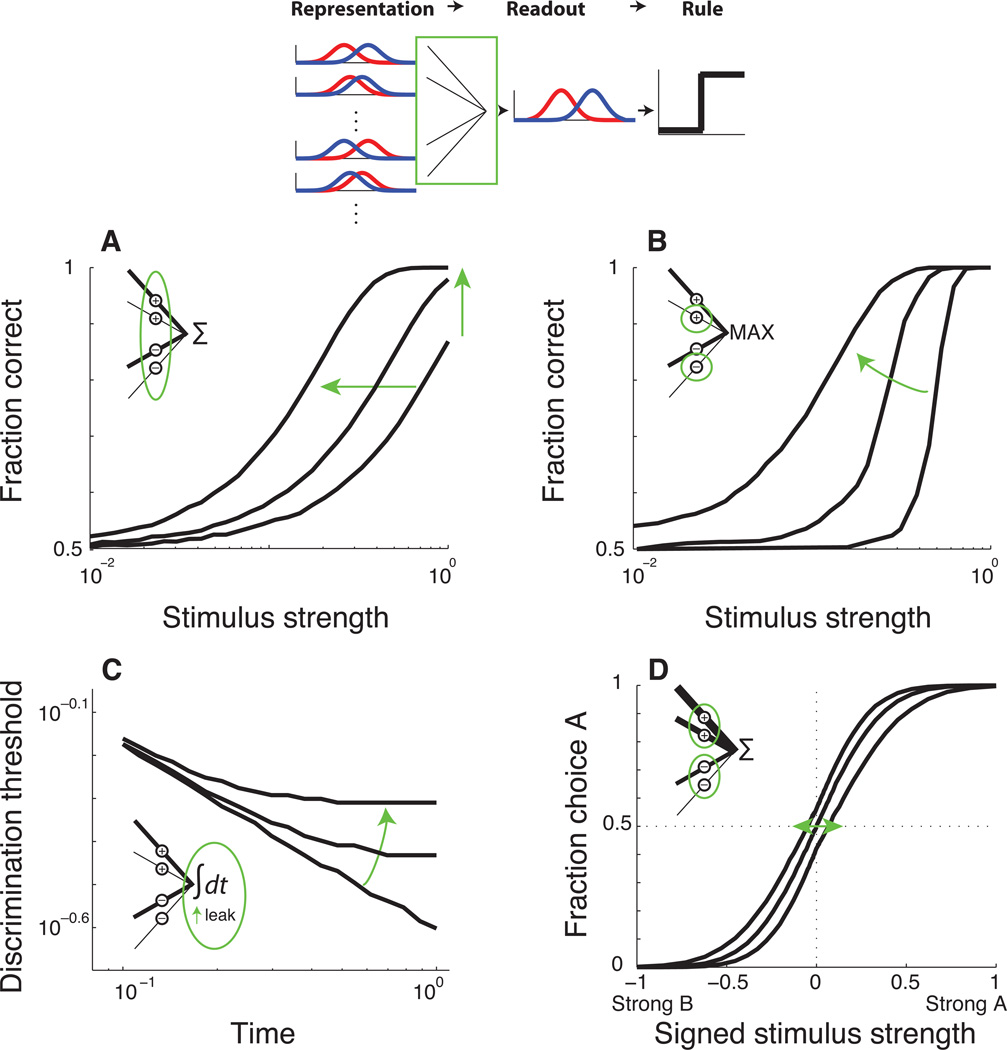
Figure 4. Effects of readout on the psychometric function.

A. Effects on threshold and lapse rate. The curves are from simulations in which the decision variable is formed as a weighted sum of sensory neurons with a variety of sensitivities to the two alternatives. As the decision variable becomes less dependent on inappropriately tuned neurons, the psychometric function shifts leftward (lower thresholds) and have higher values for the largest stimulus strength (smaller lapse rates). B. Effects on slope. The simulations use a readout scheme with a non-linear pooling operation that compares the maximum absolute value of positively versus negatively weighted sensory signals. As the decision depends on fewer unturned sensory neurons, the psychometric function shifts leftward and becomes shallower. C. Effects on time dependence. The simulations use a readout scheme in which sensory evidence is integrated over time using a leaky integrator. For this log-log plot of discrimination threshold versus stimulus duration, a slope of −0.5 (bottom curve) corresponds to a perfect integrator, with no leak. Increasing the amount of leak causes the relationship to become shallower, indicating smaller improvements in discrimination threshold for increasing stimulus presentation time. D. Effects on choice biases. Simulations use a linear pooling scheme in which the weights corresponding to one alternative are either stronger than, the same as, or weaker than the weights corresponding to the other alternative. Asymmetric weights cause horizontal shifts in the psychometric choice function. Similar effects can result from a fixed offset to the value of the decision variable or asymmetric bounds in an accumulation-to-bound decision process.

The diversity of relevant response properties in the sensory representation highlights the usefulness of readout strategies that do not simply select the appropriate sensory neurons, but also weigh and pool their outputs effectively. Consider a sensory representation consisting of only three neurons with responses that are independent of each other. These neurons respond differently during a particular 2AFC task. One has stimulus-driven responses that are the same for the two test stimuli (e.g., opposite directions of motion for a coarse-discrimination task), equivalent to d’=0. Another has responses that differ moderately for the two stimuli, equivalent to d’=1. The third has responses that differ more strongly for the two stimuli, equivalent to d’=2. Basing the decision on just one unit will of course yield perceptual sensitivity that is equivalent to the sensitivity of the given unit, ranging from completely insensitive (d’=0) to highly sensitive (d’=2). However, even higher sensitivity can be obtained using a simple additive readout scheme that takes a weighted sum of the outputs of the two sensitive units. In general, using additive, pooling readout of independent units, discrimination threshold is minimized when the relative strengths of the weights equal the relative sensitivities of the corresponding units. This idea can be easily extended to more than two neurons, following basic principles of linear discriminant analysis and other approaches (Duda & Hart, 1972; Pouget et al., 2003).

Some forms of perceptual learning are thought to reflect experience-dependent calibration of these kinds of task-specific readout strategies (Law & Gold, 2009b). One proposed mechanisms involves changes in weights that result in an increasingly selective readout of the most sensitive and informative sensory neurons to form the decision variable (Chung, Levi & Tjan, 2005; Dosher & Lu, 1998; Dosher & Lu, 1999; Gold, Bennett & Sekuler, 1999; Gold, Sekuler & Bennett, 2004; Jacobs, 2009; Law & Gold, 2009b; Li, Levi & Klein, 2004; Petrov et al., 2005). Correlates of these kinds of changes in readout have been identified in the parietal cortex of monkeys learning a coarse motion discrimination task (Law & Gold, 2008). In principle, similar mechanisms might also underlie some forms of selective attention, which can improve perceptual sensitivity by increasing the reliance of the perceptual decision on the most informative neurons for the given task (Ahissar & Hochstein, 1993; Dosher & Lu, 1999; Ito, Westheimer & Gilbert, 1998; Maunsell & Treue, 2006; Sasaki & Uka, 2009; Yu, Klein & Levi, 2004).

However, more work is needed to understand the relationship between readout and perceptual sensitivity. One open question is the nature of the neural code that both carries information about the stimulus in the sensory representation and is accessible to the readout mechanisms. Increasingly sophisticated computational techniques are being used to quantify the information content of a sensory population with respect to particular sets of stimuli (Latham & Nirenberg, 2005; Schneidman et al., 2003). In principle, these techniques can take into account different properties of individual neurons, such as the number or patterns of spikes, and of the population, such as synchrony and other forms of correlation, to establish benchmarks for the level of perceptual sensitivity that could be expected from such a representation (Jacobs et al., 2009). However, an important consideration is how the brain is able to use those signals to form the decision variable. For example, a current topic of debate is if and how the readout takes into account interneuronal correlations that can limit the information content of the sensory representation (Bair, Zohary & Newsome, 2001; Chen et al., 2006; Chen et al., 2008; Mazurek & Shadlen, 2002; Zohary, Shadlen & Newsome, 1994). Whether the readout scheme takes into account such correlations (a “faithful” decoder) or instead treats the sensory population as independent despite the presence of correlations (an “unfaithful” decoder) can have substantial effects on the resulting performance (Averbeck, Latham & Pouget, 2006; Jazayeri & Movshon, 2006; Latham & Nirenberg, 2005; Sompolinsky, Yoon, Kang & Shamir, 2001). The correlation structure within the sensory representation might also itself change with experience, which depending on the readout might or might not have an effect on behavior (Bejjanki, Beck, Lu & Pouget, 2011; Gu et al., 2011).

A second open question is how task-specific readout is learned. Learning schemes based on reinforcement-based rules and Hebbian mechanisms of synaptic plasticity have been proposed that can, in principle, produce effective decision variables for particular tasks based on past experience, including possibly taking advantage of the particular correlation structure in the sensory representation (Gutig, Aharonov, Rotter & Sompolinsky, 2003; Law & Gold, 2009a; Petrov et al., 2005). However, neural substrates of these learning processes have not yet been identified in the context of perceptual readout. Moreover, readout in the brain undoubtedly operates under more complex constraints than are captured in these models, including metabolic limits, response nonlinearities, availability of cellular and molecular mechanisms of plasticity, and uncertainty about how past experiences can inform future decisions (Britten & Heuer, 1999; Carandini & Heeger, 1994; Carandini, Heeger & Movshon, 1997; Koch et al., 2004; Kouh & Poggio, 2008; Law & Gold, 2009a; Miller & Troyer, 2002; Nassar, Wilson, Heasly & Gold, 2010; Petrov et al., 2005; Purushothaman & Bradley, 2005; Rust, Schwartz, Movshon & Simoncelli, 2005; Yu, Giese & Poggio, 2002). Thus, although examples like the readout of MT activity associated with the coarse and fine direction-discrimination tasks are at least consistent with linear weight profiles that maximize discriminability, it is not yet known if they represent general principles of readout optimization or just approximations operating under a more complex set of factors that constrain how readout is established (Hol & Treue, 2001; Jazayeri & Movshon, 2007a; Law & Gold, 2009a; Purushothaman & Bradley, 2005; Regan & Beverley, 1985).

A third open question is whether or not the readout scheme itself adds noise to the decision process (Shadlen et al., 1996). Along with the role of interneuronal correlations, this issue is of central importance to understanding why, given the high sensitivity of individual sensory neurons and the brain’s presumed access to many such neurons, subjects are not even more sensitive than they are. Studies that examine how decision computations can be implemented by more biologically plausible mechanisms will hopefully lead to a greater understanding of how those mechanisms can both enhance and limit perceptual sensitivity (Bogacz & Gurney, 2006; Grossberg & Pilly, 2008; Wong & Wang, 2006).

3.2. Effects on the slope of the accuracy function

The slope of the psychometric function describing performance accuracy versus response strength is a measure of the reliability of the subject’s performance, particularly with respect to the measured discrimination threshold. A shallow function implies that performance is similar across a wide range of stimulus values and thus measures of threshold are unreliable. In contrast, a steep function implies a more precisely defined interval of stimulus values that correspond to threshold.

Among the first attempts to interpret psychometric slope in terms of the underlying brain mechanisms focused on problems of contrast detection. In principle, an ideal observer with complete knowledge of all relevant stimulus parameters, including the time, location, magnitude, and duration of presentation, should have sensitivity (measured as d’, computed from performance) on a contrast-detection task that increases linearly as a function of stimulus contrast. However, d’ measured from human performance tends not to follow this ideal scenario but rather to increase with stimulus strength (in this case contrast, or c) raised to a power greater than one (often around two); i.e., d’ ⧜ c^b, where b > 1 (Pelli, 1985). This power-law nonlinearity can be readily measured as the slope of a cumulative Weibull function, motivating its widespread use for describing psychophysical data (Quick, 1974; Pelli, 1987).

An early interpretation of the power-law relationship between d’ and contrast, and thus of the slope of the cumulative Weibull psychometric function, focused on the representation, not readout, of sensory signals. In particular, this relationship was interpreted as the “non-linear transduction” of incoming visual information into its neural representation (Foley & Legge, 1981; Nachmias & Sansbury, 1974; Pelli, 1985; Tanner, 1961). Readout of these signals to form the decision variable was thought to involve probability summation. According to this scheme, the detection of a signal occurs when it is detected by one of a population of independent channels (i.e., neural populations) in the brain (Graham, 1985). Assuming that such channels are homogenous and detect only signals, not noise (the “high-threshold” assumption), the cumulative Weibull is the only psychometric function for which changes in the number of contributing channels affects only discrimination threshold and not slope (Green & Luce, 1975). Thus, psychometric slopes that were quantified using this function were thought to represent the non-linear relationship between signal strength and the signal-to-noise ratio of its sensory representation.

However, measured psychometric functions can be inconsistent with the assumptions that helped to motivate the use of the cumulative Weibull function. For example, under the high-threshold assumption, false alarms on a yes/no detection task (i.e., the subject indicates “yes” when no signal was presented) result only from guessing. In principle, this “guess rate” should not influence estimates of detection threshold. In practice, however, detection thresholds on a variety of tasks are affected by the guess rate (Green & Swets, 1966; Swets, 1961). Moreover, the strong assumption of homogeneity for all channels has been discredited by the observation of different psychometric slopes for different tasks and different subjects (Nachmias, 1981).

These new perspectives helped to motivate a reinterpretation of the slope of the cumulative Weibull and other psychometric functions, taking into account both the sensory representation and its readout (Kontsevich & Tyler, 1999; Pelli, 1985; Tanner, 1961; Tyler & Chen, 2000). This reinterpretation hinged on the idea that a readout based on probability summation can itself affect psychometric slope, under the assumption that not all contributing channels are equally informative. In general, increasing the number of channels that provide only noise, not signal, to the decision variable will tend to increase psychometric slope for both yes-no detection and 2AFC discrimination tasks. This phenomenon has been interpreted in terms of either uncertainty about or lack of attention to the appropriate signal-driven channels, both of which can be thought of as a form of readout (Pelli, 1985; Tyler & Chen, 2000).

These ideas are also related to readout-based theories of perceptual learning. To improve perceptual sensitivity, changes in readout typically increase the contribution of informative sensory neurons and decrease the contribution of uninformative neurons to the decision variable (Dosher & Lu, 1999; Jacobs, 2009; Law & Gold, 2009a). Assuming that the readout involves a form of probability summation implies, in turn, that improvements in perceptual sensitivity should be accompanied by changes in psychometric slope. More generally, a range of nonlinear pooling mechanisms that, like probability summation and other forms of “lower-envelope” schemes, base the decision on only one or a small number of separate sensory channels, can lead to similar relationships between psychometric threshold and slope (Fig. 4B) (Gold, Law, Connolly & Bennur, 2010; Kouh & Poggio, 2008; Purushothaman & Bradley, 2005; Yu et al., 2002).

Consistent with this idea, learning-induced decreases in discrimination threshold on a coarse direction-discrimination task were found to be accompanied by slight decreases in the slope of the psychometric function describing performance accuracy as a function of signal strength (Gold et al., 2010). These psychophysical changes corresponded to changes in how sensory information represented in area MT was read out to form the decision variable represented in area LIP, but no changes in stimulus-driven responses in MT (Law & Gold, 2008). The changes in slope were thus interpreted in terms of changes in a linear weighting function from the sensory representation to the decision variable, but pooled via a static, power-law non-linearity.

These results suggest a strong relationship between non-linear pooling mechanisms in the brain and psychometric slope. In general, input-output non-linearities can result from variety of mechanisms, including noise in the value of the membrane potential that affects spike generation in individual neurons, shunting inhibition to produce a form of divisive normalization, and interneuronal correlations that rely on signal strength (Anderson, Lampl, Gillespie & Ferster, 2000; Heeger, 1993; de la Rocha, Doiron, Shea-Brown, Josic & Reyes, 2007; Miller & Troyer, 2002; Shamir & Sompolinsky, 2004). More work is needed to determine how these mechanisms contribute to perceptual performance.

3.3. Effects on time dependence

The dependence of perceptual sensitivity on viewing duration is well established. Bloch’s law states that for relatively short viewing durations, visual sensitivity depends on the total energy content of the stimulus; i.e., the product of luminance and duration (Bloch, 1885). Psychophysically, this law holds on a variety of visual detection and discrimination tasks for up to several hundred milliseconds (Kahneman & Norman, 1964). Electrophysiological measurements from early in the visual pathway, including the retina, optic fibers, and primary visual cortex, show a similar relationship between time, intensity, and neuronal responses, implying that at least for these relatively short stimulus durations, the effects of duration on perceptual performance reflects properties of the sensory representation (Duysens, Gulyás & Maes, 1991; Scharnowski, Hermens & Herzog, 2007).

For longer durations, the relationship between duration and perceptual sensitivity probably more strongly reflects readout mechanisms. Beyond a few hundred milliseconds, Bloch’s law can either be maintained, as for the detection of low-frequency gratings, or break down, as for the detection of high-frequency gratings. These effects have been accounted for using decision models that assume that information from the brain’s sensory representation is interpreted over time via either a process of probability summation or temporal accumulation (Smith, 1998; Watson, 1979).

Decision models based on an accumulation of incoming sensory information over time have come to predominate the literature of perceptual decision-making. These models come in many forms, including race models that include multiple accumulators that compete to support the alternatives under consideration and random-walk or diffusion models that describe the process of accumulating evidence for two alternatives in terms of the drifting, noisy movements of a subatomic particle (Smith & Ratcliff, 2004). The accumulate-to-bound models described above are versions of these models in which the decision rule is to commit to a decision when a predefined amount of evidence has been accumulated. Thus, two key components of these models relate psychometric performance to viewing time: the temporal dynamics of the accumulation process, and the choice of bound height.

Certain sequential-sampling models, such as the drift-diffusion model (DDM), assume that the process of temporal accumulation is equivalent to perfect integration (Ratcliff & Rouder, 1998; Shadlen et al., 2006). That is, the arrival time of any piece of incoming information does not affect its ultimate contribution to the accumulated decision variable. Accordingly, increasing the stimulus duration has predictable effects on perceptual sensitivity. For 2AFC tasks, discrimination threshold improve proportional to the square root of stimulus duration, as has been found for monkeys performing the coarse direction-discrimination task (Gold & Shadlen, 2000; Gold & Shadlen, 2003; Kiani et al., 2008).

Other models with more complex processes of temporal accumulation have been proposed that can have more complex effects on psychophysical performance. For example, a leaky integrator, in which newly arrived information has a stronger effect on the decision than older information, can account for the dependence of discrimination threshold on viewing duration for certain visual discrimination tasks (Fig. 4C) (Usher & McClelland, 2001). Recent work has begun to examine models with more general temporal dynamics, including drift rates that can vary as arbitrary functions of time (Eckhoff, Holmes, Law, Connolly & Gold, 2008). For these cases, changes in stimulus duration could have substantial effects on psychometric sensitivity and possibly the upper asymptote of the psychometric function (lapse rate), which might fall well short of perfect accuracy for very short durations. Some tasks even appear not to depend on temporal accumulation in the readout process at all, with performance accuracy showing little dependence on stimulus durations beyond what is needed to activate the sensory detectors (Ludwig et al., 2005; Uchida et al., 2006).

The choice of bound height in accumulate-to-bound decision processes, which is a form of rule applied to the decision variable, can also affect the psychometric function. The bound height can govern the trade-off between speed and accuracy on RT tasks (Bogacz, Brown, Moehlis, Holmes & Cohen, 2006; Gold & Shadlen, 2007; Link, 1992; Smith & Ratcliff, 2004; Wickelgren, 1977). A low bound implies that the decision is based on little accumulated evidence, resulting in low accuracy but fast decisions. A high bound implies higher accuracy but longer decision times. Thus, according to this framework the interpretation of psychometric threshold requires knowledge of the bound height, because otherwise it is impossible to distinguish inherent sensitivity from the choice of speed-accuracy trade-off. For this reason, it is useful to measure and analyze both choice and RT data, often by fitting models that can distinguish the effects of the accumulated decision variable and the choice of bound height on performance (Palmer et al., 2005; Voss, Rothermund & Voss, 2004).

The idea of a decision bound that governs a trade-off between speed and accuracy might also extend to non-RT tasks. In these cases, the experimenter, not the subject, determines stimulus viewing duration but the subject nonetheless places a bound on the amount of accumulated evidence used to form the decision, ignoring subsequently presented information (Kiani et al., 2008). The implication of this idea is that even for non-RT tasks, particularly those that use stimulus-presentation durations that are longer than the typical RT, there is an underlying trade-off between speed and accuracy that might be governed by a diffusion-to-bound-like process and should be taken into account when interpreting the psychometric function.

Like other components of the psychometric function, its dependence on viewing time can be shaped by experience in a manner that suggests a flexible readout scheme. For example, improved performance on certain tasks is thought to involve the increased efficiency of a leaky accumulator (Brown & Heathcote, 2005; Pietsch & Vickers, 1997; Usher & McClelland, 2001). For RT tasks, learning is also likely to involve changes in the speed-accuracy trade-off, which must thus be distinguished from changes to the underlying decision variable (Liu & Watanabe, 2011).

3.4. Effects on lapse rate

For well-trained psychophysical subjects, lapses are thought to reflect transient, non-perceptual sources of error in performance, including temporary inattentiveness, distraction, and “finger slips.” As such, they are typically treated computationally as a separate process than the one that governs perceptual sensitivity (albeit one that must be estimated appropriately to allow for accurate estimates of other properties of the psychometric function, particularly its slope (Wichmann & Hill, 2001)). For example, the commonly used Abbott’s formulation accounts for lapses by re-scaling the entire psychometric function to match the measured upper asymptote (Finney, 1947). Accordingly, the sensory threshold is defined not as simply the stimulus value corresponding to a particular level of measured performance accuracy, but rather the level that is expected assuming no lapses.

For more naïve subjects, however, lapses might represent an incompletely or inappropriately formed decision process (Fig. 4A). Our lab recently trained monkeys to perform a coarse direction-discrimination task (Law & Gold, 2008). In their first training sessions, lapse rates and perceptual thresholds were relatively high, both measured using a psychometric function with Abbott’s formulation. As training progressed, both improved steadily, but the improvements in lapse rate occurred more rapidly than the improvements in perceptual threshold. Despite these apparently different time courses, both learning trends were accounted for by a single model that involved changes in readout of a stable sensory representation (Law & Gold, 2009a).

More specifically, the model assumed that the sensory representation consisted of neurons with noisy, MT-like direction-tuned responses. Importantly, these simulated neurons differed in terms of their sensitivity to the motion stimulus but maintained the same response properties throughout learning. Sensitive neurons had responses that differed considerably under the two direction conditions (e.g., leftward versus rightward motion) and therefore provided useful evidence for the perceptual decision. In contrast, insensitive neurons had responses that were not useful for distinguishing between the two motion directions. The model used a linear, additive readout scheme in which the outputs of the sensory neurons were scaled by individual weights and then summed to form the decision variable. Learning in the model was implemented as changes in the weights, driven by reinforcement-learning signals that were based on the difference between predicted reward, computed from the value of the decision variable, and actual (simulated) reward that was given for correct choices and withheld for errors (Sutton & Barto, 1998; Williams, 1992)

Initially, random weights provided a decision variable that did not distinguish between the two alternatives and therefore led to errors even for simulated high-coherence stimuli; i.e., a high lapse rate. Early in simulated training, appropriate direction-tuned neurons became weighted more heavily, eliminating lapses and representing a form of associative learning. Over time, stronger weights for sensitive neurons and weaker weights for insensitive neurons led to an increasingly sensitivity decision variable and lower discrimination threshold, representing a form of perceptual learning. These simulation results demonstrate that training-induced improvements in both lapse rate and discrimination threshold can, at least in principle, arise from a common neural mechanism that is based on improved readout of the sensory representation to form the decision variable.

The relationship between mechanisms of perceptual, associative, and reinforcement learning, and their effects on lapse rate and discrimination threshold, merit further study. An obvious target of study is a network of brain regions including midbrain dopamine neurons, which can encode the kind of reward prediction error used in the model described above, and the striatum and prefrontal cortex, which are primary targets of the dopaminergic projections and can reflect associative learning (Ding & Gold, 2010; Nomoto, Schultz, Watanabe & Sakagami, 2010; Pasupathy & Miller, 2005; Schultz, Dayan & Montague, 1997; Williams & Eskandar, 2006). It remains to be seen if and how these circuits influence the readout of sensory information used to form decision variables on perceptual tasks.

3.5. Effects on choices biases

A choice bias on a 2AFC task represents a tendency to choose one alternative versus the other, independent of the sensory evidence. Such biases are common, even when they are maladaptive and decrease rewarding outcomes for tasks in which the two alternatives are a priori equally probable and otherwise equally valuable to the subject (Green & Swets, 1966; Klein, 2001). Choice biases can also be adaptive, in response to asymmetric frequencies or values of the alternatives (Carpenter & Williams, 1995; Edwards, 1965; Feng, Holmes, Rorie & Newsome, 2009; Green & Swets, 1966; Hanks, Mazurek, Kiani, Hopp & Shadlen, 2011; Link & Heath, 1975; Mulder, Wagenmakers, Ratcliff, Boekel & Forstmann, 2012; Teichert & Ferrera, 2010; Voss et al., 2004). In both cases, biases must be treated appropriately by the psychometric function to ensure effective interpretation of its other features, including discrimination threshold.

Choice biases on a 2AFC task that are consistent across an entire experimental session often have a straightforward interpretation in terms of the decision rule. The decision variable can often be thought of as a difference in neural signals representing the two alternatives, reflecting the logarithm of their relative likelihoods (Gold & Shadlen, 2001). For an unbiased decision variable, this quantity will be symmetric about zero, with increasingly positive values indicating increasingly strong support for one alternative and increasingly negative values indicating increasingly strong support for the other alternative. According to Signal detection theory, a biased observer would assume a non-zero decision criterion, such that the point of subjective equality corresponds to weak evidence for one of the two choices (Green & Swets, 1966; Macmillan & Creelman, 2004). According to accumulate-to-bound models, a biased observer would set decision bounds corresponding to the two alternatives at different distances from the starting value of the decision variable (or, equivalently, shift the starting value towards one of the bounds), such that less evidence is needed to elicit one choice versus the other (Carpenter & Williams, 1995; Ratcliff & McKoon, 2008).

Other forms of bias can be more difficult to diagnose. For example, one common form of bias arises from sequential effects, in which choices reflect the recent history of choices or rewards. For these cases, choices can be balanced over an entire session, resulting in an unshifted psychometric choice function. However, choices are unbalanced over shorter time scales, which can be seen by identifying particular patterns of choices or other analyses of local choice structure (Cho et al., 2002; Gold, Law, Connolly & Bennur, 2008; Laming, 1968; Laming, 1979). Bias can also depend on the type and amount of uncertainty the subject has about the sensory evidence, which can lead to dynamics effects on the decision variable that change as more evidence is accumulated (Hanks et al., 2011). However, like overall choice biases, both choice- and time-dependent biases can reflect offsets to the decision variable, suggesting similar neural mechanisms.

An offset to the decision variable can reflect asymmetries in the sensory representation, its readout, or both. Asymmetries in the sensory representation might involve intrinsic differences in the size or tuning properties of the pools of neurons representing different, task-relevant stimulus features. In principle, these differences at the level of sensory cortical areas could arise from plasticity driven by prior sensory experience, particularly during development; perceptual training, which can affect distributions of tuning properties primary auditory, somatosensory, and, to a lesser extent, visual cortex; pathological events, including selective damage or artificial disruption at any level of the ascending sensory pathway; normal age-related changes, such as auditory hair-cell degeneration that tends to follow a high- to low-frequency gradient; and top-down modulation of sensory-driven activity by higher cortical areas, possibly reflecting feature-based or spatial attention or some forms of learning (Bovo, Ciorba & Martini, 2011; Ditterich, Mazurek & Shadlen, 2003; Gilbert et al., 2001; Maunsell & Treue, 2006; Salzman et al., 1990; de Villers-Sidani & Merzenich, 2011; Wandell & Smirnakis, 2009). For two-interval tasks, this asymmetry might also arise from time-order effects, such as interactions between sequentially presented stimuli or memory limitations, that can differentially affect the neural representations of the two stimuli at the time of the decision (Green & Swets, 1966; Macmillan & Creelman, 2004; Wickelgren, 1968; Yeshurun et al., 2008).

An asymmetry in the readout scheme might reflect an initial value that is added to balanced sensory information, akin to a shift in the decision criterion. Neural correlates of this kind of offset have been identified in the neural activity of several brain areas involved in saccadic decision-making, including area LIP, superior colliculus, and caudate (Basso & Wurtz, 1998; Ding & Gold, 2010; Dorris & Munoz, 1998; Hanks et al., 2011; Shadlen & Newsome, 2001). Similar effects, corresponding to offsets to the value of the decision variable, could arise from unbalanced weights associated with the pools of sensory neurons representing the two alternatives (Fig. 4D). Another possibility is differences in the temporal accumulation profiles between competing race-like processes, such as if one accumulator is less leaky than the other.

Readout mechanisms might also play key roles in minimizing inappropriate choice biases by calibrating the symmetry of the decision variable with respect to the alternatives. For example, a recent study showed that monkeys learning a coarse direction-discrimination task exhibited choice biases early in training, even though the task was balanced in terms of the frequency and values of the two alternatives (Gold et al., 2008). Analyzing the behavioral data using an accumulation-to-bound framework, these biases were consistent with an initial offset to the decision variable that depended on the recent history of choices. The magnitude of this offset, relative to stimulus-driven components of the decision variable, declined with training. These improvements paralleled improvements in lapse rate and discrimination threshold, which also could be accounted for by refinement of the readout scheme (Law & Gold, 2008; Law & Gold, 2009a). More generally, the brain might use various asymmetries in the readout scheme to compensate for asymmetries in the sensory representation and produce relatively unbiased choices, when appropriate.

4. Methods to distinguish representation from readout

Given that representation and readout can both have substantial effects on the psychometric function, an obvious question is if – and if so, under what conditions – their effects can be distinguished from one another. Here we describe the strengths and limitations of several psychophysical approaches that have been used to infer the contributions of representation and readout to behavior. We then summarize recent work that has begun to identify these mechanisms in the brain.

4.1. Psychophysical approaches

Many psychophysical studies of perceptual learning have been used to infer contributions of the sensory representation to perceptual sensitivity. These inferences have been based largely on the finding that under some (but not all) conditions, perceptual learning is specific to the stimulus configuration used during training (Ahissar & Hochstein, 1997; Fahle, 2005; Jeter, Dosher, Liu & Lu, 2010; Jeter, Dosher, Petrov & Lu, 2009; Zhang et al., 2010; for counter-examples, see Ahissar & Hochstein, 1997; Jeter et al., 2010; Jeter et al., 2009; Liu & Weinshall, 2000; Zhang et al., 2010). That is, training with a particular set of stimuli can lead to improved sensitivity that does not transfer across changes in properties of those stimuli, such as their location in the visual field. This specificity, which helps to distinguish perceptual learning from changes in task strategy and other forms of learning, has been used to argue that the underlying changes likely occur in early sensory areas where the specificity of neuronal tuning is comparable to the specificity of learning (Berardi & Fiorentini, 1987; Karni & Sagi, 1991; Poggio, Fahle & Edelman, 1992; Schoups, Vogels & Orban, 1995). However, this interpretation has been brought into question, because the specificity of learning can, in principle, also arise from changes in higher-order mechanisms like attention or readout (Law & Gold, 2009a; Li, Piech & Gilbert, 2004; Mollon & Danilova, 1996). Thus, several new psychophysical approaches have been developed to distinguish the effects of representation and readout on perceptual sensitivity.

One approach involves manipulations of external (stimulus) noise to infer properties of the underlying perceptual process. According to Signal Detection Theory, perceptual performance is limited by the presence of noise in the internal decision variable. These methods define various internal sources of noise in the brain, then use external noise to probe how adjusting these noise sources affects behavior (Lu & Dosher, 1999; Lu & Dosher, 2008; Mumford & Schelbe, 1968; Pelli & Farell, 1999). These effects are often measured in terms of the relationship between the level of external noise and perceptual threshold. This relationship tends to have a fairly stereotyped form. Low levels of external noise have little effect on discrimination threshold, which under those conditions is limited primarily by internal noise. In contrast, higher levels of external noise can substantially affect perceptual sensitivity, causing thresholds to increase roughly linearly as a function of increasing external noise.

Several studies examined how perceptual training can affect this relationship between perceptual sensitivity and external noise levels (Chung et al., 2005; Dosher & Lu, 1998; Dosher & Lu, 1999; Gold et al., 1999; Gold et al., 2004; Li et al., 2004). A consistent finding has been improvements in threshold across all levels of external noise. These effects have been interpreted as a combination of an improved signal-to-noise ratio of the internal decision variable, which accounts for lower thresholds at low external noise levels, and improved exclusion of external noise, which accounts for lower thresholds at high external noise levels. This combination of effects can be thought of as an improvement in the efficiency with which an internal template filters the incoming sensory data. One possible implementation of this improvement in efficiency is changes in readout that include an increasingly selective weighing of the most task-relevant sensory inputs to form the perceptual decision (Dosher & Lu, 1998; Dosher & Lu, 1999; Jacobs, 2009; Law & Gold, 2009a; Li et al., 2004; Saarinen, 1996).

Several other techniques have relied less on assumptions about different sources of internal noise in perceptual circuits and more on knowledge of the relevant tuning properties of certain populations of neurons. For example, direction-tuned neurons in area MT have roughly Gaussian-shaped direction-tuning curves with widths (at half-height) of approximately 40° and best values that cover the full 360° of motion (Albright, 1984; Law & Gold, 2008; Snowden, Treue & Andersen, 1992). As described above, the activity from this population of neurons should, in principle, be read out differently to optimize performance on the coarse- and fine-discrimination tasks. For the coarse task, the most-informative neurons are those tuned to the test directions. For the fine task, the most-informative neurons are those tuned slightly away from – and therefore respond most differently to – the two test directions. Two different psychophysical methods have been used to infer these readout schemes for the two different tasks.

One method was based on an adaptation paradigm in which an adapting stimulus was presented before each test stimulus (Hol & Treue, 2001). The adapting stimulus was designed to reduce the responsiveness of neurons tuned to particular pairs of directions, either in the test directions or offset from the test directions by fixed amounts. The associated increases in discrimination threshold were used to infer which neurons contributed most to the decision.

The other method used subthreshold motion added to the test stimulus (Jazayeri & Movshon, 2007a). The subthreshold motion was designed to increase the responsiveness of neurons tuned to particular directions. The associated choice biases were used to infer which neurons contributed most to the decision. The results from both studies were consistent with the ideas presented above, indicating different patterns of readout for the two tasks.

A final set of psychophysical approaches that might have implications for readout are tasks involving double judgments (Klein, 1985; Nachmias & Weber, 1975; Olzak & Wickens, 1999). For these tasks, the subject is asked to make two judgments about the same stimulus or stimuli presented on a single trial, for example whether or not (or in which interval) a stimulus was detected and then a judgment about the identity of the stimulus. Results from these studies have been interpreted in terms of both interactions between sensory signals relevant to the two judgments and complex decision rules (Klein, 1985). More recently, results from double-judgment tasks have been interpreted in terms of readout. For example, for a task that involved a fine direction discrimination followed by occasional estimates of motion direction, the direction estimates were consistently biased away from the actual direction, a form of perceptual illusion. These biases were interpreted in terms of a readout scheme that was formed appropriately for the more common fine-discrimination judgment and therefore not optimally for estimation (Jazayeri & Movshon, 2007b).

These kinds of methods are likely to be beneficial for understanding readout profiles for other tasks, as well. However, a limitation of these approaches is that they can only measure readout with respect to particular stimulus features that can be manipulated directly; e.g., how readout on the direction-discrimination tasks depends on motion direction. Readout is also likely to selectively target subpopulations of neurons with similar feature tuning but different sensitivities, which are not identifiable using these approaches but must instead be examined directly in the brain.

4.2. Physiological approaches

Ultimately, distinguishing the relative contributions of the sensory representation and its readout to psychophysical performance will require a better understanding of their neural implementations. In this section, we briefly summarize the strengths and limitations of some of the approaches currently used by researchers to identify and characterize these implementations.

For the sensory representation, identification of the relevant neurons typically starts with anatomical tracings across successive stages from the periphery and recordings of neural responses when relevant stimuli are presented to the subject. However, neurons that respond selectively to a particular stimulus feature are not guaranteed to contribute to perceptual tasks that target that feature. Moreover, once the relevant neurons have been identified, the nature of their collective responses that provide input to the perceptual-decision process must also be understood. Therefore, additional experimental approaches that move beyond a characterization of stimulus selectivity must be used to identify and understand the sensory representation.

Several techniques have been used to identify neurons with activity that plays a causal role in the perceptual-decision process. One commonly used technique, known as choice probability, relates trial-by-trial variability in the activity of single neurons and the subject’s choices, which can be interpreted in terms of how the activity of those neurons are read out to form the perceptual decision (Britten, Newsome, Shadlen, Celebrini & Movshon, 1996; Dodd, Krug, Cumming & Parker, 2001; Heuer & Britten, 2004; Purushothaman & Bradley, 2005; Uka & DeAngelis, 2004). However, choice probability also can be highly sensitive to interneuronal correlations in the sensory representation and top-down signals from decision-making circuits, making it difficult to interpret exclusively in terms of a sensory neuron’s causal influence on behavior (Nienborg & Cumming, 2009; Shadlen et al., 1996). Other approaches include inactivation or electrical microstimulation to perturb focal regions of the sensory representation and test for effects on behavior (Afraz, Kiani & Esteky, 2006; Celebrini & Newsome, 1995; Newsome & Pare, 1988; Nichols & Newsome, 2002; Romo, Hernandez, Zainos & Salinas, 1998; Salzman et al., 1990; Salzman, Murasugi, Britten & Newsome, 1992b; Uka & DeAngelis, 2006). However, these approaches often suffer from imprecise targeting, a problem that will hopefully be overcome by emerging optogenetic techniques to precisely target particular cell types and neurons with particular connectivity patterns (e.g., those that project directly to higher-order decision circuits).

Understanding the neural code used by a sensory population to solve a particular perceptual task requires recording neural activity in a subject performing the task. Some advances in our understanding of this code will require better measurements, such as using particular multi-electrode recording techniques to isolate the activity of single neurons when measuring inter-neuronal correlations (Ecker et al., 2010). Other advances will require a better conceptual understanding of how the brain reads out sensory signals, including whether the brain uses spike rates, spike timing, or other signals generated by the sensory representation as input to the readout process (Rieke, Warland, de Ruyter Van Steveninck & Bialek, 1999). A particular challenge will be to measure, analyze, and understand these properties only when they are relevant to a particular task (Berens, Ecker, Gerwinn, Tolias & Bethge, 2011; Mazurek & Shadlen, 2002). Using RT tasks has been a step in the right direction, allowing the subject to provide temporal bounds on when the perceptual decision process begins and ends (Luce, 1986). However, even within these bounds there can be uncertainty about the exact timing of the decision process, which in turn can lead to uncertainty about the relevance of sensory-driven responses measured during that time.

The identification and characterization of readout neurons is also a challenging problem. Two common approaches have been used. The first approach takes advantage of the roughly hierarchical organization of the sensory system to identify neurons whose complex stimulus selectivity represents the readout of the responses of neurons earlier in the pathway. For example, neurons in V1 have small receptive fields and are modulated by low-order features such as oriented bars (Hubel & Wiesel, 1968). Neurons in progressively further regions along the ventral stream of the monkey, including V2, V4, and IT, tend to have increasingly large receptive fields and selectivity for increasingly complex features (Bruce, Desimone & Gross, 1981; Desimone, Albright, Gross & Bruce, 1984; Gallant, Braun & Van Essen, 1993; Hegde & Van Essen, 2000; Kobatake & Tanaka, 1994; Pasupathy & Connor, 1999; Perrett, Rolls & Caan, 1982; Rust & Dicarlo, 2010; Tanaka, 1996). Neurons later in this pathway also tend to be affected more strongly by factors that affect perception of visual features, including attention and learning (Buffalo, Fries, Landman, Liang & Desimone, 2010; Erickson & Desimone, 1999; Erickson, Jagadeesh & Desimone, 2000; Mehta et al., 2000; Reynolds, Pasternak & Desimone, 2000). Thus, a better understanding of how this complex stimulus selectivity is generated along this pathway is likely to yield important insights into how the brain reads out sensory information for perception.

The second approach takes advantage of the fact that, for any psychophysical tasks, the perceptual decision must be transformed into a motor response. This approach searches for the earliest appearance of decision-related activity, working backwards along a motor, premotor, sensorimotor axis. This approach has led to extensive research on the frontal and parietal cortices for somatosensory, auditory and visual discrimination tasks. For example, correlates of an accumulate-to-bound process have been found in a series of interconnected brain regions in monkeys performing the coarse motion-discrimination task (Gold & Shadlen, 2007). Consistent with the task design, in which the monkeys indicate their direction decision with a saccadic eye movement to one of two visual targets, these brain regions lie in the oculomotor pathways contributing to the control of eye movements, including the lateral intraparietal area (LIP) and frontal eye field (FEF) in cortex, the superior colliculus, and the caudate nucleus of the basal ganglia (Ding & Gold, 2010; Ding & Gold, 2011; Horwitz & Newsome, 1999; Kim & Shadlen, 1999; Roitman & Shadlen, 2002). Similar decision-related signals have been found for other tasks and, using fMRI, EEG, and other non-invasive measurements of brain activity, in humans performing a variety of tasks (Heekeren, Marrett & Ungerleider, 2008; Hernández et al., 2010; Ratcliff, Hasegawa, Hasegawa, Smith & Segraves, 2007).

One ongoing challenge with this second approach is to disentangle mechanisms responsible for forming the perceptual decision with those responsible for preparing and executing the motor response. Under some conditions, such as when there is a direct, predictable mapping between the decision and the response, there might be strong overlap between decision and motor processing (Cisek, 2006; Gold & Shadlen, 2000; Gold & Shadlen, 2003). However, even under these conditions RTs undoubtedly include contributions from both decision processing and “nondecision” time including contributions from the motor system (Shadlen et al., 2006; Shankar et al., 2011). Ongoing work with novel task designs that help separate decision and motor processing is helping to address these issues and provide new insights into the relationship between formation of the perceptual decision and formation of the motor response (Bennur & Gold, 2011; Freedman & Assad, 2009; Freedman & Assad, 2011).

5. Conclusions

Signal Detection Theory has had a strong influence on the interpretation of psychophysical data by providing a quantitative framework for distinguishing sensory processing from non-sensory factors. Accordingly, this framework has allowed for direct comparisons of perceptual sensitivity and stimulus-driven responses of sensory neurons. However, “sensory processing” in the brain is complex, consisting of not just the representation of relevant stimulus information by sensory neurons, but also the interpretation, or read out, of that information to form the decision variable that guides behavior on perceptual tasks. This decision process must select, weigh, and combine information from across the population of relevant sensory neuron and over time, in a manner that takes into account both how sensory information is encoded and the task demands. In this article we reviewed recent findings that shed light on how the neural mechanisms that underlie this complex decision process can affect psychophysical performance.

Our general conclusion is that these decision processes can have substantial effects on all aspects of the psychometric function, including threshold, slope, time dependence, lapse rate, and choice biases. Many of these effects are evident in learning studies in which improvements in performance reflect refinements to the decision process, without accompanying changes to the sensory representation. Accordingly, the interpretation of the psychometric function in terms of the underlying brain mechanisms must take into account properties of both the sensory representation and its readout. These interpretations will benefit from a growing understanding of how and where in the brain these different processing stages are implemented.

Highlights.

Signal Detection Theory distinguishes between sensory processing and non-sensory decision rules in the brain.

Sensory processing is a complex process involving both the sensory representation and its readout to form the decision variable that guides behavior.

Many studies that examined the neural basis for the psychometric function focused on properties of the sensory representation.

This article reviews recent work characterizing properties of the readout process and how it can affect the psychometric function, particularly in the context of learning.

Abbreviation List

FEF

frontal eye field

LIP

lateral intraparietal area

MT

middle temporal area

ROC

receiver-operator characteristic

RT

response time

2AFC

two-alternative forced-choice