Graphical abstract
Keywords: P-glycoprotein, ADMET, In silico, Fingerprint, Machine learning methods, Association rule
Abstract
P-Glycoprotein (P-gp, ABCB1) plays a significant role in determining the ADMET properties of drugs and drug candidates. Substrates of P-gp are not only subject to multidrug resistance (MDR) in tumor therapy, they are also associated with poor pharmacokinetic profiles. In contrast, inhibitors of P-gp have been advocated as modulators of MDR. However, due to the polyspecificity of P-gp, knowledge on the molecular basis of ligand–transporter interaction is still poor, which renders the prediction of whether a compound is a P-gp substrate/non-substrate or an inhibitor/non-inhibitor quite challenging. In the present investigation, we used a set of fingerprints representing the presence/absence of various functional groups for machine learning based classification of a set of 484 substrates/non-substrates and a set of 1935 inhibitors/non-inhibitors. Best models were obtained using a combination of a wrapper subset evaluator (WSE) with random forest (RF), kappa nearest neighbor (kNN) and support vector machine (SVM), showing accuracies >70%. Best P-gp substrate models were further validated with three sets of external P-gp substrate sources, which include Drug Bank (n = 134), TP Search (n = 90) and a set compiled from literature (n = 76). Association rule analysis explores the various structural feature requirements for P-gp substrates and inhibitors.
1. Introduction
More than 600 ABC transporters are expressed in all living organisms, with 48 ABC genes having been reported in humans. Among these, ABCB1 (P-glycoprotein or P-gp) has been shown to effect the efflux of a large variety of xenobiotics out of cells using ATP hydrolysis as energy source.1–3 P-gp is characterized by a broad and polyspecific ligand recognition pattern, translocating structurally diverse molecules such as amino acids, xenobiotics (drugs/toxins), natural products (glycosides, alkaloids, etc.), lipids, steroids, across cellular membranes.4 This seems to be a genuine defense mechanism against toxins, which for example leads to multi-drug resistance (MDR) in tumor therapy.5–7 Thus, inhibitors of ABCB1 have been tested in clinical trials as potential resensitizers of drug resistant tumor cells. However, due to the inherent contribution to the ADMET (absorption, distribution, metabolism, excretion, and toxicity) properties of P-gp substrates, knowledge about the substrate/non-substrate properties of drug candidates is even more important.8–10 Thus, it has been urged by the FDA (food and drug administration) that every new molecular entity (NME) should be routinely checked whether it shows an interaction with P-glycoprotein or not.11–13
Thus, in the process of lead optimization, early identification of P-gp ligands, being either substrates or inhibitors, is of utmost importance to improve the ADMET profile of drug candidates. To support this, a considerable number of ligand- and structure-based computational models have been developed.14 These include QSAR studies,15 pharmacophore modeling,16,17 machine learning approaches18–20 and docking into homology models.21 However, due to the lack of high quality data, training and test sets are normally quite small, which limits the general applicability of the models derived.
In the present study, we developed classification models from a set of 484 substrates/non-substrate and a set of 1935 inhibitors/non-inhibitors using machine learning methods and a set of in-house generated functional-groups-based fingerprints. Subsequently, we have explored the possibility to trace back the importance of certain functional groups for substrate/inhibitor properties using the FP-growth algorithm.
2. Results and discussion
2.1. Classification models for substrates and non-substrates
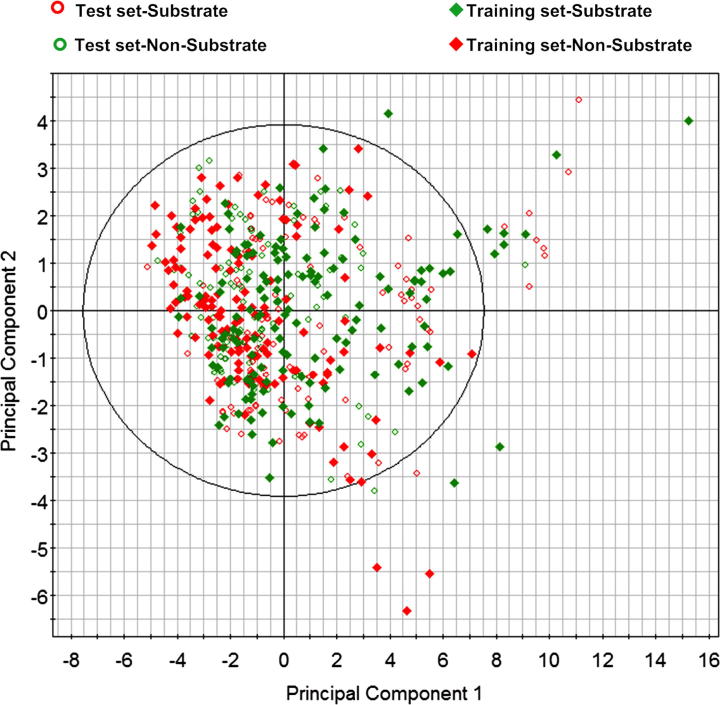
As described in the methods section, the data sets of substrates and inhibitors were separated into a training and a test set using the D-optimal onion design (DOOD). The number of compounds selected as training and test sets for substrate and inhibitor models is provided in Table 1. Initially, the data set was characterized by principal component analysis (PCA) using a set of physicochemical properties (a list of properties used for PCA is provided in Supplementary data T1). As outlined in the scores plot (Fig. 1), both data sets are evenly distributed in the chemical space. The first two principal components explain 75% of the variance in the data set. Interestingly, no distinct outlier or cluster was identified in the scores plot. Only a few compounds were slightly outside (right side of the score plot) from the main chemical space. An inspection of these compounds revealed that the majority of them are substrates taken from the Szakács data set, such as bryamycin (NSC170365) and actinomycin (NSC237671) (the chemical structure of selected outliers is provided in Supplementary data, Fig.1). In addition, the distribution of substrates and non-substrates in the data set was significantly different, for example, substrates spread throughout the score plot, whereas the majority of the non-substrates are located in the left side of the plot, where the predicted water solubility property (Log S) calculated with MOE22 dominates the region. This observation indicates that P-gp non-substrates are relatively polar compared to substrates. In addition to PCA characterization, log P distribution for substrates and non-substrates was performed. The results revealed that substrates have relatively high log P values (>5) compared to non-substrates (a distribution plot is provided in Supplementary data, Fig. 2).
Table 1.
Number of compounds in the training and test set for inhibitor and substrate models
| Models | Training set |
Test set |
Sum | ||
|---|---|---|---|---|---|
| P+a | P−b | P+a | P−b | ||
| Substrate | 142 | 140 | 101 | 101 | 484 |
| Inhibitor | 881 | 387 | 399 | 268 | 1935 |
P+: substrate or inhibitor.
P−: non-substrate or non-inhibitor.
Figure 1.
Scoring plot of the first two principal components for substrates and non-substrates in the training and test set.
Figure 2.
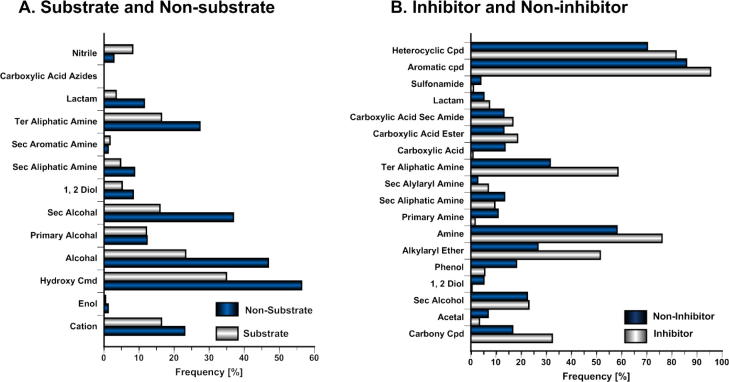
Frequency distribution of functional groups for substrate (A) and inhibitor (B) models. (For inhibitor frequency plot, the functional groups, which have frequency <5% are not shown for clarity).
Classification models for 484 substrates/non-substrates were built using a set of 13 bins, which were selected from WSE (wrapper subset evaluator) as implemented in the WEKA data mining software. A summary of the performance of the models is provided in Table 2. In general, the models developed with random forest and kappa nearest neighbor were reasonably good in predicting the test set (accuracy 67–70%), with random forest performing slightly better (MCC 0.41 vs 0.34 for kappa nearest neighbor; G-mean (0.66/0.70). Using the whole data set for establishing the model and performing a 10-fold cross validation slightly improves the validation parameters with an overall accuracy of 75%, an MCC of 0.49, and sensitivity and specificity of 74% and 76%, respectively. In the present study, we used standard (default) WEKA parameters for all methods, including the SVM method. From the SVM method, a polykernel, that is linear kernel was used; this polykernel performs better compared to the Gaussian kernel, which shows slightly poorer results compared to the linear kernel. In particular, prediction of inhibitors (accuracy = 47%) is lower than that of non-inhibitors (accuracy = 76%).
Table 2.
Accuracies of the models for substrates and non-substrate using supervised classifiers
| Data set | Methods | Confusion matrix |
Sensitivity | Specificity | G-mean | MCC | Accuracy | |||
|---|---|---|---|---|---|---|---|---|---|---|
| TP | FN | TN | FP | |||||||
| 10-Folda | kNN | 188 | 55 | 167 | 74 | 0.77 | 0.69 | 0.73 | 0.47 | 0.73 |
| SVM | 152 | 91 | 159 | 82 | 0.63 | 0.66 | 0.64 | 0.29 | 0.64 | |
| RF | 179 | 64 | 182 | 59 | 0.74 | 0.76 | 0.75 | 0.49 | 0.75 | |
| Test set | kNN | 75 | 26 | 60 | 41 | 0.74 | 0.59 | 0.66 | 0.34 | 0.67 |
| SVM | 67 | 43 | 57 | 44 | 0.61 | 0.56 | 0.59 | 0.17 | 0.59 | |
| RF | 73 | 28 | 69 | 32 | 0.72 | 0.68 | 0.70 | 0.41 | 0.70 | |
The bold letters indicate the best performing model.
Abbreviations: kNN, kappa nearest neighbor; SVM, support vector machine; RF, random forest; TP, true positive; FN, false negative; TN, true negative; FP, false positive; MCC, Matthews correlation coefficient.
Whole data set was used for 10-fold cross validation.
Despite having a validated model for classifying compounds into substrates and non-substrates, it would be very interesting to trace back which functional groups are prevalent in substrates and non-substrates. This information is of high value when it comes to designing in (e.g., preventing compounds from entering the brain) or designing out (anticancer agents, CNS active agents) substrate properties in a certain lead series. Figure 2A shows a frequency count of bins present in the final model. The main difference between substrates and non-substrates is observed in the presence of hydroxyl groups (secondary alcohols, in particular) and tertiary aliphatic amines. Based on this analysis, substrates show a lower probability of having hydroxyl groups in the molecule, than non-substrates. This observation fits well with the current view on P-gp substrates, which are of relatively hydrophobic nature, so that they are able to access the hydrophobic binding site via the membrane bilayer.23 Additionally, the data matrix was analyzed using an association rule algorithm such as FPGrowth. Although in total 26 rules could be identified, none of them was significant (data not shown). Therefore, we extended the analysis to the original fingerprints comprising 112 bins. This identified 386 rules, whereby 35% of the compounds (>35%) follow at least one of the following associations:
Rule 1 SUB = 1, Ether (123/243) → Aromatic compound (111/243)
Rule 2 SUB = 1, Amine (123/243) → Aromatic compound (115/234)
Rule 3 SUB = 1, Heterocyclic, ether (102/243) → Aromatic compound (96/243)
To exemplify rule 1, out of 243 substrates, 123 compounds bear an ether oxygen, with 111 compounds also having an aromatic group. However, as already mentioned before, these associations are by far too general to support designing in/designing out substrates properties.
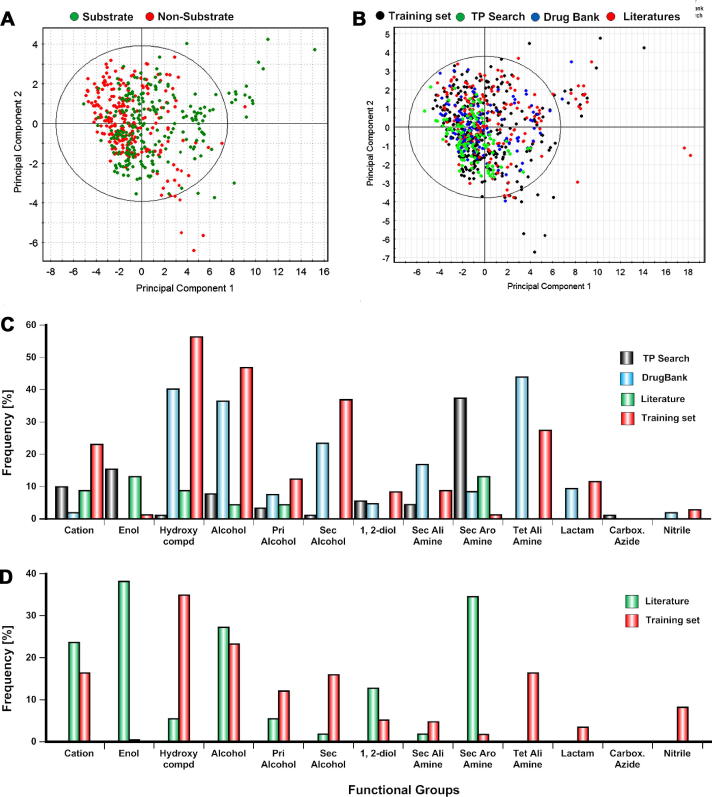
The models developed were further validated by applying them to known P-gp substrates/non-substrates extracted from publicly available data sources. For this, we considered three data sources: TP search (www.tp-search.jp), Drug Bank (www.drugbank.ca) and compounds taken from literature.18 Duplicates and overlapping compounds were removed from the respective data sets. Unfortunately, for TP search and drug bank only information on substrates was available. The overall prediction accuracy for substrates from TP search and Drug Bank was rather poor, with a correct classification rate (sensitivity) of 42% and 62% in TP search and drug bank, respectively (Table 3). For the literature compounds (n = 76) compiled by Zhi Wang et al.,18 the correct classification rate for substrates (51%) was quite similar (Table 3). However, the specificity of the model was slightly better (78%), leading to an overall accuracy of 59%. The main reason for this might be that the external compounds do not share a lot of substructures with the training set (Fig. 3C (substrate) and Fig. 3D (non-substrate)). This was further confirmed with applicability domain experiments using WSE bins with three different applicability domain methods, such as Euclidian distance, probability density and Ranges, using the Ambit Discovery tool (http://ambit.sourceforge.net). The results indicate that more than 40 compounds of the external dataset are outside of the applicability domain of the model, which in part explains the poor prediction of external compounds. Furthermore, as shown by a PCA plot generated with standard physicochemical properties (list provided in Supplementary data T1), the chemical space of substrates of the external sources was quite similar to that for non-substrates of the training set (Fig. 3A,B). A PCA plot using the WSE bins as descriptors shows an analogous picture and is provided in Supplementary data (Fig. 3).
Table 3.
Performance of the substrate prediction model for external test sets; A: TP search, B: Drug Bank, C: Wang et al.
| Data set | Compounds | Sensitivity |
Specificity |
Overall accuracy |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SVM | KNN | RF | SVM | KNN | RF | SVM | KNN | RF | ||
| Aa | 90 | 13 | 14 | 42 | — | — | — | — | — | — |
| Ba | 134 | 30 | 64 | 62 | — | — | — | — | — | — |
| C | 76 | 28 | 25 | 51 | 91 | 91 | 78 | 47 | 45 | 59 |
The bold letters indicate the best performing model.
Only substrates are available.
Figure 3.
Analysis of the external test sets: (a) scoring plot of the first two principal components, (b) scoring plot of the first two principal components for the external test sets (TP search, Drug Bank, literature compounds), (c) comparison of functional group frequency (bins) for substrates between different data source, (d) comparison of functional group frequency (bins) for non-substrates between different data sources.
2.2. Classification models for inhibitors and non-inhibitors
As described in the methods section, classification models for P-gp inhibitors and non-inhibitors were developed utilizing a set of 1935 compounds using 26 WSE bins (Table 4). In general, all obtained models were able to correctly predict more than 80% of the inhibitors with an overall prediction accuracy of >70% for the test set. However, the models generally suffer from high false-positive rates, which leads to poor performance with respect to correct prediction of inactive compounds. Among the three classification methods used, RF works significantly better than the other methods. The RF model correctly classified 334/399 inhibitors (sensitivity: 84%) and 168/268 non-inhibitors (specificity: 63%) from the test set, giving an overall accuracy and G-mean of 0.75 and 0.72, respectively. As shown in Figure 2B, there was a significant difference in the fingerprints of inhibitors and non-inhibitors. Phenols (18%), primary amines (11%) and carboxylic acids (14%) were quite prevalent in non-inhibitors compared to inhibitors. Moreover, tertiary aliphatic amine and alkylaryl ether groups were significantly more present in inhibitors (59% and 51%) compared to non-inhibitors (31% and 28%).
Table 4.
Accuracies of the models for inhibitor/non-inhibitor using supervised classifiers
| Models | Methods | Confusion matrix |
Sensitivity | Specificity | G-mean | MCC | Accuracy | |||
|---|---|---|---|---|---|---|---|---|---|---|
| TP | FN | TN | FP | |||||||
| 10-Folda | kNN | 1153 | 127 | 378 | 277 | 0.90 | 0.58 | 0.72 | 0.51 | 0.79 |
| SVM | 1153 | 127 | 307 | 348 | 0.90 | 0.47 | 0.65 | 0.42 | 0.75 | |
| RF | 1148 | 132 | 426 | 229 | 0.90 | 0.65 | 0.76 | 0.57 | 0.81 | |
| Test set | kNN | 345 | 54 | 142 | 126 | 0.86 | 0.53 | 0.68 | 0.42 | 0.73 |
| SVM | 345 | 54 | 129 | 139 | 0.86 | 0.48 | 0.65 | 0.38 | 0.71 | |
| RF | 334 | 65 | 168 | 100 | 0.84 | 0.63 | 0.72 | 0.48 | 0.75 | |
The bold letters indicate the best performing model.
Abbreviations: kNN, kappa nearest neighbor; SVM, support vector machine; RF, random forest; TP, true positive; FN, false negative; TN, true negative; FP, false positive; MCC, Matthews correlation coefficient.
Whole data set was used for 10-fold cross validation.
In addition to the classification models, association rule learning was performed with the WSE derived fingerprints and with the full-length fingerprints (provided as Supplementary data). Using WSE-based bins (n = 26), ten rules were found, whereby three were found to be non redundant (i.e., tertiary amine and secondary amine in the same rule was considered as redundant).
Rule 4 INH = 1, Tertiary amine (749/1280) → Aromatic compound (745/1280)
Rule 5 INH = 1, Alkylaryl ether (659/1280) → Aromatic compound (659/1280)
Rule 6 INH = 1, Amine, Heterocyclic (810/1280) → Aromatic compound (806/1280)
From rule 4 it can be deduced that the majority of inhibitors (66%) contain a tertiary amine group together with an aromatic moiety. The confidence of this rule is 0.99, which means that, when an aromatic moiety is present, in 99% of the cases the compound also contains a tertiary amine and is annotated as inhibitor. When association rule learning was used for the whole fingerprints, in total 317 rules were found (provided as Supplementary data). To reduce the number of rules before analyzing them, we only considered those rules, which cover more than 55% of the data set. This resulted in a set of 37 rules, with three being significant.
Rule 7 INH = 1, Ether (770/1280) → aromatic compound (759/1280)
Rule 8 INH = 1, Heterocyclic compound (1045/1280) → aromatic compound
(1017/1280)
Rule 9 INH = 1, Tertiary aliphatic amine, Tertiary amine (748/1302), Amine (749/1280) → Aromatic compounds (745/1280)
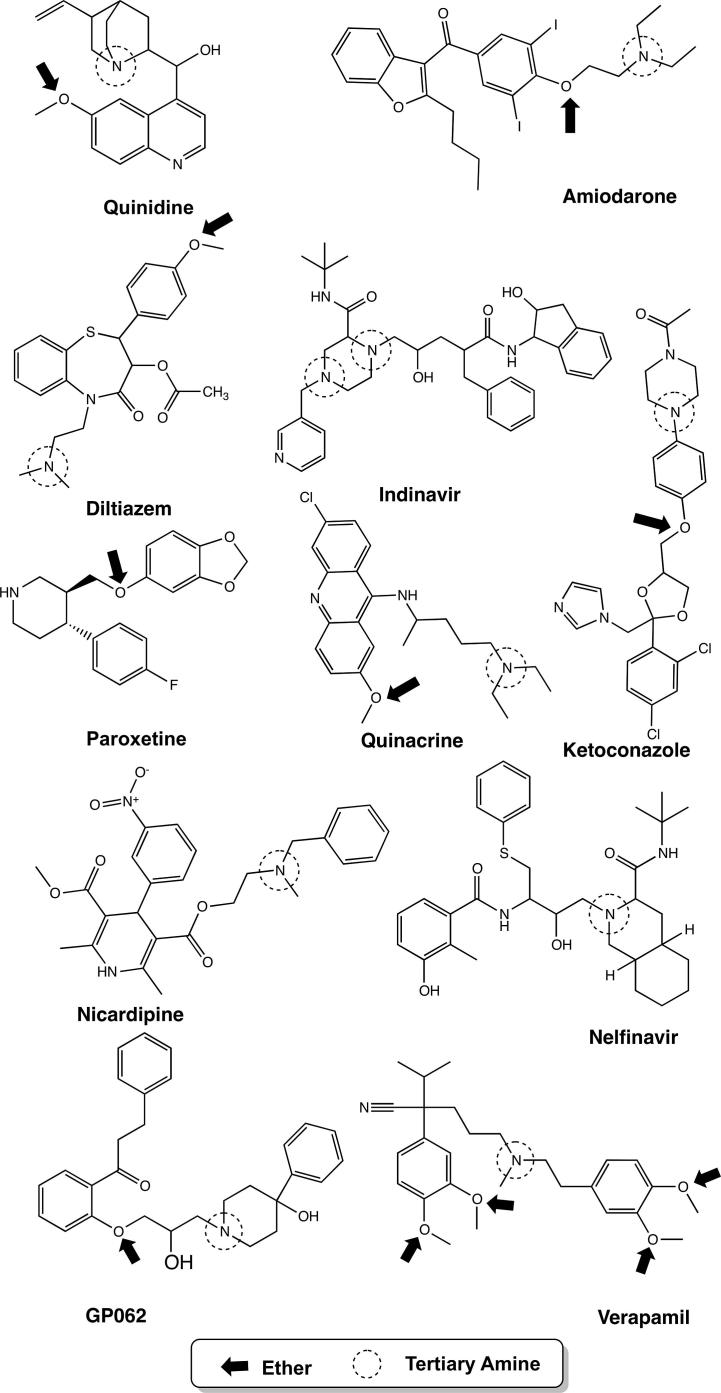
These rules quite nicely match our current knowledge on the basic pharmacophoric features for P-gp inhibitors, demonstrating that the majority of inhibitors contain aromatic moieties, heterocycles, alkylaryl ethers, tertiary amines and tertiary aliphatic amines (Fig. 4). These observations further strengthen the current notion of P-gp inhibitors of being hydrophobic (at least one aromatic ring), cationic, basic nitrogen atoms, tertiary amine, with at least two hydrogen bond acceptors.24
Figure 4.
Selected P-glycoprotein inhibitors; atoms are marked according to association rules for inhibitors. ether: arrow, tertiary amine: dotted circle.
3. Conclusions
In the present study, kappa nearest neighbor (kNN), random forest (RF) and support vector machine (SVM) were applied to a set of 484 P-gp substrates/non-substrates and a set of 1935 P-gp inhibitors/non-inhibitors using functional groups based fingerprints. Models that were built for substrate/non-substrate and inhibitor/non-inhibitor classification based on the random forest method perform better than those derived using kappa nearest neighbor or support vector machines. The random forest model correctly predicts 70% of substrates/non-substrates and 75% of inhibitors/non-inhibitors in the test set. In addition to the classification models, frequency of functional group based bins present in substrate and inhibitor models were counted, and the results indicate that the majority of non-substrates contain hydroxyl groups when compared to substrates. This indicates that molecules that are more hydrophobic are likely to act as substrates. This has been further verified from by a frequent pattern (FP) growth algorithm, which derived a set of rules for substrates. The majority of substrates (>40%) consist of an aromatic system, an ether moiety, and amine groups.
Similar rules have been derived for inhibitors, that is compounds that contain alkylaryl ethers, aromatic amines, and tertiary aliphatic amine groups are likely to be P-gp inhibitors. These features are in agreement with various previously reported QSAR models of P-gp substrates and inhibitors. Models and rules derived from this study could assist in identifying whether a compound might show an interaction with P-glycoprotein or not in an early phase of the drug development process. Furthermore, the approach of association rule analysis will also aid in a deeper understanding of the molecular basis of compound/transporter interaction.
4. Computational materials and methods
4.1. Preparation of substrate and inhibitor data sets
A set of 257 P-gp substrates and non-substrates was compiled from various literature sources. In addition, a set of 227 compounds was extracted from a data set published by Szakács et al.25 In brief, Szakács et al. correlated the mRNA levels of a given ABC transporter in the 60 cancer cell lines of the NCI60 screen with the toxicity of a given compound in these 60 cell lines. A negative correlation of these two parameters over the whole panel of tumor cells (i.e., the higher the expression rate of the transporter, the lower the toxicity of the compound) indicates that this compound is a substrate of the respective transporter. Detailed analysis of the individual compounds suggested a Pearson correlation coefficient (PCC) of −0.3 as a valuable threshold. Compounds with PCC values between −0.02 and +0.02 are considered to be ABCB1 non-substrates. These two data sets (n = 484) were merged in order to broaden the chemical space of the models.
For P-gp inhibitors, a data set of 1935 compounds was compiled from Chen et al. and Broccatelli et al.26,27 In brief, Broccatelli et al. created a data set of 1275 compounds from more than 60 literature references, as well as from the ChEMBL and WOMBAT databases. The thresholds’ values for inhibitors and non-inhibitors were assigned based on the IC50 values and the percentage of inhibition as corroborate by Rautio et al.28 While compounds with an IC50 ⩽ 15 μM, and >25–30% of inhibition were considered as inhibitors, compounds possessing an IC50 values of ⩾100 μM and <10–12% of inhibition were considered as non-inhibitors. The data set of Chen et al. was created from various literature sources using MDRR (multi-drug-resistance ratio) values measured in adriamycin-resistant P388 murine leukemia cells. Compounds were classified as inhibitors and non-inhibitors depending on their MDRR value, whereby values higher than 0.5 were assigned to inhibitors, compounds with values lower or equal to 0.4 were annotated as non-inhibitors.
For fingerprints calculation, the substrate data set of 484 compounds and the inhibitor data set of 1935 compounds were preprocessed. First, CORINA29 was used to convert 2D structures into 3D structures. Subsequently, molecules were imported into the MOE modeling software (Chemical Computing Group, version 2010.10)30 for energy minimization using the MMFF94x force field. Both data sets are available as sdf-files in Supplementary data and via our homepage (pharminfo.univie.ac.at).
4.2. Fingerprints calculation
Functional groups based fingerprints were calculated for both sets of compounds (i.e., substrates and inhibitors) using the software package checkmol,31 which extracts >200 functional groups (a list of functional groups used in the study can be found at the checkmol/matchmol homepage, (http://merian.pch.univie.ac.at/~nhaider/cheminf/cmmm.html) and creates a binary fingerprint for all compounds. Zero variance bins were removed before the classification, as they do not contain any relevant information for model building.
4.3. Selection of training and test sets
The data sets of substrates and inhibitors were separated into a training and a test set using D-optimal onion design (DOOD). DOOD is a multivariate method, used for selecting training and test sets of reasonable size, which are representative for the chemical property space defined by the molecular structures.32,33 SIMCA-P 10.5 and MODDE 7.034 were used for PCA and DOOD, respectively.
4.4. Machine learning methods
In the present study, we used support vector machine (SVM), random forest (RF) and kappa nearest neighbor (kNN) as classifiers. The WEKA (v3.6.5) data mining software35 was used for classification. These methods have been commonly used for classification of compounds with respect to their ADMET properties. Theory and applications of these methods can be found elsewhere.36 In addition to these classification methods, we have also explored association rule learning to extract the relations between the variables and to identify frequent pattern rules. This idea was introduced by Agarwal et al. in 1993,37 and since then many derivatives of the algorithm have been developed, for example, Apriori, Eclat, and FPGrowth. In the present study, we used the FPGrowth (Frequent Pattern Growth) algorithm as implemented in the WEKA (version 3.6.5) software.35 A classical example for an association rule is the customers shopping in a supermarket.
| (1) |
where X and Y refers to item sets or variables. An association rule consists of transactions and item sets:
[potatoes, onions] → [milk]
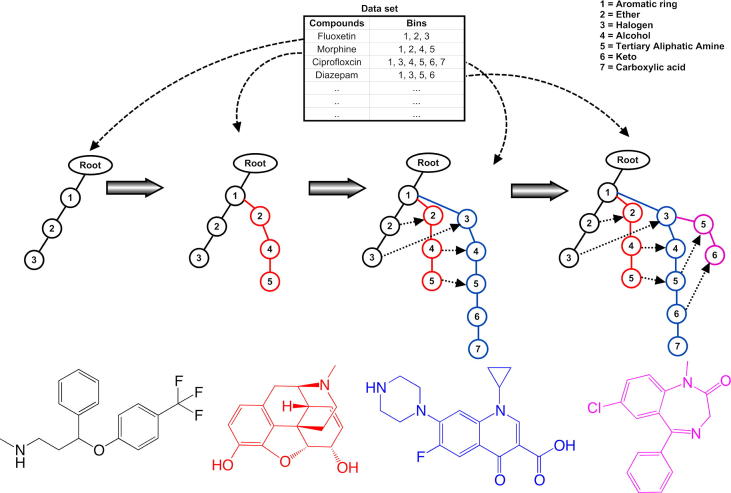
If the customer buys potatoes and onions, he/she likely also buys milk. These rules can be assessed using various statistical terms, for example, support (fraction of transactions that contains both X and Y) and confidence (measures how often items in Y appear in transactions that contain X). The FPGrowth algorithm tries to find frequent item sets based on the principle frequent pattern tree (FP-Tree) or ‘divide and conquer’ approach. FPGrowth works in two steps; (1) It constructs the FP tree from the data set (e.g., compounds and their fingerprints, as shown in Fig. 5), (2) It extracts the frequent item sets from the FP-tree.
Figure 5.
Schematic representation of the principle of the frequent pattern growth algorithm (FPGrowth).
4.5. Attribute selection and model evaluation
Best attributes for the models were selected based on a supervised attribute selection method called wrapper subset evaluator (WSE). This evaluator initially selects a subset of attributes, subsequently induces the machine-learning algorithm (e.g., random forest) to the selected subset and evaluates the resulting models (based on the overall accuracy or kappa statistic. This process is continued until the subset has high accuracy. All classification models were evaluated on basis of Matthews correlation coefficient (MCC, Eq. 2), G-mean (Eq. 3) and overall accuracy (Eq. 4) of the test set and n-fold cross validation of the whole data set. MCC is a measure for the quality of a model, and it returns a value between −1 and +1. MCC value 0 means average or random prediction, −1 is worst prediction, and +1 is perfect prediction. An MCC value above 0.4 is considered to be predictive in binary classification.38 Accuracy is the proportion of correctly predicted positive and negative classes (Eq. 4). G-mean is the geometric mean of sensitivity and specificity. G-mean provides a measure for the overall performance of a model and is used to check balanced prediction of each of two classes (Eq. 3).
| (2) |
| (3) |
| (4) |
where, TP: true positive, TN: true negative, FP: false positive, FN: false negative, sensitivity: (TP/TP+FN), specificity: (TN/TN+FP).
All classification models were further validated by 10-fold cross validation. Attributes selection and n-fold cross validation were carried out as implemented in the WEKA software.35
Acknowledgments
We gratefully acknowledge the financial assistance provided by the Innovative Medicines Initiative (eTOX, 115002) and by the Austrian Science fund (F3502). The authors are thankful to Tingjun Hou (Soochow University, China) and Gabriele Cruciani (University of Perugia, Italy) for providing P-gp inhibition data. The authors are also thankful to ChemAxon for providing a free academic license for the Standardizer, Name to Structure, and other toolkits.
Footnotes
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.bmc.2012.03.045.
Supplementary data
Supplementary Figures and Tables.
References and notes
- 1.Higgins C.F. Annu. Rev. Cell Biol. 1992;8:67. doi: 10.1146/annurev.cb.08.110192.000435. [DOI] [PubMed] [Google Scholar]
- 2.Vasiliou V., Vasiliou K., Nebert D.W. Hum. Genomics. 2009;3:281. doi: 10.1186/1479-7364-3-3-281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Davidson A.L., Dassa E., Orelle C., Chen J. Microbiol. Mol. Biol. Rev. 2008;72:317. doi: 10.1128/MMBR.00031-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dean M., Rzhetsky A., Allikmets R. Genome Res. 2001;11:1156. doi: 10.1101/gr.184901. [DOI] [PubMed] [Google Scholar]
- 5.Gottesman M.M., Fojo T., Bates S.E. Nat. Rev. Cancer. 2002;2:48. doi: 10.1038/nrc706. [DOI] [PubMed] [Google Scholar]
- 6.Gottesman M.M., Pastan I., Ambudkar S.V. Curr. Opin. Genet. Dev. 1996;6:610. doi: 10.1016/s0959-437x(96)80091-8. [DOI] [PubMed] [Google Scholar]
- 7.Szakács G., Paterson J.K., Ludwig J.A., Booth-Genthe C., Gottesman M.M. Nat. Rev. Drug Disc. 2006;5:219. doi: 10.1038/nrd1984. [DOI] [PubMed] [Google Scholar]
- 8.Szakács G., Varadi A., Ozvegy-Laczka C., Sarkadi B. Drug Discovery Today. 2008;13:379. doi: 10.1016/j.drudis.2007.12.010. [DOI] [PubMed] [Google Scholar]
- 9.Ecker G., Chiba P. Vol. 44. Wiley-VCH, Verlag GmbH & Co.; 2009. (Transporters as Drug Carriers). [Google Scholar]
- 10.Fenner K.S., Troutman M.D., Kempshall S., Cook J.A., Ware J.A., Smith D.A., Lee C.A. Clin. Pharmacol. Ther. 2009;85:173. doi: 10.1038/clpt.2008.195. [DOI] [PubMed] [Google Scholar]
- 11.Food and Drug Administration (FDA), Drug Interaction Studies–Study Design, Data Analysis, and Implications for Dosing and Labeling (2006). http://www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidances/ucm072101.pdf. (accessed Oct 2011).
- 12.Giacomini K.M., Huang S.M., Tweedie D.J., Benet L.Z., Brouwer K.L., Chu X., Dahlin A., Evers R., Fischer V., Hillgren K.M., Hoffmaster K.A., Ishikawa T., Keppler D., Kim R.B., Lee C.A., Niemi M., Polli J.W., Sugiyama Y., Swaan P.W., Ware J.A., Wright S.H., Yee S.W., Zamek-Gliszczynski M.J., Zhang L. Nat. Rev. Drug Disc. 2010;9:215. doi: 10.1038/nrd3028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang L., Zhang Y.D., Zhao P., Huang S.M. AAPS J. 2009;11:300. doi: 10.1208/s12248-009-9106-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ecker G.F., Stockner T., Chiba P. Drug Discovery Today. 2008;13:311. doi: 10.1016/j.drudis.2007.12.012. [DOI] [PubMed] [Google Scholar]
- 15.Ekins S., Kim R.B., Leake B.F., Dantzig A.H., Schuetz E.G., Lan L.B., Yasuda K., Shepard R.L., Winter M.A., Schuetz J.D., Wikel J.H., Wrighton S.A. Mol. Pharmacol. 2002;61:974. doi: 10.1124/mol.61.5.974. [DOI] [PubMed] [Google Scholar]
- 16.Penzotti J.E., Lamb M.L., Evensen E., Grootenhuis P.D. J. Med. Chem. 2002;45:1737. doi: 10.1021/jm0255062. [DOI] [PubMed] [Google Scholar]
- 17.Pajeva I.K., Globisch C., Wiese M. ChemMedChem. 2009;4:1883. doi: 10.1002/cmdc.200900282. [DOI] [PubMed] [Google Scholar]
- 18.Wang Z., Chen Y., Liang H., Bender A., Glen R.C., Yan A. J. Chem. Inf. Model. 2011;51:1447. doi: 10.1021/ci2001583. [DOI] [PubMed] [Google Scholar]
- 19.Xue Y., Yap C.W., Sun L.Z., Cao Z.W., Wang J.F., Chen Y.Z. J. Chem. Inf. Comput. Sci. 2004;44:1497. doi: 10.1021/ci049971e. [DOI] [PubMed] [Google Scholar]
- 20.Huang J., Ma G., Muhammad I., Cheng Y. J. Chem. Inf. Model. 2007;47:1638. doi: 10.1021/ci700083n. [DOI] [PubMed] [Google Scholar]
- 21.Klepsch F., Chiba P., Ecker G.F. PLoS Comput. Biol. 2011;7:e1002036. doi: 10.1371/journal.pcbi.1002036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hou T.J., Xia K., Zhang W., Xu X.J. J. Chem. Inf. Comput. Sci. 2004;44:266. doi: 10.1021/ci034184n. [DOI] [PubMed] [Google Scholar]
- 23.Gatlik-Landwojtowicz E., Aanismaa P., Seelig A. Biochemistry. 2006;45:3020. doi: 10.1021/bi051380+. [DOI] [PubMed] [Google Scholar]
- 24.Klopman G., Shi L.M., Ramu A. Mol. Pharmacol. 1997;52:323. doi: 10.1124/mol.52.2.323. [DOI] [PubMed] [Google Scholar]
- 25.Szakács G., Annereau J.P., Lababidi S., Shankavaram U., Arciello A., Bussey K.J., Reinhold W., Guo Y., Kruh G.D., Reimers M., Weinstein J.N., Gottesman M.M. Cancer Cell. 2004;6:129. doi: 10.1016/j.ccr.2004.06.026. [DOI] [PubMed] [Google Scholar]
- 26.Broccatelli F., Carosati E., Neri A., Frosini M., Goracci L., Oprea T.I., Cruciani G. J. Med. Chem. 2011;54:1740. doi: 10.1021/jm101421d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen L., Li Y., Zhao Q., Peng H., Hou T. Mol. Pharmacol. 2011;8:889. doi: 10.1021/mp100465q. [DOI] [PubMed] [Google Scholar]
- 28.Rautio J., Humphreys J.E., Webster L.O., Balakrishnan A., Keogh J.P., Kunta J.R., Serabjit-Singh C.J., Polli J.W. Drug Metab. Dispos. 2006;34:786. doi: 10.1124/dmd.105.008615. [DOI] [PubMed] [Google Scholar]
- 29.CORINA (version 3.4), Molecular Networks GmbH- Computerchemie, Erlangen: Germany. http://www.molecular-networks.com.
- 30.MOE (Molecular Operating Environment, version 2012.02), Software available from Chemical Computing Group, Inc., 1010 Sherbrooke Street West, Suite 910, Montreal, Quebec, Canada, H3A 2R7. http://www.chemcomp.com.
- 31.Haider N. Molecules. 2010;15:5079. doi: 10.3390/molecules15085079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Olsson I.M., Gottfries J., Wold S. Chemom. Intell. Lab. 2004;73:37. [Google Scholar]
- 33.Kriegl J.M., Eriksson L., Arnhold T., Beck B., Johansson E., Fox T. Eur. Pharm. Sci. 2005;24:451. doi: 10.1016/j.ejps.2004.12.009. [DOI] [PubMed] [Google Scholar]
- 34.SIMCA-P (version 10.5) and MODDE (version 7.0), software available from Umetrics AB, Umeå, Sweden, http://www.umetrics.com.
- 35.Hall M., Frank E., Holmes G., Pfahringer B., Reutemann P., Witten I. SIGKDD Explor. 2009:11. [Google Scholar]
- 36.Witten I., Frank E. 2nd ed. Morgan Kaufmann; San Francisco: 2005. Data Mining: Practical Machine Learning Tools and Techniques. [Google Scholar]
- 37.Agrawal R., Imielinski T., Swami A. SIGMOD Conf. 1993:207. [Google Scholar]
- 38.Chohan K.K., Paine S.W., Mistry J., Barton P., Davis A.M. J. Med. Chem. 2005;48:5154. doi: 10.1021/jm048959a. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures and Tables.