Characterization of the Adaptation Module of the Signaling Network in Bacterial Chemotaxis by Measurement of Step Responses

Abstract

The bacterial chemotaxis network features robust adaptation implemented by negative integral feedback. Here, we show that the adaptation module can be characterized by measurement of the response to simple step-addition and removal of a chemoattractant. The method does not rely on a particular form of the receptor module, and thus can be used to characterize other integral feedback networks.

Cellular networks often exhibit modular structures (1). For example, the bacterial chemotaxis network, which enables cells to detect and respond to chemical stimuli (2,3), is composed of a receptor module that senses changes in the environment and generates the network activity, and an adaptation module that allows the cells to maintain a steady-state activity independent of ambient conditions (4). The adaptation module for wild-type Escherichia coli was characterized recently by measurements of responses to a set of temporal exponential ramps of chemoattractant (4). Here, we developed a simpler method for characterizing the adaptation module that employs simple step-addition and removal of chemoattractant. Because of its simplicity, this method can be easily applied to systematic studies of the adaptation module in a variety of E. coli mutants and in other bacteria. Moreover, the method does not rely on a particular functional form of the receptor module (i.e., on the specific way that module output depends on input); therefore, it should be applicable to the study of adaptation modules in other cellular networks.

In the E. coli chemotaxis signaling network, binding of chemical ligands by membrane receptors modulates the activity of an associated histidine kinase, CheA, which phosphorylates the response regulator, CheY. A phosphatase, CheZ, dephosphorylates CheY-P. The activity of the receptor-kinase complex (the network activity, a) also is affected by the level of receptor methylation, m (a increases with m). Adaptation is mediated by receptor methylation and demethylation, by CheR and CheB.

Although other models have been developed to understand the precision and kinetics of adaptation in bacterial chemotaxis, e.g., by Meir et al. (5), our purpose here was to characterize the adaptation module, F(a), in the systems-level scheme proposed by Tu et al. (6). In this model, three dynamical variables are utilized to describe the chemotaxis network: the ligand concentration [L], the receptor-kinase activity a, and the methylation level m, corresponding to the network input, output, and memory, respectively. The dynamics of these variables are described with the equations a = G([L], m), and dm/dt = F(a). The timescale for ligand binding and kinase response is much shorter than that for receptor methylation and demethylation, so the dependence of a on [L] and m can be described by an algebraic equation, whereas the temporal dynamics of m can be described by a differential equation. From the network’s perfect adaptation to aspartate, dm/dt should depend explicitly only on a, according to the linear integral feedback model described previously (7). Following Tu et al. (6), the receptor-kinase activity is expressed with a two-state model,

$$G\left(\left[\mathit{L}\right],m\right)=\frac{1}{\left(1+\exp \left(f_{\text{t}}(\left[L\right],m\right)\right)},$$

where the total free energy f_t is the sum of ligand-dependent and methylation-dependent parts,

$$f_{\text{t}}=N\left(f_{\text{L}}\left(\left[L\right]\right)+f_{\text{m}}\left(m\right)\right),$$

where N is the number of receptor homodimers (binding sites) in an allosteric cluster, and the energies are in units of kT. In the Monod-Wyman-Changeux model (8), which has been shown to describe the receptor module successfully (9–13),

$$f_{\text{L}}\left(\left[L\right]\right)=\ln \left(1+\left[L\right]/K_1\right)-\ln \left(1+\left[L\right]/K_{\text{A}}\right),$$

and f_m(m) = α(m₀ − m). In these equations, α is the free-energy change per added methyl group, m₀ is the methylation level where f_m crosses zero, and K_I and K_A are the ligand dissociation constants for inactive and active receptors, respectively. During the adaptation process in a step response, [L] is constant, and m changes, so

$$\begin{array}{c}\frac{\text{d}\mathit{a}}{\text{d}\mathit{t}}=\frac{\partial a}{\partial m}\times \frac{\text{d}m}{\text{d}t}\\ =\alpha Na\left(1-a\right)\times \frac{\text{d}\mathit{m}}{\text{d}\mathit{t}}.\end{array}$$

Thus, the rate of change of the receptor methylation level can be calculated from the adaptation process if a is measured as a function of time:

$$\frac{\text{d}\mathit{m}}{\text{d}\mathit{t}}=\frac{\left(\frac{\text{d}\mathit{a}}{\text{d}\mathit{t}}\right)}{\left(\alpha Na\left(1-a\right)\right)},$$

with α = 2 and N = 6 determined previously in the characterization of the aspartate receptor module in wild-type cells (4). By plotting dm/dt versus a during adaptation to a simple step response, we can reconstruct the adaptation module, F(a).

We used fluorescence resonance energy transfer (FRET) between CheZ-CFP and CheY-YFP as an indicator of the receptor-kinase activity (14). We measured FRET as a function of time during a step-addition and removal of 0.05 mM α-methyl-DL-aspartate (MeAsp) to cells of E. coli wild-type strain RP437 (15), as shown in Fig. 1. The measurements were carried out at room temperature using a setup described previously (4,14). Fluorescence signals from a field of ∼400 cells were filtered by an eight-pole low-pass Bessel filter (3384, Krohn-Hite) with a cutoff frequency of 0.4 Hz and sampled at 1 Hz. Because the change of the FRET value, ΔFRET, is proportional to the change of receptor-kinase activity, Δa, and a is defined to lie in the range of 0 to 1, we converted the FRET values to a by measuring the full range of ΔFRET, which corresponds to the receptor-kinase activity changing from 0 to 1. This was done by measuring the ΔFRET values when adding and removing a large concentration of attractant. The peak FRET level after removal of attractant saturates at [MeAsp] > 0.1 mM, and this saturated peak FRET level was used as the FRET value corresponding to a = 1 (5).

Figure 1.

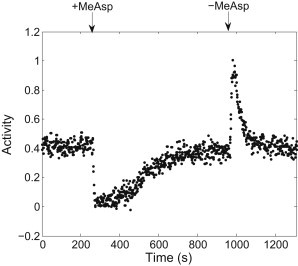
Responses of cells of E. coli wild-type strain RP437 to step-addition and removal of 0.05 mM MeAsp, showing the receptor-kinase activity as a function of time. (Arrows) Times of addition and removal of attractant.

From the step response, we calculated da/dt during the adaptation process: for each data point, da/dt was calculated by fitting a segment of 31 data points centered on the one discussed here, with a linear function and extracting the slope. We then calculated the dm/dt values and plotted them as a function of a, as shown in Fig. 2. Values for kinase activities a less than the steady-state activity a₀ were derived from the response to the addition of attractant, whereas values for activities a > a₀ were derived from the response to the removal of attractant. The data are inherently noisy when a is close to 0 or 1, corresponding to the situation in which a is not sensitive to m. This reconstruction of F(a) is similar to the result obtained in the exponential ramp experiments (4), showing a sharp transition at activity ∼0.75 and a shallow negative slope near the steady-state receptor-kinase activity a₀: F′(a₀) = −0.0090 ± 0.0012. Data were analyzed using custom scripts in MATLAB (The MathWorks, Natick, MA).

Figure 2.

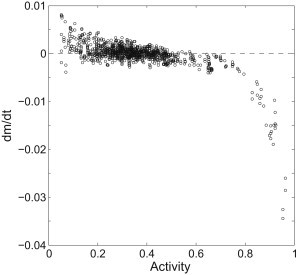
Adaptation function F(a), showing the rate of change of the receptor methylation level as a function of receptor-kinase activity, calculated for the experiment of Fig. 1, involving the step-addition and removal of 0.05 mM MeAsp.

We measured the responses of cells of wild-type E. coli to three rounds of step-addition and removal of MeAsp, with step sizes of 0.02, 0.1, and 0.5 mM, respectively, and reconstructed F(a) using these step responses, as shown in Fig. 3. The results from all three data sets collapse, with similar slopes of F(a) near a₀: F′(a₀) = −0.0099 ± 0.0013, −0.0086 ± 0.0012, and −0.0085 ± 0.0012 for step sizes of 0.02, 0.1 and 0.5 mM MeAsp, respectively. This further validates our method.

Figure 3.

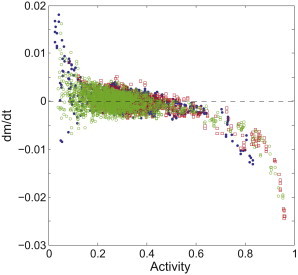
Adaptation function F(a) reconstructed from responses of cells of strain RP437 to step-addition and removal of MeAsp with various step sizes: 0.02, 0.1, and 0.5 mM MeAsp (blue dots, red squares, and green circles, respectively). All three functions collapse to a single curve, showing the insensitivity of this reconstruction to the step size.

The simplicity of our method allows it to be applied in systematic studies of the adaptation module, for example, to explore the unexplained sharp transition of F(a) at ∼a = 0.75, using various E. coli mutants.

Compared to the exponential ramp method (4), which requires a specific form of G([L], m) (linear dependence of f_L([L]) on ln([L]) and linear dependence of f_m on m), our method is not restricted to a specific form of G([L], m). In fact, during a step response of step size [L₀], a = G([L₀], m), so m can be calculated from a: m = G⁻¹([L₀], a), where G⁻¹ is the inverse function of G([L₀], m). During the adaptation process,

$$\begin{array}{c}\frac{\text{d}\mathit{a}}{\text{d}\mathit{t}}=\frac{\partial G\left(\left[L_0\right],m\right)}{\partial m}\times \frac{\text{d}\mathit{m}}{\text{d}\mathit{t}}\\ =\text{g}\left(\left[{\mathit{L}}_0\right],G^{-1}\left(\left[L_0\right],a\right)\right)\times \frac{\text{d}\mathit{m}}{\text{d}\mathit{t}},\end{array}$$

where the function g([L], m) is the derivative of G([L], m) with respect to m. Therefore, the rate of change of receptor methylation level can be calculated if a is measured as a function of time:

$$\frac{\text{d}\mathit{m}}{\text{d}\mathit{t}}=\frac{\left(\frac{\text{d}\mathit{a}}{\text{d}\mathit{t}}\right)}{\text{g}\left(\left[{\mathit{L}}_0\right],G^{-1}\left(\left[{\mathit{L}}_0\right],a\right)\right)}$$

or

$$\frac{\text{d}\mathit{m}}{\text{d}\mathit{t}}=\frac{\partial G^{-1}\left(\left[L_0\right],a\right)}{\partial a}\times \frac{\text{d}\mathit{a}}{\text{d}\mathit{t}}.$$

We can then reconstruct F(a) by plotting dm/dt versus a. Because of this generality, we expect this method to be applicable to the studies of other biological networks that feature integral feedback.