Flow Loading Induces Oscillatory Trajectories in a Bloodstream Parasite

Abstract

The dynamics of isolated microswimmers are studied in bounded flow using the African trypanosome, a unicellular parasite, as the model organism. With the help of a microfluidics platform, cells are subjected to flow and found to follow an oscillatory path that is well fit by a sine wave. The frequency and amplitudes of the oscillatory trajectories are dependent on the flow velocity and cell orientation. When traveling in such a manner, trypanosomes orient upstream while downstream-facing cells tumble within the same streamline. A comparison with immotile trypanosomes demonstrates that self-propulsion is essential to the trajectories of trypanosomes even at flow velocities up to ∼40 times higher than their own swimming speed. These studies reveal important swimming dynamics that may be generally pertinent to the transport of microswimmers in flow and may be relevant to microbial pathogenesis.

Introduction

Self-propelled microorganisms are frequently subjected to flow in various environments, be it sperm cells in the fallopian tube, pathogens in the bloodstream, or artificial swimmers created for a range of applications from drug delivery to environmental monitoring to chemical sensors. Although both theoretical and experimental studies have dealt with hydrodynamic interactions with boundaries (1) and between microorganisms leading to cooperative behavior (2–4), little has been done to examine the effects of flow in detail. In relation to bacterial transport, upstream swimming of Escherichia coli has been demonstrated in microfluidic channels (5) and has applications in medicine and aquatic environments in general. Other physical studies with external flow fields on microorganisms have been limited to studying shear effects on adhesive cells (6–8).

In this work we report on the behavior of Trypanosoma brucei brucei in microfluidic flow. T. brucei are protozoan parasites in humans and other animals. They are unicellular organisms with an elongated body tapered toward the leading end. Propulsion is mediated by a single 9+2 flagellum structure (9) that emerges from the basal body and is anchored to the remaining length of the cell toward the leading end (10), as illustrated in Fig. 1. In a static, nutrient-rich environment, T. brucei swim at ∼10 μm/s (11). African trypanosomiasis (also known as sleeping sickness) is a result of infection by T. brucei after the bite of a Tsetse fly. In the mammalian host, bloodstream-form T. brucei are intercellular parasites and are subjected to the strong shear flows within the host’s blood circulation. Despite blood flow velocities ranging from millimeters/second to meters/second, T. brucei proliferate within the bloodstream, occupy tissue spaces, and eventually invade the central nervous system via the blood-brain barrier (12,13). Furthermore, flow-mediated cell surface removal of host antibodies is believed to allow T. brucei to evade immune attack (14). Therefore, systematic studies of T. brucei behavior are required to further our understanding of the underlying physical mechanisms of these swimmers in flow.

Figure 1.

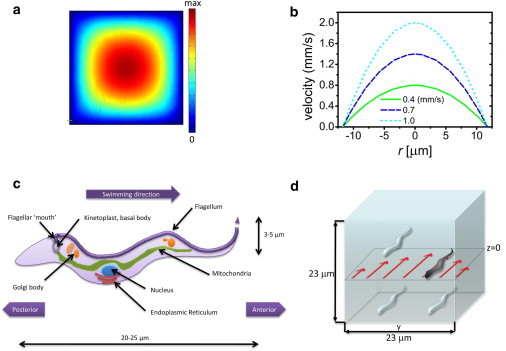
(a) Simulation of flow profile (ComSol Multiphysics) in a square channel. (b) The dotted line corresponds to parabolic velocity profile as a function of distance from the center of the channel (shown for different average flow velocities). (c) Schematic of T. brucei. (d) Only cells in the middle plane are observed in the symmetric channel.

Microfluidic tools provide the ideal platform for such studies and allow us to investigate the motion of single cells under controlled flow conditions at the relevant length scales. Furthermore, we can distinguish the role of self-propulsion from purely hydrodynamic effects by drawing a comparison between live and immotile trypanosomes. We use a symmetric channel of equal height and width, which gives us a near parabolic flow profile (see Fig. 1). For these studies, we record information only for the cells that are located in the middle plane and thus are exposed to the same flow profile in the z direction, as illustrated in Fig. 1.

The experimental setup allows us to study microswimmers (using T. brucei as a model) in pressure flow in a very well controlled environment and can be used to search for generic swimming behaviors. As presented below, this simple environment leads to a rich range of behavior that must be understood before further parameters (such as red blood cells or variations in channel geometry) can be introduced to mimic the natural habitat of trypanosomes.

The length scales of this system correspond to Reynolds numbers in the range of 10⁻⁴ to 10⁻², indicating that inertial forces are negligible and viscous forces dominate the fluid dynamics (15). Flow is predictable, and neighboring streamlines flow parallel to each other in the case of laminar flow. The influence of boundary conditions is significant and in particular affects the relation between pressure gradients and volumetric flow rates. The no-slip boundary condition (velocity U = 0 at channel walls) yields a parabolic Poiseuille flow profile, with the fluid in the center of the channel having the largest velocity (Fig. 1), as given by $U=U_{\max }\left[1-r^2/{\left(r_c/2\right)}^2\right]$, where r is the distance from the center and r_c is the diameter of the pipe. Note that the average flow velocity U_ave ≈ 0.5 U_max. The boundary condition also results in a maximum shear rate $\dot{\gamma }$ at the walls that decreases linearly toward the center of the channel given by $\dot{\gamma }\left(r\right)=\left[2U_{\max }/{\left(r_c/2\right)}^2\right]\left|r\right|$.

During locomotion, organisms generate a flow field that may influence neighboring cells and boundaries. Depending on the swimming mechanism, cells are often broadly classified as either pushers (when fluid is repelled from the body along the long axis and drawn into the sides) or pullers (when fluid is drawn in along the elongated direction and pushed out on the sides). Pullers usually swim with one or more appendages attached to the leading end of the cell (1,16). Although the flow fields generated by T. brucei are not known, we expect that due to the location of the flagellum toward the leading end, the results of our microfluidic studies may be generalized to other similar organisms and point to generic features of low Reynolds number swimmers in the presence of pressure-driven Poiseuille flow (17).

Materials and Methods

Microfluidics

Microfluidic channels are prepared as previously reported (18) using photolithography followed by soft lithography. Briefly, silicon wafers are spin-coated with photoresist (SU8-50; Micro Resist Technology, Berlin, Germany) to a height of 23 μm. This is followed by a soft-bake step at 65°C for 10 min and then 95°C for 45 min. The wafer is then covered with a photo mask (designed on AutoCAD (AutoDesk) and printed by JD Photo-Tools (Hitchin, UK)) and illuminated with UV light (λ = 365 nm, 15 mW/cm²), cross-linking the exposed areas. The remaining areas are washed away with developer. A polydimethylsiloxane (PDMS; Dow Corning, Weisbaden, Germany) replica is made by mixing the PDMS precursor with its cross-linker (10:1) and pouring this mixture onto the silicon master. The PDMS is cured by baking at 80°C for 4–6 hr. The PDMS mold is peeled off and inlet holes are made. The PDMS is then plasma-bonded to a glass slide, and tubing is connected to the resulting structure. We approximate the channel to a pipe for calculations of shear and velocity.

For flow velocities < 0.5 mm/s, hydrostatic pressure is used to control flow velocities. When higher flow velocities are required, fluid is injected and pumped through the channels using a custom-made syringe pump, and flow velocities are kept constant for each experiment. Adhesion of polystyrene beads to the interior of the microfluidic channels can cause clogging and changes to flow field. To prevent such adhesion, the channel is flushed with 1% bovine serum albumin (BSA; Sigma Aldrich, Munich, Germany) for 30 min before injection of the sample. BSA has not been associated with any changes to T. brucei motility.

Trypanosome preparation

T. brucei are cultured in HMI9 complete medium (19,20) supplemented with 10% fetal calf serum and collected at concentration of 2 × 10⁵ cells/mL. Cells are concentrated (but still kept sufficiently dilute to observe single-cell dynamics in the microfluidic channel) and resuspended in fresh medium. For cell immobilization, trypanosomes are washed twice in trypanosome dilution buffer (TDB; 5 mM KCl, 80 mM NaCl, 1 mM MgSO₄, 20 mM Na₂HPO₄, 2 mM NaH₂PO₄, 20 mM glucose (pH 7.4)) and resuspended in TDB-2DG (5 mM KCl, 80 mM NaCl, 1 mM MgSO₄, 20 mM Na₂HPO₄, 2 mM NaH₂PO₄, 20 mM 2-deoxy-D-glucose (pH 7.4)), incubated at 37°C for 10 min. 2-deoxy-D-glucose (2DG) is a stable glucose analog that is actively taken up by glucose transporters but cannot be fully metabolized and thus blocks the glycolytic pathway (21). Incubation with 2DG results in cells being reversibly immotile for up to 45 min. Although the absence of ATP may lead to changes in flagellar compliance (22), alternative methods of rendering a cell immotile result in much more significant changes in mechanical properties. Both HMI9 complete medium and TDB have a viscosity similar to that of water, as measured by an Ubbelohde viscometer (VWR, Darmstadt, Germany).

Microscopy and image processing

All experiments with microfluidic devices are conducted using a Zeiss (Jena, Germany) Axiovert inverted microscope equipped with a 100x air objective. Cells in flow are recorded with a PCO Sensicam and each movie frame is processed using a combination of MATLAB (The MathWorks, Natick, MA), and Image Pro Plus (Media Cybernetics, Rockville MD).

Polystyrene beads (Polysciences, Eppelhem Germany), 1 μm in diameter, are mixed with the sample and then injected into the channel at a sufficiently dilute concentration to avoid affecting cell motility. The motion of the beads is used to monitor the average flow velocities either by measuring the streak produced using long exposure times on the camera or by taking an average of the distances traveled by several beads from frame to frame within the channel. Sine wave trajectories (discussed below) are recorded over long distances using a 10x objective, and tracking is performed manually. Sine wave fitting for oscillating trajectories is done by first smoothing the y trajectory in time with five-point adjacent averaging in Origin (OriginLab, Northampton, MA).

Results and Discussion

Although several studies have shown that deformable vesicles and red blood cells migrate away from boundaries in pipe flow, few have examined the behavior of self-propelled entities such as bacteria and other microorganisms subjected to a flow field (5,23,24). The stroboscopic image shown in Fig. 2, which was taken with fluorescently labeled trypanosomes, illustrates that a swimming cell appears to move laterally across the width of the channel, while an immotile cell is carried in the same streamline of the flow throughout the length of the channel. At a flow velocity of 1.6 mm/s, which is much higher than the trypanosome’s swimming speed in a static environment, the trypanosome’s ability to propel itself clearly continues to play a role in its behavior when it is subjected to flow.

Figure 2.

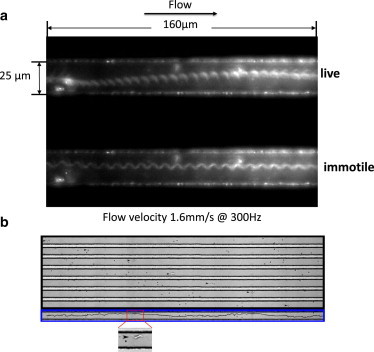
(a) Single stroboscopic image taken at 300 Hz of a live cell (top channel) and an immotile cell (lower channel), both fluorescently labeled, in a microfluidic channel. Despite the channel flow velocity of 1.6 mm/s, which is much higher than their own velocity, live T. brucei (top) are able to swim the width of the channel, whereas a dead cell stays in the same lateral position and is carried by the flow. (b) Montage of a cell moving in pressure-driven flow through a microfluidic channel. The cell (indicated by the black arrow) moves in a sinusoidal trajectory within an upstream orientation. Channel width is 23 μm. In the lowest panel, the cell’s actual trajectory is superimposed to the overlay of all frames in the montage, clearly showing the cell moving toward and away the channel wall.

To investigate the behavior of T. brucei in flow, we begin with a symmetrical channel where cells are constrained to a geometry of equal height and width of 23 μm × 23 μm (of the same length scale as the T. brucei body), which provides a well-controlled setup for studying the physics of microswimmers in parabolic flow. All observations are recorded only for cells in the middle plane (z = 0), ensuring that they are subjected to the same flow profile in the z direction, as shown in Fig. 1. A suspension of T. brucei in fresh culture medium is allowed to enter the channel. A very dilute concentration of polystyrene beads, 1 μm in diameter, is included in the cell suspension as tracers for flow.

Oscillatory trajectories in flow

Intriguingly, when we observe the cells at lower magnifications and flow velocities U_ave < 0.4 mm/s, allowing for longer observation times, we find that most cells swim upstream with the flagellum end leading (though they do not necessarily progress upstream due to the flow) from one wall to another in a sine wave trajectory, as shown in Fig. 2. The observed trajectories are well fitted by sine waves. The trajectory in Fig. 2 appears jagged due to the fast distortions of the T. brucei body during swimming, as discussed in previous work (11,25–27).

T. brucei swimming with a downstream orientation do not exhibit such oscillatory paths, but rather tend to tumble along a streamline. Tumbling cells may still produce distortion in the overall shape, and appear to rotate as a wheel.

Oscillatory trajectories at a range of flow velocities are fitted to sine waves, and the frequency and amplitude of oscillations are shown in Fig. 3 as a function of flow velocities. Increasing velocities result in increasing frequency and decreasing amplitude of the trajectories.

Figure 3.

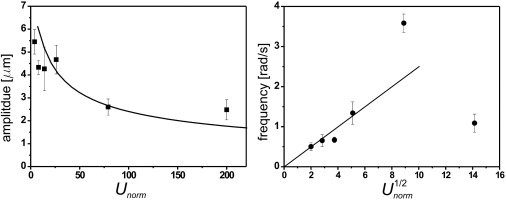
For live cells, the frequency of the oscillations increases with flow velocities while the amplitude decreases, as shown for experiment (symbols) and theory (black line/curve). Theory predicts the frequency to be proportional to the square root of velocity. The scaled velocity, U_norm, used for the abscissa is defined as the maximum flow velocity divided by the proper velocity of the trypanosomes.

It can be readily appreciated that this oscillatory behavior is a direct consequence of the interplay between the Poiseuille flow field and the active motion of the trypanosome relative to the fluid, and may be a generic feature of self-propelled microorganisms that can be deconstructed into physical terms.

To that end, consider a swimmer of length L and width l in a channel with radius r_c ≥ L/2, such that the swimmer is able to turn within the channel, as applicable to the motion of elongated flagellates such as T. brucei. The swimmer is assumed to swim with a constant velocity, u₀, along its long-axis direction relative to the liquid medium, which flows at an average velocity U_ave along the channel with a Poiseuille flow profile. If we adopt, for the sake of simplicity, a two-dimensional representation, the vorticity of the liquid flow is U_maxr/r_c², where U_max is the flow velocity in the channel center, and r is the distance from the center line. If ϕ(t) is the angle the active swimming direction of the swimmer makes with the channel axis, we have ${\partial }_{\mathit{t}}\varphi =-G{U}_{\max }r/r_c^2$, where G < 1 is a dimensionless geometry factor describing the coupling of the swimmer shape to the vorticity of the flow field. The proper motion of the swimmer entails ∂_t r = u₀ sin ϕ, such that we can directly write down the equation of motion for the swimmer direction, ϕ(t). Introducing the two characteristic frequency scales of the system, ω₀ = U_max/r_c and ω_T = u₀/r_c, we find

$${\partial }_{tt}\varphi +G{\omega }_0{\omega }_T\sin \varphi =0$$ (1)

with the Hamiltonian

$$H={\left({\partial }_t\varphi \right)}^2-\frac{{\omega }^2}{2}\cos \varphi ,$$ (2)

where we have introduced $\omega =\sqrt{G{\omega }_0{\omega }_T}$, and ϕ is defined such that ϕ = 0 corresponds to the upstream swimming direction.

As Eq. 1 shows, the angular motion of the swimmer is equivalent to the motion of a pendulum (24). Equation 2 gives rise to a phase plot that accounts for the observed tumbling and oscillatory trajectories (see Supporting Material for details). Because ω is directly linked to the flow velocity, we can use the above formulas to fit our experimental data for the amplitude and frequency of the oscillatory trajectories. As shown in Fig. 3, we find reasonable agreement with the experimental data. The best fit was obtained with G = 0.08, which seems to be a reasonable value for swimming T. brucei. In a recent analysis (28), we confirmed that the frequency for small oscillations for spheroids depends on G as stated in Eq. 1. For rigid spheroidal particles, G = 1 − (γ² − 1)/(γ² + 1), where γ = L/l is the aspect ratio of the body (29), so G = 0.08 corresponds to γ ≈ 5. T. brucei has an aspect ratio of ∼8 when it is fully stretched. Because of its undulating motion, this ratio is reduced significantly and varies with time. Thus, the geometry factor G = 0.08 may indicate the time-averaged value expected for swimming T. brucei. The top-down approach used in this model provides us with some understanding of what features lead to the observed oscillatory trajectories for swimmers in parabolic flow. We expect that this approach will not only uncover generic physical aspects of microswimmers in simple pressure flow but will also likely be applicable in a wide range of biological contexts.

Note that the trends observed here are seen for flow velocities that are many times greater than the velocity of the trypanosome itself. As the flow velocity is increased further, sine wave trajectories become less frequent and the tumbling motion of the cell begins to dominate. At flow velocities of 1 mm/s, the frequency of the trajectory oscillations deviates strongly from the predictions of the simple physical model outlined above, finally dropping to very low values. At such high flow velocities, in addition to shear stresses, it is likely that a lift force similar to that seen in vesicles (30) and red blood cells (31) may come into play, causing cells to move inward.

Cell orientation

As we have seen, T. brucei are likely to exhibit oscillatory trajectories while swimming upstream. Therefore, we investigate cell orientation as a function of velocity and channel position. Because the velocity gradient is on the length scale of the cell itself, each segment of the body may experience a different drag force, influencing cell orientation.

The frequencies of upstream and downstream swimming are summarized in relation to flow velocity in Fig. 4. We find that at low flow velocities (0.1 mm/s), most cells swim upstream (with the flagellum end leading), suggesting that T. brucei swim toward the oncoming flow field (upstream). Depending on the flow velocity, however, there may still be a net cell body movement downstream. The orientation preference is lost once the velocities increase further, and indeed begin to display a small tendency to swim downstream at 1 mm/s flow velocity. Cells that are tumbling to recover one of the two orientations are recorded as having a transition orientation (green in Fig. 4).

Figure 4.

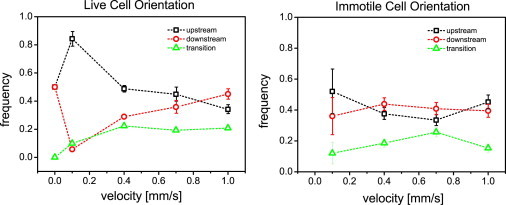
Cell orientation relative to flow for live and immotile cells. For live cells in the absence of flow, an arbitrary direction is chosen for the flow.

In contrast, no significant orientation preference across the velocity spectrum (see Fig. 4) is seen for immotile cells, suggesting that self-propulsion plays an important role in orientation, especially in the lower range of flow velocities. The propulsive force of the cell dominates and allows it to swim upstream. As the shear gradient increases, the corresponding increase in drag dominates the motion of the trypanosome, resulting in the tumbling motion of the cell seen at higher flow velocities.

Orientation order parameter

We investigate the experimentally observed cell behavior at the walls in more detail using an orientation order parameter given by

$$S=\langle \frac{3{\cos }^2\theta -1}{2}\rangle .$$ (3)

Here θ (−90 < θ < 90) is the angle of the end-to-end vector (base to flagellum tip) relative to the flow direction. When cells are aligned to the channel wall, S = 1, whereas random orientation to all possible angles yields S = 0 and an orientation perpendicular to the wall yields S = −1/2. Note that the angle θ is defined as positive if the endpoint closest to the origin of the flow is nearer to the wall than the other end. In general, θ will be similar to ϕ, but the latter relates to the swimming direction and the former relates to the cell geometry. In Fig. 5, the orientation parameter S is presented for both live and immotile cells (red and black) as a function of channel position for different flow velocities. Note that although the cell direction (upstream or downstream swimming) is represented in Fig. 4, the orientation parameter S is a measure of cell tilting with respect to the wall shown in Fig. 5.

Figure 5.

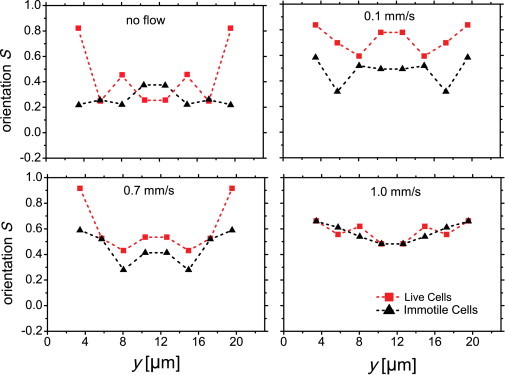
Orientation order parameter for live (red) and immotile (black) cells, shown for a range of velocities. Results are mirrored at the center for improved statistics. In the first panel, orientation without flow is measured by simply choosing a direction for flow.

In the absence of flow, a finite orientation order parameter is observed even for immotile cells due to the confinement by the walls. We note that as live cells approach the walls, they become highly aligned to the walls. Immotile cells are much less oriented across the channel. The most dramatic difference in orientation parameter between live and immotile cells in flow is seen at the lowest velocity. As the flow velocity is increased up to 1 mm/s, we see that the orientation between live and immotile cells converges. In flow, for both live and immotile cells, the orientation order parameter increases close to the walls and away from the channel center, yielding a shallow minimum at the center of the channel. This drop in orientation at the center may be attributed to both the minimum in shear and the reduced steric hindrance, which allow cells to orient, on average, more randomly. Immotile cells appear to be less oriented to the flow, which can be attributed to their tendency to tumble in flow. The results presented above also show that at 0.1 and 0.4 mm/s, self-propulsion dominates the dynamics in flow, but at the higher velocities the shear forces dominate.

The effect of shear rate on mean orientation is shown in Fig. 6. In the absence of flow (and therefore shear), live cells are more aligned than immotile cells. We observe a distinct effect at low flow velocities, showing clearly that live cells are well aligned to the boundaries (S = 0.73) at the lowest measured shear rate. Further increases in shear rate reduce the mean cell orientation. In contrast, immotile cells exhibit a much lower orientation (S = 0.48) at low shear, which shows an increasing trend as shear rate is increased. At the highest shear rate (corresponding to U_ave = 1.0 mm/s), we observe clearly that the effect of self-propulsion is weak, because the live-cell orientation and immotile-cell orientation are equivalent.

Figure 6.

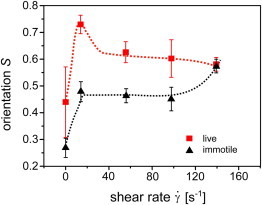
Mean orientation order parameter (for y = 2–20 μm) for live and immotile cells, shown as a function of the mean shear rate. Dashed lines are a guide to the eye.

Cell elongations

The effect of flow on the body of T. brucei is also characterized by the overall elongation of the body. We measure the distance from the flagellum tip to the base of the cell body (the end-to-end distance) for single cells as a function of average flow velocity. In Fig. 7, histograms of the end-to-end distance of the cell for both live and immotile cells show that in the absence of flow, there is no significant difference in the length distribution for live cells as compared with immotile cells. Increasing flow velocities, leading to increased shear stress, result in a more elongated cell shape for immotile cells, in agreement with simulation and experiments for semiflexible polymers (32,33). As we can see, this trend is much less pronounced in live cells. Therefore, although the onset of cell stretching due to flow is the same for live and immotile cells, the end-to-end distance of live cells appears to have little dependence on flow velocity, indicating that even at 1.0 mm/s, T. brucei are able to produce body distortions. We observe that within this range of increasing flow velocities, immotile cells begin to flatten with a linear dependence on flow velocity, whereas live cells are not further straightened. Differences in cell length are assumed to be equivalent in all populations and are therefore averaged out for data sets collected at each velocity. We can therefore liken the cell body to a spring dumbbell following Hooke’s law (cf. inset in Fig. 8), with the drag force acting on the cell body due to fluid flow acting as the stretching force. In previous work, we showed that the end-to-end distance can be used as a measure of cell stiffness (11).

Figure 7.

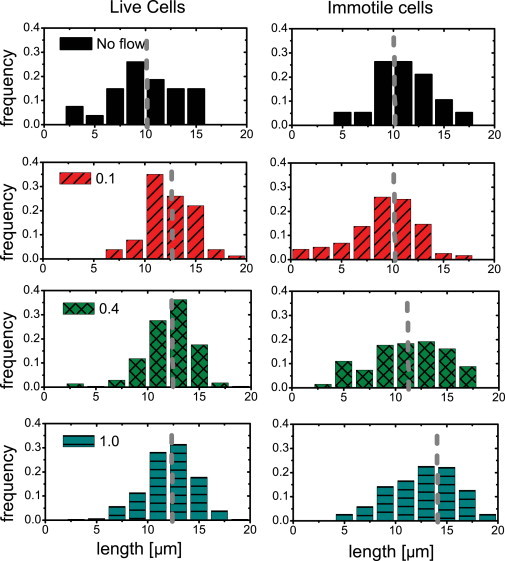
Histograms of end-to-end distance as a function of flow velocity (given in mm/s) for live and immotile cells. Without flow, both live cells and immobile cells exhibit the same average end-to-end distance. Whereas live cells show the same average elongation at all measured flow velocities, immotile cells appear to stretch in response to increased shear. The dashed line indicates the mean.

Figure 8.

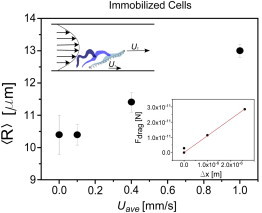
Mean end-to-end distance versus average flow velocity U_ave for immotile cells. Lower inset: Drag force resulting from fluid flow plotted as a function of cell stretching. Upper inset: Trypanosome cell body being stretched in a parabolic flow profile.

Adopting the dumbbell model, the drag force that causes cell stretching is a function of the velocities U₁ and U₂ at each end of the dumbbell and is given in good approximation by F_d = γ|U₂ − U₁|. We take a simplified approach with U₂ − U₁ ∼ U_ave. Taking the radius of the beads of the dumbbells, a, to be 1.5 μm, the drag coefficient can be estimated as γ = 6πηa = 2.8 × 10⁻⁸ kg/s. The drag forces are therefore in the piconewton range and can be plotted versus the cell stretching, given by $\Delta x=\langle R\rangle -\langle R_{eq}\rangle$, where R_eq is the end-to-end distance in the absence of flow, and yield the linear relationship shown in Fig. 8.

Cell stretching, taken as a spring, may therefore be described by Hooke’s law, F = −kx, where k is the stiffness of the cell. The slope of the line in Fig. 8 gives us the value for cell stiffness of k = 1.1 × 10⁻⁵ N/m. The obtained value is approximately twofold greater than that of reported values for red blood cell stiffness, 6 × 10⁻⁶ N/m (34,35). Elongated cells comprised of microtubule cytoskeletons, such as T. brucei, have not been studied in this context. Recent experiments on Vorticella convallaria showed that the cell body is extended in microfluidic flows, and validated the use of flow-induced load to measure cell stiffness (36). Cells that are 10- to 100-fold wider than T. brucei have been reported to have stiffnesses on the order of 10⁻⁴ to 10⁻³ N/m (36–40), reflecting the cross-sectional area A of the cell (the stiffness depends on the elastic modulus E and the length L as k = EA/L). Taking into account the potential change in cell stiffness due to ATP depletion, we find that the stiffness estimate for T. brucei found here is reasonable, and that flow loading is a straightforward method to estimate the stiffness of elongated cells.

Conclusions

Using a relatively simple experimental setup for studying self-propulsion in microfluidic parabolic flow, we observed that the model organism T. brucei exhibited fascinating behavior in flows ranging from 0.02 to 1.0 mm/s. At the lower flow velocities, T. brucei oriented upstream and oscillated from one channel wall to another, following sinusoidal paths. Further increases in flow velocity resulted in more tumbling cells. We expect that the rich range of behaviors observed here are universal physical features of swimmers in parabolic flow. Indeed, the theoretical description provided in this work points to such a generalization. Although live cells retain their ability to bend and distort their bodies, immotile cells begin to stretch as a linear function of flow velocity and therefore can be used to derive cell stiffness. A comparison with immotile cells shows that self-propulsion dominates cell dynamics at mean flow velocities up to 0.4 mm/s. How the observed behavior is affected when obstacles such as blood cells, leukocytes, or even geometrical branching, as found in the bloodstream, are introduced into the environment remains to be investigated.