Cell Mechanics, Structure, and Function Are Regulated by the Stiffness of the Three-Dimensional Microenvironment

Abstract

This study adopts a combined computational and experimental approach to determine the mechanical, structural, and metabolic properties of isolated chondrocytes cultured within three-dimensional hydrogels. A series of linear elastic and hyperelastic finite-element models demonstrated that chondrocytes cultured for 24 h in gels for which the relaxation modulus is <5 kPa exhibit a cellular Young’s modulus of ∼5 kPa. This is notably greater than that reported for isolated chondrocytes in suspension. The increase in cell modulus occurs over a 24-h period and is associated with an increase in the organization of the cortical actin cytoskeleton, which is known to regulate cell mechanics. However, there was a reduction in chromatin condensation, suggesting that changes in the nucleus mechanics may not be involved. Comparison of cells in 1% and 3% agarose showed that cells in the stiffer gels rapidly develop a higher Young’s modulus of ∼20 kPa, sixfold greater than that observed in the softer gels. This was associated with higher levels of actin organization and chromatin condensation, but only after 24 h in culture. Further studies revealed that cells in stiffer gels synthesize less extracellular matrix over a 28-day culture period. Hence, this study demonstrates that the properties of the three-dimensional microenvironment regulate the mechanical, structural, and metabolic properties of living cells.

Introduction

The mechanical properties of cells are known to influence many aspects of cell function, including mechanotransduction (1,2), migration (3), and differentiation (4). Furthermore, these properties also influence intracellular force transmission to the surrounding extracellular matrix during embryonic development, cell motility, and wound healing. Consequently, cellular mechanical properties are of fundamental importance for a wide range of processes, and changes in cell mechanics are associated with conditions such as osteoarthritis, asthma, cancer, inflammation, and malaria (5,6).

Estimation of cellular mechanical properties requires the use of computational or analytical models, the two principal types of which are structure-based models and continuum models. The former include tensegrity (2,7) and percolation models (8), which are appropriate for small finite deformations of the cell (9). By contrast, continuum models, such as linear elastic (10,11), hyperelastic (12–14), and viscoelastic models (15–18), can accommodate larger deformations. Using such models, previous studies have estimated the mechanical properties of cells based on experimental techniques such as micropipette aspiration (15,19,20), atomic force microscopy (AFM) (17,21), cytocompression (22), and laser tweezers (23). All these approaches involve manipulation of individual cells in suspension. However, the majority of cell types exist within a surrounding three-dimensional (3D) tissue microenvironment. Recent evidence suggests that the mechanical properties of the microenvironment can regulate cell structure and function (24).

The initial aim of this study was to determine the suitability of different analytical models for describing the mechanical behavior of cells with a 3D microenvironment. In addition, the study tested the hypothesis that the mechanical properties of the 3D microenvironment influence cell mechanics and that this involves changes in the organization of the actin cytoskeleton and the nucleus. To accomplish this, an inverse finite-element approach (FEA) has been implemented in ABAQUS that utilizes new and previously published experimental data describing the deformation of isolated articular chondrocytes subjected to gross compression within 3D hydrogel scaffolds (25,26). In particular, the study used data showing temporal changes in cell deformation in compressed alginate, which were associated with the viscoelastic stress relaxation of the gel. The use of chondrocytes encapsulated within 3D hydrogels provides additional relevance, since these models have been widely used to investigate mechanotransduction and as a potential tissue-engineering strategy (27,28). The study shows that the mechanical properties of the 3D cellular microenvironment influence cell mechanics, with associated changes in actin cytoskeletal organization and chromatin condensation, as well as long-term regulation of metabolic activity.

Materials and Methods

Cell deformation in 3D hydrogels

In previous studies in the host lab, the deformation of articular chondrocytes has been measured in a range of hydrogel constructs subjected to 20% gross compressive strain applied via a compression platen (25,26). The chondrocytes were isolated using a well established sequential enzyme digestion procedure and encapsulated, at a concentration of 10⁶ cells mL⁻¹, in either alginate or agarose constructs. In each case, different concentrations of gel were used, namely 1.2% and 2% (w/v) GMB low-viscosity alginate gel (Kelco, Atlanta, GA), and 1% and 3% (w/v) agarose (type IX; Sigma, St. Louis, MO). Both alginate and agarose showed characteristic viscoelastic stress relaxation over a 1-h period of static compression with mechanical properties that were dependent on the gel type and concentration (Fig. 1, a and b). After 24 h in culture in Dulbecco’s modified Eagles medium plus 20% fetal calf serum, gross static compression resulted in chondrocyte deformation from a rounded to an oblate ellipsoid morphology. This was quantified by a deformation index (I) representing the ratio of cell diameters parallel (y) and perpendicular (x) to the axis of compression (Eq. 1). The deformation index can be used to estimate the axial cell strain (ε_y) based on previously validated assumptions of symmetry and volume conservation (29) (Eq. 2):

$$I=y/x$$ (1)

$${\epsilon }_y={\left(I\right)}^{\frac{2}{3}}-1.$$ (2)

Figure 1.

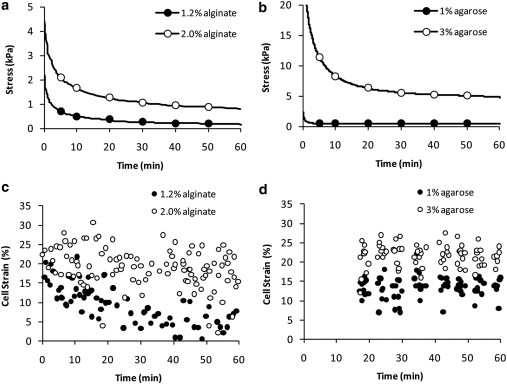
Experimental data used for modeling chondrocyte mechanical properties. The data show gross viscoelastic stress relaxation (a and b) and cell deformation (c and d) in compressed alginate (a and c) and agarose (b and d) constructs. The freshly isolated cells were cultured in the 3D constructs for 24 h and then held at 20% static compression. Applied stress and cell deformation were recorded over the subsequent 60-min period.

During the 1-h period of static compression applied after 24 h in culture, chondrocytes exhibited temporal variation in cell deformation that was dependent on the mechanical properties of the hydrogel (Fig. 1, c and d). In this study, values of cell strain were then plotted against corresponding instantaneous stress to generate cellular stress-strain data to which different computational FEA models have been fitted to estimate the material properties of the chondrocytes.

Finite-element model

A two-dimensional (2D) axisymmetric finite-element (FE) model was created using ABAQUS 6.9 with a cell volume fraction based on the experimental cell density of 10⁶ cells mL⁻¹. The cell was assumed to adopt a spherical morphology in the unstrained state, with a diameter of 10 μm based on previous measurements of isolated bovine articular chondrocytes seeded in hydrogel constructs (26). For inhomogenous models, the nucleus was assumed to be centrally located and to have a diameter of 6 μm. The density of the FE mesh was designed to increase with proximity to the cell (Fig. 2). The entire 3D model has rotational symmetry, with boundary conditions as described in Fig. 2. Large deformation was considered in the FE model analysis and Nlgeom was enabled.

Figure 2.

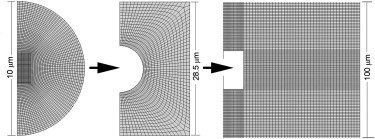
Details of the composite finite-element mesh for compression of cells in 3D hydrogels. The cell is modeled as a spherical inclusion within the gel such that the entire 3D model has rotational symmetry. Roller boundary conditions were applied to the bottom of the compression platen, with frictionless contact between the gel and the platen. The bottom of the construct was fixed in the vertical direction and the displacement was applied on the top of the construct. The symmetric boundary condition was applied at the center lines of the cell and 3D scaffold.

Linear elastic models

The cell was initially modeled as a homogenous linear elastic material. The Poisson’s ratios for alginate and agarose were taken from previous studies, with values of 0.31 (30) and 0.49 (31), respectively. An effective Poisson’s ratio of 0.49 was adopted for the chondrocyte based on published measurements of cell deformation in equivalent alginate and agarose constructs (26). The cellular Young’s modulus (E_cell) was estimated to be the value that yielded the best fit to the experimental data relating instantaneous cell strain to applied stress (Fig. 3 a). Although the cellular stress-strain behavior shows some nonlinearity, we have utilized the Young’s modulus as in numerous other studies, by considering the modulus at the point when the cell reaches its equilibrium after cellular stress relaxation.

Figure 3.

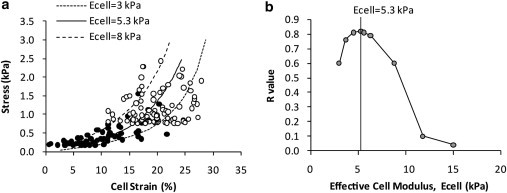
Linear elastic model with a cell modulus of 5.3 kPa provides the best fit to the data for cell deformation in 1.2% and 2% alginate gel. (a) The results of three different linear elastic models with effective moduli (E_cell) of 3, 5.3, and 8 kPa are shown against the experimental data from Fig. 1 (26). (b) The corresponding R values for these and other models are plotted against modulus, indicating that the highest R value corresponds to a cell modulus of 5.3 kPa.

It is reported that the cytoplasm has an effective Young’s modulus of 0.5–4 kPa, with a nucleus that is up to 10 times stiffer (10,32). Therefore, further studies used an inhomogenous FEA model with separate Young’s moduli for the cytoplasm (E_cyto) and the nucleus (E_nuc). The effective Poisson’s ratios for the cytoplasm and the nucleus were set at 0.49 and 0.40, respectively, based on previous experimental findings (33). Composite deformation theory (34) was used to provide a further estimate of the cell modulus (E_cell) based on the cytoplasm and nucleus moduli determined from the best fit to the experimental data (Eq. 3),

$$\frac{E_{cell}}{E_{cyto}}=\left[1+\frac{\left(\frac{m}{\left(A_n/A_c\right)}-1\right)\varphi }{1+\frac{\left(1-\varphi \right)\left(\frac{m}{\left(A_n/A_c\right)}-1\right)}{1+2A_c}}\right]\times \frac{A}{A_c},$$ (3)

where $m=E_{nuc}/E_{cyto}$, $A_n=1-2{\nu }_{nuc}/1+{\nu }_{nuc}$, $A_c=1-2{\nu }_{cyto}/1+{\nu }_{cyto}$, $A=1-2\left[{\nu }_{nuc}\varphi +{\nu }_{cyto}\left(1-\varphi \right)\right]/1+\left[{\nu }_{nuc}\varphi +{\nu }_{cyto}\left(1-\varphi \right)\right]$, and ν is Poisson’s ratio. The subscripts cyto and nuc represent the cytoplasm and nucleus, respectively. φ is the volume fraction of the nucleus, which in this case is 0.216.

Hyperelastic models

Due to its simplicity, the neo-Hookean (NH) model, also known as the Gaussian model, is one of the most widely used hyperelastic models. For example, it has been successfully used to model the deformation of single cells in a microplate compression system (35). For an incompressible material, the NH model adopts the energy function (36)

$$W=C_1\left({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2-3\right),$$ (4)

where W is the strain energy density and λ_j (j = 1,2,3) are the three principal stretch ratios. The Young’s modulus, E_cell, is given by

$${\mathit{E}}_{\mathit{cell}}=6{\mathit{C}}_1.$$ (5)

Other, more sophisticated hyperelastic models have also been developed, such as the polynomial and Ogden models. The strain energy function for the former is given by the equation (37)

$$W=\sum _{i+j=1}^N{C}_{ij}{\left({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2-3\right)}^i{\left(\frac{1}{{\lambda }_1^2}+\frac{1}{{\lambda }_2^2}+\frac{1}{{\lambda }_3^2}-3\right)}^j.$$ (6)

In this model, the Young’s modulus, E_cell, is given by

$${\mathit{E}}_{\mathit{cell}}=6\left({\mathit{C}}_{10}+{\mathit{C}}_{01}\right).$$ (7)

The Ogden model can describe a wide range of strain hardening characteristics and, as described in previous studies (36,37), it takes the form

$$W=\sum _{i=1}^n\frac{2{\mu }_i}{{\alpha }_i^2}\left({\lambda }_1^{{\alpha }_i}+{\lambda }_2^{{\alpha }_i}+{\lambda }_3^{{\alpha }_i}-3\right),$$ (8)

where α_i is strain hardening (or stiffening) exponent. The constants μ_i are related to the initial Young’s modulus, E_cell, by

$$E_{cell}=3\sum _{i=1}^n{\mu }_i$$ (9)

For all these hyperelastic models, the term with elastic volume ratio is assumed to be zero based on the assumption of constant cell volume during deformation. The derivation of the Young’s modulus is given in the Supporting Material. The NH, Ogden, and polynomial models were fitted to the experimental data describing instantaneous cell deformation in 1.2% and 2% alginate gels compressed after 24 h in culture.

Quantification of chondrocyte actin and nucleus organization in 1% and 3% agarose gels

Further experiments were performed to determine whether chondrocytes cultured in 1% and 3% agarose exhibited differences in the organization of the actin cytoskeleton and the nucleus, which may contribute to overall cellular mechanical properties. Bovine articular chondrocytes were isolated as previously described (29) and seeded in either 1% or 3% agarose (w/v; type IX; Sigma). After 1 h, 5 h, 18 h, and 24 h in culture, separate groups of cells were fixed in 4% formaldehyde (15 min at 37°) and stained with Alexa 564-Phalloidin and Hoescht-33258. Cells were then washed in phosphate-buffered saline and visualized using confocal microscopy (SP2, Leica, Wetzlar, Germany). For analysis of actin organization, a single 2D confocal section image was obtained bisecting the center of each individual cell visualized in both 1% and 3% agarose specimens. The same imaging settings were used throughout. Single 2D confocal section images were also obtained bisecting the center of each chondrocyte nuclei. Approximately 40–80 cells were visualized for each experimental condition or time point.

Actin organization was quantified by creating a region of interest in the form of a beigel consisting of two concentric circles, the outer of which follows the cell periphery and the inner with a radius 1 μm less than the outer. The mean Alexa-phalloidin intensity within the beigel region between the two circles represented the level of cortical actin staining (I_cortical) and was normalized to the mean cytoplasmic intensity within the inner circle (I_cytoplasm) in an approach similar to that previously described by Erickson et al. (38) (Eq. 10):

$$\text{cortical}\text{actin}\text{ratio}=\frac{I_{cortical}}{I_{cytoplasmic}}$$ (10)

Due to differences in the penetration of the Alexa-phalloidin into the different-density agarose gels, it was necessary to normalize the cortical actin ratio to that measured in cells fixed immediately after seeding in agarose, when it was assumed that actin organization would be the same in both gels.

Nucleus organization was quantified from the confocal images by measuring the degree of chromatin condensation using a previously validated automated image analysis approach in MatLab. The images were filtered using a Sobel edge-detection filter, and measurement of the density of edges yielded a chromatin condensation parameter that correlated well with an independent visual inspection.

Temporal changes in cell mechanics

Further experiments were conducted to examine the time course over which changes in cell mechanics develop in response to the 3D microenvironment. Isolated chondrocytes were seeded in 1% and 3% agarose gel (w/v) and confocal microscopy was used to measure cell deformation in response to 20% gross compression after both 1 and 24 h in culture, as previously described (25,26). After a 10-min period of stress relaxation, cells were visualized in the compressed agarose constructs and cell strain parallel to compression was estimated from the ratio of parallel and perpendicular cell diameters (Eqs. 1 and 2). The linear elastic models for cells in 1% and 3% agarose were used to estimate the effective cell modulus based on the mean cell strain for samples of individual cells (n = 75–100).

Measurement of extracellular matrix synthesis in 4% and 2% agarose gels

Finally, studies were conducted to examine the influence of the 3D microenvironment on the metabolic activity of the chondrocytes in terms of cell proliferation and the elaboration of extracellular matrix. Isolated bovine articular chondrocytes were seeded into either 2% or 4% agarose constructs (5 mm diameter × 5 mm height; w/v; type IX; Sigma) at a concentration of 4 × 10⁶ cells mL⁻¹. Individual constructs were cultured in 2 mL Dulbecco’s modified Eagle’s medium plus 20% fetal calf serum, with media changed every 48 h over a 28-day culture period, and all media were retained for subsequent analysis. Separate groups of constructs were removed from culture at days 1, 3, 9, 15, 22, and 28. Constructs (n = 6) and associated cumulative media samples were assayed for total sulfated glycosaminoglycan (sGAG) content using the well established DMB method. Cell proliferation within the agarose constructs was measured using a standard DNA assay. Separate constructs at each time point were fixed and processed for histology by staining the proteoglycan with Safranin O.

Results

Linear elastic properties of chondrocytes

Linear elastic FE models were fitted to experimental data describing the cell strain and instantaneous stress for chondrocytes compressed in 1.2% and 2% alginates. Fig. 3 a shows the FE model data for three selected cell moduli (E_cell = 3, 5.3, and 8 kPa) against the experimental data. The cell modulus was varied over the range 3–15 kPa and the corresponding R values were calculated. Fig. 3 b shows that the best fit (R = 0.81) was observed with an effective cell modulus of 5.3 kPa after 24 h in culture.

Hyperelastic properties of chondrocytes

Various hyperelastic models were used to describe the cell deformation in 3D alginate constructs. Both the Ogden model, with strain hardening exponents α₁ = 4, α₂ = 5.78, and α₃ = 0.71, and the polynominal model provided a reasonable fit to the experimental data as shown in Fig. 4, a and b, respectively. The NH model provided a less effective fit, particularly at higher strains (Fig. 4 c). The resulting cellular Young’s moduli (E_cell) values derived, after 24 h in culture, using the Ogden, polynomial, and NH models were 4.3, 4.4, and 3.7 kPa, respectively.

Figure 4.

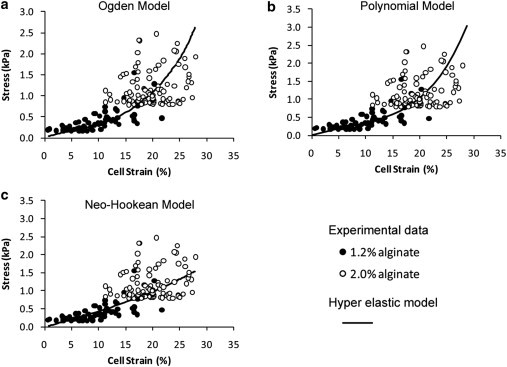
Hyperelastic models predict cell deformation in compressed alginate constructs. The results of three different hyperelastic models fitted to the experimental data of instantaneous gross stress and cell strain in 20% compressed alginate constructs as shown in Fig. 1 (26). The Ogden Model (a), the Polynomial model (b), and the NH model (c) produced effective cell moduli of 4.3, 4.4, and 3.7 kPa, respectively.

The influence of the stiffness of the 3D microenvironment on cell mechanics

The inverse FE approach using the linear elastic model was extended to chondrocytes embedded in 1% and 3% agarose gel. However, in this case, the viscoelastic stress relaxation properties of agarose are such that the cell deformation showed minimal temporal variation over the measured time period of 10–60 min after the start of compression (Fig. 1). Therefore, the effective cell modulus was varied over the range 2–25 kPa to produce a cell strain that most closely matched the experimental value (Fig. 5 a). For 1% agarose, the mean cell strain was 18.7% when compressed after 1 h in culture (data not shown) and 13.8% when compressed after 24 h (Fig. 1 d). These values of cell strain were best simulated with a cell modulus of ∼2.7 kPa at 1 h and 5.0 kPa at 24 h, the difference being statistically significant (p < 0.001) (Fig. 5 b).

Figure 5.

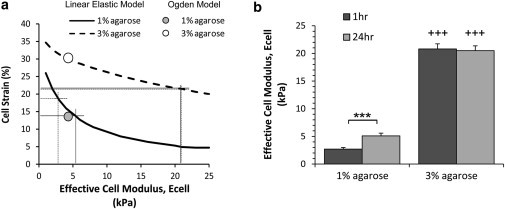
Relationship between the effective cell modulus, E_cell, and the predicted cell strain in compressed 1% and 3% agarose enables analysis of temporal changes in cell mechanics. (a) The influence of E_cell on the cell strain estimated using the linear elastic model. The hyperelastic Ogden model produced accurate estimates of cell strain in 1% agarose (14%) when optimized to experimental data for cells cultured for 24 h in alginate. However, the Ogden model overestimated the cell strain in 3% agarose (31%), suggesting that the modulus in 3% agarose may be substantially larger than that predicted in the softer alginate. The linear elastic models best match the experimental cell strain values in 1% and 3% agarose at moduli of 5.3 kPa and 20 kPa, respectively. (b) The relationship between modulus and cell strain may be used to derive the temporal changes in cell mechanics for chondrocytes in 1% and 3% agarose after 1 h and 24 h in culture. Values represent mean cell moduli ±SD based on the mean experimental cell strain values at 20% gross compression.

By contrast, in the stiffer 3% agarose the cell strain was approximately equal to the applied strain, with a mean value of ∼21% at both time points. When using the linear elastic model, this was best simulated with a cell modulus of 20 kPa, which is substantially stiffer than the moduli predicted in 1% agarose or 1.2% and 2% alginate (Fig. 5).

Similarly, the hyperelastic Ogden model was used to predict the equilibrium cell strain in 1% and 3% agarose gels compressed to 20% gross strain after 24 h in culture (Fig. 1 d). A cell modulus of 4.3 kPa was used based on the optimized value for 1.2% and 2% alginate (Fig. 4). In 1% agarose, this cell modulus value, derived for cells in alginate, produced a close estimate of the experimental cell strain obtained after 24 h in 1% agarose gel (Fig. 5 a). However the predicted cell strain in 3% agarose was substantially greater than the experimental cell strain (Fig. 5 a). This further confirmed the findings from the linear elastic model that the cell modulus in 3% agarose is substantially greater than that in the softer 1% agarose or 1.2% and 2% alginate.

Linear elastic properties of cytoplasm and nucleus

When the cell nucleus was included in the linear elastic FE model, the computed cell strain was heavily influenced by the prescribed values for E_cyto and E_nuc. As shown in Fig. 6 a, values of E_cyto = 3 kPa and E_nuc = 11 kPa result in a good agreement between the simulated cellular stress-strain relationship and the experimental data derived for 1.2% and 2% alginate compressed after 24 h in culture. The corresponding R values for various combinations of E_cyto and E_nuc are displayed in Fig. 6 b. This shows that in alginate gels, if E_cyto > 2 kPa, then the best fit occurs with E_nuc = 10–15 kPa. However it is not possible to predict a more precise value, since the model produced similar maximum R values for a variety of combinations of E_cyto and E_nuc where E_cyto = 2–5 kPa (Fig. 6 b). If the effective cytoplasm modulus E_cyto is assumed to be in the range 1–10 kPa, and the ratio E_nuc/E_cyto in the range 1–10, then the effective cell modulus given by Eq. 3 can be plotted as shown in Fig. 6 c.

Figure 6.

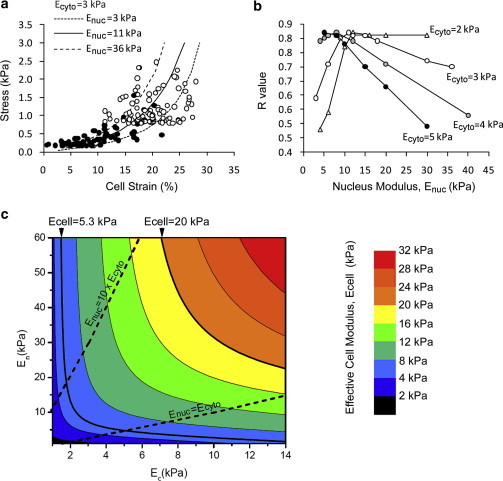
Relative influence of the cytoplasm and the nucleus on gross cell mechanics. (a) The results of the linear elastic models with nucleus moduli (E_nuc) of 3, 11, and 36 kPa and cytoplasmic modulus (E_cyto) of 3 kPa. The models have been fitted to the experimental data of instantaneous gross stress and cell strain in 20% compressed alginate constructs, as shown in Fig. 1. (b) The corresponding R values for linear elastic models with a nucleus modulus of 3–40 kPa and a cytoplasmic modulus of 2, 3, 4, or 5 kPa. The data indicate that the best fit occurs with a nucleus modulus of ∼10 kPa. (c) Contour plot showing the relative effect of cytoplasm and nucleus moduli (E_cyto and E_nuc) on the resulting cell modulus (E_cell) based on the linear elastic models. The contours are indicated separately for a cell modulus of 5.3 and 20 kPa, representing the predicted values for cells in 1% and 3% agarose.

The influence of agarose concentration on actin and nucleus organization

Chondrocytes in both 1% and 3% agarose exhibited cortical actin staining (Fig. 7 a) similar to that reported previously for isolated chondrocytes (33,39) and cells in situ within articular cartilage (40). Quantification of cortical actin intensity showed that cortical actin organization in cells in 3D agarose constructs increased with time in culture, with significant differences observed after 18 and 24 h. In cells in 3% agarose relative to those in 1% agarose, normalized actin organization increased more rapidly, such that there was a significantly greater level of organization at 18 and 24 h, with statistically significant differences (p < 0.001; Fig. 7 b).

Figure 7.

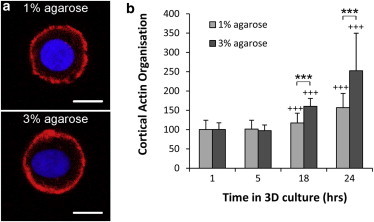
Cells in 3% agarose develop greater cortical actin organization compared to those in 1% agarose. (a) Confocal section images showing the chondrocytes after 24 h in 1% and 3% agarose gel. F-actin was labeled with Alexa 564-Phalloidin (red, outer ring) and the nuclei with Hoescht (blue, central area). Scale bars, 5μm. The level of actin organization was quantified by measuring the mean Alexa 564-Phalloidin intensity within the cortical region and dividing by the cytoplasmic intensity to yield the cortical actin ratio, which was normalized to values at 1 h to account for variation in stain penetration. (b) The normalized cortical actin ratio increased with time in culture and at 18 and 24 h was significantly greater for cells in 3% agarose compared to cells in 1% agarose (^∗∗∗p < 0.001). Values are represented as the mean ± SE (n = 40–80).

Chromatin condensation in the nucleus was successfully quantified using the Sobel edge-detection method (Fig. 8, a and b). With increasing time in culture, there was a steady reduction in chromatin condensation, with significant differences detected after 5 h. Cells in 3% agarose showed a slower reduction in chromatin condensation such that after 24 h in culture these cells had a significantly greater level of chromatin condensation compared to those in 1% agarose (p < 0.001; Fig. 8 c).

Figure 8.

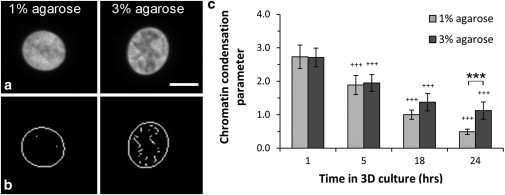
Cells in 3% agarose develop greater chromatin condensation compared to those in 1% agarose. (a) Confocal section images of chondrocytes in 1% and 3% agarose gel showing the nuclei labeled with Hoescht and the higher level of chromatin condensation in the 3% gel after 24 h in culture. Scale bars, 5 μm. (b) Corresponding images that have been digitally filtered to reveal the density of edges, from which the chromatin condensation parameter was calculated (see text for details). (c) Chromatin condensation decreased with time in culture, but by 24 h the levels were significantly greater for cells in 3% agarose (^∗∗∗p < 0.001). Values are represented as the mean ± SE (n = 60).

Extracellular matrix synthesis is regulated by the composition of pericellular microenvironment

Chondrocytes in both 2% and 4% agarose synthesized proteoglycan, as detected by substantial increases in sGAG content. Cells in the softer, 2% agarose synthesized more sGAG than did those in the 4% agarose, with statistically significant differences in sGAG content both within the constructs (Fig. 9 a) and released to the media (Fig. 9 b). The proteoglycan retained within the agarose constructs formed a dense pericellular matrix around individual cells or groups of divided cells. In the 2% agarose, the pericellular matrix and associated clumps of cells were of a spherical morphology. By contrast, these chondron-like structures in 4% agarose were noticeably more elongated and columnar, as shown in Fig. 9, c and d. There was no significant difference in the proliferation of cells in the two gels as quantified by the DNA assay (data not shown).

Figure 9.

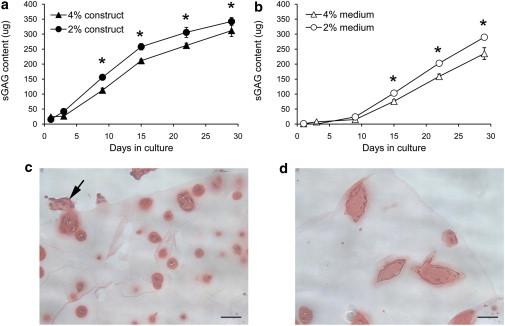
Cells in 2% agarose synthesize more proteoglycan than cells in 3% agarose. (a) sGAG content retained within the 2% and 4% agarose constructs. (b) Cumulative amount of sGAG released to the associated culture media over a 28-day culture period. Values represent mean ± SD for n = 6 constructs. Differences are statistically significant at p < 0.05. (c and d) Staining with Safranin O revealed that the proteoglycan formed a dense pericellular matrix around individual cells and groups of recently divided cells, with a more elongated columnar morphology in the stiffer scaffolds. In some cases the cells and matrix expanded out of the agarose constructs (arrow).

Discussion

This study utilized both new and previously published experimental data describing the deformation of isolated bovine articular chondrocytes compressed in different concentrations of agarose and alginate gel (Fig. 1) (25,26). These model systems maintain chondrocytic phenotype, with the cells adopting a rounded morphology and actin cytoskeletal organization similar to that observed in situ (40). The models have proved popular for examining the role of cell deformation in chondrocyte mechanotransduction (27,29) and the potential benefits of mechanical stimulation within a tissue-engineering strategy for cartilage repair (28). The mechanical properties of chondrocytes embedded in these hydrogels is therefore important for understanding the cellular response to compression and learning more about the relationship between cell mechanics and the biophysical properties of their extracellular environment.

The experimental cell deformation data and corresponding instantaneous stress in the gel were modeled using an inverse finite-element approach with either a linear elastic or hyperelastic model (Fig. 2). These models assume that the cell is in a state of mechanical equilibrium under the experimental conditions. This is justified by the fact that the time constant for the 3D constructs (26,41) is substantially greater than that for the chondrocytes, which is ∼30 s (15,16,18). Therefore, under the test conditions of 20% compressive strain applied at a strain rate of 20% min⁻¹, it is reasonable to assume that the chondrocyte reaches equilibrium before stress relaxation of the constructs. At these levels of strain and strain rate, it is generally accepted that the linear elastic model accurately describes the behavior of viscoelastic materials such as living cells. Indeed, this study demonstrates a close agreement between the optimal linear elastic model and the experimental data for cell deformation in 1.2% and 2% alginate gels (Fig. 3). Using the linear elastic model, the cell modulus was estimated at 5.3 kPa after 24 h in 3D culture. This modulus value is almost 10 times larger than the values previously reported for isolated chondrocytes in suspension subjected to localized deformation using micropipette aspiration, 0.5–1 kPa (25,42,43), or atomic force microscopy, 0.2–0.5 kPa (44). The values presented are closer to the value of 1–3 kPa, obtained by cytocompression, which produces a similar gross cell deformation (18,22). Indeed, it should be noted that the results agree well with previous estimates of 3–4 kPa based on cell deformation in 3D scaffolds, although the modeling in those previous studies is less sophisticated than that employed here (25,26,45). In this study, three different hyperelastic models, namely the Ogden, polynomial, and NH, were also used to fit the experimental data for cell deformation in alginate. The associated values for cell moduli in alginate matched very closely with those generated using the linear elastic model (Fig. 4). The fit was noticeably better for the Ogden and polynomial models, compared to the more simplistic NH model, indicating the suitability of these two hyperelastic models, as well as the linear elastic model, for describing cell deformation behavior in compressed 3D alginate gels.

The models were then extended to describe the cell deformation behavior in 1% and 3% agarose. The 1% agarose has a relaxation modulus similar to that of 1.2% and 2% alginate, whereas the 3% agarose is at least five times stiffer, with a relaxation modulus of ∼25 kPa at 20% compressive strain (Fig. 1). Using a modulus value of 5.3 kPa derived for 1.2% and 2% alginate, the linear elastic and Ogden hyperelastic models accurately predicted the cell strain in 1% agarose compressed after 24 h in culture (Fig. 5 a). However, in the stiffer, 3% agarose, both models significantly overestimated the cell deformation at 24 h. It was only by increasing the cell modulus to 20 kPa that the linear elastic model generated cell strains that matched the experimental data (Fig. 5 b). Using the linear elastic model to estimate cellular Young’s moduli from measurements of cell strain indicates that cells in 1% agarose show a small increase in stiffness over 24 h, whereas those in the 3% agarose scaffolds appear to rapidly reach a peak modulus of ∼5 kPa (Fig. 5 b). These data therefore suggest that the cells adapt to the mechanical properties of the surrounding 3D scaffold by altering their cellular mechanical properties. This is supported by previous studies in 2D systems, which reported that cell stiffness is regulated by the properties of the underlying substrate (46). For example, primary epithelial cells show an increase in stiffness associated with culture on plastic substrates (47), whereas epithelial carcinoma cells show a similar stiffening with passage on glass (48).

The linear elastic model facilitates the examination of the mechanical contribution of specific intracellular components of the cell to its overall mechanical response. Using this approach, we show that the nucleus is several times stiffer than the cytoplasm, in agreement with previous studies (10,32). The difference in Young’s modulus between cells in 1% and 3% agarose may be associated with differences in the nucleus and/or the cytoplasmic modulus (Fig. 6). The latter is largely governed by the properties of the actin cytoskeleton (46), which in chondrocytes in situ or in 3D culture forms a cortical mesh (Fig. 7 a) (29). Actin organization of cells in 2D monolayer culture is known to be regulated by the mechanical properties of the substrate (49,50). Here, we demonstrate a similar phenomenon in 3D, such that chondrocytes in agarose show an increase in cortical actin organization over the culture period, with cells in 3% agarose having greater organization than those in 1% agarose after 18 and 24 h in culture (Fig. 7 b). This correlates with the increase in cell modulus and supports the suggestion presented in previous studies that endothelial cells also show increases in actin morphology and cell mechanics after culture in stiffer 3D gels (51).

In addition, we show a difference in nucleus morphology with a reduction in chromatin condensation during culture, which suggests that changes in nucleus mechanics are not responsible for the increased cell modulus in 3D scaffolds (Fig. 8 b). However, cells in 3% agarose did show higher levels of condensation after 24 h, possibly associated with the changes in actin organization, as reported for cells in 2D monolayer cultures (52).

Examination of the early changes in cell mechanics and organization indicates that after only 1 h in culture, cells in 3% agarose are already substantially stiffer than those in 1% agarose, based on differences in the cell strain analyzed using the linear elastic model. However, at this time point there are no differences in actin organization or chromatin condensation between cells in 1% and those in 3% agarose. The reason for this is unclear, but it may be the result of other factors influencing cell mechanics at these early time points or of inaccuracy in the modeling of cells in stiffer 3D gels. One possibility is that the modeling assumes a single Poisson’s ratio of 0.49 for both the cell and agarose based on previous studies. However, conservation of cell volume suggests that the cell Poisson’s ratio increases with cell strain, with a value of 0.59 at 20% strain. Thus, the higher levels of cell strain predicted in stiffer 3D scaffolds may not occur in practice.

Finally, in addition to showing how the mechanical properties of the 3D scaffold influence cell mechanics and structural organization, we have also shown alterations in matrix synthesis and accumulation, with cells in softer gels synthesizing more proteoglycan (Fig. 9). This has important implications for the development of tissue-engineering scaffolds, suggesting a necessary compromise between the ability to provide structural support and the need to maximize matrix synthesis. The presence of this pericellular matrix ultimately prevents cell deformation in compressed hydrogels, such that it is not possible to derive data describing the mechanical properties of cells maintained in 3D culture for longer than 24 h (53). However, it is likely that the presence of pericellular matrix will further modulate cellular structure/function and mechanics.

In summary, this study uses an array of computational and experimental approaches to model the mechanical properties of chondrocytes in 3D scaffolds. We demonstrate that chondrocytes appear significantly stiffer when cultured in 3D scaffolds compared to when tested in suspension cultures. Using this approach, we demonstrate how the mechanical properties of the 3D microenvironment regulate cell mechanics such that stiffer scaffolds produce stiffer cells. Furthermore, we demonstrate that differences in the mechanical properties of the 3D scaffold are associated with alterations in the mechanical, structural, and downstream metabolic behavior of the cells. Thus, changes in extracellular mechanics caused by factors such as aging, injury, disease, and development may regulate cell mechanics, with resulting changes in cell structure and function.