Transcription Stochasticity of Complex Gene Regulation Models

Abstract

Transcription is regulated by a multitude of factors that concertedly induce genes to switch between activity states. Eukaryotic transcription involves a multitude of complexes that sequentially assemble on chromatin under the influence of transcription factors and the dynamic state of chromatin. Prokaryotic transcription depends on transcription factors, sigma-factors, and, in some cases, on DNA looping. We present a stochastic model of transcription that considers these complex regulatory mechanisms. We coarse-grain the molecular details in such a way that the model can describe a broad class of gene-regulation mechanisms. We solve this model analytically for various measures of stochastic transcription and compare alternative gene-regulation designs. We find that genes with complex multiprotein regulation can have peaked burst-size distributions in contrast to the geometric distributions found for simple models of transcription regulation. Burst-size distributions are, in addition, shaped by mRNA degradation during transcription bursts. We derive the stochastic properties of genes in the limit of deterministic switch times. These genes typically have reduced transcription noise. Severe timescale separation between gene regulation and transcription initiation enhances noise and leads to bimodal mRNA copy number distributions. In general, complex mechanisms for gene regulation lead to nonexponential waiting-time distributions for gene switching and transcription initiation, which typically reduce noise in mRNA copy numbers and burst size. Finally, we discuss that qualitatively different gene regulation models can often fit the same experimental data on single-cell mRNA abundance even though they have qualitatively different burst-size statistics and regulatory parameters.

Introduction

Transcription operates in a stochastic manner and depends on many molecular factors. Recent studies suggest that eukaryotic transcription proceeds in a quasiordered sequence of covalent histone modifications and protein complex formation on chromatin (1–3). Activators recruit a multitude of proteins to initiate transcription (4). Nucleosomes are repositioned and evicted to facilitate DNA access and protein complex assembly, culminating in an assembled elongation-competent RNA polymerase II (5). Dozens of proteins in large assemblies have been implicated in transcription regulation, e.g., SAGA, mediator, SWI/SNF, and generalized transcription factors (6). Although prokaryotic transcription often relies on a smaller number of proteins, gene regulation still depends on several factors, such as transcription factors, a sigma-factors, RNA polymerase, and in some cases DNA looping.

Single-cell studies show that transcription can proceed in a bursty fashion and bring about large cell-to-cell heterogeneity (7–10). Although bursts in prokaryotes have been mostly attributed to translation or leaky repression (11–14), the origin of bursts in eukaryotes is less clear. Transcription bursts in yeast have been linked to the quality of the TATA box and its role in determining the frequency of transcription reinitiation (15). Nucleosome remodeling and eviction have been shown to influence the rate and noise of gene expression (16–19).

The stochastic model of transcription that is most commonly used is the two-state model of gene expression. Its advantage is that the burst-size distribution and the stationary mRNA copy-number distribution can be obtained analytically (11,14,20,21). In this model, a gene switches between an on-and off-state and mRNA is produced during the on-phase. It is assumed that each of these processes relies on a single rate-limiting step and as a result, these processes are described by first-order reactions (10,20,22–26). Although this is indeed what is expected for a simple regulation mechanism, involving a single protein that induces gene switching between two activity states, even many prokaryotic genes are known to have more complex regulatory mechanisms. For eukaryotic genes, which typically involve large numbers of regulatory proteins and cofactors, there is no a priori reason to assume that a single step for each transition would be rate-limiting. A few experimental and theoretical studies do therefore consider multistep models where transitions between on-and off-state include multiple reactions (7,16,18,28,29). In these studies, the design of the model was guided by prior knowledge about the system, either in terms of different possible nucleosome states (for the PHO5 gene (16,18)) or of known complexes of general transcription factors (7). Theoretical studies that are more recent extend these approaches and calculate stochastic measures for systems with arbitrary promoter complexity while retaining synthesis and degradation as single-step reactions (30–32).

In this work, we derive stochastic models for gene expression starting from the probability distributions for the lifetimes of on-and off-states as well as the waiting times between consecutive transcription initiation events. In this way, we can deal with complex molecular mechanisms for transcription regulation in a coarse-grained manner. In contrast to previous methods, the approach is not limited to a specific Markov chain description of possible promoter states. Instead, we offer analytical solutions for families of waiting-time distributions for on-and off-states where the shape of the waiting-time distribution is a parameter of the model. Hereby we can efficiently model a whole range of different gene-regulation mechanisms. Our approach allows us to treat the number of promoter states and possible transitions between them as variables, which are incorporated into the waiting-time distribution for gene state transitions. Through this approach, we can directly compare the stochastic properties of genes. In this article, we focus on comparisons of the probability distributions of mRNA copy numbers and of burst size and consider several novel extensions, such as mRNA degradation during the gene’s on-phase and genes with deterministic switch times. Finally, we discuss contemporary limitations of model-based analysis of experimental data on single molecule counting of mRNA (e.g., mRNA FISH).

Results

Complex transcription regulation mechanisms

Transcription regulation typically depends on the concerted action of several proteins. In prokaryotes, transcription regulation is typically less complex than in eukaryotes but also there several proteins are required. Experimental evidence suggests that the eukaryotic mechanism follows an ordered, multistep and cyclic mechanism involving a sequence of transitions between distinct chromatin states (1–3,33). One interpretation of this data is that each transition involves reversible protein complex formation on chromatin followed by irreversible histone modifications, as shown in Fig. 1 A. These modifications sensitize chromatin for the assembly of the next complex in the sequence. We shall refer to this model as the “molecular ratchet model”. In this model, some of the chromatin states are transcriptionally permissive, and together make up the on-phase of the gene and allow for (repeated) multistep assembly of the preinitiation complex and promoter escape.

Figure 1.

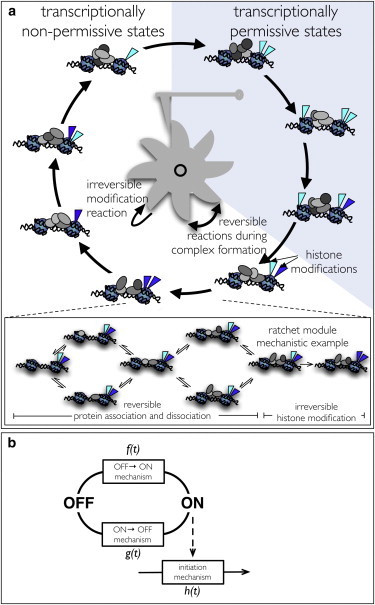
Molecular-ratchet model of the basal design of eukaryotic transcription. (a) A eukaryotic gene is displayed that switches between on- and off-states via a sequence of transitions that involve reversible protein complex formation on chromatin followed by covalent-histone modifications that mark progress and sensitize chromatin for the next protein complex assembly. (b) Coarse-grained view of the molecular ratchet where the duration distributions of the on- and off-states and transcription initiation (involving PIC formation, open complex formation, and promotor escape) are given by general first-passage time distributions f(t), g(t), and h(t). The first-passage time distributions can be obtained from a molecular mechanism for ratchet transitions.

In the molecular ratchet model, the time that a single gene spends in its on- or off-state and the time between consecutive transcription initiation events are random variables that depend on the kinetics of the underlying molecular mechanisms. These times are sampled from the waiting-time distributions f(t), g(t), and h(t) (Fig. 1 B), which correspond to the first-passage time distribution of the underlying molecular mechanism. In analytical studies, the waiting-time distributions for gene switching and transcription initiation are typically modeled as exponential distributions, corresponding to single first-order reactions (14,20,21,34). However, recent data (35,36) indicate that lifetimes of a eukaryotic gene’s off-state can have peaked (nonexponential) distributions. These findings suggest that the underlying molecular mechanisms are more complex than single first-order reactions. Our aim is to derive models with the least number of parameters and which are flexible enough to describe a broad class of transcription mechanisms. To achieve this we have to approximate the complex molecular mechanisms involved in transcription regulation by suitable waiting time distributions, i.e., f(t), g(t), and h(t).

Limited experimental information exists on protein assembly mechanisms and histone-modification kinetics. Random (37,38) as well as sequential (39) assembly mechanisms have been reported. Our analysis indicates that gamma-distributions can model a wide range of molecular mechanisms relevant for gene switching and transcription initiation. In Fig. 2, the first-passage time distribution is shown for a protein complex formation process relevant for transcription regulation. It is a peaked waiting-time distribution that can be approximated by a gamma-distribution parameterized with the same mean and variance of the assembly-time probability density corresponding to the actual molecular mechanism. In the Supporting Material, different mechanisms (sequential, preferentially random, and random) are explored using realistic kinetic parameters (see Fig. S3 in the Supporting Material). We find in all cases that the first-passage time distributions can be approximated by gamma-distributions as long as no severe timescale separation occurs (see Fig. S5).

Figure 2.

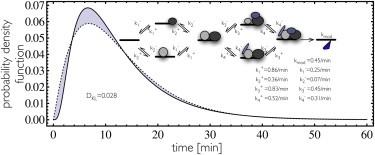
First-passage time (duration) distribution for a single-transition mechanism. A single-ratchet transition composed out of reversible protein complex assembly followed by irreversible covalent histone modification has a peaked waiting time distribution (solid line) that can be approximated by a gamma-distribution with the same mean and variance (dotted line).

Burst-size probability distributions for different transcription mechanisms

Transcription often proceeds in a bursty fashion (8,12,14,15,23). This indicates that, while the gene is in its on-state, several transcription initiation events can occur (20). For a gene with exponential waiting times for gene switching and transcription initiation, the burst size is geometrically distributed (12,14). In this section, we will derive the probability distribution for burst sizes for genes with complex transcription mechanisms.

We define the probability distribution for the burst size p_b(B = b) as the distribution of the number of transcription initiation events per single on-phase. The probability density function of the waiting time between transcription initiation events is denoted by h(t) (Fig. 1 b). The probability that at least b mRNA’s are formed during the lifetime of the on-state, t_on, is given by

$$p_b\left(B\ge b|T_{on}=t_{on}\right)=\underset{0}{\overset{t_{on}}{\int }}h{\left(t\right)}^{\left(b\right)}dt,$$

where the probability density function h(t)^(b) equals the b^th convolution of h(t), given by

$${\mathcal{L}}^{-1}\left(\mathcal{L}{\left(h\left(t\right)\right)}^b\right),$$

where ℒ(·) denotes the Laplace transform. The probability that exactly b initiation events occur in a time span t_on is given by the probability mass function,

$$p_b\left(B=b|T_{on}=t_{on}\right)=p_b\left(B\ge b|T_{on}=t_{on}\right)-p_b\left(B\ge b+1|T_{on}=t_{on}\right).$$

The burst-size distribution results after integrating over all T_on times,

$$p_b\left(B=b\right)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{p}_b\left(B=b|T_{on}=t_{on}\right)g\left(t_{on}\right))d{t}_{on}.$$ (1)

This equation applies to a general waiting-time distribution (i.e., molecular mechanisms) for the on-state and for transcription initiation. The moments of this distribution can be determined from the Laplace transforms of h(t) (see the Supporting Material).

For exponentially distributed waiting times for the on-state and transcription initiation Eq. 2 simplifies to a geometric distribution, p_b(B = b) = p(1 − p)^b, which was also found by others using combinatorics (11,14). Here p = k_g/(k_h + k_g) equals the probability for a step in the on-to-off transition. In this case, the mean burst-size 〈b〉 is given by the mean on-time (k⁻¹_g) divided by the mean initiation time (k⁻¹_h). The noise in burst-size, 〈δ²b〉/〈b〉², equals 1 + 1/〈b〉 and cannot reduce to <1. The burst-size distribution remains geometric as long as the on-state has an exponentially distributed waiting time even when general waiting-time distributions, h(t), are considered for the initiation process.

To explore how nonexponential waiting times for switching and transcription initiation (for complex molecular mechanisms) influence the burst-size distribution, we consider Erlang-distributed duration times for the on-phase and transcription initiation. The Erlang-distribution E(N,k) is a special case of a gamma-distribution and gives the distribution of the waiting times for a sequence of N first-order reactions with rate constant k. In the most general case, with Erlang-distributed initiation times (a series of N_h reactions with rate constant k_h) and Erlang-distributed on-lifetimes (a series of N_g reactions with rate constant k_g), the burst-size distribution is given by

$$p_b\left(B=b\right)=\sum _{i=b{N}_h}^{\left(b+1\right)N_h-1}\left(\begin{array}{c}i+N_g-1\\ i\end{array}\right)p^{N_g}{\left(1-p\right)}^i,$$ (2)

where p = k_g/(k_h + k_g) equals the probability for a step in the on-to-off transition. This burst-size distribution can be a peaked distribution and is therefore qualitatively different from the previous two transcription designs (Fig. 3).

Figure 3.

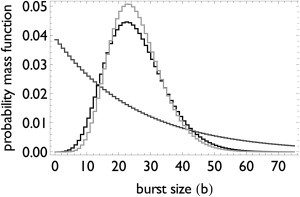
Nonexponential on-state time distributions make the burst-size distribution peaked. The on-to-off transition and the initiation mechanism were modeled with Erlang (solid, light-shaded) or exponential (dark-shaded) distributions. The average duration of the on-state was kept constant while the initiation rate was adjusted to achieve a mean burst-size of 25 initiations per on-phase. The initiation time is exponentially distributed (solid line) and Erlang-distributed (light-shaded line). A nonexponentially distributed initiation time has a small effect on the burst-size dispersion.

When N_h is set to 1 in Eq. 2, the initiation waiting-time distribution becomes exponentially distributed and the on-to-off transition remains Erlang-distributed. This design leads to a negative binomial burst-size distribution,

$$p_b\left(B=b\right)=\left(\begin{array}{c}b+N_g-1\\ b\end{array}\right)p^{N_g}{\left(1-p\right)}^b.$$ (3)

This distribution is qualitatively different from a geometric distribution in its noise properties: it is a peaked distribution with tunable dispersion. The mean burst-size corresponds again to a ratio of timescales, 〈b〉 = N_gk_h/k_g. The noise in burst-size,

$$\frac{\langle {\delta }^{2}b\rangle }{{\langle b\rangle }^2}=\frac{\langle {\delta }^2{\tau }_{on}\rangle }{{\langle {\tau }_{on}\rangle }^2}+\frac{1}{\langle b\rangle }=\frac{1}{N_g}+\frac{1}{\langle b\rangle },$$

decreases when the lifetimes of the on-to-off are less dispersed. Having in addition a multistep mechanism for initiation (Eq. 2) further reduces the noise, but only slightly (Fig. 3). Therefore, the multistep design of the on-to-off transition can reduce burst-size noise by making the burst-size distribution peaked.

The effective burst-size distribution: consideration of mRNA degradation during the burst phase

So far, degradation of mRNA during the on-phase was neglected. This is assumed in most studies of transcription bursts. A more realistic measure for the burst-size statistics is the distribution of the number of remaining transcripts at the end of a single on-phase, taking into account mRNA synthesis and degradation. This distribution we refer to as the effective burst-size distribution, $p_{b_e}$. The distribution of the remaining number of mRNAs produced during a certain period of time given zero^th-order transcription and first-order mRNA degradation kinetics is known analytically (see Eq. 1, and Hemberg and Barahona (40)). Substitution of this relationship for p_b(B = n|T_on = t_on) into Eq. 1 yields the effective burst-size distribution as function of the on-duration distribution, g(t). For an exponentially distributed lifetime of the on-state, the effective burst-size distribution equals (with k_d as the rate constant for mRNA degradation),

$$p_{b_e}\left(B_e=b_e\right)={\left(\frac{k_h}{k_d}\right)}^{b_e}\Gamma {\left[\frac{k_d+k_g}{k_d}\right]}_1{F}_{1R}\left[1+b_e,\frac{k_d+k_g}{k_d}+b_e,-\frac{k_h}{k_d}\right].$$ (4)

In this equation, Γ denotes the gamma-function and F_1R the regularized and confluent hypergeometric function of the first kind. Equation 4 is explored in Fig. 4. The effective burst-size converges to the steady-state level of mRNA when the gene is rarely in the off-state. At low turnover of mRNA, the nonexponentially distributed on-durations can make the effective burst-size distribution peaked. Then, the distribution approximates Eq. 3.

Figure 4.

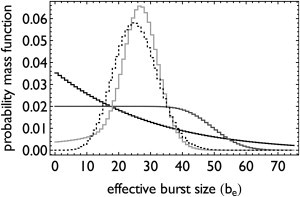
High mRNA turnover or nonexponentially distributed on-lifetime can make the effective burst-size distribution peaked. All models have an exponential distribution for the initiation mechanism. The on-to-off transition was modeled with an Erlang distribution (N = 10, dotted black line) and with exponential distributions otherwise with a fixed average duration. For all models the initiation rate constant was adjusted to fix the mean effective burst-size to 25. The average mRNA lifetimes are 10τ_on (solid black, dotted black), 1τ_on (dark-shaded), and 0.1τ_on (light-shaded). At high turnover (light-shaded), mRNA can almost attain its steady-state level given transcription and degradation kinetics and the mRNA burst-size becomes peaked. At low turnover of mRNA (black lines), the burst-size can become peaked for nonexponentially distributed on-to-off transition durations (dotted black).

If the lifetime of the on-state is Erlang-distributed, the mean and noise of the effective burst-size distribution can be calculated as

$$\begin{array}{c}\langle b_e\rangle =\frac{k_h}{k_d}\left(1-{\left(\frac{k_g}{k_d+k_g}\right)}^{N_g}\right),\\ \frac{\langle \delta b_e^2\rangle }{{\langle b_e\rangle }^2}=\frac{1}{\langle b_e\rangle }+\frac{{\left(\frac{k_g}{2k_d+k_g}\right)}^{N_g}-{\left(\frac{k_g}{k_d+k_g}\right)}^{2N_g}}{{\left({\left(\frac{k_g}{k_d+k_g}\right)}^{N_g}-1\right)}^2}.\end{array}$$

Inspection of the expressions in this equation indicates that noise in burst-size can be tuned above as well as below the noise of geometrically distributed bursts. These equations indicate at the large N_g the effective burst size converges to k_h/k_d. In the noise equation, the numerator of the second term is typically positive.

Noise in mRNA copy numbers for genes with short on-periods

The probability to have a certain copy number of mRNAs at stationary state depends on the kinetics and mechanisms of transcription and degradation. The associated probability distributions for mRNA have been derived for a number of gene systems, mostly dealing with the two-state model (21,23,41) or for more complex models using simulation (7,18,28). These studies suggest that transcription bursts enhance noise in mRNA copy numbers. In this section, we will study whether the complex transcription mechanisms for gene switching can compensate for this type of noise enhancement. We developed a method for calculating the moments of mRNA copy number distributions for genes with general lifetime distributions for switching (see the Supporting Material). Here, we first discuss this model in its stochastic hybrid system limit (42) where the durations of the on-state are infinitesimally short. As part of this description, bursts are solely characterized by their mean burst-size and noise level.

For an Erlang-distributed lifetime of the off-state, the noise in the steady-state mRNA distribution can be expressed as

$$\frac{\langle {\delta }^{2}n\rangle }{{\langle n\rangle }^2}=\frac{\langle b\rangle }{2\langle n\rangle }\left(\underset{\text{nonexponential}\text{effect}}{\underbrace{\frac{1+{\left(\frac{k_f}{k_f+k_d}\right)}^{N_f}}{1-{\left(\frac{k_f}{k_f+k_d}\right)}^{N_f}}-\frac{2k_f}{N_f{k}_d}}}+\frac{\langle \delta b^2\rangle }{{\langle b\rangle }^2}+\frac{1}{\langle b\rangle }\right).$$ (5)

This equation indicates that the noise in mRNA levels increases with the mean burst size and its noise. More sequential steps in the transition from off- to on-state decrease the noise. This suggests that a reduction in the noise in the lifetime distribution of the off-state leads to a reduction in the noise of the resulting copy-number distribution. The multistep design already proved beneficial for the reduction of burst-size noise, but then it led to an increase in the number of reactions for the on-to-off-transition. Thus, multistep transitions lead to a reduction in the noise of burst-size and mRNA.

The nonexponential term is largest when degradation is slow (k_d ≪ k_g). In the absence of degradation, the nonexponential term becomes 1/N_f, which is equal to the noise of gamma-distributed lifetimes for the off-state. In this limit, the equation reduces to the equation given in Pedraza and Paulsson (43). In more realistic regimes, when the half-life of mRNA is of the same order as the duration of the off-state, the deviation of the nonexponential term from 1 is less pronounced.

The application of Eq. 5 is limited to systems with short lived on-states, e.g., leaky repression. Fig. S5 shows the relative deviation of the mRNA noise of the instantaneous burst model compared to a model with gamma-distributed switch times. For the Lac/Ara promoter in Escherichia coli for which on- and off-duration distributions have been measured with an MS2 construct (14), the relative deviation of Eq. 5 from the switching model lies between 25 and 50% for typical lifetimes of bacterial mRNAs of 5–10 min.

Noise in mRNA copy numbers for a gene with deterministic switch times

The multistep sequential design of a eukaryotic transcription cycle can cause the waiting-time distributions for gene switching to have low noise. Accordingly, an interesting limit of the ratchet model is then a deterministic-switch model. We have derived an analytical expression for the complete probability distribution for mRNA copy numbers (see the Supporting Material). Simulations show that Erlang-distributed switch times with N ≥ 5 show qualitatively the same behavior as a deterministic switch model (see Table S1 in the Supporting Material). This suggests that quite some eukaryotic genes could be close to the deterministic limit of gene switching.

In Fig. 5, the copy-number distribution is explored numerically. Severe timescale separation can induce bimodal distributions of mRNA across cell populations; the same applies to the stationary mRNA distribution for the single-step gene switch model (20). However, the noise in mRNA is smaller in the case of deterministic switching, as we shall see next. This suggests that eukaryotes can reduce mRNA noise by tuning the design of complex transcription mechanisms. The noise in the stationary state mRNA copy number can be expressed analytically as

$$\frac{\langle {\delta }^{2}n\rangle }{{\langle n\rangle }^2}=\frac{1}{\langle n\rangle }+\frac{\left(1-e^{k_d{\tau }_{off}}\right)\left(1-e^{k_d{\tau }_{on}}\right)}{1-e^{k_d\left({\tau }_{on}+{\tau }_{off}\right)}}\frac{{\tau }_{on}+{\tau }_{off}}{k_d{\tau }_{on}^2}+\frac{{\tau }_{off}}{{\tau }_{on}}.$$ (6)

The mean mRNA level is given by

$$\langle n\rangle =\frac{{\tau }_{on}}{{\tau }_{on}+{\tau }_{off}}\frac{k_h}{k_d}.$$

The sum of the last two terms in this equation is always larger than zero and increases with shorter on-times and longer off-times: genes that are infrequently in the on-state are more noisy than highly active genes, which converge to Poissonian noise.

Figure 5.

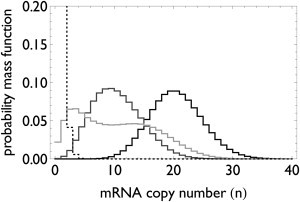
Stationary mRNA copy number distributions for the deterministic gene switch as function of on- and off-durations. A gene controlled by a deterministic switch with transcription rate 0.5 mRNA min⁻¹ and a mRNA lifetime of 40 min. If the gene is always in the on-state, the mRNA is Poisson-distributed with mean 20 molecules per cell (black). With 40 min in the on- and the off-state, the mean mRNA level goes down (dark-shaded). With infrequent switching (100 min in on- and off-state), the mRNA distribution becomes bimodal (light-shaded). When the gene is 1 min in the on-state and 60 min in the off-state, the distribution becomes nearly exponential with a mean of ≈0.3 molecules per cell (dashed black).

Time-resolved single-molecule mRNA counting allows for model discrimination

Complex formation, DNA looping, transcription initiation, and mRNA synthesis cannot yet all be tracked at single-molecule resolution in one experiment. The question is, then, how much information about the underlying transcription mechanisms is actually captured by the contemporary experimental data, and to what extent are the contemporary analytical models capable of discriminating alternative transcription mechanisms?

The advantage of our model is that it captures a broad range of different transcription mechanisms, ranging from simple to very complex transcription mechanisms. In addition, the waiting-time distributions for f(t), g(t), and h(t) can generally by approximated by gamma-distributions, which require only two parameters each. This leads to a model with at least seven parameters. The experimental data that are often at hand are mRNA copy-number distributions—for instance, those measured by mRNA-FISH labeling (10,23,44,45) or RT-qPCR on individual cells (46–49).

Often the simplest gene switch model is used to fit mRNA copy-number distributions. Such a model has exponential waiting-time distributions for f(t), g(t), and h(t). We shall show next that such fits may be misleading because models with nonexponential waiting times, which can have very different burst statistics, can fit the data often equally well (Fig. 6 and see Table S2 and Table S3).

Figure 6.

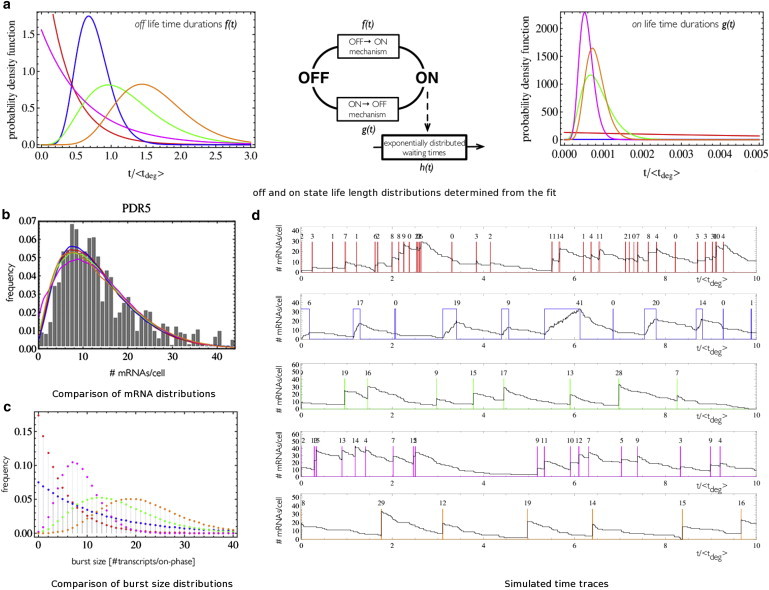
Stationary single-cell mRNA data contain only very limited information about the transcription mechanism. (a) Lifetime distributions of on- and off-states that were determined from choosing a combination of shape parameters for both states and then determining the rate parameters for both lifetime distributions as well as the rate constant for h(t) by matching the first three moments of the experimental data: (i.) (Red) N_on = 1, N_off = 1. (ii.) (Blue) N_on = 1, N_off = 10. (iii.) (Green) N_on = 5, N_off = 5; (magenta) N_on = 10, N_off = 1; and (orange) N_on = 10, N_off = 10. (b) Experimental data for PDR5 from Chubb et al. (8) (shaded bars) and the mRNA distributions of the fitted models. (c) Burst size distributions vary greatly between the fitted models. (d) Time-traces for the models described in panel a. (Colored lines) On- and off-states. (Black lines) Time-traces of simulations (50). (Numbers on top) Burst sizes.

We fitted the mRNA distributions for the five genes measured by Zenklusen et al. (10) to models with Erlang-distributed lifetimes of on- and off-states. The rate constants for transcription initiation and state switching were calculated such that the first three moments of the steady-state distribution of the model matched the moments of the experimental data. The mRNA distributions of the models were obtained from stochastic simulations (50). The quality of the fit, as measured by the χ² value, did not differ significantly between models with different values for N_g and N_f. The failure to discriminate between alternative transcription mechanisms on the basis of the stationary mRNA distribution was perhaps to be expected for the three house-keeping genes (MDN1, DOA1, KAP104). Zenklusen et al. (10) already showed that these distributions could be fitted by a Poisson distribution, suggesting a model with a short off-state. In this regime, the shapes of the distributions of the lifetimes of both states do not significantly affect the steady-state mRNA distribution as is indicated by Fig. S6 b. More surprisingly, we could not use the mRNA distribution for the two bursting genes (PDR5, POL1) in the data set to distinguish different transcription initiation models (see Fig. 6).

The different models with multistep and single-step on-to-off-switch mechanisms used in the fit vary vastly in their fractions of time that the gene is in the off-state, in total transcription cycle duration relative to the average time for degradation, and in burst-size distributions (Fig. 6, see Table S2). Even though these parameters do also vary between the different models fitted to the three housekeeping genes, a closer look at mRNA time traces reveals that those differences are less informative, as the on- and off-phases are not distinguishable from the time traces of the mRNA production events alone. This was further confirmed by calculations of the burst significance (21). For all models fitted to mRNA distributions of the three housekeeping genes, the burst significance was <0.1 (even though the fraction of time the gene is in the off-state according to the model can be significant, e.g., for DOA1; see Table S3), whereas all the models for the two bursting genes showed high burst significances (>0.85).

Fig. 7 exemplifies further how inferring parameters from a fit to the two-state model with exponentially distributed waiting times may be misleading. We simulated the distribution for a model where the lifetimes of both on- and off-state follow an Erlang distribution with four steps and used this simulated data for a fit with the exponential two-state model. The parameter range inferred from this fit on a 90% confidence level does not include the true parameters used to generate the distribution. In general, how the significant the parameter discrepancy is between simple and complex models depends on the parameter regime. The differences are largest for a bursting gene model in a bimodal regime of mRNA copy numbers. For genes with on-state durations longer than off-state durations, the fits between exponential and nonexponential models are in good agreement. This demonstrates that the static distributions of mRNA copy numbers contain only limited information about the underlying mechanisms and burst statistics. Time traces of mRNA copy numbers (e.g., measured with MS2 tagged mRNAs (51–53)) does allow for a discrimination of the different transcription mechanisms (see Fig. S9).

Figure 7.

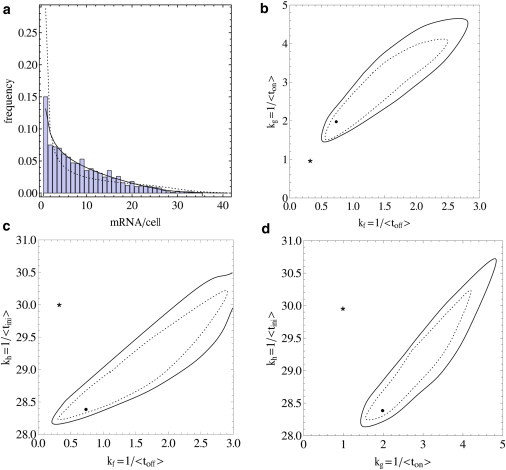
Parameters estimated with the two-state model with exponentially distributed waiting times can be misleading. (a) Histogram shows the copy number distribution obtained by simulating a model with nonexponentially distributed lifetimes for on- and off-state. Both distributions were modeled as Erlang distributions with four steps and average times of 〈t_on〉 = 1 and 〈t_off〉 = 3. (Solid line) Best fit to the first three moments of the simulated data using the exponential two-state model. (Dashed line) Distribution for an exponential two-state model that has the same average lifetimes for on- and off-state as the nonexponential model used to simulate the data. (b–d) Contours show 99% and 90% confidence levels for a parameter fit to the exponential two-state model. (Solid dot) Best fit. (Asterisk) Parameters of the nonexponential model used to generate the data.

Discussion

In this work, we have explored the consequences of complex molecular mechanisms for transcription regulation using nonexponentially distributed lifetimes of gene states for stochastic transcription. Such lifetime distributions occur naturally as a consequence of protein complex formation mechanisms in transcription regulation under the condition that the associated reactions occur on similar timescales. Recently, in eukaryotes, experimental evidence for nonexponentially distributed lifetimes of gene states was found (35,36). In prokaryotes, even though the gene regulation mechanisms do involve several molecules, the waiting times for gene switching in some cases have been found to be exponentially distributed (11,14). We found that nonexponential waiting times for gene switching have an influence on the burst size and mRNA distribution across a cell population and cause a reduction in transcription noise. The methods we propose can be extended to handle specific nonexponential waiting-time distributions when more mechanistic knowledge of the transcription initiation mechanism becomes available, as many of our equations do not depend explicitly on the type of waiting-time distribution for gene states.

Many studies aim at inference of kinetic parameters and burst sizes from experimental data on single cells. Often the stationary mRNA distribution (measured with RNA Fish) across a cell population is fitted to either the two-state transcription model or models tailored to the gene under investigation based on prior knowledge. Our results highlight the importance of the type of waiting-time distributions for gene switching in inference studies. Different kinetic parameters and burst sizes can be fit to the same distribution. Time-resolved single-molecule counting of mRNA, first carried out using a bacteriophage-derived protein MS2 (8,14,53) and recently with PP7 (54), are promising methods that do suffer less from the limitations we discussed. The disadvantage to these methods is that these experiments are more invasive and that genetic engineering is required.

The molecular ratchet model is a step toward quantitatively modeling eukaryotic gene regulation. The modular nature of the ratchet model allows for various extensions. Specific coarse-grained waiting time distributions can be used that derive from molecular mechanisms that could, for instance, incorporate chromatin looping. The integration of such models with time-resolved single-cell technologies will undoubtedly give more insight into the basal design and regulation of gene expression.