Abstract
The pathway to membrane fusion in synthetic and biological systems is thought to pass through hemifusion, in which the outer leaflets are fused while the inner leaflets engage in a hemifusion diaphragm (HD). Fusion has been proposed to be completed by lysis of the expanded HD that matures from a localized stalklike initial connection. However, the process that establishes the expanded HD is poorly understood. Here we mathematically modeled hemifusion of synthetic vesicles, where hemifusion and fusion are most commonly driven by calcium and membrane tension. The model shows that evolution of the hemifused state is driven by these agents and resisted by interleaflet frictional and tensile stresses. Predicted HD growth rates depend on tension and salt concentration, and agree quantitatively with experimental measurements. For typical conditions, we predict that HDs expand at ∼30 μm2/s, reaching a final equilibrium area ∼7% of the vesicle area. Key model outputs are the evolving HD tension and area during the growth transient, properties that may determine whether HD lysis occurs. Applying the model to numerous published experimental studies that reported fusion, our results are consistent with a final fusion step in which the HD ruptures due to super-lysis HD membrane tensions.
Introduction
Membrane fusion is essential for diverse biological processes including intracellular transport, exocytosis, and fertilization and is a key step in cell invasion by enveloped viruses such as HIV and influenza (1,2). Fusion consists in the merging of bilayer membrane-enclosed compartments by reconnection of the four lipid leaflets into a single bilayer, a process requiring force that is thought to be provided by fusion proteins (1–5). An obstacle to understanding protein-mediated fusion is that much of the underlying biophysics, even in the absence of proteins, is not established. A large research effort, both theoretical (6–10) and experimental (see Table 1), has aimed to uncover these basic mechanisms by studying fusion of protein-free lipid membranes where the driving forces are most commonly provided by calcium or other divalent cations, osmotically generated membrane tension (11,12) or PEG polymer (3).
Table 1.
Hemifusion predictions for published experimental fusion studies
| System | Ref. | System properties |
Estimated parameters |
Critical values |
Model predictions |
Symbol | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rves | Lipids | [Cation] | ϵcation (%) | Y0 (mN/m) | (mN/m) | Rcrit (nm) | Fcrit (kT) | Yeq (mN/m) | (mN/m) | Ahd/Aves (%) | Rhd | τeq | |||
| GUV-GUV | (17) | 10 μm | PC, PS, PE | 2 mM Mg2+ | 6.0 | 7.7 | 15 | 2 | 23 | 1.6 | 3.2 | 9.3 | 6.0 μm | 23 s | ● |
| (17) | 10 μm | PC,PS, PE | 6 mM Ca2+ | 6.7 | 8.7 | 17 | 2 | 20 | 4.0 | 8.2 | 16.7 | 8.2 μm | 21 s | ■ | |
| (32) | 5 μm | PS | 5 mM Ca2+ | 6.8 | 9.0 | 18 | 3 | 107 | 0 | 0 | 6.8 | 2.6 μm | 5 s | ▾ | |
| (33) | 16 μm | PC, PE | 25 μM Ca2+ | 0.1 | 1.4 | 2.8 | 10 | 124 | 1.4 | 2.8 | 2.9 | 5.4 μm | 66 s | ▴ | |
| LUV-LUV | (43) | 50 nm | PA | 0.1 mM Mg2+ | 3.8 | 5.0 | 10 | 1 | 4 | 0 | 0 | 3.8 | 19 nm | 0.4 ms | X |
| (32) | 50 nm | PS | 5 mM Ca2+ | 6.8 | 9.0 | 18 | 3 | 107 | 0 | 0 | 6.8 | 26 nm | 0.2 ms | Right triangle | |
| SUV-SUV | (26) | 25 nm | PA | 0.5 mM Mg2+ | 4.8 | 6.3 | 13 | 1 | 3 | 0 | 0 | 4.8 | 11 nm | 0.1 ms | ○ |
| (25,44) | 25 nm | PS | 1.5 mM Ca2+ | 6.4 | 8.4 | 17 | 4 | 115 | 0 | 0 | 6.4 | 13 nm | 0.1 ms | □ | |
| (41) | 35 nm | PS, PE | 4 mM Ca2+ | 5.6 | 7.3 | 15 | 0 | −0.2 | 0 | 0 | 5.5 | 16 nm | 0.1 ms | + | |
Experiments cover a representative range of vesicle radii Rves, lipid compositions, and cation concentrations. Tensions, condensation factors, and critical factors were calculated using similar procedures to those we used to analyze experiments of Nikolaus et al. (17) (see text). Model predictions were calculated from Eqs. 10–12, and 14 (vesicles in bulk solution) except for Nikolaus et al. (17) and Estes et al. (33), where Eqs. 4–6 were solved numerically with Eq. 9 (substrate-adhered vesicles). Symbols correspond to graphical markers in Fig. 6A. The results show that HD growth time τeq and equilibrium radius increase with vesicle size but depend weakly on lipid composition. In most experiments, the initial HD tensions are well above lysis (∼8 mN/m (21)), suggesting that hemifusion equilibrium was not reached but instead fusion occurred during HD growth by HD lysis.
Considerable evidence has emerged that the fusion pathway is multistage and passes through a key intermediate, the hemifused state, in which only the proximal leaflets of the two apposing bilayers are fused (Fig. 1) (13–16). Direct visualizations of the hemifused state revealed that the unfused distal leaflets engage one another to form a new bilayer region, the hemifusion diaphragm (HD). A broad range of sizes has been reported, including ∼20 μm HDs in hemagglutinin-mediated cell-bilayer hemifusion (16), ∼10 μm HDs between pure lipidic giant unilamellar vesicles (GUVs) (17), and ∼5 nm HDs in synaptic vesicles (13). In macroscopic suspended or supported synthetic bilayer systems, HDs reach diameters of ∼10 μm (18–20). In many other cases, HDs were not visualized but hemifusion was inferred from outer leaflet lipid mixing. Examples include studies of protein-free fusion and hemifusion (11,12), exocytosis (14), vacuole fusion (15), and viral fusion (5).
Figure 1.
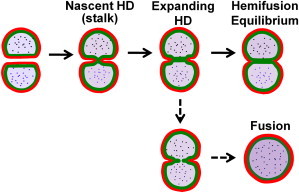
Multistage pathway to fusion through hemifusion. Divalent cations and membrane tension drive membrane bilayers to hemifusion and fusion. Evidence suggests the pathway to vesicle fusion begins with an initial hemifused connection (fused outer monolayers, red) that is a minimally sized hemifusion diaphragm (HD), i.e., the stalk, and tension- and cation-induced leaflet-condensation forces drive HD expansion to a final equilibrium state (dead-end hemifusion) unless HD tension is sufficient to cause rupture (fusion).
Here, we study the mechanisms whereby divalent cations and membrane tension drive hemifusion of protein-free membranes on the pathway to fusion. Recently, we showed theoretically that the final hemifused equilibrium state is characterized by an expanded HD whose size depends on tension, vesicle areas, and salt concentration (10). In this study, we mathematically model the kinetics, from the moment a hemifusion connection is nucleated between two membranes to the establishment of the mature HD. We predict the time for HDs to grow to equilibrium and we compute the time-dependent HD tension during growth. These quantities are likely critical to the fusion process that may follow hemifusion, as fusion requires the HD to rupture and the rupture probability of a membrane depends on both the magnitude and time-dependence of its tension (21). A further complication is the fact that the process of hemifusion lowers the tension (10,17). The kinetics of the HD is presumably also important in biological fusion, thought to entail HD lysis similarly to synthetic membranes. For example, influenza virions establish hemifused connections with supported bilayers, but it is not known if these connections matured into fully expanded HDs in the ∼10 s before complete fusion occurred (5).
The initial hemifusion connection may be a minimally sized HD, the stalk—the structure and energetics of which have been extensively analyzed theoretically (6,9). Our aim is to predict the evolution from such a localized connection to an equilibrated HD (Fig. 1). Experimentally tracking this evolution has been technically challenging as HDs can be short-lived (22) and in some cases are presumably smaller than optical resolution limits. Recently Nikolaus et al. (17) directly tracked the kinetics of HD growth between synthetic GUVs using bilayer-spanning peptides excluded from hemifused regions. At lower salt concentrations, 2 mM Mg2+, stable HDs developed with areas ∼9% of the vesicle area, corresponding to HD diameters in the range 6–40 μm for the 6–55 μm GUVs employed (17). At higher concentrations, 6 mM Ca2+, rapid fusion occurred and in some cases sequences were captured where short-lived HDs expanded at rates ∼20 μm2/s for ∼1 s. HD growth was terminated either by rupture of the HD, a fusion event, or vesicle lysis (17).
What forces do divalent cations exert on membranes and how might these drive membranes along the pathway to fusion? Divalent cations are known to condense membranes through electrostatic forces that lower repulsions between anionic or zwitterionic lipid headgroups, causing membrane areas to decrease by factors ϵcation ≈ 3–7% (23,24). When constraints are present to oppose this condensation tendency (e.g., constant vesicle volume), high membrane tensions result: γ ≈ 1–10 mN/m (25,26). Another effect of divalent cations is membrane-membrane adhesion, which could destabilize bilayers (22).
In a previous study, we showed that, after nucleation of a hemifusion connection, divalent cation-induced membrane tension and condensation effects expand HDs to a state of hemifused equilibrium (10). In typical experiments such as those of Nikolaus et al. (17), only outer vesicle leaflets contact the divalent cation solution. Condensation forces are thus selectively exerted on these leaflets, a situation favoring HD growth (see Fig. 2). We showed that the cationically elevated membrane tension is a second driving force, because the tendency of tension to reduce membrane surface area is satisfied by HD formation as the HD is a bilayer shared by the two vesicles (8–10). The predicted size dependencies of equilibrium HDs on vesicle areas and membrane tensions were in close quantitative agreement with the measurements by Nikolaus et al. (17).
Figure 2.
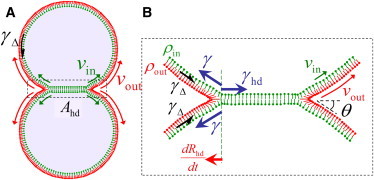
Hemifusion diaphragm growth model. (A) Hemifused vesicle pair with contact angle θ and (B) blowup of HD of area Ahd boxed in panel A. The driving force for HD growth sums’ contributions from membrane tension γ and cation-induced condensation effects (Eq. 1). The net force compresses (expands) the outer (inner) leaflets, increasing the difference in leaflet lipid densities ρout, ρin, which increases the interleaflet tension γΔ opposing HD growth. The lipid velocities υout, υin in each leaflet are unequal, and their relative sliding is opposed by interleaflet friction. The balance of tensile and frictional forces determines the HD boundary velocity, dRhd/dt, and the evolution of HD tension γhd.
Here our emphasis is the HD growth process. Our immediate goal is to explain the ∼20-μm2/s growth rates measured in Nikolaus et al. (17). HD expansion kinetics has also been measured in noncationic systems. Macroscopic suspended bilayers (SBLs) forced together by pressure grew HDs at rates ∼100 μm/s up to ∼1 mm sizes (18) whereas density-depleted supported bilayers grew ∼50 μm HDs at speeds ∼20 μm/s (19). PEG polymer solution grew ∼50 μm HDs at ∼5 μm/min in supported bilayers (20) and the HD expansion kinetics were quantitatively modeled as depending on PEG-driven monolayer tension and frictional forces (8).
Our starting point is the equilibrium analysis of Warner and O’Shaughnessy (10), where it was shown that there is a net thermodynamic driving force for HD expansion, , which is a combination of the membrane tension γeq and the cationic condensation factor ϵcation,
| (1) |
where kΔ is the interleaflet modulus (see below). The physics of hemifusion involve two classes of membrane tension: the familiar bilayer tension, γ, and the interleaflet tension, γΔ, which reflects asymmetry between the two leaflets of the bilayer. The latter tension grows in proportion to the difference Δρ between the outer and inner leaflet densities, γΔ = kΔ(Δρ/ρ0) (10,27). Here the reference density ρ0 is the initial lipid leaflet density before hemifusion. HD expansion compresses the outer leaflets, thereby triggering interleaflet tension, which opposes HD growth (Fig. 2). The equilibrium HD area and tension are determined by a balance of this resisting force with the expansion force of Eq. 1, leading to
| (2) |
where is the mean vesicle area of the hemifused vesicle pair (10). This relation accurately reproduced the experimental measurements of Nikolaus et al. (17), with a best-fit value kΔ = 19 ± 5 mN/m very close to values of the modulus independently measured by extraction of membrane tubes with high interleaflet areal difference from GUVs 23 ± 9 mN/m (28). The result of Eq. 2 is valid for all but the smallest HDs, for which line tension due to leaflet-bending stresses along the HD perimeter becomes an important effect (8–10).
In the following sections we develop a mathematical model predicting the time-dependent HD area and tension, Ahd(t) and γhd(t). The growing HD excites a spatially inhomogeneous field of interleaflet density differences and tensions over the two-vesicle hemifusion complex whose maximum is at the HD boundary. Technically, the HD supplies a moving boundary condition for the relaxation of these fields to uniformity (equilibrium), and the relaxation and HD growth are mutually dependent. Solving this moving boundary problem yielded the HD growth velocity and the time to reach its equilibrium size. Our predictions agree quantitatively with the measurements of Nikolaus et al. (17) and qualitatively describe HD measurements in SBL-SBL systems. We also applied our analysis to a range of published experiments where hemifusion was signaled but HD sizes were not tracked. To this end we first extended the equilibrium analysis of Warner and O’Shaughnessy (10) to the situation where hemifusion occurs in bulk suspension, realized in most of these experiments. An important output of our model is the evolving HD tension γhd(t), which can reach super-lysis levels that rupture the HD and cause fusion (7,18). We used this information to qualitatively describe the complete hemifusion-fusion pathway and to explain the observations of Nikolaus et al. (17) that, before equilibrium was reached, HD growth terminated either in HD rupture or vesicle lysis.
Model
Model of HD growth kinetics
Throughout, tension, density, and velocity variables (γ, ρout, ρin, Δρ, vout, vin, and Δv, see below) refer to the major portion of the vesicle-vesicle hemifused complex that excludes the HD. We will solve the density and velocity evolution dynamics in that region, for which the HD boundary supplies a boundary condition. In the equilibrium state, the outer leaflets of each vesicle are pulled out of the HD region and compressed, whereas in the non-HD region there is a uniform interleaflet density difference Δρ ≡ ρout − ρin, where ρout, ρin denote lipid densities in each leaflet (Fig. 2) (10). To achieve this, starting from a localized hemifused connection, the outer leaflets must have slid over the inner leaflets. In Evans and Yeung (27), it was argued that in situations involving relative leaflet displacements in lipid membranes, the principal resistance is the interleaflet frictional stress λΔv. Here λ is the interleaflet friction coefficient and Δv ≡ vout − vin is the difference between the lipid velocities in each leaflet. Below, we will show that, during HD expansion, balance of thermodynamic tensile forces and interleaflet frictional stresses determines the evolution of the time- and space-dependent density and velocity difference fields and the HD growth rate. HD equilibrium is reached after a characteristic relaxation timescale over which Δρ reaches uniformity.
The force balance equates the frictional and interleaflet tensile stresses at each point in the membrane bounding the hemifused vesicle-vesicle complex: −λΔv = ∇γΔ, where the gradient is taken in the surface. Here the interleaflet tension depends on the local areal strain Δρ/ρ0:
| (3) |
The continuity equation dΔρ/dt = −ρ0∇⋅(Δv) then yields
| (4) |
These equations evolve the velocity and density interleaflet difference at every location r in the membrane that defines the surface of the hemifused complex (Fig. 2). Their form is that of the diffusion equation with effective diffusion coefficient D. The same equations were previously derived to model extraction of membrane tubes from vesicles (27). A similar equation was used to describe PEG-mediated HD growth between mica-supported bilayers (8). In that model only outer leaflet dynamics were considered and the boundary conditions were qualitatively different from those employed here (see below).
The connection with HD dynamics arises via the boundary condition at the rim of the growing HD of radius Rhd(t). Now in the hemifused topology, the HD leaflets and the inner vesicle leaflets are connected and thus have equal chemical potentials, but unequal densities. To leading order in the difference between the mean lipid densities of the HD and inner leaflets, it was shown in Warner and O’Shaughnessy (10) that in equilibrium a fundamental global relationship relates the interleaflet and bilayer tensions: γΔ = γ/2. During HD growth, this global relationship now applies locally at the HD boundary owing to the leaflet connectivity between HD and non-HD regions. Using this in Eq. 3, one finds that the density difference at the rim is proportional to the HD driving force for growth,
| (5) |
This is the dynamic boundary condition for the density difference field dynamics (Eq. 4). Note that the driving force ftherm(t) is now time-dependent as vesicle tension γ(t) relaxes throughout HD growth because the presence of an HD decreases the total bilayer area; in the following subsection the tension falloff is calculated and shown to depend only on the current HD area.
In the Supporting Material, we show that the HD growth velocity itself depends on the relative leaflet velocity at the rim, , which in turn depends on the local density gradient (Eq. 4). The HD expansion rate is
| (6) |
Thus, calculation of the HD growth rate amounts to solving a moving boundary problem. The diffusion-like expressions from Eq. 4 are solved with the density condition at the moving HD boundary from Eq. 5, and the density solution then yields the HD growth velocity through Eq. 6. This allows the boundary location in Eq. 5 to be continuously updated.
Decay of vesicle tension during HD growth
To solve the growth kinetics above, we need the time-dependent vesicle tension γ(t) appearing in the driving force of Eq. 5. During the transient that leads to hemifusion equilibrium of a vesicle pair, the vesicle membrane tension decreases from the value before hemifusion, γ0, because HD growth decreases the total bilayer surface area (Fig. 2). Thus, the driving force progressively diminishes. Generally, the bilayer tension change depends on the change in the mean of the leaflet lipid densities, ,
| (7) |
where K is the bilayer elastic modulus (27,29). It follows that the bilayer tension γ (in contrast to the interleaflet tension γ▵) is essentially constant over the entire membrane surface because relaxation of gradients in the mean density is fast, as no relative leaflet motion is required so that only relatively weak hydrodynamic drag forces are involved (27,28,30). The time decay of the tension depends on whether or not the hemifusing vesicles adhere to a substrate. Let us now analyze these two practically important cases, assuming no leakage (fixed vesicle volume on experimental timescales). For the experiments of Nikolaus et al. (17), this assumption is valid, as five of the six GUVs that were tracked had constant volume during the HD growth episodes that lasted seconds (see the Supporting Material). We note that leakage was absent in other experiments under similar conditions (31,32). For simplicity, our analysis will assume small HD area relative to the vesicle area.
Hemifusion of vesicles in bulk suspension (no substrate adhesion)
Typical experiments track fusion of vesicles in bulk solution. The presence of an HD squeezes the lipids in the non-HD regions and increases the density by amount ρ0Ahd/(2Aves) to leading order in the small quantity Ahd/Aves (Fig. 2). Then from Eq. 7 the tension has a simple linear dependence on the HD area Ahd(t),
| (8) |
We used this relation to continuously update the boundary condition of Eq. 5.
Hemifusion of vesicles adhered to a substrate
In the experiments of Nikolaus et al. (17) and Estes et al. (33), vesicles were observed on a substrate or coverslip, and in hemifusion equilibrium vesicle-substrate contact angles of adhering vesicles were measured (17). Adhesion has the effect of buffering the vesicle tension: attachment to the substrate stretches the vesicle, thus decreasing the membrane density and so increasing the tension. In the Supporting Material, we show this leads to a significantly slower decay of tension:
| (9) |
Here W is the adhesion surface energy density that determines the contact angle θs according to Young’s equation, W = γ(1 = cosθs) (34). Thus, tension buffering by surface adhesion increases the tension by Δγadh relative to the value in Eq. 8 for vesicles in bulk suspension. When we solved our HD growth models for this case, at each time Eq. 9 was implicitly solved for the above-referenced tension using the same HD area. This was then used to update the boundary condition of Eq. 5.
Asymmetric hemifusion
The model and results above assumed the two hemifusing vesicles are identical. In the Supporting Material we generalized the analysis to hemifusion of vesicles with arbitrary size and tension (see Eqs. S3–S7 in the Supporting Material). The physics of asymmetric hemifusion are similar, but now two density fields Δρ1, Δρ2 follow the diffusion-like equation of Eq. 4, one for each vesicle. The boundary condition for each vesicle depends on the corresponding driving force
analogously to Eq. 5. In the generalization of Eq. 6, the HD expansion rate depends on the mean of the gradients of Δρ1 and Δρ2 at the HD boundary. An important difference is that there is now net flow of outer leaflet lipids from the less tense to the more tense vesicle and the tension decay of Eq. 9 is correspondingly more complex.
Results
Model predictions for HD growth kinetics agree with measurements from another study
We first applied our model to the experiments of Nikolaus et al. (17), the only quantitative measurements of HD growth kinetics during vesicle-vesicle hemifusion, to our knowledge. These experiments tracked the growth of HDs on the pathway to either fusion or vesicle lysis. The predicted time course of HD sizes agreed with the experimental measurements, and the calculated tensions explained the observed fusion events. Three GUV pairs with lipid composition 60% DOPC, 20% DOPS, and 20% DOPE adhered to the coverslip and were hemifused in 6 mM Ca2+ (Fig. 3, A–C). In each case, an HD grew at ∼30 μm2/s, and then ruptured to give fusion (vesicle pairs 1 and 2, blue and red in Fig. 3, respectively) or the smaller vesicle lysed (green pair).
Figure 3.
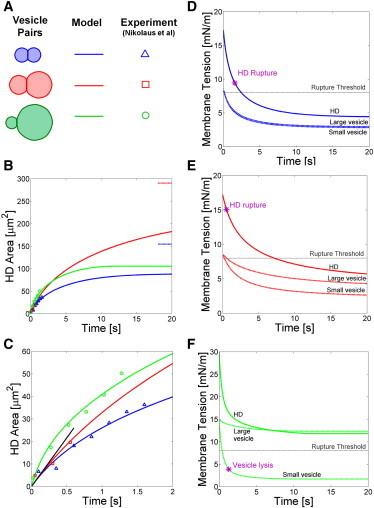
Hemifusion diaphragm growth kinetics: model predictions versus experiment of Nikolaus et al. (17). (A) Legend. Three hemifused pairs were experimentally studied: blue pair (vesicle areas = 824 μm2, = 887 μm2), red pair (1550 and 3260 μm2), and green pair (422 and 5030 μm2). HD growth terminated in HD rupture (blue and red pairs) or vesicle lysis (green pair, smaller vesicle). (B) HD size evolution. (Data points) Experiment and (solid lines) model predictions. (Dashed lines) Predicted final equilibrium area that would have been attained had HDs not ruptured (blue and red pair). (C) Short time kinetics in panel B. (Blue and red pairs) Model fitted to data using estimated initial tension γ0 = 8.7 mN/m (see main text) yielding best-fit value for interleaflet friction coefficient λ = 1.1 (±0.2) × 109 N s/m3. (Green pair) Model fitted to data using initial tension as fitting parameter, yielding best-fit value γ0 = 15 ± 2 mN/m. (Solid black line) Short time analytical model prediction (Eq. 13) for red and blue pairs. (D–F) Predicted evolutions of vesicle and HD tensions. HD tensions are consistent with observed HD rupture in panels D and E. In all cases the initial vesicle tensions exceeded the rupture threshold.
Parameter values
We first estimated the model parameters for these experimental conditions. The 6 mM Ca2+ increases membrane tension and selectively condenses the outer vesicle leaflets (see Introduction). To quantify these effects we computed the composition-weighted average tension and condensation factor based on measured or estimated values for the pure lipid species under these conditions (23–25) (see the Supporting Material for details). This gave γ0 = 8.6 mN/m for the prehemifusion tension and ϵcation = 6.5% for the cation-induced condensation factor. The vesicle diameters were directly measured in Nikolaus et al. (17), while the vesicle-substrate adhesion energy for this system was previously calculated, W = 1.1 mN/m (10).
HD area
Using these parameter values, the system of model equations (Eqs. 4 and 7, and see Eq. S3 and Eq. S7 in the Supporting Material) was solved numerically for each vesicle pair using a standard finite difference technique (35). Numerical predictions of Ahd(t) are plotted in Fig. 3, B and C, along with the measured data. We fit the predicted HD trajectories Ahd(t) to those measured experimentally for the blue and red vesicle pairs using the interleaflet friction coefficient as a fitting parameter, yielding λ = 1.1(±0.2) ± 109 N s/m3 (see the Supporting Material for details of fitting procedure). This is in reasonable agreement with the value λ = 4.6(±2.4) ± 108 N s/m3 measured in SOPC GUVs (30) and lies within the range λ = 5 × 107 – 5 × 109 N s/m3 reported for DOPC monolayers deposited on substrate-fixed hydrocarbon leaflets (36).
Whereas the blue and red vesicle pairs grew HDs at indistinguishable rates, the green pair produced faster growth, suggesting its membrane tension was higher. Such variations could reflect variable proximity to the micropipette used to inject concentrated Ca2+ into the solution (J. Nikolaus, Humboldt University, personal communication, 2011). Using the above best fit λ-value, for the green pair we fit for the initial membrane tension that yielded γ0 = 15 ± 2 mN/m. Overall, the model-predicted HD area evolutions are consistent with experiment for all three pairs (Fig. 3, B and C).
Vesicle tensions and HD tension
We used the model to calculate the time-dependent vesicle and HD tensions during HD growth, solved for concurrently with HD area (Fig. 3, D–F). For the blue and red pairs, the predicted vesicle tension decays from the initial value γ0 = 8.6 mN/m, eventually reaching the equilibrium value ∼3–4 mN/m, whereas the HD tension begins at ∼17 mN/m and decays to ∼5 mN/m in equilibrium. Now these two experimental growth trajectories were both interrupted by HD rupture at the times indicated in the plots in Fig. 3, D and E. Consistent with these observations, the model-predicted HD tensions at the instants of HD rupture exceed the rupture threshold ∼8 mN/m measured in Evans et al. (21).
Hemifusion in bulk suspension: HD growth rates, equilibrium size, and equilibrium tension
In the previous section, the experiments of Nikolaus et al. (17) were analyzed, where tension is buffered because the hemifusing vesicles are adhered to a substrate. In this section we apply the model to a second class of experiments, where the vesicles are in bulk suspension (Table 1) and the tension decay during HD growth is far more pronounced (compare to Eqs. 8 and 9). For simplicity, symmetric hemifusion is treated below.
HD equilibrium
Using Eq. 8 in Eq. 2 gives the equilibrium HD area and tension
| (10) |
where the driving force and membrane tension in the equilibrium state are
| (11) |
Note that by the time equilibrium has been attained, the driving force has decayed by the factor
| (12) |
relative to its prehemifused value when the tension was γ0. To apply the above results to experimental systems we will estimate the initial tension γ0 from published membrane tension measurements in the presence of divalent cations and use Eq. 12 for the decay factor. This differs from our procedure for the experiments of Nikolaus et al. (17) where contact angles gave a readout of the equilibrium tension (10). Note also that the cation-induced tension and condensation factor are physically related: we estimate that typically γ0 ≈ (K/2)ϵcation. Using this relation in the expressions above shows that cation-induced stresses are almost completely relaxed by HD growth. This contrasts with situations with vesicle-substrate adhesion where vesicle and HD tensions remain high.
Micron-sized vesicles grow HDs in ∼0.1 s
We numerically solved the model equations for vesicles sizes in the micron range having typical lipid composition, with a range of initial hemifusion driving forces corresponding to calcium concentrations ∼1 mM to ∼3 mM. The initial HD areal growth rate increased with driving force but was independent of vesicle area. The equilibrium HD size was approached after times in a range ∼0.05 s (smallest vesicles, highest driving force) to ∼0.15 s (largest vesicles, smallest driving force) (Fig. 4, B and F). Final equilibrium areas increased linearly with the initial driving force (Fig. 4 E), consistent with the analytical predictions of Eq. 10.
Figure 4.
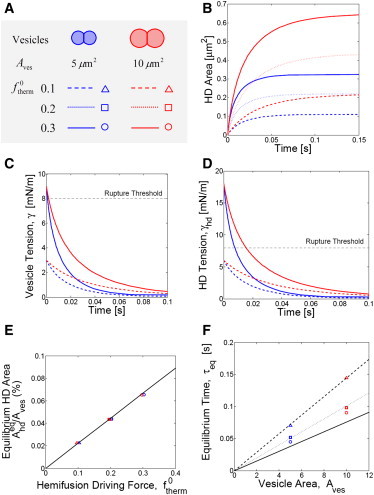
Model predictions for vesicle hemifusion in bulk solution. (A) Legend. Results are shown for three values of the thermodynamic driving force and for two hemifusing pairs, each with identical vesicles (symmetric hemifusion). Lipid composition: 60% DOPC, 20% DOPS, 20% DOPE. (B) HD area versus time. Initial growth rates depend only on the driving force. (C) Vesicle and (D) HD tensions versus time (for clarity, results for intermediate driving force not shown.) For the higher driving force, the vesicle and HD tensions exceed the rupture threshold, suggesting fusion or vesicle lysis would be the end state. For the lower driving force, dead-end hemifusion is predicted. (E) Normalized equilibrium HD area versus driving force and (F) time for HD to grow to equilibrium size versus vesicle area. (Black solid lines) Analytical predictions (Eqs. 10 and 14). (Colored symbols) Exact numerical model solutions. Numerical solutions confirm the analytically predicted scaling law τeq ∼ Aves, and the analytical solution quantitatively reproduces numerical solutions except for the largest driving force in panel F due to finite driving force corrections to the predicted prefactor b in Eq. 14.
The evolutions of vesicle and HD tensions are shown in Fig. 4, C and D, respectively. At high driving forces their initial values exceed the rupture threshold, but with time decay to subthreshold values. This suggests that HD rupture could interrupt HD growth, but, if avoided in the early episode, the final outcome would then be stable hemifusion.
Initial HD growth rates are independent of vesicle size
How does the HD growth rate depend on the sizes of the hemifusing vesicles, membrane tension and salt concentration? For early times, shortly after formation of a localized hemifusion connection, we could solve the HD growth kinetic equations Eqs. 4–6 exactly (see Appendix). This showed that 1), the HD area increases linearly in time and 2), the initial growth rate is the same for all vesicle sizes, but 3), it increases with tension and salt concentration:
| (13) |
Thus for times less than the HD equilibration time τeq, the HD area increases at a rate that increases almost linearly (to within a logarithmic factor) with the initial driving force, , set by the initial tension and the salt condensation factor. From numerical solutions we find the prefactor c = 10.6 for small driving forces . In Fig. 5 we plot the predictions of Eq. 13 for a range of vesicle tensions (0 < γ < 10 mN/m) and condensation factors (0 < ϵcation < 0.07).
Figure 5.
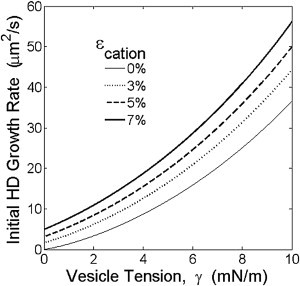
Model predictions for initial rate of growth of hemifusion diaphragm area. Exact analytical predictions of Eq. 13 are plotted. HD areal growth rates increase with membrane tension γ and divalent cationic outer leaflet condensation factor ϵcation, independently of vesicle areas.
These short time analytical predictions agree qualitatively with the experiments of Nikolaus et al. (Fig. 3 C), including the vesicle size-independence of the early growth rate and the linear dependence on time. They are also confirmed by numerical solutions, also shown in Fig. 3 C. An important technical point is that the linear dependence on time might not be expected because our moving boundary equations describing HD growth are formally equivalent to a two-dimensional reaction-diffusion system (see Appendix) where inverse logarithmic time dependencies typically arise (37,38). If the HD growth rate had this time dependence, the curvature in Fig. 3 C would be far greater (there is a small curvature due to finite time corrections). Its absence arises because the HD expansion is just fast enough to cancel the logarithmic time factor, leading to a constant slope in Eq. 13.
Hemifusion equilibration time is proportional to vesicle area
How long does it take for a HD to grow to its equilibrium size? From our model equations (Eqs. 4–6), it is simple to show that, for symmetric hemifusion, the HD equilibration time is directly proportional to vesicle area Aves,
| (14) |
where the prefactor b depends very weakly on the driving force (see below). This result can be understood as follows. The kinetic equations describe diffusive-like propagation of an outer leaflet compression wave Δρ(r,t) extending outward from the rim of the growing HD. The compressed portion of the outer leaflet extends the diffusion distance ∼(Dt)1/2 away from the HD into the non-HD part of each hemifused vesicle where D = kΔ/λ is the effective diffusivity. Because HD equilibration requires complete outer leaflet compression the equilibrium timescale is essentially the diffusion time Aves/D for the entire vesicle area.
Using an equilibrium criterion that HD area reach 95% of its final value, we verified this result by numerical solution of the kinetic equations that showed the prefactor b depends logarithmically on the dimensionless driving force, b = 0.11 ln(1/), for small forces. Fig. 4 F shows that the dependence of the equilibration time on vesicle area predicted by Eq. 14 is consistent with numerical solutions for the six vesicle pairs of Fig. 4 A.
HD growth depends on divalent cation concentration and lipid composition
Next we applied our model to representative divalent cation-driven bulk suspension fusion studies published in recent years spanning a wide vesicle size range, from ∼50-nm SUVs to ∼100-nm unilamellar vesicles (LUVs) to micron-scale GUVs (see Table 1). Fusion was reported but hemifusion was not tracked, with the exception of Nikolaus et al. (17). Our results suggest that, in many cases, hemifusion preceded fusion. For each experiment, analogously to our procedure for Nikolaus et al. (17) described above, we used the reported cation concentration and lipid composition to estimate the vesicle tension and condensation factor based on linear composition dependence and published data for pure lipid species. Together with the reported vesicle sizes, we used these parameters in Eqs. 10–12 to predict the equilibrium HD size and equilibration time, taking the values of the interleaflet modulus kΔ and friction coefficient λ obtained by fitting the data of Nikolaus et al.
For these salt conditions we find HDs are ∼3–10% of the vesicle area. The results are listed in Table 1 and plotted in Fig. 6 A: HDs between hemifusing GUVs grow to ∼3–10 μm in ∼8–100 s, whereas in SUV and LUV systems HD sizes of ∼11–27 nm develop after ∼0.1–0.5 ms. For most experimental conditions we found the HD tension initially exceeds the membrane lysis threshold, but would drop safely below it if the HD can reach equilibrium (Table 1).
Figure 6.
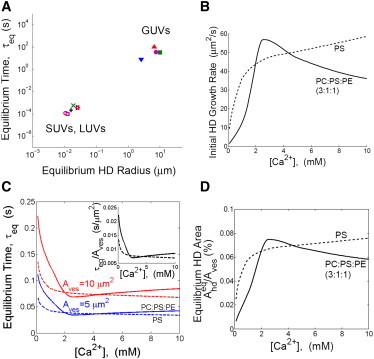
Effect of salt concentration on hemifusion diaphragm kinetics and equilibrium size. (A) Model predictions for equilibrium HD radius (Eq. 10) and equilibration time (Eq. 13) for the conditions of published experiments. Each marker represents one experiment in Table 1. (B–D) Predictions for vesicles pairs with membranes of pure DOPS (dashed lines) or a DOPC/DOPS/DOPE (3:1:1) mixture (solid lines). (B) Initial HD growth rate (Eq. 13). (C) HD equilibration time (Eq. 14) for two vesicle pairs each with identical vesicles. (Inset) The predicted ratio of equilibration time to vesicle area depends on cation concentration only and follows a universal curve. (D) Normalized equilibrium HD area (Eq. 10).
To document the effect of calcium concentration over a broad range, we then calculated initial HD growth rates, equilibration times, and equilibrium HD sizes for [Ca2+ ] up to 10 mM (Fig. 6, B–D). We considered two lipid compositions: pure DOPS membranes (e.g., Ohki (25) and Rand et al. (32)) and a mixture of 60% DOPC, 20% DOPS, 20% DOPE (e.g., Nikolaus et al. (17)). For each [Ca2+ ] value the tension and condensation factor were computed (as described above for the experiments of Table 1) and input into our model results. Interestingly, the predicted HD growth rate increases monotonically with [Ca2+ ] for pure DOPS whereas for mixed lipid vesicles a maximum is reached near 2.5 mM Ca2+. The maximum arises because the reported lipid condensation strength of PC peaks at this concentration (23). Correspondingly, the lipid mixture equilibration time and equilibrium area reach minimum and maximum values, respectively, at about the same calcium level (Fig. 6, C and D).
Discussion
Calcium drives HD areal growth at typical rates ∼10–50 μm2/s
Fusion of protein-free membranes in the presence of calcium or magnesium cations has been widely studied (Table 1). Here we showed that divalent cations provide driving forces for hemifusion on the pathway to fusion. Consider membranes of typical lipid composition, 60% DOPC, 20% DOPS, 20% DOPE, in typical salt conditions, 6 mM Ca2+. Our mathematical model then predicts that a localized stalklike hemifusion connection between two vesicles expands at a rate ∼30 μm2/s and grows to a final equilibrium area that is ∼7% of the vesicle area. Thus, 50-nm diameter SUVs grow 20 nm HDs in ∼0.1 ms, whereas 20 μm GUVs grow ∼8 μm HDs in ∼30 s. Applied to the GUV-GUV hemifusion-fusion study of Nikolaus et al. (17), the model quantitatively reproduced the observed behavior in which spontaneously nucleated hemifusion connections grew at rates ∼20 μm2/s into micron-sized HDs from a small initial size, less than optical resolution.
Expansion of a hemifusion connection compresses the outer monolayers and reduces the total bilayer area (Fig. 2). Correspondingly, our analysis showed that cations drive HD expansion by 1), selective outer monolayer condensation, and 2), increasing the membrane tension. As both effects are concentration- and composition-dependent, the areal growth rate, the final equilibrium HD size, and the HD equilibration time all depend on cation concentration and lipid composition (Fig. 6). For example, for the composition of Nikolaus et al. (17), we predict that increasing Ca2+ from 1 mM to 6 mM increases the initial HD growth rate from ∼10–40 μm2/s.
Our study emphasized micron-scale or larger vesicles where HD line tension effects are unimportant once an initial kinetic barrier is overcome. This is reflected in the equilibrium HD radius being much larger than the critical radius, , a condition that holds for many of the experiments in Table 1 involving even SUVs (∼70 nm) or LUVs (∼100 nm). However, for the smallest vesicles HD line tension and curvature stress effects may become important in which case our framework provides a guide only.
Membrane tension drives hemifusion even in the absence of cations
In synthetic fusion systems tension can be generated by osmotic gradients (11,12), micropipette aspiration (39), or by SBL lipid reservoirs (see below) (18). In vesicle-SBL experiments with Ca2+, fusion requires osmotically generated tension (11), whereas in computer simulations tension promoted hemifusion and fusion without Ca2+ (40). Our model revealed the mechanism whereby tension drives hemifusion, originating from the fact that HD formation reduces total bilayer surface area. For example, we predict that increasing tension from 2 to 8 mN/m increases the initial HD growth rate from ∼3 to 25 μm2/s (Fig. 5, ϵcation = 0) and the equilibrium HD area increases from ∼1 to 5% of the vesicle area (Eq. 11).
The model is consistent with the observed kinetics of hemifusion between macroscopic suspended bilayers
Though our model addressed vesicle-vesicle hemifusion, at short times when the HD is much smaller than the vesicles the predictions apply equally well to hemifusion between macroscopic SBLs, typically ≲1 mm in size. Now three key experimental findings reported in such SBL systems (18) were 1), the HD area grows linearly in time and 2), the growth rate increases with increasing membrane tension, but 3), is independent of SBL area. As the SBL tension is maintained constant by a lipid reservoir attaching it to a solid orifice across which the bilayer is suspended (41), the short time HD growth law predicted by the model from Eq. 13 is expected to apply for minutes. It follows that the model’s predictions are in agreement with all three of these key observations.
Evolution of the hemifusion diaphragm from a stalk
After nucleation, the initial hemifusion connection may be a collapsed HD, known as a stalk. Due to the effective line-tension Thd of the HD rim, expansion of the stalk is expected to be free-energetically costly (8–10). In Warner and O’Shaughnessy (10), we showed that, in consequence, the stalk is metastable, and before HD expansion can begin it must grow to a critical radius Rcrit = Thd/(2kΔ) to overcome a free energy barrier of height Fcrit = πThdRcrit. Thereafter, the HD expands according to the kinetics described in this article and the line-tension free energy contribution is rapidly overwhelmed by that from the expansion driving force, ftherm. Using these results, we calculated the free energy barriers and critical HD radii for each of the experiments listed in Table 1 after using Kozlovsky et al. (7) and Kooijman et al. (42) to estimate the line tension as a function of lipid composition. For the experiments of Nikolaus et al. to which we compared our model predictions in this study, the estimated barrier height is ∼24 kT. Consistent with their observations of expanding HDs, this is less than the ∼40 kT barrier that can be surmounted on timescales of seconds as estimated from membrane electroporation experiments (4).
For all other experiments of Table 1 the barriers would be overcome on experimental timescales, with the exception of Estes et al. (33), where very low salt concentrations were used and in studies of pure phosphatidylserine (PS) membranes whose positive spontaneous membrane curvature leads to high line-tension. Our model predicts that phosphatidic acid (PA) lipids by contrast are highly hemifusogenic, having large negative spontaneous curvature (42) and thus presenting very small (a few kT) energy barriers to HD growth. This may be a factor in the low threshold cation concentration required to fuse PA lipid membranes (26,43) compared to that for PS membranes (25,44).
A model for the complete hemifusion-fusion pathway
Our analysis of hemifusion kinetics provides a framework to model the full pathway to fusion via hemifusion. Our analysis determines, for the first time to our knowledge, the evolution of HD area and tension during the hemifusion transient, both of which have been proposed to promote fusion through HD rupture (7,10,11,18). If fusion requires that the HD tension exceed the lysis threshold for sufficiently long, then we can use our own analysis to deduce whether or not fusion occurs under given experimental conditions. For example, in the experiments of Nikolaus et al, our model predicts that the HD tensions for two pairs (blue and red pairs in Fig. 3) exceeded the measured rupture threshold tensions (e.g., 8 mN/m measured in Evans et al. (21)), consistent with their eventual rupture to give fusion. Similarly, our estimates for the initial HD tensions in the other experiments of Table 1 are all super-lysis except for Estes et al. (33), suggesting that the fusion that was observed in these studies may have been produced by tension-driven HD rupture. On the other hand, because HD tension decays during growth (Fig. 4, C and D), our model suggests that a dead-end hemifused state will result if the initial tension is low or if an early super-lysis episode is survived, consistent with the equilibrium HDs observed in Nikolaus et al. (17) in low salt. Such effects were demonstrated in computer simulations of fusion, where high tension promoted fusion through rupture of small but expanding HDs, before membrane tension was relaxed by HD expansion (45).
Effects of vesicle-vesicle adhesion
In some cases, adhesion of the vesicles precedes their hemifusion, an effect neglected by our analysis. In the experiments of Nikolaus et al. (17), to which we quantitatively compared our model predictions, such effects are apparently weak: at high salt (6 mM Ca2+), small adhesion zones and contact angles were seen initially, typically eliminated by the growing HD, whereas at low salt (2 mM Mg2+) adhesion was absent in their equilibrium hemifused complexes. However, in other fusing systems such as the pure DOPS vesicles of Rand et al. (32), substantial adhesion zones are seen. In such cases, the production of an HD decreases the outer leaflet area available for adhesion. Thus, adhesion is expected to retard HD growth and produce smaller equilibrium HDs, as the driving force for hemifusion is reduced (ftherm of Eqs. 1 and 5). Fusion kinetics will also be affected: for a given vesicle tension, adhesion lowers the HD tension due to the finite contact angle that adjusts the force balance at the HD rim; on the other hand, vesicle and HD tensions tend to be greater as adhesion deforms and stretches the vesicles (32). These two tendencies are expected to suppress and enhance fusion, respectively.
Implications for biological fusion
Hemifusion in biological systems is commonly observed (13–16). Presumably the fusion machinery operates within the constraints of the membrane biophysics established in this work. Calcium pulses regulate fusion events in cells and activate calcium sensors that could include synaptotagmin (1). Our work suggests that such pulses may also induce significant local membrane tension and lipid condensation (10) because local cellular concentrations rise to typical levels of 25–300 μM Ca2+ (46) that could locally generate dimensionless driving forces ftherm ∼ 0.5–4% (10). Using these forces in Eq. 14, for 50–200-nm secretory vesicles our model suggests Ca2+ pulses would create ≲10 nm HDs on an equilibration timescale of ∼0.1–1 ms. Interestingly, this timescale is of the same order as the millisecond timescales thought to characterize neurotransmitter release following the calcium pulse (47).
Experimental outlook
Our modeling study motivates several experiments. Divalent cations drive hemifusion because they increase membrane tension and decrease membrane area. The dependencies of these effects on cation concentration are key input data for our model. We estimated tensions and condensation factors by taking composition-weighted sums of literature values measured for pure lipid species (23–25). The estimated condensation factors ϵcation are similar to those computed from simulations of PC/PS mixtures (48). However, a far superior procedure would be to independently measure these properties over a range of Ca2+ and Mg2+ concentrations in membranes with the same lipid composition as the hemifusing membranes.
Although the experimental method of Nikolaus et al. enables direct measurement of HD and vesicle sizes, the membrane tension and condensation factors are not directly available and both are controlled by divalent cation concentration in an unknown manner. A powerful experimental approach would be to hemifuse micropipette-aspirated GUVs (a similar approach was used to study EuCl3-mediated fusion pore expansion in Haluska et al. (39)). Then the tension γ would be controlled by the pipette aspiration pressure, whereas the condensation factor ϵcation could be precisely determined for each concentration by setting the tension to zero, measuring the equilibrium HD area and using the relation ϵcation = (Eq. 2). Thus, the HD area would provide a direct readout of the cationic condensation factor and the hemifusion driving force could be directly controlled.
Acknowledgments
We thank J. Nikolaus and A. Herrmann for critical discussions and access to experimental data before publication of Nikolaus et al. (17), including numerical values of the sizes of HDs shown in Figs. 1 and S1 of that publication.
The National Science Foundation is gratefully acknowledged for funding (for J.W.) through Integrative Graduate Education and Research Traineeship, Research Foundation of the City University of New York grant No. 404340001A.
Appendix: Derivation of Early Time HD Growth Law, Eq. 10
In this Appendix we show the HD area grows linearly in time for short times, = βD, where D = kΔ/λ and β is a time-independent factor depending on the driving force for HD growth, ftherm. Defining the shifted density field p(r,t) ≡ Δρ∗ − Δρ, where Δρ∗ is the value at the HD rim, r = Rhd(t), the diffusion-like equation of Eq. 8 becomes
| (15) |
For short times the geometry is effectively planar as the region where Δρ is substantial is much smaller than the vesicle radius. The HD boundary velocity is given by
proportional to the current. These dynamics are equivalent to a two-dimensional reaction-diffusion system with an infinitely strong reaction sink in the HD region r > Rhd(t). The quantity we seek is the reaction rate, , equal to the current per unit length of sink boundary times 2πRhd. Thus . The complexity is that the sink is growing in size.Let Q be the sink reaction rate per particle. Below, we will take the limit Q → ∞ to obtain the solution of Eq. 15. For finite Q, the solution would obey
| (16) |
where G(r – r′, t − t′) is the probability a particle at r′ at time t′ arrives at r at time t. Now the average value of p in the sink region obeys
| (17) |
where
| (18) |
depends only on the magnitude r′ = |r′| by symmetry. Multiplying both sides of Eq. 17 by QAhd(t) and noting we have
| (19) |
where
| (20) |
is the probability a particle on the HD perimeter at t′ lies within the HD region r ≤ Rhd(t) at t, and is a constant unit radial vector. We assumed Q is so large that within the sink p(r,t) is substantial only near r = Rhd(t).
We now make the Ansatz Ahd(t) = βDt. Thus, in Eq. 19, (t′) is constant and after taking Q → ∞, one has
| (21) |
after using the boundary condition of Eq. 9 of the main text for Δρ∗.
Thus, if the Ansatz is true, then self-consistently the time integral of S in Eq. 21 must be constant. Using Ahd(t) = βD in Eq. 20, one finds this time integral,
is a function of β only and has the value (4πD)−1 ln1/β for β << 1. This verifies the Ansatz. Moreover, it follows that in the limit of small β, Eq. 21 can be written β = 4πftherm/D ln(1/β), whose leading-order solution is
| (22) |
This proves our small time HD growth-rate result of Eq. 10 in the main text, with prefactor c = 4π = 12.57. Our numerical solutions verify this behavior, albeit with a slightly lower value c = 10.6 for the ftherm values used (see main text). The above result is valid for small β, i.e., small driving force ftherm << 1.
Supporting Material
References
- 1.Jahn R., Lang T., Südhof T.C. Membrane fusion. Cell. 2003;112:519–533. doi: 10.1016/s0092-8674(03)00112-0. [DOI] [PubMed] [Google Scholar]
- 2.Harrison S.C. Viral membrane fusion. Nat. Struct. Mol. Biol. 2008;15:690–698. doi: 10.1038/nsmb.1456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lentz B.R., Lee J.K. Poly(ethylene glycol) (PEG)-mediated fusion between pure lipid bilayers: a mechanism in common with viral fusion and secretory vesicle release? Mol. Membr. Biol. 1999;16:279–296. doi: 10.1080/096876899294508. (Review) [DOI] [PubMed] [Google Scholar]
- 4.Chernomordik L.V., Kozlov M.M. Protein-lipid interplay in fusion and fission of biological membranes. Annu. Rev. Biochem. 2003;72:175–207. doi: 10.1146/annurev.biochem.72.121801.161504. [DOI] [PubMed] [Google Scholar]
- 5.Floyd D.L., Ragains J.R., van Oijen A.M. Single-particle kinetics of influenza virus membrane fusion. Proc. Natl. Acad. Sci. USA. 2008;105:15382–15387. doi: 10.1073/pnas.0807771105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kozlovsky Y., Kozlov M.M. Stalk model of membrane fusion: solution of energy crisis. Biophys. J. 2002;82:882–895. doi: 10.1016/S0006-3495(02)75450-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kozlovsky Y., Chernomordik L.V., Kozlov M.M. Lipid intermediates in membrane fusion: formation, structure, and decay of hemifusion diaphragm. Biophys. J. 2002;83:2634–2651. doi: 10.1016/S0006-3495(02)75274-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hed G., Safran S.A. Initiation and dynamics of hemifusion in lipid bilayers. Biophys. J. 2003;85:381–389. doi: 10.1016/S0006-3495(03)74482-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Katsov K., Müller M., Schick M. Field theoretic study of bilayer membrane fusion. I. Hemifusion mechanism. Biophys. J. 2004;87:3277–3290. doi: 10.1529/biophysj.103.038943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Warner J.M., O’Shaughnessy B. The hemifused state on the pathway to membrane fusion. Phys. Rev. Lett. 2012;108:178101. doi: 10.1103/PhysRevLett.108.178101. [DOI] [PubMed] [Google Scholar]
- 11.Chanturiya A., Chernomordik L.V., Zimmerberg J. Flickering fusion pores comparable with initial exocytotic pores occur in protein-free phospholipid bilayers. Proc. Natl. Acad. Sci. USA. 1997;94:14423–14428. doi: 10.1073/pnas.94.26.14423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chernomordik L., Chanturiya A., Zimmerberg J. The hemifusion intermediate and its conversion to complete fusion: regulation by membrane composition. Biophys. J. 1995;69:922–929. doi: 10.1016/S0006-3495(95)79966-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zampighi G.A., Zampighi L.M., Wright E.M. Conical electron tomography of a chemical synapse: vesicles docked to the active zone are hemi-fused. Biophys. J. 2006;91:2910–2918. doi: 10.1529/biophysj.106.084814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wong J.L., Koppel D.E., Wessel G.M. Membrane hemifusion is a stable intermediate of exocytosis. Dev. Cell. 2007;12:653–659. doi: 10.1016/j.devcel.2007.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jun Y., Wickner W. Assays of vacuole fusion resolve the stages of docking, lipid mixing, and content mixing. Proc. Natl. Acad. Sci. USA. 2007;104:13010–13015. doi: 10.1073/pnas.0700970104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Melikyan G.B., White J.M., Cohen F.S. GPI-anchored influenza hemagglutinin induces hemifusion to both red blood cell and planar bilayer membranes. J. Cell Biol. 1995;131:679–691. doi: 10.1083/jcb.131.3.679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nikolaus J., Stöckl M., Herrmann A. Direct visualization of large and protein-free hemifusion diaphragms. Biophys. J. 2010;98:1192–1199. doi: 10.1016/j.bpj.2009.11.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chernomordik L.V., Melikyan G.B., Chizmadzhev Y.A. Biomembrane fusion: a new concept derived from model studies using two interacting planar lipid bilayers. Biochim. Biophys. Acta. 1987;906:309–352. doi: 10.1016/0304-4157(87)90016-5. [DOI] [PubMed] [Google Scholar]
- 19.Helm C.A., Israelachvili J.N., McGuiggan P.M. Molecular mechanisms and forces involved in the adhesion and fusion of amphiphilic bilayers. Science. 1989;246:919–922. doi: 10.1126/science.2814514. [DOI] [PubMed] [Google Scholar]
- 20.Kuhl T., Guo Y.Q., Hui S.W. Direct measurement of polyethylene glycol induced depletion attraction between lipid bilayers. Langmuir. 1996;12:3003–3014. [Google Scholar]
- 21.Evans E., Heinrich V., Rawicz W. Dynamic tension spectroscopy and strength of biomembranes. Biophys. J. 2003;85:2342–2350. doi: 10.1016/s0006-3495(03)74658-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Arnold K. Elsevier Science; New York: 1995. Handbook of Biological Physics. [Google Scholar]
- 23.Uhríková D., Kucerka N., Balgavý P. Structural changes in dipalmitoylphosphatidylcholine bilayer promoted by Ca2+ ions: a small-angle neutron scattering study. Chem. Phys. Lipids. 2008;155:80–89. doi: 10.1016/j.chemphyslip.2008.07.010. [DOI] [PubMed] [Google Scholar]
- 24.Mattai J., Hauser H., Shipley G.G. Interactions of metal ions with phosphatidylserine bilayer membranes: effect of hydrocarbon chain unsaturation. Biochemistry. 1989;28:2322–2330. doi: 10.1021/bi00431a051. [DOI] [PubMed] [Google Scholar]
- 25.Ohki S. A mechanism of divalent ion-induced phosphatidylserine membrane fusion. Biochim. Biophys. Acta. 1982;689:1–11. doi: 10.1016/0005-2736(82)90182-1. [DOI] [PubMed] [Google Scholar]
- 26.Ohki S., Ohshima H. Divalent cation-induced phosphatidic acid membrane fusion. Effect of ion binding and membrane surface tension. Biochim. Biophys. Acta. 1985;812:147–154. doi: 10.1016/0005-2736(85)90532-2. [DOI] [PubMed] [Google Scholar]
- 27.Evans E., Yeung A. Hidden dynamics in rapid changes of bilayer shape. Chem. Phys. Lipids. 1994;73:39–56. [Google Scholar]
- 28.Waugh R.E., Song J., Zeks B. Local and nonlocal curvature elasticity in bilayer membranes by tether formation from lecithin vesicles. Biophys. J. 1992;61:974–982. doi: 10.1016/S0006-3495(92)81904-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rawicz W., Olbrich K.C., Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000;79:328–339. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Raphael R.M., Waugh R.E. Accelerated interleaflet transport of phosphatidylcholine molecules in membranes under deformation. Biophys. J. 1996;71:1374–1388. doi: 10.1016/S0006-3495(96)79340-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shoemaker S.D., Vanderlick T.K. Calcium modulates the mechanical properties of anionic phospholipid membranes. J. Colloid Interface Sci. 2003;266:314–321. doi: 10.1016/s0021-9797(03)00582-4. [DOI] [PubMed] [Google Scholar]
- 32.Rand R.P., Kachar B., Reese T.S. Dynamic morphology of calcium-induced interactions between phosphatidylserine vesicles. Biophys. J. 1985;47:483–489. doi: 10.1016/S0006-3495(85)83941-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Estes D.J., Lopez S.R., Mayer M. Triggering and visualizing the aggregation and fusion of lipid membranes in microfluidic chambers. Biophys. J. 2006;91:233–243. doi: 10.1529/biophysj.105.076398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Puech P.-H., Brochard-Wyart F. Membrane tensiometer for heavy giant vesicles. Eur. Phys. J E Soft Matter. 2004;15:127–132. doi: 10.1140/epje/i2003-10157-8. [DOI] [PubMed] [Google Scholar]
- 35.Douglas J., Gallie T.M. On the numerical integration of a parabolic differential equation subject to a moving boundary condition. Duke Math. J. 1955;22:557–571. [Google Scholar]
- 36.Merkel R., Sackmann E., Evans E. Molecular friction and epitactic coupling between monolayers in supported bilayers. J. Phys. (Paris) 1989;50:1535–1555. [Google Scholar]
- 37.Carslaw H.S., Jaeger J.C. Oxford University Press; London, UK: 1959. Conduction of Heat in Solids. [Google Scholar]
- 38.Durning C.J., O’Shaughnessy B. Diffusion controlled reactions at an interface. J. Chem. Phys. 1988;88:7117–7128. [Google Scholar]
- 39.Haluska C.K., Riske K.A., Dimova R. Time scales of membrane fusion revealed by direct imaging of vesicle fusion with high temporal resolution. Proc. Natl. Acad. Sci. USA. 2006;103:15841–15846. doi: 10.1073/pnas.0602766103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Shillcock J.C., Lipowsky R. Tension-induced fusion of bilayer membranes and vesicles. Nat. Mater. 2005;4:225–228. doi: 10.1038/nmat1333. [DOI] [PubMed] [Google Scholar]
- 41.Chanturiya A., Scaria P., Woodle M.C. The role of membrane lateral tension in calcium-induced membrane fusion. J. Membr. Biol. 2000;176:67–75. doi: 10.1007/s00232001076. [DOI] [PubMed] [Google Scholar]
- 42.Kooijman E.E., Chupin V., Rand P.R. Spontaneous curvature of phosphatidic acid and lysophosphatidic acid. Biochemistry. 2005;44:2097–2102. doi: 10.1021/bi0478502. [DOI] [PubMed] [Google Scholar]
- 43.Sundler R., Papahadjopoulos D. Control of membrane fusion by phospholipid head groups. I. Phosphatidate/phosphatidylinositol specificity. Biochim. Biophys. Acta. 1981;649:743–750. doi: 10.1016/0005-2736(81)90179-6. [DOI] [PubMed] [Google Scholar]
- 44.Wilschut J., Papahadjopoulos D. Ca2+-induced fusion of phospholipid vesicles monitored by mixing of aqueous contents. Nature. 1979;281:690–692. doi: 10.1038/281690a0. [DOI] [PubMed] [Google Scholar]
- 45.Grafmüller A., Shillcock J., Lipowsky R. The fusion of membranes and vesicles: pathway and energy barriers from dissipative particle dynamics. Biophys. J. 2009;96:2658–2675. doi: 10.1016/j.bpj.2008.11.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Schneggenburger R., Neher E. Presynaptic calcium and control of vesicle fusion. Curr. Opin. Neurobiol. 2005;15:266–274. doi: 10.1016/j.conb.2005.05.006. [DOI] [PubMed] [Google Scholar]
- 47.Llinás R., Sugimori M., Silver R.B. The concept of calcium concentration microdomains in synaptic transmission. Neuropharmacology. 1995;34:1443–1451. doi: 10.1016/0028-3908(95)00150-5. [DOI] [PubMed] [Google Scholar]
- 48.Vernier P.T., Ziegler M.J., Dimova R. Calcium binding and head group dipole angle in phosphatidylserine-phosphatidylcholine bilayers. Langmuir. 2009;25:1020–1027. doi: 10.1021/la8025057. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


