Abstract
Ultrahigh-resolution optical coherence tomography (UR-OCT) has been used for the first time to our knowledge to study single-cell basal cell carcinoma (BCC) in vitro. This noninvasive, in situ, label-free technique with deep imaging depth enables three-dimensional analysis of scattering properties of single cells with cellular spatial resolution. From three-dimensional UR-OCT imaging, live and dead BCC cells can be easily identified based on morphological observation. We developed a novel method to automatically extract characteristic parameters of a single cell from data volume, and quantitative comparison and parametric analysis were performed. The results demonstrate the capability of UR-OCT to detect cell death at the cellular level.
OCIS codes: (170.1530) Cell analysis, (170.4500) Optical coherence tomography, (100.2960) Image analysis, (170.1870) Dermatology
1. Introduction
The aim of cancer therapies is mainly to stop cell proliferation or induce cell death. Cell death regulation is important for normal development and homeostasis [1]. Cancer cells escape from death signals and continue their abnormal proliferation. Therefore, the ability to induce death in cancer cells has been a crucial biomarker for the efficacy of chemotherapeutic agents. However, individual cancer cells, even from the same population, vary greatly in their response to cell death stimuli [2–4]. Some cancer cells are easily killed, but others remain resistant. This cell-to-cell variability might be attributed to genetic, epigenetic or proteomic factors, the presence of cancer stem cells and different stages of the cell cycle [5–10]. In the context of the tumor microenvironment, the reasons for variable cancer cell response to treatment further include variations in tissue drug concentration, local oxygen concentration, cytokine profile, interaction between cancer cells, and host immune response. Measuring the response at the single-cell level provides further pharmacokinetic and pharmacodynamic information, which aids drug development and regimen design [11,12]. Fluorescence microscopy can be used to detect cell death at the single-cell level after cancer cells have been labeled by genetically engineered reporters or exogenous fluorescent dyes [13–16]. Despite great success employing fluorescence microscopy in mouse intravital observations, the requirement for labeling and possible phototoxicity circumvents its use in human subjects. Furthermore, the limited imaging depth of fluorescence microscopy also places restrictions on clinical application. Therefore, developing a microscopic technology with noninvasive, in situ, label-free, single-cell spatial resolution may serve this long-term need. In this paper, we report the detection of cell death at the single-cell level using ultrahigh-resolution optical coherence tomography (UR-OCT).
Optical coherence tomography is widely used in clinical medicine, especially in ophthalmology and cardiology because of the ability of imaging deep within tissue [17]. After the first trial using OCT for three-dimensional tomography on cell-based tissue models [18], OCT emerged as a promising technique for detecting multiple cell activities and responses to environmental stimuli [19–21]. Traditionally, clinical OCT is relatively low in resolution and mainly used to characterize architectural morphology [22]. An improvement in OCT technology currently provides axial resolution to approximately 1 μm and lateral resolution to 2 μm [22–24]. In this report, we demonstrated that UR-OCT not only provides three-dimensional in situ single-cell imaging but is also able to delineate subcellular structure (i.e., the nucleus).
Dead cells cannot be differentiated from live cells based merely on size. Many parametric analytic methods have been used to address this issue, including speckle fluctuation in time-lapse images [25–27]. It was confirmed that back-scattering signals are lower in apoptotic cells [28], which is most likely due to the perturbation of mitochondrial morphology during apoptosis [29]. Nuclear disintegration after chromatin condensation provides high-signal-intensity peaks that facilitate the identification of apoptotic cells.
Other nonlinear optical techniques, such as second/third harmonic generation microscopy [30], coherent anti-stoke Raman scattering microscopy [31], and stimulated Raman scattering microscopy [32], also provide alternative choices for label-free imaging with subcellular spatial resolution. Because these techniques make use of nonlinear signals originating from light-material interactions within the specimen as a source of contrast, femtosecond or picosecond pulse lasers are usually used to efficiently excite nonlinear processes. In view of the high peak power of these pulse lasers, combined with the risk of damaging the specimen under illumination with high intensity, the application of these nonlinear microscopy techniques remains in the field of pre-clinical research.
In this study, we aimed to use a homemade UR-OCT system to image single-cell basal cell carcinoma (BCC) in three dimensions and differentiate between live and dead BCC cells by not only morphological recognition but also parametric analysis. A BCC cell line was used because BCC is the most common skin cancer, and we are familiar with it [33,34]. An image analysis approach was also developed to automatically extract deterministic information of a single cell.
2. Materials and methods
2.1. Sample preparation
The BCC cell line was tested to be free of mycoplasma and other trivial contaminants. BCC cells were cultured in RPMI 1640 (Invitrogen, Carlsbad, CA) supplemented with 10% fetal calf serum (FCS), 100 mg/ml penicillin and 100 mg/ml streptomycin and maintained in an incubator at 37 °C with 5% CO2. Prior to the experiment, grown cells were trypsinized and collected by centrifugation. Samples for OCT scanning were prepared by mixing a BCC cell suspension with thawed Matrigel solution (BD Bioscience, Bedford, MA) 1:1, and injecting 25 μl of the suspension, which corresponded to 5000 cells per sample, into round-grooved glass-slides. To prevent environmental effects during the experiment, all of the samples were fixed with 2% paraformaldehyde and mounted with cover-slips.
2.2. Confocal microscopy
The samples for confocal microscopy were prepared similarly to the typical procedure, except that the cells were stained before being injected into round-grooved glass-slides. Before staining, the BCC cells were suspended in Hank’s balanced salt solution (HBSS) supplemented with 2% FCS (HBSS+) and centrifuged to replace HBSS+ with the stain. To stain the nucleus and cell membrane, the BCC cells were incubated with Hoechst and CellMask (Invitrogen, Carlsbad, CA) solution (diluted 1:1 in HBSS+) for 15 minutes and 5 minutes, respectively, and then washed again in HBSS+. The samples were observed under a commercial confocal microscope system (LSM 510 META, Carl Zeiss, Oberkochen, Germany).
2.3. UR-OCT system
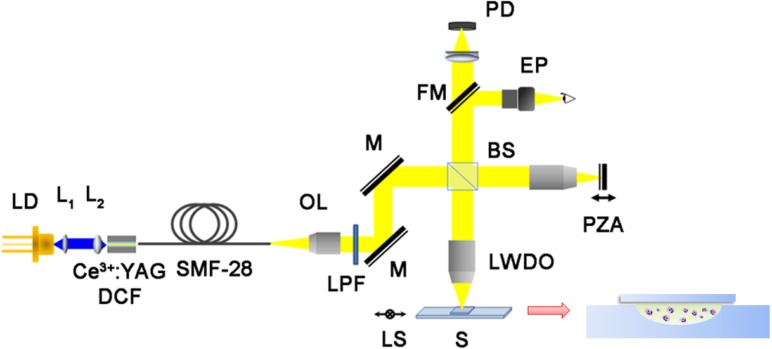
The design and operating principle of the UR-OCT system was similar to our previous report [35]. However, the light source was improved, and a parallel light system setup was adopted to achieve better transverse resolution. Figure 1 is a schematic representation of the system. The original light source was a Ce3+:YAG double-clad crystal fiber, which was fabricated by the codrawing laser-heated pedestal growth technique and pumped by a 446-nm blue laser diode (NDB-7112E, Nichia, Tokushima, Japan). Amplified spontaneous emission of this active fiber was butt-coupled into a silica fiber (SMF-28-10, THORLABS, Newton, New Jersey) to produce a high-brightness pigtailed fiber light source. The output spectrum had a center wavelength of 560 nm, and the full-width at half-maximum bandwidth was approximately 100 nm, which corresponded to 1.45 μm depth resolution in air and approximately 1.1 μm in bio-samples. Transverse resolution was measured to be 2.6 μm when a 10x long working distance objective (NT59-877, Edmund Optics Inc., Barrington, New Jersey) was utilized as the focusing lens; thus, cellular spatial resolution could be achieved. The probing power was 42 μW, which is well below the safe occupational exposure level established by the American National Standards Institute (ANSI Z 136.1). Depth scanning was accomplished by a piezo actuator (P-601.30L, PI, Karlsruhe, Germany) with a scanning range of 200 μm. The A-scan repetition rate was 2 Hz. Based on the above operational conditions, the system sensitivity was 82.3 dB. To compensate for the differences in dispersion and optical path length between the sample arm and reference arm, hardware compensation was adopted using the same optical elements, such as an objective lens and cover glass, in both sample and reference arms.
Fig. 1.
A schema of UR-OCT system. LD: laser diode; L1 and L2: 40X and 60X aspheric lenses; OL: 4X objective lens; LPF: long-pass filters; M: mirror; BS: beam splitter; LWDO: 10X long working distance objective; FM: flipper mirror; PZA: piezo actuator; S: sample; LS: 2D linear stage; EP: eyepiece; PD: photo diode.
2.4. Data analysis algorithm and statistical methods
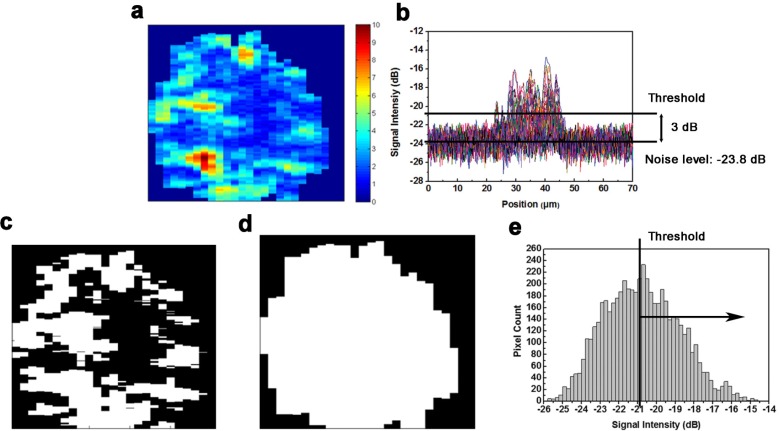
Several parameters were defined based on the intensity and spatial distribution of the back-scattering signal for single-cell analysis. Quantitative analysis could be performed because back-scattering signal characteristics were closely associated with morphological and physiological differences between live and dead BCC cells. In this study, each cell was analyzed in a three-dimensional manner. Two-dimensional image analysis was unable to completely describe a whole cell and may lead to biased conclusions. To avoid power fluctuation of the light source, the signal intensity was normalized by the reflection intensity of the lower surface of the cover glass. For each data volume, the normalized noise level was measured, and any pixel whose normalized intensity was 3 dB higher than the noise level was considered for signal analysis (Figs. 2a and 2b). Pixels whose intensity was lower than the 3 dB threshold were disregarded because we could not easily distinguish them from noise fluctuation. Therefore, a binary image called a “mask” can be constructed from each B-scan (Fig. 2c) by assigning considered pixels’ value to logical one and assigning disregarded pixels’ value to logical zero. In this way, the considered pixels and their total number inside a data volume for single-cell analysis were obtained. The signal average was defined by computing the mean value of considered pixel intensity for each cell. The signal average can be considered as the total scattering capability of a single cell to the incident light. To compute the spatial density of a cell, defined as cellular density, the cell volume must first be evaluated. This evaluation could be performed by identifying the cell region of each B-scan from its corresponding mask (Fig. 2d). For every column in a mask, the segment between the first and last nonzero pixel was regarded as within the cell region; thus, the pixel number of the cell region of a B-scan could be computed, and the cell volume was obtained by summing the total pixel number in cell regions. Cellular density was calculated as the ratio of the number of total analyzed pixels and the total pixel number in a cell volume (Fig. 2e). Finally, the average dynamic range of a cell was defined as the mean value of the dynamic range of each A-scan within the data volume. We averaged the dynamic range of each A-scan because the sampling rate was the highest along the z-axis. The average dynamic range can be thought of as the scattering capability of the main scatterers in a cell. Note that the dynamic range was defined as the ratio of the maxima and noise level of the A-scan. After obtaining the characteristic parameters of single BCC cells, Student’s t-test was used to evaluate the differences in these parameters between the normal group and the dead group. All of the tests were two-tailed, and a P-value < 0.05 was considered to be statistically significant. The linear relationship between these parameters was evaluated based on Pearson's linear regression model. All of the statistical tests were performed using STATA 8.2 software (StataCorp, College Station, TX).
Fig. 2.
For each B-scan, intensity image (a) was transform into binary image by applying a threshold (b) which was higher than noise level by 3 dB on every pixels (c). The corresponding image of cell region which was found by automatically boundary detecting method (d). Cellular density can also calculated by dividing the area above the threshold and the total area of the bell shape intensity distribution diagram (e).
3. Results
3.1. UR-OCT images
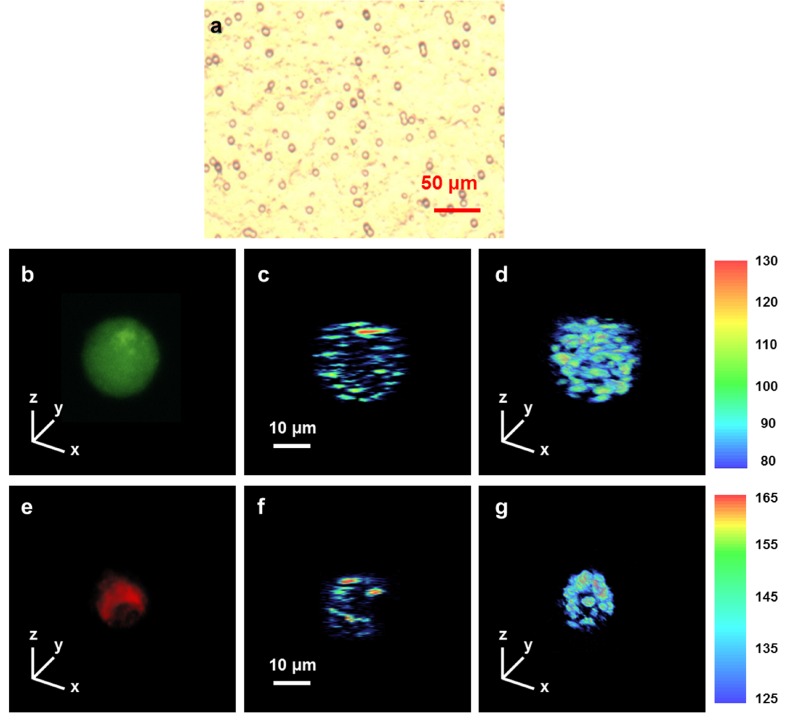
Figure 3 shows the microscopic image of a BCC cell line suspended in Matrigel solution and typical UR-OCT/confocal microscopy images of live and dead BCC cells. In this study, dead BCC cells were prepared by mixing 80 μM celecoxib with a cell suspension for 16 hours to induce cell death. Celecoxib has been used in combination with other chemotherapeutic agents, including docetaxel and erlotinib, in clinical trials for non–small-cell lung cancers [36,37]. A previous report demonstrated the important role of cyclooxygenase-2 in the progression of BCC. Preliminary studies also showed that celecoxib induces dose- and time-dependent killing of BCC. The viability of live cells was confirmed by positive calcein staining by confocal microscopy (Fig. 3b) before they were imaged with UR-OCT. The dead cells were verified by positive propidium staining (Fig. 3e) and subsequently observed with UR-OCT. In Fig. 3(a), BCC cells cultured in a non-restricted three-dimensional environment generally showed a round shape with diameter ranged from 15 to 22 μm. In UR-OCT images, the back-scattered light intensity is demonstrated by the contrast of transition from blue (low intensity) to red (high intensity). In two-dimensional cross-sectional images (Figs. 3c and 3f), we observed that the signal distribution of a live BCC cell was easily identified as a round shape. In addition to the clear boundary of the live BCC cell, signals from intracellular organelles were also observed. In contrast, the back-scattering signal of dead BCC cells was concentrated only on some main scatterers whose relative position could not be easily described by a specific geometry, suggesting that the cell had disintegrated into apoptotic bodies. The three-dimensional images (Figs. 3d and 3g) show that the contour of live BCC cells was spherical and intact, while dead BCC cells showed an irregular and shrinking appearance. The difference in UR-OCT imaging between live and dead BCC cells can be correlated with common knowledge of the apoptotic process at the cellular level.
Fig. 3.
Microscopic image of BCC cell line and UR-OCT/confocal microscopy images of live and dead BCC cells. BCC cell line was suspended in Matrigel and imaged by a bright-field microscope (a). Live and dead BCC cells were randomly selected from the sample and scanned by UR-OCT and confocal microscopy. Live cell were encoded in green (b) and dead cell which was were encoded in red (e), according to the calcein and propidium’s fluorescence spectrum. Two-dimensional cross-sectional imaging (c, f) were performed across the center of each cell. Three-dimensional imaging of the whole cell (d, g) were realized by combining several cross-sectional images whose covering range were slightly larger than the size of the cells.
3.2. Confocal microscopy observation
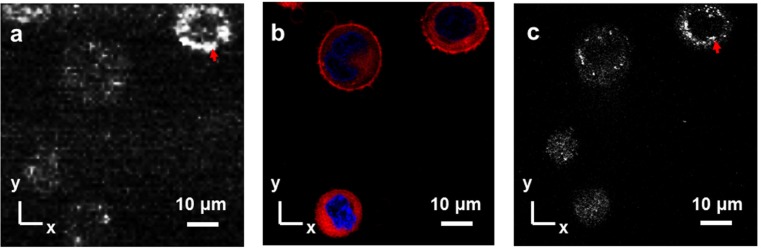
A comparison of the UR-OCT en face image with a confocal microscope image of the same cell was also performed (Figs. 4a -4c). Several BCC cells in which the nucleus and cell membrane were previously stained were imaged with UR-OCT, and several x-y planes were summed to provide an en face image, which was consistent with the image obtained with confocal microscopy (Fig. 4a). A confocal fluorescence microscope (CFM) image with the nucleus in blue and the plasma membrane in red was acquired (Fig. 4b). Note that the cytoplasm of these cells was also stained unexpectedly. Comparing Figs. 4a and 4b, the relative position and the shape of BCC cells in the UR-OCT image could be perfectly correlated to the CFM image. To illustrate the origin of back scattering, confocal reflectance microscope (CRM) image was also acquired (Fig. 4c). In the CRM image, we observed that the back-scattered signals were concentrated on some small organelles, and the position of the nucleus showed a hollow morphology. The phenomenon was also found in the UR-OCT image, suggesting that the main scatterers in UR-OCT were small organelles, such as mitochondria or the Golgi apparatus, instead of the relatively larger nucleus.
Fig. 4.
Co-registered BCC cells image of UR-OCT and confocal microscopy. En face image of UR-OCT (a) with corresponding CFM and CRM images (b, c) of BCC cells. The CFM and CRM images were acquired before UR-OCT imaging since the fluorescence decayed rapidly after staining procedure. Red arrows, strong scattering from small organelles.
3.3. Signal characteristics of UR-OCT single-cell images
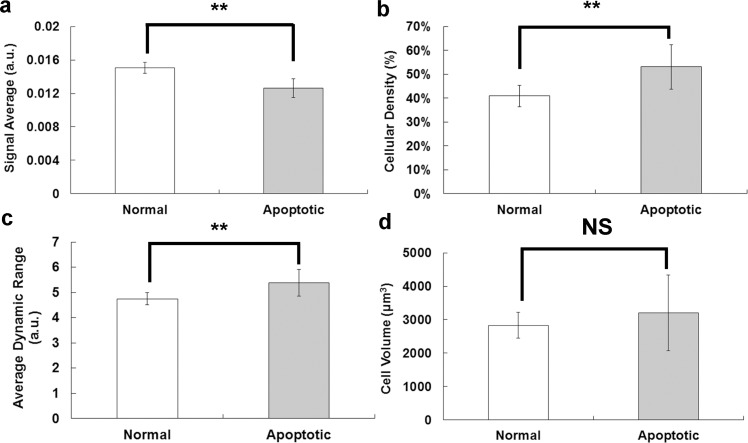
Based on the previously mentioned parameter definitions, the signal average of the live group was significantly higher than the dead group (live group, ; dead group, ; P = 0.0006) (Fig. 5a ), suggesting that back-scattered light intensity was higher for live BCC cells. However, the cellular density of the live group was significantly lower than the dead group (live group, ; dead group, ; P = 0.0125) (Fig. 5b). Moreover, the average dynamic range of the three-dimensional image was also significantly lower for the live group than the dead group (live group, ; dead group, ; P = 0.0208) (Fig. 5c). The higher cellular density and dynamic range for the dead group were consistent with the characteristic properties of apoptotic cells. Nevertheless, there was no significant difference in cell volume between live and dead groups, showing the heterogeneous nature of the size distribution of original BCC cells (normal group, 2827.5 μm3; apoptotic group, 3210.7 μm3; P = 0.4229) (Fig. 5d).
Fig. 5.
Different properties between live and dead BCC cells. (a) Signal average; (b) cellular density; (c) average dynamic range; (d) cell volume of BCC cells. White bar, normal group (n = 7); black group, apoptotic group (n = 7); **P < 0.05. NS, not significant.
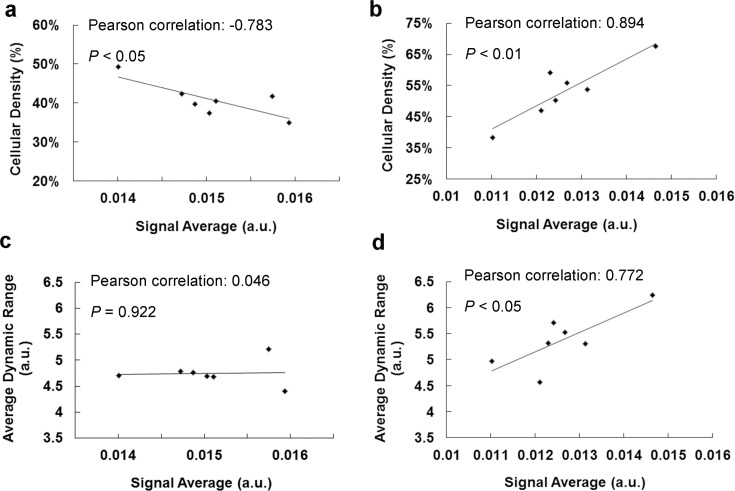
The relationships of different parameters of BCC cells were further illustrated by scatter plots. In the dead group, the signal average was highly correlated with cellular density (Pearson’s correlation 0.894, P < 0.01), but it was highly negatively correlated with cellular density in the live group (Pearson’s correlation −0.783, P < 0.05) (Figs. 6a and 6b). Moreover, the signal average had a high positive correlation with the average dynamic range in the dead group (Pearson’s correlation 0.772, P < 0.05) but appeared to be uncorrelated in the live group (Pearson’s correlation 0.046, P = 0.922) (Figs. 6c and 6d). The results suggested that the distinct relationships of these parameters could originate from intrinsic morphological differences between live and dead BCC cells.
Fig. 6.
Correlation of signal average, cellular density, and average dynamic range between live and dead BCC cells. Scatter plots of cellular density and signal average, average dynamic range and signal average of live (a, c) and dead group (b, d). Significant positive correlations of the three parameters were observed in dead group.
4. Discussion
The mechanism of light scattering from biological cells has been investigated, and scattering at large angles, which corresponds to back-scattered OCT signals, could be mainly due to small organelles and structures within organelles [38,39]. These previous reports are consistent with our observation from en face images of UR-OCT and confocal microscopy. In flow cytometry, dead cells can be identified on the basis of changes in scattering by plotting the intensity of light scattered forward and at 90° [28], and the formation of apoptotic bodies can be characterized by a decrease in both forward and side scattering [40]. Based on these previous reports, it can be assumed that light scattering is higher for live than dead BCC cells, because the number of main scatterers in UR-OCT imaging, such as mitochondria, in live cells should be higher than in apoptotic cells, and the morphology of these scatterers is relatively intact compared with apoptotic bodies, which leads to a stronger back-scattering light intensity. In this study, the signal average was significantly higher in live BCC cells than dead BCC cells, which was in good agreement with the previously mentioned hypothesis. Our result suggests that dead BCC cells have a generally much weaker scattering potential than their live counterparts. Interestingly, our experimental result also showed that the average dynamic range was significantly higher in dead BCC cells. In apoptotic cells, back-scattered signals may originate from locally condensed chromatin and fragmented nuclei [28]. The results that the average dynamic range was higher but the signal average was lower in dead BCC cells reflected that back-scattering signals of apoptotic BCC cell were only concentrated on some main scatterers. These scatterers induced locally strong scattering signals, but the average signal intensity for a whole cell remained low due to the relatively weaker scattering capability of other scatterers.
The nuclei in live BCC cells are unbroken and occupy a large ratio of the total cell volume, which can be confirmed by UR-OCT and confocal microscope images. Due to the low contribution of back-scattered signals from the nucleus and considering cellular shrinkage and nuclear rupture during the cell death process, it can be predicted that live BCC cells would have lower cellular density than dead BCC cells. As expected, our experimental result showed that cellular density was significantly lower in live BCC cells, suggesting that UR-OCT imaging can be used to identify dead BCC cells based on the integrity of nuclear morphology. Note that the higher cellular density of apoptotic BCC cells can be intuitively related to the shrinking morphology, but it cannot be concluded that the dead BCC cells had a smaller average size than live BCC cells, because there was no difference in the size of live and dead BCC cells (Fig. 5d).
Further examination of the relationships between characteristic parameters of single cells provided even deeper insight into intracellular structure. It has been reported that the scattering cross section increases significantly as the nuclear-cytoplasmic ratio increases [38]. In live BCC cells, cellular density decreased as the nuclear-cytoplasmic ratio increased. Therefore, the signal average should increase as cellular density decreases. In this study, the measured signal average was significantly negatively correlated with cellular density in live BCC cells, which indicated that light scattering is enhanced as the nuclear-cytoplasmic ratio increases. In addition, the size distribution of main scatterers in live BCC cells, such as mitochondria, should have high homogeneity, which means that these scatterers also have similar scattering capability. The experimental result showed that the average dynamic range was independent of the signal average for different live BCC cells, which suggests that the difference in scattering capability between different cells is most likely due to the difference between the numbers of scatterers inside the cells.
In dead BCC cells, there was no well-defined nuclear-cytoplasmic ratio, so the previous analysis by [38] cannot be directly linked to the experimental result. Nevertheless, light scattering may originate from the condensed chromatin of dead cells, and it was assumed that the refractive index increase linearly with the amount of DNA [41]. The higher concentration of DNA corresponded to a higher average dynamic range of the dead BCC cells, and so did the signal average. Our experimental result showed that the signal average had a significantly positive correlation with the average dynamic range in dead BCC cells, which implied that the light-scattering properties of dead BCC cells was highly correlated with the chromatin condensation process. Moreover, due to the shrinkage of dead cells, it can be assumed that the higher cellular density corresponded to a higher concentration of DNA content. The measured cellular density of dead BCC cells was positively correlated with the signal average, which also agrees well with our assumption.
5. Conclusions
Three-dimensional single-cell imaging and the analysis of live and dead BCC cells utilizing UR-OCT were demonstrated for the first time. The apoptotic process involves a series of morphological changes, and there are many new scatterers generated. The morphological change-induced scatterers affected the scattering properties of dead cells. Therefore, the death of a single cell can be detected by not only direct imaging but also parametric analysis. In this study, we defined the signal average, cellular density, average dynamic range, and cell volume as characteristic parameters of single cells. Based on these parameters, three effective parameters were found, with P-value less than 0.05. Correlations between these parameters also provide complementary information to three-dimensional imaging. This technique is believed to be an important noninvasive methodology that provides morphological and quantitative information for detecting cell death at cellular level.
Acknowledgments
This work was supported by grants from the National Science Council, Executive Yuan, Taiwan (NSC 100-3113-P-002-008). The authors would like to thank Dr. Chung-Liang Chien and Chuan-Chuan Chao for assistance with confocal microscopy.
References and links
- 1.Spencer S. L., Sorger P. K., “Measuring and modeling apoptosis in single cells,” Cell 144(6), 926–939 (2011). 10.1016/j.cell.2011.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gascoigne K. E., Taylor S. S., “Cancer cells display profound intra- and interline variation following prolonged exposure to antimitotic drugs,” Cancer Cell 14(2), 111–122 (2008). 10.1016/j.ccr.2008.07.002 [DOI] [PubMed] [Google Scholar]
- 3.Huang H. C., Mitchison T. J., Shi J., “Stochastic competition between mechanistically independent slippage and death pathways determines cell fate during mitotic arrest,” PLoS ONE 5(12), e15724 (2010). 10.1371/journal.pone.0015724 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sharma S. V., Lee D. Y., Li B., Quinlan M. P., Takahashi F., Maheswaran S., McDermott U., Azizian N., Zou L., Fischbach M. A., Wong K. K., Brandstetter K., Wittner B., Ramaswamy S., Classon M., Settleman J., “A chromatin-mediated reversible drug-tolerant state in cancer cell subpopulations,” Cell 141(1), 69–80 (2010). 10.1016/j.cell.2010.02.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cohen A. A., Geva-Zatorsky N., Eden E., Frenkel-Morgenstern M., Issaeva I., Sigal A., Milo R., Cohen-Saidon C., Liron Y., Kam Z., Cohen L., Danon T., Perzov N., Alon U., “Dynamic proteomics of individual cancer cells in response to a drug,” Science 322(5907), 1511–1516 (2008). 10.1126/science.1160165 [DOI] [PubMed] [Google Scholar]
- 6.Niepel M., Spencer S. L., Sorger P. K., “Non-genetic cell-to-cell variability and the consequences for pharmacology,” Curr. Opin. Chem. Biol. 13(5-6), 556–561 (2009). 10.1016/j.cbpa.2009.09.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Raj A., van Oudenaarden A., “Nature, nurture, or chance: stochastic gene expression and its consequences,” Cell 135(2), 216–226 (2008). 10.1016/j.cell.2008.09.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rando O. J., Verstrepen K. J., “Timescales of genetic and epigenetic inheritance,” Cell 128(4), 655–668 (2007). 10.1016/j.cell.2007.01.023 [DOI] [PubMed] [Google Scholar]
- 9.Reya T., Morrison S. J., Clarke M. F., Weissman I. L., “Stem cells, cancer, and cancer stem cells,” Nature 414(6859), 105–111 (2001). 10.1038/35102167 [DOI] [PubMed] [Google Scholar]
- 10.Spencer S. L., Gaudet S., Albeck J. G., Burke J. M., Sorger P. K., “Non-genetic origins of cell-to-cell variability in TRAIL-induced apoptosis,” Nature 459(7245), 428–432 (2009). 10.1038/nature08012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Earley S., Vinegoni C., Dunham J., Gorbatov R., Feruglio P. F., Weissleder R., “In vivo imaging of drug-induced mitochondrial outer membrane permeabilization at single-cell resolution,” Cancer Res. 72(12), 2949–2956 (2012). 10.1158/0008-5472.CAN-11-4096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Orth J. D., Kohler R. H., Foijer F., Sorger P. K., Weissleder R., Mitchison T. J., “Analysis of mitosis and antimitotic drug responses in tumors by in vivo microscopy and single-cell pharmacodynamics,” Cancer Res. 71(13), 4608–4616 (2011). 10.1158/0008-5472.CAN-11-0412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Albeck J. G., Burke J. M., Aldridge B. B., Zhang M., Lauffenburger D. A., Sorger P. K., “Quantitative analysis of pathways controlling extrinsic apoptosis in single cells,” Mol. Cell 30(1), 11–25 (2008). 10.1016/j.molcel.2008.02.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nicholls S. B., Chu J., Abbruzzese G., Tremblay K. D., Hardy J. A., “Mechanism of a genetically encoded dark-to-bright reporter for caspase activity,” J. Biol. Chem. 286(28), 24977–24986 (2011). 10.1074/jbc.M111.221648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pittet M. J., Weissleder R., “Intravital imaging,” Cell 147(5), 983–991 (2011). 10.1016/j.cell.2011.11.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Weissleder R., Pittet M. J., “Imaging in the era of molecular oncology,” Nature 452(7187), 580–589 (2008). 10.1038/nature06917 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., et, “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tan W., Oldenburg A. L., Norman J. J., Desai T. A., Boppart S. A., “Optical coherence tomography of cell dynamics in three-dimensional tissue models,” Opt. Express 14(16), 7159–7171 (2006). 10.1364/OE.14.007159 [DOI] [PubMed] [Google Scholar]
- 19.Liang X., Graf B. W., Boppart S. A., “Imaging engineered tissues using structural and functional optical coherence tomography,” J. Biophotonics 2(11), 643–655 (2009). 10.1002/jbio.200910048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kuo W. C., Chan C. H., Chou C. H., Cheng J. C., “Swept source optical coherence tomography for radiation-enhanced hepatocellular carcinoma cell invasion imaging,” Phys. Med. Biol. 54(13), 4289–4297 (2009). 10.1088/0031-9155/54/13/021 [DOI] [PubMed] [Google Scholar]
- 21.Rey S. M., Povazay B., Hofer B., Unterhuber A., Hermann B., Harwood A., Drexler W., “Three- and four-dimensional visualization of cell migration using optical coherence tomography,” J. Biophotonics 2(6-7), 370–379 (2009). 10.1002/jbio.200910027 [DOI] [PubMed] [Google Scholar]
- 22.Liu L., Gardecki J. A., Nadkarni S. K., Toussaint J. D., Yagi Y., Bouma B. E., Tearney G. J., “Imaging the subcellular structure of human coronary atherosclerosis using micro-optical coherence tomography,” Nat. Med. 17(8), 1010–1014 (2011). 10.1038/nm.2409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Häusler G., Lindner M. W., “Coherence radar and spectral radar—new tools for dermatological diagnosis,” J. Biomed. Opt. 3(1), 21–31 (1998). 10.1117/1.429899 [DOI] [PubMed] [Google Scholar]
- 24.Vakhtin A. B., Kane D. J., Wood W. R., Peterson K. A., “Common-path interferometer for frequency-domain optical coherence tomography,” Appl. Opt. 42(34), 6953–6958 (2003). 10.1364/AO.42.006953 [DOI] [PubMed] [Google Scholar]
- 25.Bagnaninchi P. O., Holmes C., Drummond N., Daoud J., Tabrizian M., “Two-dimensional and three-dimensional viability measurements of adult stem cells with optical coherence phase microscopy,” J. Biomed. Opt. 16(8), 086003 (2011). 10.1117/1.3606561 [DOI] [PubMed] [Google Scholar]
- 26.Dunkers J. P., Lee Y. J., Chatterjee K., “Single cell viability measurements in 3D scaffolds using in situ label free imaging by optical coherence microscopy,” Biomaterials 33(7), 2119–2126 (2012). 10.1016/j.biomaterials.2011.11.058 [DOI] [PubMed] [Google Scholar]
- 27.Joo C., Akkin T., Cense B., Park B. H., de Boer J. F., “Spectral-domain optical coherence phase microscopy for quantitative phase-contrast imaging,” Opt. Lett. 30(16), 2131–2133 (2005). 10.1364/OL.30.002131 [DOI] [PubMed] [Google Scholar]
- 28.Darzynkiewicz Z., Juan G., Li X., Gorczyca W., Murakami T., Traganos F., “Cytometry in cell necrobiology: analysis of apoptosis and accidental cell death (necrosis),” Cytometry 27(1), 1–20 (1997). [DOI] [PubMed] [Google Scholar]
- 29.Reis Y., Bernardo-Faura M., Richter D., Wolf T., Brors B., Hamacher-Brady A., Eils R., Brady N. R., “Multi-parametric analysis and modeling of relationships between mitochondrial morphology and apoptosis,” PLoS ONE 7(1), e28694 (2012). 10.1371/journal.pone.0028694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rehberg M., Krombach F., Pohl U., Dietzel S., “Label-free 3D visualization of cellular and tissue structures in intact muscle with second and third harmonic generation microscopy,” PLoS ONE 6(11), e28237 (2011). 10.1371/journal.pone.0028237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Evans C. L., Potma E. O., Puoris’haag M., Côté D., Lin C. P., Xie X. S., “Chemical imaging of tissue in vivo with video-rate coherent anti-Stokes Raman scattering microscopy,” Proc. Natl. Acad. Sci. U.S.A. 102(46), 16807–16812 (2005). 10.1073/pnas.0508282102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhang X., Roeffaers M. B., Basu S., Daniele J. R., Fu D., Freudiger C. W., Holtom G. R., Xie X. S., “Label-free live-cell imaging of nucleic acids using stimulated Raman scattering microscopy,” ChemPhysChem 13(4), 1054–1059 (2012). 10.1002/cphc.201100890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tjiu J. W., Liao Y. H., Lin S. J., Huang Y. L., Tsai W. L., Chu C. Y., Kuo M. L., Jee S. H., “Cyclooxygenase-2 overexpression in human basal cell carcinoma cell line increases antiapoptosis, angiogenesis, and tumorigenesis,” J. Invest. Dermatol. 126(5), 1143–1151 (2006). 10.1038/sj.jid.5700191 [DOI] [PubMed] [Google Scholar]
- 34.Tjiu J. W., Chen J. S., Shun C. T., Lin S. J., Liao Y. H., Chu C. Y., Tsai T. F., Chiu H. C., Dai Y. S., Inoue H., Yang P. C., Kuo M. L., Jee S. H., “Tumor-associated macrophage-induced invasion and angiogenesis of human basal cell carcinoma cells by cyclooxygenase-2 induction,” J. Invest. Dermatol. 129(4), 1016–1025 (2009). 10.1038/jid.2008.310 [DOI] [PubMed] [Google Scholar]
- 35.Tsai C. C., Chen T. H., Lin Y. S., Wang Y. T., Chang W., Hsu K. Y., Chang Y. H., Hsu P. K., Jheng D. Y., Huang K. Y., Sun E., Huang S. L., “Ce3+:YAG double-clad crystal-fiber-based optical coherence tomography on fish cornea,” Opt. Lett. 35(6), 811–813 (2010). 10.1364/OL.35.000811 [DOI] [PubMed] [Google Scholar]
- 36.Csiki I., Morrow J. D., Sandler A., Shyr Y., Oates J., Williams M. K., Dang T., Carbone D. P., Johnson D. H., “Targeting cyclooxygenase-2 in recurrent non-small cell lung cancer: a phase II trial of celecoxib and docetaxel,” Clin. Cancer Res. 11(18), 6634–6640 (2005). 10.1158/1078-0432.CCR-05-0436 [DOI] [PubMed] [Google Scholar]
- 37.Reckamp K. L., Krysan K., Morrow J. D., Milne G. L., Newman R. A., Tucker C., Elashoff R. M., Dubinett S. M., Figlin R. A., “A phase I trial to determine the optimal biological dose of celecoxib when combined with erlotinib in advanced non-small cell lung cancer,” Clin. Cancer Res. 12(11), 3381–3388 (2006). 10.1158/1078-0432.CCR-06-0112 [DOI] [PubMed] [Google Scholar]
- 38.Drezek R., Dunn A., Richards-Kortum R., “Light scattering from cells: finite-difference time-domain simulations and goniometric measurements,” Appl. Opt. 38(16), 3651–3661 (1999). 10.1364/AO.38.003651 [DOI] [PubMed] [Google Scholar]
- 39.Mourant J. R., Freyer J. P., Hielscher A. H., Eick A. A., Shen D., Johnson T. M., “Mechanisms of light scattering from biological cells relevant to noninvasive optical-tissue diagnostics,” Appl. Opt. 37(16), 3586–3593 (1998). 10.1364/AO.37.003586 [DOI] [PubMed] [Google Scholar]
- 40.Darzynkiewicz Z., Bedner E., Smolewski P., “Flow cytometry in analysis of cell cycle and apoptosis,” Semin. Hematol. 38(2), 179–193 (2001). 10.1016/S0037-1963(01)90051-4 [DOI] [PubMed] [Google Scholar]
- 41.Drezek R., Guillaud M., Collier T., Boiko I., Malpica A., Macaulay C., Follen M., Richards-Kortum R., “Light scattering from cervical cells throughout neoplastic progression: influence of nuclear morphology, DNA content, and chromatin texture,” J. Biomed. Opt. 8(1), 7–16 (2003). 10.1117/1.1528950 [DOI] [PubMed] [Google Scholar]