The sliding-helix voltage sensor

Abstract

The voltage sensor (VS) domain of voltage-gated ion channels underlies electrical excitability of living cells. We simulate a mesoscale model of the VS domain to determine the functional consequences of some of its physical elements. Our mesoscale model is based on VS charges, linear dielectrics and whole-body motion, applied to an S4 ‘sliding helix’. The electrostatics under voltage-clamped boundary conditions are solved consistently using a boundary element method. Based on electrostatic configurational energy, statistical-mechanical expectations of the experimentally observable relation between displaced charge and membrane voltage are predicted. Consequences of the model are investigated for variations of: S4 configuration (α- and 3₁₀-helical), countercharge alignment with S4 charges, protein polarizability, geometry of the gating canal, screening of S4 charges by the baths, and fixed charges located at the bath interfaces. The sliding helix VS domain has an inherent electrostatic stability in the explored parameter space: countercharges present in the region of weak dielectric always retain an equivalent S4 charge in that region but allow sliding movements displacing 3 to 4 e₀. That movement is sensitive to small energy variations (< 2kT) along the path dependent on a number of electrostatic parameters tested in our simulations. These simulations show how the slope of the relation between displaced charge and voltage could be tuned in a channel.

1 Introduction

Electrical signaling via voltage-gated ion channels depends upon the function of the voltage sensor (VS), identified with the S1–S4 domains of voltage-gated K⁺ channels. Atomic structures for this domain, and their variation under function, are an active field of investigation (Jiang et al 2003; Long et al 2005a,b, 2007; Payandeh et al 2011). However, crystallography destroys the transmembrane electrical field and thus the physical force regulating channel conductance via VS configuration. Therefore computational molecular modeling has been used to construct the range of natural channel configurations from crystallographic information, and molecular dynamics (MD) simulations have been developed to test aspects of these atomic models (Yarov-Yarovoy et al 2006; Pathak et al 2007; Campos et al 2007; Nishizawa and Nishizawa 2008; Bjelkmar et al 2009; Delemotte et al 2010; Schow et al 2010; Schwaiger et al 2011; Khalili-Araghi et al 2012).

The applicability of MD simulations to this system is restricted by the wide gap existing between the time scale of atomic motion (femtoseconds) and the time scale of channel gating (milliseconds). Furthermore, important structural aspects are collective properties of many atoms and as such are not effectively tested by atomic-level simulation. We therefore use mesoscale models of the VS domain to simulate thermodynamic properties and consequences of atomistic and non-atomistic parameters. These simulations are solved under the boundary conditions of a voltage-clamp experiment. Statistical-mechanical expectations are computed for variables of interest. The relation between membrane potential and displaced gating charge is constructed. Our results provide a physical perspective on the structure-function relationship at a level above the atomic.

The mesoscale model, simulation setup and methods used here are those described by Peyser and Nonner (2012). In brief, the VS domain is represented by point charges embedded in a homogeneous dielectric (protein) and incorporated into a simulation cell composed of a membrane dielectric, bath dielectrics, and encapsulating electrodes. The simulated VS domain is not coupled to other parts of the channel (in particular not to the parts that implement the ‘gate’ of the ionic pore). This isolated VS model is a necessary step toward the construction of a mesoscale model of a full gated channel.

We explore variations of two reference models representing the sliding S4 helix in a generic α-helical or 3₁₀-helical geometry. Model aspects at the atomistic and non-atomistic scales are varied to examine both their importance for voltage sensing and the spectrum of their effects. We address the engineering questions: what are the conditions needed for a sliding helix to sense membrane voltage, and what are the ranges of physical characteristics produced? Since computed consequences include the relation between gating charge and voltage, they directly pertain to experimental information.

Specifically, here we vary the geometrical arrangement of VS charges, the electrical polarizability assigned to the VS protein domain, the geometry of the gating canal through which the S4 helix slides, and the screening of S4 charges emerging into the aqueous phases by charged groups in locations along the S4 path. All of these variations modify the gating charge-voltage relation, often effecting multiple characteristics simultaneously. In turn, a given characteristic of that relation can be similarly modified by the variation of distinct parameters, a degeneracy that complicates function-structure considerations. The 3₁₀-helical S4 segment produces less voltage sensitivity than the α-helical S4 segment in otherwise identical models.

2 Model and boundary conditions

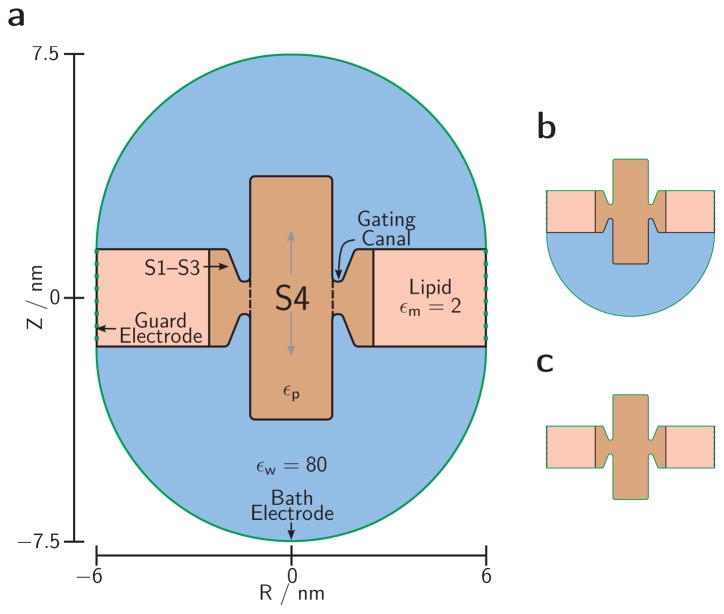
The simulation cell and metric details of the tested models are shown here in Fig. 1 and in the geometry table (Online Resource S2). In Fig. 1, the cell is represented by an axial cross-section of the radially symmetric three-dimensional domain swept by rotating that cross-section about its vertical axis. The external boundaries (in green) are electrode surfaces kept at controlled electrical potentials to establish voltage-clamp conditions. The blue zones represent aqueous baths (with a dielectric coefficient ε_w = 80). The pink zone is a region of small dielectric coefficient (ε_m = 2) representing the lipid membrane. The brown zone represents the region of the channel protein that we model. This region is assigned a dielectric coefficient of ε_p = 4 unless noted otherwise. These dielectrics are piecewise uniform and therefore have sharp boundaries (solid lines).

Fig. 1. Simulation cell.

(a) The 3D setup is produced by rotating this cross-section about its vertical axis. Green lines are electrode surfaces bounding the cell. Black lines are dielectric boundaries separating uniform dielectric regions: baths (blue), membrane lipids (pink), and protein (brown) with dielectric coefficient ε_p (varied between 2 and 16). Charges on the protein side chains (see Fig. 2) are embedded in the protein dielectric region in varied geometries. We simulate a single VS sensor domain (S1–S4) modeled as a central S4 cylinder surrounded by a ring of protein material including the S1–S3 transmembrane domains. The junction between these protein domains is narrowed to less than the membrane thickness by circular invaginations (‘vestibules’) leading up to the ‘gating canal’ through which the S4 helix glides to travel through the rest of the protein (dashed line). Precise lengths defining this geometry are specified in the geometry table (Online Resource S2). (b, c) Modified simulation cells used for simulating high ionic strength for the external bath (b) or for both baths (c) by placing the respective electrode(s) directly on the membrane and protein

The protein region represents the matrix of the S4 helix as a central cylinder surrounded by the other parts of the VS domain which together form a dielectric environment distinct from the dielectric environment of the membrane lipid. Included in the protein region are the invaginations which allow the baths to extend into the planes defining the lipid phase of the membrane (vestibules of the the gating canal). Metric details of tested models are given in the geometry table (Online Resource S2).

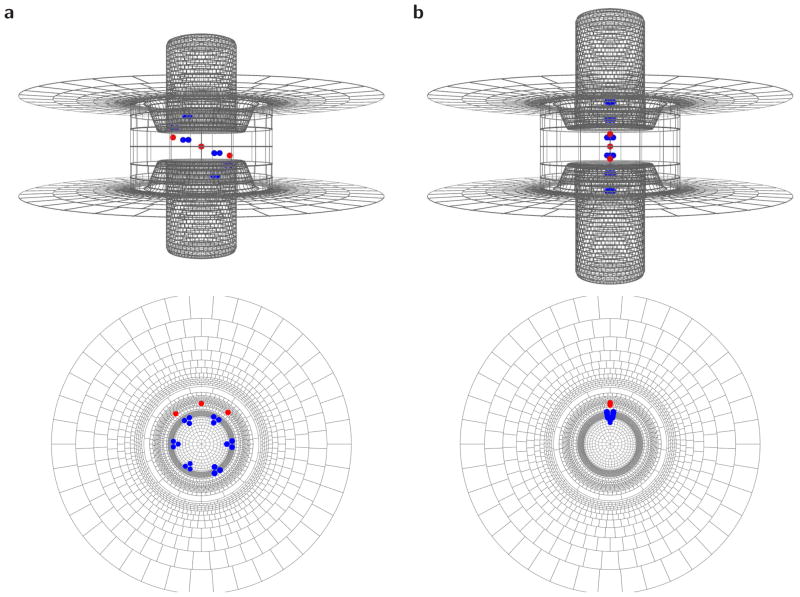
The formal charges of the VS protein in the two tested conformations of the S4 segment (α-helical and 3₁₀-helical) are shown together with the dielectric boundary surfaces in Fig. 2. The charged guanido group of each arginine residue of the S4 segment is represented as three point charges of 1/3 e₀ on a circle of radius 0.122 nm (blue spheres in Fig. 2). The centers of the S4 arginine charges are arranged on a curve defined by arginine side chains on an α- or 3₁₀-helix backbone, where every third amino acid is an arginine. For the α-helix, charged residues are separated by 0.45 nm in the transmembrane direction and 60° leftward around the helix; for the 3₁₀-helix, charged residues are separated by 0.6 nm and 0°. Negatively charged residues contributed by the S2 and S3 transmembrane segments of the natural VS domain are modeled as single point charges of −1 e₀ rather than several partial charges (because, unlike the moving S4 charges they do not move relative to the interfaces between non-polar and polar environments). In our ‘reference’ models, these countercharges are arranged on a curve parallel to the curve on which S4 charges are centered (red spheres in Fig. 2); the offset from the helix axis of the countercharge curve is 0.466 nm larger than the radius of the curve of the centers of the (triplets of) S4 charges (see the geometry table Online Resource S2). Axial and angular intervals between countercharges are two-thirds the interval between the S4 charges (Peyser and Nonner 2012). Point charges are arranged at a minimal distance of 0.2 nm from the protein/water boundary.

Fig. 2.

VS charge positions and dielectric boundary surfaces in an α-helical (a) and a 3₁₀-helical model (b). Blue symbols: S4 charges, each represented as three point charges of 1/3 e₀; Red symbols: countercharges in the S2 and S3 segments, each represented as a single point charge of −1 e₀. The dielectric boundary surface is divided into curved surface elements whose size is chosen dependent on distance from point charges and local surface curvature. This surface grid is used in solving the induced-charge calculation. The figure is drawn using perspective-enhancing features. The geometries shown here (a & b) reflect the base models in the geometry table (Online Resource S2, α (1) & 3₁₀ (1) respectively). For the range of motion of the S4 in these models, see supplementary animations (Online Resources S8 & S9, respectively)

We analyze two degrees of freedom for VS charge movement, translation along the helix axis and rotation about that axis. The curve on which the centers of S4 charge triplets are aligned can be both translated along the helix axis and rotated about that axis. The model S4 charges move like parts of a solid body. The countercharges are stationary in their assigned positions, while the ensemble of S4 charges slides within the dielectric envelope provided by the S4 matrix shown in Fig. 1. The protein dielectric itself does not accompany the movement of the charges. With the S4 dielectric matrix extended far enough into the baths, keeping the S4 dielectric stationary has negligible electrostatic consequences because the dielectric of the model is uniform within the S4 matrix. Simulating S4 motion this way reduces computational demands of model exploration by several orders of magnitude.

The bath electrodes encapsulating the simulation cell provide Dirichlet boundary conditions corresponding to a voltage clamp. The voltage V_m is applied across the bath electrodes by imposing the potentials +V_m/2 and −V_m/2 at the internal and external bath electrodes. At the surface where the membrane region meets the cell boundary, a set of guard electrodes (forming rings around the cell) maintain a graded potential varying linearly from the potential applied at the inner bath electrode to that of the outer bath electrode. These guard electrodes impose at the membrane edge a potential similar to the potential existing in a macroscopic system at a location far from the protein.

The bath electrodes, besides establishing the voltage clamp, substitute for the screening by bath ions of uncompensated protein charge. Screening by the ions in an aqueous bath is equivalent to the screening provided by charge on a metal foil placed in the water a distance away from the protein boundary. (According to the Debye-Hückel theory approximation, an electrode distance of ~0.8 nm corresponds to physiological bath ionic strength.) The electrode location shown in Fig. 1a corresponds to a bath solution in the low millimolar range. An alternate configuration, a simulation cell with one or both bath regions omitted and the electrodes placed directly on the membrane and protein boundaries (Fig. 1b,c), establishes screening at the Onsager limit (approached at exceedingly large ionic strength). Results obtained with the two alternate electrode placements allow us to examine the possible range of screening effects at far smaller computational cost than the costs of a simulation with explicit bath ions.

A simulation setup as shown in Fig. 1 tests a single VS domain which is not interacting with other parts of the channel protein, in particular the parts mediating the gating of the conductive pore. This model VS domain operates as an ‘idling’ transducer of electrical force. The forces acting between a VS domain and other parts of the natural channel are not known. The reactions of model voltage-sensors to such forces can be explored by simulations which include hypothesized force fields in addition to the electrostatic force field (Peyser and Nonner 2012). Characteristics of the ‘load’ acting on the integral VS domain may be inferred in this manner. However, here we report simulations of the idle VS domain.

3 Methods

3.1 Electrostatics

Our simulations involve electrostatic interactions among the charged groups of the VS protein, the electrode charges and the charges induced on sharp dielectric boundaries. In solving these electrostatics, we take advantage of the fact that all charges other than the point source charges of the protein are distributed on a few boundary surfaces rather than distributed throughout a volume.

The primary task in solving the electrostatics is determining the charge distributions on the electrode and dielectric boundaries, distributions which are initially unknown for a given configuration of protein charges and applied voltage. To compute charge induced on dielectric boundaries we use the method of Boda et al (2006). The application of this method to our simulation system, and its extension to also compute the charges on electrodes, have been described in Peyser and Nonner (2012).

The secondary tasks in solving the electrostatics are the computation of displaced charge that flows between the bath electrodes when charges in the VS domain change positions, and the computation of the electrostatic energy of the system for a given VS configuration and applied voltage. Both computations are done efficiently using the Ramo-Shockley theorem (as revisited by He 2001). For details of these computations, we refer the reader again to Peyser and Nonner (2012).

Displaced charge is computed in two steps:

1. Set all point source charges to zero and apply +1/2 volt at the internal and −1/2 volt at the external bath electrode. Solve for the unknown electrode and induced boundary charges. From these charges, an electric potential V₀(r) can be computed for any geometrical location r of the simulation cell.

2. In a simulation with the actual point source charges q_k present and arbitrary potentials +V_m/2 and −V_m/2 applied at the internal and external bath electrodes, determine the displaced charge Q_k from the relation:

   $$Q_k=-q_k{V}_0({\mathbf{r}}_k)/1\text{volt}.$$ (1)

   Note that Q_k = 0 for all geometrical positions r_k where V₀(r_k) = 0, and Q_k varies between −q_k/2 and +q_k/2 as the position of q_k is varied from the internal to the external bath electrode.

   When several point source charges are in the simulation, the total displaced charge is the algebraic sum of the displaced charges defined by Eq. 1 for each point source charge:

   $$Q=\sum _k{Q}_k.$$ (2)

Electrostatic energy is computed as the algebraic sum of two terms:

$$W=W_1+W_2.$$ (3)

The first term is a voltage-independent configurational energy:

$$W_1=\frac{1}{2}\sum _k{q}_k{V}^{V_{\mathcal{E}}=0}({\mathbf{r}}_k),$$ (4)

where V^V_ℰ=0 (r_k) is the potential produced at location r_k by all charges in the system excluding the point charge q_k itself (but including the charges induced on dielectric boundaries and the charges on electrodes) when all electrode surfaces ℰ E are grounded (V_ℰ = 0).

The second term is due to the applied voltage:

$$W_2=-{QV}_{\text{m}},$$ (5)

where V_m is the voltage applied between the bath electrodes in the simulation, and Q is the total charge displacement associated with the arrangement of VS charges in the simulation. The membrane voltage V_m (defined as internal minus external potential) is created in our simulations by equal and opposite potentials V_m/2 and −V_m/2 imposed at the internal and external bath electrodes.

Since we are concerned with the change of electrostatic energy associated with the change in S4 position, we present energy (and displaced charge) as relative to a reference S4 position. The reference S4 position is the S4 position giving the displaced charge Q = 0 (due to rotational symmetry of electrodes and dielectrics in our simulations, only the translational reference position is specified by Q = 0; we choose the rotational reference position zero). The electrostatic energy at the reference position is independent of the applied voltage V_m because of Eq. 5.

3.2 Statistical mechanics

Displaced gating charge is experimentally measured from ensembles of channels and thus is an ensemble average. Our electrostatic calculations yield both the displaced charge and the electrostatic part of the configurational energy for a given configuration of a simulated VS model. We consider whole-body movements of S4 charge in two degrees of freedom: translation along the S4 axis and rotation about that axis. Our computational method is efficient enough to allow systematic sampling of energy over this configuration space. We represent each dimension by 51 equally spaced grid nodes and compute the electrostatic energy for the 2601 nodes of the two-dimensional space (see Fig. 3c,d).

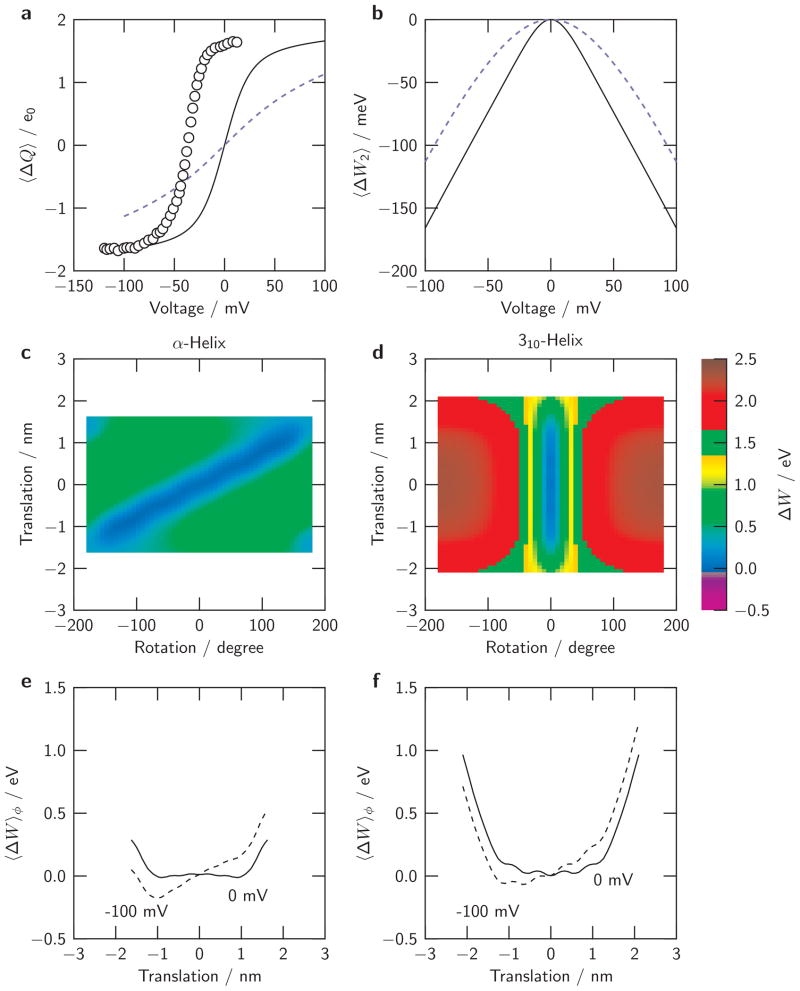
Fig. 3.

Theoretical predictions and underlying energetics of the reference models. (a) Expectations of the displaced-charge/voltage relation for the α-helical (solid line) and 3₁₀-helical (dashed line) S4 models, and an experimental relation (circles; from Fig. 2a of Seoh et al (1996)). (b) Expectations for the energy due to the applied voltage for the models in panel a. (c, d) pseudo-color maps of electrostatic energy for the translational and rotational degrees of freedom in S4 position. (e, f) Translational energy profiles (expectations of energy over the rotational degree of freedom)

The energy samples define a canonical partition function describing the consequences of the electrostatics on the distribution of an ensemble in the discretized configuration space:

$$\mathcal{Q}=\sum _{i,j}{e}^{-\mathrm{\Delta }{W}_{ij}/k_{B}T},$$ (6)

where i and j are the indices of the translational and rotational discrete positions; ΔW_{i j} is the electrostatic configurational energy with the voltage sensor at translational position i and rotational position j; k_B is the Boltzmann constant; and T = 298.15 K is the absolute temperature. The sampled rotational range is 360°, and a typical translational range is−1.625 nm to +1.625 nm relative to the central position of the S4 charges in α-helical models (±2.102 nm for 3₁₀-helical models). Restricting the configuration space in this manner is equivalent to including hard-wall potentials in the Hamiltonian (Eq. 3).

The probability associated with a particular VS configuration defined by translation i and rotation j is

$$P_{ij}=\frac{1}{\mathcal{Q}}{e}^{-\mathrm{\Delta }{W}_{ij}/k_{B}T},$$ (7)

and the expectation (mean) value of a random variable X is

$$\langle X\rangle =\sum _{i,j}{X}_{ij}{P}_{ij}.$$ (8)

The expectation for ΔW₂, the part of the electrostatic energy that depends on the applied electrical field, has a simple relationship to the expectation of displaced charge:

$$\langle \mathrm{\Delta }{W}_2\rangle =-\sum _{i,j}\mathrm{\Delta }{Q}_{ij}{V}_{\text{m}}{P}_{ij}=-\langle \mathrm{\Delta }Q\rangle V_{\text{m}}.$$ (9)

We also determine the expectations of random variables over the rotational degree of freedom φ for a particular translational position i:

$${\langle X_i\rangle }_{\phi }=\frac{{\sum }_j{X}_{ij}{e}^{-\mathrm{\Delta }{W}_{ij}/k_{B}T}}{{\sum }_j{e}^{-\mathrm{\Delta }{W}_{ij}/k_{B}T}}.$$ (10)

3.3 Online Supplementary Materials

Supplementary figures (Online Resources S3–S6) and the associated animations (Online Resources S8–S11, respectively) illustrate VS geometry or movement in four of the simulations presented in this paper. They show the mean positions of VS charges superimposed on the distribution of charge density in the microscopic system, as explained in the supplementary text (Online Resource S1, Section S2). In the animations, voltage is ramped from −100 to +100 mV.

The standard α-helical model is displayed in terms of its three-dimensional geometry (Online Resource S3), and its geometrical behavior is shown in the associated animation (Online Resource S8). As seen as well in Fig. 3a, most of the charge rearrangement occurs within the range ±50 mV, as opposed to the more continuous movement in the 3₁₀ model as shown in its figure (Online Resource S4) and associated animation (Online Resource S9). Note as well that the expectation values for the ensembles of charge positions marked by the spheres do not fully characterize the most probable charge positions for a single snapshot of the VS domain, as represented by the blue shading.

Two variations of the α-helical model are illustrated as well (Online Resources S5 and S6, and the respective animations S10 and S11). The configuration distribution of the case where ε_p = 16 from Fig. 5 is displayed in one figure (Online Resource S5); note that in the associated animation (Online Resource S10), an increased variance in charge distribution can be seen in the larger volume of blue shading at mid-range voltages where the charge-voltage slope is smaller. The three-dimensional representation of outline 4 from Fig. 6 is also shown (Online Resource S6), where the gating vestibule is reduced and shifted. The midpoint shift in the charge-voltage curve can be seen as a shift in charge position distributions in the associated animation (Online Resource S11).

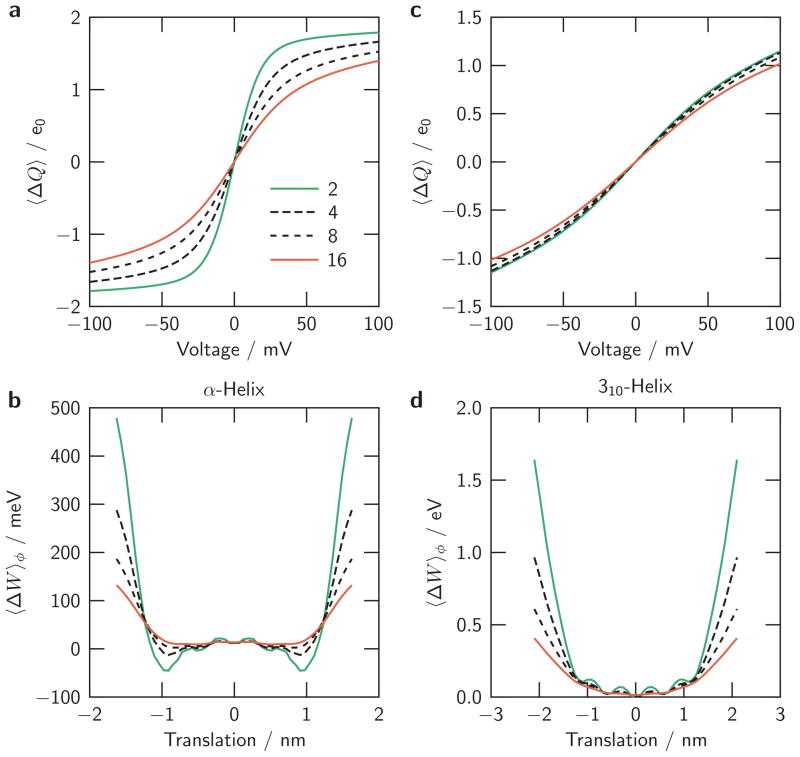
Fig. 5. Effects of protein dielectric coefficient.

The α-helical (a, b) and 3₁₀-helical (c, d) models are solved for 4 different settings of ε_p as indicated in panel a. (a, c) translational energy profiles; (b, d) expectations of the displaced-charge/voltage relation

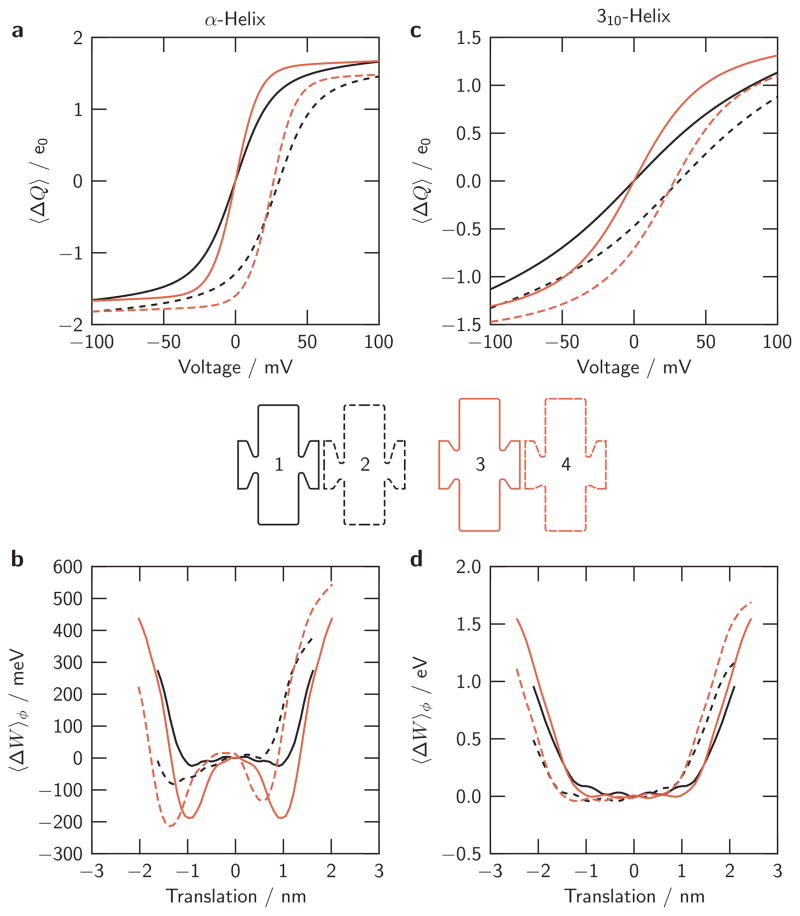
Fig. 6. Consequences of gating canal geometry.

Length and position of the gating canal (and hence its vestibules) are varied as shown by the outlines of the VS protein between the graphs. Outline 1 is our reference α-helical S4 model, with Outlines 2–4 being variations of that model as specified in the table (Online Resource S2), rows α (1–4). The line patterns & colors in both the graphs of the charge-voltage relations (a) and the underlying translational energy profiles (b) correspond to the line patterns & colors used for the outlines of the VS shapes. Outline 4 can be seen in a supplementary 3-dimensional figure (Online Resource S6). (c, d): the corresponding relations computed for the 3₁₀-helical model. Shapes 1–4 are as in the α outlines, remapped for 3₁₀ helices according to the geometry table (Online Resource S2), rows 3₁₀ (1–4)

4 Results and Discussion

We study a mesoscale model of the VS domain to gain insight into the physics underlying voltage sensing by a sliding helix. The energetics and charge-voltage relations are computed by simulations with stepwise varied model parameters to assess the kind and extent of effects that the parameter has in the model. The variation changes one parameter at a time (where possible) in a set of parameters that defines a reference model.

We follow two parallel lines of study throughout the paper, distinguished by the configurations assigned to the S4 segment: α-helical or 3₁₀-helical. Hence, two distinct reference models are implemented as a basis for variation. We use the reference models already described in previous work (Peyser and Nonner 2012). It is important to note that these models are not intended to constitute optimal models. Their choice is more or less arbitrary. Better choices might be made with the results of parameter variations in hand. We do not attempt such optimization at this stage. The reference models have been defined in Section 2.

These reference models predict charge-voltage relations as shown in Fig. 3a. The charge displaced in the α-helical model (solid line) is similar in magnitude to that measured in a typical experiment (circles). Thus the α-helical sliding-helix model can account for the bulk of the displaced gating charge. The slopes of these charge voltage relations are also similar. In contrast, the 3₁₀-helical model (dashed line) yields a smaller total charge and smaller slope over the tested range of voltage. Both simulated charge-voltage curves are centered about the origin of the voltage axis, whereas the experimental curve (from Fig. 2A of Seoh et al 1996) is centered about a negative voltage. The experiment was conducted with full channels, each comprising four VS domains and a gated conductive pore. In this paper we analyze equilibrium properties of the isolated VS domain as a step toward constructing models of a full channel.

The contribution of the applied electrical field to the electrostatic energy (ΔW₂, Eq. 5) is shown in Fig. 3b. Like the displaced charge shown in Fig. 3a, the work shown is the expectation of the respective random variable (Eq. 9). This work is zero when the applied voltage is zero and becomes negative for both polarities of applied voltage. The α-helical model (solid line) predicts a larger variation in work per applied voltage than the 3₁₀-helical model (dashed line), quantifying in another way the voltage sensitivities of these reference models.

Pseudo-color maps of the electrostatic configurational energies for these models at an applied voltage of zero are shown in Fig. 3c,d. These maps are constructed by computing the configurational electrostatic energy (Eq. 3) on a grid of translational and rotational positions of the sliding helix. These maps are the basis for computing a partition function that is discretized on the grid. The partition function is used to compute the expectation values of the displaced charge and the work picked-up (Fig. 3a,b). The energy maps, and the differences between these maps for the two models, have been discussed in Peyser and Nonner (2012).

Results of the model variations are represented in the following using the charge-voltage relation. The underlying energy maps are analyzed as ‘translational energy profile’, a one-dimensional map computed by averaging, for each discrete translational position, configurational energy over the full rotation. Translational energy profiles for the reference models are shown in Fig. 3e,f for applied voltages of 0 and −100 mV. Due to the symmetry of the models, the profiles at +100 mV (not shown) mirror the profiles for −100 mV. The applied voltage simply tilts the energy profile about the translational origin.

4.1 Position of countercharges

Charge balance by the formation of ion pairs in the membrane region of the VS domain appears to be important for proper function, and in some instances for proper protein folding (Papazian et al 1995; Seoh et al 1996). Residues with anionic side chains are preserved in the S2 and S3 segments. Anionic head groups of membrane phospholipid seem to be essential (Schmidt et al 2006). Crystallographic structures suggest alignment of cationic S4 residues with anionic residues on S2 and S3 in (open) Kv2.1/Kv1.2 chimeric channels (Long et al 2007; Tao et al 2010). Modeling based on molecular dynamics simulation suggests such alignments in both open and closed channels (Khalili-Araghi et al 2010; Jensen et al 2012). Because our mesoscale models are not restricted to a particular atomic structure, they allow us to test basic geometrical concepts of the S4-charge-countercharge interaction.

The reference models include three countercharges positioned so that they can interact periodically with S4 charges moving through the gating canal (Fig. 2). S4 charges and countercharges are arranged on parallel curves separated by a radial offset. The S4 helix can translate along and rotate about its axis whereas the countercharges are fixed. In the α-helical S4 model, the countercharges are fixed on a helix, and the average S4 trajectory follows that of a screw. In the 3₁₀-helical S4 model, the countercharges are fixed on a straight line, and the average S4 trajectory follows that of a piston (graphs not shown). The countercharges of both reference models are spaced at a (rotational and translational) interval which is 2/3s that of the S4 charges. Thus no more than one S4 charge can be in the nearest possible alignment with a countercharge in any S4 position. The maps of electrostatic energy show an energy trough confining the S4 segment but not impeding S4 motion within the trough by substantial barriers (Fig. 3). countercharges and S4 charges of these models thus form a stable electrostatic system that allows for the movements needed for voltage sensing.

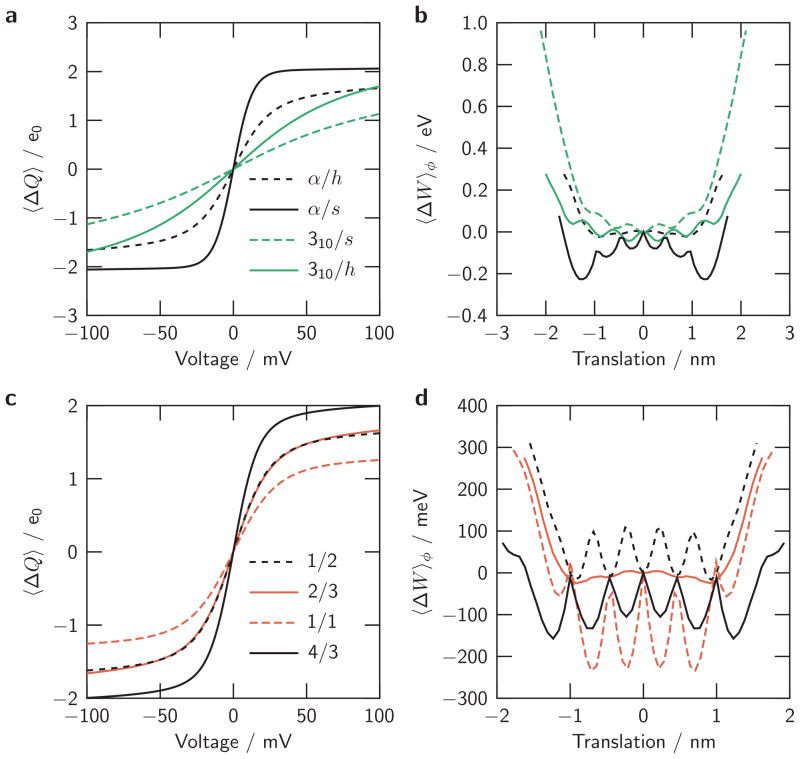
In real channels, S4 charges and countercharges are likely to align in less regular geometries than in the mesoscale models of Fig. 3. To determine some possible consequences of countercharge arrangement for voltage sensing, we (1) swap the countercharge geometries of the two reference models in Fig. 2 so that the countercharges of the α-helical S4 segment are arranged on a straight line parallel to the S4 axis while the corresponding countercharges of the 3₁₀-helical S4 segment (whose charges form a straight array) are arranged on a helical curve around the S4 helix; and (2) vary, in the model with α-helical S4 segment and helical countercharge alignment, the (rotational and translational) interval between the countercharges.

In the first test, combining either S4 helical configuration with the ‘wrong’ countercharge configuration produces a voltage sensor with greater total charge movement and greater voltage sensitivity as measured by the slope of the charge-voltage relation (solid lines in Fig. 4a) compared to the models with the ‘matched’ countercharge configuration (dashed lines). Translational energy profiles reveal a longer energy trough for the models with the ‘wrong’ countercharge configuration (Fig. 4b), which allows for a larger range of translation for the S4 segment and thus larger charge movement. Energy near the edges of the trough is lowered with respect to the ‘matched’ countercharge configuration. As will be discussed in Section 4.2, such a change in translational energy profile increases the slope of the charge-voltage relation. Energy ripples within the energy trough are increased by the ‘wrong’ countercharge arrangements but remain small enough for fast dynamic responses of the S4 segment.

Fig. 4. Consequences of countercharge geometry.

Expectations of displaced-charge/voltage relations (a, c) and translational energy profiles (b, d). Top panels: swapping countercharge geometries among the reference α-helical and 3₁₀-helical S4 models. Bottom panels: varying the counter-charge spacing in the reference α-helical S4 model.

In the second test using the α-helical S4 model, we vary the ratio of countercharge to S4 charge interval: 1/2, 2/3, 1/1, and 4/3. The ratios 2/3 and 4/3 do not allow more than one S4 charge to be closest to a countercharge over the entire range of S4 motion, whereas the ratios 1/2 and 1/1 allow multiple simultaneous alignments. Again, there are substantial effects on the charge-voltage relation (Fig. 4c). The total charge moved and the slope of the relation vary non-monotonically with countercharge interval: 1/1 < 1/2 ≈ 2/3 < 4/3. Translational energy profiles exhibit larger energy barriers for S4 motion in the models allowing multiple alignments of S4 charges and countercharges (Fig. 4d). The barrier size, however, does not exceed ≈0.25 eV (10 kT).

These variations of countercharge geometry all preserve the basis for voltage sensing: a trough of electrostatic energy that limits S4 movements while allowing the play necessary for voltage sensing. In all tested cases, strong voltage sensitivity maps to less perfect alignment of S4 charges with countercharges. Since charge-charge interaction is moderated by electrical polarization in the charge environment, we tested the described countercharge geometries over a range of the protein dielectric coefficient, ε_p (see also next section). Over the range 2 ≤ ε_p ≤ 16, voltage sensitivity maps to less perfect alignment of S4 charges with countercharges.

The tested countercharge geometries involve equally spaced countercharges. More simulations are needed to test non-periodic spacing of countercharges, specific geometries emerging from structural work, and geometries of charge deletion mutants involving putative countercharges (Seoh et al 1996). For the purpose of a sensitivity analysis, our reference models appear to be suitable because their voltage sensitivities leave space for both improvement and degradation by variation of parameters.

4.2 Polarizability of the protein

We describe the electrical polarizability in the VS domain by a dielectric coefficient ε_p that is uniform throughout the VS protein region. This coefficient summarizes readjustments of electrons, atoms and groups of atoms in response to S4 helix movement, implying a large number of internal degrees of freedom beyond the two degrees of freedom in whole-body motion sampled explicitly. Although our mesoscale model does not explicitly deal with the physics underlying polarization in the VS domain, a polarizability parameter allows one to investigate the extent to which the characteristics of voltage sensing depend on protein polarizability. We assess the consequences of linear polarization for model behavior by varying ε_p over a range of values used in other theoretical studies of proteins (reviewed by Schutz and Warshel 2001). Our computations give consistent solutions for a system with piecewise homogeneous linear dielectrics and include appropriate boundary conditions.

In the model with α-helical S4 segment, variation of ε_p from 2 to 16 alters the charge-voltage relation (Fig. 5a). The steepness of the relation is reduced as ε_p is increased, both near the midpoint of the curves and in their approaches to saturation at extreme voltages. Translational energy profiles reveal an energy trough flanked by regions of higher energy (Fig. 5b). Both the walls of the trough and the energy variations inside the trough are reduced in magnitude as ε_p is increased from 2 to 16. Energy variation inside the trough is always small — even with ε_p = 2, that variation does not exceed 0.05 eV (~2 kT).

Small differences of the translational energy profiles thus result in substantially different charge-voltage relations. With ε_p = 2 there are two distinct energy minima, about 0.05 meV deep, at the ±1 nm translations from the central position (Fig. 5b). With ε_p = 16, the bottom of the energy trough is almost flat in the absence of an applied voltage. Apparently, these differences in energy profiles are enough to make the S4 helix dwell mostly in one of two low-energy positions located near the ends of S4 travel range, or (in the absence of an applied voltage) these differences allow the S4 helix to assume any position within its travel range with uniform likelihood. For a graphical representation, see the discrete distribution of charge in the animation (Online Resource S8) with ε_p = 4 and the continuous distribution in the animation (Online Resource S10) with ε_p = 16.

Analytical expressions for the bistable and continuous S4 distributions are given in Supplementary Materials. These expressions are formally equivalent to the ‘two-state Boltzmann distribution’ of the channel literature (Hodgkin and Huxley 1952) and to a distribution derived by Neumcke et al (1978), but they apply more generally (e.g., to the movement of a solid body bearing distributed point charges that can move in and out of the electrical field across the membrane). The supplementary figure (Online Resource S7) illustrates two analytical charge-voltage relations for an S4 segment displacing 3 elementary charges over its range of travel. The bistable charge-voltage relation is three times as steep at its midpoint than the continuous relation. Charge displacement saturates exponentially in the bistable relation, but hyperbolically ( $\propto V_{\text{m}}^{-1}$) in the continuous relation.

Published theoretical studies of the VS domain have used a single fixed protein dielectric coefficient, such as ε_p = 15 (Lecar et al 2003) or ε_p = 10 (Grabe et al 2004). In our simulations, we vary the protein dielectric coefficient from 2 to 16, finding rather small (but important) effects on the translational energy profile. That profile is dominated by an energy trough spanning the translational range where the intrinsic countercharges of the VS domain overlap with an equivalent number of S4 charges. This trough is in fact deeper for smaller values of ε_p than for larger values (Fig. 5a), providing greater stability for the transmembrane position of the S4 segment. With charge balance established inside the region of weak dielectric, charge induced on the aqueous boundaries of the dielectric is small — interaction of that induced charge with S4 charges does not dominate the translational energy profile.

Analogous computations with the 3₁₀-helical model reveal that varying ε_p has smaller effects than those observed for the α-helical model (Fig. 5c,d). A slightly U-shaped translational energy profile is expressed for all tested ε_p, and therefore the charge distribution in the 3₁₀ model does not tend to saturate crisply at large voltages of either polarity. The 3₁₀-helical model in the presented form has difficulty producing steep charge-voltage relations like those observed in biological channels. On the other hand, the energetic differences determining slope are not large: the seemingly unfavorable characteristics of the 3₁₀-helical S4 segment might be overcome by energy contributions not included in the model. Since we are modeling a single voltage sensor, our models for instance would not account for any coupling that exists among the VS domains of the full biological channels.

These simulations with varied dielectric coefficient indicate that protein polarizability is not crucial for the electrostatic stability of a sliding-helix VS domain that balances S4 charges with countercharges. On the other hand, the degree of polarizability contributes to determining the relation between voltage and displaced charge to an extent that depends on S4 helical structure.

4.3 Geometry of the gating canal

About 10 consecutive residues of the S4 segment are inaccessible to hydrophilic reagents applied to resting channels from either the extracellular or intracellular side (reviewed by Gandhi and Isacoff 2002). If the S4 domain is α-helical and oriented perpendicular to the membrane plane, then the inaccessible translational range is only ~1.35 nm long and thus shorter than the lipid core of the membrane. Thus the S4 helix is thought to move across the hydrophobic region in a short ‘gating canal’ that forms an electrical seal between water pockets extending toward the canal from either side (vestibules). One consequence of this arrangement is that most of the applied voltage drops over the short length of the gating canal and is thereby ‘focused’ on the interval of S4 charges dwelling in the canal itself.

Short of a simulation, approximate inferences can be made of electrostatic consequences of the length of the gating canal. If the queue of S4 charges spans the gating canal plus the range of S4 travel, then the instantaneous force F exerted by the applied field on n S4 charges simultaneously present in the canal of length D is approximately F = ne₀V_m/D. With S4 charges spaced at the uniform and fixed interval d, canal length and number of charges in the canal are related by D ≈ n × d. The electrical force acting on the S4 charges F ≈ e₀V_m/d is then independent of the length of the gating canal, dependent only on the spacing between S4 charges. The instantaneous work done by the field on the S4 charges as the S4 moves through the canal is given by W = Fmd ≈ me₀V_m, where m is the number of S4 charges that travel across one of the gating canal mouths during the motion associated with the work W. This work does not depend on the length of the gating canal. Moreover, the S4 charges travel the same distance md per unit work regardless of the length of the gating canal, D. Voltage sensitivity (defined by force or work picked up per unit applied voltage) does not depend on the focusing of the electric field by the gating canal itself, as long as the queue of S4 charges extends across the gating canal.

To assess more fully the consequences of gating canal geometry, we simulate varied canal lengths and canal positions with respect to the membrane planes of the VS model (Fig. 6). (The metrics of these gating pores are fully specified in Table 1 of Supplementary Materials.) Starting with the geometry of our reference model for the α-helical VS domain (VS protein outline 1 in Fig. 6), we shift the canal 0.4 nm toward the intracellular membrane plane (outline 2). Two further variations include reduction of the vestibule length on both sides by one half, thereby lengthening the gating canal (outline 3) and a shift of that lengthened gating canal (outline 4, supplementary figure: Online Resource S6). When we shift the gating canal, all negative countercharges of the VS domain are shifted as well. When we lengthen the gating canal, the axial spacing of countercharges is not changed. The spacing of S4 charges is kept constant as well.

For both the centered and the shifted gating canals, lengthening the canal increases the slope of the charge-voltage relation while maintaining the amplitude of charge displacement between ±100 mV (Fig. 6a, line patterns and colors in the graph correspond with the protein outlines below the graph). Shifting the position of the gating canal shifts the charge-voltage relation along both the voltage axis and the charge axis (towards the intracellular side) while maintaining the slope typical of the canal length. These shifts indicate that asymmetries of the vestibules of the gating canal bias the voltage sensed by the S4 segment.

The underlying energetics are summarized in Fig. 6b. Lengthening the gating canal increases the depth of the energy minima at the ends of the range of travel, thus promoting the bistable behavior of the VS domain associated with a steep slope of the charge-voltage relation. Shifting the position of the gating canal shifts and tilts the energy profile and therefore shifts the S4 geometrical range of travel and preferred positions. The translational spacing between the minima at either end of the energy trough is not changed by these variations of gating canal geometry, and therefore the total charge displaced remains unchanged.

The respective experiments for 3₁₀-helices in Fig. 6c,d behave like their α-helical counterparts. However for all of these variations, the mid-point slopes stay small relative to the α-helices, due to the flatness of the energy profile in Fig. 6d and the resulting wide distribution in VS translation for most potentials.

The observed invariance of the total charge displaced in these simulations conforms to our approximation (W = me₀V_m). Geometrical S4 travel relative to the center of the membrane tends to follow the position of the gating canal. A longer gating canal giving less ‘focusing’ of the applied electric field results in a steeper charge-voltage relation. The latter two relationships are due to the self-energy contribution to the configurational energy as defined by Eq. 4 — that is, to the electric field when V_m = 0 is applied to the bath electrodes. In this section’s simulations, the countercharges to the S4 charges are aligned to the center of the septum of the gating canal which, when the gating canal is shifted, varies from the center of the membrane and the S4 protein region. The countercharges’ mutual spacing continues to be constant. With a longer canal, there is a longer gap between the outermost countercharge and the central end of the vestibule on each side. The energy minima of the translational energy profile are located at the S4 translational coordinate associated with the trailing charge of the S4 helix vacating the poorly screened stretch of the gating canal (see supplementary animation, Online Resource S11, for associated charge distributions).

This ‘paradoxical’ effect of gating canal length is indirect, a consequence of the changing relationship between countercharges and dielectric boundaries. These simulations show that the geometry of the dielectrics forming the gating canal and its vestibules help determine the steepness and midpoint position of the charge-voltage relation. The steepness of that relation as well as the total amount of charge displaced do not follow the degree of ‘focusing’ of the applied electric field (i.e., the field strength) in the canal.

4.4 Screening of VS charge exposed to the aqueous solutions

The translocation of S4 charge across the membrane necessarily shifts a high local density of protein charge across the membrane. Therefore the energetics of S4 translation should depend on the screening on either side of the membrane of S4 charges by bath ions. We have thus far reported on VS models under symmetrical screening conditions. Under those conditions, any screening effects on S4 energetics are masked by mutual compensation. Strongly asymmetrical screening should unmask the contribution of screening to the energetics. Our simulations do not include explicit bath ions, as we explore screening effects instead by varying the distance of the bath electrodes from the membrane and VS protein surfaces (see Section 2). The two extreme electrode placements shown in Fig. 1a,c are equivalent to low millimolar ionic strength baths and exceedingly large ionic strength baths. Using the electrodes to study screening approximately captures electrostatics at the mean-field level, but not specific effects due to high densities of exposed S4 charge or lyotropic adsorption of anions (Dani et al 1983).

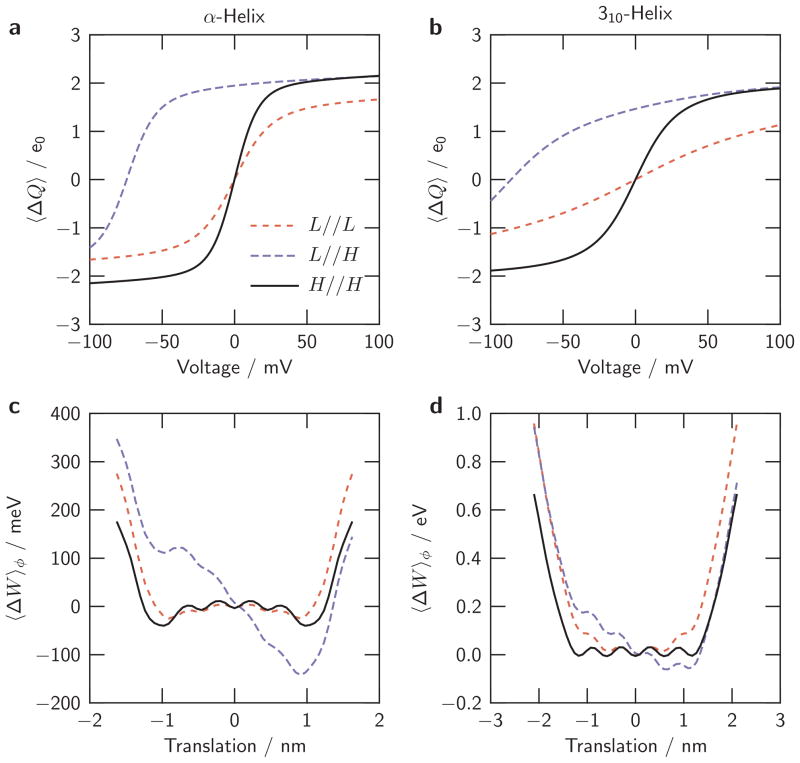
We compute the charge-voltage relations for our reference α-helical model with three electrode configurations (Fig. L//L, symmetrical low ionic strength: both electrodes far from the membrane and protein; H//H, symmetrical high ionic strength: both electrodes are directly on the surface of the membrane and protein; and L//H: low internal and high external ionic strength: the internal electrode is far from the membrane and protein and the external electrode is directly on the membrane and protein. The charge-voltage relation for the H//H configuration (solid line) reveals a larger total displaced charge and a steeper slope compared with the L//L configuration (dotted line). The increase in total displaced charge at symmetrical ‘high ionic strength’ has two sources: the increase in electric distance between the geometrical S4 positions (as discussed by Islas and Sigworth 2001); and the increase in the S4 geometrical range of travel between ±100 mV, as indicated by the spacing of the energy minima of translational energy profiles (Fig. 7c). The increase in slope is due to the deeper translational energy minima at the extreme positions, which promote bistable behavior as discussed earlier.

Fig. 7. Consequences of screening by the baths.

(a, c) The reference α-helical S4 model is simulated with varied electrode arrangements to mimic varied ionic strength of the baths (see Fig. 1). Labels in panel a indicate the internal//external ‘ionic strengths’ (H, high; L, low). (a, b) Charge-voltage relations, (c, d) translational energy profiles. (b, d) Simulations of the reference 3₁₀-helical S4 model.

The simulation for the asymmetrical L//H configuration yields a left-shifted charge-voltage relation (long-dashed line in Fig. 7a). The S4 charges are attracted toward the external side where screening is more effective. The magnitude of this shift quantifies the range of the effect that asymmetrical screening of S4 charges can produce. The screening of bath-exposed S4 charges contributes substantially to the energetics of S4 translation. That energetic bias is masked by mutual compensation when ionic strengths are equally high or low on both sides.

The 3₁₀-helical model produces substantially less voltage sensitivity than the α-helical model when we simulate the models with ‘low ionic strength’ electrode placement. Given the effects of screening on voltage sensitivity seen in Fig. 7a, it is interesting to see to what extent strong screening ‘rescues’ voltage sensitivity of the 3₁₀-helical model. In fact, exceedingly large ionic strength increases voltage sensitivity substantially (solid line in Fig. 7b) in terms of both increased maximal slope and total charge displaced in the simulated potential range. However, this ‘rescue’ is incomplete relative to the equivalent relation for the α-helical model (solid line in Fig. 7a). The corresponding translational energy profiles for the 3₁₀-helical model are shown in Fig. 7d.

Islas and Sigworth (2001) found small voltage shifts (<10 mV) when studying the effects of intracellular variation of ionic strength on charge-voltage relations of Shaker channels. They interpreted these observations in terms of the Gouy-Chapman theory of the electrical double layer. In those terms, small shifts indicate a low density of membrane surface charge. In our simulations (Fig. 7a,b), a unilateral variation of screening causes a large shift even though the model does not include surface charge. Screening of S4 charges by a bath of low ionic strength reduces the electrostatic energy less than 7a): the screening of such S4 charges by a bath of high ionic strength. This effect does not require fixed surface charges, but arises from the S4 charges themselves. In contrast to the interpretation given by Islas and Sigworth (2001), the absence of a voltage shift may indicate that fixed negative charge exists at the intracellular end of the gating canal, but that such charge is largely neutralized by the positive S4 charges exposed to the intracellular baths at the midpoint of the S4 segment’s range of travel. The S4 charge exposed in this configuration then faces a matching density of negative fixed charge regardless of the ionic strength of the bath.

The screening of sliding-helix charges that become exposed to the external or internal aqueous solution is important for both the steepness of the charge-voltage relation as well as for the position on the voltage axis. Since fixed countercharges on the channel protein or associated lipids might dominate the screening effects of free ions in the aqueous solutions, we assess in the following section the effects of fixed countercharges on VS characteristics.

4.5 Consequences of fixed ‘surface charge’

The existence of ‘surface charge’ acting on the VS domain was inferred by Frankenhaeuser and Hodgkin (1957) and many subsequent studies (reviewed by Hille (2001)). Negative charges on residues of the extracellular loop connecting the S5 and pore-forming P-loop segments of Kv channels determine the voltage for activating the channel (Elinder et al 1998; Elinder and Århem 1999). One residue is conserved in that region — E418 for ShakerB — while others are variable. E418 is involved in mediating activation-related slow inactivation and has been proposed to interact at close range with the outermost S4 charge (R362) when the S4 segment is in the activating position (Larsson and Elinder 2000; Elinder et al 2001). Furthermore, Schmidt et al (2006) have shown that negatively charged phospholipids need to be present in the membrane if voltage-gated K⁺ channels are to function.

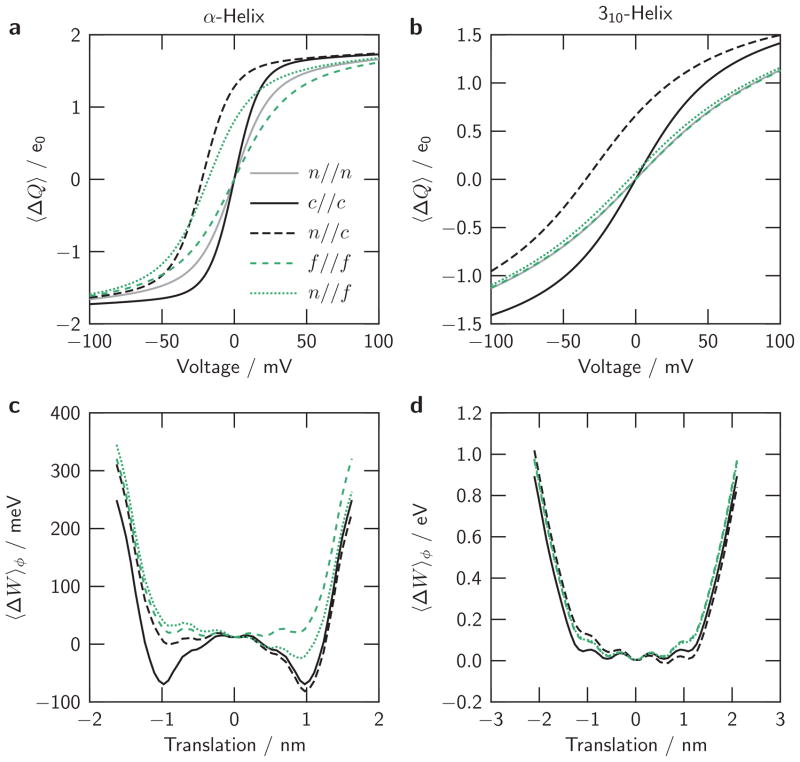
We model surface charge with discrete charges by placing a point charge of −e₀ into the baths at a z position corresponding to the position of the terminal S4 charge when the S4 has been translated by ±1 nm, the range of translation by voltage found in the reference models. Two variations are studied: either a single charge in the external bath, or two charges, one in each bath at symmetrical distances in the translational direction. For the α-helix, that distance is ±2.125 nm from the center of the lipid bilayer; and for the 3₁₀-helix, that distance is ±2.7 nm. The charges are given the same radial distance from the S4 axis as the countercharges located inside the protein. Two angular positions are tested: a ‘close’ one aligned with the terminal S4 charge, and a ‘far’ one turned 180° away from that S4 charge.

The charge-voltage relations for our reference α-helical S4 model with surface charge(s) in four different geometries are shown in Fig. 8a: one external charge in the far position (dotted line); one external and one internal surface charge, with both in the far positions (short-dashed line); one external charge in the close position (long-dashed line); and one external and one internal charge, with both in the close positions (solid line). The far external charge alone shifts the charge-voltage relation, producing the signature of a surface charge. The combination of far external and far internal surface charges slightly reduces the slope of the charge-voltage relation with respect to the model without surface charges (compare light gray line). The combination of close internal and close external charge does not produce a shift (due to symmetry) but does steepen the slope of the charge-voltage curve. With only the close external charge, the charge-voltage relation is shifted, and at negative voltage, the asymptote is slightly less steep relative to the asymptote with both surface charges. Thus surface charges have position-dependent effects on both the midpoint and slope of charge-voltage relations.

Fig. 8. Consequences of ‘surface charge’.

Reference α-helical (a, c) and reference 3₁₀-helical (b, d) S4 models with discrete surface charge(s) added in four variations of geometrical position (detailed in text). The labels in panel a specify: n, no surface charge; c, charge in ‘close’ position; f, charge in ‘far’ position. (a, b) Mean charge-voltage relations; (c, d) Translational energy profiles

The translational energy profiles from those four surface-charge simulations are shown in Fig. 8c. Far external surface charge chiefly tilts the profile (dotted line), whereas far surface charges on both sides (short-dashed line) remove the energy wells near the ends of the energy trough. Close external and internal charges, however, create deeper energy wells at either end of the range of S4 motion (solid line). With only a close external charge, an energy well is added at the external end of the range of S4 motion, while energy at the intracellular end of the range is raised (long-dashed line). The energy well resulting from close interaction with a surface charge increases the electrostatic contribution to S4 transmembrane stability as well, since it lowers the electrostatic energy of that S4 position relative to more extreme S4 positions. This does not occur when the interaction with the surface charge is far.

The model with the 3₁₀-helical S4 segment responds to surface charge in the close position(s) much more strongly than to surface charge in the far position(s) (Fig. 8b,d). The far surface charge in this helix geometry is always on the opposite side of all charges of the S4 helix. The close surface charge(s) increase the slope of the charge-voltage relation. This increase is smaller than that for the α-helical model, with the translational energy profiles maintaining an overall U-shape (Fig. 8d) in contrast to the profiles computed with the α-helical model (Fig. 8c).

Elinder et al (2001) estimated the contribution by individual surface charges to voltage shift in K⁺ channel charge-voltage relations using the voltage shifts of ionic conductance observed with varied Mg²⁺ concentrations. Our simulated shifts are in the range of those estimated shifts. Using Gouy-Chapman theory, Elinder et al (2001) interpreted the varied shifts estimated for different charged residues in terms of the distance between the S4 charges and the charged residues. For the α-helical S4 model, our consistent simulations with a ‘close’ and a ‘far’ surface charge show only a small effect on the voltage shifts due to the distance between S4 and the surface charge (long-dashed and dotted lines in Fig. 8a). In contrast, the 3₁₀-helical S4 model predicts a larger effect on voltage shifts (Fig. 8b), comparable to those observed by Elinder et al (2001).

The screening of sliding-helix charges by protein (or lipid) charges exposed to the aqueous solutions provides a channel with a means to control the midpoint as well as the steepness of its charge-voltage relation. Assessments of such screening charges need to consider the specific surface charge location and S4 helix configuration.

5 Conclusion

The sliding helix voltage sensor has an innate electrostatic stability if the S4 charges not exposed to water are balanced by fixed countercharges. This balance restricts the range of S4 travel to the range displacing from ~3 to 4 charge equivalents across the membrane field. The electrostatic restriction of travel at the extremes of physiological membrane potential leads to robust VS behavior over a range of conditions and geometrical variations. Whether the geometry is α-helical, 3₁₀ helical, in high ionic concentration or low, this basic structural issue produces reversible gating-charge displacement in response to change in transmembrane potential.

On the other hand, between those extremes the energy landscape for a given membrane potential varies between models: from almost flat to two energy minima separated by a broad barrier. Those variations lead to distinct charge displacement patterns, implying distinct dynamics not investigated here. S4 helix configuration, countercharge arrangement, protein dielectric, gating canal geometry, and fixed surface charges alter the behavior of the system, ranging from systems that can be approximated by two-state Boltzmann models all the way to continuous model systems. This results in a family of voltage-sensors with easily perturbed voltage sensitivity despite their robust behavior at their limits. Features not made explicit in our models will likely play a role in that region of sensitivity. Characteristics determined by small electrostatic energy differences show that the physics of the VS domain needs to be solved consistently for conclusive results.

These results suggest a problem with the 3₁₀-helical S4 structure: in the parameter space we studied, the 3₁₀ models tend towards poor voltage-sensitivity in contrast with α-helical models, which show both higher voltage-sensitivity across parameters and broader responsiveness to variation of model parameters.

Our simulations elucidate electrostatic principles making a sliding helix a robust sensor that can report voltage with a range of possible set points and sensitivities. These ‘forward’ simulations give insight by calculating the consequences of specific physical models. The ‘inverse’ problem of determining the underlying physics from experimental observation is hard (Cubitt et al 2012). We suggest that forward simulation can efficiently explore the terrain for designing and interpreting experiments, as well as provide knowledge for understanding the functional implications of structure.

Here we have simulated the equilibrium characteristics of the VS domain. The dynamics of voltage sensing is crucial as well for fast electrical signaling by ion channels. Our electrostatic computations provide an energy functional for models of the VS domain. A general and efficient method for extending these computations toward dynamics can use Onsager’s variational principle to compute the time evolution of least energy dissipation (Doi 2011).