Abstract
In this article, we develop an admixture F model (AFM) for the estimation of population-level coancestry coefficients from neutral molecular markers. In contrast to the previously published F model, the AFM enables disentangling small population size and lack of migration as causes of genetic differentiation behind a given level of FST. We develop a Bayesian estimation scheme for fitting the AFM to multiallelic data acquired from a number of local populations. We demonstrate the performance of the AFM, using simulated data sets and real data on ninespine sticklebacks (Pungitius pungitius) and common shrews (Sorex araneus). The results show that the parameterization of the AFM conveys more information about the evolutionary history than a simple summary parameter such as FST. The methods are implemented in the R package RAFM.
Keywords: coancestry, identity by descent (IBD), FST, admixture F model (AFM), Bayesian inference
IN the fields of animal and plant breeding, coancestry coefficients are often used as measures of relatedness between individuals (Bink et al. 2008). For example, in a noninbred population the coancestry between full-sibs or between a parent and an offspring is , and the coancestry between half-sibs is (Lynch and Walsh 1998). Coancestry is the same as probability of identity by descent (IBD) at the limit of a low mutation rate and given a noninbred ancestral population. Two genes are said to be identical by descent if and only if they have not mutated since the most recent common ancestor.
Individual-level coancestry coefficients (or probabilities of IBD) are useful in gene mapping, because they tell how much the genomes of two individuals are expected to resemble each other; i.e., they summarize the expected level of genetic similarity. In analogy, population-level coancestry coefficients can be used as measures of relatedness between local populations, and they can be combined with phenotypic data to detect signals of selection in quantitative traits, as opposed to those caused by random drift (Merilä and Crnokrak 2001; Mckay and Latta 2002; Ovaskainen et al. 2011).
Coancestry coefficients can be calculated directly, if pedigree information is available, but their estimation for natural populations is often challenging. One approach for doing so is to use the link between coancestry coefficients and coalescence times (Rousset 2004). Coalescence time distributions can be solved, at least numerically, for a population that is in a stationary state, assuming that the demographic parameters are known (Bahlo and Griffiths 2001). However, in the context of evolutionary ecology of natural populations, this is rarely the case, as there is often limited direct information on demographic history, and it can be unrealistic to assume any kind of stationarity. Instead, a common approach is to infer the demographic history using neutral molecular markers genotyped from the present generation. One statistical framework for estimating coancestry coefficients in this way is given by the F model (Falush et al. 2003; Gaggiotti and Foll 2010). However, this approach suffers from the structural limitation that the subpopulations are assumed to have radiated independently from the ancestral population, so that there has been no recent gene flow. Consequently, the F model cannot account for limited gene flow and small population size as alternative sources of genetic differentiation (Gaggiotti and Foll 2010).
In animal and plant breeding, a number of alternative methods have been developed for estimating coancestry coefficients from molecular marker data for pairs of individuals. Bink et al. (2008) survey seven such methods, concluding that the surveyed estimators have poor statistical properties, except in the special case that the allele frequencies are known for a hypothetical reference population. Furthermore, as Fernandez and Toro (2006) point out, many of these estimators have undesired mathematical properties; e.g., they may yield logically incompatible estimates for different pairs of individuals. Software by Maenhout et al. (2009) removes some of these flaws by post hoc modification of the parameter estimates.
In this article, we focus on the case where neutral genotypic data are available for a set of subpopulations, and the problem is to infer the matrix of coancestry coefficients among these local populations. We model the demographic histories of the subpopulations by an admixture of evolutionary independent lineages, thus extending the F model in a way that relaxes the structural assumption noted above. We use an admixture of independent lineages as a phenomenological model for the evolutionary history of a metapopulation where local populations experience a limited level of gene flow. Apart from Gaggiotti and Foll (2010), our method is also a generalization of that of Fu et al. (2005), because we consider multiallelic loci and a more general population structure than the case of clustered subpopulations. With these extensions, our model contains both gene flow and pure random drift as factors influencing the level of differentiation. Contrary to the “pairwise methods” used in animal and plant breeding, both the original F model and our model permit writing the likelihood of individual-level data directly as a function of population-level coancestry coefficients. In the following, we first introduce the modeling approach and then its Bayesian parameterization that we have implemented in the R-package RAFM, and finally we illustrate the modeling approach with the help of simulated and real data.
The Modeling Approach
Coefficients of coancestry
Our main interest is in the estimation of population-level coefficients of coancestry, denoted by for a pair of populations (A, B). We define as the average coancestry between the subpopulations,
| (1) |
where is the coancestry coefficient of individuals i and i′, and nA is the number of individuals in population A. We note that the definition of Equation 1 allows for the possibility that the level of coancestry is not identical for all pairs of individuals with i ε A and i′ ε B. A priori, in lack of this information, is assumed to depend only on the populations A and B, and thus it can be used interchangeably with for calculating the covariance of allelic states as detailed in Supporting Information, File S1.
We follow Rousset (2004) and call two gene copies IBD if they originate from the same ancestral copy and are identical by state; i.e., they have not mutated since their divergence. The coancestry coefficients and the probabilities of IBD for neutral loci are often used interchangeably, but they have a slight difference (we denote the latter by and for the individual and subpopulation levels, respectively). The probability of IBD can be written by using the coalescence time distribution for two gene copies in populations A and B as (Rousset 2004), e.g., for a model with discrete generations:
| (2) |
In this equation, CAB,t is the probability that the two gene copies coalesce exactly t generations before present, and μ is the per-locus per-generation probability of mutation. Bahlo and Griffiths (2001) derive formulas that allow the numerical computation of , assuming that the migration rates between the subpopulations and their relative sizes are known. These formulas enable estimating from demographic parameters, but this approach typically assumes that population dynamics have remained stationary over a long period of time (Bahlo and Griffiths 2001; Wilkinson-Herbots 2003; Wilkinson-Herbots and Ettridge 2004; Bhattacharya et al. 2007).
Sometimes the biological context is such that there has been a major perturbation, such as the last ice age, after which the subpopulations have diverged from a common ancestral pool. In this case, instead of assuming stationarity, it is more natural to consider a finite population history of T generations. In this case,
| (3) |
where the expectation is taken over the distribution of pedigrees generated by the demographic model. The approximation is justified if the mutation rate is low compared to the number of generations.
The relationship between coancestry and FST
FST is one of the most widely used statistics in population genetics, and it is routinely used as a measure of genetic differentiation (Rousset 2002, 2004; Whitlock 2011). Depending on the definition of θ, FST can be defined through coancestry, probability of IBD, or probability of identity by state as
| (4) |
where
| (5) |
and is the number of populations. In this article, we define FST through population-level coancestry. In Equation 5, is the average coancestry within subpopulations, and is the average coancestry between subpopulations. In line with the coalescent-based definition of FST (Rousset 2004), we do not weight the averages, e.g., by the sizes of the local populations. We are chiefly interested in estimating the coancestry coefficients and investigating the properties of the admixture F model (AFM), but we also report FST (defined through the coancestry-based variant of Equations 4 and 5) estimates because of the centrality of FST in the literature.
The AFM
In this section, we extend the F model (Falush et al. 2003; Gaggiotti and Foll 2010) to an AFM that allows for gene flow among the local populations. As is the case with the original F model, we assume that the local populations are derived from a common ancestral population and consider the limit of a small mutation rate, i.e., the situation that relates to Equation 3.
Denoting the frequency of allele u at locus j in the ancestral generation by qju, the expectation and variance of the allele frequency in population A can be written as
| (6) |
where φ is a factor that depends on the demographic model (Lynch and Walsh 1998). For an isolated population of a constant effective size,
| (7) |
(Lynch and Walsh 1998). A convenient distributional form that satisfies the above is
| (8) |
where
| (9) |
in absence of mutation. By Equation 9, a small value of a corresponds to a small effective population size or a large number of generations T, both of which imply a high amount of random genetic drift. The Dirichlet distribution is just a convenient approximation for the distribution of allele frequencies under pure random drift, as their true distribution is difficult to implement in a statistical model (see File S2). Also the truncated normal distribution is often used to approximate this distribution (Nicholson et al. 2002; Balding 2003; Coop et al. 2010). However, the truncated normal distribution is more difficult to adapt to the multiallelic case than the Dirichlet distribution as the frequency distribution is constrained by the condition . For a discussion on the relative accuracy of the Dirichlet and truncated-normal approximations, see File S2 and Figure S1.
To extend the model for subpopulations that may have experienced gene flow since their divergence from a common ancestral population, we assume an admixture of nε evolutionary independent lineages (Figure 1). The allele frequencies in each lineage are distributed as in Equation 8; i.e., we assume for locus j and lineage k,
| (10) |
where ak measures the amount of drift experienced by this lineage. The allele frequencies in locus j in local population A are defined as a mixture the lineage-specific frequencies, namely
| (11) |
We constrain the lineage loadings kAk to sum up to unity over the lineages, , implying that vector pAj is a proper frequency distribution. Setting the lineage-loading matrix to the identity matrix yields the special case of fully independent demes (the F model of Falush et al. 2003). Technically, our construction is analogous to factor analysis (Gorsuch 1983), with lineages as factors and lineage loadings kAk as factor loadings.
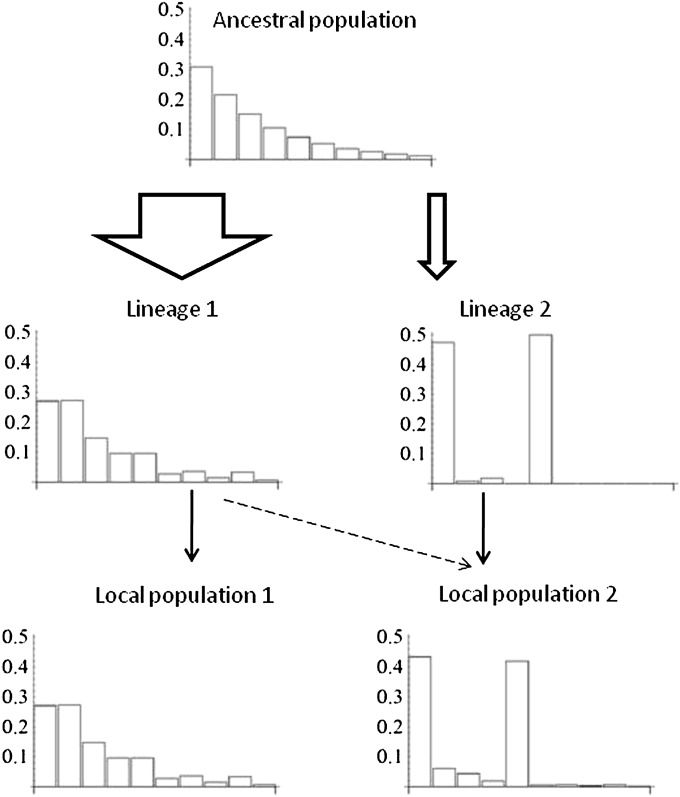
Figure 1 .
Schematic presentation of the admixture F model (AFM), in which subpopulations are constructed as admixtures of independent lineages. The histograms represent allele frequencies in a particular locus in the ancestral generation, in two independent lineages, and in two present subpopulations. In this example, lineage 1 has been subject to little drift (parameter value a1 = 100). In contrast, only two alleles remain at high frequency in lineage 2 as a result of much drift (a2 = 0.5). Population 1 is identical to lineage 1 (k11 = 1, k12 = 0). Population 2 is mainly derived from lineage 2, but has received some gene flow from lineage 1 (k21 = 0.1, k22 = 0.9). These parameter values give population-level coancestry coefficients , , and , yielding FST = 0.22.
A convenient property of the AFM is that the subpopulation-level coancestry coefficients depend on the model parameters in a very simple way (Table 1). As shown in File S1,
| (12) |
Table 1 . List of main parameters and symbols.
| Dimensions | |
|---|---|
| No. distinct alleles in locus j | nj |
| No. loci | |
| No. lineages | nε |
| No. subpopulations | |
| Coalescent theory | |
| Probability of IBD for two gene copies in populations A and B | |
| Probability that two gene copies from populations A and B have coalesced exactly t generations before present | CAB,t |
| Time since population divergence | T |
| Per-generation per-locus rate of mutation | μ |
| Per-capita probability of migration | m |
| Coancestry coefficients | |
| Coancestry among subpopulations | matrix with elements |
| Mean within-population coancestry | |
| Mean between-population coancestry | |
| Allele frequencies | |
| Allele frequencies in the ancestral generation | qj = (qju); u = 1, … , nj |
| q = (qj); j = 1, … , nL | |
| Allele frequencies in lineages | zkj = (zkju); u = 1, … , nj |
| zk = (zkj); j = 1, … , nL | |
| z = (zk); k = 1, … , nL | |
| Allele frequencies in subpopulations | pAj = (pAju); u = 1, … , nj |
| pA = (pAj); j = 1, … , nL | |
| p = (pA); A = 1, … , nP | |
| Parameters measuring evolutionary history | |
| Lineage loadings | matrix k with element kAk |
| Genetic drift | a = (ak); k = 1, … , nL |
| Identity by state | |
| Indicator variable for the allele copy k in locus j of individual i being of the allelic type u | xijku |
| Data, i.e., observed allele counts on the sample As of individuals originating from subpopulation A | |
| xAj = (xAju); u = 1, … , nj | |
| xA = (xAj); j = 1, … , nL | |
| x = (xA); A = 1, … , nP | |
Thus, after fitting the AFM to data it is straightforward to obtain an estimate of the matrix of population-to-population coancestry coefficients. By construction, this matrix will be always positive definite, avoiding the logical problems from which some of the earlier methods suffered (Fernandez and Toro 2006).
Assuming no genetic structure within subpopulations, i.e., a random distribution of alleles among and within individuals, the genotype of each individual in subpopulation A is a multinomial random variable, xij ∼ Multinomial(2, pAj). Notably, inbreeding due to a small population size is represented by a high intrapopulation coancestry , whereas an increased level of inbreeding due to assortative mating could be added to the model by assuming a dependency between the allelic states of the two gene copies within an individual, but we do not consider that in this article.
Parameter estimation with Bayesian inference
To parameterize the AFM with Bayesian inference, prior distributions need to be defined for the primary parameters q, α, and k. We assume the distributional forms
mainly for the sake of mathematical convenience. Indexes j, k, and A refer to loci, lineages, and subpopulations, respectively. In the case studies below, we assume the values , μa = 2, We set the number of lineages equal to the number of subpopulations and assume that lineage A makes the dominant contribution to subpopulation A, i.e., that the matrix k is diagonally dominant. To do so, we let
| (13) |
and truncate the prior by the requirement that for all k ≠ A. This specification links each population with a particular lineage by assuming that lineage A makes a dominating contribution to population A. It also ensures that label switching is not possible, thus improving the mixing of the Markov chain Monte Carlo (MCMC) algorithm (Gelman and Carlin 2004).
The number of alleles (nj) in locus j in the ancestral generation is generally unknown, as some alleles may have disappeared after the lineages have diverged or are not present in the sampled individuals. Due to the aggregation property of the Dirichlet distribution, all of the unobserved alleles can be binned into a single unobserved class. Thus, we define nj as the number of distinct alleles observed in locus j plus one.
The directed acyclic graph that illustrates the link from the primary parameters (k, α, q) through the derived parameters (z, p) to the data x is shown in Figure 2. Given the data x, the posterior density can be decomposed as
| (14) |
with the distributional form of each factor being specified above. As noted above, the coancestry coefficients are not directly involved in the estimation procedure, but their posterior distribution is determined by that of (k, α) (Equation 12). We use the adaptive random-walk Metropolis–Hastings algorithm of Ovaskainen et al. (2008) to sample the posterior density π(k, α, q | x). More details of the algorithm can be found in File S3, and it is implemented in the R package RAFM.
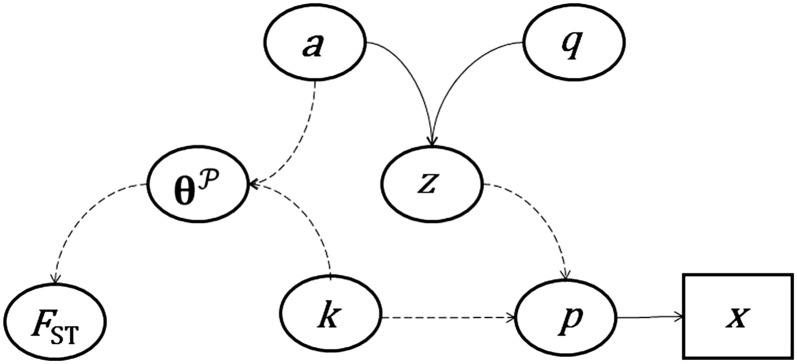
Figure 2 .
A directed acyclic graph (DAG) describing the dependencies among model parameters and data. Solid arrows imply probabilistic links and dashed arrows deterministic relationships. The process that is assumed to have generated the genotype data (x) involves the ancestral allele frequencies (q), the amount of genetic drift experienced by the lineages (a), the allele frequencies in the lineages (z), and the lineage loadings, i.e., the contributions of lineages to the local populations (k). Derived parameters include allele frequencies in the subpopulations (p) and the matrix of population-level coancestry coefficients (θP) from which FST can be computed.
Numerical Examples
We tested the performance of the method described above with two kinds of simulated data: data generated by the AFM itself and data generated through individual-based pedigrees that we in turn generated by a demographic model with continuous migration among subpopulations. The first type of data was used to investigate the performance of the estimation scheme in the ideal case that the data follow the structural assumptions of the model. The second type of data was used to examine whether a mixture of independent lineages can yield a good approximation of a more realistic demography in the sense of providing an accurate estimate of the matrix and whether the parameters α and k correlate with the demographic parameters in an intuitive way.
Case studies with data generated by the AFM
First, we considered populations A and B and assumed the parameter values k = (0.9, 0.1; 0.1, 0.9) and α = (2.7, 2.7), which leads to and consequently FST = 0.18. As a default case, we assumed that nA = nB = 100 individuals from each population were genotyped for loci, each having nj = 4 allelic variants that were equally common in the ancestral generation. To test the dependency of parameter estimates on sample size, we varied each of these parameters in turn, considering nA = nB = 10, 100, 1000; and nj = 2, 4, 8. Figure 3 shows how the accuracy of the estimated FST value increases with sample size. As expected from earlier research (Gaggiotti and Foll 2010; Wang and Hey 2010), increasing the number of loci improves the accuracy much more rapidly than increasing the number of individuals. Analogously, increasing the number of alleles per each locus, i.e., increasing the level of polymorphism, brings more resolution to the data, and thus it also rapidly improves parameter estimates. Contrary to the case studies of Jost (2008), but consistent with the fact that FST is defined through coancestry, the estimates of FST do not decrease when the polymorphism of marker loci increases (Figure 3A).
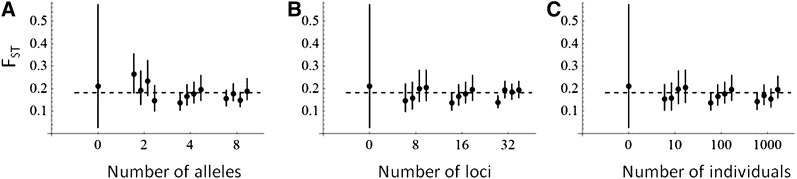
Figure 3 .
Accuracy of parameter estimates increases with allelic polymorphism and sample size. The solid circles with the error bars show the estimate (posterior median and 95% central credibility interval) of FST obtained by fitting the AFM to simulated data generated by the AFM. The default values of four alleles, 16 loci, and 100 individuals are assumed except for the parameter that is varied in each panel: level of polymorphism (A), number of loci (B), and number of individuals sampled from each subpopulation (C). The true value of FST = 0.18 is indicated by the dashed line, and the cases with sample size 0 show the prior distribution. For parameter values used in generating the data, see Case studies with data generated by the AFM in the main text.
To test whether local drift and lack of gene flow could be separated as alternative causes of genetic differentiation, we repeated the above (with the default sample size) with the off-diagonal value of k set to 0.05, 0.15, 0.25 and the value of α adjusted so that FST = 0.18 in all cases (Figure 4). Note that gene flow sets an upper limit to population differentiation: given a value of gene flow (i.e., off-diagonal of k), there is an upper limit to FST, namely the one produced by α = (0, 0). While the separation of gene flow and migration is not possible in the standard F model (Gaggiotti and Foll 2010), Figure 4A shows that the parameters k and α are identifiable in the AFM, if sufficient data are available. As a consequence, it is possible to estimate a full matrix (Figure 4B), not only the summary parameter FST.
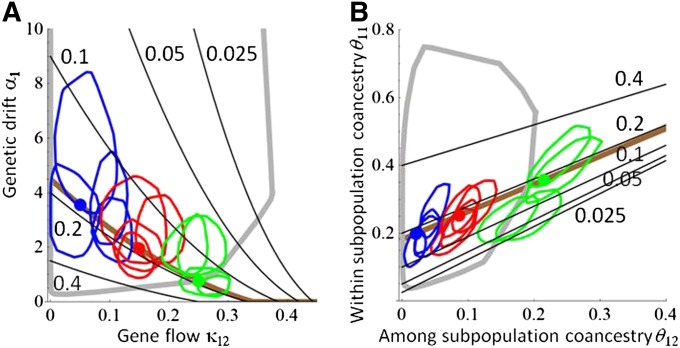
Figure 4 .
Separation of genetic drift and gene flow as causes of genetic differentiation. In the simulated case study consisting of two identical populations, FST and the subpopulation-level coancestry coefficients depend on the parameters a1 = a2 (measuring genetic drift) and k12 = k21 (measuring gene flow). The black lines show isoclines of FST in (k12, a1) space (A) and in (θ12,θ11) space (B). The brown line shows the isocline of FST = 0.18 corresponding to the true value in all three simulated scenarios, and the solid circles show the true parameter values for each of the scenarios. The lines show the parameter estimates of the fitted models, measured by 75% polytope quantiles of the posterior distributions. The thick gray lines show the 75% polytope quantiles for the prior distribution.
Case studies with an individual-based model
We constructed pedigrees for subpopulations with nonoverlapping, constant-size generations consisting of equal numbers of males and females. For each individual in the ancestral population, we randomized the two allele copies for each locus assuming four allelic variants with equal frequency qju = 0.25. The two parents of each individual in the subsequent generations were randomized (independently of each other) with probability 1 − m among the individuals of the same subpopulation and with probability m among the individuals of the other subpopulation (thus implying a per-capita migration rate m). We modeled diploidic inheritance for 32 unlinked loci. To vary the level of gene flow and genetic drift, we considered three scenarios, in each of which the two subpopulations had diverged 50 generations ago. In the baseline scenario 1, we assumed 200 individuals per population and m = 0.001. In scenario 2, we increased the amount of drift (and thus also FST) by assuming 50 individuals per subpopulation. Finally, scenario 3 differed from the baseline scenario 1 by having a higher amount of gene flow, m = 0.02. As the purpose of this simulation study was to examine whether the AFM is able to approximate individual-based pedigrees rather than to test its statistical power (which we demonstrate in Figures 3 and 4), we assumed that large data sets were available, i.e., 100 individuals per subpopulation genotyped for 32 loci (even for the smaller subpopulations), each having four allelic variants in the ancestral generation. We created four replicate data sets for each of the scenarios 1–3.
Figure 5 shows that the AFM can mimic individual-based pedigrees in the sense that the parameters that measure gene flow (k) and genetic drift (α) vary in line with the individual-level parameters of the three demographic scenarios. Increasing local population size decreases α, and increasing gene flow increases the off-diagonal elements of k. Figure 5B shows that our approach performs well also for estimating FST from the individual-based data, although there is a slight bias upward for scenario 2 with a high amount of drift. Here the true values of the coancestry coefficients were computed from the simulated pedigree, using first the standard recursive relationships (File S1) and then averaging the individual-level coancestries over the natural subpopulations (not the genotyped individuals), according to Equation 1. For comparison, the Weir–Cockerham estimator (Weir and Cockerham 1984), implemented in FSTAT (Goudet 1995), gives very similar results (Figure 5B). Thus, the novelty of our approach is not in estimation of FST, but in separating gene flow and genetic drift as causal factors behind the observed level of differentiation. This separation is needed to estimate the full coancestry matrix , which in turn is needed, e.g., for detecting signals of natural selection in quantitative-genetic studies (Ovaskainen et al. 2011).
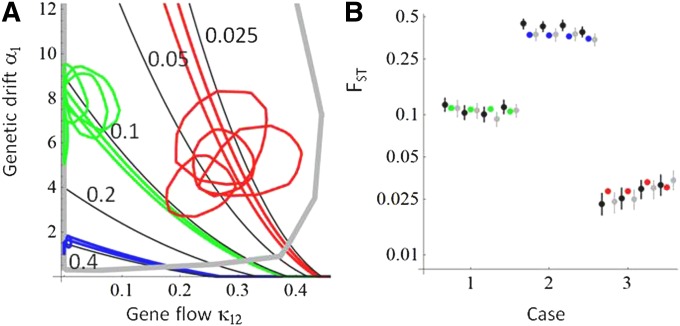
Figure 5 .
The AFM fitted to data generated by individual-based simulations of two identical subpopulations. The green color refers to baseline scenario 1 in which data were simulated assuming little gene flow and little random drift, blue refers to scenario 2 with a higher amount of drift, and red refers to scenario 3 with a higher amount of gene flow. (A) The 75% credible sets of the estimated parameters are plotted in (k12, a1) space. The colored lines show the isoclines of the minimal and maximal true FST values among the four replicate data sets generated for each scenario. (B) The FST values estimated by our method (black circles and error bars show the posterior median and 95% central credibility interval) are compared to the true values (colored circles) and to the Weir–Cockerham estimates (gray circles and error bars show the ML estimate and its 95% confidence interval) given by FSTAT (Goudet 1995). For parameter values used to generate the data, see Case studies with an individual-based model in the main text.
Case studies with real data
Here we illustrate our model’s output with two natural data sets. Both of these data sets are included in the R package RAFM (Karhunen 2012). The first data set consists of 183 ninespine sticklebacks genotyped for 12 microsatellite markers (a subset of data used by Shikano et al. 2010), and it comprises four populations: Baltic Sea (60°13′N, 25°11′E), White Sea (66°18′N, 33°25′E), pond Bynästjärnen in Sweden (64°27′N, 19°26′E), and pond Pyöreälampi in Finland (66°15′N, 29°26′E). The pond populations are likely to have experienced a very high amount of drift, and all populations are likely to have remained reproductively isolated from each other since the last ice age (Shikano et al. 2010). Thus, the demographic assumptions of Equation 3 and the AFM are at least approximately in line with the biological context.
For the ninespine sticklebacks, the median (95% credibility interval) of FST given by the AFM was FST = 0.34 (0.31–0.37). The Weir–Cockerham estimator yielded a higher estimate, the point estimate (95% confidence interval) being FST = 0.50 (0.44–0.55). The median estimates of the within-population coancestries were 0.02, 0.10, 0.57, and 0.68 for the White Sea, Baltic Sea, Swedish pond, and Finnish pond populations, respectively. These numbers may be compared to population-specific FST values, i.e., θi of Weir and Hill (2002), calculated from pairwise FST values given by FSTAT (Goudet 1995): 0.13, 0.09, 0.77, and 0.98 in the same order. Thus, as expected intuitively, the pond populations have experienced much more drift than the sea populations. In our analysis, the White Sea population is more diverse than the Baltic Sea population, which may reflect a higher effective population size in the White Sea that is in direct contact with the Arctic Ocean. In line with the expectation of no recent gene flow due to geographic barriers, the level of between-population relatedness was very low in our analysis (median estimates of all off-diagonal terms of the matrix were in the range 10−5−10−3, attributable to numerical noise from the MCMC).
The second data set originates from a much smaller spatial setting, containing samples of the common shrew (Sorex araneus) on islands on the lake Sysmä (62°40′N, 31°20′E) and the surrounding mainland in Finland (Hanski and Kuitunen 1986). Here we utilize data from the mainland, two large islands (L1 and L3, areas 3.8 and 4.4 ha), and two small islands (S5 and S10, areas 0.7 and 0.4 ha). The islands form two pairs, each consisting of a large and a small island, so that the distance between L1 and S5, as well as the distance between L3 and S10, is <500 meters, but the distance between any other pair of islands is at least 1300 meters. The diameter of the lake is ∼3 km, and thus the size of the study system is comparable to the potential migration distances of shrews (Hanski and Kuitunen 1986).
The small spatial scale is reflected by the low overall degree of population differentiation, the AFM yielding the estimate FST = 0.08 (0.06–0.09) and the Weir–Cockerham estimator giving FST = 0.05 (0.04–0.07). As expected from variation in population size, the within-subpopulation relatedness is lower for the mainland (median estimate 0.01) than for the islands (0.12, 0.10, 0.09, and 0.08 for L1, L3, S5, and S10, respectively). These findings are in line with the population-specific FST estimates (0.01, 0.12, 0.09, 0.09, and 0.06 in the same order). The only off-diagonal terms that are ≥0.01 in the median estimate are between the mainland and the island L1 (0.01) and between the islands L3 and S10 (0.01) that are located close to each other, but it is hard to draw conclusions on a more general pattern based on this observation. This is in line with the discriminant function analysis based on metrical traits by Hanski and Kuitunen (1986), which also revealed little indication of isolation by distance.
Discussion
The AFM can be used to infer population-level coancestry coefficients from genotypic data. Mathematically, the AFM is a generalization of the model of Fu et al. (2005) for multiallelic data and a more general population structure. As discussed above, the estimates of also relate to coalescent theory and thus to the definition of FST by Rousset (2004). Using the AFM for estimating FST is justified subject to two conditions: First, we have assumed that the subpopulations have diverged from a common ancestral population at some time in the past. Second, we have assumed that the mutation rate is low compared to the time elapsed since divergence or at least compared to the influence of potential gene flow after time since divergence. If these two conditions are met, is close to its coalescent-based analogy (), and thus it can be used for calculating the coalescent-based FST (Slatkin 1991, 1995; Rousset 2004). The AFM models the allele frequencies by an admixture of evolutionary independent lineages, but this assumption is less restrictive. As the simulations show, it can also be used to mimic the effects of continuous gene flow (Figure 5).
The parameters of the AFM convey information about the demographic history of the local populations, as we have demonstrated with the simulated data and the two natural data sets. Using the AFM, it is possible to analyze the level of connectivity between the subpopulations (as characterized by k) and the relative effective population sizes of the underlying evolutionary lineages. However, it is not possible to disentangle the absolute effective population sizes and the number of generations after divergence (as they are not identifiable on basis of a alone), nor it is possible to deduce per-capita rates of migration.
Apart from demography, the AFM also makes a number of assumptions regarding the type of genetic data. As discussed above, the mutation rate is assumed to be low, suggesting that using microsatellite markers should be avoided. As usual in population-genetic studies, we have also assumed that the markers used are selectively neutral. Thus, markers subject to diversifying (stabilizing) selection are likely to cause an upward (downward) bias in the estimate of FST, as is the case of FST estimates obtained by other methods (Excoffier et al. 2009). Third, we have ignored genotyping error, which is known to increase the sampling variation of FST estimates (Bonin et al. 2004; Herrmann et al. 2010). The implementation of these features to the present framework would be an important extension that we hope to be addressed by future work. Finally, we have used the Dirichlet distribution to model random genetic drift within each of the independent lineages. This approximation should be taken with some criticism (Nicholson et al. 2002; Balding 2003). Some authors have used truncated normal distribution in place of Dirichlet for estimating FST (Nicholson et al. 2002; Weir and Hill 2002; Coop et al. 2010). However, both of these statistical models are approximations of the true model, and both of them have their limitations, which we discuss in File S2.
For the molecular ecologists and population geneticists, FST is probably a more familiar variable than the matrix . While most authors consider FST as a parameter, some consider it as an estimator or a point estimate of this parameter. For different types of data and different mutation models, a full “alphabet soup of related indices have been developed” (Whitlock 2011, p. 1083), which may cause part of the confusion. There has also been recent discussion concerning the aptitude of FST for measuring genetic differentiation (Jost 2008; Whitlock 2011). Some authors have reported that locus-specific values correlate with the polymorphism of the marker loci (Hedrick 2005; Carreras-Carbonell et al. 2006; Jost 2008). By the canonical definition (Equation 4), FST is fully determined by the coalescent, so that it is logically independent of ancestral polymorphism. On the other hand, a high rate of mutation of course shows both in FST and in the present level of polymorphism. At the limit of a low mutation rate, FST reduces into a function of expected coalescence times (Slatkin 1991, 1995; Rousset 2002, 2004; Whitlock 2011) that are independent of polymorphism. In line with this, our coancestry-based FST is a function of coancestry coefficients and the pedigree that do not depend on the ancestral polymorphism.
Jost (2008) pointed out that FST can have low values even if the subpopulations do not share any alleles. In terms of coancestry coefficients, this implies for two different populations. As illustrated by the y-axis of Figure 4, the value of FST can range anywhere between zero and one also in this case. However, unlike Jost (2008), we do not consider this as a problematic feature of FST. From the viewpoint of Equation 4, FST is just a summary statistic of the subpopulation-to-subpopulation coancestry matrix . A more detailed understanding of population structure can clearly be obtained by considering the entire matrix , rather than a single scalar. Like Whitlock (2011), we still consider FST to be a very useful quantity in population genetics, e.g., for the reason that it is the relevant statistic for FST−QST comparisons that attempt to find signals of stabilizing and disruptive selection in quantitative traits (Merilä and Crnokrak 2001; Mckay and Latta 2002), although we note that also this analysis can be done more effectively using the full matrix of population-level coancestries (Ovaskainen et al. 2011).
Supplementary Material
Acknowledgments
We thank Christopher Wheat, Juha Merilä, and Michael Whitlock for helpful comments; Takahito Shikano for providing the ninespine stickleback data; and Ilkka Hanski for providing the common shrew data. Our research was supported by the Academy of Finland (grants 124242, 129636, and 250444 to O.O. and the work by M.K. partly covered by grants 213491, 129662, 118673, and 134728 to Juha Merilä) and the European Research Council (starting grant 205905 to O.O.).
Footnotes
Communicating editor: M. A. Beaumont
Literature Cited
- Bahlo M., Griffiths R. C., 2001. Coalescence time for two genes from a subdivided population. J. Math. Biol. 43: 397–410 [DOI] [PubMed] [Google Scholar]
- Balding D. J., 2003. Likelihood-based inference for genetic correlation coefficients. Theor. Popul. Biol. 63: 221–230 [DOI] [PubMed] [Google Scholar]
- Bhattacharya S., Gelfand A. E., Holsinger K. E., 2007. Model fitting and inference under latent equilibrium processes. Stat. Comput. 17: 193–208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bink M. C. A. M., Anderson A. D., Van De Weg W. E., Thompson E. A., 2008. Comparison of marker-based pairwise relatedness estimators on a pedigreed plant population. Theor. Appl. Genet. 117: 843–855 [DOI] [PubMed] [Google Scholar]
- Bonin A., Bellemain E., Eidesen P. B., Pompanon F., Brochmann C., et al. , 2004. How to track and assess genotyping errors in population genetics studies. Mol. Ecol. 13: 3261–3273 [DOI] [PubMed] [Google Scholar]
- Carreras-Carbonell J., Macpherson E., Pascual M., 2006. Population structure within and between subspecies of the Mediterranean triplefin fish Tripterygion delaisi revealed by highly polymorphic microsatellite loci. Mol. Ecol. 15: 3527–3539 [DOI] [PubMed] [Google Scholar]
- Coop G., Witonsky D., Di Rienzo A., Pritchard J. K., 2010. Using environmental correlations to identify loci underlying local adaptation. Genetics 185: 1411–1423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L., Hofer T., Foll M., 2009. Detecting loci under selection in a hierarchically structured population. Heredity 103: 285–298 [DOI] [PubMed] [Google Scholar]
- Falush D., Stephens M., Pritchard J. K., 2003. Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164: 1567–1587 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez J., Toro M. A., 2006. A new method to estimate relatedness from molecular markers. Mol. Ecol. 15: 1657–1667 [DOI] [PubMed] [Google Scholar]
- Fu R., Dey D. K., Holsinger K. E., 2005. Bayesian models for the analysis of genetic structure when populations are correlated. Bioinformatics 21: 1516–1529 [DOI] [PubMed] [Google Scholar]
- Gaggiotti O. E., Foll M., 2010. Quantifying population structure using the F-model. Mol. Ecol. Res. 10: 821–830 [DOI] [PubMed] [Google Scholar]
- Gelman A., Carlin J. B., 2004. Bayesian Data Analysis Chapman & Hall/CRC, Boca Raton, FL.
- Gorsuch R. L., 1983. Factor Analysis. Lawrence Erlbaum, Hillsdale, NJ [Google Scholar]
- Goudet J., 1995. FSTAT (Version 1.2): a computer program to calculate F-statistics. J. Hered. 86: 485–486 [Google Scholar]
- Hanski I., Kuitunen J., 1986. Shrews on small islands: epigenetic variation elucidates population stability. Holarct. Ecol. 9: 193–204 [Google Scholar]
- Hedrick P. W., 2005. A standardized genetic differentiation measure. Evolution 59: 1633–1638 [PubMed] [Google Scholar]
- Herrmann D., Poncet B. N., Manel S., Rioux D., Gielly L., et al. , 2010. Selection criteria for scoring amplified fragment length polymorphisms (AFLPs) positively affect the reliability of population genetic parameter estimates. Genome 53: 302–310 [DOI] [PubMed] [Google Scholar]
- Jost L., 2008. G(ST) and its relatives do not measure differentiation. Mol. Ecol. 17: 4015–4026 [DOI] [PubMed] [Google Scholar]
- Karhunen M., 2012. RAFM: Admixture F-model. Available at: http://CRAN.R-project.org/package=RAFM [DOI] [PMC free article] [PubMed]
- Lynch M., Walsh B., 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, New York [Google Scholar]
- Maenhout S., De Baets B., Haesaert G., 2009. CoCoa: a software tool for estimating the coefficient of coancestry from multilocus genotype data. Bioinformatics 25: 2753–2754 [DOI] [PubMed] [Google Scholar]
- Mckay J. K., Latta R. G., 2002. Adaptive population divergence: markers, QTL and traits. Trends Ecol. Evol. 17: 285–291 [Google Scholar]
- Merilä J., Crnokrak P., 2001. Comparison of genetic differentiation at marker loci and quantitative traits. J. Evol. Biol. 14: 892–903 [Google Scholar]
- Nicholson G., Smith A. V., Jonsson F., Gustafsson O., Stefansson K., et al. , 2002. Assessing population differentiation and isolation from single-nucleotide polymorphism data. J. R. Stat. Soc. Ser. B Stat. Methodol. 64: 695–715 [Google Scholar]
- Ovaskainen O., Rekola H., Meyke E., Arjas E., 2008. Bayesian methods for analyzing movements in heterogeneous landscapes from mark-recapture data. Ecology 89: 542–554 [DOI] [PubMed] [Google Scholar]
- Ovaskainen O., Karhunen M., Zheng C., Arias J. M. C., Merilä J., 2011. A new method to uncover signatures of divergent and stabilizing selection in quantitative traits. Genetics 189: 621–632 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousset F., 2002. Inbreeding and relatedness coefficients: What do they measure? Heredity 88: 371–380 [DOI] [PubMed] [Google Scholar]
- Rousset F., 2004. Genetic Structure and Selection in Subdivided Populations. Princeton University Press, Princeton, NJ [Google Scholar]
- Shikano T., Shimada Y., Herczeg G., Merila J., 2010. History vs. habitat type: explaining the genetic structure of European nine-spined stickleback (Pungitius pungitius) populations. Mol. Ecol. 19: 1147–1161 [DOI] [PubMed] [Google Scholar]
- Slatkin M., 1991. Inbreeding coefficients and coalescence times. Genet. Res. 58: 167–175 [DOI] [PubMed] [Google Scholar]
- Slatkin M., 1995. A measure of population subdivision based on microsatellite allele frequencies. Genetics 139: 457–462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., Hey J., 2010. Estimating divergence parameters with small samples from a large number of loci. Genetics 184: 363–379 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir B. S., Cockerham C. C., 1984. Estimating F-statistics for the analysis of population-structure. Evolution 38: 1358–1370 [DOI] [PubMed] [Google Scholar]
- Weir B. S., Hill W. G., 2002. Estimating F-statistics. Annu. Rev. Genet. 36: 721–750 [DOI] [PubMed] [Google Scholar]
- Whitlock M. C., 2011. G′(ST) and D not replace F(ST). Mol. Ecol. 20: 1083–1091 [DOI] [PubMed] [Google Scholar]
- Wilkinson-Herbots H. M., 2003. Coalescence times and F-ST values in subdivided populations with symmetric structure. Adv. Appl. Probab. 35: 665–690 [Google Scholar]
- Wilkinson-Herbots H. M., Ettridge R., 2004. The effect of unequal migration rates on F(ST). Theor. Popul. Biol. 66: 185–197 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.