Diffusion models of protein folding

Abstract

In theory and in the analysis of experiments, protein folding is often described as diffusion along a single coordinate. We explore here the application of a one-dimensional diffusion model to interpret simulations of protein folding, where the parameters of a model that “best” describes the simulation trajectories are determined using a Bayesian analysis. We discuss the requirements for such a model to be a good approximation to the global dynamics, and several methods for testing its accuracy. For example, one test considers the effect of an added bias potential on the fitted free energies and diffusion coefficients. Such a bias may also be used to extend our approach to determining parameters for the model to systems which would not normally explore the full coordinate range on accessible time scales. Alternatively, the propagators predicted from the model at different “lag” times may be compared with observations from simulation. We then present some applications of the model to protein folding, including Kramers-like turnover in folding rates of coarse-grained models, the effect of non-native interactions on folding, and the effect of the chosen coordinate on the observed position-dependence of the diffusion coefficients. Lastly, we consider how our results are useful for the interpretation of experiments, and how this type of Bayesian analysis may eventually be applied directly to analyse experimental data.

1 Introduction

At first sight, the folding of a protein appears to be a staggeringly intricate and complex process, with the formation of the specific native structure requiring the correct arrangement of thousands of protein atoms. In fact, just such a description of folding can be obtained from classical molecular dynamics simulations with atomistic force fields, which are now able to access the necessary time scales to sample complete folding trajectories,^1–3 or folding transition paths. However, the important events along the folding pathway are not easily identified simply by viewing a folding trajectory by itself. In particular, by their very nature, transition states are only transiently visited and remain hidden within the overwhelming number of conformations committed either to the folded or the unfolded state. Fortunately, the energy landscape theory of protein folding suggests an enormous simplification: as a consequence of an energy landscape funneled toward the folded state, it should be possible to represent the folding dynamics using a one-dimensional (1D), or low-dimensional reaction coordinate.^4–8 Since significant movement along this collective coordinate involves the crossing of many local barriers, it appears diffusive at long times. Projecting the complicated multidimensional trajectories onto a “good” 1D coordinate helps identify the configurations present as the protein progresses towards the folded state.^9,10 Furthermore, such low-dimensional projections provide a framework to characterise the folding dynamics in terms of a diffusion model.^7,11,12

From the perspective of experiments, too, the ability to describe folding as diffusion along a 1D coordinate is very useful. Firstly, many single molecule experiments explicitly measure dynamics along a distance coordinate, e.g., fluorescence resonance energy transfer (FRET)¹³ or optical tweezers.¹⁴ Secondly, experiments with high time resolution (e.g., ultrafast laser temperature jump) often probe only one or a few observable quantities (tryptophan fluorescence, infra-red absorption).^15–17 The ability to map dynamics onto a low dimensional description greatly facilitates the interpretation of such experiments in terms of a simple physical model.^18,19

The minimal description of 1D diffusion (without “memory”) requires a free energy surface and diffusion coefficient to be specified. While the former can be straightforwardly obtained by a variety of methods both from simulation²⁰ and (less straightforwardly) from experiment,^21,22 determining diffusion coefficients along collective coordinates poses a more challenging problem. In early diffusive descriptions based on lattice models of folding⁷ and on all-atom explicit solvent simulations of the helix-coil transition,¹¹ the diffusion coefficient was simply assumed to be constant and matched to the equilibrium relaxation dynamics in the unfolded well, and to the folding times, respectively. However, a projection of the high-dimensional dynamics onto a 1D coordinate in general makes the resulting diffusion coefficient dependent on the position along the coordinate. This position-dependence of the diffusion coefficient in protein folding has been the subject of a number of recent studies,^12,23–30 with some studies concluding that the diffusion coefficient varies strongly along the reaction coordinate (although the exact nature of the variation varies widely between studies^24–26,30) and others that the position-dependence is relatively weak.^12,23

Here, we present the theory and methodology for determining local diffusion coefficients (and free energies) on a reaction coordinate. The basis of our approach is a Bayesian analysis to determine the model parameters most consistent with molecular simulation trajectories, via the likelihood (given in terms of the model propagators) and any prior assumptions about the parameters. We illustrate the application of the model to simulation data using Langevin dynamics simulations of a coarse-grained representation of a small protein. Several tests are presented for the accuracy of the model, including the addition of a bias potential, and comparison of the propagators estimated from simulation with those predicted from the model, at different “lag” times. We also discuss where 1D diffusion models may break down when the fraction of native contacts is used as a reaction coordinate. Further applications of the model to protein folding are presented, including the effect of non-native interactions, the origin of Kramers-like turnover and the influence of the chosen coordinate. Finally, we discuss the implications for experiment, and possible future direct application to experimental data.

2 Theory

The dynamics of the molecular system occurs in a high-dimensional phase space that includes both protein and solvent coordinates. Here we are interested in developing a reduced description for the system dynamics projected onto a 1D coordinate. For systems obeying the laws of classical mechanics, Zwanzig’s projection-operator formalism provides the theoretical framework to construct such low-dimensional dynamical models.³¹ The projected dynamics can be described by a generalised Langevin equation or, equivalently, a generalised Fokker-Planck equation. The memory kernels and noise terms entering these equations are complex functions of the underlying dynamics in phase space, making this formal approach of primarily theoretical interest for processes such as protein folding.⁴

Here we simply assume (and later test) that the slow folding dynamics can be described by Smoluchowski diffusion on the 1D free energy surface F(Q) for a suitably chosen coordinate Q,

$$\frac{\partial p}{\partial t}=ℒp$$ (1)

where the diffusion operator is

$$ℒ=\frac{\partial }{\partial Q}D(Q)e^{-\beta F(Q)}\frac{\partial }{\partial Q}{e}^{\beta F(Q)}.$$ (2)

β = (k_BT)⁻¹ is the reciprocal temperature, and p = p(Q,t|Q₀,t₀) is the propagator or Green’s function, i.e., the probability density of Q at time t, given that the system started from Q₀ at time t₀. We then construct such a diffusion model by determining F(Q) and the position dependent diffusion coefficient D(Q) by projection of simulation trajectories collected for a detailed molecular system onto Q.³² Specifically, we use time series Q_i = Q(t_i) collected at times t_i = t₀ + iΔt spaced at intervals Δt. Assuming that the molecular system was initialised from a state with all phase space variables drawn from an equilibrium Boltzmann distribution and Q = Q₀ picked from an equilibrium distribution p_eq(Q) = exp[−βF(Q)]/ ∫ dQ′ exp[−βF(Q′)], then the probability of a particular trajectory segment i = 0,1, …, M is given by the product of propagators,

$$L=p_{\text{eq}}(Q_0){\displaystyle \prod _{i=1}^M}p(Q_i,t_i|Q_{i-1},t_{i-1}).$$ (3)

Here we have assumed that the dynamics is Markovian (i.e., memory-less) and described by the Smoluchowski diffusion equation, eqn (1). The path probability L defines a likelihood function that can be evaluated explicitly for a trajectory and given F(Q) and D(Q). Both long equilibrium trajectories and short trajectories initialised at different Q₀ can be used as input. If the trajectory is initialised from states conditional on Q = Q₀ (i.e., with an equilibrium distribution in all phase space variables on a hypersurface of fixed Q), the factor p_eq(Q₀) is removed from the likelihood L. Data from multiple (short) trajectories α can be combined, with each trajectory contributing a likelihood L_α to the product defining the overall likelihood, L = Π_α L_α. We note that in this approach detailed balance and microscopic time reversibility are satisfied by construction, simply because they are satisfied in the entire space of models considered.

Here we use the observed propagators, as sampled from simulation trajectories, to construct a diffusion model. Other observables can be used as well, such as the round-trip time between sufficiently distant Q points²⁸ or the mean first passage time.²⁷ In a variant³³ of the above approach, a Gaussian approximation is used for the short-time propagators instead of numerically solving eqn (1) for p(Q,Δt|Q₀,0). In a similar vein, if the free energy landscape is sufficiently flat, and if the dynamics is sufficiently Markovian even at short times Δt, one can also extract D(Q) simply from the short-time expansion of the diffusive propagator, D(Q) ≈ var(Q|Δt)/2Δt, using the variance of trajectories after time Δt starting from Q (this approach has been applied to protein folding in several instances^24,25 and is considered further below).

The likelihood function L in eqn (3) allows us to use Bayesian or maximum-likelihood approaches.³² For given F(Q) and D(Q), we can calculate p(Q_i,t_i|Q_i−1,t_i−1) = p(Q_i,t_i − t_i−1|Q_i−1,0) explicitly, such that L = L[Q₀,Q₁, …, Q_M|F(Q),D(Q)]. In a maximum-likelihood framework one variationally maximises L or lnL with respect to F(Q) and D(Q). In a Bayesian framework, one can in addition specify priors p_prior[F(Q),D(Q)] and then sample F(Q) and D(Q) according to the posterior distribution L × p_prior[F(Q),D(Q)]. This sampling is conveniently done in a suitably chosen function space. Here we have chosen functions F(Q) and D(Q) that are piecewise linear and continuous at points Q_i = iΔQ and i = …, −1,0,1, …. This discretisation is convenient also because it lends itself to an efficient numerical solution of the Smoluchowski equation, eqn (1), via matrix diagonalisation.³⁴ However, other basis sets can be used as well. To ensure scale invariance, the discretised D(Q_i) = D_i are sampled with a prior p_prior = Π_i 1/D_i, corresponding to uniform distributions of lnD_i. In addition, one can also impose smoothness on a scale given by ε by multiplying the prior with

$$L_{\text{smooth}}={\displaystyle \prod _i}\text{exp}[-{(D_i-D_{i-1})}^2/2{\epsilon }^2].$$ (4)

In practice, we collect statistics for the number of transitions N_ij from bin j around Q_j to bin i around Q_i after lag time Δt, summed over all trajectories. By solving the discretised Smoluchowski equation for given F(Q) and D(Q),^32,34 we calculate the transition probabilities p_ij(Δt) = p(bin i,Δt|bin j,0). The log-likelihood function (for fixed initial states Q₀) then becomes a double sum over bins,

$$\text{ln }L={\displaystyle \sum _{i,j}}{N}_{\mathit{\text{ij}}}\text{ ln }{p}_{\mathit{\text{ij}}}.$$ (5)

For infinitely long equilibrium trajectories we expect N_ij = N_ji on average because of time reversibility. We then maximize lnL + lnL_smooth by performing a Monte Carlo optimization of the discretised F(Q) and D(Q) functions.

A number of tests can be used to confirm that the underlying dynamics is indeed described accurately by a diffusion model. The simplest test uses different lag times Δt to ensure that the dynamics is sufficiently Markovian. It is typically found that for short lag times, the predicted dynamics is faster than the limiting behavior obtained for long lag times. From a plot of the first non-trivial eigenvalue λ₂ of the diffusion operator versus lag time Δt, one can estimate the temporal extent of the memory as the time it takes to reach a plateau. One could argue that the diffusion model is a meaningful description of two-state folding when the limiting behavior is reached for lag times that are shorter than the mean waiting times spent in the folded and unfolded states, and also shorter than the mean transition path duration between the two wells. The latter can be calculated by generalizing eqn (16) in ref 35 to position-dependent diffusion,

$$\langle {\tau }_{\text{TP}}\rangle ={\displaystyle {\int }_{Q_0}^{Q_1}}{\mathit{\text{dQe}}}^{-\beta F(Q)}\varphi (Q)[1-\varphi (Q)]\times {\displaystyle {\int }_{Q_0}^{Q_1}}\mathit{\text{dQ}}\prime e^{\beta F(Q\prime )}/D(Q\prime )$$ (6)

where transition paths are defined as trajectories passing directly from Q₀ to Q₁ or back. The splitting probability (or committor) satisfies $\varphi (Q)={\displaystyle {\int }_{Q_0}^Q}\mathit{\text{dQ}}\prime e^{\beta F(Q\prime )}/D(Q\prime ){[{\displaystyle {\int }_{Q_0}^{Q_1}}\mathit{\text{dQ}}″e^{\beta F(Q″)}/D(Q″)]}^{-1}.$ .

Additional tests compare the predicted dynamics of Q to that observed in the simulation trajectories. Such a comparison can be performed at the level of the propagators, by comparing transition events collected at different lag times to the predicted propagators. In addition, one can compare correlation functions. The most relevant autocorrelation function is that of Q itself, 〈Q(t)Q(0)〉, which is here directly related to the folding-unfolding dynamics and should decay as exp(λ₂t) at long times. More stringent tests³⁶ can be performed by projecting Q(t) onto the left eigenfunctions of the diffusion operator ℒ. The auto-correlation functions should be single-exponential, and the cross-correlations should vanish at all times.

Another useful test involves the addition of a term V(Q) to the total potential. For true 1D diffusion, this term would only affect the estimated free energies F(Q) and not the diffusion coefficients D(Q). Therefore, comparison of diffusion coefficients calculated with or without such a term serves as a test of how well the dynamics can be represented as 1D diffusion. For a two-state system (such as often found in protein folding), the matrix of transitions between Q bins, N_ij, will be heavily biased towards transitions within the stable states, with less data for dynamics on the barrier itself, the region most important for determining folding rates; for slow folding proteins it will not be possible to sample reactive events at all in equilibrium simulations. An obvious choice for the additional potential is then to set V(Q) = −F(Q).³⁷ This choice requires that F(Q) be determined beforehand using umbrella sampling or another suitable method for determining the potential of mean force on Q.³⁸ In the simulations with the bias, a cubic spline potential may be used to represent F(Q), resulting in smooth derivatives for molecular dynamics.

It is interesting to compare and contrast the 1D diffusion equation description of the folding dynamics to that of kinetic master equations³⁶

$$\mathbf{ṗ}(t)=\mathbf{\text{Kp}}(t),$$ (7)

or Markov state models^39–41

$$\mathbf{p}(t+\mathrm{\Delta }t)=\mathbf{\text{Tp}}(t),$$ (8)

where p(t) = (p₁(t), p₂(t), …, p_N(t))^T is the vector of probabilities of the N states, K is the kinetic rate matrix, and T is the transition matrix (with T = exp(ΔtK) for a given K). As pointed out by Bryngelson and Wolynes⁴ in the construction of their folding dynamics model, for an appropriately chosen coordinate in a suitable continuum limit the master equation description reduces to a diffusion model. This reduction to a diffusion model can be accomplished by another projection operation, as follows.

If the N-state master equation (or Markov state model) is consistent with essentially two-state like folding dynamics, there is only one slow relaxation process corresponding to the first non-trivial eigenvalue λ₂, which is separated by a time-scale gap from the N − 2 faster relaxation processes (with eigenvalues λ₁ = 0 > λ₂ ≫ λ₃ … for the master equation, and λ₁ = 1 > λ₂ ≫ λ₃ … for the Markov state model). By ordering the N states according to the corresponding left-hand eigenvector^36,42 of the kinetic rate matrix (or transition matrix), ψ⁽²⁾K = λ₂K (or ψ⁽²⁾T = λ₂T), one can construct the “best” reduced 1D master equation (Markov state model): ${\psi }_{i_1}^{(2)}<{\psi }_{i_2}^{(2)}<\dots <{\psi }_{i_N}^{(2)}$. If an order parameter can be found that, more or less, preserves the 1D ordering of the states, Q(i) < Q(j) if ${\psi }_i^{(2)}<{\psi }_j^{(2)}$, and if the microscopic states are sufficiently dense along Q (i.e., there are no large gaps between neighbouring ${\psi }_{i_k}^{(2)}$), one can construct the desired 1D Fokker-Planck equation in the continuum limit by reverting the steps used for discretisation.³⁴ This reduced representation gives up detail concerning fast relaxations within the folded and unfolded states, but faithfully retains the relevant two-state folding dynamics.

3 Simulations

We use simulations of a coarse-grained folding model to illustrate the fitting of a diffusion model for folding. As an example, we choose the B1 domain of streptococcal protein G, which has served as a paradigm in folding studies of small, single domain proteins.^43–46 The three-dimensional structure of the α/β protein G is shown in Fig. 1. We initially constructed a Gō-like model based on the native structure of protein G⁴⁷ using a standard procedure.⁴⁸ This model represents each residue by a single “bead” centered on the α carbon, and includes rigid bond constraints for consecutive atoms in the chain, harmonic terms for angle bending, knowledge-based terms for torsional rotation, and a non-bonded pair potential including a “desolvation” barrier. Since Gō-like models tend to generate energy landscapes that are smoothly funnelled toward the native state, we anticipate that the dynamics of this model may be well-captured by a single coordinate.

Fig. 1.

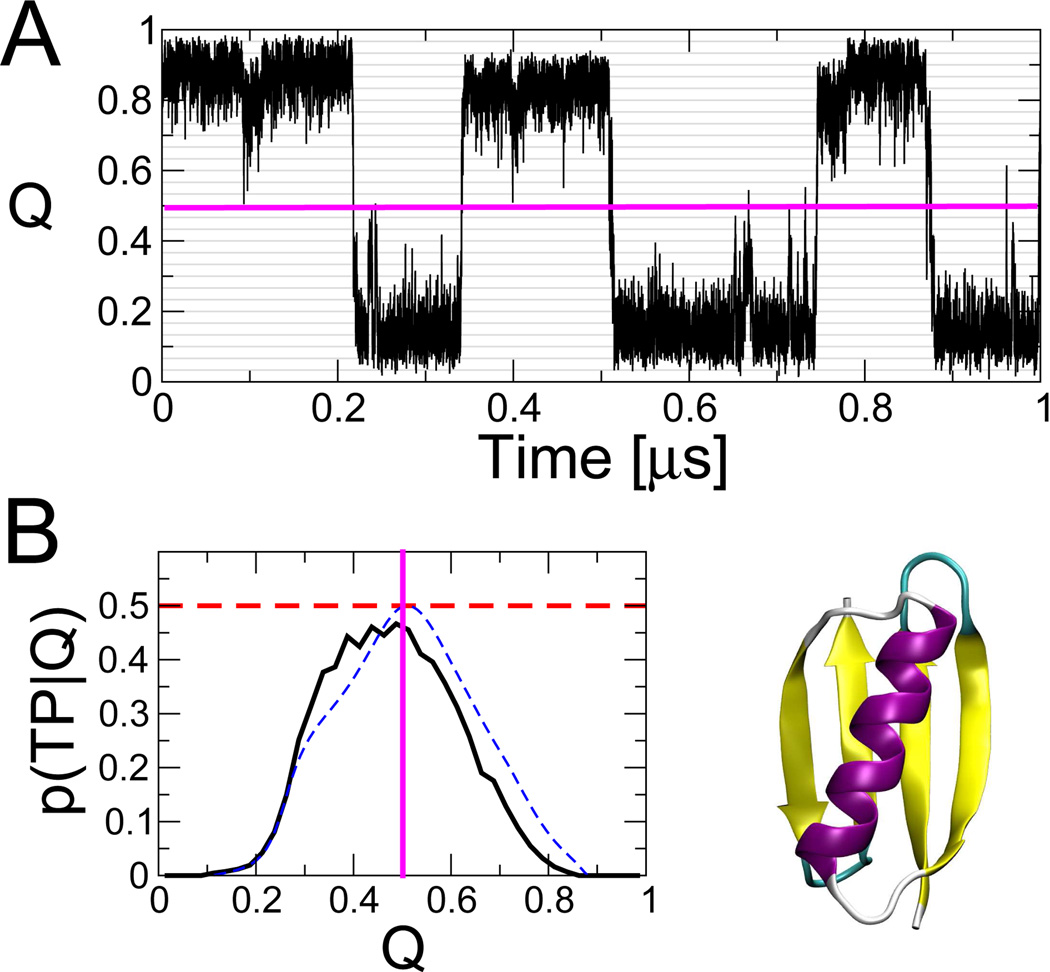
Folding dynamics of protein G Gō model (protein structure shown, lower right). (A) Example of an equilibrium folding trajectory projected onto the fraction of native contacts, Q; (B) Probability of being on a transition path, p(TP|Q), with dashed horizontal line indicating the theoretical maximum for diffusive dynamics. The blue dashed line shows p(TP|Q) calculated from the 1D diffusion model. Simulation details in ref 12.

As an alternative to a purely Gō-like model we also investigate the effect of replacing the repulsive pair potential for non-native interactions with a transferable pair potential. To do this we use a recently described model for protein-protein binding⁴⁹ to add “non-Gō” interactions to the energy, i.e, interactions specified by the identity of the residues rather than by their native structure. The non-bonded energy in the presence of non-Gō interactions is given by:

$$V_{\text{nb}}={\displaystyle \sum _{\underset{(i,j)}{\text{native}}}}{V}_{\mathrm{G}\mathrm{ō}}(r_{\mathit{\text{ij}}})+{\displaystyle \sum _{\underset{(i,j)}{\text{non}-\text{native}}}}{V}_{\text{ng}}(r_{\mathit{\text{ij}}})+{\displaystyle \sum _{\underset{(i,j)}{\text{all}}}}{V}_{\text{elec}}(r_{\mathit{\text{ij}}})$$ (9)

Here, the V_ng(r_ij) and V_elec(r_ij) are, respectively, the modified Lennard-Jones potential and Debye-Hückel type (model “a” in ref 49).

All simulations are run using Langevin dynamics at the folding temperature of the Gō model (310 K), with a friction coefficient of 0.1 ps⁻¹. Fig. 1 A shows representative fragments of a trajectory projected onto the fraction of native contacts Q. This coordinate has been successfully used to describe the folding dynamics of several small two-state proteins.^7,10,23 For protein G, Q is a reasonably good coordinate, in the sense that it captures folding transition states at a single value of the coordinate. If we define transition states x as those having the highest probability of being on transition paths between folded and unfolded states, p(TP|x), then for a good coordinate these states will be concentrated around a single Q^‡, for which p(TP|Q) = 〈p(TP|x)〉 _Q(x)=Q is maximal. In Fig. 1 B, we show that the p(TP|Q) is sharply peaked for both of these proteins, with a maximum approaching the theoretical limit of 0.5 for diffusive dynamics.³⁵ A good coordinate is important to avoid artificial memory effects, as caused for example by metastable states that overlap in projection.⁵⁰

4 Fitting of 1D diffusion models

Before describing the application of diffusion models to questions connected to protein folding, we first discuss here some of the technical issues encountered in fitting diffusion models to simulation (or experimental) data. There are a number of choices to be made in the analysis, since the projected dynamics must be discretised in space, and a suitable “lag time” must be chosen for the construction of the model, such that the dynamics appears Markovian. We also consider the choice of a smoothening prior applied to the diffusion coefficients.

The choice of the width of the bins in Q used for constructing the transition matrix N_ij is a trade-off between the need for local accuracy of F(Q) and D(Q), and that for obtaining sufficient statistics from an equilibrium trajectory, and for solving eqn (1) accurately. If the free energy and diffusion coefficient are slowly varying along the coordinate, a reasonable result may be obtained with fewer bins, but sharp variations are possible, as is the case for the d_RMS coordinate presented below. For all the examples presented we have used 30 bins, which appears to be a reasonable compromise for the coordinates studied here.

4.1 Lag time test for Markovian dynamics

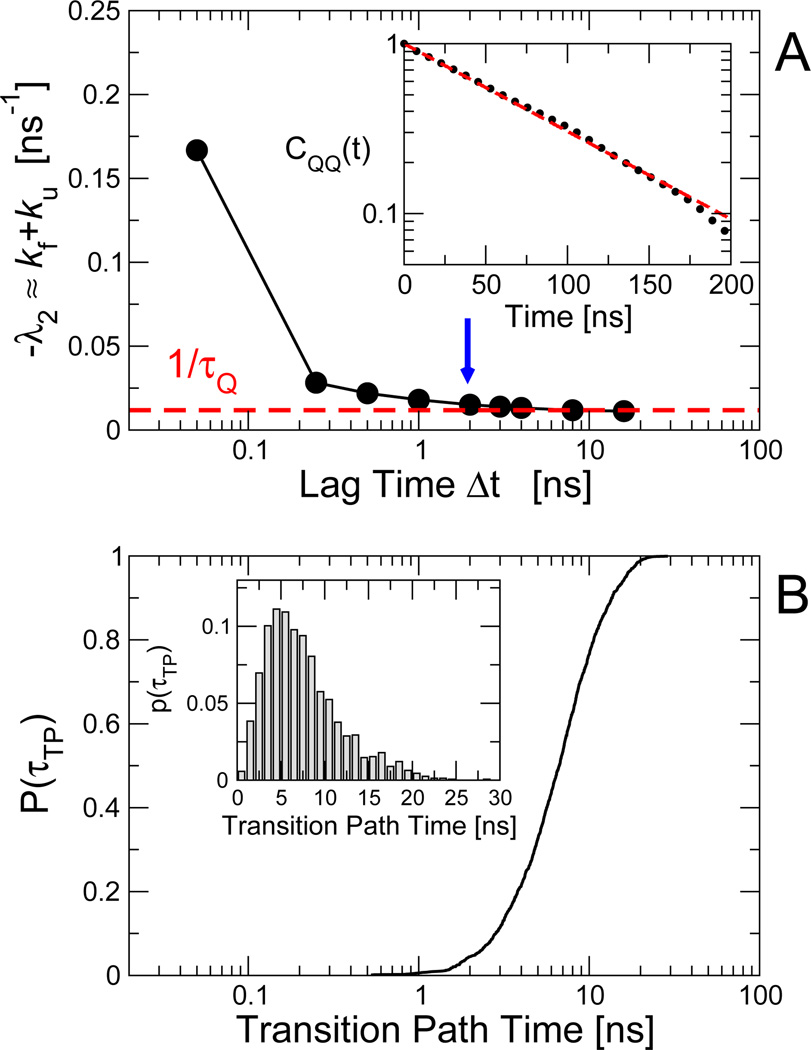
As discussed above, one of the simplest tests for diffusive dynamics is that the estimated diffusion coefficients should not depend on the chosen lag time, provided it is sufficiently long. Lag times that are too short will generally result in an overestimation of the diffusion coefficients, due to memory effects still present on shorter time scales. As an illustrative example, we use equilibrium simulations of protein G. We construct transition matrices N_ij with different lag times Δt, and use the Bayesian formalism to fit the most likely distribution of diffusion models that reproduce the data. In Fig. 2 A, we show the dependence of the negative of the first non-zero eigenvalue of the diffusion operator, −λ₂. Note that for a two-state system, we expect that −λ₂ ≈ k_f + k_u, with k_f and k_u the folding and unfolding rates, respectively.

Fig. 2.

Construction of diffusive models. (A) Dependence of the slowest relaxation rate, given by the negative of the first non-zero eigenvalue λ₂ of the diffusion operator, on the “lag time” Δt for the protein G Gō model. The inset shows the Q autocorrelation function C_QQ(t), whose relaxation rate k_Q is given by the broken red line in the main panel. For a lag time of 2 ns (blue arrow in (A), the resulting position-dependent free energies F(Q) and diffusion coefficients are shown in Fig. 3 A and B, respectively. (B) Cumulative distribution of transition path durations for protein G Gō model. The inset shows the corresponding probability density on a linear scale.

After an initial rapid decay, the slowest eigenvalue converges fairly slowly with increasing lag time, reaching convergence after ~ 2 – 3 ns. We have also computed the relaxation time from the Q autocorrelation function, shown in Fig. 2 A, inset. The decay is well-described by single exponential relaxation, with correlation time τ_Q in good agreement with −1/λ₂ at long lag times. The decay of the correlation function makes it clear that the required lag time is indeed much shorter than the mean waiting time in the stable (folded, unfolded) states.

The transition path duration is accurately captured by the diffusion model, with 〈τ_TP〉 = 7.5 ± 0.15 ns from simulation versus 7.30 ns from eqn (6). This barrier crossing time (for direct crossings³⁵ from Q = 0.1 to Q = 0.9) is also longer than the time Δt ≈ 2 ns required for the dynamics along Q to become diffusive. In Fig. 2 B we show the cumulative distribution of barrier crossing times. In the case of protein G, we can see that the lag time required for convergence is indeed shorter than the majority of transition path times. Below we will present additional results showing that the analysis is sensitive to the diffusion coefficient on the barrier top.

As a further test, we compare in Fig. 1 B the probability p(TP|Q) of being on a transition path obtained directly from simulations to the prediction from the diffusion model, p(TP|Q) = 2ϕ(Q)[1 − ϕ(Q)]. We find that the 1D diffusion model overall accounts well for the distribution of “transition states”. In particular, the maxima of the two curves, corresponding to the isocommittor surface in the 1D model, are nearly coincident. However, on the folded side of the peak the p(TP|Q) from simulation is somewhat lower than that of the 1D model, suggesting the possible presence of a “hidden state”. Indeed, the trajectory segment in Fig. 1 A shows distinct steps within the folded basin.

4.2 Smoothening prior

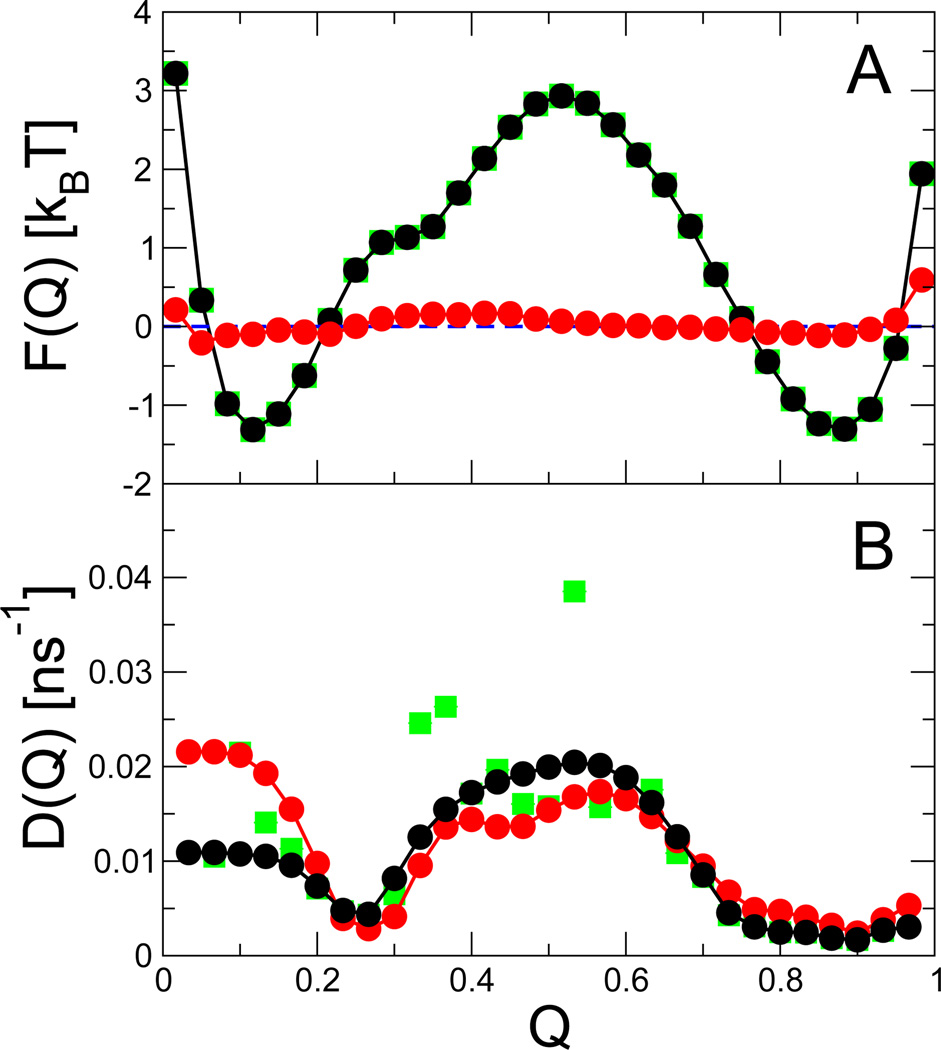
In Fig. 3 we show the position-dependent diffusion coefficients and free energies obtained from the above analysis with a lag time of 2 ns (green symbols). There is some variation of the diffusion coefficient with position, with the defining feature being a maximum in the barrier region. The slow diffusion in the unfolded state arises because, even though diffusion may be rapid in Cartesian space, the average time taken to make or break a contact is long. By contrast, in the folded state, diffusion is slow due to the small fluctuations in Cartesian position. The maximum in the diffusion coefficient reflects an imperfect cancellation of these competing effects.¹²

Fig. 3.

Free energy and diffusion coefficient for protein G Gō model. (A) Free energy F(Q) from unbiased simulations (black) and from simulations with an added biasing potential V(Q) = −F(Q) (red). (B) Diffusion coefficients D(Q) from equilibrium simulations on the unbiased surface (black), and on the biased surface (red), obtained with a smoothening prior and ε = 10⁻³ ns⁻¹. The green squares show F(Q) (hidden) and D(Q) obtained without such a prior.

Because of the sparse data on the barrier, the estimate for the diffusion coefficient there is relatively noisy. Our expectation that D(Q) is a smoothly varying function of Q can be expressed in terms of a smoothening prior, eqn (4). We show also in Fig. 3 the results of applying a smoothening prior (black symbols). The free energy estimates are unaffected, but the noise in the diffusion coefficients in the barrier region is much reduced.

4.3 Bias potential

A useful complement to the above diffusion analysis is to place an additional bias potential V(Q) on the reaction coordinate Q. Firstly, if the dynamics can truly be represented as 1D diffusion on a given time scale, the added potential should only affect the estimated free energies and not the diffusion coefficients. A careful choice of the potential can moreover extend the range of applicability of the diffusion analysis, by lowering the barrier and enhancing the sampling of Q in regions rarely visited in unbiased trajectories. This allows the method to be applied to systems that would otherwise be stuck in one region during equilibrium trajectories.

The most obvious choice of such a bias potential is simply the inverse of the free energy surface, V(Q) = −F(Q).³⁷ In the cases where F(Q) is not known a priori, it can be estimated by an initial umbrella sampling simulation. As proof of principle, we apply this potential here to protein G, for which we also have good estimates of the diffusion coefficient from unbiased dynamics. We use umbrella sampling to estimate the free energy surface, and implement the bias as a cubic spline on Q. The added potential effectively flattens the free energy surface, shown in Fig. 3 A; the small deviations near the end points are due to inaccuracies in the estimated potential of mean force used to construct the bias.

The diffusion coefficients estimated from the bias potential are generally in good agreement with those from the equilibrium simulation, demonstrating that even with sparse sampling on the barrier, the Bayesian method is able to determine accurate diffusion coefficients. The agreement is particularly good for Q > 0.2, with only small deviations in the barrier region. However, for Q < 0.1, the D(Q) obtained from trajectories on the biased surface is about twice as large as the original D(Q). A likely cause for this discrepancy is that the added bias populates substantially more unfolded structures with Q ≈ 0 that are rarely visited without bias. In this fully unfolded region of configuration space, Q is unlikely to be the slowest coordinate, such that the apparent dynamics along Q depends on the region of configuration space that is populated and accordingly on the applied biasing potential. The deviations at small Q thus remind us of the fact that the diffusion model is only an approximation designed to capture the apparent dynamics for a given thermodynamic state of the system.

4.4 Propagator test of barrier dynamics

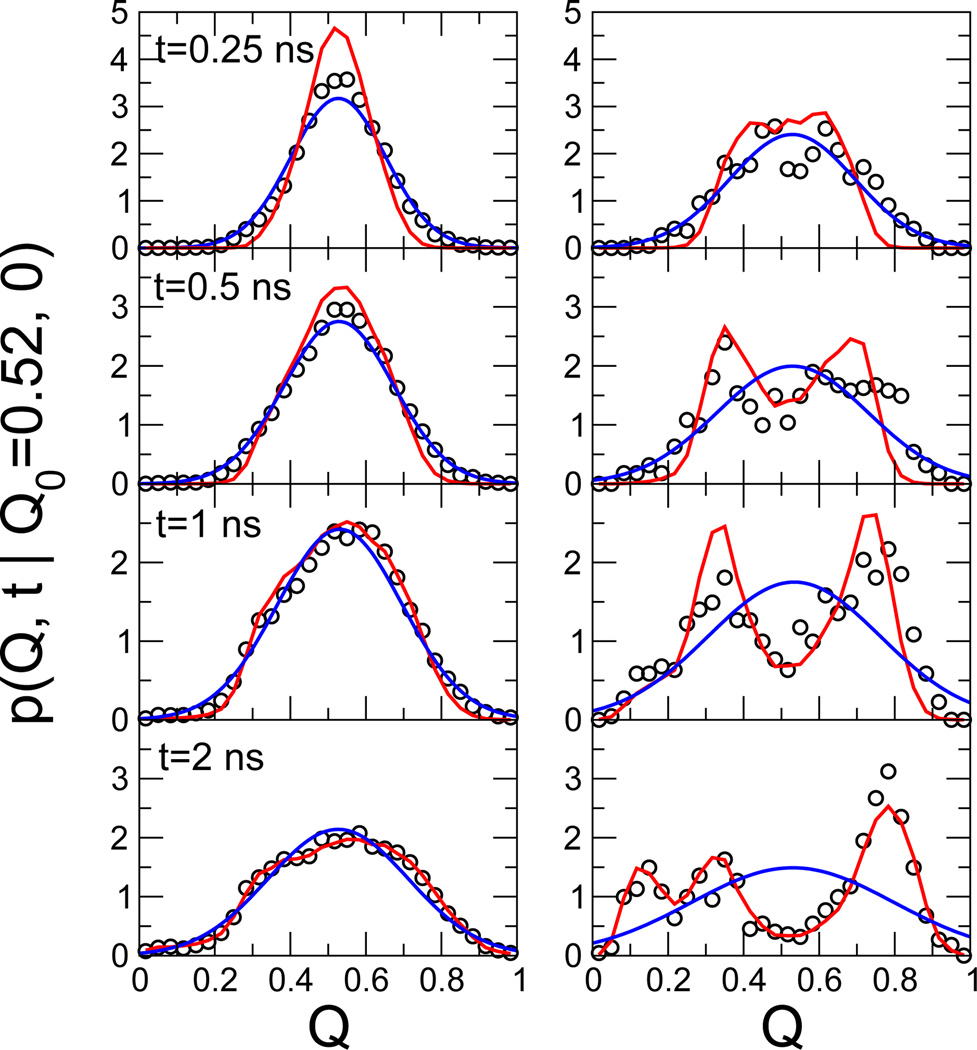
A further test for the accuracy of the diffusion model is a comparison of the propagators estimated directly from the simulation with those calculated from the model. We find for our protein G model that the dynamics at the top of the folding barrier is accurately reproduced by the diffusion model. The propagators for trajectories starting from near the barrier top (Q ≈ 0.52), as calculated from the diffusion model obtained for a lag time Δt = 2 ns, accurately reproduce the transitions observed in the explicit simulations with the added bias potential V(Q) = −F(Q) (Fig. 4 left panels) and without (right panels). Results are shown for different lag times t = 0.25, 0.5, 1, and 2 ns (top to bottom). Also included are the results of Gaussian fits based on the actual mean and variance. We find that at short times, D from a Gaussian fit would be too fast, even for the flattened Q surface. The reason for the deviations from Gaussians even for a flat surface is the position dependence of D(Q). In contrast, the 1D diffusion model accounts well for the dynamics on the folding barrier seen in the explicit simulations, with only small deviations at the shortest time of 0.25 ns.

Fig. 4.

Dynamics at the top of the folding barrier. Propagators p(Q, t|Q₀ = 0.52, 0) are shown for simulations (open circles) on the flat surface with V(Q) = −F(Q) added (left panels) and for the unperturbed system (right panels), collected at times t = 0.25, 0.5, 1, and 2 ns (top to bottom). Red lines are the predictions of the diffusion model, eqn (1), and blue lines are Gaussian fits based on the actual mean and variance.

5 Applications

5.1 Origin of Kramers-like turnover in folding kinetics

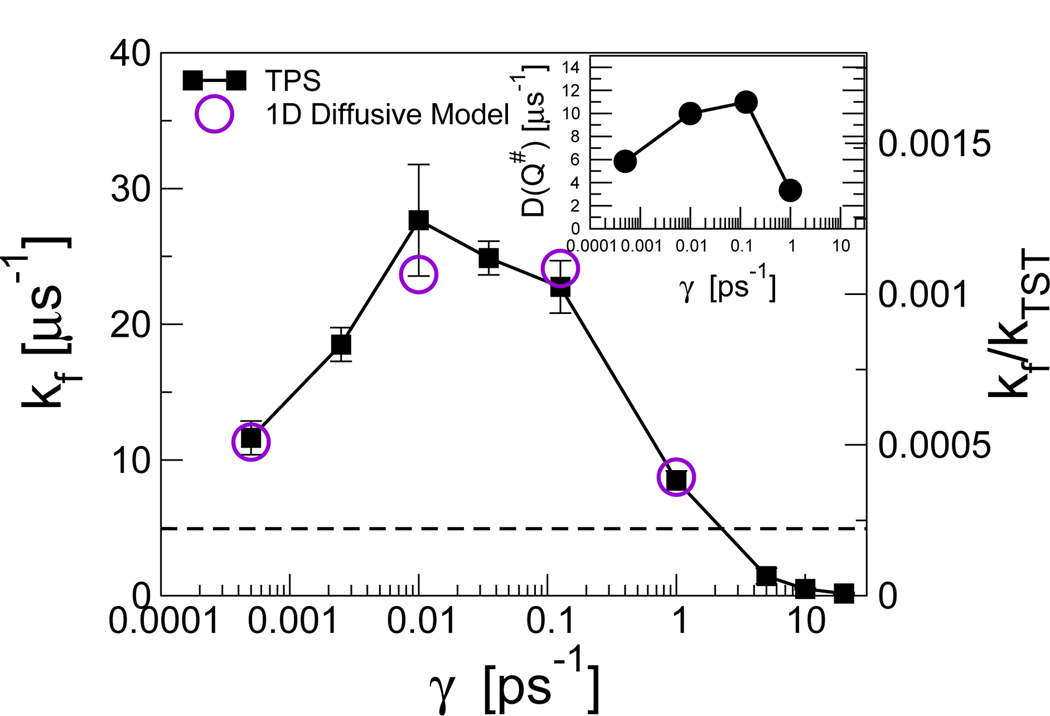
An initially surprising result that emerged from studies of the friction-dependence of protein folding rates in Langevin dynamics simulations of simple folding models was a “turnover” in rate at low friction.^23,51 This is illustrated by the friction-dependent folding rate for the helix bundle protein prb_7–53, determined by transition-path sampling simulations (Fig. 5). Such a turnover in rates is expected for 1D barrier crossing by Kramers’ rate theory: at high friction, the theory predicts that the rate will depend linearly on the reciprocal of the friction γ. In the underdamped limit, however, the rate will decrease again such that at zero friction the rate also vanishes.

Fig. 5.

Apparent Kramers turnover in friction-dependent folding rate k_f(γ) for three-helix bundle prb_7–53. Rates from transition path sampling and the diffusive model are indicated by filled squares and empty circles, respectively. The horizontal dashed line indicates the limiting rate for Hamiltonian dynamics, i.e., for γ = 0 (without friction). The inset shows the corresponding turnover in friction-dependent diffusion coefficients at the barrier top, D(Q^‡;γ). Data from ref 23.

While this turnover may be anticipated for 1D models, it was a surprising finding in the context of high-dimensional protein folding, albeit in the context of a highly simplified model. The slowdown at low friction in the 1D case is due to weak exchange of energy with the heat bath, resulting in dynamics that is dominated by inertia. The system has either insufficient energy to cross the barrier, or if it does, is unable to dissipate the energy while in the product state and returns to the reactant state immediately. However, the protein has many more degrees of freedom, making such an inertial scenario unlikely. We investigated this by mapping the projected dynamics along Q onto a 1D diffusive model. We found that the diffusive model fits the data well at all friction coefficients studied, in contrast to the picture of inertia-dominated dynamics at low friction. The rates from the fit to the diffusive model agree well with those determined independently from transition-path sampling (Fig. 5). Rather than the turnover occurring via a switch of the global dynamics from overdamped to inertial, it results from a turnover in the diffusion coefficients D(Q) themselves. This can be seen from the turnover in the diffusion coefficient at the barrier top in the inset to Fig. 5.

The turnover in the position-dependent diffusion coefficients suggests that the origin of the effect must be the low-dimensional microscopic transitions on the rough energy landscape. A useful analogy is the variation of diffusion coefficients with friction in a simple jump-diffusion model, where the diffusion on the global coordinate arises from hopping between many local minima.⁵² At long times, motion on such a landscape appears diffusive, with a diffusion coefficient proportional to the hopping rate between minima; it is this rate for crossing microscopic barriers that varies in a Kramers-like way with friction. For example, we have shown that simple models for the microscopic dynamics using coarse-grained peptide fragments do indeed give a Kramers-like dependence of rotamer transition rates on friction.²³

5.2 Effect of non-native interactions on protein folding dynamics

The profiles of diffusion coefficients for the Gō-like models presented to this point revealed relatively weak dependence of the diffusion coefficient on the position along the reaction coordinate. It may be argued that this is at least partially due to the “smooth” energy landscape of the Gō model; a rougher energy surface might be expected to exhibit stronger features in the diffusion coefficient profile. What might the effect of realistic non-native contacts be? To address this question, we have replaced the original repulsive non-native contacts in the Gō model with a transferable model for the non-native interactions. That is, the nature of the interaction between a given pair of amino acids is dependent only on their types, and not their relative position in the native structure. Specifically, we use a coarse-grained protein interaction potential originally developed for binding.

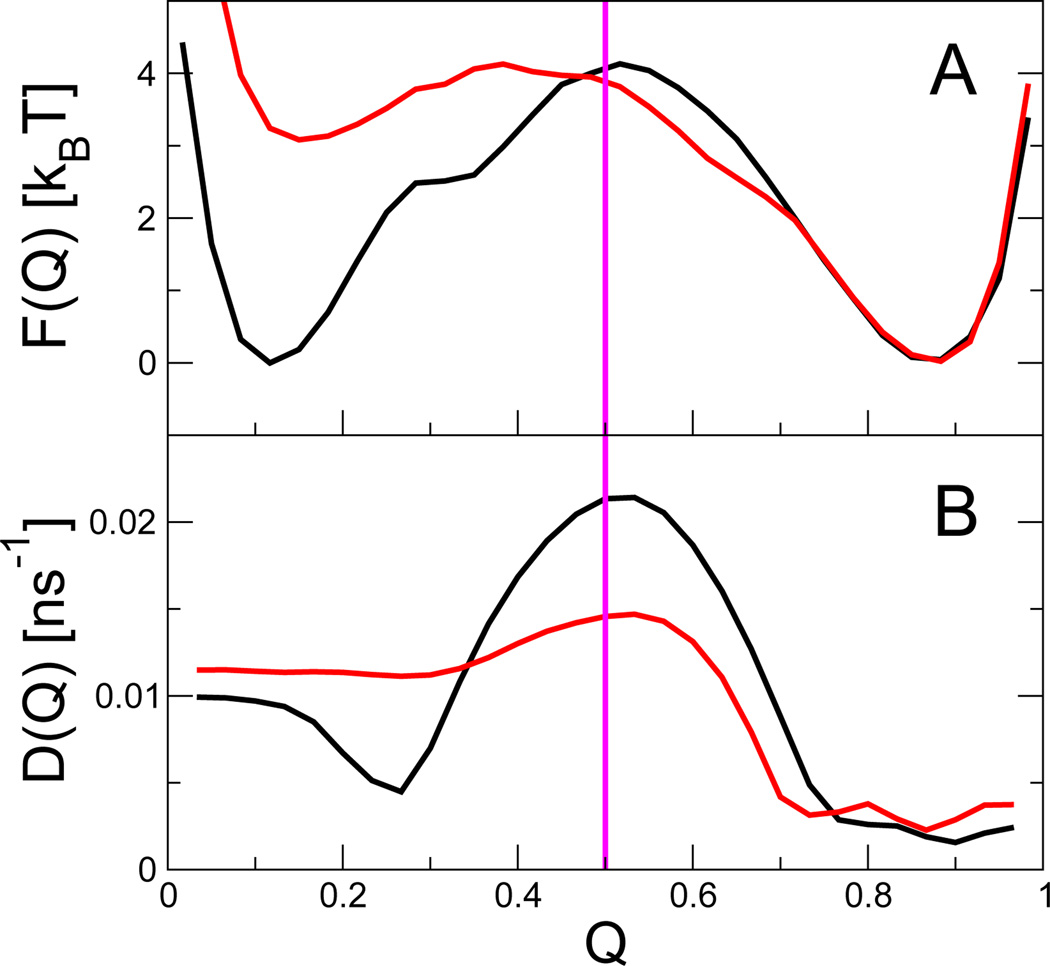
The effect of adding such non-native interactions on the free energies and dynamics of the coarse-grained folding models is shown in Fig. 6. We find that the free energy profiles are significantly altered, with the barrier being lowered and the folded state being stabilized. While the latter effect has a more mundane origin,¹² the lowering of the barrier due to weak non-native interactions was an effect predicted by earlier theoretical⁵³ and computational⁵⁴ studies. Those studies, however, only considered directly the effect of non-native interactions on the free energies, rather than on the dynamics. Remarkably, we find that the non-native interactions also significantly modulate the fitted diffusion coefficients (Fig. 6B), the main effect being a reduction in diffusion coefficient near the barrier top. In the case of fast-folding proteins, the effect can be nearly strong enough to cancel the lowering of the barrier height.¹²

Fig. 6.

Effect of adding non-Gō contacts to the (A) free energies and (B) diffusion coefficients for protein G. Black and red curves correspond to the original Gō model, and to the model with added non-Gō interactions, respectively. Data from ref 12.

5.3 Effect of chosen coordinate on position dependence of diffusion coefficients

For the given projections of protein G dynamics onto the folding coordinate Q, we find, apart from a moderate increase in diffusion coefficient near the barrier top, that the diffusion coefficients in both the folded and unfolded states are remarkably similar. This result is in apparent contrast to suggestions that diffusion should slow dramatically as the native state is approached, where increased local barriers in a compact protein impede chain motion,²⁶ and from experimental evidence of slower diffusion for more collapsed states.⁵⁵

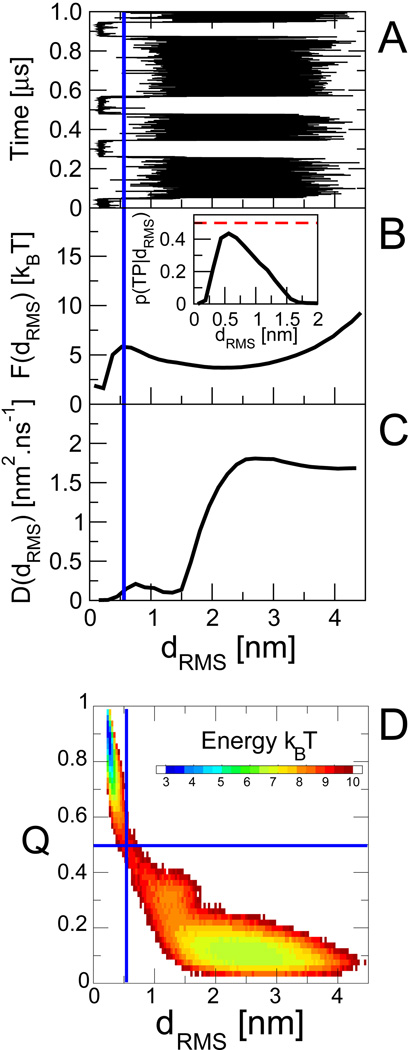
To gain some insight into the effects of compaction on diffusion, we have studied the dynamics projected onto an alternative reaction coordinate, the distance matrix RMS, d_RMS, defined as $d_{\text{RMS}}(\mathbf{R})={(N^{-1}{\mathrm{\Sigma }}_{(i,j)}{(d_{\mathit{\text{ij}}}(\mathbf{R})-d_{\mathit{\text{ij}}}^0)}^2)}^{1/2}$ , where the sum runs over the N native contact pairs (i, j) separated by a distance $d_{\mathit{\text{ij}}}^0$ in the native state and d_ij(R) in configuration R. This coordinate is a sensitive probe of native structure formation similar to Q close to the native state, but is closely related to the radius of gyration far from the native state. In contrast to Q it probes the fluctuations in Cartesian space more directly.

The dynamics on d_RMS results in a very different picture from the projection on Q.¹² The diffusion coefficient is reduced by around two orders of magnitude in progressing along the coordinate from unfolded to folded. This qualitative difference between Q and d_RMS can be understood by considering the relationship between them. In Fig. 7 D, we plot free energy surfaces as a function of d_RMS and Q. We see that the two coordinates are strongly correlated, being approximately related by a one-to-one mapping. However, this mapping is a highly non-linear transformation, explaining the differences in diffusion coefficient: in the unfolded state at low Q and large d_RMS, the mapping compresses the large Cartesian-space fluctuations of d_RMS (Fig. 7 A) into small fluctuations of Q (Fig. 1 A). By contrast, in the folded state, the small fluctuations in Cartesian space are stretched by projection onto Q, because many contacts can be broken or formed for very small Cartesian-space displacements.

Fig. 7.

Dynamics and free energy for d_RMS reaction coordinate. (A) Projection of the trajectories onto d_RMS. Corresponding position-dependent free energies (B) and diffusion coefficients (C) obtained from Bayesian fitting. (D) Two-dimensional potential of mean force F(d_RMS,Q), showing the relationship between the two coordinates. Data from ref 12.

When two coordinates are both ideal reaction coordinates, it should be possible to construct a bijective mapping between them (since a degenerate mapping would imply that one coordinate is less informative about reaction progress than the other). Given such a mapping s(r) : r → s, a simple variable transformation may be made to relate the free energies and diffusion coefficients on the two coordinates, namely βF(s) = βF(r) + ln |ds/dr| and D(s) = D(r)(ds/dr)². We have shown previously that this mapping may be used to interchange both free energies and diffusion coefficients between Q and d_RMS, obtaining almost identical results to those from a direct analysis on each coordinate.¹² Using these relations, it is also possible to transform any 1D coordinate to one along which the diffusion coefficient is position-invariant.^12,28,56,57 Remarkably, we find that the Q coordinate is an inspired choice, coming close to position-invariant D without any transformation, therefore closely approximating the 1D diffusion scenario with constant D commonly envisaged when describing folding.

5.4 Experimental applications

Most of this article has focused on the interpretation of folding simulation data using diffusion models. However, diffusion models are increasingly being used to interpret experimental data,^18,19 and our results also have implications for these applications. One of the assumptions often necessary in experimental analyses is that the diffusion coefficient D is position-independent. However, since often an arbitrary coordinate is assumed to describe the folding dynamics¹⁸ (with the experimental signal being dependent on the position along the coordinate), the above analysis shows that assuming a constant D does not result in any loss of generality – any 1D coordinate can be transformed into one along which diffusion is position-independent.

The results from the analysis of diffusion coefficients in simulations may also be used to analyze some of the assumptions made in interpreting experiments. For example, when applying the overdamped solution of Kramers theory to experiment, it is often necessary to assume that the curvature of the free energy surface at the barrier top and in the wells are similar (with position-invariant D).^55,58,59 By mapping the dynamics in our Gō model to a coordinate where D is position-invariant, we showed that in fact the curvatures of the barrier and minimum are indeed equal within a factor of two.¹²

However, the same analysis presented here could also be applied, in principle, directly to experimental data. Data from single-molecule pulling and FRET experiments would clearly be the most appropriate for this purpose, with different complications arising in each case. For the FRET experiments, the coordinate probed, the distance between the chromophore labels, is close to that whose dynamics we would like to characterize. However, in addition to the model for the dynamics of the coordinate given here, a model would also be needed for the emission of photons by donor and acceptor chromophores. Recent theoretical work describing photon trajectories of multi-state molecules⁶⁰ would probably be a useful starting point for the analysis. On this basis, our likelihood-based construction of the underlying diffusion model would have to be extended to what amounts to a hidden-Markov model. From the experimental side, however, a much higher photon detection efficiency will be needed to make this application practical.

Similarly, for the pulling experiments, time resolution is also a limitation since it would not be possible to describe dynamics on the barrier if the effective sampling time is longer than the time taken for barrier crossing. A second complication in this case is that the coordinate measured is in fact the length of a larger system including not only the molecule of interest, but also flexible linkers. The dynamics of such linkers, and of the pulling apparatus itself (cantilever, bead, etc.) would therefore need to be accounted for in any diffusion analysis.

Even bulk experiments provide information about effective diffusion coefficients of protein conformational coordinates. In a relatively direct probe of the chain dynamics, contact quenchers are used to report on the formation of close spatial contacts.^61,62 With fast quenchers,⁶³ such experiments amount to measurements of the first-passage time distribution to contact, which contains information about the distribution and dynamics of the dye-quencher distance. Effective average end-to-end diffusion coefficients have been extracted, for instance, for small unfolded peptides.⁶⁴

Given the rapid advances that have been made in various single molecule technologies over the past decade, however, we are optimistic that direct determination of diffusion coefficients and free energies from these experiments may be possible in the not too distant future.

6 Concluding remarks

We have shown how 1D diffusion models can be fitted to protein folding dynamics trajectories, and that such models become a good description of the global dynamics after some initial lag time. Applications of the model to various protein folding scenarios have yielded useful insights in the context of coarse-grained folding models. In future it will be interesting to apply such models to the analysis of atomistic simulation data.³ On the basis of such an analysis, conclusions drawn from simplified models and atomically detailed simulation models can be compared. Moreover, diffusion models constructed from atomistic simulations may also suggest ways in which theory and coarse-grained models can be modified to more accurately capture the folding dynamics. Finally, we anticipate that 1D diffusion models should be particularly useful in the interpretation of single molecule experiments that probe motions along one (or a few) coordinate(s), once these measurements attain sufficient time resolution.